A quantitative confidence signal detection model: 1. Fitting psychometric functions

Abstract

Perceptual thresholds are commonly assayed in the laboratory and clinic. When precision and accuracy are required, thresholds are quantified by fitting a psychometric function to forced-choice data. The primary shortcoming of this approach is that it typically requires 100 trials or more to yield accurate (i.e., small bias) and precise (i.e., small variance) psychometric parameter estimates. We show that confidence probability judgments combined with a model of confidence can yield psychometric parameter estimates that are markedly more precise and/or markedly more efficient than conventional methods. Specifically, both human data and simulations show that including confidence probability judgments for just 20 trials can yield psychometric parameter estimates that match the precision of those obtained from 100 trials using conventional analyses. Such an efficiency advantage would be especially beneficial for tasks (e.g., taste, smell, and vestibular assays) that require more than a few seconds for each trial, but this potential benefit could accrue for many other tasks.

measuring thresholds is probably the most common psychophysical procedure in use today; applications range from experimental psychology to neuroscience to economics to engineering. Fitting psychometric functions using categorical data analyses (Agresti 1996) that describe the relationship between a stimulus characteristic (e.g., amplitude) and a subject's forced-choice categorical responses provides a standard approach used to estimate thresholds (Green and Swets 1966; Macmillan and Creelman 2005).

A recent comprehensive analysis (Garcia-Perez and Alcala-Quintana 2005) concluded that only maximum likelihood methods should be used when accuracy and precision of psychometric function fit parameters is important and, furthermore, showed that more than 100 forced-choice trials are generally required to yield acceptable fit parameter estimates. Because such perceptual threshold tests are common and because many trials are needed to yield accurate and precise psychometric fits, studies spanning 50 yr (Garcia-Perez and Alcala-Quintana 2005; Green 1990; Hall 1968, 1981; Harvey 1986; Kaernbach 1991; Kontsevich and Tyler 1999; Leek 2001; Lim and Merfeld 2012; Pentland 1980; Shen et al. 2015; Shen and Richards 2012; Taylor and Creelman 1967; Treutwein 1995; Watson and Pelli 1983; Watt and Andrews 1981; Wetherill and Levitt 1965; Wichmann and Hill 2001a,b) have reported efforts to improve threshold test efficiency (i.e., to reduce the number of trials), but only modest efficiency improvements have accumulated. (For a brief review of these papers, see Karmali et al. 2015, who also present a theoretic analysis of these sampling issues, accompanied by both simulations and human data.) This is probably due to the fact that binary/binomial distributions inherently have high variability at near-threshold stimulus levels, where the maximal information can be attained on each trial (Wetherill 1963).

While forced choice procedures are simple and robust, many subjects also know how confident they are for each response. Confidence is a belief in the validity of what we believe and is widely considered a form of metacognition (Drugowitsch et al. 2014; Fleming and Dolan 2012; Grimaldi et al. 2015; Lau and Rosenthal 2011) because it involves self-monitoring of perceptual performance. In other words, confidence reflects self-assessment of the conviction in a decision.

Confidence has been studied in humans using a variety of techniques (Balakrishnan 1999; García-Pérez and Alcalá-Quintana 2011, 2012; Garcia-Perez and Peli 2014; Hsu and Doble 2015; Okamoto 2012; Sawides et al. 2013) including probability judgments (Baranski and Petrusic 1994; Björkman 1994; Ferrell 1995; Ferrell and McGoey 1980; Juslin et al. 1998; Keren 1991; Lichtenstein et al. 1982; Stankov 1998; Stankov et al. 2012; Suantak et al. 1996). In fact, as noted in a recent review (Grimaldi et al. 2015), confidence probability judgments (i.e., confidence ratings provided using a nearly continuous scale between 0 and 100% or 50 and 100%) provide the most common assessment of confidence.

One common use of confidence recordings is in “confidence calibration” studies where confidence is compared with actual performance, where a data set may be classified as “well-calibrated” or classified as indicative of “overconfidence” or “underconfidence” (Baranski and Petrusic 1994; Björkman 1994; Ferrell and McGoey 1980; Juslin et al. 1998; Keren 1991; Lichtenstein et al. 1982; Stankov 1998; Suantak et al. 1996). Specifically, imagine that a subject reported 90% confidence that a given motion was rightward for 10 separate trials at a given stimulus level. On average, perfect calibration (Bjorkman et al. 1993; Ferrell 1995; Keren 1991; Lichtenstein et al. 1982; Stankov et al. 2012) of these confidence reports is assumed when 9 out of 10 of these trials are in the rightward direction, while overconfidence would be indicated by 5 out of 10 being rightward.

To our knowledge, probability judgments have never before been directly used to help estimate psychometric function parameters. Typically, confidence is not recorded. Sometimes a confidence rating (e.g., “uncertain”) is recorded (Balakrishnan 1999; García-Pérez and Alcalá-Quintana 2011, 2012; Garcia-Perez and Peli 2014; Hsu and Doble 2015; Okamoto 2012; Sawides et al. 2013) and used as part of a psychometric fit procedure, but these approaches do not model how confidence quantitatively changes as the stimulus is varied. Instead these approaches include one additional decision boundary for each added category (e.g., “uncertain”) and typically add one free parameter to the fit algorithm for each additional decision boundary.

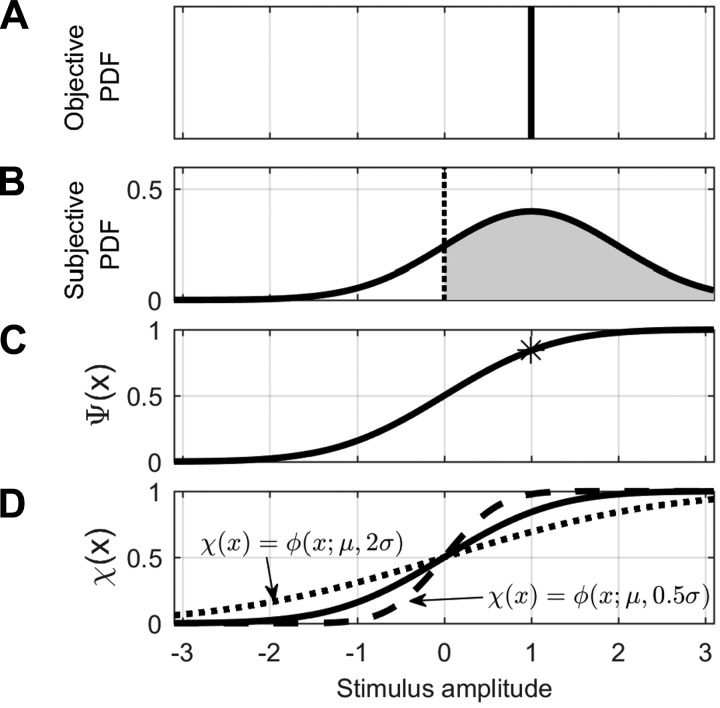
We now introduce our confidence signal detection (CSD, pronounced “kissed”) model, which combines a confidence function (Fig. 1D) with a standard signal detection model (Fig. 1, A–C). We use an example to illustrate the relationship between psychometric functions and confidence for a direction-recognition forced-choice task. A typical perceptual direction-recognition paradigm begins with well-controlled stimuli that are either positive or negative; the subject's task is to determine whether the motion is positive (“rightward”) or negative (“leftward”). Typically, the stimuli provided to a subject (Fig. 1A) are well controlled (i.e., have little variation). The standard signal detection model suggests that neural noise contributes to perception (Goris et al. 2014; Tolhurst et al. 1981), which is represented by the probability density function (PDF) shown in Fig. 1B. Signal detection theory advocates that a single sample from this probability distribution, often called the decision variable, is available to the subject for each trial. If the decision variable sampled from this PDF for an individual trial is negative, the subject reports negative (e.g., leftward) motion and if the sampled decision variable is positive, the subject reports positive (e.g., rightward) motion. For the stimulus and noise PDF shown, positive motion will, on average, be reported 84% of the time. When this process is repeated for different stimulus amplitudes, it leads to a fitted psychometric function, ($\widehat{\Psi }\left(x\right)$), that represents subject performance as a function of stimulus amplitude (Fig. 1C). Large positive stimuli will almost always be correctly reported as positive, and large negative stimuli will almost always be correctly reported as negative. Stimuli in between lead to the sigmoidal shape shown. With enough data, this fitted psychometric function ($\widehat{\Psi }\left(x\right)$) is assumed to converge to a psychometric function that is representative of the subject's underlying noise distribution, $\widehat{\Psi }\left(x\right)\approx \Psi \left(x\right)$.

Fig. 1.

Relationship among decision variables, psychometric functions [Ψ(x)], and confidence functions [χ(x)] in our confidence signal detection (CSD) model. A: The stimulus for this example is well controlled having an amplitude of +1.0 with little variation, so the objective probability density function (PDF) is a delta function. B: signal detection model assumes additive noise. For this example, Gaussian noise having zero-mean and a SD of 1 is added to the stimulus of +1.0 and leads to the subjective PDF shown. The dotted vertical line at zero represents a decision boundary. If a sampled decision variable falls to the right of the decision boundary, represented by the gray area, the subject decides positive. If the sampled decision variable falls to the left, the subject decides negative. For this example, 84% of the decision variables lead to the subject deciding positive. C: asterisk located at (1, 0.84) represents the example data point illustrated in the previous panel. When this process is repeated for a variety of different stimulus levels, it yields a psychometric function, Ψ(x) (black curve). D: similarly, a relationship between confidence and the stimulus for an individual trial can be represented by a confidence function [χ(x)]. The psychometric function represents average subject performance, and confidence is defined as well calibrated when confidence matches average subject performance (Bjorkman et al. 1993; Ferrell 1995; Keren 1991; Lichtenstein et al. 1982; Stankov et al. 2012). Therefore, well-calibrated confidence matches the psychometric function [χ(x) = Ψ(x)] and is plotted as the solid curve. Also shown are confidence functions that represent overconfidence (dashed) and underconfidence (dotted).

So far, we have simply introduced the conventional signal detection approach; we now add a confidence model. If we happen to sample a very positive decision variable for one trial (e.g., if the stimuli were very large), we should have high confidence that the motion was positive. If we happen to sample a positive decision variable near the decision boundary on another trial, we should again decide that the motion was positive but have much less confidence in that decision. Like the empiric relationship captured by a psychometric function ($\widehat{\Psi }\left(x\right)$), a quantitative empiric relationship between confidence and the stimulus can be represented by a confidence function ($\widehat{\chi }\left(x\right)$). As for the psychometric function, with enough data, this empiric confidence function is assumed to be representative of neural processes that can be captured by a confidence function, $\widehat{\chi }\left(x\right)\approx \chi \left(x\right)$. Figure 1D shows three example confidence functions that are each modeled as Gaussian cumulative distribution functions (CDFs); the solid curve represents well-calibrated confidence (χ(x) = Ψ(x)), the dashed curve represents overconfidence, and the dotted curve represents underconfidence.

As will be described in detail in Confidence maximum likelihood fit technique, we utilize this CSD model to help improve psychometric parameter estimates. More specifically, we present a new confidence analysis technique that utilizes this CSD model. We will introduce, develop, and investigate this model using previously published analytic, simulation, and experimental approaches. To help evaluate the contributions that confidence can make to psychometric function estimation, we report the following: 1) human studies for a direction-recognition task in which the subjects were required to report whether they rotated toward their left or right, and 2) simulation results for psychometric functions that range from 0 to 1, which are used for direction-recognition data analysis (Chaudhuri et al. 2013; Merfeld 2011). We report that psychometric functions estimated using confidence probability judgments require about five times fewer trials to yield the same performance as conventional forced-choice psychometric methods.

Such improved test efficiency might be realized for any forced-choice task where confidence can be reported but may be especially important for perceptual tasks involving olfaction, gustation, or equilibrium (or any other task where individual trials take tens of seconds) (Linschoten et al. 2001) as well as for clinical applications where more efficient and/or more precise perceptual measures could lead to improved patient diagnoses (Merfeld et al. 2010). Nonetheless, while the promise of a fivefold improvement in efficiency is appealing, we do not, at this time, advocate replacing standard forced-choice analyses with this confidence probability-judgment analyses because confidence in perceptual decisions is not well-understood and our CSD model is not validated. We instead present this CSD model and new analysis method as deserving of further study.

METHODS

Confidence maximum likelihood fit analysis.

This section presents the new maximum likelihood analysis developed to help estimate psychometric function fit parameters. This technique simultaneously fits both a conventional psychometric function ($\widehat{\Psi }\left(x\right)$) and a confidence function ($\widehat{\chi }\left(x\right)$) to confidence probability judgments. appendix a presents flow charts that outline this fitting technique (see Fig. A1, left, for a specific model and see Fig. A1, right, for a generalized flow chart).

To introduce the new technique we assume that the fitted psychometric function can be represented by a Gaussian cumulative distribution function (ϕ) having two fit parameters ($\widehat{\mu },\hspace{0.17em}\widehat{\sigma }$):

$$\widehat{\Psi }\left(x\right)=\varphi \left(x;\widehat{\mu },\widehat{\sigma }\right)$$ (1)

where $\widehat{\mu }$ represents shifts in the psychometric function (i.e., mean value of the noise distribution) and $\widehat{\sigma }$ represents the width of the psychometric function (i.e., SD of the noise distribution), which is often referred to as the threshold for direction-recognition tasks. Assuming that subjects based their confidence assessment on the signal used to make their decision, we modeled the fitted confidence function as a Gaussian cumulative distribution function having one additional free parameter, a confidence-scaling factor $(\widehat{k}$) that scales this average confidence function to account for underconfidence or overconfidence, as previously demonstrated in Fig. 1D:

$$\widehat{\chi }\left(x\right)=\varphi \left(x,\widehat{\mu },\widehat{k}\widehat{\sigma }\right)$$ (2)

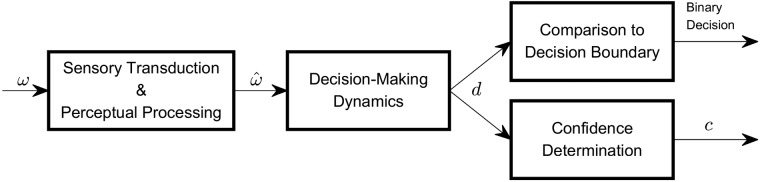
We assume a Gaussian confidence function for simplicity, but other shapes of the confidence function were investigated via simulations to evaluate the impact of this assumption. Noise was not explicitly included in this relationship; noise may be present in the mapping from a decision variable to the confidence response, and we evaluate the impact of additive noise via simulations. While the rest of this paper focuses on using this CSD model to fit data, Fig. 2 helps schematically illustrate the neural processing underlying the model.

Fig. 2.

Schematic representation of pertinent neural processing. For the experimental investigations herein, the stimulus is angular velocity (ω), which is transduced and processed via pertinent perceptual mechanisms to yield a perceptual representation of angular velocity ($\widehat{\omega }$); these representations could readily be generalized to any perceptual process. This perceptual signal may be further filtered (e.g., Merfeld et al. 2016) to yield a decision-variable (d) used both to make the binary decision, by comparing the decision variable to the decision boundary, and via additional neural manipulations to yield confidence (c) in the decision. The latter confidence calculations may be performed “correctly” [i.e., c = χ(d) = ϕ(d,μ,σ)], yielding well-calibrated data. Alternatively, these confidence calculations could be miscalibrated [i.e., c = χ(d) = ϕ(d,μ,kσ)], where k ≠ 1, leading to overconfidence (k < 1) or underconfidence (k > 1). Furthermore, as we will evaluate via simulations, the confidence function may be independent of the noise distribution that defines the psychometric function (i.e., confidence function is not Gaussian for this application).

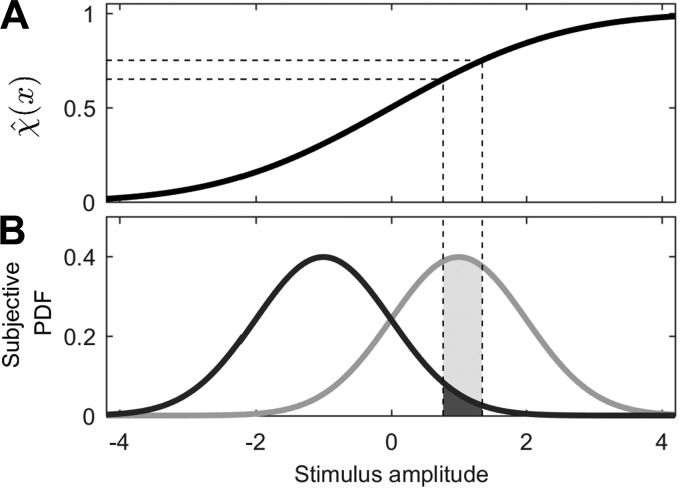
Figure 3 schematically demonstrates the maximum likelihood calculation for an individual trial. For each confidence probability judgment (c_j) provided by the subject, we can calculate the corresponding decision variable via the inverse Gaussian CDF:

$${\widehat{x}}_j={\widehat{\chi }}^{-1}\left(c_j\right)={\varphi }^{-1}\left(c_j;\widehat{\mu },\widehat{k}\widehat{\sigma }\right)$$ (3)

Fig. 3.

Illustration of how confidence probability judgments from individual trials contribute to a maximum likelihood psychometric function fit. A: given a confidence probability judgment, we can use the inverse fitted confidence function (${\widehat{\chi }}^{-1}\left(c_j\right)$) to calculate a modeled decision variable to accompany that judgment. More specifically, given upper and lower limits to a confidence probability judgment (dashed horizontal lines), we can use the inverse fitted confidence function to calculate the corresponding upper and lower decision variable limits (dashed vertical lines). B: given the estimated decision variable range shown by the dashed vertical lines, we can calculate the probability that the given stimulus (s_j) and psychometric function noise model would yield that confidence probability judgment. Two examples are illustrated. The light curve shows the decision variable PDF for the stimulus having an amplitude of +1.0 shown in Fig. 1B and the light shaded area represents the probability of the confidence probability judgment for a +1.0 stimulus. The dark curve shows the PDF for a stimulus having an amplitude of −1.0, and the dark shaded area represents the probability for a −1.0 stimulus. High confidence that the motion is positive is much more probable (i.e., much more likely) for the +1 stimulus than for the −1 stimulus.

where c_j represents a confidence probability judgment, ${\widehat{\chi }}^{-1}\left(c_j\right)$ represents the inverse fitted confidence function, and ϕ⁻¹ represents the inverse cumulative Gaussian. The precise probabilistic interpretation of a confidence probability judgment depends on the resolution of the subjective scale provided the subject. Our subjects provided a confidence probability judgment using a scale that had a resolution of 1%. Therefore, when a subject provided a confidence probability judgment of 70%, we set the lower (c_j^lower) and upper (c_j^upper) bin limits to 69.5 and 70.5%, respectively. With the use of Eq. 3, lower (x_j^lower) and upper (x_j^upper) decision variable limits can be calculated for a given confidence probability judgment, c_j.

As illustrated schematically (Fig. 3B), we can then calculate the probability (p_j), which in this context is commonly called the “likelihood,” that a decision variable for an individual trial falls in this range using the relationship:

$$p_j=\widehat{\Psi }\left(x_j^{\text{upper}}\right)-\widehat{\Psi }\left(x_j^{\text{lower}}\right)=\varphi \left(x_j^{\text{upper}};s_j+\widehat{\mu },\widehat{\sigma }\right)-\varphi \left(x_j^{\text{lower}};s_j+\widehat{\mu },\widehat{\sigma }\right)$$ (4)

where s_j is the stimulus provided on that trial.

Repeating this process for each of the N trials, we can then calculate the log likelihood by simply summing the log of each of the individual trial likelihoods, which can be written as:

$$L\left(\widehat{\mu },\widehat{\sigma },\widehat{k};\overrightarrow{c},\overrightarrow{s}\right)={\displaystyle \sum _{j=1}^N\log \left(p_j\right)}$$ (5)

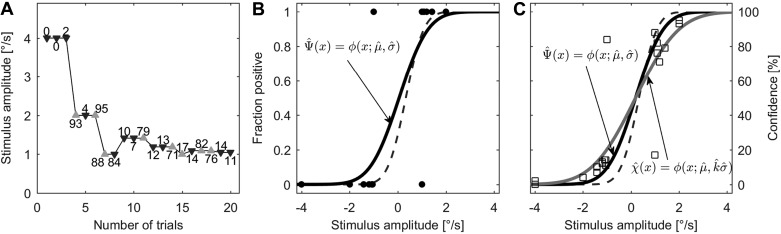
We find the maximum likelihood fit by numerically finding the three fit parameters ($\widehat{\mu },\widehat{\sigma },\widehat{k}$) that maximize the value of this log likelihood function. This method assumes that the confidence judgment utilizes the same decision variable as the binary decision-making process. Our methods also assume that all processes and mechanisms (e.g., decision boundary, confidence estimation, etc.) are stationary (i.e., constant) across time. This stationarity assumption is standard for psychometric function fits as well. Figure 4 shows example fitted functions.

Fig. 4.

Example fits for a human test. A: example stimulus track, including confidence probability judgments, is shown for first 20 trials. Upward-pointing gray triangles and downward-pointing black triangles represent rightward and leftward trials, respectively. B: following 20 binary forced-choice trials, a conventional psychometric function (black curve), $\widehat{\Psi }\left(x\right)=\varphi \left(x;\widehat{\mu }=0.05,\widehat{\sigma }=0.95\right)$, was fit to the binary forced-choice data points shown. C: given the same 20 trials with confidence probability judgments, a psychometric function (black curve), $\widehat{\Psi }\left(x\right)=\varphi \left(x;\widehat{\mu }=0.19,\widehat{\sigma }=0.91\right)$, and a confidence function (gray curve), $\widehat{\chi }\left(x\right)=\varphi \left(x;\widehat{\mu }=0.19,\widehat{k}\widehat{\sigma }=1.43\right)$, were simultaneously fit to the confidence data. All example data are from one of the human data sets (Fig. 5, D, H, and L) presented herein. For comparison, the fitted psychometric function determined after 100 binary forced-choice trials using conventional methods, $\widehat{\Psi }\left(x\right)=\varphi \left(x;\widehat{\mu }=0.33,\widehat{\sigma }=0.59\right)$, is also shown via dashed lines in B and C. Half-scale (50 to 100%) probability judgments provided by subjects have been converted to full-scale (0 to 100%) judgments as described in methods.

Data analysis.

To provide a direct comparison of this new fitting method to standard binary forced-choice fitting methods, we fit psychometric curves to the binary data using a maximum likelihood approach (Chaudhuri and Merfeld 2013; Lim and Merfeld 2012). For our forced-choice direction-recognition task, the subject's directional responses are binary (e.g., left or right) and the psychometric function ranges from 0 to 1. A Gaussian distribution was fitted to the data in MATLAB using a generalized linear model using a probit link function. (An example of a psychometric function fit to binary data is shown in Fig. 4B).

The general technique used to fit a psychometric function and a confidence function to the confidence data was described earlier (Fig. 3). To find the maximum likelihood parameter estimates we minimized the negative of the likelihood via a numeric optimization algorithm (MATLAB's fmincon function). The initial value for the confidence-scaling factor ($\widehat{k}$) was assumed equal to 1.0; initial values for the psychometric function parameters ($\widehat{u},\widehat{\sigma }$) were set equal to the values obtained by the general linear model fit of the binary forced-choice data.

Human studies.

Basic methods mimicked those used in our earlier studies (Chaudhuri et al. 2013; Valko et al. 2012). Each subject was seated in a racing-style chair with a five-point harness; his or her head was fixed relative to the chair and platform via an adjustable helmet. Each subject wore a pair of noise cancelling earpieces that also provided the ability to communicate with the experimenter. All motions were performed in complete darkness. Subjects performed a binary forced-choice direction-recognition task in response to upright whole body yaw rotation. Aural white noise began playing in the subject's earpiece 300 ms before motion commenced and ended when the motion ended. This aural cue was provided to mask any potential directional auditory cues and also informed the subject when a trial began and ended. When the motion and white noise ended, the iPad illuminated and subjects were required to report the motion direction perceived and a confidence probability judgment. Single cycles of sinusoidal acceleration at 1 Hz were used as the motion stimuli. Motion stimuli were generated using a MOOG 6DOF motion platform. There was a pause of at least 3 s between motions. An adaptive sampling procedure, a standard 3-Down/1-Up (3D/1U) staircase using parameter estimation by sequential testing (PEST) rules (Taylor and Creelman 1967), was utilized. The initial stimulus amplitude was 4°/s. Figure 4A shows an example stimulus track for the first 20 trials. There were 100 trials in each experiment.

Subject responses, both the direction responses (i.e., left or right) and quantitative confidence probability judgments having a resolution of 1%, were recorded using an iPad. Before each trial, the iPad backlighting was turned off. When the trial ended, the iPad was automatically illuminated to display sliders (one on the left and one on the right) that ranged from 50 to 100%. The subject tapped on the left side of the iPad to report perceived motion to the left and tapped on the right side to report perceived motion to the right. Subjects could then move the selected slider up/down to indicate their confidence. To avoid biasing the subject's confidence responses, no indication of slider position was displayed until the subject touched the screen to indicate their confidence (i.e., no initial slider position). The subject's responses, both direction (left/right) and confidence (50 to 100%), were displayed on the screen. The subject could adjust his or her response until satisfied; they then tapped a button labeled “Confirm.” At the beginning of the testing, the subjects practiced for a few trials to be sure that they understood the task.

These human studies utilized a half-range task in which subjects used a scale between 50 and 100%, inclusive. Confidence probability judgment tasks can be full-range tasks or half-range tasks (Galvin et al. 2003; Lichtenstein et al. 1982). Full-range scales range between 0 and 100%, while half-range scales range between 50 and 100%. For our half-range task, a subject might report that they perceived negative motion and report 84% confidence. For a full-range task with the subject asked to report his or her confidence that the motion was positive, the equivalent response would be a 16% confidence that the motion was positive. To plot, model, and fit the data, we used this mathematical equivalence to convert each half-range confidence rating to a full-range rating.

Subject instructions emphasized that the motion direction would be selected randomly and that the directions of previous motions would have no impact on the next motion direction. Instructions also emphasized that we had no expectation regarding how their confidence assessments would be distributed and that it was important that they report the confidence that they experienced for each specific trial. Subjects were specifically informed that “…if you are guessing much of the time, this is OK, and if you are very certain much of the time, this is OK, too.” Subjects were not ever provided any information regarding their confidence indications. During the initial training that never exceeded 10 practice trials, subjects were informed whether their left/right responses were correct or incorrect. During test sessions, subjects were never informed whether their responses were correct or incorrect.

Four healthy human subjects (2 male, 2 female, 26–34 yr old) were each tested on 6 different days. Informed consent was obtained from all subjects before participation in the study. The study was approved by the local ethics committee and was performed in accordance with the ethical standards laid down in the 1964 Declaration of Helsinki.

An author (Y. Yi) participated as one of the subjects. Since the computer randomized the motion direction for each trial just before the trial and since the adaptive staircase targets stimuli where all subjects should get ∼20% of the trials incorrect, this subject did not have information to guide his binary reports or confidence judgments on each individual trial. More importantly, as noted in the results, this subject's responses did not differ from the other subjects in any noticeable manner.

Simulations.

All simulations were performed in MATLAB R2015a (The Mathworks) on the Harvard Orchestra computation cluster using parallel IBM BladeCenter HS21 XMs with 3.16 GHz Xeon processors and 8 GB of RAM. These simulations used the same standard adaptive sampling procedure used for the human studies. Specifically, we used a 3D/1U staircase having 100 trials. The simulated 3D/1U staircases began at a stimulus level of four. The size of the change in stimulus magnitude was determined using PEST (parameter estimation by sequential testing) rules (Taylor and Creelman 1967).

For all four simulated data sets included herein, the psychometric function, Ψ(x) = ϕ(x;μ = 0.5,σ = 1), and the fitted psychometric function, $\widehat{\Psi }\left(x\right)=\varphi \left(x;\widehat{\mu },\widehat{\sigma }\right)$, were modeled as cumulative Gaussians.

For the first simulated data set (see Figs. 8, A, E, and I, and 9, A and E), the confidence function was modeled as “well-calibrated,” meaning that the confidence function equaled the psychometric function, χ(x) = Ψ(x) = ϕ(x;μ = 0.5,σ = 1). For the second simulated data set (see Figs. 8, B, F, and J, and 9, B and F), the confidence function was modeled as “underconfident” with a confidence-scaling factor (k) of 2, yielding a confidence function of χ(x) = ϕ(x;μ = 0.5,σ = 2). For the last two simulated data sets (see Figs. 8, C, G, and K, and 9, C and G), the confidence function was linear, crossing the 0.5 confidence level with a bias of 0.5 (μ = 0.5) and with a slope of 0.1443 (m = 0.1443), χ(x) = m(x − μ) + 0.5 = 0.1443x + 0.428, which yielded confidence saturations at −2.96 (“zero”) and +3.96 (“one”).

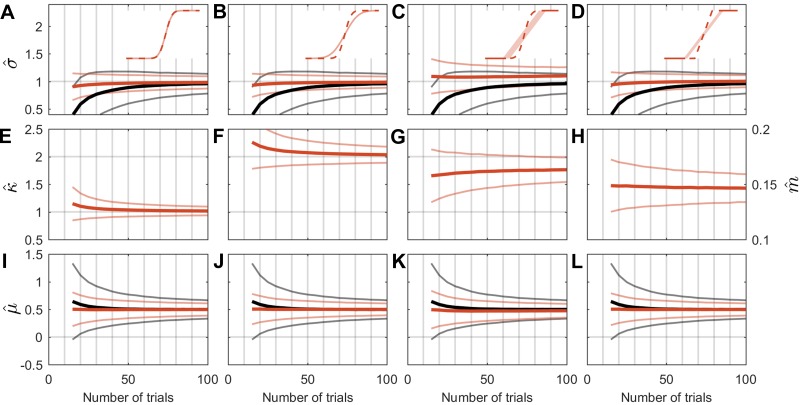
Fig. 8.

Summary of simulation parameter estimates as trial number increases. As illustrated via insets, each column represents different simulated combinations of the confidence function (red solid curves) and the fitted confidence function (red dashed curves). A, E, and I: well-calibrated subject (k = 1) when both confidence and confidence fit functions are cumulative Gaussians. B, F, and J: underconfident subject (k = 2) when both confidence and confidence fit functions are cumulative Gaussians. C, G, and K: underconfident subject when the confidence function is linear, χ(x) = m(x − μ) + 0.5 = 0.1443x + 0.428, with added zero-mean uniform noise [U(−0.1,+0.1)], and the confidence fit function is a cumulative Gaussian. D, H, and L: underconfident subject with the same linear confidence function with added zero-mean uniform noise [U(−0.05,+0.05)] when the confidence fit function is linear, $\widehat{\chi }\left(x\right)=\widehat{m}\left(x-\widehat{\mu }\right)+0.5$. A–D: fitted psychometric width parameter ($\widehat{\sigma }$). E–G: fitted confidence-scaling factor ($\widehat{k}$). H: fitted slope of confidence function. I–L: fitted psychometric function bias ($\widehat{\mu }$). Thick black curves show average conventional forced-choice parameter estimates, which are identical for all conditions. Thick red curves show average parameter estimates determined by fitting confidence probability judgments. Errors bars (thin gray curves and thin red curves, respectively) represent SD of parameter estimates.

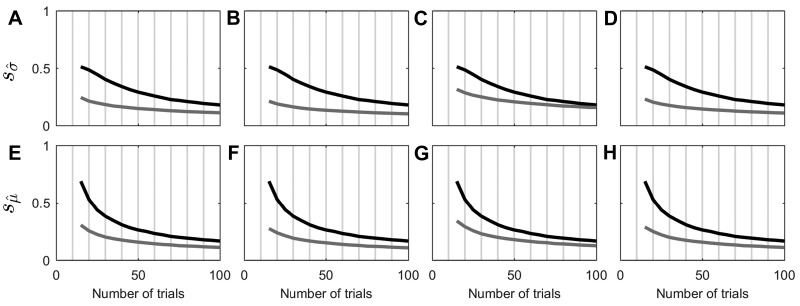
Fig. 9.

SD of simulation parameter estimates as trial number increases. Each column represent the same conditions as Fig. 8. A–D: fitted psychometric width parameter ($\widehat{\sigma }$). E–H: fitted psychometric function bias ($\widehat{\mu }$). Black curves show SD of conventional forced-choice parameter estimates, which are identical for all conditions. Gray curves show SD of parameter estimates determined via our CSD model fit.

For the first three simulated data sets (see Figs. 8, A–C, E–G, and I–K, and 9, A–C and E–G), we fit the data by modeling the fitted confidence function as the three-parameter Gaussian CDF introduced as Eq. 3, $\widehat{\chi }\left(x\right)=\varphi \left(x;\widehat{\mu },\widehat{k}\widehat{\sigma }\right)$. For the last simulated data set (see Figs. 8, D, H, and L, and 9, D and H), we fit the data by modeling the fitted confidence function as a linear model of confidence, $\widehat{\chi }\left(x\right)=\widehat{m}\left(x-\widehat{\mu }\right)+0.5$, which matched the form of the simulated confidence function.

Two simulation data sets included additive noise. For the simulations (see Figs. 8, C, G, and K, and 9, C and G), the noise distribution was modeled as zero-mean uniform noise having width of 20% (−10 to +10%), U(−0.1, +0.1). We intentionally chose a large noise range to demonstrate the small impact of such confidence noise. The relative stability of human confidence ratings suggest that this simulated noise level overestimates the actual contributions of confidence noise. For context, recognize that this noise distribution means that if the confidence function yielded a confidence rating of 70%, that the noise would lead to a report of between 60 and 80%, essentially yielding roughly three functional confidence bins between 50% (just guessing) and 100% (certain). We chose uniform noise because we could strictly control the noise range without any impact to the noise distribution. This was important because confidence must stay in the range 0 to 100%. To keep the noise zero-mean when the confidence function yielded a confidence of >90% (or <10%), the limits on the noise distribution were reduced to keep the confidence judgment in the range of 0 to 100%. For example, if the simulation yielded a mean confidence of 94% for an individual trial, the noise distribution was modeled as zero-mean uniform with a range of −6 to 6% [i.e., U(−0.06, +0.06)] for that trial. This had no impact on most trials, as confidence usually was lower than 90%. For the simulations (see Figs. 8, D, H, and L, and 9, D and H), the noise distribution was again modeled as zero-mean uniform noise but with a width of 10% (−5 to +5%), U(−0.05, +0.05).

RESULTS

Human studies.

Fitted psychometric function ($\widehat{\mu },\widehat{\sigma }$) and confidence scaling ($\widehat{k}$) parameters for each of our four subjects for yaw rotation about an earth-vertical rotation axis are shown in Figs. 5 (mean) and 6 (SD); parameter fits are plotted vs. the number of trials in increments of 5 trials starting at the 15th trial. [To demonstrate raw performance for individual test sessions, appendix b (see Fig. B1) presents the parameter fits for each of the six individual tests for each subject.] As described in the methods, all parameter estimates are determined using maximum likelihood methods.

Fig. 5.

Summary of human psychometric parameter estimates as trial number increases. Each column represents fitted parameters for 1 subject. A–D: average fitted psychometric width parameter ($\widehat{\sigma }$). E–H: average fitted confidence scaling factor ($\widehat{k}$). I–L: average fitted psychometric function bias ($\widehat{\mu }$). Thick black curves show average psychometric parameter estimates calculated using conventional forced-choice analyses. Thick red curves show average parameter estimates determined by fitting confidence probability judgment data. Errors bars (thin gray curves and thin red curves, respectively) represent SD of parameter estimates.

Fig. 6.

SD of human psychometric parameter estimates as trial number increases. Each column represents fitted parameters for one subject in the same order as Fig. 5. A–D: SD of the fitted psychometric width parameter ($\widehat{\sigma }$). E–H: fitted psychometric function bias ($\widehat{\mu }$). Black curves show SD of psychometric parameter estimates calculated using conventional forced-choice analyses. Gray curves show SD of parameter estimates determined via our CSD model fit.

Consistent with previous studies utilizing adaptive procedures (e.g., Chaudhuri and Merfeld 2013; Garcia-Perez and Alcala-Quintana 2005), the conventional estimates of the width of the psychometric function ($\widehat{\sigma }$) took between 50 and 100 trials to stabilize (Fig. 5, A–D, black curves). More specifically, using these conventional psychometric methods, the estimated width parameter ($\widehat{\sigma }$) was significantly lower after 20 trials than after 100 trials (repeated measures ANOVA, n = 4 subjects, P = 0.011).

In contrast, estimates of the width parameter ($\widehat{\sigma }$) using our confidence fit technique required fewer than 20 trials to reach stable levels (Fig. 5, A–D, red curves). Specifically, the width parameter ($\widehat{\sigma }$) estimated using confidence probability judgments was not significantly different after 20 trials than for 100 trials (repeated-measures ANOVA, n = 4 subjects, P = 0.251). Furthermore, the estimated width parameter after 20 trials using confidence probability judgments was not significantly different from the estimated width parameter after 100 trials using conventional psychometric fit methods (repeated-measures ANOVA, n = 4 subjects, P = 0.907).

Furthermore, the parameter estimates obtained using conventional psychometric fits (Fig. 6, black traces) were more variable than the fits obtained using our CSD model (Fig. 6 gray traces). In fact, the precision of the psychometric width estimate using the confidence model was about the same after 20 trials (average SD of 0.124 across subjects) as the conventional psychometric fit estimate after 100 trials (0.129).

The estimates of the shift of the psychometric functions ($\widehat{\mu }$) showed a qualitatively similar pattern; the estimates that utilized confidence reached stable levels a little sooner and were more precise than the estimates provided by the conventional analysis. We also note that three of our subjects seemed well calibrated (Fig. 5, E–G) with fitted confidence-scaling factors near 1, while the second subject had a fitted confidence-scaling factor near 2 (Fig. 5H), suggesting substantial underconfidence.

Simulations.

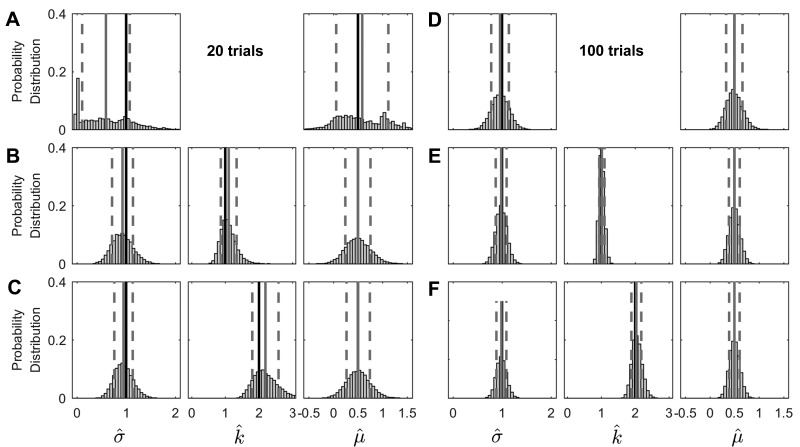
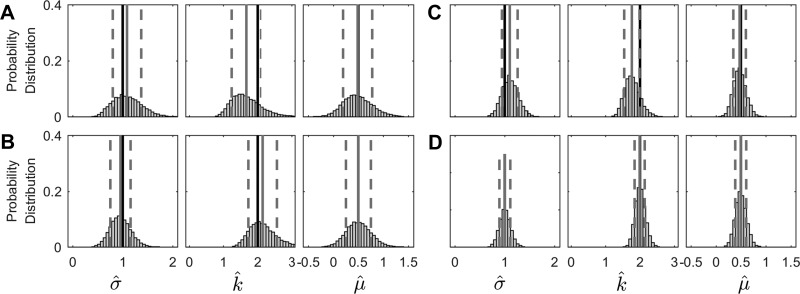
We also simulated tens of thousands of test sessions to test the confidence fit procedures more thoroughly. The simulations were designed to mimic the human studies with the obvious difference being that we defined the simulated psychometric [Ψ(x)] and confidence [χ(x)] functions. Since we knew these simulated functions, this allowed us to quantify parameter fit accuracy. For all simulated data sets, we fit the conventional binary forced-choice data and compared and contrasted these fits with the CSD fits. Histograms show fitted parameters after 20 (Fig. 7, A–C) and 100 (Fig. 7, D–F) trials for 10,000 simulations. After as few as 20 trials, the CSD fit parameters demonstrated relatively tight distributions (Fig. 7, B and C) compared with the binary fits that show ragged distributions (Fig. 7A). After 100 trials, the binary fit parameters demonstrated relatively tight distributions (Fig. 7D) that mimicked those found for the CSD fit parameters after 20 trials (Fig. 7, B and C). The CSD fit parameters after 100 trials (Fig. 7, E and F) demonstrated higher precision (i.e., lower variance) than the binary fit parameters after 100 trials (Fig. 7D). (See Fig. B2 for similar histograms for 100 trials for the other 2 simulation data sets.)

Fig. 7.

Parameter distributions show parameter estimates for 10,000 simulated experiments with 20 and 100 trials. The columns from left to right represent the fitted psychometric width parameter ($\widehat{\sigma }$), the fitted confidence scaling factor ($\widehat{k}$), and the fitted psychometric function bias ($\widehat{\mu }$) as shown on the x-axis at bottom. A and D: fitted parameters of conventional binary forced-choice parameter estimates. B and E: fitted parameters estimates determined via our CSD model fit for a well-calibrated subject (k = 1). C and F: fitted parameters estimates determined via our CSD model fit for an underconfident subject (k = 2). The solid black line shows the actual parameter value (i.e., μ = 0.5 or σ = 1), the solid gray line shows the mean of fitted parameters, and the dashed gray lines indicate SD on each side of the mean.

Mimicking the format previously used for the human data (Figs. 5 and 6); simulation parameter fits are plotted vs. the number of trials in increments of 5 trials starting at the 15th trial. The black curves in Figs. 8 and 9 show the fitted psychometric function parameters for the binary forced choice data; the red (Fig. 8) and gray (Fig. 9) curves show the fitted psychometric and confidence function parameters fit using the CSD model. (To provide direct quantitative comparisons, appendix b summarizes data from all simulations in tabular form.)

The simulated data (Figs. 8, A, E, and I, and 9, A and E and Tables B1–B3, row 2) show that the CSD model yielded fit parameters that accurately matched those simulated when the simulated subject's confidence was well calibrated (k = 1), where “well calibrated” means that the subject's confidence matches the psychometric function, χ(x) = ϕ(x;μ + 0.5,kσ = 1). Even when the subject's confidence was not well calibrated (k = 2), the confidence fit parameters matched the three confidence function parameters well (Figs. 8, B, F, and J, and 9, B and F, and Tables B1–B3, row 3). In fact, except that the fitted confidence-scaling factor ($\widehat{k}$) settles near a value of 2 (Fig. 8F) instead of 1 (Fig. 8E), the average psychometric parameter estimates for an underconfident subject appeared nearly the same as for a well-calibrated subject. Indeed, the fitted psychometric width parameter ($\widehat{\sigma }$) demonstrated a lower SD for an underconfident subject than for a well-calibrated subject (see appendix b).

To demonstrate robustness, we utilized the same Gaussian confidence fit model (Eq. 2) while simulating a confidence model that differed from the Gaussian confidence fit model in two ways. First, we modeled the confidence function as a linear function (slope of 0.1445; i.e., σ = 2) instead of a cumulative Gaussian. In addition, secondly, we added zero-mean uniform noise, U(−0.1,0.1), to the simulated confidence response. Despite these differences, the confidence fit of these simulated data mimics the earlier confidence fits well (Figs. 8, C, G, and K, and 9, C and G, and Tables B1–B3, row 4). The primary difference is that the parameter fit precision was not as good as for the first two simulation sets described above but was still better than for the conventional fits. For example, despite the severe noise (−10% to +10%), the fit precision for the width parameter ($\widehat{\sigma }$) after 20 trials utilizing confidence matched the fit precision after about 50 trials using conventional analyses.

Finally, to demonstrate the flexibility of the confidence fit technique, we model the same linear confidence function from the previous paragraph, but we now add less extreme zero-mean uniform noise levels U(−0.05,0.05) and fit a linear confidence function that mimics the linearity of the true confidence function used for these simulations. The fit accuracy and precision were very good (Figs. 8, D, H, and L, and 9, D and H, and Tables B1–B3, row 5), demonstrating that the fitted psychometric function and confidence function need not be similar in form. (For some conventional confidence metrics, including goodness of fit parameters, see Table B4.)

DISCUSSION

This paper introduces a new confidence CSD model (Fig. 1) and then uses this model to develop a confidence analysis technique (Fig. 3) that utilizes confidence probability judgments to help yield more efficient psychometric function fits. The primary novelty of the new technique is the introduction of a confidence function, alongside confidence probability judgments to help improve psychometric function fit efficiency. The introduction of a fitted confidence function yields two benefits. First, it provides a way to incorporate confidence probability judgments into a psychometric fit procedure. Second, while it does not require that the confidence function differ from the psychometric function, it allows these two functions to differ from one another.

We assumed that the binary decision variable is used to determine confidence probability judgments. Of course, if confidence does not correlate in some manner with the sampled decision variable used to make a decision, this would lead to erroneous results but empirical data presented suggest that, at least for yaw rotation thresholds, this does not appear to be a substantive concern.

We specifically note that while we utilized confidence probability judgments and a confidence function, similar benefits may accrue by replacing 1) the confidence function and confidence recordings with a magnitude estimation function accompanied by magnitude estimation recordings (e.g., I rotated +3°) or other analogous perceptual functions and associated recordings or 2) the confidence probability judgments by another confidence assay accompanied by an appropriate model of the confidence assay. Such potential benefits would need to be investigated theoretically and empirically via behavioral studies and simulations as provided herein for confidence probability judgments.

In this paper, we focus nearly exclusively on improving the efficiency of psychometric parameter fits, but the fitting technique shown herein also calculates a confidence-scaling factor, which may independently prove useful for studies of confidence calibration. More generally, the confidence modeling approach described herein (Fig. 1) may benefit studies of confidence calibration, but such topics require separate study.

Human studies.

Our human experimental data showed that stable psychometric function parameters could be estimated in as few as 20 trials (Figs. 5 and 6). In fact, these human data demonstrated no significant differences between the psychometric function parameters estimated after 20 trials using confidence data and the same parameters estimated after 100 trials using conventional methods. These findings suggest that the number of trials required to estimate psychometric fit parameters could be reduced by roughly 80% simply by collecting a confidence probability judgments and utilizing the confidence information in the manner shown.

Not one of these four subjects had performed an experiment utilizing a confidence probability judgment before our studies of confidence and none were provided any feedback, except during the initial practice that consisted of 10 trials when subjects were informed whether their responses were correct or incorrect. No specific feedback regarding confidence was ever provided during the course of the study. Despite intentionally limiting the training and feedback, each subject yielded a coherent data set across the six test sessions. It is worth noting that all four subjects were experienced observers; one of the subjects was an author (Y. Yi), but there was nothing noteworthy about his data as he was not the subject whose confidence-scaling factor was near 2.

For our task, we minimize the potential impact of aftereffects from the previous trial (Coniglio and Crane 2014; Crane 2012a,b) by requiring at least 3 s between the end of a stimulus and the start of the next stimulus (Chaudhuri et al. 2013). Therefore, providing confidence did not require much, if any, additional time to complete each trial than a conventional binary forced-choice task for our direction-recognition task, but this may not be true for all other tasks. Nonetheless, an 80% improvement in efficiency may be well worth a little more time on each trial even for those tasks that do not include such a mandatory intertrial interval.

We also want to note at least a possible concern/limitation. While we did not attempt to test children for this study, it seems highly likely that forced-choice tasks can be taught more readily to children and probably even some adults (e.g., elderly patients) than the confidence probability judgment task we utilized. Some simple form of training with feedback may prove beneficial but we intentionally avoided any feedback for this initial study. We also specifically note that a better understanding of confidence would be required for maximal utilization of this new CSD psychometric analysis.

For example, the benefit of confidence training for perceptual tasks needs to be studied. For knowledge tasks, investigations show that simple and short training sessions that provide direct confidence calibration information can lead to improved calibration (Lichtenstein and Fischhoff 1980; Stone and Opel 2000) and that such improvement might generalize to tasks beyond the one calibrated (Lichtenstein and Fischhoff 1980). If generalized calibration occurs, such training could help calibrate confidence before testing as part of the process by which subjects are taught the requisite tasks; this may be particularly useful for clinical testing. Alongside existing measures (e.g., the Brier score and its calibration and resolution components; Yates 1990), our confidence-scaling factor might be useful to help determine if confidence calibration is an individual trait and to help train confidence calibration. Beyond improving psychometric parameter estimation, a specific benefit of our confidence modeling approach may be that it only requires about 20 to 50 trials (e.g., Figs. 5 and 6) to provide relatively stable calibration feedback. This is substantially fewer trials than the hundreds of trials used before (Lichtenstein and Fischhoff 1980; Stone and Opel 2000) because the calibration plots and the Brier score partitions used previously are sensitive to sample size (Lichtenstein and Fischhoff 1980).

Simulations.

Simulations confirmed that this new fitting technique yields accurate psychometric parameter estimates and also confirmed a marked efficiency improvement. Even simulations that assumed 1) a confidence model that was not matched by the fitting model and 2) large additive confidence noise, likely greater than actual confidence noise, yielded psychometric function parameter estimates that matched the simulated psychometric function much more efficiently than conventional psychometric fits (i.e., 20 trials compared with 50–100 trials). If the assumed confidence function is wrong, it could lead to biased predictions. However, simulations show that even assuming the wrong confidence function did not cause major difficulties.

Simulations showed that this new fitting method works well for psychometric functions that range from 0 to 1. As noted above, we also verified experimentally that this fitting method works well for a specific vestibular direction-recognition task, but we did not verify experimentally that this new fitting technique works for other tasks/modalities. Nonetheless simulation results should be generally applicable to all tasks yielding psychometric functions that range from 0 to 1. Furthermore, there is no fundamental reason to believe that this technique cannot be applied to other tasks, like detection tasks (i.e., yes/no tasks) or to two-alternative forced choice detection tasks where the subject identifies the interval (or location) when (or where) the signal occurred, having different psychometric ranges (e.g., 0.5 to 1). However, we have not yet determined the extent to which our findings generalize to psychometric functions having other ranges.

In closing, we have developed a new CSD model (Fig. 1) and then used this new model to develop a confidence analysis technique (Fig. 3) that utilizes confidence probability judgments that can reduce the number of trials needed to provide good psychometric parameter estimates. Human studies (Figs. 5 and 6) using a direction-recognition task and a psychometric function that varies from 0 to 1 and extensive simulations (Figs. 7–9) suggest that about 20 trials using this new confidence fit method can match the performance typically achieved only after about 100 trials using conventional fit methods.

GRANTS

This research was supported by National Institute of Child Health and Human Development Grants R01-DC-04158 and R56-DC-12038.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: Y.Y. performed experiments; Y.Y. and D.M.M. analyzed data; Y.Y. and D.M.M. interpreted results of experiments; Y.Y. and D.M.M. prepared figures; Y.Y. and D.M.M. drafted manuscript; Y.Y. and D.M.M. edited and revised manuscript; Y.Y. and D.M.M. approved final version of manuscript; D.M.M. conception and design of research.

Appendix A: FLOW CHART FOR CONFIDENCE FIT PROCESS

Figure A1 provides a flow chart for the confidence fit process.

Fig. A1.

Flow chart for confidence fit process.

Appendix B: SIMULATED FIT PARAMETERS

Tables B1, B2, and B3 included in this appendix summarize results from 10,000 simulated test sessions for direct quantitative comparisons. These fit parameters are the same as shown graphically in Figs. 8 and 9. Tables B1 and B3, row 5, quantitatively present the fitted psychometric parameters using the conventional binary methods; these were graphically presented in Figs. 8 and 9 as black curves. Tables B1–B3, rows 1–4, quantitatively present the fitted psychometric and confidence scaling parameters found using the CSD fit; these were graphically presented in Figs. 8 and 9 as red or gray curves. Specifically, Tables B1–B3, row 1, quantitatively presents fit parameters for a well-calibrated subject (k = 1) when both confidence and confidence fit functions were cumulative Gaussians (Figs. 8, A, E, and I, and 9, A and E). The Tables B1–B3, row 2, quantitatively presents fit parameters for an underconfident subject (k = 2) when both confidence and confidence fit functions were cumulative Gaussians (Figs. 8, B, F, and J and 9, B and F). The Tables B1–3, row 3, quantitatively presents fit parameters an underconfident subject when the confidence function is linear, χ(x) = m(x − μ) + 0.5 = 0.1443x + 0.428, with added zero-mean uniform noise [U(−0.1,+0.1)], and the confidence fit function was a cumulative Gaussian (Figs. 8, C, G, and K, and 9, C and G). The Tables B1–B3, row 4, present fit parameters for an underconfident subject with the same linear confidence function with added zero-mean uniform noise [U(−0.05,+0.05)] when the confidence fit function was linear, $\widehat{\chi }\left(x\right)=\widehat{m}\left(x-\widehat{\mu }\right)+0.5$ (Figs. 8, D, H, and L, and 9, D and H). Table B4 shows some conventional parameters that summarize different characteristics of the fit, including goodness of fit. Figure B1 presents the parameter fits for each of the six individual tests for each subject. Figure B2 shows similar histograms for 100 trials for the other 2 simulation data sets.

Table B1.

Fitted width parameter ($\widehat{\sigma }$)

	Trials
	20		40		60		80		100
Fig. 8, A, E, and I	0.926	(0.213)	0.960	(0.163)	0.973	(0.139)	0.977	(0.121)	0.983	(0.111)
Fig. 8, B, F, and J	0.946	(0.188)	0.971	(0.144)	0.980	(0.125)	0.984	(0.111)	0.987	(0.102)
Fig. 8, C, G, and K	1.053	(0.279)	1.041	(0.218)	1.045	(0.189)	1.050	(0.166)	1.058	(0.153)
Fig. 8, D, H, and L	0.955	(0.203)	0.984	(0.156)	0.995	(0.134)	0.999	(0.119)	1.003	(0.109)
Binary	0.588	(0.484)	0.841	(0.340)	0.914	(0.257)	0.944	(0.209)	0.959	(0.179)

Table B2.

Fitted confidence scaling factor ($\widehat{k}$)

	Trials
	20		40		60		80		100
Fig. 8, A, E, and I	1.102	(0.234)	1.045	(0.137)	1.029	(0.107)	1.021	(0.090)	1.016	(0.079)
Fig. 8, B, F, and J	2.189	(0.389)	2.089	(0.245)	2.058	(0.194)	2.043	(0.164)	2.034	(0.146)
Fig. 8, C, G, and K	1.752	(0.464)	1.814	(0.360)	1.845	(0.308)	1.859	(0.272)	1.868	(0.248)
Fig. 8, D, H, and L	0.148	(0.022)	0.148	(0.018)	0.147	(0.015)	0.147	(0.014)	0.146	(0.013)

Table B3.

Fitted bias parameter ($\widehat{\mu }$)

	Trials
	20		40		60		80		100
Fig. 8, A, E, and I	0.499	(0.255)	0.494	(0.175)	0.496	(0.143)	0.497	(0.123)	0.497	(0.111)
Fig. 8, B, F, and J	0.505	(0.237)	0.500	(0.167)	0.500	(0.137)	0.500	(0.120)	0.499	(0.107)
Fig. 8, C, G, and K	0.486	(0.283)	0.468	(0.193)	0.469	(0.158)	0.471	(0.136)	0.473	(0.122)
Fig. 8, D, H, and L	0.503	(0.249)	0.496	(0.173)	0.498	(0.143)	0.498	(0.124)	0.497	(0.110)
Binary	0.588	(0.529)	0.514	(0.308)	0.501	(0.232)	0.498	(0.191)	0.498	(0.166)

Table B4.

Conventional confidence metrics for human and simulated data

	BS		REL		RES		UNC		Deviance Binary		Deviance CSD
Subject 1	0.150	(0.015)	0.081	(0.013)	0.181	(0.016)	0.249	(0.001)	92.6	(8.7)	789.0	(40.8)
Subject 2	0.127	(0.021)	0.074	(0.017)	0.192	(0.016)	0.246	(0.003)	75.3	(10.1)	752.6	(44.8)
Subject 3	0.145	(0.020)	0.081	(0.011)	0.185	(0.019)	0.249	(0.001)	93.6	(9.5)	791.3	(31.0)
Subject 4	0.147	(0.025)	0.076	(0.014)	0.176	(0.012)	0.247	(0.004)	79.2	(12.8)	821.0	(20.6)
Fig. 8, A, E, and I	0.135	(0.019)	0.095	(0.015)	0.207	(0.015)	0.247	(0.004)	79.3	(8.0)	764.6	(37.4)
Fig. 8, B, F, and J	0.141	(0.015)	0.091	(0.012)	0.198	(0.016)	0.247	(0.004)	79.3	(8.0)	807.9	(18.2)
Fig. 8, C, G, and K	0.152	(0.015)	0.093	(0.013)	0.188	(0.017)	0.247	(0.004)	79.3	(8.0)	830.7	(22.7)
Fig. 8, D, H, and L	0.150	(0.014)	0.092	(0.013)	0.190	(0.017)	0.247	(0.004)	79.3	(8.0)	788.0	(21.7)

Brier Score (BS) and its 3 decomposed components: reliability (REL), resolution (RES), and uncertainty (UNC) are shown. For definitions and descriptions, see Brier 1950; Murphy 1973, 1972. We use the formulation commonly used today, which results by dividing Brier's original formulation by 2. Deviance for each of 2 fits are also shown. Mean (SD) across 6 trials for each subject and across 10,000 simulations for each simulated data set are provided.

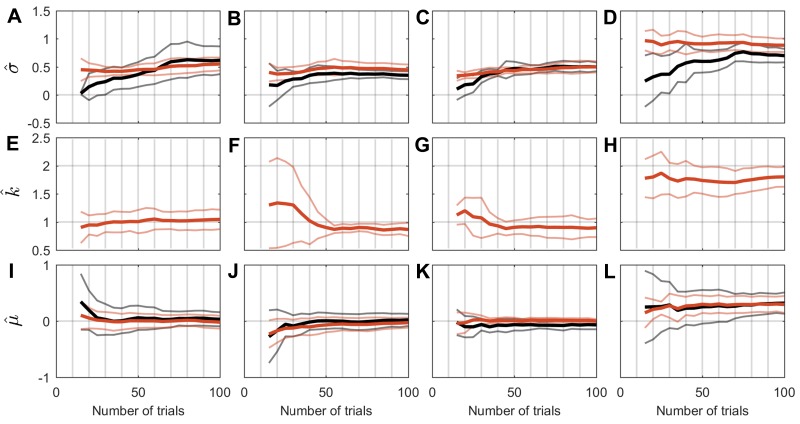
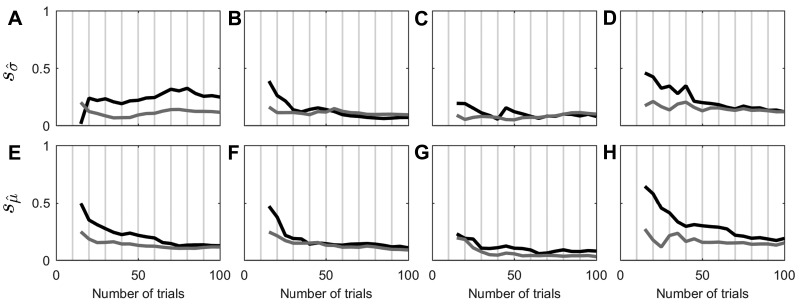
Fig. B1.

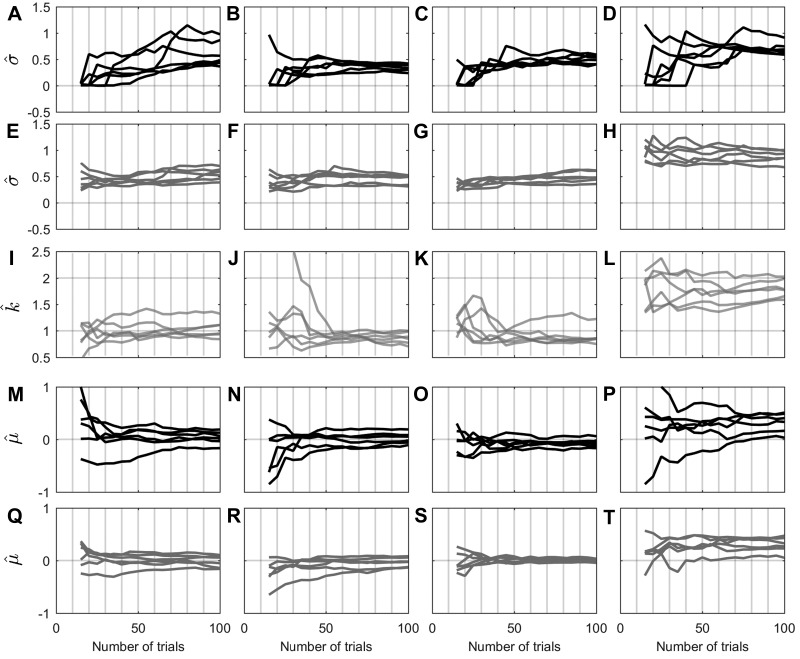
Human psychometric width parameter ($\widehat{\sigma }$), confidence scaling factor ($\widehat{k}$), and bias parameter ($\widehat{\mu }$) estimates as trial number increases for each subject for each of 6 test sessions. Each column shows fitted parameters for one subject. A–D: fitted psychometric width parameter using conventional forced-choice analyses. E–H: fitted psychometric width parameter for CSD model fit. I–L: fitted confidence scaling factor for CSD model fit. M–P: fitted psychometric function bias using conventional forced-choice analyses. Q–T: fitted psychometric function bias for CSD model fit.

Fig. B2.

Parameter distributions show parameter estimates for 10,000 simulated experiments with 20 and 100 trials in the same order as Fig. 6. A and C: fitted parameters estimates determined via our CSD model fit for an underconfident subject when the confidence function is linear, χ(x) = m(x − μ) + 0.5 = 0.1443x + 0.428, with added zero-mean uniform noise [U(−0.1,+0.1)], and the confidence fit function is a cumulative Gaussian. B and D: fitted parameters estimates determined via our CSD model fit for an underconfident subject with the same linear confidence function with added zero-mean uniform noise [U(−0.05, +0.05)] when the confidence fit function is linear, $\widehat{\chi }\left(x\right)=\widehat{m}\left(x-\widehat{\mu }\right)+0.5$. The solid black line shows the actual parameter value (i.e., μ = 0.5 or σ = 0.5), the solid gray line shows the mean of fitted parameters, and the dashed gray lines indicate SD on each side of the mean.