Abstract
How neuronal activity of motor cortex is related to movement is a central topic in motor neuroscience. Motor-cortical single neurons are more closely related to hand movement velocity than speed, that is, the magnitude of the (directional) velocity vector. Recently, there is also increasing interest in the representation of movement parameters in neuronal population activity, such as reflected in the intracranial EEG (iEEG). We show that in iEEG, contrasting to what has been previously found on the single neuron level, speed predominates over velocity. The predominant speed representation was present in nearly all iEEG signal features, up to the 600–1000 Hz range. Using a model of motor-cortical signals arising from neuronal populations with realistic single neuron tuning properties, we show how this reversal can be understood as a consequence of increasing population size. Our findings demonstrate that the information profile in large population signals may systematically differ from the single neuron level, a principle that may be helpful in the interpretation of neuronal population signals in general, including, for example, EEG and functional magnetic resonance imaging. Taking advantage of the robust speed population signal may help in developing brain–machine interfaces exploiting population signals.
Keywords: brain–machine interface, ECoG, population signals, tuning, velocity
Introduction
There is an increasing interest in understanding how movement is represented in intracranial electroencephalography (iEEG) signals. This interest is due, among other factors, to (1) the growing popularity of the iEEG as a tool to study human cortical functions in general and motor control in particular (Mukamel and Fried 2012), and (2) the application in brain–machine interfaces (BMIs) that aim to reconstruct movement from brain activity recordings in paralyzed patients (Lebedev and Nicolelis 2006; Schwartz et al. 2006; Vaadia and Birbaumer 2009; Milekovic et al. 2012).
A number of different kinematic parameters and their relation to motor-cortical activity have been previously studied using voluntary movement paradigms that broadly fall into 2 categories: (1) “event-related” tasks (Pfurtscheller and Lopes da Silva 1999), where subjects make repetitive, short-duration movements of up to a few seconds, for example, after a “go” cue followed by a period of rest, or (2) continuous movement tasks, lasting for longer periods from tens of seconds up to several minutes. The category of the event-related tasks (e.g., center-out movements) was already described with an impressive degree of detail in most of the available neuronal signals: single unit activity (SUA) (Ashe and Georgopoulos 1994), local field potential (LFP) (Mehring et al. 2003), electrocorticogram (ECoG) (Ball et al. 2009), scalp EEG, or magnetoencephalography (MEG) (Waldert et al. 2008). First results were also demonstrated in the continuous movement tasks in SUA (Paninski et al. 2004), LFP (Mehring et al. 2003), ECoG (Schalk et al. 2007), and EEG (Bradberry et al. 2010). Among the many different kinematic parameters, movement direction turned out to be strongly represented especially in SUA (Georgopoulos et al. 1982), but also in LFP (Mehring et al. 2003), and to some degree also in ECoG (Ball et al. 2009), and even in EEG or MEG (Waldert et al. 2008). Besides velocity (Paninski et al. 2004; Pistohl et al. 2008), other important parameters investigated were position (Pistohl et al. 2008), acceleration (Bourguignon et al. 2011; Hammer et al. 2013), or speed (Jerbi et al. 2007).
Another factor leading to diversity among studies is that there are many different signal components that can be extracted from analog population signals. iEEG, for example, is typically investigated either in its temporal domain or as a power modulation in different frequency bands. The time domain signal is usually low-pass filtered, yielding the so-called low-pass filtered component (LFC). The LFC was shown multiple times to be very informative about some of the major kinematic parameters such as direction (Ball et al. 2009), velocity (Pistohl et al. 2008), position (Schalk et al. 2007), or acceleration (Hammer et al. 2013). The ECoG power spectrum is analyzed in many different frequency bands (Sauseng and Klimesch 2008): δ (0–4 Hz), θ (4–8 Hz), α (8–12 Hz), β (13–30 Hz), low γ (30–45 Hz), high γ (55 to ∼300 Hz); very little is currently known about the representation of movement in even higher iEEG frequency bands (>300 Hz).
As a consequence, results on motor-cortical iEEG are dispersed among different studies, investigating different sets of kinematic parameters, signal features, and decoding algorithms. For example, Ball et al. (2009) investigated decoding of movement direction both in ECoG LFC and in different frequency band power modulations, but not of other kinematic parameters. Moreover, different studies typically used different decoding methods, such as a Kalman filter used by Pistohl et al. (2008) or a linear discriminant analysis used by Ball et al. (2009), hindering a direct, quantitative comparison of the results. It is hence currently not clear whether there is a systematic difference between population signals and single neuron activity with respect to which movement parameters are strongly represented.
Therefore, we designed continuous motor tasks and systematically analyzed neuronal population activity from iEEG recordings covering parts of the motor cortex in patients suffering from intractable epilepsy. From the executed movements we derived direction, position, velocity, speed (magnitude of velocity), acceleration, and magnitude of acceleration and analyzed not only their decoding, but also their representation (tuning) in different iEEG signal features. An important aspect of the data analysis was to clarify how the observed properties of motor-cortical iEEG could be understood also from the perspective of SUA recordings (Ashe and Georgopoulos 1994).
One of the first striking observations we made was that speed of movement (the magnitude of the velocity vector) was the best represented of all kinematic variables in nearly all iEEG signal features investigated, up to the 1-kHz signal range. Such a result is in clear contrast to the situation as was previously documented in SUA, where the directional tuning was shown to be much stronger than the SUA tuning to speed (Schwartz and Moran 1999).
We show that the observed robust speed representation in iEEG can be understood based on previously described properties of directional- and speed-tuning of SUA (Moran and Schwartz 1999). We used the model of firing rate for a single motor cortex neuron proposed by Moran and Schwartz (1999) to simulate the firing rate of a whole neuronal population (similar to Waldert et al. 2009). Several studies demonstrated considerable complexity and heterogeneity of movement-related SUA in motor cortex deviating from the “canonical” Moran and Schwartz model (Sergio et al. 2005; Churchland and Shenoy 2007). As such deviations can act as noise with respect to speed and directional tuning terms in our model, we also investigated various levels of such noise.
The ensuing numerical model reproduced the predominance of speed- over direction-related information in neuronal population activity consisting of many thousands of neurons. Our findings thus demonstrate that the information profile in large population signals may substantially differ from the single neuron level. We anticipate the same principle to be useful for understanding the relation between the single neuron level and physiological population signals, such as in EEG and fMRI, in general.
Materials and Methods
Subjects
Nine subjects with iEEG electrodes in the area of hand/arm motor cortex participated in 2 different continuous movement tasks, after giving their informed consent. The site of the implantation was selected exclusively based on the clinical requirements for the surgical evaluation in these patients with pharmaco-resistant epilepsy. The study was approved by the University Clinics' Ethics Committees in Freiburg, Germany, and Prague, Czech Republic. Detailed information about subjects (S1–S9), electrode type, and location is provided in Table 1.
Table 1.
Subject information
| Sex (age) | Pathology | Electrode type, location | Hand/arm channels | Sampling rate (Hz) | Task | |
|---|---|---|---|---|---|---|
| S1 | F (47) | Cryptogenic | 64-Contact ECoG grid, right frontal | 14 | 2500 | 1-D |
| S2 | M (46) | FCD right inferior frontal gyrus | 64-Contact ECoG grid, right fronto-temporal | 12 | 2500 | 1-D |
| S3 | M (50) | cryptogenic | 64-Contact ECoG grid, right fronto-lateral | 8 | 2500 | 1-D |
| S4 | M (13) | FCD left insular | 62-Contact SEEG, left operculo-insular | 13 | 1000 | 1-D |
| S5 | F (29) | Gliosis right parietal cortex | 62-Contact SEEG, left and right fronto-parietal | 12 | 8000 | 1-D |
| S6 | F (22) | FCD left superior frontal gyrus | 28-Contact ECoG grid, left fronto-parietal | 9 | 2000 | 1-D |
| S7 | M (30) | FCD right rolandic cortex | 48-Contact ECoG grid, right fronto-parietal | 13 | 1024 | 2-D |
| S8 | M (14) | FCD right frontal cortex | 64-Contact ECoG grid, right frontal | 11 | 256 | 2-D |
| S9 | M (27) | FCD left SMA | 64-Contact ECoG grid, left fronto-parietal | 11 | 1024 | 2-D |
SEEG, stereoelectroencephalography; FCD, focal cortical dysplasia; SMA, supplementary motor area.
Continuous Motor Tasks
The tasks were designed to produce continuous, natural hand/arm movements, which would be close to casual, every-day behavior. The experimental data were recorded by using the software described by Fischer et al. (2014) and consisted of several 3–5 min recording sessions. All pauses without movement longer than 200 ms were rejected from the analysis (see below) to ensure the continuous nature of the motor task.
The first task was the car-driving computer game as described in detail by Hammer et al. (2013), a one degree-of-freedom (1-D) task, as the control of the car was restricted to the horizontal dimension (left/right). Subjects were instructed to drive a car with a gaming steering wheel on a randomly curved road displayed on a computer screen (Fig. 1A). For subjects S1 to S3 in the present study (corresponding to subjects S1–S3 in Hammer et al. 2013), the upward (vertical) car scrolling speed was held constant throughout the recording sessions, while for subjects S4–S6 the vertical scrolling speed of the car was varied in the different recording sessions in order to test the resilience of the decoding results for different distributions of the kinematic variables.
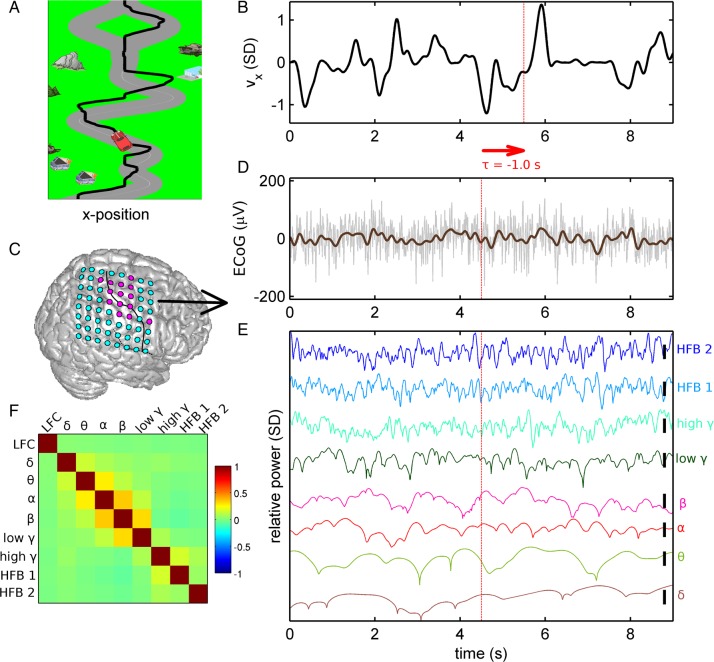
Figure 1.
ECoG recording in the continuous car-driving task. (A) Subjects were instructed to steer a car (red) on a randomly curved road (gray). Trajectory of the car is marked as a black line (note that the trajectory was not displayed to the subjects). (B) Velocity time series corresponding to the trajectory shown in A, normalized to unit standard deviation. (C) Example of ECoG grid position (subject S1) visualized on a standard brain. Electrodes with hand/arm motor response upon electrical stimulation mapping colored in magenta (otherwise in cyan). Black line: central sulcus identified from post-implantation MRI of the individual patient. (D) Raw ECoG (gray) and LFC (brown) aligned with the velocity data in B. Note the definition of the time offset τ: For example, τ = −1.0 s indicates that the iEEG feature vector precedes movement execution. (E) Relative power modulations (colored traces) in the different frequency bands investigated: δ (0–4 Hz), θ (4–8 Hz), α (8–12 Hz), β (13–30 Hz), low γ (30–45 Hz), high γ (55–300 Hz), and high-frequency bands “HFB 1” (300–600 Hz) and “HFB 2” (600–1000 Hz). (F) The correlation coefficients of the different iEEG signal features (LFC and power modulations), computed as mean over all subjects, motor channels, and recording sessions.
The second task was the target pursuit task as described in detail by Pistohl et al. (2008), a 2 degree-of-freedom (2-D) task, where a computer cursor was controlled on the whole plane of the computer monitor. To perform this task, the subjects S7–S9 were instructed to move a cursor using either a gaming joystick or a manipulandum to a target appearing on a computer monitor randomly in 1 of 9 possible locations arranged as 3 × 3 grid. As soon as one target was reached, another, new target appeared in a different location to which the subjects navigated the cursor again. Only those subjects with coverage of hand/arm motor area and with ECoG recordings without strong epileptic discharges were included in the present analysis, corresponding to subjects S4 to S6 in the study by Pistohl et al. (2008).
Continuous Kinematic Variables
During all motor tasks, rotation of the steering wheel (car-driving task) or movement of the joystick/manipulandum (in target pursuit) was linearly translated into car/cursor position on the screen (see Fig. 1A, black line). Movement velocity and acceleration were estimated by a 5-point derivative approximation (Abramowitz and Stegun 1970) from the recorded position. All kinematic variables were normalized to their standard deviation (SD) and smoothed (eighth order Butterworth with 10-Hz cut-off frequency and zero-phase shift), with the exception of movement direction. The directional vector was derived by normalization to unit length from the velocity vector. To exclude pauses during the otherwise continuous movement task, for example, on the straight parts of the road, the pauses were defined whenever speed was continuously below 0.05 SD for longer than 200 ms. The corresponding time windows were excluded from further analysis (both decoding model estimation and tuning, see below). We examined the following kinematic variables: direction, position, velocity, speed, acceleration, and magnitude of acceleration.
As some of the most important observations and hypothesis in this study concern speed of movement, we would like to underline the distinction between speed and velocity. Velocity v(t) is defined as a vector variable, having a certain direction and a magnitude, while speed s(t) = ||v(t)|| is defined as the magnitude of the velocity vector, that is, a scalar variable with only positive values. While velocity also includes information about direction of movement, speed only reflects how fast or slow this movement was, irrespective of direction. Thus velocity, but not speed, captures also the basic properties of directional tuning, because direction of movement is indicated by direction of the velocity vector.
iEEG Recording and Pre-Processing
ECoG electrode grid arrays (see an example of subject S1 in Fig. 2C), with 10-mm interelectrode distance, 4-mm electrode diameter, and 2.4-mm brain surface contact diameter, were subdurally implanted in each subject, with the exception of subjects S4 and S5 who were implanted with intracranial stereoelectroencephalography (SEEG, cylindrical electrode contacts with 0.8-mm diameter, 2-mm height, and 1.5-mm interelectrode distance). Throughout this study, we use the term iEEG to refer to both, ECoG and SEEG. The raw iEEG recordings were common-average re-referenced. All data analysis was performed in Matlab (version R2011b, The MathWorks Inc., Natick, MA).
Figure 2.
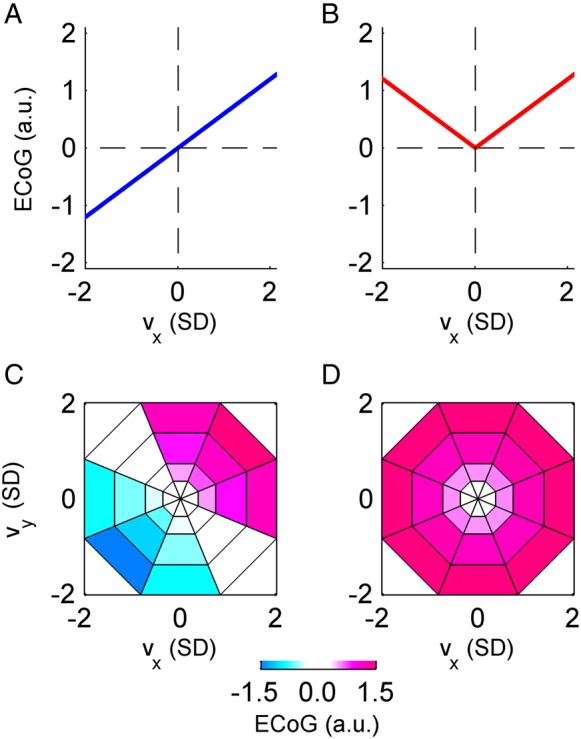
Tuning functions expected in the case of “perfect” velocity and speed dependence. (A) The expected “perfect” velocity tuning function in the 1-D case is a (scaled) identity function, and (B) for speed it is a (scaled) absolute value function. Similarly, in the 2-D case, the “perfect” velocity tuning (C) has a maximum response for a certain preferred direction (in this example oriented north-east), while “perfect” speed tuning (D) shows a radially symmetrical response. These “perfect” tuning patterns were used to classify the significantly tuned iEEG features as velocity-type or speed-type.
Individual iEEG electrodes (ECoG or SEEG) were electrically stimulated to produce functional mapping underneath/around each electrode contact (Pistohl et al. 2008; Hammer et al. 2013). In all patients, the implantations covered parts of the hand/arm motor cortex as verified by electrical stimulation mapping (ESM). The number of electrodes which induced ESM hand/arm motor responses in each subject is given in Table 1.
Time-Domain LFC Analysis
Previous studies (Mehring et al. 2003; Schalk et al. 2007; Pistohl et al. 2008; Waldert et al. 2008; Ball et al. 2009; Hammer et al. 2013) consistently reported the best motor decoding results from the time-domain LFC in different neuronal population signals (LFP, ECoG, EEG, and MEG). To derive the LFC in the present study, the iEEG data were high-pass filtered (sixth order Butterworth with 0.1-Hz cut-off frequency and zero-phase shift) to remove offsets and slow drifts. Amplitudes were normalized to the SD of each game session. To extract the LFC (Fig. 1D), a low-pass filter was used (eighth order Butterworth with 4.0-Hz cut-off frequency and zero-phase shift) (Waldert et al. 2008).
Spectral Analysis
As in many previous iEEG motor decoding studies (e.g., Rickert et al. 2005), we used the short time Fourier transformation (STFT) for time–frequency decomposition. The time-resolved power spectral density, P(f,t), was computed in 10-ms steps from the common average re-referenced iEEG data. In order to better estimate the power modulation at different frequencies, the STFT Hanning window size w was adjusted based on the frequency band f of interest as follows: w = 2 s for 0 Hz ≤ f< 4 Hz, w = 1 s for 4 Hz ≤ f< 8 Hz, w = 0.5 s for 8 Hz ≤ f< 30 Hz, w = 0.25 s for 30 Hz ≤ f< 55 Hz, w = 0.125 s for 55 Hz ≤ f< 1000 Hz, where f is the frequency of a band of interest. The relative power, RP(f,t), was normalized to the mean (denoted here by 〈…〉) power of each STFT frequency bin over time in each game session (RP(f,t) = P(f,t)/<P(f,t)>t). This procedure of spectral whitening avoids dominance of the power in lower frequencies, as the lower frequencies in neuronal population signals have higher magnitudes due to the 1/f power decay (Miller et al. 2009). The frequency band relative power, FBRP(t), was averaged over a defined frequency band (f1 → f2): FBRP(t) = <RP(f,t)>[f1,f2], log-transformed, and normalized to zero mean and unit SD.
We examined time-resolved spectral power modulations of iEEG frequency bands (Fig. 1E) up to approximately two-fifth of the sampling rate (Nunez and Srinivasan 2006). The lower frequency bands (<50 Hz) were defined in the traditional way (Sauseng and Klimesch 2008), namely: δ (0–4 Hz), θ (4–8 Hz), α (8–12 Hz), β (13–30 Hz), low γ (30–45 Hz). The higher frequencies (>50 Hz) were divided into 3 broad frequency bands: high γ (55–300 Hz), “high-frequency band 1” (HFB 1) in the range 300–600 Hz, and “high-frequency band 2” (HFB 2) between 600–1000 Hz. Note that which of the highest frequency bands (>300 Hz) could be analyzed depended on the sampling rate in each subject. Thus, for example, only data of 4 subjects (S1–S3 and S5, c.f. Table 1) could be analyzed in HFB 2 (600–1000 Hz). The correlation matrix of the different investigated iEEG signal features showed low, but positive correlations among the 3 high-frequency bands “high γ”, “HFB 1”, and “HFB 2” (Fig. 1F). The positive sign of the correlations may suggest that these high-frequency bands share a common physiological origin (cf. Miller et al. 2014). On the other hand, the low values of these correlations may be a consequence of high-frequency (amplifier) noise. The highest correlations were observed between the α and β bands (CC = 0.35 ± 0.11, mean ± SD over all subjects).
Statistical Analysis Using Surrogate iEEG Datasets
To assess statistical significance, surrogate datasets were constructed by the approach described by Pistohl et al. (2008), that is, by computing the Fourier transform (FT) of the raw iEEG time-series in each recording session, randomly shuffling the phases of all complex-valued FT coefficients (different shuffling for different sessions), while preserving their magnitudes, and transforming the shuffled data back to time-series by inverse FT (Faes et al. 2004). These surrogate iEEG datasets have identical power spectra as the original signals and hence according to the Wiener–Khinchin theorem also preserve their autocorrelations (Khinchin 1934), but their time-courses are not systematically correlated with the original iEEG datasets and hence also with the behavioral task. The surrogate iEEG datasets were used to assess the significance of decoding accuracy as well as the tuning strength (see below).
Decoding Model
Multiple linear regression (MLR) (Georgopoulos et al. 2005; Bradberry et al. 2010; Hammer et al. 2013) was used for decoding kinematic variables with the following prediction step:
where ŷ(t) is the predicted (kinematic) variable at time t, xch(t + τ) is the predicting iEEG feature vector extracted from selected channels ch with a certain time offset τ. τ< 0 implies that the iEEG feature vector precedes movement execution and can therefore be used to truly predict the decoded movement variable, as would be required in real-time applications. βch(τ) are the regression coefficients for an MLR model built with the time offset τ.
The predictors, xch(t), were either the STFT frequency band power or the LFC of the iEEG signal. To allow for an offset in the prediction model, each feature vector x included an additional value of x0 = 1 followed by samples of processed iEEG signal from selected channels ch (e.g., channels that induced hand/arm motor response upon ESM). The predicted variable, ŷ(t), was the x-component and in case of the 2-D task also the y-component of the vector kinematic variables: that is, direction, position, velocity, and acceleration, as well as the scalar kinematic variables: speed (the magnitude of the velocity vector) and the magnitude of the acceleration.
Accuracy of Prediction Assessment
The decoding performance of the MLR model was assessed by cross-validation. The recorded datasets were split into N non-overlapping, continuous movement parts (so-called “validation folds,” each lasting 30 s), where N − 1 of these folds were used to build the MLR decoding model (training set) and the remaining validation fold was predicted (test set) and evaluated for goodness of prediction by the correlation coefficient (CC) between the actual and the predicted movement. This was repeated N times, so that each movement validation fold was tested exactly once. The result was a mean CC over all test sets for each subject, signal feature, and time offset τ. The significance of decoding (e.g., comparing 2 different signal features, or comparing real and surrogate datasets) was assessed by the Wilcoxon rank sum test between the CCs of all movement validation folds. In the case of multiple testing over different parameters (e.g., signal features, subjects), the P-values of the Wilcoxon rank sum test were submitted to false discovery rate (FDR) correction (Benjamini and Hochberg 1995).
Velocity Tuning Analysis
To better understand the predominance of speed in our decoding results (see Results), we further sought to clarify the relationship between directional and speed representation in iEEG signal features. Both direction and speed are naturally contained in the velocity vector, and therefore any prominent representation of either speed or direction should become apparent by investigating the iEEG as a function of movement velocity. Thus, the characterization of velocity representation (or tuning) in iEEG was our next step. To this end, the distribution of velocity v(t), was divided into several bins, the sizes of which were adjusted such that each bin contained an approximately equal amount of velocity samples (Golub et al. 2014). In the 1-D task, where v(t) = vx(t), velocity was divided into Nx = 15 bins. In the 2-D task, the velocity vector v(t) was represented in polar coordinates better reflecting its distribution (Paninski et al. 2004), v(t) = [s(t), φ(t)], where s(t) is speed and φ(t) direction of movement. The v(t) was binned into Ns= 4 bins (for the radial component) and Nφ = 8 (for the angular component). For a selected velocity bin, all samples of the velocity falling into this “bin” were detected. From these detected samples, corresponding iEEG feature samples with a certain time offset τ (Fig. 1D) were extracted. The final tuning value was calculated as the mean of all such extracted iEEG signal features. This procedure was repeated for all velocity bins v, time offsets τ and iEEG channels ch.
After processing a dataset of particular iEEG features (frequency band power or LFC) for each subject, the result was a multidimensional tuning array of [v, τ, ch], a subset of which in the case of ECoG grids could be plotted on the brain surface. The values of the ECoG grid channels ch (at a certain time offset τ and a selected velocity bin v) were topographically ordered, color-coded, and—for easier orientation—interpolated (see Results). Another important subset of the tuning array [v, τ, ch] in our analysis was the so-called “velocity tuning response”, consisting of all velocity bins v (at a particular time offset τ and iEEG channel ch). The velocity tuning response retained the mean modulation of the processed data given the (binned) velocity and played a crucial role in deciding if the modulation was statistically significant or not (see the following paragraph).
Significance of Tuning
We assessed the statistical significance of tuning based on its signal-to-noise ratio (SNR) as previously done in LFP (Rickert et al. 2005). The SNR was computed as the variance of the “tuning curve” divided by the mean “sample-by-sample” fluctuations, where the “tuning curve” was represented by the velocity tuning response as defined above, while “samples” corresponded to the samples from which the values of velocity tuning response were computed. The SNR(τ, ch) was computed for each time offset τ and channel ch separately.
To test for significant deviations of the SNR values from the null SNR distribution, 2.000 surrogate datasets from the iEEG recordings of each subject (as described above) were used. The P-values (for each τ and ch) were computed as the probability of the SNR values from the 2.000 surrogate datasets being equal to or higher than the SNR from the real iEEG. P-values were submitted to FDR correction (q-level = 0.001) for multiple testing (e.g., over τ and ch).
Comparison of Velocity- and Speed-Tuning Strength
Secondly, we also classified the significant velocity tuning responses as “velocity-type”, “speed-type”, or “undefined”. This classification allowed us to compute and compare the tuning profiles for these classes, and particularly how close these profiles were to the profiles to be expected in the case of perfect speed and velocity tuning (Fig. 2). The classification rule that we applied was that if the fit of a significant velocity tuning response to either a “perfect” velocity or to a “perfect” speed-tuning profile had a coefficient of determination R2 > 0.5, then it was assigned as velocity-type or speed-type, respectively. Else, it was labeled as “undefined.” The “perfect” tuning profiles were obtained from a perfectly velocity-tuned or speed-tuned variable, for example, by submitting the x-velocity or speed themselves—instead of iEEG features—to the tuning analysis. Thus, in the 1-D task, the “perfect” velocity-type tuning profile was the (scaled) identity function of the velocity bins (Fig. 2A), while the “perfect” speed-type tuning profile was the (scaled) absolute value function (Fig. 2B). Similarly, in the 2-D case, the “perfect” velocity-type tuning profile in polar coordinates (Fig. 2C) corresponded to a cosine function for direction and linear speed scaling (cf. Paninski et al. 2004). Therefore, the 2-D velocity-type tuning had a maximum response for a certain preferred direction (PD) and a minimum for the opposite (anti-PD) direction, resembling the well-known directional cosine tuning (Georgopoulos et al. 1982). Analogically, the “perfect” speed-type tuning in polar coordinates was a radially symmetrical linear increase in polar coordinates (Fig. 2D). As the PD of the 2-D velocity-type tuning was a priori unknown, we computed the R2 between the investigated velocity tuning response and all possible PD orientations (i.e., the 8 directional bins as shown in Fig. 2) of the “perfect” velocity-type tuning profile and considered only the maximum R2 value for subsequent classification.
Velocity Tuning Model as a Function of Neuronal Population Size
Our goal was to find out how our empirical results of a predominance of speed over velocity in the iEEG signal could possibly be reconciled with the fact that on the SUA level, velocity tuning has been shown to be dominating over speed tuning. Therefore, we constructed a numerical model of neuronal population activity based on previously established experimental evidence from SUA discharges in motor cortex. Such a model is by no means aspiring to describe realistic biophysical mechanisms underlying the motor cortex activity. Rather, the model was reduced to the necessary components to allow for an intuitive insight into how the tuning properties of neuronal population activity might be fundamentally different than those of the individual neurons comprising this activity, following the model by Waldert et al. on population cosine tuning. Adapting this approach, we investigated the neuronal population firing rate computed as the sum of the instantaneous discharges of individual neurons (Waldert et al. 2009). Therefore,
where P is the neuronal population activity, N is the number of underlying neurons, rn is the discharge rate of the n-th neuron at time t.
The firing rate of the neuronal population was modeled as a scalar sum of the N individual, underlying neurons. It might be worth pointing out, to avoid possible confusion, that this constitutes a difference to the summation applied in the population vector algorithm for SUA-based BMI control (Georgopoulos et al. 1986), where the firing rates of individual neurons serve as weights in the vectorial sum along the axis of their estimated PDs.
Although there has been an extensive debate about which, if any, movement-related parameters are “represented” by SUA of motor cortex in a functional sense (Mussa-Ivaldi 1988; Fetz 1992; Todorov 2000; Churchland and Shenoy 2007; Graziano 2011), it is commonly accepted that many task- and movement-related parameters are at least to some degree correlated with the SUA of motor cortex, including, for example, movement direction (Georgopoulos et al. 1982), velocity (Ashe and Georgopoulos 1994), position (Kettner et al. 1988), acceleration (Flament and Hore 1988), force (Evarts 1968), or distance to target (Fu et al. 1995). We based our model on that proposed by Moran and Schwartz (1999), because it explicitly considers 2 parameters, which together unambiguously define continuous movement velocity, namely, direction and speed. Thus, the model of motor-cortical activity (following eq. 1 in Moran and Schwartz 1999) had the following form:
The discharge rate rn(t) of n-th neuron is thus a function of movement speed s(t) and movement direction φ(t). It consists of 3 terms: (1) a nondirectional component of linearly tuned speed scaled by factor Sn (reflecting a strength of the speed tuning), (2) a directional component of cosine tuned velocity scaled by Vn (reflecting a strength of velocity tuning) and with a preferred direction (PD) of discharge αn, and (3) a task-unrelated noise term ϵn(σ, t), with the noise drawn from a normal distribution of width σ.
Because of the summation in neuronal population activity PN, we assumed, without the loss of generalization, same values of Sn and Vn for all neurons (Sn = S, and Vn = V). We set PDs randomly in the interval [−π, π], as several studies indicate that the spatial arrangement of PDs in motor cortex on the macro-scale level (order of millimeters) is approximately random (Amirikian and Georgopoulos 2003; Ben-Shaul et al. 2003). There is considerable complexity in movement-related SUA in motor cortex deviating from the “canonical” Moran and Schwartz model (Sergio et al. 2005; Churchland and Shenoy 2007). As such deviations can act as noise with respect to speed and directional tuning terms in our model, we also investigated various levels of such noise. Thus, the task-unrelated noise term ϵn(t, σ) for each neuron was drawn from a normal distribution of width σ in the range from 0.01 (small level of noise) to 10 (larger level of noise). We computed R2 values between the ensemble nondirectional response and movement speed, as described in Moran and Schwartz (1999) or Churchland and Shenoy (2007). This allowed us to verify the predictions of our model with a certain parameter settings (tuning strengths of velocity, speed, and noise level) to their experimental observations of many SUAs recorded during center-out reaching tasks in monkey motor cortex. For a discussion of other assumptions and limitations for a similar model of motor-cortical tuning properties see Waldert et al. (2009).
We computed firing rates of populations of variable sizes N during conditions corresponding to a center-out reaching task (Georgopoulos et al. 1982; Golub et al. 2014). In particular, we investigated 2-D movements to 8 circular equidistant directions and with 6 different levels of speed (1%, 20%, 40%, 60%, 80%, or 100% of maximum speed). One simulation of N neurons, during which the PDs remained fixed, included 300 trials. The neuronal population size N was varied on the log-scale from 1 (corresponding to SUA) to 106 neurons. The simulations were repeated 100 times (including re-shuffling of PDs for each simulation). Similar to the real iEEG data, the SNR of direction and speed tuning, defined as a variance of class means over trial-by-trial variance (Rickert et al. 2005), was computed as an average over all simulations.
We also investigated the “reversal point” where speed SNR became larger than directional SNR as a function of the different relevant parameters of our model. The reversal point was defined as the minimum number of neurons, where SNRspeed was significantly greater than SNRdirection (Wilcoxon rank sum test, P < 0.01, FDR corrected for multiple testing over different neuronal population sizes). The population size N was varied from 1–10 in each order of magnitude ranging from units up to one million (i.e., N = 1, 2, 3, …, 10, 20, 30, …, 100, 200, 300, …, 1 000 000). The significance was tested over the different repetitions of each simulation with given parameter settings. The model had 3 different parameters: strength of the velocity tuning V, strength of the speed tuning S, and level of noise σ. We set V = 1 and varied S, hence exploring different ratios of velocity-to-speed tuning. Furthermore, we explored the impact of different values of σ.
Results
Speed as the Overall Best-Decodable Kinematic Variable Across iEEG Features
First, we systematically compared the decodability of the kinematic variables direction, position, velocity, acceleration, speed, and the magnitude of acceleration from iEEG power modulations averaged across predefined standard frequency bands, such as the δ (0–4 Hz), θ (4- Hz), α (8–12 Hz), β (13–30 Hz), low γ (30–45 Hz), high γ (55–300 Hz), and—if the sampling rate allowed—even high-frequency bands HFB 1 (300–600 Hz) and HFB 2 (600–1000 Hz), as well as from the LFC obtained by low-pass filtering (0–4 Hz) of the time-domain signal. To ensure comparability of the decoding results, we applied the same decoding algorithm (multiple linear regression) and the same feature vector template of a fixed length to extract the iEEG signal components for each subject (see Materials and Methods for further details). In this analysis, we used only iEEG feature samples at the time of movement execution (i.e., time offset τ = 0 s), and from motor-cortical channels (i.e., with hand/arm motor response after ESM). Similar results, equally supporting the conclusions of our study, were also obtained with a causal time offset (iEEG leading movement execution, τ = −100 ms).
An example in Figure 3A illustrates a 9-s time-segment of both real movement speed (blue curve) and the decoded speed (red curve) from high γ (55–300 Hz) power modulations in subject S2, together with the CC between the real and predicted speed. The grand average (mean ± SEM over all 9 subjects) is shown in Figure 3B. The statistical significance of decoding results was tested between real iEEG data and the surrogate datasets (Wilcoxon rank sum test at 0.01 significance level, FDR corrected for multiple testing).
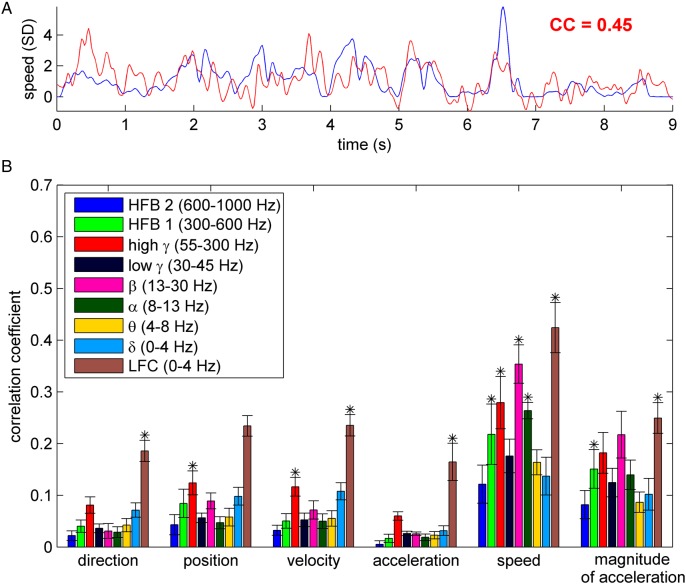
Figure 3.
Decoding of kinematic variables. (A) An example of the time course of the decoded (red) and the real (blue) movement speed. The goodness of prediction was evaluated by means of the correlation coefficient (CC). In this example, speed was predicted from high γ (55–300 Hz) power modulation in subject S2. (B) Kinematic variables (direction, position, velocity, acceleration, speed, and magnitude of acceleration) decoded from different frequency bands, using only channels with hand/arm motor response upon ESM. Decoding accuracy (DA) was evaluated by CC (y-axis) between the real and predicted kinematic variable (here shown grand mean ± SEM over all 9 subjects). The stars indicate significant DA in all 9 subjects (Wilcoxon rank sum test at 0.01 significance level, FDR corrected). Decoding movement speed from the LFC, high γ and β bands yielded the highest DA of all movement parameters/signal components.
A striking observation was that DA was larger for the nondirectional movement speed (i.e., the magnitude of velocity) than for direction or velocity in all frequency bands investigated. Also the DA of the magnitude of acceleration was more than 3-fold larger than its directional counterpart (i.e., acceleration itself) in nearly all frequency features (Fig. 3B). The LFC (0–4 Hz) and the high γ power (55–300 Hz) offered the best decoding of direction, position and velocity, while the lower frequency power modulations were not informative (e.g., α and β bands). These results are consistent with previous reports of decoding kinematic variables both in the “event-related” (e.g., center-out) as well as in the continuous tasks (Rickert et al. 2005; Pistohl et al. 2008; Ball et al. 2009). The overall best-decodable kinematic parameter was speed from time-domain LFC (0–4 Hz), and power modulations of the β (13–30 Hz) and high γ (55–300 Hz) bands.
Kinematic variables may be correlated, depending on the task design. In our case, the most correlated variables were velocity with direction (CC = 0.59 ± 0.15, mean ± SD over subjects), and also speed with magnitude of acceleration (CC = 0.41 ± 0.05). Therefore, it was not possible to unambiguously separate their representation. Importantly, speed was not correlated with either the x- or y-components of velocity (CC = 0.02 ± 0.01) or direction (CC = 0.00 ± 0.02).
Movement Speed is Decodable from iEEG Signals up to 600–1000 Hz
To further delineate the iEEG signals informative on movement speed, we performed a decoding analysis that was resolved both in time and frequency (time referring to the offset between movement execution and the iEEG signal used for decoding, see Fig. 1). In the lower frequency range (<50 Hz), we divided the spectrum into the traditional frequency bands as indicated in Figure 3B, while in higher frequencies (>50 Hz), we examined bands of 30 Hz bandwidth, up to 1000 Hz. We show the results of subjects S1–S3 (see Table 1), as those were the recordings with the largest (8 × 8) ECoG grids (Fig. 4A) and highest sampling rates, which enabled us to address the question of speed representation up to 1 kHz. The other subjects, in those frequency bands that the sampling rate allowed to investigate, showed similar results. Overall, movement velocity was not well decodable from any band power feature (Fig. 4B), with the exception of a certain amount of information in the high γ (55–300 Hz) and δ (0–4 Hz) bands, consistent with previous reports (Pistohl et al. 2008; Ball et al. 2009). Speed, on the other hand, was much better decodable and had a clear peak of decoding in the β band (13–30 Hz) and a second, broader peak in higher frequencies, most prominent in the high γ band (55–300 Hz), even reaching to the frequency range of 600–1000 Hz (Fig. 4C).
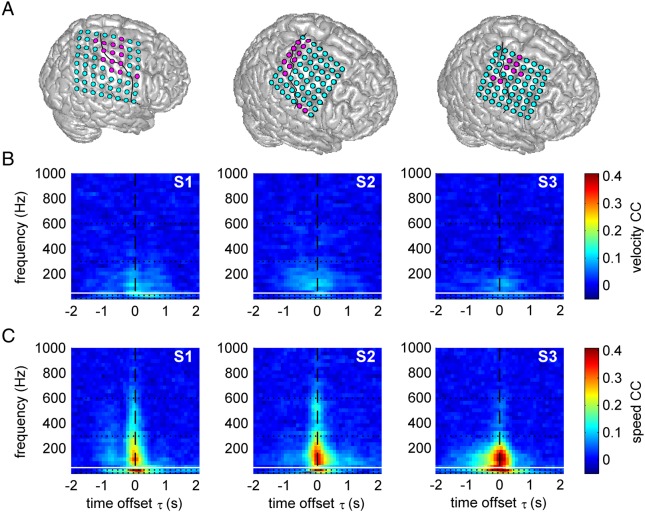
Figure 4.
Time–frequency resolved decoding of velocity and speed from ECoG power modulations. (A) Position of ECoG grids in S1–S3. Magenta: electrodes with hand-arm motor response upon ESM used for decoding; solid black line: central sulcus. Results for movement velocity (B) and speed (C), both from the 1-D task. Values refer to the mean CC over all test sets. The horizontal white line at 50 Hz indicates the frequency position of line noise. Speed was better decodable than velocity, up to very high frequencies (>600 Hz).
Spatially Resolved Decoding of Velocity and Speed
Besides the high temporal resolution, another advantage of iEEG is its high spatial accuracy that allowed us to examine the exact cortical sources of speed- and velocity-related activity in the human cortex. To obtain the highest possible spatial resolution, we used the iEEG data from the individual iEEG channels for decoding (all results for time offset τ = 0 s). This allowed creating decoding maps of the mean CC values of the predictions (cf. Fig. 4A). In all frequency bands these maps had plausible spatial topologies, with the most pronounced effects in the hand/arm area of the motor cortex (Fig. 5). Higher CCs for speed than for velocity also dominated the spatially resolved results (see β and high γ results of S3 for a particularly clear effect).
Figure 5.
Spatially resolved decoding of velocity and speed. For the region covered by the ECoG grids in S1–S3, velocity and speed decoding results are shown in the left and right columns, respectively. Gray lines: central sulcus. First row: letters indicate electrical stimulation responses (black—motor response, gray—sensory response; H—hand, A—arm, O—orofacial, E—eyes, L—leg, S—shoulder, N—neck); remaining rows: only hand/arm motor channels.
Intriguingly, for speed, there was a spatially very focal DA distribution observed in the HFB 2 (600–1000 Hz), with its spatial maximum in the hand/arm area of the premotor cortex. Robust speed decoding was also prominent in the LFC, however, the speed decoding maps based on the LFC had generally different and more complex spatial distributions than those based on high γ or β power modulations. Delineating the sources of movement-related information in the LFC and how they differ from those of power modulations in higher frequencies will require further investigation beyond the present study.
Speed-Related iEEG Power Changes
We further investigated speed-related iEEG power changes in nonoverlapping, consecutive frequency bands of 10-Hz width covering the entire frequency spectrum up to 1000 Hz (Fig. 6). As described in Materials and Methods (see Velocity tuning analysis), movement velocity was normalized to unit SD and its absolute value (corresponding to movement speed) was binned into 7 discrete bins. In each frequency band, the average power modulation (computed as mean over all motor channels of subjects S1–S3) of the fastest speed (>1.6 SD) was compared with that of the slowest speed (<0.1 SD). The significance of the power modulation was compared with the results obtained from the surrogate iEEG datasets (see Materials and Methods). There was a clear power decrease in low frequencies (<50 Hz) and a power increase in high frequencies (>50 Hz) for the fastest speed bin, significant even in the very high-frequency band, up to 1000 Hz.
Figure 6.
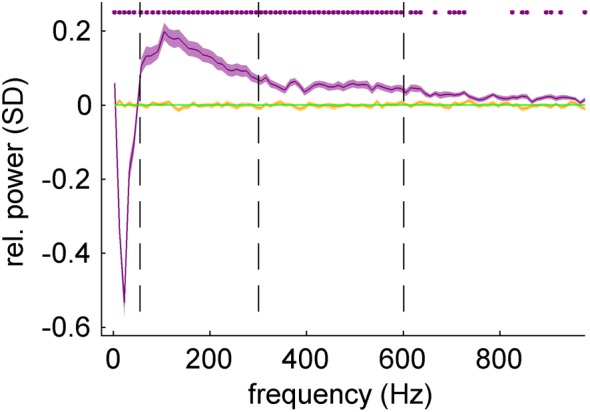
Speed-related iEEG power changes in motor cortex. The frequency spectrum of iEEG was divided into nonoverlapping bands of 10-Hz width. For each frequency band, the iEEG band power corresponding to the fastest speed (purple curve) was computed with respect to the slowest speed (green line). The slowest speed was thus taken as a reference point and was equal to zero. Statistical significance (purple stars) of the power modulation (FDR corrected, q-level = 0.05) was tested against the results obtained from surrogate iEEG datasets (orange curve). There was a clear relative power decrease in lower frequencies (<50 Hz) and a relative power increase in the higher frequencies (>50 Hz) statistically significant (P < 0.05, FDR corrected) even in the highest frequencies (up to 1 kHz).
The power increase in the high frequencies was most pronounced in the high γ band (peak in the frequency band 105–115 Hz), and attenuated in even higher frequencies. This could be accounted for by the amplifier noise (we observed the increasing noise effect in the power spectral density plot around 300 Hz, where the 1/f power decay became less steep). A similar frequency profile without any significant difference (P > 0.05, FDR corrected for multiple testing over different frequency bands) was obtained from the Hilbert transformation of band-pass filtered data (10th order Butterworth filter with zero-phase shift).
Cortical Activation During the 1-D Motor Task
The high DA of movement speed from nearly all iEEG signal features was quite surprising, especially when contrasted with the rather low DA of velocity, which was reported to play a dominant role on the level of SUA (Moran and Schwartz 1999; Golub et al. 2014). To clarify the representation of the directional and speed components of velocity, we analyzed the iEEG features as a function of movement velocity (velocity tuning).
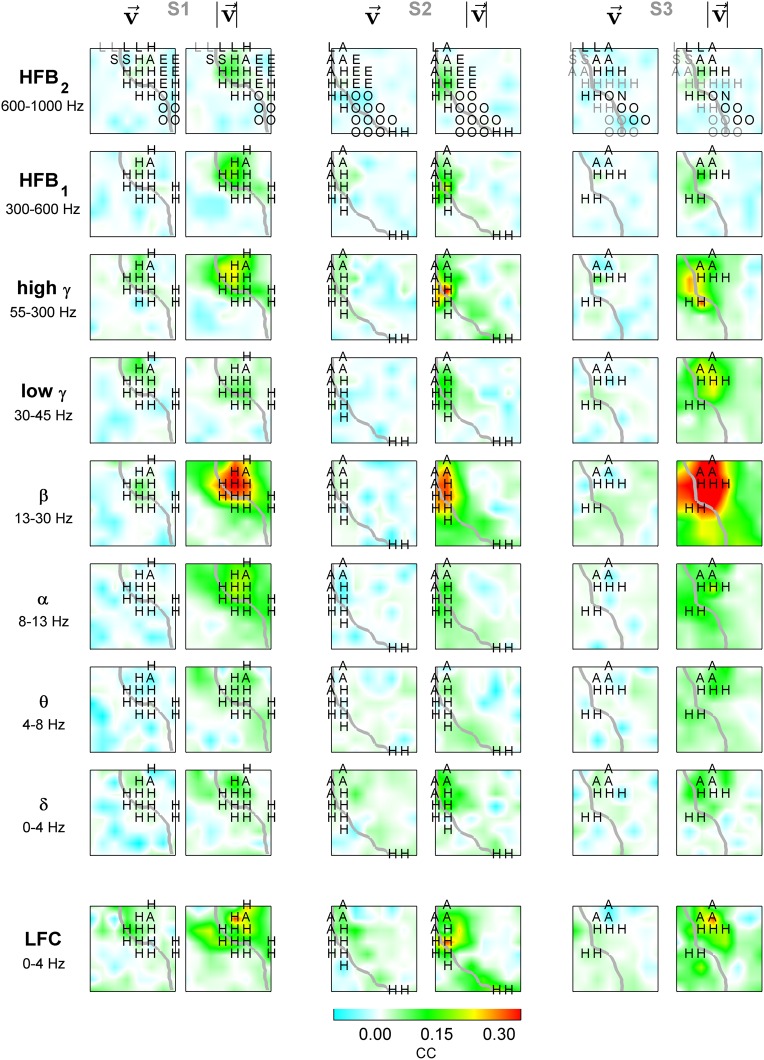
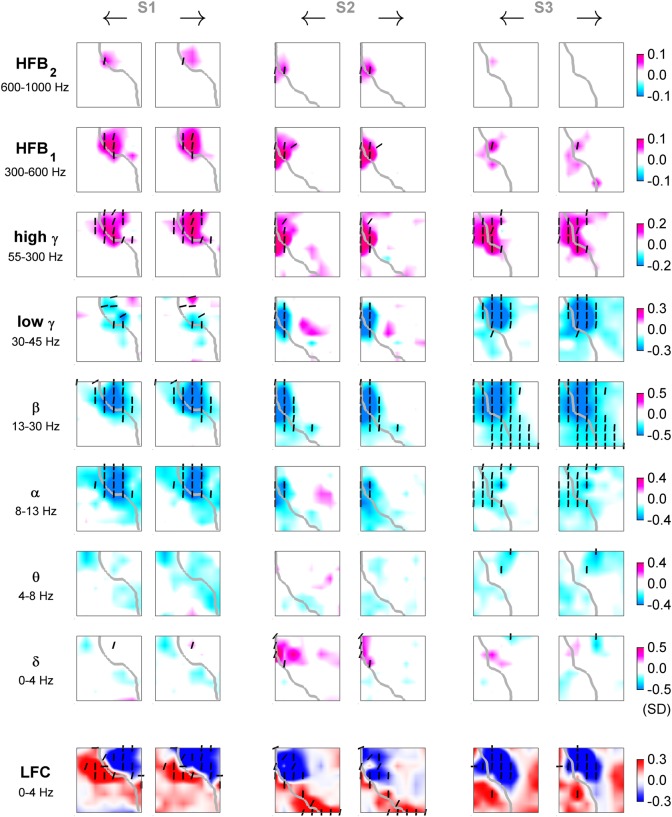
From the velocity tuning analysis, we observed a movement-related increase of iEEG power in high frequencies (>50 Hz) accompanied by a simultaneous decrease of power in lower frequencies (<50 Hz). The power increase was significant in subjects S1 and S2 even in the highest frequency band (600–1000 Hz). The LFC formed spatially more complex, dipole-like patterns (Fig. 7). The activations (taken relative to zero speed and simultaneous to movement execution) were spatially focal in high frequencies (>50 Hz), most prominent in the high γ band, and broader in lower frequencies (<50 Hz), most prominent in the β band. Moreover, these activations had a large degree of overlap with respect to movement direction and most of the significantly tuned channels were close to the “perfect” speed-tuning function (cf. vertical orientation of dashes in Fig. 7). Such direction-unspecific activations were complementary to the high DA of speed (cf. Fig. 5). As a complement to the above single-channel decoding analysis (Fig. 5), we plotted the average power modulation (or LFC activation) as the ECoG grid tuning maps for the fastest left and right velocity bins at the time offset τ = 0 s (Fig. 7). For easier comparison, the slowest, “zero-velocity” bin was taken as a reference point (i.e., by definition, the frequency band power = 0 and the LFC activation = 0 for all channels in the “zero-velocity” bin).
Figure 7.
ECoG relative power (or LFC) for fastest movements to opposite directions: 1-D task. Tuning for fastest left (odd columns) and right (even columns) movements of subjects S1–S3 in different frequency bands (rows) and time domain LFC (bottom row). Each panel represents an interpolated ECoG grid with delineated central sulcus (gray). Significantly tuned ECoG channels (black dashes) were compared (by R2) to the “perfect” velocity- and speed-type tuning profiles. The angle of the dashes (defined as arctan ) indicates the degree of speed-type (vertical orientation) or velocity-type (horizontal orientation) tuning. Increase of power in high-frequency bands (>50 Hz) was accompanied by a simultaneous power decrease in lower frequencies (<50 Hz). LFC showed patterns of spatially complex, dipole-like cortical activations.
iEEG Signal Features as Functions of Movement Velocity
The tuning profile over all velocity bins of the significantly tuned speed-type channels in the different frequency bands of iEEG (e.g., in high γ, β bands, or LFC) closely resembled the absolute value function or its negative sign version (Fig. 8B). In the previous analysis (Fig. 7), we saw the topographic ECoG feature modulations in different frequency bands, but only for the 2 fastest left and right velocity bins, and only at a single time offset τ = 0 s (with respect to movement execution). Here, we investigated the tuning of all significantly tuned iEEG features (frequency band power or LFC of channels at different time offsets sampled in steps of 100 ms) as a function of all velocity bins (see Materials and Methods).
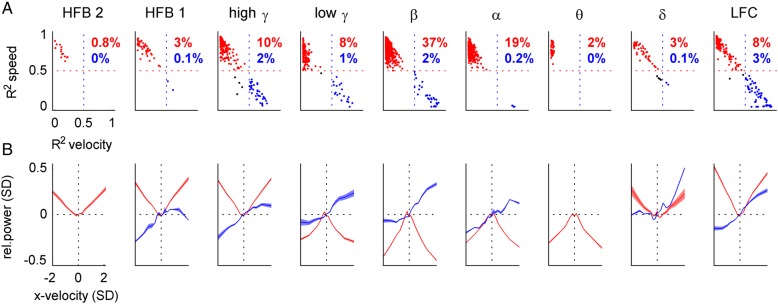
Figure 8.
Velocity and speed tuning profiles of iEEG features. We investigated velocity tuning functions of the iEEG features (columns, indicated by title) from all recorded channels, sampled in steps of 100 ms at different time offsets τ with respect to movement execution. (A) Scatter plots of R2 values of the correlation of iEEG features with the “perfect” velocity-type (x-axis) and speed-type (y-axis) tuning profiles. If the speed or velocity R2 was >0.5, an instance was classified as speed-type (red) or velocity-type (blue), respectively (percentages of these instances in red and blue). For example, in the β band, 37% of all (n = 348) significantly tuned channels at different time offsets were classified as speed-type. (B) Velocity tuning profiles (mean ± SEM) of iEEG features classified as speed-type (red) or velocity-type (blue). The power modulation was taken relative to that of zero velocity (dotted horizontal black line). Movement velocity was normalized to unit SD, direction of movement is indicated by the sign of velocity (positive = right, negative = left). The power in the higher frequency bands (>50 Hz) closely resembled the “perfect” speed tuning, linearly increasing with magnitude of velocity, irrespective of its direction.
First, we compared the tuning functions of all significantly tuned iEEG channels fitted to the “perfect” velocity-type (Fig. 2A) or speed-type (Fig. 2B) profiles. Scatter plots of the against are shown in Figure 8A. If the (or ), then such a significantly tuned function was classified as speed-type (Fig. 8A, red dots) or velocity-type (Fig. 8A, blue dots), respectively.
Next, we plotted the speed-type or velocity-type tuning functions (mean ± SEM) for all velocity bins (Fig. 8B). The average power modulation in high frequencies (>50 Hz) of the speed-type channels closely matched the absolute value function of velocity (Fig. 8B, red curves), while the low frequency (<50 Hz) power modulations were similar to the negatively signed absolute value function of velocity.
Much fewer channels were classified as velocity-type than as speed-type. The largest group (3%) of tuning functions labeled as velocity-type tuning of all examined iEEG features was found in the LFC (Fig. 8B, right panel, blue), consistent with the high DA of velocity from this iEEG signal feature. Note that for a meaningful average, the inverse in sign for the tuning functions of some channels was necessary (by a factor of −1), thereby enforcing positive LFC activation for the movements to the right.
Cortical Activation During the 2-D Motor Task
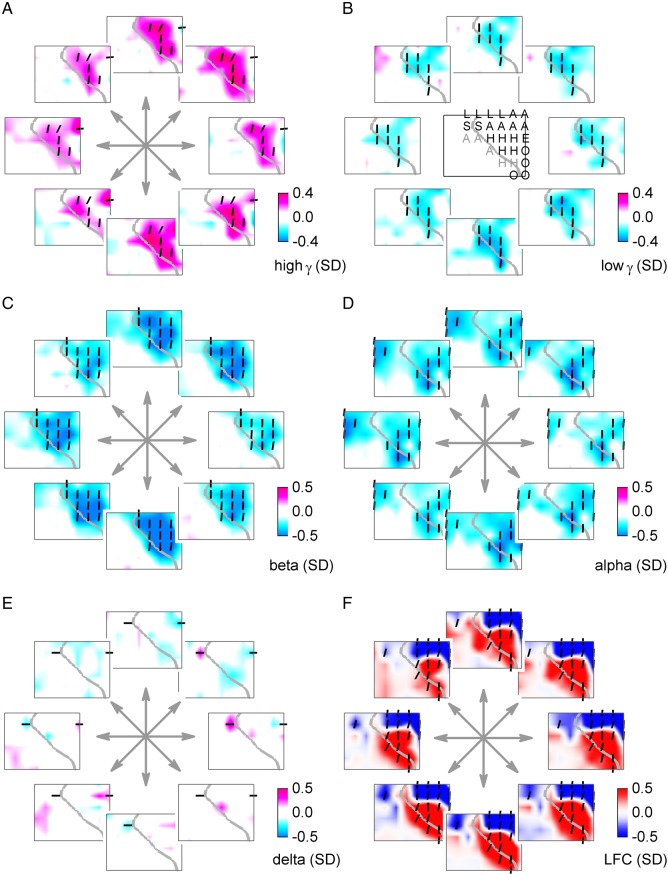
The increase of power in high γ band (55–300 Hz) in the hand/arm area of the motor cortex and the simultaneous decrease in lower frequencies (<50 Hz), most pronounced in the β (13–30 Hz) band, was apparent also in the 2-D target pursuit task (Fig. 9). Due to the lower sampling frequencies in these ECoG recordings, they could only be analyzed up to the high γ band. Most of the significantly tuned channels with a power-increase were most similar to the speed-type tuning (Fig. 9, vertical bars). No clear, consistent modulation was found in the δ power (Fig. 9E), in contrast to the time-domain LFC signal (Fig. 9F), which represented the same frequency band, but retained phase information. The LFC tuning maps revealed—similarly as in the 1-D task—larger, dipole-like patterns of coherent and ordered cortical activations. Thus, the observations of tuning analysis in the 2-D target pursuit task were very consistent with those of the 1-D task (Fig. 7).
Figure 9.
ECoG relative power (or LFC) for fastest movements to different directions: 2-D task. Velocity tuning of (A) high γ (55–300 Hz), and (B) low γ (30–45 Hz). (C) β (13–30 Hz), (D) α (8–12 Hz), (E) δ (0–4 Hz) power modulations, and (F) the time-domain LFC (0–4 Hz). Movement directions are indicated by arrows. The ECoG grid schema of subject S7 with ESM labels (same annotation as in Fig. 5) is shown in the middle of B. Significantly tuned ECoG channels (P < 0.001) were compared (by R2) with the “perfect” 2-D velocity- and speed-type tuning profiles. The angle of the dashes (defined as arctan ) indicates the degree of speed-type (vertical orientation) or velocity-type (horizontal orientation) tuning. The ECoG power modulation is relative to that of zero velocity. Consistent with the 1-D car-driving task, relative power in high-frequency bands (>50 Hz) increased irrespective of movement direction, accompanied by a simultaneous power decrease in lower frequencies (<50 Hz), in the 2-D target pursuit task as well. Similarly, the LFC showed large-scale, dipole-like activation patterns.
Numerical Modeling of Speed- and Velocity-Related Neuronal Population Activity
Astonishingly, a simple numerical model of the firing rate in large neuronal populations (see Materials and Methods) predicted the predominance of nondirectional, speed tuning over that of directional tuning—a situation that is completely reversed to that on the level of individual motor neurons (Moran and Schwartz 1999; Golub et al. 2014). Moreover, the model predicted an increase of spiking rate during high-speed movements. The single-neuron discharges were based on the velocity-tuning model proposed by Moran and Schwartz (1999), with a directionally independent, linear speed tuning (scaled by factor S) and a velocity cosine tuning (scaled by factor V). Thus, movement speed modulated the discharge activity both irrespective of movement direction and as a gain factor to movement direction.
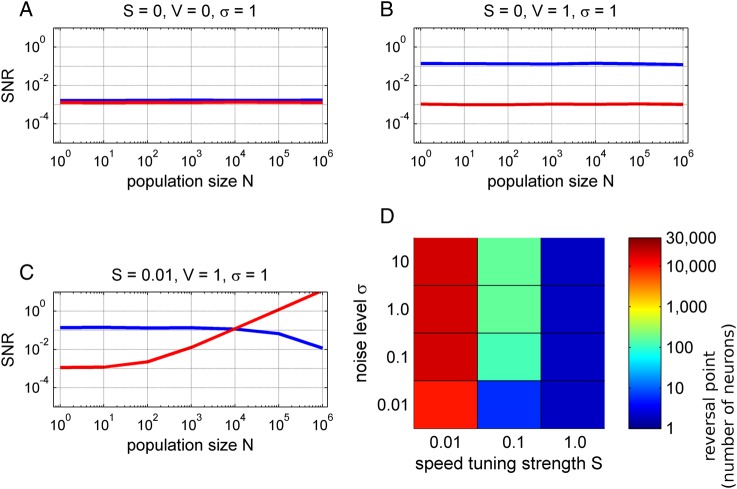
We assessed the SNR of the directional and speed tuning as a function of the neuronal population size in 3 different models. First, we wanted to indicate a “noisy, baseline level” of a model without any directional or speed-related information (Fig. 10A). The SNR of neither speed nor direction depended on the population size N. Next, we considered only the velocity tuning without the directionally independent speed term (i.e., setting S = 0). The speed tuning remained at the baseline level (Fig. 10B, red), but the directional tuning was significantly increased and, importantly, constant for different population sizes (Fig. 10B, blue) as analytically derived by Waldert et al. (2009). Although such a result might appear as somewhat counter-intuitive, the sum of N cosines with random phases (which was one of the assumptions of the model) will again result in a cosine function with a random phase and an amplitude of N1/2. The Gaussian noise term of the population ensemble will also grow as a N1/2, thus yielding a constant SNR, independent of the population size (Waldert et al. 2009).
Figure 10.
Simulation of neuronal population activity in motor cortex. We simulated a 2-D, center-out task with different movement speeds and directions. The population activity was modeled as a sum of N motor-cortical neurons, the discharges of which consisted of (1) a linear speed tuning (scaled by factor S), (2) a velocity cosine tuning (scaled by factor V) with a random PD and (3) a Gaussian noise term. We investigated the SNR (y-axis) of directional tuning (blue) and speed tuning (red) as a function of the neuronal population size N (x-axis). (A) Noise model indicated a baseline SNR in absence of any speed or velocity tuning. (B) Velocity tuning model. The SNR of directional tuning was independent of the population size. The speed-tuning SNR remained at the baseline level. (C) Model with velocity and speed tuning. For small populations, the directional SNR (blue) dominated the speed SNR (red), as observed in SUA studies. The situation reversed in large neuronal populations (N > 10.000) and the speed SNR dominated that of movement direction. The directional SNR even decreased for large populations (N = 106), because the strong speed effect masked the cosine velocity tuning. (D) Analysis of the reversal points (color-coded), defined as minimum population size where speed SNR is significantly greater than the directional SNR, as a function of model parameters. The velocity cosine tuning was fixed (V = 1) and the speed tuning strength S was varied together with the task-unrelated Gaussian noise level σ. In summary, the model showed that the tuning properties of neuronal populations might be quite different, depending on their size, from the level of SUA.
Finally, the model accounted for both velocity tuning (V = 1) and speed tuning (S = 0.01). Note that the strength of the speed tuning was set to only 1% that of the velocity tuning. Therefore, for small neuronal populations, the directional SNR clearly dominated that of speed, as experimentally observed for SUA (Moran and Schwartz 1999). However, as more and more neurons were summed up, the speed term started to grow linearly with population size N (Fig. 10C). Eventually, for large-enough populations, the speed SNR surpassed that of direction (at the reversal point N = 10 000) and clearly dominated over the directional SNR—a situation that is opposite to the level of SUA. There was even a decrease of directional SNR for large neuronal populations (N > 105), because the strong speed tuning masked the directional modulations (note that we included movements of different speeds in computation of the directional SNR). This could have a profound influence on the directional information in large-scale population signals, such as EEG.
The values of the parameters in the model resulting in the curves as shown in Figure 10C were set rather conservatively in the sense of a relatively weak speed tuning strength S. To explore the position of the reversal point for a broader range of parameters, we independently varied the strength of speed tuning S, as well as the noise level σ, while keeping the magnitude of velocity cosine tuning V = 1 (Fig. 10D). Quite intuitively, the weaker the strength of speed tuning and the larger the noise value, the more neurons were required to reach the reversal point where the speed SNR surpassed the directional SNR. Interestingly, when compared with published data for some realistic settings (i.e., speed-to-velocity tuning strength ratio of 0.1 (cf. Moran and Schwartz 1999), and a noise level of σ = 10), our model predicted the R2 of 0.4 between speed and the speed-dependent population activity, similar to the experimental observation of Churchland and Shenoy (2007) (see also Discussion). In this case, only a few hundreds of neurons would be sufficient for the speed to dominate over direction in the population signal (Fig. 10D).
Discussion
The presented results enabled a direct comparison of decoding accuracies of different kinematic parameters during continuous movement tasks using different frequency features of the iEEG signal within the same decoding algorithm (Figs 3–5). Such a comprehensive overview was up to now missing in the literature. We also complemented the decoding with the tuning analysis (Figs 6–9), which allowed a further insight into the representation of the iEEG features in motor cortex during the continuous movement tasks (up to now also absent in the literature). Moreover, we offered a theoretical explanation of our results based on previous models of motor cortex SUA (Fig. 10), trying to bridge the gap between results of SUA and those of large-scale neuronal populations.
Predominance of Speed Over Velocity in iEEG
Probably the most striking observation in the comparison of the DAs of the kinematic parameters was the dominating representation of movement speed (or magnitude of the velocity vector), especially when compared with the decoding of x- or y-components of velocity itself (Fig. 3B). Significant decoding of direction, position, velocity, and acceleration were obtained consistently in all subjects from LFC (0–4 Hz) and high γ power (55–300 Hz) of iEEG. Surprisingly, the nondirectional movement speed and also magnitude of acceleration were robustly represented in motor cortex (Fig. 3B) in nearly all frequency features investigated, including power of very high-frequencies (600–1000 Hz), where the iEEG signal is assumed to predominantly reflect the compound spiking activity of the underlying neuronal population (Miller et al. 2014, see below).
The tuning analysis of continuous movements corroborated the predominance of speed over velocity observed in the decoding results (Figs 7–9), and revealed 2 distinct frequency-specific phenomena, namely, a speed-related increase in high-frequency bands (>50 Hz) and a simultaneous decrease of power in lower frequencies (<50 Hz). Such reciprocal modulations are a general signature of cortical “activation” (Chen et al. 1998; Miller et al. 2012). We found that these continuous movement-related modulations closely matched the brain responses established in “event-related” paradigms: first, a broadband and spatially focal high γ (>50 Hz) power increase, well-known in event-related paradigms (often called event-related synchronization—Crone et al. 1998; Crone et al. 2006; Miller et al. 2007), and second, a simultaneous, spatially more widespread power decrease in the α (8–12 Hz) and β (13–30 Hz) bands (also called event-related desynchronization—Pfurtscheller and Lopes da Silva 1999), likely involving brain activation-related modulations of oscillations in large-scale, inter-areal and also cortico-subcortical networks. The reciprocal modulation of low and high frequency components, well-documented in event-related paradigms, thus also shapes spectral responses in continuous conditions.
Properties of the Low-Pass Frequency Component
We also analyzed the time-domain LFC, as it is generally considered a particularly rich source of movement-related information (LFP: Mehring et al. 2003; ECoG: Schalk et al. 2007; MEG: Jerbi et al. 2007; EEG: Bradberry et al. 2010), which could be confirmed here as well. A novel observation of the present study was that the directionally tuned LFC was organized in spatially coherent maps (Figs 7 and 9G). These spatially organized activation patterns may open a window for investigation of the cortical sources of the directionally tuned ECoG components using source estimation techniques (Dümpelmann et al. 2012). Slow oscillations may represent changes in the balance of excitatory and inhibitory synaptic input (Eccles 1951; Mitzdorf 1985), likely reflecting a sum of local (e.g., motor and sensory) activity (Bansal et al. 2011). As suggested by Edwards et al. (2009), the presence of LFC activation does not guarantee an increase in high γ, whereas high γ activation generally overlaps that of the LFC—in line with our observation of the LFC activations being spatially more extended than those in high γ (cf. Figs 7 and 9).
Predominance of Speed Over Velocity as a Consequence of Population Size
The observed dominance of nondirectional movement speed over the direction-specific movement velocity is in clear contrast to previous findings on the level of SUA, where the directional or velocity tuning dominated that of speed (Flament and Hore 1988; Moran and Schwartz 1999; Golub et al. 2014). For example, Moran and Schwartz proposed a model of motor-cortical SUA as a function of movement velocity (hence including both speed and direction), consisting of an independent speed-tuned term and a velocity tuning (Moran and Schwartz 1999). These findings were further corroborated by Golub et al. (2014) where the independent speed and direction tuning best fitted the real SUA data.
Considering directional tuning only, Waldert et al. (2009) proposed a model of neuronal population firing rate activity and predicted that (under certain assumptions, see below) the SNR of directional tuning could be independent of its size even in the absence of any preferential spatial arrangement of PDs over the surface of motor cortex, and, hence, the same as in the case of SUA (Fig. 10B). We extended this model of neuronal population activity (see also Materials and Methods) to explicitly account not only for movement direction, but also for the speed tuning, building on published results of velocity-dependent discharges in SUA proposed by Moran and Schwartz (1999). Despite its simplicity, the neuronal population activity model makes an important prediction: SNRspeed will become much higher than SNRdirection when moving to larger population sizes in the range of thousands of neurons (Fig. 10C).
The above model was based on several assumptions: (1) The discharges of motor-cortical neurons considered only movement velocity and consisted of a linear speed term, cosine-tuned velocity with a certain (neuron-specific) PD, and task-unrelated Gaussian noise. These assumptions are in line with the findings and model proposed by Moran and Schwartz (1999). To account for the fact that there is a considerable complexity and heterogeneity of movement-related SUA in motor cortex deviating from the “canonical” Moran and Schwartz model (Sergio et al. 2005; Churchland and Shenoy 2007) and that thus may contribute to the noise, we also investigated the impact of the noise term over a broad parameter range (see Materials and Methods). (2) Random orientation of PDs within the simulated population. Several studies indicate that the spatial arrangement of PDs in motor cortex is—at least on a large spatial scale (>1 mm)—indeed approximately random (Amirikian and Georgopoulos 2003; Ben-Shaul et al. 2003; Naselaris et al. 2006; Georgopoulos et al. 2007; Stark et al. 2009). (3) The assumption that population signals can be approximately described as a sum of their instantaneous SUA firing rates (Waldert et al. 2009; Moran 2010). This may be especially correct for high γ responses (Ray et al. 2008; Manning et al. 2009; Ray and Maunsell 2011; see below).
Speed is Represented in Very High (600–1000 Hz) iEEG Frequencies
One interesting hypothesis proposed that the broad-band shifts of iEEG power could be a marker of local cortical activity (Miller et al. 2014). Namely, that it is a signature of asynchronously arriving synaptic inputs in the dendrites of pyramidal neurons (Bédard et al. 2006; Miller et al. 2007). According to our model of neuronal population activity (Fig. 10C), high-speed movements were characterized by a linear increase of mean firing rate of the underlying neuronal population relative to slow or even no movements. This increase of mean firing should, in turn, be reflected by a broadband iEEG power increase (Manning et al. 2009; Mollazadeh et al. 2009; Ray and Maunsell 2011). The fact that we saw the increase as a band limited phenomena in high frequencies (>50 Hz), could be due to the masking effect of rhythmic, low-frequency activity, especially in the β band (Miller et al. 2014). Thanks to the high-sampling frequency of some of our recordings (see Table 1), we were indeed able to show the approximately linear power increase with movement speed not only in the high γ (55–300 Hz) band, but even in the 300–1000 Hz frequency range of iEEG (Fig. 8B). Spectral changes might, in principle, affect all frequencies equivalently (Miller et al. 2014). However, we observed an attenuation of tuning strength with increasing frequencies (>300 Hz), which likely, at least in part, is due to the amplifier noise floor. The ultra-high frequency range was previously only rarely investigated. Signals in this range have been suggested to reflect summed action potentials of pyramidal cells (Curio et al. 1994; Edwards et al. 2005; Fedele et al. 2012). In our case, we were able to observe significant, meaningful physiological activity in the very high frequencies (Fig. 7) up to approximately 1000 Hz. As we used standard clinical amplifiers, our results likely underestimate the information content in these ultra-high frequencies. Our findings could hence further incite the interest in these ultra-high frequency signals and in low-noise amplifiers designed for optimally capturing them (Fedele et al. 2015).
Previous Reports on Movement Speed in Neuronal Population Signals
The prediction of the model that the SNR of speed should grow with the underlying neuronal population size, together with the hypothesis that the high-frequency range closely correlates to the mean firing rate of the underlying population, seems to be in concordance with previously published studies. In order to fully test the model's predictions, we would have to measure population signals of different, defined sizes—which was not possible here, due to the constraints of the clinical requirements of our subjects. However, in large neuronal populations, such as those reflected by LFP, studies of monkey motor cortex (Mehring et al. 2003; Bansal et al. 2011; Perel et al. 2013) reported that hand movement speed was actually better predictable from the LFP than from SUA or MUA, precisely as predicted by our model. Robust representation of movement speed in high γ iEEG of human motor cortex was also recently reported by Anderson et al. (2012). These results are very much in line with our hypothesis that speed tuning increases with the number of the neurons that the neuronal population signal comprises.
Neuronal Population Size Needed for Speed Dominance
How many neurons would be needed for the speed-related signal to dominate over that of movement direction? From the Figure 10C, the reversal point NRP (where SNRspeed > SNRdirection) is around 10.000 neurons. However, as shown in Figure 10D, the value of the reversal point, NRP, is dependent on a number of factors: speed-tuning strength S (increasing S decreases NRP), and also the width σ of the task-unrelated Gaussian noise (increasing σ increases NRP). Reports on the values of the speed-tuning strength S or the level of noise σ in human motor cortex are currently not available. In monkey motor cortex, Moran and Schwartz calculated the nondirectional speed-tuning strength S to be approximately 10% of that of the directional tuning (cf. Fig. 10A in Moran and Schwartz 1999). Interestingly, there was a remarkable agreement between the predictions of our simple model (using V = 1, S = 0.1, and σ = 1) and the experimental results of Moran and Schwartz (1999), when computing the R2 between speed and the neuronal population activity for number of neurons N = 1066 as in their study: our model predicted R2 = 0.98, while Moran and Schwartz reported value of R2 = 0.99. Therefore, the model's parameter setting of V = 1, S = 0.1, and σ = 1 might be quite realistic. In this case, the reversal point was NRP = 160 neurons (Fig. 10D). A similar analysis was carried out also by Churchland and Shenoy (2007), where they computed the ensemble nondirectional response for N = 137 neurons. Their R2 = 0.95, while our model predicted 0.98 (taking into account the higher number of trials in their study). These high correlations were achieved especially in the initial (ballistic) part of the movement. However, when considering the entire speed profile of the center-out reaching, the correlation between speed and the neuronal population activity dropped down (R2 = 0.61). We were able to simulate this decrease of R2 by simply increasing the noise level, σ = 8. Such an increase of noise may be interpreted as a consequence of larger variability of the SUAs in motor cortex during the latter (i.e., slow down) part of the movement.
How many neurons contribute to the ECoG signal? The diameter of the contact area with the cortical surface of the individual ECoG electrodes used in our study was 2.4 mm. Assuming a density of ∼105/mm2 neurons in human cortex, there are approximately 500 000 neurons directly beneath the contact area (Ray et al. 2008). However, due to volume conduction not all neurons contributing to a recorded signal must be directly underneath the recoding electrode (Dümpelmann et al. 2012), and conversely, not all neurons in the direct vicinity can be expected to be task-modulated (e.g., 75% of direction-modulated cells in monkey motor cortex were found by Georgopoulos et al. 1982). The number of neurons contributing to the ECoG may also depend on parameters such as the correlation structure of neuronal firing patterns, as has been recently shown for the LFP (Katzner et al. 2009; Lindén et al. 2011; Einevoll et al. 2013; Łęski et al. 2013). In summary, it appears highly plausible that the population size N reflected in the movement-related signal measured with individual ECoG electrodes is far above a few hundreds neurons and thus above the reversal point in Figure 10C.
Relevance of Speed Information in BMI Control
Our model predicts that speed tuning reduces the directional information especially in very large neuronal populations, as we observed a decrease of directional SNR in the presence of strong speed-related discharges (Fig. 10C). In this case, speed effectively masked the directional tuning properties. This could have a profound influence on EEG-based BMIs striving to exploit directional-related signal components (Waldert et al. 2009).
Many previous BMI studies based on single neuron activity noted a difficulty in reconstructing movement speed, and hence appropriate stopping signals (Carmena et al. 2003; Kim et al. 2008; Ganguly and Carmena 2009; Golub et al. 2014). Our results strongly suggest that BMIs might greatly benefit from incorporating speed information derived from the population level, as reflected in intracranial EEG, alongside the already widely used directional signals. This might be achieved by multi-scale recordings of both, single neuron activity and EEG-like signals. Speed information could further enhance the currently prevailing approach of decoding movement velocity (e.g., Pistohl et al. 2008) by utilizing the inverse relationship between curvature of trajectory and speed of movement (Lacquaniti et al. 1983; Schwartz 1994; Golub et al. 2014). Another possibility how speed information might be utilized is by alternative control paradigms, where speed would be the decoded and also the control variable, for example, as in the 2-target right-justified box task, where the speed-related iEEG activity would control the 1-D vertical cursor movement (Wolpaw et al. 2003; Wander et al. 2013).
Conclusions
In summary, we have characterized the representation of different hand movement parameters in the iEEG of human motor cortex more extensively than before. As a novel feature, we empirically demonstrated and theoretically explained pronounced speed tuning in the high γ iEEG, dominating over directional tuning, which is in opposition to the situation that was previously revealed on the single-neuron level at least in nonhuman primates. Assuming a similar basic cellular functional organization in human motor cortex, we propose that this reversal in the information content can be understood based on a simple model of tuning properties as a function of population size. We have argued that the representation SNRdirection >> SNRspeed on the single neuron level may be very different, even reversed, if the speed tuning is constructively summed up across the population, and may only become evident in large enough population averages, arguing against a “scale chauvinism” (Nunez and Srinivasan 2010) putting exclusive emphasis on the micro-scale of neuronal recording. Instead, multiscale techniques, such as a combination of recordings from single neurons for directional information with recordings from large populations for speed information, may enable better insight into cortical function as well as more efficient BMI control.
Funding
This work was supported by the DFG grant EXC 1086 BrainLink-BrainTools to the University of Freiburg, Germany. Funding to pay the Open Access publication charges for this article was provided by DFG grant EXC 1086.
Notes
We would like to thank the subjects for participating in our study, the medical staff of the university clinics both in Freiburg and Prague for their help in conducting our experiments. Namely, Pavel Čelakovský for his technical assistance. Conflict of Interest: None declared.
References
- Abramowitz M, Stegun IA. 1970. Handbook of mathematical functions with formulas, graphs, and mathematical tables. Dover, Ninth printing. Table 25.2. [Google Scholar]
- Amirikian B, Georgopoulos AP. 2003. Modular organization of directionally tuned cells in the motor cortex: is there a short-range order? Proc Natl Acad Sci USA. 100:12474–12479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson NR, Blakely T, Schalk G, Leuthardt EC, Moran DW. 2012. Electrocorticographic (ECoG) correlates of human arm movements. Exp Brain Res. 223:1–10. [DOI] [PubMed] [Google Scholar]
- Ashe J, Georgopoulos AP. 1994. Movement parameters and neural activity in motor cortex and area 5. Cereb Cortex. 4:590–600. [DOI] [PubMed] [Google Scholar]
- Ball T, Schulze-Bonhage A, Aertsen A, Mehring C. 2009. Differential representation of arm movement direction in relation to cortical anatomy and function. J Neural Eng. 6:016006. [DOI] [PubMed] [Google Scholar]
- Bansal AK, Vargas-Irwin CE, Truccolo W, Donoghue JP. 2011. Relationships among low-frequency local field potentials, spiking activity, and three-dimensional reach and grasp kinematics in primary motor and ventral premotor cortices. J Neurophysiol. 105:1603–1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bédard C, Kröger H, Destexhe A. 2006. Does the 1/f frequency scaling of brain signals reflect self-organized critical states? Phys Rev Lett. 97:118102.1. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. 1995. Controlling the false discovery rate: a practical and powerful approach to multiple testing. JRSSB. 57:289–300. [Google Scholar]
- Ben-Shaul Y, Stark E, Asher I, Drori R, Nadasdy Z, Abeles M. 2003. Dynamical organization of directional tuning in the primate premotor and primary motor cortex. J Neurophysiol. 89:1136–1142. [DOI] [PubMed] [Google Scholar]
- Bourguignon M, De Tiège X, Op de Beeck M, Pirotte B, Van Bogaert P, Goldman S, Hari R, Jousmäki V. 2011. Functional motor-cortex mapping using corticokinematic coherence. Neuroimage. 55:1475–1479. [DOI] [PubMed] [Google Scholar]
- Bradberry TJ, Gentili RJ, Contreras-Vidal JL. 2010. Reconstructing three-dimensional hand movements from noninvasive electroencephalographic signals. J Neurosci. 30:3432–3437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carmena JM, Lebedev MA, Crist RE, O'Doherty JE, Santucci DM, Dimitrov DF, Patil PG, Henriquez CS, Nicolelis MA. 2003. Learning to control a brain-machine interface for reaching and grasping by primates. PLoS Biol. 1:E42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen R, Yaseen Z, Cohen LG, Hallett M. 1998. Time course of corticospinal excitability in reaction time and self-paced movements. Ann Neurol. 44:317–325. [DOI] [PubMed] [Google Scholar]
- Churchland MM, Shenoy KV. 2007. Temporal complexity and heterogeneity of single-neuron activity in premotor and motor cortex. J Neurophysiol. 97:4235–4257. [DOI] [PubMed] [Google Scholar]
- Crone NE, Miglioretti DL, Gordon B, Lesser RP. 1998. Functional mapping of human sensorimotor cortex with electrocorticographic spectral analysis. II. Event-related synchronization in the gamma band. Brain. 121:2301–2315. [DOI] [PubMed] [Google Scholar]
- Crone NE, Sinai A, Korzeniewska A. 2006. High-frequency gamma oscillations and human brain mapping with electrocorticography. Prog Brain Res. 159:275–295. [DOI] [PubMed] [Google Scholar]
- Curio G, Mackert BM, Burghoff M, Koetitz R, Abraham-Fuchs K, Härer W. 1994. Localization of evoked neuromagnetic 600 Hz activity in the cerebral somatosensory system. Electroencephalogr Clin Neurophysiol. 91:483–487. [DOI] [PubMed] [Google Scholar]
- Dümpelmann M, Ball T, Schulze-Bonhage A. 2012. sLORETA allows reliable distributed source reconstruction based on subdural strip and grid recordings. Hum Brain Mapp. 33:1172–1188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eccles JC. 1951. Interpretation of action potentials evoked in the cerebral cortex. Electroencephalogr Clin Neurophysiol. 3:449–464. [DOI] [PubMed] [Google Scholar]
- Edwards E, Soltani M, Deouell LY, Berger MS, Knight RT. 2005. High gamma activity in response to deviant auditory stimuli recorded directly from human cortex. J Neurophysiol. 94:4269–4280. [DOI] [PubMed] [Google Scholar]
- Edwards E, Soltani M, Kim W, Dalal SS, Nagarajan SS, Berger MS, Knight RT. 2009. Comparison of time-frequency responses and the event-related potential to auditory speech stimuli in human cortex. J Neurophysiol. 102:377–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Einevoll GT, Kayser C, Logothetis NK, Panzeri S. 2013. Modelling and analysis of local field potentials for studying the function of cortical circuits. Nat Rev Neurosci. 14:770–785. [DOI] [PubMed] [Google Scholar]
- Evarts EV. 1968. Relation of pyramidal tract activity to force exerted during voluntary movement. J Neurophysiol. 31:14–27. [DOI] [PubMed] [Google Scholar]
- Faes L, Pinna GD, Porta A, Maestri R, Nollo GD. 2004. Surrogate data analysis for assessing the significance of the coherence function. IEEE Trans Biomed Eng. 51:1156–1166. [DOI] [PubMed] [Google Scholar]
- Fedele T, Scheer HJ, Burghoff M, Curio G, Körber R. 2015. Ultra-low-noise EEG/MEG systems enable bimodal non-invasive detection of spike-like human somatosensory evoked responses at 1 kHz. Physiol Meas. 36:357–368. [DOI] [PubMed] [Google Scholar]
- Fedele T, Scheer HJ, Waterstraat G, Telenczuk B, Burghoff M, Curio G. 2012. Towards non-invasive multi-unit spike recordings: mapping 1kHz EEG signals over human somatosensory cortex. Clin Neurophysiol. 123:2370–2376. [DOI] [PubMed] [Google Scholar]
- Fetz EE. 1992. Are movement parameters recognizably coded in the activity of single neurons? Behav Brain Sci. 15:679–690. [Google Scholar]
- Fischer J, Milekovic T, Schneider G, Mehring C. 2014. Low-latency multi-threaded processing of neuronal signals for brain-computer interfaces. Front Neuroeng. 7:1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flament D, Hore J. 1988. Relations of motor cortex neural discharge to kinematics of passive and active elbow movements in the monkey. J Neurophysiol. 60:1268–1284. [DOI] [PubMed] [Google Scholar]
- Fu QG, Flament D, Coltz JD, Ebner TJ. 1995. Temporal encoding of movement kinematics in the discharge of primate primary motor and premotor neurons. J Neurophysiol. 73:836–854. [DOI] [PubMed] [Google Scholar]
- Ganguly K, Carmena JM. 2009. Emergence of a stable cortical map for neuroprosthetic control. PLoS Biol. 7:e1000153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos AP, Kalaska JF, Caminiti R, Massey JT. 1982. On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. J Neurosci. 2:1527–1537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos AP, Langheim FJ, Leuthold AC, Merkle AN. 2005. Magnetoencephalographic signals predict movement trajectory in space. Exp Brain Res. 167:132–135. [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP, Merchant H, Naselaris T, Amirikian B. 2007. Mapping of the preferred direction in the motor cortex. Proc Natl Acad Sci USA. 104:11068–11072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos AP, Schwartz AB, Kettner RE. 1986. Neuronal population coding of movement direction. Science. 233:1416–1419. [DOI] [PubMed] [Google Scholar]
- Golub MD, Yu BM, Schwartz AB, Chase SM. 2014. Motor cortical control of movement speed with implications for brain-machine interface control. J Neurophysiol. 112:411–429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graziano MSA. 2011. New insights into motor cortex. Neuron. 71:387–388. [DOI] [PubMed] [Google Scholar]
- Hammer J, Fischer J, Ruescher J, Schulze-Bonhage A, Aertsen A, Ball T. 2013. The role of ECoG magnitude and phase in decoding position, velocity, and acceleration during continuous motor behavior. Front Neurosci. 7:200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jerbi K, Lachaux JP, N'Diaye K, Pantazis D, Leahy RM, Garnero L, Baillet S. 2007. Coherent neural representation of hand speed in humans revealed by MEG imaging. Proc Natl Acad Sci USA. 104:7676–7681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katzner S, Nauhaus I, Benucci A, Bonin V, Ringach DL, Carandini M. 2009. Local origin of field potentials in visual cortex. Neuron. 61:35–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kettner RE, Schwartz AB, Georgopoulos AP. 1988. Primate motor cortex and free arm movements to visual targets in three-dimensional space. III. Positional gradients and population coding of movement direction from various movement origins. J Neurosci. 8:2938–2947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khinchin A. 1934. Korrelationstheorie der stationären stochastischen Prozesse. Mathematische Annalen. 109:604–615. [Google Scholar]
- Kim SP, Simeral JD, Hochberg LR, Donoghue JP, Black MJ. 2008. Neural control of computer cursor velocity by decoding motor cortical spiking activity in humans with tetraplegia. J Neural Eng. 5:455–476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacquaniti F, Terzuolo C, Viviani P. 1983. The law relating the kinematic and figural aspects of drawing movements. Acta Psychol (Amst). 54:115–130. [DOI] [PubMed] [Google Scholar]
- Lebedev MA, Nicolelis MA. 2006. Brain-machine interfaces: past, present and future. Trends Neurosci. 29:536–546. [DOI] [PubMed] [Google Scholar]
- Łęski S, Lindén H, Tetzlaff T, Pettersen KH, Einevoll GT. 2013. Frequency dependence of signal power and spatial reach of the local field potential. PLoS Comput Biol. 9:e1003137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindén H, Tetzlaff T, Potjans TC, Pettersen KH, Grün S, Diesmann M, Einevoll GT. 2011. Modeling the spatial reach of the LFP. Neuron. 72:859–872. [DOI] [PubMed] [Google Scholar]
- Manning JR, Jacobs J, Fried I, Kahana MJ. 2009. Broadband Shifts in Local Field Potential Power Spectra Are Correlated with Single-Neuron Spiking in Humans. J Neurosci. 29:13613–13620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehring C, Rickert J, Vaadia E, Cardoso de Oliveira S, Aertsen A, Rotter S. 2003. Inference of hand movements from local field potentials in monkey motor cortex. Nat Neurosci. 6:1253–1254. [DOI] [PubMed] [Google Scholar]
- Milekovic T, Fischer J, Pistohl T, Ruescher J, Schulze-Bonhage A, Aertsen A, Rickert J, Ball T, Mehring C. 2012. An online brain-machine interface using decoding of movement direction from the human electrocorticogram. J Neural Eng. 9:046003. [DOI] [PubMed] [Google Scholar]
- Miller KJ, Hermes D, Honey CJ, Hebb AO, Ramsey NF, Knight RT, Ojemann JG, Fetz EE. 2012. Human motor cortical activity is selectively phase-entrained on underlying rhythms. PLoS Comput Biol. 8:e1002655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KJ, Honey CJ, Hermes D, Rao RP, denNijs M, Ojemann JG. 2014. Broadband changes in the cortical surface potential track activation of functionally diverse neuronal populations. Neuroimage. 85:711–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KJ, Leuthardt EC, Schalk G, Rao RPN, Anderson NR, Moran DW, Miller JW, Ojemann JG. 2007. Spectral changes in cortical surface potentials during motor movement. J Neurosci. 27:2424–2432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KJ, Sorensen LB, Ojemann JG, den Nijs M. 2009. Power-law scaling in the brain surface electric potential. PLoS Comput Biol. 5:e1000609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitzdorf U. 1985. Current source-density method and application in cat cerebral cortex: investigation of evoked potentials and EEG phenomena. Physiol Rev. 65:37–100. [DOI] [PubMed] [Google Scholar]
- Mollazadeh M, Aggarwal V, Thakor NV, Law AJ, Davidson A, Schieber MH. 2009. Coherency between spike and LFP activity in M1 during hand movements. Neural Eng. 2009. NER ‘09. 4th International IEEE/EMBS Conference on, pp. 506–509. [Google Scholar]
- Moran D. 2010. Evolution of brain–computer interface: action potentials, local field potentials and electrocorticograms. Curr Opin Neurobiol. 20:741–745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran DW, Schwartz AB. 1999. Motor cortical representation of speed and direction during reaching. J Neurophysiol. 82:2676–2692. [DOI] [PubMed] [Google Scholar]
- Mukamel R, Fried I. 2012. Human intracranial recordings and cognitive neuroscience. Annu Rev Psychol. 63:511–537. [DOI] [PubMed] [Google Scholar]
- Mussa-Ivaldi FA. 1988. Do neurons in the motor cortex encode movement direction? An alternative hypothesis. Neurosci Lett. 91:106–111. [DOI] [PubMed] [Google Scholar]
- Naselaris T, Merchant H, Amirikian B, Georgopoulos AP. 2006. Large-Scale organization of preferred directions in the motor cortex. ii. Analysis of local distributions. J Neurophysiol. 96:3237–3247. [DOI] [PubMed] [Google Scholar]
- Nunez PL, Srinivasan R. 2006. Electric fields of the brain: the neurophysics of EEG. (2nd ed.) New York: Oxford University Press. [Google Scholar]
- Nunez PL, Srinivasan R. 2010. Scale and frequency chauvinism in brain dynamics: too much emphasis on γ band oscillations. Brain Struct Funct. 215:67–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paninski L, Fellows MR, Hatsopoulos NG, Donoghue JP. 2004. Spatiotemporal tuning of motor cortical neurons for hand position and velocity. J Neurophysiol. 91:515–532. [DOI] [PubMed] [Google Scholar]
- Perel S, Sadtler PT, Godlove JM, Ryu SI, Wang W, Batista AP, Chase SM. 2013. Direction and speed tuning of motor-cortex multi-unit activity and local field potentials during reaching movements. Conf Proc IEEE Eng Med Biol Soc. 2013:299–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfurtscheller G, Lopes da Silva FH. 1999. Event-related EEG/MEG synchronization and desynchronization: basic principles. Clin Neurophysiol. 110:1842–1857. [DOI] [PubMed] [Google Scholar]
- Pistohl T, Ball T, Schulze-Bonhage A, Aertsen A, Mehring C. 2008. Prediction of arm movement trajectories from ECoG-recordings in humans. J Neurosci Methods. 167:105–115. [DOI] [PubMed] [Google Scholar]
- Ray S, Crone NE, Niebur E, Franaszczuk PJ, Hsiao SS. 2008. Neural correlates of high-gamma oscillations (60-200 hz) in macaque local field potentials and their potential implications in electrocorticography. J Neurosci. 28:11526–11536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ray S, Maunsell JH. 2011. Different origins of gamma rhythm and high-gamma activity in macaque visual cortex. PLoS Biol. 9:e1000610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rickert J, Oliveira SC, Vaadia E, Aertsen A, Rotter S, Mehring C. 2005. Encoding of movement direction in different frequency ranges of motor cortical local field potentials. J Neurosci. 28:8815–8824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sauseng P, Klimesch W. 2008. What does phase information of oscillatory brain activity tell us about cognitive processes? Neurosci Biobehav Rev. 32:1001–1013. [DOI] [PubMed] [Google Scholar]
- Schalk G, Kubánek J, Miller KJ, Anderson NR, Leuthardt EC, Ojemann JG, Limbrick D, Moran DW, Gerhardt LA, Wolpaw JR. 2007. Decoding two-dimensional movement trajectories using electrocorticographic signals in humans. J Neural Eng. 4:264–275. [DOI] [PubMed] [Google Scholar]
- Schwartz AB. 1994. Direct cortical representation of drawing. Science. 265:540–542. [DOI] [PubMed] [Google Scholar]
- Schwartz AB, Cui XT, Weber DJ, Moran DW. 2006. Brain-controlled interfaces: movement restoration with neural prosthetics. Neuron 52:205–220. [DOI] [PubMed] [Google Scholar]
- Schwartz AB, Moran DW. 1999. Motor cortical activity during drawing movements: population representation during lemniscate tracing. J Neurophysiol. 82:2705–2718. [DOI] [PubMed] [Google Scholar]
- Sergio LE, Hamel-Paquet C, Kalaska JF. 2005. Motor cortex neural correlates of output kinematics and kinetics during isometric-force and arm-reaching tasks. J Neurophysiol. 94:2353–2378. [DOI] [PubMed] [Google Scholar]
- Stark E, Drori R, Abeles M. 2009. Motor Cortical activity related to movement kinematics exhibits local spatial organization. Cortex. 45:418–431. [DOI] [PubMed] [Google Scholar]
- Todorov E. 2000. Direct cortical control of muscle activation in voluntary arm movements: a model. Nat Neurosci. 3:391–398. [DOI] [PubMed] [Google Scholar]
- Vaadia E, Birbaumer N. 2009. Grand challenges of brain computer interfaces in the years to come. Front Neurosci. 3:151–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waldert S, Pistohl T, Braun C, Ball T, Aertsen A, Mehring C. 2009. A review on directional information in neural signals for brain–machine interfaces. J Physiol Paris. 103:244–254. [DOI] [PubMed] [Google Scholar]
- Waldert S, Preissl H, Demandt E, Braun C, Birbaumer N, Aertsen A, Mehring C. 2008. Hand movement direction decoded from MEG and EEG. J Neurosci. 28:1000–1008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wander JD, Blakely T, Miller KJ, Weaver KE, Johnson LA, Olson JD, Fetz EE, Rao RP, Ojemann JG. 2013. Distributed cortical adaptation during learning of a brain-computer interface task. Proc Natl Acad Sci USA. 110:10818–10823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolpaw JR, McFarland DJ, Vaughan TM, Schalk G. 2003. The Wadsworth Center brain-computer interface (BCI) research and development program. IEEE Trans Neural Syst Rehab Eng. 11:204–207. [DOI] [PubMed] [Google Scholar]