Modeling the Control of Planar Cell Polarity

Abstract

A growing list of medically important developmental defects and disease mechanisms can be traced to disruption of the Planar Cell Polarity (PCP) pathway. The PCP system polarizes cells in epithelial sheets along an axis orthogonal to their apical-basal axis. Studies in the fruitfly, Drosophila, have led to the concept of a modular system controlling PCP. The components of the PCP signaling modules, and the effector systems with which they interact, function together to produce emergent patterns. Experimental methods allow the manipulation of individual PCP signaling molecules in specified groups of cells; these interventions not only perturb the polarization of the targeted cells at a subcellular level, but also perturb patterns of polarity at the multicellular level, often affecting nearby cells in characteristic ways. These kinds of experiments should, in principle, allow one to infer the architecture within and between modules, but the relationships between molecular interactions and tissue-level pattern are sufficiently complex that they defy intuitive understanding. Mathematical modeling has been an important tool to address these problems. This review explores the emergence of a local signaling hypothesis, and describes how a local intercellular signal, coupled with a directional cue, can give rise to global pattern. We will discuss the critical role mathematical modeling has played in guiding and interpreting experimental results, and speculate about future roles for mathematical modeling of PCP. Mathematical models at varying levels of abstraction have and are expected to continue contributing in distinct ways to understanding the regulation of PCP signaling.

The orientation of epithelial cells along an axis orthogonal to the apical-basal axis is referred to as Planar Cell Polarity (PCP). PCP signaling controls the polarity of numerous epithelial cells in both Drosophila and vertebrates (Fig. 1). In Drosophila, the most intensively studied planar polarized tissue is the fly wing, in which each cell produces a trichome (“hair”), that in wildtype, emerges from the distal side of the cell and points distally[1]. PCP mutants cause disruption of this pattern. PCP also orients asymmetric cell divisions such that fate determinants are properly inherited by a single daughter (i.e. the Drosophila pI sensory organ precursor cells[2–4]), and determines rotation and chirality of cell clusters in the Drosophila eye[5–7]. In vertebrates, the PCP signaling modules identified in flies are conserved, and interact with diverse systems to produce planar polarized structures[8–12]. Defects in PCP result in a range of developmental anomalies and diseases including open neural tube defects[13], polycystic kidneys[8, 11, 13, 14], conotruncal heart defects[15–18], and disruption of sensory hair cell polarity causing deafness[19–29]. PCP is also believed to underlie the directed migration of malignant cells during invasion and metastasis[30–34]. A growing body of evidence suggests that the molecular mechanisms controlling PCP in flies are well conserved in vertebrates, though perhaps with some additional layers of regulation (reviewed in[8, 12]). Unfortunately, the PCP signaling modules and their interactions are as yet poorly understood, thereby limiting the potentially substantial opportunities for therapeutic interventions.

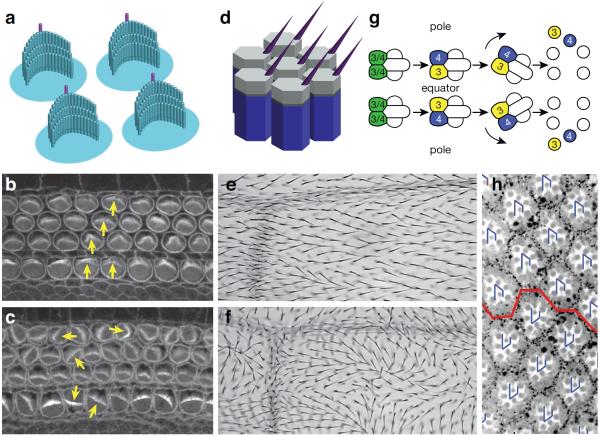
Figure 1.

Planar cell polarity. (a) Cartoon of cochlear hair cells showing asymmetrically localized and coordinately oriented kinoclila (purple) and stereocilia (blue). (b) Wild type and (c) Lp/Lp mutant cochlear hair cells stained with phalloidin to show actin. Orientation of some cells is denoted with arrows. (d) Cartoon of Drosophila pupal wing cells with nascent hairs emerging from the distal vertex and pointing distally. (e) Wild type and (f) dishevelled1 wings showing hair polarity (distal is right). (g) Chiral and oriented ommatidia in the fly eye. Equipotent R3/R4 cells (green) differentiate to R3 (equatorial; yellow) and R4 (polar; blue) according to their relative position along the equatorial-polar axis. Ommatidia then rotate in opposite directions in the dorsal (top) and ventral (bottom) eye fields. (h) Wild type eye showing ommatidia in the dorsal (top) and ventral (bottom) eye fields. Orientation is noted with blue arrows. Images in (b) and (c) were kindly provided by M. Montcouquiol and M. Kelley.

The collective PCP of cells in an epithelium constitutes a large scale pattern. The typical wildtype pattern is a simple parallel array, but mutations of PCP signaling components may produce more complex patterns. Clonal disruption of the PCP signaling mechanism not only disrupts polarity within the clone, but in some cases causes characteristic changes in the polarity of neighboring, non-mutant cells. These mutant patterns, described below, hold important clues to understanding the signaling mechanisms governing PCP.

The goal of this review is to describe how various different forms of mathematical modeling have contributed in different ways to understanding the relationship between the molecular signaling events underlying PCP and the large scale patterning that is observed in wild-type and mutant animals. Mathematical modeling has allowed investigators to test predictions concerning perturbation of the molecular machinery, and therefore better understand those molecular mechanisms. In addition, it has provided a window into understanding control features that allow the system to function robustly. We will highlight the role mathematical modeling has played in this process, and suggest that mathematical modeling will become an increasingly important tool in deciphering the relationship between molecular mechanisms and the resultant developmental patterns they control. We will not attempt to provide an exhaustive discussion of what's known and not known about the molecular details of PCP signaling, either in vertebrates or in Drosophila, nor to describe the variations observed in different planar polarized tissues, though these are important topics. Several excellent reviews discuss these topics[6, 9, 35–37].

1. Planar cell polarity

1.1 Drosophila as a model system for PCP

The greatest strides in understanding PCP have been made using Drosophila as a model system. A powerful set of genetic, molecular and cell biological tools, together with easily observable phenotypes, make Drosophila an extremely attractive system for investigating the controls governing PCP.

1.2 The genetic basis for PCP

PCP in Drosophila is seen in most cells secreting the adult cuticle[38]. These cells each produce a single trichome, or hair, and the hairs are polarized with respect to the axis of the body or appendage (Fig. 1). Hair polarity has been most intensively studied in the wing and to a lesser extent in the abdomen. Studies of the hair producing cells of the wing have been the most informative in revealing the connections between molecular signaling and large scale patterning, so these will be the focus of our discussion, with some reference also to work in the eye and abdomen.

Genetic and molecular analyses in Drosophila suggest that the PCP signaling components may be divided into three modules: a global directional cue, a core module, and a suite of tissue specific effector modules that respond to the upstream modules to produce morphological asymmetry in individual tissues. The “core” PCP module coordinates polarity between neighboring cells in all tissues, and includes Frizzled (Fz[39]), Flamingo (Fmi; aka Starry night[40, 41]), Van gogh (Vang[42, 43]), Prickle-spiny-legs (Pk[44]), Dishevelled (Dsh[45, 46]) and Diego (Dgo[47, 48]). Early genetic analyses of the core PCP genes led to the view that the core components signal in a linear fashion from the receptor, Fz[49], through a downstream, cytoplasmic transducing protein, Dsh[50], providing output to the various effector modules (reviewed in[50, 51]). Most effector components show some tissue specificity, and while less is known about them as compared to the upstream components, a reasonable view is that they couple signaling from the core proteins to the cell-type specific responses required to generate PCP in the individual tissues (reviewed in[7, 50, 52]). Like the core module, the global module also influences PCP in all tissues, and comprises the golgi protein Four-jointed (Fj[53]), and the atypical cadherins Dachsous (Ds[54]) and Fat(Ft[55–59]). These proteins were proposed to function upstream of the core components, transducing global directional information to the core PCP proteins[56, 60–62]. While this view has been challenged, with some arguing that the global and core modules function in parallel[63, 64], we believe the arguments for the parallel model are not compelling (reviewed in [37]).

1.3 Cellular phenotypes correlate with activity of the core PCP module

The cellular phenotypes of wild-type and mutant hair cells in the wing, first characterized in detail by Wong and Adler[1], are diagnostic for the three tiers of the mechanism, and as described below, correspond to molecular asymmetry (or lack thereof) within the cell. The location for prehair initiation is the critical event in establishing polarity: for hairs emerging away from the center of the cell, the hair is always observed to point outward from the center[1]. In wildtype, the uniform placement of the nascent prehairs at the distal edge of the cell reflects the ability of the cell to distinguish that edge on a molecular level. Mutation of the core PCP genes causes the prehairs to initiate and grow at (dsh) or at a variable distance from (fz, dsh, vang, pk, fmi, and dgo) the center of the cell, reflecting a complete or partial failure to achieve molecular asymmetry (Fig. 2). Mutants affecting the downstream effector module in wing cells (inturned, fuzzy, multiple wing hairs, the Drok pathway) typically produce multiple prehairs that often initiate at aberrant locations around the cell periphery (Fig. 2)[1, 65], reflecting uncoupling of the effector systems from the molecular asymmetry produced by the core proteins. Mutants in the global components fj, ds and fat do not abolish cellular asymmetry, invariably producing prehairs at the periphery as in wild-type cells[61]. However, the prehairs often fail to correctly choose the distal edge. Furthermore, the prehair locations chosen by neighboring cells are highly correlated in swirling patterns, reflecting a loss of overall directionality, yet keeping intact the ability of the core module to produce subcellular asymmetry and to coordinate local alignment.

Figure 2.

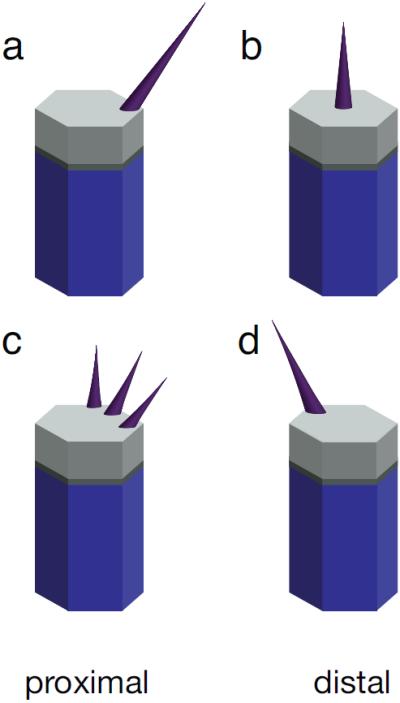
Cellular phenotypes of wing hair cells. (a) Wild type, (b) core gene mutants, (c) downstream effector mutants, and (d) global directional mutants.

Considerable attention has been paid to the fact that in mutants of the core PCP genes, the prehairs do not adopt a random polarity, instead forming stereotypical patterns in which hairs on a given region of the wing tend to point in a given direction. These mutants produce little or no molecular asymmetry of PCP proteins, and prehairs tend to grow at or near the center of the cell. Therefore, the stereotypical patterns of hair orientation seen in core mutants arise through an unknown mechanism not obviously related to the PCP signaling pathway.

1.4 Clonal phenotypes: autonomy and non-autonomy

Beyond polarizing individual cells, PCP mechanisms function across epithelia to produce emergent, large scale, patterns. In wildtype fly wing and abdomen, the pattern is a simple parallel array of polarized cells, each producing its hair on the same side of the cell. However, the patterns become more interesting when clones of cells lose or overexpress one or more components of the system, as described below (Fig. 3). The resulting patterns indicate transmission of polarity information between cells, and have served as a rich source of clues to the mechanism that underlies polarization.

Figure 3.

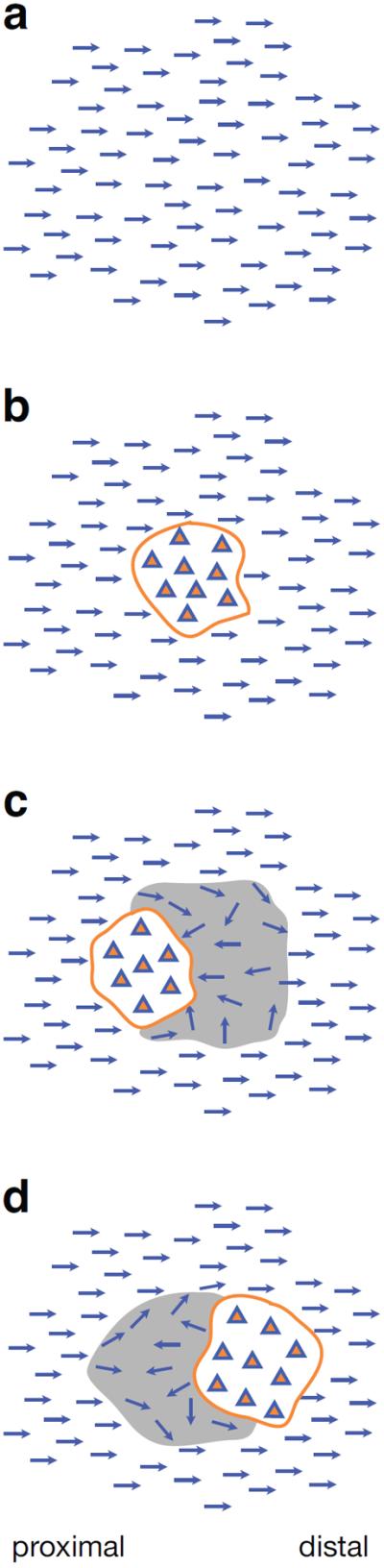
Cartoons of clonal phenotypes. (a) Wild type polarity with all hairs pointing distally. (b) A cell autonomous mutant clone (orange outline) showing loss of polarity within the clone (triangles) and normal polarity surrounding the clone. (c) Mutant clone with distal domineering non-autonomy (grey shaded area) characteristic of fz mutant clones. (d) Mutant clone showing proximal domineering non-autonomy characteristic of vang mutant clones. See Figure 7 for phalloidin stained pupal wing clones showing these phenotypes.

A dominant non-cell-autonomous effect on PCP was first noticed in experiments in which transplanted tissue repolarized neighboring tissue[66]. Clones mutant for the core PCP genes fz and vang similarly produce misorientation of neighboring, non-mutant tissue, a phenomenon referred to as domineering non-autonomy[42, 67, 68]. Remarkably, fz mutants induce polarity reversals on the distal side of clones, while vang induces polarity reversal on the proximal side (Fig. 3). While most fz clones display domineering non-autonomy, some alleles produce nearly autonomous polarity defects[69], as do the remaining core PCP genes[40, 45, 46, 67, 70]. Overexpression clones of the core components each produce a characteristic non-autonomous effect as well (summarized in[71]). Clones of the upstream components ds and fat often, but do not always produce PCP defects[42, 61, 72]. However, those that do sometimes produce domineering non-autonomy, and the direction of the domineering non-autonomy is less predictable than around fz and vang clones[42, 61]. Results are largely similar for the abdomen[62, 73, 74].

1.5 Domineering non-autonomy and the diffusible factor (“factor X”) models

The observation of domineering non-autonomy prompted researchers to propose models in which cells respond to an initial cue by making and secreting a diffusible second factor, resulting in a distribution gradient that determines polarity[38, 73, 75–84] (Fig. 4). These models, referred to as the “factor X” models for the unidentified diffusible factor, were first formalized with reference to phenotypes in the eye[76]. In the eye, Wingless (Wg; a Wnt protein) signals in a gradient that is highest at the poles and lowest at the equator. Wehrli and colleagues proposed that Wg signaling induces the dose dependent secretion of a diffusible factor X, which in turn regulates Fz signaling via the gradient of factor X distribution. Clonal disruption of the response to Wg would perturb the factor X gradient both in the mutant and the neighboring wild-type tissue, inducing a gradient reversal that would cause the observed non-autonomy. A variation of this model was subsequently offered to explain the fz and vang clonal phenotypes in the wing. In response to an unknown, graded, upstream signal, Fz and Vang were proposed to regulate production of a diffusible “factor Z” whose gradient is read out to produce polarity[38, 78]. The factor X and factor Z models may be unified: since factor Z might feed back through Fz, factor X and factor Z could be the same molecule.

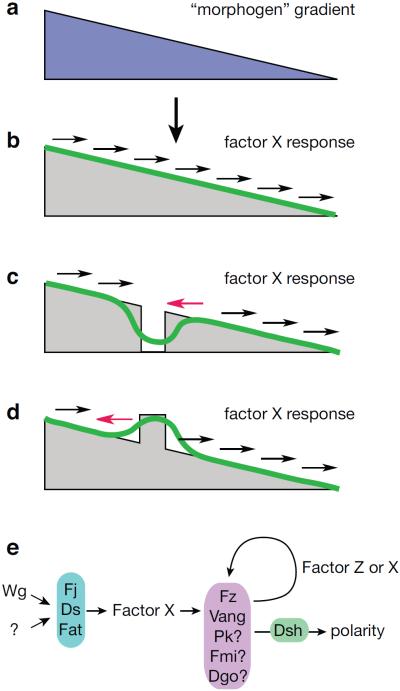
Figure 4.

Diffusible factor model. An upstream signal (a; blue), such as Wg in the eye, induces a proportional expression of a diffusible factor X (gray). (b) In wild type, factor X distributes in a gradient (green) whose slope determines polarity (arrows). (c) In clones that do not respond to the upstream signal, the factor X expression profile results in a distribution profile (green) with slope reversal, causing polarity reversal distal to the clone (red arrow). (d) Clones with augmented response to the upstream factor result in a distribution profile showing polarity reversal on the proximal side of the clone. (e) Factor X and factor Z signaling scheme.

These models have also been asked to account for the observation that clones of cells mutant for most fz alleles, including null alleles, produce domineering non-autonomy, but clones of cells mutant for certain fz alleles produce a nearly cell autonomous phenotype[67–69]. In addition, dsh mutant cell clones produce nearly cell autonomous polarity disruptions[45, 46, 71]. The diffusible factor models explain these observations by positing that Fz mediates two separably mutable signaling functions: a cell autonomous, Dsh dependent, signaling function and a Dsh independent non-autonomous signal[41, 42, 72, 85]. The non-autonomous signal might be mediated by factor Z, that is produced in a dose dependent response to Fz signaling, while the autonomous Dsh dependent signal would initiate cell polarization[38, 78].

Despite its attractiveness, challenges exist for the diffusible factor model. Although the model proposes an autonomous Dsh dependent Fz signaling pathway and a separably mutable non-autonomous Fz signal, dsh clones show a small though significant amount of non-autonomy([71, 86] and P. Adler, personal communication) that is difficult to reconcile with this distinction. Furthermore, while the molecular mechanism of Fz signal transduction is not well understood, there is no molecular evidence for separable signals upstream of Dsh. The controversial proposal that Fz signals through a heterotrimeric G protein suggests that the G protein would function in Dsh dependent pathways[87] (see[88] for review of evidence from higher organisms). Finally, despite tremendous efforts, diffusible factors X or Z have not been identified[73]. A Wnt protein is a logical candidate for factor X or Z, but no Wnt has been identified to play this role in the fly [73, 89]. In contrast, Wnt proteins have been shown to function in vertebrate PCP pathways (see [90–92] for examples). The evidence, while somewhat difficult to interpret, is most consistent with Wnts being permissive rather than having an instructive role as predicted by factor X models[90, 92–94].

1.6 The molecular basis of subcellular asymmetry

The finding that core PCP proteins localize asymmetrically within the cell paved the way for a more mechanistic understanding of subcellular asymmetry. Uemura and colleagues found that fmi mutants display PCP phenotypes, and that Fmi protein appears to localize to both the proximal and distal sides of wing cells prior to prehair formation, where it most likely forms a homodimer spanning the intercellular boundary[40]. This was the first molecular indication that this boundary becomes specialized during PCP signaling, although its bipolar localization indicated that Fmi could not be the component that distinguishes proximal from distal within the cell. Two subsequent reports identified unipolar protein localization and therefore a molecular basis for distinguishing one side of the cell from the other. Fz and Dsh were both found to localize to the distal side of the cell before prehair formation[95, 96]. Subsequently, Pk and Vang were found to localize proximally, and Dgo distally with Fz and Dsh[47, 97, 98]. These findings suggested that localization of core proteins provides cues for morphologic cellular asymmetry.

1.7 A local signaling model for Fz dependent PCP signaling

The possibility that distally localized Fz and Dsh designate the distal side of cells for prehair initiation raised the critical question of how these proteins achieve their asymmetric localization. Based on genetic mosaics, subcellular localization and biochemical assays, Tree et al.[70] proposed a feedback loop mechanism that mediates a competition between proximal and distal proteins displayed on adjacent surfaces of neighboring cells (Fig. 5). This model had features similar to insightful models proposed earlier by Adler and colleagues that were proposed without the benefit of subcellular localization data[42, 99]. Largely based on mosaic analyses of clones lacking or overexpressing individual components, it was deduced that these proteins communicate at cell boundaries, with the distal proteins (Fmi, Fz, Dsh, Dgo) recruiting the proximal proteins (Fmi, Vang, Pk) to adjacent cell boundaries, and vice versa. Through the function of a the feedback mechanism, these proteins become strongly polarized[71, 97]. Mutual exclusion of proximal and distal complexes appears to promote an all-or-none accumulation in one or the other orientation. This module therefore behaves as a bistable switch, producing a strongly biased accumulation of complexes oriented in one direction, and producing local alignment between neighboring cells.

Figure 5.

Cartoon of the Fz feedback loop proposed by Tree et al. and Amonlirdviman et al.[71, 97](bottom). A cartoon of a possible mechanism for Fj, Ds and Ft function that biases Fz feedback loop function is also shown (top). Pale symbols represent species with reduced concentration.

Specific roles for the core proteins in this process are not well understood. Fmi, Fz and Vang are thought to communicate information between cells, while the remaining proteins appear to participate in amplifying asymmetry[40, 74, 89, 100]. Functionally asymmetric Fmi homodimers have been proposed to communicate information between adjacent cells[89], though others have suggested that Fz and Vang communicate directly[101]. Dgo competes with Pk for binding to Dsh[48, 102], suggesting that Dgo may reinforce the difference between the proximal and distal complexes. Aside from the demonstration of some binding interactions ex vivo, the feedback competition mechanism is very poorly understood at a biochemical level.

More recently, directed vesicular transport and recycling of PCP components have been implicated as intrinsic parts of this mechanism[37, 103–105]. While it is likely that these are important elements of the mechanism, and will undoubtedly attract considerable attention in the future, they are just now being incorporated into mathematical modeling efforts, so will not be discussed at length here.

Though not as extensive, studies of the fly eye are consistent with a similar mechanism[60, 95, 98]. Subcellular localization has not yet been examined in the abdomen, though it seems likely that findings will be similar. It's important to point out that most of the observations that contributed to the local feedback model could also be consistent with a factor X model. Furthermore, it is not intuitively obvious to all observers[38, 72] that the local feedback loop model can explain the range of autonomous and non-autonomous clonal phenotypes that have been observed.

1.8 The global directional cue

In addition to a local alignment mechanism, the PCP process requires a global directional cue to orient cell polarity with respect to the tissue axes. Based on data from both eye and wing, a model involving Fat, Ds, and Fj was proposed as an alternative to hypothetical diffusible factors in providing a global directional signal[60, 61]. This global module is proposed to function by converting expression gradients of Fj and Ds into asymmetric subcellular arrays of Fat-Ds heterodimers. Fat and Ds colocalize in uniformly distributed puncta in the marginal zone, forming heterodimers that are proposed to occur in a biased orientation along the proximal-distal axis[61]. Golgi localized Fj acts on both Fat and Ds, perhaps via an ectokinase activity to make Fat a stronger ligand, and Ds a weaker ligand, for the other[106]. The graded expression of Fj and Ds [58, 60–62, 74], therefore produce an excess of Fat-Ds heterodimers in one orientation relative to the other, at proximal-distal boundaries, according to the Fj and Ds gradients [61] (Fig. 5). Directional information present in the transcriptional gradients of Fj and Ds is thereby converted into subcellular gradients of Ds and Fat, which then signal to downstream components by an unknown mechanism to regulate orientation of polarization. An attractive model is that these components orient or polarize the apical microtubule web along which PCP components traffic [37, 105, 107, 108]. The protein phosphatase subunit Wdb and the transcription factor Atrophin may have roles in transducing the Fat signal[80, 108].

Gradients of Fj and Ds gradients are present in eye, wing and abdomen, and are therefore good candidates for providing a global signal[58, 60–62]. Interestingly, these gradients may also control tissue size through a mechanism that senses their steepness[109]. This model leaves several additional questions unanswered. If directional information is encoded in the gradients of Fj and Ds, then flattening these gradients should disrupt polarity, and this is seen in the eye[110]. However, the same intervention in the wing produces only a mild polarity phenotype, indicating that in this tissue, another source of directional information is likely to exist([110],see also[111]). Furthermore, in the abdomen, the gradients of Fj and Ds are reversed in anterior and posterior compartments, yet the hairs point posteriorly in both. Similarly, these gradients are oriented oppositely with respect to the direction of Fz accumulation in the eye and wing. Therefore, the signal from this system must be interepreted differently in different compartments.

Disruption of the global module highlights an important feature of the core module. Activity of the core module ensures that within small fat clones, cells almost always have normal polarity, and even within large clones, cells have a strong tendency to local alignment with their neighbors[61, 72]. This tendency toward local alignment is also evident in the domineering non-autonomy seen in wildtype tissue near some mutant clones. Mutant clones that reverse the direction of core protein recruitment in wildtype cells at a clone boundary will propagate the reversed polarity for some distance through wildtype tissue [61, 71].

2. Mathematical modeling of PCP

A variety of modeling strategies to understand PCP have been adopted, with a range of strengths and weaknesses. At one extreme models have been developed to relate the activities or localization of specific PCP proteins to pattern formation. Among the limitations of these is that they require computationally intensive numerical methods to analyze the model and identify parameters. Investigators interested in exploring more global properties of the PCP signaling system have developed a number of more abstracted models that sacrifice capturing (and therefore predicting) molecular detail but allow analytical exploration of parameters and larger scale model behaviors.

2.1 Testing molecular models of PCP with mathematical modeling

A persistent challenge in understanding PCP has been to relate the molecular observations to the emergent polarity patterns evident in and around mutant clones, and therefore to draw inferences about molecular relationships from the clonal phenotypes. Several distinct “bottom-up”[112] mathematical models based on proposed functions of the core PCP protein have been used in efforts to understand the relationship between molecular mechanisms and patterning.

Lawrence et al.[74] created a simple algebraic model to test their proposal that Fz activity can be represented by a scalar value in each cell, and that a comparison of Fz activation levels between cells determines the direction of polarization (Fig. 6). This model is intuitively appealing, but notably, it discards the notion that asymmetrically localized proteins play a role in polarization, and instead suggests that these localizations are more likely a result of polarization.

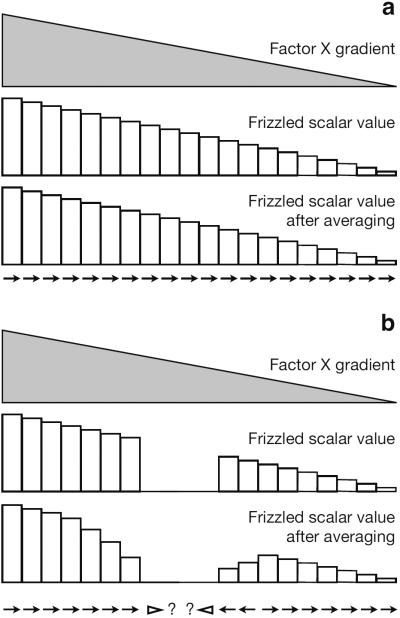
Figure 6.

Schematics of the Lawrence et al. algebraic model. (a) In wild type, the factor X gradient (gray) initiates Fz activation at scalar levels in each cell. After averaging, the resulting Fz levels are compared with neighbors to produce a vector determining polarity (arrows). (b) A wing with a fz clone cannot produce Fz within the clone, and after averaging, the scalar levels of Fz in neighboring cells are affected, altering the resulting polarity.

Forced expression gradients of Fz direct polarity from high toward low Fz levels[83]. Drawing on this observation, as well as a variety of other results, Lawrence and colleagues proposed that factor X, in an unspecified way involving, and most likely resulting from Fj, Fat and Ds function, induces a scalar level of Fz activation in individual cells, depending on their relative position with respect to the factor X gradient. Subsequently, each cell compares its level of Fz activation with its neighbors, using a mechanism requiring Fmi in each cell and Vang in the cell sensing the Fz activity level in its neighbor. Each cell is then proposed to adjust its Fz activity level from that determined by the initial scalar level toward an average of that in each of its neighbors. In a rough gradient, this would have the effect of smoothing the gradient. However, in and around clones that either reduce or abolish Fz activity (fz clones), or conversely elevate Fz activity (vang clones), the gradient would be modified such that it would reverse its slope on either the distal or proximal sides, respectively. Finally, at the conclusion of the averaging process, the comparison process would determine a vector that describes the cells' polarity.

One dimensional lines of cells were numerically simulated to demonstrate that this mathematical model recapitulates the distal domineering non-autonomy near a fz clone (Fig. 6). By proposing that Vang antagonizes Fz activity cell autonomously, it also recapitulates the proximal domineering non-autonomy near a vang clone. Furthermore, the distance to which domineering non-autonomy reverses polarity is controlled by a variable that represents the relative amount by which the averaging between neighbors and the reading of the original factor X gradient influence the adjusted scalar Fz value at each step. The model is attractive in that it provides an intuitive connection between the biological model and the resulting polarity, and it provides a demonstration that a model including factor X plus scalar Fz activation might explain at least some of the observed PCP phenotypes. Yet because the model is not based on specific molecular interactions between signaling components, it cannot be used to gain a mechanistic understanding of these interations. Furthermore, there is no experimental evidence for a tissue wide Fz expression gradient, nor for an activating modification that could produce an activity gradient during planar polarization[95, 99].

Amonlirdviman et al.[71] have described a mathematical model designed to test the feasibility of the asymmetric protein/Fz feedback loop model proposed by Tree et al.[70]. This model proposed that the autonomy or domineering non-autonomy of fz, vang, dsh and pk clones, and a variety of other phenotypes results simply from the dynamics of the proposed interactions (Fig. 7). In this model, the global directional cue is provided as an asymmetric input to each cell that results from the graded expression of Fj, Ds and, in the wing, other unknown signals, transmitted through Fat.

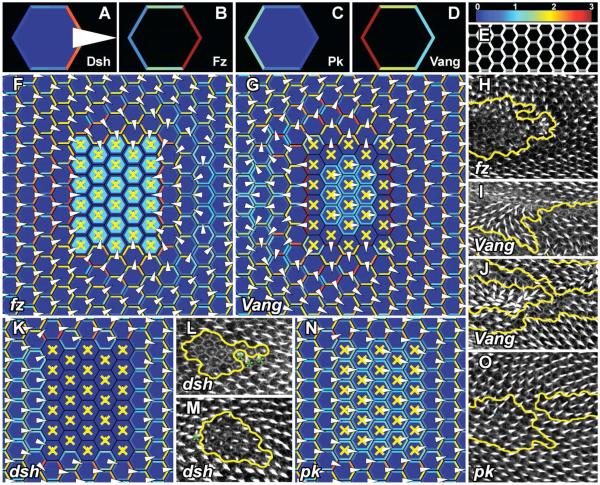
Figure 7.

Simulation results from the Amonlirdviman et al. model, reprinted from[71]. Wild-type results showing the final distributions of Dsh (A), Fz (B), Pk (C) and Vang (D). The same color scale is used in all figures, where 1 is scaled to the initial uniform concentration of Dsh and the scale is truncated so that concentrations greater than 3 are shown in red. (E) Simulated distribution of Dsh displayed as an intensity representing total Dsh concentrations, corresponding to the appearance of Dsh∷GFP in wild-type experiments. Simulation results of several PCP phenotypes showing the final distribution of Dsh with predicted hair growth directions derived from the vector sum of Dsh (F,G,K and N) and corresponding pupal wings (H-J,L,M and O). Greater Dsh asymmetry is represented by hair placement at increasing distances from the cell center. When Dsh asymmetry does not exceed the threshold value, the hair is depicted at the center of the cell. Mutant cells are designated with yellow. (H) fz^R52 clones. (I and J) Vang^A3 clones. (L and M) dsh^V26 mutant clones. (O) pk-sple¹³ clones. Asterisks mark non-autonomous effects near dsh clones.

The Amonlirdviman model represents the proposed Fz feedback loop solely as reactions between Dsh, Fz, Vang and Pk to form protein complexes, with a feedback inhibition term and a global asymmetric input. These interactions are represented in a series of reaction-diffusion partial [71] and ordinary[113, 114] differential equations that define the concentrations of proteins or protein complexes, and their evolution over time, at each location within each cell of a simulated two-dimensional cell grid. Given these equations, and a set of starting protein concentrations, one can then simulate the evolution of protein localization over time. Fmi and Dgo were not explicitly modeled, yet the logic of the model is retained if they participate in the explicitly modeled interactions. The final polarity of a cell is taken as the vector sum of Dsh within that cell. Since the values for the parameters needed to instantiate the model are not known, they were identified through an optimization procedure in which the model was asked to simulate a representative set of PCP phenotypes. The first experiment was, therefore, to ask if a set of parameters could be identified that would produce a large set of characteristic PCP phenotypes. The results showed that the proposed feedback loop mechanism can recapitulate all PCP phenotypes that were examined, demonstrating that the Fz competition machine, combined with the global directional cue, is sufficient to explain domineering non-autonomy and other phenotypes, despite features of the model that are counterintuitive to some (Fig. 7; [38, 72]). The model is robust to parameter perturbation. In addition, the model was challenged to simulate some of the non-intuitive phenotypes observed by Lawrence and colleagues in the abdomen[74], and it did this remarkably well without prior knowledge of the observed biological result (K. Amonlirdviman, J. Axelrod C. Tomlin and P. Lawrence; unpublished results).

The Amonlirdviman model also led to a new insight important for understanding autonomous versus non-autonomous fz alleles. The model demonstrated that a Dsh mutant protein rendered nearly incapable of being recruited to the plasma membrane in the presence of Fz (Dsh¹) produced a nearly (though not completely) cell autonomous clonal phenotype. It therefore followed that autonomous fz alleles should recruit Dsh poorly, yet retain the ability to recruit Vang in the neighboring cell. In contrast, non-autonomous fz alleles should exhibit impaired interactions with both Dsh and Vang. Simulations showed this to be the case. Based on these predictions, the cell autonomous fz alleles were then experimentally demonstrated to retain their ability to recruit Vang to the boundary of neighboring cells while losing their ability to recruit Dsh to the plasma membrane. In contrast, non-autonomous alleles were shown to lose their interactions with both Dsh and Vang. The model therefore yielded a prediction that was experimentally confirmed, lending insight into the biological process.

The mode by which the global Fat mediated directional signal impinges on the core module is not known. The Amonlirdviman model, and a subsequently modified version[115] allowed the authors to test the feasibility of global inputs in several different forms, including an identical gradient across each cell (as suggested by Ma et al.[61]), a scalar gradient across the tissue (similar to that suggested by Lawrence and colleagues[74]) and a monotonic gradient across the tissue (Fig. 8). The results demonstrated that any of these forms of global directional input can produce correct results in conjunction with the feedback loop model. Therefore, the other conclusions drawn from this work do not depend on the specific mechanism that is implemented. Additional experimental results will be required to distinguish between these possible modes of global module signaling.

Figure 8.

Global signaling paradigms tested by the Amonlirdviman et al. model[71]. (a) Non-globally varying, constant slope within each cell, as suggested by the global signaling model depicted in Figure 5 (top). (b) Globally varying, uniform within each cell, similar to that proposed by Lawrence et al.[74]. (c) Globally varying, constant slope. This signal can be viewed as a combination of the forms shown in (a) and (b). Depending on whether the intercellular or intracellular components predominate, the slope can be in either direction. As shown, the subcellular asymmetry dominates, as in (a).

The Amonlirdviman model demonstrates the feasibility of the proposed biological model to explain characteristic phenotypes without invoking diffusible factors, and provides insight into the molecular basis of autonomous and non-autonomous fz alleles. The underlying molecular interactions are explicitly defined, though they certainly reflect a simplification of the true molecular mechanism. The cost of increased detail is a potential loss of intuition: with 10 differential equations and about 30 parameters, the key shortcoming of the Amonlirdviman model is in its complexity. In addition, it fails to provide testable predictions that might distinguish between models for the mechanism by which Fat activity influences the Fz feedback loop.

A third molecular-based mathematical model, presented by Le Garrec and colleagues, is a reaction-diffusion model using stochastic difference equations[116]. The authors model a system based on a graded extracellular Fz ligand and asymmetric protein localization dependent on intracellular feedback loops (Fig. 9). The model aims to test the requirements for such an extracellular ligand, and to ask whether introduction of intercellular interactions might be mediated by Fmi dimerization. The underlying biological model, while similar to that modeled by Amonlirdviman et al., differs in several essential ways. The authors used trial and error to explore how the model would react to a variety of initial ligand conditions, and found that to achieve the correct results for wildtype and mutant clones, the ligand should be assumed to be expressed at a limiting level in a gradient from proximal to distal. Ligand-receptor (Fz) binding is rapid and irreversible, and the free ligand gradient must disappear early in the signaling process. The feedback loops adopt two hypothetical feedback mechanisms, different from those of Tree et al.[70], as shown in Fig. 9. Fmi is modeled as an agent mediating the interaction between Fz and Vang, and has higher affinity for heterotypic FzFmi-FmiVang complexes than for either homotypic complex including only Fz or only Vang. Furthermore, complex assembly is restricted to an ordered set of additions, eliminating some possible species, and finally an activated form of Fz (ligand bound, denoted Fz*) and Dsh (Fz bound, denoted Dsh*) are assumed. Variables were instantiated by manual adjustment to achieve desired wildtype and mutant clonal phenotypes, and to be within reasonable physiological limits.

Figure 9. Axelrod and Tomlin.

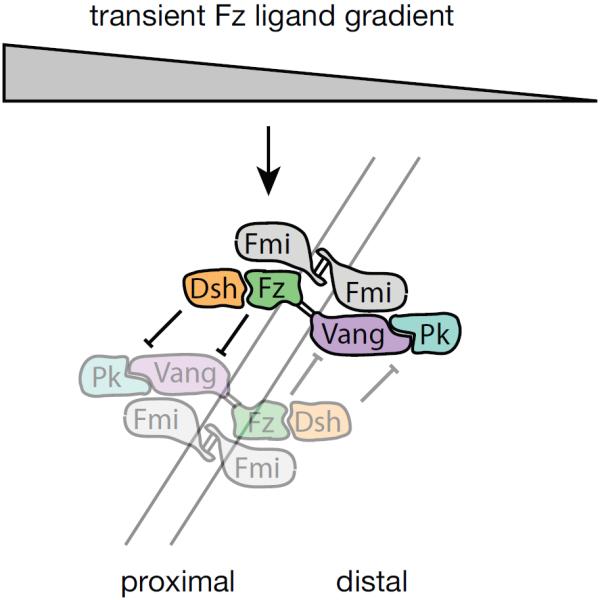
Signaling mechanism modeled by Le Garrec et al.[116] using reaction-diffusion stochastic difference equations. Note that the feedback loops differ from those in Figure 5.

The model succeeds in capturing many characteristic PCP phenotypes, and demonstrates that Fmi mediated intercellular interactions can produce correct results, as had been suggested though not tested by Amonlirdviman et al.[71], and subsequently experimentally demonstrated[89]. The model encodes intrinsic stochastic variation, and the results demonstrate that the model structure is robust. This model has more recently been extended to the fly eye, describing the relationship between PCP and Notch signaling[117].

The Le Garrec model predicts a number of conditions that have not been experimentally validated. First, the model makes a strong prediction that the initial extracellular gradient of ligand must be proximal to distal, and must be shallow and short lived. This may be at odds with a number of findings. It is not clear that a ligand for Fz exists in PCP signaling in the fly[73, 89], and the irreversibility of ligand binding would suggest an affinity orders of magnitude higher than that measured for Fz and Wnts[118]. Irreversible activition of Fz might occur by a different mechanism that is activated in a transient and graded fashion (see for example [119]). A more vexing problem is that the transient nature of the activation is difficult to reconcile with the experimental observation that active Fz can be present in only the second half (or only the first half) of the 30 hour polarization period and still achieve reasonably good polarity[120]. A second unvalidated condition is the hypothesized intracellular feedback mechanisms that are not based on experimental evidence. It is difficult to know what impact this might have on the simulation results, though it is curious that a feedback mechanism similar to that proposed earlier[70, 71] apparently did not produce the correct results in this context.

2.2 Understanding swirling PCP patterns with mathematical modeling

A modified version of the Amonlirdviman model was used, in conjunction with biological experiments, to ask whether the variable swirling patterns seen within fat clones could be attributed to irregularities in cell packing[113]. Biological experiments were consistent with a causative effect of irregular cell packing on formation of swirls, and modeling was invoked to ask whether cell packing is sufficient to explain the swirling patterns. The mathematical model was modified to simulate PCP on a cell grid captured from images of wings, and was shown to be capable of predicting the presence of a swirl from the cell geometry, allowing the authors to conclude that one need not postulate anything other than the activity of the core module operating in the context of a given cell packing to account for the swirls. Core module function is therefore sensitive to cell packing, but combination with a distributed global directional cue robustly overcomes the noise produced by irregular packing.

A simple model of macroscopic polarity behavior, inspired by ferromagnets and not tied to specific molecular interactions, was reported by Wang and Nathans[121]. Iterative interactions between cells in a two-dimensional grid produced many small swirls that progressively merged to fewer, larger swirls. A surprisingly weak initial global polarity was sufficient to rapidly cause the pattern to converge to a parallel one.

A model inspired by dielectric dipoles was developed by Zhu to explore the effect of cell packing on production of swirls[122]. In this model, cells are described by equations often used to represent polarizing dielectric molecules. The model, designed to test the contribution of cell geometry to producing swirling patterns, simulates different cell packing arrangements by permitting or disallowing the influence of possible neighboring cell “dipoles” within a cell grid. While abstract in conception, the model, based on a 2D grid, requires numerical analysis. The relationship between cell packing and a directional cue (representing an initial polarization) in producing polarity patterns was explored. Similar to the Owen model described below, simulations showed that anisotripic propagation of molecular orientation produces swirling patterns, but that when present, global cues predominate in determining polarity. This conclusion holds for both whole fields, and within clones of cells, in which weakened or absent global cues greatly increased the sensitivity of swirling patterns to cell packing. Interestingly, the shape of clone boundaries contributes to production of swirling patterns as well.

Burak and Shraiman developed a model that incorporates and evaluates the effects of noise (stochasticity) on polarization[123]. Their model represents polarization in terms of generic complexes in a ferromagnet-type model. A simple model of bistability is assumed, with nonlocal inhibition, to produce dipoles. Stochasticity is modeled as white Gaussian noise. As in other models, polarization in the absence of a global signal produced swirls, and these were seen to be noise dependent. A global cue exerted as either a boundary signal or a weak bulk signal were examined in the context of noise. The weak bulk orienting signal but not the boundary signal was shown to compete with local noise to produce correct polarization within a realistic time frame. A gradient of the bulk global cue of 0.1% between cells is enough to produce normal polarity before a swirling pattern becomes fixed. The authors suggest that imposition of an artificial gradient of defined steepness to compete with the endogenous signal would be a way to measure the gradient of the endogenous global directional cue.

2.3 An analytical model of PCP signaling

Owen and colleagues have worked on a class of models representing juxtacrine signaling in an epithelial sheet with a single ligand and receptor, and feedback coupling levels of each on adjacent cells[124]. In exploring the properties of a model for lateral inhibition, they relaxed a prior assumption of homogeneous ligand and receptor distribution around the cell surface to allow for cell polarization and included diffusion. Using these conditions, the authors identified conditions in which a wildtype planar polarization occurred. In a cell grid, domineering non-autonomy such as that seen near a fz or vang clone could be observed.

These properties were explored further in[125] using a mathematical model which abstracts PCP activity to two variables per cell while capturing the mechanisms of feedback and diffusion in a compelling way. Ligand and receptor are equivalent to proximal and distal PCP complexes, and are coupled by negative feedback between adjacent surfaces of neighboring cells. Contributions of diffusion, the strength of feedback, and the strength of the initial directional cue were explored. The authors concluded that polarization occurs for all parameter sets in which there is sufficiently strong feedback and sufficiently weak diffusion. A weak, distributed, initial polarization signal is sufficient to initiate polarization, and the system can overcome variations in initial conditions across the cell array, as would be expected in vivo. Providing global directional information from a boundary source gave traveling wave models that showed a broader range of behaviors more difficult to reconcile with experimental results. The model makes interesting quantitative predictions that would be interesting to test, but would require defining experimental interventions that modify strength of feedback or diffusion rates.

2.4 PCP signaling and primitive streak formation

One final, interesting, model does not aim to understand PCP mechanisms, but rather invokes PCP to explain the stereotypical cell migration pattern seen during primitive streak formation in the chick epiblast[126]. Using a grid-free cell-based model in which cells behave as ferromagnets, Newman showed that an initial pattern of PCP based on known patterns of gene expression, together with a coupling of cell velocity and direction to the average PCP vector of cells in the neighborhood, is sufficient to reproduce the observed pattern of cell migration. This appealing model awaits experimental confirmation.

Conclusion

While research efforts integrating biological experimentation and mathematical modeling have demonstrated that feedback based on asymmetric protein localization at cell boundaries is a feasible mechanism for core module function in PCP, our understanding of the specific molecular mechanisms is still rudimentary. Furthermore, our understanding of how the global, core, and effector modules are connected together is lacking. Future efforts should be aimed at probing the PCP system from its molecular level interactions, through its multicellular behavior, to the tissue-level effects. More detailed models of each of the modules will allow us to better understand how mutation of specific components compromises function, and how signals from module to module may be received and interpreted. Thus the best strategies will likely be those that employ a hierarchy of mathematical models, from detailed mechanistic models to representations that abstract the function of each module to just a few variables.

Finally, what about the future of mathematical modeling methods in biology? A commonly asked question is “How have the equations improved our intuitive understanding of how the system works?” Intuition not only allows us to describe in words the behavior of the system, it is necessary in generating likely hypotheses for the function of connected or related biological mechanisms. Simple models comprised of a few parameterized equations, or more complex models that can be represented as simple interconnections of such, win out in this respect. Seeking simplifications in biological modeling can be compared to engineering design, in which mathematical analyses are almost always performed on simple abstracted models, prior to the numerical simulations that validate the design on large-scale, complex models more closely representing the true system dynamics. It seems likely that the best modeling efforts will be those that develop hierarchies of equations, which, for example, connect the low level detailed dynamics of molecular interaction, with a higher level abstract view of the basic functionality involved, such as amplification, feedforward, and feedback.