Mapping Brain Anatomical Connectivity Using Diffusion Magnetic Resonance Imaging: Structural connectivity of the human brain

In 2009, the National Institutes of Health ambitiously launched the Human Connectome Project (HCP) [1] to promote engineering capabilities for imaging and analyzing brain connections. One of the primarily promoted technologies is diffusion Magnetic Resonance (dMR) imaging which non-invasively maps brain connectivity at a macroscopic scale by measuring water molecules’ anisotropic diffusion constrained by neural fibers. Following years of steady advancement, dMR imaging technique has reached unprecedented spatial and angular resolution, and its computational analysis methods, stimulated by growing research needs, have also blossomed. This is achieved by joint contributions from various areas: signal processing, applied mathematics, network analysis, etc. In this review and tutorial article, we outline the milestones on this exciting path of interdisciplinary technology development, with the aim of bringing these advancements to engineers outside the medical imaging community.

This article covers key components in the workflow to map structural connectivity of the human brain, including data acquisition, neural fiber orientation modeling, image processing, tractography, and applications to brain studies. For each topic, basic theories are reviewed, and major breakthroughs and state-of-the-art technologies are discussed. Along with an overview of existing technologies, we also attempt to provide an outlook of future challenges in building a comprehensive connectivity map that integrates genetic and functional information.

Diffusion MR Imaging

At a microscopic scale, water molecules in an isotropic medium move freely in all directions in a jittery and erratic fashion. This random walk was first noticed in 1827 by Scottish botanist Robert Brown, and explained physically by Albert Einstein in 1905, and later rigorously modelled as a mathematical stochastic process by Norbert Wiener. Movement of these tiny molecules not only inspired mathematicians to develop elegant theories now widely used in financial analysis, but is also utilized by medical engineers to “look” through the human brain in vivo at its sophisticated neural network. In an anisotropic medium, such as brain tissues containing neuronal fibers, water molecules move faster along than across structural constraints. By measuring their anisotropic diffusion, we can infer the underlying structure of neuronal fibers. Figure 1 shows a typical information flow of studying brain connectivity using dMR imaging: neural fibers introduce anisotropic diffusion (a) and influence magnetic resonance (MR) signals generated from spinning protons (b); diffusion magnetic resonance (dMR) signals are collected along many diffusion directions (c) and then reconstructed at each voxel location as fiber orientation distributions (d); local fiber structures are assembled and “weaved” together as long fiber tracks (e) to build a network (g) connecting brain cortex regions (f); these networks are further investigated for their relationship with brain’s function and development. We will elaborate this procedure step by step in the following sections.

Figure 1.

Information flow of structural connectivity analysis. (a) Water molecules move faster along than across neuronal fibers. (b) Diffusion affects the electromagnetic waves radiated by precessing protons. (c) dMR imaging captures diffusion signals along different directions and forms images. (d) Fiber orientation distributions (FODs) are reconstructed from diffusion images. (e) Fiber tracks are simulated from FOD images. (f) The brain cortex is segmented into many regions using structural MR images, for example with software FreeSurfer [2]. (g) Connectivity networks between cortex regions are constructed from fiber tracks.

Let us first look at how dMR signals are generated. Understanding the generation procedure is important for the processing and interpretation of dMR images. It also sheds light on the potential limitations and caveats of using dMR images. We start with excitation of protons in a magnetic field and then explain how diffusion affects signal resonation, with formulations in the so called k-space and q-space. The relationship between diffusion and magnetic resonation is the key to dMR imaging and its data analysis.

Nuclear Magnetic Resonance

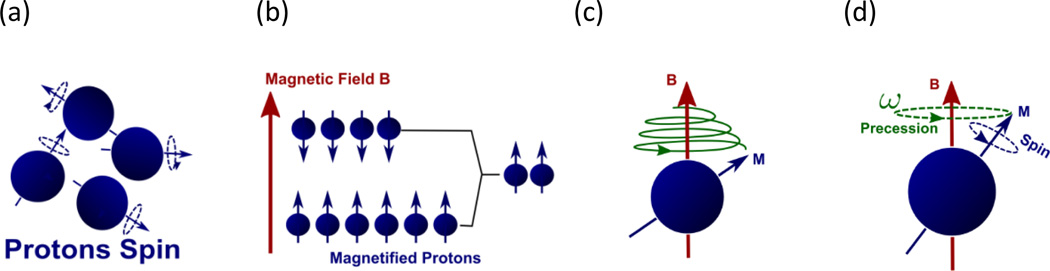
A proton/hydrogen, spinning with its positive electrical charge, forms a tiny magnetic moment along its spin axis. Under normal circumstances, protons spin randomly in all directions (Figure 2a). In the presence of an external magnetic field, they align with the field, getting polarized (Figure 2b). In this case, if the spin axis is perturbed away from the field direction, it will rotate in a spiral path to gradually realign with the magnetic field (Figure 2c). This is analogous to the motion of a rotating gyroscope hung on a rope. Perturbation from the equilibrium is called “excitation”, and restoration is called “relaxation”.

Figure 2.

Nuclear magnetic resonance. (a) Protons spin randomly, each forming a tiny magnetic moment. (b) In the presence of a magnetic field B, protons align with the field. Some spin “down” against the field and more spin “up” along the field. The net magnification is along the field. (c) If a proton is perturbed from the field direction, it will return to its equilibrium in a spiral path, similar to a rotating gyroscope hung on a rope. In this process, it radiates electromagnetic waves. (d) The spiral path has a precession component and the frequency is determined by the Larmor equation ω = γB where γ is the gyromagnetic ratio [3]. In our body, there are a numerous number of protons which can be used to generate magnetic resonance signals.

The spiral return to equilibrium consists of three different motions. The first is precession (Figure 2d) around the field direction at the Larmor frequency (named after Sir Joseph Larmor, 1875 ∼ 1942) ω = γB where γ is the gyromagnetic ratio [3]. This Larmor precession is essential in MR imaging. We can transmit radio waves at this frequency to excite protons, and the excited protons will in return radiate electromagnetic waves at the same frequency in their precession. To maximize the radiated energy, protons are flipped by 90 degrees in excitation, perpendicular to the field direction. This resonated radio wave is collected as a function of time, and its Fourier transform shows a peak near the Larmor frequency, reflecting protons’ spin density. If a magnetic field with a linear gradient is applied, then protons’ spatial location will be “encoded” into their precession frequencies. In this way, we can recover spatial density of spinning protons in the Fourier domain, as elaborated in the “k-space” and “q-space” sections later. The other two motions are the precession plane’s moving toward the equilibrium and shrinkage of the precession radius. Usually they are exploited to produce image contrast ratio [3], but here we will not go into their details.

K-space

If a gradient g is added to a uniform magnetic field B, then protons at location r precess at their local Larmor frequency γ(B + g · r). The radio wave they radiate, as a function of time, is s(r)e^iγBt e^iγ(g·r)t where the magnitude s(r) reflects the amount of local magnification and is the interest of imaging. Because the carrier wave e^iγBt can be removed with a heterodyne mixer² in the receiver [3], it effectively reduces to s(r)e^iγ(g·r)t. Instead of naturally referencing with time t, Sir Peter Mansfield and Grannell in 1973 introduced a vector k = γgt [4]. In k-space [5], the total signal collected from all protons in a volume V turns out to be

$$S(k)={\int }_{v}s(r)e^{ik\cdot r}\mathit{\text{dr}}$$ Eq.(1)

Eq. (1) clearly reveals that local signal s(r) can be reconstructed from S(k) with the Fourier transform [4]. This relationship lies in the heart of spatial reconstruction, and Mansfield received a Nobel Prize for the imaging techniques developed based on it.

q-space

In a homogeneous field, exchange of protons between different locations does not affect local signals because they all precess at the same Larmor frequency in the same phase after their initial excitation. When protons precess at different phases spatially, then their movement in and out of a location will mix phases and hence reduce signal magnitude. If we can encode proton’s displacement into their phase shift, then we will be able to quantitatively deduce their displacement from the signals reduced by phase mixture.

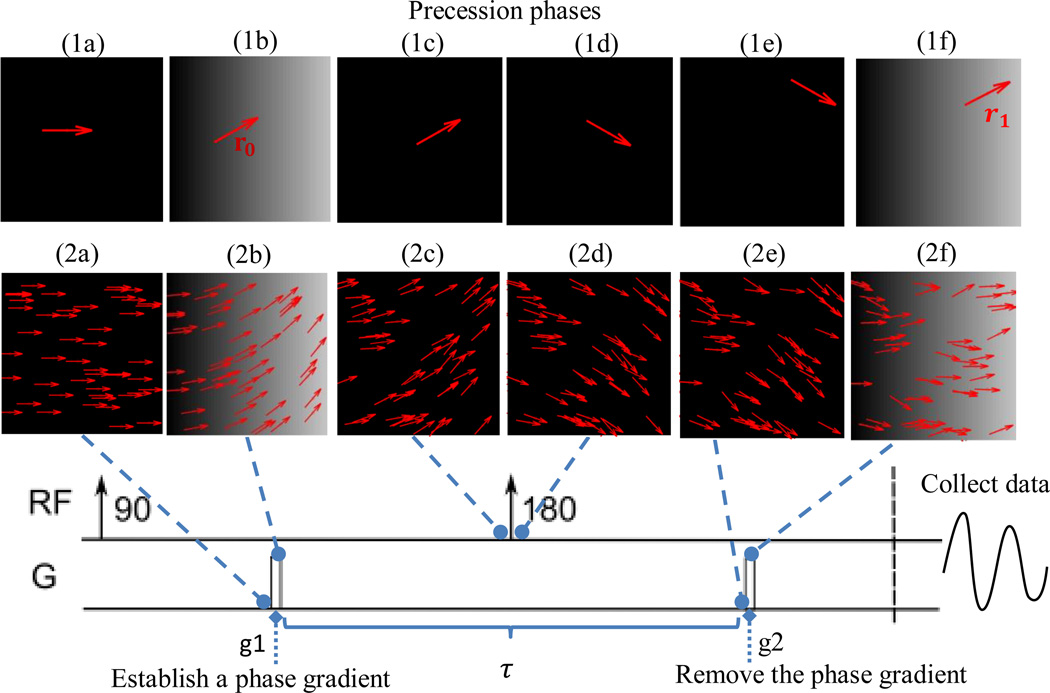
Stejskal and Tanner in 1965 [6] invented a widely used scheme that makes such deduction of diffusivity from MR possible, as sketched in Figure 3. After excitation, a strong gradient pulse g is applied for a short duration δ to establish a phase gradient q. If δ is so short that protons have hardly displaced before the establishment of q, protons at location r₀ will almost instantly receive a phase shift of q · r₀. Later, a radio frequency pulse is transmitted to flip the spinning protons by 180 degrees. This flipping technique, invented by Hahn in 1950 [7], reverses the phase gradient spatially and negates the initially received phase shift to — q · r₀. After time τ of the first gradient pulse, a second gradient pulse is applied to remove the reversed phase gradient. Protons having migrated to a location r₁ will receive a phase shift q · r₁. In this way, the displacement from r₀ to r₁ is translated to a net phase shift q · (r₁ — r₀). If we denote the displacement vector as v ≡ r₁ — r₀, then the net phase shift is solely determined by the displacement vector, independent of the initial location. Diffusion duration is controlled by the interval τ between the two gradient pulses.

Figure 3.

Paradigm of Stejskal and Tanner’dMR imaging scheme [6]. (1a) - (1f) illustrate phase change of a single spinning proton. (1a) before application of the first gradient pulse g₁, its phase is 0; (1b) during g₁, it receives a phase shift q · r₀ at its location r₀; (1c-1d) the 180-degree pulse reverses the phase gradient and negates the initially received phase tag to –q · r₀; (1e) immediately before application of the second gradient pulse, the proton has moved to a new location r₁; (1f) the second gradient pulse exerts a phase shift q · r₁ on the proton. The net phase shift the proton received is q·(r₁ − r₀). If we define displacement vector v ≡ r₁ − r₀, then the phase shift is q·v, independent of the starting location r₀. (2a) - (2f) illustrate how diffusion causes phase incoherence among protons, at the same snapshot time points of (1a)-(1f). Due to displacement, protons cannot restore their initial phases, with some shifted forward and some backward, so their phases become incoherent and the signal is reduced.

The total signal s_τ(q) in the Stejskal-Tanner experiment is integration of all possible displacement signals in terms of e^iq·v and weighted with average displacement probability P_τ(v) = ∫ P_τ(r → r + v)p(r)dr, where p(r) is the spin density at location r and P_τ(r → r + v) is the probability of moving from r to r + v after time τ. P_τ(V) averages displacement probability over start locations, and is called the “ensemble average propagator”. If s₀ is the signal without the two gradient pulses, then s_τ(q) relates to s₀ through superposition of all phase shifts as

$$s_{\tau }(q)=s_0\int P_{\tau }(v)e^{iq\cdot v}\mathit{\text{dv}}.$$ Eq.(2)

Eq. (2) bears a close resemblance to Eq. (1) and similarly we call the space formed by phase gradient “q-space”. The ensemble average diffusion propagator P_τ(v) can be obtained from s_τ(q) with the Fourier transform. Please note that Eq. (2) assumes that the two gradient pulses are so short that their phase shifts have perfectly tagged protons’ location before the protons have hardly displaced. However, this is not true in practice, so Eq. (2) is inaccurate in most cases.

Diffusion propagator of isotropic media is a Gaussian distribution with variance 2Dτ where D is the diffusion coefficient. Because the Fourier transform of a Gaussian distribution is still a Gaussian, the diffusion signal in this case also has a Gaussian format: s_τ(q) = s₀e^−|q|2Dτ. As aforementioned, this equation is inaccurate due to the unneglectable gradient pulse duration δ. Adjusted for rectangle gradient pulses, s_τ(q) becomes s₀e^{−|q|2D(τ–δ/3)}. The |q|²(τ - δ/3) term determines how sensitive s_τ(q) is to the diffusion coefficient D, and Basser, Mattiello, and Le Bihan [8] coined the name b-value for it. The direction of a q vector can be assigned to the b-value derived from it. In this way, we get a b-vector from a q vector.

There are several schemes to sample b vectors. Sampling b-vectors of the same magnitude is called single-shell acquisition. Sampling b-vectors of multiple magnitudes is called multi-shell acquisition. Sampling b-vectors laid on a 3D lattice is called diffusion spectrum imaging.

Data Acquisition

Innovative engineering ideas are often needed for turning elegant theories into practical, efficient and affordable technologies, and such is the case of dMR image acquisition. One of the major difficulties encountered with dMR imaging is its acquisition time, because it essentially collects data for a six-dimensional space: three dimensions for k-space and the other three dimensions for q-space. In the early days of MR imaging, it typically took 10 ∼ 20 minutes to scan a non-diffusion structural image of 64×64 pixels [9]. Nowadays, the protocol developed in the Human Connectome Project takes about 55 minutes to scan the whole brain twice at the 1.25mm resolution (about 150×150×150 pixels) in 270 different diffusion directions [10]. This amazing speed-up is achieved with a series of breakthroughs.

Echo-Planar Imaging (EPI)

was invented by Sir Peter Mansfield in 1977 [11]. This technique made it possible to obtain an individual MR slice in the time frame of 50∼100 msec. After selectively exciting a slice of an image with the radio frequency determined by a gradient pulse along the z direction, EPI efficiently traverses k-space by modulating the field gradient in the x and y directions, as illustrated in Figure 4. It first sends negative gradient pulses in both x and y directions to initialize the scan at the left lower corner in k-space. Then it alternatively switches between positive and negative gradients along the x direction, iterating forth and back in k-space. Meanwhile, whenever it reverses x-gradient direction, it sends a short positive gradient pulse along the y direction, to start the scan with a new y coordinate in k-space. In this way, k-space is iterated over in a zig-zag manner and a slice of the image can be scanned in one excitation. Because gradient pulses along the x direction control protons’ precession frequency and those along the y direction each time shift their phases, they are respectively called the frequency-encoding and phase-encoding direction. Please note that it takes much longer time for EPI to move one step along the phase-encoding direction than the frequency-encoding direction. This will make artifacts more pronounced along the former than the latter, as discussed later.

Figure 4.

Echo-Planar Imaging (EPI). The left panel shows gradient pulses and the right panel shows the corresponding path in k-space. In the company of a gradient pulse in the z-direction (left, blue), a radio frequency selectively excites a slice of an image. Then negative gradient pulses (left, yellow) along the x and y directions initializes the scan at the left lower corner of k-space, as shown by the yellow arrow on the right. As the x-gradient switches (left, red boxes), it travels back and forth in k-space. Whenever the x-gradient changes direction, a short gradient pulse in the y-direction (left, green boxes) is applied to move the scan in the x direction to a new y-coordinate in k-space. If data are sampled at s₀, s₁ …, s_n in each scan of an x-direction line, then it takes time T_x to move one step in the x direction and T_y in the y direction. T_y is much longer than T_x.

Parallel Imaging

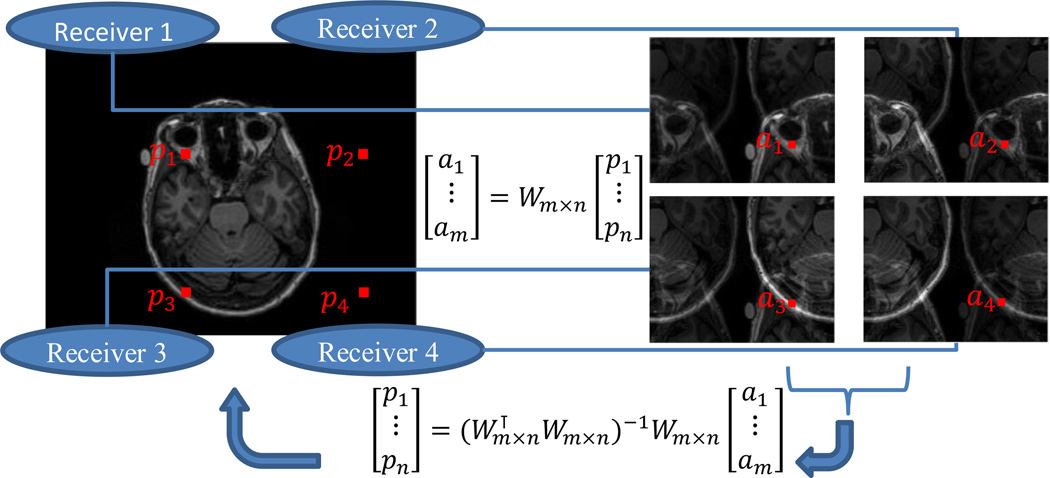
exploits receivers’ localized spatial sensitivity to reconstruct an image with reduced sampling in k-space. Ordinarily, if k-space is under-sampled, the reconstructed image in a reduced field of view (FOV) shows overlapping effect, i.e., aliasing. In the aliased view, a pixel value is the linear combination of its aliasing pixels in the full view. If multiple receiver coils are placed at different locations, each of their reconstructed images takes a different linear combination, due to their different spatial sensitivity. With many different linear combinations, it is possible to separate all the aliasing pixels provided that the number of receiver coils is at least the under-sample rate. The separation can be achieved in two ways, either in the image domain, as the Sensitivity Encoding (SENSE) [12] does (Figure 5), or in the frequency domain, as the Generalized Auto-calibrating Partially Parallel Acquisitions (GRAPPA) [13] does.

Figure 5.

Parallel imaging with the SENSE [12]. Suppose that we have m=4 receivers, and in image acquisition under-sample k-space by 2 in both the x axis and the y axis. Each pixel in the reduced field of view, has n = 4 aliasing pixels. The n aliasing pixels [p₁,…,p_n] are linearly combined with a sensitivity matrix W_m×n in each of the reconstructed images, resulting [a₁,…,a₂] in the reduced field of view. The full view image can be recovered by solving a linear problem for each of the aliased pixels.

Multi-Band Multi-Slice Imaging

excites multiple image slices by transmitting multi-band radio frequencies and reconstructs the excited slices with signals collected by multiple receivers [14]. Because the signal received by each coil is a unique linear combination of the excited slices, they can be separated as long as the number of receivers is not less than the number of excited slices. The multi-band multi-slice technique can be used together with parallel imaging to achieve two-way acceleration [15].

Compressed Sensing

in its theory, ensures that data sparse in a domain can be reconstructed without much information loss by sporadically sampling them in another almost random domain. Because there is only a limited number of crossing fibers at one voxel, it is possible to reconstruct diffusion displacement distribution in a compressed way. To further accelerate dMR imaging with compressed sensing, various sparse bases have been proposed, including wavelets [16], spherical ridgelets [17], and adaptive dictionaries [18].

Artifacts of dMR Imaging

As shown in previous sections, dMR imaging encodes protons’ location by their precession phase and recovers spatial information such as voxel location and displacement by transforming signals from the frequency domain, such as k-space or q-space, to spatial domain. This is the essential rule of MR imaging. When assumptions establishing the phase-location relationship are violated, then artifacts come in, and some might be very insidious. Here we briefly go through some of them, without diving into details of their related MR pulse sequences, but explain from k-space and q-space perspectives.

Gibbs Ringing

also known as truncation or spectral leakage, appears as spurious ripples around sharp edges. It is a consequence of reconstructing images from MR signals with the Fourier transform. With an infinitely wide frequency band any signals can be almost perfectly represented. However in MR imaging practice we can only sample a finite number of frequencies. As a result, high frequency oscillation required to represent sharp edges are truncated and such truncation shows in the reconstructed images as ripples near high-contract edges, as shown in Figure 6.

Figure 6.

Gibbs Ringing. (a) When sharp edges are approximated with truncated Fourier series, the missing high frequency components produce ripples around the edges. (b) An MR image with Gibbs ringing. (c) The same image low-pass filtered. (d) The same image corrected with a total-variation method. Images (b)∼(d) are reproduced from [20].

Because usually fewer samples are taken in the phase-encoding direction, the Gibbs artifact is most prominent along this direction. One remedy is to increase the number of phase-encoding steps or reduce the field of view. However it can never be eliminated because it fundamentally lies in the Fourier reconstruction rule of MR imaging. Low-pass filtering in k-space [19] is a straight-forward post-processing method to minimize Gibbs ringing, but this may blur the image and lower its quality. More complicated methods, such as total-variation [20], have also been developed.

Geometric Distortion

There is no free lunch. As EPI accelerates imaging speed, it also brings a very insidious artifact: geometric distortion. With a homogenous gradient field, protons’ spatial location can be linearly mapped to their precession phase or frequency. What will happen if the gradient varies spatially, or equivalently, the magnetic field is non-linear? The result is not additive noise overlaid on a “noise-free” image, but spatial distortion, because the mapping between spatial location and signal phase becomes non-linear. Even with a scanner producing a perfect linear magnetic field, tissues with different magnetic susceptibility still introduces local nonlinear gradients.

Geometric distortion is far more obvious in the phase-encoding direction than in the frequency-encoding direction. If there is a nonlinear background gradient other than the controlled one, it shifts protons’ precession all over the time during the image acquisition procedure, and its effect accumulates. For the frequency-encoding direction, the accumulation time for each sample step is just the interval between two sampled points. For the phase-encoding direction, the accumulation time for each scan line is the interval between the start time points of two lines. This is much longer than that for the frequency-encoding direction, and consequently accumulates much more distortion effect. Distortion along the frequency-encoding direction usually is at the sub-voxel level, while along the phase-encoding direction it could be 3 ∼ 10 voxels.

Geometric distortion can be corrected by unwarping with an estimated background field map [21]. Distortion stretches regions where the unwanted background gradient is along the encoding direction and squeezes where it is against. If the same image is scanned twice, with opposite encoding directions, then it will experience two opposite distortions. With the two distorted images, it is possible to estimate the distortion field [22], as shown in Figure 7. Stretched regions can be better restored than squeezed ones, because they still hold all intensity information.

Figure 7.

Example of geometric distortion. (a) shows two diffusion MR images collected with opposite phase-encoding directions. (b) is the estimated field map from (a) by nonlinear registration. (c) is the corrected image. These figures are reproduced from [22].

Eddy Currents

A time-varying magnetic field generates an electrical field, and in turn a time-varying electrical field generates a magnetic field. When strong magnetic gradient pulses are switched on and off rapidly, which is common in dMR imaging, they induct electrical currents on conductive surface of MR scanners. The currents, called “Eddy currents” may persist and produce a magnetic gradient other than the controlled one. As explained previously, such an extra gradient will lead to geometric distortion.

It is better to suppress the effect of Eddy currents during acquisition than post-processing. It can be reduced first at the source with shielded gradient coils, and further by using a special twice-refocused spin echo [23]. It can also be corrected in the post-processing stage with an estimated field map.

Fat Shift

So far we have assumed that all protons have the same gyromagnetic ratio γ so in a magnetic field with a homogeneous gradient their Larmor frequency should be linearly associated with their location. However, we also have a considerable amount of fat in the scalp whose protons precess with a much higher gyromagnetic ratio, in long chains of carbons with 1–3 hydrogen atoms. Because spatial location in MR imaging is encoded with phase or equivalently frequencies, fat signals in the reconstructed image will not appear additively at the location of scalp, but instead, map to locations where water protons precess with the same Larmor frequency as they do! In a magnetic field of 3 Tesla, fat protons precess with a frequency 400 Hz higher than water protons do. The phase-encoding dimension of a typical EPI has around 30 Hz per pixel, so the 400 Hz difference will show as a shift of a dozen of pixels in the phase-encoding direction.

Another reason makes fat-shift more harming to dMR imaging than other modalities. The diffusion coefficient of fat is much lower than that of water, so their signal attenuation, according to equation S = S₀e^−bD, is stronger than that of water protons. Therefore, fat shift appears as bright curved lines in dMR images, or as dark lines in derived diffusion coefficient images, as shown in Figure 8.

Figure 8.

Example of fat shift. (a) An image with fat-shift (left), and the derived apparent diffusion coefficient (ADC) image (right). (b) An image of the same subject with fat-shift suppressed (left), and the derived ADC image. These figures are reproduced from [24].

This fat-shift effect can be suppressed by various methods and there is no simple answer to “which is the best?”. The most widely use one is to first excite fat protons at its frequency and remove their phase coherence with a “dephasing” gradient pulse before imaging. As fat protons are dephased, their MR signal becomes very weak in comparison with that of water protons, though they still spin and precess.

Reconstruction of Fiber Orientation Distributions

Diffusion signals captured by dMR imaging distinguish from fibers’ spatial distribution in the following senses. First, they reflect the Brownian motion restricted by neuronal fibers, rather than neuronal fibers themselves. Second, they are average of diffusion signals within voxels, not a detailed microscopic image. Voxel resolution of dMR images is usually 2mm or so, and those acquired in the Human Connectome Project is 1.25mm [25]. On the other hand, the diameter of the axon is at the micrometer (µm) level [26]. Therefore, it is impossible to reconstruct the exact fiber structure with dMR images. However, it is possible to estimate statistical properties of neuronal fibers from dMR images by modelling diffusion property of brain tissues. As an inverse problem, such estimation topically involves a representation of fiber orientation distributions (FODs) and a forward model to relate FODs to diffusion signals. After briefly introducing two popular representations of FODs, diffusion tensors and spherical harmonics, we will discuss the essential part of reconstruction: signal generation models.

Diffusion Tensors

In the early 1990s, it was only feasible to scan the brain in a few directions. The limited angular resolution did not support complicated models, so fiber orientation distributions were depicted with the most concise anisotropic model: Gaussian distributions determined by symmetric, positive definite matrices, which are called “diffusion tensors” [8]. The principle eigenvector of a diffusion tensor reflects the dominant fiber direction, and its eigenvalues characterize rotation-invariant properties. The tensor model is unable to effectively account for crossing fibers, as shown in Figure 9. In the presence of crossing fibers, it usually reduces to a nearly isotropic diffusion “ball” or a thin and round “plate”. Such side effect will lead fiber track simulation to propagate in wrong directions when fibers actually cross each other, which is not rare in the brain. To solve this problem, high-order diffusion tensors have been proposed [27].

Figure 9.

A patch of an FOD image represented with 8^th-order spherical harmonics (a) and 2^nd-order diffusion tensor (b). For the spherical harmonic representation, FOD values in different directions are shown as radius length and each direction is color-coded by linearly combining the red, green and blue color according to the x, y, and z components of unit directional vectors. For the diffusion tensor representation, FODs are rendered as ellipsoids and color-coded according to their principal eigenvector. Diffusion tensors cannot faithfully represent crossing fibers.

Spherical Harmonics

Breakthroughs in dMR imaging have made it practical to scan the brain in a hundred or even more directions in a reasonable time, resolving the problem of crossing fibers [10]. To fully utilize such high angular resolution in data acquisition, a probabilistic distribution F defined on a unit sphere S² has been employed, replacing diffusion tensors. Similar to that every smooth function in a linear space can be represented with a set of sine and cosine functions, a smooth spherical function can also be represented with a set of orthonormal functions oscillating on the sphere at different frequencies: spherical harmonics [28], as shown in Figure 10. The more frequency bands are employed, the more details can be represented. Because spherical harmonic functions are essentially polynomials, they are interchangeable with high-order tensors [27].

Figure 10.

Spherical harmonics, at the 0-order, 2^nd-order and 4^th-order. Function values are color-coded from blue (low) to red ( high).

The purpose of dMR imaging is not to just estimate diffusion coefficients, but to relate with underlying fiber orientation distributions and tissue composition. Because it is an ill-posed inverse problem, such estimation must be done with highly simplified signal generation models. As an emerging field under active exploration and also due to lack of validation with microscopic images, researchers have not reached agreement and many issues are still controversial.

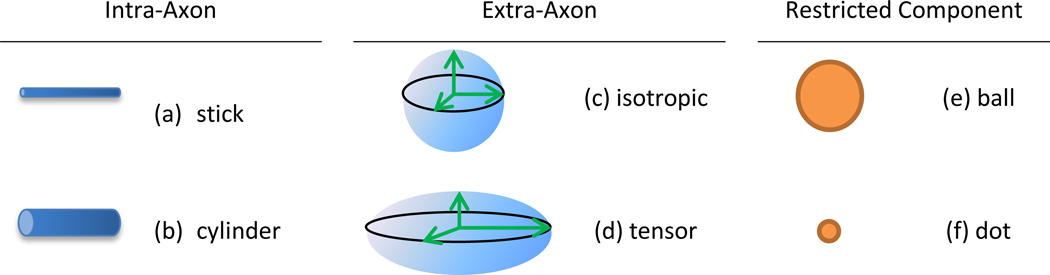
Given an FOD F and a diffusion model H for fibers, the diffusion signal is the convolution of F and H on a unit sphere: F *_s² H (where *_s² denotes spherical convolution) plus contributions from other tissues. The estimation of F relies on diffusion models for neuronal fibers and other restrictive biological structures. A comprehensive analysis [29] has proposed three types of components to characterize dMR signals: intra-axonal compartments, extra-axonal compartments and highly restricted compartments. The total diffusion signal is approximated by the sum of the three components. It should be noted that such models are just an abstraction and simplification of the underlying complicated microscopic structure. There are also different options. For example, another study [30] shows that highly restricted compartments are unnecessary and only contribute very little to dMR signals.

The intra-axonal compartment represents contributions from neuronal fibers. A neuronal fiber, a thin and long geometric object, can be abstracted as a stick (Figure 11a) which only allows water molecules to move along its longitudinal direction [31], or a slim cylinder (Figure 11b) which allows limited transverse motion [32]. For the cylinder model, fiber diameters can be further weighted with a random distribution, such as the gamma distribution [33], to handle their inhomogeneity. However, estimation of axon diameters is a difficult issue and only possible with very high gradients [34].

Figure 11.

Diffusion models for reconstructing fiber orientation distributions.

The extra-axonal compartment accounts for hindered diffusion not directly related to neuronal fibers. Because they should not have a dominant direction, they could be modeled as an unbounded homogeneous material (Figure 11c) with unknown diffusivity d [31], or an unknown diffusion tensor D (Figure 11d) [32].

The highly restricted component is for water molecules trapped in so tiny structures that a magnetic field gradient can hardly affect their diffusion signals. Their diffusion profile can be treated as a small ball [29] (Figure 11e), or more restrictively a “dot” (Figure 11f) that completely prevents water molecules from moving [29, 35].

Figure 12 shows that diffusion models affect reconstruction results significantly. In this example, the stick+ball+dot model solved with convex optimization [35] yields sharper and more stable results.

Figure 12.

Reconstruction of FODs for a small brain region. The region of interest is the red box in (a). FODs reconstructed with a stick+ball+dot model and convex optimization [35] are shown in (b); those with spherical deconvolution of diffusion distributions [36] are in (c), and those with a stick+ball model and Markov Chain Monte Carlo (MCMC) [37] are in (d). Diffusion models affect reconstruction results significantly. In this example, the model-based and regularized method (b) [35] yields sharper and more stable results. (e) Estimated fraction of the intra-axon, extra-axon and restricted water components. This figure is reproduced from [35].

FOD Image Processing

Reconstruction of FODs ends at the stage of extracting voxel-wise fiber information from dMR images. Afterward processing will not directly handle dMR images, but in most cases directly work with FOD images. Tasks applicable to ordinary scalar-valued images, such as enhancement, segmentation, and registration, can also be performed with FOD images. Here we will not discuss these image processing tasks themselves, but focus on a fundamental level: manifold structures of FODs. Manifold structures are not only the driving force behind many image processing tasks, but also need special treatment for FODs.

Many image processing methods are built upon interaction between voxel values. For example, in image smoothing, neighboring voxels exert forces on the central one to make its value gradually coherent with theirs. By defining different driving forces, various effects can be achieved [38]. In image registration, voxel-interaction forces between two images drive them to spatially deform and gradually become similar to each other. Even interpolation involves this kind of voxel interaction. The interpolated value can be regarded as the one in balance with the weighted forces from its neighbors. In general, many image processing methods can be formulated as the minimization of an energy function involving interaction forces between voxels.

Processing FOD images is challenging because each voxel is a spherical function whose mathematical properties are much more complicated than a simple intensity scalar. Even fundamental tasks such as interpolation, smoothing, segmentation and registration must be redesigned. To utilize well-developed image processing frameworks, it is crucial to develop suitable manifold structures for FODs.

Log-Euclidean Manifold for Diffusion Tensors

The simplest manifold structure for diffusion tensors is the linear one. Given two diffusion tensors D₁ and D₂, represented as symmetric positive-definite matrices, their distance is ║D₁ − D₂║₂. However, this structure has a noticeable defect: the linear average of two diffusion tensors may produce a tensor whose determinant is greater than both of them. The determinant, in the scenario of diffusion, has solid physical meaning: its square root is proportional to the width of the diffusion region. It is undesirable to have the region expanded. As a remedy, Arsigny et al. in 2006 introduced the log-Euclidean manifold [39]: the distance between two diffusion tensors is ║log(D₁) − log(D₂)║₂. This manifold essentially maps a diffusion tensor D to its matrix logarithm log(D). Because D is symmetric and positive-definite, log(D) is unique.

Hyper-Spherical Manifold

The full description of FODs is a non-negative spherical function F: S² → R_>0 whose integral on the sphere equals one. In resemblance to the problem with diffusion tensors, linear combination of spherical functions disperses probability density on the sphere and hence reduces its angular focus. Cheng, et al. [41] proposed a hyper-spherical manifold of FODs. Because ∫_u∈S2 F(u)du = 1, its square-rooted function $f=\sqrt{F}\ge 0$ satisfies ∫_u∈S²f²(u)du = 1, or equivalently, the norm of f is one. This implies that f resides on a unit sphere in a hyper-space, a well-studied manifold. On this manifold, the distance between two FODs is the length of the great arc connecting them, and the interaction force is in the tangent plane of the hyper-sphere.

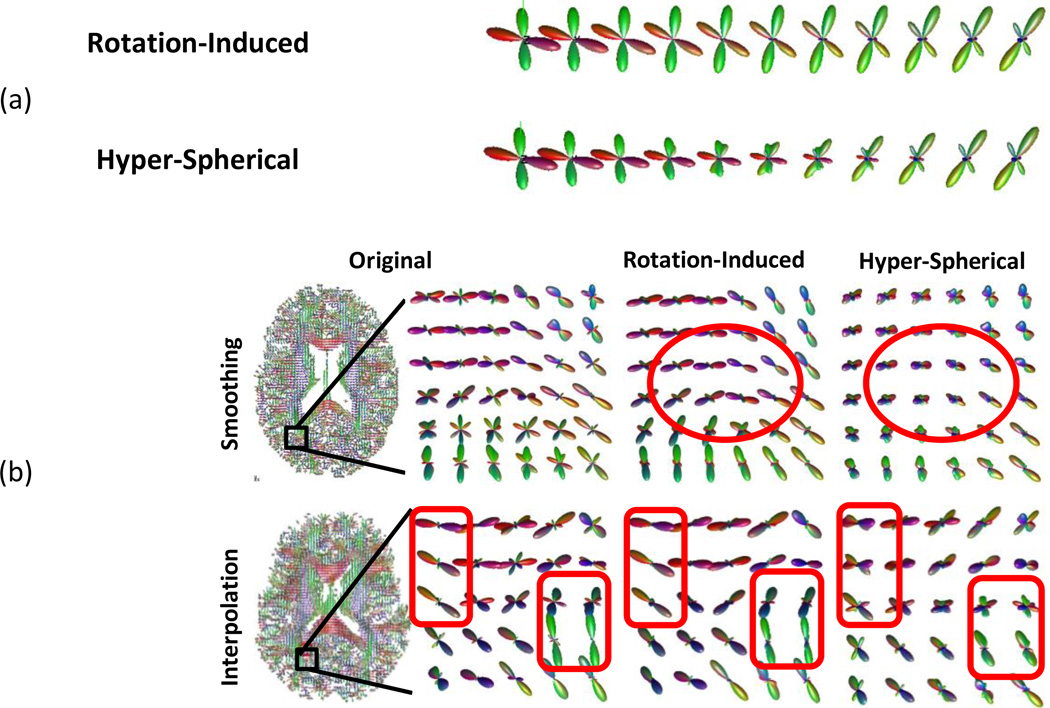
Rotation-Induced Spherical Manifold

Though the hyper-spherical manifold reduces the angular dispersion of FODs, it does not directly handle the main cause of dispersion: FODs’ difference in orientation. As neuronal fibers extend in the brain, they do not take straight paths, but turn gradually to make curves. Li et al. [40] proposed a rotation-induced manifold to directly handle this orientational difference. The rotational-induced manifold treats tangent vectors on the hyper-spherical surface differently: whichever can be realized by rotation is associated with a parameter λ_rot while whichever purely reflects shape differences is associated with a constant one. This unequal treatment does not change the topology, but defines a new Riemannian metric. By setting λ_rot smaller than one, FODs’ orientational difference is under-weighted, and consequently FODs with similar shapes but different orientations are “squeezed” closer. If λ_rot equals zero, then the manifold reduces to a quotient space completely discarding differences caused by rotation. Figure 13 compares between the rotation-induced and the hyper-spherical manifolds, showing that manifold structures can lead to very different processing effects. Reisert and Kiselev have provided a framework [42] for embedding fiber continuity into FOD reconstruction. It is very interesting to utilize these FOD manifolds in their framework.

Figure 13.

(a) Trajectories connecting two FODs on the rotation-induced and the hyper-spherical manifolds. FOD values in different directions are shown as radius length and each direction is color-coded by linearly combining the red, green and blue color according to the x, y, and z components of unit directional vectors. (b) Examples of smoothing (the first row) and interpolating (the second row) FODs. The right column shows the original image and highlighted regions. The middle and left columns show the results of the rotational-induced and the hyper-spherical manifolds, respectively. The highlighted red boxes show that the hyper-spherical manifold mixes curving fibers instead of aligning them, introducing the “swelling” effect. This figure is reproduced from [40].

Simulation of Fiber Tracks

Based on local fiber orientation, tractography simulates fiber paths stretching from one brain region to another, to statistically model geometric and connectional properties of the fiber network. Millions of tracks can be simulated, grouped as bundles and later analyzed with graph theory. It should be noted that simulated fiber tracks do not represent real neuronal fibers, but reflect their spatial and orientational distribution statistically. A single simulated fiber track does not have much realistic meaning, but statistics derived from a huge number of tracks are useful.

Tractography methods can be classified into two broad categories: local methods and global methods. Local methods “grow” a “neuronal fiber” from a seed step by step with the guidance of local fiber orientation. Usually, it becomes the simulation of an ordinary differential equation $(\text{ODE}):\frac{\mathit{\text{dr}}}{\mathit{\text{dt}}}=G(r)$ where r is the current location of a fiber point, G(r) is the fiber direction at this point, and $\frac{\mathit{\text{dr}}}{\mathit{\text{dt}}}$ is the growing velocity of the fiber. G(r) can be either deterministic or stochastic [37, 43]. If it is deterministic, it usually follows the FOD’s peak closest to the previous track direction. In this case, a fiber track is determined by its initial seed location and direction. If it is stochastic, the direction is randomly sampled according to the FOD. Probabilistic tractography explores more possibilities than deterministic ones. ODEs of higher orders or more sophisticated models can be used. Some methods [44] employ the 4^th order Runge-Kutta method, instead of the 1^st order explicit Euler method, to reduce errors. Local tractography algorithms usually run quite fast, but they share a common problem: local errors accumulate and propagate. To regularize the problem, most algorithms impose an upper bound on the curvature of their fiber tracks to avoid sharp turns.

Another approach treats tractography as an inverse problem: finding a set of fiber tracks that “generate” signals to match the diffusion MR image [45]. The advantage of this method is very obvious: to optimize an objective function, fiber tracks interact with each other, which may lead to more stable results, and may also avoid repetitively sampling similar fibers. However, it is very challenging to jointly solve such a problem with a huge number of fiber tracks. Therefore, it usually takes much longer computation time than local methods. Reisert et al. [46] in 2011 reduced the computation to a practical range of several hours for about 10^5 fiber tracks. They formulated an energy function

$$E=E(\text{Tracks})+E(\text{Tracks,Data})$$

where E(Tracks) prefers smooth and long tracks, and E(Tracks,Data) is the difference between track-generated signals and the real dMR image. The energy function is minimized with simulated annealing, instead of a deterministic method. Each time, an operation on track segments is randomly proposed: creation, removal, move, join, and so on. Then the proposed operation is accepted or rejected stochastically based on the energy change it introduces. Daducci et al. implemented this global tractography method into a software package Connectome Mapper [47].

Applications to Brain Research

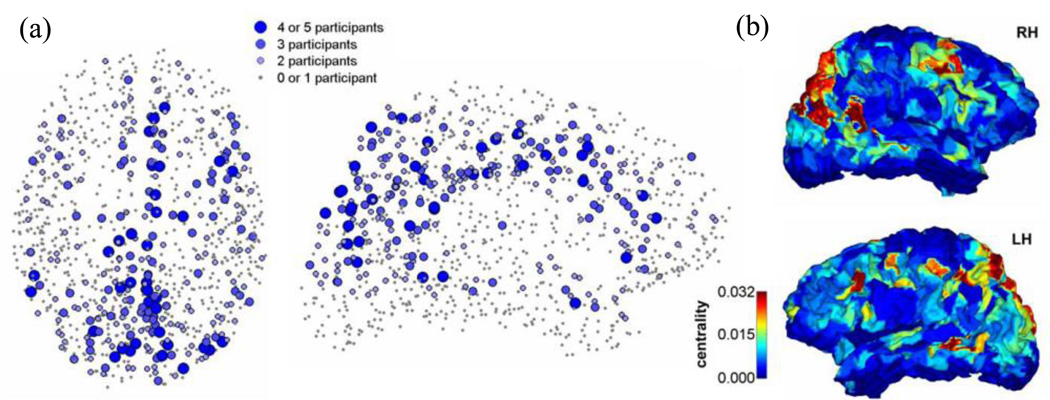
Connectivity information captured by dMR imaging has been investigated for understanding the brain’s structure, function and its relationship with neurological disorders. A study on five healthy young males conducted by Hagmann et al. [48] revealed that brain regions are not connected equally but some play more central roles than others (Figure 15). For each subject, they simulated nearly 3 million fiber tracks with a fixed step size of 1mm, and then derived a connectivity matrix between 998 regions on the cortex surface each of approximately 1.5 cm². Based on graph theory, they found that brain regions within the posterior medial, parietal cerebral cortex, and several temporal and frontal lobes form a highly mutually connected network, and meanwhile constitute hubs linking other regions. Functional activities of these regions are also highly coupled when the brain is at rest.

Figure 15.

Connectivity centrality of brain regions. (a) Region centrality obtained from high-resolution connection matrices of 5 participants. The plot shows how consistently region centrality ranked in the top 20% among the 998 regions. (b) Lateral views of the right and left cerebral hemispheres showing connectivity centrality, averaged across all five participants. This figure is reproduced from [48].

From childhood to adulthood, the brain experiences profound development to reach its peak of intelligence and mental capacity. Comparing the brains of 439 individuals aged 12 to 30, Dennis et al. [49] found that not all connections are strengthened during the development, but some are “pruned”. They scanned the subjects with high angular resolution diffusion imaging (HARDI), reconstructed their fiber networks, and analyzed the networks with graph theory and linear regression regarding subjects’ gender and age. It was found that fiber density relating to the frontal cortex decreases, but those relating to the temporal cortex increases, as shown in Figure 16.

Figure 16.

Comparing the brains of 439 individuals aged 12 to 30 with high angular resolution diffusion imaging, Dennis et al. [49] found that not all connections are strengthened during development, but some are pruned. The figure only shows connections with significant correlation with age. Node size is proportional to number of connections, and thickness of connection edges is proportional to relative fiber density. This figure is reproduced from [49].

Many mental disorders are related to abnormal functional integration caused by aberrant brain connectivity. Using diffusion tensor imaging and tractography, Zalesky et al. [50] compared the anatomic connectivity network of 74 schizophrenia patients with 32 control subjects matched in age and gender. They found that connectivity involving the medial frontal, parietal/occipital and the left temporal lobe shows statistically significant difference between the patients and the control subjects.

Future Scope

Advances in dMR imaging have provided a platform for investigating brain connectivity in vivo at an unpreceded spatial and angular resolution. Current acquisition and analyzing techniques have not reached their full potential yet. Under active development, in the foreseeable future they shall be more efficient, more accurate and more reliable in the established framework.

As these techniques are becoming more and more accessible, it is important to explore their clinical applications such as brain surgical planning, prognosis of recovery from trauma, stroke, etc. A connectivity network reconstructed from a patient’s dMR images may provide valuable information for surgeons to more precisely locate the spot of intervention, or for doctors to better predict the mental impact of trauma or hemorrhage. A single imaging modality such as dMR might be insufficient for explaining the underlying physiological or pathological changes. In order to obtain a more comprehensive understanding of these changes, it is important to take advantage of multimodal imaging data like functional MR imaging and positron emission tomography for biochemical and metabolic information. These clinical applications, in return, will inspire more engineering and methodological innovations.

As dMR imaging provides in-vivo and indirect view of brain’s structural connectivity at a macroscopic level, it is important to verify and further investigate its relationship with microscopic images. Referring to high resolution images at the neuron level may help identify signal signatures related to certain specific tissues. In 2013, the breaking-through CLARITY technology by Chuang et al. [51] has made it possible to optically image an intact brain structure in 3D at the resolution of individual neurons. CLARITY removes light-blocking fatty membranes from the brain, and makes it transparent. With high resolution microcopies, it can image brain’s long-range projections, local circuit wiring, cellular relationships, subcellular structures, protein complexes, nucleic acids and neurotransmitters. Though dMR imaging cannot achieve such super resolution, CLARITY does not replace it because CLARITY is a post-mortem technique and unavailable for in-vivo diagnosis. As an in-vivo and macroscopic technology, dMR imaging can be further investigated with microscopic references to improve its value for clinical diagnosis.

A comprehensive and multi-scale description of brain connectivity, function and development requires integrating information from multiple imaging modalities, functional tasks, and genetic data. Such challenging integration will actively adopt cutting-edge technologies in data science. A connectivity map on the cortical surface forms a four-dimensional space, though sparse. Correlating with genomic data [52] introduces one more dimension with a numerous number of genetic alleles. Overlaying functional tasks brings up even more varieties. Such explosive complexity has pushed researcher to seek solutions beyond classical regression models, but in recent achievements of machine learning, for instance, deep learning.

The need for standardization will arise as our knowledge about brain connectome continues to expand. Fusion of complex information will naturally lead to more detailed and specialized definition of brain regions and fiber bundles, as shown in “Dense Individualized and Common Connectivity-Based Cortical Landmarks” [53] by Zhu et al. A systematic and precise naming catalog for anatomic structures and functional tasks will be needed for researchers around the world to report and exchange their results in shared databases. Extendable digital storage formats to accommodate complex connectivity information and processing protocols are also important for experiment replication and validation. A standardized neuroinformatics platform will boost collaboration and lead to large-scale investigation, as that having been witnessed in the field of genomics.

Figure 14.

Two tractography methods. The local method, as illustrated in (a), each time grows a fiber track step by step according local fiber information. The global method, as illustrated in (b), improves a set of fiber tracks by disconnecting, joining, removal and creation of fibers, in the aim of minimizing an energy function that matches fiber tracks and the FOD image through a generative model. (c) Fiber bundles simulated with a local tractography method seeded in a ball region. (d) An example of fiber tracks simulated by Daducci et al.’s global tractography method [47]. In sub-figures (c) and (d), fiber tracks are color-coded with the directional vector from their start point to their end point, with the red, green and blue color respectively for the left-right, back-front and up-down directions. Subfigure (d) is reproduced from [47].