Abstract
We present and evaluate a method for kernel regression estimation of fiber orientations and associated volume fractions for diffusion MR tractography and population-based atlas construction in clinical imaging studies of brain white matter. This is a model-based image processing technique in which representative fiber models are estimated from collections of component fiber models in model-valued image data. This extends prior work in nonparametric image processing and multi-compartment processing to provide computational tools for image interpolation, smoothing, and fusion with fiber orientation mixtures. In contrast to related work on multi-compartment processing, this approach is based on directional measures of divergence and includes data-adaptive extensions for model selection and bilateral filtering. This is useful for reconstructing complex anatomical features in clinical datasets analyzed with the ball-and-sticks model, and our framework’s data-adaptive extensions are potentially useful for general multi-compartment image processing. We experimentally evaluate our approach with both synthetic data from computational phantoms and in vivo clinical data from human subjects. With synthetic data experiments, we evaluate performance based on errors in fiber orientation, volume fraction, compartment count, and tractography-based connectivity. With in vivo data experiments, we first show improved scan-rescan reproducibility and reliability of quantitative fiber bundle metrics, including mean length, volume, streamline count, and mean volume fraction. We then demonstrate the creation of a multi-fiber tractography atlas from a population of 80 human subjects. In comparison to single tensor atlasing, our multi-fiber atlas shows more complete features of known fiber bundles and includes reconstructions of the lateral projections of the corpus callosum and complex fronto-parietal connections of the superior longitudinal fasciculus I, II, and III.
Keywords: diffusion MRI, tractography, atlasing, interpolation, multi-fiber, image processing
1. Introduction
Diffusion MR imaging provides an in-vivo probe of tissue microstructure that enjoys numerous applications to neuroscience and clinical studies. This is due to its unique ability to image local patterns of water molecule diffusion, which reflect physical properties of biological tissue [1]. These patterns enable the quantification of brain white matter microstructure, as diffusion exhibits anisotropy due to the geometry of neuronal axon projections [2]. This is useful for making local measurements of fiber orientations through diffusion modeling [3] and more global fiber bundle reconstructions through tractography [4] [5]. In addition, atlas-based reconstructions can reveal population-wide features of anatomy and serve as a reference for comparing individuals [6]. Both tractography and population-based atlasing are applications that depend on a number of basic image processing tasks, including interpolation, smoothing, and fusion [7]. For tractography, interpolation is needed when determining fiber orientations off the voxel grid, and smoothing is needed to control errors due to noise and other image artifacts. For atlas construction, interpolation is needed to resample images into a common space, and fusion is needed to derive a composite image from a population. This paper develops and evaluates methods for performing these tasks with support for multiple distinct fibers, which are important for resolving complex sub-voxel fiber configurations due to crossings and partial volume effects [8].
In particular, the goal of this work is to develop and evaluate methods for model-based image processing that are useful for interpolation, smoothing, and fusion tasks with the multi-compartment ball-and-sticks diffusion model. For this, we derive a kernel regression framework for estimating fiber orientation mixtures, which represent multiple fiber orientations per voxel and associated volume fractions. In contrast to signal-based image processing, this approach estimates fiber models from a collection of fiber models contained in volumetric parametric maps. This is accomplished by extending a kernel regression image processing framework for vector-valued images [9] and building on prior work on model-based diffusion MRI processing [10] [11]. We show how this formulation generalizes a variety of tasks and allows for simple data-adaptive extensions for bilateral filtering and model-selection, which may be generally useful for parametric model-based image processing. Our experimental evaluation first characterizes performance with computational phantoms, and then explores applications to quantitative tractography-based analysis of fiber bundles and multi-fiber atlas construction.
The rest of the paper is organized as follows. In Secs. 2 and 3, we discuss related work and background material. In Sec. 4, we describe our proposed model-based estimator, outline optimization techniques, and describe its application to streamline tractography. In Sec. 5, we describe experimental evaluation of our approach with computational phantoms and in vivo clinical data. The synthetic data experiments evaluate the performance of our method in relation to fiber orientations, volume fractions, compartment count, and tractography-based connectivity. The in vivo data experiments first measure the scan-rescan reproducibility and reliability of fiber bundles metrics in individual subjects. We then build a multi-fiber tractography atlas from 80 healthy subjects to study population-wide properties of white matter. In Secs. 6 and 7, we discuss our results and conclude.
2. Related work
In this section, we briefly review related work and outline the distinguishing features of the present approach.
This paper examines a model-based approach for diffusion MRI processing. This contrasts with signal-based approaches that apply filters to the vector-valued diffusion-weighted MRIs, while accounting for factors such as the gradients strengths, directions, and Rician noise [12]. Model-based approaches instead operate on lower-dimensional mathematical representations of the diffusion signal [7]. Previous work has developed such approaches for single diffusion tensors [13] and orientation distribution functions (ODFs) [14, 15]. We differ by considering multi-compartment models, which are a parametric alternative to ODFs with the advantage of compartment-specific measures and isotropic diffusion modeling. However, two notable challenges for processing multi-compartment models are model selection (to determine the number of compartments) and compartment matching (to solve the combinatorial problem of finding corresponding compartments among some set of voxels) [16].
The approach is related to some prior work on multi-fiber model-based image processing. Yap et al. proposed an approach for multi-fiber atlas construction with fiber orientations extracted from ODF peaks [17], which dealt with similar computational problems but was not designed for parameteric models. The present work differs by considering atlas construction with the ball-and-sticks diffusion model and by relaxing some assumptions on fiber correspondence and fiber count. The prior work of Taquet et al. [10] first explored the idea of parametric model-based interpolation of multi-tensors and its application to tractography and atlas construction, developing a rich framework for multi-tensor processing based on Gaussian mixture simplification [18]. Our work differs by considering directional measures of divergence that are compatible with the ball-and-sticks model. This is necessary because the Burg matrix divergence employed by the full multi-tensor framework is not well-defined for the anisotropic stick compartments, so we instead develop a divergence measure based on the directional Watson distribution to serve the same purpose. We also differ by incorporating data-adaptive extensions to support both bilateral filtering and model selection, in contrast to previous work that employed only spatial kernel weights and local-maximum model selection. Some of the methods presented here have been explored in previous conference work [11] [19], but those included neither the full data-adaptive kernel regression estimator nor the full experimental results presented here.
3. Background
Our work focuses on image analysis with multi-fiber ball-and-sticks diffusion models, which falls into the multi-compartment class of diffusion models [20]. This is a multi-tensor constrained to include an isotropic ”ball” compartment and a number of completely anisotropic ”stick” compartments. These constraints allow the model to achieve good performance for single shell gradients with low b-value acquisitions at intermediate field strengths [21], which are common in clinical applications. The ball compartment can account for isotropic diffusion, and the volume fractions associated with each compartment can account for partial volume effects and mixtures of bundles at crossings. There is also evidence that the volume fraction maps provide a quantitative measure for clinical studies [22]. With this model, the predicted diffusion-weighted signal S is given by:
| (1) |
for a particular gradient encoding direction g⃗, b-value b, and baseline signal S0. This includes N fiber compartments with fiber orientations ‖vj‖ = 1, fiber volume fraction 0 ≤ fj ≤ 1, , and shared diffusivity d > 0. It’s important to note that there is no sign associated with fiber orientations, so there is an equivalence vj ~ −vj. We use the following parameterization to denote a fiber orientation mixture M with N compartments: . In our experiments, we fit the model to the diffusion signal with the Bayesian approach of Behrens et al. implemented in the FSL software library [23].
4. Methods
In this section, we present our model-based kernel regression estimator for fiber orientation mixtures, followed by a description of extensions for data-adaptive processing. We then outline the necessary optimization routines and practical implementation details. Finally, we describe how this can be applied to deterministic streamline tractography.
4.1. Kernel Regression Estimation
We now formulate our approach for kernel regression estimation of fiber orientation mixtures, which is the main contribution of the paper. This builds on the prior work of Takeda et al. on kernel regression image processing for scalar and vector data [9] and prior multi-compartment processing [11] [18]. The general idea of kernel regression, however, has also been proposed in several other contexts as the moving average, kernel smoothers, etc. [24]. The simplest of such is the Nadaraya-Watson estimator (NWE) [25], which we focus on here. Given a collection of data and a desired regression function ŷ(x0) evaluated at point x0, the NWE assumes a product kernel density distribution for observed data and takes the regression function to be the conditional expectation ŷ = E(y|x0). This can be simply expressed by the following least-squares problem:
| (2) |
| (3) |
with a kernel function K and bandwidth parameter h. In practice, larger values of h produce a smoother estimate. The kernel K can be chosen from a variety of options, but we use the standard Gaussian. The advantage of this approach is that it makes few assumptions about the structure of the data and consequently generalizes well to a number of tasks. In particular, Takeda et al. [9] presented a general framework for image processing based on this approach, showing it can be used for interpolation, smoothing, and fusion. The goal here is to further extend this approach to model-based estimation of fiber orientation mixtures.
The primary limitation of the standard kernel regression approach is the assumption of vector-valued images, for which the Euclidean distance ‖x − y‖ is a reasonable measure of discrepancy. This assumption breaks down for diffusion model-valued image data due to various constraints and the non-Euclidean geometry of the models, e.g. fiber volume fractions and orientations. This issue can be addressed by instead considering a model-based measure of discrepancy and by performing optimization over the constrained space of models. Given an input position p0 and local neighborhood of data with , we formulate this extended estimator M̂ (p0) as follows:
| (4) |
| (5) |
given a positional bandwidth parameter hp. We denote the neighborhood size here as C, and in practice, we choose a neighborhood sufficiently large to include three standard deviations of the Gaussian kernel, e.g. a 7×7×7 window of 1 mm3 voxels for hp = 1 mm. We define the model-based discrepancy for fiber mixtures as follows:
| (6) |
given a single fiber distance :
| (7) |
The above definition of is a matching-based distance that accounts for the combinatorial structure of the model by minimizing the sum-squared distances across all possible matching functions π between compartments in M and those in M̂. This formulation happens to allow efficient optimization and makes no assumptions on compartment ordering or total count. Both and also have interesting relationships to statistical measures of divergence, which are discussed in the appendix.
4.2. Data-adaptive Extension: Model Selection
The estimator puts no constraints on the complexity of the estimated model, so some mechanism is needed to perform model selection. One solution is to choose a fixed number of compartments; however, this can overestimate in some areas and underestimate in others. Data-driven approaches can instead use the fiber counts from the local neighborhood to estimate the model complexity, e.g. the local-maximum estimator used in prior work [18]. Another more conservative data-driven approach is to use the average fiber count (rounded to the nearest integer). We propose another data-driven approach that works by extending the estimator in Eq. 4 to include a regularization term for the number of compartments N:
| (8) |
given a regularization parameter λ. The goal of this approach is to choose the fiber count that best supports the fiber orientation data in the local neighborhood, rather than just the counts. In later experiments, we compare these different model selection approaches to assess their strengths and weaknesses.
4.3. Data-adaptive Extension: Bilateral Filtering
In addition to performing model selection, the estimator can be simply modified to allow for bilateral filtering. The goal here is to avoid blurring interesting features at boundaries of anatomical structures. This issue has been studied for standard kernel regression estimators, and one solution is to include additional weights that reflect similarity between data values [9] [26]. We include this idea by adding a data-adaptive factor as follows:
| (9) |
| (10) |
| (11) |
given a bandwidth parameter hm and a reference model M0.
This can be optimized with the same routines as Eq. 8; however, it is more computationally costly because the adaptive kernel weights Km cannot be precomputed like the spatial kernel weights Kp. For voxelwise smoothing, the reference can be the original input model; for tractography, it can be the model from the previous step in tracking; for interpolation, it can be the estimate without the bilateral factor Km.
4.4. Optimization
Next, we describe optimization routines for the proposed estimator and outline some practical issues for implementation.
The estimator in Eq. 8 involves an optimization problem in which the weighted sum of model-based distances must be minimized, subject to a regularization term for model selection. Substitution of dm and df gives a simpler form:
| (12) |
given the kernel weights ki in Eq. 10. This is equivalent to solving the weighted axial DP-means clustering problem [27], which is similar to the k-means algorithm with two extensions. First, clustering is performed with axial variables [28], which are equivalent to fiber orientations. Second, the number of clusters is estimated from the data as in the DP-means algorithm, a name derived from its relation to Dirichlet Process mixture models [29]. An iterative algorithm for solving this is presented in Algo. 1, and further discussion is in the appendix.
Algorithm 1.
axial DP-means clustering
| Input: | ||||
| : the input weights and orientations | ||||
| λ: the regularization parameter | ||||
| Kmax: a maximum number of clusters | ||||
| Output: | ||||
| K̂: estimated number of clusters | ||||
| : estimated cluster weights and orientations | ||||
| /* Initialize | */ | |||
| K̂ ← 1, | ||||
| while not converged do | ||||
| /* Assign cluster labels | */ | |||
| for l=1 to L do | ||||
| for k=1 to K̂ do | ||||
| /* Optionally increment clusters | */ | |||
| if mink Dlk > λ & K̂ < Kmax then | ||||
| K̂ ← K̂ + 1, v̂K ← vl, πl ← K̂ | ||||
| else | ||||
| πl ← argmink Dlk | ||||
| /* Update cluster centers | */ | |||
| for k=1 to K̂ do | ||||
| ŵk ← ∑l wlδ(k, πl) | ||||
| return | ||||
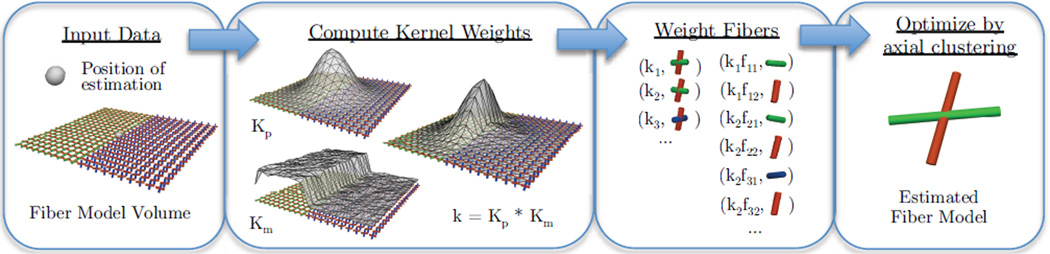
The full procedure for using the estimator is summarized in Fig. 1 and detailed in Algo. 2. This process proceeds by first collecting fiber models in a local neighborhood of the point of estimation, then kernel weights are computed by the product of spatial and data-adaptive factors. These weights are normalized to sum to one and then distributed among the fiber compartments of each model. The above clustering problem is then solved to estimate the output number of compartments, fiber orientations, and volume fractions. A summary of the algorithms parameters is shown in Table 1.
Figure 1.
A flowchart illustrating the steps in the proposed method, detailed in Algo. 2. The input is a position for estimation and model-valued volumetric data. Then, kernel weights are computed from the product of spatial and data-adaptive factors and normalized to sum to one. Then, weights are distributed among the fiber compartments and multiplied by volume fraction. Finally, the estimated model is found by a clustering-based optimization procedure, detailed in Algo. 1.
Algorithm 2.
fiber orientation mixture estimation
| Input: | ||||
| p0: the input spatial position for estimation | ||||
| M0: the input reference model | ||||
| : the local neighborhood of C position/model pairs | ||||
| Ni: the number of fibers in the i-th local model | ||||
| fij: the volume fraction of the j-th fiber of the i-th local model | ||||
| vij: the fiber orientation of the j-th fiber of the i-th local model | ||||
| hpos: the spatial positional bandwidth | ||||
| hdir : the bilateral data-adaptive bandwidth | ||||
| λ: the model complexity regularization parameter | ||||
| Kmax: the maximum number of fiber compartments | ||||
| Output: | ||||
| K̂: estimated number of fiber compartments | ||||
| : estimated model | ||||
| /* Compute sum-normalized model weights | */ | |||
| Ksum ← 0 | ||||
| for i=1 to C do | ||||
| Ksum ← Ksum + ki | ||||
| for i=1 to C do | ||||
| ki ← ki/Ksum | ||||
| /* Compute fiber weights | */ | |||
| L ← 0, Fsum ← 0 | ||||
| for i=1 to C do | ||||
| for j=1 to Ni do | ||||
| wL ← ki * fij, vL ← vij | ||||
| L ← L + 1, Fsum ← Fsum + fij | ||||
| /* Optimize by clustering with Algo. 1 | */ | |||
| for k=1 to K̂ do | ||||
| f̂k ← ŵk * Fsum | ||||
| return | ||||
Table 1.
A summary parameters used for estimation, including a range of values found in our evaluation and experiments.
| Symbol | Name | Description | Range |
|---|---|---|---|
| hp | Spatial bandwidth | Specifies the size of the region used for estimation | 1.0–3.0 mm |
| hm | Data-adaptive bandwidth | Specifies the sensitivity to local data structure | 0.3–0.6 |
| λ | Regularization | Specifies how conservative the model selection should be | 0.99–0.9999 |
| Kmax | Maximum complexity | Specifies an upper bound on the number of fiber compartments | 2–3 |
There are also some practical issues to note when implementing this. First, the procedure is only guaranteed to find a local minima, which depends on the starting conditions. This can be helped by performing several random restarts and taking the solution with the overall minimum, e.g. 10 restarts with shuffling in our implementation. There may be some rare configurations where the minimum is not well-defined, e.g. strictly orthogonal fibers. If this occurs, the known model with highest weight can be chosen; however, we check for this condition and never encountered it in practice. Finally, the kernel weights must be normalized by their total sum, as this ensures the total volume fraction of the fiber compartments is conserved and the estimated model volume fractions also sum to one.
4.5. Tractography
We applied the above estimator to deterministic tractography using a generalization of the standard streamline approach to account for multiple fibers. In the standard approach, a fiber trajectory is considered a 3D space curve whose tangent vector is equated with the fiber orientation of the voxelwise diffusion models. This process proceeds by evolving a solution to a differential equation with some initial condition at a given seed position. Typically, some geometric criteria are also used to stop and exclude fibers, including angle threshold and minimum and maximum length [30].
This approach must be adapted when multiple orientations are present [16], and we use the following modifications. During tracking, one of the N possible fiber compartments must be chosen for the next step, so we choose the fiber with the smallest angular difference to the previous step, among those below a given angle threshold. We also incorporate additional volume fraction termination criteria, where tracking is stopped if the volume fraction of the chosen fiber compartment is below a given threshold. Finally, we use the proposed model-based estimator for interpolation and smoothing during tracking. We also retain the volume fraction parameter during tracking in order to estimate statistics across fiber bundles.
5. Experiments and Results
This section describes the evaluation of our method with four experiments, including a discussion of the datasets, experimental design, evaluation metrics, and results in each experiment. Two synthetic data experiments were conducted with computational phantoms to assess the ability of clustering-based optimization to match compartments and also to measure performance of our proposed model selection and bilateral filtering extensions. Two in vivo data experiments were conducted with clinical scans to assess the practical benefits of our approach in modeling human brain white matter fiber bundles. The first investigated scan-rescan reliability of quantitative fiber bundle metrics, and the second investigated population-level features of white matter by constructing a multi-fiber tractography atlas from 80 subjects.
All statistical analysis was performed using R 3.1.1 and ggplot2 [31]. Unless stated otherwise, the estimation parameters were hp = 1.5 mm, hm = 0.5, λ = 0.99, and the kernel support radius was 5 voxels. All experiments fit two-fiber compartment ball-and-sticks diffusion models with the Markov-Chain Monte-Carlo procedure implemented in FSL XFIBRES [20].
5.1. Datasets and Preprocessing
Synthetic datasets
We generated datasets from two types of computational phantoms, which were defined and synthesized with the ball-and-sticks diffusion model as follows.
The first type of phantom represents a complex boundary between fiber bundles for voxel-based analysis. The phantom included two fibers per voxel and represented two adjacent and perpendicular bundles with a fixed volume fraction of 0.4 with a third bundle that crosses both with a volume fraction varied between 0.2 and 0.4. This left an isotropic volume fraction of 0.2 to 0.4, depending on the condition. Diffusion-weighted images were synthesized with with S0 = 10000, d = 0.0017 mm2/s, 1 mm3 voxels, and dimensions 30×30×5.
The second phantom represents a more complex set of bundles for both voxel-based and connectivity-based analysis. This included three bundles with a crossing and branching structure. Diffusion-weighted images were synthesized with S0 = 10000, d = 0.0017 mm2/s, 1 mm3 voxels, and dimensions 71×71×15, as described in Leemans et al. [32].
All images were synthesized with seven baseline volumes, 64 diffusion-weighted volumes with b-value 1000 s/mm2 to match the clinical imaging data. Rician noise was introduced by adding Gaussian noise with standard deviation σsynth to the complex signal and taking the modulus, using Camino [33]. Noise level is reported by the signal-to-noise ratio in decibels, S NR(dB) = 20 log10(S0/σsynth).
Human brain datasets
Clinical data included diffusion-weighed volumes acquired from healthy volunteers with a GE 1.5T scanner with a voxel size of 2mm3 and image size 128×128 and 72 slices. For each volunteer, a total of 71 volumes were acquired, with seven T2-weighted volumes (b-value = 0 s/mm2) and 64 diffusion-weighted volumes with distinct gradient encoding directions (b-value = 1000 s/mm2). 80 volunteers were scanned with ages ranging between 25 and 65 years and roughly equal numbers between sexes. An additional five volunteers were scanned with three repetitions each to assess scan-rescan reproducibility and reliability. The noise level was estimated to be 22.05 dB using two manually drawn regions-of-interest and the Rician corrected method in [34], .
Diffusion-weighted MRI data was preprocessed using FSL [23] as follows. First, the diffusion-weighted MRIs were corrected for motion and eddy current artifacts by affine registration to the first T2-weighted volume using FSL FLIRT with the mutual information cost function. The gradient encoding directions were rotated to account for the alignment [35], and non-brain tissue was removed using FSL BET.
The 3×5 scan-rescan volumes were used for assessing reproducibility and reliability in the third experiment. For the fourth experiment, a diffusion tensor atlas was constructed from the other 80 subjects. This was done by first fitting single tensor models using FSL DTIFIT and then constructing a population-specific template by deformable tensor registration using DTI-TK [36] [37]. The resulting deformation fields were retained for creation of the multi-fiber atlas, and the single tensor atlas was retained for comparison.
5.2. Synthetic Data Experiment with Boundary Phantom
Design
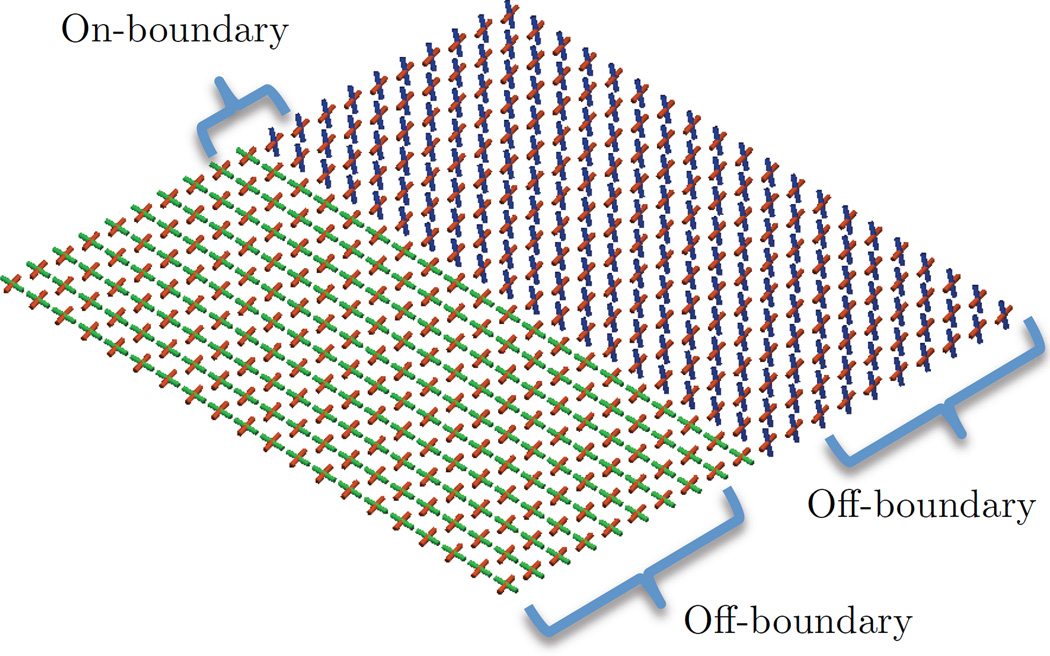
The first experiment was conducted with the boundary phantom (shown in Fig. 3) and was designed to test the fiber matching and bilateral filtering features. For this, we defined two regions of interest: an “on-boundary” two-voxel window, and the remaining “off-boundary” voxels. The proposed estimator was compared to a so called “rank-based” estimator, which is meant to serve as a point of comparison to evaluate compartment matching. This rank-based method sorts fibers in each model based on their volume fraction, and then each compartment is processed independently as if it were a multi-channel volume. We hypothesized that this rank-based approach would introduce greater angular errors than our approach. To test performance relative to previous work, we also compared the bilateral estimator (Eq. 9) to one with only spatial weights (Eq. 4), which we will refer to as “linear”. We hypothesized that the bilateral factor would have lower error at the boundary between bundles. In each condition, we introduced noise and measured deviation from the ground truth with evaluation metrics similar to Ramirez-Manzanares et al. [38]. For this, fibers were matched to the ground truth, and the total angular error and volume fraction error was computed in each voxel and averaged within each region of interest. SNR was varied from 15 to 25, the data-adaptive bandwidth parameter hm was varied from 0.1 to 1.0, and crossing bundle volume fraction was varied from 0.2 to 0.4. Each condition was repeated 20 times to obtain the sample mean and uncertainty. To exclude effects related to model selection, the number of fiber compartments was assumed to be known and fixed at two; however, the next experiment investigates performance of the model selection component.
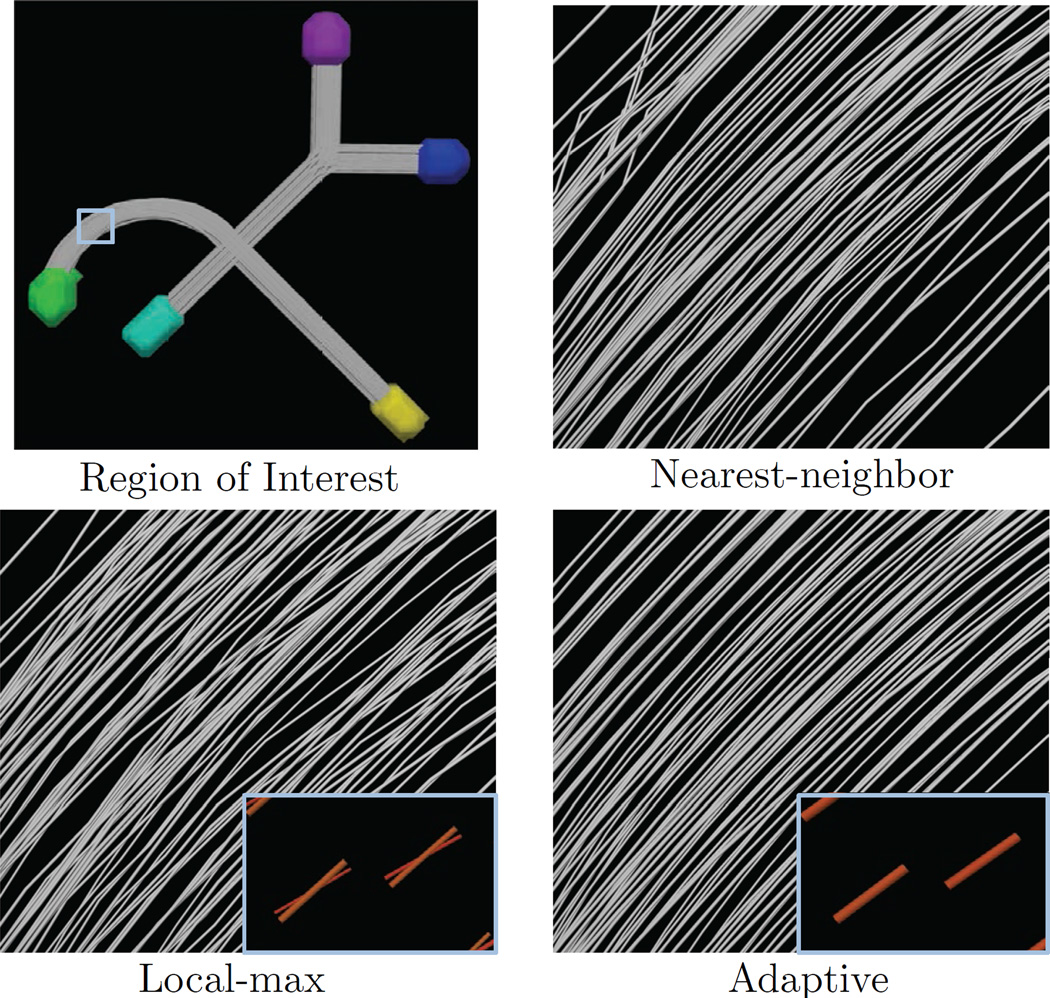
Figure 3.
The phantom used in the first experiment in Sec. 5.2. This represents a complex boundary between fiber bundles and includes “off-boundary” and “on-boundary” regions-of-interest.
Results
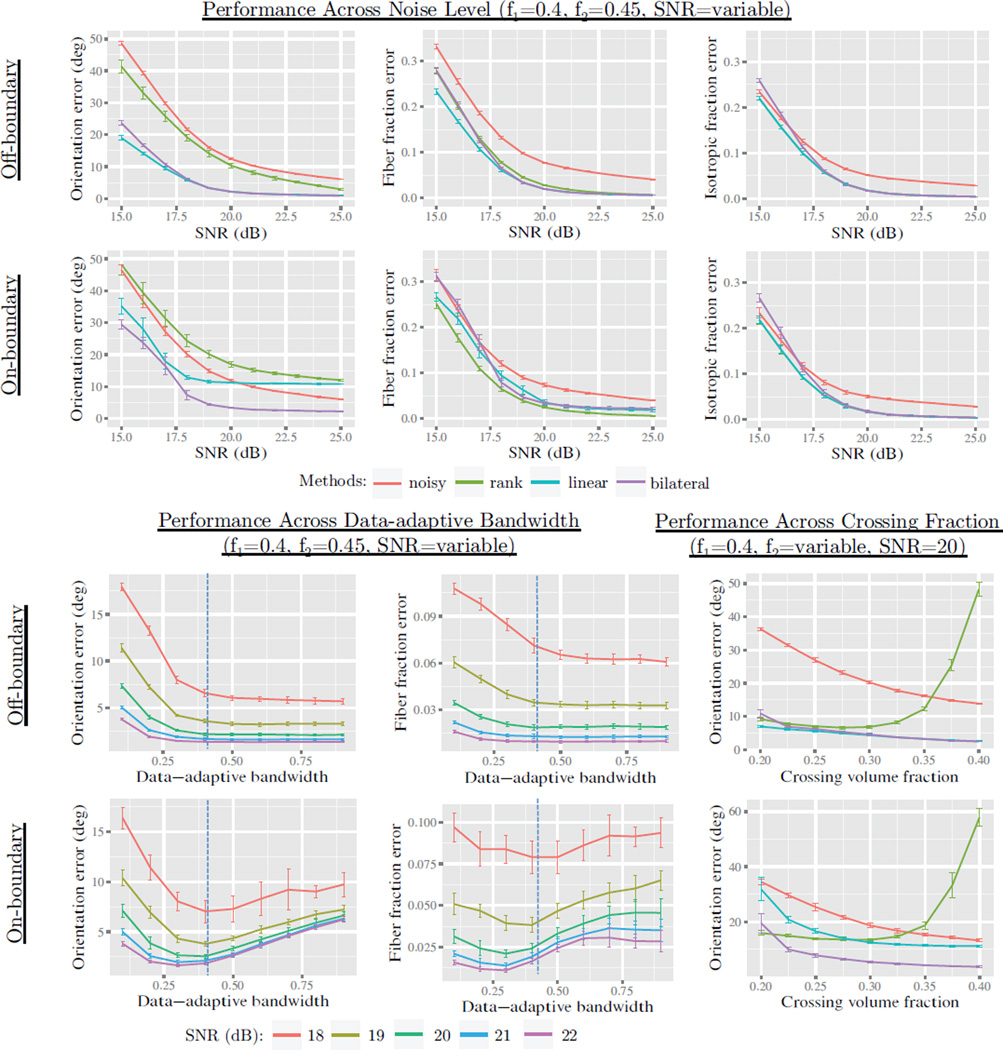
Results are shown in Figs. 4 and 5. We found isotropic and fiber volume fraction error was similarly lowered in all methods; however the rank-based method had slightly lower error on-boundary. We found rank-based orientation error to be significantly higher than the other methods in all cases. We found both linear and rank-based to introduce significant orientation error at the boundary, exceeding that of noise for SNR > 20. Bilateral filtering significantly reduced the error on-boundary with a negligible increase elsewhere. Upon varying the adaptive bandwidth, we found error had a local minima with good overall performance from 0.3 to 0.5, depending on the SNR. Upon varying the crossing bundle fraction, we found rank-based estimation to introduce very high orientation error when the bundle volume fractions were within 0.05.
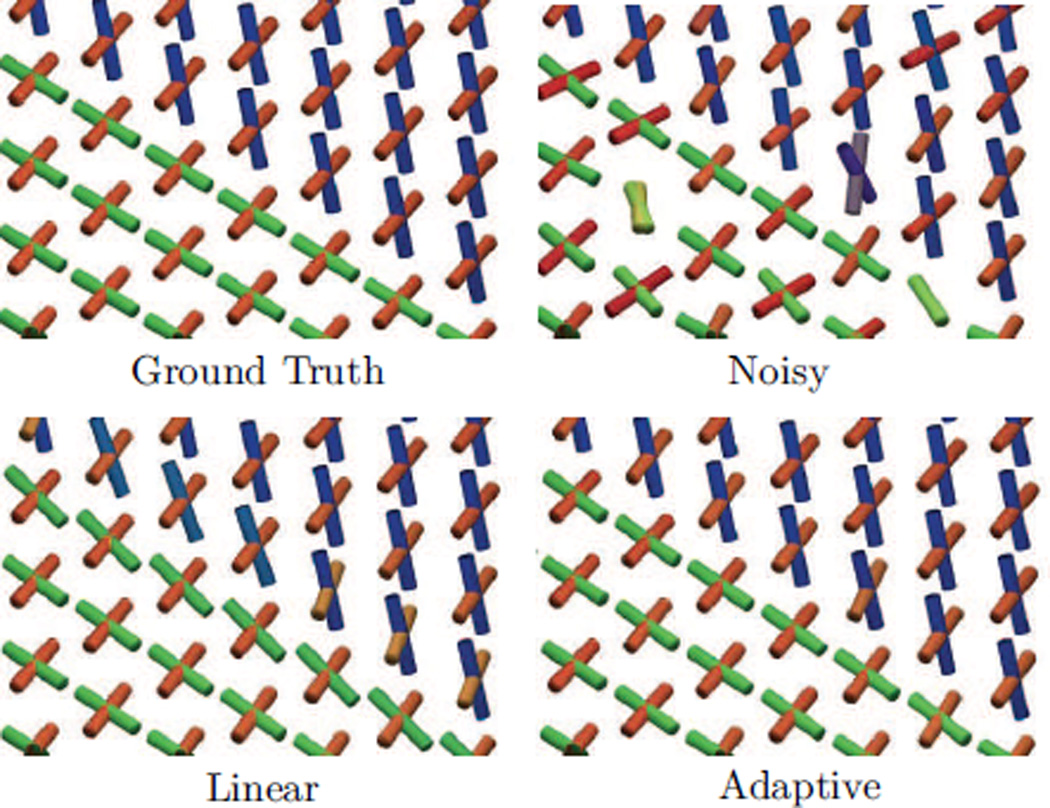
Figure 4.
Qualitative results from the first experiment described in Sec. 5.2. The first panel shows the ground truth phantom at the boundary voxels. The second panel shows fibers fit after adding Rician noise at S NR = 21.5. The third and fourth panels show smoothing results using linear (Eq. 4) and bilateral (Eq. 9) kernel weights. The results show that both estimation techniques reduce noise-induced angular error; however, adaptive estimation can avoid the orientation blurring at the boundary voxels, due to the inclusion of the Km kernel weights.
Figure 5.
Results from the first experiment in Sec. 5.2. The labels on the left indicate the region where results were aggregated, and each plot shows either orientation or volume fraction error rates. The plot titles also show the volume fraction of the compartments (f1 and f2). The top two rows show results with SNR from 15 to 25, comparing the noisy, rank-based, linear, and adaptive estimation conditions (with hp = 1.5 and hm = 0.5). We see that all methods perform well at reducing volume fraction, with rank-based estimation performing slightly better with on-boundary fiber fractions. We see that rank-based estimation rates poorly in orientation error, particularly in regions where bundle volume fractions are within 0.05 apart. We also see that linear estimation introduces high orientation error in on-boundary voxels, while adaptive estimation avoids this issue. By sweeping across the data-adaptive parameter hm, we see a local minima in orientation error occurs between 0.3 and 0.5, depending on the SNR.
5.3. Synthetic Data Experiment with Bundle Phantom
Design
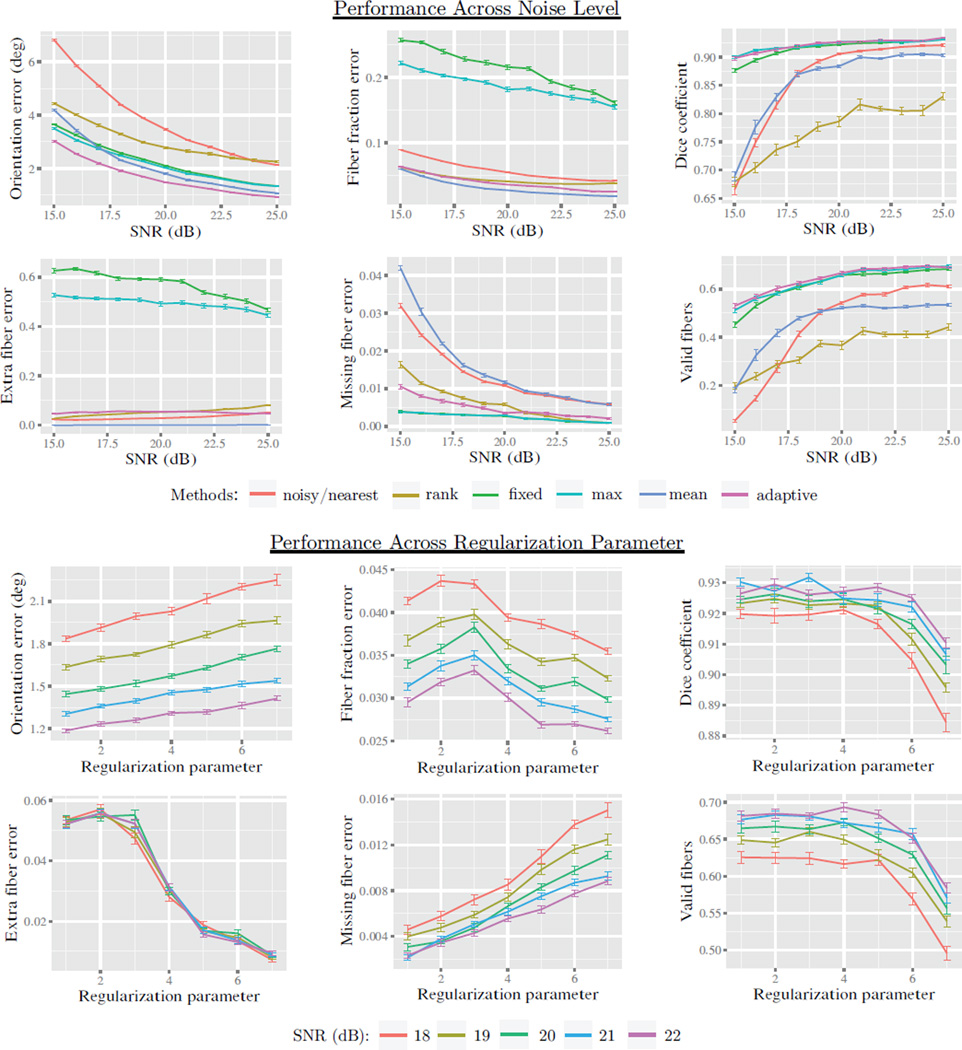
The second experiment was conducted with the bundle phantom (shown in Fig. 6) and was designed to test the model selection methods and to assess performance in connectivity mapping. The adaptive model selection (Eq. 8) technique was compared with the following alternatives: “fixed” (always two fibers), “mean” (rounded local average number of fibers), “max” (local maximum of fiber count, like [18]). We tested both voxel-wise errors and tractography-based connectivity errors. Voxel-wise conditions measured orientation error, volume fraction error, and also “missing” and “extra” fibers error [38]. We also tested connectivity measures derived from deterministic streamline tractography. For this, we manually delineated volumetric masks representing ”white matter” along bundle trajectories and ”gray matter” regions at bundle endpoints. These gray matter masks were used to seed deterministic tractography, and the resulting tracks were then compared to the manually delineated ground truth. For each bundle, we assessed performance by measuring the valid fiber rate (fraction of seeds that reach their intented target) and the Dice overlap coefficient D(A, B) = 2 vol(A ∩ B)/(vol(A) + vol(B)), given bundle mask A and ground truth B [39]. Tractography was performed with 5 seeds per voxel, step size 0.5 mm, 45° angle threshold. Noise was varied from 15 to 25, and the regularization parameter was varied across seven levels, which are listed in Fig. 8. Tractography was performed with nearest-neighbor interpolation as a baseline, and rank-based esimation was also performed in all conditions for comparison. We hypothesized that mean selection would be most conservative and adaptive selection would improve connectivity mapping and help control extra fiber error while not significantly increasing missing fiber error. All conditions were repeated twenty times to measure the sample mean and uncertainty.
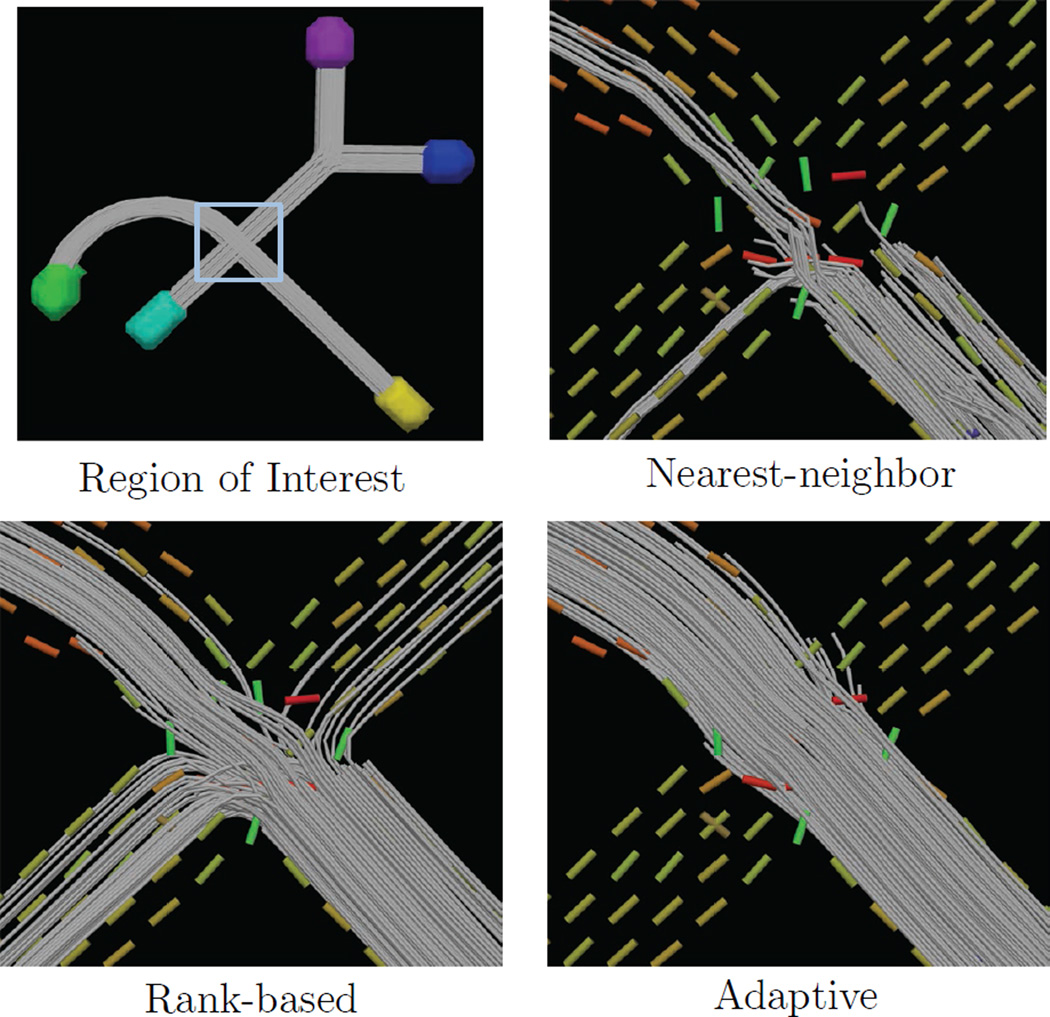
Figure 6.
Results from the second experiment in Sec. 5.3 The first panel shows the phantom and region-of-interest, and the following three panels show tractography using nearest-neighbor, rank-based, and adaptive estimation (SNR = 14). We see that nearest neighbor includes early terminations due to high orientation error and compartment count error. We also compare to the rank-based approach, which creates many spurious connections due to poor matching of compartments in the crossing region. Adaptive estimation can improve both of these issues through smoothing and clustering-based compartment matching.
Figure 8.
Results from the second experiment in Sec. 5.3 using the phantom shown in Fig. 6. Evaluation was first performed by measuring voxel-wise orientation error, volume fraction error, missing fiber error, extra fiber error (lower is better). Tractography-based evaluation was performed to evaluate performance in connectivity mapping using the Dice coefficient and fraction of valid connections (higher is better). Several methods for model selection were compared including: fixed count, local-max selection, mean selection, and our proposed adaptive selection. We also included rank-based estimation and nearest neighbor interpolation to serve as a baseline. The top two rows show performance across noise levels from SNR 15 to 25. We see that adaptive estimation provided significantly lower orientation error than other methods. Across all noise levels, fixed and local-max selection introduced a high volume fraction error and extra fiber error, due to “fiber-splitting”. Adaptive performance significantly reduced these errors with a slight increase in missing fiber error. We also varied the regularization parameter and plotted with semilog axes, x = log10(1 − λ). We found performance to be acceptable between λ = 0.99 and 0.9999, with a tradeoff between extra and missing fiber error.
Results
Results are shown in Figs. 6, 7, and 8. We found similar results for isotropic volume fraction as Exp. 1. Volume fraction error was significantly higher in fixed and max selection, with linear and adaptive performing best. Orientation error was reduced in all conditions with adaptive selection performing best by a small margin. Fixed and max selection showed very high extra fiber error with linear and adaptive performing best. Fixed and max selection had the lowest missing fiber error, with adaptive selection being slightly higher. For tractography-based measures, rank-based estimation performed poorly, nearest and linear selection were better and comparable to each other. We found adaptive, max, and fixed to perform very well, with adaptive performing slightly better in most cases. Upon varying the regularization parameter, we found orientation error, fraction error, and tractography performance to be rather stable, but the extra and missing fiber error varied somewhat. This variation, however, was small compared to the errors introduced with max and fixed selection. After inspecting the results, we found max and fixed selection to be sensitive to noise and problems in model fitting, resulting in over-estimated model complexity such as “fiber splitting”, shown in Fig. 7.
Figure 7.
Results from the second experiment in Sec. 5.3. The first panel shows the phantom and region-of-interest, and the following three panels show tractography results using nearest neighbor interpolation, local-max model selection, and adaptive model selection (Eq. 8). This shows how local-max selection can sometimes introduce “fiber splitting” due to noise (SNR 16.5 shown). Adaptive selection can reduce this effect, resulting in smoother streamline curves and lower orientation and volume fraction errors (see Fig. 8).
5.4. In vivo Data Experiment for Individual Subjects
Design
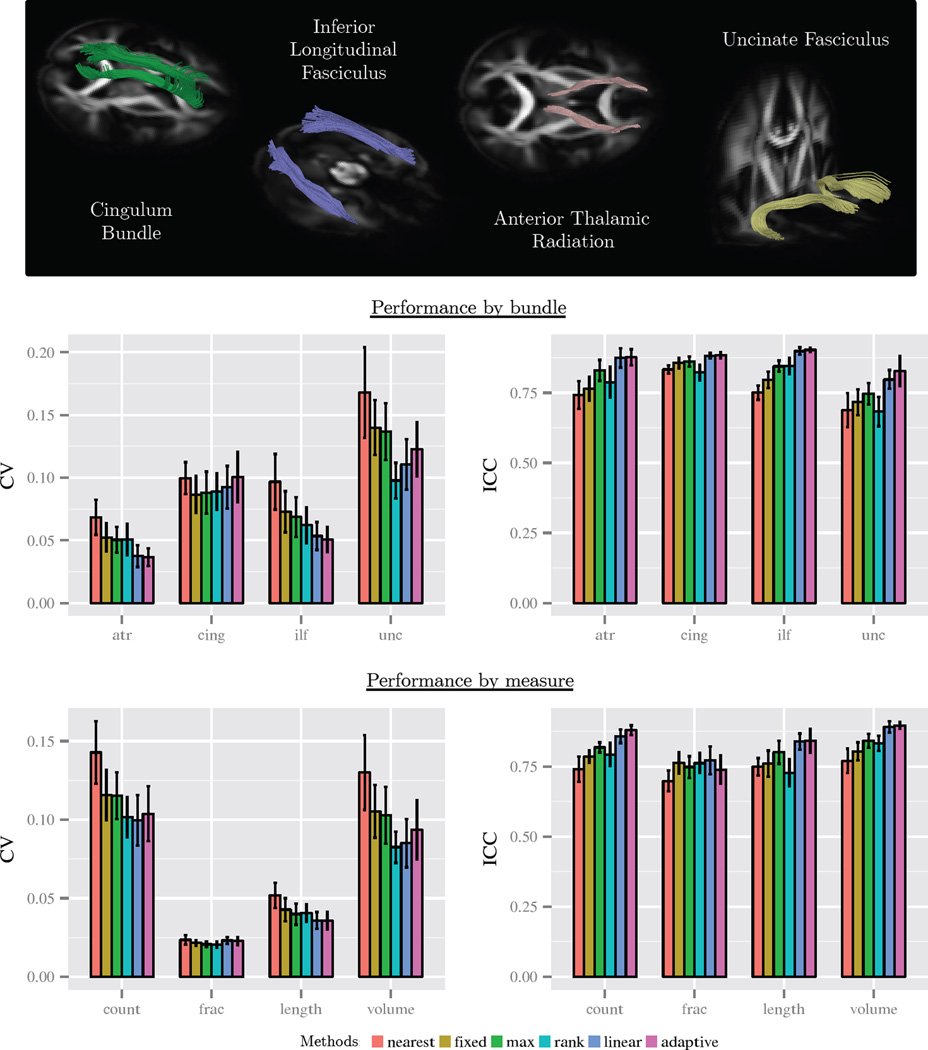
The third experiment tested the reproducibility and reliability of quantitative tractography metrics obtained with the proposed method in in vivo human brain data. For this, we extracted fiber bundles from the scan-rescan dataset, including the following structures: anterior thalamic radiation (atr), cingulum bundle (cing), inferior longitudinal fasciculus (ilf), and uncincate fasciculus (unc) in each hemisphere. Fiber bundles were selected from whole-brain streamline tractography using a multiple region-of-interest approach guided by anatomical references [40] [41]. For each bundle, three masks (two inclusion, one exclusion) were manually delineated in the population specific atlas with ITK-SNAP [42] and then deformed to each subject. Tractography was performed with the following methods: nearest-neighbor interpolation, rank-based estimation with fixed selection, linear estimation with fixed selection, linear estimation with max selection, and our proposed adaptive kernel-based estimation. Tracking parameters included two seeds per voxel, and angle threshold 45°, step size 1.0 mm, minimum volume fraction 0.1, and minimum length 10 mm.
We computed four metrics for each bundle: the mean length, mean volume fraction, total volume, and streamline count. Reproducibility and reliability were measured with the coefficient of variation (CV) and the intra-class correlation coefficient (ICC). The CV was measured by σs/μs and averaged across subjects, given the within-subject mean μs and standard deviation σs. A lower CV score indicates higher reproducibility and has units that are normalized to allow comparison across bundle metrics. The ICC was measured by , given the between-subjects variance and within-subjects variance . A larger ICC indicates more variance between subjects than within subjects. This takes a maximum value of one, and values above 0.75 indicate high reliability. The implementation used the R ’ICC’ package [43].
Results
Results are shown in Fig. 9. We found that linear and adaptive kernel-based estimation generally had lower or roughly equal scan-rescan error (CV) compared to other methods. With adaptive estimation, bundle length had a CV of 3.56%, streamline count had a CV of 10.37%, total volume had a CV of 8.01%, and mean volume fraction had a CV of 2.3%. We found that linear and adaptive estimation had the highest reliability (ICC) in all cases. With adaptive estimation, total volume had an ICC of 0.88, fiber count had an ICC of 0.88, bundle length had an ICC of 0.84, and mean volume fraction had an ICC of 0.72. Mean volume fraction had good and similar performance across all methods. We also found that given the same number of seed points, linear and adaptive estimation both had a much greater number of surviving streamlines than either nearest-neighbor or rank-based estimation.
Figure 9.
Quantitative results from the third experiment described in Sec. 5.4. Scan-rescan reproducibility and reliability were measured for fiber bundle metrics of eight fiber bundles. Reproducibility was measured with the coefficient of variation (CV), which gives a normalized measure of error across scans. Reliability was measured with the intra-class correlation (ICC), which indicates the proportion of total variation that exists between subjects. A lower CV and a high ICC are preferable, with an ICC above 0.75 being highly reliable. The top row shows reference visualizations of the bundles. The middle row shows results by bundle type, with aggregation across bundle measures and hemisphere. The bottom row shows results by bundle measure, with aggregation across bundle type. We found linear and adaptive estimation to show an improvement in nearyly all cases by the ICC metric and improvement in most cases by the CV metric.
5.5. In vivo Data Experiment for Atlas Construction
Design
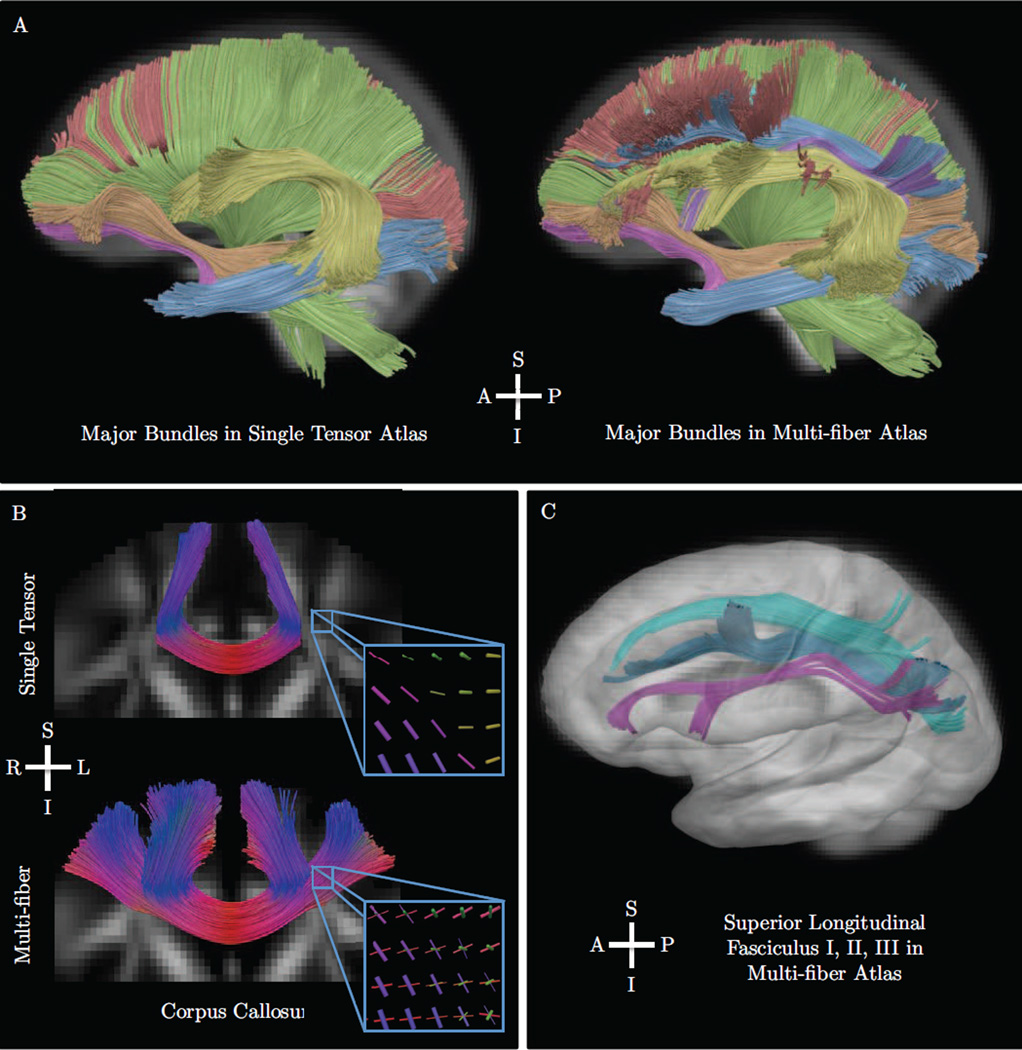
The fourth experiment examined the construction of a multi-fiber tractography atlas with the 80 subject population. For this, we used the deformation fields computed with DTI-TK to resample the multi-fiber models to diffusion atlas space. Interpolation was performed using our approach, and fibers were reoriented by the local Jacobian and normalized to unit length, i.e. Jv/‖Jv‖ given Jacobian J and fiber orientation v. Multi-fiber fusion was then performed with our method to produce an average volume to represent the population. For comparison, standard single tensor tractography was performed in the diffusion tensor atlas with a minimum fractional anisotropy of 0.15. The single tensor atlas was created with the deformable registration algorithm in DTI-TK using finite strain tensor reorientation and the deviatoric tensor similarity metric. [36] [37]. In both atlases, major fiber bundles were manually delineated from whole brain tractography. For the multi-fiber atlas, the corpus callosum and superior longitudinal fasciculus I, I, and III were interactively tracked and manually delineated with guidance from atlas-space averaged Freesurfer gray matter labels. The lateral projections of the corpus callosum were selected based on left and right lobular regions. The superior longitudinal fasciculus I, II, and III were delineated by selecting connections between parietal cortex and superior, middle, and inferior subdivisions of frontal cortex, respectively.
Results
Visualizations of the results are shown in Figs. 10 and 11. We found the multi-fiber atlas to include nearly all features of the major bundles in the single tensor atlas. In addition, the multi-fiber atlas included more complete anatomical features of several bundles. In particular, the arcuate fasciculus included projections to inferior frontal gray matter, and the corpus callosum included lateral projections connecting the left and right hemispheres of frontal gray matter. We also found reconstructions of the three portions of the superior longitudinal fasciculus [44], which included crossings with numerous other bundles. We found the superior longitudinal fasciculus I crossed the corona radiata and superior projections of the corpus callosum. The superior longitudinal fasciculus II was found to cross the frontal lateral projections of the corpus callosum. Slice-based visualizations in Fig. 11 show examples of other crossings found in the multi-fiber atlas, including an axial slice of the brainstem and a sagittal slice of the corona radiata.
Figure 10.
Results from the fourth experiment described in Sec. 5.5, which included the construction of a multi-fiber atlas of 80 normal human subjects. Our proposed method was used for interpolation and fusion with deformation fields computed by DTI-TK. The top panel (A) shows a comparison of major bundles in the standard single-tensor atlas and our proposed the multi-fiber atlas. Bundles include the corona radiata (green), inferior longitudinal fasciculus (blue), inferior fronto-occipital fasciculus (orange), uncinate fasciculus (pink), corpus callosum (red), and the arcuate fasciculus (yellow). We found the multi-fiber atlas included nearly all features found in the single tensor atlas and more complete reconstructions of the frontal projections of the arcuate and lateral projections of the corpus callosum. The bottom panels show tractography results for complex fiber bundles including the lateral projections of the corpus callosum (B) and fronto-parietal connections of the superior longitudinal fasciculus I, II, III (C). The detail view in panel B also shows a triple crossing inferred at the intersection of the corona radiata, superior longitudinal fasciuculus, and corpus callosum. The three portions of the superior longitudinal fasciculus are also shown in panels A and C and include crossings with the corona radiata and corpus callosum. These reconstructions compare favorably to related work that examined these bundles in single human diffusion MRI reconstructions, dissection, and tracing studies in non-human primates.
Figure 11.
Results from the fourth experiment described in Sec. 5.5, which included the construction of a multi-fiber atlas of 80 normal human subjects. The top row shows principal tensor orientations overlaid on fractional anisotropy, and the bottom row shows fibers from the multi-fiber atlas overlaid on total fiber volume fraction. Fiber tube thickness reflects fractional anisotropy and per-fiber volume fraction in the top and bottom rows, respectively. The left column (A) shows an axial slice of the brainstem, demonstrating crossing fibers of cerebellar and pyramidal tracts. The right column (B) shows a sagittal slice demonstrating crossing fibers of the corona radiata and superior longitudinal fasciculus I.
6. Discussion
In two synthetic data experiments, we evaluated the major features of our approach, including compartment matching, model selection, and bilateral filtering. To assess performance in compartment matching, we compared our method to the “rank-based” method, which matches solely based on volume fractions. The first experiment showed how our approach can avoid large errors that occur with the rank-based estimator when crossing bundles have similar volume fraction. The second experiment showed how this problem arises during tractography, and how clustering-based matching can avoid the invalid connections of the rank-based approach. We also showed how orientation blurring can occur at bundle boundaries when using kernel weights derived only from spatial information. The first experiment showed how the bilateral filtering extension can reduce this effect by incorporating the structure of the data into the kernel weights. We also evaluated the proposed data-adaptive approach for model selection and compared it with previously proposed alternatives. We found “max” selection to always out-perform “fixed” selection and good performance in some cases; however, we found that both fixed and max selection can overestimate the number of fibers in even low noise conditions. These extra fibers give rise to compartment splitting, which both reduces the expected volume fraction and introduces orientation errors that are visible in tractography. We found the data-adaptive approach to reduce this effect, with only a small increase in missing fiber error. In general, these synthetic data experiments also showed our approach to significantly reduce noise-induced errors in fiber orientation and volume fraction and to improve connectivity mapping.
In the first in vivo data experiment, we examined the practical benefit of our approach for fiber bundle modeling in individual subjects. We found our approach provided reliable and reproducible results for quantitative fiber bundle metrics, including mean length, mean volume fraction, total volume, and streamline count. Among the measures, mean length and mean volume fraction performed best. Streamline count and total volume are perhaps less reliable due to their dependence on the pose and sampling resolution of the voxel grid. While past work has evaluated length-based measures [45], it is less clear how volume fraction can be used as an index of white matter [22] [46]. The results provide evidence that fiber bundle volume fraction may be a clinically useful measure in terms of reproducibility; however, it remains unclear exactly how this measure relates to others, such as fractional anisotropy, fiber orientation dispersion, and apparent fiber density [47] [48]. The scan-rescan results can also serve as a reference for gauging the significance of group differences of fiber bundle metrics in clinical imaging studies.
In the second in vivo data experiment, we examined an application to multi-fiber atlas construction, using our approach for interpolation during image resampling and fusion. We found the resulting atlas to include complex fiber bundle features not found in single tensor atlases [36]. In particular, the results included atlas-based reconstructions of the superior longitudinal fasciculus I, II, and III, all of which compare favorably to prior work on single subject reconstructions, post-mortem dissection, and tracing studies in non-human primates [44] [49] [50]. This method is potentially useful for constructing population-specific brain atlases, where it can be used to examine population-wide features of anatomy or serve as a reference for mapping bundles in individual subjects.
The software implementation consisted of custom Java code with experiments run on a Sun Grid Engine to allow for parallelized processing of simulation and human subject data. The fusion algorithm ran on a single Intel 2.8 GHz Core i5 processor and took 30 minutes for the 80 subject population. The primary computational bottleneck of this step was main memory usage, which required 6GB total. If applied to a larger population or with a higher sampling resolution, this issue could be addressed by decomposing the co-registered volumes into a number of overlapping blocks, performing fusion of each block, and then reconstructing the full atlas from the results.
There are a number of limitations and interesting open issues to note. First, we make use of tensor-based registration; however, some work has found multi-compartment registration to be beneficial [18] [51] [52]. Note, however, that dm is more of a divergence than a strict distance as it is not symmetric, so this may not be suitable for registration, where inverse-consistency is desirable. Second, it may be beneficial to investigate applications to other parametric diffusion models. The bilateral filtering and adaptive model selection techniques could be similarly applied to the full multi-tensor framework by substitution of df. The kernel regression framework could also be applied to models that incorporate microstructural information, such as NODDI [53] and ball-and-rackets [54]. This could be accomplished either by extending the proposed divergence measure to include variable Watson κ parameters or perhaps by a more general formulation with a Bingham divergence. Finally, there is a variety of applications to which this approach could be applied and further evaluated. Here we looked at fiber bundle mapping, but this could also be useful for brain network construction and visualization for surgical planning and guidance.
The approach is also related to more general image processing with orientation data, which touch research areas outside of MRI. Early approaches in directional statistics examined methods for dealing with axial data, a term more common in the statistics literature that applies equally well to fiber orientations [55]. In computer vision and graphics, filtering [56] [57] [58] [59], anisotropic diffusion [60] and bilateral filtering [61] have been developed for orientation fields, e.g. in analyzing fingerprints, hair, or textures. In the diffusion MRI literature, methods for fiber orientation regularization have also been proposed using Markov random fields [62], variational methods [63], and cohelicity [64]. The present work may have applications to those other areas, but this paper is limited to applications to neuroimaging with diffusion MRI and the ball-and-sticks model.
7. Conclusion
In this paper, we presented and evaluated a model-based kernel regression framework for estimating fiber orientation mixtures from model-valued image data. This framework generally supports image interpolation, smoothing, and fusion with the ball-and-sticks diffusion model and is compatible with scanner protocols with standard clinical field strengths, single shells, and low b-values. The kernel regression formulation also allows for simple and efficient data-adaptive extensions for model selection and bilateral filtering, and these general design of these components may potentially be applied to image processing with other multi-compartment parametric models. We experimentally evaluated our approach with synthetic data from computational phantoms and in vivo clinical data from human subjects. First, we showed our approach can address issues related to compartment matching and model selection, and can avoid orientation blurring at bundle boundaries and fiber splitting due to noise. The evaluation showed significant reductions in noise-induced orientation and volume fraction errors and improved reliability in connectivity mapping. Through in vivo data experiments, we tested the practical value of our approach in analyzing individual subjects, showing improved scan-rescan reproducibility and reliability of quantitative fiber bundle metrics. We then demonstrated the creation of a multi-fiber tractography atlas from a population of 80 human subjects. In comparison to single tensor atlasing, our results show more complete features of known fiber bundles and include reconstructions of lateral projections of the corpus callosum and complex fronto-parietal connections of the superior longitudinal fasciculus. This atlas-based approach could be used to either study population-wide features of anatomy or to aid fiber bundle mapping in individual subjects.
Figure 2.
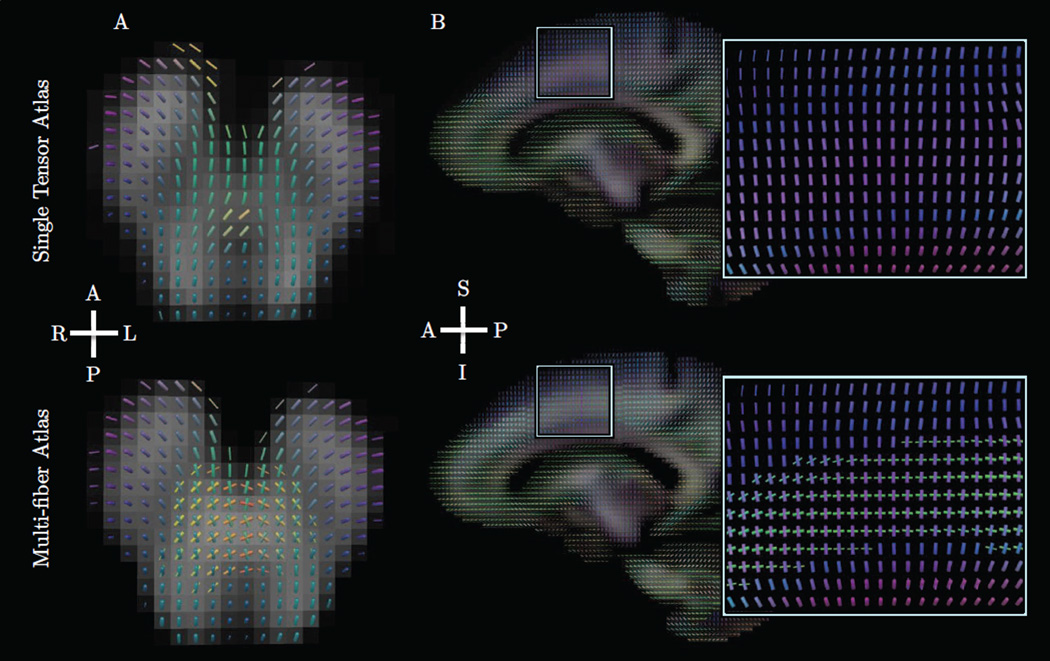
Example uses of the proposed estimator for interpolation, smoothing, and fusion tasks. Slices were taken from average human brain data at the junction of the corpus callosum (pink), corona radiata (blue), and cingulum (green). Fibers are colored according to their orientation, and thickness encodes volume fraction. The top panel shows interpolation at twice the original resolution, demonstrating continuity of both fiber orientations and volume fractions. The middle panel shows smoothing to reduce noise-induced angular error. The bottom panel shows fusion of 80 aligned subjects to produce an atlas representing the population.
Highlights.
-
*
Develops framework for tractography and atlasing with fiber orientation mixtures
-
*
Includes data-adaptive extensions for model selection and bilateral filtering
-
*
Shows improvements in fiber orientation, fraction, count, and connectivity metrics
-
*
Shows improvements in reproducibility/reliability of fiber bundle metrics
-
*
Shows reconstruction of complex fiber bundles in population atlas of 80 subjects
Acknowledgments
We would like to thank the anonymous reviewers for their constructive comments. This work was supported by the Brown Institute for Brain Science Graduate Research Award 2014, NIH/NINDS grant R01 NS052470, NIH/NIMH grant R01 MH085604, and NIH grant R01 EB004155.
Appendix
In the above analysis, we employ (Eq. 7) as a measure of discrepancy between fiber orientations. This turns out to have some useful geometric and statistical properties. For example, given an orientation v, consider the mapping ϕ(v) = vvT, also known as the Veronese-Whitney embedding, the dyadic product, or Knutsson mapping [65] [66] [67]. This can be imagined to take points on the sphere to a higher dimensional sphere and to fold its antipodes to give ϕ(v) = ϕ(−v). The Euclidean distance under this mapping is then equivalent to up to a scalar factor: The extrinsic mean is then given by μ = ∑i wiϕ(vi), which must be projected to the nearest orientation by argminv ‖ϕ(v)−μ‖2. This can be solved in closed form by finding the principal eigenvector of μ [66]. This formulation also has a statistical interpretation, as is equivalent to the Bregman divergence between Watson distributions of equal dispersion [68] [27], and the weighted average is equivalent to the maximum likelihood estimate of the direction of a Watson distribution [69]. These results support prior work suggesting a relationship between extrinsic means and maximum likelihood estimates for data in ℝℙn [70].
A connection can also be drawn between df and prior work using Gaussian mixture simplification with the Burg matrix divergence, dburg(A, B) = tr(AB−1) − log(det(AB−1)) − 3. While dburg cannot be directly applied to the sticks due to their low rank, it can be applied to sticks that are approximated by an “inflated” positive definite tensor with δ added to the second and third eigenvalues. If this approach is applied to a pair of stick orientations a and b to produce inflated tensors Ain f and Bin f, then dburg can be reduced to dburg(Ain f, Bin f) = (δ + 1/δ − 2) sin2(θ), given angle θ between a and b. If , then , so the use of Gaussian mixture simplification with inflated sticks is then equivalent to the “linear” and “max” conditions in the experiments. We ran a simulation experiment to numerically verify this and also found the ”inflated stick” Burg divergence implementation to take 40 times longer on average.
For multi-fiber analysis, we employ (Eq. 6) to measure discrepancy between mixtures of fiber orientations, and this too has useful geometric and statistical features. The form of dm allows the kernel regression estimator in Eq. 8 to be algebraically reduced to the simpler form in Eq. 12, which is equivalent to a clustering problem. The first sum-of-squares term has a statistical interpretation as hard clustering with a mixture of Watsons [28], and the additional regularization term has a statistical interpretation as the small-variance asymptotic limit of a Dirichlet process mixture, as in the DP-means algorithm [29]. Taken together, these make up the axial DP-means clustering problem in Eq. 12. This is theoretically well-grounded because the Watson distribution is an exponential family, and df is the associated Bregman divergence [27]. The work of Jiang et al. also demonstrates that the general form of Algo. 1 converges, albeit to a local minima [71]. To avoid instability due to local minima, we use random restarts with shuffling of the order of the input and take the solution with the overall minimum of Eq. 12.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. Journal of magnetic resonance. 2011;213(2):560–570. doi: 10.1016/j.jmr.2011.09.022. [DOI] [PubMed] [Google Scholar]
- 2.Pierpaoli C, Basser PJ. Toward a quantitative assessment of diffusion anisotropy. Magnetic resonance in Medicine. 1996;36(6):893–906. doi: 10.1002/mrm.1910360612. [DOI] [PubMed] [Google Scholar]
- 3.Vos SB, Viergever MA, Leemans A. Multi-fiber tractography visualizations for diffusion MRI data. PloS one. 2013;8(11):e81453. doi: 10.1371/journal.pone.0081453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Catani M, Howard RJ, Pajevic S, Jones DK. Virtual in vivo interactive dissection of white matter fasciculi in the human brain. NeuroImage. 2002;17(1):77–94. doi: 10.1006/nimg.2002.1136. [DOI] [PubMed] [Google Scholar]
- 5.Wakana S, Caprihan A, Panzenboeck MM, Fallon JH, Perry M, Gollub RL, Hua K, Zhang J, Jiang H, Dubey P, et al. Reproducibility of quantitative tractography methods applied to cerebral white matter. NeuroImage. 2007;36(3):630–644. doi: 10.1016/j.neuroimage.2007.02.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mori S, Oishi K, Faria AV. White matter atlases based on diffusion tensor imaging. Current opinion in neurology. 2009;22(4):362. doi: 10.1097/WCO.0b013e32832d954b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lenglet C, Campbell JS, Descoteaux M, Haro G, Savadjiev P, Wassermann D, Anwander A, Deriche R, Pike GB, Sapiro G, et al. Mathematical methods for diffusion MRI processing. NeuroImage. 2009;45(1):S111–S122. doi: 10.1016/j.neuroimage.2008.10.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tuch DS, Reese TG, Wiegell MR, Makris N, Belliveau JW, Wedeen VJ. High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magnetic Resonance in Medicine. 2002;48(4):577–582. doi: 10.1002/mrm.10268. [DOI] [PubMed] [Google Scholar]
- 9.Takeda H, Farsiu S, Milanfar P. Kernel regression for image processing and reconstruction. Image Processing, IEEE Transactions on. 2007;16(2):349–366. doi: 10.1109/tip.2006.888330. [DOI] [PubMed] [Google Scholar]
- 10.Taquet M, Scherrer B, Benjamin C, Prabhu S, Macq B, Warfield SK. Interpolating multi-fiber models by gaussian mixture simplification; Biomedical Imaging (ISBI), 2012 9th IEEE International Symposium on, IEEE; 2012. pp. 928–931. [Google Scholar]
- 11.Cabeen RP, Bastin ME, Laidlaw DH. Estimating constrained multi-fiber diffusion MR volumes by orientation clustering. Medical Image Computing and Computer-Assisted Intervention–MICCAI. 2013:82–89. doi: 10.1007/978-3-642-40811-3_11. [DOI] [PubMed] [Google Scholar]
- 12.Becker S, Tabelow K, Voss HU, Anwander A, Heidemann RM, Polzehl J. Position-orientation adaptive smoothing of diffusion weighted magnetic resonance data (POAS) Medical image analysis. 2012;16(6):1142–1155. doi: 10.1016/j.media.2012.05.007. [DOI] [PubMed] [Google Scholar]
- 13.Pennec X, Fillard P, Ayache N. A Riemannian framework for tensor computing. International Journal of Computer Vision. 2006;66(1):41–66. [Google Scholar]
- 14.Goh A, Lenglet C, Thompson PM, Vidal R. A nonparametric riemannian framework for processing high angular resolution diffusion images and its applications to ODF-based morphometry. NeuroImage. 2011;56(3):1181–1201. doi: 10.1016/j.neuroimage.2011.01.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yeh F-C, Tseng W-YI. NTU-90: a high angular resolution brain atlas constructed by q-space diffeomorphic reconstruction. NeuroImage. 2011;58(1):91–99. doi: 10.1016/j.neuroimage.2011.06.021. [DOI] [PubMed] [Google Scholar]
- 16.Qazi AA, Radmanesh A, O’Donnell L, Kindlmann G, Peled S, Whalen S, Westin C-F, Golby AJ. Resolving crossings in the corticospinal tract by two-tensor streamline tractography: Method and clinical assessment using fmri. NeuroImage. 2009;47:T98–T106. doi: 10.1016/j.neuroimage.2008.06.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yap P-T, Gilmore JH, Lin W, Shen D. PopTract: population-based tractography, Medical Imaging. IEEE Transactions on. 2011;30(10):1829–1840. doi: 10.1109/TMI.2011.2154385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Taquet M, Scherrer B, Commowick O, Peters JM, Sahin M, Macq B, Warfield SK. A mathematical framework for the registration and analysis of multi-fascicle models for population studies of the brain microstructure, Medical Imaging. IEEE Transactions on. 2014;33(2):504–517. doi: 10.1109/TMI.2013.2289381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cabeen RP, Laidlaw DH. Bilateral filtering of multiple fiber orientations in diffusion MRI. MICCAI Workshop on Computational Diffusion MRI. 2014:193–202. [Google Scholar]
- 20.Behrens T, Berg HJ, Jbabdi S, Rushworth M, Woolrich M. Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? NeuroImage. 2007;34(1):144–155. doi: 10.1016/j.neuroimage.2006.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wilkins B, Lee N, Gajawelli N, Law M, Lepor N. Fiber estimation and tractography in diffusion mri: Development of simulated brain images and comparison of multi-fiber analysis methods at clinical b-values. NeuroImage. 2015;109(0):341–356. doi: 10.1016/j.neuroimage.2014.12.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jbabdi S, Behrens TE, Smith SM. Crossing fibres in tract-based spatial statistics. NeuroImage. 2010;49(1):249–256. doi: 10.1016/j.neuroimage.2009.08.039. [DOI] [PubMed] [Google Scholar]
- 23.Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. FSL. NeuroImage. 2012;62(2):782–790. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- 24.Lehmann TM, Gonner C, Spitzer K. Survey: Interpolation methods in medical image processing, Medical Imaging. IEEE Transactions on. 1999;18(11):1049–1075. doi: 10.1109/42.816070. [DOI] [PubMed] [Google Scholar]
- 25.Watson GS. Smooth regression analysis, Sankhyā: The Indian Journal of Statistics. Series A. 1964:359–372. [Google Scholar]
- 26.Hamarneh G, Hradsky J. Bilateral filtering of diffusion tensor magnetic resonance images. Image Processing, IEEE Transactions on. 2007;16(10):2463–2475. doi: 10.1109/tip.2007.904964. [DOI] [PubMed] [Google Scholar]
- 27.Cabeen RP, Laidlaw DH. White matter supervoxel segmentation by axial DP-means clustering. MICCAI Workshop on Medical Computer Vision. Large Data in Medical Imaging. 2014:95–104. [Google Scholar]
- 28.Sra S, Jain P, Dhillon I. Technical Report TR-07-05. Austin: Dept. of CS, Univ. of Texas; Modeling data using directional distributions: Part II. [Google Scholar]
- 29.Kulis B, Jordan MI. Revisiting k-means: New algorithms via bayesian nonparametrics; Proceedings of the 29th International Conference on Machine Learning (ICML-12); 2012. [Google Scholar]
- 30.Zhang S, Demiralp C, Laidlaw DH. Visualizing diffusion tensor MR images using streamtubes and streamsurfaces, Visualization and Computer Graphics. IEEE Transactions on. 2003;9(4):454–462. [Google Scholar]
- 31.Wickham H. ggplot2: elegant graphics for data analysis. New York: Springer; 2009. [Google Scholar]
- 32.Leemans A, Sijbers J, Verhoye M, Van der Linden A, Van Dyck D. Mathematical framework for simulating diffusion tensor MR neural fiber bundles. Magnetic resonance in medicine. 2005;53(4):944–953. doi: 10.1002/mrm.20418. [DOI] [PubMed] [Google Scholar]
- 33.Cook P, Bai Y, Nedjati-Gilani S, Seunarine K, Hall M, Parker G, Alexander D. Camino: open-source diffusion-mri reconstruction and processing. 14th scientific meeting of the international society for magnetic resonance in medicine, Vol. 2759; 2006; Seattle WA, USA. [Google Scholar]
- 34.Dietrich O, Raya JG, Reeder SB, Reiser MF, Schoenberg SO. Measurement of signal-to-noise ratios in mr images: Influence of multichannel coils, parallel imaging, and reconstruction filters. Journal of Magnetic Resonance Imaging. 2007;26(2):375–385. doi: 10.1002/jmri.20969. [DOI] [PubMed] [Google Scholar]
- 35.Leemans A, Jones DK. The b-matrix must be rotated when correcting for subject motion in DTI data. Magnetic Resonance in Medicine. 2009;61(6):1336–1349. doi: 10.1002/mrm.21890. [DOI] [PubMed] [Google Scholar]
- 36.Zhang H, Yushkevich PA, Rueckert D, Gee JC. Unbiased white matter atlas construction using diffusion tensor images. Medical Image Computing and Computer-Assisted Intervention–MICCAI. 2007:211–218. doi: 10.1007/978-3-540-75759-7_26. [DOI] [PubMed] [Google Scholar]
- 37.Zhang H, Avants BB, Yushkevich PA, Woo JH, Wang S, McCluskey LF, Elman LB, Melhem ER, Gee JC. High-dimensional spatial normalization of diffusion tensor images improves the detection of white matter differences: an example study using amyotrophic lateral sclerosis, Medical Imaging. IEEE Transactions on. 2007;26(11):1585–1597. doi: 10.1109/TMI.2007.906784. [DOI] [PubMed] [Google Scholar]
- 38.Ramirez-Manzanares A, Cook PA, Hall M, Ashtari M, Gee JC. Resolving axon fiber crossings at clinical b-values: An evaluation study. Medical physics. 2011;38(9):5239–5253. doi: 10.1118/1.3626571. [DOI] [PubMed] [Google Scholar]
- 39.Dice LR. Measures of the amount of ecologic association between species. Ecology. 1945;26(3):297–302. [Google Scholar]
- 40.Catani M, De Schotten MT. A diffusion tensor imaging tractography atlas for virtual in vivo dissections. Cortex. 2008;44(8):1105–1132. doi: 10.1016/j.cortex.2008.05.004. [DOI] [PubMed] [Google Scholar]
- 41.Zhang Y, Zhang J, Oishi K, Faria AV, Jiang H, Li X, Akhter K, Rosa-Neto P, Pike GB, Evans A, et al. Atlas-guided tract reconstruction for automated and comprehensive examination of the white matter anatomy. NeuroImage. 2010;52(4):1289–1301. doi: 10.1016/j.neuroimage.2010.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, Gerig G. User-guided 3d active contour segmentation of anatomical structures: significantly improved efficiency and reliability. NeuroImage. 2006;31(3):1116–1128. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]
- 43.Wolak ME, Fairbairn DJ, Paulsen YR. Guidelines for estimating repeatability. Methods in Ecology and Evolution. 2012;3(1):129–137. [Google Scholar]
- 44.De Schotten MT, Dell’Acqua F, Forkel SJ, Simmons A, Vergani F, Murphy DG, Catani M. A lateralized brain network for visuospatial attention. Nature neuroscience. 2011;14(10):1245–1246. doi: 10.1038/nn.2905. [DOI] [PubMed] [Google Scholar]
- 45.Correia S, Lee SY, Voorn T, Tate DF, Paul RH, Zhang S, Salloway SP, Malloy PF, Laidlaw DH. Quantitative tractography metrics of white matter integrity in diffusion-tensor MRI. NeuroImage. 2008;42(2):568–581. doi: 10.1016/j.neuroimage.2008.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Jeurissen B, Leemans A, Tournier J-D, Jones DK, Sijbers J. Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging. Human brain mapping. 2013;34(11):2747–2766. doi: 10.1002/hbm.22099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Raffelt D, Tournier J-D, Rose S, Ridgway GR, Henderson R, Crozier S, Salvado O, Connelly A. Apparent fibre density: a novel measure for the analysis of diffusion-weighted magnetic resonance images. NeuroImage. 2012;59(4):3976–3994. doi: 10.1016/j.neuroimage.2011.10.045. [DOI] [PubMed] [Google Scholar]
- 48.Riffert TW, Schreiber J, Anwander A, Knösche TR. Beyond fractional anisotropy: extraction of bundle-specific structural metrics from crossing fiber models. NeuroImage. 2014;100:176–191. doi: 10.1016/j.neuroimage.2014.06.015. [DOI] [PubMed] [Google Scholar]
- 49.De Schotten MT, DellAcqua F, Valabregue R, Catani M. Monkey to human comparative anatomy of the frontal lobe association tracts. Cortex. 2012;48(1):82–96. doi: 10.1016/j.cortex.2011.10.001. [DOI] [PubMed] [Google Scholar]
- 50.Schmahmann JD, Pandya DN, Wang R, Dai G, D’Arceuil HE, de Crespigny AJ, Wedeen VJ. Association fibre pathways of the brain: parallel observations from diffusion spectrum imaging and autoradiography. Brain. 2007;130(3):630–653. doi: 10.1093/brain/awl359. [DOI] [PubMed] [Google Scholar]
- 51.Taquet M, Scherrer B, Commowick O, Peters J, Sahin M, Macq B, Warfield SK. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2012. Springer; 2012. Registration and analysis of white matter group differences with a multi-fiber model; pp. 313–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Du J, Goh A, Qiu A. Diffeomorphic metric mapping of high angular resolution diffusion imaging based on Riemannian structure of orientation distribution functions, Medical Imaging. IEEE Transactions on. 2012;31(5):1021–1033. doi: 10.1109/TMI.2011.2178253. [DOI] [PubMed] [Google Scholar]
- 53.Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. NeuroImage. 2012;61(4):1000–1016. doi: 10.1016/j.neuroimage.2012.03.072. [DOI] [PubMed] [Google Scholar]
- 54.Sotiropoulos SN, Behrens TEJ, Jbabdi S. Ball and rackets: Inferring fiber fanning from diffusion-weighted mri. NeuroImage. 2012;60(2):1412–1425. doi: 10.1016/j.neuroimage.2012.01.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Watson GS. Distributions on the circle and sphere. Journal of Applied Probability. 1982:265–280. [Google Scholar]
- 56.Aach T, Mota C, Stuke I, Muhlich M, Barth E. Analysis of superimposed oriented patterns. Image Processing, IEEE Transactions on. 2006;15(12):3690–3700. doi: 10.1109/tip.2006.884921. [DOI] [PubMed] [Google Scholar]
- 57.Muhlich M, Aach T. Analysis of multiple orientations. Image Processing, IEEE Transactions on. 2009;18(7):1424–1437. doi: 10.1109/TIP.2009.2019307. [DOI] [PubMed] [Google Scholar]
- 58.Westin C-F, Knutsson H. Representation and estimation of tensor-pairs. New Developments in the Visualization and Processing of Tensor Fields. 2012:267–280. [Google Scholar]
- 59.van Vliet LJ, Faas FG. Multi-orientation analysis by decomposing the structure tensor and clustering. Pattern Recognition, 2006. ICPR 2006. 18th International Conference on. 2006;3:856–860. [Google Scholar]
- 60.Perona P. Orientation diffusions. Image Processing, IEEE Transactions on. 1998;7(3):457–467. doi: 10.1109/83.661195. [DOI] [PubMed] [Google Scholar]
- 61.Paris S, Briceño HM, Sillion FX. Capture of hair geometry from multiple images. ACM Transactions on Graphics (TOG) 2004;23(3):712–719. [Google Scholar]
- 62.Poupon C, Clark C, Frouin V, Regis J, Bloch I, Le Bihan D, Mangin J-F. Regularization of diffusion-based direction maps for the tracking of brain white matter fascicles. NeuroImage. 2000;12(2):184–195. doi: 10.1006/nimg.2000.0607. [DOI] [PubMed] [Google Scholar]
- 63.Coulon O, Alexander DC, Arridge S. Diffusion tensor magnetic resonance image regularization. Medical image analysis. 2004;8(1):47–67. doi: 10.1016/j.media.2003.06.002. [DOI] [PubMed] [Google Scholar]
- 64.Savadjiev P, Campbell JS, Pike GB, Siddiqi K. 3D curve inference for diffusion MRI regularization. Medical Image Computing and Computer-Assisted Intervention–MICCAI. 2005:123–130. doi: 10.1007/11566465_16. [DOI] [PubMed] [Google Scholar]
- 65.Knutsson H, Westin C-F, Andersson M. Representing local structure using tensors II. Image Analysis. 2011:545–556. [Google Scholar]
- 66.Bhattacharya R, Patrangenaru V. Large sample theory of intrinsic and extrinsic sample means on manifolds. I. Annals of statistics. 2003:1–29. [Google Scholar]
- 67.Rieger B, van Vliet LJ. Representing orientation in n-dimensional spaces. Computer Analysis of Images and Patterns. 2003:17–24. [Google Scholar]
- 68.Garcia V, Nielsen F. Simplification and hierarchical representations of mixtures of exponential families. Signal Processing. 2010;90(12):3197–3212. [Google Scholar]
- 69.Sra S, Karp D. The multivariate Watson distribution: Maximum-likelihood estimation and other aspects. Journal of Multivariate Analysis. 2013;114:256–269. [Google Scholar]
- 70.Brun A, Westin C-F, Herberthson M, Knutsson H. Intrinsic and extrinsic means on the circle-a maximum likelihood interpretation, Acoustics. Acoustics, Speech and Signal Processing, 2007. ICASSP 2007. IEEE International Conference on. 2007;3:III–1053. [Google Scholar]
- 71.Jiang K, Kulis B, Jordan MI. Small-variance asymptotics for exponential family dirichlet process mixture models. Advances in Neural Information Processing Systems. 2012:3158–3166. [Google Scholar]