mlRho – a program for estimating the population mutation and recombination rates from shotgun-sequenced diploid genomes

Abstract

Improvements in sequencing technology over the past 5 years are leading to routine application of shotgun sequencing in the fields of ecology and evolution. However, the theory to estimate evolutionary parameters from these data is still being worked out. Here we present an extension and implementation of part of this theory, mlRho. This program can efficiently compute the following three maximum likelihood estimators based on shotgun sequence data obtained from single diploid individuals: the population mutation rate (4N_eμ), the sequencing error rate, and the population recombination rate (4N_ec). We demonstrate the accuracy of mlRho by applying it to simulated data sets. In addition, we analyse the genomes of the sea squirt Ciona intestinalis and the water flea Daphnia pulex. Ciona intestinalis is an obligate outcrosser, while D. pulex is a cyclic parthenogen, and we discuss how these contrasting life histories are reflected in our parameter estimates. The program mlRho is freely available from http://guanine.evolbio.mpg.de/mlRho.

Introduction

Over a quarter of a century after its inception, the shotgun approach remains the method of choice for sequencing long stretches of DNA (Sanger et al. 1982). An idealized shotgun run returns Poisson-distributed coverage of the template with a certain error rate. Recent advances in sequencing technology have made the shotgun procedure available to the evolution and ecology community (Shendure & Ji 2008). This has sparked interest in inferring evolutionary parameters directly from assembled shotgun reads (Johnson & Slatkin 2006; Hellmann et al. 2008; Lynch 2008; Jiang et al. 2009; Lynch 2009). The main challenge in this work is to account for uneven coverage and the errors introduced by the widening spectrum of sequencing chemistry on offer.

Johnson & Slatkin (2006) developed a method for estimating the scaled mutation rate, θ = 4N_eμ, where N_e is the effective population size and μ is the probability of mutation per generation per nucleotide. In addition, they estimate the scaled exponential population growth rate. Both statistics are computed from metagenomics data, where every read is assumed to originate from a different organism, although ascertainment and correct species assignment is difficult with such data sets.

By contrast, Hellmann et al. (2008) have developed an estimator of θ for one or a few diploid individuals. Their method incorporates sequencing error as a known parameter, which is assumed to be small. However, current second-generation sequencing instruments can have error rates on the order of the sampled genetic diversity. Jiang et al. (2009) have derived an estimator of θ that is similar to that of Hellmann et al. (2008). In addition, they extended the method of Hudson (2001) to estimate the scaled recombination rate ρ = 4N_ec, where c is the probability of recombination. They use a threshold scheme to classify positions in assembled shotgun reads as heterozygous or homozygous and apply a set of rules to account for sequencing error.

To overcome the problem of unknown error rates and to account for binomial sampling of parental alleles, Lynch (2008) has proposed maximum likelihood methods for estimating a number of genetic parameters from assembled shotgun data obtained from diploid individuals. Here we present mlRho, an implementation of his maximum likelihood estimators for θ and sequencing error. We also follow his suggestion to estimate the rate of recombination from the correlation between the zygosity at pairs of nucleotide positions. For this purpose, we make explicit the link between the zygosity correlation and ρ and θ. We demonstrate the usefulness of these derivations by applying mlRho to simulated data sets and to the genomes of the sea squirt Ciona intestinalis and the water flea Daphnia pulex.

Ciona intestinalis is a diploid benthic urochordate with a compact genome of 160 Mb, mostly sequenced from a single individual (Dehal et al. 2002). It is a self-sterile hermaphrodite and has one of the highest recombination densities (centimorgan, cM/bp) known in animals (Kano et al. 2006).

Daphnia pulex is a diploid planktonic crustacean with a genome size of approximately 200 Mb. The sequenced strain was chosen for its low genetic diversity to facilitate subsequent genome assembly. Under favourable environmental conditions Daphnia reproduce parthenogenetically but switch to sexual reproduction in response to harsher conditions. We discuss how these diverse life-history traits are reflected in our estimations of ρ and θ for the two organisms.

Approach

Homo- and heterozygous pairs of positions

Consider a population of N_e diploid individuals evolving under the standard neutral model, i.e. population size is constant, no selection acts on any locus, and the population is in equilibrium. The fraction of loci with distinct alleles is known as the population heterozygosity, denoted by H. The expected heterozygosity, given θ = 4N_eμ, is

$${\mathbb{E}}_{\theta }[H]=\frac{\theta }{1+\theta }\approx \theta ,$$ (1)

where the approximation holds under the infinite sites model, that is, if θ ≪ 1.

Now consider pairs of sites at some constant distance that undergo reciprocal recombination with probability c. We call H₀ the fraction of pairs of sites that are both homozygous, and H₂ the fraction of pairs of sites that are both heterozygous. Using eqn (4) of Strobeck & Morgan (1978) we can write the expectation for the fraction of homozygous pairs among all pairs of positions separated by a fixed distance as

$${\mathbb{E}}_{\mathrm{\theta },\rho }[H_0]=\frac{18+13\rho +{\rho }^2+36\theta +22{\theta }^2+4{\theta }^3+\rho (6\theta +{\theta }^2)}{(1+\theta )(18+13\rho +{\rho }^2+54\theta +40{\theta }^2+8{\theta }^3+\rho (\rho \theta +19\theta +6{\theta }^2))},$$ (2)

and the expectation for the fraction of heterozygous pairs as

$${\mathbb{E}}_{\mathrm{\theta },\rho }[H_2]=\frac{{\theta }^2(36+14\rho +{\rho }^2+36\theta +6\rho \theta +8{\theta }^2)}{(1+\theta )(18+13\rho +{\rho }^2+54\theta +40{\theta }^2+8{\theta }^3+\rho (\rho \theta +19\theta +6{\theta }^2))}.$$ (3)

Note that there are only three types of pairs: homozygous, heterozygous and mixed, which means that

$${\mathbb{E}}_{\theta ,\rho }[H_0]+{\mathbb{E}}_{\theta ,\rho }[H_2]+2({\mathbb{E}}_{\theta }[H]-{\mathbb{E}}_{\theta ,\rho }[H_2])=1.$$

Expressions (1)–(3) are therefore connected through

$$2{\mathbb{E}}_{\theta }[H]+{\mathbb{E}}_{\theta ,\rho }[H_0]-{\mathbb{E}}_{\theta ,\rho }[H_2]=1$$

and thus we may write

$${\mathbb{E}}_{\theta ,\rho }[H_0]=\frac{1}{{(1+\theta )}^2}+\mathrm{\Delta }\frac{\theta }{{(1+\theta )}^2},$$ (4)

$${\mathbb{E}}_{\theta ,\rho }[H_2]=\frac{{\theta }^2}{{(1+\theta )}^2}+\mathrm{\Delta }\frac{\theta }{{(1+\theta )}^2}$$ (5)

with

$$\mathrm{\Delta }=\frac{\theta (18+\rho +18\theta +\rho \theta +4{\theta }^2)}{18+13\rho +{\rho }^2+54\theta +40{\theta }^2+8{\theta }^3+\rho (\rho \theta +19\theta +6{\theta }^2)},$$ (6)

where Δ is the zygosity correlation introduced by Lynch (2008). Note that Δ converges to 0 in the limit of large recombination rates ρ. This is clear because the first terms on the right-hand sides of eqns (4) and (5) describe the familiar formulas for the expected number of homo/heterozygotes if loci are independent. So, Δ measures the deviation from independence of loci, which we call ‘zygosity correlation’. Formulas for Δ could also be obtained for models other than the standard neutral model investigated by us.

The formalism established so far suffices to estimate θ and ρ from error-free sequencing data. To incorporate sequencing error into our model, we follow the approach taken by Lynch (2008): consider mapped shotgun sequencing reads from one diploid individual. At each position in the genome we count the four different nucleotides, n: = (n_A,n_C,n_G,n_T), and call such a quartet of counts a profile, while the sum of counts, n = n_A + n_C + n_G + n_T, is the coverage of the profile’s position. We further denote the genome-wide nucleotide frequencies p_A, p_C, p_G, p_T and the sequencing error per base of shotgun read ε. We can now express the probability of obtaining a certain profile given that the position is truly homozygous as

$$P_{\epsilon }^{\text{ho}}(\underset{\_}{n})=\sum _{i\in \{\mathrm{A},\mathrm{C},\mathrm{G},\mathrm{T}\}}{p}_{i}B(n-n_i;n;\epsilon ),$$

where B(k;n;p) is the binomial probability of k successes in n trials, each success with probability p. Conversely, given that a position is truly heterozygous, the probability of its profile is

$$P_{\epsilon }^{\text{he}}(\underset{\_}{n})=\sum _{\begin{array}{c}i,j\in \{\mathrm{A},\mathrm{C},\mathrm{G},\mathrm{T}\}\\ i\ne j\end{array}}\frac{p_i{p}_j}{1-{\sum }_i{p}_i^2}B\left(n-n_i-n_j;n;\frac{2}{3}\epsilon \right)B\left(n_i;n_i+n_j;\frac{1}{2}\right).$$

The probability that a site is heterozygous is

$$\frac{\theta }{1+\theta }\approx \theta ,$$

and hence the total probability of a profile is

$$P_{\theta ,\epsilon }(\underset{\_}{n})=(1-\theta )P_{\epsilon }^{\text{ho}}(\underset{\_}{n})+\theta P_{\epsilon }^{\text{he}}(\underset{\_}{n}).$$

We can now express the probability of observing pairs of profiles at distinct sites separated by some fixed recombination distance, n_a = (n_Aa,n_Ca,n_Ga,n_Ta) and n_b =(n_Ab,n_Cb,n_Gb,n_Tb) as

$$\begin{array}{l}{P}_{\theta ,\rho ,\epsilon }({\underset{\_}{n}}_a,{\underset{\_}{n}}_b)={\mathbb{E}}_{\theta ,\rho }[H_0]P_{\epsilon }^{\text{ho}}({\underset{\_}{n}}_a)P_{\epsilon }^{\text{ho}}({\underset{\_}{n}}_b)\\ +{\mathbb{E}}_{\theta ,\rho }[H_2]P_{\epsilon }^{\text{he}}({\underset{\_}{n}}_a)P_{\epsilon }^{\text{he}}({\underset{\_}{n}}_b)\\ +\frac{1}{2}(1-{\mathbb{E}}_{\theta ,\rho }[H_0]-{\mathbb{E}}_{\theta ,\rho }[H_2])[P_{\epsilon }^{\text{ho}}({\underset{\_}{n}}_a)P_{\epsilon }^{\text{he}}({\underset{\_}{n}}_b)]\\ +P_{\epsilon }^{\text{he}}({\underset{\_}{n}}_a)P_{\epsilon }^{\text{ho}}({\underset{\_}{n}}_b)].\end{array}$$

For a given distance, let N(n_a,n_b) be the number of pairs of positions across the genome with profiles (n_a,n_b) in our shotgun sequencing data. These pairs of positions are not completely independent; by nevertheless treating them as independent, we use what is known as a ‘composite likelihood’ approach, which allows us to compute the log likelihood of the desired parameters θ, ρ and ε as

$$logL(\theta ,\rho ,\epsilon )=\sum _{{\underset{\_}{n}}_a,{\underset{\_}{n}}_b}N({\underset{\_}{n}}_a,{\underset{\_}{n}}_b)log{P}_{\theta ,\rho ,\epsilon }({\underset{\_}{n}}_a,{\underset{\_}{n}}_b).$$ (7)

Maximizing this function with respect to θ, ρ and ε yields maximum likelihood estimators for these parameters. As an alternative to estimating ρ, we can estimate Δ using the formalism established by Lynch (2008).

Implementation

When looking at genome-scale data, two things are needed to find the maximum of eqn (7): (i) an efficient method for counting the number of sites with each observed profile, and (ii) a fast and accurate procedure for multidimensional maximization of the target functions. We implemented profile counting using a binary search tree. Binary search trees are a standard data structure described, for example, by Knuth (1998, 426ff), and Kernighan & Ritchie (1988, p. 139ff) give a simple but effective implementation. For the function maximization we used the simplex algorithm by Nelder & Mead (1965) as implemented in the GNU Scientific Library (Galassi et al. 2005). Confidence intervals were determined by calculating the values of an estimator where the likelihood was two log units below the maximum. Note that under our composite likelihood approach these confidence intervals will tend to be too narrow. The resulting program, mlRho, can be tested via a web interface at http://guanine.evolbio.mpg.de/mlRho. The C source code for the stand-alone version of mlRho is also freely available from this web site.

As detailed in its documentation, the input of mlRho is a table of counts of the four nucleotides at every position. However, genome assembly programs usually do not produce such profiles as output. We therefore also provide the program ace2pro, which converts files in ACE format to profiles. The ACE file format was developed for the widely used assembly viewer consed (Gordon et al. 1998) and is generated by a number of assembly programs. The program ace2pro is also freely available from the mlRho web page.

Testing

Turing (1946, p.45) wrote with characteristic perspicacity about programming errors, which he called ‘snags’, that ‘up to a point it is better to let the snags be there than to spend such time in design that there are none (how many decades would this course take?)’. Our approach to Turing’s point of diminishing returns on testing was twofold. (i) We compared mlRho with an independent earlier implementation of the estimation procedure for θ and ε by ML. (ii) We wrote software to simulate shotgun sequencing data with defined genetic diversity, recombination rate and sequencing error for analysis by mlRho.

Two procedures are necessary to simulate shotgun sequencing data: template generation and the sequencing itself. For template generation we used the coalescent program ms (Hudson 2002), which simulates haplotypes under neutrality conditioned on θ and ρ. These haplotypes were converted to the corresponding DNA sequences using our program ms2dna, which can be downloaded freely from the mlRho web page.

We simulated shotgun sequencing using our program sequencer. This takes a set of simulated or empirical input sequences and returns shotgun reads in FASTA or profile format. The user can vary a number of parameters, including average read length, coverage and error rate. Again, sources and documentation for the program can be downloaded freely via the mlRho web page.

Application

In addition to the simulated data sets, we analysed the genomes of the sea squirt, C. intestinalis (Dehal et al. 2002), and the water flea, D. pulex. Ciona intestinalis was shotgun sequenced to a coverage of 8.3 yielding 2326 scaffolds spanning 114.5 × 10⁶ bp (Dehal et al. 2002). The assembled reads from this genome project were published as part of a study on diploid genome reconstruction (Kim et al. 2007) and can be obtained from http://www-rcf.usc.edu/~lilei/diploid.html. A program to convert these data to profiles, asm2pro, is available from the mlRho web site. Analysis of the Daphnia genome was carried out on the best assembled half of its 200 Mb genome (A. Tucker, personal communication). This comprised 90.7 Mb covered 8.4-fold. In both genomes only sites with a minimum coverage of four were included in the analysis.

Results

Simulations

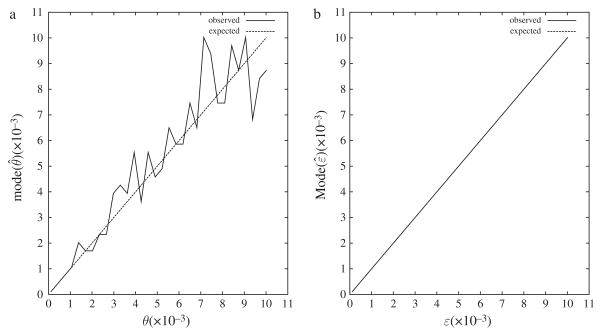
We began by asking of the previously established joint estimator of θ and ε (Lynch 2008): given a large number of simulated data sets conditioned on some value of θ or ε, what are the most likely values of the corresponding parameters? The hallmark of a ML estimator is, of course, that these two statistics coincide, i.e. that, say, θ̂ is located where P(profiles|θ) is maximal. We investigated this by simulating 10⁴ diploid genomes of length 1 Mb and coverage 10 for a range of values of θ and ε. Figure 1a shows that for θ there seems to be no systematic deviation from the ideal diagonal. The fit between estimator and parameter is almost perfect for ε, as demonstrated in Fig. 1b.

Fig. 1.

The mode of distributions of the population mutation rate, mode (θ̂) (a) and of the sequencing error rate, mode (ε̂) (b) as a function of the corresponding simulated parameter. Each parameter value investigated was simulated 10⁴ times. In (a), ε = 4 × 10⁻⁴ and in (b) θ = 10⁻³.

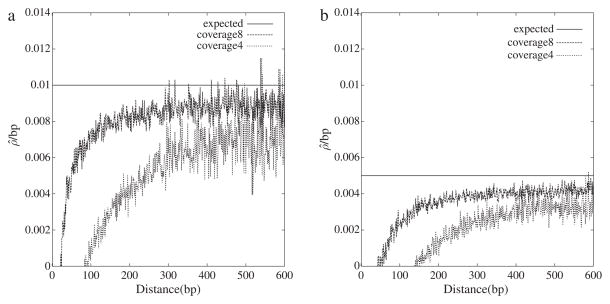
In order to study our new estimator of the recombination rate, we simulated 1000 pairs of sequences each 100 kb long with θ = 0.01 and two different recombination rates, which were in silico sequenced with an error of ε = 10⁻⁴ to a coverage of 4 or 8. In Fig. 2a we can see that with increasing distance the estimated recombination rate approaches the simulated value of ρ = 0.01, without reaching it. However, an increase in coverage from four to eight improved the fit between theory and experiment. This was also observed with a simulated recombination rate of ρ = 0.005 (Fig. 2b) and suggests that our estimator becomes unbiased in the limit of large coverage.

Fig. 2.

The maximum likelihood estimator of the population recombination rate per base pair, ρ̂/bp, as a function of pairwise distance for two coverages. Each graph is based on a single simulated data set consisting of 1000 pairs of 100 kb sequences (contigs) with θ = 0.01 and ρ = 0.01 (a) or ρ = 0.005 (b). This data set was in silico shotgun sequenced to a coverage of four or eight with an error rate of ε = 10⁻⁴.

The genomes of Ciona intestinalis and Daphnia pulex

Using the program mlRho, we calculated θ̂ = 0.0111 and θ̂ = 0.0011 for C. intestinalis and D. pulex respectively. By applying a correction for low coverage (Lynch 2008), we obtained θ̂ = 0.0116 ≈ 0.012 for C. intestinalis and θ̂ = 0.00116 ≈ 0.0012 for D. pulex. Thus, C. intestinalis is 10 times more diverse than D. pulex.

The estimated error rate was similarly high in both sequencing projects, with D. pulex having a 7% higher value of ε̂= 0.00121 than C. intestinalis (ε̂ = 0.00113). However, when compared with the mutation rate, we see a great difference here: while in C. intestinalis there were 10 times more genuine polymorphisms than errors, in D. pulex genetic diversity is almost identical to the error rate.

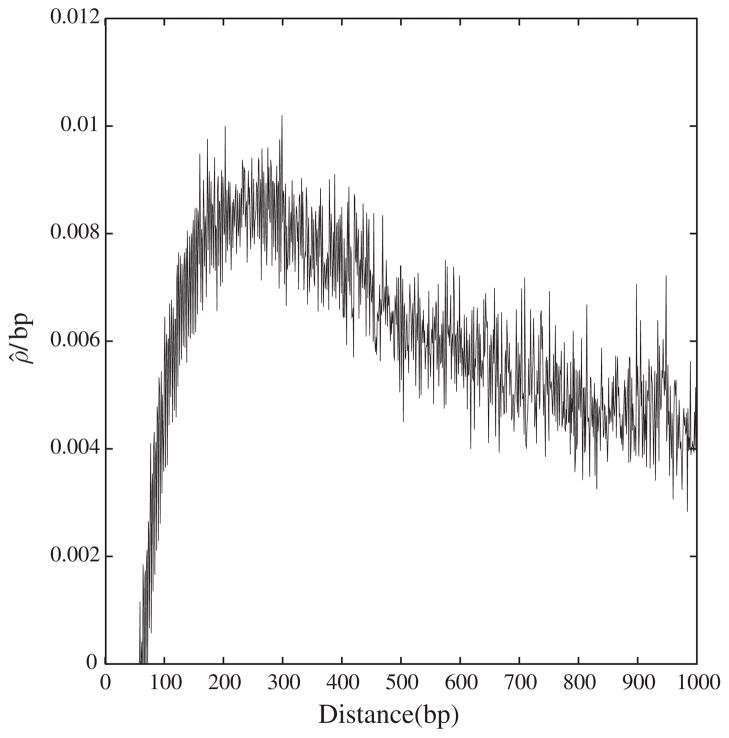
Figure 3 shows ρ̂ as a function of distance for the genome of C. intestinalis. This has a markedly different shape compared with the simulations shown in Fig. 2, which reach a plateau for distances greater than approximately 400 bp. By contrast, the curve for C. intestinalis peaks at approximately 200 bp at a value close to 0.0085 and reaches roughly half this value at distance 1000. In D. pulex, the lower confidence level of all estimates at distances between 1 and 3000 was zero. This means that the recombination rate in this organism is below the sensitivity of our detection method.

Fig. 3.

The new estimator of recombination rate per base pair, ρ̂/bp, as a function of distance between sites in the genome of Ciona intestinalis.

Discussion

The most significant impact of second-generation sequencing technology on the field of evolution and ecology is likely to be the widespread application of shotgun sequencing to non-model organisms. Such applications create a number of challenges, which can be divided into two classes: data handling and data interpretation. Perhaps the most difficult aspects of data handling are quality control and read assembly. Both of these have been dealt with extensively in the now classical early genome projects (Ewing & Green 1998; Ewing et al. 1998; Myers et al. 2000). However, the advent of second-generation sequencing technology has rekindled interest in quality control and assembly algorithms (Brockman et al. 2008; Hernandez et al. 2008).

The interpretation of shotgun sequencing experiments, on the other hand, is undergoing a qualitative shift in the hands of evolutionary biologists. Where previously the goal of the experiment was to determine a consensus genome sequence, the focus now switches to computing population genetic parameters from these data (Begun et al. 2007). This has recently inspired a number of theoretical studies (Johnson & Slatkin 2006; Hellmann et al. 2008; Lynch 2008, 2009; Jiang et al. 2009).

One of these was concerned with the estimation of population genetic parameters from diploid individuals (Lynch 2008). It served as the starting point for the present investigation, which we began by implementing the published maximum likelihood estimation of the mutation and error rates. Lynch (2008) had already shown how these two estimators behave as a function of coverage and that they are unbiased in the limit of high coverage. Here we complemented this result by showing for a range of parameter values that θ̂ and ε̂ behave, indeed, as maximum likelihood estimators (Fig. 1).

Our mutation rate of θ̂ = 0.012 for the genome of C. intestinalis is identical to the value published in two earlier studies (Dehal et al. 2002; Kim et al. 2007). Similarly, our value of θ̂ = 0.0012 for the genome of D. pulex agrees with conventional diversity computations carried out on the same data set (not shown).

A necessary, although often neglected, prerequisite for genome-wide parameter computations is an efficient implementation of a given estimation procedure. This is particularly relevant for recombination rates, which need to be recalculated for many distance classes. Our program mlRho makes such computations feasible on the scale of whole genomes.

The estimator of the population recombination rate implemented in mlRho is an extension of previous work on zygosity correlation (Lynch 2008). It might appear counter-intuitive that it is possible to infer ρ from unphased polymorphism data obtained from just two chromosomes. However, recall that recombination leads to variation of coalescent times along a chromosome. This results in increased clustering of polymorphisms, or greater correlation in zygosity, Δ, which is the signal picked up by our method. Under the neutral model studied here, ρ is a known function of Δ. On the other hand, if the assumption of neutrality is violated, we can still compute Δ using mlRho, but the relationship of this statistic to ρ is then unknown.

Given the neutral model, the resulting ρ estimator is sensitive to small variations in the frequencies of homozygous and heterozygous pairs of positions, which leads to the strong fluctuations observed in the simulations (Fig. 2) and in the analysis of the Ciona genome (Fig. 3).

In contrast to the substantial recombination rate diagnosed in C. intestinalis, we could not measure the recombination rate in D. pulex. Of course, this does not mean that D. pulex has no recombination; in fact, recombination in Daphnia is well documented (Omilian et al. 2006). Our result merely draws attention to the limited sensitivity of the method and that results obtained by it should be treated as lower bounds. This bounding property was already demonstrated in the simulations, where the estimator levelled off close to, but consistently below the simulated parameter value (Fig. 2a and b). Jiang et al. (2009) also observed that with low coverage their approach leads to an under-estimation of ρ.

The analysis of recombination in C. intestinalis further illustrates that the model underlying the estimation is violated leading to the hump-shaped graph. This model assumes a neutral equilibrium population affected only by mutation and reciprocal recombination. However, it cannot be ruled out that gene conversion plays a significant role in C. intestinalis (Kano et al. 2006) as well as in D. pulex (Omilian et al. 2006).

In addition, population structure might distort the estimation of ρ. In an unstructured population the recombination rate between sites located on different chromosomes should be maximal. With population structure, sites between chromosomes continue to have correlated genealogies and hence finite ρ. The linkage groups for C. intestinalis are known and it would therefore be feasible to investigate the population structure of this organism by measuring inter-chromosomal recombination rates.

Moreover, the exceptionally low genetic diversity of the sequenced strain of D. pulex may well be the result of a recent population bottleneck, violating the assumption of constant population size. It will be interesting to see how violations of specific model assumptions are reflected in the graph of ρ̂ as a function of distance.

In spite of these provisos, the conclusion that C. intestinalis has a genome that is more frequently recombining than the sequenced strain of D. pulex does make biological sense. During his thesis research in embryology, Castle discovered the self-incompatibility of C. intestinalis gametes over a century ago (Carlson 2004, p. 155). Castle went on to become one of the pioneers of mammalian and especially mouse genetics (Snell & Reed 1993), but his result in Ciona was the first example of self-incompatibility in animals. Today C. intestinalis is reported to have the exceptionally high recombination ratio of 20–40 cM/Mb. This is greater than the recombination ratio observed in social hymenopterans, which in turn have exceptionally high recombination densities among multicellular eukaryotes (Wilfert et al. 2007). Now, if we take the maximum of ρ̂ ≈ 0.0085 at face value (Fig. 3), we would get an estimate of c/μ = 0.7, which is only slightly higher than human (0.6) and lower than Drosophila melanogaster (3.8) (Lynch 2007, p. 89).

In contrast to the outcrosser C. intestinalis, Daphnia is a cyclical parthenogen that reproduces asexually for indefinite numbers of generations before switching to sexual reproduction. This life history is expected to result in the low recombination rates observed by us, even though asexual Daphnia strains are known to engage in frequent ameiotic recombination (Omilian et al. 2006).

The starting point of this work was the implementation, testing and initial application of theory established by Lynch (2008). Our extension of this theory to estimate ρ has left two main issues for future work: first, the statistical properties of ρ̂ need to be investigated more systematically. Second, it will be interesting to compute ρ̂ from other individual diploid genomes, most notably the growing number of ‘private’ human genomes obtained since the pioneering work in this field by Levy et al. (2007). Our program mlRho provides a robust and efficient foundation for such future studies.