Prior knowledge or freedom of interpretation? A critical look at a recently published classification of “novel” Zn binding sites

Abstract

In a recently published paper [Yao, S., Flight, R.M., Rouchka, E.C. & Moseley, H.N. (2015). Proteins 83, 1470–1487] the authors propose novel Zn coordination patterns in protein structures, apparently discovered using an unprejudiced approach to the information collected in the Protein data Bank (PDB), which they advocate as superior to the prior-knowledge-informed paradigm. In our assessment of those propositions we demonstrate here that most, if not all, of the ‘new’ coordination geometries are fictitious, as they are based on incorrectly interpreted protein crystal structures, which in themselves are often not error-free. The flaws of interpretation include partial or wrong Zn sites, missed or wrong ligands, ignored crystal symmetry and ligands, etc. In conclusion, we warn against using this and similar meta-analyses that ignore chemical and crystallographic knowledge, and emphasize the importance of safeguarding structural databases against bad apples.

1. Introduction

A recently published paper describes a new classification of Zn binding sites in protein structures using a sophisticated mathematical apparatus combining statistical methods and elements of machine learning,¹ hereinafter denoted as Y2015, and figures therein annotated using a ‘Y’ prefix, as in ‘Fig. Y1′ or ‘Fig. YS1′. The authors claim to have discovered novel and previously uncharacterized coordination geometries of Zn sites in proteins. In their opinion, the advantage of their method lies in the fact that it is unbiased as it is not based on prior belief of what is present in the datasets at hand. Although elimination of prejudice sounds like a good idea in science, we note that a credo stated like that can be quite precarious if, as demonstrated recently,² solid prior chemical knowledge does not lay the groundwork for the intended analyses and interpretations. Apparently, some fundamental rules of chemistry were not utilized in the analysis of Y2015, as some figures show such unlikely ‘features’ as protein D-amino acids (Fig. Y6 B1 and D1, partially reprinted here in Fig. 1). We find it appropriate to evoke here the message of a recently published (in Proteins) April Fools Day Special Paper³ which explores ‘Zn-catalyzed formation of triple and quadruple cysteine bridges’ based on experimental ‘evidence’ taken from PDB-deposited crystal structures. The message is that the data in the PDB, when used indiscriminately and without understanding, can support even the most absurd hypotheses.

Fig. 1.

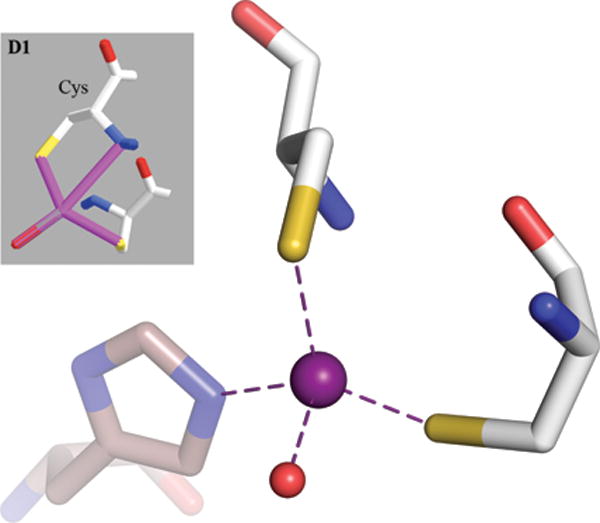
The gray insert is a copy of the original Fig. Y6D1 from Y2015 (reprinted with the permission of John Wiley and Sons) showing a ‘bidentate interaction of cysteine with its Sγ and backbone N atoms’. In reality, there is no bidentation and the Zn coordination sphere is completed by a histidine residue from a symmetry-related molecule, shown with brown, transparent sticks. The difference in the orientation of the two views comes from the fact that the original image was inverted, giving rise to D-cysteines, and it is not possible to keep this orientation while retaining the proper (L) chirality of the Cα atoms. The PDB code of the illustrated structure is 4A48.

Briefly, the method used by Y2015 was as follows. A survey of the PDB entries containing Zn ions and a preliminary classification of the Zn sites into ‘known coordination geometries’ (those being tetrahedral, trigonal bipyramidal, and octahedral, complete or incomplete) resulted in high standard deviations for the ligand-metal-ligand angles. From this the authors concluded that some of the Zn sites might have been artificially forced into known standard geometries instead of, perhaps, being classified as novel sites. In particular, the authors were surprised by the presence of angles much smaller than 90°, with a normal-like bimodal distribution centered at 32 and 53° which, they claimed, have not been investigated in any previous study. The authors acknowledge that 83% of these ‘compressed angles’ are the result of coordination by bidentate ligands (such as the carboxylate group, -COO⁻). [Parenthetically, we note here that actually the first paper presenting a thorough classification of Zn binding sites in proteins by Alberts et al.,⁴ that Y2015 do cite, does describe the average angle for a bidentate interaction of Zn with a carboxylate group as 55.9 ± 2.6°]. Based on this preliminary analysis, Y2015 divided the Zn sites into normal and compressed-angle ones, with the latter group containing such unusually small (<< 90°) ligand-Zn-ligand angles. Finally, they used a clustering approach aimed at discovering novel coordination geometries among the four-coordinated Zn ions and conclude that the identified clusters in the compressed-angle group ‘have not been described in the literature and from this perspective can be viewed as novel coordination geometries’.

In this work, we present a critical assessment of some of the methodological aspects of the approach used by Y2015, and especially of the results and proposed interpretations. In addition, errors in the underlying Zn-containing PDB structures are discussed and, where possible, corrected.

2. Methods

2.1. Summary of the methods used by Y2015

Y2015 extracted the PDB data sets that contained at least one Zn ion and excluded those sites that belonged to zinc clusters (Zn-Zn distance ≤ 3 Å). They defined the initial coordination spheres as all the ligand atoms within 1.3–3.2 Å of each zinc center. Next, they compared the angles in each coordination sphere to the ideal angles in the three ‘major coordination geometries’: tetrahedral, trigonal bipyramidal, and octahedral, checking all the permutations of the ligands/angles and selecting the geometry that gave the smallest variance. They calculated the mean values and variances of the angles for each coordination geometry, as well as the mean values and variances of the bond distances for each of the ligand atom type. Subsequently, they redefined the coordination spheres using the obtained bond length statistics and chose those spheres that gave the highest χ² probability. Next, they used an iterative algorithm where in each cycle they defined the best-fitting coordination geometries (CGs) and spheres, and then updated the bond statistics until the calculations have converged. The fitting was again done with χ² probabilities using both the bond length and angle values.

The next move was to divide all the Zn sites using a RandomForest machine learning algorithm into three groups: normal, compressed, and super-compressed. Initially, the data were grouped as follows. The normal group contained sites for which the smallest angle was > 68°, for the compressed group the smallest angle was between 58° and 38°, and for the super-compressed group the smallest angle was below 38°. These data were used to train the classifier, which was then applied to the set of overlapping data points (smallest angle between 58 and 68°), as well as to the training data itself.

The groups were then subjected to clustering using a k-means algorithm, where a dataset is divided into a preselected number of clusters based on the distances between the data points. The output clusters were assigned to novel or known coordination geometries. The authors presented the angle statistics for each cluster in the normal and compressed-angle groups and their average χ² probabilities of belonging to any of the known coordination geometries. For each cluster they picked a representative case that is closest to the cluster center. Finally, the authors presented the three-dimensional structures of each representative case in Supplementary materials (Fig. YS1 and YS2).

2.1. Outline of the present analysis

We divide the list of problems that we encountered in the paper by Y2015 into two categories: general problems with the assumptions (such as the implication of the N-H amide group as a coordination bond ligand), as well as problems with the analyzed Zn centers. The second group includes misrepresentations of the identified Zn sites with respect to the actual coordinates in the PDB files as well as disordered, partial, or incorrectly modeled coordination spheres that were not (but should have been) filtered out during a preliminary quality control check of the input data.

For each structural figure presented by Y2015, we downloaded the corresponding PDB⁵ atomic coordinate file and electron density maps, if available, from the Uppsala EDS server,⁶ in which we identified the site shown in the original figure and compared it with what was really present in the structure. In the cases where the coordinates were not in agreement with the electron density, we downloaded the structure factors from the PDB and corrected the model to improve the fit. For two structures, 3IFE (Fig. 2E) and 1XTL (Fig. 2F), we carried out re-refinement in Refmac5⁷ and manual rebuilding in Coot.⁸ For both cases we note a drop in R/R_free, which in part may reflect the improvement of the refinement protocols when compared with those available at the time of the original deposits. Our figures were prepared with PyMol⁹ and the displayed electron density maps were calculated via the CCP4 suite¹⁰ using the Fourier coefficients either produced by Refmac5 or downloaded from the Uppsala EDS server.

Fig. 2.

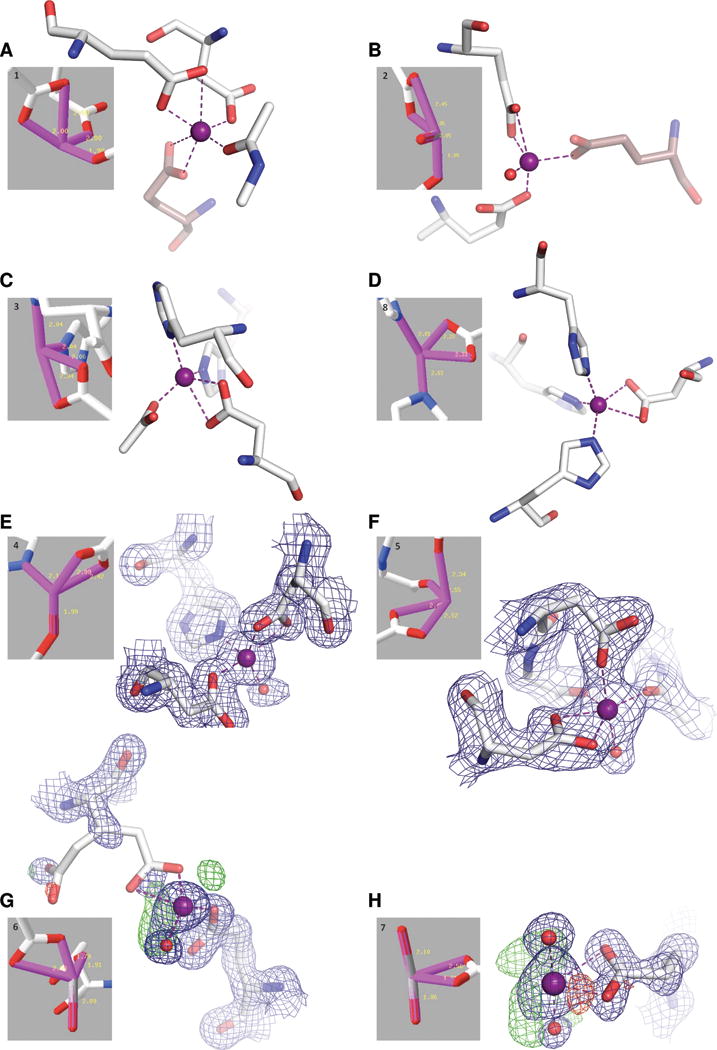
The figure shows a reprint of the original Fig. YS2 from Y2015 (reprinted with the permission of John Wiley and Sons) presenting 3D structures for each of the representative Zn sites of the compressed-angle clusters (gray inserts). For each site we also show a new figure, prepared by us. Examples A–D are presented using exactly the same coordinates as deposited in the PDB. The difference with respect to the figure presented by Y2015 was simply the inclusion of all the ligands found in the crystal structure. For A and B, the missing residues come from a symmetry-related molecule (shown with brown, transparent sticks). The missing ligands in the cases C and D could have been rejected by the χ² test employed by Y2015 to define the final coordination spheres. E and F show two structures which were of very poor quality. In both cases, the selected Zn sites were incorrectly modeled in the deposited coordinates. We have re-refined both these structures and show the corrected coordinates with the corresponding 2mF_o−DF_c electron density map contoured at 1.5σ (calculated in CCP4 from the coefficients produced by Refmac5). For structure G, the crystal was soaked using 0.5 M ZnCl₂ and for structure H the crystal was grown in the presence of 0.2 M zinc acetate, leading to numerous non-specific Zn binding sites. Both sites have partial Zn occupancy (0.5 and 0.6, respectively) and are not well-ordered, as indicated by the electron density maps. The 2mF_o−DF_c map (blue) is contoured at 1.3σ in G and at 1.5σ in H, while for the mF_o−DF_c map the contour is 3.0σ (positive - green, negative - red) in both G and H. The maps were calculated in CCP4 using the Fourier coefficients downloaded from the Uppsala Electron Density Server (EDS). The PDB codes and Zn site identifiers are as follows: A, 2EJ1, Zn700A; B, 2Z45, Zn1002A; C, 4EWL, Zn401B; D, 3QW0, Zn500D; E, 3IFE, Zn411A; F, 1XTL, Zn1331A; G, 1K9Z, Zn404A; H, 4FTF, Zn202A.

3. Results

In the following subsections we take a closer look at some of the unusual stereochemical features proposed by Y2015 and analyze them one by one, providing possible explanations of the apparently non-standard geometries and suggesting different interpretations that would be in agreement with the accepted rules of chemistry.

3.1. General problems with the assumptions

3.1.1. Implication of N-H amide groups as Zn ligands

The authors claim to have noticed 57 cases of cysteine residues forming a bidentate interaction using the Sγ and backbone nitrogen atoms. As an sp² hybridized N-H amide nitrogen atom is not a plausible ligand for coordination of a zinc ion, this would be only possible for N-terminal cysteine with unprotonated sp³ –NH₂ amino group. We examined the only example for which the PDB code was given (4A48) and found it to look quite different from the representation in the authors’ original figure (Fig. 1). The differences in the orientation between the original and our image stem from the fact that the original picture had been inverted, giving rise to D-cysteines, and that it was not possible to maintain the same orientation while retaining the correct L chirality of the Cα atoms. This example is not a case of an N-terminal cysteine residue, and the Zn-N distance is above 3 Å, which is significantly longer than the standard Zn-N bond (2.0 Å). In reality, 4A48 represents a very well-defined tetrahedral site with the fourth ligand being a histidine residue from a symmetry-related molecule (shown in Fig. 1 with transparent brown sticks), which was apparently overlooked by Y2015.

3.1.2. Zn-P coordination

Even more striking is the detection of 182 Zn-P coordination bonds, with an average bond length of 2.97 Å and a standard deviation of 0.12 Å (Table YIII). Such direct metal-phosphorus bonds do exist, but are very rare and are generally only found in phosphine derivatives, which are not present in biological systems. On top of that, the expected length of a Zn-P bond is ~2.4 Å. A query of the Cambridge Structural Database (CSD),¹¹ which stores the coordinates of over 800,000 small-molecule organic and organometallic crystal structures, for compounds containing Zn-P bonds produces 45 hits, but not a single one with a Zn-P distance within the interval of 2.97 ± 0.36 Å, corresponding to three standard deviations from the Y2015 analysis. These implied Zn-P bonds may have originated from bidentate phosphate groups coordinating Zn²⁺ ions through their O atoms. This could also explain the Zn-ligand angle distribution centered at ~32°, since with a phosphate group coordinating a metal ion symmetrically (or almost symmetrically) using two of its O atoms, the O-Zn-P angles would be close to 32° (see, for example, Zn601A in the data set 4KAV, or Zn501B in 5A1F). A similar situation would also exist for sulfate ions.

3.1.3. Incorrect definition of coordination spheres

Y2015 use the Zn-ligand distances only to create the initial list of possible Zn ligands. All ligand combinations from this list are subsequently scored against the obtained bond-length statistics and the ‘best’ coordination sphere is defined as the one giving the highest χ² probability. Subsequently, this ‘best’ coordination sphere can be updated based on another χ² goodness-of-fit test, now using both the bond lengths and bond angles, with mean values calculated for each possible coordination geometry. We strongly suspect that in some cases (see section 3.2.1) this method of coordination sphere definition inadvertently eliminated some of the ligands (possibly the key ones, because of the short Zn-X contact) with bond distances to Zn shorter than the mean-value-based threshold. The authors do not present these intermediate bond statistics, only the final values obtained after outlier rejection, so it is not possible to repeat the calculations using exactly the same parameters. It also appears that their method has a strong bias towards tetra-coordinated sites as they constitute over 95.7% of all the identified Zn sites. While this is the most common coordination number for zinc, such a high proportion is very surprising. Indeed, as we show in section 3.2.1, many of the presented Zn sites were in reality not tetra–coordinated, but contained higher numbers of ligands.

3.2. Re-analysis of the output clusters

No list of PDB entries corresponding to the clusters identified in Y2015 was provided, only a figure for one representative structure per cluster was shown (Figs. YS1 and YS2, the latter reprinted here as Fig. 2). We inspected each of the representative sites for both normal- and compressed-angle clusters and found a number of problems. In our evaluation, we have focused on the compressed-angle clusters, presented by the authors as novel Zn coordination geometries. We found that for about one half of the representative cases the actual atom coordinates are different from what is shown in the original figure of Y2015. Surprisingly, some of the ligand groups from the deposited structures were simply overlooked by Y2015 (Fig. 2A–D). For the other half of the representative Zn centers, the electron density maps revealed disordered or incorrectly modeled sites, the inclusion of which in such an analysis indicates a lack of proper validation and quality control of the input data.

3.2.1. Some of the Zn ligands not taken into account

Almost exactly 50% of the representative Zn sites of the compressed group fall into this category of problems. One reason appears to be that symmetry-related molecules were not taken into account (Fig. 2A and B). No simple explanation exists for two other examples (Fig. 2C and D). For both these sites, the missing ligand is the one with the shortest distance to the Zn ion: an acetate ion with the Zn-O distance of 1.90 Å (4EWL), and a histidine residue with its Nɛ2 atom 1.91 Å from the metal ion (3QW0). Possibly, these omissions were caused by the authors’ method of defining the coordination spheres, which used a χ² goodness-of-fit filter on both sides (also for short Zn-X bonds) of the mean. We can only assume that this approach may have caused ligands with ‘too short distances’ compared to the mean to be eliminated.

3.2.2. Partial or wrong Zn sites and ligands

The Zn center shown in Fig. 2E (PDB ID 3IFE) has the occupancy of 0.7. A water molecule in two alternative positions (with Zn distances of 1.99 and 2.27 Å) is present in the deposited coordinates file but it was not included in the authors’ figure. Also, another Zn ion is present in the PDB file 3IFE with 0.2 occupancy, 3.6 Å away from the first metal center. Using the deposited structure factor data for refinement in Refmac5⁷ and rebuilding in Coot,⁸ we were able to obtain a model characterized by a very significant drop of R/R_free from 14.9/17.2 to 11.6/15.7%. In the new model the low-occupancy Zn ion turned out to be absent altogether. This non-existent Zn ion had contributed to the overall confusion in the area of the higher-occupancy Zn site. After modeling of one additional water molecule, the major site could be classified as tetrahedral by the CheckMyMetal (CMM) server¹² with a gRMSD of 11.5°.

Perhaps the most interesting case is the cluster 5 representative, Fig. 2F (1XTL). The Zn site selected as the example (Zn 1331A) is also a pointed example of an incorrectly modeled coordination sphere. After some minor corrections and inclusion of proper restraints, the site presented in Fig. 2F becomes a well-defined octahedron with a gRMSD value of 7.4°, in which one site is vacant due to the absence of electron density for a water molecule, and in which the bidentate aspartate ligand acts as one super-atom.¹²

3.2.3. Non-functional Zn sites

In the next two examples the crystals were either grown in the presence of high concentration (0.2 M) of Zn²⁺ ions (4FTF, Fig. 2H), or soaked using a 0.5 M solution of ZnCl₂ (1K9Z, Fig. 2G). As a result, we observe extensive non-specific Zn binding at the peripheries of the macromolecules and the two presented sites were exactly such examples. The occupancies of those Zn ions are 0.5 (G) and 0.6 (H). The electron density maps indicate a possible presence of additional water molecules, whereas the glutamate ligand in Fig. 2G lacks any interpretable electron density altogether. Our attempts to correct the modeling did not yield sensible results and we suspect that both of these sites are disordered. Clearly, they were not the best choices for defining canonical coordination geometry. Moreover, both structures contain many more such incidental sites and probably they were all included in the analysis. Unfortunately, the authors did not distinguish between functional and non-functional metal binding sites, even though their declared aim was to explore the structure-function relationship of Zn metalloproteins.

3.3. Errors in the input PDB structures

We also noticed serious and troubling errors in two PDB structures used as examples of the input in the Y2015 analysis. The first one is a 1.55 Šstructure of peptidase T from Bacillus anthracis (3IFE, unpublished), which contains two Zn binding sites, both of which are occupied in the deposited coordinate file. The first one (Zn 411A) seems to be reasonably ordered with 0.7 occupancy and a B factor of 20 Ų. The average B factor of the surrounding ligand atoms is ~15 Ų. One of the ligands is a water molecule in two alternative positions. The second site was modeled with 0.2 occupancy and has the temperature factor of ~29 Ų. Our corrections included the removal of the second Zn site, addition of another water ligand and refinement of anisotropic temperature factors (not modeled in the deposited coordinates). This approach resulted in a dramatic improvement of R/R_free from 14.9/17.2 to 11.6/16.0%, and a better geometry of the Zn binding site (Fig. 2E).

The second problematic structure is that of the P104H mutant of SOD-like protein from Bacillus subtilis, determined at 2.0 Å resolution (1XTL).¹³ Its PDB validation report reveals 47 bond length and 86 bond angle outliers, 115 close contacts, five Ramachandran violations, and 53 side chain (rotamer) outliers. The deposited model contains protein fragments with grave violations of peptide bond planarity and incorrect conformation of the ligands of some of the Zn sites (Zn 1331A, Zn 1329B, Zn 1328C, Zn 1330D). After our rather cursory corrections the R/R_free values dropped from 23.7/29.9 to 22.7/28.7% and all the Zn sites acquired an acceptable Zn binding geometry (see an example in Fig. 2F).

4. Discussion

The source of the above problems with the Y2015 analysis seems to lie in insufficient understanding of crystallographic data and, possibly, errors and other deficiencies of the software tools employed. A recent work about Zn binding sites¹⁴ cautions about the dangers of overlooking symmetry-related molecules during classification of Zn coordination geometries, but unfortunately it is not found among the references presented by Y2015. It is understandable that manual inspection of every single case in such a large dataset would be difficult, but the highlighted examples are those selected by the authors as the representative cases of their clusters and it is troubling that the apparent ‘novelty’ did not encourage their closer examination. Particularly worrisome is the fact that such errors were not intercepted by the reviewers of a very respectable journal, which is generally regarded as a standard-setting venue in protein research.

Another set of problems is created by the choice of the Zn sites themselves. In order to perform a meaningful meta-analysis, it is essential to ensure proper quality control of the input data. It has been pointed out more than once that one bad apple can spoil a whole bushel of decent data points.¹⁵ All that the authors seem to have done in this respect was to limit the resolution of the input structures to better than 3 Å, and examine the B factors of the ligands involved in unusual angles and to compare them to the average B factor for all the ligands. The occupancy of the ligands or of the metal ion itself was not analyzed at all. Three of the compressed-angle representative Zn sites are only partially occupied (between 0.5 and 0.7), which should have prompted their closer inspection and extra care in the analysis of their geometry.

The Protein Data Bank is an extremely valuable source of data, used as an indispensable resource by countless scientists, most notably in life-science- and medicinally-oriented research. Unfortunately, some of the deposited data are not free from mistakes, inaccuracies, mis- and especially over-interpretations, and even blatant errors. To use these data indiscriminately and without adherence to the basic principles of chemistry and crystallography is a recipe for disaster, or at least science fiction.

The key point is that fortunately we do have extremely well validated prior knowledge about macromolecular stereochemistry and interactions. This knowledge comes predominantly from high-accuracy X-ray diffraction studies (reported in the CSD, as well as in the PDB itself), and also from spectroscopic and quantum chemical studies. Without this knowledge, the field of macromolecular crystallography would not exist in its present form. Taking this knowledge into account cannot be viewed as introducing bias but, on the contrary, it is essential for meaningful interpretation of macromolecular crystal structures. Disregard of the chemical knowledge, as well as of the rules of crystallography, will inevitably lead to deplorable lack of credibility of the results and conclusions. Since the Y2015 paper presents an overview and not just a case study, its ripple effect, if not stopped, could be particularly damaging. We can only hope that our voice will alert the community and encourage greater care in the use of the data contained in the PDB, with the goal to improve the quality of the scientific outcome in structural biology.

On the positive side, we wish to note that the mathematical procedure developed by Y2015 is very interesting and might be applied, after appropriate elimination of the flaws pointed out in this paper, in other meta-analyses of structural data. However, such a mathematical approach should not be trusted as an omnipotent panacea that will miraculously make scientific discoveries all by itself. Instead, it should always be used in combination with sound knowledge of chemistry, crystallography, and other disciplines of science.

5. Conclusions

As a summary, we must conclude that the paper by Y2015, despite the announcement made in its title, does not actually present any novel Zn binding sites. The ‘novel’ coordination geometries are either misrepresented or based on erroneously modeled Zn sites in protein crystal structures. The field of Zn coordination by macromolecules is sufficiently well grounded on the previous, competent studies, such as those presented in^4,14,16. As another conclusion we reiterate the opinion that the field of structural biology should continue to be on the lookout and safeguard itself against fallacious data-mining meta-analyses, as well as against individual bad apples (macromolecular structures, especially with small-molecule components) that contaminate our repositories.¹⁵