Development of a deformable dosimetric phantom to verify dose accumulation algorithms for adaptive radiotherapy

Abstract

Adaptive radiotherapy may improve treatment outcomes for lung cancer patients. Because of the lack of an effective tool for quality assurance, this therapeutic modality is not yet accepted in clinic. The purpose of this study is to develop a deformable physical phantom for validation of dose accumulation algorithms in regions with heterogeneous mass. A three-dimensional (3D) deformable phantom was developed containing a tissue-equivalent tumor and heterogeneous sponge inserts. Thermoluminescent dosimeters (TLDs) were placed at multiple locations in the phantom each time before dose measurement. Doses were measured with the phantom in both the static and deformed cases. The deformation of the phantom was actuated by a motor driven piston. 4D computed tomography images were acquired to calculate 3D doses at each phase using Pinnacle and EGSnrc/DOSXYZnrc. These images were registered using two registration software packages: VelocityAI and Elastix. With the resultant displacement vector fields (DVFs), the calculated 3D doses were accumulated using a mass-and energy congruent mapping method and compared to those measured by the TLDs at four typical locations. In the static case, TLD measurements agreed with all the algorithms by 1.8% at the center of the tumor volume and by 4.0% in the penumbra. In the deformable case, the phantom's deformation was reproduced within 1.1 mm. For the 3D dose calculated by Pinnacle, the total dose accumulated with the Elastix DVF agreed well to the TLD measurements with their differences <2.5% at four measured locations. When the VelocityAI DVF was used, their difference increased up to 11.8%. For the 3D dose calculated by EGSnrc/DOSXYZnrc, the total doses accumulated with the two DVFs were within 5.7% of the TLD measurements which are slightly over the rate of 5% for clinical acceptance. The detector-embedded deformable phantom allows radiation dose to be measured in a dynamic environment, similar to deforming lung tissues, supporting the validation of dose mapping and accumulation operations in regions with heterogeneous mass, and dose distributions.

Introduction

In adaptive radiotherapy for lung cancer patients, treatment plans can be developed using four-dimensional computed tomography (4DCT) images.[1] A respiratory cycle can be divided into multiple phases, with radiation dose at each phase being calculated using the 4D images and warped to a reference image to estimate the total dose delivered at each treatment fraction.[2] Based on the dose computed for the delivered treatment fractions, the initial treatment plan can be reoptimized. This process is known as image-guided adaptive treatment planning (IGATP).[3] The key steps in IGATP include deformable image registration (DIR), dose mapping and accumulation, and plan reoptimization. DIR and dose accumulation algorithms while fundamental to the development of a high-quality adaptive plan are difficult to evaluate.[4,5] This therefore necessitates the development of a platform for validation of different dose accumulation techniques before their clinical implementation.[6]

Deformable phantoms are a valuable tool to evaluate DIR and dose calculation algorithms. Chang et al.[7] developed a physical, deformable phantom and used it to verify the Demon's algorithm implemented in Insight Segmentation and Registration Toolikit,[8] based on the center of the registered images. Liu et al.[9] developed a deformable abdominal phantom to evaluate an in-house developed registration algorithm based on the implanted fiducials in liver. With a deformable gel phantom, Yeo et al.[10] evaluated the performance of 12 DIR algorithms in the case of mass and density conserving deformation in low-contrast regions. Serban et al.[11] developed a deformable 4D phantom and evaluated a nonlinear registration algorithm (ANIMAL) using landmarks embedded in the phantom. Szegedi et al.[12] used a fresh tissue phantom implanted with electromagnetic tracking fiducials to verify the accuracy of 4D tissue deformation reconstruction. Compared to the verification of DIR performance, dosimetry accuracy is an end point for quality assurance of adaptive radiation therapy. Few studies were reported in this direction.

Recently, Cherpak et al.[13] combined electromagnetic positioning probe with a MOSFET dosimeter to track the dose delivered in a deformable phantom. Their results showed a good agreement between the measured doses and the treatment-planned doses for adaptive radiation delivery. Vinogradskiy et al.[14] used a moving thoracic phantom to validate the accuracy of a 4D dose calculation algorithm. The phantom had one-dimensional compressible inserts with thermoluminescent dosimeters (TLDs) embedded. With a landmark-based DIR performed on this phantom, they compared TLD measurements with calculated doses and evaluated whether the performance of the 4D dose calculation algorithm varied between different motion patterns and treatment plans. As this phantom essentially is of one-dimensional compression, the impact of conventional DIR errors on 4D dose calculation algorithms was not evaluated. Niu et al.[15] evaluated a gel dosimetry phantom using an in-house developed, mechanical model-based software for image registration, and the Pinnacle treatment planning system (TPS) for dose calculation. Because of its limited compressibility and heterogeneity, the developed gel phantom works better for landmark or mechanical model-based registration methods rather than image intensity-based algorithms such as B-spline or demons-based registrations.

When heterogeneous materials are compressed, dose mapping and accumulation algorithms may have errors in accumulated dose.[6] It is important to verify these algorithms with results measured in a similar environment. In this study, we developed a new deformable phantom, acquired its 4DCT images, and verified the stability of its repeating deformation. To demonstrate the dosimetric capability of this phantom, we verified different dose accumulation algorithms, implemented TLD verification procedures for this phantom, and compared the accumulated doses with the TLD measured results. We showed that this phantom offered several advantages over the previously described works. The novelty of this study is the development of the detector-embedded, compressible and heterogeneous lung phantom with deformation driven by a motor and remotely controlled by a computer. We demonstrated the capacity of this phantom in measuring dynamically delivered dose and performed dose accumulation using different 4D dose calculation techniques including 4D Monte Carlo (MC) simulations. To our knowledge, no one has ever verified deformable dose accumulation techniques with data measured in heterogeneous, compressible lung tissues.

Materials and Methods

Development of a deformable lung phantom

A deformable phantom was developed in collaboration with the laboratory of Smart Sensors and Integrated Microsystems, Wayne State University. The phantom consists of a motor-driven piston that compresses a deformable insert contained in an acrylic exterior which is 30 cm in diameter by 35 cm in length [Figure 1a]. The deformable insert consists of a heterogeneous sponge material and a tissue-equivalent tumor composed of bolus material approximately 3.1cm × 3.1 cm × 4.3 cm. The sponge is enclosed in a latex cylinder which is compressed by a piston to simulate diaphragm motion. The phantom components are changeable modular so that dosimeters can be inserted in both the heterogeneous sponge and tumor. Software developed in LabVIEW (National Instruments Corporation, Austin, TX) is capable of driving the piston in a sine waveform with a peak-to-peak amplitude of up to 3.8 cm, at a speed of up to 7.5 cm/s. Patient-derived waveforms can also be imported from files derived from motion tracking systems. The impact of patient-specific breathing patterns on dose accumulation algorithms would be addressed in a different study.

Figure 1.

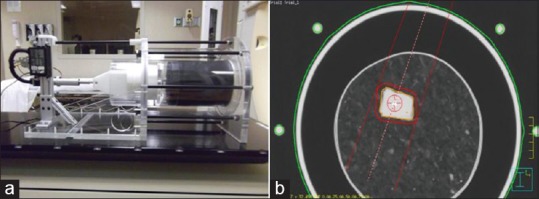
(a) Lung phantom; (b) planning target volume consisting of tumor volume on the maximum intensity projection dataset plus 5 mm isotropic margin

Four-dimensional computed tomography image acquisition of the deformable phantom

To simulate clinical scenarios, a phantom motion was programmed in a sinusoidal pattern with an amplitude of 1.5 cm and a period of 5 s. 4DCTs were acquired using a multislice CT scanner equipped with a bellows pneumatic belt (Philips Brilliance CT Big Bore Oncology, Philips Healthcare, Andover, MA). The bellows consist of a rubber air belt attached to a pressure transducer. As the phantom moves, the air pressure change within the bellows is detected by the transducer, and the signal is digitized and transmitted to the scanner for 4DCT image reconstruction. The CT scanner was operated at 120 kVp, 800 mAs/slice, 0.5 s tube rotation, pitch of 0.06, and 2 mm slice thickness. The images were binned into 4 phases to mimic our clinical practice and exported to the Pinnacle TPS for subsequent treatment planning and delivery. After 4DCT scanning, isocenter was set to the center of the tumor in the untagged CT image, and the phantom external was tattooed using the laser system. This same setup was used at the time of dose delivery for target localization.

Since 4DCT acquisition and dose delivery were performed at different times, reproducibility of the phantom deformation and target localization during compressional cycles need to be verified. The phantom was scanned twice using the same experimental setup and programmed breathing period. The end-exhale (EE) phases (i.e. the largest scale of deformation) were selected for verification. Since voxel sizes could be different between the two scans, the second 4DCT images were interpolated to be consistent to the first one. Image differences between the EE phases were calculated, and spatial deviations between landmarks were measured to illustrate the consistency of deformation between trials.

Treatment planning and delivery

Tumor targets were delineated on the maximum-intensity projection of the 4DCT images to form an internal target volume (ITV). To avoid using multiple beams that may average out the dosimetric differences, a single AP beam plan was developed so that the sensitivity of typical measurement positions in relation to the beam's orientation (e.g., beam edge, downstream) could be accurately evaluated. The ITV was expanded by 5 mm to generate a planning target volume (PTV) [Figure 1b], and the jaw opening was set to 6.7 cm × 5.7 cm to match the edges of the PTV. The multileaf collimator was not used to avoid introducing additional uncertainty from leakage. The number of monitor units (MU) for this beam was set to 250.

The phantom was setup to tattoos and was treated with the developed treatment plan on a Trilogy 21EX linear accelerator (Varian Medical Systems, Palo Alto, CA) under the same sinusoidal motion pattern as used during 4DCT acquisition. The MU was assumed to be delivered evenly among these phases. To minimize the dose error induced by the unsynchronized tumor motion and beam-on time, the dose rate was reduced to 200 MU/min. In this case, about 16 MU would be delivered during each breathing cycle and 4 MU for each phase. If one phase was missed during the delivery of 250 MU, the induced error would be <1.6%. The requirement of the dose rate reduction can be removed when a gating technique is used.

Four-dimensional dose calculations

To calculate the 4D dose, CT images were registered from the end-inhale (EI) phase, when the sponge was uncompressed, to each of the other phases. For the heterogeneous sponge shown in Figure 1b, two intensity-based DIR algorithms implemented in VelocityAI (Velocity Medical Solutions, Atlanta, GA) and Elastix (University Medical Center Utrecht) were verified. VelocityAI has a mutual information (MI) based B-Spline algorithm with multipass deformable settings. Elastix is also an MI-based but open-source software package for nonrigid image registration.[16] The displacement vector field (DVF) from each registration was output to Hertz, an in-house developed system for 4D treatment planning.[17,18]

Treatment plans were exported from Pinnacle to Hertz, which was integrated with EGSnrc/BEAMnrc to calculate MC dose.[19,20] With the EGSnrc dosimetry system, the treatment head components of the Trilogy 21EX linear accelerator were modeled for a 6 MV photon beam,[17,21] and the source distribution was simulated using a Gaussian function with 1.4 mm full-width at half maximum in both X- and Y-directions. The generated phase space file contained approximately 165 million particles. The CT images of the phantom were converted to the material–mass–density tables using the CT-create program, where a 55 material ramp was used in the Hounsfield unit (HU)-to-density conversion.[21] To test the sensitivity of the phantom to different dose calculation algorithms, the dose was calculated on each phase of the 4DCT using three different algorithms: Analytic anisotropic algorithm (AAA) in Eclipse, collapsed cone convolution superposition algorithm (CCCS) in Pinnacle, and MC method in EGSnrc. The doses calculated at each phase were exported directly to Hertz for dose reconstruction. With the mass-and-energy congruent mapping method,[18,22] the dose was calculated at each phase and warped back to EI phase (0%) using their VelocityAI and Elastix DVFs. The mapped dose was equally weighted and accumulated on the EI phase to get the 4D dose.

Phantom dose measurement

TLDs (TLD-100, ThermoFisher Scientific Pittsburgh, PA) of dimension 3.2 mm × 3.2 mm × 0.89 mm were used to measure the doses delivered to the phantom. The irradiated TLDs were read by the Harshaw 3500, a TLD reader from ThermoFisher Scientific Pittsburgh, PA. Before radiation measurement, TLDs were annealed for 1 h at high temperature (400°C) and 24 h at low temperature (80°C).[23,24] To reduce uncertainties induced by electron fading at low-energy states, the readout process involved 10 min of preheating at low temperature (100°C) followed by readout, following a protocol outlined by the TLD reader manufacturer. For more details on the TLD dosimeter and its annealing procedures, readers may refer to the literature.[25,26] To generate a calibration curve for dose conversion, TLDs were placed in a solid water phantom at depth d_max and irradiated by a 10 cm × 10 cm, 6 MV photon beam. 10, 60, 100, 200, and 300 MUs were delivered, and the calibration curve for these TLDs was generated. The linearity of the curve was represented as its correlation coefficient to the linear function y = 0.0998x + 7.8064 with R² = 0.9986.

The deformable lung insert held multiple TLDs in the simulated lung and tumor. Four deformable positions (DP) inside or around the tumor were evaluated: Point T is located inside the tumor [Figure 2a] and points 1, 2, and 3 are inferior, superior, and posterior to the tumor, respectively [Figure 2b]. Three TLDs were grouped in a small plastic bag with readings averaged at each location for better statistics. The three TLDs were contoured on the planning image so that the average TLD doses could be compared to the average of the doses computed by different algorithms within each contour.

Figure 2.

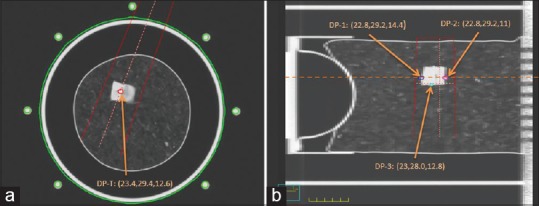
Thermoluminescent dosimeter points of measurement: (a) Tumor point in an axial cut; (b) inferior (DP-1), superior (DP-2) and posterior (DP-3) points in a sagittal cut

In this study, an adult chest protocol was used for all the 4DCT scans. As TLDs were inserted in the lung phantom before the 4DCT scans, the response of these TLDs to the 4DCT scan was subtracted from all TLD measurements. To measure the 4DCT dose, three TLDs were placed in the phantom which was scanned twice. The resultant TLD readings were interpreted to get the average 4DCT dose.

Results

The developed phantom and its deformation

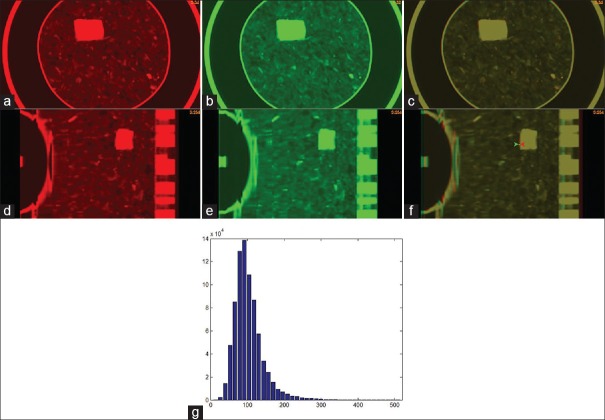
The deformable phantom was scanned twice. To mimic clinical scenarios, the second setup followed the tattoos marked at the time of the first scan. To compensate the voxel-spacing difference between the two image sets, the second 4DCT images [Figure 3b] were scaled so that the resultant image can be compared to that of the first 4DCT image [Figure 3a]. The axial cuts of the two images at the EE phase were overlaid as shown in Figure 3c, and their corresponding sagittal cuts are shown in Figure 3d–f. Multiple locations on the overlaid images were manually checked using a measurement tool shown in Figure 3f. It was found that the 4DCT scans can be repeated with the deviation of the tumor and TLDs <1.1 mm. The intensity distribution of the sponge in the first 4DCT image is shown in Figure 3g, and the average HU of the sponge is −880.

Figure 3.

The axial cut of the end-exhale phase images in (a) the first four-dimensional computed tomography scan, and (b) the second four-dimensional computed tomography scan; (c) the overlay of the two images in (a) and (b); (d-f) the sagittal cuts of the images shown in (a-c); (g) the computed tomography image intensity of the sponge in Pinnacle (X) versus the number of voxels (Y)

DIRs were performed from the EI phase [Figure 4a and d] to each of the other phases using Elastix and VeloctiyAI, respectively. With the derived DVFs, the EE image was warped to the EI phase and the two warped images were subtracted from the EI image with the axial cuts shown in Figure 4b and c, and with the sagittal cuts shown in Figure 4e and 4f.

Figure 4.

(a) An axial cut of the end-inhale image; (b) and (c) the Elastix and VelocityAI-warped end-exhale images subtracted by the end-inhale image; (d-f) the sagittal cuts corresponding to (a-c)

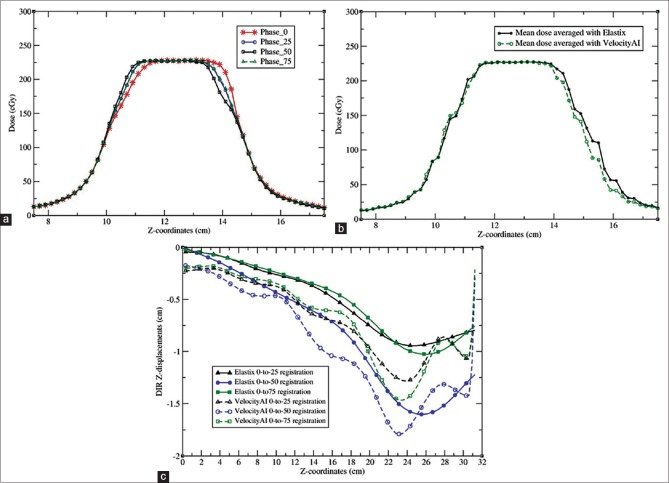
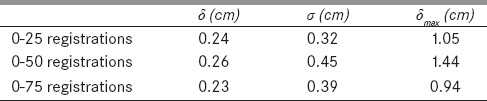
The DVFs calculated by the two algorithms differ by 2.6 mm on average with the maximum up to 1.44 cm. Large differences mainly appeared at image boundaries as illustrated in Figure 5c. The general comparisons of the two registration algorithms are shown in Table 1. More quantitative evaluation of DIRs performed on this phantom was previously reported in Stanley et al.[27]

Figure 5.

(a) The profiles of the Pinnacle doses calculated on the images of phase 0, 25, 50 and 75; (b) the profiles of the doses accumulated with the Elastix and VelocityAI algorithms; (c) the profiles of the Z-displacements from the Elastix and VelocityAI registrations

Table 1.

The mean difference (δ) and standard deviation (σ) between the displacement vector fields of the Elastix and VelocityAI-based deformable registrations performed from phase 0 to phase i, i=25, 50, and 75

Verification of static dose calculations with thermoluminescent dosimeter measurements

Since the electron and mass densities of the phantom materials are different from those of patients, the first test was to check if the clinical algorithms could generate accurate dose predictions for the static phantom. The doses computed by the AAA, CCCS, and MC were compared to the TLD measurements at four static positions (SP). SP-T was inside the tumor, SP-A was out of the field, SP-B was in the left penumbra of the field, and SP-C was inferior to tumor but within the field. SP-A and SP-B were sensitive to the phantom's setup [Figure 6a], and SP-C could be subject to the capability of these algorithms in heterogeneity correction. The doses calculated by CCCS are shown in Figure 6a, and by MC in Figure 6b.

Figure 6.

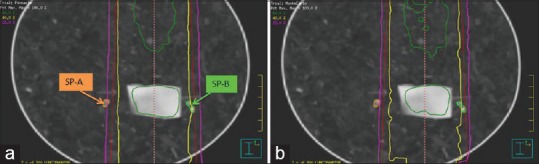
Iso-dose lines calculated by (a) Pinnacle and (b) EGSnrc/DOSXYZnrc

The average of the 4DCT dose measured by three TLDs is 10.3 cGy. After the subtraction of the CT dose, the TLD measured treatment dose agrees well with the computed dose in tumor and their maximum difference is <1.8%. The doses in the other three locations are shown in Table 2 where the mean and standard deviation of the computed doses in the volume contoured at each location are represented by D and σ. The relative dose error r is calculated by r%=100*|D-D_TLD|/D₀, where D_TLD is the mean of the three TLD doses measured at each location, and D₀ is the mean of the TLD doses measured in the tumor.

Table 2.

The thermoluminescent dosimeter measured doses (cGy) and computed doses were compared at four static points: SP-T, SP-A, SP-B, and SP-C

From Table 2, it can be found that at SP-C, the computed and measured doses are within 2.8%, but there are relatively large differences at other locations. At SP-A, the three algorithms in AAA, CCCS, and MC are different from the TLD measurements by 6.0%, 5.5%, and 2.4%, respectively, in relation to the prescribed dose. The large differences could be caused by phantom setup errors and insufficient validations of the clinical algorithms in regions out of the field. Note that the TLD readings for SP-B were acquired only at three locations [Figure 6]. The average of the three readings may slightly differ from the dose averaged within the SP-B contours [Figure 6]. This may help explain the relatively large difference between the TLD and MC doses. While large variations can be observed in the SP-B and SP-C contours, the mean doses computed by each algorithm are within 4% of the TLD measurements.

Verification of deformable dose calculations with thermoluminescent dosimeter measurements

With the treatment plan described in the section of Treatment planning and delivery, radiation dose was delivered with the Trilogy 21EX system to the phantom that was undergoing sinusoidal breathing patterns and related deformations. The developed plan was exported from Pinnacle to Hertz for MC dose calculation and for 4D dose accumulation. The DVF calculated by VelocityAI and Elastix were exported to Hertz. 3D dose volumes calculated with Pinnacle and EGSnrc/DOSXYZnrc for each of the four phases were warped to the EI phase using an in-house developed, mass-and-energy congruent mapping method.[18,22]

Figure 5a shows the dose profiles along the line marked in Figure 2b. The doses were calculated with Pinnacle on the phase images 0, 25, 50, and 75. The dose distributions computed with these phase images show obvious differences in the penumbra regions where the dose was reduced from 80% to 20% within 1.2 cm, i.e., 5% dose reduction per millimeter. The wide penumbra is due to the extended traveling range of scattered electrons in the low-density lung phantom. Furthermore, the tumor-scattered dose in the penumbra regions varies between these phases, and the computed and TLD-measured doses at the points DP-1 and DP-2 depend on the phantom's deformation and the tumor's positions within the beam [Figure 5]. The doses computed in each phase were warped to phase 0 and summed with equal weights to obtain the total dose. The profiles of the accumulated doses by the Elastix and VelocityAI registration algorithms are shown in Figure 5b, and the profiles of the displacements generated by these registrations in the Z-axis are shown in Figure 5c. The accumulated doses at the locations of DP-T, DP-1, DP-2, and DP-3 are listed in Table 3. The mean and standard deviation of the accumulated doses in the volume contoured at each location are represented by D and σ. The relative dose accumulation error is r%=100*|D-D_TLD|/D₀, where D_TLD and D₀ are defined in the same way as in Table 2.

Table 3.

The accumulated doses were compared to their thermoluminescent dosimeter measurements at the four locations: DP-T, DP-1, DP-2, and DP-3

The accumulated doses and the TLD measurements were compared at DP-T, DP-1, DP-2, and DP-3. The means of the TLD measured doses (±standard deviation) at the four locations are 224.4 (±6.7), 195.9 (±5.9), 209.8 (±6.3), and 198.1 (±6.0), respectively. At DP-T, all the accumulated doses are within 2% of the measured data. At DP-1, the Pinnacle dose reconstructed with the Elastix DVF agreed to the TLD measurement within 2.5%. However, when the VelocityAI DVF was used, the computed and measured doses differed by 11.8% at the same location. For the 3D dose calculated by EGSnrc/DOSXYZnrc, the total doses accumulated with the two DVFs were within 5.7% of the TLD measurements. Since image registration errors can induce large-dose accumulation errors in the beam penumbra region but have less consequence in homogeneous dose regions, the TLD-based dosimetric phantom will be used as a benchmark tool mainly for evaluation of the overall performance of dose accumulation algorithms, instead of their underlying DIRs.

Discussion

Adaptive treatment planning involves several computational algorithms including 3D dose calculation, DIR, dose warping, and summation. It is of paramount importance to verify the accuracy of these algorithms with physical phantom measurements. Several phantoms have been developed, each focusing on different parts of the 4D or adaptive plan procedure. However, these phantoms are either limited to one direction[14] or made of homogeneous materials[15] which are more suitable to validating 4D dose reconstructed by nonintensity-based registration methods. In contrast, the phantom developed in this study is composed of a heterogeneous, compressible sponge with TLD dosimeters implanted for dose measurement. Different from the homogeneous gel phantom, the phantom developed in this study was used to verify those 4D dose calculation algorithms that use intensity-based DIRs.

The adaptive planning algorithms implemented in Hertz involve two intensity-based image registration algorithms. Based on the Pinnacle calculated 3D doses, the total dose accumulated by the Elastix DVFs is within 2.5% of the TLD measurement at the location inferior to the tumor while the dose accumulated by the VelocityAI DVFs differs from the measurement by 11.8%. Note that in the superior-inferior direction, the phantom has large scales of deformation which may affect the dose coverage of the moving target. The accuracy of a 4D dose calculation algorithm depends on many factors including DIR and dose interpolation. Uncertainties in the DIR may induce errors in the accumulated dose, especially in the region of a moving target. The phantom developed in this study was designed to measure radiation dose, so it cannot detect DIR errors in dose-homogeneous region. Additional validation tools should be included when evaluating the performance of an image registration and its related dose accumulation. Acceptance tests for an adaptive planning software package should include comparisons with phantom measurements.[28] The phantom developed in this study makes it possible to perform TLD-based dosimetric verifications for the 4D dose calculation algorithms implemented in the software package.

As shown in Figure 6, the TLD dosimeters can be identified in the CT images, and grouping three TLDs can reduce the uncertainty of their average readings to 3%. While the readings in beam penumbra regions may be compromised by the finite size of TLDs, Table 2 shows the mean doses calculated in the tumor are about 250 cGy with the standard deviations <3.4 cGy. It should be mentioned that the fidelity of dose accumulation depends on the DIR and dose mapping algorithms as well as the dose accumulation weights assigned to individual phases. In this study, we equalized the dose contributions from individual phases and reduced the dose rate to 200 MU/min to minimize the synchronization uncertainties between the phantom's deformation and beam-on time. The dose rate reduction is not required if a gating technique is adopted for the synchronization. Nevertheless, the impact of patient-specific phase weighting factors on the accumulated dose, especially for irregular breathing patterns,[29] remains to be investigated in future studies.

If there are large errors identified in a given 4D dose calculation algorithm, it should be investigated further if these errors are from DIR or from dose interpolation. As a key component in adaptive radiotherapy, DIRs may induce large errors in accumulated doses. Virtual phantoms are often used to evaluate the performance of these registrations, but the lack of imaging artifacts and phase-to-phase changes in lung density compromises the realism of the simulated images in these phantoms. Furthermore, dose errors may come from the operation of dose interpolation, instead of the positional mapping. This type of errors cannot be identified without comparison with dose measurement. An acceptance test for an adaptive TPS should include comparisons between computed and measured doses.[28] As virtual phantoms can provide voxel-wise quantification of some DIR errors, combining the use of both the physical and virtual phantoms will improve the quality of the acceptance test.

Conclusions

In this study, a motor-controlled compressible phantom was developed to verify the dose accumulation algorithms on deformable structures, and the doses accumulated with different DIR and dose calculation algorithms were compared with TLD measurement results. The developed phantom may serve as an important QA tool for verification of dose accumulation algorithms for adaptive radiation therapy.

Financial support and sponsorship

This study was supported by the National Institutes of Health, grant number R01 CA140341..

Conflicts of interest

There are no conflicts of interest.