Abstract
Recent high-resolution computational fluid dynamics (CFD) studies have detected persistent flow instability in intracranial aneurysms (IAs) that was not observed in previous in silico studies. These flow fluctuations have shown incidental association with rupture in a small aneurysm dataset. The aims of this study are to explore the capabilities and limitations of a commercial cfd solver in capturing such velocity fluctuations, whether fluctuation kinetic energy (fKE) as a marker to quantify such instability could be a potential parameter to predict aneurysm rupture, and what geometric parameters might be associated with such fluctuations. First, we confirmed that the second-order discretization schemes and high spatial and temporal resolutions are required to capture these aneurysmal flow fluctuations. Next, we analyzed 56 patient-specific middle cerebral artery (MCA) aneurysms (12 ruptured) by transient, high-resolution CFD simulations with a cycle-averaged, constant inflow boundary condition. Finally, to explore the mechanism by which such flow instabilities might arise, we investigated correlations between fKE and several aneurysm geometrical parameters. Our results show that flow instabilities were present in 8 of 56 MCA aneurysms, all of which were unruptured bifurcation aneurysms. Statistical analysis revealed that fKE could not differentiate ruptured from unruptured aneurysms. Thus, our study does not lend support to these flow instabilities (based on a cycle-averaged constant inflow as opposed to peak velocity) being a marker for rupture. We found a positive correlation between fKE and aneurysm size as well as size ratio. This suggests that the intrinsic flow instability may be associated with the breakdown of an inflow jet penetrating the aneurysm space.
Keywords: computational fluid dynamics, hemodynamics, flow fluctuations, intracranial aneurysms, rupture risk
Introduction
IAs or pathological out-pouchings of the arteries in the brain, occur in approximately 3% of the population [1]. Continued growth of aneurysms can lead to their eventual rupture, resulting in a high rate of mortality and morbidity [2]. Image-based CFD studies have shown that hemodynamics can stratify aneurysm rupture status [3–6]. However, it is unclear if these simulations, under limited spatial and temporal resolutions, and often low-order discretization schemes, can capture intra-aneurysmal flow instabilities, which could affect rupture potential [7,8].
In Vitro and in vivo studies have uncovered the presence of flow instability through audible thrills or murmurs (termed bruit) in IAs. in vivo, velocity fluctuations have been found in some patients intra-operatively prior to aneurysm clipping. However, their association with rupture has not been determined [9–12]. Similarly, in vitro particle image velocimetry measurements [13] and flow visualization in experimental glass models have also noted unstable flow within vasculature models [12,14,15].
In CFD studies of IAs, such flow instabilities have been reported under imposed high-resolution settings [7,16]. Moreover, in a small number of MCA aneurysms (12 total, seven ruptured), Valen-Sendstad et al. [17] found that five ruptured bifurcation aneurysms showed flow fluctuations despite the use of a steady, high-inflow condition. Therefore, the authors suggested that this characteristically unstable flow has the potential to be associated with rupture. However, such flow instabilities in IAs have not been independently verified by other groups or in a larger cohort. Likewise, the possibility of flow instability as a rupture predictor can only be tested in a large IA data set.
To this end, the objectives of the current study were as follows: first, this study explored the capabilities and limitations of first- and second-order CFD discretization schemes, as well as temporal and spatial resolution (i.e., time step and mesh size), particularly in capturing velocity fluctuations in IAs. As CFD becomes more widely used in the biomedical field, it is important to understand the methodology behind the cfd solvers with particular consideration to the parameters being studied. This is especially critical for users of commercial CFD packages, as they are often treated as “black boxes” with limited understanding of the impact of the underlying setting and internal schemes. As previously suggested [18,19], disregarding the ramifications of these settings could lead to different aneurysmal hemodynamics and neglect flow characteristics that may be relevant to aneurysm pathophysiology.
Second, we explored if the flow instability observed by Valen-Sendstad et al. [17] could be observed in a larger patient dataset. Similar to previous studies, we use a steady flow as the inlet boundary condition in order to investigate if inherent flow fluctuations arise without the variability of a pulsatile waveform. However, we choose to impose a cycle-averaged inlet boundary condition, thus investigating if flow fluctuations arise at a nominal flow rate. Third, we analyzed if fKE, as a metric to quantify flow instability, could be a marker for IA rupture in our larger data set. Finally, we examined the mechanisms by which flow instabilities may arise by analyzing velocity fluctuations and their correlation to aneurysm geometrical parameters.
Our patient cohort consisted of 56 MCA aneurysms including 12 that were ruptured. We quantified aneurysmal fKE in the same manner as turbulence kinetic energy in turbulent flow analysis. With an imposed steady inflow boundary condition, we analyzed aneurysm-averaged fKE in ruptured and unruptured aneurysms, and bifurcation and sidewall aneurysms to see if there is a statistically significant difference between IA groups. We aimed to test if ruptured IAs have stronger flow instability as compared to unruptured IAs as suggested previously [17], and gain insight into the geometric characteristics which may give rise to flow fluctuations.
Methods
Patient Dataset.
Fifty-six MCA aneurysms from 52 patients from our center were examined, which were collected retrospectively under Institutional Review Board approval from 2006 to 2014. This patient dataset was partially derived from a previously analyzed cohort from 2006 to 2011 [6]. Digital subtraction angiographic images were taken using a Toshiba Infinix C-arm 3D rotational angiography system, with 512(×3) matrix and 250 μm voxel size (Toshiba Medical Systems Corp., Tustin, CA). Selection of the patient dataset was continuous and determined based on the MCA location and if the 3D image quality was sufficient for segmentation. Rupture was determined at the time of imaging, and 12 aneurysms were classified as such. Forty-seven MCA aneurysms were classified as bifurcation aneurysms (including ten ruptured) and nine as sidewall aneurysms (including two ruptured). Bifurcation aneurysms are those that arise at the apex of a split from a main artery into two or more daughter arteries. Following the definition by Dhar et al. [20], we calculated the average aneurysm size to be 5.80 ± 2.81 mm for ruptured aneurysms and 4.47 ± 2.28 mm for unruptured aneurysms (no statistical difference between the groups, p = 0.160).
Table 1 summarizes the demographic information of the study population. We chose MCA aneurysms based on their relatively high rupture prevalence as well as to be able to easily compare with results from previous studies [17] without introducing variability of aneurysm location.
Table 1.
Patient Demographic Information
| Unruptured (n = 44) | Rutpured (n = 12) | |
|---|---|---|
| Patient Characteristics | ||
| Female sex (%) | 29 (66%) | 4 (33%) |
| Age, years (mean ± st. dev) | 62 ± 11 | 57 ± 10 |
| Aneurysm Characteristics | ||
| IA Size, mm (mean ± st. dev) | 4.47 (2.28) | 5.80 (2.81) |
| Bifurcation (%) | 37 (84%) | 10 (83%) |
| Sidewall (%) | 7 (16%) | 2 (17%) |
Computational Methods.
Aneurysm geometries were reconstructed from 3D angiographic images and segmented using vascular modeling toolkit (VMTK) [21]. Generation of surface meshes were based on zero level set and fast marching cube algorithms in VMTK [22] and the aneurysm domain was isolated and cleaned in ANSYS ICEM CFD (ANSYS, Inc., Canonsburg, PA). The proximal (inlet) MCA branch was extended by a minimum of 12 vessel diameters before the aneurysm to allow for sufficient flow development. The average MCA inlet diameter was 2.74 ± 0.42 mm. The outlets were extended to the next bifurcation. Unstructured volumetric meshes were generated in ANSYS ICEM CFD. Tetrahedral elements were used with four refined prism layers at the wall at one-tenth the size of the maximum volumetric element size for the first prism layer and a height ratio of 1.2 to define the other prism element size.
CFD simulations were run in the commercial solver, STAR-CD (CD-adapco, Melville, NY). The transient Navier–Stokes equations were solved under the Newtonian fluid assumption. The mass and momentum equations for an incompressible flow are expressed below in Eqs. (1) and (2), respectively,
| (1) |
| (2) |
where is Cartesian coordinates ( = 1, 2, 3), is the absolute fluid velocity component in the direction , the pressure, is density, and is viscosity. Due to the relatively low Reynolds number in our simulations, a turbulent flow model was not investigated in this study.
The Algebraic Multigrid algorithm was used to solve the linear system of equations that were obtained when the Navier–Stokes equations were discretized in the computational domain. The computational domain was initialized at zero pressure and velocity. A rigid wall and no-slip boundary condition were assumed and blood was modeled as a Newtonian fluid with a constant density and viscosity of 1056 kg/m3 and 3.5 cP, respectively. A relaxation factor of 0.7 was used for the momentum equation, with a minimum residual tolerance of 1 × 10−7(scaled, unitless).
As in previous studies [17], in order to investigate intrinsic flow instability that may be present in some aneurysms, independent of pulsatile flow dynamics, a constant inflow was imposed at the inlet of each vascular model. A flow rate of 120 mL/min was applied at the inlet. According to a phase-contrast MR imaging study of 88 subjects, this corresponds to the cycle-averaged flow rate in the MCA [23]. This resulted in an average inflow velocity of 0.36 ± 0.10 m/s and average Reynolds number of 287 ± 51. The outlet condition was based on the principle of minimum work, where the flow split is proportional to the cube of the outlet diameters [24].
Each simulation was run for a total of six periods, or flow-throughs, which allowed for sufficient convergence of the solution. A period was defined as the volume of the computational domain divided by the volumetric flow rate. The final three periods were used as output for our analysis. Simulations were run at the Center for Computational Research for an average of 36 hr on an 8-core Intel Xeon L5520 processor (2.27 GHz). Simulation time was typically halved when utilizing first-order discretization schemes. Postprocessing and visualization, in which the aneurysm was isolated, was performed in Tecplot 360 (Tecplot, Inc., Bellevue, WA).
Quantification of Flow Fluctuations and Classification of Stable Versus Unstable Aneurysm Flow.
We decompose the instantaneous velocity, , into mean velocity, , and fluctuating components of velocity, , in the direction of ( = 1, 2, 3):
| (3) |
where the overbar represents the nodal average over time.
To quantify the kinetic energy per unit mass of these fluctuations, we define fKE as
| (4) |
This definition is mathematically equivalent to turbulence kinetic energy, which was used previously [17,25]. (However, note that the fluctuations are not necessarily fully developed turbulence.) To compare among different aneurysm cases, we isolated the aneurysm sac and calculated a spatially averaged fKE for each IA, termed aneurysmal or aneurysm-averaged fKE.
The classification of “stable” and “unstable” aneurysms in terms of velocity fluctuations was initially based on the observations of velocity at a monitoring point in the aneurysm dome. Consistent with previous literature [17], the fKE threshold for unstable flow was preliminarily set to >10−4 m2/s2. Adjustment of this threshold was later assessed based on the flow characteristics of our cohort and the calculation of fluctuation intensity, , defined as
| (5) |
which quantified the percentage of flow that is fluctuating and is mathematically equivalent to turbulence intensity.
To further characterize the nature of the flow instabilities, we performed a frequency analysis of the velocity magnitude at the monitoring point in the aneurysm dome for the final three periods. The dominant frequencies of each of the stable cases, which exhibited unstable flow fluctuations, were found using a power spectral density estimate that was calculated using the fast Fourier transform (FFT) algorithm in matlab R2014b (The MathWorks Inc., Natick, MA). The FFT algorithm decomposes and sorts frequencies present in the discrete time signal. The relative magnitude or densities of each frequency were displayed as the power spectral density curves.
Sensitivity Analysis.
To establish the appropriate numerical settings necessary to capture the underlying aneurysmal flow instabilities, we varied the CFD discretization schemes, and spatial and temporal resolutions for one of the MCA aneurysm cases (UR1), as shown in Fig. 1. This aneurysm exhibited flow instability when second-order discretization schemes were used. A steady-inflow condition at the inlet of the aneurysm was set and transient CFD simulations were run under various conditions of testing. In addition, in order to examine the sensitivity of our simulations to the inflow rate, the inflow was varied in the known physiologic range. Aneurysmal fKE and velocity magnitude were calculated and compared for different simulation settings.
Fig. 1.
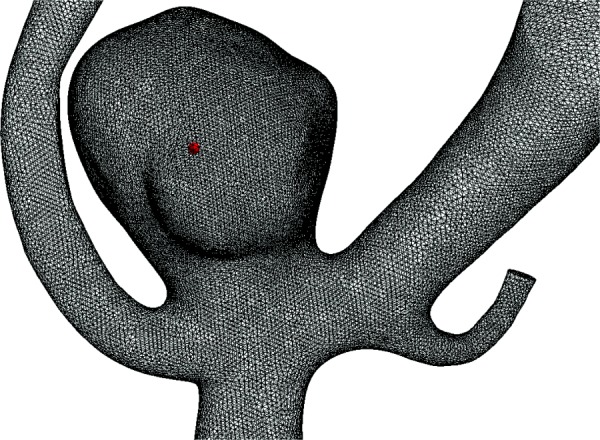
An unruptured MCA case, UR1, using the sensitivity tests is shown with a mesh consisting of 2.2 × 106 elements. A monitoring point at the center of the aneurysm dome, shown by the red dot, was used for illustration of the flow fluctuations and frequency analysis.
Discretization Scheme Selection.
To examine solution sensitivity to CFD discretization settings, first- and second-order spatial and temporal discretization schemes were tested. For temporal discretization, a first- and second-order semi-implicit method for pressure-linked equations (SIMPLE) schemes were used (Star-CD 2013 v4.2). For spatial discretization schemes, a first-order upwind-differencing (UD) scheme, and second-order UD and central-differencing (CD) schemes were tested. In both first- and second-order simulations, a second-order CD scheme was used in mass conservation. A series of five tests were conducted which investigated various combinations of the aforementioned discretization schemes. The discretization tests included: (1) first-order temporal and first-order spatial; (2) first-order temporal, and second-order spatial (UD); (3) second-order temporal and first-order spatial (UD); (4) second-order temporal and second-order spatial (UD); and (5) second-order temporal and second-order spatial (CD). These tests were performed using a fine mesh (maximum element size of 0.13 mm, 2.2 × 106 elements) and small time-step (dt = 0.4 ms).
Grid Resolution.
To determine the appropriate mesh element size for capturing flow fluctuations, a grid-independence study was performed. Using second-order temporal and spatial discretization schemes and a time step of 0.4 ms (for grids ≤2 × 106 elements) or 0.3 ms (for grids >2 × 106 elements), the unstructured grids in this aneurysm were refined from 200,000 to 4.7 × 106 tetrahedral elements. This corresponded to a maximum element size decreasing from 0.30 mm to 0.10 mm.
Temporal Resolution.
As with grid resolution, a temporal resolution study was performed to confirm that the appropriate time step was chosen. The time step was varied based on the Courant–Friedrichs–Lewy (CFL) condition. Given the inflow rate and maximum element size, we calculated CFL and varied it from 2 to 0.125. For a computational domain of 2.2 × 106 elements, this corresponded to a time step of 0.80–0.05 ms. Additionally, to ensure both grid and time step independence, CFL was varied for a mesh of 4.7 × 106 elements from 2 to 0.25. This corresponded to a time step of 0.65–0.16 ms.
Inflow Sensitivity.
To examine the potential effect of fKE on changing inflow rate, we varied the steady inlet flow rate across the physiologic range in the single MCA case. With second-order temporal and spatial discretization schemes, a mesh of 2.2 × 106 elements, and CFL number of 1, we performed three tests with flow rates of 108 [26], 120 (nominal) [23], and 161 mL/min [27].
Statistical Analysis.
After determining the appropriate discretization order, grid and temporal resolutions, we applied these conditions to simulate flow in all 56 MCA cases under constant cycle-averaged inflow rate. To compare among different IA groups, we calculated group-averaged aneurysmal fKE (e.g., ruptured versus unruptured; bifurcation versus sidewall) and used a Wilcoxon rank-sum test (for abnormally distributed data) to assess if the IAs groups could be differentiated. A p-value of <0.05 was considered statistically significant. We tested three groups of aneurysms:
-
(i)
Ruptured (n = 12) and unruptured (n = 44) IAs
-
(ii)
Sidewall (n = 9) and bifurcation (n = 47) type IAs
-
(iii)
Bifurcation only, ruptured (n = 10), and unruptured (n = 37) IAs
Furthermore, to examine if there was any correlation of the flow instability to aneurysm geometric features and inlet velocity, a Kendall's tau-b correlation analysis was performed. Kendall's tau-b correlation assesses the number of concordant (agreeable increases or decreases) and discordant (disagreeable increases or decreases) pairs between two ordered variables without assuming normally distributed data or a linear relation relationship. Statistical analysis was performed in IBM SPSS Statistics Version 22.0 (IBM Corporation, Armonk, NY).
The morphologic parameters included in the analysis were IA size, size ratio (SR), aspect ratio (AR), undulation index (UI), ellipticity index (EI), nonsphericity index (NSI), vessel angle, aneurysm inclination angle, IA neck diameter, and parent vessel size [20,28]. Morphologic calculations were performed using previously developed algorithms [20] programmed in matlab R2014b. Detailed definitions of these morphologic parameters can be found in our previous publications [20]. Briefly, size is the maximum perpendicular height of the aneurysm, SR is the relative aneurysm-to-parent vessel size, AR is the aneurysm-to-neck size, UI is the degree of surface concavity, EI is a measure of the aneurysm elongation, NSI is a measure of the deviation of the aneurysm from a hemisphere, vessel angle is the angle between the parent vessel to the aneurysm, aneurysm inclination angle is the angle of inclination between the aneurysm and the neck plane, neck diameter is the average diameter at the aneurysm orifice, and parent vessel size is the average diameter of feeding artery.
Results
Sensitivity Analysis Results
Discretization Scheme Selection.
In the single test case (UR1), we examined the ability of first- and second-order spatial and temporal discretization schemes to capture flow instability. Results of aneurysmal fKE for the five combinations of discretization schemes are shown in Fig. 2(a). It can be seen that CFD simulations under both first-order spatial and first-order temporal discretization schemes do not exhibit any appreciable flow fluctuations. The aneurysmal fKE was 8.4 × 10−12 m2/s2, much below the threshold of 10−4 m2/s2. However, when either temporal or spatial second-order discretization schemes were used, the aneurysm exhibited unstable flow. The greatest degree of velocity fluctuation was captured with both second-order temporal and spatial discretization schemes. There was no appreciable difference when using an UD or a CD spatial discretization scheme as aneurysm-averaged fKE was found to be 9.38 × 10−4 m2/s2 and 9.32 × 10−4 m2/s2, respectively.
Fig. 2.
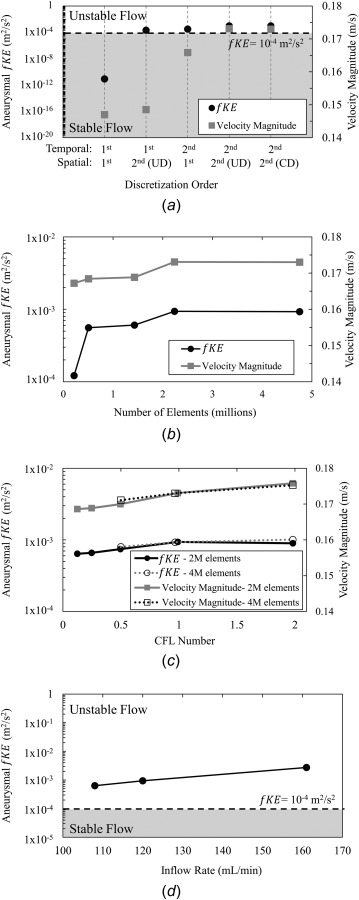
The results of sensitivity tests on a single unruptured MCA case. (a) The discretization scheme sensitivity tests showing aneurysm-averaged fKE and velocity magnitude for five combinations of first- and second- order discretization schemes. The stable (gray) and unstable regimes which were initially defined by the threshold of aneurysmal fKE of 10−4 m2/s2 (dashed line). Results showed that second-order temporal and spatial discretization schemes are necessary to capture flow fluctuations. (b) Grid-independence study showing convergence of aneurysm-averaged fKE and velocity magnitude between 2.2 × 106 and 4.7 × 106 elements. (c) Time step-independence study showing the aneurysm-averaged fKE and velocity magnitude with successive refinement of the CFL number. For simulations with both 2.2 × 106 and 4.7 × 106 elements, no appreciable change in fluctuation energy and velocity magnitude was found for a CFL number of 1. (d) The results of inflow rate sensitivity tests, where flow rate was varied in the physiologic range. Aneurysmal fKE increased with increasing inflow rates, but the case retained unstable flow characteristics.
Based on these results, we applied a second-order temporal and second-order spatial (UD) discretization scheme for the remaining simulations. We chose an UD scheme over a CD scheme for spatial discretization due to its reported good functionality with unstructured grids [29].
Grid Resolution.
As shown in Fig. 2(b), convergence of aneurysmal fKE and velocity magnitude was reached at a grid resolution between 2.2 × 106 and 4.7 × 106 elements. We therefore adopted a maximum element size of 0.13 mm for our study. In our MCA cohort, this corresponded to an average of 2.7 × 106 elements (range 1.5–7 × 106). This spatial resolution is higher than typical CFD simulations with approximately 500,000 elements [6,30–33].
To assess the quality of the spatial resolution of our simulations that use a maximum element size of 0.13 mm, we calculated the viscous length scale defined in the equations given below [34]
| (6) |
| (7) |
where is the friction velocity at the vessel wall, is the shear deformation tensor, ν is kinematic viscosity, and Δl is the maximum element size. We found = 2.5 for a maximum element size of 0.13 mm. Similar to previous studies [25], we assume that because is on the same order of 1, that the flow field could be considered spatially resolved.
Temporal Resolution.
Figure 2(c) shows the variation of aneurysmal fKE and velocity magnitude with a changing temporal resolution. No appreciable change in aneurysm-averaged fKE and velocity was found between CFL number of 1 and 0.5 for meshes of 2 and 4 × 106 elements (corresponding to a time step of 0.4 ms and 0.3 ms, respectively). Furthermore, at a CFL number equal to 1, there was no appreciable change in aneurysm-averaged fKE between the two mesh sizes (9.38 × 10−4 and 9.27 × 10−4 m2/s2 for 2 and 4 × 106 elements, respectively), which ensured both grid independence and time step independence. We also noted that the solution was less dependent on the time step as compared to the discretization order and grid resolution. Therefore, we adopted a criterion of CFL equal to 1 for each case in our MCA cohort. This corresponded to an average time step of 0.23 ms. This is much smaller than typical pulsatile simulations where 1–10 ms is common [3,6]. Table 2 summarizes the discretization schemes, and spatial and temporal resolutions, for lower-resolution CFD studies and compares them to that of the current CFD studies.
Table 2.
Typical settings of lower- and high-resolution IA CFD simulations
| Lower-resolution CFD | High-resolution CFD | |
|---|---|---|
| Numerical scheme | ||
| Spatial discretization (order) | UD (1st) | UD (2nd) |
| Temporal discretization (order) | SIMPLE (1st) | SIMPLE (2nd) |
| Spatial resolution | ||
| Number of elements (× 106) | 0.5 | 2.6 |
| Range (× 106) | 0.3–1.0 | 1.3–6.5 |
| Max element size (mm) | 0.3 | 0.13 |
| Temporal resolution | ||
| Average time step (ms) | 1.0 | 0.23 |
| Simulated number of periods | 3 | 6 |
| Number of periods examined | 1 | 3 |
UD, upwind differencing spatial discretization scheme; SIMPLE, semi-implicit method for pressure-linked equations temporal discretization scheme
We further compared our time step against the viscous time scale defined in Eq. (8),
| (8) |
We found = 1.3 ms for a simulation time step of 0.23 ms. Therefore, our transient simulation time step was smaller than the viscous time scale.
Inflow Sensitivity.
Figure 2(d) shows the variation of aneurysmal fKE across the physiological range of inlet flow rates. Although fKE increased with flow rate, the change did not result in a shift from the unstable (gray region in Fig. 2(d)) to the stable flow regime. When inflow rate was changed from 108 to 161 mL/min aneurysm-averaged fKE increased from 6.35 × 10−4 to 2.73 × 10−3 m2/s2, respectively.
Classification of Stable Versus Unstable Aneurysm Flow.
For each of the 56 aneurysms in our cohort, we applied second-order discretization and high grid and temporal resolutions established previously and quantified aneurysmal fKE. Figure 3 shows the distribution of IA size and aneurysmal fKE in our cohort. From these data, we defined a threshold of fKE greater than 5 × 10−5 m2/s2 for unstable flow. This threshold best discriminates the aneurysms with appreciable flow fluctuations from those with small or negligible instabilities. Additionally, we verified the classification of stable versus unstable flow based on . Cases with unstable flow exhibited between 5% and 9%, and cases with stable flow exhibited of less than 1%, further supporting the designation of cases to the unstable and stable flow regimes.
Fig. 3.
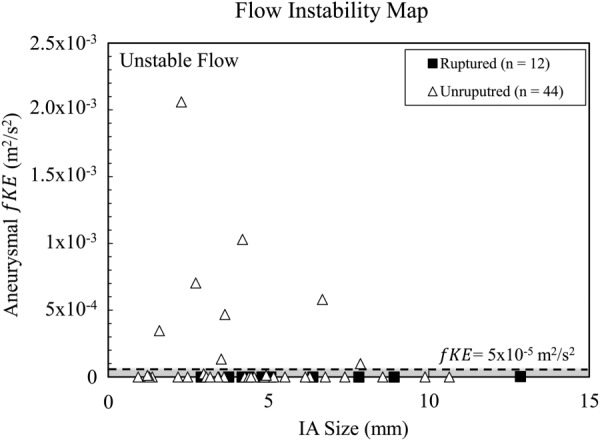
The distribution of aneurysm-averaged fluctuation energy for all MCA cases in comparison to aneurysm size. The flow instability map where eight cases were found to have unstable flow. The dashed line demarks the verified threshold for unstable flow fKE > 5 × 10−5 m2/s2). All other cases were classified as stable (gray) in terms of velocity fluctuations.
Based on this verified threshold, each of the 56 MCA aneurysms was classified as stable or unstable in terms of velocity fluctuations. Eight cases showed appreciable amounts of velocity fluctuations within the aneurysm and were classified as unstable flow (fKE > 5 × 10−5 m2/s2). All other cases (n = 48), including all ruptured cases, were found to have stable flow, reflected in low fKE. A visual examination of fKE contours shows, in Fig. 4(a), the eight cases with unstable flow, UR1–UR8, and in Fig. 4(b), four representative unruptured, UR9–UR12 and four ruptured, R1–R4, cases with stable flow. It is interesting to note that all the cases exhibiting flow instability, or high aneurysmal fKE, were unruptured bifurcation aneurysms. Furthermore, each of the eight unstable flow cases also show the presence of an inflow jet as shown in Fig. 5.
Fig. 4.
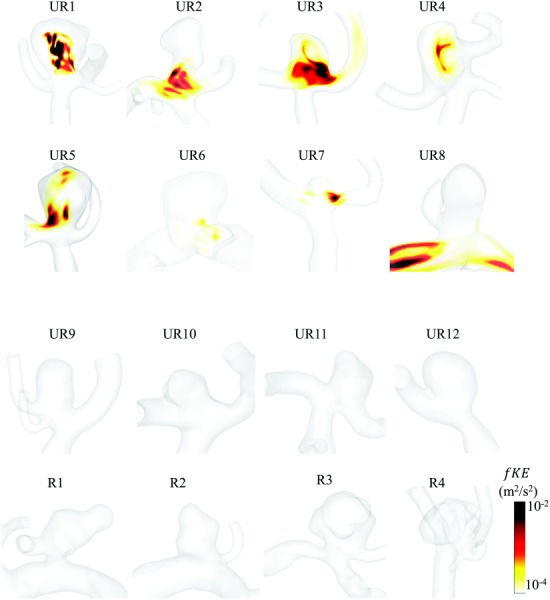
Volumetric rendering of fKE in the eight IA cases with unstable flow and eight representative IA cases with stable flow. (a) The eight unstable flow cases (fKE > 5 × 10−5), all of which were unruptured bifurcation aneurysms. (b) Representative stable flow cases including four unruptured (top row) and four ruptured (bottom row) IAs.
Fig. 5.
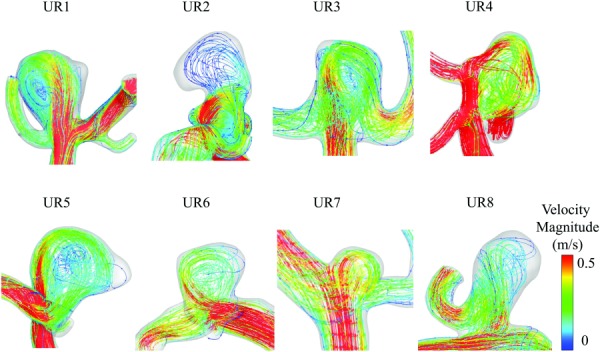
Streamlines colored by velocity magnitude of the eight unstable flow cases. Each case was a bifurcation aneurysm with a distinct inflow jet. The velocity fluctuations may have arisen from complex interaction of the parent vessel and aneurysms geometry leading to the instability of the inflow jet, which penetrated the aneurysm and subsequently broke down.
To further illustrate the dichotomy of cases with stable and unstable flow, a monitoring point arbitrarily chosen at the center of the aneurysm sac shows either the convergence of velocity or continued oscillations after three periods. Figure 6(a) shows velocity magnitude at a monitoring point for the eight cases with unstable flow, and, likewise, Fig. 6(b) shows the eight representative unruptured and ruptured cases. After three periods, unstable flow cases demonstrated persistent velocity fluctuations, where the stable flow cases converged to a single solution.
Fig. 6.
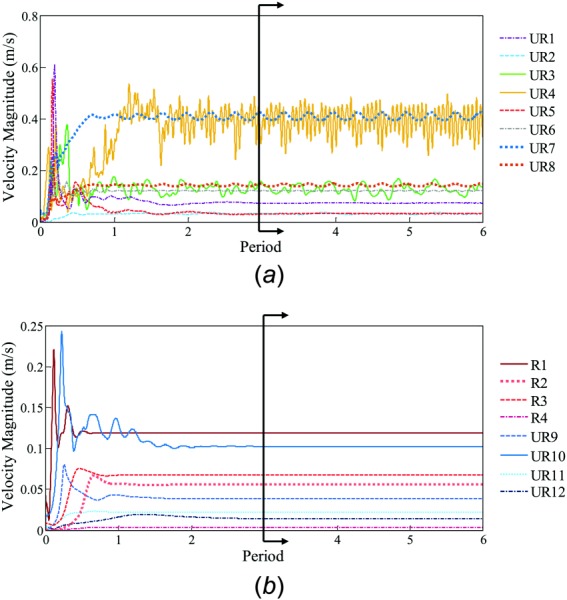
CFD solutions under second-order discretization schemes of velocity magnitude versus time at a monitoring point in each of the 16 aneurysms in Fig. 4. (a) The eight unstable flow cases, which demonstrated persistent velocity fluctuations, and thus, high aneurysm-averaged fKE in the last three periods. (b) The eight representative stable flow cases, which showed no fluctuations, and thus, low aneurysm-averaged fKE.
Furthermore, when velocity fluctuations of the final three periods at the monitoring point were examined in the frequency domain, each of the cases with unstable flow exhibited a dominant frequency. Figure 7(a) shows the dominant frequencies for the eight cases with unstable flow. For cases UR1 through UR8, the frequencies were 102, 15, 11, 89, 110, 108, 25, and 6 Hz. Furthermore, as shown in a representative case, UR1, when the final three periods (Fig. 7(b)) were examined in the frequency domain (Fig. 7(c)), a continuous distribution of frequencies was not present as would be expected in fully developed turbulent flows.
Fig. 7.
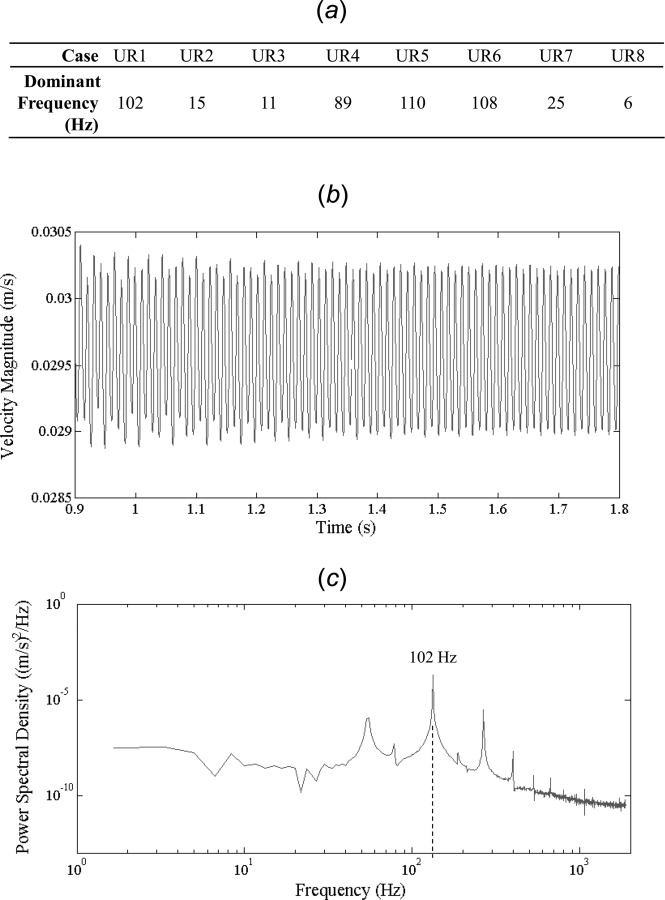
The frequency analysis results at a monitoring point in the aneurysm dome. (a) The dominant frequencies in the eight cases with unstable flow. (b) Velocity magnitude versus time at a monitoring point in the aneurysm for the final three periods of a representative case (UR1). (c) Power spectral density (note the log-log scale) of the last three periods for one representative case, UR1. The case shows a dominant frequency of 102 Hz.
Verification of Discretization Schemes.
To verify that second-order spatial and temporal discretization schemes are indeed required to capture the flow instability, we re-ran CFD for these eight cases with unstable flow using first-order discretization schemes (SIMPLE and upwind differencing and schemes for temporal and spatial discretization, respectively). Figure 8 shows velocity magnitude at monitoring point in the aneurysm as a function of time. In contrast to Fig. 6(a), all but a single case (UR3) stabilized after three periods. This is consistent with our finding from the sensitivity analysis (Fig. 2) that second-order discretization schemes are required in order to capture this unstable flow phenomenon.
Fig. 8.
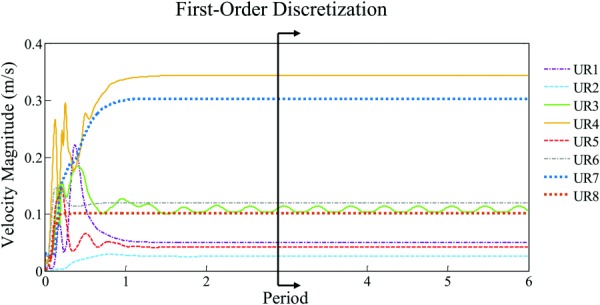
To demonstrate the necessity of second-order discretization schemes, each of the eight cases found to have unstable flow in high-resolution simulations were run using first-order discretization. After three periods, all cases except for one case (UR3, green), were found to have stable flow.
Statistical Analysis.
Table 3 shows statistical analysis in the three previously presented aneurysm groups. No statistical difference was observed between groups based on aneurysm-averaged fKE. Ruptured and unruptured IAs had a group averaged fKE of 4.88 × 10−4 and 1.14 × 10−3 m2/s2, respectively (p = 0.566). Sidewall and bifurcation type IAs had group averaged fKE of 8.29 × 10−3 and 1.06 × 10−4 m2/s2, respectively (p = 0.877). Likewise, within the bifurcation aneurysms, ruptured and unruptured groups had a group averaged fKE of 5.46 × 10−7 and 1.32 × 10−4 m2/s2, respectively (p = 0.287). The finding that aneurysmal fKE in ruptured and unruptured IAs is statistically indistinguishable is contrary to our initial hypothesis that ruptured aneurysms would have a higher prevalence of flow instability and thus, higher fKE. This data shows that, in our cohort, the prevalence of flow instability, quantified by aneurysmal fKE, is not a predictor for rupture.
Table 3.
Results of statistical analysis comparing three different aneurysm groups
| Aneurysm group | Aneurysmal fKE (m2/s2) | p-value | |
|---|---|---|---|
| I | Ruptured | 4.88 × 10−5 ± 1.67 × 10−4 | 0.566 |
| Unruptured | 1.14 × 10−4 ± 3.66 × 10−4 | ||
| II | Sidewall | 8.29 × 10−5 ± 2.19 × 10−4 | 0.877 |
| Bifurcation | 1.06 × 10−4 ± 3.54 × 10−4 | ||
| III | Ruptured, bifurcation | 5.46 × 10−7 ± 1.18 × 10−6 | 0.287 |
| Unruptured, bifurcation | 1.32 × 10−4 ± 3.97 × 10−4 |
Finally, Table 4 shows the correlation analysis of aneurysmal fKE to aneurysm geometric parameters and inlet velocity. Aneurysmal fKE was found to be positively correlated to both increasing IA size and SR (p = 0.001and 0.002, respectively). The other geometric parameters investigated: AR, UI, EI, NSI, aneurysm angle, vessel inclination angle, IA neck diameter, and parent vessel size were found to have no correlation to aneurysmal fKE. Furthermore, there was found to be no correlation between fKE and inlet velocity.
Table 4.
Correlation analysis of morphologic parameters and inlet velocity to aneurysmal fKE
| Comparison parameter | Stable flow (n = 48) (Mean ± st. dev) | Unstable flow (n = 8) (Mean ± st. dev) | Kendall's tau-b correlation coefficient | p-value |
|---|---|---|---|---|
| IA Size (mm) | 4.85 ± 2.61 | 4.35 ± 1.80 | 0.316 | 0.001a |
| SR | 2.54 ± 1.36 | 2.29 ± 0.99 | 0.293 | 0.002 a |
| AR | 1.27 ± 0.59 | 1.24 ± 0.60 | 0.140 | 0.144 |
| UI | 0.076 ± 0.056 | 0.072 ± 0.052 | 0.095 | 0.320 |
| EI | 0.14 ± 0.06 | 0.13 ± 0.07 | 0.116 | 0.082 |
| NSI | 0.17 ± 0.07 | 0.16 ± 0.08 | 0.162 | 0.091 |
| Aneurysm angle (deg) | 87.2 ± 7.29 | 87.4 ± 3.6 | −0.065 | 0.500 |
| Inclination angle (deg) | 44.7 ± 21.7 | 41.4 ± 24.4 | −0.069 | 0.475 |
| Neck diameter (mm) | 3.95 ± 1.48 | 3.74 ± 1.19 | 0.138 | 0.149 |
| Parent vessel (mm) | 2.00 ± 0.55 | 1.80 ± 0.32 | −0.013 | 0.893 |
| Inlet velocity (m/s) | 0.29 ± 0.12 | 0.37 ± 0.11 | −0.187 | 0.168 |
Indicates statistically significant
Discussion
In this study, we have verified that second-order discretization schemes and sufficient spatial and temporal resolutions are required for CFD to capture intrinsic flow instability that arises in some aneurysms under steady inflow. We applied that these CFD settings to a large cohort of patient aneurysms and explored if there was a difference in fKE between ruptured and unruptured aneurysm groups. We have found that these flow instabilities were present in 8 of 56 aneurysms, all of which were unruptured bifurcation aneurysms, and that fluctuation energy was not associated with rupture. Furthermore, we explored the possible correlation of the flow instability to aneurysm geometrical features and found that these flow fluctuations might be correlated to larger aneurysm sizes and size ratios.
Our findings that the flow fluctuations is not associated with aneurysm rupture status is opposite to the incidental correlation that was found by Valen-Sendstad et al. [17], who observed appreciable fluctuation energy (>10−4 m2/s2) in five of 12 MCA aneurysms, all of which were ruptured. Like in our current study, they applied a steady inflow in transient simulations to observe the intrinsic fluctuations that occur without the effect of pulsatile waveforms. However, the steady inflow boundary condition of our study was a cycle-averaged inflow rate, as opposed to a constant inlet velocity, corresponding to peak systole [17].
To examine if our inlet boundary assumption was reasonable, we performed a sensitivity analysis. Results showed that aneurysmal fKE moderately increased with increasing inflow within the physiologic range. However, this variation was not sufficient to alter the flow stability status in this aneurysm. Among different aneurysms in our cohort, there was no correlation between inlet velocity and fKE. We suspect that the choice of inlet velocity within the physiologic range may not drastically alter the flow stability map (Fig. 3) such that ruptured and unruptured aneurysms in this cohort would be segregated, according to fKE. However, we cannot conclude which inflow assumption is better. Future research utilizing a systolic inlet velocity conditions can be performed in order to recapitulate prior studies [17].
It should be clarified that when discussing aneurysm natural history, unstable aneurysms are usually referred to as those that are growing and may have a higher propensity for rupture [35], while stable aneurysms are referred to those that appear to have stabilized and do not exhibit growth. Such pathology-based dichotomy is not the focus of our study. Our study concerns itself with a type of flow dynamics-based instability. In a number of CFD studies in the past, a connection between complex and unstable flow patterns and ruptured aneurysms has been observed, and there has been evidence that unstable flow, manifested in multiple or time-varying vortices, is associated with ruptured aneurysms [6,36–39]. Therefore, it is reasonable to investigate whether the persistent flow fluctuations emerging under a steady inlet boundary condition could be associated with rupture. Our large patient dataset has positioned us to explore if there is a statistical difference in the flow fluctuations between ruptured and unruptured aneurysm groups.
The dichotomy of stable and unstable flow cases was verified by the calculation of fluctuation intensity, and the observation of velocity magnitude at a monitoring point in the aneurysm sac. Cases with stable flow are those with aneurysmal fKE of less than 5 × 10−5 m2/s2, and with fluctuation intensities of less than 1%. It is possible that the small, “negligible” fluctuations exhibited by the cases with stable flow could be numerical fluctuations. This, however, requires rigorous verification studies and was not the focus of our study; rather, we sought to identify the significant fluctuations that were previously unexpected.
We conjecture that the observed unstable flow fluctuations in this study are due to the existence of an unstable, oscillating jet issued from the parent vessel into the “open space” of the aneurysm sac [15]. In each of the eight cases with unstable flow in our cohort, an inflow jet was identified, as shown in Fig. 5. We suspect that the geometric features of these aneurysms may have “tripped” the flow, even at lower Reynolds numbers (Re = 287 ± 51). Additionally, we have noticed that regardless of the rupture status of the IA, all of the cases that have unstable flow in our study are bifurcation aneurysms (i.e., those that arise from the apices of a split from a parent to two or more daughter arteries), while none are sidewall aneurysms. The presence of velocity fluctuations in bifurcation and not sidewall aneurysms is consistent with previous findings [17].
To explore the mechanism by which such velocity instabilities may arise, we examined if there was any correlation between aneurysmal fKE and geometric features. Several relevant geometric parameters included IA size, size ratio (the ratio of IA height to parent vessel), and aspect ratio (the ratio of IA height to neck diameter), all of which characterize the sudden expansion of the aneurysm space from the parent vessel. In addition, vessel angle (the angle between the inlet vessel and neck plane) and aneurysm inclination angle (the inclination of the aneurysm to the neck plane) influence the presence and penetration of an inflow jet. We found a positive correlation of aneurysmal fKE with IA size and size ratio. However, there is no association between aneurysmal fKE with vessel angle and aneurysm inclination angle. This may be attributed to the fact that our cohort was dominated by bifurcation aneurysms, all which tend to be endowed with a jet.
Clinical and experimental evidence suggests that these velocity fluctuations could occur in vivo. Several in vivo studies have reported audible bruits or palpable thrills in human IAs [9–11,40,41]. Most notably, Ferguson et al. found an audible bruit in 10 of 17 patients that had an average dominant frequency of 460 ± 130 Hz, and which they attributed to fluid turbulence [9]. However, the same study noted that the “turbulent” flow occurred at a Reynolds number of 400 ± 10 in glass model aiming at representing bifurcation aneurysms. Therefore, this flow, similar to the observed instabilities in our study, may not be truly turbulence. Steiger and Reulen [41] also noted low-frequency fluctuations in the range of 10–30 Hz in intra-operative recordings. Four of our cases showed similar low-frequency fluctuations, but whether they are related to the bruit in vivo requires further investigation. Additionally, as previously suggested [19], higher frequency fluctuations may be suppressed in certain cfd solvers and therefore, such fluctuations must be confirmed in vivo, experimentally, and using different solvers.
This study has several limitations. First, while in vivo blood flow is pulsatile, this study used a constant flow at the inlet boundary to drive the flow dynamics in order to examine the intrinsic flow instabilities. Previous studies have shown that disturbances are suppressed during flow acceleration and amplified during deceleration at the beginning of diastole [7,42], suggesting that the dynamic nature of the inlet waveform may cause unexpected perturbations of the flow. If such instabilities persist in pulsatile flow requires future investigation.
Secondly, we assumed rigid wall in our CFD, while in vivo bruit could be related to the flexible nature of the aneurysm wall [10]. Flow simulation studies based on fluid–structure interaction in aneurysms are difficult due to the lack of patient-specific wall thicknesses and material properties.
Thirdly, for lack of patient-specific flow measurement, we used a typical cycle-averaged MCA inflow rate as inlet boundary condition in all of the cases. It is possible that simulations conducted with a steady flow at peak systolic conditions [17] could change some of the stable cases into unstable cases. Future investigations should scrutinize the inlet flow assumption and what conditions may cause a transition from stable to unstable flow regime. Furthermore, future studies using patient-specific inflow rates and waveforms will help to determine the relevance of flow fluctuations in aneurysm rupture.
Finally, although larger than previous studies, our patient cohort (n = 56) is still rather small and limited to a single center. Moreover, this cohort contains only cross-sectional data of ruptured and unruptured IAs and thus, does not allow us to directly examine the propensity of future rupture.
Conclusions
In this study, we demonstrated that high-resolution CFD, which incorporates second-order spatial and temporal discretization, and high grid and temporal resolutions, are required to detect flow instabilities in IAs. Under these CFD settings, and at a cycle-averaged steady inflow rate, we found flow instability in 8 of 56 MCA aneurysms, all of which were unruptured bifurcation aneurysms. A quantitative measure of these flow instabilities, or aneurysmal fKE, could not differentiate ruptured from unruptured aneurysm. Thus, our study does not lend support to such flow instabilities being a marker for MCA IA rupture. We found a positive correlation between aneurysmal fKE and aneurysm size and as well as size ratio, implicating a possible link of velocity fluctuations to the breakdown of an impingement jet in the aneurysm space.
Acknowlegment
The support and resources for this work were provided from the Center for Computational Research at the University at Buffalo. The authors would also like to thank Kristian Valen-Sendstad and David Steinman for stimulating conversation, and Rob Damiano and Nikhil Paliwal for help in preparation of this manuscript.
The support for this work was partially provided by NIH Grant (No. R01 NS091075-01) and a grant from Toshiba Medical Systems Corp.
Dr. Xiang is the Principal Investigator of NIH Grant (No. R03 NS 090193-01) and co-Investigator of NIH Grant (No. R01 NS 091075-01). Dr. Levy has shareholder/ownership interests with Intratech Medical Ltd and Blockade Medical LLC and is a principal investigator for Covidien U.S. SWIFT PRIME Trials. Dr. Meng is the Principal Investigator of NIH Grant (No. R01 NS 091075-01). Other financial support includes Abbott for carotid training for physicians. The other authors have no other conflict of interests to disclose.
Contributor Information
Nicole Varble, Department of Mechanical , and Aerospace Engineering, , University at Buffalo, , The State University of New York, , Buffalo, NY 14203;; Toshiba Stroke and Vascular Research Center, , The State University of New York, , Buffalo, NY 14203
Jianping Xiang, Toshiba Stroke and Vascular Research Center, , The State University of New York, , Buffalo, NY 14203; , Department of Neurosurgery, , University at Buffalo, , The State University of New York, , Buffalo, NY 14203.
Ning Lin, Department of Neurosurgery, , University at Buffalo, , The State University of New York, , Buffalo, NY 14203; , Department of Neurosurgery, , Weill Cornell Medical , Center/New York Presbyterian Hospital, , New York, NY 10065.
Elad Levy, Toshiba Stroke and Vascular Research Center, , The State University of New York, , Buffalo, NY 14203; , Department of Neurosurgery, , University at Buffalo, , The State University of New York, , Buffalo, NY 14203.
Hui Meng, Department of Mechanical , and Aerospace Engineering, , University at Buffalo, , The State University of New York, , Buffalo, NY 14203; , Toshiba Stroke and Vascular Research Center, , The State University of New York, , Buffalo, NY 14203; , Department of Neurosurgery, , University at Buffalo, , The State University of New York, , Buffalo, NY 14203; , Department of Biomedical Engineering, , University at Buffalo, , The State University of New York, , Buffalo, NY 14203 , e-mail: huimeng@buffalo.edu.
Nomenclature
- =
fluctuation intensity;
- fKE =
fluctuation kinetic energy;
- =
pressure
- =
instantaneous component of velocity ( = 1, 2, 3)
- =
friction velocity at the wall;
- =
fluctuating component of velocity
- =
time-averaged velocity
- =
Cartesian coordinates ( = 1, 2, 3)
- =
shear deformation tensor
- =
viscous length scale;
- =
viscous time scale;
- =
maximum element size
- =
viscosity
- =
kinematic viscosity
- =
density
Abbreviations
- AR =
aspect ratio
- CD =
center differencing, spatial discretization scheme
- CFD =
computational fluid dynamics
- EI =
ellipcity index
- IA =
intracranial aneurysm
- MCA =
middle cerebral artery
- NSI =
nonsphericity index
- SIMPLE =
semi-implicit method for pressure-linked equations, temporal discretization scheme
- SR =
size ratio
- TKE =
turbulence kinetic energy
- UD =
upwind differencing, spatial discretization scheme
- UI =
undulation index
References
- [1]. Vlak, M. H. , Algra, A. , Brandenburg, R. , and Rinkel, G. J. , 2011, “ Prevalence of Unruptured Intracranial Aneurysms, With Emphasis on Sex, Age, Comorbidity, Country, and Time Period: A Systematic Review and Meta-Analysis,” Lancet Neurol., 10(7), pp. 626–636. 10.1016/S1474-4422(11)70109-0 [DOI] [PubMed] [Google Scholar]
- [2]. Wiebers, D. O. , 2003, “ Unruptured Intracranial Aneurysms: Natural History, Clinical Outcome, and Risks of Surgical and Endovascular Treatment,” Lancet, 362(9378), pp. 103–110. 10.1016/S0140-6736(03)13860-3 [DOI] [PubMed] [Google Scholar]
- [3]. Cebral, J. R. , Mut, F. , Weir, J. , and Putman, C. M. , 2011, “ Association of Hemodynamic Characteristics and Cerebral Aneurysm Rupture,” AJNR Am. J. Neuroradiol., 32(2), pp. 264–270. 10.3174/ajnr.A2274 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4]. Jou, L. D. , Lee, D. H. , Morsi, H. , and Mawad, M. E. , 2008, “ Wall Shear Stress on Ruptured and Unruptured Intracranial Aneurysms at the Internal Carotid Artery,” AJNR. Am. J. Neuroradiol., 29(9), pp. 1761–1767. 10.3174/ajnr.A1180 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5]. Shojima, M. , Oshima, M. , Takagi, K. , Torii, R. , Hayakawa, M. , Katada, K. , Morita, A. , and Kirino, T. , 2004, “ Magnitude and Role of Wall Shear Stress on Cerebral Aneurysm: Computational Fluid Dynamic Study of 20 Middle Cerebral Artery Aneurysms,” Stroke, 35(11), pp. 2500–2505. 10.1161/01.STR.0000144648.89172.0f [DOI] [PubMed] [Google Scholar]
- [6]. Xiang, J. , Natarajan, S. K. , Tremmel, M. , Ma, D. , Mocco, J. , Hopkins, L. N. , Siddiqui, A. H. , Levy, E. I. , and Meng, H. , 2011, “ Hemodynamic-Morphologic Discriminants for Intracranial Aneurysm Rupture,” Stroke, 42(1), pp. 144–152. 10.1161/STROKEAHA.110.592923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7]. Valen-Sendstad, K. , Piccinelli, M. , and Steinman, D. A. , 2014, “ High-Resolution Computational Fluid Dynamics Detects Flow Instabilities in the Carotid Siphon: Implications for Aneurysm Initiation and Rupture?,” J. Biomech., 47(12), pp. 3210–3216. 10.1016/j.jbiomech.2014.04.018 [DOI] [PubMed] [Google Scholar]
- [8]. Valen-Sendstad, K. , and Steinman, D. A. , 2014, “ Mind the Gap: Impact of Computational Fluid Dynamics Solution Strategy on Prediction of Intracranial Aneurysm Hemodynamics and Rupture Status Indicators,” AJNR. Am. J. Neuroradiol., 35(3), pp. 536–543. 10.3174/ajnr.A3793 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9]. Ferguson, G. G. , 1970, “ Turbulence in Human Intracranial Saccular Aneurysms,” J. Neurosurg., 33(5), pp. 485–497. 10.3171/jns.1970.33.5.0485 [DOI] [PubMed] [Google Scholar]
- [10]. Olinger, C. P. , and Wasserman, J. F. , 1977, “ Electronic Stethoscope for Detection of Cerebral Aneurysm, Vasospasm, and Arterial Disease,” Surg. Neurol., 8(4), pp. 298–312. [PubMed] [Google Scholar]
- [11]. Sekhar, L. N. , and Wasserman, J. F. , 1984, “ Noninvasive Detection of Intracranial Vascular Lesions Using an Electronic Stethoscope,” J. Neurosurg., 60(3), pp. 553–559. 10.3171/jns.1984.60.3.0553 [DOI] [PubMed] [Google Scholar]
- [12]. Stehbens, W. E. , 1975, “ Flow in Glass Models of Arterial Bifurcations and Berry Aneurysms at Low Reynolds Numbers,” Q. J. Exp. Physiol. Cogn. Med. Sci., 60(3), pp. 181–192. 10.1113/expphysiol.1975.sp002310 [DOI] [PubMed] [Google Scholar]
- [13]. Ford, M. , Nikolov, H. , Milner, J. S. , Lownie, S. P. , DeMont, E. M. , Kalata, W. , Lowth, F. , Holdsworth, D. W. , and Steinman, D. A. , 2008, “ PIV-Measured Versus CFD-Predicted Flow Dynamics in Anatomically Realistic Cerebral Aneurysm Models,” ASME J. Biomech. Eng., 130(2), p. 021015. 10.1115/1.2900724 [DOI] [PubMed] [Google Scholar]
- [14]. Roach, M. R. , Scott, S. , and Ferguson, G. G. , 1972, “ The Hemodynamic Importance of the Geometry of Bifurcations in the Circle of Willis (Glass Model Studies),” Stroke, 3(3), pp. 255–267. 10.1161/01.STR.3.3.255 [DOI] [PubMed] [Google Scholar]
- [15]. Simpkins, T. , and Stehbens, W. , 1973, “ Vibrational Behavior of Arterial Aneurysms,” Lett. Appl. Eng. Sci., 1, pp. 85–100. [Google Scholar]
- [16]. Ford, M. D. , and Piomelli, U. , 2012, “ Exploring High Frequency Temporal Fluctuations in the Terminal Aneurysm of the Basilar Bifurcation,” ASME J. Biomech. Eng., 134(9), p. 091003. 10.1115/1.4007279 [DOI] [PubMed] [Google Scholar]
- [17]. Valen-Sendstad, K. , Mardal, K. A. , and Steinman, D. A. , 2013, “ High-Resolution CFD Detects High-Frequency Velocity Fluctuations in Bifurcation, but not Sidewall, Aneurysms,” J. Biomech., 46(2), pp. 402–407. 10.1016/j.jbiomech.2012.10.042 [DOI] [PubMed] [Google Scholar]
- [18]. Antiga, L. , and Steinman, D. A. , 2009, “ Rethinking Turbulence in Blood,” Biorheology, 46(2), pp. 77–81. 10.3233/BIR-2009-0538 [DOI] [PubMed] [Google Scholar]
- [19]. Khan, M. O. , Valen-Sendstad, K. , and Steinman, D. A. , 2015, “ Narrowing the Expertise Gap for Predicting Intracranial Aneurysm Hemodynamics: Impact of Solver Numerics Versus Mesh and Time-Step Resolution,” Am. J. Neuroradiol., 36(7), pp. 1310–1316. 10.3174/ajnr.A4263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20]. Dhar, S. , Tremmel, M. , Mocco, J. , Kim, M. , Yamamoto, J. , Siddiqui, A. H. , Hopkins, L. N. , and Meng, H. , 2008, “ Morphology Parameters for Intracranial Aneurysm Rupture Risk Assessment,” Neurosurgery, 63(2), pp. 185–196; Discussion 196–187. 10.1227/01.NEU.0000316847.64140.81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21]. Antiga, L. , and Steinman, D. A. , 2004, “ Robust and Objective Decomposition and Mapping of Bifurcating Vessels,” IEEE Trans. Med. Imaging, 23(6), pp. 704–713. 10.1109/TMI.2004.826946 [DOI] [PubMed] [Google Scholar]
- [22]. Antiga, L. , Piccinelli, M. , Botti, L. , Ene-Iordache, B. , Remuzzi, A. , and Steinman, D. A. , 2008, “ An Image-Based Modeling Framework for Patient-Specific Computational Hemodynamics,” Med. Biol. Eng. Comput., 46(11), pp. 1097–1112. 10.1007/s11517-008-0420-1 [DOI] [PubMed] [Google Scholar]
- [23]. Stock, K. W. , Wetzel, S. G. , Lyrer, P. A. , and Radu, E. W. , 2000, “ Quantification of Blood Flow in the Middle Cerebral Artery With Phase-Contrast MR Imaging,” Eur. Radiol., 10(11), pp. 1795–1800. 10.1007/s003300000378 [DOI] [PubMed] [Google Scholar]
- [24]. Oka, S. , and Nakai, M. , 1987, “ Optimality Principle in Vascular Bifurcation,” Biorheology, 24(6), pp. 737–751. [DOI] [PubMed] [Google Scholar]
- [25]. Valen-Sendstad, K. , Mardal, K. A. , Mortensen, M. , Reif, B. A. , and Langtangen, H. P. , 2011, “ Direct Numerical Simulation of Transitional Flow in a Patient-Specific Intracranial Aneurysm,” J. Biomech., 44(16), pp. 2826–2832. 10.1016/j.jbiomech.2011.08.015 [DOI] [PubMed] [Google Scholar]
- [26]. Enzmann, D. R. , Ross, M. R. , Marks, M. P. , and Pelc, N. J. , 1994, “ Blood Flow in Major Cerebral Arteries Measured by Phase-Contrast Cine MR,” Am. J. Neuroradiol., 15(1), pp. 123–129.http://www.ajnr.org/content/15/1/123.abstract [PMC free article] [PubMed] [Google Scholar]
- [27]. Valdueza, J. M. , Balzer, J. O. , Villringer, A. , Vogl, T. J. , Kutter, R. , and Einhaupl, K. M. , 1997, “ Changes in Blood Flow Velocity and Diameter of the Middle Cerebral Artery During Hyperventilation: Assessment With MR and Transcranial Doppler Sonography,” Am. J. Neuroradiol., 18(10), pp. 1929–1934.http://www.ajnr.org/content/18/10/1929.abstract [PMC free article] [PubMed] [Google Scholar]
- [28]. Raghavan, M. L. , Ma, B. , and Harbaugh, R. E. , 2005, “ Quantified Aneurysm Shape and Rupture Risk,” J. Neurosurg., 102(2), pp. 355–362. 10.3171/jns.2005.102.2.0355 [DOI] [PubMed] [Google Scholar]
- [29].CD-Adapco, 2013, “ STAR-CD Methodology,” Ver. 4.2, CD-Adapco, Melville, NY.
- [30]. Boussel, L. , Rayz, V. , McCulloch, C. , Martin, A. , Acevedo-Bolton, G. , Lawton, M. , Higashida, R. , Smith, W. S. , Young, W. L. , and Saloner, D. , 2008, “ Aneurysm Growth Occurs at Region of Low Wall Shear Stress: Patient-Specific Correlation of Hemodynamics and Growth in a Longitudinal Study,” Stroke, 39(11), pp. 2997–3002. 10.1161/STROKEAHA.108.521617 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31]. Chatziprodromou, I. , Tricoli, A. , Poulikakos, D. , and Ventikos, Y. , 2007, “ Haemodynamics and Wall Remodelling of a Growing Cerebral Aneurysm: A Computational Model,” J. Biomech., 40(2), pp. 412–426. 10.1016/j.jbiomech.2005.12.009 [DOI] [PubMed] [Google Scholar]
- [32]. Kim, M. , Ionita, C. , Tranquebar, R. , Hoffmann, K. R. , Taulbee, D. B. , Meng, H. , and Rudin, S. , 2006, “ Evaluation of an Asymmetric Stent Patch Design for a Patient Specific Intracranial Aneurysm Using Computational Fluid Dynamic (CFD) Calculations in the Computed Tomography (CT) Derived Lumen,” Proc. SPIE, 6143, p. 61432G. 10.1117/12.651773 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33]. Jiang, J. , and Strother, C. , 2009, “ Computational Fluid Dynamics Simulations of Intracranial Aneurysms at Varying Heart Rates: A ‘Patient-Specific’ Study,” ASME J. Biomech. Eng., 131(9), p. 091001. 10.1115/1.3127251 [DOI] [PubMed] [Google Scholar]
- [34]. Pope, S. B. , 2000, Turbulent Flows, Cambridge University Press, Cambidge, UK. [Google Scholar]
- [35]. Xiang, J. , Tutino, V. M. , Snyder, K. V. , and Meng, H. , 2014, “ CFD: Computational Fluid Dynamics or Confounding Factor Dissemination? The Role of Hemodynamics in Intracranial Aneurysm Rupture Risk Assessment,” Am. J. Neuroradiol., 35(10), pp. 1849–1857. 10.3174/ajnr.A3710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36]. Byrne, G. , and Cebral, J. , 2013, “ Vortex Dynamics in Cerebral Aneurysms,” arXiv:1309.7875, epub.http://arxiv.org/abs/1309.7875
- [37]. Byrne, G. , Mut, F. , and Cebral, J. , 2014, “ Quantifying the Large-Scale Hemodynamics of Intracranial Aneurysms,” Am. J. Neuroradiol., 35(2), pp. 333–338. 10.3174/ajnr.A3678 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38]. Castro, M. A. , Putman, C. M. , Sheridan, M. J. , and Cebral, J. R. , 2009, “ Hemodynamic Patterns of Anterior Communicating Artery Aneurysms: A Possible Association With Rupture,” Am. J. Neuroradiol., 30(2), pp. 297–302. 10.3174/ajnr.A1323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39]. Cebral, J. R. , Mut, F. , Weir, J. , and Putman, C. , 2011, “ Quantitative Characterization of the Hemodynamic Environment in Ruptured and Unruptured Brain Aneurysms,” Am. J. Neuroradiol., 32(1), pp. 145–151. 10.3174/ajnr.A2419 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40]. Shaaf, M. , Cagle, S. K. , and Farris, B. K. , 1994, “‘ Mickey Mouse’ Aneurysm Presenting With Cranial Bruit: Case Report,” Neurosurgery, 35(3), pp. 509–512; Discussion 512. 10.1227/00006123-199409000-00021 [DOI] [PubMed] [Google Scholar]
- [41]. Steiger, H. J. , and Reulen, H. J. , 1986, “ Low Frequency Flow Fluctuations in Saccular Aneurysms,” Acta Neurochir., 83(3–4), pp. 131–137. 10.1007/BF01402392 [DOI] [PubMed] [Google Scholar]
- [42]. Nerem, R. M. , Seed, W. A. , and Wood, N. B. , 1972, “ An Experimental Study of the Velocity Distribution and Transition to Turbulence in the Aorta,” J. Fluid Mech., 52(1), pp. 137–160. 10.1017/S0022112072003003 [DOI] [Google Scholar]


