Motion robust PPG-imaging through color channel mapping

Abstract

Photoplethysmography (PPG)-imaging is an emerging noninvasive technique that maps spatial blood-volume variations in living tissue with a video camera. In this paper, we clarify how cardiac-related (i.e., ballistocardiographic; BCG) artifacts occur in this imaging modality and address these using algorithms from the remote-PPG literature. Performance is assessed under stationary conditions at the immobilized hand. Our proposal outperforms the state-of-the-art, blood pulsation imaging [Biomed. Opt. Express 5, 3123 (2014). ], even in our best attempt to create diffused illumination. BCG-artifacts are suppressed to an order of magnitude below PPG-signal strength, which is sufficient to prevent interpretation errors.

1. Introduction

Photoplethysmography (PPG) is a non-invasive optical technique to detect blood-volume variations in the microvascular bed of tissue. This is possible because blood has a higher absorption than bloodless skin, so an increase in blood-volume will decrease the intensity of the light reflected from the skin. PPG-based devices have been proven effective to monitor relevant physiological variables that include cardiac activity, respiration and thermal regulation [1]. The standard visualization modality of PPG sensor data is a one-dimensional, time-varying envelope signal. An attractive and more evolving extension of this concept is PPG-imaging; i.e., a modality at which a skin region of interest (RoI) is spanned by a two-dimensional array of PPG sensors. PPG-images are obtained by quantifying the local PPG signal strength or phase shift within each sensor (e.g., by similarity with reference functions or standard deviation [2]).

PPG-images were first described by Verkruysse et al. [3]. They recorded facial skin affected by port wine stains after laser therapy and used the resulting data to obtain maps of the amplitude and phase of the spatially varying PPG signals. Subsequently, others have explored the distinguishing feature of mapping local PPG-data to propose applications for clinical diagnosis and skin perfusion monitoring [4–6]. Of particular relevance is the state-of-the-art blood pulsation imaging (BPI) algorithm [2], whereby PPG-amplitude and phase maps are obtained as the normalized inner-product between a low-noise reference PPG-function and individual sensor-elements over a skin RoI. A limitation, however, is the fact that the illuminator is a green LED. As will be shown in this paper, a punctual light source often amplifies motion artifacts, which is a serious concern in PPG-imaging.

Typical approaches to enhance motion robustness rely on at least one of the following strategies: (a) RoI stabilization by optical flow and/or tracking [7, 8]; (b) provision of invariance to unstable lighting by normalization of signals (i.e., the pulsatile/varying signal component, AC, divided by the albedo, DC, component) in all PPG-image sensors [5]; (c) noise removal by bandpass filtering in a predefined range or “locked-in” at the harmonics of the pulse-rate frequency [2]; (d) correlation with a normalized PPG-reference waveform [5]; and (e) using polarizers both on the cameras and on the illuminators [2, 9]. Another possible signal processing approach to enhance motion robustness is subtraction of the obtained PPG-images by a soft mask for which correction factors are higher at the noisier PPG-sensors (located at contours and high-contrast regions of the image [3]). Similarly, hard masks may be used to prune sensors affected by high-amplitude distortions [7]. Still, none of these alternatives is effective against periodic distortions that are synchronous with remote-PPG signals. Modulation of the reflected light by cardiac related micro-motion of the skin (ballistocardiographic; BCG-motion) is a relevant example. If we do not distinguish these two different signal sources, we cannot make conclusions about local PPG-strength (PPG-imaging), because the BCG signal may locally increase or decrease the PPG-signal.

Micro-motion of the head due to cardiac activity (BCG-motion) was reported by Balakrishnan et al. by using a camera [10], who also demonstrated the feasibility of remotely extracting the pulse rate from hair and even from a mask attached to the face. For a better understanding of the modulation of light by BCG, our group investigated the magnifying effect of the illumination angle on a non-skin (flat, opaque) surface attached to the head. By recording this surface under lateral versus frontal illumination conditions, the strength of the signal changed by almost an order of magnitude. PPG-imaging systems are most susceptible to this kind of artifacts when lighting is neither uniform nor orthogonal, as light flux variations amplify the modulation caused by subtle BCG motions [11]. If arterial motion at the carotid artery is strong enough to cause head motion, it is unsurprising that BCG-motion is also observed in skin sites at the vicinity of arteries, so contamination of PPG-images still needs to be addressed.

In our previous work, we proposed to eliminate BCG-artifacts in PPG-images during image acquisition by preferring orthogonal lighting conditions (e.g., by deploying several diffused light sources around the skin RoI) [11]. However, practical constraints for data acquisition are rarely compatible with the pursuit of perfect orthogonality. This is why canceling motion artifacts during signal processing is advantageous. In this paper, we propose to improve the PPG-image formation pipeline by applying channel-mapping to orthogonalize PPG-signals from BCG-artifacts. To this end, we investigate two established options from the remote-PPG literature: the chrominance (CHROM) [12] and the blood-volume pulse signature methods [13]. Both rely on linear combinations of normalized sensor data in red, green and blue. Recognizing that distortions in normalized RGB signals have the same gain, CHROM seeks to achieve a linear combination of color channels where disturbing motions are cancelled out and PPG data from different color channels is enforced. Conversely, the PBV-method explores the fact that PPG signals have known ratios in the red, green and blue channels. When these are the coefficients of a pulse-blood-volume (PBV) “signature” vector, the least-mean-squared criteria can be suitably applied to separate distortions from actual signals. Despite being conceptually complementary, both map (by linear combination of RGB data) the desired PPG-signals to a direction that is orthogonal to motion artifacts. For this reason, we refer to CHROM and PBV as motion robust channel-mapping methods.

Similar to the BPI imager [2], we extract a reference PPG signal at the palm and obtain PPG-images as normalized inner-product between this reference and the streams from the skin-sensors array. However, we improve motion-robustness over BPI by using data from multiple (RGB) channels—rather than restricting acquisition to the green wavelength—so that the input data can be mapped using the steering weights of CHROM or PBV. The aims of this investigation are twofold: 1) raise awareness to contamination of PPG-images by BCG-artifacts; 2) assess the robustness of our imagers against BCG-artifacts. To this end, we start by demonstrating BCG-artifacts at the human wrist. Then, we describe our proposed algorithms to minimize these and provide benchmarking results against BPI.

2. Materials and methods

2.1. Ballistocardiographic artifacts

To understand the challenges posed by BCG-artifacts, we first derive insights from Lambertian theory. We consider a living skin surface that is subject to cardiac-induced motion. Examples could be skin in the vicinity of arteries (e.g., carotid artery at the neck [3], radial artery at the wrist [14]), or facial skin experiencing cardiac-related head motion [10]. Similar to the BPI imager [2, 14], we will consider the wrist’s skin in the vicinity of the radial artery, as a site for PPG-image acquisition. Figure 1 depicts a convenient choice for the XYZ reference axis, where: skin motion at the vicinity of the radial artery appears mostly as rotation about the X-axis; the XoY plane of the reference axis is tangent to a small skin site in the vicinity of the radial artery; and α (YoZ plane) is the angle between incident light and normal to skin.

Fig. 1.

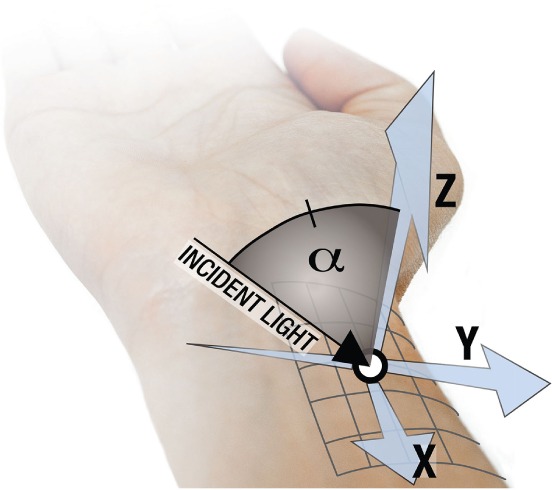
Vicinity of the radial artery as a working scenario for BCG-artifacts in PPG-images.

We assume the absence of voluntary motions and dominance of skin-motion induced by pulse in a single degree of freedom, e.g., rotation about the X axis (nomenclature: θ_X, θ_Y and θ_Z, for the X, Y and Z axis; see Fig. 1). We further assume the light intensity, I, to be constant over the skin surface and that illumination is provided by a punctual, distant light source located in the YoZ plane, resulting in a light incident angle α. Finally, we neglect specular reflections, so we assume that subsurface scattering is the dominant mechanism by which light is reflected from the skin surface to the camera. Using the Inverse Square Law, I is expressed as

$$I=\frac{I_0}{R^2}\Vert {\hat{\mathbf{e}}}_{\mathbf{r}}\cdot {\hat{\mathbf{e}}}_{\mathbf{n}}\Vert ,$$ (1)

where ê_r and ê_n are unit vectors of the incident light direction and surface-normal, respectively, R is distance to source and I₀ is a constant. For distant light sources, small perturbations in R² are negligible, but BCG-motion still influences brightness, I, over the skin RoI by modulating the inner-product ê_r·ê_n. By applying Euler’s rotation theorem, the normal to skin surface ê_n(t) is given by

$${\hat{\mathbf{e}}}_{\mathbf{n}}(t)={\mathbf{R}}_Z({\theta }_Z(t)){\mathbf{R}}_Y({\theta }_Y(t)){\mathbf{R}}_X({\theta }_X(t)){\hat{\mathbf{e}}}_{\mathbf{n},0},$$ (2)

where the sign of the angles is positive for counterclockwise rotation, ê_n,0 = (0,0,1)^T is the baseline normal vector to the surface and R_X, R_Y and R_Z are the rotation matrixes about the X, Y and Z axis, respectively. For convenience, we will omit the explicit time dependence (t) of all signals. The components of ê_n are as displayed in Eq. (3).

$$\{\begin{array}{l}{e}_{n,X}=\cos {\theta }_Z\sin {\theta }_Y\cos {\theta }_X+\sin {\theta }_Z\sin {\theta }_X\hfill \\ e_{n,Y}=\sin {\theta }_Z\sin {\theta }_Y\cos {\theta }_X-\sin {\theta }_X\cos {\theta }_Z\hfill \\ e_{n,Z}=\cos {\theta }_Y\cos {\theta }_X\hfill \end{array}$$ (3)

Recognizing that θ_X, θ_Y, θ_Z are small, the Taylor-series expansion justifies assuming sin(θ_i) ≈ θ_i and cos(θ_i) ≈ 1. By further recognizing that the mixed product term θ_Zθ_Y is much smaller than θ_X, ê_n is rewritten as follows:

$$\{\begin{array}{l}{e}_{n,X}\approx {\theta }_Y,\hfill \\ e_{n,Y}\approx -{\theta }_X,\hfill \\ e_{n,Z}\approx 1.\hfill \end{array}$$ (4)

The average brightness at a RoI over the skin surface, I, can now be expressed as

$$I=(-e_{n,Y}\sin \alpha +e_{n,Z}\cos \alpha )\frac{I_0}{R^2}.$$ (5)

Equation (5) can simplified by particularizing e_n,Y and e_n,Z to (4). Therefore,

$$I\approx ({\theta }_X\sin \alpha +\cos \alpha )\frac{I_0}{R^2}.$$ (6)

It is apparent from (6) that I consists of a constant (“DC”) component and motion-induced, (“AC”) which is modulated by θ_X. So we define the ratio BCG = I_BCG,AC/I_DC as the relative BCG-artifact signal, where I_BCG,AC = θ_X sin αI₀/R² and I_DC = cos(α)I₀/R². BCG reduces to BCG = tan(α)θ_X, from which it can be observed that tan(α) is a factor amplifying rotation w.r.t. the orientation of the light source. As such, the combined effect of BCG-artifacts and PPG signals in brightness intensity recorded in a given camera channel, I_C, is modeled as a mixed product of scattering of light through the skin signals, PPG, and BCG-artifacts:

$$I_C\approx ({\beta }_{C}PPG+1)(BCG+1)\cos \alpha \frac{I_0}{R^2},$$ (7)

where β_C is a parameter characterizing relative spectral reflectance in the camera channel C. Because β_C PPG and BCG are small, it is reasonable to arrive at the following approximation for the polluted signal in each camera sensor:

$$I_C\approx ({\beta }_{C}PPG+BCG+1+n_{AWGN,C})\cos \alpha \frac{I_0}{R^2},$$ (8)

where the mixed product term β_C PPGBCG ≪1 was neglected and $n_{AWGN,C}~(0,{\sigma }_C^2)$ stands for additive white Gaussian (AWGN) noise. In the absence of voluntary wrist motions, the term cos αI₀/R² is constant and easily removed when I_C is normalized to AC/DC, resulting in i_C:

$$i_C\approx {\beta }_{C}PPG+BCG+n_{AWGN,C}.$$ (9)

Note that the above formulation has implications for all wavelengths; i.e., BCG motion artifacts are intensity variations that affect all wavelengths in the same relative amount. This property holds, irrespective of whether illumination is provided by a single point source, or if multiple point sources coexist. Stated another way, diffuse light-sources and pixel-averaging cannot change the fact that motion changes the intensity (but not the chrominance) of the reflected light.

From Eq. (9), it is apparent that recovering PPG from i_C requires PPG-imagers to eliminate sensor noise and BCG-artifacts. However, like PPG signals, artifacts are periodic and related with the pulse-rate, so addressing artifacts is not as straightforward as noise and random motion distortions. Indeed, for non-cardiac related sources, methods can safely rely on the periodicity of the desired PPG-signal, and assume that noise and interferences have a Gaussian distribution. Examples range from simply filtering in the spacial or temporal domains to independent component analysis [15] and maximum ratio combining [7]. Unfortunately, however, these strategies will likely recover a scaled version of the compound signal f = β_C PPG+BCG, rather than β_C PPG. One might argue that this is generally not a problem in the remote-PPG domain, where the goal is to determine pulse-rate. So BCG-artifacts enforcing PPG are actually beneficial for performance, whereas signal loss at skin sites where artifacts are in opposition of phase with PPG is compensated by the fact that PPG-image sensors are merged to a large skin region-of-interest (RoI) [16]. However, when it comes to PPG-imaging, accurately quantifying PPG-amplitude at every skin site is paramount.

At this stage, it is reasonable to ask whether the magnitude of the artifact component (BCG) in each sensor-element is indeed strong enough in comparison with the intended signal, β_C PPG, and, if so, what options are there to promote robustness against BCG-artifacts. Clearly, if illumination would be perfectly uniform, there would be no dependence on the angle between normal to skin and lighting. Consequently, the inner-product term, ∥ê_r·ê_n∥, would be absent from Eq. (1) onwards and micro-motion would not affect skin brightness. Even when the illuminator is a single punctual light source, BCG-artifacts are still ameliorated if the source is distant and orthogonal to the skin surface (i.e., the tangent of the incident angle amplifying BCG is minimized). Proper illumination for PPG-image acquisition comes with the added benefit of robustness against other sources of motion noise. Yet, this may not be always possible to achieve since the skin is generally curved.

An additional strategy to eliminate BCG effects in PPG-imaging may start by recognizing that motion artifacts have no wavelength dependence, whereas remote-PPG signals do. These are the principles of CHROM and PBV, which have been proven effective at separating remote-PPG signals from motion sources and form the core of our motion robust imagers, further referred to as CHROM-imager (CHROMi) and PBV-imager (PBVi).

2.2. Motion robust channel-mapping methods

2.2.1 Chrominance-based method (CHROM)

CHROM was designed to estimate the pulse-rate from the chrominance (i.e., channel differences) of the skin [12]. The output signal is as follows:

$$S_{CHROM}=X_f-\alpha Y_f,\text{with}\alpha =\frac{\text{std}(X_f)}{\text{std}(Y_f)},$$ (10)

where X_f = R_f − G_f and Y_f = R_f/2 + G_f/2 − B_f are orthogonal chrominance-based signals with subscript (f) denoting filtering around the fundamental (and possibly multiples) of the pulse-rate frequency. The adjustment parameter α accounts for imprecision in skin-tone standardization; otherwise, α takes the value of one. Since motion artifacts have the same intensity in the normalized RGB channels of the video camera, the contributions of BCG or other interfering motions cancel out in the resulting chrominance signal. The correctly mapped signal, S_CHROM, is a linear combination of the PPG signal components in RGB:

$$S_{CHROM}=PP{G}_f\left[3(1-\alpha /2){\beta }_R-2(1+\alpha /2){\beta }_G+3\alpha /2{\beta }_B\right]+n_{RGB},$$ (11)

where n_RGB is the equivalent sensor noise after band-pass filtering and linear combination according to Eq. (10), and β_C, C ∈ {R,G,B}, translates wavelength dependence of PPG strength.

2.2.2 Blood-volume pulse signature method

The relative PPG-amplitude as a function of wavelength, λ, is determined both by the optical contrast of blood and bloodless skin, and the penetration depth of the light. The spectrum of the reflected PPG signal is a combination of the absorption spectra of the oxygenated arterial blood and that of the microvascular bed of tissue, normalized by the baseline non-pulsatile component. The relative-PPG spectrum is wavelength-dependent and peaks around 550 nm (i.e., green region of the spectrum). The simulations of [17] further indicate that the pulsatile activity in green is stronger than in red. For green, there is much less light being reflected from deeper skin layers, but the contrast with the skin is much higher than for red. More recently, the simulations of Huelsbusch have also been used by de Haan et al. [13]. Recognizing this physiological property as an opportunity, Haan et al. derived the PBV-method which exploits the characteristic relative strength—referred to as “signature”—of normalized PPG-signals in multiple wavelengths or regions of the spectrum.

Since economy RGB-cameras incorporate Bayer filters (central frequencies: about 450 nm, 550 nm and 650 nm; channel bandwidth: about 100 nm), these can be used as a low-cost multispectral cameras, providing input to the PBV-method. In this case, the signature for the relative-PPG signal is a three-dimensional vector whose components are the root-mean-squared standard deviation (STD) of the PPG signal’s amplitude in the normalized R, G and B channels. We denote this vector as p_bv = (p_R, p_G, p_B)^T or p_bv = κ(β_R, β_G, β_B)^T, where κ is factor normalizing the L2-norm of p_bv to unity.

In this paper, p_bv was determined experimentally as the standard deviation of the fundamental of the normalized signals in the R, G and B channels. Since the p_bv-vector is not subject dependent, it could be calculated from one subject only. However, care was required to minimize sensor noise and motion interference. Note that sensor noise is different in all channels, but is zero mean and Gaussian distributed. Conversely, the corruption by motion changes the intensity of the light entering the skin by changing distance to the light-source, or, more importantly, by changing the orientation of the skin-surface with respect to (w.r.t.) the light-source. Motion distortions are identical for all wavelengths. Although we recognize that using the STD operator as a primary source for estimating the PPG amplitude in RGB will likely cause a bias error (particularly for the smaller amplitude red channel), we were still able to ameliorate the problem by considering a reasonably long recording of the palm lasting about 2 minutes (sampling rate, 20 Hz). Additionally, the strides were normalized as AC/DC and filtered to the fundamental of the pulse-rate. We hoped to minimize motion distortions in our estimate of the amplitude ratios in RGB (i.e., the PBV-vector) by acquiring videos under homogeneous lighting conditions and by mechanical stabilization of the fingers (see section 2.3 for details).

Having p_bv, the task of optimally separating PPG signals from motion-related interferences can be formulated as a least mean squares (LMS) problem:

$$S_{PBV}{\mathbf{M}}^T={{\mathbf{p}}_{\mathbf{bv}}}^T$$ (12)

where M = [R_f, G_f, B_f]^T is an augmented matrix constructed by combining strides of filtered and normalized red, green and blue data. Since strides may be required to last 10–20 sec [12], L can easily exceed 200 samples on a sampling frequency of 20 Hz. This is why the pseudoinverse of M^T, required to solve Eq. (12), is better avoided by prior computation of the covariance matrix of M, S = M^T M, size (3 × 3). The LMS problem is now restated as follows:

$$S_{PBV}={{\mathbf{p}}_{\mathbf{bv}}}^T{\mathbf{S}}^{-1}{\mathbf{M}}^T$$ (13)

The compound product W_PBV = p_bv^T S⁻¹ [Eq. (13)] is the (three-dimensional) steering weight vector of the PBV-method. Once determined for a specific illuminator and recording settings, W_PBV correctly maps PPG data irrespective of the characteristics of subject, skin site or kind of interfering motions.

2.2.3 Pitfalls of adapting remote-PPG algorithms to PPG-imaging

In order to achieve motion-robustness in imaging by channel mapping, care should be taken w.r.t. signal-to-noise ratio (SNR) of PPG-images and proper calibration of CHROM and PBV.

Resolution vs. SNR

Given the noise specifications of a camera, PPG-imaging involves balancing spatial resolution and SNR of the PPG-image. On one extreme, an imager may output PPG-images with low spatial resolution, but low quantization noise in each image sensor. Conversely, the PPG-image may be large so as to account for the spatial variations within a body region, but the PPG-signal will be more affected by noise. Sensor noise is a less serious problem in remote-PPG literature than it is for imaging, as the skin RoIs for signal extraction are made as large as the input video allows. In the remote-PPG literature efforts are directed to coping with specular reflections, large body motions or challenging lighting conditions. Thus, stride processing with a window length, L, as short as 32–64 samples (at a sampling frequency within 15–30 Hz) has been recommended for heart-rate detection. However, when it comes to PPG-imaging, a calibration test is advised to ensure the suitability of L (see Section. 3.1.1).

Calibration of the steering weights of CHROM and PBV

Large body motions are common in remote-PPG applications, but PPG-imaging protocols typically require subjects to remain still during recordings and the contribution of skin motion to the received signal can be small. Consequently, determining α = std(X_f)/std(Y_f) in CHROM and S⁻¹ in PBV becomes numerically unstable. This potential threat may be overcome by introducing the effect of a pulsating light source, which is equivalent to adding AWGN noise, $l_{\text{added}}~(0,\sqrt{(}N))$, to the data from a reference skin RoI, $I_C^{\text{ref}}$, with C ∈ {R, G, B}. Mathematically:

$$I_C^{\text{ref}}\approx (1+{\beta }_{C}PPG+n_C^{\text{ref}})\cos \alpha \frac{I_0}{R^2}[1+l_{\text{added}}].$$ (14)

As long as l_added ≪ 1, Eq. (14) is approximated by

$$I_C^{\text{ref}}\approx (1+{\beta }_{C}PPG+l_{\text{added}}+n_C^{\text{ref}})\cos \alpha \frac{I_0}{R^2}.$$ (15)

As before, we proceed by expressing the received signal in each channel as normalized AC/DC; i.e., the fraction of the pulsatile variation over the mean signal intensity, so that the obtained signal, $i_C^{\text{ref}}\approx ({\beta }_{C}PPG+l_{\text{added}}+n_C^{\text{ref}})$, is made independent of the illuminator’s intensity, I₀, and location. The steering weights of PBV are obtained from the data matrix $M=[i_R^{\text{ref}}{i}_G^{\text{ref}}{i}_B^{\text{ref}}]$. Finally, the covariance matrix for the reference skin RoI, S^ref−1, is stabilized, and so is W_PBV = p_bv^T S^ref−1 [Eq. (13)]. Likewise, α of CHROM is corrected if X_f and Y_f are obtained from $i_R^{\text{ref}}$, $i_G^{\text{ref}}$ and $i_B^{\text{ref}}$. In practice, a calibration stage is required to compute the steering weights for PBV and CHROM (W_CHROM = [3(1−α/2);−2(1+α/2);+3α/2]; See Eq. 16 of [12]). To this end, $I_C^{\text{ref}}$ should be obtained from a large reference skin RoI, where a parameter regulating the noise gain of l_added is increased until optimal results are achieved. For example, in this investigation, data was acquired at a reference RoI in the subject’ s palm and the noise gain factor affecting light modulation, N, was varied from 0.0 to 0.1. Figure 2 provides a geometrical view of the calibration process for CHROMi and PBVi. As the strength of multiplicative noise increases, the trajectories defined by the weight vectors converge to the plane for which the sum of its components amounts to zero; i.e., W_R +W_G + W_B = 0. As such, artifacts have the same gain in normalized red, green and blue and are eliminated in the output signal.

Fig. 2.

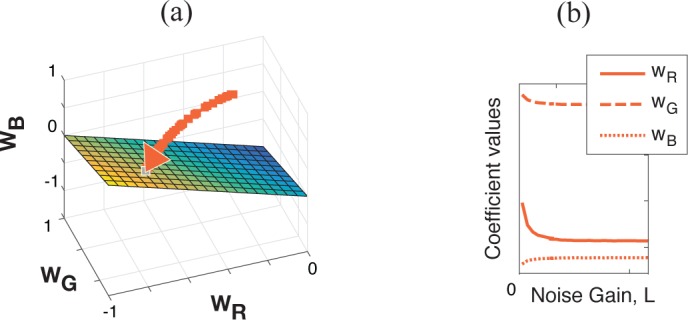
The normalized weight vectors of the color channel mapping methods converge to the W_R +W_G +W_B = 0 plane for increasing noise gain of the modulated light, L. Visualization (a) in the RGB space and (b) coefficient values as a function of L.

Note that the final weights for PBVi and CHROMi may differ. For these methods to have same units as BPI, i.e., AC/DC units of the green channel, PPG-images need to be scaled by the factors $C_{PBV}=1/({\mathbf{W}}_{\mathbf{PBV}}^{\mathbf{T}}{\mathbf{p}}_{\mathbf{bv}})$ and $C_{CHROM}=1/({\mathbf{W}}_{\mathbf{CHROM}}^{\mathbf{T}}{\mathbf{p}}_{\mathbf{bv}})$.

2.3. Motion-robust PPG-imaging framework

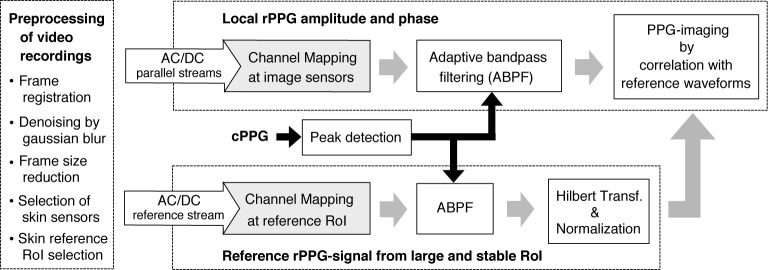
This section describes our framework for PPG-imaging (see Fig. 3), where the input signals originate from channel mapping. Similar to BPI, our imagers are offline MATLAB implementations whose core components are a reference PPG-signal and an sensor-element array.

Fig. 3.

Framework of the proposed motion robust PPG-imagers. After frame preprocessing, remote-PPG (rPPG) signals are acquired in each sensor-element, mapped according to CHROM or PBV algorithms (gray box), and correlated with a reference PPG signal from the palm. The instantaneous pulse-rate is obtained by contact PPG (cPPG).

Preprocessing

First, we registered frames w.r.t. the central frame of the video sequence. We used the RealTITracker toolbox [18], which implements the Horn-Schunk algorithm to ensure stabilization against small movements, even at wrinkles and contours of the skin. The resulting frames were subsequently denoised by Gaussian blurring (kernel size, 45) and reduced in size, horizontally and vertically, by a factor of 5. Each pixel in the obtained images will be referred to as a sensor-element. Finally, skin sensors were segmented from background (dark, textureless) by color thresholding and a large reference skin RoI (RoI Skin) was manually demarcated at the palm.

Reference remote-PPG-signal

To obtain a reference remote-PPG (rPPG) signal, a raw RGB stream was extracted from a user-defined RoI at the palm. The reference signal was first lowpass filtered to extract its “DC” component (9th order Butterworth filter; cutoff frequency, 20 bpm) and normalized as AC/DC. The signals were processed in strides of 128 samples (corresponding to about 10 cardiac cycles) with an overlapping factor of 50%. Each stride was detrended, multiplied with a Hanning window and filtered in the frequency domain by selection of heart-rate component(s). The heart-rate measurements from pulse oximetry were used to select either one or three harmonics of the heart-rate. We refer to this strategy as adaptive bandpass filtering (ABPF). The signal was then linearly combined according to the PBV or CHROM steering weights, Hilbert-transformed and normalized to unit norm as $\Sigma \mathit{\text{Re}}[{\tilde{x}}_{\text{ref}}]{\tilde{x}}_{\text{ref}}=1$.

Local rPPG amplitude

The initial processing stages in each sensor-element are similar to those of the reference remote-PPG-signal, i.e., the raw RGB streams in each column m and line n of the sensor array were normalized to AC/DC, mapped according to CHROM or PBV and adaptively bandpass filtered. The value of the PPG-image at (m, n) is the normalized innerproduct between X_Skin and s_m,n; i.e, $PPG{I}_{m,n}=\sqrt{2/L}{\Sigma }_{l=1}^L{s}_{m,n}(l){\tilde{x}}_{\text{Ref}}(l)$.

2.4. Performance assessment

2.4.1 Benchmarking algorithm

BPI [2] is the benchmarking algorithm considered in this investigation. We did not implement BPI’s latest version [5] because the reference PPG-signal is modeled as a trellis of handcrafted triangular waveforms, so modeling error would occur when remote-PPG waveforms have prominent dichrotic notches, particularly with children [19], or under alternative protocols where the hand would be lowered below the heart level [20].)

2.4.2 Subjects and experimental protocol

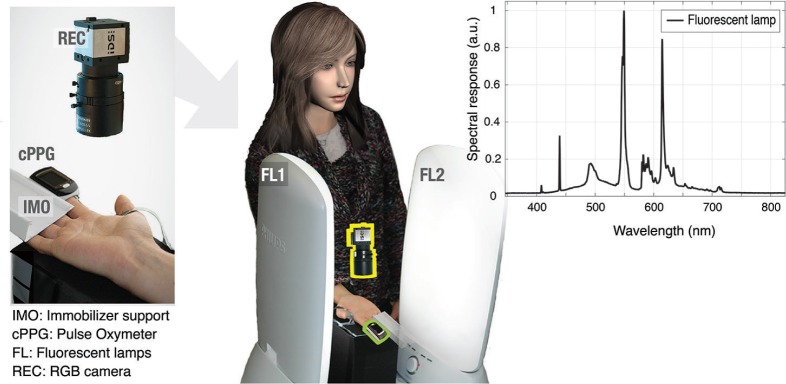
The performance of all imagers was evaluated in recordings from 7 subjects (ages, 25 to 40 yrs; gender: 6 males, 1 female). The study was approved by the Internal Committee Biomedical Experts of Philips Research and an informed consent was obtained from each subject. An RGB camera (model USB UI-2230SE-C, IDS, Germany; global shutter, CCD, 8 bits per color channel) and a pulse oximeter (model CMS50E, Contec, China) were synchronized and the recordings stored in an uncompressed data format (frame rate, 20 Hz; frame size, 520 × 400 pixels).

Figure 4 depicts the setup for data acquisition. Subjects were asked to sit and have their hand immobilized, about 20 cm below the level of the heart, with the palm facing the ceiling. To minimize non-cardiac movements, explicit instructions were given to avoid voluntary hand movements during recordings. Illumination was provided by fluorescent lamps (model HF3319/01, Philips). These were used to implement the contrasting situations of nearly homogeneous versus somewhat lateral lighting conditions. For the rest of this paper we shall briefly talk of “lateral” and “homogeneous” illumination. The area of both light sources (about 50 cm × 25 cm) is large in comparison with the hand. When only the right-side lamp was active, the illuminating pattern was identified as lateral. Adding the second illumination surface yields a good attempt to realize diffuse illumination although we emphasize that is it not perfect. The fluorescent lamps have discrete peaks at red, green and blue (about 440 nm, 550 nm, and 625 nm, respectively; see Fig. 4), which is beneficial to minimize inter-channel interference.

Fig. 4.

Setup for PPG-image acquisition at the palm and wrist.

To minimize specular reflections, a cross-polarization strategy was implemented by covering the illuminators and objective of the camera with linear polarizing film. Note that addressing the issue of specular reflections does not eliminate the issue of BCG-motion per se; BCG-motion is not only about specularly reflected light, but also about diffusely reflected light. The latter is affected by orientation changes of the skin-surface, which modulates the amount of incoming light. Consequently, all signal components (also the diffusely reflected light) are modulated. Hence, polarizing strategies alone cannot solve BCG effects, although these effects would possibly be more severe if the polarizers were not used.

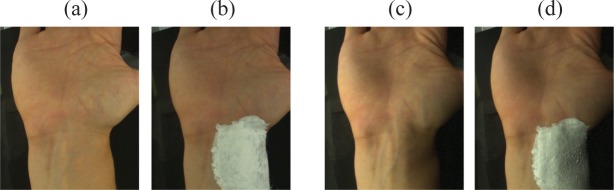
Four consecutive recordings of 2 min each were performed for uniform and lateral lighting conditions, with and without pen corrector ink over the skin in the vicinity of the brachial artery (see Fig. 5). The purpose of the recordings where skin was covered by opaque ink was to isolate BCG-artifacts, so that the artifact cancellation performance of imagers could be quantitatively compared (see Section 2.4.3). The normal-skin recordings were used to confirm PPG-images for each subject.

Fig. 5.

Recordings acquired using (a-b) homogeneous and (c-d) lateral illumination.

2.4.3 Bechmarking metrics

Unfortunately, there is no ground truth method to evaluate the agreement of PPG-imagers. However, it is still possible to evaluate the proposed imagers based on artifact cancellation performance by devising a protocol that isolates the BCG component in a skin site. To this end, we took the skin covering the brachial artery as a convenient RoI (see Fig. 5(b) and 5(d)). This region shows strong pulse-induced skin motion, as confirmed visually under lateral lighting conditions and further by Wu et al. using the Eulerian video magnification algorithm [21]. We performed consecutive recordings where BCG-artifacts are minimized or amplified by recreating, respectively, homogeneous and lateral lighting conditions. In all recordings, the skin at the vicinity of the brachial artery was covered by opaque ink to ensure that the measured amplitude in (polluted) PPG-images at a RoI defined over ink (ROI_Ink) was due to BCG-artifacts only. BCG-artifact cancellation is assessed by quantifying the normalized root mean squared (NRMS) error of the PPG-images at the ROI_Ink. Normalization is done by dividing absolute RMS-errors by the RMS PPG-signal strength, measured at the palm under homogeneous illumination conditions. As such, despite the inherent effort of acquiring data twice at a number of subjects, the assessment procedure based on the normalized RMS error does not require estimates of the PPG signals at the inspection sites and effectively allows quantifying the remnant energy of BCG-artifacts after attempts to compensate for it.

3. Results

3.1. Preliminary tests

3.1.1 Defining the window length

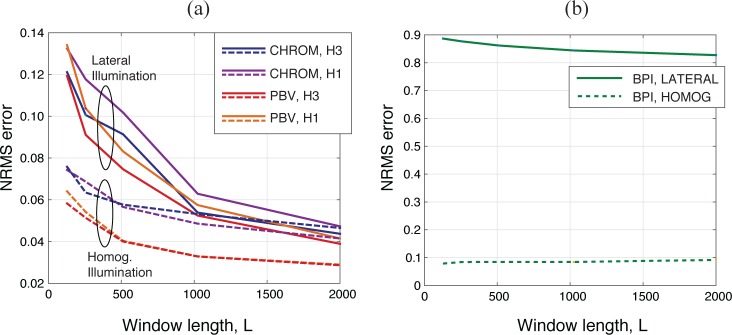
As shown in Fig. 6(a), when the window length is increased from 128 to 2000 frames (sampling rate, 20 Hz), the normalized RMS error (defined in Section 2.4.3) in CHROMi and PBVi decays by the inverse of the window length. This holds true when the methods use filtered versions of the PPG signals with only the fundamental of the pulse-rate (“1H”), or three harmonics (“3H”). Although 1000 frames would already provide a good tradeoff between computational load and performance, taking all the 2000 frames available provides best results and is, therefore, our choice to evaluate CHROMi and PBVi. For the same settings, the normalized RMS error of BPI does not show a decaying tendency; malfunctioning is particularly critical under lateral illumination, irrespective of window length (see Fig. 6(b)).

Fig. 6.

Effect of window length on the NRMS error of (a) the proposed imagers and (b) BPI. CHROMi and PBVi are implemented with one vs. three harmonics of the pulse-rate (H1 vs. H3) and tested at the wrist under homogenous and lateral illumination conditions.

As also seen in Fig. 6(a) and 6(b), under nearly homogeneous illumination conditions, artifact suppression can be achieved with less frames and the BPI error is minimized. This translates to the observation that, as long as temporal-spatial averaging are adjusted so as to minimize sensor noise, CHROMi and PBVi provide more reliable results than its single-channel counterpart, BPI, even under nearly homogenous lighting conditions.

3.1.2 Artifacts in the vicinity of the brachial artery

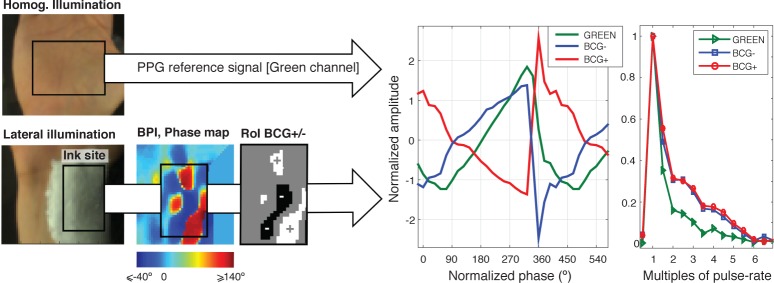
Figure 7 shows average waveforms for artifact signals extracted from a ROI_Ink at the wrist. For comparison, the average PPG waveform from the reference RoI at the palm (green channel) was also included in the plot. BCG and PPG signals were obtained from two consecutive recordings of the same subject, under homogeneous and lateral lighting conditions. The left part of Fig. 7 shows sample frames for each (top, homogeneous; bottom, lateral). As in section 2.3, signals were normalized in amplitude as AC/DC. Cycles were demarcated by using the peaks provided by contact-PPG, rescaled to unit standard deviation per cardiac cycle and resized to 23 samples per cycle. We followed the convention that 0 – 23 samples corresponds to a range of 360 degrees. When the same average waveform is repeated twice for visualization purposes, the scale of the repetition waveform ranges from 360 to 720°.

Fig. 7.

Sample average BCG and remote-PPG waveforms acquired at the green channel at the wrist and palm, respectively [Subject A]. BCG waveforms may be in phase or in phase-opposition, and are morphologically different from the reference remote-PPG.

The RoIs for extraction of counter-phase BCG-artifacts were refined by selecting sensors that correspond to hotspots and coldspots in the BPI phase maps. User-defined thresholds of ≤−40 and ≥140 were applied to query the opposing BCG− and BCG+ signals The application of the BPI maps as scores map, and the corresponding selection mask is illustrated at the middle panel of Fig. 7. It is unequivocal that BCG-artifacts have different waveforms from remote PPG signals in green, and are either in-phase or opposite-phase, depending on the orientation of the skin-surface w.r.t. the light-source (confirmed by the overlap of the amplitude spectrum for in-phase and opposite phase artifacts). BCG waveforms have a sharper systolic slope than PPG-green at the palm. The FFT spectrum further confirms the higher harmonic content of the BCG signals in comparison with its PPG counterpart from the palm.

3.2. PPG image formation

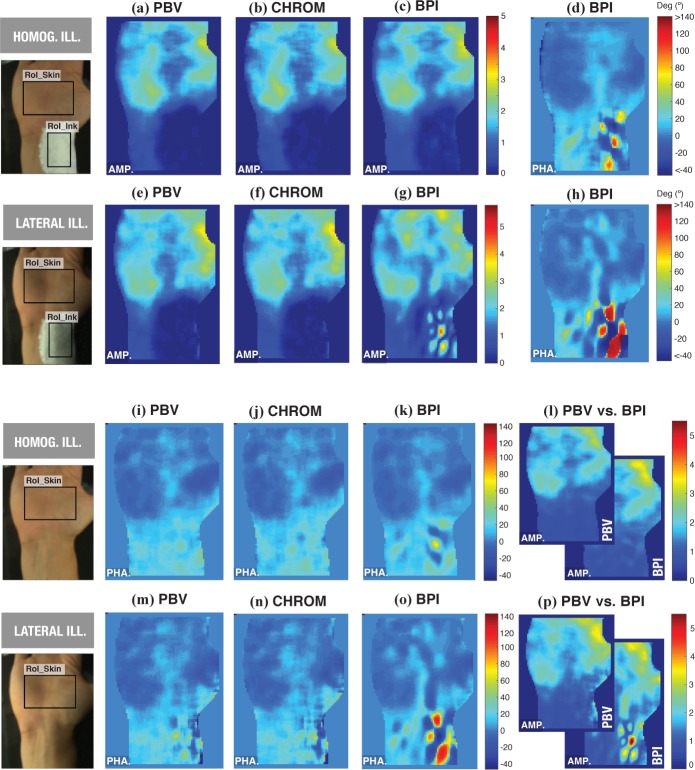
Figures 8(a-p) are PPG amplitude and phase maps obtained for one subject (A: female, 30 yrs), using the proposed channel mapping algorithms, side-by-side with BPI under homogeneous and lateral lighting conditions. The efficacy of lighting conditions to minimize BCG-artifacts is the first observation suggested by the contrast of this set of images. Clearly, lateral lighting conditions cause stronger BCG effects in the vicinity of arteries. Still, even under homogeneous illumination, BCG patterns at the wrist remain visible. Depending on the selected body-part, orthogonal illumination may be very hard to achieve, particularly for curved skin-surfaces. Whereas BPI is unable to cope with this interference, channel mapping algorithms robustly cancel out this interfering source, though inaccuracies may occur, particularly under lateral lighting conditions, when the average brightness at a skin site is low and/or the magnitude of artifacts is much stronger than PPG.

Fig. 8.

PPG amplitude (“AMP.”) and phase (“PHA.”) images, obtained using CHROM, PBV and BPI under homogeneous and lateral lighting conditions [Subject A].

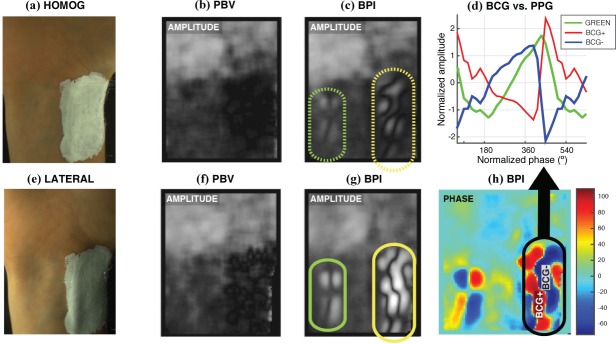
We assessed, qualitatively, the efficacy of artifact-cancellation by PBVi and CHROMi in the remaining subjects from our database. For example, Fig. 9 illustrates results for a test subject (B: male, 27 yrs) whose BCG-artifacts occurred in the vicinity of both the brachial and ulnar arteries. As before, whereas BPI amplitude maps are polluted, the CHROM and PBV imagers efficiently removed these artifacts from the ink RoI. Also included are average waveforms obtained in the vicinity of the brachial artery, by merging ink sensors of cold and hotspots in phase maps from BPI (named BCG− and BCG+, respectively). It can be observed that the BCG− and BCG+ waveforms are in opposition of phase with one another and contain more energy in higher-order harmonics than PPG signals. The observation that the palm has stronger PPG- signals than the wrist was confirmed in the remaining five subjects from our study. Similarly, although the skin motion patterns observed in phase maps are highly varying among subjects, 180-degree phase phase shifts are systematically strong over the brachial artery.

Fig. 9.

BCG-artifact patterns contaminate BPI amplitude maps, but are correctly eliminated by the PBV-imager [Subject B].

3.3. Artifact suppression performance

Table 1 summarizes the NRMS errors measured at the wrist (ROI_Ink) on recordings from the 7 subjects measured in this study. Only recordings containing ink on the inspection site were analyzed. This procedure allows isolation of the interfering source. BPI is compared with the CHROM and PBV imagers, under contrasting illumination conditions. The benefit of considering three harmonics of the cardiac rate frequency, rather than the fundamental only, was further taken into comparison. It is clear that, under the challenging lateral lighting conditions, both CHROMi and PBVi improve over BPI by an order of magnitude and keep artifacts within less than 5% (AC/DC) of the rPPG average amplitude at the palm. Under homogeneous illumination conditions, channel mapping offers a threefold benefit and contributes to the best performance of this comparative study. A last observation is that higher-order harmonics of the pulse-signal improve performance, though only marginally.

Table 1.

Normalized RMS-Error in PPG-Images at a Non-skin RoI

Illumination	PBVi (%)		CHROMi (%)		BPI (%)
	1H	3H	1H	3H	1H
Homogeneous	2.2±1.1	2.6±1.1	2.1±0.9	2.5±1.1	6.5±0.8
Lateral	4.5±1.8	4.9±2.2	4.1±1.9	4.6±2.1	31.2 ±13.3

Accronyms and abbreviations: BPI, Blood Pulsation Imager, CHROMi, Chrominance-based imager; PBVi, p_bv-signature Imager; 1H/3H, one/three harmonics of the pulse-rates.

4. Discussion

This paper considers, for the first time, cancellation of ballistocardiographic artifacts in remote PPG-images by means of signal processing. As this kind of motion is synchronous with the cardiac signal, common strategies to enhance the motion robustness are ineffective against this interfering source, and risks are that artifacts are confounded with actual PPG signals. BCG-artifacts in PPG-images have only been recognized as such by Verkruysse et al. [3] and Blanik et al. [6], and, so far, only our previous work was conducted to minimize this problem by means of proper illumination during image acquisition.

In this paper, we took a step further for improving validity of PPG-images by demonstrating that two motion-robust channel mapping algorithms previously reported for heart-rate detection in the remote-PPG literature, namely CHROM and PBV, can be extended to imaging. These offer the promise of eliminating motion sources in remote PPG sensor-elements, irrespective of whether they are cardiac-related or from other sources, with the added benefit of compensating artifacts resulting from non-orthogonal illumination in curved skin-surfaces. However, CHROM and PBV were validated for pulse-rate measurements, but not for multi-point amplitude and phase measurements. Since the sensor sub-RoIs of the PPG-images are small in comparison with the (merged skin) RoIs used for a single point estimates in the remote-PPG literature, additional measures to overcome the penalty in signal-to-noise ratio. In this regard, our core innovation resides in extracting the weights of the PBV and CHROM papers from the reference palm, which were, subsequently, applied at all sensors locations in the skin. Because the palm may be static and, consequently, contain little motion distortion, we proposed to artificially modulate the intensity of the illuminator so as to mimic interference and overcome the instability of the least-mean-squares method to provide steering weights to separate motion from PBV signal.

Performance gains resulting from motion robust channel-mapping are cumulative with additional practices or signal processing approaches aiming at improved PPG-image formation. The overall procedure taken in this investigation consisted of three steps: 1. demonstrating BCG-artifacts at the wrist, 2. proposing channel mapping to eliminate motion artifacts in PPG-images, and 3. assessing the proposed imagers against BPI.

Eliminating BCG-artifacts by channel mapping

Our first insights were derived from waveforms of sensors over skin covered by opaque ink, in the vicinity of the brachial artery, as well as from non-corrected PPG-images containing this site. This allowed us to confirm that artifacts are magnified under lateral illumination and are clearly visible as hotspots in PPG-amplitude maps and as neighboring cold/hotspots in phase maps from the BPI-imager. From Fig. 7 and Fig. 9, we were further also able to observe the shape resemblance and phase-inversion of the average waveforms for BCG+ and BCG− sensors, which confirms that phase opposition in polluted BPPs reflects the pulse-related displacement of the (curved) skin w.r.t. the light source. The joint representation of the normalized Fourier coefficients for remote-PPG signals (a surrogate of blood-volume variations at the capillary bed) and BCG-artifacts (a surrogate of arterial motion) further confirms that these signals are slightly different and must not be confused.

The importance of the finding that PPG and BCG have different shapes must not be underestimated, as the validity of the complex inner product as a principle to measure phase is threatened. Even when BCG signals are not in sign opposition with PPG, the result of computing phase maps by using the Hilbert operator (complex inner product) will be affected by apparent phase lags which are just caused by changes of the pulse-shape due to different fractions of BCG and PPG signals. Removing the BCG-fraction, eliminates this source of phase-errors.

Using the same recordings, we demonstrated the feasibility of concealing BCG-artifacts by mapping normalized data from the PPG sensor-elements prior to forming PPG-images. Using our CHROM- or PBV-based imaging frameworks, we observed that the PPG-amplitude in the palm region is stronger than at the wrist, for all subjects. In the corrected phase images, we observed differences, in the order of 20–30 degrees, between the center of the palm and wrist, and the periphery of the palm; these are largely independent of illumination conditions, i.e., lateral or homogeneous illumination show similar results. Pulse-induced skin motion patterns are most prominent under non-uniform lighting conditions, though, to a minor extent, BCG-artifacts also occur under uniform lighting conditions, at high spatial frequency sites, as are edges, wrinkles, and even the texture of the skin. In this investigation, both algorithms performed comparably. In practical scenarios, the preference from one method over the other should depend upon the relative ease of estimating the blood-volume pulse vector, p_bv, or the trust in the assumed “standard skin-tone vector”. We further assessed performance benefits resulting from the inclusion of two additional harmonics of the pulse-rate frequency and found that it resulted in just marginal improvements in detail and NRMS performance of the resulting PPG-images.

Implications for earlier publications

Migraine

The interpretation of our motion-corrected PPG-maps and BCG maps suggests that the local phase shifts in blood pulsation phase maps (BPP), obtained using BPI imagers, reflects spatially-varying enforcement/attenuation in each sensor by BCG-signals, depending on the incident angle of light w.r.t. skin-surface. It is, therefore, surprising that artifact-contaminated BPP maps have been shown successful as biomarkers of the migraine pathophysiology [9]. Although the test-set may be too small to rule out accidental correlation, lateral inversion of average waveforms in migrainers was significant and the side-to-side lateralization of blood perfusion was attributed to dysfunction of the autonomic vascular control in the face. Since no attempt was made in the migraine study to distinguish between BCG and PPG signal, the phase maps cannot be trusted, although we admit that without the source material, we also cannot prove that the conclusion is certainly incorrect.

Using a green LED as a lighting source, Zaproudine et al. applied the BPI imager to measure faces of migrainers and healthy patients. One observes that the published amplitude maps are contaminated by BCG-artifacts, particularly at sites where the angles with incident light largely deviate from orthogonality (e.g., hair and facial edges). The investigation considered three local RoIs located at the forehead and at the right and left cheeks. For a light source placed frontally and 2 meters away from the forehead, the incident angle of the light w.r.t. skin is less than 10 degrees, which indeed suggests that BCG effects are a minor concern. However, the cheeks are a curved surface; for these, the incident angles is likely to exceed 45 degrees (particularly for thin-faced subjects), hence justifying our concerns.

Counter-phase PPG waveforms

More recently, artifact-contaminated maps obtained using the BPI-imager have motivated Kamshilin et al. [14] to substantiate a new interpretation of remote photophethysmography, and an attempt was made to use this new model to explain the strongly pulsatile counter-phase PPG waveforms which were detected as local hotspots in the [non-corrected, BCG plus PPG] amplitude and phase maps at the wrist (e.g., vicinity of the radial artery). We highlight that a new physiological model is not required to explain counter-phase relations in PPG-images. Our experiments in skin covered by opaque ink, complemented with the corresponding motion-corrected maps, prove that these find explanation in the motion pattern of the skin. However, we emphasize that the new model may explain elements for which our observations do not provide an alternative explanation. For example, our decontaminated PPG-images show much reduced regional phase and amplitude differences, but BCG-motion clearly provides no explanation for the remaining smaller variations.

Remote tonometry

Nippolainen et al. [22] evaluated the palm and wrist of fifty-six subjects using the BPI-imager under LED (lateral) lighting conditions [2]. Specifically, an attempt was made to explain a possible correlation between age and amplitude of hotspots (in polluted PPG-amplitude images) at the vicinity of wrist arteries. Although the authors acknowledge the resemblance between the waveforms collected by sensor-elements over the arteries of the wrist and pulse-pressure waveforms, it was not recognized that BCG-artifacts at the selected spots are much stronger than PPG.

Limitations

In addition to performance deterioration when the weights of PBVi or CHROMi are slightly off (e.g., inaccuracies in the estimation of the PBV vector), these imagers have decreased image sensitivity w.r.t. its single channel counterparts. This is because, in contrast to the initial implementation of BPI, featuring the use of a monochrome camera, this investigation was conducted using a regular RGB camera, so the obtained recordings have lower signal-to-noise ratios, particularly in the red and blue channels. Moreover, the linear combination of channels is optimized to steer PBV-signals from interfering source(s), rather than minimizing sensor noise.

Efforts were made to conform to parameter choices described in the literature, namely generating PPG-images from as little as 10 cardiac cycles. Yet, best results were achieved for 100 sec, though 1 minute could have already been a safe option. This window length is in agreement with the pioneering algorithm of Verkruysse et al., Pulse Amplitude Mapping algorithm, where 10 consecutive amplitude maps of 5–6 seconds could be obtained using a regular RGB camera, and then averaged into a final amplitude map. Although this setting suits the scope of this investigation, it might be prohibitive for applications whose relaxation times are in the order of seconds to minutes (e.g., vasodilation and vasoconstriction of local vessels [23]).

In Fig. 8 we demonstrated that both the CHROM and PBV imagers can eliminate artifacts in PPG images of amplitude and phase. However, numerical errors are visible at the corrected sites under the severe lateral lighting conditions, i.e., where the magnitude of artifacts exceeded PPG by more than an order of magnitude. However, if efforts are made to achieve homogeneous illumination, this problem is minimized, with the benefit of overall image improvement [24].

5. Conclusion

This paper demonstrated that both CHROMi and PBVi are effective against BCG-artifacts. From the PPG-images obtained in a number of subjects, our NRMS benchmarking results showed that PBVi and CHROMi perform comparably and reduce BCG-artifacts to less than 10% of the reference PPG signal strength at the palm. Both imagers outperform BPI by more than an order of magnitude. Motion-robust channel mapping is, therefore, among the good practices that improve the validity of PPG-imaging and push the boundaries of what can be obtained from this technique. Finally, integrating PBV or CHROM into PPG-imaging frameworks enforces trust into PPG-images and helps preventing interpretation errors.