Evaluation of range-separated hybrid density functionals for the prediction of vibrational frequencies, infrared intensities, and Raman activities

Abstract

We present an assessment of different density functionals, with emphasis on range-separated hybrids, for the prediction of fundamental and harmonic vibrational frequencies, infrared intensities, and Raman activities. Additionally, we discuss the basis set convergence of vibrational properties of H₂O with long-range corrected hybrids. Our results show that B3LYP is the best functional for predicting vibrational frequencies (both fundamental and harmonic); the screened-PBE hybrid (HSE) density functional works best for infrared intensities, and the long-range corrected PBE (LC-ωPBE), M06-HF, and M06-L density functionals are almost as good as MP2 for predicting Raman activities. We show the predicted Raman spectrum of adenine as an example of a medium-size molecule where a DFT/Sadlej pVTZ calculation is affordable and compare our results against the experimental spectrum.

I. Introduction

Kohn–Sham density functional theory (DFT)¹ has become an efficient computational chemistry tool for the accurate prediction of a variety of molecular properties. Common local, semilocal, and hybrid density functional approximations (DFAs) are, however, unsuccessful for several applications including, but not limited to, polarizability of long chains² and charge-transfer and Rydberg excitations.³ Many of the failures of common DFAs can be traced back to the self-interaction error (SIE) they include.⁴ One-electron self-interaction error (1e–SIE) can be defined as inexactness for one-electron systems. (The complementary concept of many-electron self-interaction error has recently been emphasized.^5,6) An important manifestation of 1e–SIE is the incorrect long-range behavior of the exchange–correlation (XC) potential. In molecules, the XC potential of semi-local functionals decays exponentially along with the density, while the asymptotic form of the exact potential is −1/r.^7,8

In recent years, it has been suggested^3,9–13 to introduce range separation into the exchange component of the XC potential as a means of recovering the exact −1/r asymptote. This can be implemented by splitting the Coulomb operator into short-range (SR) and long-range (LR) components by a scheme like

$$\frac{1}{r_{12}}=\frac{\text{erfc}(\omega r_{12})}{\underset{\text{SR}}{\underbrace{r_{12}}}}+\frac{\text{erf}(\omega r_{12})}{\underset{\text{LR}}{\underbrace{r_{12}}}},$$ (1)

where r₁₂ is the interelectronic distance and ω is a parameter defining the extent of the short and long ranges. Admixing exact (Hartree–Fock-type, HF) exchange into SR and LR separately gives a general expression for a hybrid functional with range separation¹³

$$E_{\text{xc}}=a{E_x}^{\text{SR-HF}}(\omega )+(1-a){E_x}^{\text{SR-DFA}}(\omega )+b{E_x}^{\text{LR-HF}}(\omega )+(1-b){E_x}^{\text{LR-DFA}}(\omega )+{E_c}^{\text{DFA}}.$$ (2)

In screened hybrids (such as HSE^14,15), the coefficient b = 0, while in long-range corrected hybrids (such as LC-ωPBE^13,16), a = 0 and b = 1. The importance of middle-range exchange has recently been assessed.^17,18 Long-range correction with 100% LR-HF exchange (b = 1) does not work properly for all common DFAs previously available. Yanai and coworkers¹⁹ proposed a “Coulomb-attenuating method” where b ≠ 1. The most obvious consequence of not including 100% LR-HF exchange is that one loses the correct asymptotic behavior of the XC potential.

The success of density functional theory for vibrational spectroscopy has been well documented.^20–22 Density functional approximations, especially hybrids, outperform HF and other simple wavefunction methods (such as MP2) for the prediction of fundamental frequencies.²² DFT has also been successful in quantitative assessments of infrared intensities and Raman activities.^23,24

It has long been known that the accurate prediction of infrared and Raman intensities is difficult because of their dependence on dipole moment and polarizability derivatives. These properties sample the tail of the density and require the use of large, diffuse basis sets.^25,26 Electronic correlation effects are also important. The long-range corrected functionals discussed above, which recover the correct asymptotic XC potential, should improve the description of the tail of the density compared to semilocal functionals. Indeed, long-range correction has been shown to improve properties such as polarizabilities of long chains²⁷ and excitation energies.²⁸ Thus we were prompted to examine the performance of long-range corrected density functionals for predicting infrared and Raman intensities.

Long-range exact exchange is formally and computationally problematic in metals and small-band-gap systems.²⁹ If we were to study molecules on the surface of a metal, ^30–32 we would like to be able to predict infrared intensities and Raman activities accurately enough without the inclusion of long-range HF exchange. Thus, we also explored the behavior of a screened hybrid density functional, HSE, for predicting these properties. HSE has been successful in describing the electronic structure of solids, significantly improving the band gaps predicted by local and semi-local DFAs.²⁹

II. Computational details

All calculations were performed using the development version of the GAUSSIAN³³ suite of programs. Full geometry optimizations were carried out for all molecules enforcing the proper point group symmetry of the ground state. Calculations that broke symmetry, where the symmetric geometry was a transition state (TS) or a higher-order saddle point, were discarded from the data sets (see Tables). Tight convergence criteria were used for both the scf and the optimization procedure [Gaussian keywords scf = tight and opt = tight]. All calculations use at least a pruned (99 590) numerical integration grid (Gaussian keyword integral (grid = ultrafine)). This grid turned out to be insufficient for some calculations, particularly with the M06 meta-GGAs. These calculations yielded relatively large imaginary frequencies for molecular rotations. Accordingly, we used larger integration grids (974 or 70 × 140 = 9800 angular points) for several calculations with the M06 functionals, including all of the M06-HF and M06-L Raman activities. We also used these large grids for all Raman activity calculations using the Sadlej pVTZ basis set. A few other calculations⁷² required larger grids for proper geometry convergence. Otherwise, larger integration grids do not change the reported statistics (up to round-off errors).

Harmonic frequencies and dipole moment derivatives were computed analytically for HF and all DFAs. Derivatives of the polarizability tensor were computed analytically for HF and by numerical differentiation of the analytic dipole derivatives with respect to the electric field for all DFAs. Static Raman activities (zero-frequency, non-resonant) were computed in the double harmonic approximation, ignoring cubic and higher force constants and omitting second and higher order polarizability derivatives. Infrared intensities were computed analytically within the double harmonic approximation. We used the convention theory—experiment to report mean errors (MEs).

The DFT approaches employed here consisted of the Becke three-parameter functional³⁴ with the Lee–Yang–Parr correlation functional³⁵ (B3LYP), the Perdew–Burke–Ernzerhof exchange and correlation functional^36,37 (PBE), the global hybrid version of the PBE functional^38,39 (PBEh), the long-range corrected PBE functional^13,16 (LC-ωPBE), the Heyd–Scuseria–Ernzerhof screened-PBE hybrid functional^14,15, (HSE), the Hamprecht–Cohen–Tozer–Handy exchange and correlation functional^40–42 (HCTH or HCTH/407), two members of the Minnesota 06 family of density functionals^43–45 (M06-L and M06-HF), and the “Coulomb-attenuating method” version of B3LYP¹⁹ (CAM-B3LYP) density functional. The density functionals used in this work can be classified as semi-local (PBE, HCTH, and M06-L), global hybrids (B3LYP, PBEh, and M06-HF), and range-separated hybrids (HSE, LC-ωPBE, and CAM-B3LYP). HCTH, M06-L, and M06-HF have a large number of empirical parameters fitted to extensive data sets. Of particular interest to this study, LC-ωPBE includes 100% LR-HF exchange, CAM-B3LYP uses 65% LR-HF exchange, and M06-HF incorporates 100% HF exchange in the entire range.

Three basis sets were considered for the assessment of frequencies and intensities. 6–31G(d) is split-valence, double zeta augmented with one set of polarization functions on heavy atoms.^46,47 It is commonly used for vibrational spectroscopy because it constitutes a good compromise between computational cost and accuracy for the prediction of vibrational frequencies. Moreover, it has been used to predict infrared intensities at the HF level which are qualitatively correct.⁴⁸ Sadlej pVTZ^49,50 (polarized valence triple zeta) is a medium size basis set designed to give accurate molecular polarizabilities.⁷³ It has been shown in ref. 24 that it is also very accurate for the prediction of Raman activities (which depend on the derivative of the polarizability tensor) with several density functionals. Lastly, aug-cc-pVTZ^51–53 (augmented correlation-consistent polarized valence triple zeta) is a large basis set used here to estimate the convergence of vibrational properties in the basis set limit. We investigated the basis set dependence of vibrational frequencies, infrared intensities, and Raman activities of H₂O using Dunning’s cc-pVnZ, aug-cc-pVnZ, and d-aug-cc-pVnZ series, with n = 2–5.⁵⁴

III. Results and discussion

A Estimation of vibrational frequencies

It is well known that harmonic vibrational frequencies calculated from electronic structure methods generally overestimate fundamental frequencies.⁵⁵ Fundamental frequencies are the experimentally measured frequencies associated with the transition from the ground to the first excited vibrational state. This overestimation can be traced back to the neglect of anharmonicity (neglecting cubic and higher force constants), the approximate treatment of electron correlation, and the use of a finite basis set. Several algorithms have been proposed for predicting experimental fundamental frequencies from computed harmonic frequencies. Of these, probably the most popular are uniform rescaling and dual rescaling (where different scaling factors are used for low and high-frequency modes). Herein we adopt uniform rescaling and estimate scaling factors suitable for the various density functionals considered with 6–31G(d), Sadlej pVTZ, and aug-cc-pVTZ.

We used the F1 set (122 molecules with a total of 1066 frequencies; molecules contain ≤ 4 heavy atoms (1st–2nd row), ≤ 10 total atoms) compiled by Pople et al.⁵⁶ to assess the performance of the various density functionals and to estimate optimum uniform scaling factors. AlCl₃, BF₃, B₂H₆, and BH₃CO were excluded from the set in DFT/Sadlej pVTZ calculations because there are no basis available for B and Al. Additionally, we excluded C₄H₂ (diacetylene) in calculations using the Sadlej pVTZ basis set because all methods predict it to have a slightly bent minimum. Merrick et al.²² have computed optimum scaling factors and estimated RMS errors for a large list of density functionals using Pople-type basis sets with the F1 set. Halls et al.⁵⁷ have later developed scaling factors for HF, MP2, and various DFAs for use along with the Sadlej pVTZ basis set over a slightly reduced F1 set.

Optimum scaling factors are calculated in order to minimize the residuals given by

$$\mathrm{\Delta }=\sum _i^N{(\lambda {\omega }_i^{\text{theor}}-{\tilde{\nu }}_i^{\text{expt}})}^2,$$ (3)

where ${\omega }_i^{\text{theor}}$ and ${\tilde{\nu }}_i^{\text{expt}}$ are the ith theoretical harmonic frequency and the ith experimental fundamental frequency (in cm⁻¹), and the index i runs over all the N vibrational modes considered. This leads to the following expression for the scale factor λ

$$\lambda =\frac{{\sum }_i^N{\omega }_i^{\text{theor}}{\tilde{\nu }}_i^{\text{expt}}}{{\sum }_i^N{({\omega }_i^{\text{theor}})}^2}.$$ (4)

The results of our assessment are shown in Table 1.

Table 1.

Assessment of computed harmonic vibrational frequencies (both scaled and unscaled) vs. experimental fundamentals for different functionals. Mean error (ME), mean average error (MAE), and root mean square error (RMS) are all given in cm⁻¹. Methods are sorted, for each basis set, according to the value of the last column (same for all tables in this paper)

Basis set	Method	Unscaled			Scale factor	Scaled
		ME	MAE	RMS		ME	MAE	RMS
6-31G(d)	M06-HFa	97.7	102.3	133.5	0.9317	−3.0	35.5	53.8
	HF	167.9	169.8	202.3	0.8952	5.7	34.8	52.5
	HCTH	31.5	48.6	68.3	0.9696	−11.3	31.0	44.0
	PBE	6.3	33.8	48.7	0.9874	−11.3	30.6	43.8
	LC-ωPBE	90.5	94.0	120.3	0.9367	−2.5	28.3	42.0
	M06-L	49.5	59.1	80.6	0.9600	−7.7	28.1	40.7
	PBEh	65.0	70.3	93.6	0.9512	−5.5	24.8	37.8
	HSE	63.6	69.1	92.2	0.9520	−5.7	24.8	37.6
	B3LYP	48.5	57.5	76.9	0.9612	−6.9	24.3	37.1
	CAM-B3LYP	71.5	75.6	97.8	0.9485	−3.3	22.6	36.7
Sadlej pVTZ	M06-HF	79.7	86.9	120.7	0.9398	−8.7	39.3	54.9
	HF	144.1	146.3	179.8	0.9075	2.2	35.9	54.9
	HCTHb	10.2	45.2	64.3	0.9797	−18.1	41.6	54.1
	PBEa	−16.5	40.3	51.6	0.9988	−18.2	40.4	51.6
	LC-ωPBE	65.5	72.7	102.7	0.9491	−8.6	36.7	49.3
	M06-La	30.1	46.4	69.8	0.9703	−11.9	33.3	47.4
	PBEh	42.2	54.2	80.5	0.9625	−11.5	34.5	46.8
	HSE	40.9	53.2	79.3	0.9632	−11.8	34.3	46.6
	CAM-B3LYP	45.6	55.7	80.6	0.9615	−9.7	31.6	44.4
	B3LYPa	24.6	42.5	63.0	0.9734	−12.9	32.4	43.2
aug-cc-pVTZ	HF	147.5	149.5	178.9	0.9075	6.2	37.0	55.6
	M06-HF	86.8	91.6	123.2	0.9369	−5.7	34.0	50.6
	HCTHb	16.5	37.0	56.4	0.9788	−13.1	32.7	43.3
	LC-ωPBE	71.3	75.4	101.3	0.9479	−4.3	30.8	42.8
	PBEb	−7.5	31.6	42.7	0.9956	−13.5	31.6	42.1
	PBEh	48.8	54.7	77.8	0.9610	−7.0	26.4	38.1
	HSE	48.0	54.0	77.0	0.9613	−7.2	26.2	37.7
	M06-L	41.5	49.5	70.2	0.9655	−7.5	25.9	37.1
	CAM-B3LYP	56.6	60.9	82.4	0.9573	−4.8	23.3	35.2
	B3LYP	35.8	45.1	64.3	0.9687	−8.5	24.0	35.0

^aC₄H₆ (2-butyne) was excluded because it converged to a TS or a higher-order saddle point when using D_3h symmetry.

^bCH₃COCH₃ (acetone) was excluded because it converged to a TS when using C_2v symmetry.

It should be noted that our results vary slightly from the results shown in ref. 22 for the 6–31G(d) basis set. In particular, the RMS errors reported herein are ca. 3 cm⁻¹ larger than the ones previously reported. This discrepancy appears to arise from the way one matches the computed harmonic frequencies to the experimental fundamentals. In previous studies,¹⁶ the authors seem to have sorted all computed frequencies of a given molecule and compared them directly to the experimental fundamentals without considering the symmetry of modes. Here, we consider the symmetry of the mode in the matching algorithm: modes are required to have the previously assigned symmetry. Indeed, there are only few cases (for the largest molecules) in which symmetry makes a difference. Ignoring symmetry underestimates the error of a given method to accurately predict experimental fundamentals. This is why we discard calculations in which molecules break symmetry.

In general, the scaling factors for all functionals are closer to unity than those for HF. The scaling factor for LC-ωPBE (0.9479 with the aug-cc-pVTZ basis) is the lowest one of all DFAs. We also note that the scaling factors for the Sadlej pVTZ and aug-cc-pVTZ basis are about 0.01 larger than the ones for 6–31G(d). It is interesting to note that Sadlej pVTZ does not seem to be the best basis for estimating fundamental frequencies with density functionals; it gives root mean square errors that are ca. 8–10 cm⁻¹ larger than those for aug-cc-pVTZ, whereas 6–31G(d), once scaled, gives root mean square errors that are only slightly larger than the corresponding ones for aug-cc-pVTZ. This observation does not hold for HF, whose RMS error computed with Sadlej pVTZ is even slightly smaller than the one from aug-cc-pVTZ computations. From the results shown in Table 1, the best functionals for predicting fundamental frequencies are B3LYP and its “Coulomb-attenuating method” version (CAM-B3LYP). Indeed, B3LYP/6-31G(2df,p) is used to estimate thermal corrections from computed frequencies in G3X theory.⁵⁸

From comparison of unscaled RMS errors, it seems that inclusion of HF exchange in the long-range (CAM-B3LYP, LC-ωPBE, and M06-HF) tends to degrade the performance of the parent density functional for the prediction of fundamental frequencies.

Experimentally, there is the possibility of measuring not only the fundamental but also other transitions, especially for diatomic molecules. One can then fit these energies to a polynomial to estimate the harmonic frequencies. It is interesting to assess the behavior of different functionals for the prediction of these “experimental” harmonic frequencies. The errors in the estimation of harmonic frequencies are not due to the harmonic approximation, but result only from the use of finite basis sets, approximate treatment of electron correlation, and experimental uncertainties.

We have used two different sets to evaluate the performance of density functionals in predicting harmonic vibrational frequencies. The T82F set⁵⁹ consists of 82 diatomic molecules, radicals, and cations; most experimental harmonic frequencies in this set were taken from the CRC Handbook of Chemistry and Physics and deemed reliable. The T32F (introduced here) is a combination of the 28 experimental harmonics used by Besler et al.⁶⁰ and the 4 experimental harmonics used by Tew et al.;⁶¹ we feel very confident about the accuracy of the experimental values in this second set. A total of 11 molecules are included in the T32F set: CH₄, HCN, C₂H₂, CO₂, H₂O, H₂CO, NH₃, HF, N₂, CO, and F₂. Be₂ was omitted from the T82F set for HF, as it is unbound. A few molecules failed to converge and were omitted (see Table 2). Several molecules had to be excluded from the T82F set in DFT/Sadlej pVTZ calculations because there are no basis available for B and Al: B₂, BH, BF, BCl, BN, BO, BS, Al₂, AlH, AlCl, AlO, and AlS. The results of our assessment are shown in Table 2. HF significantly overestimates the harmonic frequencies. Hybrids incorporating a significant amount of HF exchange, such as M06-HF and LC-ωPBE, also overestimate harmonic frequencies, though not as much as HF does. LC-ωPBE performs better than its PBE parent in the T32F set, but not in the T82F set. Interestingly, PBE and HCTH underestimate harmonic frequencies whereas all other functionals tend to overestimate them. B3LYP gives the best results for the prediction of harmonic frequencies.

Table 2.

Assessment of computed harmonic vibrational frequencies vs. experimental harmonic frequencies for different functionals, details as in Table 1

Basis set	Method	T82F set			T32F set
		ME	MAE	RMS	ME	MAE	RMS
6-31G(d)	HF	112.3	143.3	190.8	198.4	198.4	211.2
	M06-HF	81.4	108.6	150.5	91.1	103.5	131.0
	PBE	−34.3	47.7	70.1	−51.4	72.3	99.9
	LC-ωPBE	75.3	83.9	103.3	65.3	73.2	90.9
	CAM-B3LYP	41.6	56.5	77.8	41.0	62.8	78.2
	HCTH	−16.0	44.0	61.0	−10.8	57.4	74.1
	PBEh	36.0	47.4	70.3	39.1	58.1	73.0
	HSE	32.8	46.1	68.9	37.5	58.1	72.5
	B3LYP	7.2	39.5	57.3	12.1	57.5	71.0
	M06-L	21.1	45.7	62.2	14.1	53.7	63.9
Sadlej pVTZ	HF	110.5	136.4	191.7	171.0	171.0	192.3
	M06-HFa	73.1	96.7	141.1	68.5	82.4	112.2
	PBE	−49.3	58.2	77.4	−73.4	79.9	96.2
	LC-ωPBE	57.6	69.2	92.8	35.2	60.0	75.1
	HCTH	−30.4	52.3	64.5	−30.3	48.1	62.2
	CAM-B3LYP	25.4	51.5	72.6	10.8	45.1	61.6
	M06-L	10.3	42.2	57.4	−5.3	45.2	59.7
	PBEh	23.6	44.5	67.9	14.9	45.0	59.7
	HSE	20.2	43.9	66.6	13.0	44.4	58.4
	B3LYP	—7.3	41.7	56.7	−13.7	43.1	55.4
aug-cc-pVTZ	HF	114.2	137.2	192.2	174.3	174.3	194.5
	M06-HFb	47.0	115.1	182.0	77.5	88.7	118.1
	PBE	−37.3	46.2	62.6	−60.6	67.6	85.8
	LC-ωPBE	62.8	70.2	92.1	44.2	63.2	79.1
	CAM-B3LYP	34.9	48.0	69.5	27.0	47.8	64.6
	PBEh	30.0	41.3	63.5	23.7	45.0	60.3
	HSE	27.1	40.4	62.0	22.7	44.1	59.2
	HCTH	−19.8	41.2	52.5	−21.6	41.1	53.6
	M06-Lb	19.8	37.7	51.0	7.9	41.2	53.2
	B3LYP	3.9	34.0	48.1	2.8	39.3	51.4

^aBeF was excluded from T82F because of SCF convergence issues.

^bBeH was excluded from T82F because of SCF convergence issues.

B Assessment of infrared intensities

In a previous study, Halls and Schlegel²³ concluded that the agreement of electronic structure methods with respect to QCISD for the prediction of infrared intensities follows the order: hybrid DFT > MP2 > local DFT ≈ gradient-corrected DFT > HF, with hybrid functionals offering an excellent performance. Galabov et al.⁶² have shown that inclusion of electron correlation (at the QCISD, CCSD or CCSD(T) levels of theory) and extended basis sets (such as aug-cc-pVTZ) are needed to achieve quantitative agreement for infrared intensities between theoretical predictions and experimentally determined values. It should be noted that experimental infrared intensities are difficult to measure because of overlapping bands, resonances, intensity sharing, etc., limiting the accuracy to around ±10%.

Halls and Schlegel²³ compared the results of infrared intensities at the QCISD/6–311+G(3df,3pd) and CCSD(T)/TZ(2df,2pd) levels for a small number of molecules. The authors found good agreement between both theoretical methods, but both showed large discrepancies with respect to experimental values. Therefore, a large fraction of the difference may be attributed to the experimental uncertainties and the double harmonic approximation. We compare our calculated intensities against experiment and against high-level ab initio results already reported in the literature. DFT and ab initio results should ultimately converge to the same limit within the double harmonic approximation. Our test set is a combination of the sets used by Halls and Schlegel²³ and Galabov et al.:⁶² HF, CO, H₂O, HCN, C₂H₂, H₂CO, NH₃, C₂H₄, CH₂F₂, CH₄ and SiH₄. The results are shown in Table 3. We did not consider CO₂ as part of our test set because there is a large disagreement between experimental and ab initio results: the experimental intensity of the σ_u⁺ mode is 548 km mol⁻¹, while the theoretical intensities are 749, 634 and 708 km mo⁻¹ at the CCSD/TZ(2df,2pd), CCSD(T)/TZ(2df,2pd), and QCISD/6–311+G(3df,3pd) levels, respectively.^23,63

Table 3.

Assessment of computed infrared intensities for different functionals vs. experimental and high-level ab initio results. The test set consists^a of HF, CO, H₂O, HCN, C₂H₂, H₂CO, NH₃, C₂H₄, CH₂F₂, CH₄ and SiH₄. Mean error (ME), mean average error (MAE), and root mean square error (RMS) are all given in km mol⁻¹

Basis set	Method	High level ab initiob			Experimental
		ME	MAE	RMS	ME	MAE	RMS
6-31G(d)	HF	36.0	37.9	82.8	37.9	44.5	93.6
	M06-L	20.3	27.6	63.1	22.2	31.7	74.0
	LC-ωPBE	10.1	17.9	33.3	12.1	23.8	45.9
	CAM-B3LYP	7.6	16.4	28.5	9.5	21.8	41.0
	B3LYP	6.4	16.8	29.4	8.3	21.3	40.8
	HSE	7.9	15.4	27.5	9.8	20.7	39.0
	PBEh	7.7	15.3	26.9	9.6	20.7	38.6
	HCTH	2.0	18.8	30.4	3.9	20.4	38.3
	PBE	−0.1	18.5	30.4	1.9	20.4	37.2
	M06-HF	3.8	18.1	30.1	5.7	21.0	34.8
Sadlej pVTZ	HF	24.0	24.8	40.6	25.9	30.1	50.2
	M06-HF	4.2	18.9	26.4	6.2	23.0	30.2
	M06-L	4.1	10.6	16.8	6.0	12.3	22.1
	LC-ωPBE	3.2	10.7	15.7	5.2	15.8	21.8
	CAM-B3LYP	5.1	9.0	13.9	7.0	14.4	21.4
	PBE	−2.8	11.5	22.6	−0.9	11.4	21.0
	HCTH	−0.1	9.7	18.2	1.8	11.6	19.5
	PBEh	2.0	9.5	16.4	3.9	13.3	19.3
	HSE	2.2	9.2	15.8	4.1	13.1	19.1
	B3LYP	3.5	6.9	11.8	5.4	11.9	18.9
aug-cc-pVTZ	HF	25.6	26.0	43.1	27.5	30.5	52.6
	M06-HF	4.3	18.9	28.0	6.3	22.1	28.2
	LC-ωPBE	4.6	9.8	14.2	6.6	14.8	20.8
	CAM-B3LYP	6.4	8.2	12.1	8.3	14.4	20.6
	M06-L	3.1	8.7	13.6	5.1	11.8	20.4
	PBE	−1.7	11.2	21.2	0.2	10.5	19.2
	HCTH	1.6	10.0	18.2	3.5	11.0	18.9
	B3LYP	4.8	6.2	10.2	6.7	11.2	18.2
	PBEh	3.3	8.7	14.2	5.2	12.1	17.5
	HSE	3.5	8.5	13.7	5.4	11.9	17.4

^aOnly those modes for which experimental intensities were available were considered; modes that are inactive were not considered, and degenerate modes were considered only once.

^bQCISD/6-311+G(3df,3pd) for HF, CO, NH₃, C₂H₄, and CH₂F₂;²³ CCSD(T)/aug-cc-pVTZ for the rest of the set.⁶²

In general, all functionals show similar behavior and the results are much better than the predictions of HF. Taking aug-cc-pVTZ as a basis, HSE and PBEh are the best performers when comparing against experiment, whereas comparison against ab initio results yields B3LYP and CAM-B3LYP as the best performers. PBE and HCTH give results in greatest disagreement with respect to ab initio results. When comparing against experimentally determined intensities, the long-range corrected hybrids LC-ωPBE and CAM-B3LYP are among the worst performers, although the RMS error is only ca. 3 km mol⁻¹ larger than that for the best performers. M06-HF gives even larger errors. It is evident that 6–31G(d) is an insufficient basis set for the prediction of infrared intensities, giving RMS errors much larger than either the Sadlej pVTZ or the aug-cc-pVTZ basis. Most methods show very similar behavior with the Sadlej pVTZ and aug-cc-pVTZ basis. There is also a reasonable agreement when comparing results against experiment or against high-level ab initio computations.

C Assessment of Raman activities

Halls and Schlegel²⁴ have shown that DFAs are almost as good as MP2 for the prediction of Raman activities. They observed that the difference between HF and MP2 is not as large as for infrared intensities. In addition, the convergence with basis set is slower for Raman activities than for infrared intensities, in agreement with the observation that Raman activities require a better description of the tail of the density. The density near the nuclei is held tightly by the nuclear charges, whereas the tail of the density is more polarizable and thus becomes important in the prediction of the Raman response, which depends on the derivative of the polarizability. Our test set is the same as that used in ref. 24: N₂, H₂O, CH₄, C₂H₂, C₂H₄, C₂H6, CH₂F₂ and NH₃. A total of 29 vibrational modes were considered (degenerate modes were considered only once). The results of our assessment are shown in Table 4.

Table 4.

Assessment of computed Raman activities for different functionals vs. experimental results. The test set consists^a of N₂, H₂O, CH₄, C₂H₂, C₂H₄, C₂H₆, NH₃ and CH₂F₂. Mean error (ME), mean average error (MAE), and root mean square error (RMS) are all given in Å⁴ amu⁻¹

Basis set	Method	ME	MAE	RMS
6-31G(d)	MP2b	−8.4	30.2	50.4
	M06-L	1.0	33.0	50.2
	HF	0.9	30.2	49.2
	LC-ωPBE	−6.5	29.4	48.9
	M06-HF	−0.1	29.4	48.9
	CAM-B3LYP	−4.0	29.5	48.7
	B3LYP	−2.7	30.0	48.5
	PBE	−2.3	30.5	48.1
	HSE	−3.0	29.5	47.8
	PBEh	−3.3	29.4	47.8
	HCTH	−5.0	29.0	47.5
Sadlej pVTZ	PBE	13.6	15.7	29.3
	HCTH	13.0	15.1	28.8
	B3LYP	10.9	13.5	25.2
	HF	8.6	15.1	25.1
	M06-L	6.5	15.0	24.4
	HSE	9.1	12.3	23.1
	PBEh	8.7	12.2	22.7
	M06-HF	6.2	11.1	21.4
	MP2b	7.4	11.5	19.7
	CAM-B3LYP	7.0	10.9	17.6
	LC-ωPBE	1.7	11.2	17.4
aug-cc-pVTZ	PBE	9.7	12.9	25.6
	HCTH	8.1	12.4	24.0
	HF	5.9	14.6	23.7
	B3LYP	7.0	12.0	22.4
	HSE	5.9	11.7	21.1
	PBEh	5.7	11.7	20.9
	CAM-B3LYP	4.5	11.8	19.8
	LC-ωPBE	−1.2	12.0	17.9
	M06-L	0.3	12.4	17.7
	M06-HF	−2.7	11.6	17.3
	MP2b	2.3	10.0	16.7

^aOnly those modes for which experimental activities were available were considered; modes that are inactive were not considered, and degenerate modes were considered only once.

^bFrom ref. 24.

As in the case of infrared intensities, the 6–31G(d) basis set is insufficient, with RMS errors close to 50 Å⁴ amu⁻¹. As observed by Halls and Schlegel,²⁴ all functionals show a similar performance with large basis sets. LC-ωPBE is among the best DFT performers with both the Sadlej pVTZ and the aug-cc-pVTZ basis sets, giving results comparable to those of MP2. Interestingly, all methods but LC-ωPBE tend to overestimate the Raman activities with the Sadlej basis set; in the case of the aug-cc-pVTZ basis, all methods performing well (as judged by the RMS) give a mean error close to zero. CAM-B3LYP also performs well, though not as well as LC-ωPBE, suggesting that 100% HF exchange in the long range improves the predicted Raman activities. However, M06-L, which does not include HF exchange, performs also very well in conjunction with the aug-cc-pVTZ basis.

D Basis set convergence of vibrational properties

Electronic structure methods that can be used to estimate molecular properties are characterized by an approximate treatment of electron correlation and an incomplete basis set, thus limiting the accuracy of the computation. It is important to study how different molecular properties converge with respect to the size of the basis set for a given theoretical method. Water (H₂O) has previously been used to assess this convergence for ab initio methods.^48,62,64 In Table 5, we present an assessment of the basis set convergence of the vibrational properties of water with the long-range corrected LC-ωPBE density functional using Dunning’s basis set series. The same assessment performed with the PBE and PBEh functionals is included as part of the supporting information for this paper.

Table 5.

Basis set dependence of the harmonic vibrational frequencies (in cm⁻¹), infrared intensities (in km mol⁻¹), and Raman activities (in Å⁴ amu⁻¹) for the vibrational modes of water computed with the LC-ωPBE density functional

Basis set	a1			a1			b2			CPUa
	ω	IIR	IRaman	ω	IIR	IRaman	ω	IIR	IRaman
Sadlej pVTZ	1624.18	78.37	0.99	3881.73	8.47	91.71	3995.79	76.93	21.21	2
cc-pVDZ	1642.36	60.70	5.75	3849.73	9.69	65.35	3954.29	39.40	32.03	1
cc-pVTZ	1623.12	73.91	4.04	3887.89	7.12	64.85	3988.95	56.84	24.06	3
cc-pVQZ	1618.43	77.84	2.46	3889.33	7.90	71.36	3989.81	68.05	23.30	13
cc-pV5Z	1615.16	79.58	1.70	3890.49	8.94	75.22	3991.88	75.04	22.58	116
aug-cc-pVDZ	1605.46	75.88	1.64	3874.10	7.35	87.57	3984.69	74.25	22.36	2
aug-cc-pVTZ	1613.66	80.49	0.94	3880.90	8.40	89.23	3982.69	78.17	22.15	6
aug-cc-pVQZ	1614.97	80.92	0.75	3887.26	8.59	89.46	3988.68	78.97	21.83	47
aug-cc-pV5Z	1614.88	80.94	0.70	3889.51	8.52	89.80	3991.27	78.60	21.75	460
d-aug-cc-pVDZ	1611.75	78.74	0.71	3874.34	8.00	90.49	3986.75	75.56	21.92	2
d-aug-cc-pVTZ	1614.50	80.66	0.67	3881.51	8.12	91.34	3985.26	77.49	21.89	12
d-aug-cc-pVQZ	1614.83	80.91	0.67	3887.01	8.60	90.35	3988.45	78.74	21.78	126
d-aug-cc-pV5Z	1614.84	80.96	0.66	3889.60	8.55	90.29	3991.32	78.62	21.73	1292
Experimentalb	1649	64.0	0.9	3832	2.98	108.0	3943	43.3	19.2

^aRelative CPU time for a frequency calculation at the optimized structure.

^bExperimental harmonic frequencies from ref. 60, vibrational intensities from ref. 69, and Raman activities from ref. 70 and 71.

Regarding the computed harmonic frequencies, the two high frequency modes are almost converged with a triple-ζ quality basis set (cc-pVTZ), while the low-frequency a₁ mode requires, at the triple-ζ level, inclusion of a set of diffuse functions (aug-cc-pVTZ). Typically, scaling factors are used to correct for both of these deficiencies in computed values. In fact, the use of scaling factors also allows one to use a lower quality basis set (the scaling factor will be slightly different and will include contributions from basis set effects). It is interesting to notice that, at the quintuple-ζ level, inclusion of diffuse functions has a marginal effect on the prediction of harmonic frequencies. This confirms that it is not needed to describe very accurately the tail of the wavefunction (or the density) to get accurate harmonic frequencies, which is not the case for infrared intensities or Raman activities.

Inclusion of diffuse functions is almost mandatory for an accurate estimation of Raman activities (observe, for instance, that the predicted values for the two a₁ modes are far from converged even at the cc-pV5Z level). The aug-cc-pVTZ basis set seems to be acceptably close to the converged values, although inclusion of a second set of diffuse functions (d-aug-cc-pVTZ) may significantly improve the prediction for the low-frequency a₁ mode.

For the prediction of infrared intensities, the aug-cc-pVTZ basis gives results very close to convergence, while working without diffuse functions is not recommended. It is interesting to note that d-aug-cc-pVDZ (that is, including two sets of diffuse functions with a double-ζ basis set) yields very similar results to those of aug-cc-pVTZ for both infrared intensities and Raman activities.

The best compromise between accuracy and computational efficiency seems to be the Sadlej pVTZ basis sets, which gives results very close to those of aug-cc-pVTZ while being only slightly more expensive than aug-cc-pVDZ and cheaper than the d-aug-cc-pVDZ basis. Comparison of the results shown in Table 5 and those reported in the ESI^† shows that the convergence of vibrational properties with basis sets is rather similar for PBE, PBEh, and LC-ωPBE, an observation that was difficult to estimate a priori.

With respect to experimental results, a very good estimate of the absolute Raman activities can be obtained with LC-ωPBE as one approaches the basis set limit. Indeed, the converged values are much closer to experiment than those for infrared intensities (vide supra). However, we recall that absolute infrared intensities are challenging to measure experimentally, and that LC-ωPBE gives infrared intensities close to other density functionals.

E Raman spectrum of adenine

We were interested in evaluating the predicting power of DFT/Sadlej pVTZ computations for the Raman spectrum of middle-size molecules. We chose adenine as our target molecule for this purpose.

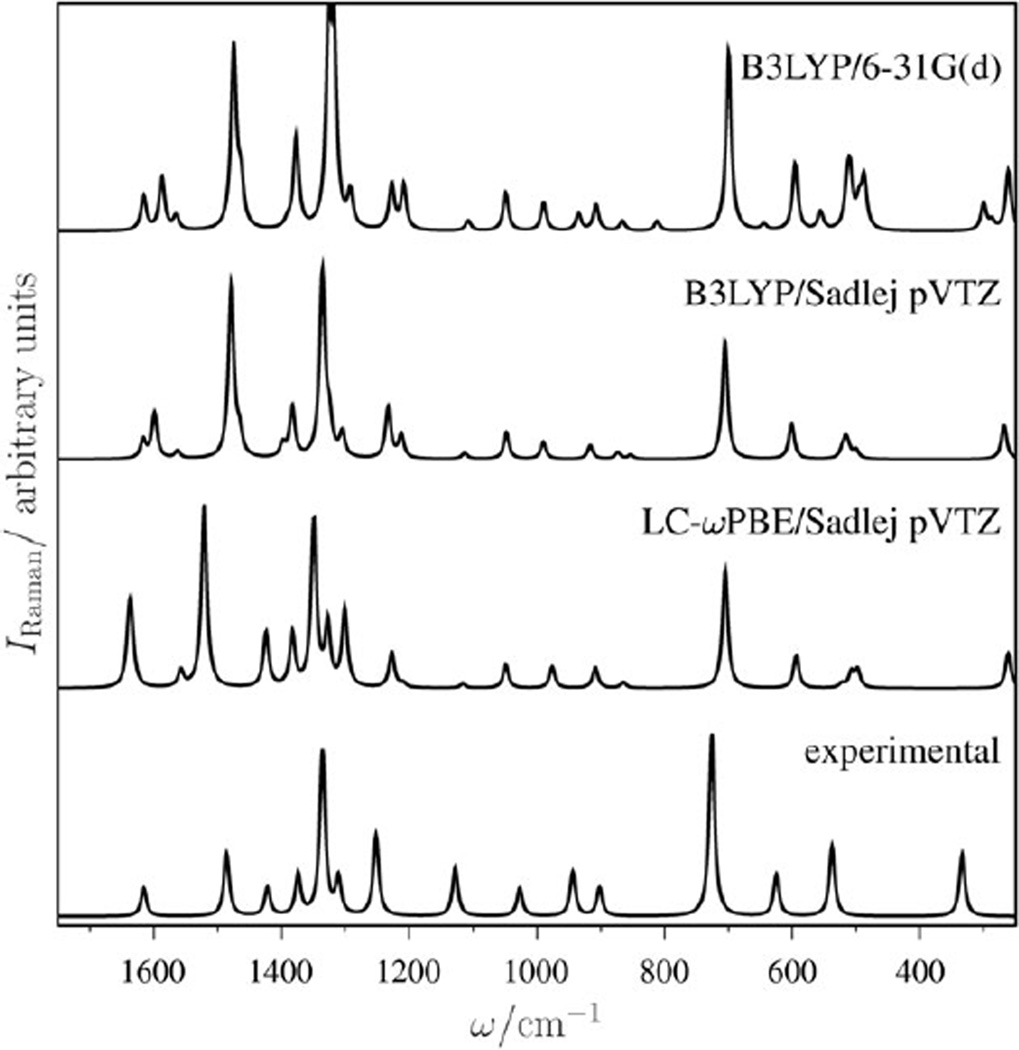
There has been some controversy over whether adenine has a planar or non-planar equilibrium geometry.⁶⁵ It is not our intention to solve this issue here. We note that LC-ωPBE/Sadlej pVTZ predicts a planar (C_s) minimum, while B3LYP/6–31G(d) and B3LYP/Sadlej pVTZ predict a minimum slightly distorted from planarity, in which the NH₂ group retains its pyramidal configuration. The computed theoretical spectra at the B3LYP/6–31G(d), B3LYP/Sadlej pVTZ, and LC-ωPBE/Sadlej pVTZ levels in the 300–1700 cm⁻¹ region are shown in Fig. 1, along with the experimental spectrum for comparison purposes. Fig. 1 plots the calculated relative Raman intensities against scaled frequencies. The Raman intensity of a vibrational mode p with frequency ω_p is proportional to R_p/ω_p, where R_p is the “Raman activity” calculated using Placzek’s approximation and reported by a program such as GAUSSIAN. (Theoretical details of Placzek’s approximation for Raman intensities may be found in the textbook by Barron.⁶⁶) A 5 cm⁻¹ Lorentzian broadening was added to each of the peaks. The frequencies and relative intensities of the peaks in adenine’s experimental spectrum were obtained from the Spectral Database for Organic Compounds, SDBS, from the National Institute of Advanced Industrial Science and Technology (http://riodb01.ibase.aist.go.jp/sdbs/). These were measured from a powder sample using a 4880 Å source. The “experimental” spectrum in Fig. 1 is these tabulated frequencies and intensities, plotted with a Lorentzian broadening as a guide to the eye. This approach suffices for our purposes, as we did not attempt to calculate the Raman peak shapes.

Fig. 1.

Experimental and theoretical (zero-frequency, non-resonant) Raman spectrum of adenine.

There is a good overall agreement between the computed spectrum using LC-ωPBE and the experimental spectrum. The relative intensities of all low-frequency modes are underestimated, and the predicted frequencies for low-frequency modes are slightly overestimated while for high-frequency modes are underestimated. The feature at approximately 1100 cm⁻¹ from the experimental spectrum describing an in-plane motion appears severely underestimated (in relative intensity) in all theoretical spectra. The theoretical spectra at the B3LYP level are also in good agreement with experiment. In general, the frequencies predicted with B3LYP are in better agreement with experiment than those from LC-ωPBE, consistent with the results from previous sections.

IV. Conclusions

We have shown that long-range corrected hybrids, LC-ωPBE in particular, improve the accuracy of common DFAs for the prediction of Raman activities. The one-parameter LC-ωPBE gives frequencies and Raman activities approaching the highly parametrized “density¹⁶ functional for spectroscopy” (M06-HF).⁴⁴ Previous studies showed that LC-ωPBE is also very good for thermochemical kinetics. The observation that HSE does not degrade results from PBEh for the prediction of vibrational properties is encouraging, as this functional is particularly suitable to be used in molecule–metal interfaces using periodic boundary conditions. Inclusion of long-range exchange tends to degrade a functional’s performance for vibrational frequencies and infrared intensities. This is especially true for M06-HF. However, the CAM-B3LYP and LC-ωPBE functionals still appear to provide acceptable accuracy for these properties. As in previous investigations, B3LYP with an empirical scale factor provides very accurate predictions of experimental fundamental and harmonic vibra-tional frequencies. The LC-ωPBE/Sadlej pVTZ adenine Raman spectrum is in good agreement with the experimental one, further demonstrating that long-range corrected functionals can be routinely applied to predicting the vibrational spectra of medium-sized molecules.