Abstract
Density functional theory incorporating hybrid exchange–correlation functionals has been extraordinarily successful in providing accurate, computationally tractable treatments of molecular properties. However, conventional hybrid functionals can be problematic for solids. Their nonlocal, Hartree–Fock-like exchange term decays slowly and incorporates unphysical features in metals and narrow-bandgap semiconductors. This article provides an overview of our group’s work on designing hybrid functionals for solids. We focus on the Heyd–Scuseria–Ernzerhof screened hybrid functional [J. Chem. Phys. 2003, 118, 8207], its applications to the chemistry and physics of solids and surfaces, and our efforts to build upon its successes.
I. Introduction
The chemistry and physics of solids and surfaces has a long history of theoretical and practical importance. A topical but by no means exhaustive list of examples includes semiconductor doping, heterogeneous catalysis, and the chemistry of actinide solids. Creation and manipulation of semiconductor defects is essential to modern electronics. Heterogeneous catalysis by metal and metal oxide surfaces is essential in fields such as industrial chemical production, pollution control,1 and solar energy conversion.2 The physical properties and surface chemistry of novel refractory actinide compounds are important for safer and more efficient utilization of nuclear power.3,4
The electronic structure of extended systems has been modeled since the birth of quantum mechanics.5–8 Such investigations provide essential complements to experiments, particularly for experimentally challenging systems such as actinides. The density functional theory (DFT),9,10 which originated in studies of solids,11 has become the most widely used method for predicting the electronic structure and properties of solids and large molecules.12,13 DFT provides a rigorous framework for simple models of the many-body effects that dominate the computational cost of wavefunction-based electronic structure calculations.14 Simple semilocal density functionals can accurately model many ground state properties including lattice parameters and bulk moduli.15 They also provide a starting point for higher-level treatments of many-body effects, surfaces, defects, and time-dependent properties.8,16
Unfortunately, semilocal density functionals have some inherent drawbacks. They tend to over-delocalize electrons due to their intrinsic self-interaction error (see below). This makes them problematic for localized subsystems such as defects, surface states, and d and f block elements. They also systematically underestimate band gaps, often mistakenly assigning metallic behavior to semiconductors.17,18 Molecular quantum chemists often correct similar problems by using “hybrid” density functionals that incorporate a fraction of nonlocal exact exchange (see below). Hybrid functionals such as the widely used B3LYP19,20 are enormously successful in quantum chemistry. However, computational and formal problems have prevented their widespread application to solids and surfaces.
Our research group is engaged in designing novel hybrid density functionals for extended systems. This feature article summarizes our efforts to date. After briefly reviewing density functional theory in section II and approximate exchange–correlation functionals in section III, we discuss the Heyd–Scuseria–Ernzerhof (HSE) screened hybrid21 in section IV. Section V reviews some applications of HSE to outstanding problems in the physics and chemistry of solids and surfaces. The results illustrate the power of the screened exchange approximation, and indicate areas where successors to HSE can make a contribution. We discuss our recent work on successors to HSE in section VI, and our broader conclusions in section VII. This article is necessarily focused on our own work, and will not discuss all of the recent progress made by other groups investigating range-separated hybrid functionals and applications of DFT to extended systems.
II. Density functional theory
Density functional theory is based on the Hohenberg–Kohn theorems.11 These show that the ground-state energy of an N-electron system is a unique and variational functional of the electron density ρ(r).22,23 An N-electron system in an external potential vext(r) arising from nucleii and applied electric fields has a ground state total electronic energy
| (1) |
where ρ(r) is the ground state density at point r and the universal density functional F[ρ] accounts for the electrons’ kinetic and interaction energies.11 (We use atomic units throughout, ħ = |e| = me = 1.)
The functional dependence of F[ρ] is not known analytically, and must be approximated in practical calculations. Kohn and Sham approximated the bulk of F[ρ] by obtaining ρ(r) from a reference system of N noninteracting electrons moving in an effective potential veff(r). This potential may in principle be selected to return the exact ground-state energy and density. The energy is
| (2) |
Here the term in ∇2 gives the kinetic energy of the noninteracting electrons, u(r) is the classical Coulomb potential of the N-electron density, and the exchange–correlation (XC) functional EXC[ρ] is an “everything else” term containing the remainder of F[ρ]. {ϕi(r)} are the one-electron orbitals occupied by the non-interacting electrons. They satisfy
| (3) |
where the effective potential is given by
| (4) |
The exchange–correlation potential vXC(r) is obtained from the functional derivative
| (5) |
Modern Kohn–Sham calculations typically use a spin-dependent formalism, with different electron densities, orbitals, and exchange–correlation potentials for ↑-spin and ↓-spin electrons. Janak’s theorem shows that, if the KS orbitals are evaluated with the exact exchange–correlation functional, the noninteracting system’s highest occupied orbital energy is the negative of the real system’s ionization potential (work function).24
The Hohenberg–Kohn theorems ensure that eqn (2) yields the exact ground-state energy, provided that we use the exact, universal exchange–correlation functional EXC[ρ]. Systematic approximations to the exchange–correlation energy and potential of a given system have a computational effort that is at least comparable to the corresponding wavefunction-based approximations.25–30 However, one of DFT’s main attractions is that simple approximate exchange–correlation functionals can in practice provide accurate (albeit unsystematic) results with a computational cost comparable to mean-field calculations.
III. Approximate exchange–correlation functionals
The broad applicability of modern density functional theory results from the development of a range of increasingly complicated and (ideally) increasingly accurate approximate exchange–correlation functionals. We briefly review these approximations here. The extensive review by Staroverov and Scuseria provides more details.13
The simplest approximate functional is the local spin-density approximation (LSDA). The LSDA approximates the exchange–correlation energy density at point r as a functional of the electron spin densities ρσ(r). (Here σ = ↑,↓ and ρ= ρ↑ + ρ↓.) Generalized gradient approximations (GGAs) extend LSDA by incorporating a dependence on the density gradient ∇ρσ(r). The first-order gradient correction to the exchange–correlation potential diverges in finite systems,31 and various GGAs correct this divergence in various ways.32–35 Meta-GGAs incorporate the noninteracting kinetic energy densities
| (6) |
or ∇2ρσ(r). LSDA, GGAs, and meta-GGAs are “semilocal” functionals, whose exchange–correlation energy density at r depends only on the density and KS orbitals in an infinite-simal region around r.36
An important characteristic of semilocal exchange–correlation functionals is their intrinsic self-interaction error (SIE).37 Briefly, SIE refers to the fact that semilocal exchange–correlation functionals allow electrons to interact with themselves. One convenient definition of this effect is the one-electron self-interaction error. In any one-electron system, the electron-electron Coulomb repulsion in eqn (2) must be exactly cancelled by the exchange–correlation interaction EXC[ρ]. Semilocal approximations to the exchange–correlation functional are generally insufficiently flexible to provide this cancellation. This is defined as one-electron SIE.37 This effect can cause significant errors even in many-electron systems.38–40
Another definition of SIE is the many-electron self-interaction error recently emphasized in the literature.41–45 The exact energy of an N-electron system is piecewise linear with respect to fractional occupancy N, with derivative discontinuities as N passes through integers.46,47 Semilocal functionals and Hartree–Fock theory both predict nonlinearities in the energy as a function of N, as well as incorrect energies at integer N. These two errors define the many-electron SIE.41–45
Self-interaction error tends to over-delocalize electrons.44 This over-delocalization produces systematic errors for localized states such as defects and surfaces. However, Kohn–Sham DFT calculations that combine semilocal functionals with spatial and spin symmetry breaking can have the benefit of mimicking nondynamical, left-right electron correlation in chemical bonds.48–50 This enables simple, mean-field Kohn–Sham calculations to accurately treat systems that would otherwise require expensive multideterminant wave-function calculations. Modern exchange–correlation functionals generally seek to balance the undesirable effects of self-interaction error with semilocal functionals’ desirable simulation of static, nondynamical correlation.
One of the most useful classes of density functionals are “hybrids” incorporating a fraction of exact nonlocal (Hartree–Fock-type, HF) exchange. HF exchange is defined by
| (7) |
| (8) |
Here r12 = |r1 − r2| and {ϕiσ(r)} are the σ-spin orbitals of the noninteracting Kohn–Sham reference system (eqn (3)). Hybrid functionals are formally justified by an adiabatic connection between the real system and the noninteracting reference system.19,51 A more empirical justification is that admixture of one-electron-SIE-free HF exchange tunes the amount of nondynamical correlation included by a semilocal functional, and the resulting balance between the desirable and undesirable effects of self-interaction error. A related empirical justification is that semilocal functionals tend to overestimate the strength of covalent bonds, while Hartree–Fock theory tends to underbind. Mixing these approximations yields a useful cancellation of errors for molecular thermochemistry. Several other properties (including band gaps, section IV A) can also benefit from cancellation of error in hybrid functionals.
Hybrid exchange–correlation functionals dramatically improve many molecular properties relative to semilocal functionals, and are essential tools in modern computational chemistry.19,48,51 But they are problematic in solids. One problem is computational. In metals, the Kohn–Sham one-particle density matrix of eqn (8) decays very slowly in r12. This makes it computationally expensive to evaluate eqn (7) numerically.52 A more fundamental problem is that the exchange interactions at large r12 are exactly cancelled by correlation in the uniform electron gas,53 and approximately cancelled by correlation in metals and narrow-bandgap semiconductors. 54–56 Calculations combining exact exchange with approximate correlation functionals can yield qualitatively incorrect results in such systems. For example, Hartree–Fock calculations (exact exchange and no correlation) on the uniform electron gas incorrectly predict a vanishing density of states at the Fermi level.8
IV. The Heyd–Scuseria–Ernzerhof functional
The screened hybrid functional of Heyd, Scuseria, and Ernzerhof21 was proposed to extend the successes of hybrid functionals into the solid state, by avoiding the problematic effects of long-range HF exchange. This functional partitions the Coulomb operator in eqn (7) into two ranges
| (9) |
and incorporates only short-range (SR) HF exchange. The parameter ω in eqn (9) controls the definition of the two ranges. The error function in eqn (9) is chosen for computational convenience, as the range-separated HF exchange can be evaluated analytically when the KS orbitals are expanded in Gaussian or plane wave basis sets.
HSE is based on the PBEh global hybrid57,58 of the Perdew–Burke–Ernzerhof (PBE)33 GGA. PBEh incorporates 25% full-range HF exchange, 75% full-range PBE exchange, and 100% PBE correlation. The fraction of HF exchange is based on perturbation theory arguments.59 HSE includes 25% short-range HF exchange and no long-range HF exchange. The range-separation parameter ω is selected empirically, and is set to 0.11 Bohr−1 in the latest version of the functional (HSE06).60
HSE is related to the screened hybrid functionals of Bylander and Kleinman17 and Seidl and coworkers,61 and to screened Coulomb operator methods previously developed in quantum chemistry.62–64 HSE is also closely connected with a large body of work on long-range-corrected hybrids. These functionals combine wavefunction theory in the long range with a DFT approximation for short-range exchange–correlation.65–74 They can provide efficient wavefunction expansions due to the semilocal treatment of the correlation cusp. However, they are in a sense completely opposite to HSE, and are not generally intended for solids. Their inclusion of long-range HF exchange is problematic for metals and small-bandgap semiconductors for the reasons discussed above.54–56 (Additionally, these long-range-corrected functionals are often treated with multiconfigurational self-consistent field methods, a non-size-consistent approximation that is not appropriate for extended systems.) The observation that both screened and long-range-corrected functionals can provide accurate molecular thermochemistry75 led us to investigate the “middle-range” hybrid functionals discussed in section VI.
Our numerical tests of HSE use the Gaussian suite of programs.76 These perform periodic boundary condition calculations using atom-centered Gaussian orbitals, fast multipole method treatments of Coulomb interactions,77 and sophisticated numerical screening procedures for efficient evaluation of screened exchange78 and its second derivatives.80,79 We have also extended these programs for correlated wavefunction calculations (Laplace-transformed Møller–Plesset perturbation theory) on infinite systems,81,82 and applied them to outstanding problems in nanotechnology83 and biophysics.84 Hybrid density functional calculations in solids are also regularly performed with the CRYSTAL85,86 and VASP87–89 programs.
The remainder of this section discusses two of HSE’s important properties: its accurate treatment of band gaps, and its model for range-separated semilocal exchange.
A HSE band gaps
One of HSE’s most important aspects is its ability to accurately predict semiconductor band gaps. To rationalize this, we must briefly discuss the calculation of band gaps within density functional theory. Further details are presented in the recent reviews of Rinke and coworkers90 and Kümmel and Kronik.91 Numerical results for HSE band gaps are discussed in section V.
The fundamental band gap of an N-electron system is defined as the difference between its ionization energy and electron affinity
| (10) |
| (11) |
Here E(N) is the ground state energy of the N electron system, and f denotes some fraction of an electron. (The fundamental gap is thus a property of ground state systems, and in principle accessible within ground state DFT.) A related quantity is the optical gap, defined as the system’s first electronic excitation energy. Relaxation effects tend to make optical gaps smaller than fundamental gaps. However, the two are often rather similar in semiconductors.
Janak’s theorem24 allows the partial derivatives in eqn (11) to be expressed in terms of the exact highest-occupied Kohn–Sham eigenvalues as
| (12) |
where is the ith KS orbital energy for an N electron system. The exact Kohn–Sham energy is piecewise linear with respect to the number of electrons,46,47 such that is constant for 0 < f < 1. This lets us rewrite eqn (12) as
| (13) |
Rewriting eqn (13) in terms of quantities obtained from the N-electron system gives
| (14) |
| (15) |
| (16) |
The derivative discontinuity ΔXC(N) results from a discontinuous shift in vXC(r) as the electron number passes through integer values.92–94 This discontinuity is intrinsic to Kohn–Sham theory, and is generally nonzero for the exact exchange–correlation functional. Additionally, the many-electron self-interaction error of approximate exchange–correlation functionals makes their total energy E(N + f) generally nonlinear (and non-constant) for 0 < f < 1.41–43 Yang and coworkers have recently pointed out that this invalidates the approximation of eqn (13).44 This effect can produce significant errors in the Kohn–Sham band gaps predicted for continuous systems, even though the large system size gives an apparent linearity in E(N).45
It is common practice to approximate band gaps using the band energy differences of eqn (15). As we have seen, the band energy differences obtained from a semilocal exchange–correlation functional introduce several sources of error: errors in the orbital energies at integer occupancy, nonlinearities in orbital energies at fractional occupancy due to many-electron SIE, and neglect of the derivative discontinuity. In the remainder of this section, we show that HSE band energy differences can approximately correct for these sources of error.
Unlike LSDA and GGAs, hybrids like HSE include an approximate derivative discontinuity.44 This can be incorporated into the band energy differences of eqn (15) using the generalized Kohn–Sham (GKS) approach. GKS treatments of hybrid functionals replace the noninteracting Kohn–Sham reference system with a system containing some part of the electron-electron interaction.61,95,96 (For example, the HSE reference system contains 25% of the short-range interaction.) This interaction provides a nonlocal contribution to the exchange–correlation potential, similar to the nonlocal exchange present in Hartree–Fock theory. The resulting GKS band energy differences incorporate the functional’s approximate derivative discontinuity. For completeness, we note that hybrid functionals may also be treated within the Kohn–Sham framework. This requires using the optimized effective potential (OEP) method25–27,97–100 or approximations thereto99,101–106 to determine the local potential. However, OEP band energy differences lack the derivative discontinuity, which must be evaluated separately.44,90,92 Moreover, OEP has been shown to have computational and formal issues in finite Gaussian basis sets.103,104
In addition to incorporating a derivative discontinuity, HSE (like other hybrid functionals) can approximately correct for the other errors intrinsic to predicting band gaps from semilocal band energy differences. HSE’s inclusion of a fraction of one-electron-SIE-free HF exchange tends to correct for the effects of one-electron SIE on the orbital energies. Hartree–Fock and semilocal DFT functionals generally have opposite many-electron self-interaction errors,41–45 such that hybrids like HSE tend to reduce the many-electron SIE107 that makes eqn (13) a poor approximation for eqn (12). (The range-separated hybrid functional of ref. 73 was explicitly constructed to have minimal many-electron SIE.) It is interesting to note that inclusion of screened exchange makes HSE’s generalized Kohn–Sham reference system qualitatively similar to the quasiparticles used to evaluate the self-energy in many-body GW theory.17,61,108–111 HSE appears to provide a very good starting point for perturbative GW corrections, suggesting that the corrections are generally small.16,112
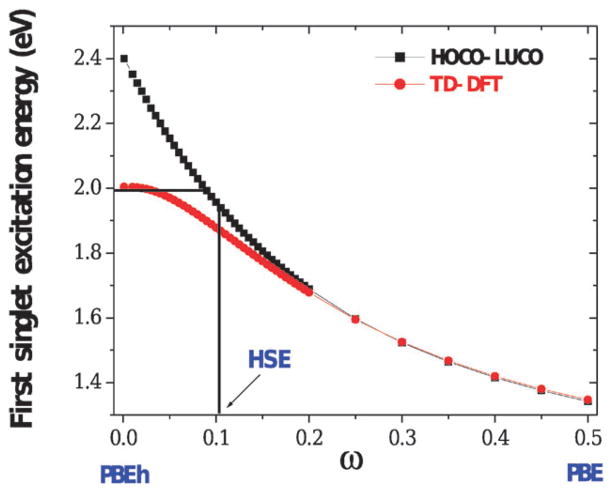
Brothers and coworkers recently provided a different rationalization of HSE’s success for semiconductor band gaps.113 The authors show that HSE’s GKS band energy differences reproduce the accurate optical gaps predicted by time-dependent density functional theory (TDDFT) calculations with the PBEh global hybrid.114 More generally, they show that band energy differences evaluated with screened HF exchange can always reproduce optical band gaps from TDDFT calculations with full-range HF exchange. The “excitonic” effects incorporated by nonlocal exchange were assessed more thoroughly in ref. 115. Importantly, for typical systems, the accurate TDDFT PBEh optical gaps were reproduced with a range-separation parameter ω that is fairly close to the fixed ω = 0.11 Bohr−1 of HSE06. Fig. 1 illustrates this for a model system, an infinite dimerized hydrogen chain with a nonzero band gap. This result helps rationalize HSE’s success. It also provides a motivation for the more sophisticated local-range-separated approximations discussed in section VI. The observation that HSE predicts optical rather than fundamental band gaps suggests that HSE will underestimate the fundamental band gaps of wide-bandgap systems. Numerical results in section V suggest that this is indeed the case.
Fig. 1.
Generalized Kohn–Sham band energy difference (“HOCO–LUCO”) and TDDFT first optical excitation energy for an infinite dimerized hydrogen chain. Results are evaluated for screened hybrids of the PBE GGA with 25% short-range HF exchange, and plotted as a function of the range-separation parameter ω. The GKS band gap, evaluated with the HSE06 ω=0.11 Bohr, is quite close to the accurate TDDFT optical excitation energy obtained with the full-range PBEh global hybrid (ω = 0).
B Approximate exchange holes
Another important aspect of HSE’s success appears to be the approximation used for the range-separated semilocal exchange. As discussed above, the HSE exchange–correlation functional incorporates 25% short-range HF exchange, 75% short-range PBE exchange, and 100%long-range PBE exchange. The short-range exchange energy predicted by a semilocal density functional is evaluated following eqn (7) as
| (17) |
Here is a semilocal model for the angle-averaged exchange hole about a σ-spin electron at point r1. (Physically, a reference electron at r1 digs an exchange–correlation “hole” hXC(r1,r2) in the density ρ(r2) about r1. This exchange–correlation hole gives the difference between the reference electron’s true interaction with the other N − 1 electrons, and its mean-field Coulomb interaction with the N-electron density ρ(r2).) The short-range HF exchange energy is obtained by substituting the exact exchange hole
| (18) |
(see eqn (7)) into eqn (17). The exchange hole obeys a number of exact constraints: for example, it is negative definite, normalized to −1, and equals −ρσ(r1) at interelectronic separation r12 = 0.
Several investigators have proposed model exchange holes that reproduce the energies of a “parent” semilocal exchange functional. Such models are nonunique. Even the LSDA exchange energy, which can be directly obtained from the exchange hole of the homogeneous electron gas, can also be constructed from non-oscillating models.116,117 HSE uses the PBE exchange hole model by Ernzerhof and Perdew,118 which obeys several exact constraints by construction. We showed in ref. 119 that the Ernzerhof and Perdew model appears to provide better range-separated hybrids than the simple and widely-used LSDA-based model of Iikura and coworkers.120 A long-range-corrected PBE functional (0% short-range, 100% long-range HF exchange, see ref. 72) using the Ernzerhof and Perdew hole model provided molecular thermochemistry and kinetics that were significantly more accurate than the same functional constructed using the hole model of Iikura and coworkers. The latter model has the wrong normalization and on-top curvature in inhomogeneous systems, and appears to yield results rather similar to range-separated LSDA. Thus, HSE’s success results at least in part from its accurate range-separated GGA exchange. One drawback of Ernzerhof and Perdew’s model is that the integral over r12 in eqn (17) cannot be performed fully analytically.121 More recent GGA hole models attempt to remedy this while still satisfying as many exact constraints as possible.68,70,71,119,122–124
V. Applications of HSE
This section provides an overview of recent applications of the Heyd–Scuseria–Ernzerhof screened hybrid functional. The discussion is organized according to the systems studied: beginning with molecular properties, and proceeding through semiconductors, d and f block materials, and surfaces and nanostructures. The results illustrate the power of the screened exchange approximation and provide a rationale for the more sophisticated successors to HSE discussed in section VI.
A Molecules
While it was designed for solids, the HSE functional provides a reasonably accurate treatment of small and medium-sized molecules. Table 1 reproduces results from ref. 125 on HSE’s performance for molecular thermochemistry, classical reaction barrier heights, and atomic total energies. HSE gives results comparable to its “parent” global hybrid PBEh, and is competitive with other global hybrid approximations. Results from the long-range-corrected hybrid LC-ωPBE (ref. 72) are discussed in section VI. We note that the computational benefits of screened exchange in extended systems are likely to carry over to large molecules. In such systems, HSE should provide results comparable to PBEh with a significantly reduced computational effort.
Table 1.
HSE’s performance for molecular properties. Mean absolute errors (MAE) in the G3 set of molecular heats of formation126 (kcal mol−1), the HTBH38 and NHTBH38 sets of hydrogen-transfer and non-hydrogen-transfer reaction barrier heights127,128 (kcal mol−1), and the total energies of atoms H–Ar (mH/electron). Results from ref. 125
| Functional | G3/99 | HTBH38 | NHTBH38 | Atoms |
|---|---|---|---|---|
| PBE | 22.2 | 9.7 | 8.6 | 8.6 |
| PBEh | 6.7 | 4.6 | 3.6 | 7.1 |
| LC-ωPBE | 4.3 | 1.3 | 2.4 | 5.1 |
| HSE06 | 4.9 | 4.6 | 3.9 | 6.2 |
B Semiconductors: band gaps, lattice parameters, and defects
Perhaps the most important success of HSE is its accurate treatment of semiconductors. An extensive study of 40 systems (35 semiconductors plus the insulators C (diamond), BN, AlN, MgO, MgS) compared experimental band gaps vs. band energy differences calculated with HSE and semilocal functionals. 129 Error statistics from this study are reproduced in Table 2. HSE dramatically improves the band gaps relative to the LSDA, the PBE33 GGA, and the TPSS130 meta-GGA. This study also showed that HSE provides the best overall predictions of lattice constants. A later study explicitly incorporating relativistic effects found comparable results.131 While several methods exist for predicting band gaps, HSE is rather unique in its ability to accurately treat both band gaps and other ground state properties, without incorporating material-dependent empirical parameters.
Table 2.
Band gap error statistics for 40 solids, from ref. 129. Mean errors (ME) and mean absolute errors (MAE) in eV
| LSDA | PBE | TPSS | HSE | |
|---|---|---|---|---|
| ME | −1.14 | −1.13 | −0.98 | −0.17 |
| MAE | 1.14 | 1.13 | 0.98 | 0.26 |
The accurate semiconductor band gaps shown in Table 2 were reproduced by Paier and coworkers in HSE calculations using plane-wave basis sets.132 This study showed that HSE improves upon the PBEGGA for the lattice constants and bulk moduli of a variety of solids, and is comparable to PBEh and somewhat degraded from PBE for atomization energies. The study also indicated some interesting deficiencies of HSE, possibly resulting from its use of a universal range-separation parameter ω and a universal fraction of short-range HF exchange. HSE apparently includes too much HF exchange in metals, where it tends to overestimate bandwidths. Conversely, it may include too little HF exchange in large-bandgap solids such as NaCl and Ar, where it underestimates the fundamental gap.132 However, we recall that the the arguments of ref. 113 suggest that HSE is more appropriate for optical gaps. Large optical gaps are difficult to characterize experimentally, but are generally smaller than the fundamental gap. Regardless, the position-dependent mixing functions and range separations discussed in section VI could provide a route to further exploring these effects. It is worth noting in this context that HSE appears to significantly improve upon the B3LYP global hybrid for lattice constants, bulk moduli, and atomization energies of several representative solids.133
In addition to these bulk properties, HSE can also accurately treat semiconductor defects. A recent study by Batista and coworkers showed that HSE accurately predicts the formation energy of silicon point defects, with results approaching computationally expensive diffusionMonte Carlo calculations.134 Such localized defect states are problematic for semilocal density functionals due to the delocalizing effects of self-interaction error.45 Accurate semilocal DFT treatments of defects tend to require additional approximations such as ad hoc surface energy corrections or functionals explicitly designed to treat surfaces.135 Ref. 134 also showed that HSE was the only tested density functional to accurately predict the energy difference between the semiconducting diamond and metallic β-tin phases of Si.
C Transition metals, lanthanides, and actinides
Another particularly successful application of HSE is to systems with a mixture of itinerant and localized electrons. Transition metal d electrons, and lanthanide and actinide f electrons, can either participate in metallic bonding or localize to atoms where they contribute to magnetic properties. 8 The delicate balance between itinerancy and localization can produce multiple competing ground states and phases. A proper theoretical description requires adequate treatment of the strong electron correlations that lead to electron localization. Semilocal density functionals appear to lack this, and often yield qualitatively incorrect predictions for the band gaps and magnetic properties of such systems. Explicit localization,136 “scissor operator” methods,137 or LDA+U138,139 can provide useful insights into these problems. However, the rather ad hoc nature of such approaches makes them problematic for treating new materials. In contrast, HSE has been shown to provide accurate treatments of many such systems, without the need for system-dependent adjustable parameters or decisions of which electrons to localize.
Hay and coworkers showed that HSE correctly predicts lattice constants and band gaps of the lanthanide oxides CeO2 and Ce2O3.140 Similar results were obtained in plane-wave calculations by Da Silva and coworkers, who also indicated some deficiencies in the thermochemical predictions.141 (The role of HF exchange in lanthanide oxides was previously illustrated in the Hartree–Fock calculations of Gennard and coworkers.142) Prodan and coworkers showed that HSE provides an accurate treatment of some uranium and plutonium oxides, including a correction to the metallic behavior predicted by semilocal functionals. 143 A later systematic study of actinide dioxides showed an interesting transition between localized vs. itinerant behavior, resulting from coupling between the actinide f and oxygen 2p bands.144 Uddin and coworkers showed that HSE, unlike semilocal functionals, predicts a nonzero band gap for platinum oxide.145 Applications to platinum nitride were also reported.146 Marsman and coworkers used plane-wave calculations to demonstrate that HSE is significantly more accurate than LSDA for the band gaps, lattice constants, and local spin magnetic moments of a small set of transition metal monoxides.147 However, ref. 132 showed that HSE overestimates the magnetic moment of Fe. Kasinathan and coworkers studied the pressuredependent Mott transition of MnO using a variety of localization corrections: LDA+U, explicit Perdew–Zunger37 one-electron self-interaction corrections, approximate pseudopotential SIC, and HSE.148 The role of HF exchange in the balance between localization and itinerancy was also explored by Doll and coworkers in B3LYP investigations of gadolinium nitride.149
D Molecules at surfaces
In a recent application to surface chemistry, HSE has provided a partial solution to the “CO/Pt(111) puzzle”.150 The (111) surfaces of cubic-close-packed metals are composed of triangles of metal atoms. Adsorbates such as CO (carbon monoxide) may bind on top of a single surface atom, to a bridge site between two surface atoms, or in a threefold site equidistant from three surface atoms. A simplified picture of the metal–CO bond is a σ bond from the lone pair on C, plus π backbonding from the metal into unoccupied CO π orbitals.151 While the σ bond is strongest at the top site, the π backbonding is increased at threefold sites. CO is known experimentally to preferentially bind top sites at low coverage. However, an extensive survey showed that semilocal density functionals predict binding at threefold sites at low coverage.150 This has been rationalized as a consequence of the underestimated HOMO–LUMO gap predicted by semilocal functionals, leading to excessive π backbonding and an incorrect site ordering.151 (Semilocal functionals systematically under-estimate HOMO–LUMO gaps due to the derivative discontinuity and self interaction errors discussed in section IV A).
Stroppa and coworkers showed that hybrid functionals, including HSE and PBEh, reduce the π backbonding and predict binding preferences that are closer to experiment.152 Similar results were obtained by Doll for the B3LYP global hybrid.153 However, the authors of ref. 152 also argued that HSE’s overestimate of metal bandwidths increases the π backbonding, such that the threefold site is still weakly favored for Pt(111).152 This result provides an interesting rationalization for more sophisticated functionals incorporating a position-dependent admixture of HF exchange (section VI). Functionals incorporating less HF exchange than HSE in metallic regions, and the same amount of HF exchange as HSE in molecules, should provide smaller metal bandwidths and improved site predictions.
E Carbon nanostructures
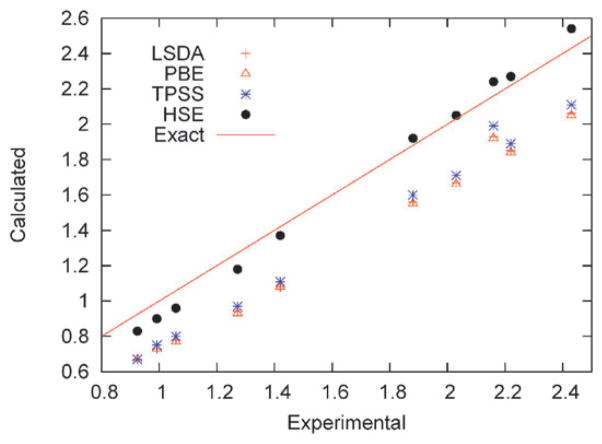
HSE has been extensively applied to carbon nanostructures such as nanotubes and nanoribbons. The screened exchange approximation is invaluable for such systems due to their large unit cells. Barone and coworkers showed that HSE provides accurate first optical excitation energies and optical spectra for metallic nanotubes,154 with accuracy comparable to previous global hybrid calculations on semiconducting nanotubes.155 Fig. 2 illustrates the HSE excitation energy predictions. HSE was also used to investigate the work functions of pristine and doped semiconducting nanotubes.156
Fig. 2.
Calculated versus experimental first optical excitation energies (eV) for metallic and semiconducting single-wall carbon nanotubes (ref. 154). The LSDA and PBE results are nearly indistinguishable on this scale.
An important recent application has been to semiconducting graphene nanoribbons, one-dimensionally periodic strips of a single layer of graphite. Density functional calculations predict zigzag nanoribbons these systems to be spin-polarized, with ↑ spin polarization on one side of the ribbon and ↓ on the other. These have been proposed as “half-metallic” systems that could preferentially conduct one spin flavor under the influence of transverse electric fields157 or asymmetric edge substitution.158 Recent HSE calculations on armchair nanoribbons predict width-dependent band gap oscillations similar to those found in tight-binding calculations. 159,160 The HSE predictions were later confirmed experimentally. 161,162 A detailed study of edge substitution suggested that edge oxidation could enhance the half-metallic behavior of zigzag graphene nanoribbons, lowering the applied field needed to induce half-metallicity.163 A particularly interesting set of recent studies suggests that the spin polarization predicted for nanoribbons may also occur in finite graphene nanoparticles.164,165
F Other systems
The HSE screened hybrid has begun to be applied in a number of other fields. A recent benchmark study showed that HSE provides rather accurate results for molecular vibrational frequencies, infrared intensities, and Raman activities.166 This suggests that HSE may be applicable to modeling properties such as surface-enhanced vibrational spectroscopy of molecules at metal surfaces.167 A density functional study of the large organometallic dye copper phthalocyanine showed that the HSE orbital energies provide a reasonable approximation to the experimental photoelectron spectrum.168 A study of polymeric nitrogen has relevance to energy storage via high energy density materials.169 A recent HSE simulation of a large water cluster provided a significant milestone in applying hybrid functionals to ab initio molecular dynamics simulations.170 HSE has also been applied to magnetic coupling in molecular systems.171 Such applications will be enriched by the successors to HSE discussed below.
VI. Successors to HSE
The survey presented in section V suggests that, while the HSE exchange–correlation functional is quite accurate for a variety of systems, it is limited by its use of a constant fraction of short-range exchange and a constant range-separation parameter ω in all materials. That these are limitations is unsurprising, as PBE (ω → ∞) and PBE hybrid (ω → 0) are respectively good for metals33 and optimal for molecules.59 In fact, it is rather surprising how well HSE works with fixed parameters (see e.g. ref. 113). Regardless, our recent work has involved constructing successors to HSE by developing more flexible admixtures of range-separated exchange. We discuss three approaches: multiple range separation, local admixture of screened exchange, and local range separation.
A Multiple range separation
Our first attempt at extending HSE is the multiple-range-separated hybrid of Henderson, Izmaylov, Scuseria, and Savin (HISS).125,172 This functional was inspired by the work of Vydrov and coworkers, who showed that admixture of either short-range or long-range HF exchange improves molecular thermochemistry and reaction barriers relative to semilocal functionals.75 It was also inspired by the observation that HSE gives rather poor predictions for chemical reaction barriers in molecules: comparable to PBE hybrid, but significantly worse than the long-range-corrected LC-ωPBE functional (see Table 1).72,121 But while LC-ωPBE performs very well for molecular systems, it is neither computationally efficient nor particularly accurate in solids, for which its inclusion of 100% long-range HF exchange is problematic.
The HISS functional is a three-range hybrid that attempts to combine the strengths of HSE and LC-ωPBE (i.e. to yield accurate thermochemistry and reaction barriers, while giving an efficient and accurate treatment of the electronic structure of extended systems). To this end, it writes the exchange–correlation energy as
| (19) |
where the middle range “MR” of the Coulomb operator 1/r12 is defined by
| (20) |
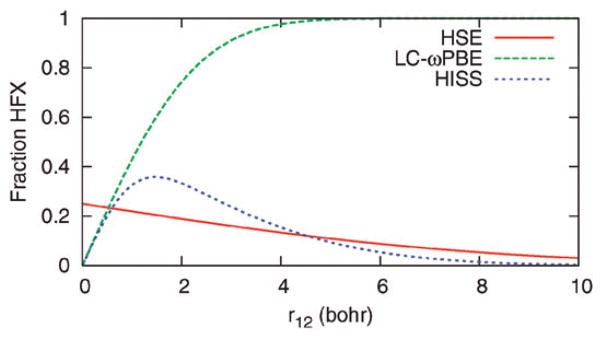
and cMR, ωSR and ωLR are empirical parameters. The current HISS functional (“HISS-B” in ref. 172) uses cMR = 0.6. Fig. 3 shows the fraction of HF exchange included by HSE, HISS, and LC-ωPBE as a function of interelectronic separation r12.
Fig. 3.
Fraction of HF exchange included as a function of interelectronic separation r12. Screened hybrid HSE, long-range-corrected hybrid LC-ωPBE, and middle-range hybrid HISS.
Preliminary investigations show that the HISS functional provides accuracy generally comparable to that of LC-ωPBE for diverse molecular properties such as thermochemistry, reaction barriers, geometries and vibrational frequencies, and so on.125 At the same time, it provides an accurate treatment of semiconductor band gaps (noting, however, that while HSE somewhat underestimates band gaps (Table 2), HISS tends to slightly overestimate them). These results are encouraging and suggest that HISS may be able to properly describe reactions at surfaces or barriers in solids (e.g. barriers to defect formation or mobility). However, further investigations are necessary.
B Local admixture of screened exchange
A second approach to extending HSE is to introduce a position-dependent admixture of short-range exact exchange, while keeping the range-separation parameter ω constant. This is a straightforward generalization of existing local hybrid functionals.173–182 Local hybrid functionals contain a position-dependent fraction of HF exchange, giving an exchange–correlation energy
| (21) |
Here is the energy obtained from a semilocal exchange–correlation functional and is the σ-spin exchange energy density predicted by the corresponding exchange functional. (The rest of this section suppresses spin dependence for conciseness.) The HF exchange energy density (in the conventional gauge183,182) is constructed from eqn (7) and (8) as
| (22) |
A local hybrid’s performance is governed by the choice of mixing function f(r) and the choice of semilocal exchange functional. The general local hybrid form was suggested by Burke and coworkers183 as early as 1998, but specific forms of f(r) were not proposed or implemented until later.36,173 Jaramillo, Scuseria, and Ernzerhof173 were the first to propose and implement a local hybrid with
| (23) |
| (24) |
(The kinetic energy τ(r) is defined in eqn (6).) This mixing function correctly incorporates no HF exchange in the uniform electron gas, where combinations of full-range HF exchange and semilocal correlation are problematic as discussed above. It incorporates 100% HF exchange in one-electron regions where HF exchange is the exact exchange–correlation functional. Unfortunately, its thermochemical performance is rather poor.173 Later, Kaupp and coworkers175,177,179 showed that empirically parameterized mixing functions can provide accurate molecular thermochemistry and reaction barriers in local hybrids of LSDA exchange. These authors also developed a self-consistent treatment of local hybrids using the LHF/CEDA approximation to the optimized effective potential. 174,178 We recently presented nonlocal density matrix similarity metrics that show promise for constructing local hybrids of LSDA and GGA exchange.176,180
We have begun exploring local hybridization of short-range HF exchange. This approach should enable straightforward extension of local hybrids to metals and narrow-bandgap semiconductors. Our preliminary results involve a local admixture of short-range HF exchange into LSDA, using the empirical mixing function f(r) = ατW/τ proposed in ref. 175. Numerical tests with the HSE06 range separation parameter ω = 0.11 Bohr−1 and α ~ 1/2 give molecular thermochemistry comparable to HSE, and reaction barriers that improve somewhat upon HSE.184
C Local range separation
Our most sophisticated approach to extending HSE is to let the range-separation parameter ω of eqn (9) be an explicit function of position: ω = ω(r). This approach was previously suggested by Toulouse and coworkers for semilocal DFT correlation.70 There are two difficulties inherent to this approach: the choice of the functional form of ω(r), and the evaluation of the corresponding local-range-separated HF exchange. We will discuss these issues in brief here; for a more through discussion, see ref. 185.
The first question facing this approach is how to define ω(r). One route is to exploit the connections between this term and the microscopic dielectric constant of many-body GW calculations. 61,110 Another is to select ω(r) such that the total exchange hole, obtained as the sum of range-separated HF and DFT model exchange holes, is properly normalized to −1 at each point. Assuming that ω(r) can be written as a semilocal functional of the density and the density gradient, simple dimensional arguments imply that ω(r) = kF(r)F(s(r)), where kF = (3π2ρ)1/3, s = |∇ρ|/(2kFρ), and F(s) is arbitrary. Preliminary empirical tests of F(s) = α + βs + γs2 suggests that F(s) ≈ βs suffices.
The second and more daunting question is how to evaluate the HF exchange energy density given a position dependent ω. This can be written in a straightforward generalization of eqn (22) as
| (25) |
(Spin dependence is again suppressed for conciseness.) However, like eqn (22), this expression is unsuitable for practical computation as it requires the integration with respect to r′ to be carried out anew at each point r. Assuming that the integration with respect to r is done numerically, the total computational cost of evaluating the local-range-separated HF exchange energy becomes , where Ngrid is the size of the numerical integration grid and NAO is the size of the atomic orbital (AO) basis set. Conventional local hybrids generally use the resolution of the identity approximation introduced by Della Sala and Görling.99 This yields an expression for the HF-type exchange energy density
| (26) |
Here {χμ(r)} is the AO basis and the matrix Q is given by
| (27) |
If the AO basis set is used for the resolution of the identity, P is the one-particle density matrix in the AO basis, S is the overlap matrix, and
| (28) |
| (29) |
is the matrix representation of the HF exchange operator. This may be extended to range-separation interactions by screening the two-electron integrals in eqn (29). However, in the case that ω is also position dependent, we would have a different matrix Q(r) at every point in space r, and the computational savings of the resolution of the identity approximation would be negligible.
To date there is no ideal solution to this problem. Recently, Krukau, Scuseria, Perdew, and Savin185 proposed to approximate the HF exchange hole using a semilocal model. This model exchange hole123 takes the unscreened (full-range) HF exchange energy density as a parameter, and is constructed to yield this input exchange energy density in the full-range limit. The authors used this model exchange hole to evaluate eqn (25). Early results have been encouraging, but further work is needed. Other approaches, which attempt to directly approximate the integral of eqn (25), are also being pursued.
VII. Concluding remarks
The screened exchange approximation appears to be a very powerful tool for density functional treatments of condensed systems. The HSE screened hybrid provides a reasonably accurate and computationally tractable treatment of ground-state properties and band energies, while incorporating only a single, universal empirical parameter. Its successors also show a great deal of promise. However, we can identify several unresolved formal and computational issues, as well as applications that require more detailed investigations.
While the formal details of range-separated DFT exchange have been extensively investigated over the past two decades, several interesting issues remain. One is to further elucidate the connections between the screened exchange of HSE and the screened exchange present in many-body GW theory. Such investigations may provide new insight into appropriate choices for the local range separation parameters and local exchange admixtures in HSE’s successors. We are particularly interested in nonempirical treatments of these quantities.
The computational issues inherent to range-separated hybrids also remain important. Despite extensive efforts towards computationally efficient implementations, HSE is still rather more expensive than semilocal functionals. Another significant problem is the need for a computationally tractable treatment of the locally-range-separated HF exchange energy density of eqn (25). We are also interested in extending local hybrids of range-separated exchange to solids. Finally, we hope at some point to resolve the “paradox” of screened hybrids at metal surfaces: long-range exact exchange is intractable in the bulk metal, but likely to be essential above the metal surface.
We are actively pursuing applications of HSE and its successors to new systems. We are particularly interested in applying HISS and local-range-separated functionals to metal bandwidths and CO adsorbtion, properties that were identified as problematic for HSE. We plan to apply HISS to defect migration in solids, in the hope that its accurate treatment of molecular reaction barriers will carry over to condensed systems. We are interested in further applications of HSE and its successors to reactions and spectroscopy at metal surfaces. Such systems, which bridge the divide between molecules and solids, seem ideally suited for screened hybrid functionals. We hope that these theoretical and computational investigations will yield new insight into fundamental and practical improvements to the density functional theory for extended systems.
Acknowledgments
This work was supported by the National Science Foundation (CHE-0807194), the Department of Energy (DE-FG02-04ER15523), ARO-MURI (DAAD-19-03-1-0169), and the Welch Foundation (C-0036). BGJ acknowledges additional support from a training fellowship from the National Library of Medicine to the Keck Center for Interdisciplinary Bioscience Training of the Gulf Coast Consortium (5T15LM07093).
Biographies

Benjamin G. Janesko joined the group after a PhD with David Yaron at Carnegie Mellon University. He has worked on local hybrid functionals and models of surface-enhanced vibrational spectroscopy.

Thomas M. Henderson joined the group after a PhD with Rodney Bartlett at the University of Florida and a postdoc at the Tyndall National Institute in Ireland. He has worked on range-separated and locally-range separated hybrid functionals.

Gustavo E. Scuseria is the Robert A. Welch Professor of Chemistry at Rice University. He is Associate Editor of the Journal of Chemical Theory and Computation. During the last 25 years, his research group has pioneered methodologies in coupled cluster theory, linear scaling electronic structure methods, and density functional theory, especially for periodic systems with main applications fullerenes, carbon nanotubes, graphene nanoribbons, and bulk actinide oxides.
References
- 1.Hoffmann MR, Martin ST, Choi W, Bahnemann DW. Chem Rev. 1995;95:69. [Google Scholar]
- 2.Kudo A, Kato H, Tsuji I. Chem Lett. 2004;33:1534. [Google Scholar]
- 3.Ogawa T, Akabori M, Kobayashi F, Haire RG. J Nucl Mater. 1997;247:215. [Google Scholar]
- 4.Ogawa T, Kobayashi F, Sato T, Haire RG. J Alloys Compd. 1998;271:347. [Google Scholar]
- 5.Bloch F. Z Phys. 1928;52:555. [Google Scholar]
- 6.Slater JC. Phys Rev. 1951;81:385. [Google Scholar]
- 7.Slater JC, Kostler GF. Phys Rev. 1954;94:1498. [Google Scholar]
- 8.Harrison WA. Solid State Theory. McGraw-Hill Book Company; New York: 1970. [Google Scholar]
- 9.Parr RG, Yang W. Density-Functional Theory of Atoms and Molecules. Oxford University Press; New York: 1989. [Google Scholar]
- 10.Dreizler M, Gross EKU. Density Functional Theory: An Approach to the Quantum Many-Body Problem. Springer; Berlin: 1990. [Google Scholar]
- 11.Hohenberg P, Kohn W. Phys Rev. 1964;B136:864. [Google Scholar]
- 12.Martin RM. Electronic Structure: Basic Theory and Practical Methods. Cambridge University Press; Cambridge: 2004. [Google Scholar]
- 13.Scuseria GE, Staroverov VN. In: Theory and Applications of Computational Chemistry: The First 40 Years. Dykstra CE, Frenking G, Kim KS, Scuseria GE, editors. Elsevier; Amsterdam: 2005. [Google Scholar]
- 14.Kurth S, Perdew JP, Blaha P. Int J Quantum Chem. 1999;75:889. [Google Scholar]
- 15.Fuchs M, Bockstedte M, Pehlke E, Scheffler M. Phys Rev B. 1998;57:2134. doi: 10.1103/physrevb.52.2550. [DOI] [PubMed] [Google Scholar]
- 16.Fuchs F, Furthmüller J, Bechstedt F, Shishkin M, Kresse G. Phys Rev B. 2007;76:115109. [Google Scholar]
- 17.Bylander DM, Kleinman L. Phys Rev B. 1990;41:7868. doi: 10.1103/physrevb.41.7868. [DOI] [PubMed] [Google Scholar]
- 18.Staroverov VN, Scuseria GE, Tao J, Perdew JP. Phys Rev B. 2004;69:075102. [Google Scholar]
- 19.Becke AD. J Chem Phys. 1993;98:5648. [Google Scholar]
- 20.Stephens PJ, Devlin FJ, Chabalowski CF, Frisch MJ. J Phys Chem. 1994;98:11623. [Google Scholar]
- 21.Heyd J, Scuseria GE, Ernzerhof M. J Chem Phys. 2003;118:8207. [Google Scholar]; Heyd J, Scuseria GE, Ernzerhof M. J Chem Phys. 2006;124:219906E. [Google Scholar]
- 22.Levy M. Proc Natl Acad Sci U S A. 1979;76:6062. doi: 10.1073/pnas.76.12.6062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lieb EH. Int J Quantum Chem. 1983;24:243. [Google Scholar]
- 24.Janak JF. Phys Rev B. 1978;18:7165. [Google Scholar]
- 25.Ivanov S, Hirata S, Bartlett RJ. Phys Rev Lett. 1999;83:5455. [Google Scholar]
- 26.Görling A. Phys Rev Lett. 1999;83:5459. [Google Scholar]
- 27.Yang W, Wu Q. Phys Rev Lett. 2002;89:143002. doi: 10.1103/PhysRevLett.89.143002. [DOI] [PubMed] [Google Scholar]
- 28.Grabowski I, Hirata S, Ivanov S, Bartlett RJ. J Chem Phys. 2002;116:4415. doi: 10.1063/1.1809605. [DOI] [PubMed] [Google Scholar]
- 29.Bartlett RJ, Grabowski I, Hirata S, Ivanov S. J Chem Phys. 2005;122:034104. doi: 10.1063/1.1809605. [DOI] [PubMed] [Google Scholar]
- 30.Bartlett RJ, Schweigert IV, Lotrich VF. THEOCHEM. 2006;771:1. [Google Scholar]
- 31.Langreth DC, Mehl MJ. Phys Rev Lett. 1981;47:446. [Google Scholar]
- 32.Becke AD. Phys Rev A. 1988;38:3098. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 33.Perdew JP, Burke K, Ernzerhof M. Phys Rev Lett. 1996;77:3865. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]; Perdew JP, Burke K, Ernzerhof M. Phys Rev Lett. 1997;78:1396E. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 34.Perdew JP, Wang Y. Phys Rev B. 1992;45:13244. doi: 10.1103/physrevb.45.13244. [DOI] [PubMed] [Google Scholar]
- 35.Perdew JP, Chevary JA, Vosko SH, Jackson KA, Pederson MR, Singh DJ, Fiolhais C. Phys Rev B. 1992;46:6671. doi: 10.1103/physrevb.46.6671. [DOI] [PubMed] [Google Scholar]
- 36.Perdew JP, Schmidt K. In: Density Functional Theory and its Application to Materials. Van Doren V, Van Alsenoy C, Geerlings P, editors. American Institute of Physics; 2001. [Google Scholar]
- 37.Perdew JP, Zunger A. Phys Rev B. 1981;23:5048. [Google Scholar]
- 38.Vydrov OA, Scuseria GE. J Chem Phys. 2004;121:8187. doi: 10.1063/1.1794633. [DOI] [PubMed] [Google Scholar]
- 39.Vydrov OA, Scuseria GE. J Chem Phys. 2005;122:184107. doi: 10.1063/1.1897378. [DOI] [PubMed] [Google Scholar]
- 40.Vydrov OA, Scuseria GE, Perdew JP, Ruzsinszky A, Csonka GI. J Chem Phys. 2006;124:094108. doi: 10.1063/1.2176608. [DOI] [PubMed] [Google Scholar]
- 41.Ruzsinszky A, Perdew JP, Csonka GI, Vydrov OA, Scuseria GE. J Chem Phys. 2006;125:194112. doi: 10.1063/1.2387954. [DOI] [PubMed] [Google Scholar]
- 42.Mori-Sánchez P, Cohen AJ, Yang W. J Chem Phys. 2006;125:201102. doi: 10.1063/1.2403848. [DOI] [PubMed] [Google Scholar]
- 43.Vydrov OA, Scuseria GE, Perdew JP. J Chem Phys. 2007;126:154109. doi: 10.1063/1.2723119. [DOI] [PubMed] [Google Scholar]
- 44.Cohen AJ, Mori-Sánchez P, Yang W. Phys Rev B. 2008;77:115123. doi: 10.1103/PhysRevLett.100.146401. [DOI] [PubMed] [Google Scholar]
- 45.Mori-Sánchez P, Cohen AJ, Yang W. Phys Rev Lett. 2008;100:146401. doi: 10.1103/PhysRevLett.100.146401. [DOI] [PubMed] [Google Scholar]
- 46.Perdew JP, Parr RG, Levy M, Balduz JL., Jr Phys Rev Lett. 1982;49:1691. [Google Scholar]
- 47.Yang W, Zhang Y, Ayers PW. Phys Rev Lett. 2000;84:5172. doi: 10.1103/PhysRevLett.84.5172. [DOI] [PubMed] [Google Scholar]
- 48.Gritsenko OV, Schipper PRT, Baerends EJ. J Chem Phys. 1997;107:5007. [Google Scholar]
- 49.Cremer D. Mol Phys. 2001;99:1899. [Google Scholar]
- 50.Baerends EJ, Gritsenko OV. J Chem Phys. 2005;123:062202. doi: 10.1063/1.1904566. [DOI] [PubMed] [Google Scholar]
- 51.Becke AD. J Chem Phys. 1993;98:1372. [Google Scholar]
- 52.Heyd J, Scuseria GE. J Chem Phys. 2004;121:1187. doi: 10.1063/1.1760074. [DOI] [PubMed] [Google Scholar]
- 53.Zecca L, Gori-Giorgi P, Moroni S, Bachelet GB. Phys Rev B. 2004;70:205127. [Google Scholar]
- 54.Monkhorst HJ. Phys Rev B. 1979;20:1504. [Google Scholar]
- 55.Delhalle J, Calais JL. Phys Rev B. 1987;35:9460. doi: 10.1103/physrevb.35.9460. [DOI] [PubMed] [Google Scholar]
- 56.Gell-Mann M, Brueckner KA. Phys Rev. 1957;106:364. [Google Scholar]
- 57.Adamo C, Barone V. J Chem Phys. 1999;110:6158. [Google Scholar]
- 58.Ernzerhof M, Scuseria GE. J Chem Phys. 1999;110:5029. [Google Scholar]
- 59.Perdew JP, Ernzerhof M, Burke K. J Chem Phys. 1996;105:9982. [Google Scholar]
- 60.Krukau AV, Vydrov OA, Izmaylov AF, Scuseria GE. J Chem Phys. 2006;125:224106. doi: 10.1063/1.2404663. [DOI] [PubMed] [Google Scholar]
- 61.Seidl A, Görling A, Vogl P, Majewski JA, Levy M. Phys Rev B. 1996;53:3764. doi: 10.1103/physrevb.53.3764. [DOI] [PubMed] [Google Scholar]
- 62.Gill PMW, Adamson RD. Chem Phys Lett. 1996;261:105. [Google Scholar]
- 63.Adamson RD, Dombroski JP, Gill PMW. Chem Phys Lett. 1996;254:329. [Google Scholar]
- 64.Gill PMW, Adamson RD, Pople JA. Mol Phys. 1996;88:1005. [Google Scholar]
- 65.Savin A, Flad HJ. Int J Quantum Chem. 1995;56:327. [Google Scholar]
- 66.Leininger T, Stoll H, Werner HJ, Savin A. Chem Phys Lett. 1997;275:151. [Google Scholar]
- 67.Toulouse J, Colonna F, Savin A. Phys Rev A. 2004;70:062505. [Google Scholar]
- 68.Toulouse J, Savin A, Flad HJ. Int J Quantum Chem. 2004;100:1047. [Google Scholar]
- 69.Henderson TM, Bartlett RJ. Phys Rev A. 2004;70:022512. [Google Scholar]
- 70.Toulouse J, Colonna F, Savin A. J Chem Phys. 2005;122:014110. doi: 10.1063/1.1824896. [DOI] [PubMed] [Google Scholar]
- 71.Goll E, Werner HJ, Stoll H. Phys Chem Chem Phys. 2005;7:3917. doi: 10.1039/b509242f. [DOI] [PubMed] [Google Scholar]
- 72.Vydrov OA, Scuseria GE. J Chem Phys. 2006;125:234109. doi: 10.1063/1.2409292. [DOI] [PubMed] [Google Scholar]
- 73.Cohen AJ, Mori-Sánchez P, Yang W. J Chem Phys. 2007;126:191109. doi: 10.1063/1.2741248. [DOI] [PubMed] [Google Scholar]
- 74.Stoll H, Savin A. In: Density Functional Methods in Physics. Dreizler R, da Providencia J, editors. Plenum; New York: 1985. p. 177. [Google Scholar]
- 75.Vydrov OA, Heyd J, Krukau AV, Scuseria GE. J Chem Phys. 2006;125:074106. doi: 10.1063/1.2244560. [DOI] [PubMed] [Google Scholar]
- 76.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA, Jr, Vreven T, Scalmani G, Mennucci B, Barone V, Petersson GA, Caricato M, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Li X, Hratchian HP, Peralta JE, Izmaylov AF, Kudin KN, Heyd JJ, Brothers E, Staroverov VN, Zheng G, Kobayashi R, Normand J, Sonnenberg JL, Ogliaro F, Bearpark M, Parandekar PV, Ferguson GA, Mayhall NJ, Iyengar SS, Tomasi J, Cossi M, Rega N, Burant JC, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Chen W, Wong MW, Pople JA. Gaussian Development Version, Revision G.01. Gaussian, Inc; Wallingford CT: 2007. [Google Scholar]
- 77.Kudin KN, Scuseria GE. Phys Rev B. 2000;61:16440. [Google Scholar]
- 78.Izmaylov AF, Scuseria GE, Frisch MJ. J Chem Phys. 2006;125:104103. doi: 10.1063/1.2347713. [DOI] [PubMed] [Google Scholar]
- 79.Izmaylov AF, Scuseria GE. J Chem Phys. 2007;127:144106. doi: 10.1063/1.2790024. [DOI] [PubMed] [Google Scholar]
- 80.Izmaylov AF, Brothers EN, Scuseria GE. J Chem Phys. 2006;125:224105. doi: 10.1063/1.2404667. [DOI] [PubMed] [Google Scholar]
- 81.Ayala PY, Kudin KN, Scuseria GE. J Chem Phys. 2001;115:9698. [Google Scholar]
- 82.Izmaylov AF, Scuseria GE. Phys Chem Chem Phys. 2008;10:3421. doi: 10.1039/b803274m. [DOI] [PubMed] [Google Scholar]
- 83.Kudin KN, Bettinger HF, Scuseria GE. Phys Rev B. 2001;63:045413. [Google Scholar]
- 84.Improta R, Barone V, Kudin KN, Scuseria GE. J Am Chem Soc. 2001;123:3311. doi: 10.1021/ja003680e. [DOI] [PubMed] [Google Scholar]
- 85.Towler MD, Zupan A, Causà M. Comp Phys Comm. 1996;98:181. [Google Scholar]
- 86.Dovesi R, Saunders VR, Roetti C, Orlando R, Zicovich-Wilson CM, Pascale F, Civalleri B, Doll K, Harrison NM, Bush IJ, D’Arco Ph, Llunell M. CRYSTAL06 User’s Manual. University of Torino; Torino: 2006. [Google Scholar]
- 87.Kresse G, Hafner J. Phys Rev B. 1993;48:13115. doi: 10.1103/physrevb.48.13115. [DOI] [PubMed] [Google Scholar]
- 88.Kresse G, Furthmüller J. Comput Mater Sci. 1996;6:15. [Google Scholar]
- 89.Kresse G, Furthmüller J. Phys Rev B. 1996;54:11169. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
- 90.Rinke P, Qteish A, Neugebauer J, Scheffler M. Phys Status Solidi B. 2008;245:929. [Google Scholar]
- 91.Kümmel S, Kronik L. Rev Mod Phys. 2008;80:3. [Google Scholar]
- 92.Perdew JP, Levy M. Phys Rev Lett. 1983;51:1884. [Google Scholar]
- 93.Sham LJ, Schlüter M. Phys Rev Lett. 1983;51:1888. [Google Scholar]
- 94.Godby RW, Schlüter M, Sham LJ. Phys Rev Lett. 1986;56:2415. doi: 10.1103/PhysRevLett.56.2415. [DOI] [PubMed] [Google Scholar]
- 95.Neumann R, Nobes RH, Handy NC. Mol Phys. 1996;87:1. [Google Scholar]
- 96.The wavefunction of the interacting GKS reference system may be treated with multideterminant methods, as in ref. 64–73. However, we restrict ourselves here to single-determinant treatments.
- 97.Sharp RT, Horton GK. Phys Rev. 1953;90:317. [Google Scholar]
- 98.Talman JD, Shadwick WF. Phys Rev A. 1976;14:36. [Google Scholar]
- 99.Della Sala F, Görling A. J Chem Phys. 2001;115:5718. [Google Scholar]
- 100.Krieger JB, Li Y, Iafrate GJ. Phys Rev A. 1992;45:101. doi: 10.1103/physreva.45.101. [DOI] [PubMed] [Google Scholar]
- 101.Krieger JB, Li Y, Iafrate GJ. Phys Rev A. 1992;46:5453. doi: 10.1103/physreva.46.5453. [DOI] [PubMed] [Google Scholar]
- 102.Gritsenko OV, Baerends EJ. Phys Rev A. 2001;64:042506. [Google Scholar]
- 103.Staroverov VN, Scuseria GE, Davidson ER. J Chem Phys. 2006;124:114103. doi: 10.1063/1.2194546. [DOI] [PubMed] [Google Scholar]
- 104.Izmaylov AF, Staroverov VN, Scuseria GE, Davidson ER. J Chem Phys. 2007;127:084113. doi: 10.1063/1.2768351. [DOI] [PubMed] [Google Scholar]
- 105.Staroverov VN, Scuseria GE, Davidson ER. J Chem Phys. 2006;125:081104. doi: 10.1063/1.2345650. [DOI] [PubMed] [Google Scholar]
- 106.Izmaylov AF, Staroverov VN, Scuseria GE, Davidson ER, Stoltz G, Cancés E. J Chem Phys. 2007;126:084107. doi: 10.1063/1.2434784. [DOI] [PubMed] [Google Scholar]
- 107.Vydrov OA, Scuseria GE, Perdew JP. J Chem Phys. 2007;126:154109. doi: 10.1063/1.2723119. [DOI] [PubMed] [Google Scholar]
- 108.Hedin L. Phys Rev. 1965;139:A796. [Google Scholar]
- 109.Gygi F, Baldereschi A. Phys Rev Lett. 1989;62:2160. doi: 10.1103/PhysRevLett.62.2160. [DOI] [PubMed] [Google Scholar]
- 110.Sánchez-Friera P, Godby RW. Phys Rev Lett. 2000;85:5611. doi: 10.1103/PhysRevLett.85.5611. [DOI] [PubMed] [Google Scholar]
- 111.Onida G, Reining L, Rubio A. Rev Mod Phys. 2002;74:601. [Google Scholar]
- 112.Schleife A, Rödl C, Fuchs F, Furthmüller J, Bechstedt F. Appl Phys Lett. 2007;91:241915. [Google Scholar]
- 113.Brothers EN, Izmaylov AF, Normand JO, Barone V, Scuseria GE. J Chem Phys. 2008;129:011102. doi: 10.1063/1.2955460. [DOI] [PubMed] [Google Scholar]
- 114.The PBEh global hybrid of full-range HF exchange provides accurate TDDFT valence excitations in molecules.57,186–188 While PBEh TDDFT has not been extensively investigated in extended systems, it seems reasonable to assume that similar accuracy will be achieved.
- 115.Izmaylov AF, Scuseria GE. J Chem Phys. 2008;129:034101. doi: 10.1063/1.2953701. [DOI] [PubMed] [Google Scholar]
- 116.Perdew JP, Wang Y. Phys Rev B. 1992;46:12947. doi: 10.1103/physrevb.46.12947. [DOI] [PubMed] [Google Scholar]; Perdew JP, Wang Y. Phys Rev B. 1997;56:7018E. [Google Scholar]
- 117.Gori-Giorgi P, Perdew JP. Phys Rev B. 2002;66:165118. [Google Scholar]
- 118.Ernzerhof M, Perdew JP. J Chem Phys. 1998;109:3313. [Google Scholar]
- 119.Henderson TM, Janesko BG, Scuseria GE. J Chem Phys. 2008;128:194105. doi: 10.1063/1.2921797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Iikura H, Tsuneda T, Yanai T, Hirao K. J Chem Phys. 2001;115:3540. [Google Scholar]
- 121.Heyd J, Scuseria GE. J Chem Phys. 2004;120:7274. doi: 10.1063/1.1668634. [DOI] [PubMed] [Google Scholar]
- 122.Perdew JP, Burke K, Wang Y. Phys Rev B. 1996;54:16533. doi: 10.1103/physrevb.54.16533. [DOI] [PubMed] [Google Scholar]; Perdew JP, Burke K, Wang Y. Phys Rev B. 1998;57:14999. [Google Scholar]
- 123.Constantin LA, Perdew JP, Tao J. Phys Rev B. 2006;73:205104. [Google Scholar]
- 124.Bahmann H, Ernzerhof M. J Chem Phys. 2008;128:234104. doi: 10.1063/1.2937447. [DOI] [PubMed] [Google Scholar]
- 125.Henderson TM, Izmaylov AF, Scuseria GE, Savin A. J Comp Theor Chem. 2008;4:1254. doi: 10.1021/ct800149y. [DOI] [PubMed] [Google Scholar]
- 126.Curtiss LA, Raghavachari K, Redfern PC, Pople JA. J Chem Phys. 2000;112:7374. [Google Scholar]
- 127.Zhao Y, Lynch BJ, Truhlar DG. J Phys Chem A. 2004;108:2715. [Google Scholar]
- 128.Zhao Y, Gónzales-García N, Truhlar DG. J Phys Chem A. 2005;109:2012. doi: 10.1021/jp045141s. [DOI] [PubMed] [Google Scholar]; Zhao Y, Gónzales-García N, Truhlar DG. J Phys Chem A. 2006;109:4942. [Google Scholar]
- 129.Heyd J, Peralta JE, Scuseria GE, Martin RL. J Chem Phys. 2005;123:174101. doi: 10.1063/1.2085170. [DOI] [PubMed] [Google Scholar]
- 130.Tao J, Perdew JP, Staroverov VN, Scuseria GE. Phys Rev Lett. 2003;91:146401. doi: 10.1103/PhysRevLett.91.146401. [DOI] [PubMed] [Google Scholar]
- 131.Peralta JE, Heyd J, Scuseria GE, Martin RL. Phys Rev B. 2006;74:073101. [Google Scholar]
- 132.Paier J, Marsman M, Hummer K, Kresse G, Gerber IC, Ángyán JA. J Chem Phys. 2006;124:154709. doi: 10.1063/1.2187006. [DOI] [PubMed] [Google Scholar]
- 133.Paier J, Marsman M, Kresse G. J Chem Phys. 2007;127:024103. doi: 10.1063/1.2747249. [DOI] [PubMed] [Google Scholar]
- 134.Batista ER, Heyd J, Hennig RG, Uberuaga BP, Martin RL, Scuseria GE, Umrigar CJ, Wilkins JW. Phys Rev B. 2006;74:121102R. [Google Scholar]
- 135.Mattsson AE, Wixom RR, Armiento R. Phys Rev B. 2008;77:155211. [Google Scholar]
- 136.Skorodumova NV, Ahuja R, Simak SI, Abrikosov IA, Johansson B, Lundqvist BI. Phys Rev B. 2001;64:115108. doi: 10.1103/PhysRevLett.89.166601. [DOI] [PubMed] [Google Scholar]
- 137.Gunnarsson O, Schönhammer K. Phys Rev Lett. 1986;56:1968. doi: 10.1103/PhysRevLett.56.1968. [DOI] [PubMed] [Google Scholar]
- 138.Anisimov VI, Zaanen J, Andersen OK. Phys Rev B. 1991;44:943. doi: 10.1103/physrevb.44.943. [DOI] [PubMed] [Google Scholar]
- 139.Cococcioni M, de Gironcoli S. Phys Rev B. 2005;71:035105. [Google Scholar]
- 140.Hay PJ, Martin RL, Uddin J, Scuseria GE. J Chem Phys. 2006;125:034712. doi: 10.1063/1.2206184. [DOI] [PubMed] [Google Scholar]
- 141.da Silva JRF, Gangduglia-Pirovano MV, Sauer J, Bayer V, Kresse G. Phys Rev B. 2007;75:045121. [Google Scholar]
- 142.Gennard S, Corà F, Catlow CRA. J Phys Chem B. 1999;103:10158. [Google Scholar]
- 143.Prodan ID, Scuseria GE, Martin RL. Phys Rev B. 2006;73:045104. [Google Scholar]
- 144.Prodan ID, Scuseria GE, Martin RL. Phys Rev B. 2007;756:033101. [Google Scholar]
- 145.Uddin J, Peralta JE, Scuseria GE. Phys Rev B. 2005;71:155112. [Google Scholar]
- 146.Uddin J, Scuseria GE. Phys Rev B. 2005;72:035101. [Google Scholar]; Uddin J, Scuseria GE. Phys Rev B. 2005;72:119902E. [Google Scholar]
- 147.Marsman M, Paier J, Stroppa A, Kresse G. J Phys: Condens Matter. 2008;20:064201. doi: 10.1088/0953-8984/20/6/064201. [DOI] [PubMed] [Google Scholar]
- 148.Kasinathan D, Kuneš J, Koepernik K, Diaconu CV, Martin RL, Prodan ID, Scuseria GE, Spaldin N, Petit L, Schulthess TC, Pickett WE. Phys Rev B: Condens Matter Mater Phys. 2006;74:195110. [Google Scholar]
- 149.Doll K. J Phys: Condens Matter. 2008;20:075214. [Google Scholar]
- 150.Feibelman PJ, Hammer B, Norskov JK, Wagner F, Scheffler M, Stumpf R, Watwe R, Dumesic J. J Phys Chem B. 2001;105:4018. [Google Scholar]
- 151.Kresse G, Gil A, Sautet P. Phys Rev B. 2003;68:073401. [Google Scholar]
- 152.Stroppa A, Termentzidis K, Paier J, Kresse G, Hafner J. Phys Rev B. 2007;76:195440. [Google Scholar]
- 153.Doll K. Surf Sci. 2004;573:464. [Google Scholar]
- 154.Barone V, Peralta JE, Scuseria GE. Nano Lett. 2005;5:1830. doi: 10.1021/nl0509733. [DOI] [PubMed] [Google Scholar]
- 155.Barone V, Peralta JE, Wert M, Heyd J, Scuseria GE. Nano Lett. 2005;5:1621. doi: 10.1021/nl0506352. [DOI] [PubMed] [Google Scholar]
- 156.Barone V, Peralta JE, Uddin J, Scuseria GE. J Chem Phys. 2006;124:024709. doi: 10.1063/1.2150213. [DOI] [PubMed] [Google Scholar]
- 157.Son YW, Cohen ML, Louie SG. Nature. 2006;444:347. doi: 10.1038/nature05180. [DOI] [PubMed] [Google Scholar]
- 158.Kan E-j, Li Z, Yang J, Hou JG. J Am Chem Soc. 2008;130:4224. doi: 10.1021/ja710407t. [DOI] [PubMed] [Google Scholar]
- 159.Ezawa M. Phys Rev B. 2006;73:045432. [Google Scholar]
- 160.Barone V, Hod O, Scuseria GE. Nano Lett. 2006;6:2748. doi: 10.1021/nl0617033. [DOI] [PubMed] [Google Scholar]
- 161.Han MY, Özyilmaz B, Zhang Y, Kim P. Phys Rev Lett. 2007;98:206805. doi: 10.1103/PhysRevLett.98.206805. [DOI] [PubMed] [Google Scholar]
- 162.Chen Z, Lu YM, Rooks MJ, Avouris P. Phys E. 2007;40:228. [Google Scholar]
- 163.Hod O, Barone V, Peralta JE, Scuseria GE. Nano Lett. 2007;7:2295. doi: 10.1021/nl0708922. [DOI] [PubMed] [Google Scholar]
- 164.Hod O, Peralta JE, Scuseria GE. Phys Rev B. 2007;76:233401. [Google Scholar]
- 165.Hod O, Barone V, Scuseria GE. Phys Rev B. 2008;77:035411. [Google Scholar]
- 166.Jiménez-Hoyos CA, Janesko BG, Scuseria GE. Phys Chem Chem Phys. 2008;10:6621. doi: 10.1039/b810877c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167.Aikens CM, Schatz GC. J Phys Chem A. 2007;110:13317. doi: 10.1021/jp065206m. [DOI] [PubMed] [Google Scholar]
- 168.Marom N, Hod O, Scuseria GE, Kronik L. J Chem Phys. 2008;128:164107. doi: 10.1063/1.2898540. [DOI] [PubMed] [Google Scholar]
- 169.Uddin J, Barone V, Scuseria GE. Mol Phys. 2006;104:745. [Google Scholar]
- 170.Guidon M, Schiffmann F, Hutter J, VandeVondele J. J Chem Phys. 2008;128:214104. doi: 10.1063/1.2931945. [DOI] [PubMed] [Google Scholar]
- 171.Rivera P, Moreira IPR, Illas F, Scuseria GE. J Chem Phys. 2008 doi: 10.1063/1.3006419. in press. [DOI] [PubMed] [Google Scholar]
- 172.Henderson TM, Izmaylov AF, Scuseria GE, Savin A. J Chem Phys. 2007;127:221103. doi: 10.1063/1.2822021. [DOI] [PubMed] [Google Scholar]
- 173.Jaramillo J, Scuseria GE, Ernzerhof M. J Chem Phys. 2003;118:1068. [Google Scholar]
- 174.Arbuznikov AV, Kaupp M, Bahmann H. J Chem Phys. 2006;124:204102. doi: 10.1063/1.2196883. [DOI] [PubMed] [Google Scholar]
- 175.Bahmann H, Rodenberg A, Arbuznikov AV, Kaupp M. J Chem Phys. 2007;126:011103. doi: 10.1063/1.2429058. [DOI] [PubMed] [Google Scholar]
- 176.Janesko BG, Scuseria GE. J Chem Phys. 2007;127:164117. doi: 10.1063/1.2784406. [DOI] [PubMed] [Google Scholar]
- 177.Arbuznikov AV, Kaupp M. Chem Phys Lett. 2007;440:160. [Google Scholar]
- 178.Arbuznikov AV, Kaupp M. Chem Phys Lett. 2007;442:496. [Google Scholar]
- 179.Kaupp M, Bahmann H, Arbuznikov AV. J Chem Phys. 2007;127:194102. doi: 10.1063/1.2795700. [DOI] [PubMed] [Google Scholar]
- 180.Janesko BG, Scuseria GE. J Chem Phys. 2008;128:084111. doi: 10.1063/1.2831556. [DOI] [PubMed] [Google Scholar]
- 181.Arbuznikov AV, Kaupp M. J Chem Phys. 2008;128:214107. doi: 10.1063/1.2920196. [DOI] [PubMed] [Google Scholar]
- 182.Tao J, Staroverov VN, Scuseria GE, Perdew JP. Phys Rev A. 2008;77:012509. [Google Scholar]
- 183.Burke K, Cruz FG, Lam KC. J Chem Phys. 1998;109:8161. [Google Scholar]
- 184.Janesko BG, Krukau AV, Scuseria GE. J Chem Phys. 2008;129:124110. doi: 10.1063/1.2980056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185.Krukau AV, Scuseria GE, Perdew JP, Savin A. J Chem Phys. 2008;129:124103. doi: 10.1063/1.2978377. [DOI] [PubMed] [Google Scholar]
- 186.Adamo C, Scuseria GE, Barone V. J Chem Phys. 1999;111:2889. [Google Scholar]
- 187.Jacquemin D, Perpéte EA, Vydrov OA, Scuseria GE, Adamo C. J Chem Phys. 2007;127:094102. doi: 10.1063/1.2770700. [DOI] [PubMed] [Google Scholar]
- 188.Jacquemin D, Perpéte EA, Scuseria GE, Ciofini I, Adamo C. J Comput Theor Chem. 2008;4:123. doi: 10.1021/ct700187z. [DOI] [PubMed] [Google Scholar]