Near-Infrared Grating Spectrometer for Mobile Phone Applications

Abstract

Near-infrared (NIR) spectroscopy is a well-established technique for the chemical analysis of organic and inorganic matter. Accordingly, spectroscopic instrumentation of different complexity has been developed and is currently commercially available. However, there are an increasing number of new mobile applications that have come into focus and that cannot be addressed by the existing technology due to size and cost. Therefore, a new miniaturized scanning grating spectrometer for NIR spectroscopy has been developed at Fraunhofer IPMS. It is based on micro–electro–mechanical systems (MEMS) technology, and has been designed to meet the requirements for mobile application, regarding spectral range, resolution, overall size, robustness, and cost. The MEMS spectrometer covers a spectral range from 950 nm to 1900 nm at a resolution of 10 nm. The instrument is extremely small and has a volume of only 2.1 cm³. Therefore, it is well suited for integration, even into a mobile phone. A first sample of the new spectrometer has been manufactured and put into operation. The results of a series of test measurements are in good agreement with the requirements and specifications.

Introduction

Miniaturized spectroscopic devices are currently the subject of extensive research and development. There are various approaches with their individual advantages and disadvantages.^1–4 Reducing the physical dimensions while maintaining the optical performance compared to compact or desktop systems is certainly one of the biggest challenges common to all approaches. The reasons for the difficulties in downsizing a spectrometer are, amongst others, the scaling effects of optical and mechanical tolerances, assembly issues, and a limited number of suitable materials in terms of cost and reliability. This is particularly evident for a system to be integrated into a mobile phone.

The approach to miniaturized spectrometers pursued at Fraunhofer IPMS is a grating type instrument based on the Czerny–Turner design. At first sight such a scanning system may seem outdated, since most current grating instruments are based on linear sensor arrays without the need for scanning. However, in near-infrared (NIR) spectroscopy, where line detectors are still very expensive, it is almost mandatory to use single detectors in conjunction with a monochromator for price-sensitive markets like the mobile phone business. As NIR is considered to be a very interesting spectral range for mobile applications, a miniaturized scanning grating spectrometer for the near-infrared has been developed.

As already indicated, the development of a miniaturized spectroscopic instrument is a challenging task. Considerable effort is needed to build a fully functional system that meets all specifications. This is due to the fact that almost all of the main spectrometer components have to be substantially modified or even developed from scratch. This is especially true for the scanning mechanism, which is the core element of any monochromator. It turned out that MEMS devices are very well suited to being used as a scanning grating in such miniaturized systems, and thereby enabling the development of extremely compact, yet powerful, instruments.

In this paper the development of a new extremely miniaturized scanning grating spectrometer for the near-infrared spectral range is described. It is organized as follows. First, the design requirements for such a spectrometer, based on possible applications, are discussed. Second, relevant information concerning micro–electro–mechanical systems (MEMS) devices and their use for spectrometer design will be given. Subsequently, the design process, along with some typical constraints, is explained in detail and the results in terms of an optimized design are presented. Third, the realization of a first fully functional sample is described in detail. Finally, the outcome of the characterization and first measurements with the new spectrometer are presented.

Design Requirements

Volume applications for mobile NIR spectroscopy are mainly aimed at the analysis of organic matter. In this context C–C, C–H, and C–O bonds play an important role. Even though their spectra can be evaluated much more easily in the mid-infrared (MIR), also known as the “fingerprint region” (wavelengths beyond 2.5 µm), there are some arguments in favor of the NIR. Strong absorption in the fingerprint region prevents the radiation from deeply penetrating into the material. Therefore, spectral information can only be gathered from near the surface of a sample. On the other hand, the penetration depth is considerably larger in the NIR. For this reason, much more information about a sample can be gained. This advantage comes at the cost of more complex data analysis. To extract the relevant information from the NIR, spectral–chemometric evaluation is needed.

The NIR spectral region can be divided in two main regions. The first reaches from 780 nm to 1900 nm. It can be addressed with sensors operating at ambient temperature. The second is the extended range up to 2500 nm. It requires intense cooling of the detectors to ensure an acceptable signal-to-noise level. Even though some interesting bands can be detected between 1900 nm and 2500 nm the additional effort required for detector cooling inhibits its use for most mobile applications. Operation without additional bandpass or order sorting filters is favorable but limits the range to a single decade. As prominent bands are 1446 nm for water and 1650 nm to 1800 nm for carbon compounds, the range either from 900 nm to 1800 nm or from 950 nm to 1900 nm is appropriate. The second option has been selected here for the MEMS spectrometer.

The requirements for spectral resolutions in this region are intermediate due to the broad structure of the overtone and combination bands. It can be assumed that 9 nm to 10 nm resolution is sufficient for most applications. On the other hand, the long-term stability of the wavelength scale is much more relevant as model data must match with spectra measured on site. Here 1 nm is the minimum requirement for long-term stability.

For the reliable evaluation of spectra it is important to ensure sufficient signal level and low noise. Ignoring scattering effects, absorption measurements in a transmission setup for fluids in cuvettes or solids of well-defined thickness can be evaluated by direct correlation of the intensities of the light source I₀ with the transmitted signal I. This is due to the Beer–Lambert law

$$A=\text{lo}{\text{g}}_{10}(\frac{I_0}{I})=\varepsilon \mathrm{cl}$$ (1)

where the optical path length l is the most relevant quantity. The properties of the material to be analyzed are contained in the molar absorptivity ε and the molar concentration c. The limits of detection are dominated by detector noise, provided that internal stray light is sufficiently suppressed. In this context it should be noted that measurements in diffuse reflection are in general more demanding than those in transmission. Diffuse reflection is inherently connected with scattering processes that redistribute the radiation over the whole hemisphere. This not only leads to a greater loss of signal, but also to an amount of stray light. However, the detected signal in the spectrometer must exceed scattered light by some orders of magnitude. This is of paramount importance for mobile applications as, for the majority of cases, diffuse reflection measurements will be the method of choice.

Independent of the spectral setup, the signal-to-noise ratio (SNR), typically given for the lowest signal level that can be detected, contributes to the performance description of a spectrometer. Very often the absorbance A is used for the characterization. Then, by considering absorption measurements for mobile analysis, A = 3.3 to A = 4 should be sufficient for most applications. Table 1 gives the percentage of transmitted radiation, the corresponding absorbance and the required bit resolution Q necessary for an analog-to-digital converter (ADC) to minimally meet the I/I₀ ratio.

Table 1.

Percentage of transmitted radiation through a sample, the corresponding absorbance A and the required bit resolution Q for an applied ADC to minimally meet the I/I₀ ratio.

I/I0 (%)	A	$Q>\text{lo}{\text{g}}_2(\frac{I_0}{I})$
0.05	3.3	11
0.01	4.0	13.3

Finally, different applications are associated with specific requirements for the size of the spectrometer. Several tasks in the field of process automation or machine mounted measurement units can be addressed with systems featuring an outline of approximately 10 cm × 10 cm × 5 cm. Mobile units for handheld applications would benefit from a reduced size in the range below 5 cm × 2 cm × 2 cm. Further miniaturization is required if the spectrometer is to be integrated into a mobile phone. Applications like nutrition advice will need simultaneous spectral analysis on selected spots under the guidance of the user with imaging by the camera and display device. To fit into a modern mobile phone, the spectrometer's volume must be as low as possible, and the thickness must not exceed 6 mm.

To summarize, it is very promising to be able to design a spectrometer for 950 nm to 1900 nm spectral range with a resolution of 10 nm or below. Wavelength stability must be at least 1 nm for lifetime. The system should provide a signal-to-noise performance to ensure measurements with A = 3.5 to A = 4. These measurements may take 0.5 s to 1 s time. For stand-alone handheld systems the size may be around 5 cm × 2 cm × 2 cm, including the standard interface and battery in the case of wireless operation. For integration into a mobile phone, the device thickness must not exceed 6 mm, and the surface area might be up to 20 mm × 20 mm.

Micro–Electro–Mechanical Systems Devices

The strategy for the development of a miniaturized grating spectrometer is based on two major assumptions. First, as the movable diffraction grating is the key component in the system, it is vital to have a small and robust scanning grating device. Second, for efficient assembly it is very advantageous to be able to minimize the number of components to be mounted. Therefore, the monolithic integration of all functional elements into a much smaller number of parts, and the subsequent assembly of those parts into a hybrid stack, forming the final system, is the method of choice. In order to successfully apply the described procedure, as a first step it is essential to maximize the number of functional elements within one component.

Micro–electro–mechanical systems technology and MEMS devices are ideally suited for the implementation of highly integrated and robust systems, as required for mobile applications. A MEMS device can include a movable element, such as a tiltable plate with a diffraction grating on top, and the corresponding driving mechanism. Micro–electro–mechanical systems devices fabricated at Fraunhofer IPMS are based on single crystalline silicon and are actuated by an electrostatic driving mechanism. Due to the materials used and the lithographic definition of all structures, these devices combine very good mechanical and optical properties with excellent structural precision. Special emphasis is put on the very high quality grating structures achievable with this technology, stable grating rotation and the resonant electrostatic comb drive with its low power consumption, long-term stability, and large mechanical deflection amplitude. To give a brief insight into the characteristics of different MEMS driving mechanisms in terms of angles of deflection, three typical values are listed in Table 2.

Table 2.

Exemplary oscillating MEMS driving mechanisms with the corresponding typical angular deflection. The electrostatic comb drive is used in the MEMS spectrometer.

Driving mechanism	Angle of deflection	Reference
Electrostatic, comb drive (IPMS solution)	±11°	5
Electrostatic, plane electrodes	±5.5°	6
Galvanometric	±5.5°	7

The main advantage of MEMS technology is that all of the important elements of the device are implemented to the highest precision. This is due to the semiconductor manufacturing processes used for MEMS technology. Therefore, the springs holding the plate, the lines of the grating, and the comb structures of the driving mechanism are not only precisely defined but also aligned to each other within the same chip. Following from these advantages it seems appropriate to integrate further elements. In the case of a spectrometer, the entrance and exit slits are ideal candidates. Thus, the approach pursued is to add the two slits to the MEMS chip, thereby ensuring extreme alignment accuracy between them and with respect to the grating. Besides the precision gained with this approach, the assembly process can be significantly simplified.

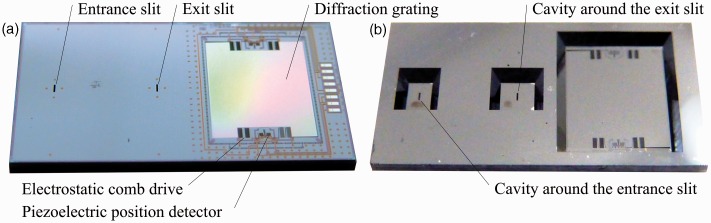
Detection of the position of the deflection angle of the grating is required to cover the deviations from the ideal sinusoidal movement of the electrostatic comb drive, as well as the demand for high wavelength accuracy and stability. The MEMS device employed in the miniaturized grating spectrometer is depicted in Figure 1. Following the considerations mentioned above, the dimensions of the component part are 9.6 mm × 5.3 mm × 0.5 mm, which includes two optical slits, a single cavity located underneath each slit, and a position detector, in addition to the electrostatically driven diffraction grating.

Figure 1.

Scanning grating MEMS device, dimensions 9.6 mm × 5.3 mm × 0.5 mm, with its electrostatically driven tiltable diffraction grating, a position detection for the deflection of the grating plate as well as an entrance and exit slit with a cavity located underneath. (a) face up and (b) face down.

Despite the larger number of integrated features in the MEMS chip it can be fabricated with some minor modifications to the process flow for more-or-less standard devices. It should be noted that MEMS technology is particularly suitable for volume production, which is one major requirement for integration into mobile phones.

Spectrometer Design

The design process for the miniaturized MEMS spectrometer involves both optical and mechanical aspects. Additionally, some assembly issues should not be overlooked, even in the early design stages. This is mainly due to the rather strict requirements of the application. The spectrometer must have a very small outline, along with the need for high volume production and, at the same time, the optical specifications must be met. In fact, it is the demand for high volume production that imposes the most severe constraints. In this context one should consider the consequences of the term “high volume” for the production of a spectrometer. Compared to the market for ordinary spectrometers the mobile phone market is extremely large, possibly comprising hundreds of millions of units per year. It is clear that such markets can only be addressed with an adequate assembly strategy, which in turn calls for a suitable design approach. This leads to additional design constraints when compared to more conventional systems.

First-Order Layout

The first step in the design process is to choose a suitable system from one of the well-known spectrometer designs as a starting point for further optimization. Over the past decades a number of different designs and mountings have been described in the literature.⁸ Some of these, like the famous Czerny–Turner design or Fastie–Ebert design, have been used (and are still being used) as the basis for many commercially available instruments. This is being done for good reason, since the Czerny–Turner design exhibits some valuable properties. First of all, this type of mounting is made for plane diffraction gratings that can be manufactured with a high level of quality. It is well-suited to the use of MEMS devices as described above. Second, due to the inherent symmetry in the Czerny–Turner design, odd aberrations like coma cancel out. This is very beneficial for aberration correction in general, and to achieving good image quality and thereby good spectral resolution in a monochromator (spectrometer) in particular. Moreover, the Czerny–Turner design offers more degrees of freedom for aberration correction than the Fastie–Ebert design, which in principle would also fulfill the above-mentioned conditions. This provides the main argument for selecting the Czerny–Turner design as the starting point for the system.

Having decided in favor of the Czerny–Turner design, a first-order layout of the system had to be made. Here, the properties of the MEMS device set some important limitations. The lateral dimensions of the scanning grating itself are limited for mechanical reasons to about 3 mm. For good light throughput the spectrometer should have an f/# of 4 or even less. Given the f/# and the size of the grating, the focal length is

$$f=\mathrm{Df}/\#$$ (2)

where D denotes the maximum diameter of an inscribed circle of the square diffraction grating. In general, the more light a spectrometer gathers the better. Even faint signals might then be detected. Setting the width of the entrance slit aside, this is associated with a smaller f/#. Because the grating size is constant, an increase in throughput can only be achieved by reducing the focal length. In Table 3, the resulting focal lengths for different f/# are listed along with the associated numerical aperture (NA). In addition, typical means for light coupling at the entrance are given for reference. To have some design margin and to avoid stray light, the target f/# has been set to 2.8 rather than 4. This implies a focal length of 8.4 mm and an underfilling of the aperture.

Table 3.

Spectrometer focal length for different F/# and numerical apertures (NA); grating size 3 mm × 3 mm.

F/#	Numerical aperture	Focal length (mm)	Light coupling
4	0.125	12	SM optical fiber, NA = 0.12
2.8	0.178	8.4	Typical free air
2.3	0.22	6.9	MM optical fiber, NA = 0.22
2	0.25	6	Typical free air

There is another reason for the somewhat lengthy treatment of throughput here. As described above, the MEMS scanning grating chip is a resonantly driven device with a resonant frequency on the order of 100 Hz. This is quite fast for a scanning spectrometer. A small f/# and hence a large throughput is of considerable importance for a good SNR in this case.

Another MEMS grating property to be taken into account is its limited deflection amplitude of approximately ±10°. This is in great contrast to bench-top spectrometers where the grating rotation is, in principle, unlimited (360°). The main impact of this characteristic is on the attainable spectral range and, to some extent, on the resolution. The former is directly related to the grating rotational amplitude for a given angular dispersion (line spacing on the grating). As far as resolution is concerned, this can be adjusted within limits by choosing an appropriate slit width in conjunction with a given value for angular dispersion. The well-known grating equation

$$\frac{m\lambda }{g}=\text{sin}(\alpha )+\text{sin}(\beta )$$ (3)

is the starting point of a search for a reasonable arrangement of the main components under specific constraints. Here, α is the angle of incidence on the grating and β is the angle of diffraction. The grating constant and order of diffraction are denoted by g and m, respectively. Since the focal length is comparatively small, the angular dispersion

$$\frac{\text{d}\beta }{\text{d}\lambda }=\frac{m}{g\cos (\beta )}$$ (4)

will have to be rather large in order to obtain the desired spectral resolution. This leads to the assumption that the spectrometer can only be operated in the ±1 diffraction order and with g on the order of λ.

The next step was to match the minimum and maximum wavelength of the specified spectral range to the deflection amplitude of the oscillating grating. Inserting the corresponding values into Eq. 3 results in a nonlinear system of equations. The solution of these equations is described in the literature.⁹ Without going into further detail here, it can be stated that the equations can be solved analytically. One of the advantageous solutions is as follows. The required spectral range from 950 nm to 1900 nm can be covered with a maximum amplitude of ±10° at a grating constant of 1.6 µm. The angles amount to α = 42° and β = 13°, respectively. Therefore, these values have been adopted for the first-order layout.

Due to the manufacturing process the grating exhibits a trapezoidal line profile. The diffraction efficiency varies between 30% and 50% across the spectral range. The rest of the diffracted radiation is distributed among the other orders, mainly the zero and +1st order.

Interestingly enough, the solution is strongly influenced by the geometry of the setup. That is, the attainable spectral range does not only depend on the deflection amplitude but also upon the angle that the rays given by Eq. 3 make with the spectrometer axis, which is an axis of symmetry with respect to the two mirrors. It is highly favorable to keep that angle as small as possible to maximize spectral range. Such small angles are normally associated with avoiding aberrations, but here it has an additional meaning.⁹

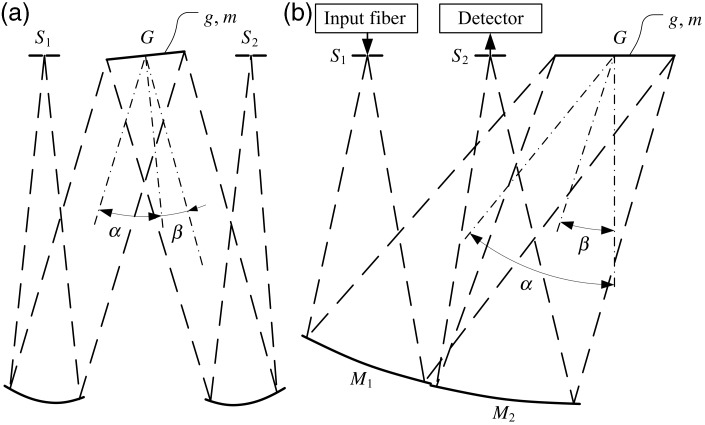
The next question was how a Czerny–Turner design must be modified for an appropriate assembly strategy. The above-mentioned demand for high volume production can best be met by the use of modern micro-assembly platforms. Fast automated pick-and-place machines are capable of putting together optical systems with an extraordinarily high precision, if necessary. Such machines are optimized for a situation where all components are to be stacked on top of each other like plane substrates. Therefore, this implies a planar (quasi two-dimensional) mounting concept. The most striking implication of this approach is that, when the MEMS chip is mounted on a plane substrate, the diffraction grating in its rest position will be parallel to the surface of that substrate. According to Figure 2a, for the conventional Czerny–Turner design the angles α and β would then be the same. The grating would behave like a simple plane mirror. The solution to that challenge is a change from the classic Czerny–Turner design.¹⁰

Figure 2.

Czerny–Turner monochromator design in two different configurations: (a) classical setup with tilted grating, (b) modified version with an in-plane grating optimized for micro-assembly, G: the grating; M1: collimating mirror; M2: refocussing mirror; S1: entrance slit; S2: exit slit.

In order for the grating to not act as a plane mirror, one part of the ray path must be flipped so that both the entrance and exit slits lie on the same side of the grating. This way, the setup can be operated in the ±1st diffraction order as shown in Figure 2b. However, the two mirrors for collimation and refocusing must then also be placed on that same side. It can be seen how deeply the first-order layout of the system is influenced by the assembly strategy. At this point it is worthwhile to note that for the first-order layout it makes no large difference on which side the mirrors are set as long as the focal lengths and distances are correct. However, this does not in general hold for aberration correction. For the modified version it is more complicated to achieve good image quality.

Due to the planar mounting concept the ray bundles have to be (nearly) telecentric at the slit positions. Furthermore, the two mirrors will have to be off-axis sections of at least plane symmetric optical surfaces.

The first-order layout was completed with the definition of slit widths. This has been done so as to meet the requirement for 10 nm resolution, determined by a convolution of the image of the entrance slit and the exit slit.¹¹ Entrance and exit slits have widths of 52 µm and 48 µm, respectively.

Optimization

In order to meet the specification for spectral resolution the system must have good image quality. That is, the image of the entrance slit should be nearly free from optical aberrations. As is known from aberration theory, the leading terms are the primary, or Seidel aberrations.¹² For their correction, different methods have been established. First in the series is spherical aberration. Since the system is relatively fast, spherical aberration will definitely be present and has to be corrected. The usual approach adopted here is to use conic surfaces. The second aberration is coma. As mentioned above, this cancels out due to the symmetry of the system, like any other odd aberration. On the other hand, astigmatism is more of a problem. As an even aberration it adds up in a symmetric configuration like the Czerny–Turner design. One way of dealing with this issue is to use biconic surfaces. These have different radii and conic constants in two orthogonal directions. Field curvature is not critical, because the slits are comparatively narrow, and thus the effective field is small. The anamorphic imaging property induced by the diffraction grating itself¹¹ can also be addressed by the biconics due to their different focal lengths. The optimization has been done with commercially available optical design software.

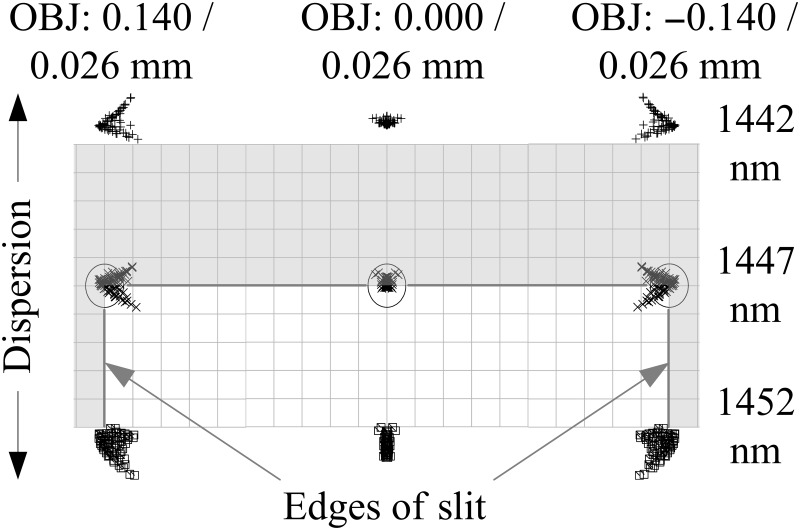
The result after a number of optimization runs is depicted in Figure 3. It shows a spot diagram for some points that define the center line through the entrance slit. The maximum scale of 0.048 mm corresponds to the width of the exit slit. The circles in the diagram indicate the Airy radius. The ray trace data is given for three wavelengths that represent one central wavelength that lies near the middle of the spectral range and its two neighbors. In accordance with the goal of spectral resolution they are 10 nm apart.

Figure 3.

Spot diagram for three different field points representing the center line of the entrance slit, maximum scale of 0.048 mm corresponds to the width of the exit slit, and ray trace data for three different wavelengths near mid-spectral range.

First, it can be seen that the spot size is near the diffraction limit. Hence, the image quality is quite good for a spectrometer. Second, the requirement for a spectral resolution of 10 nm is safely met. The spots for the two adjacent wavelengths are outside the area of the exit slit. Figure 4 shows the same situation for another three spots that define one edge of the entrance slit. The only difference is that now the spots for one of the neighboring wavelengths lies at the center of the slit. Even though some unwanted light for these points obviously enters the exit slit the resolution is still preserved. This is due to the resolution criterion given by the convolution of the two slit functions (resulting in a triangle function).¹¹

Figure 4.

Spot diagram for three different field points representing the edge of the entrance slit, maximum scale of 0.048 mm corresponds to the width of the exit slit, and ray trace data for three different wavelengths near mid-spectral range.

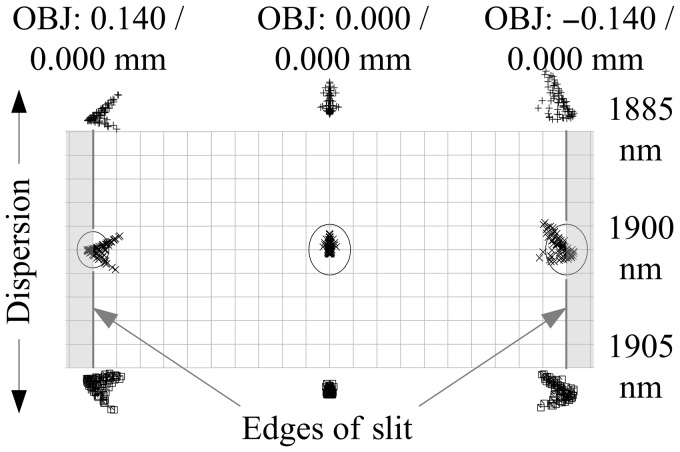
For completeness, a third spot diagram is shown in Figure 5. Here, the central wavelength is at the upper limit of the spectral range. All other parameters are similar to Figure 3. Again, it can be seen that the image quality and the resolution are within the specification.

Figure 5.

Spot diagram for three different field points representing the center line of the entrance slit, maximum scale of 0.048 mm corresponds to the width of the exit slit, and ray trace data for three different wavelengths at the upper limit of the spectral range.

The general outline of the optimized system is as illustrated in Figure 2b. The results of the design are in good agreement with the requirements.

Spectrometer Realization

Some aspects concerning the design and assembly strategy have already been discussed in the sections above. It has been pointed out that MEMS is an enabling technology, with the possibility of integrating the optical slits into the scanning grating chip and thereby to allow for a simplified assembly of a stack of hybrid components. The objectives behind these efforts are to facilitate both miniaturization and high volume production.

In order to enable mass production of possibly hundreds of millions of units per year, it is vital to replace traditional manufacturing techniques for spectrometers and to abandon common alignment procedures. Instead, the overall system layout must be adapted for the use of modern micro-assembly platforms. These platforms are optimized for the highly accurate and fast assembly of optical systems consisting of a number of plane component parts. That is, all parts of the spectrometer will have to be designed so that they can be put together as a stack. Recalling the design presented in Figure 2b, the spectrometer consists of seven functional elements, provided that the grating, driving mechanism, and position detection are counted as one unit. Due to the high degree of integration of the MEMS device, only the two mirrors, the input fiber, and the detector remain as separate parts. In the assembled component stack, the fiber and detector are located in the two cavities of the MEMS as depicted in Figure 1b, exactly behind the entrance or the exit slit. With respect to Figure 2b, the surfaces of the mirrors have a similar orientation and are placed in close proximity, making them highly suitable for integration in a common optics substrate. In the setup shown in Figure 6b, this component is made of aluminum. The optical surfaces were fabricated by ultra-precision machining.¹⁰ At a later stage, the optics substrate may be manufactured using plastics or glass with replicating processes like micro-injection molding, injection compression molding, or precision molding. It is assumed that a change in manufacturing processes can be facilitated without profoundly revising the overall concept.

Figure 6.

(a) Assembly process for the production of a hybrid integrated grating spectrometer from individual component parts into the complete system; (b) cross-sectional view of the complete system with the optical path highlighted (red).

As the input fiber is intended to be replaced by an entrance optics in further developments, and infrared detectors cannot be integrated in any of the process flows described above, these components will remain separate. In Figure 7a, all six component parts and the flow of the assembly process for the miniaturized grating spectrometer are shown. An illustration of the cross-sectional view of the assembled system with the optical path highlighted (red) is depicted in Figure 7b.

Figure 7.

(a) SMA fiber connector; (b) demonstration model of a miniaturized spectrometer based on a grating monochromator with a volume of 2.1 cm³ and a power consumption of 1.9 W; (c) rendered CAD half-section of the demonstration system with the optical path highlighted (red, orange, green and blue).

There are two component parts not mentioned so far: the carrier substrate and the spacer; the spacer includes an insert for stray light suppression as described below. The carrier substrate, with a surface area of 12 mm × 17 mm, is made of FR-4 and contains basic electronic circuits. It serves as the planar mounting platform for the detector and the MEMS as well as the input fiber that is attached to the back side. In accordance with Table 3, mirrors and slits have to be located at a defined distance in order to establish the correct focal distance. This function is performed by a spacer made of aluminum with the dimensions 15 mm × 10 mm × 9.1 mm. The only feature not depicted in Figure 7 is a small inlet that fits perfectly into the spacer. This inlet can be regarded as a part of the spacer and contains simple structures for stray light suppression. For the demonstration setup this component part is fabricated from a black plastics by rapid prototyping. Further details concerning the system assembly can be found in other publications.¹⁰

The first fully functional sample of the MEMS spectrometer has been assembled with a commercially available micro-assembly platform following the scheme depicted in Figure 7 and illustrated in Figure 6b. A subminiature version A (SMA) fiber connector is shown for reference (Figure 6a). As can be seen the spectrometer is quite small compared to all of the conventional NIR spectrometers that are available. A sectional drawing of the system is given in Figure 7b. The ray path within the system is indicated. The characterization and results of the first operational system are given in the next section.

As for all time-discrete spectroscopic approaches, signal processing is an important issue for the miniaturized spectrometer. This is the case, with the MEMS scanning grating chip oscillating with a frequency in the order of 100 Hz, which is quite fast for a scanning spectrometer. The discrete analog front-end electronics of the spectrometer performs the analog preprocessing and digitization of the measured intensity of the detector as well as of the signal for the measured grating deflection angle. Both analog readings are each simultaneously sampled and converted by individual 16-bit ADCs, at 500 kHz sampling frequency. With data sampled on just one tilt excursion of the grating, this translates to 2500 data points within each spectrum. Even though the angular velocity of the MEMS grating is not constant, the sampling density is sufficient to cover the required 1 nm wavelength stability and 10 nm spectral resolution.

Characterization and Results

After the successful assembly of a first sample of the MEMS spectrometer, the associated driving and readout electronics were put into operation. For the characterization of the whole setup several measurements were made.

The first parameter to be tested was spectral resolution. For this purpose a special test setup was established in the laboratory. Light from a broadband Xe short arc lamp was coupled into a monochromator. Its parameters were set so that the light output had a spectral bandwidth of less than 1 nm at a central wavelength of 1446 nm. This narrow-band light output was then coupled into the fiber of the spectrometer. The result of the measurement is depicted in Figure 8. It shows the average of the detected signal over 100 measurements. Figure 8a shows the whole spectral range from 950 nm to 1900 nm, and Figure 8b shows a magnified section of the single peak. Since the MEMS is operated at 100 Hz this implies a total measurement time of 1 s. From these data the spectral resolution at full width half-maximum (FWHM) was found to be 10 nm. Moreover, for numerous measurements the fluctuation of the aforementioned peak wavelength was observed to be less than 1 nm, meeting the requirement for long-term stability. Thereby, that stability was confirmed for up to several hours of continuous measurement under laboratory conditions.

Figure 8.

Spectrum of a Xe short arc lamp source filtered by a monochromator to a peak of less than 10 nm, measured with MEMS microspectrometer with 100× averaging. (a) The whole spectral range from 950 nm to 1900 nm; (b) a magnified section of the single peak.

The two spectra displayed in Figure 8 reveal a baseline intensity of about 16%. In order to gain some insight into the characteristics of the baseline, additional measurements were made. Firstly, the spectrum of the broadband Xe short arc lamp filtered by a monochromator was measured without and with 10× averaging. Except for the number of averaging steps, the setup was identical to that used for the results displayed in Figure 8. The numerical findings for 1×, 10×, and 100× averaging in terms of mean value and standard deviation of the baseline as well as peak intensity and SNR are listed in Table 4. The SNR is derived as the ratio of the peak intensity and the standard deviation of the baseline. The analysis of the baseline signal shows no distinctive features, except an expected decrease of noise.

Table 4.

Mean value, standard deviation, peak intensity, and SNR of the spectrum of a Xe short arc lamp source filtered by a monochromator with 1×, 10×, and 100× averaging.

Parameter/averaging	1×	10×	100×
Baseline intensity mean value (a.u.)	0.1665	0.1664	0.1663
Baseline intensity SD (a.u.)	0.0073	0.0025	0.0015
Peak intensity (a.u.)	0.9951	0.9844	0.9900
SNR (a.u.)	136	391	643

Secondly, a spectrum was taken with the Xe short arc lamp switched off. As before, the rest of the setup remained unchanged. This dark spectrum, shown in Figure 9, displayed for the whole normalized intensity range (Figure 9a) of the MEMS microspectrometer and (Figure 9b) a magnified view of the noise, exhibiting an intensity distribution of I = (0.1603 ± 0.0014) atomic units (a.u.) at 1σ with 100× averaging. By comparison with the numbers given in Table 4, the ratio of the baseline intensity related to electronic effects like dark current or other DC offsets can be estimated. Accordingly, only a very small part of the baseline intensity of about I = 0.006 a.u. (0.6 %) is related to stray light. For the first fully operational miniaturized MEMS microspectrometer, this is a very promising result that emphasizes the findings described above. Therefore, the baseline is attributed to a DC offset in the measurement electronics.

Figure 9.

Dark spectrum measured with MEMS spectrometer with 100× averaging. The spectrum is displayed (a) for the whole normalized intensity range of the MEMS microspectrometer and (b) as a magnified view of the noise.

Furthermore, there are no other peaks present; the spectrum is very “clean”. The absence of ghosts and side lobes indicates that the MEMS grating is of high quality and that there is not much stray light from the grating surface. This may seem somewhat surprising, since in a spectrometer this small there is not much room for baffles to suppress stray light, even though an inset for that purpose was deployed (see the previous section above). Nevertheless, the special embodiment of the MEMS slits and the inset along with the coatings in the system appear to be very effective.

To see how the spectrometer performs with a broadband light input the whole spectrum of the Xe short arc lamp was recorded. The result is shown in Figure 10. All major peaks in the spectrum are well resolved. To compare this performance with that of a commercially available instrument, some reference measurements with a Hiperscan (HiperScan GmbH, Dresden, Germany) SGS 1900 were made. The resulting data are also shown in Figure 10.

Figure 10.

Whole spectrum of the Xe short arc lamp measured with SGS 1900 and MEMS microspectrometer.

It can be seen that the two spectra are in reasonably good agreement. Differences are mainly due to a currently imperfect baseline correction of the MEMS spectrometer. However, this is not a serious issue, since it can be addressed by an improved version of the software and some minor changes to the readout electronics. Some important parameters of the MEMS spectrometer in comparison with the SGS 1900 are listed in Table 5. It is apparent that the new MEMS spectrometer performs at the same level as the SGS 1900 concerning spectral range and resolution, though some improvements will have to be made regarding baseline correction and SNR.

Table 5.

Important parameters of the microspectrometer and the corresponding values for the Hiperscan SGS 1900 for comparison.

Parameter	SGS 1900	Microspectrometer
Resolution (nm)*	10	10
Baseline intensity (a.u.)	0.066	0.166
SNR (a.u.)†	1700	643
Volume (cm³)	722.4	2.1
Weight (g)	800	8.4
Power consumption (W)‡	5.3	1.9

*Confirmed at several measurement points within spectral range;

†measured at 1446 nm with 100× averaging;

‡including complete readout electronics.

Some additional measurements have been made to demonstrate the spectrometer's capabilities for a simple real-world application. A setup for the measurement of absorption spectra of ethanol solutions was created. This setup consisted of a halogen light bulb as light source and fused silica cuvettes containing ethanol solutions. The light source and the cuvette holder were connected by an optical fiber, and the second port of the holder was attached to the input fiber of the MEMS spectrometer. All samples were measured in transmission and mixed using a mechanical pipetting aid. The spectra for a number of different ethanol solutions were recorded. The results are shown in Figure 11. As can be seen, the different ethanol concentrations can be well differentiated in the spectra. It should be noted that the data given in Figure 11 corresponds to transmission intensity rather than absorbance.

Figure 11.

Spectrum of ethanol solutions varying from pure water to pure ethanol, measured with microspectrometer at 100× averaging.

However, some fluctuations between neighboring spectra are also present. These effects can be attributed to imperfections in the nominal sample concentrations. This was confirmed by reference measurements with a SGS 1900.

Conclusions

The realization of a scanning grating spectrometer that is both sufficiently miniaturized to fit into a mobile phone and is suitable for mass production while still having good optical performance is a challenging task. Miniaturization is mainly facilitated by the rigorous integration of all functional elements into a minimum number of component parts. Mass production requires special manufacturing methods like batch processing or replicating techniques. This set of requirements can be met by a modified Czerny–Turner design optimized for a planar orientation and a good spatial arrangement of the main components.

The overall system approach is being enabled by the use of MEMS technology. The MEMS device employed in the spectrometer combines an electrostatically driven diffraction grating with a sensor for the detection of its deflection angle. Additionally, the entrance and the exit slit are integrated as well. A further benefit results from the manufacturing of the two required mirrors in a common optics substrate. The same applies for the spacer with its internal features for stray light suppression, keeping the MEMS device and optics substrate at the correct focal position and significantly improving SNR. All major component parts were mounted by a modern micro-assembly platform. In contrast to classical spectrometers, the usual alignment procedures can be omitted.

First measurements confirm compliance with the basic specifications. The miniaturized spectrometer, comparable in size to a sugar cube and with a weight of only 8.4 g, has a spectral range from 950 nm to 1900 nm at a resolution of 10 nm. Furthermore, the SNR was identified to be 643 for the first demonstrational setup, as recorded in Table 5.

Even though the new spectrometer meets all of the major design requirements there is still room for improvements. To ensure the detection of even fainter spectral features, a better SNR in conjunction with a better baseline correction is needed. This involves both software and hardware, for example signal shielding and processing. Besides improvements in signal quality, the electronics can be subject to a further size reduction by the use of an application-specific integrated circuit (ASIC) with the minimum required circuitry.

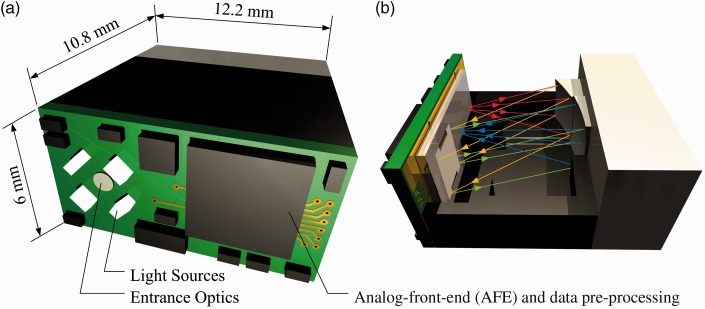
Although the spectrometer is extremely miniaturized already, it could be made even smaller. This could be achieved by mechanical optimization. Through the reduction of wall thicknesses and an optimized arrangement of the inner parts, an overall size of 12.2 mm × 6 mm × 10.8 mm seems to be attainable. A CAD model of one possible embodiment of such an optimized system is depicted in Figure 12. Most notably, all electronics and input optics would be included in such an optimized version of the MEMS spectrometer. With those improvements all requirements for integration into flat mobile phones will be fulfilled.

Figure 12.

(a) Rendered image of a further miniaturized version of the microspectrometer with dimensions 12.2 mm × 6 mm × 10.8 mm; (b) a sectional view of the same system with the optical path (red, orange, green, and blue) highlighted. The proposed system includes free space entrance optics as well as analog front-end and data pre-processing to a stand-alone spectral sensor module.

Conflict of Interest

The authors report there are no conflicts of interest.

Funding

This work was supported by Fraunhofer Vintage-Class-Research-Group “M(O)EMS für die mobile multi-Analytik” (MObilA).