Summary
The growth of nonresponse rates for social science surveys has led to increased concern about the risk of nonresponse bias. Unfortunately, the nonresponse rate is a poor indicator of when nonresponse bias is likely to occur. We consider in this paper a set of alternative indicators. A large-scale simulation study is used to explore how each of these indicators performs in a variety of circumstances. Although, as expected, none of the indicators fully depicts the impact of nonresponse in survey esti mates, we discuss how they can be used when creating a plausible account of the risks for nonresponse bias for a survey. We also describe an interesting characteristic of the FMI that may be helpful in diagnosing NMAR mechanisms in certain situations.
Keywords: Bias, Missing data, Nonresponse, Nonresponse indicators, Survey data quality measures
1. Introduction
Nonresponse rates have been increasing over the recent past (de Leeuw and de Heer, 2002; Curtin et al., 2005; Atrostic et al., 2001; Petroni et al., 2004; Brick and Williams, 2013). This growth in nonresponse rates has prompted concerns about the quality of survey data. In a review of the research on the problem, Groves (2006) recommended that survey researchers focus more on limiting bias than on attaining high response rates. This point was further strengthened by a review of specialized “gold standard” studies of nonresponse bias (Groves and Peytcheva, 2008). This review found that the response rate was not a good predictor of when nonresponse bias might occur. As a result, survey designers and statisticians have been seeking alternative measures that may be more useful in predicting nonresponse bias.
Several indicators have been proposed and explored theoretically (e.g. Schouten et al., 2009; Wagner, 2010). However, there has not been a large-scale simulation study of the performance of these indicators in a variety of circumstances. In particular, little is known about how these indicators perform under different missing data mechanisms. Little and Rubin (2002) define three missing data mechanisms. The first is Missing Completely at Random (MCAR). Under this mechanism, the observed data are essentially a simple random sample of the full sample. This pattern of missingness does not lead to biased estimates, but can lead to increased variance due to smaller sample sizes. The second mechanism is described as Missing at Random (MAR). This mechanism indicates that conditioning on observed data will eliminate bias from estimates. For example, this corresponds to the assumption in weighting class adjustments that respondents within each cell are a random subsample of the cell. Under this missingness mechanism, if response rates differ across the cells, reweighting the responses back to the proportions in each class will produce unbiased estimates. The final mechanism is Not Missing at Random (NMAR). This mechanism corresponds to the situation where the missingness is a function of unobserved data. In other words, there is no strategy that will eliminate all bias from estimates without making at least some untestable assumptions – for example, positing a model for missing data that is not estimated from observed data.
In this paper we examine a set of indicators for the risk of nonresponse bias through simulation studies. Using the classification described by Wagner (2012), we group these indicators into three categories: the response rate; indicators involving complete auxiliary data and the response indicator variable; and indicators involving complete auxiliary data, the response indicator variable, and the observed survey data. We also examine measures of model fit. The simulations vary response rates, missing data mechanisms, and correlations between the complete auxiliary data (e.g. sampling frame data) and the survey data. The results of these simulations are used to demonstrate the strengths and weaknesses of each indicator. For the sake of simplicity, we examine only the simple random sample case throughout the paper. While we anticipate that many of the results observed in our simulation studies will hold after taking into account the specific features of more complex sample designs, we leave this exploration to future research.
The paper proceeds as follows. In section 2, we discuss the set of nonresponse bias indicators considered in this study. Section 3 describes the simulation study design and discusses the results, including the overall relationship between nonresponse bias and the proposed indicators under the three missing mechanisms. Section 4 focuses on the concept of “maximal absolute bias,” derived from the R-indicator (Schouten, et al., 2009). Section 5 considers the special situation of the fraction of missing information (FMI) indicator in the NMAR setting. Section 6 considers the behavior of the nonresponse bias indicators after adjustment for nonresponse using nonresponse weights. The paper concludes with suggestions for improved nonresponse evaluations as well as suggestions for future research.
2. Measures for the risk of nonresponse bias
2.1 A review of nonresponse bias
In order to understand and evaluate alternative indicators to the response rate for the risk of nonresponse bias, it is important to understand the source of nonresponse bias. Nonresponse bias occurs when there are systematic differences between respondents and nonrespondents. A well known illustration of this problem is the use of the unadjusted respondent mean to estimate the population mean. Assuming equal sampling probabilities, the complete-case estimator of the population mean is given by
| (1) |
where r is the number of respondents on the sample and ri is the response indicator for the ith element in the sample, that is,
The bias of this estimator can be viewed through two different perspectives. The first approach is deterministic; it assumes that the population can be divided into two groups, respondents and nonrespondents (Cochran, 1977). Under this approach, the nonresponse bias of the unadjusted respondent mean is given by
| (2) |
where N is the overall population size, M is the population size of the nonrespondent's group, and are the population means of a given survey variable Y of the respondents and nonrespondents, respectively, and is the proportion of respondents in the population, which is also called the population response rate. It is important to note that while we have a sample estimate of , in most practical situations, we do not have a sample estimate of .
A more general perspective for nonresponse bias is stochastic: it assumes that every element in the population has a probability of responding the survey, if requested. This is usually referred to as a response propensity and it is denoted by ρi = P(ri = 1), 0 ≤ ρi ≤ 1, i = 1, …, N. In most nonresponse adjustment strategies, we assume that all response propensities are positive in order to be able to estimate them. Then, under this stochastic approach, the nonresponse bias of the unadjusted mean is given approximately (Bethlehem, 1988) by
| (3) |
where is the population covariance between a given survey variable Y and the response propensity ρ, and is the overall population response propensity mean. Observe that the sample response rate can be considered an estimator for this latter parameter.
The deterministic approach for nonresponse bias is actually a special case of the stochastic approach, in which every element in the population has a response propensity of either ρi = 0 or ρi = 1, that is, everyone is either a respondent or a nonrespondent with certainty.
Notice that while the first term on the bias expression under both approaches can be estimated by the sample response rate, the second term cannot be estimated in most practical situations. The second term is only available in specialized studies that have a “gold standard” measure available. This might be one of the reasons that the first term – the response rate—has commonly been used as an indicator for the risk of the nonresponse bias. On the other hand, if the difference between and varies across different response rates, then there might be no relationship between the response rate and nonresponse bias. Increasing the response rate, in such a situation, may increase, decrease, or have no impact on the nonresponse bias depending upon for which subjects the change occurs.
While the response rate, in the absence of any other information, is the only available indicator for the risk of nonresponse bias, it only provides partial evidence of the risk of nonresponse bias. However, the nonresponse bias can be further explored when other auxiliary variables, denoted X, are available for the entire sample. Such variables are typically taken from the sampling frame or result from paradata, that is, data generated by the process of collecting data (Couper, 1998; Couper and Lyberg, 2005; Kreuter, 2013). Suppose that H subgroups can be formed using the auxiliary variable X, which may be continuous or categorical. Then, under the deterministic approach the nonresponse bias can be rewritten (Kalton and Kasprzyk, 1986) as
| (4) |
where is the proportion of elements in the hth subgroup, and are the population means of the respondents and nonrespondents of a given survey variable Y in the hth subgroup, respectively, is the population response rate in the hth subgroup and . Note again that the are not observed. The first component, on the one hand, can be estimated as a difference between adjusted and unadjusted means where the adjustments are the inverses of the response rates in the H subgroups. Such an estimate would eliminate bias due to this first component, but not that due to the second component. The first component corresponds to an “MAR component” that can be eliminated through standard adjustment procedures. The second piece corresponds to an “NMAR component” in that the differences between respondents and nonrespondents on the survey variable Y remain after conditioning upon the variables used to create the H subgroups. These two pieces can vary independently such that one may be zero while the other is non-zero. They may have opposite signs, thereby creating perverse situations where removing the first component may increase the overall bias of an estimate. This situation occurs when the sign of the relationship between the population respondent mean and the population response rate is the opposite of the difference between the population means for the nonrespondents and respondents, . For example, if subgroups with larger respondent means also have larger response rates, but the nonrespondent mean is larger than the respondent mean in these subgroups, the absolute nonresponse bias of a weighted adjusted mean would be larger than the unadjusted respondent mean, . This formulation generalizes to settings other than that in which cell weighting adjustments are employed.
Usually, in survey practice, subgroups of cases are formed using sampling frame variables or paradata and their response rates are monitored throughout the data collection period (Wagner, et al., 2012). In the case where there is much variability among these response rates, effort is made to equalize them by seeking to increase the levels of groups with low response rates. The coefficient of variation of subgroup response rates may also be used as a summary measure for that purpose. It is interesting to notice, however, that, unless this extra effort reduces Cov(Y, ρ), the nonresponse biases might not be reduced. The auxiliary data used to guide data collection effort may also be used to form nonresponse adjustment weights. A usual method to deal with nonresponse is by weighting the respondents to compensate for the nonrespondents within subgroups, also called nonresponse adjustment cells, formed by the auxiliary information. For a given nonresponse adjustment cell, the nonresponse weight is the inverse of the response rate on that cell. Response propensity adjustments are a generalization of this cell approach in which the response indicator is modeled using logistic regression, with fully-observed covariates as predictors.
This discussion provides a framework within which to discuss nonresponse bias. We now turn to descriptions of various indicators that may be related to nonresponse bias.
2.2 Indicators for nonresponse bias
In this section, we discuss the indicators investigated by our simulation study. These indicators are organized into two sections: indicators using auxiliary variables only and indicators using auxiliary variables and survey variables together.
2.2.1 Indicators using auxiliary variables only
Indicators using auxiliary variables can be estimated at the survey level. That is, there is a single indicator for the entire survey. This simplifies their calculation, but relies upon the strong assumption that a single indicator can adequately capture the risk of nonresponse bias across all of the statistics produced by a survey. Following the notation from the previous section, we will denote the survey outcome variable as Y and a fully observed covariate as X. We will also introduce an unobserved confounding variable, denoted Z. These X, Y, and Z may be either a single variable or a vector of variables depending upon the context.
Variability in nonresponse weights, var(Wnr)
Whether nonresponse weights are formed via adjustment cells or a response propensity model, a higher level of variability of these weights could indicate a larger risk for nonresponse bias, since it allows the covariance between Y and ρ to potentially increase. Hence, the variance of such weights is an alternative indicator to the response rate for the risk of nonresponse bias. A general form of nonresponse weighting adjustment takes the nonresponse weight, Wnr, to be the inverse of an estimate of the response propensity. That is, , where is the estimated response propensity for the ith respondent. For example, in weighting cells nonresponse adjustments, in which the sample is divided into H weighting cells according to auxiliary variables observed for both respondents and nonrespondents, the response propensity is estimated by the response rate of the cell, that is, , i ∈ h, where nh is the sample size and nrh is the number of respondents in cell h. More generally, the response propensities can be estimated using a set of auxiliary variables observed for respondents and nonrespondents, X, by a logistic regression. The variability of the nonresponse weights can then be measured by the variance of these weights:
where . A key assumption of this indicator is that if the respondents vary in their observed characteristics greatly from those of the sample, then there is a risk of nonresponse bias. This assumption might not be true. For instance, if X is unrelated to Y, then variation in X is not an indicator of potential bias in Y.
Särndal and Lundström (2010) propose a similar measure, the coefficient of variation of the nonresponse adjustments, where these nonresponse adjustments are based upon a calibration procedure. They label this indicator “H3.” A related measure, the variance of poststratification weights – or the product of the poststratification and nonresponse weights -- can also be used as a nonresponse bias indicator.
R-Indicator,
Schouten, et al. (2009) adapted this idea of using the variability of the predicted response propensities as a measure of survey quality, proposing the R-Indicator:
| (5) |
where is the mean of the predicted response propensities. Since , the R-Indicator varies between 0 and 1, with lower values indicating a larger risk for nonresponse bias, a similar reasoning to that which motivates the use of the variability in nonresponse weights as an indicator. Särndal (2011) proposed several related “balance” indicators. These are based upon a metric of the distance between the sample and responders on a set of covariates. Särndal defines one of these balance indicators, BI3, as , where is estimated from the sample using design weights. Särndal notes that this measure is very similar to the R-Indicator and, in some circumstances (i.e. under simple random sampling, maximum likelihood estimates of the logistic regression model, and with categorical covariates), they will be equivalent. The assumption of this indicator is similar to that of the variation of the nonresponse weights. A lack of balance on observed characteristics X for the respondents with respect to the sample is an indication that Y may also be imbalanced.
Coefficient of Variation of Subgroup Response Rates, cv(RRsub)
This indicator is similar to the R-Indicator, but it requires categorical auxiliary data observed for both respondents and nonrespondents in order to define subgroups. Similarly to the weighting cell nonresponse adjustment, let be the response rate in the hth subgroup with nrh respondents out of the nh sampled elements, h = 1,…, H. The coefficient of variation of subgroup response rates is then defined as
where is the overall response rate. Large variation in subgroup response rates is taken as an indication that there is a risk of nonresponse bias.
Area Under the Curve/Pseudo-R2
These indicators are meant to evaluate the model used to predict the response propensities. The Area Under the Curve (AUC), which is also the C statistic for binary outcomes, is one such measure. It ranges from 0.5 to 1. Higher values of AUC indicate a better predictive model and, therefore, a higher risk for nonresponse bias under the assumption that a strong relationship between auxiliary predictors X and the response indicator R reflects an imbalance among responders with respect to X.
Similarly, the pseudo-R2 (Nagelkerke, 1991) is another measure of the predictive power of a logistic regression model for the response propensity:
It is scaled to vary between 0 and 1, with high values of the pseudo-R2 also indicating a strong association between the observed data and the response indicator and increased risk of nonresponse bias. This is similar to the assumption underlying the other balance indicators.
2.2.2 Indicators using auxiliary variables and survey variables together
Despite adding information through the auxiliary variables, the alternative indicators discussed in the previous section do not incorporate the relationship between the response propensity and a given survey variable Y. However, developing indicators that include survey data presents two issues. First, the survey data are only available for responders. Second, using survey data implies that the indicators will be at the variable level, as opposed to the indicators estimated at the level of the survey. For these indicators, each survey statistic could have a different value and, potentially, some of them might have a high risk of nonresponse bias, while others do not. This feature, however, may also be viewed as a strength, since nonresponse bias is a statistic-level issue that may vary depending on the outcome variable or, more generally, the analysis of interest.
Fraction of Missing Information, FMI
Wagner (2010) suggested using the Fraction of Missing Information (FMI) as a survey quality measure. The FMI was developed in the missing data and multiple imputation literature (Dempster, et al., 1977; Rubin 1987) as a measure of uncertainty about the values imputed for missing elements. More precisely, it is the proportion of the total variance of a survey estimate explained by the between-imputation variability. The underlying idea is that if the FMI is large, it means that there is much uncertainty about the imputed values of nonrespondents and, therefore, this may indicate a large risk for nonresponse bias. The most straightforward method to estimate FMI is to multiply impute, say M times, the missing data for the nonrespondents under a model, estimating for each of the M imputed dataset the parameter θ by . The FMI is then estimated by:
| (6) |
where is the between-imputation variance, is the average of the estimates using the M fully-imputed datasets, is the total variance of the estimate and is the within-imputation variance, which is the average of the M estimate's variances computed using the M fully-imputed datasets. If the missing values are filled in using a relationship between X and Y estimated from the observed data, then the assumption underlying the imputation model is that the data are MAR when conditioning on X. As we will show, violations of this assumption can lead to biased estimates of the FMI.
Correlation between Nonresponse Weights and Survey Variables, corr(Wnr,Y)
Another indicator of this type is the correlation between nonresponse weights and survey variable:
Little and Vartivarian (2005) showed that the effectiveness of a nonresponse adjustment depends both on the associations of the survey variable with the auxiliary variables used in the adjustments and also with the response propensities. The correlation between the nonresponse weights and the survey variable can be used as a proxy of the former, but may be a biased estimate of corr(X,Y) if this relationship is different among nonrespondents, i.e. NMAR, since corr(Wnr,Y) is computed only over the respondents. Särndal and Lundstrom (2010) propose two similar measures. They label |corr(Wnr,Y)|×cvw, where cvw is the coefficient of variation of the weights, as H1 and corr(Y,X)×cvw as H2. Another similar indicator, the W indicator developed by Schouten (2007), can be used as an indicator for the risk of nonresponse bias, even though it was not proposed for this purpose. As with the correlation between nonresponse weights and survey variables, this measure is an indicator for the range of potential nonre-sponse bias. It is based upon the correlation of predicted values for Y (predicted from a model estimated using covariates X and estimated regression coefficients β) and R and Y. Using our notation, it can be written:
The * indicates that these data or estimates are available for respondents only. This strategy assumes that the estimates from the respondents of the coefficients β and the correlation between the predicted values and the respondent Y is the same as that for the full sample. In this way, it relies upon assumptions similar to the correlation between the nonresponse adjustments and respondent Y values.
Indicators that incorporate the survey variables on top of the auxiliary variables and the response indicator might be able to better capture the risk of nonresponse bias. On the other hand, they also rely on model assumptions about the relationship of the auxiliary and outcome variables. If these assumptions are not met, the conclusions made using such indicators might be invalid. However, this is also true for the other indicators, except that they might make stronger and less explicit assumptions. Brick and Jones (2008) explore the extent to which the form of the weighting (propensity scores, calibration, raking, etc) may influence nonresponse bias. They find that the choice of which auxiliary variables to include is more important than the method used to develop the weights.
Using a set of simulation studies, we demonstrate the conditions under which a representative subset of indicators may or may not be useful for identifying when nonresponse bias is likely to occur. In the first simulation study, we examine different mechanisms for the missing data (MCAR, MAR, and NMAR). In the second simulation, we focus on the NMAR mechanism.
3. Simulation study
3.1 Study design
Two simulation studies were conducted, each one using k = 1,000 simulations with sample sizes n = 1,000 for each simulation to estimate a population mean . Each simulation included one observed explanatory variable X and another unobserved Z. In both studies the following conditions were varied:
-
■
Missing mechanism
-
■
Response rate
-
■
Correlation between the explanatory and survey variables
-
■
Correlation between the response propensities and the explanatory variables
The first simulation study considers a broader range of these parameters. In this simulation study, a total of 3 × 19 × 19 = 1,083 different simulation studies were conducted using:
-
■
3 missing mechanisms: Missing Completely at Random (MCAR), Missing At Random (MAR) and Not Missing At Random (NMAR)
-
■
19 response rates varying from 0.05 to 0.95 with 0.05 increments
-
■
19 correlations between auxiliary variable (X or Z) and survey variable varying from 0.05 to 0.95 with 0.05 increments
For the NMAR mechanism in this study, only the unobserved variable Z was used to generate the missing pattern.
The focus of the second simulation study was the NMAR mechanism. In this case, the missing mechanism was generated using both the observed and unobserved variables X and Z. This corresponds to varying the strength of the first and second components of the expression developed by Kalton and Kasprzyk (4). The X variable determines the magnitude of the first (observable) component while the Z variable determines the magnitude of the second (unobservable) component. A total of 35 = 243 different simulation studies were conducted using:
-
■
3 response rates: 0.2, 0.4 and 0.7
-
■
3 correlations between the observed variable X and survey variable Y: low, medium and high
-
■
3 correlations between the unobserved variable Z and survey variable Y: low, medium and high
-
■
3 correlations between the response propensities and the observed variable X: low, medium and high
-
■
3 correlations between the response propensities and the unobserved variable Z: low, medium and high
The levels low, medium and high correspond, respectively to correlations of 0.05, 0.20 and 0.70. The only exception is when the correlations between the response propensities and both covariates X and Z were high. In those cases, due to a restriction problem, they were set as approximately 0.54 for both correlations.
The data and missing mechanism generation was done in the same way for both simulation studies. First, a sample of size n = 1,000 of a random vector (Y, X, Z) was generated with
| (7) |
The covariances σyx and σyz vary accordingly to the specified correlations. Then, for each one of the 1,000 elements, a response propensity, ρi, was computed using a logistic regression model, given by
| (8) |
In the first simulation study, the coefficients β0, β1 and β2 were varied to meet the specified response rates and missing data mechanisms (see Appendix 1). In the second simulation study, the values of β1 and β2 varied according to the correlations between the response propensities and the observed and unobserved variables, X and Z respectively; while the coefficient β0 was set to adjust the overall response rate (see Appendix 2 for a 40% response rate example).
For each one of the 1000 elements a random number ui ~ Uniform(0,1) was generated and if ui < ρi, then that element was classified as respondent, (ri = 1). Otherwise, it was treated as a nonrespondent (ri = 0). The value for the survey variable Y was treated as missing for nonrespondents.
For each simulation, we calculated the response rate and several statistics from each of the other categories described earlier. From the indicators using auxiliary variables only, we calculated the variance of the nonresponse adjustment weights, the R-Indicator and the coefficient of variation of subgroup response rates. For the R-Indicator, only the X variable was used as a predictor in the response propensity model. Likewise, only the X variable was used to define the subgroups for the coefficient of variation of the subgroup response rates. The subgroups were formed by using the quintiles of the observed variable X as cut-off points.
As examples of the indicators using auxiliary variables X and the survey data Y from respondents, we calculated the FMI and the correlation of the nonresponse adjustment weights and the survey data. For the FMI, multiple imputation was done using only the observed variable X as a covariate in a regression model estimated from the observed data and, because of computational constraints, M = 10 multiple imputations. In practice, a larger number of imputations may be needed to reliably estimate the FMI (Graham, et al. 2007). In these simulations, the reliability issue is less important as we performed 1,000 replications.
For the model fit statistics, we calculated the AUC and Pseudo-R2 of the logistic regression models predicting response, again using X as the predictor. These statistics form a representative set of the many statistics that could be estimated given the input data. We also computed two different estimates of the mean of Y: 1) the unadjusted respondent mean, and 2) an adjusted mean, where the adjustments are the inverse of estimated response propensities using X as a predictor in a logistic regression model. This allowed us to compare the indicators to the bias of each estimate (unadjusted and adjusted). We can make these comparisons under the various scenarios described earlier. A key question is whether these indicators can be good predictors of when bias is likely.
The simulations and analysis were performed in R 2.13.2 (R Development Core Team, 2011) with survey (Lumley, 2004; Lumley, 2012), mice (van Buuren and Groothuis-Oudshoorn, 2011) and rms (Harrell Jr, 2014) packages.
3.2 Results
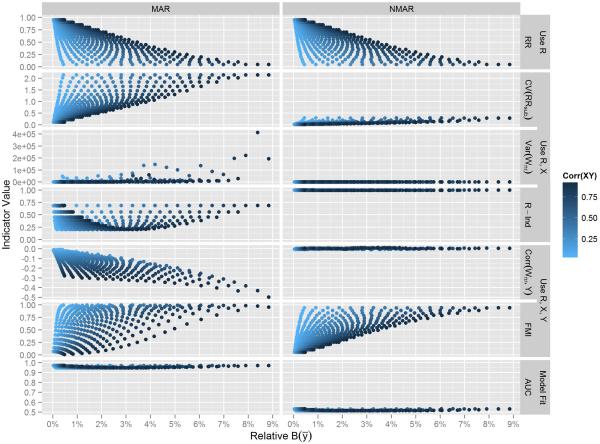
Figure 1 presents some of the results from the first simulation study. We have omitted the MCAR simulation results in order to simplify the presentation. As expected, the MCAR mechanism does not lead to biased estimates. In Figure 1, the relative bias of the unadjusted respondent mean is on the x-axis. The y-axis presents the level of each indicator. The shade of the dot represents the strength of the correlation between X and Y. The top row of the figure plots the relative bias against the response rate for the two mechanisms shown (MAR and NMAR). The next three rows display the results for indicators that depend upon the relationship between the X variable (available for all cases, e.g. sampling frame data or paradata) and the response indicator R. These indicators include the coefficient of variation of subgroup response rates cv(RRsub), the variance of nonresponse adjustment weights (var(Wnr) where the adjustments are based on X), and the R-Indicator. A third type of indicator includes those based upon the relationship between the complete data X and the survey variable Y. These indicators are presented in the next two rows of Figure 1 and include the correlation of the nonresponse weights Wnr and the survey variable Y, and the FMI which uses X to impute missing values of Y. Finally, some indicators monitor the model fit. The area under the curve (AUC) for the model predicting the probability of response using X as a predictor is an example of this type of indicator.
Figure 1.
Indicators (y-axis) vs. Nonresponse Relative Bias (x-axis) of the respondent mean
From a review of Figure 1, several interesting patterns emerge. From the first row of plots for the response rate, it can be seen that, for a given association between the survey variable and the auxiliary variable X (represented by the shading of the points), the nonresponse bias is a decreasing function of the response rate. The response rates do place a limit on the bias. However, although it may be obvious from the definitions, we can also see that it is not possible to distinguish from the response rate which missing mechanism is underlying the nonresponse error. Although the response rate places a limit on the potential bias, this does not mean that a higher response rates leads to smaller nonresponse bias, since the latter also depends on the association of the outcome and auxiliary variable. For example, if by increasing the response rate, the nature of the association between the outcome and auxiliary variable changes, there might be an increased in the nonresponse bias if that change actually makes that association stronger, even though this increase in response reduces the range of the potential nonresponse bias.
Although the response rate is associated with the magnitude of the nonresponse bias range, it is important to notice that the range, or maximum bias, is never known to the survey practitioner. In other words, higher response rates (under the same level of association between nonresponse and the survey outcome) only guarantees a smaller range of the nonresponse bias, but its real magnitude, and therefore the bias itself, will most likely be an unknown for any given survey variable. Other than for proportions, placing a limit on this bias will require making assumptions about the missing mechanism. We will return to this question in the next section.
Indicators using both the response indicator and auxiliary variables show a similar pattern, but with different levels of correlation between the indicator and the nonresponse bias. For instance, the coefficient of variation of the subgroup response rates (cv(RRsub)) presents a very similar pattern to the response rate, but with the inverse relationship: for a given association between the outcome and auxiliary variables, the larger the cv(RRsub), the larger the nonresponse bias is. It is still not possible to distinguish the different missing data mechanism based on the value of this indicator for a given survey. Therefore, although it appears that this indicator performs better as an indication of the potential maximum nonresponse bias, this information is, in virtually every practical situation, hidden since we cannot know the missingness mechanism. Further, when the mechanism is NMAR, low values of the cv(RRsub) may give the misleading impression that the risk of nonresponse bias is low. The plot of the cv(RRsub) under the NMAR mechanism shows consistently low estimates of this indicator even as the bias increases. Unless one knows the mechanism, interpretation of this indicator is difficult.
The R-Indicator and the variance of the nonresponse weights var(Wnr) seem not to perform well in terms of indicating the magnitude of the bias. Under the NMAR mechanism, the R-Indicator is unrelated to the bias. Under the MAR mechanism, lower values of the R-Indicator appear to be associated with the magnitude of the bias, however, the range of the R-Indicator is limited with the larger biases. On the other hand, these indicators do identify when the missing mechanism is MAR versus when it is either MCAR (not shown) or NMAR. The indicators behave the same under either the MCAR or NMAR situations, basically indicating that the response set is well balanced with respect to X. When the situation is MAR, these indicators show a lack of balance. When the R-Indicator is very large, the missing mechanism tends to be MCAR or NMAR. Of course, knowing the distinction would be crucial information for judging the bias. The variance of the nonresponse weights var(Wnr) behaves similarly, but in the opposite direction. That is, very large values of the variance of the nonresponse weights tend to indicate a MAR mechanism. Again, the problem is that is not possible to make a distinction whether the missing mechanism is MCAR or NMAR using these indicators.
The AUC also presents a similar pattern, but in this case, when the missing mechanism is MCAR or NMAR it assumes values around 0.50, indicating a weak fit of the model where X predicts the response indicator R, while under the MAR mechanism, as this indicator increases, so does the nonresponse bias.
Indicators that use the survey data for the observed cases suffer limitations similar to those of other indicators. The FMI ranges from 0 to 1, but just as the previous indicators, larger values tend to indicate a large range on the maximum bias when the missing mechanism is MAR or NMAR. These ranges are more apparent when the X variable is strongly correlated with Y. The correlation between the nonresponse weight and the survey variable corr(Wnr,Y) presents an interesting pattern under MAR mechanism: with large negative correlation, the largest nonresponse bias tends to be very large, but this tends to rapidly decrease as this correlation approaches to zero.
In sum, as expected, none of the indicators reveal the magnitude of the nonresponse bias or even whether it exists. They do provide limited evidence on potential mechanisms. This evidence is limited to descriptions of the relationships between X and R and X and Y.
4. Maximal absolute bias
As noted in the previous section, none of the indicators used to evaluate the risk of non-response bias can specifically identify whether this bias is present in the estimation of the mean of a given survey variable, but some of them are at least able to present an indication whether the range of the nonresponse bias will increase or decrease, depending on the size of those indicators. Hence, as an alternative to the well know strategy of maximizing the response rate as a solution for nonresponse bias, it has been suggested that it may be useful to minimize the “maximal absolute bias” (Schouten, et al., 2009; Buellens and Loosveldt, 2012). This measure, a function of the R-Indicator, is defined as
| (9) |
where R(ρ) is the R-Indicator, is the overall population response propensity mean and S (y) is the standard deviation of the survey outcome Y.
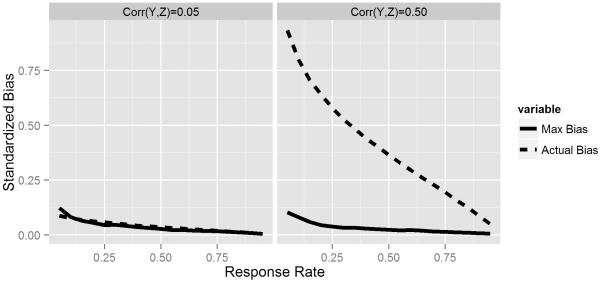
However, using such a strategy can be misleading as this measure directly depends on the adequacy of the model estimating the R-Indicator. If this model is misspecified, by not including important predictors of the response indicator, for example, this measure might actually underestimate the true maximal nonresponse bias. As an illustration of this situation, we used the results from the simulation conducted under NMAR missing mechanism of the first study. In this set of simulations, the R-Indicator is estimated using an observed covariate X, although the missing mechanism is generated through an unobserved covariate Z. In the graphs below we compare the maximal absolute bias computed with the misspecified R-Indicator and the true nonresponse standard bias of the respondent mean, across different response rates and associations between the survey outcome Y and the unobserved covariate Z.
The results of these simulations confirms that in most cases, the maximal absolute bias measure using a misspecified model to estimate the R-Indicator underestimates the true nonresponse bias. This gap tends to decrease as the response rate increases, mostly because the true nonresponse bias rapidly decreases as well. This pattern is the opposite for the association between Y and Z: as it increases, the difference between the estimated and the true bias also increases. There are only two instances in which the estimated maximal absolute bias was larger than the true nonresponse bias: when the association of Y and Z is low (corr(Y, Z) = 0.05) and the response rate is low (RR = 0.05 and RR = 0.10). This illustrates how placing a bound on the maximal absolute bias relies upon an untestable assumption about the missing mechanism.
5. Bias of the FMI under NMAR
The second simulation study revealed an interesting characteristic of the FMI. Wagner (2010), following Rubin (1987), observed that the FMI is bounded on the upper end by the nonresponse rate. However, this is only true under the MAR assumption. Here, we define the “bias” of the FMI as the difference of the FMI estimated with the incorrectly specified missingness model (i.e. the model that just uses X) and the FMI under the correctly specified model (i.e. that using both X and Z). In our simulations, the bias of the estimated FMI can be quite extreme when unobserved factors (Z, in our simulations) are powerful drivers of the nonresponse process.
Table 1 shows the relative bias of the FMI under a variety of simulated conditions. The columns define the relationships between the Y outcome variable and both X (observed) and Z (unobserved) variables. The first level of the columns shows the correlations of of Y and X (Low=0.05, Medium=0.20, High=0.70). Nested within these correlations are the correlations of Y and Z (low=0.05, Medium=0.20, High=0.70). The rows show the correlations between the response indicators R and the covariates X (observed) and Z (unobserved). The bias of the FMI can be extreme under two different conditions: if the unobserved covariate (Z) is a powerful predictor of response(these are the Corr(R,Z) rows marked “High”), or if the unobserved covariate is a powerful predictor of the survey outcome variable (Y) (these are the Corr(Y,Z) rows marked “High”). A positive bias (overestimate of the FMI) is highlighted in light gray. This occurs when the unobserved covariate Z is highly correlated with Y. In this case, we have overestimated our ability to predict Y, hence we have a strong positive bias on the FMI. A negative bias (underestimate fo the FMI) is highlighted in dark gray. This occurs when the unobserved covariate (Z) is a strong predictor of response. This results when we have relatively weak prediction of R from the observed X but have at least some ability to predict Y. These two features can sometimes “cancel each other out” as in the two cells highlighted in black. Kreuter and Olson (2011) explore a similar phenomenon for multivariate adjustment models.
Table 1.
The relative bias of the FMI under various simulated NMAR conditions for a 40% response rate
| Corr(Y,X) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Low | Medium | High | ||||||||
| Corr(Y,Z) | ||||||||||
| Corr(R,X) | Corr(R,Z) | Low | Medium | High | Low | Medium | High | Low | Medium | High |
| Low | Low | −0.99% | 0.24% | 35.79% | 0.55% | 1.16% | 38.06% | −0.10% | 6.33% | 1250.96% |
| Medium | −3.74% | −2.51% | 29.58% | −3.08% | −0.69% | 34.36% | −6.78% | −1.04% | 1111.53% | |
| High | −29.20% | −29.41% | −18.83% | −30.42% | −30.04% | −20.13% | −40.53% | −40.64% | −200.48% | |
| medium | Low | 0.57% | 1.40% | 32.65% | 0.84% | −0.13% | 40.57% | −0.36% | 5.09% | 1208.11% |
| Medium | −4.22% | −2.34% | 27.13% | −3.40% | −1.56% | 32.43% | −5.11% | 1.18% | 1105.40% | |
| High | −27.63% | −27.96% | −19.54% | −29.26% | −27.81% | −17.23% | −39.46% | −37.86% | 212.31% | |
| High | Low | −29.20% | −29.41% | −18.83% | −30.42% | −30.04% | −20.13% | −40.53% | −40.64% | 200.48% |
| Medium | −1.90% | −1.84% | 10.21% | −1.53% | −0.83% | 11.77% | −2.55% | 2.45% | 522.1 | |
| High | −15.34% | −15.08% | −7.55% | −14.94% | −14.78% | −5.36% | −21.53% | −20.47% | 353.43% | |
This bias may be useful in detecting NMAR mechanisms. If it appears that the estimated FMI is much higher than the nonresponse rate, and there are a sufficient number of imputations (perhaps as many as 200; Graham et al., 2007), then this may indicate that the missing data are NMAR. For the data in Table 1, this condition was obtained in the bottom two rows of the table.
6. Nonresponse bias after adjusting for nonresponse
While our analyses up until now have focused on unadjusted means, in practice, adjustments would typically be made to compensate for possible nonresponse bias if information is available for such corrections. A common form of correction is done through nonresponse adjustment weighting. A nonresponse-weighted adjusted mean is given by
| (10) |
where is the inverse of the response rate on the adjustment class c. Its nonresponse bias is given by
| (11) |
in the deterministic setting, and
| (12) |
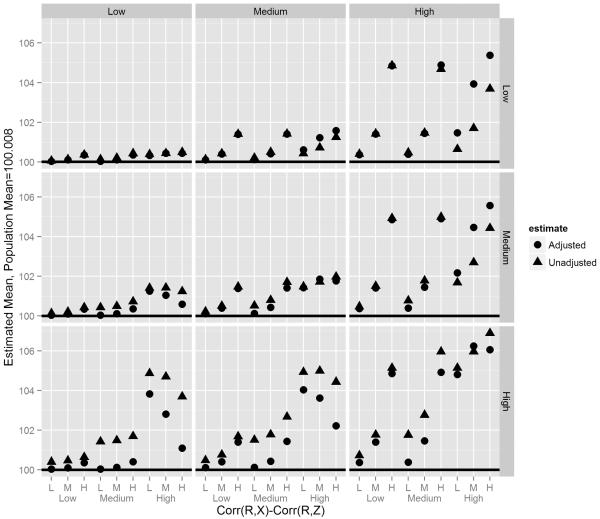
in the stochastic setting. We note that nonresponse weights eliminate the portion of the bias estimable from the observed data -- the first term in Kalton and Kasprzyk's formulation (4). The second component of the original bias in (4) still remains. It is therefore worth analyzing under which circumstances the nonresponse weight-adjusted mean presents a smaller bias than the respondent mean. For that purpose, we used data from the second NMAR simulation study and compared both the respondent mean and the nonresponse-weighted mean estimators with the population mean across different scenarios. In Figure 3, the results of such a comparison are presented.
Figure 3.
Respondent Mean vs. Nonrespondent Weighted Mean vs. Overall Mean by Corr(Y,X), Corr(Y,Z), Corr(R,X) and Corr(R,Z) under a 40% response rate
As expected, in general, the bias of both respondent mean and the nonresponse weighted-adjusted mean increase as the correlations of X and Y, Z and Y, and both response propensity and Y increase. Also, the weighting adjustment seems to perform well when the correlation of X and Y is high and the correlation of Z and Y is not large.
In most cases, the nonresponse-weight adjusted mean resulted in less bias than the respondent mean, as would be expected. However, in general we see that the difference between the two estimators was not large. Moreover, there were some cases in which both estimates were very similar or even situations where the adjusted estimator presented a larger bias than the unadjusted. The latter situation occurred when the correlation of Z and Y and the correlation of the response propensity and Z were high, and the correlation of X and Y was not high. In this case, the first and second components of the bias expression might have different signs, with the second component dominating the overall bias compared to the first component. Therefore, eliminating the first component of the nonresponse bias by making a nonresponse weighting adjustment actually increases the bias compared to the respondent mean. This highlights the importance of having strong correlations between auxiliary variables X and Y when making nonresponse adjustments.
It is also important to analyze the behavior of the indicators for the bias of this nonresponse weight adjusted mean. For simplicity, we do not present a new figure as the pattern of all indicators is exactly the same as seen for the bias of the respondent mean in Figure 1. The only difference we find is that the range of the bias of this nonresponse adjusted mean under MAR is smaller, as would be expected, since the weighting strategy matches the missing mechanism in this case. Hence, the same conclusions made previously for the unadjusted mean are valid here as well.
7. Conclusion
Each of the indicators explored in the simulation study revealed weaknesses. Of course, the response rate yielded no evidence about the nature of the missing data. However, it does have a limiting function on the magnitude of any nonresponse bias. In the case of a proportion, we can provide limits to the nonresponse bias by assuming that none of the nonresponders have the condition (for the lower limit) or that all the nonresponders have the condition (for the upper limit). Unfortunately, in the case of continuous measures, the limits on the bias for any particular variable and response rate are not known. This strongly limits the utility of the response rate as in indicator of the risk of nonresponse bias.
On the other hand, balance indicators such as the coefficient of variation of subgroup response rates, the R-Indicator, and Särndal's BI3 indicator have the advantage of indicating when responders and nonresponders differ on fully-observed characteristics, such as those available for all elements on the sampling frame. In this case, these imbalances are an indirect indicator of nonresponse bias on the survey variables for which the nonresponders are not observed. A key assumption, therefore, of these indicators is that the selectivity observed on the fully-observed characteristics is mimicked by the survey outcome variables, which are not fully observed. Further, this same assumption is needed for each variable collected by the survey. Model fit statistics for response propensity models provide very similar information to this type of indicator. In sum, this class of indicators gives some limited evidence about whether the data are MAR vs MCAR, but do not allow us to rule out the NMAR possibility. Further, a correctly specified model is needed in order to bound the potential biases, as was shown with the “maximal absolute bias” indicator.
As with indicators which involve the partially-observed survey data, they explore, at a variable level, the relationship between R and Y. Understanding these relationships across a series of Y variables may aid in the evaluation of the risk of nonresponse bias. It directly tests the assumption of indicators based on the relationship of X and R that this relationship is similar to that of X and Y. However, the full relationship of X and Y cannot be explored in the presence of nonresponse (i.e. the relationship between X and YNR is not known). The FMI, one such indicator, may be badly biased when the missing mechanism is NMAR. The simulations also revealed that situations where the FMI is greater than the nonresponse rate may actually indicate that the missing mechanism is NMAR. Whether such situations occur in actual survey data collections has yet to be explored.
It is clear that no indicator solves the problem of monitoring and evaluating survey data collections with respect to the risk of nonresponse bias. Each of the indicators reviewed here (and any others that could be developed) provides only partial evidence. This is the nature of the missing data problem. There can be no certainty about the consequences of having missing data. Evaluating the risk requires assumptions about how the data are missing. The sensitivity of our conclusions to those assumptions needs to be carefully evaluated. Andridge and Little (2011) provide an example of how one might test a broad range of assumptions about the nature of the missing survey data. A constellation of views, involving multiple indicators may help validate and test these assumptions and, thus, provide a more convincing picture of the likely impact of missing data.
Many journals have the practice of reporting response rates. This is a compact way of describing the quality of a survey. The information contained in such evaluations is also very low. Of course, substantive journals would have a difficult time requiring that comprehensive analyses of nonresponse be included in every manuscript. However, it might be reasonable to expect that these analyses are conducted and reported as stand-alone products that can be referenced by other substantive articles. Of course, that does not absolve researchers from the responsibility to investigate how missing data might alter the conclusions of their own research.
Future research in this area should be concerned with the relationship between these indicators and the risk of nonresponse bias in fully-adjusted estimates. This question, by its nature, must be treated empirically as there can be no definitive theoretical answer. The goal should be to identify indicators or sets of indicators that provide an indication of the risk of bias that can be used as a guide during data collection. Such indicators would be useful for comparing the effectiveness of design features in relation to reducing nonresponse bias. Further, these measures would be useful inputs into “responsive designs” (Groves and Heeringa, 2006) that seek to make mid-course adjustments to the data collection based on indicators of errors and costs. For instance, FMI values greater than the nonresponse rate may indicate the there is a NMAR mechanism behind the missing data. A closely related question has to do with the consequences of tailoring survey data collections to these indicators. Does this tailoring lead to less bias (or lower cost or variance) in adjusted estimates? This research would require specialized “gold standard” studies across a variety of situations, including very realistic and common situations. Such a task is a necessary to complete if these indicators are to become part of current data collection protocols.
Figure 2.
True Standard Nonresponse Bias vs. Maximal absolute bias
Acknowledgements
The authors would like to thank the anonymous reviewers, the editor and the co-editor-in-chief for their useful comments and suggestions that have greatly improved this paper. This work was supported by the Eunice Kennedy Shriver National Institute of Child Health & Human Development [5R03HD070012-02 to J.W.]. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the National Institute of Child Health & Human Development.
Appendix 1.
: Values of β0,β1 and β2 for the first simulation study
| RR | MCAR | MAR | NMAR | ||||||
|---|---|---|---|---|---|---|---|---|---|
| β0 | β1 | β2 | β0 | β1 | β2 | β0 | β1 | β2 | |
| 0.05 | −2.94 | 0.00 | 0.00 | −27.18 | 2.00 | 0.00 | −27.18 | 0.00 | 2.00 |
| 0.10 | −2.20 | 0.00 | 0.00 | −25.64 | 2.00 | 0.00 | −25.64 | 0.00 | 2.00 |
| 0.15 | −1.73 | 0.00 | 0.00 | −24.52 | 2.00 | 0.00 | −24.52 | 0.00 | 2.00 |
| 0.20 | −1.39 | 0.00 | 0.00 | −23.69 | 2.00 | 0.00 | −23.69 | 0.00 | 2.00 |
| 0.25 | −1.10 | 0.00 | 0.00 | −22.93 | 2.00 | 0.00 | −22.93 | 0.00 | 2.00 |
| 0.30 | −0.85 | 0.00 | 0.00 | −22.25 | 2.00 | 0.00 | −22.25 | 0.00 | 2.00 |
| 0.35 | −0.62 | 0.00 | 0.00 | −21.68 | 2.00 | 0.00 | −21.68 | 0.00 | 2.00 |
| 0.40 | −0.41 | 0.00 | 0.00 | −21.06 | 2.00 | 0.00 | −21.06 | 0.00 | 2.00 |
| 0.45 | −0.20 | 0.00 | 0.00 | −20.55 | 2.00 | 0.00 | −20.55 | 0.00 | 2.00 |
| 0.50 | 0.00 | 0.00 | 0.00 | −20.00 | 2.00 | 0.00 | −20.00 | 0.00 | 2.00 |
| 0.55 | 0.20 | 0.00 | 0.00 | −19.45 | 2.00 | 0.00 | −19.45 | 0.00 | 2.00 |
| 0.60 | 0.41 | 0.00 | 0.00 | −18.90 | 2.00 | 0.00 | −18.90 | 0.00 | 2.00 |
| 0.65 | 0.62 | 0.00 | 0.00 | −18.32 | 2.00 | 0.00 | −18.32 | 0.00 | 2.00 |
| 0.70 | 0.85 | 0.00 | 0.00 | −17.74 | 2.00 | 0.00 | −17.74 | 0.00 | 2.00 |
| 0.75 | 1.10 | 0.00 | 0.00 | −17.08 | 2.00 | 0.00 | −17.08 | 0.00 | 2.00 |
| 0.80 | 1.39 | 0.00 | 0.00 | −16.28 | 2.00 | 0.00 | −16.28 | 0.00 | 2.00 |
| 0.85 | 1.73 | 0.00 | 0.00 | −15.50 | 2.00 | 0.00 | −15.50 | 0.00 | 2.00 |
| 0.90 | 2.20 | 0.00 | 0.00 | −14.34 | 2.00 | 0.00 | −14.34 | 0.00 | 2.00 |
| 0.95 | 2.94 | 0.00 | 0.00 | −12.86 | 2.00 | 0.00 | −12.86 | 0.00 | 2.00 |
Appendix 2.
: Values of β0, β1 and β2 for the second simulation study (40% response rate)
| Corr(X.R) | Corr(Z,R) | β0 | β1 | β2 |
|---|---|---|---|---|
| Low | Low | −1.40 | 0.05 | 0.05 |
| Medium | −3.20 | 0.06 | 0.22 | |
| High | −21.35 | 0.13 | 1.90 | |
| Medium | Low | −3.20 | 0.22 | 0.06 |
| Medium | −5.05 | 0.23 | 0.23 | |
| High | −30.90 | 0.64 | 2.32 | |
| High | Low | −21.35 | 0.13 | 1.90 |
| Medium | −30.90 | 2.32 | 0.64 | |
| High* | −64.20 | 3.10 | 3.10 |
In this case the high level of Corr(X,R) and Corr(Z,R) is High ≈ 0.54.
References
- Andridge RR, Little RJA. Proxy pattern-mixture analysis for survey nonresponse. Journal of Official Statistics. 2011;27(2):153–180. [Google Scholar]
- Atrostic BK, Bates N, Burt G, Silberstein A. Nonresponse in US Government Household Surveys: Consistent Measures, Recent Trends, and New Insights. Journal of Official Statistics. 2001;17(2):209–226. [Google Scholar]
- Beullens K, Loosveldt G. Should high response rates really be a primary objective? Survey Practice. 2012;5(3) [Google Scholar]
- Bethlehem JG. Reduction of Nonresponse Bias Through Regression Estimation. Journal of Official Statistics. 1988;4(3):251–261. [Google Scholar]
- Brick JM, Jones ME. Propensity to Respond and Nonresponse Bias. Metron. 2008;66:51–73. [Google Scholar]
- Brick JM, Williams D. Explaining Rising Nonresponse Rates in Cross-Sectional Surveys. The ANNALS of the American Academy of Political and Social Science. 2013;645(1):36–59. [Google Scholar]
- Cochran WG. Sampling Techniques. 3rd edition Wiley; New York: 1977. [Google Scholar]
- Couper MP. Measuring Survey Quality in a CASIC Environment; Proceedings of the Survey Research Methods Section of the American Statistical Association; 1998. pp. 41–49. [Google Scholar]
- Couper MP, Lyberg L. The Use of Paradata in Survey Research; Proceedings of the International Statistical Institute Meetings; 2005. pp. 1–5. [Google Scholar]
- Curtin R, Presser S, Singer E. Changes in Telephone Survey Nonresponse over the Past Quarter Century. Public Opinion Quarterly. 2005;69(1):87–98. [Google Scholar]
- de Leeuw E, de Heer W. Trends in Household Survey Nonresponse: A Longitudinal and International Comparison. In: Groves RM, editor. Survey Nonresponse. John Wiley & Sons; New York: 2002. pp. 41–54. [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of the Royal Statistical Society. Series B (Methodological) 1977;39(1):1–38. [Google Scholar]
- Graham J, Olchowski A, Gilreath T. How Many Imputations are Really Needed? Some Practical Clarifications of Multiple Imputation Theory. Prevention Science. 2007;8(3):206–213. doi: 10.1007/s11121-007-0070-9. [DOI] [PubMed] [Google Scholar]
- Groves RM. Nonresponse Rates and Nonresponse Bias in Household Surveys. Public Opinion Quarterly. 2006;70(5):646–675. [Google Scholar]
- Groves RM, Heeringa SG. Responsive design for household surveys: tools for actively controlling survey errors and costs. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2006;169(3):439–457. [Google Scholar]
- Groves RM, Peytcheva E. The Impact of Nonresponse Rates on Nonresponse Bias: A Meta-Analysis. Public Opinion Quarterly. 2008;72(2):167–189. [Google Scholar]
- Harrell FE., Jr. rms: Regression Modeling Strategies. R package version 4.2-0. 2014 http://CRAN.R-project.org/package=rms.
- Kalton G, Kasprzyk D. Treatment of missing survey data. Survey Methodology. 1986;12:1–16. [Google Scholar]
- Kreuter F, Olson K. Multiple auxiliary variables in nonresponse adjustment. Sociological Methods & Research. 2011;40(2):311–332. [Google Scholar]
- Kreuter F. Improving Surveys with Paradata: Analytic Use of Process Information. Wiley; 2013. [Google Scholar]
- Little RJA, Rubin DB. Statistical Analysis with Missing Data. Wiley; Hoboken, N.J.: 2002. [Google Scholar]
- Little RJA, Vartivarian S. Does Weighting for Nonresponse Increase the Variance of Survey Means? Survey Methodology. 2005;31(2):161–168. [Google Scholar]
- Lumley T. survey: analysis of complex survey samples. R package version 3. 2012:28–2. [Google Scholar]
- Lumley T. Analysis of complex survey samples. Journal of Statistical Software. 2004;9(1):1–19. [Google Scholar]
- Nagelkerke NJD. A Note on a General Definition of the Coefficient of Determination. Biometrika. 1991;78(3):691–692. [Google Scholar]
- Petroni R, Sigman R, Willimack D, Cohen S, Tucker C. Response Rates and Non-response in Establishment Surveys BLS and Census Bureau. Presented to the Federal Economic Statistics Advisory Committee. 2004:1–50.
- R Core Team . R: A language and environment for statistical computing. R Foundationfor Statistical Computing; Vienna, Austria: 2013. URL http://www.R-project.org/ [Google Scholar]
- Rubin DB. Multiple imputation for Nonresponse in Surveys. Wiley; New York: 1987. [Google Scholar]
- Särndal C-E. The 2010 Morris Hansen Lecture Dealing with Survey Nonresponse in Data Collection, in Estimation. Journal of Official Statistics. 2011;27(1):1–21. [Google Scholar]
- Särndal C-E, Lundström S. Design for Estimation: Identifying Auxiliary Vectors to Reduce Nonresponse Bias. Survey Methodology. 2010;36:131–144. [Google Scholar]
- Schouten B. A selection strategy for weighting variables under a not-missing-at-random assumption. Journal of Official Statistics. 2007;23:51–68. [Google Scholar]
- Schouten B, Cobben F, Bethlehem JG. Indicators for the representativeness of survey response. Survey Methodology. 2009;35(1):101–113. [Google Scholar]
- van Buuren S, Groothuis-Oudshoorn K. mice: Multivariate Imputation by Chained Equations in R. Journal of Statistical Software. 2011;45(3):1–67. [Google Scholar]
- Wagner J. The Fraction of Missing Information as a Tool for Monitoring the Quality of Survey Data. Public Opinion Quarterly. 2010;74(2):223–243. [Google Scholar]
- Wagner J. A Comparison of Alternative Indicators for the Risk of Nonresponse Bias. Public Opinion Quarterly. 2012;76(3):555–575. doi: 10.1093/poq/nfs032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner J, West BT, Kirgis N, Lepkowski JM, Axinn WG, Ndiaye SK. Use of Paradata in a Responsive Design Framework to Manage a Field Data Collection. Journal of Official Statistics. 2012;28(4):477–499. [Google Scholar]