A novel toxicity scoring system treating toxicity response as a quasi-continuous variable in Phase I clinical trials

Abstract

In almost all current Phase I designs, toxicity response is treated coarsely as a binary indicator of dose limiting toxicity (DLT) and a lot of useful toxicity information is discarded. We are the first to establish a novel toxicity scoring system to treat toxicity response as a quasi-continuous variable and utilize all toxicities in Phase I trial. The generally accepted and objective parts, such as a logistic function, grade and type of toxicity, and whether the toxicity is DLT, are used so that the toxicity scoring system is relatively objective. Our toxicity scoring system has been successfully applied to an isotonic design (ID) [1] to develop an extended isotonic design (EID). Simulation study and application of EID to the data of a real Phase I trial demonstrate that EID can always estimate a more accurate maximum tolerated dose (MTD) according to the exact toxicity profile under any toxicity profiles without additional cost or length of the trial. These cannot be accomplished in designs using a binary indicator of DLT, such as Standard 3+3 design, ID, and continual reassessment method (CRM) [2]. Moreover, our EID is relatively objective, model free, and simple to use. Our toxicity scoring system can also be applied to other designs, such as CRM and escalation with overdose control (EWOC) [3], to improve their efficiency and accuracy in MTD estimation by utilizing all toxicities. Our novel toxicity scoring system and EID may help to begin a new era in which toxicity response is treated as a continuous variable.

1. Introduction

As one of the most important steps in drug development, a Phase I clinical trial is the first clinical trial in human subjects after the laboratory and animal study for a therapeutic agent showing a potential cure effect of disease. The main purpose of a cancer Phase I trial is to estimate its MTD under safe administration and acceptable level of adverse events using toxicity responses of a small number of patients treated at different dose levels [4,5].

In almost all of the current Phase I designs, toxicity response is reduced to be a binary indicator as 1 for DLT and 0 for no DLT. In the National Cancer Institute (NCI) common toxicity criteria [9], the DLT is defined as a group of grade 3 or 4 non-hematologic and grade 4 hematologic toxicities as well as death (grade 5) [4,5]. In practice, patients usually have multiple toxicities and there are some correlations between different toxicities, such as fever and fatigue. Some patients even have multiple DLTs and DLTs are not equally severe, for example a grade 4 non-reversible renal toxicity is much more severe than a grade 3 reversible neutropenia [6–8]. Similarly, among “non-toxicities”, grades 0, 1, and 2 toxicities are not equally severe and a further differentiation of them will provide a more reliable basis for safety monitoring and dose allocation [6–8]. When toxicity response is treated as a binary variable, only the “worst” toxicity among all toxicities of each patient is considered and further dichotomized into a binary indicator of DLT so that a lot of useful toxicity information is ignored. A phase I trial is a small study with only a small amount of information so that all toxicity information of all patients is very valuable and should be fully utilized in order to maximize its efficiency [6–8].

So far, there are only a few studies trying to propose a Phase I design in which toxicity response can be differentiated beyond binary [6–8]. In 2000, Wang et al. [6] first brought up the idea of differentiating toxicity beyond binary by proposing an extended CRM in which a weight is used to reflect the differentiation in the severity of grade 3 and 4 toxicities during dose allocation. Through simulation study, the extended CRM has been shown to reduce the chance of selecting the higher dose level as MTD by giving more impact to grade 4 toxicities. In 2004, Bekele and Thall [7] applied a total toxicity burden (TTB) to measure qualitatively the severity of multiple toxicities in real trials. The dose allocation procedure (increasing, staying at the same dose, or decreasing) is based on the comparison between the observed TTB and the average TTB value, TTBc, of the same outcome in a hypothetical collection of all possible outcomes. The estimated MTD is the dose with the average TTBc value of the “staying at the same dose”. In 2006, Yuan et al. [8] proposed a quantitative method called Quasi-CRM in which a numeric equivalent toxicity score was employed to incorporate the impact of toxicity grade on the dose escalation decision of the standard CRM by using the quasi-Bernoulli likelihood. The Quasi-CRM was shown to be superior over the standard CRM and comparable to the Bekele and Thall method [7] in some simulation studies. Unfortunately, the fact that patients usually have multiple toxicities was not considered in their study [8].

A toxicity scoring system which calculates an equivalent score measuring the composite severity of multiple toxicities can be a good solution for the common cases of multiple toxicities per patient. To our knowledge, no such a comprehensive toxicity scoring system for Phase I trials has been proposed in the literature. In this study, we propose a novel toxicity scoring system to measure quantitatively and comprehensively the overall severity of multiple toxicities per patient. In order to reduce the arbitrariness and stay in the current track of Phase I clinical trial practice, the generally accepted and relatively objective components, such as a logistic function, grade and type of toxicity, and whether the toxicity is DLT, are used to establish our toxicity scoring system. At last we demonstrate that our system can be easily incorporated into the common designs to treat toxicity response as a quasi-continuous variable and increase the accuracy and efficiency of MTD estimation by simulation study and application to the data of a real Phase I clinical trial.

2. A novel toxicity scoring system

In the NCI common toxicity criteria (NCI 2003) [9], according to their severities and types, toxicities are classified into 5 grades as follows:

• Grade 0: no toxicity;

• Grade 1: mild toxicity;

• Grade 2: moderate toxicity;

• Grade 3: severe toxicity;

• Grade 4: life-threatening toxicity; and

• Grade 5: death.

The DLT is usually defined as a group of grade 3 or higher non-hematologic toxicities and grade 4 hematologic non-transient toxicities.

2.1. A mapping between adjusted grade and original toxicity

DLTs are usually pre-defined specifically in each trial. In order to take into account the classification of DLT and imitate what is done conventionally using the NCI grades, a mapping between adjusted grade and original toxicity has been proposed (Table 1). In the mapping, we further differentiate grade 3 toxicities into grade 3 non-DLT and grade 3 DLT, and grade 4 toxicities into grade 4 non-DLT and grade 4 DLT. It is assumed that low grade non-DLT is less severe than high grade non-DLT, non-DLT is less severe than DLT, and grade 3 DLT is less severe than grade 4 DLT. Therefore we assign an adjusted grade for toxicity: 0 for grade 0 toxicity, 1 for grade 1 toxicity, 2 for grade 2 toxicity, 3 for grade 3 non-DLT, 4 for grade 4 non-DLT, 5 for grade 3 DLT, and 6 for grade 4 DLT (Table 1). Drug-related death (grade 5) is not considered because when it happens the trial needs to be suspended and re-evaluated. But if necessary, a new highest adjusted grade, such as 7, can be assigned to death.

Table 1.

Mapping of adjusted grade and original toxicity.^a

Original grade/whether DLT	Grade 0	Grade 1	Grade 2	Grade 3 non-DLT	Grade 4 non-DLT	Grade 3 DLT	Grade 4 DLT
Adjusted grade	0	1	2	3	4	5	6

^aDLT: dose limiting toxicity.

2.2. Equivalent toxicity score

Equivalent toxicity score (ETS) is defined as a quantitative measurement of the overall toxicity severity for each patient. The mapping between adjusted grade and original toxicity in Section 2.1 is flexible because the estimated ETS of each patient will be further normalized to a range from 0 to 1 in Section 2.3.

Suppose that there are n₁, n₂, …, n_K patients who received dose levels d₁, d₂, …, d_K, (d₁ ≤ d₂ ≤ … ≤ d_K) respectively. Let T_j,k,i be the ith (1≤i≤I) toxicity of the jth (1≤j≤n_k) patient among the n_k patients who received the dose level d_k (1≤k≤K). Its NCI toxicity grade is G_j,k,i and the corresponding adjusted grade after the mapping is $G_{j,k,i}^{\prime }$.

Let the maximum adjusted grade, $G_{j,k,max}^{\prime }$, among all I toxicities of the patient j at the dose level d_k be defined as:

$$G_{j,k,max}^{\prime }=\underset{1\le i\le I}{max}(G_{j,k,i}^{\prime }).$$

Let the ETS for patient j at the dose level d_k be defined as S_j,k. In order to make the range of ETS start from 0, the ETS for a patient with no toxicity is defined as 0 as below:

$$S_{j,k}=0.$$

The ETS for a patient who has only 1 toxicity (adjusted grade=1) is arbitrarily assigned as 0.1 in order to match the value of ETS calculated with Eq. (1).

$$S_{j,k}=0.1.$$

In order to imitate the generally accepted NCI toxicity grade and make the range of ETS start from 0, the ETS for a patient who has only 1 toxicity (adjusted grade ≥ 2) is estimated as below:

$$S_{j,k}=G_{j,k,max}^{\prime }-1.$$

The ETS for the patient who had 2 or more toxicities (adjusted grade ≥ 1) is estimated by a logistic function with 3 parameters (w, α, and β) selected by an investigator as below:

$$S_{j,k}=G_{j,k,max}^{\prime }-1+\frac{exp(\mathrm{\alpha }+\mathrm{\beta }\ast (\sum _{i=1}^I\frac{w_i{G}_{j,k,i}^{\prime }}{G_{j,k,max}^{\prime }}-1\left)\right)}{1+exp(\mathrm{\alpha }+\mathrm{\beta }\ast (\sum _{i=1}^I\frac{w_i{G}_{j,k,i}^{\prime }}{G_{j,k,max}^{\prime }}-1\left)\right)}.$$ (1)

A logistic function is employed in the above equation because the range of its value (from 0 to 1) fits the gap between two consecutive adjusted toxicity grades and it is commonly used to model dose–toxicity relationship in Phase I clinical trials.

The parameter w_i ranging from 0 to 1 is a weight for the correlation of the ith toxicity with other toxicities of the same patient. The weight increases with a decreasing correlation. If the toxicity is independent of other toxicities, its weight is 1. On the other hand, the weight of a toxicity which is a “duplicate” of other toxicities is 0. The assignment of a weight for toxicity needs extensive involvement of physicians and is subjective.

The value of α mainly reflects the differences in the impacts on ETS of the “worst” toxicity and other toxicities of the same patient. According to our toxicity scoring system, for 2 patients with the same maximum adjusted grade, the first patient with 1 toxicity and the other one with 2 toxicities with the same maximum adjusted grades, the difference of ETS, Δ, for the 2 patients is as below:

$$\mathrm{\Delta }=S_2-S_1=\frac{exp(\mathrm{\alpha }+\mathrm{\beta })}{1+exp(\mathrm{\alpha }+\mathrm{\beta })}\ge \frac{exp(\mathrm{\alpha })}{1+exp(\mathrm{\alpha })},\forall \mathrm{\beta }\ge 0.$$

Because the ETS for a patient with no toxicity or only grade 0 toxicity is arbitrarily assigned as 0 and the ETS for a patient who has only 1 toxicity (adjusted grade = 1) is arbitrarily assigned as 0.1, it is consistent for Δ to be close to 0.1 too. Therefore α = − 2 is an approximately appropriate choice for the consistency of our toxicity scoring system.

$$\mathrm{\Delta }\ge \frac{exp(\mathrm{\alpha })}{1+exp(\mathrm{\alpha })}\ge \frac{exp(-2)}{1+exp(-2)}\ge 0.12,\forall \mathrm{\alpha }\ge -2.$$

The value of parameter β represents the increasing “speed” of ETS by additional toxicity. Beta has to be greater than or equal to 0 (β≥0) in order to enforce the constraint that ETS is a non-decreasing function of the “non-worst” toxicities. When β is equal to 0, our method reverts to the method counting only the maximum grade for each patient. Therefore we will only investigate situations (β>0) that are different from the standard method of escalation. The integer part of ETS depends on the maximum adjusted grade of toxicities for each patient. The values of parameters α and β only have influences on the decimal part of ETS. Fig. 1 shows some examples on the decimal part of ETS contributed by other toxicities with the same maximum adjusted grade besides the “worst” toxicity using different values of β while α = − 2 and all w_i = 1. We can explore and verify some appropriate and applicable values for β using some real trial data. In later section, we recommend some workable values (0.5 or 0.25 or 0.1) for β based on the data of a real clinical trial.

Fig. 1.

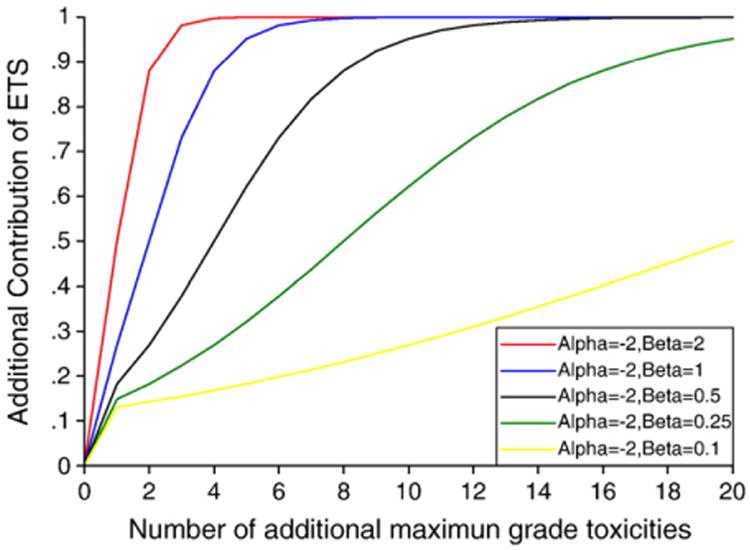
Decimal part of ETS contributed by other toxicities with maximum adjusted grade besides the “worst” toxicity using different values of β while α=−2 and all w_i =1.

2.3. Normalized equivalent toxicity score

The ETS of each patient is further normalized to be a normalized equivalent toxicity score (NETS) in the range of 0 to 1. The NETS of patient j treated with dose level d_k is defined as

$$S_{j,k}^{\ast }=S_{j,k}/S_{max}$$

where S_max<∞ is the ETS for a patient with the most severe overall toxicities among all patients and it is 6 in our toxicity scoring system presented in Table 1. If we want to further differentiate non-DLT and DLT among grade 2 toxicities or consider a grade 5 toxicity (death), a different mapping may be proposed and the S_max will become a different number, such as 7, 8, or 9. But it will not change under different mappings that $S_{j,k}^{\ast }$, ε [0, 1], k = 1, 2, …, K. The NETS, $S_{j,k}^{\ast }$, is discrete and not exactly continuous because of the finite number of possible toxicities [9] so that it is called quasi-continuous and can be viewed as fractional events.

2.4. Characteristics of toxicity scoring system

A summary of toxicity scoring system is presented in Table 2. For example, for a patient whose “worst” toxicity is a grade 3 DLT, the maximum adjusted grade is 5 and the range of ETS for the patient is from 4 to 5 depending on the additional toxicities of the patient besides the “worst” toxicity (a grade 3 DLT), the range of NETS is from 2/3 to 5/6 and the corresponding mid-range NETS is 0.75 ((2/3 + 5/6)/2 = 0.75). It is similar for other cases. The maximum adjusted toxicity grade minus 1 is the integer part of ETS and the maximum adjusted toxicity grade is the highest possible ETS of each patient. A large number of toxicities of the same adjusted grade will generate an ETS just slightly less than that generated by a single toxicity of the next higher adjusted grade so that ETS preserves the relative order of the highest adjusted toxicity grade of each patient. The ETS of 4.0 is the cut point separating patients with or without DLT. In this way, the ETS not only retains the information provided by a binary indicator of DLT, but also can further differentiate two patients who both have or do not have DLT by their different overall toxicity profiles. All toxicities are taken into account while low grade toxicity contributes less and high grade toxicity contributes more to ETS.

Table 2.

Summary of toxicity scoring system.^a

Most severe toxicity	Maximum adjusted grade	Range of ETSb	Range of NETSb	Mid-range NETS
Grade 0	0	0	0	0
Grade 1	1	[0.1–1)	[1/60–1/6)	0.092
Grade 2	2	[1–2)	[1/6–1/3)	0.25
Grade 3 non-DLT	3	[2–3)	[1/3–½)	0.417
Grade 4 non-DLT	4	[3–4)	[1/2–2/3)	0.583
Grade 3 DLT	5	[4–5)	[2/3–5/6)	0.75
Grade 4 DLT	6	[5–6)	[5/6–1)	0.917

^aDLT: dose limiting toxicity. ETS: equivalent toxicity score. NETS: normalized equivalent toxicity score.

^bThe symbol “[” means that the following number is included and the symbol “)” means that the before number is excluded from the range.

3. Determination of target normalized equivalent toxicity score

In designs treating toxicity response as a binary indicator of DLT, the target toxicity level (TTL) is the probability of DLT of the estimated MTD. In designs treating toxicity response as a continuous variable, its analog is the target normalized equivalent toxicity score (TNETS). The determination of TNETS is a clinical decision based on the target toxicity profile (TTP) at MTD level. In order to define a TTP, physicians or investigators of the Phase I trial are asked some questions as below:

1. If the treatment were to become standard, what proportion of patients would get a DLT and still be acceptable for all patients?

   A). 20%; B). 33%; C). 50%; D). Others, specify _________.

2. Within a selected total probability of DLT for a patient who is treated at MTD level, what ratios for grade 3 DLT and grade 4 DLT do you find acceptable?

   A). 1:1; B). 2:1; C). 1:2; D). Others, specify ________.

3. Among patients treated at MTD level, many will not have DLT, but must still have some side effects, what is the smallest percentage of patients who will have no toxicity or grade 0 toxicity that would be acceptable?

   A). 0%; B). 5%; C). 10%; D). Others, specify ________.

4. Within a selected total probability of non-DLT after deduction of the probability for no toxicity or grade 0 toxicity in question 3), for a patient who is treated at MTD level, what are the ratios for grade 1 toxicity, grade 2 toxicity, grade 3 non-DLT, and grade 4 non-DLT that would be acceptable?

   A). 1:1:1:1; B). 4:3:2:1; C). 1:2:3:4; D). Others, specify ___.

For example, if the TTL is pre-specified as 33% in designs treating toxicity response as a binary variable, then correspondingly, the highest acceptable probability of DLT in the design treating toxicity response as a continuous variable is also defined as 33%. Further, we can assume that the probabilities of grade 3 and 4 DLT should be equal (1:1) and non-DLT toxicity probabilities of each grade should also be equal (1:1:1:1) as well as a certain probability of no toxicities, such as 7%. Therefore, the corresponding TTP is consisting of 7%, 15%, 15%, 15%, 15%, 16.5% and 16.5% for grade 0 toxicity or no toxicity, grade 1 toxicity, grade 2 toxicity, grade 3 non-DLT, grade 4 non-DLT, grade 3 DLT, and grade 4 DLT being the “worst” toxicity, respectively (Table 3). The mid-range NETS values are 0, 0.092, 0.25, 0.417, 0.583, 0.75, and 0.917 for grade 0 toxicity, grade 1 toxicity, grade 2 toxicity, grade 3 non-DLT, grade 4 non-DLT, grade 3 DLT, and grade 4 DLT being the “worst” toxicity with maximum adjusted grade for a patient, respectively (Table 2). Therefore the TNETS, q*, is determined to be 0.476 (0.07*0+ 0.15*0.092 + 0.15*0.250 + 0.15*0.417 + 0.15*0.583 + 0.165*0.75 + 0.165*0.917 = 0.476) for designs treating toxicity response as a quasi-continuous variable (Table 3). If one has a desired TTP, it should hold for all studies. Otherwise, a TTP and the corresponding TNETS can be determined in a similar way with the answers to the 4 questions above.

Table 3.

TNETS based on TTP with 33% DLT and ratios (1:1:1:1 and 1:1).^a

Target toxicity profile	67% non-DLT toxicity (1:1:1:1)					33% DLT (1:1)		TTL = 33%
	Grade 0 or none	Grade 1	Grade 2	Grade 3 non-DLT	Grade 4 non-DLT	Grade 3 DLT	Grade 4 DLT	TNETS = 0.476
	7%	15%	15%	15%	15%	16.5%	16.5%	100% (sum)
Mid-range NETS	0	0.092	0.25	0.417	0.583	0.75	0.917	NA
Contribution	0	0.0138	0.0375	0.0626	0.0875	0.1238	0.1513	0.476 (Sum)

^aDLT: dose limiting toxicity. TNETS: targeted normalized equivalent toxicity score. TTP: targeted toxicity profile. TTL: targeted toxicity level.

4. An application of toxicity scoring system to a Phase I design

In order to evaluate its feasibility and performance, the toxicity scoring system needs to be applied to some common Phase I designs to develop new designs which can increase the accuracy and efficiency of MTD estimation by treating toxicity response as a quasi-continuous variable and utilizing all toxicities.

4.1. An extended isotonic design

In 2001, Leung and Wang proposed an ID, a simple model free approach using isotonic regression (IR), and demonstrated that ID performed substantially better than the standard Phase I design and compared favorably with CRM [2], Storer's Up-and-Down Designs [10], and EWOC design [3]. But toxicity response was treated as a binary DLT in ID. In this study, we couple our toxicity scoring system with ID to develop a new EID.

4.1.1. Design

In EID, the NETS and TNETS are used to replace the binary indicator of DTL and TTL of ID, respectively. First, NETS is estimated for each patient by utilizing fully all his/her toxicities. The average NETS (ANETS) of n_k patients in the dose level d_k, $S_k^{\ast }$, is defined as

$$S_k^{\ast }=\frac{1}{n_k}\sum _{j=1}^{n_k}{S}_{j,k}^{\ast }\text{where}k=1,2,\dots ,K.$$

The ANETS of each dose level is an analog to the probability of DLT of each dose level in designs treating toxicity response as a binary DLT. The new concept of EID is to utilize all toxicities by applying the ANETS, $S_k^{\ast }$, in the IR instead of probability of DLT during the dose allocation procedure and estimation of the MTD.

The ANETS $(S_k^{\ast })$ at dose level k (1 ≤ k ≤ K) may not satisfy the only assumption of EID, a non-decreasing dose–toxicity relationship. When it is violated among the range from dose d_r to dose d_h with d_r below d_k (r≤k) and d_h above d_k (h≥k), a pooled estimate of ANETS (PANETS) at dose d_k, q̂_r,k,h, is estimated with a pool adjacent violator algorithm (PAVA) as below:

$${\widehat{q}}_{r,k,h}=\frac{\sum _{i=r}^h(S_i^{\ast }{n}_i)}{\sum _{i=r}^h(n_i)}.$$

The final PANETS at dose level k, q̂_k, satisfying a non-decreasing dose–toxicity relationship among all K dose levels is estimated with IR as below:

$${\widehat{q}}_k=\underset{k\le h\le K}{min}\left(\underset{1\le r\le k}{max}\right({\widehat{q}}_{r,k,h}\left)\right).$$

Let q* be the TNETS and find a MTD with a PANETS, q̂_MTD, such that |q̂_MTD−q*|≤|q̂_i −q* for all i=1 to K. The rules of EID are summarized below:

Start from the lowest dose level d_k, k =1:

1. Treat a cohort of M (such as 3) patients at d_k and evaluate their toxicity responses.

2. Update the PANETS, q̂_i, of each dose d_i (i =1 to K) after the addition of toxicity responses of the current cohort using IR. Let, q̂_k, be the PANETS of the current dose level and a dose level for the next cohort is decided according to the following rule:

   If q̂_k<q*, then

   • Escalate if q*−q̂_k≥q̂_{k + 1} −q*, where k<K
   • Continue at the same dose, otherwise
   If q̂_k≥q*, then

   • De-escalate if q*−q̂_k−1<q̂_k−q*, where k>1
   • Continue at same dose, otherwise

   Dose escalation or de-escalation can only do one dose level at a time and no dose may be skipped.

3. Iterate between steps 1 and 2 until stop when a fixed total number of cohorts have been used and the recommended MTD is not the highest dose level ever tested or 3 consecutively cohorts have been treated at the same dose level.

4. The recommended dose level for the next cohort is the MTD.

4.2. Simulation studies

As the sample size of a Phase I trial is small (20–80), large sample properties are not appropriate for evaluating a Phase I trial design and simulation studies under different dose– toxicity assumptions are the most convincing ways to evaluate different methods [10]. Therefore, simulation studies are conducted to compare EID with ID [1], Standard 3 + 3 design [11], and CRM [2,12–14] in the aspects of MTD estimation, sample size, trial length (number of cohorts used), and patient distribution by dose levels (therapeutic effect for participants).

4.2.1. Simulation scenarios

Table 4 summarizes the exact toxicity profiles of 3 different scenarios. For example, in the Target-Scenario, the probability is 0.20 for a grade 3 non-DLT being the “worst” toxicity with maximum adjusted grade among all toxicities of a patient treated at dose level 1. The probabilities of DLTs are 8%, 24%, 33%, 44%, 56%, and 76% for dose levels 1, 2, 3, 4, 5, and 6, respectively, in all 3 scenarios. But the exact toxicity profiles are different across the 3 scenarios. The ANETS for each dose level calculated in the same way as for TNETS in Section 3 varies according to the exact toxicity profile across the 3 scenarios. In Target-Scenario, like in the TTP used to calculate the TNETS, the probability being the “worst” toxicity for each kind of non-DLT toxicities is the same (ratio=1:1:1:1) and that for each kind of DLTs is the same too (ratio=1:1). The Target-Scenario has a target toxicity profile so that DLT probability and ANETS match pretty well in measuring the overall toxicity severity of each dose level and the true MTD is the same (dose level 3) in designs treating toxicity response as a binary (TTL=33%) or quasi-continuous variable (TNEST=0.476). The toxicity profiles of other 2 scenarios deviate from that of the Target-Scenario. In the Under-Toxic-Scenario, toxicity profile skews to low grade toxicity and each dose level is less toxic with smaller ANETS. On the contrast, in the Over-Toxic-Scenario, the toxicity profile skews to high grade toxicity and each dose level is more toxic with bigger ANETS.

Table 4.

True toxicity profiles of different scenarios.^a

Scenario	The “worst” toxicity	Maximum adjusted grade	Mid-range NETS	Probability that the toxicity is the “worst” toxicity with the maximum adjusted grade a patient will have when treated at the dose level
				1	2	3	4	5	6
Target-Scenario	0	0	0	0.11	0.09	0.07	0.05	0.03	0.01
	1	1	0.092	0.2	0.16	0.15	0.12	0.1	0.05
	2	2	0.25	0.2	0.17	0.15	0.13	0.1	0.06
	3 non-DLT	3	0.417	0.2	0.17	0.15	0.13	0.1	0.06
	4 non-DLT	4	0.583	0.21	0.17	0.15	0.13	0.11	0.06
	3 DLT	5	0.75	0.04	0.12	0.165	0.22	0.28	0.38
	4 DLT	6	0.917	0.04	0.12	0.165	0.22	0.28	0.38
	ANETS for the dose			0.341	0.427	0.476	0.54	0.607	0.713
	Probability of DLTs for the dose			0.08	0.24	0.33	0.44	0.56	0.76
Under-Toxic-Scenario	0	0	0	0.11	0.09	0.07	0.05	0.03	0.01
	1	1	0.092	0.324	0.268	0.24	0.204	0.164	0.092
	2	2	0.25	0.243	0.201	0.18	0.153	0.123	0.069
	3 non-DLT	3	0.417	0.162	0.134	0.12	0.102	0.082	0.046
	4 non-DLT	4	0.583	0.081	0.067	0.06	0.051	0.041	0.023
	3 DLT	5	0.75	0.06	0.16	0.22	0.3	0.37	0.51
	4 DLT	6	0.917	0.02	0.08	0.11	0.14	0.19	0.25
	ANETS for the dose			0.269	0.363	0.41	0.483	0.556	0.67
	Probability of DLTs for the dose			0.08	0.24	0.33	0.44	0.56	0.76
Over-Toxic-Scenario	0	0	0	0.11	0.09	0.07	0.05	0.03	0.01
	1	1	0.092	0.081	0.067	0.06	0.051	0.041	0.023
	2	2	0.25	0.162	0.134	0.12	0.102	0.082	0.046
	3 non-DLT	3	0.417	0.243	0.201	0.18	0.153	0.123	0.069
	4 non-DLT	4	0.583	0.324	0.268	0.24	0.204	0.164	0.092
	3 DLT	5	0.75	0.02	0.08	0.11	0.14	0.19	0.25
	4 DLT	6	0.917	0.06	0.16	0.22	0.3	0.37	0.51
	ANETS for the dose			0.408	0.486	0.526	0.593	0.653	0.751
	Probability of DLTs for the dose			0.08	0.24	0.33	0.44	0.56	0.76

^aDLT: dose limiting toxicity. NETS: normalized equivalent toxicity score. ANETS: averaged normalized equivalent toxicity score.

4.2.2. Designs in simulation

4.2.2.1. Extended isotonic design

The detailed design of EID in the simulation is described in Section 4.1.1. The TNETS level is set to be 0.476 as in Section 3. Three patients per cohort are used and a maximum of 20 cohorts can be used. In the case all tested dose levels are overdosed, the first dose level is determined as MTD. On the other hand, the highest dose level is MTD when all tested dose levels are under-dosed.

4.2.2.2. Isotonic design

ID is set up similarly as EID except that a binary indicator of DLT and a TTL of 33% are used instead of NETS and TNETS.

4.2.2.3. Standard 3 + 3 design with dose de-escalation

The Standard 3 + 3 design with dose de-escalation [11], called Standard design in this study, is still the most widely used Phase I design. Three (3) patients are assigned to the first dose level. If no DLT is observed, the trial proceeds to the next dose level and another cohort of 3 patients is enrolled. If at least 2 out of the 3 patients experience at least 1 DLT, then the dose level decreases; otherwise, if only 1 patient experiences the DLT, then 3 more patients are enrolled at the same dose level. If none of the 3 additional patients experience DLT, the dose will be escalated; otherwise, the dose level decreases. Dose reduction continues until a dose level is reached at which 6 patients have been treated and at most 1 DLT is observed. The MTD is defined as the highest dose level at which at most 1 of 6 patients experiences DLT, and the immediate higher dose level has at least 2 patients who experience DLTs. In the case all tested dose levels are overdosed, the first dose level is selected as MTD. On the other hand, the highest dose level is MTD in case all tested dose levels are under-dosed.

4.2.2.4. Continuous reassessment method

CRM is a representative of model-based designs [2,12–14]. We simulate a Likelihood-based modified CRM [12–14] in which toxicity response is treated as a binary outcome and a two-parameter (α, β) logistic model is employed to depict the dose–toxicity relationship. The parameters can be updated with the Bayesian method or maximum likelihood estimation (MLE) method, both of which have been shown to perform similarly by simulation studies [12]. In our simulated CRM, the MLE method and 3 patients per cohort are used. The trial starts with the lowest dose level and keeps escalating one dose level at a time until a DLT occurs, and thereafter the MLE is employed to update parameters α and β after each additional cohort. The probability of DLT for each dose level is re-updated with the updated parameters α and β. The recommended dose level for next cohort is the one which has a probability of DLT closest to the TTL (33%). The trial stops when the same dose has been recommended for 3 consecutive cohorts or a maximum 20 cohorts have been treated. MTD is there commended dose level for the next cohort after the trial stops.

4.2.3. Simulation results

Comparisons of performances in MTD estimation between the 4 designs are summarized in Table 5. The simulation results are the same for designs treating toxicity response as a binary variable (ID, Standard design, and CRM) because of the same DLT pattern even though toxicity profiles are different substantially across the different scenarios. These demonstrate that the designs treating toxicity response as a binary variable can only utilize the probability of DLTs, but discard a lot of valuable toxicity information and fail to differentiate a more detailed toxicity profile. In the contrast, the simulation results from the 3 scenarios are different for EID, demonstrating that treating toxicity response as a quasi-continuous variable with our toxicity scoring system can successfully differentiate the toxicity profile and utilize all toxicities in MTD estimation.

Table 5.

Percentages of each dose levels recommended as MTD in different scenarios.^a

Scenario	Dose levelb	Probability of DLTs for the dose	ANETS for the dose	Percentages (%) the dose chosen as MTD
				EIDc	IDd	Standardd	CRMd
Target-Scenario	1	0.08	0.34	12	16	45	10
	2	0.24	0.43	33	34	33	34
	3	0.33	0.48	35	34	17	35
	4	0.44	0.54	17	14	4	19
	5	0.56	0.61	3	2	0.4	2
	6	0.76	0.71	0.1	0	0	0
Under-Toxic-Scenario	1	0.08	0.27	37	16	45	10
	2	0.24	0.36	15	34	33	34
	3	0.33	0.41	30	34	17	35
	4	0.44	0.48	36	14	4	19
	5	0.56	0.56	15	2	0.4	2
	6	0.76	0.67	1	0	0	0
Over-Toxic-Scenario	1	0.08	0.41	36	16	45	10
	2	0.24	0.49	40	34	33	34
	3	0.33	0.53	20	34	17	35
	4	0.44	0.59	4	14	4	19
	5	0.56	0.65	0.3	2	0.4	2
	6	0.76	0.75	0	0	0	0

^aDLT: dose limiting toxicity. MTD: maximum tolerated dose. EID: extended isotonic design. ID: isotonic design. ANETS: averaged normalized equivalent toxicity score.

^bThe dose level in bold and with underline is the true MTD.

^cDesigns treating toxicity response as quasi-continuous variable is targeted with TNETS≤0.476.

^dDesigns treating toxicity response as binary variable is targeted with TTL≤0.33.

In Target-Scenario, EID, ID, and CRM correctly estimate the true MTD (dose level 3). The percentages of each dose level chosen as MTD are pretty similar between EID and ID and CRM. These suggest that designs treating toxicity response as a binary or quasi-continuous variable perform similarly when toxicity profile is similar to the target toxicity profile. Dose level 1 is the most frequently estimated MTD by Standard design. Standard design obviously (17.3%) underestimates the MTD compared with the other 3 designs (>31%), consistent with report by Chen et al. [15].

In the Under-Toxic-Scenario, the true MTD is dose level 4 which has a higher probability of DLT than 33%. EID estimates the correct MTD (dose level 4) according to the exact toxicity profile instead of the coarse probability of DLT while MTD is obviously underestimated in ID (dose level 3), Standard design (dose level 1), and CRM (dose level 3). On the other hand, in the Over-Toxic-Scenario, the true MTD is dose level 2 which has a lower probability of DLT than 33%. EID can estimate the correct MTD (dose level 2) according to the exact toxicity profile while ID, Standard design, and CRM fail to “recognize” the deviation of toxicity profiles. These simulation results demonstrate that designs treating toxicity response as a quasi-continuous variable can always estimate a more accurate MTD according to the exact toxicity profile under any scenarios while designs treating toxicity response as a binary variable cannot.

The simulation results about the comparison of distribution of patients, sample size, and number of cohorts across 4 designs are not shown because of space limit. The distribution of patients, sample size, and the number of cohorts are the same across scenarios in the ID, Standard design, and CRM. However, they are different across the 3 scenarios in EID. In Target-Scenario in which the true MTD is the same for all designs, the patient distributions, sample size, and study length are similar in ID, CRM, and EID except Standard design. Standard design needs obviously a smaller sample size and patient distribution skews heavily to the low dose levels because of two reasons. First, it estimates a MTD with about 22% DLTs [15] while others target a MTD with 33% DLT or 0.476 TNETS so that obviously fewer dose levels need to be tested as dose escalates from the lowest level to an underestimated MTD. Second, each dose level can only be treated with no more than 6 patients. In deviated scenarios, there is no way to compare because their estimated MTDs are different. Overall, EID does not require additional cost and extended length of trial while improving its MTD estimation.

4.3. Application of EID to data of a real Phase I clinical trial

Ultimately, to assess adequately EID's utility, it is necessary to evaluate its performance in real Phase I clinical trials. We apply EID to data of a real trial from Children's Oncology Group, A90712, which is a Phase I study of motexafin gadolinium and involved field radiation therapy for intrinsic pontine glioma of childhood. The main purpose of the study is to determine the MTD and schedule of motexafin gadolinium given prior to radiation therapy using Standard 3 + 3 design with dose de-escalation. The starting dose is 1.7 mg/kg/dose from Monday to Friday for 3 weeks and there are a total of 9 dose levels. DLTs are defined as any grade 4 hematologic toxicity that persists for more than 7 days or that requires platelet transfusions for a period of time exceeding 7 days during the assigned weeks of concurrent chemotherapy and radiation therapy and grade 3 or 4 non-hematologic toxicity with the exception of grade 3 nausea and/or vomiting which can be controlled within 7 days. Patients of A90712 had various toxicities from no toxicity to multiple toxicities. The toxicity profile of the patients is very different from the TTP employed to define the TNETS (0.476). The toxicity distribution skews extremely to low grade and less severe toxicities without any grade 4 non-DLT toxicities or grade 4 DLTs among all patients so that the overall toxicity profile of study A09712 is an extreme under toxic scenario (Table 6).

Table 6.

Summary of dose level and toxicity of patients in A09712.^a

Dose level	Treatment	Toxicities
		Patient 1	Patient 2	Patient 3	Patient 4	Patient 5	Patient 6
1	1.7 mg/kg/dose M–F*3w	2G2 3G1	None	1G2 2G1	1G2 4G1
2	1.7 mg/kg/dose MWF*6w	1G1	None	2G1	2G1
3	1.7 mg/kg/dose M–F*6w	3G2 5G1	1G2 1G1	1G1	None
4	1.9 mg/kg/dose M–F*6w	None	1G1	1G3DLT 2G3 5G2 1G1	1G2 2G1	4G1	1G2 3G1
5	3.4 mg/kg/dose M–F*6w	1G2 1G1	2G1	2G1	None
6*	4.4 mg/kg/dose M–F*6w	1G2 1G1	2G2 1G1	2G2 2G1	1G3DLT 2G3 2G2 2G1	2G2 2G1	1G3 3G2 6G1
7	5.5 mg/kg/dose M–F*6w	1G2	1G2 1G1	2G2 2G1	1G3DLT 1G2 2G1	1G3DLT 1G3 2G2 1G1	2G2 6G1
8	7.1 mg/kg/dose M–F*6w	2G2 1G1	2G2 1G1	2G2 2G1	1G3DLT 1G3 2G2 3G1	1G3DLT 1G3 4G2 5G1
9	9.2 mg/kg/dose M–F*6w	1G3DLT 2G3 4G2 2G1	1G3DLT 1G2 1G1

nGm: n grade m non-DLT toxicities. nGmDLT: n grade m DLT toxicities.

^*Recommended maximum tolerated dose (MTD) by original Standard 3+3 design with dose de-escalation.

^aM: Monday. F: Friday. w: week. DLT: dose limiting toxicity.

We conduct pseudo-trials of EID with patients of A09712. Bootstrap method (sampling with replacement) is used to randomly sample a patient at a time from the patient pool at the right dose level and 3 patients per cohort are used. The toxicities and treated dose levels of sampled patients are used in the pseudo-trials with EID, but their entry orders in the original trial are ignored. An ETS ranging from 0 to 6.0 is calculated for each patient according to his/her toxicities and our toxicity scoring system, and then divided by the maximum ETS (6.0) to obtain NETS with the range 0 to 1. The TNETS is set to be 0.476 and no new dose levels can be added ad hoc during a pseudo-trial. The recommended new dose level for the next coming cohort is still the highest existing dose level when further escalation beyond the lowest existing dose level is warranted and it is still the lowest existing dose level when further de-escalation below the lowest existing dose level is warranted. The comparison outcomes are the percentage of each dose level chosen as MTD, average sample size, and average cohort number. A total of 40,000 simulations are conducted in each situation. In order to explore the appropriate values of β and investigate their impacts on MTD estimation, we conduct similar pseudo-trials in the same setting except that patients' NETSs are estimated with 5 different values (2, 1, 0.5, 0.25, and 0.1) of β while α is fixed as −2 and weight w_i = 1 for all toxicities.

The pseudo-trial with EID is summarized in Table 7. The original A09712 trial recommended dose level 6 as MTD, but the pseudo-trials most frequently recommend dose level 8 as MTD among all cases with 5 different values of β. The dose level 6 recommended in the original A09712 is a substantially underestimated MTD with a far less toxic effect. The pseudo-trials with EID identify correctly dose level 8 as MTD according to the exact toxicity profile. The following Phase II trial further confirms that dose level 6 is an underestimated MTD and dose level 8 is the correct MTD after adjustment for the deviation of the extremely under toxic profile of A97012. In the Phase II trial, a review board consisting of physicians, study coordinators, and statisticians reviewed both the overall toxicity profile and efficacy of the agent to achieve an optimized MTD. The important components of overall toxicity profile are the incidence, type, grade, severity, timing, and duration of all treatment related toxicities. The measurements for the efficacy of agent are clinical response rate (complete response and partial response), event free survival, and overall survival. These results demonstrated that EID can adjust for the deviation of toxicity profile and always estimate a correct MTD with the target toxicity level to ensure therapeutic effect of chemical agent.

Table 7.

Simulation results with data of A09712 with different values of β while α=−2 and w_i=1 for all toxicities.

Dose level	Probability (%) the dose chosen as maximum tolerated dose (MTD)
	β=0.1	β=0.25	β=0.5	β=1	β=2
1	0	0	0	0	0
2	0	0	0	0	0
3	0	0	0	0.05	0.3
4	0.01	0.02	0.02	0.07	0.2
5	0	0	0	0.02	0.2
6a	1.6	2.0	2.9	7.0	20.2
7	7.3	8.0	11.1	23.0	34.5
8b	83.5	83.7	83.0	69.9	44.6
9	7.5	6.3	3.1	0.03	0.01
Average sample size	41.0 (4.5)	41.1 (4.7)	41.1 (5.0)	41.1 (5.9)	40.0 (7.1)
Average number of cohorts	13.7 (1.5)	13.7 (1.6)	13.7 (1.7)	13.8 (2.0)	13.3 (2.4)
Original sample size	40
Original cohort number	13

^aThe MTD recommended by original trial with Standard 3+3 design with dose de-escalation.

^bThe most frequently recommended MTD by pseudo-trials with extended isotonic design (EID).

The probabilities are 0 for the cases that MTD cannot be estimated because the ANETSs of all existing dose levels are all either bigger or smaller than the TNETS (0.476). The frequency of correctly estimating dose level 8 as MTD decreases from 83.5% to 44.6% with the increasing values of β, suggesting that the value of β can substantially affect the performance of EID. But the decreases are very small, less than 1%, when the value of β increases from 0.1 to 0.5. The average sample sizes (about 41 patients) and number of cohorts (about 13.7 cohorts) of the pseudo-trials with EID are pretty stable regardless the different β values used and similar to those (40 patients and 13 cohorts) of the original trial, respectively. Therefore, we recommend the use of EID with β as 0.1, 0.25, or 0.5 and α as −2 in practical Phase I clinical trials.

5. Discussion

In real trials, a patient usually has multiple toxicities so that no design can claim to be able to treat toxicity response as a continuous variable and utilize all toxicities if the case of multiple toxicities per patient is not considered and multiple toxicities are not measured comprehensively and quantitatively [6–8]. We propose a novel toxicity scoring system to treat toxicity response as a quasi-continuous variable, estimate the overall toxicity severity of patient quantitatively, and utilize all toxicities in Phase I clinical trials. Binary DLT has been generally accepted and used, our toxicity scoring system is a natural extension along this track from binary to ordinal and finally to quasi-continuous. The significant separation of patients with (ETS≥4.0) or without (ETS<4.0) DLT is retained in the toxicity scoring system. To reduce arbitrariness and be relatively objective, our toxicity scoring system is based on the generally accepted toxicity grade and type as well as study specific definition of DLT.

On the other hand, our toxicity scoring system is also flexible. The mapping between adjusted grade and original toxicity can be modified according to practical needs. For example, the impact of different types of toxicities with same grade can be differentiated by assigning a higher adjusted grade to a more severe toxicity and a lower one for the less severe toxicity. A relative higher adjusted grade can be assigned to non-reversible toxicity than to reversible toxicity, or to long lasting toxicity than to transient toxicity, or to non-hematological toxicity than to hematological toxicity. Vice versa, different toxicities of different grades can be assigned the same adjusted grade if they are close in overall severity. Based on the adjusted grade of toxicity, a scoring function may be obtained by interpolating between them and continuous adjusted grade can be assigned to toxicity of continuous measurement, such as neutropenia. Moreover, there is still some “wiggle room” left for investigators by choosing different values for the parameter β and weight w_i for each toxicity because Phase I trial usually has its specific aims and considerations. Therefore, a balance between flexibility and objectiveness is achieved well in our toxicity scoring system.

Our toxicity scoring system depends on the same assumption as the binary DLT that the relative order of scores for patients is decided by their “worst” toxicities. But its clinical and biological meaning is open to discuss. Whether the assumption is the best way to deal with toxicity response is still debatable. For example, it is unsure which is more severe between a patient with numerous (such as N> 1,000,000) grade 2 toxicities and another with only 1 grade 3 non-DLT. Moreover, toxicity types should be further differentiated and incorporated into the toxicity scoring system with involvement of physicians.

The toxicity scoring system has been successfully applied to ID, one of the common Phase I designs, to develop an EID which can always estimate a more accurate MTD according to the exact toxicity profile under any toxicity profiles, especially deviated profiles. EID is robust because it only requires a generally accepted assumption of a non-decreasing dose– toxicity relationship. EID is a rule-based design so that it is simple to use. Application of EID to A97012 data further shows that EID is not very sensitive to the chosen values of parameter β in the toxicity scoring system because IR [16] is coupled with the NETS to estimate MTD. IR depends mainly on the relative order of overall toxicity severity and is not sensitive to the exact score so that it can reduce the impact from the arbitrariness of the toxicity scoring system.

Lots of Phase I designs have been proposed in the literature [4,5]. They can be classified by their algorithm as two major groups: rule-based and model-based. Standard 3 + 3 design and ID are rule-based designs. CRM and EWOC are typical model-based designs. Rule-based designs and model-based designs have their own advantages and disadvantages [4,5]. ID is chosen as a framework to couple with the toxicity scoring system to create a successful EID in this study because of its semi-parametric characteristics. In our toxicity scoring system, NETS and TNETS are analogs to a binary indicator of DLT and TTL, respectively, which are the two most important factors in the designs treating toxicity response as a binary DLT. By applying the NETS and TNETS to a design treating toxicity response as a binary DLT, we can transform it into a design which can always estimate a more accurate MTD by treating toxicity response as a quasi-continuous variable and utilizing all toxicities. Application of our toxicity scoring system to the EWOC is ongoing and will be reported in the future. Our toxicity scoring system may also be applied to one or two arm non-adaptive Phase II trials in radiation oncology and other disciplines whose primary outcomes are toxicities.

In summary, we are the first in the literature to propose a novel toxicity scoring system to treat toxicity response as a quasi-continuous variable and utilize all toxicities. Simulation studies and practical applications demonstrate that our toxicity scoring system has been successfully applied to develop an EID which can estimate a more accurate MTD according to exact toxicity profile instead of coarse probability of DLT without additional cost and extended length of trial. Moreover, our EID is model free, relatively objective, robust, and simple to use. Therefore, our novel toxicity scoring system and EID would be of great practical value in the field of Phase I clinical trial and will help to begin a new era in which toxicity response is treated as a quasi-continuous variable and all toxicities are utilized.