Morphometry of anatomical shape complexes with dense deformations and sparse parameters

Abstract

We propose a generic method for the statistical analysis of collections of anatomical shape complexes, namely sets of surfaces that were previously segmented and labeled in a group of subjects. The method estimates an anatomical model, the template complex, that is representative of the population under study. Its shape reflects anatomical invariants within the dataset. In addition, the method automatically places control points near the most variable parts of the template complex. Vectors attached to these points are parameters of deformations of the ambient 3D space. These deformations warp the template to each subject’s complex in a way that preserves the organization of the anatomical structures. Multivariate statistical analysis is applied to these deformation parameters to test for group differences. Results of the statistical analysis are then expressed in terms of deformation patterns of the template complex, and can be visualized and interpreted. The user needs only to specify the topology of the template complex and the number of control points. The method then automatically estimates the shape of the template complex, the optimal position of control points and deformation parameters. The proposed approach is completely generic with respect to any type of application and well adapted to efficient use in clinical studies, in that it does not require point correspondence across surfaces and is robust to mesh imperfections such as holes, spikes, inconsistent orientation or irregular meshing.

The approach is illustrated with a neuroimaging study of Down syndrome (DS). Results demonstrate that the complex of deep brain structures shows a statistically significant shape difference between control and DS subjects. The deformation-based modeling is able to classify subjects with very high specificity and sensitivity, thus showing important generalization capability even given a low sample size. We show that results remain significant even if the number of control points, and hence the dimension of variables in the statistical model, are drastically reduced. The analysis may even suggest that parsimonious models have an increased statistical performance.

The method has been implemented in the software Deformetrica, which is publicly available at www.deformetrica.org.

1. Introduction

Non-invasive imaging methods such as Magnetic Resonance Imaging (MRI) enable analysis of anatomical phenotypic variations over large clinical data collections. For example, MRI is used to reveal and quantify effects of pathologies on anatomy, such as hippocampal atrophy in neurodegenerative diseases or change in neuronal connectivity in neurodevelopmental disorders. Subject-specific digital anatomical models are built from the segmentation and labeling of structures of interest in images. In neuroanatomy, these structures of interest are often volumes whose boundaries take the form of 3D surfaces. For a given individual, the set of such labeled surfaces, which we call an anatomical complex, is indicative of the shape of different brain objects and their relative position. Our goal is to perform statistics on a series of such anatomical complexes from subjects within a given population. We assume that the complex contains the same anatomical structures in each subject, so that interindividual differences are not due to the presence or absence of a structure or a split of one structure into two. The quantification of phenotypic variations across individuals or populations is crucial to find the anatomical substrate of neurologic diseases, for example to find an early biomarker of disease onset or to correlate phenotypes with functional or genotypic variables. Not only the quantification, but also the description of the significant anatomical differences are important in order to interpret the findings and drive the search for biological pathways leading to pathologies.

The core problem is the construction of a computational model for such shape complexes that would allow us to measure differences between them and to analyze the distribution across a series of complexes. Geometric morphometric methods make use of the relative position of carefully defined homologous points on surfaces, called landmarks (Bookstein, 1991; Dryden and Mardia, 1998). Landmark-free methods often use geometric characteristics of the surfaces. They therefore need to make strong assumptions about the topology of the surface, for example limiting analysis to genus zero surfaces (Chung et al., 2003; Boyer et al., 2010) or using medial representations (Styner et al., 2005; Bouix et al., 2005; Gorczowski et al., 2010) or Laplace-Beltrami eigenfunctions (Reuter et al., 2006). Such methods can rarely be applied to raw surface meshes resulting from segmentation algorithms since such meshes may include small holes, show irregular sampling or split objects into different parts.

More important, such methods analyze the intrinsic shape of each structure independently, therefore neglecting the fact that brain anatomy consist of an intricate arrangement of various structures with strong interrelationships. By contrast, we aim at measuring differences between shape complexes in a way that can account for both the differences in shape of the individual components and the relative position of the components within the complex. This goal cannot be achieved by concatenating the shape parameters of each component or by finding correlations between such parameters (Tsai et al., 2003; Gorczowski et al., 2010), as such approaches do not take into account the fact that the organization of the shape complex would not change, and in particular, that different structures must not intersect.

One way to address this problem is to consider surfaces as embedded in 3D space and to measure shape variations induced by deformations of the underlying 3D space. This idea stems from Grenanders group theory for modeling objects (Grenander, 1994), which revisits morphometry by the use of 3D space deformations. The similarity between shape complexes is then quantified by the “amount” of deformation needed to warp one shape complex to another. Only smooth and invertible 3D deformations (i.e., diffeomorphisms) are used, so that the internal organization of the shape complex is preserved during deformation since neither surface intersection nor shearing may occur. The approach determines point correspondences over the whole 3D volume by using the fact that surfaces should match as a soft constraint. The method is therefore robust to segmentation errors in that exact correspondences among points lying on surfaces are not enforced. In this context, a diffeomorphism could be seen as a low-pass filter to smooth shape differences. In this paper, it is our goal to show that the deformation parameters capture the most relevant parts of the shape variations, namely the ones that would distinguish between normal and disease.

Here, we propose a method that builds on the implementation of Grenanders theory in the LDDMM framework (Miller et al., 2006; Vaillant et al., 2007; McLachlan and Marsland, 2007). The method has 3 components: (i) estimation of an average model of the shape complex, called the template complex, which is representative of the population under study; (ii) estimation of the 3D deformations that map the template complex to the complex of each subject; and (iii) statistical analysis of the deformation parameters and their interpretation in terms of variations of the template complex. The first two steps are estimated simultaneously in a combined optimization framework. The resulting template complex and set of deformations are now referred to as an atlas.

Previous attempts to estimate template shapes in this framework offered little control over the topology of the template, whether it consists in the superimposition of a multitude of surface sheets (Glaunès and Joshi, 2006) or a set of unconnected triangles (Durrleman et al., 2009). The topology of the template may be chosen as one of a given subject’s complex (Ma et al., 2008), but this topology then inherits the mesh imperfections that result from an individual segmentation. In this paper, we follow the approach initially suggested by Durrleman et al. (2012), which leaves the choice of the topology of the template with number of connected components to the user. This method estimates the optimal position of the vertices so that the shape of the template complex is an average of the subjects complexes. Here, we extend this approach in order to guarantee that no self-intersection could occur during the optimization.

The set of deformations that result from warping the template complex to each subjects complex captures the variability across subjects. The deformation parameters quantify how the subjects anatomy is different from the template, and can be used in a statistical analysis in the same spirit as in Vaillant et al. (2004) and Pennec (2006). We follow the approach initiated in Durrleman et al. (2011, 2013), which uses control points to parameterize deformations. The number of control points is fixed by the user, and the method automatically adjusts their position near the most variable parts of the shape complex. The method therefore offers control over the dimension of the shape descriptor that is used in statistics, and thus avoids an unconstrained increase with the number of surfaces and their samplings (Vaillant and Glaunès, 2005). We show that statistical performance is not reduced by this finite-dimensional approximation and that the parameters can robustly detect subtle anatomical differences in a typical low sample size study. We postulate that in some scenarios, the statistical performance can even be increased, as the ratio between the number of subjects and the number of parameters becomes more favorable.

An important key element of the method is a similarity metric between pairs of surfaces. Such a metric is needed to optimize the deformation parameters that enable the best matching between shape complexes. We use the varifold metric that has been recently introduced in Charon and Trouvé (2013). It extends the metric on currents (Vaillant and Glaunès, 2005) in that it considers the non-oriented normals of a surface instead of the oriented normals. The method is therefore robust to possible inconsistent orientation of the meshes. It also prevents the “canceling effect” of currents, which occurs if two surface elements with opposite orientation face each other, and which may cause the template surface to fold during optimization. Otherwise, the metric inherits the same properties as currents: it does not require point-correspondence between surfaces and is robust to mesh imperfections such as holes, spikes or irregular meshing (Vaillant and Glaunès, 2005; Durrleman et al., 2009).

This paper is structured as follows to give a self-contained presentation of the methodology and results. We first focus on the main steps of the atlas construction, while discussing the technical details of the theoretical derivations in the appendices. We then present an application to neuroimage data of a Down syndrome brain morphology study. This part focuses on the new statistical analysis of deformations that becomes possible with the proposed framework, and it also presents visual representations that may support interpretation and findings in the context of the driving clinical problem. The analysis also includes an assessment of the robustness of the method in various settings.

2. Mathematical Framework

2.1. Kernel formulation of splines

In the spline framework, 3D deformations ϕ are of the form ϕ(x) = x +v(x), where v(x) is the displacement of any point x in the ambient 3D space, which is assumed to be the sum of radial basis functions K located at control point positions {c_k}_k=1,…,Ncp:

$$v(x)=\sum _{k=1}^{N_{\text{cp}}}K(x,c_k){\alpha }_k.$$ (1)

Parameters α₁, …, α_Ncp are vector weights, N_cp the number of control points and K(x, y) is a scalar function that takes any pair of points (x, y) as inputs. In the applications, we will use the Gaussian kernel $K(x,y)=exp(-{\mid x-y\mid }^2/{\sigma }_V^2)$, although other choices are possible such as the Cauchy kernel $K(x,y)=1/(1+\mid x-y^2\mid /{\sigma }_V^2)$ for instance.

It is beneficial to assume that K is a positive definite symmetric kernel, namely that K is continuous and that for any finite set of distinct points {c_i}_i and vectors {α_i}_i:

$$\sum _i\sum _{j}K(c_i,c_j){{\alpha }_i}^T{\alpha }_j\ge 0,$$ (2)

the equality holding only if all α_i vanish. Translation invariant kernels are of particular interest. According to Bochner’s theorem, functions of the form K(x – y) are positive definite kernels if and only if their Fourier transform is a positive definite operator, in which case (2) becomes a discrete convolution. This theorem enables an easy check if the previous Gaussian function is indeed a positive-definite kernel, among other possible choices.

Assuming K is a kernel allows us to define the pre-Hilbert space V as the set of any finite sums of terms K(., c)α for vector weights α. Given two vector fields v₁ = Σ_i K(., c_i)α_i and $v_2={\sum }_{j}K(.,c_j^{\prime }){\beta }_j$, (2) ensures that the bilinear map

$${\langle v_1,v_2\rangle }_V=\sum _i\sum _{j}K(c_i,c_j^{\prime }){{\alpha }_i}^T{\beta }_j$$ (3)

defines an inner-product on V. This expression also shows that any vector field v ∈ V satisfies the reproducing property:

$${\langle v,K(.,c)\alpha \rangle }_V=v{(c)}^T\alpha ,$$ (4)

defined for any point c and weight α. The space of vector fields V could be “completed” into a Hilbert space by considering possible infinite sums of terms K(., c)α, for which (4) still holds. Such spaces are called Reproducing Kernel Hilbert Spaces (RKHS) (Zeidler, 1991).

Using matrix notations, we denote c and α (resp. c′ and β) in ℝ^3N (resp. ℝ^3M) the concatenation of the 3D vectors c_i and α_i (resp. $c_j^{\prime }$ and β_j), so that the dot product (3) writes 〈v₁, v₂〉_V = α^T K(c, c′)β, where K(c, c′) is the 3N × 3M matrix with entries $K(c_i,c_j^{\prime }){\mathrm{I}}_{3\times 3}$.

2.2. Flows of diffeomorphisms

The main drawback of such deformations is their noninvertibility, as soon as the magnitude of v(x) or its Jacobian is “too” large. The idea to build diffeomorphisms is to use the vector field v as an instantaneous velocity field instead of a displacement field. To this end, we make the control points c_k and weights α_k to depend on a “time” t that plays the role of a variable of integration. Therefore, the velocity field at any time t ∈ [0, 1] and space location x is written as:

$$v_t(x)=\sum _{k=1}^{N_{\text{cp}}}K(x,c_k(t)){\alpha }_k(t)$$ (5)

for all t ∈ [0, 1]

A particle that is located at x₀ at t = 0 follows the integral curve of the following differential equation:

$$\frac{dx(t)}{dt}=v_t(x(t)),x(0)=x_0,$$ (6)

This equation of motion also applies for control points. Using matrix notations, their trajectories follow the integral curves of

$$\stackrel{.}{\mathbf{c}}(t)=\mathbf{K}(\mathbf{c}(t),\mathbf{c}(t))\mathit{\alpha }(t),\mathbf{c}(0)={\mathbf{c}}_0.$$ (7)

At this stage, point trajectories are entirely determined by time-varying vector weights α_k(t) and initial positions of control points c₀.

For each time t, one may consider the mapping x₀ → ϕ_t(x₀), where ϕ_t(x₀) is the position at time t of the particle that was at x₀ at time t = 0, namely the solution of (6). At time t = 0, ϕ₀ = Id_ℝ³ (i.e., ϕ₀(x₀) = x₀). At any later time t, the mapping is a 3D diffeomorphism. Indeed, it is shown in Miller et al. (2006) that (6) has a solution for all time t > 0, provided that time-varying vectors α_k(t) are square integrable. It is also shown that these mappings are smooth, invertible and with smooth inverse. In particular, particles cannot collide, thus preventing self-intersection of shapes. At any space location x, one can find a particle that passes by this point at time t via backward integration, thus preventing shearing or tearing of the shapes embedded in the ambient space.

For a fixed set of initial control points c₀, the time-varying vectors α(t) define a path (ϕ_t)_t in a certain group of diffeomorphisms, which starts at the identity ϕ₀ = Id_ℝ³, and ends at ϕ₁, the latter representing the deformation of interest. We aim to estimate such a path, so that the mapping ϕ₁ brings the template shapes as close as possible to the shapes of a given subject. The problem is that the vectors, which enable us to reach a given ϕ₁ from the identity, are not unique. It is natural to choose the vectors that minimize the integral of the kinetic energy along the path, namely

$$\frac{1}{2}{\int }_0^1{\Vert v_t\Vert }_V^{2}dt=\frac{1}{2}{\int }_0^1\mathit{\alpha }{(t)}^T\mathbf{K}(\mathbf{c}(t),\mathbf{c}(t))\mathit{\alpha }(t)dt.$$ (8)

We show in Appendix A that the minimizing vectors α(t), considering c(0) and c(1) fixed, satisfy a set of differential equations. Together with the equations driving motion of control points (7), they are written as:

$$\{\begin{array}{l}{\stackrel{.}{c}}_k(t)=\sum _{p=1}^{N_{\text{cp}}}K(c_k(t),c_p(t)){\alpha }_p(t)\hfill \\ {\stackrel{.}{\alpha }}_k(t)=-\sum _{p=1}^{N_{\text{cp}}}{\alpha }_k{(t)}^T{\alpha }_p(t){\nabla }_{1}K(c_k(t),c_p(t))\hfill \end{array}$$ (9)

Denoting $\mathbf{S}(t)=\left(\begin{array}{c}\mathbf{c}(t)\\ \mathit{\alpha }(t)\end{array}\right)$ the state of the system of control points at time t, (9) could be written in short as

$$\stackrel{.}{\mathbf{S}}(t)=F(\mathbf{S}(t)),\mathbf{S}(0)=\left(\begin{array}{c}{\mathbf{c}}_0\\ {\mathit{\alpha }}_0\end{array}\right).$$ (10)

The flow of deformations is now entirely parameterized by initial positions of control points c₀ and initial vectors α₀ (called momenta in this context). Integration of (10) computes the position of control points c(t) and momenta α(t) at any time t from initial conditions. Control points and momenta define, in turn, a time-varying velocity field v_t via (5). Any configuration of points in the ambient space, concatenated into a single vector X₀, follows the trajectory X(t) that results from the integration of (6). Using matrix notation, this ODE is written as Ẋ(t) = v_t(X(t)) = K(X(t), c(t))α(t) with X(0) = X₀, which can be further shortened to:

$$\stackrel{.}{\mathbf{X}}(t)=G(\mathbf{X}(t),\mathbf{S}(t)),\mathbf{X}(0)={\mathbf{X}}_0$$ (11)

A given set of initial control points c₀ defines a sub-group of finite dimension of our group of diffeomorphisms. Paths of minimal energy, also called geodesic paths, are parameterized by initial momenta α₀, which play the role of the logarithm of the deformation ϕ₁ in a Riemannian framework. Integration of (10) computes the exponential map. It is easy to check that ||v_t||_V is constant along such geodesic paths. Therefore, the length of the geodesic path that connects ϕ₀ = Id_ℝ³ to ϕ₁ (i.e., ${\int }_0^1{\Vert v_t\Vert }_{V}dt$) simply equals the norm of the initial velocity (i.e., ||v₀||_V).

2.3. Varifold metric between surfaces

Deformation parameters c₀, α₀ will be estimated so as to minimize a criterion measuring the similarity between shape complexes. To this end, we define a distance between surface meshes in this section, and show how to use it for shape complexes in the next section. If the vertices in two meshes correspond, then the sum of squared differences between vertex positions could be used. However, finding such correspondences is a tedious task and is usually done by deforming an atlas to the meshes. This procedure leads to a circular definition, since we need this distance to find deformations between meshes! Among distances that are not based on point correspondences, we will use the distance on varifolds (Charon and Trouvé, 2013). In the varifold framework, meshes are embedded into a Hilbert space in which algebraic operations and distances are defined. In particular, the union of meshes translates to addition of varifolds. The inner-product between two meshes 𝒮 and 𝒮′ is given as:

$${\langle \mathcal{S},{\mathcal{S}}^{\prime }\rangle }_{W^{\ast }}=\sum _p\sum _q{K}^W(c_p,c_q^{\prime })\frac{{\left(n_p^T{n}_q^{\prime }\right)}^2}{\left|n_p\right|\left|n_q^{\prime }\right|}$$ (12)

where c_p and n_p (resp. $c_q^{\prime }$ and $n_q^{\prime }$) denotes the centers and normals of the faces of 𝒮 (resp. 𝒮′). The norm of the normals |n_p| equals the area of the mesh cell. K^W is a kernel, typically a Gaussian function with a fixed width σ_W.

The distance between 𝒮 and 𝒮′ then simply writes: $d_W{(\mathcal{S},{\mathcal{S}}^{\prime })}^2={\Vert \mathcal{S}-{\mathcal{S}}^{\prime }\Vert }_{W^{\ast }}^2={\langle \mathcal{S},\mathcal{S}\rangle }_{W^{\ast }}+{\langle {\mathcal{S}}^{\prime },{\mathcal{S}}^{\prime }\rangle }_{W^{\ast }}-2{\langle \mathcal{S},{\mathcal{S}}^{\prime }\rangle }_{W^{\ast }}$. One notices that the inner-product, and hence the distance, does not require vertex correspondences. The distance measures shape differences in the difference in normals directions, by considering every pair of normals in a neighborhood of size σ_W. It considers meshes as a cloud of undirected normals and therefore does not make any assumptions about the topology of the meshes; one mesh may consist of several surface sheets, have small holes or have irregular meshing. Differences in shape at a scale smaller than the kernel width σ_W are smoothed, thus making the distance robust to spikes or noise that may occur during image segmentation. The inner-product resembles the one in the currents framework (Vaillant and Glaunès, 2005; Durrleman et al., 2009), except that $\frac{{\left(n_p^T{n}_q^{\prime }\right)}^2}{\left|n_p\right|\left|n_q^{\prime }\right|}$ now replaces $\left(n_p^T{n}_q^{\prime }\right)$. With this new expression, the distance is invariant if some normals are flipped. It does not require the meshes to have a consistent orientation. Contrary to other correspondence-free distance such as the Hausdorff distance, the gradient of this distance with respect to the vertex positions is easy to compute, which is particularly useful for optimization.

We explain now how (12) is obtained. In the varifold framework, one considers a rectifiable surface embedded in the ambient space as an (infinite) set of points with undirected unit vectors attached to them. The set of undirected unit vectors is defined as the quotient of the unit sphere in ℝ³ by the two elements group {±Id_ℝ³}, and is denoted 𝕊↔. We denote u↔ the class of u ∈ ℝ³ in 𝕊↔, meaning that u, u/ |u| and −u/ |u| are all considered as the same element: u↔. In a similar construction as the currents, we introduce square-integrable test fields ω which is function of space position x ∈ ℝ³ and undirected unit vectors u↔ ∈ 𝕊↔. Any rectifiable surface could integrate such fields ω thanks to:

$$\mathcal{S}(\omega )={\int }_{{\mathrm{\Omega }}_{\mathcal{S}}}\omega (x,\overleftrightarrow{n(x)})\mid n(x)\mid dx,$$ (13)

where x denotes a parameterization of the surface 𝒮 over a domain Ω_S, and where n(x) denotes the normal of 𝒮 at point x. This expression is invariant under surface re-parameterization. It shows that the surface is a linear form on the space of test fields W. The space of such linear forms, denoted W^* the dual space of W, is the space of varifolds.

For the same computational reasons as for currents, we assume W to be a separable RKHS on ℝ³ × 𝕊↔ with kernel 𝒦 chosen as:

$$\mathcal{K}\left(\left(x,\overleftrightarrow{u}\right),\left(y,\overleftrightarrow{v}\right)\right)=K^W(x,y){\left(\frac{u^{T}v}{\mid u\mid \mid v\mid }\right)}^2.$$ (14)

It is the same kernel as currents for the spatial part K^W, and a linear kernel for the set of undirected unit vectors.

The reproducing property (4) shows that:

$$\omega (x,\overleftrightarrow{n(x)})={\langle \omega ,\mathcal{K}\left((x,\overleftrightarrow{n(x)}),(.,.)\right)\rangle }_W.$$

Plugging this equation in (14) leads to

$$\mathcal{S}(\omega )={\langle \omega ,{\int }_{{\mathrm{\Omega }}_{\mathcal{S}}}\mathcal{K}\left((x,\overleftrightarrow{n(x)}),(.,.)\right)\mid n(x)\mid dx\rangle }_W.$$

The second part of the inner-product could be then identified with the Riesz representant of the varifold 𝒮 in W, denoted ${\mathcal{L}}_W^{-1}(\mathcal{S})$.

Therefore, the inner-product between two rectifiable surfaces 𝒮 and 𝒮′ is ${\langle \mathcal{S},{\mathcal{S}}^{\prime }\rangle }_{W^{\ast }}=\mathcal{S}({\mathcal{L}}_W^{-1}({\mathcal{S}}^{\prime }))=$

$${\int }_{{\mathrm{\Omega }}_{\mathcal{S}}}{\int }_{{\mathrm{\Omega }}_{{\mathcal{S}}^{\prime }}}{K}^W(x,x^{\prime }){\left(\frac{n{(x)}^{T}n(x^{\prime })}{\mid n(x)\mid \mid n(x^{\prime })\mid }\right)}^2\mid n(x)\mid \left|n^{\prime }(x)\right|{\mathit{dxdx}}^{\prime }$$ (15)

The expression in (12) is nothing but the discretization of this last equation.

For 𝒮 a rectifiable surface and ϕ a diffeomorphism, the surface ϕ(𝒮) can still be seen as a varifold. Indeed, a change of variables shows that for ω ∈ W, ϕ(𝒮)(ω) = 𝒮(ϕ ★ ω) where $\varphi ★\omega (x,\overleftrightarrow{n})=\mid {(d_x{\varphi }^{-1})}^{T}n\mid \omega (\varphi (x),\overleftrightarrow{{(d_x{\varphi }^{-1})}^{T}n})$ (Charon and Trouvé, 2013). Therefore, the varifold metric can be used to search for the diffeomorphism ϕ that best matches 𝒮 to 𝒮′ by minimizing $d_W{(\varphi (\mathcal{S}),{\mathcal{S}}^{\prime })}^2={\Vert \varphi (\mathcal{S})-{\mathcal{S}}^{\prime }\Vert }_{W^{\ast }}^2$.

In practice, the deformed varifold is computed by moving the vertices of the mesh and leaving unchanged the connectivity matrix defining the mesh cells. This scheme amounts to an approximation of the deformation by a linear transform over each mesh cell. Therefore, the distance ${\Vert \varphi (\mathcal{S})-{\mathcal{S}}^{\prime }\Vert }_{W^{\ast }}^2$ is only a function of X(1), i.e. A(X(1)), where we denote X₀ the concatenation of the vertices of the mesh 𝒮 and X(1) the position of the vertices after deformation. Indeed, from the coordinates in X(1), we can compute centers and normals of faces of the deformed mesh that can be then plugged into (12) to compute the distance ${\Vert \varphi (\mathcal{S})-{\mathcal{S}}^{\prime }\Vert }_{W^{\ast }}^2$.

Note that the varifold framework extends to 1D mesh representing curves in the ambient space, by replacing normals by tangents. In its most general form, varifold is defined for sub-manifolds with tangent-space attached to each point and uses the concept of Grassmannian (Charon and Trouvé, 2013).

2.4. Distances between anatomical shape complexes

The above varifold distance between surface meshes extends to a distance between anatomical shape complexes. An anatomical complex 𝒪 is the union of labeled surface meshes, each label corresponding to the name of an anatomical structure. Meshes are pooled according to their labels into S₁, …, S_N, where each S_k contains all vertices and edges sharing the same label k. Let ${\mathcal{O}}^{\prime }=\{{\mathbf{S}}_1^{\prime },\dots ,{\mathbf{S}}_N^{\prime }\}$ be another shape complex with the same number N of anatomical structures, but where the number of vertices and connected components in each ${\mathbf{S}}_k^{\prime }$ may be different than in S_k. The similarity measure between both shape complexes is then defined as the weighted sum of the varifold distance between pairs of homologous structures:

$$d_W{(\mathcal{O},{\mathcal{O}}^{\prime })}^2=\sum _{k=1}^N\frac{1}{2{\sigma }_k^2}{\Vert {\mathbf{S}}_k-{\mathbf{S}}_k^{\prime }\Vert }_{W^{\ast }}^2$$ (16)

The values of σ_k balance the importance of each structure within the distance. They are set by the user.

This distance cannot be used ‘as’ in a statistical analysis, since it is too flexible and, by construction, does not penalize changes in the organization of shape complexes. The idea is to use the distance on diffeomorphisms as a proxy to measure distances between shape complexes, the distance on varifolds being used to find such diffeomorphisms. Let 𝒪 and 𝒪′ be two shape complexes and {ϕ_t}_t∈[0,1] be a geodesic path connecting ϕ₀ = Id_ℝ³ to ϕ₁ such that, ϕ₁(𝒪) = 𝒪′. We can then define the distance between 𝒪 and 𝒪′ as the length of this geodesic path, which equals the norm of the initial velocity field v₀. Formally, we define:

$$d_{\varphi }{(\mathcal{O},{\mathcal{O}}^{\prime })}^2={\Vert v_0\Vert }_V^2={\mathit{\alpha }}_0^T\mathbf{K}({\mathbf{c}}_0,{\mathbf{c}}_0){\mathit{\alpha }}_0,$$ (17)

for a given set of initial control points c₀ and with α₀ such that ${\varphi }_1^{{\mathit{\alpha }}_0}(\mathcal{O})={\mathcal{O}}^{\prime }$.

However, it is rarely possible to find such a diffeomorphism that exactly matches 𝒪 and 𝒪′. It is even not desirable since such a matching will be likely to capture shape differences that are specific to these two shape complexes and that poorly generalize to other instances. We prefer to replace the expression in (17) with the following relaxed formulation:

$$d_{\varphi }{(\mathcal{O},{\mathcal{O}}^{\prime })}^2={\mathit{\alpha }}_0^T\mathbf{K}({\mathbf{c}}_0,{\mathbf{c}}_0){\mathit{\alpha }}_0\text{with}{\mathit{\alpha }}_0=\underset{\mathit{\alpha }}{argmin}{d}_W({\varphi }_1^{\mathit{\alpha }}(\mathcal{O}),{\mathcal{O}}^{\prime }).$$ (18)

In this expression, the distance between varifolds d_W is used to find the deformed shape complex ϕ₁(𝒪) that is the closest to the target complex 𝒪′ and the distance in the diffeomorphism group between 𝒪 and ϕ₁(𝒪) quantifies how far the two shape complexes are. The minimizing α₀ gives the relative position of ϕ₁(𝒪) (which is similar to 𝒪′) with respect to 𝒪₀.

In the following, 𝒪 will represent the template shape complex that will be a smooth mesh with a simple topology and regular meshing. By construction, the deformed template ϕ₁(𝒪) is as smooth and regular as the template itself, whereas the subjects’ shape complex 𝒪′ may have irregular meshing, small holes, spikes, etc.. On the one hand, d_W is flexible and loose in the sense that it measures a global discrepancy between the deformed template ϕ₁(𝒪) and the observation 𝒪′, but does not provide an accurate and computable description of the shape differences. On the other hand, d_ϕ captures only shape differences that are consistent with a smooth and invertible deformation of the shape complex 𝒪, leaving in the residual norm d_W (ϕ₁(𝒪), 𝒪′) all other differences including noise and such very small scale mesh deformations. Deformations can be seen as a smoothing operator that captures only certain kind of shape variations and encode them into a descriptor α₀, which will be used in the statistical analysis. The varifold metric d_W allows us to compute this distance d_ϕ without the need to smooth meshes, to build single connected components, to control for mesh quality, etc.

2.5. Atlas construction method

We are now in a position to introduce the estimation of an atlas from a series of anatomical shape complexes segmented in a group of subjects. An atlas refers here to a prototype shape complex, called a template, a set of initial control points located near the most variable parts of the template and momenta parameterizing the deformation of the template to each subject’s complex.

For N_su subjects, let {𝒪₁, …, 𝒪_Nsu} be a set of N_su surface complexes, each complex 𝒪_i being made of labeled meshes 𝒮_i,1, …, 𝒮_i,N. We define the template shape complex, denoted 𝒪₀, as a Fréchet mean, which is defined as the minimizer of the sample variance: 𝒪₀ = arg min_𝒪Σ_i d_ϕ(𝒪, 𝒪_i)². The computation of d_ϕ in (18) requires the estimation of a diffeomorphism ϕ by minimizing the varifold metric d_W (ϕ(𝒪), 𝒪_i). The combination of the two minimization problems leads to the optimization of the single joint criterion:

$$E({\mathcal{O}}_0,{\mathbf{c}}_0\{{\mathit{\alpha }}_0^i\})=\sum _{i=1}^{N_{\text{su}}}\left\{\sum _{k=1}^N\frac{1}{2{\sigma }_k^2}{d}_W{({\varphi }_1^{{\mathit{\alpha }}_0^i}({\mathcal{S}}_{0,k}),{\mathcal{S}}_{i,k})}^2+{({\mathit{\alpha }}_0^i)}^T\mathbf{K}({\mathbf{c}}_0,{\mathbf{c}}_0){\mathit{\alpha }}_0^i\right\}.$$ (19)

The sum ${\sum }_{i=1}^N{({\mathit{\alpha }}_0^i)}^T\mathbf{K}({\mathbf{c}}_0,{\mathbf{c}}_0){\mathit{\alpha }}_0^i={\sum }_{i=1}^N{\Vert v_0^i\Vert }^2$ is the sample variance. This term attracts the template complex to the “mean” of the observations. The other term with the varifold metric acts on the deformation parameters so as to have the best matching possible between the template complex and each subject’s complex. The weights σ_k can be now interpreted as Lagrange multipliers. The momentum vectors ${\mathit{\alpha }}_0^i$ parameterize each template-to-subject deformation. We assume here that they are all attached to the same set of control points c₀, thus allowing the comparison of the momentum vectors of different subjects in the statistical analysis.

We further assume that the topology of the template complex is given by the user, so that the criterion depends only on the positions of the vertices of the template meshes. The number of control points is also set by the user, so that the criterion depends only on the positions of such points. In practice, the user gives as input of the algorithm a set of N meshes (typically ellipsoid surface meshes) whose number of vertices and edges connecting the vertices are not be changed during optimization. The user also gives a regular lattice of control points as input of the algorithm. Optimization of (19) finds the optimal position of the vertices of the template meshes, the optimal position of the control points and the optimal momentum vectors.

Let ${\mathbf{S}}_0^i=\{c_{0,p},{\alpha }_{0,p}^i\}$ denote the parameters of $v_0^i$, and X₀ the vertices of every template surface concatenated into a single vector. The flow of diffeomorphisms results from the integration of N_su differential equations, as in (10): Ṡⁱ(t) = F(Sⁱ(t)) with ${\mathbf{S}}^i(0)={\mathbf{S}}_0^i$. As in (11), X₀ follows the integral curve of N_su differential equations: Ẋⁱ(t) = G(Xⁱ(t), Sⁱ(t)) with Xⁱ(0) = X₀. The final value ${\mathbf{X}}^i(1)={\varphi }_1^{v_0^i}({\mathbf{X}}_0)$ gives the position of the vertices of the deformed template meshes, from which we can compute centers and normals of each face of the deformed meshes, pool them according to mesh labels and compute each term of the kind $d_W{({\varphi }_1^{{\mathit{\alpha }}_0^i}({\mathcal{S}}_{0,k}),{\mathcal{S}}_{i,k})}^2$ using the expression in (12). Therefore, the varifold term essentially depends on the vector Xⁱ(1) and is denoted A(Xⁱ(1)). By contrast, the norm of the initial velocity, ${{\mathit{\alpha }}_0^i}^{T}K({\mathbf{c}}_0,{\mathbf{c}}_0){\mathit{\alpha }}_0^i$ depends only on the initial conditions ${\mathbf{S}}_0^i$ and is written as $L({\mathbf{S}}_0^i)$. The criterion (19) can be rewritten now as:

$$E({\mathbf{X}}_0,\{{\mathbf{S}}_0^i\})=\sum _{i=1}^{N_{\text{su}}}\left(A({\mathbf{X}}^i(1))+L({\mathbf{S}}_0^i)\right),s.t.\{\begin{array}{ll}{\stackrel{.}{\mathbf{S}}}^i(t)=F({\mathbf{S}}^i(t))\hfill & {\mathbf{S}}^i(0)={\mathbf{S}}_0^i\hfill \\ {\stackrel{.}{\mathbf{X}}}^i(t)=G({\mathbf{X}}^i(t),{\mathbf{S}}^i(t))\hfill & {\mathbf{X}}^i(0)={\mathbf{X}}_0^i\hfill \end{array}.$$ (20)

We notice that the parameters to optimize are the initial conditions of a set of coupled ODEs and that the criterion depends on the solution at time t = 1 of these equations. The gradient of such a criterion is typically computed by integrating a set of linearized ODEs, called adjoint equations, like in Durrleman et al. (2011); Vialard et al. (2012); Cotter et al. (2012) for instance. The derivation is detailed in Appendix B. As a result, the gradient is given as:

$$\{\begin{array}{l}{\nabla }_{{\mathit{\alpha }}_0^i}E={\mathit{\xi }}^{\alpha ,i}(0)+{\nabla }_{{\mathit{\alpha }}_0^i}L({\mathbf{S}}_0^i)\hfill \\ {\nabla }_{{\mathbf{c}}_0}E=\sum _{i=1}^{N_{\text{su}}}\left({\mathit{\xi }}^{c,i}(0)+{\nabla }_{{\mathbf{c}}_0}L({\mathbf{S}}_0^i)\right)\hfill \end{array},{\nabla }_{{\mathbf{X}}_0}E={\sum }_{i=1}^{N_{\text{su}}}{\mathit{\theta }}^i(0),$$

where the auxiliary variables ξⁱ(t) = {ξ^c,i(t), ξ^α,i(t)} (of the same size as Sⁱ(t)) and θⁱ(t) (of the same size as X₀) satisfy the linear ODEs (integrated backward in time):

$$\{\begin{array}{l}{\stackrel{.}{\mathit{\theta }}}^i(t)=-{\left({\partial }_{1}G({\mathbf{X}}^i(t),{\mathbf{S}}^i(t))\right)}^T{\mathit{\theta }}^i(t),{\mathit{\theta }}^i(1)={\nabla }_{{\mathbf{X}}^i(1)}A\hfill \\ {\stackrel{.}{\mathit{\xi }}}^i(t)=-({\partial }_{2}G{({\mathbf{X}}^i(t),{\mathbf{S}}^i(t))}^T{\mathit{\theta }}^i(t)-d_{{\mathbf{S}}^i(t)}{F}^T{\mathit{\xi }}^i(t),{\mathit{\xi }}^i(1)=0\hfill \end{array}.$$

Data come into play only in the gradient of the varifold metric with respect to the position of the deformed template ∇_Xⁱ(1)A (derivation is straightforward and given in Appendix C). This gradient indicates in which direction the vertices of the deformed template have to move to decrease the criterion. This decrease could be achieved in two ways, by optimizing the shape of the template complex or the deformations matching the template to each complex. The vector θⁱ transports the gradient back to t = 0 where it is used to update the position of the vertices of the template complex. The vector ξⁱ interpolates at the control points the information in θ;ⁱ, which is located at the template points, and is used at t = 0 to update deformation parameters. A striking advantage of this formulation is that one single gradient descent optimizes simultaneously the shape of the template complex and deformation parameters.

By construction, only the positions of the vertices of the template shape complex are updated during optimization. The edges in the template mesh remain unchanged, so that no shearing or tearing could occur along the iterations. However, the method does not guarantee that the template meshes do not self-intersect after an iteration of the gradient descent. To prevent such self-intersection, we propose to use a Sobolev gradient instead of the current gradient, which was computed for the L² metric on template points X₀. The Sobolev gradient for the metric given by a Gaussian kernel K^X with width σ_X, is simply computed from the L² gradient as:

$${\nabla }_{x_{0,k}}^{X}E=\sum _{i=1}^{N_{\text{su}}}\sum _{p=1}^{N_{\mathrm{x}}}{K}^X(x_{0,k},x_{0,p}){\theta }_p^i(0).$$ (21)

We show in Appendix D that this new gradient ∇^XE is the restriction to X₀ of a smooth vector field u_s. Denoting X₀(s) the positions of the vertices of the template meshes at iteration s of the gradient descent, we have that X₀(s) = ψ_s(X₀(0)) where ψ_s is the family of diffeomorphisms integrating the flow of u_s. At convergence, the template meshes, therefore, have the same topology as the initial meshes.

Eventually, the criterion is minimized using a line search gradient descent method. The algorithm is initialized with template surfaces given as ellipsoidal meshes, control points located at the nodes of a regular lattice and momenta vectors set to zero (i.e., no deformation). At convergence, the method yields the final atlas: a template shape complex, optimized positions of control points and deformation momenta.

2.6. Computational aspects

2.6.1. Numerical schemes

The criterion for atlas estimation is minimized using a line search gradient descent method combined with Nesterov’s scheme (Nesterov, 1983). Differential equations are integrated using a Euler scheme with prediction correction, also known as Heun’s method, which has the same accuracy as the Runge-Kutta scheme of order 2. Sums over the control points or over template points are computed using projections on regular lattices and FFTs using the method in Durrleman (2010, Chap. 2).

The method has been implemented in a software called “Deformetrica”, which can be downloaded freely at www.deformetrica.org.

2.6.2. Parameter setting

The method depends on the kernel width for the deformation σ_V, for the varifolds σ_W and for the gradient σ_X, as well as the weights σ_k that balance each data term against the sum of squared geodesic distances between template and observations.

The kernel widths σ_V and σ_W compare with the shape sizes. The varifold kernel width σ_W needs to be large enough to smooth noise and to be sensitive to differences in the relative position between meshes (Durrleman, 2010, Ch. 1); otherwise values that are too small tend to make the shapes orthogonal. However, too large values tend to make all shape alike and therefore alter matching accuracy. The deformation kernel width σ_V compares with the scale of shape variations that one expects to capture. Deformations are built essentially by integrating small translations acting on the neighborhoods of radius σ_V. With smaller values, the model considers more independent local variations and the information in larger anatomical regions is not well integrated. With larger values, the model is based on almost rigid deformations.

The value of σ_X is essentially a fraction of σ_V : σ_V or 0.5σ_V work well in practice. The weights σ_k are chosen so that data terms have the same order of magnitude as the sum of squared geodesic lengths. Values that are too small over-weight the importance of the data term and prevent the template from converging to the “mean” of the shape set. Values that are too large alter matching accuracy and thus shape features captured by the model.

A reasonable sampling of control points is reached for a distance between two control points being equal to the deformation kernel width σ_V. Finer sampling often induces a redundant parameterization of the velocity fields as shown in Durrleman (2010). Nonetheless, coarser sampling also may be sufficient for the description of the observed variability, as shown in the next experiments.

Kernel widths are chosen after few trials to register a pair of shape complexes. The weights σ_k were then assessed while building an atlas with 3 subjects. The initial distribution of the control points was always chosen as the nodes of a regular lattice with step σ_V or a down-sampled version of it. We always keep σ_X = 0.5σ_V. A qualitative discussion about the effects of parameter settings can also be found in Durrleman (2010).

We will show that the method works well without fine parameter tuning and that statistical results are robust with respect to changes in parameter settings.

3. Application to a Down syndrome neuroimaging study

We evaluate our method on a dataset of 3 anatomical structures segmented from MRIs of 8 Down syndrome (DS) subjects and 8 control cases. The hippocampus, amygdala and putamen of the right hemisphere (respectively in green, cyan and orange in figures) form a complex of grey matter nuclei in the medial temporal lobe of the brain. This study aims to detect complex non-linear morphological differences between both groups, thus going beyond size analysis, which already showed DS subjects to have smaller brain structures than controls (Korenberg et al., 1994; Mullins et al., 2013). Whereas our sample size is small in view of standard neuroimaging studies, the previous findings in neuroimaging of DS suggest large morphometric differences. We therefore hypothesize that such differences would also be reflected in the shapes of anatomical structures, so that the proposed method could demonstrate its strength to differentiate intra-group variability from inter-group differences. To discard any linear differences, including size, we co-register all shape complexes using affine transforms.

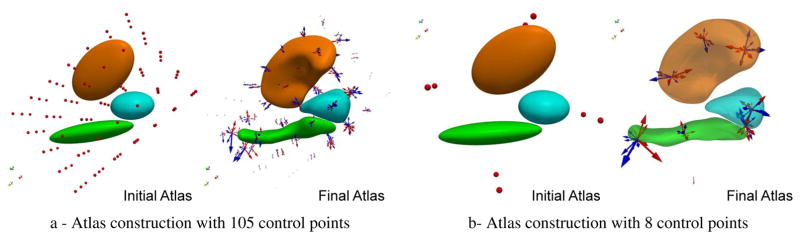
We then construct an atlas using all data, setting σ_V = 10 mm, σ_W = 5 mm, σ_X = σ_V /2 and σ_k = σ_V for all nuclei, and control points initially located at the nodes of regular lattice of step σ_V, yielding a set of 105 points. Robustness of results with respect to these values is discussed in Sec. 3.6.

The resulting template shape complex (Fig. 1-a) averages the shape characteristics of every individual in the dataset. The position of each subject’s anatomical configuration (either DS or controls) with respect to the template configuration is given by initial momentum vectors located at control point positions (arrows in Fig. 1). These momentum vectors lie in a finite-dimensional vector space, whose dimension is 3 times the number of control points. Standard methods for multivariate statistics can be applied in this space. The resulting statistics are expressed in terms of a set of momentum vectors. The template shape complex can be deformed in the direction pointed by the statistics via the integration of the geodesic shooting equations (10) followed by the flow equations (11). This procedure, also known as tangent-space statistics, is a way to translate the statistics into deformation patterns, and hence eases the interpretation of the results.

Figure 1.

Atlas estimated from different initial conditions. Left: 105 control points with initial spacing equal to the deformation kernel width σ_V = 10 mm, Right: 8 control points. Arrows are the momentum vectors of DS subjects (red) and controls (blue). Control points that were initially on a regular lattice move to the most variable place of the shape complex during optimization. Arrows parameterize space deformations and are used as a shape descriptor of each subject in the statistical analysis.

In the following sections, we show how such statistics can be computed and visualized, using the Down syndrome data as a case study.

3.1. Group differences

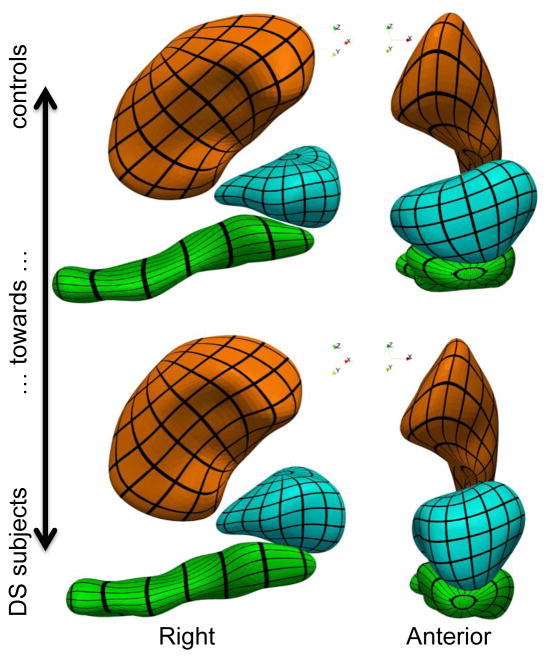
The first step is to show the differences between healthy controls (HC) and DS subjects that have been captured by the atlas. We compute the sample mean of the momenta for each group separately: ${\overline{\mathit{\alpha }}}^{HC}=\frac{1}{N_{\text{su}}^{HC}}{\displaystyle \sum _{i\in HC}}{\mathit{\alpha }}^i$ and ${\overline{\mathit{\alpha }}}^{DS}=\frac{1}{N_{\text{su}}^{DS}}{\displaystyle \sum _{i\in DS}}{\mathit{\alpha }}^i$, where HC (resp. DS) denotes the set of indices corresponding to healthy controls (resp. DS subjects). We then deform the template complex in the direction of both means, thus showing anatomical configurations that are typical of each group (Fig. 2). The figure shows that nuclei of DS subjects are turned toward the left part of the brain, with another torque that pushes the hippocampus tail (its posterior part) toward the superior part of the brain, and the head toward the inferior part. These two torques are more pronounced near the hippocampus/amygdala boundary than in the hippocampus tail or upper putamen region. The DS subjects’ amygdala also has lesser lateral extension than that of the controls.

Figure 2.

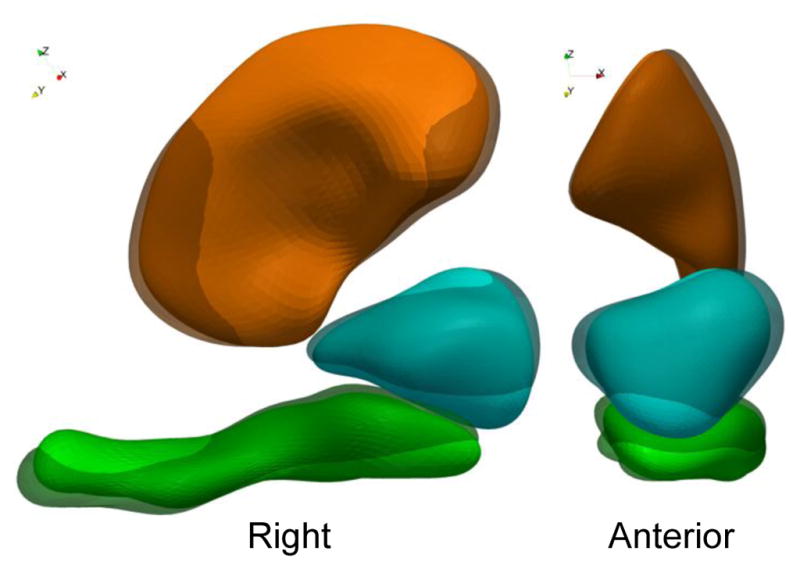
Template complex deformed using the mean deformation of controls (transparent shapes) and DS subjects (opaque shapes), which illustrates the anatomical differences that were found between both groups.

We perform Linear Discriminant Analysis (LDA) to exhibit the most discriminative axis between both groups in the momenta space. For this purpose, we compute the initial velocities of the control points vⁱ = K(c₀, c₀)αⁱ. The sample covariance matrix of these velocities, assuming equal variance in both groups, is given by:

$$\mathrm{\sum }=\frac{1}{N_{\text{su}}}\left(\sum _{i\in HC}({\mathbf{v}}^i-{\overline{\mathbf{v}}}^{HC}){\left({\mathbf{v}}^i-{\overline{\mathbf{v}}}^{HC}\right)}^T+\sum _{i\in DS}({\mathbf{v}}^i-{\overline{\mathbf{v}}}^{DS}){({\mathbf{v}}^i-{\overline{\mathbf{v}}}^{DS})}^T\right).$$

The direction of the most discriminative axis in the velocity space is defined as ${\mathbf{v}}_{\pm }^{\mathit{LDA}}=\overline{\mathbf{v}}+{\mathrm{\sum }}^{-1}({\overline{\mathbf{v}}}^{HC}-{\overline{\mathbf{v}}}^{DS})$ where $\overline{\mathbf{v}}=\frac{1}{2}({\overline{\mathbf{v}}}^{HC}+{\overline{\mathbf{v}}}^{DS})$. The associated momentum vectors are given as: ${\mathit{\alpha }}_{\pm }^{\mathit{LDA}}=\mathbf{K}{({\mathbf{c}}_0,{\mathbf{c}}_0)}^{-1}{\mathbf{v}}_{\pm }^{\mathit{LDA}}$. The anatomical configurations are generated deforming the template shape complex in the two directions ${\mathit{\alpha }}_{\pm }^{\mathit{LDA}}$. We normalize the directions, so that their norm equals the norms between the means: ${\Vert {\mathit{\alpha }}_{\pm }^{\mathit{LDA}}\Vert }_{W^{\ast }}={\Vert {\overline{\mathit{\alpha }}}^{HC}-{\overline{\mathit{\alpha }}}^{DS}\Vert }_{W^{\ast }}$. Therefore, the sum of the geodesic distance between the template complex and each of the deformed complexes is twice the norm between the means.

Results in Fig. 3 reveal similar thinning effects and torques as in Fig. 2. The figure also shows that putamen structures of DS subjects are more bent than those of controls.

Figure 3.

Most discriminative deformation axis showing the anatomical features that are the most specific to the DS subjects as compared to the controls. Differences are amplified, since the distance between the two configurations is twice the distance between the means (black grids are mapped to the surface for visualization only)

Remark 3.1

Note that if the number of observations is smaller than 3 times the number of control points, then Σ is not invertible, and we use instead the regularized matrix Σ + εI₃. In practice, we use ε = 10⁻², which leads to a condition number of the covariance matrix of order 1000. Statistics are not altered if this number is increased to 0.1 and 1, for which the condition number become 100 and 10 (results not shown).

Remark 3.2

Note that we perform the statistical analysis using the velocity field sampled at the control points v = K(c₀, c₀)α and the usual L² inner-product. However, it would seem more natural to use the RKHS metric on the momenta α instead. Using the RKHS metric amounts to using ṽ = K^1/2α so that the inner-product becomes (ṽⁱ)^Tṽ^j = α^iT K(c₀, c₀)α^j, which is the inner-product between the velocity fields in the RKHS V. One can easily check that without regularization (ε = 0), the most discriminant axis is the same in both cases, as will be the LDA and ML classification criteria introduced in the sequel. Using the identity matrix as a regularizer for the sample covariance matrix above amounts to using the matrix K(c₀, c₀)⁻¹ as a regularizer in the RKHS space. More precisely, the matrix Σ + εI₃ becomes Σ̃ + εK(c₀, c₀)⁻¹ where Σ̃ is the sample covariance matrix of the ṽⁱ’s. It is natural to use this regularizer, since the criterion for atlas construction precisely assumes the momentum vectors to be distributed with a zero-mean Gaussian distribution with covariance matrix K(c₀, c₀)⁻¹ (which leads to ${\Vert v_0^i\Vert }_V^2={{\mathit{\alpha }}_0^i}^T\mathbf{K}{\alpha }_0^i$ in (19)). For this reason, the same matrix is used in Allassonnière et al. (2007) as a prior in a Bayesian estimation framework.

3.2. Statistical significance

We estimate the statistical significance of the above group differences using permutation tests in a multivariate setting. In our experiments, the number of subjects is always smaller than the dimension of the concatenated momentum vectors, which is 3 times the number of control points. In this case the distribution Hotelling T² statistics cannot be computed and we use permutations to give an estimate of this distribution.

Let (u_k, ${\lambda }_k^2$) be the eigenvectors and eigenvalues sorted in decreasing order of the sample covariance matrix Σ (without regularization, i.e., ε = 0). We truncate the matrix up to the N_modes largest eigenvalues that explain 95% of the variance: $\mathrm{\sum }^{\sim }={\sum }_{k=1}^{N_{\text{modes}}}{\lambda }_k^2{u}_k{u}_k^T$. Its inverse is given by: ${\mathrm{\sum }^{\sim }}^{-1}={\sum }_{k=1}^{N_{\text{modes}}}\frac{1}{{\lambda }_k^2}{u}_k{u}_k^T$. We then compute the T² Hotelling statistics as:

$$T^2=\frac{N_{\text{su}}-2}{4}{({\overline{\mathbf{v}}}^{HC}-{\overline{\mathbf{v}}}^{DS})}^T{\mathrm{\sum }^{\sim }}^{-1}({\overline{\mathbf{v}}}^{HC}-{\overline{\mathbf{v}}}^{DS}).$$

To estimate the distribution of the statistics under the null hypothesis of equal means, we compute the statistics for 10⁵ permutations of the subjects’ indices i. Each permutation changes the empirical means and within-class covariance matrices, and thus the selected subspace and the statistics. The resulting p-value equals p = 2.6 10⁻⁴, thus showing that our shape descriptors are significantly different between DS and HC subjects at the usual 5% level. The anatomical differences highlighted in Fig. 2 and 3 are not due to chance.

3.3. Sensitivity and specificity using cross-validation

Over-fitting is a common problem of statistical estimations in a high dimension low sample size setting. We perform leave-out experiments to evaluate the generalization errors of our model, namely its sensitivity and specificity.

We compute an atlas with the same parameter setting and initial conditions but with one control and one DS subject data out, yielding 8² = 64 atlases. Note that this is a design choice since one does not necessarily need to have balanced groups to apply the method. For each experiment, we register the template shape complex to each of the left-out complex by minimizing (19) for N_su = 1 and considering template and control points of the atlas fixed. The resulting momentum vectors are compared with those of the atlas. We classify them based on Maximum Likelihood (ML) ratios and LDA.

Let α^test be the initial momenta parameterizing the deformation of the template shape complex to a given left-out shape complex (seen as a test data), and v^test = K(c₀, c₀)α^test. In this section, v̄, v̄^HC and v̄^DS denotes the sample mean using only the training data (7 HC and 7 DS). In LDA, we write the classification criterion as:

$$C({\mathbf{v}}^{\mathit{test}})={({\mathbf{v}}^{\mathit{test}}-\overline{\mathbf{v}})}^T{\mathrm{\sum }}^{-1}({\overline{\mathbf{v}}}^{HC}-{\overline{\mathbf{v}}}^{DS}),$$ (22)

where Σ denotes the regularized sample covariance matrix of training data (for ε = 10⁻², see Remark 3.1). For a threshold η, the test data is classified as healthy control if C(v^test) > η and DS subject otherwise. ROC curves are built when the threshold η is varied. For estimating classification scores, we estimate the threshold η on the training dataset so that the best separating hyperplane (orthogonal to the most discriminative axis Σ⁻¹(v̄^HC − v̄^DS)) is positioned at equal distance to the two classes. This threshold value is used for classifying the test data.

For classifying in a Maximum Likelihood framework, we compute the regularized sample covariance matrices ${\mathrm{\sum }}_{DS}=\frac{1}{N_{\text{su}}^{Ds}}\sum _{i\in DS}({\mathbf{v}}^i-{\overline{\mathbf{v}}}^{DS}){({\mathbf{v}}^i-{\overline{\mathbf{v}}}^{DS})}^T$ and ${\mathrm{\sum }}_{HC}=\frac{1}{N_{\text{su}}^{HC}}\sum _{i\in HC}({\mathbf{v}}^i-{\overline{\mathbf{v}}}^{HC}){({\mathbf{v}}^i-{\overline{\mathbf{v}}}^{HC})}^T$. The classification criterion, also called the Mahalanobis distance, is given by:

$$C({\mathbf{v}}^{\mathit{test}})={({\mathbf{v}}^{\mathit{test}}-{\overline{\mathbf{v}}}^{DS})}^T{\mathrm{\sum }}_{DS}^{-1}({\mathbf{v}}^{\mathit{test}}-{\overline{\mathbf{v}}}^{DS})-{({\mathbf{v}}^{\mathit{test}}-{\overline{\mathbf{v}}}^{HC})}^T{\mathrm{\sum }}_{HC}^{-1}({\mathbf{v}}^{\mathit{test}}-{\overline{\mathbf{v}}}^{HC})$$ (23)

and the classification rule remains the same.

The very high sensitivity and specificity reported in Table 1 (first row) show that the anatomical differences between DS and controls that were captured by the model are not specific to this particular dataset, but are likely to generalize well to independent datasets.

Table 1.

Classification with 105 control points using LDA and ML classifiers. Scores (in percentage) are computed using our descriptor for shape complexes (first row), only one structure at a time (rows 2–4) or a composite descriptor (fifth row).

	LDA		ML
	specificity	sensitivity	specificity	sensitivity
Shape complex	98 (63/64)	100 (64/64)	100 (64/64)	100 (64/64)
Hippocampus	97 (62/64)	87 (56/64)	92 (59/64)	100 (64/64)
Amygdala	98 (63/64)	100 (64/64)	91 (58/64)	100 (64/64)
Putamen	75 (48/64)	100 (64/64)	98 (63/64)	100 (64/64)
Composite	97 (62/64)	100 (64/64)	100 (64/64)	100 (64/64)

3.4. Shape complexes versus individual shapes

In this section, we aim to emphasize the differences between using a single model for the shape complex and using different models for each individual component of a shape complex.

We perform the same experiments as described above, but for each of the three structures independently. The atlas of each structure has its own set of control points and momentum vectors. The hypothesis of equal means for DS and control subjects is rejected with a probability of false positive of p = 3.5 10⁻³ for the hippocampus, p = 4.7 10⁻³ for the putamen and p = 1.2 10⁻⁴ for the amygdala. The statistical significance is lower for the hippocampus and the putamen than for the shape complex (p = 2.6 10⁻⁴), and higher for the amygdala. The classification scores reported in Table 1 (rows 2 to 4) show that none of the structures alone may predict the subject’s status with the same performance as the shape complex. Although the model for the amygdala has a higher statistical significance, it has a lower specificity in the Maximum Likelihood approach.

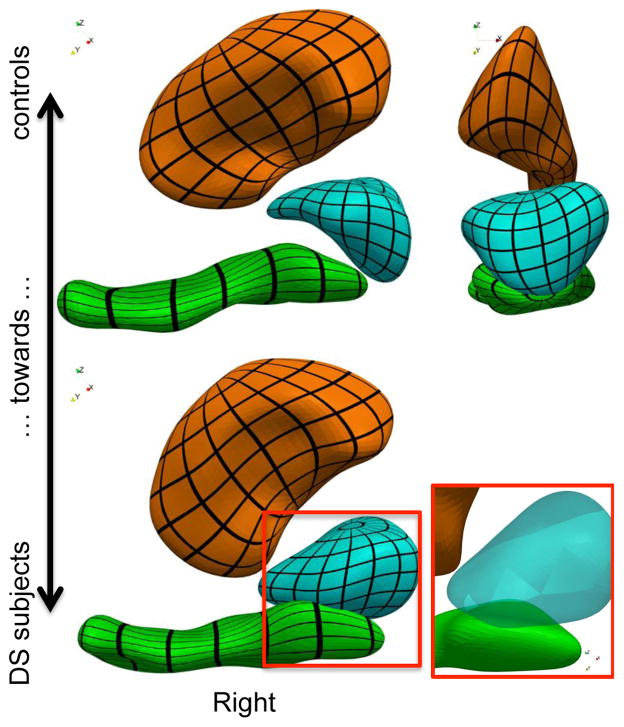
For visualization of results from individual analyses, we deform each structure along its most discriminative axis. Because the 3 deformations are not combined into a single space deformation, intersections between surfaces occur (Fig. 4). The deformation of the amygdala, though highly significant, is not compatible with the deformation of the hippocampus. From an anatomical point of view, both parts of the amygdala/hippocampus boundary should vary together, since almost nothing separates the two structures at the image resolution.

Figure 4.

Most discriminative deformation axis computed for each structure independently. Surface intersection occurs in the absence of a global diffeomorphic constraint. (black grids are mapped to the surface for visualization only)

The shape complex analysis in Fig 2 and 3 showed that the most discriminative effects involve deformations of specific subregions, and in particular the most lower-anterior part of the complex where the amygdala is located. Therefore, it is not surprising that this structure shows higher statistical performance than the hippocampus and putamen in an independent analysis of each structure. However, the most discriminative deformations of each structure are not consistent among themselves, thus misleading the interpretation of the findings. By contrast, the shape complex analysis shows that the discriminative effect is not specific to the amygdala but to the whole lower anterior part of the medial temporal lobe with strong correlations between parts of the structures within this region. The shape complex model may be slightly less significant, but it highlights shape effects that can be interpreted in the context of anatomical deformations related to underlying neurobiological processes.

One could argue that independently analyzing each structure does not take into account the correlations among structures. To mimic what previously reported shape analysis methods do, we build a composite shape descriptor vⁱ by concatenating the velocities of each individual atlas ${\mathbf{v}}_1^i,{\mathbf{v}}_2^i$ and ${\mathbf{v}}_3^i$ (for each structure s = 1, 2, 3 and subject i, ${\mathbf{v}}_s^i=\mathbf{K}({\mathbf{c}}_{0,s},{\mathbf{c}}_{0,s}){\mathit{\alpha }}_s^i$ where ${\alpha }_s^i$’s are the initial momenta in each atlas). We use this composite descriptor to compute means, sample covariance matrices, most discriminative axis and classification scores as above. This approach achieves a classification nearly as good as with the single atlas method (Table 1, last row) with a very high statistical significance p < 10⁻⁵. The direction of the most discriminative axis v^LDA takes into account the correlations between each structures. However, this vector does not parameterize a single diffeomorphism– only each of its three components does. To display these correlations, we compute the initial momentum vectors associated with each component: ${\mathit{\alpha }}_s^{\mathit{LDA}}=\mathbf{K}{({\mathbf{c}}_{0,s},{\mathbf{c}}_{0,s})}^{-1}{\mathbf{v}}_s^{\mathit{LDA}}$ for s = 1, 2, 3, and then deform each structure using a different diffeomorphism. Even in this case, surfaces intersect, thus showing that this way of taking into account correlations does not prevent generating anatomical configurations that are not compatible with the data (Inline Supplementary Figure S1). By contrast, the single atlas method proposed in this work integrates topology constraints into the analysis by the use of a single deformation of the underlying space, and therefore correctly measures correlations that preserve the internal organization of the anatomical complex.

3.5. Effects of dimensionality reduction

Our approach offers the possibility to control the dimension of the shape descriptor by choosing the number of control points given as input to the algorithm. In 3D, the dimension of the shape descriptor is 3 times the number of control points. In this section, we evaluate the impact of this dimensionality for atlas construction and statistical estimations given our low sample size setting.

We start with 105 control points on a regular lattice with spacing equal to the deformation kernel width σ_V and then successively down-sample this lattice. With only 8 points, the number of deformation parameters is decreased by more than one order of magnitude and the initial ellipsoidal shapes still converge to a similar template shape complex (Fig. 1-b). The main reason for it is that control points are able to move to the most strategic places, noticeably at the tail of the hippocampus and the anterior part of the amygdala where the variability is the greatest. Qualitatively, the most discriminant axis is stable when the dimension is varied (Inline Supplementary Figure S2), as is the spectrum of the sample covariance matrices of the momentum vectors (Inline Supplementary Figure S3). The method is able to optimize the “amount” of variability captured for a given dimension of deformation parameters. Nevertheless, the residual data term at convergence increases. The initial data term (i.e., varifold norm) decreases by 97.8% for 105 points, and only by 93.3 for 8 points, thus showing that the sparsest model captured less variability in the dataset (Table 2).

Table 2.

Decrease of the data term during optimization for different number of control points and σ_V = 10 mm

Number of CP	8	12	16	24	36	105	600
Decrease of data term (in % of initial value)	93.3	94.8	94.6	95.8	96.7	97.9	97.8

If there could be an infinite number of control points, their optimal locations would be on surface meshes themselves. Therefore, one might place one control point at each vertex (Vaillant and Glaunès, 2005; Ma et al., 2008). In our case, such a parameterization would involve 23058 control points. Nonetheless, this number can be arbitrarily increased or decreased by up/down sampling of the initial ellipsoids, regardless of the variability in the dataset! We increase the number of control points to 650 and notice that the estimated template shapes are the same as with 105 control points (results not shown), and that the atlas explains the same proportion of the initial data term (Table 2). Therefore, increasing the number of control points does not allow us to capture more information, which is essentially determined by the deformation kernel width σ_V, but distributes this information over a larger number of parameters. This conclusion is in line with Durrleman et al. (2009), who show that such high dimensional parameterizations are very redundant.

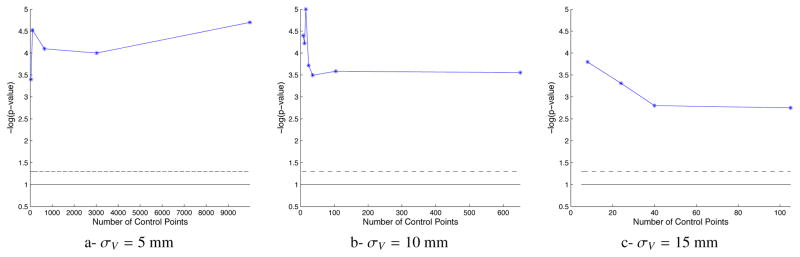
The statistical significance, as measured by the p-value associated with the Hotelling T² statistics, is not increased with higher dimensions (Fig. 5-b). It is even smaller than in small dimensions, the maximum being reached for 16 control points (p < 10⁻⁵). Leave-2-out experiments give 100% specificity and sensitivity using the ML approach, regardless of the number of control points used. To highlight differences, we performed classification using the hippocampus shape only. Again, the performance of the classifier does not necessarily decrease with the number of control points (Table 3). ROC curves in Fig. 6 show that the atlases with 48 and 18 control points have poorer performance than atlases with 12 and 8 control points.

Figure 5.

Statistical significance of the group means difference for a varying number of control points. The solid (resp. dashed) lines correspond to the 0.1 (resp. 0.05) significance thresholds, respectively. The ability of the classifier to separate DS subjects to controls is little altered by the deformation kernel width σ_V. Increasing the number of control points, and hence the dimensionality of the atlas, does not necessarily increase statistical performance.

Table 3.

Classification ratios based solely on hippocampus shape. LDA and ML classification are performed with a varying number of control points in the atlas. Ratios are in percentages. Reducing the number of control points to 12 or 8 may increase statistical performance.

	# Control Points	48	18	12	8	4
LDA	specificity	97 (62/64)	91 (58/64)	92 (59/64)	95 (61/64)	78 (50/64)
	sensitivity	87 (56/64)	89 (57/64)	89 (57/64)	89 (57/64)	81 (52/64)
ML	specificity	92 (59/64)	92 (59/64)	97 (69/64)	97 (62/64)	84 (54/64)
	sensitivity	100 (64/64)	100 (64/64)	98 (63/64)	100 (64/64)	97 (62/64)

Figure 6.

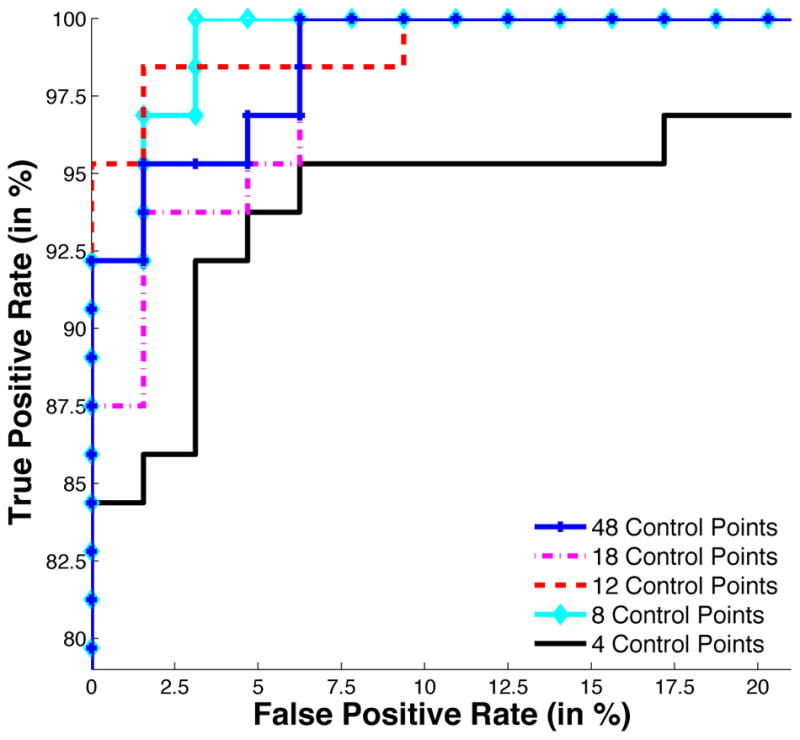
ROC curves for hippocampus classification using a different number of control points in the atlas and ML classifier. Atlases with 48 and 18 control points exhibit poorer performance than those with 12 and 8 control points.

These results suggest that using atlases of small dimension could have even greater statistical power, especially in a small sample size setting. Nevertheless, two different dimensionality reduction techniques compete with each other in these experiments. The first is the use of a small set of control points, which is a built-in dimensionality reduction technique, which has the advantage to optimize simultaneously the information captured in the data and the encoding of this information in a space of fixed dimension. The second is a post-hoc dimensionality reduction using PCA when computing classification scores that project shape descriptors into the subspace, explaining 95% of the variance captured. The variation of the p-values, when the number of modes selected in the PCA is varied, shows that a number of modes optimizes the statistical significance, between 6 and 8 modes (Inline Supplementary Figure S5). For each number of modes, an optimal number of control points also maximizes significance, and this number is never greater than 105 when one control point is placed at every σ_V.

It is difficult to distinguish the effects of the two techniques in such a low sample size setting. With 8 control points and a few dozen or more subjects, we could estimate full-rank covariance matrices and would not need the post-hoc dimensionality reduction techniques. A fair comparison between post-hoc and built-in dimensionality reduction would be then possible. Our hypothesis is that, in this regime, the trend of increased statistical significance when the number of control points is decreased would be amplified. Indeed, the ratio between the number of variables to estimate and the number of subjects is more favorable in such a scenario, thus making the statistical estimations more stable.

3.6. Effects of parameter settings

We assess the robustness of the results with respect to parameter settings. We change the values of the deformation and varifold kernel widths by ±50%, namely by setting σ_V = 5, 10 or 15mm and σ_W = 2.5, 5, or 7.5 mm. Other settings are kept fixed, namely the weights σ_k = 10 mm, the gradient kernel width σ_X = 0.5σ_V and the initial distance between control points, which always equals σ_V. Classification scores are reported in Table 4 and show a great robustness of the statistical estimates, noticeably for the ML method. We note a decrease in the specificity in the LDA classifier for the large deformation kernel width σ_V = 15 mm. With large deformation kernel widths, the atlas captures more global shape variations, which might not be as discriminative as more local changes. This effect is more pronounced with increased varifold width σ_W, as surface matching accuracy decreases, thus further reducing the variability captured in the atlas. These results show that the performance of the atlas is stable for a large range of reasonable values, and therefore that they are not due to fine parameter tuning.

Table 4.

Classification scores when deformation and varifold kernel widths are varied. Regularization of the covariance matrices ε = 10⁻². Results are overall very stable when settings are varied. Very large kernel widths penalize the matching accuracy between the template and the subject shape complexes, thus eventually altering classification performance.

		LDA		ML
		specificity	sensitivity	specificity	sensitivity
σV = 5	σW = 2.5	98 (63/64)	100 (64/64)	100 (64/64)	100 (64/64)
	σW = 5	98 (63/64)	100 (64/64)	100 (64/64)	100 (64/64)
	σW = 7.5	98 (63/64)	100 (64/64)	100 (64/64)	100 (64/64)
σV = 10	σW = 2.5	98 (63/64)	100 (64/64)	100 (64/64)	100 (64/64)
	σW = 5	98 (63/64)	100 (64/64)	100 (64/64)	100 (64/64)
	σW = 7.5	94 (60/64)	100 (64/64)	100 (64/64)	100 (64/64)
σV = 15	σW = 2.5	89 (57/64)	100 (64/64)	100 (64/64)	100 (64/64)
	σW = 5	83 (53/64)	100 (64/64)	100 (64/64)	100 (64/64)
	σW = 7.5	84 (54/64)	100 (64/64)	100 (64/64)	100 (64/64)

The shape of the template also depends on the parameter setting, and notably the deformation kernel width σ_V. With larger values, the template shape captures more rigid variations, which translates into a smoother shape. With smaller values, the template captures finer details in the data (Inline Supplementary Figure S4)

The dimension of the atlas is intrinsically linked with the deformation kernel width. Deformations with smaller σ_V need more control points to potentially deform every small region of the shape complex. Deformations with larger σ_V have fewer degrees of freedom and could be decomposed using fewer control points. Placing one control point at the nodes of lattice of step σ_V yields 15 control points for σ_V = 15 mm, 105 control points for σ_V = 10 mm and 650 control points for σ_V = 5 mm. We build an atlas for each of these values of σ_V and with down/up sampling the set of associated control points. All these atlases show a good significance level, far below the usual 0.05 threshold. On average, the statistical significance is decreased with increasing σ_V, as the atlas represents a coarser and coarser description of the variability within the dataset (Fig. 5). With σ_V = 15 mm (Fig. 5-c), the maximum significance is reached for 8 control points, and the significance is decreased with increasing dimensionality. With σ_V = 5 mm (Fig. 5-a), the same trend is observed, except an unexpected increase in statistical significance at very high dimensions. These results show that the discussion about dimensionality reduction in the previous section does not depend on a particular choice of deformation kernel width.

We also assess the influence of the amount of regularization in the covariance matrices ε, which otherwise are singular. We increase the value used in the previous experiment from ε = 10⁻² to ε = 0.1, ε = 1 and ε = 10. With these values, the condition number of the covariance matrix decreased from 1000 to 100, 10 and 1 respectively. A decrease in the sensitivity of the classifier was detected only for ε = 10, that is when the regularization became of the same order as the largest eigenvalues of the matrix. The choice of this setting has, therefore, very little influence on the classification results.

It is clear that the weights σ_k’s also should have been adjusted. As noted in Akin and Mumford (2012), adjusting the weights could increase matching accuracy, and possibly increase statistical performance. As explained in Sec. 2.6.2, these values were chosen so that the data term has the same order of magnitude as the sum of squared geodesic distances. However, it is clear from a statistical point of view that these values measure noise variance, and therefore should be estimated from the data and not fixed by the user. This estimation could be done in a Bayesian framework by adapting to varifolds the method proposed in Allassonnière et al. (2007, 2010) for images.

Overall, these experiments demonstrate the reproducibility of our results under various parameter settings. They show that the method could be applied in real cases without fine parameter tuning.

4. Discussion and Conclusion

This paper presents a comprehensive framework for the statistical analysis of shape complexes extracted from 3D anatomical images. The method can deal with raw surfaces resulting from nearly any segmentation methods thanks to its robustness to noise, mesh imperfections and inconsistencies in mesh orientation. The scheme estimates a template shape complex with a fixed topology that is representative of the anatomy, and computes modes of deformation that preserve template structure and capture variability in data. Such topology constraints lead to modes of variations that are anatomically realistic and interpretable. The proposed approach therefore contrasts with the study of correlations between shape models that are estimated independently for each component within a shape complex. Given a typical neuroimaging study of a complex of deep brain structures in Down syndrome subjects, the method can find discriminative anatomical features with high statistical significance and small generalization errors, even with a limited number of observations. We show the robustness of these results in various experimental settings, demonstrating the effectiveness of the method without fine parameter tuning. The scientific community can evaluate the method by downloading the software Deformetrica, which is freely available at www.deformetrica.org.

The statistical analysis on deformations that we proposed is essentially multivariate. Statistics show the correlations between the deformation patterns in every region of the brain. The visualization of the deformations gives a comprehensive view of how these local deformations are combined into a consistent deformation of the underlying tissue. This analysis is therefore in strong contrast with voxel-based methods, which test at every voxel the difference in image intensities (Ashburner and Friston, 2000) or the difference in the Jacobian determinant of the template-to-subject deformations (Thompson et al., 2000). In particular, the analysis of the Jacobian determinant only indicates local contraction or expansion of the tissue, while ignoring more complex deformations patterns such as torques or a shift between two structures. Such cofounding effects may be misleading when interpreting the results.

In contrast to such mass-univariate methods, our multivariate approach also avoids the problem of correction for multiple comparisons. The dimension of the variables used in the statistical analysis is essentially determined by the deformation kernel width σ_V and therefore by the scale of anatomical variants that are captured by the model. In the current scheme, the choice of the number of control points is left to the user, using a practical heuristics that consists in placing one point for every deformation kernel width σ_V. We show that this number could be even drastically reduced without altering statistical significance and generalization ability of the model. This built-in dimensionality reduction may lead to increased statistical performance as suggested by our results, although our initial results need to be confirmed and supported using more subjects and different datasets. The fact that the dimension is determined by the user before any experiments allows one to adjust the scale σ_V according to the number of available subjects, and also eases the power calculations and sample sizes estimates required in clinical trials. This finite-dimensional setting also paves the way for estimating mean and covariance matrices during the optimization in a Bayesian framework, following research by Allassonnière et al. (2007) and Allassonnière and Kuhn (2009). Constraining statistical inference to take place in a small dimensional space is likely to increase the convergence speed of the statistical estimates, as compared to performing the inference in very high dimensions and then performing post-hoc dimensionality reduction, using PCA for instance.

Cross-validation showed the very good prediction capability of our model. The prediction of Down syndrome based on neuroimaging data has little clinical interest, since subjects are characterized by their genotype and especially the copy number of chromosome 21, which is known with very high confidence. However, the shape deformation studies as shown here may give new insights into anatomical changes linked to genetics, and associations between morphologic differences and cognitive and behavioral scores. Nonetheless, our model is completely generic and can be applied to different pathologies for which the clinical status may be more difficult to assess. This prediction capability of the method demonstrates its potential in computer-aided diagnosis or prognosis in studies where a subject’s status is based only on clinical diagnosis with limited reproducibility, such as in neurodegenerative diseases, or for pre-diagnostic prediction of disease onset based on image data. Shape descriptors, which encode the joint shape variability of sets of anatomical structures with a small number of parameters, would be preferable to study correlations between anatomical phenotypes and genotype, in the spirit of Korbel et al. (2009)), where these image-derived parameters can take the place of clinical variables.

Appendix A Geodesic equations

We derive here the minimum action principle of Lagrangian mechanics. A variation δα(t) of the time-varying momentum vectors α(t) induces a variation of the control point positions δc(t), which in turn induces a variation δE of the quantity $E={\int }_0^1\mathit{\alpha }{(t)}^T\mathbf{K}(\mathbf{c}(t),\mathbf{c}(t))\mathit{\alpha }(t)dt$.

Since ċ = K(c, c)α, we have

$$\delta \stackrel{.}{\mathbf{c}}=\mathbf{K}(\mathbf{c},\mathbf{c})\delta \mathit{\alpha }+d_{\mathbf{c}}(\mathbf{K}(\mathbf{c},\mathbf{c})\mathit{\alpha })\delta \mathbf{c},$$ (24)

and

$$E={\int }_0^1{\alpha }^T\stackrel{.}{\mathbf{c}}dt.$$ (25)

Therefore, we have

$${\stackrel{.}{\mathbf{c}}}^T\delta \mathit{\alpha }={\mathit{\alpha }}^T\mathbf{K}(\mathbf{c},\mathbf{c})\delta \mathit{\alpha }={\mathit{\alpha }}^T\delta \stackrel{.}{\mathbf{c}}-{\mathit{\alpha }}^T{d}_{\mathbf{c}}(\mathbf{K}(\mathbf{c},\mathbf{c})\mathit{\alpha })\delta \mathbf{c}$$ (26)

and

$$\begin{array}{l}\delta E={\int }_0^1\left({\stackrel{.}{\mathbf{c}}}^T\delta \mathit{\alpha }+{\mathit{\alpha }}^T\delta \stackrel{.}{\mathbf{c}}\right)dt\\ ={\int }_0^1\left(2{\mathit{\alpha }}^T\delta \stackrel{.}{\mathbf{c}}-{\mathit{\alpha }}^T{d}_{\mathbf{c}}(\mathbf{K}(\mathbf{c},\mathbf{c})\mathit{\alpha })\delta \mathbf{c}\right)dt.\end{array}$$ (27)

Assuming δc(0) = δc(1) = 0, integration by parts yields:

$$\delta E=-{\int }_0^1{\left(2\stackrel{.}{\mathit{\alpha }}+d_{\mathbf{c}}{(\mathbf{K}(\mathbf{c},\mathbf{c})\mathit{\alpha })}^T\mathit{\alpha }\right)}^T\delta \mathbf{c}dt$$ (28)

The linear ODE with source term (24) shows that there is a one-to-one relationship between δc and δα. Since δα is arbitrary, so is δc and

$$\stackrel{.}{\mathit{\alpha }}=-\frac{1}{2}{d}_{\mathbf{c}}{(\mathbf{K}(\mathbf{c},\mathbf{c})\mathit{\alpha })}^T\mathit{\alpha }$$ (29)

along extremal paths.

K(c, c)α is a 3N_cp vector, whose kth coordinate is the 3D vector: ${\sum }_{p=1}^{N_{\mathrm{x}}}K(c_k,c_p){\alpha }_p$. Therefore,

$$d_{c_i}{(\mathbf{K}(\mathbf{c},\mathbf{c})\mathit{\alpha })}_k=\sum _{p=1}^{N_{\text{cp}}}{\alpha }_p{\nabla }_{1}K{(c_k,c_p)}^T\delta (i-k)+{\alpha }_i{\nabla }_{2}K{(c_k,c_i)}^T$$ (30)

Using the fact that K is symmetric (hence ∇₁K(x, y) = ∇₂K(y, x)) we have:

$${\stackrel{.}{\alpha }}_i=-\frac{1}{2}\sum _{k=1}^{N_{\text{cp}}}{(d_{c_i}{(\mathbf{K}(\mathbf{c},\mathbf{c})\mathit{\alpha })}_k)}^T{\alpha }_k=-\left(\sum _{k=1}^{N_{\text{cp}}}{\nabla }_{1}K(c_i,c_k){\alpha }_k^T\right){\alpha }_i$$ (31)

Appendix B Gradient of the atlas criterion

We provide here the differentiation of the criterion for atlas construction:

$$E({\mathbf{X}}_0,{\mathbf{c}}_0,\{{\mathit{\alpha }}_0^i\})=\sum _{i=1}^{N_{\text{su}}}\left(A({\mathbf{X}}^i(1))+L({\mathbf{S}}_0^i)\right)$$ (32)

subject to:

$$\{\begin{array}{ll}{\stackrel{.}{\mathbf{S}}}^i(t)=F({\mathbf{S}}^i(t))\hfill & {\mathbf{S}}^i(0)=\{{\mathbf{c}}_0,{\mathit{\alpha }}_0^i\}\hfill \\ {\stackrel{.}{\mathbf{X}}}^i(t)=G({\mathbf{X}}^i(t),{\mathbf{S}}^i(t))\hfill & {\mathbf{X}}^i(0)={\mathbf{X}}_0\hfill \end{array}$$ (33)

where

$$L({\mathbf{S}}_0^i)={{\mathit{\alpha }}_0^i}^{T}K({\mathbf{c}}_0,{\mathbf{c}}_0){\mathit{\alpha }}_0^i$$ (34)

X is a vector of length 3N_x, where N_x is the number of points in the template shape, c and α are two vectors of length 3N_cp each, where N_cp is the number of control points, so that S is a vector of length 6N_cp.

$F(\mathbf{S})=\left(\begin{array}{l}{F}^c(\mathbf{c},\mathit{\alpha })\hfill \\ F^{\alpha }(\mathbf{c},\mathit{\alpha })\hfill \end{array}\right)$ is a vector of length 6N_cp, which is decomposed into two vectors of size 3N_cp. The kth coordinate (among N_cp) of F^c and F^α is the 3D vector:

$$\begin{array}{ll}{F}^c{(\mathbf{S})}_k=\hfill & \sum _{p=1}^{N_{\text{cp}}}K(c_k(t),c_p(t)){\alpha }_p(t)\hfill \\ F^{\alpha }{(\mathbf{S})}_k=-\hfill & \sum _{p=1}^{N_{\text{cp}}}{\alpha }_k{(t)}^T{\alpha }_p(t){\nabla }_{1}K(c_k(t),c_p(t))\hfill \end{array}$$ (35)

G(X, S) is a vector of size 3N_x. Its kth coordinate (among N_x) is the 3D vector:

$$G{(\mathbf{X},\mathbf{S})}_k=\sum _{p=1}^{N_{\text{cp}}}K(x_k(t),c_p(t)){\alpha }_p(t)$$ (36)

Similarly,

$$L({\mathbf{S}}_0^i)=\sum _{p=1}^{N_{\text{cp}}}\sum _{q=1}^{N_{\text{cp}}}{{\alpha }_{0,p}^i}^{T}K(c_{0,p},c_{0,q}){\alpha }_{0,q}^i$$ (37)

B.1 Gradient in matrix form

The differentiation of the criterion can be done for each subject i independently. Therefore, we differentiate only one term of the sum in (32) for a generic subject’s index i that we omit in the rest of this section for clarity purposes.

A small perturbation δS₀ induces a perturbation of the motion of the control points and momenta δS(t), which, in turn, induces a perturbation of the template points’ trajectory δX(t) and then of the criterion δE, which we write, thanks to the chain rule

$$\delta E={({\nabla }_{\mathbf{X}(1)}A)}^T\delta \mathbf{X}(1)+{({\nabla }_{{\mathbf{S}}_0}L)}^T\delta {\mathbf{S}}_0.$$ (38)

According to (33), the perturbations δS(t) and δX(t) satisfy the linearized ODEs:

$$\begin{array}{ll}\stackrel{.}{\delta }\mathbf{S}(t)=d_{S(t)}F\delta \mathbf{S}(t)\hfill & \delta \mathbf{S}(0)=\delta {\mathbf{S}}_0\hfill \\ \delta \stackrel{.}{\mathbf{X}}(t)={\partial }_{1}G\delta \mathbf{X}(t)+{\partial }_{2}G\delta \mathbf{S}(t)\hfill & \delta \mathbf{X}(0)=\delta {\mathbf{X}}_0\hfill \end{array}$$

The first ODE is linear. Its solution is given by:

$$\delta \mathbf{S}(t)=exp\left({\int }_0^t{d}_{\mathbf{S}(u)}\mathit{Fdu}\right)\delta {\mathbf{S}}_0.$$ (39)

The second ODE is linear with source term. Its solution is given by:

$$\delta \mathbf{X}(t)={\int }_0^{t}exp\left({\int }_u^t{\partial }_1\mathit{Gds}\right){\partial }_{2}G(u)\delta \mathbf{S}(u)du+exp\left({\int }_0^t{\partial }_{1}G(s)ds\right)\delta {\mathbf{X}}_0$$ (40)

Plugging (39) into (40) and then into (38) leads to:

$$\{\begin{array}{ll}{\nabla }_{{\mathbf{S}}_0}E\hfill & ={\int }_0^1\left({R_{0t}}^T{\partial }_{2}G{(\mathbf{X}(t),\mathbf{S}(t))}^T{V_{t1}}^T{\nabla }_{\mathbf{X}(1)}A\right)dt+{\nabla }_{{\mathbf{S}}_0}L\hfill \\ {\nabla }_{{\mathbf{X}}_0}E\hfill & ={V_{01}}^T{\nabla }_{\mathbf{X}(1)}A\hfill \end{array},$$ (41)

where we denoted $R_{st}=exp\left({\int }_s^t{d}_{\mathbf{S}(u)}\mathit{Fdu}\right)$ and $V_{st}=exp\left({\int }_s^t{\partial }_{1}G(\mathbf{X}(u),S(u))du\right)$.

Let us denote θ(t) = V_t1^T∇_X(1)A, g(t) = ∂₂G(t)^T θ(t) and $\mathit{\xi }(t)={\int }_t^1{R_{ts}}^{T}g(s)ds$, so that the gradient (41) can be rewritten as:

$$\{\begin{array}{ll}{\nabla }_{{\mathbf{S}}_0}E\hfill & ={\int }_0^1{R_{0s}}^{T}g(s)ds+{\nabla }_{{\mathbf{S}}_0}L=\mathit{\xi }(0)+{\nabla }_{{\mathbf{S}}_0}L\hfill \\ {\nabla }_{{\mathbf{X}}_0}E\hfill & =\mathit{\theta }(0)\hfill \end{array}.$$

Now, we need to make explicit the computation of the auxiliary variables θ(t) and ξ(t). By definition of V_t1, we have V₁₁ = Id and dV_t1/dt = V_t1∂₁G(t), which implies that θ(1) = ∇_X(1)A and θ̇(t) = −∂₁G(t)^T θ(t).

For ξ(t), we notice that $R_{ts}=\text{Id}-{\int }_t^s\frac{{dR}_{us}}{du}du=\text{Id}+{\int }_t^s{R}_{us}{d}_{\mathbf{S}(u)}F(u)du$. Therefore, using Fubini’s theorem, we get:

$$\begin{array}{l}\mathit{\xi }(t)={\int }_t^1{R_{ts}}^{T}g(s)ds\\ ={\int }_t^1\left(g(s)+d_{\mathbf{S}(s)}{F}^T{\int }_s^1{R_{su}}^{T}g(u)du\right)ds\\ ={\int }_t^1\left(g(s)+d_{\mathbf{S}(s)}{F}^T\mathit{\xi }(s)\right)ds.\end{array}$$

This last equation is nothing but the integral form of the ODE given in the main text.

Given the actual values of S₀ and X₀, one needs to integrate the geodesic shooting equations and the flow equation in (33) forward in time to give the full path of parameters S(t) and template shape points X(t). Then, one needs to compute the gradient of the data term ∇_X(1)A, which is given in Appendix C. This term indicates in which direction one has to move the vertices of the deformed template shape in order to better match the observations. This term is transported back to time t = 0 by the coupled linear equations satisfied by ξ and θ. The values of time t = 0 of these auxiliary variables are used to update the deformation parameters (position of control points and momenta) and the position of the vertices of the template surfaces.

B.2 Gradient in coordinates

Expanding the variables ${\mathbf{S}}^i(t)=\{c_{0,k}(t),{\alpha }_{0,k}^i(t)\},{\mathbf{X}}^i(t)=\{X_k^i(t)\},{\mathit{\theta }}^i(t)=\{{\theta }_k^i(t)\}$ and ${\mathit{\xi }}^i(t)=\{{\xi }_k^{c,i}(t),{\xi }_k^{\alpha ,i}(t)\}$, we have

$$\begin{array}{ll}{\nabla }_{c_{0,k}}E\hfill & =\sum _{i=1}^{N_{\text{su}}}{\xi }_k^{c,i}(0)+{\nabla }_{c_{0,k}}L({\mathbf{S}}_0^i)\hfill \\ {\nabla }_{{\alpha }_{0,k}^i}E\hfill & =\sum _{i=1}^{N_{\text{su}}}{\xi }_k^{\alpha ,i}(0)+{\nabla }_{{\alpha }_k^i}L({\mathbf{S}}_0^i)\hfill \\ {\nabla }_{x_{0,p}}E\hfill & =\sum _{i=1}^{N_{\text{su}}}{\theta }_p^i(0)\hfill \end{array}$$

where the gradient of L is given as (from now on, we omit the subject’s index i for clarity purposes):

$$\begin{array}{l}{\nabla }_{{\alpha }_{0,k}}L=2\sum _{p=1}^{N_{\text{cp}}}K(c_{0,k},c_{0,p}){\alpha }_{0,p}\\ {\nabla }_{c_{0,k}}L=2\sum _{p=1}^{N_{\text{cp}}}{{\alpha }_{0,p}}^T{\alpha }_{0,k}{\nabla }_{1}K(c_{0,k},c_{0,p})\end{array}$$

The term ∂₁G(X(t), S(t)) is a block-matrix of size 3N_cp × 3N_x whose (k, p)th 3 × 3 block is given as:

$$d_{X_k}G{(\mathbf{X}(t),\mathbf{S}(t))}_p=\sum _{j=1}^{N_{\text{cp}}}{\alpha }_j(t){\nabla }_{1}K{(X_p(t),c_j(t))}^T\delta (p-k)$$

so that the vector θ(t) is updated according to:

$$-{\stackrel{.}{\theta }}_k(t)=\sum _{p=1}^{N_{\text{cp}}}{\alpha }_p{(t)}^T{\theta }_k(t){\nabla }_{1}K(X_k(t),c_p(t))$$ (42)

The terms ∂_c^gG(X(t), S(t)) and ∂_αG(X(t), S(t)) are both matrices of size 3N_x × 3N_cp, whose (k, p) block is given, respectively, by:

$$\begin{array}{l}{d}_{c_k}{G}_p={\alpha }_k{\left({\nabla }_{1}K(c_k,X_p)\right)}^T\\ d_{{\alpha }_k}{G}_p=K(c_k,X_p){\mathrm{I}}_3\end{array}$$

The differential of the function $F(\mathbf{S})=\left(\begin{array}{c}{F}^c(\mathbf{c},\mathit{\alpha })\\ F^{\alpha }(\mathbf{c},\mathit{\alpha })\end{array}\right)$ can be decomposed into 4 blocks as follows:

$$d_{\mathbf{S}(t)}F=\left(\begin{array}{ll}{\partial }_{\mathbf{c}}{F}^c\hfill & {\partial }_{\mathit{\alpha }}{F}^c\hfill \\ {\partial }_{\mathbf{c}}{F}^{\alpha }\hfill & {\partial }_{\mathit{\alpha }}{F}^{\alpha }\hfill \end{array}\right)$$ (43)

Therefore, the update rules for the auxiliary variables ξ^c(t) and ξ^α(t) are given as:

$$\{\begin{array}{l}-{\stackrel{.}{\xi }}_k^c(t)=\sum _{p=1}^{N_{\mathrm{x}}}{\alpha }_k{(t)}^T{\theta }_p(t){\nabla }_{1}K(c_k(t),X_p(t))+{({\partial }_{\mathbf{c}}{F}^c)}^T{\xi }^c{(t)}_k+{({\partial }_{\mathbf{c}}{F}^{\alpha })}^T{\xi }^{\alpha }(t_k)\hfill \\ -{\stackrel{.}{\xi }}_k^{\alpha }(t)=\sum _{p=1}^{N_{\mathrm{x}}}K(c_k(t),X_p(t)){\theta }_p(t)+{({\partial }_{\alpha }{F}^c)}^T{\xi }^c{(t)}_k+{({\partial }_{\alpha }{F}^{\alpha })}^T{\xi }^{\alpha }{(t)}_k\hfill \end{array}$$

with

$$\begin{array}{ll}{({\partial }_c{F}^c)}^T{\xi }^c{(t)}_k=\hfill & \sum _{p=1}^{N_{\text{cp}}}\left({\alpha }_p{(t)}^T{\xi }_k^c(t)+{\alpha }_k{(t)}^T{\xi }_p^c(t)\right){\nabla }_{1}K(c_k(t),c_p(t))\hfill \\ {({\partial }_c{F}^{\alpha })}^T{\xi }^{\alpha }{(t)}_k=\hfill & \sum _{p=1}^{N_{\text{cp}}}{\alpha }_k{(t)}^T{\alpha }_p(t){\nabla }_{1,1}K{(c_k(t),c_p(t))}^T\left({\xi }_p^{\alpha }(t)-{\xi }_k^{\alpha }(t)\right)\hfill \\ {({\partial }_{\alpha }{F}^c)}^T{\xi }^c{(t)}_k=\hfill & \sum _{p=1}^{N_{\text{cp}}}K(c_k(t),c_p(t)){\xi }_j^c(t)\hfill \\ {({\partial }_{\alpha }{F}^{\alpha })}^T{\xi }^{\alpha }{(t)}_k=\hfill & \sum _{p=1}^{N_{\text{cp}}}{\nabla }_{1}K{(c_k(t),c_p(t))}^T\left({\xi }_p^{\alpha }(t)-{\xi }_k^{\alpha }(t)\right){\alpha }_p(t)\hfill \end{array}$$

In these equations, we supposed the kernel symmetric: K(x, y) = K(y, x). If the kernel is a scalar isotropic kernel of the form K = f(||x − y||²)I₃, then we have:

$$\begin{array}{l}{\nabla }_{1}K(x,y)=2f^{\prime }({\Vert x-y\Vert }^2)(x-y)\\ {\nabla }_{1,1}K(x,y)=4f^{″}({\Vert x-y\Vert }^2)(x-y){(x-y)}^T+2f^{\prime }({\Vert x-y\Vert }^2){\mathrm{I}}_3\end{array}$$

Appendix C Gradient of the varifold metric for meshes

We derive here the gradient of the varifold metric with respect to the position of the vertex of the mesh. Let 𝒮 be a triangular mesh. For each face f_k, we denote n_k its normal, p_k its center and u_k = n_k/ |n_k|^1/2. Let 𝒯 be another triangular mesh, m_k its normal, q_k its center and v_k = m_k/ |m_k|^1/2. Our goal is to compute the gradient of d(𝒮, 𝒯)² with respect to x_i, a given vertex of 𝒮. The chain rule gives:

$${\nabla }_{x_i}d{(\mathcal{S},\mathcal{T})}^2=\sum _{f_k\ni x_i}{(d_{x_i}{n}_k)}^T{(d_{n_k}{u}_k)}^T{\nabla }_{u_k}d{(\mathcal{S},\mathcal{T})}^2+{(d_{x_i}{p}_k)}^T{\nabla }_{p_k}d{(\mathcal{S},\mathcal{T})}^2,$$ (44)

where we sum over all the faces that have x_i among their vertices.

Given the inner-product between varifolds (see main text), we have:

$${\nabla }_{u_k}d{(\mathcal{S},\mathcal{T})}^2=4\left(\sum _{i=1}^{N_{\mathcal{S}}}{K}^W(p_k,p_i)u_i{u}_i^T-\sum _{j=1}^{N_{\mathcal{T}}}{K}^W(p_k,q_j)v_j{v}_j^T\right)u_k,$$ (45)

and denoting p_k,d the dth coordinate of the 3D vector p_k,

$${\left({\nabla }_{p_k}d{(\mathcal{S},\mathcal{T})}^2\right)}_d=2u_k^T\left(\sum _{i=1}^{N_{\mathcal{S}}}\frac{\partial K^W(p_k,p_i)}{{\partial }_{p_{k,d}}}{u}_i{u}_i^T-\sum _{j=1}^{N_{\mathcal{T}}}\frac{\partial K^W(p_k,q_j)}{{\partial }_{p_{k,d}}}{v}_j{v}_j^T\right)u_k$$ (46)

Finally, for a face f_k, we have $n_k=\frac{1}{2}(X_1-X_0)\times (X_2-X_0)$ and $p_k=\frac{1}{3}(X_0+X_1+X_2)$, where we denote X₀, X₁, and X₂ the vertices of the face. If we denote e the edge opposite to the vertex x_i (i.e., e = X₂ − X₁ if x_i = X₀), we have for a generic 3D-vector V:

$${(d_{x_i}{n}_k)}^{T}V=\frac{1}{2}e\times V\text{and}{(d_{x_i}{p}_k)}^{T}V=\frac{1}{3}V.$$ (47)

and since u_k = n_k/ |n_k|^1/2,

$$d_{n_k}{u}_k=\frac{1}{{\mid n_k\mid }^{1/2}}\left({\mathrm{I}}_3-\frac{1}{2}\frac{n_k{n}_k^T}{{\mid n_k\mid }^2}\right)=\frac{1}{\mid u_k\mid }\left({\mathrm{I}}_3-\frac{1}{2}\frac{u_k{u}_k^T}{{\mid u_k\mid }^2}\right)$$ (48)

The gradient is computed by plugging (45), (46), (47) and (48) into (44). The gradient is computed by scanning each face of the mesh 𝒮 and adding the contribution of this face to each of its vertices.

One can easily verify that (44) is independent of the ordering of the vertices, thus showing its invariance with respect to the local orientation of the mesh.

Appendix D Diffeomorphic template evolution

The purpose of this section is to prove that no self-intersection may occur during the optimization of the template shape, by showing that the updates of the template follow a geodesic flow of diffeomorphisms. Using notations of the main text, ∇E_x0,p is the gradient of the criterion with respect to the position of the vertex x_0,p of the current template using the L² metric, and ∇^XE_x0,p its smoothed version using a metric given by a Gaussian kernel with width σ_X > 0, K^X, so that:

$${\nabla }_{x_0,k}^{X}E=\sum _{p=1}^{N_X}{K}^X(x_{0,k},x_{0,p})\nabla E_{x_{0,p}}=-u_s(x_{0,k}),$$

where u_s is a vector field in V^X, the RKHS associated with the Gaussian kernel K^X. In particular, if ψ_s is the flow associated with integration of u_s, we get X₀(s) = ψ_s(X₀(0)). An important point to be verified here is that this flow exists and generates a continuous curve s → ψ_s of C¹ diffeomorphisms so that the template components cannot degenerate or self-intersect. Let Ω_X be the open set of the configurations X₀ such that all the mesh faces associated with X₀ are non-degenerated (positive area) and that any pairs of distinct vertices do not coincide in space. The total energy $E({\mathbf{X}}_0,\{{\mathbf{S}}_0^i\})$ is C¹ on an open set Ω_X × ℝ^N_s so that the local existence of the gradient descent follows from the Cauchy-Lipschitz theorem. Now, if we consider a maximal solution on [0, s_f[, we will prove below (and this is the key estimate) that

$${\int }_0^{s_f}{\mid u_s\mid }_{V^X}^{2}ds\le E_0\doteq E({\mathbf{X}}_0(0),\{{\mathbf{S}}_0^i(0)\})<\infty$$ (49)

so that the flow ψ_s is a flow of C¹ diffeomorphisms staying at a bounded distance $d_X(\text{Id},{\psi }_s)\le \sqrt{E_0}$ from the identity and X₀(s) = ψ_s(X₀(0)) stays in a compact set of Ω_X. In particular, since the differential dψ and dψ⁻¹ can be controlled uniformly by d_X(Id, ψ), we get that no face can degenerate during the gradient descent, that the distance between two distinct vertices or two surface patches (up to the continuous limit) cannot vanish.

Now, we prove (49). From the RKHS property of the kernel we get

$$\begin{array}{l}{\mid u_s\mid }_{V^X}^2=\sum _{p=1}^{N_{\mathrm{x}}}{\left(\nabla E_{x_{0,p}}\right)}^T\left(\sum _{q=1}^{N_x}{K}^X(x_{0,p},x_{0,q})\nabla E_{x_{0,q}}\right)\\ =-\sum _{p=1}^{N_{\mathrm{x}}}{\left(\nabla E_{x_{0,p}}\right)}^T{u}_s(x_{0,p})\\ \le -\sum _p{\left(\nabla E_{x_{0,p}}\right)}^T\frac{d{x}_{0,p}}{ds}\underset{\ge 0}{\underbrace{-\sum _{i=1}^{N_{\text{su}}}{\left({\nabla }_{{\mathbf{S}}_0^i}E\right)}^T\frac{d{\mathbf{S}}_0^i}{ds}}}=-\frac{dE}{ds}\end{array}$$

so that ${\int }_0^{s_f}{\mid u_s\mid }_{V^X}^{2}ds\le E(X_0(0))-E(X_0(s_f))\le E(X_0(0))$ (we use here that E ≥ 0) and ${\int }_0^{s_f}{\mid u_s\mid }_{V^X}^{2}ds<\infty$.