Abstract
Hospital readmission is a key marker of quality of health care. Notwithstanding its widespread use, however, it remains controversial in part because statistical methods used to analyze readmission, primarily logistic regression and related models, may not appropriately account for patients who die prior to experiencing a readmission event within the timeframe of interest. Towards resolving this, we describe and illustrate the semi-competing risks framework, which refers to the general setting where scientific interest lies with some non-terminal event (e.g. readmission), the occurrence of which is subject to a terminal event (e.g. death). Although a number of statistical analysis methods have been proposed for semi-competing risks data, we describe in detail the use of illness-death models primarily because of their relation to well-known methods for survival analysis and the availability of software. We also describe and consider in detail a number of existing approaches that could, in principle, be used to analyze semi-competing risks data including composite endpoint and competing risks analyses. Throughout we illustrate the ideas and methods using data on N=49,763 Medicare beneficiaries hospitalized between 2011–2013 with a principle discharge diagnosis of heart failure.
Keywords: death, readmission, survival analysis
Introduction
Hospital readmission is a key marker of quality of health care, has been used to investigate variation in quality among patients in a broad range of clinical contexts1–10 and has become an important policy measure11, 12. Notwithstanding its widespread use, however, readmission remains controversial as a measure of quality13–16. Among the concerns raised, whether and how patient deaths are handled in the analyses and reported represents an important challenge. Joynt and Jha (2012), for example, note that “Factoring a hospital’s mortality rate into its readmission-penalty calculation could ensure that the best institutions … are not inappropriately penalized”15.
In the literature, analyses of readmission have generally been conducted with the use of logistic regression models for the binary outcome of “readmission within 30 days”17. Such models are also used by CMS in their calculation of risk-adjusted readmission rates18. Practically, if a patient dies within the 30-day interval prior to experiencing a readmission event they are counted as not having experienced the event throughout the interval. That is, person-time after death contributes to the analysis of readmission even though a patient, by definition, cannot experience a readmission during this time. Arguably, a more appropriate approach would be to explicitly treat death as a competing force that is considered simultaneously with readmission. To this end, researchers could, in principle, use competing risks analysis19–22. One key feature of these methods is that they are specifically designed for settings where patients can experience one of a number of so-called terminal events, terminal in the sense that if a patient experiences an event of any given type they cannot subsequently experience an event of any other type. Readmission, in contrast, is non-terminal, in the sense that the occurrence of a readmission event does not preclude the patient from death. Consequently, although a typical dataset will contain some information on dependence between readmission and death, competing risks analyses do not make use of it.
As an alternative, this paper considers embedding the analysis of readmission within the semi-competing risks framework23, 24. As we elaborate upon, a key benefit of this framework is the explicit use of information on the timing of readmission events post-death which provides a means to acknowledge and characterize dependence between the two events. In addition to describing semi-competing risks data and analysis, we describe a range of well-known methods that analysts may consider including the use of a composite endpoint. As we emphasize throughout, key differences across the various methods we present lie in the interpretation of the model components as well as the extent to which information on the dependence between the two events is exploited. Although the ideas and methods are useful in a broad range of settings, we illustrate them using data on N=49,763 Medicare beneficiaries hospitalized between 2011–2013 with a principle discharge diagnosis of heart failure.
Semi-Competing Risks Data
General structure
Semi-competing risks refers to the setting where primary interest lies with some non-terminal event, the occurrence of which is subject to a terminal event. Although we focus on hospital readmission as the non-terminal event, the notion is much more general and could refer to the incidence or recurrence of any health outcome, the discontinuation of treatment, or dropout. Typically, the terminal event is death although it can also refer to other phenomena. For example, one could view treatment discontinuation as terminal if the non-terminal event is a treatment-related toxicity.
Intuitively, one can think of patients in the semi-competing risks setting as transitioning through a series of “states”. For example, in the Medicare data we present patients are initially in a “Discharged” state (see Figure 1(a)). As time progresses, a patient could transition into the state of being “Readmitted” or of being “Dead”. If a patient transitions into the “Readmitted” state they could subsequently transition into the “Dead” state although these transitions cannot occur in the reverse order.
Figure 1.
Graphical representation of the states that patients can transition between under the semi-competing risks and competing risks frameworks. (a) Semi–competing risks. (b) Competing risks.
Medicare data
Table 1 reports on N=49,763 Medicare fee-for-service beneficiaries aged 65 or older who were hospitalized between 2011–2013 and subsequently discharged with a principle diagnosis of heart failure at one of 141 hospitals in the six New England states (CT, MA, ME, NH, RI, VT). Additional eligibility criteria for inclusion were that patients had at least 12 months of prior enrollment in Medicare Part A, had not transferred to some other acute care facility and had been discharged to their home, an intensive care or skilled nursing facility (ICF/SNF) or to hospice care. Applying these criteria, some patients had more than one eligible hospitalization between 2011–2013; for the purposes of this paper, we selected one hospitalization at random.
Table 1.
Patient characteristics and 30-day outcomes for N=49,573 Medicare beneficiaries hospitalized in one of the six New England states between 2011–2013 and discharged with a principle diagnosis of heart failure.
| Distribution | 30-day outcomes, % | |||||
|---|---|---|---|---|---|---|
| N | % | Readmission and death |
Readmission and censored |
Death without readmission |
Censored | |
| Total | 49,763 | 100.0 | 2.8 | 15.7 | 7.0 | 74.4 |
| Gender | ||||||
| Female | 27,775 | 55.8 | 2.7 | 15.5 | 6.9 | 74.8 |
| Male | 21,988 | 44.2 | 3.0 | 15.9 | 7.2 | 74.0 |
| Age, years | ||||||
| 65–74 | 10,590 | 21.3 | 1.9 | 18.1 | 3.3 | 76.8 |
| 75–84 | 16,160 | 32.5 | 2.6 | 16.0 | 5.7 | 75.8 |
| 85–94 | 19,851 | 39.9 | 3.5 | 14.7 | 9.0 | 72.8 |
| 95+ | 3,162 | 6.4 | 3.5 | 12.0 | 14.6 | 69.8 |
| Race | ||||||
| White | 46,412 | 93.3 | 2.9 | 15.6 | 7.3 | 74.2 |
| African-American | 1,979 | 4.0 | 2.0 | 16.9 | 3.4 | 77.8 |
| Other | 1,372 | 2.8 | 2.3 | 16.8 | 4.5 | 76.3 |
| Length of stay, days | ||||||
| 1–3 | 20,528 | 41.3 | 1.7 | 14.6 | 4.5 | 79.1 |
| 4–6 | 17,847 | 35.9 | 3.0 | 15.8 | 6.6 | 74.6 |
| 7–13 | 9,626 | 19.3 | 4.3 | 17.1 | 11.5 | 67.1 |
| 14+ | 1,762 | 3.5 | 6.2 | 19.1 | 15.9 | 58.7 |
| Discharge location | ||||||
| Home | 13,899 | 27.9 | 1.2 | 14.4 | 1.5 | 82.8 |
| Home with care | 17,893 | 36.0 | 2.3 | 17.8 | 3.1 | 76.8 |
| ICF/SNF | 16,332 | 32.8 | 5.1 | 15.9 | 9.6 | 69.5 |
| Hospice | 1,639 | 3.3 | 0.6 | 1.2 | 71.9 | 26.3 |
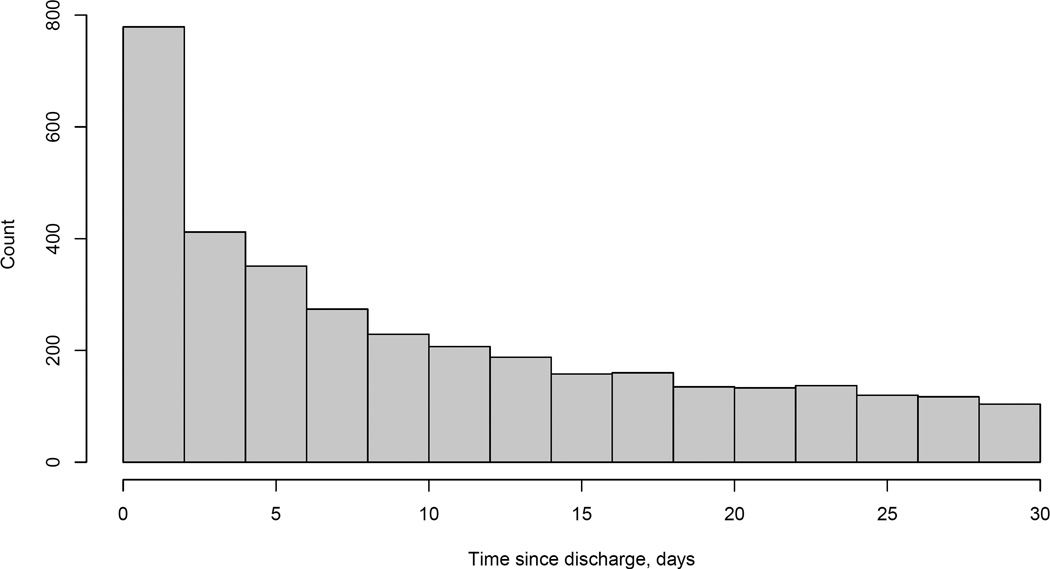
Table 1 also provides a summary of 30-day outcomes, overall and within levels of the factors reported. From the first row, we see 2.8% of patients experienced a readmission event and subsequently died within 30 days. We also see that 15.7% experienced a readmission event without subsequently dying within 30 days, so that the overall 30-day readmission rate was 18.5%. Similarly, combining the patients who experienced both events within 30 days with the 7.0% who died with 30 days without a readmission event, the overall 30-day mortality rate was 9.8%. Focusing on the 7.0% of patients who died within 30 days without a readmission event, Figure 2 provides a histogram of the death times for this group; nearly half of the 3,504 patients (48.2%) died within one week and more than two-thirds (69.6%) within two weeks.
Figure 2.
Distribution of the time to death for the 3,504 patients who died within 30 days of being discharged and without experiencing a readmission event.
Finally, we note that 74.4% of patients did not experience either event during the 30-day interval post-discharge and were therefore censored. Most of these patients were censored administratively at 30 days, although a small percentage (2.2%) lost their fee-for-service eligibility prior to experiencing either event and prior to the 30-day mark; in the analyses presented below person-time for these patients was censored accordingly.
Beyond the overall rates, Table 1 reveals substantial variation in the distribution of the four outcome types across levels of certain factors. We see, for example, that the rates at which patients are readmitted within 30-days post-discharge decrease from 18.1% among 65–74 years to 12.0% among patients 95 years or older. Furthermore, this decrease is accompanied by a substantial increase in the rate of death without readmission (from 3.3% to 14.6%) and an increase in the rate of death with readmission (from 1.9% to 3.5%). In contrast the rates at which patients are experiencing a readmission event, a death event or both are all increasing as the length of stay for the initial hospitalization stay increases; correspondingly, the rate at which patients are surviving to 30 days without either event decreases dramatically from 79.1% among those whose stay was 1–3 days to 58.7% among those whose stay was 14 or more days. Last, we find considerable variation in the distribution of the four outcome types across levels of discharge destination. Perhaps most dramatic is the very low readmission rate among patients discharged to a hospice facility (1.8% overall), while the rate at which patients are experiencing a death event without readmission is very high (71.9%). Across the other three major discharge destinations, considerable variation exists in the rate at which patients die without a readmission event (1.5–9.6%), as well as in the rate at which patients experience both events (1.2–5.1%).
The Illness-Death Model
To formalize the structure of semi-competing risks data, let T1 denote the time to the non-terminal event and T2 the time to the terminal event. The central challenge in analyzing semi-competing risks data is in developing an interpretable model for T1 while simultaneously acknowledging potential dependence between T1 and T2. In the statistical literature a number of methods for the analysis of semi-competing risks data have been recently proposed23–34. In this paper we focus on one of these approaches, the illness-death model. While other methods are mentioned briefly in the Discussion, we focus on on the illness-death model since it builds naturally and intuitively on well-known methods for survival analysis in standard settings, and because software is readily available.
Towards formally describing the illness-death, consider again Figure 1(a). Viewing T1 and T2 as time-to-event outcomes, one can specify the rates at which patients transition between the three states using three transition-specific hazard functions:
| (1) |
| (2) |
| (3) |
The first of these is the hazard rate for readmission from discharge at a given point in time, t1, given that neither the readmission nor the death event has occurred prior to time t1. The second is the corresponding hazard rate for death from discharge at a given time, t2, given that neither the readmission nor the death event has occurred prior to time t2. Finally, h3(t2|t1) is the hazard for death from readmission at time t2 given that a readmission event was observed at time T1=t1 and that a death event had not occurred prior to time t2.
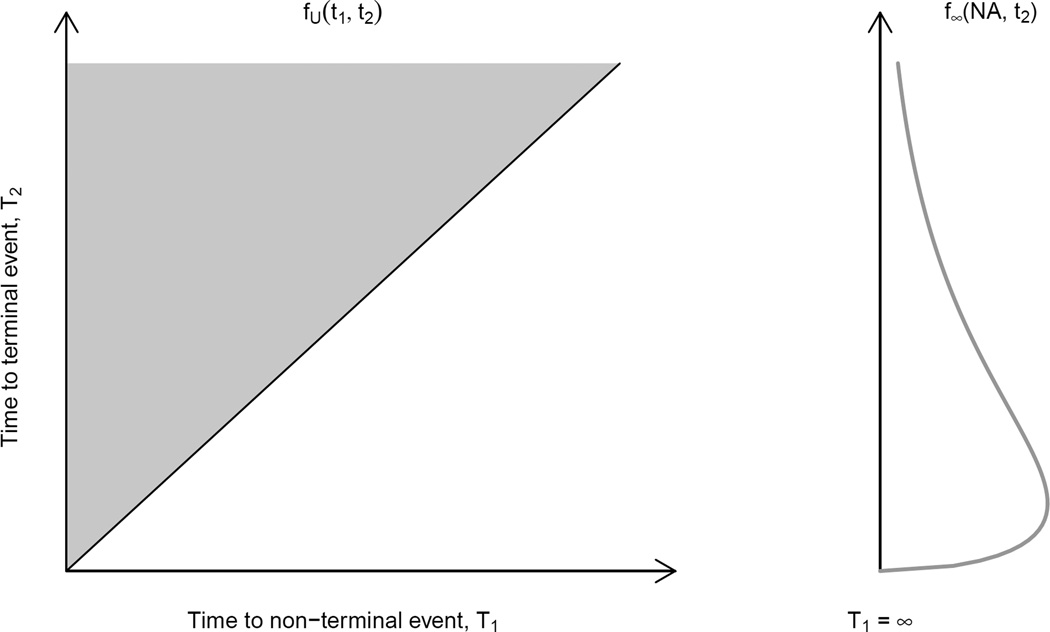
Collectively, the three hazard functions given by (1)–(3) can be shown to define the joint distribution of (T1, T2) as consisting of two components24, 30. From Figure 3, the first component corresponds to instances where both events are experienced. That is, it indicates the distribution on the so-called upper wedge on which T1 < T2 (i.e. a readmission event is observed prior to a death event). The second component corresponds to instances where only a death event is experienced. Mathematically, since the induced joint distribution on the upper wedge does not integrate to 1.0, the balance of probability is attributed along the line T1=∞. As discussed by Xu et al30, this strategy is, arguably, preferable to analysis strategies that assume some latent distribution for (T1, T2) on the lower wedge for which T1 > T2.
Figure 3.
Graphical representation of the joint distribution of (T1, T2) based on the illness-death model.
While expressions (1)–(3) formally define the three hazard functions, as in standard survival analyses, one can adopt model structure for each in order to examine covariate effects and to obtain estimates of absolute risk. By far the most common structure is the Cox model35. In the semi-competing risks context, the basic Cox model set-up can be extended as follows:
| (4) |
| (5) |
| (6) |
where γi is a patient-specific frailty and Xi is a vector of patient-specific covariates24, 30. In expression (4), h01(t1) denotes the baseline hazard function (i.e. the hazard for a population of patients with X=0) for readmission from discharge while β1 denotes the vector of log-hazard ratios that characterize the effects of X on the hazard for readmission from discharge. More specifically, the jth component of exp(β1) can be interpreted as the hazard ratio for readmission corresponding the jth covariate in X conditional on the fact that a death event has not occurred, holding the remaining elements of X and γi fixed. Similarly, h02(t2) in expression (5) denotes the baseline hazard function for death from discharge while the components of exp(β2) can be interpreted as hazard ratios for death corresponding to the covariates in X conditional on the fact that a readmission event has not occurred. Finally, h03(t2|t1) in expression (6) corresponds to the conditional baseline hazard function for death given that a readmission event occurred at time t1 and exp(β3) denotes the analogous hazard ratio parameters.
Additionally, each transition-specific model includes a shared patient-specific frailty, denoted γi. These frailties are analogous to random effects in mixed effects models for longitudinal36, in that they serve as a device for accounting for residual correlation between T1 and T2 due to the collective impact of patient-specific covariates not included in Xi. While useful for the purposes of inference, it is important to note that their inclusion has an impact on the interpretation of the regression coefficients. Specifically, in addition acknowledging the cause-specific nature of hazards (4)–(6), one should acknowledge that β1, β2, and β3 are patient-specific and therefore distinct from their marginal counterparts. From a practical perspective, the patient-specific frailties are typically assumed to arise from a Gamma(θ−1, θ−1) distribution, parameterized so E[γ]=1 and V[γ]=θ. As in standard mixed effects models the variance of the frailties dictates the extent of induced correlation between T1 and T2, and can be estimated and reported along with the other components of the model.
Finally, analyses for the illness-death model can proceed either within the frequentist30 or Bayesian paradigms24, allowing analysts to either adopt a parametric distribution for the three baseline hazard functions (e.g. a Weibull) or specify them non-parametrically. As a function of two continuous variables, h03(t2|t1) has the potential to be very complex and therefore difficult to specify parametrically or estimate non-parametrically. In practice, analysts resolve this by making one of two simplifying assumptions. In the first h03(t2|t1) is assumed to be independent of t1 so that expression (6) becomes:
| (7) |
This representation is often referred to as the Markov model since it does not depend on the timing of the readmission event. Intuitively, one can interpret this model as stating that a patient’s risk for death at any given time post-discharge, say t2, is initially governed by the hazard given in expression (5); if and when they experience a readmission, their risk for death is subsequently governed by the hazard given in expression (7). An alternative to the Markov assumption is one where expression (6) is replaced by
| (8) |
so that the risk of death at a given time post-discharge for a patient who has experienced a readmission event at time t1 depends on the time since readmission (i.e. t2−t1, the so-called sojourn time), rather than the time since discharge. This representation is referred to as the Semi-Markov model. Generally, when choosing between these specifications, the primary consideration will be the extent to which model (7) or model (8) better characterizes risk post-readmission from either from the perspective of scientific plausibility or in terms of goodness-of-fit, or possibly both.
Alternative Analysis Strategies
To clarify the importance of specific features of the illness-death model, it is instructive to consider alternative modeling strategies that analysts will generally be familiar with and may use to analyze semi-competing risks data.
Univariate logistic regression
As mentioned in the Introduction, analyses of readmission are typically conducted using logistic regression models. To formalize this, let Yi=0/1 indicate whether or not the ith patient was readmitted within 30 days post-discharge. The logistic regression model relating Xi to Yi is given by:
| (9) |
In the presence of death as a competing risk, however, the interpretation of results based on this model is complicated by the fact that it specifies a patient’s risk as being linear on the logit scale throughout the 30-day window even though such an assumption is not well-defined if a patient has died prior to the 30-day mark. Consequently, even though one can fit the model (in the sense of running some computer code), the estimates correspond to some mixture of the effect of X for patients who were at risk throughout and the effect of X for patients who could not have experienced the event during portions of person-time.
Univariate survival analysis
To explicitly acknowledge when a patient is at risk to experience the non-terminal event during the 30-day interval, one could use standard survival analysis methods. In terms of regression analyses, one way forward would be to build a model for the marginal hazard of readmission:
| (10) |
Note, we refer to this hazard as “marginal” in the sense that it does not condition on death as a competing risk and is therefore distinct from the hazard given by expression (1). Typically researchers model marginal hazard functions with a univariate Cox model such as:
| (11) |
In addition to not conditioning on death as a competing risk, we note that, in contrast to expression (4) for the illness-death model, the specific choice of expression (11) does not include a patient-specific frailty. Hence, although β* and β1 both speak to the association between X and readmission, their precise interpretations differ and they may or may not be numerically the same.
Operationally, estimation for model (11) typically proceeds on the basis of the usual partial likelihood treating death as a censoring mechanism. An important drawback of this approach, however, is that if there is dependence between readmission and death (as noted in Table 1) then the resulting estimate will not be guaranteed to be consistent for β* although, assuming proportional hazards holds, it will be consistent for its cause-specific counterpart (see below). In this sense, caution is needed to ensure an appropriate interpretation of the results.
Composite endpoints
Instead of treating death as a censoring mechanism, analysts may consider incorporating it as a component of the outcome by defining and analyzing a composite endpoint37. Towards this, let Tc = min(T1,T2) denote the time from discharge to the first of readmission or death. One could perform a standard survival analysis for Tc by fitting the model:
| (12) |
Assuming that the remaining forms of censoring are independent, estimation and inference for βc could proceed as usual. The main drawback of this approach, however, is that the interpretation of βc requires viewing it as a mixture of the effects of X on both readmission and death, so that scientific attention is shifted away from readmission as the primary outcome. Consequently, in attempting to resolve a statistical issue the primary scientific questions have been altered.
Competing risks analysis
Finally, analysts could use the competing risks framework, specifically building models for the two hazards of the sub-distribution or two cause-specific hazard functions19–22, 38. Focusing on the cause-specific hazard functions, an analysis could proceed by fitting the following two models:
| (13) |
| (14) |
for the two cause-specific hazards given by expressions (1) and (2). As with β* in expression (11), the superscript “*” has been added to emphasize the distinction between the components in (13) and (14) from the corresponding components in (4) and (5). For example, while both β1 and β1* are both cause-specific parameters, the interpretation of β1 also requires acknowledging the fact that the model conditions on the patient-specific frailties. As such, β1 and β1* may not be equivalent numerically. Nevertheless, one could proceed with estimation and inference for either cause-specific hazard function by using the standard partial likelihood treating the other event as a censoring mechanism. The primary drawback of applying the competing risks framework to the study of readmission, however, is that post-readmission death events and their timing are ignored (see Figure 1(b)). That is, information that could be used to inform an understanding of dependence between readmission and death, and hence joint distribution of the two events, is essentially thrown away.
Results
Here we present results from a series of analyses that apply the methods discussed above to N=49,763 Medicare beneficiaries. For all analyses we considered the factors listed in Table 1, together with an indicator of the New England state in which the hospitalization occurred. For simplicity, we take the baseline hazard functions for all survival models to be structured according to a Weibull distribution, although note that current methods and software permit a more flexible specification24. Furthermore, we restrict attention to results for the illness-death model based on the Markov specification for h3(t2|t1), given by expression (7). Finally, all of the analyses were conducted using the freely-available SemiCompRisks package for R39.
Focusing on the univariate analyses, Table 2 shows that the general conclusions based on the logistic regression analysis and the survival analysis with readmission as the primary outcome are very similar (see the first two sets of columns). Both analyses, for example, indicate small-to-moderate associations for gender and age, and a strong association for length of stay. In regard to discharge destination, while there is little evidence of a meaningful difference in risk for readmission between patients discharged to home without care and those discharged to either a ICF or SNF (e.g. HR 1.05; 95% CI 1.00–1.10), patients discharged to their home without care have significantly lower risk of readmission than those with care (e.g. HR 0.77; 95% CI 0.72–0.81). This is, arguably, due to unadjusted case-mix differences, specifically in the distribution of comorbid conditions; patients being discharged to their home without care are likely healthier than those discharged to their home with care, and therefore less likely to be readmitted.
Table 2.
Estimates of odds ratio (OR) and hazard ratio (HR) parameters, together with associated 95% confidence intervals (CI), from a series of analysis applied to the Medicare heart failure data*.
| Univariate analyses | Semi-competing risks anlaysis | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Logistic regression | Survival analysis | |||||||||||
| Readmission | Readmission | Composite endpoint | Readmission | Death prior to readmission |
Death post- readmission |
|||||||
| OR | 95% CI | HR | 95% CI | HR | 95% CI | HR | 95% CI | HR | 95% CI | HR | 95% CI | |
| Gender | ||||||||||||
| Female | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | ||||||
| Male | 1.06 | (1.01, 1.11) | 1.07 | (1.02, 1.11) | 1.11 | (1.07, 1.15) | 1.11 | (1.05, 1.17) | 1.34 | (1.23, 1.46) | 1.29 | (1.15, 1.45) |
| Age, years | ||||||||||||
| 65–74 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | ||||||
| 75–84 | 0.89 | (0.84, 0.95) | 0.91 | (0.86, 0.96) | 0.98 | (0.93, 1.03) | 0.90 | (0.84, 0.97) | 1.40 | (1.2, 1.62) | 1.36 | (1.13, 1.64) |
| 85–94 | 0.86 | (0.80, 0.91) | 0.89 | (0.84, 0.94) | 1.01 | (0.96, 1.07) | 0.89 | (0.83, 0.96) | 1.93 | (1.67, 2.23) | 1.98 | (1.66, 2.36) |
| 95+ | 0.71 | (0.64, 0.80) | 0.78 | (0.70, 0.86) | 1.07 | (0.99, 1.16) | 0.82 | (0.72, 0.93) | 3.30 | (2.75, 3.97) | 2.52 | (1.93, 3.30) |
| Race | ||||||||||||
| White | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | ||||||
| African-American | 0.93 | (0.83, 1.05) | 0.93 | (0.83, 1.03) | 0.88 | (0.80, 0.97) | 0.89 | (0.78, 1.02) | 0.60 | (0.45, 0.8) | 0.72 | (0.51, 1.02) |
| Other | 1.01 | (0.88, 1.15) | 1.02 | (0.90, 1.15) | 0.98 | (0.88, 1.09) | 1.05 | (0.89, 1.23) | 0.82 | (0.60, 1.12) | 0.85 | (0.58, 1.24) |
| Length of stay, days | ||||||||||||
| 1–3 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | ||||||
| 4–6 | 1.13 | (1.07, 1.19) | 1.12 | (1.06, 1.17) | 1.11 | (1.06, 1.16) | 1.15 | (1.08, 1.22) | 1.18 | (1.06, 1.31) | 1.34 | (1.15, 1.55) |
| 7–13 | 1.31 | (1.23, 1.40) | 1.31 | (1.24, 1.39) | 1.41 | (1.34, 1.47) | 1.47 | (1.37, 1.59) | 1.97 | (1.76, 2.22) | 1.64 | (1.39, 1.93) |
| 14+ | 1.63 | (1.45, 1.83) | 1.63 | (1.47, 1.80) | 1.73 | (1.59, 1.88) | 2.03 | (1.76, 2.34) | 2.79 | (2.31, 3.38) | 2.01 | (1.55, 2.59) |
| Discharge destination | ||||||||||||
| Home | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | ||||||
| Home with care | 0.75 | (0.71, 0.80) | 0.77 | (0.72, 0.81) | 0.75 | (0.71, 0.79) | 0.70 | (0.65, 0.75) | 0.51 | (0.44, 0.61) | 0.71 | (0.58, 0.86) |
| ICF/SNF | 1.02 | (0.97, 1.08) | 1.05 | (1.00, 1.10) | 1.28 | (1.22, 1.33) | 1.13 | (1.06, 1.21) | 2.95 | (2.65, 3.29) | 2.54 | (2.22, 2.91) |
| Hospice | 0.07 | (0.05, 0.10) | 0.18 | (0.13, 0.26) | 5.95 | (5.58, 6.36) | 0.63 | (0.43, 0.93) | 151.8 | (126.2, 182.6) | 15.3 | (7.04, 33.2) |
Adjusted for State
From the results for the composite endpoint analysis (see the third set of columns) we see a dramatic shift in the hospice association (HR 5.95; 95% CI 5.58–6.36) suggesting that death plays an important role in the analysis of these patients. A similar but less dramatic shift is also seen for the ICF/SNF association: in contrast to the non-significant association when readmission is taken as the outcome, the association is statistically significant under the composite endpoint analysis (HR 1.28; 95% 1.22–1.33).
While a comparison across the univariate analyses provides insight into the role that death plays in the analysis of readmission, the results from the illness-death model provide a more formal assessment. Focusing on the variance component, there is clear evidence of between-patient heterogeneity that is not accounted for by X and, consequently, that T1 and T2 are positively correlated: θ is estimated to be 2.60 (95% CI 2.34, 2.89) and a likelihood ratio test for the inclusion of the patient-specific frailties into the model40 was highly statistically significant (p < 0.001). The practical impact of this can be seen in several of the risks factors, most notably the length of stay and the discharge destination variables. We see, for example, that substantive differences in the effects of a 7–13 day stay (HR 1.47 vs 1.31) and a stay of 14 days or longer (HR 2.03 vs 1.63). We also find substantive differences in the effects of being discharged to an ICF/SNF; under the univariate analysis the HR is estimated to be 1.05 and is not statistically significant; under the semi-competing risks analysis it is estimated to be 1.13 and is statistically significant. Also of note is that for several of the risk factors there are meaningful differences in the associations for death pre- and post-readmission. This is most evident for the length of stay and discharge destination variables but also manifests for African-Americans. That these differences exist also speaks to the dependence between readmission and death as outcomes.
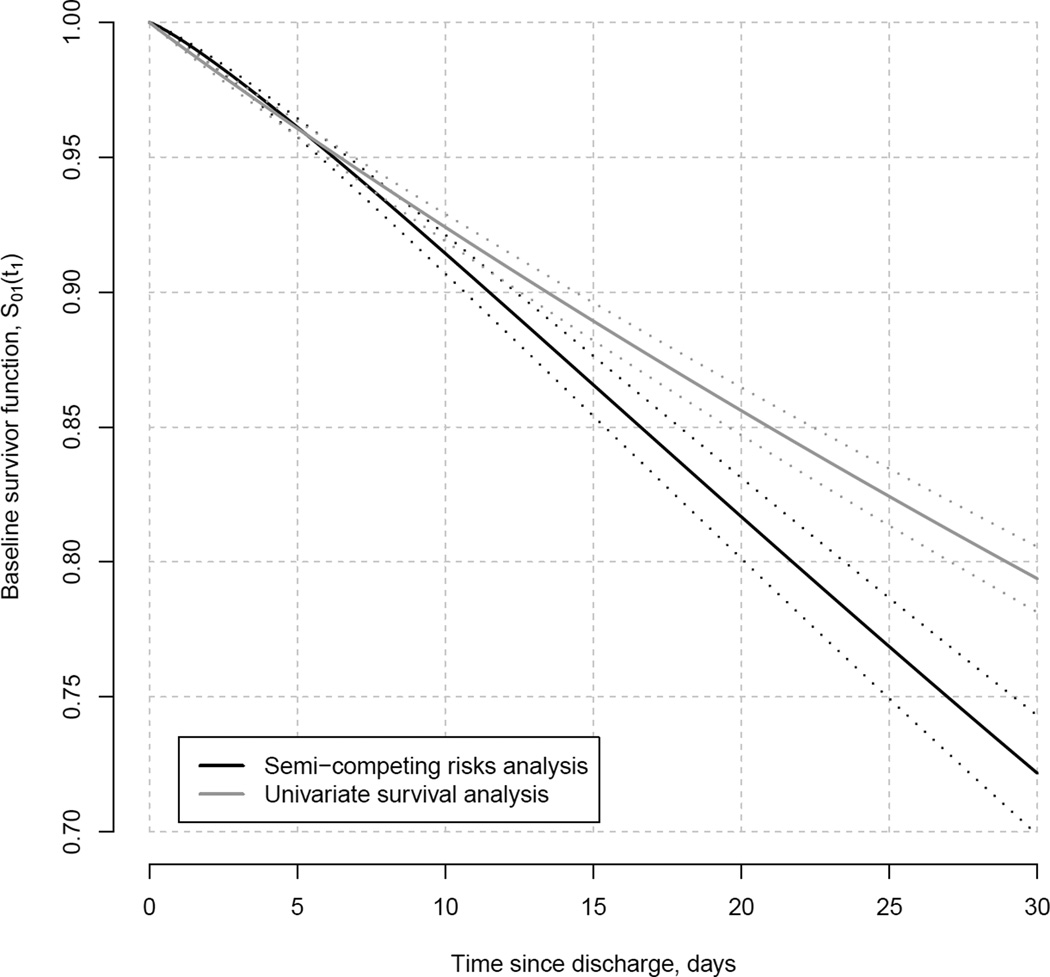
Finally, Figure 4 provides results for the baseline survivor function corresponding to h01(t1) in expression (4), and denoted S01(t1). Note, this function is the readmission-specific survivor function for a white, female patient aged 65–74 years, admitted to a hospital in MA for heart failure, hospitalized for no longer than 3 days and subsequently discharged alive to their home with care. Overall the univariate survival analysis generally indicates better (baseline) survival, with respect to readmission, across the first 30 days post-discharge relative to that indicated by the semi-competing risks analysis. This overestimation is likely due to the univariate analysis erroneously assuming death to be an independent censoring mechanism. Given the strong evidence of dependence between readmission and death, this assumption is likely unrealistic. Nevertheless the univariate analysis, intuitively, takes patients who do not die to be representative of those who do die, a consequence being that the higher (latent) risk for readmission among those who die is not accounted for adequately. In the semi-competing risks analysis, however, the dependence between readmission and death is formally part of the model specification, so that the higher (latent) risk for readmission among those who die is taken into account; hence, the baseline survivor function for readmission is estimated to be lower.
Figure 4.
Estimates and point-wise 95% confidence intervals for the readmission-specific baseline survivor function from the Markov illness-death model.
Discussion
In this paper we reviewed the semi-competing risks framework as a means investigating variation in risk for a non-terminal event in settings where occurrence of the event is subject to a terminal event. We have also described a range of approaches that researchers may use to analyze semi-competing risks data. In principle, each of these approaches estimate different quantities (as highlighted by the notation we adopt), so that they could be viewed as addressing different scientific questions. As we have elaborated upon, however, the potentially informative role that death plays as a dependent competing risk, both in terms of the impact on parameter interpretation and estimation, requires specific consideration. Although our goal is not to be prescriptive in the analysis of semi-competing risks data (arguably, the science should play the most important role in how to move forward), we believe that key benefits of the semi-competing risks framework are that: (i) estimates of risk factor associations for the non-terminal event explicitly account for the terminal event as a dependent competing risk; (ii) statistical inference accounts for within-patient correlation between the two event times via the use of patient-specific frailties; and, (iii) the quantification of the dependence via the variance component θ and the interplay between h2(t2) and h3(t2|t1).
Throughout this paper we have focused on the estimation of covariate effects on the risk of readmission while considering the potential role that death plays in the analysis. While covariate effects are of interest in a broad range of settings, they are not always of primary interest. In the context that motivates the application we present, for example, primary interest lies with characterizing and understanding variation in hospital-specific readmission rates. Towards this, appropriate modeling of covariate effects remains crucial since its purpose is to ensure control for case-mix adjustment. Nevertheless, the extent to which the semi-competing risks framework provides improved characterization of between-hospital variation in readmission rates over, say, the competing risks framework is not known and is the subject of our on-going research41. Given the inherent inability of competing risks analyses to identify dependence between events, the semi-competing risks framework has substantial promise in efforts to investigate how hospital-specific readmission and mortality rates vary jointly42.
Although the Medicare data and analyses we present serve primarily to illustrate the ideas and methods, several aspects of the example deserve comment. First, our analyses do not attempt to incorporate a comprehensive risk adjustment such as one based on using the CMS-HCC model43 risk score, nor do they include other risk factors for readmission and/or death such as whether or not the patient had a do-not-resuscitate order. Including these into the models would likely change the results in Table 2 and Figure 4, specifically by accounting for some of the between-patient variation currently absorbed by the patient-specific frailties. Second, the methods and analysis of the Medicare data set assumes X to be the same for all three transition-specific hazards. This restriction is not necessary, either theoretically or with respect to use of the code available in the SemiCompRisks package. As such, analysts may choose to include different sets of covariates into the three models as appropriate for their specific scientific contexts. Third, for simplicity we restrict attention to the Weibull distribution for the baseline hazard functions in all analyses. While often considered reasonable, the Weibull distribution will not be sufficiently flexible in all settings. Recent work in the statistical literature, however, provides methods that permit researchers to either avoid specifying the baseline hazard functions30 (as is typically done for the Cox model) or to specify very flexible shapes24, 44. Examination and comparison of model fit across alternative specifications, a critical feature of most analyses, would help in deciding modeling assumptions are reasonable. While methods towards this have been developed in the competing risks context45, to the best of our knowledge they have not in the semi-competing risks context and is therefore an important avenue for future work.
Beyond extensions that permit flexible specification of the baseline hazard function, the statistical literature is rich with methods for a broad range of settings that build on the one presented here. For example, methods exist to accommodate more general multi-state data structures including those for settings where the timeframe is relatively long and the non-terminal event is potentially recurrent (e.g. if interest lies with a patients experience in the first year post-discharge then they may experience more than one readmission)46, 47 and/or there are more than one type of non-terminal event31, 48. Beyond the multi-state approach, two other general frameworks have been proposed in the literature. Briefly, instead of directly modeling the transition-specific hazard functions, the first of these frameworks considers the two marginal event-specific survivor functions23, 49, 50. These are then linked via a copula, a mathematical construct used to specify the joint distribution of two variables (and, hence, their dependence). The second framework is grounded in the principles of causal inference, specifically principle stratification, so that the focus is on defining and estimating causal effects of a particular treatment51, 52. As mentioned, the choice to focus on the illness-death model was primarily due to its relation to well-known methods for survival analysis and the availability of software. While we view all of these methods as being complementary in helping researchers address a broad range of scientific questions, a more comprehensive comparison of these methods represents an important ongoing extension of our work.
Footnotes
Conflict of Interest Disclosures: None.
References
- 1.Krumholz HM, Parent EM, Tu N, Vaccarino V, Wang Y, Radford MJ, Hennen J. Readmission after hospitalization for congestive heart failure among Medicare beneficiaries. Arch Intern Med. 1997;157:99–104. [PubMed] [Google Scholar]
- 2.Keenan PS, Normand S-LT, Lin Z, Drye EE, Bhat KR, Ross JS, Schuur JD, Stauffer BD, Bernheim SM, Epstein AJ. An administrative claims measure suitable for profiling hospital performance on the basis of 30-day all-cause readmission rates among patients with heart failure. Circ Cardiovasc Qual Outcomes. 2008;1:29–37. doi: 10.1161/CIRCOUTCOMES.108.802686. [DOI] [PubMed] [Google Scholar]
- 3.Jencks SF, Williams MV, Coleman EA. Rehospitalizations among patients in the Medicare fee-for-service program. N Engl J Med. 2009;360:1418–1428. doi: 10.1056/NEJMsa0803563. [DOI] [PubMed] [Google Scholar]
- 4.Krumholz HM, Merrill AR, Schone EM, Schreiner GC, Chen J, Bradley EH, Wang Y, Wang Y, Lin Z, Straube BM. Patterns of hospital performance in acute myocardial infarction and heart failure 30-day mortality and readmission. Circ Cardiovasc Qual Outcomes. 2009;2:407–413. doi: 10.1161/CIRCOUTCOMES.109.883256. [DOI] [PubMed] [Google Scholar]
- 5.Krumholz HM, Lin Z, Drye EE, Desai MM, Han LF, Rapp MT, Mattera JA, Normand SL. An administrative claims measure suitable for profiling hospital performance based on 30-day all-cause readmission rates among patients with acute myocardial infarction. Circ Cardiovasc Qual Outcomes. 2011;4:243–252. doi: 10.1161/CIRCOUTCOMES.110.957498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Joynt KE, Orav EJ, Jha AK. Thirty-day readmission rates for Medicare beneficiaries by race and site of care. JAMA. 2011;305:675–681. doi: 10.1001/jama.2011.123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Epstein AM, Jha AK, Orav EJ. The relationship between hospital admission rates and rehospitalizations. N Engl J Med. 2011;365:2287–2295. doi: 10.1056/NEJMsa1101942. [DOI] [PubMed] [Google Scholar]
- 8.Tsai TC, Joynt KE, Orav EJ, Gawande AA, Jha AK. Variation in surgical-readmission rates and quality of hospital care. N Engl J Med. 2013;369:1134–1142. doi: 10.1056/NEJMsa1303118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bradley E, Yakusheva O, Horwitz LI, Sipsma H, Fletcher J. Identifying patients at increased risk for unplanned readmission. Med Care. 2013;51:761. doi: 10.1097/MLR.0b013e3182a0f492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Girotti ME, Shih T, Dimick JB. Racial disparities in readmissions and site of care for major surgery. J Am Coll Surg. 2014;218:423–430. doi: 10.1016/j.jamcollsurg.2013.12.004. [DOI] [PubMed] [Google Scholar]
- 11.Centers for Medicaid and Medicare Services. Hospital Inpatient Quality Reporting Program. [accessed 1st August, 2015];2013 https://www.cms.gov/Medicare/Quality-Initiatives-Patient-Assessment-Instruments/HospitalQualityInits/HospitalRHQDAPU.html.
- 12.Centers for Medicaid and Medicare Services. Readmissions Reduction Program. [accessed 1st August, 2015];2013 http://www.cms.gov/Medicare/Medicare-Fee-for-Service-Payment/AcuteInpatientPPS/Readmissions-Reduction-Program.html.
- 13.Axon RN, Williams MV. Hospital readmission as an accountability measure. JAMA. 2011;305:504–505. doi: 10.1001/jama.2011.72. [DOI] [PubMed] [Google Scholar]
- 14.Joynt KE, Jha AK. Thirty-day readmissions - truth and consequences. N Engl J Med. 2012;366:1366–1369. doi: 10.1056/NEJMp1201598. [DOI] [PubMed] [Google Scholar]
- 15.Joynt KE, Jha AK. A path forward on Medicare readmissions. N Engl J Med. 2013;368:1175–1177. doi: 10.1056/NEJMp1300122. [DOI] [PubMed] [Google Scholar]
- 16.Hawn MT. Unintended Consequences of the Hospital Readmission Reduction Program. Ann Surg. 2015;261:1032–1033. doi: 10.1097/SLA.0000000000001150. [DOI] [PubMed] [Google Scholar]
- 17.Normand S-LT. Statistical Methods for Profiling Providers of Medical Care: Issues and Applications. J Am Stat Assoc. 1997;92:803–814. [Google Scholar]
- 18.Ash A, Fienberg S, Louis T, Normand S, Stukel T, Utts J COPSS-CMS White Paper Committee. Statistical issues in assessing hospital performance. 2012 [Google Scholar]
- 19.Fine JP, Gray RJ. A proportional hazards model for the subdistribution of a competing risk. J Am Stat Assoc. 1999;94:496–509. [Google Scholar]
- 20.Klein JP, Andersen PK. Regression modeling of competing risks data based on pseudovalues of the cumulative incidence function. Biometrics. 2005;61:223–229. doi: 10.1111/j.0006-341X.2005.031209.x. [DOI] [PubMed] [Google Scholar]
- 21.Putter H, Fiocco M, Geskus RB. Tutorial in biostatistics: competing risks and multi-state models. Stat Med. 2007;26:2389–2430. doi: 10.1002/sim.2712. [DOI] [PubMed] [Google Scholar]
- 22.Dignam JJ, Zhang Q, Kocherginsky M. The use and interpretation of competing risks regression models. Clin Cancer Res. 2012;18:2301–2308. doi: 10.1158/1078-0432.CCR-11-2097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fine JP, Jiang H, Chappell R. On semi-competing risks data. Biometrika. 2001;88:907–919. [Google Scholar]
- 24.Lee KH, Haneuse S, Schrag D, Dominici F. Bayesian semiparametric analysis of semicompeting risks data: investigating hospital readmission after a pancreatic cancer diagnosis. J R Stat Soc Ser C Appl Stat. 2015;64:253–273. doi: 10.1111/rssc.12078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dignam JJ, Wieand K, Rathouz PJ. A missing data approach to semi-competing risks problems. Stat Med. 2007;26:837–856. doi: 10.1002/sim.2582. [DOI] [PubMed] [Google Scholar]
- 26.Peng L, Fine JP. Regression modeling of semicompeting risks data. Biometrics. 2007;63:96–108. doi: 10.1111/j.1541-0420.2006.00621.x. [DOI] [PubMed] [Google Scholar]
- 27.Putter H, Fiocco M, Geskus R. Tutorial in biostatistics: competing risks and multi-state models. Stat Med. 2007;26:2389. doi: 10.1002/sim.2712. [DOI] [PubMed] [Google Scholar]
- 28.Hsieh JÄ, Wang W, Adam Ding A. Regression analysis based on semicompeting risks data. J R Stat Soc Ser B. 2008;70:3–20. [Google Scholar]
- 29.Meira-Machado LF, de Una-Alvarez J, Cadarso-Suarez C, Andersen P. Multi-state models for the analysis of time-to-event data. Stat Methods Med Res. 2008 doi: 10.1177/0962280208092301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Xu J, Kalbfleisch JD, Tai B. Statistical analysis of illness-death processes and semicompeting risks data. Biometrics. 2010;66:716–725. doi: 10.1111/j.1541-0420.2009.01340.x. [DOI] [PubMed] [Google Scholar]
- 31.Barrett JK, Siannis F, Farewell VT. A semi-competing risks model for data with interval-censoring and informative observation: An application to the MRC cognitive function and ageing study. Stat Med. 2011;30:1–10. doi: 10.1002/sim.4071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.van den Hout A, Fox J-P, Entink RHK. Bayesian inference for an illness-death model for stroke with cognition as a latent time-dependent risk factor. Stat Methods Med Res. 2015;24:769–787. doi: 10.1177/0962280211426359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zeng D, Chen Q, Chen M-H, Ibrahim JG. Estimating treatment effects with treatment switching via semicompeting risks models: an application to a colorectal cancer study. Biometrika. 2012;99:167–184. doi: 10.1093/biomet/asr062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhang Y, Chen M-H, Ibrahim JG, Zeng D, Chen Q, Pan Z, Xue X. Bayesian gamma frailty models for survival data with semi-competing risks and treatment switching. Lifetime Data Anal. 2014;20:76–105. doi: 10.1007/s10985-013-9254-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Therneau TM, Grambsch PM. Modeling survival data: extending the Cox model. Springer Science & Business Media; 2000. [Google Scholar]
- 36.Diggle P, Heagerty P, Liang K-Y, Zeger S. Analysis of longitudinal data. Oxford University Press; 2002. [Google Scholar]
- 37.Gomez G, Lagakos SW. Statistical considerations when using a composite endpoint for comparing treatment groups. Stat Med. 2013;32:719–738. doi: 10.1002/sim.5547. [DOI] [PubMed] [Google Scholar]
- 38.Latouche A, Allignol A, Beyersmann J, Labopin M, Fine JP. A competing risks analysis should report results on all cause-specific hazards and cumulative incidence functions. J Clin Epidemiol. 2013;66:648–653. doi: 10.1016/j.jclinepi.2012.09.017. [DOI] [PubMed] [Google Scholar]
- 39.Team RC. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria, 2012. 2014 [Google Scholar]
- 40.Self SG, Liang K-Y. Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under nonstandard conditions. J Am Stat Assoc. 1987;82:605–610. [Google Scholar]
- 41.Lee KH, Dominici F, Schrag D, Haneuse S. Hierarchical models for semi-competing risks data with application to quality of end-of-life care for pancreatic cancer. J Am Stat Assoc. 2016 doi: 10.1080/01621459.2016.1164052. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Krumholz HM, Lin Z, Keenan PS, Chen J, Ross JS, Drye EE, Bernheim SM, Wang Y, Bradley EH, Han LF. Relationship between hospital readmission and mortality rates for patients hospitalized with acute myocardial infarction, heart failure, or pneumonia. JAMA. 2013;309:587–593. doi: 10.1001/jama.2013.333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Pope GC, Kautter J, Ellis RP, Ash AS, Ayanian JZ, Ingber MJ, Levy JM, Robst J. Risk adjustment of Medicare capitation payments using the CMS-HCC model. Health Care Financ Rev. 2004;25:119–141. [PMC free article] [PubMed] [Google Scholar]
- 44.Rondeau V, Mazroui Y, Gonzalez JR. frailtypack: an R package for the analysis of correlated survival data with frailty models using penalized likelihood estimation or parametrical estimation. J Stat Softw. 2012;47:1–28. [Google Scholar]
- 45.Beyersmann J, Allignol A, Schumacher M. Competing risks and multistate models with R. Springer Science & Business Media; 2011. [Google Scholar]
- 46.Ghosh D, Lin D. Marginal regression models for recurrent and terminal events. Stat Sin. 2002;12:663–688. [Google Scholar]
- 47.Kneib T, Hennerfeind A. Bayesian semi parametric multi-state models. Stat Modelling. 2008;8:169–198. [Google Scholar]
- 48.Siannis F, Farewell V, Head J. A multi-state model for joint modelling of terminal and non-terminal events with application to Whitehall II. Stat Med. 2007;26:426. doi: 10.1002/sim.2342. [DOI] [PubMed] [Google Scholar]
- 49.Lakhal L, Rivest LÄ, Abdous B. Estimating survival and association in a semicompeting risks model. Biometrics. 2008;64:180–188. doi: 10.1111/j.1541-0420.2007.00872.x. [DOI] [PubMed] [Google Scholar]
- 50.Chen Y-H. Maximum likelihood analysis of semicompeting risks data with semiparametric regression models. Lifetime Data Anal. 2012;18:36–57. doi: 10.1007/s10985-011-9202-4. [DOI] [PubMed] [Google Scholar]
- 51.Zhang JL, Rubin DB. Estimation of causal effects via principal stratification when some outcomes are truncated by death. J Educ Behav Stat. 2003;28:353–368. [Google Scholar]
- 52.Tchetgen Tchetgen EJ. Identification and estimation of survivor average causal effects. Stat Med. 2014;33:3601–3628. doi: 10.1002/sim.6181. [DOI] [PMC free article] [PubMed] [Google Scholar]