Mechanisms of small molecule–DNA interactions probed by single-molecule force spectroscopy

Abstract

There is a wide range of applications for non-covalent DNA binding ligands, and optimization of such interactions requires detailed understanding of the binding mechanisms. One important class of these ligands is that of intercalators, which bind DNA by inserting aromatic moieties between adjacent DNA base pairs. Characterizing the dynamic and equilibrium aspects of DNA-intercalator complex assembly may allow optimization of DNA binding for specific functions. Single-molecule force spectroscopy studies have recently revealed new details about the molecular mechanisms governing DNA intercalation. These studies can provide the binding kinetics and affinity as well as determining the magnitude of the double helix structural deformations during the dynamic assembly of DNA–ligand complexes. These results may in turn guide the rational design of intercalators synthesized for DNA-targeted drugs, optical probes, or integrated biological self-assembly processes. Herein, we survey the progress in experimental methods as well as the corresponding analysis framework for understanding single molecule DNA binding mechanisms. We discuss briefly minor and major groove binding ligands, and then focus on intercalators, which have been probed extensively with these methods. Conventional mono-intercalators and bis-intercalators are discussed, followed by unconventional DNA intercalation. We then consider the prospects for using these methods in optimizing conventional and unconventional DNA-intercalating small molecules.

INTRODUCTION

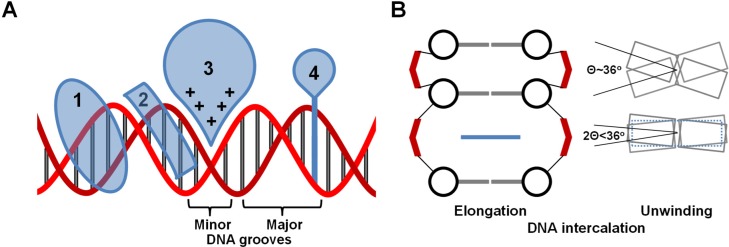
The unveiling of the self-assembled molecular structure of DNA (1–3) was shortly followed by exploring applications of DNA–ligand complexes formed by diverse binding modes such groove binding and DNA intercalation (4–8). Although non-intercalative small molecule-DNA binding modes are of interest, they are less well-studied with single molecule methods and have been previously reviewed (9). These modes will therefore be introduced briefly, followed by detailed discussion of intercalators, which can be tuned to have a wide range of specific DNA binding properties. Pioneering research by L. S. Lerman predicted (10) and confirmed (6–8) DNA–ligand intercalation, in which a planar aromatic moiety is non-covalently inserted between adjacent DNA base pairs (6–8,10–13), which stabilizes the double-stranded DNA (dsDNA) helix (14,15). The identification of intercalation as a DNA binding mode was first motivated by studying genetic transformation, potential mutagens, and to explain the DNA–acridine interaction mechanism (10,16,17), one of the early clinically used antitumor synthetic small molecule drugs (18). DNA intercalators, which can be cationic or neutral, disrupt the continuity of the encoded genome, in contrast to ligands that bind DNA electrostatically or into the major or minor grooves (12,19) (Figure 1A). Single DNA intercalation events result in DNA helix unwinding, which can exceed 50% of the native twist (11,20,21), as well as helix elongation that almost doubles the natural base pair separation (6,8,10,20,22,23) in order to accommodate the intercalating moiety (see Figure 1B). While the DNA helix unwinding that accompanies intercalation compensates for the helix extension and maximizes base-intercalator stacking, the DNA–ligand complex deformation maintains crucial aspects of the native DNA backbone structure, such as the nearly invariant distance between the adjacent phosphate groups (10,11,13,20,24). Such an invasive, yet reversible, DNA binding mode provides the basis for a wide range of applications in which DNA molecules are targeted, probed or integrated into assembly processes.

Figure 1.

(A) Schematic diagrams of different DNA binding modes: 1 is a major groove binder, 2 is a minor groove binder, 3 represents electrostatic/allosteric binding and 4 is an intercalator. The DNA backbone is in red and the base pairs in gray. (B) Diagrammatic Illustration of intercalated DNA helix elongation (left) and unwinding (right). The phosphate groups are shown in red, the deoxy sugar in black, the base pairs in gray and the intercalator in blue. The diagrams illustrate that the separation between the intercalated base pairs is nearly doubled, while more than half of the native DNA helix twist is unwound to compensate for the elongation.

There is interdisciplinary interest in DNA intercalation due to its broad range of applications. For instance, X-ray crystal structures established that DNA intercalation is a common mode of action for naturally occurring antibiotics such as Actinomycin D (ActD) and daunomycin, as well as the antimalarial drug cryptolepine (1,7,24–26). Employed in DNA-targeting antitumor therapeutics, DNA intercalators were found to act as topoisomerase II poisons, disrupt helicase activity and cause ribosomal frame-shift mutations (13,19,27,28). Consequently, both natural and synthetic DNA intercalating drugs are studied and rationally optimized for growing pharmaceutical interests (12,13,18,19,29–31). Furthermore, the optical properties associated with ‘light-switch’ synthetic intercalators upon DNA binding has become of great interest for visualization applications (31–40). In this regard, maintaining the native mechanical properties of stained DNA molecules is explored in ongoing research (23,25,41,42). The reversibility of DNA intercalation also enables a controllable mechanism for integrating DNA into synthetic biology. For example, nano-films of DNA origami loaded with intercalating drugs are demonstrated as a means of controlled release of anti-cancer agents for localized drug delivery (43). DNA intercalation was also recently utilized to dynamically modulate the parameters of a DNA-nanoparticle supper-lattice (44).

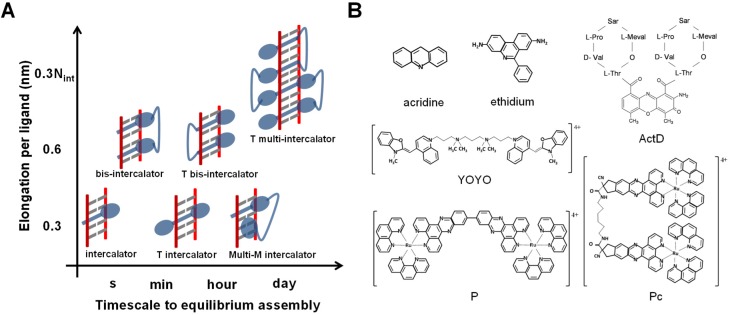
The molecular assembly of DNA intercalation can be classified according to the number of intercalating events per ligand, and the overall timescale to reach the equilibrium state as shown in Figure 2A. DNA intercalation can involve the insertion of one intercalating moiety (mono-intercalator), two intercalating moieties (bis-intercalator) or multi-intercalating moieties. Here each intercalation moiety elongates the natural DNA contour length by typical reported values of 0.2–0.4 nm (22,23,45–47). However, the timescale for reaching the final DNA–ligand intercalation state ranges over six orders of magnitude, depending on the structural deformation of the DNA that governs the intercalation complex assembly. In particular, conventional intercalators that involve direct insertion of the intercalating unit have relatively fast association kinetics that can be from milliseconds such as for DNA mono-intercalation by ethidium (48), up to seconds as observed for the bis-intercalator YOYO (49). For unconventional intercalators, which involve pre-intercalation DNA base pair threading (50,51) or groove binding accommodation (45) of non-intercalating moieties, can exhibit extremely slow kinetics that range from minutes to days (45–47,52,53). Examples for a variety of intercalators from different classifications are shown in Figure 2B.

Figure 2.

(A) DNA intercalators as classified by the number of intercalation events per ligand, elongation per ligand and typical timescale to reach the equilibrium intercalative state. The intercalators are shown in blue, the DNA backbone in red and the base pairs in gray. M stands for mode, and T for threading. (B) Examples of intercalators from different classifications.

The DNA–intercalator complex molecular self-assembly process is investigated in bulk by different experimental means. Pioneering studies used X-ray diffraction to confirm and characterize the intercalation mode of DNA-Proflavine binding (6). Another early approach employed thermal denaturation to examine DNA–acridine complexes (54). Stopped-flow techniques provided some of the first kinetics studies of DNA intercalation (55). Other bulk approaches include NMR (56), gel electrophoresis (57), fluorescence spectroscopy (33), mass spectrometry (58), and linear and circular dichroism spectroscopy (59). While providing efficiently high statistical significance, bulk studies of DNA intercalation can be constrained by several experimental and systematic challenges such as a limited range of detected concentration and uncontrolled non-intercalative molecular processes (12,46). However, single-molecule force spectroscopy enables direct and real time measurement of the progressing dynamic assembly of ligands into single B-DNA as well as non B-DNA structures such as the G-quadruplex, with precise control of the experimental conditions (60–63). Force spectroscopy determines the mechanical properties of the DNA–ligand complex, and it has outstanding sensitivity to distinguish intercalation from other binding modes. The unwinding and elongation of the DNA during an intercalation event provides mechanical signatures traceable by single molecule techniques such as atomic force microscopy (AFM) (64–66), optical tweezers (OT) (22,52,67) and magnetic tweezers (MT) (21,68). The mechanical response due to the binding of each ligand to its binding site is averaged over the total binding events accruing along the along the DNA lattice, which improves the statistical significance of the measurement. The instrumental basis of each single-molecule technique is available in related instrumental method reviews (62,69–72). Herein, we focus on surveying the recent progress in determining the equilibrium and dynamic characteristics of DNA–ligand intercalation. The review lays out the experimental data acquisition methods, the developed analysis framework, and the governing molecular mechanisms of different DNA intercalating systems. In addition to discussing the equilibrium and kinetic characteristics of conventional and unconventional intercalators, the review also covers recent progress in optimizing DNA intercalation properties for rational drug design and living cell imagining applications.

SINGLE-MOLECULE FORCE SPECTROSCOPY

In force spectroscopy experiments, a single DNA molecule is stretched and the force experienced by the molecule is measured as a function of its extension (61,62). These force-extension (F-L) curves provide insights into the elastic properties of the nucleic acid molecule. Various reversible binding modes can be characterized by observing the changes in the DNA F-L curves obtained in the presence of these reversibly binding molecules. Multiple force spectroscopy studies using OT (22,52,67) have measured the DNA binding properties of intercalators precisely. These techniques measure binding properties at the single molecule level to characterize DNA intercalating drugs. In general the DNA-drug binding properties are obtained as a function of force and extrapolated to obtain these properties in the absence of force (22).

Single-molecule DNA stretching measurements

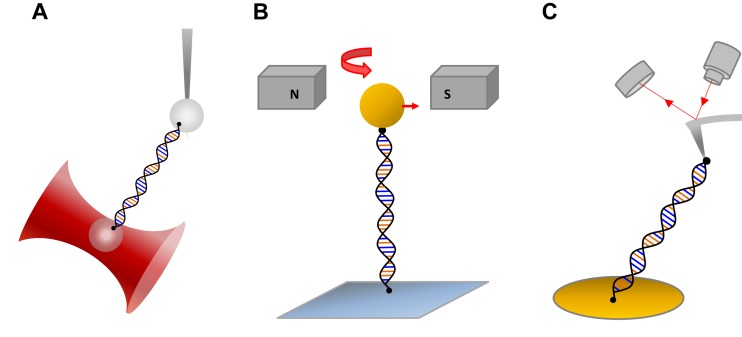
Typical OT experiments use polystyrene beads or cylinders coated with streptavidin to chemically attach a single DNA molecule that is labeled with biotin on the opposite strands (Figure 3A). The bead attachment to the opposite strands of DNA allows the DNA to freely rotate about its axis. This torsionally unconstrained DNA configuration is commonly used to investigate the DNA interactions of intercalators. The unconstrained DNA configuration relieves any torsional strain caused by the unwinding of the DNA double helix, so that only the change in DNA extension is measured. One of these beads is held by the optical trap while the other bead is held by a micropipette tip, glass plate or another optical trap that can be moved with the help of piezoelectric controls to provide stretching of DNA. When the DNA is stretched to a known extension, the bead in the trap will be displaced in proportion to the force exerted on the trapped bead by the DNA. The bead displacement causes the laser to deflect after passing through the bead. By calibrating the force as a function of laser displacement using known forces, the force exerted on the DNA is determined by measuring the laser displacement. In MT experiments a single DNA molecule is attached between the glass plate of a flow cell and a magnetic bead. The magnetic bead is then moved with the help of a moving magnet to stretch the DNA (Figure 3B). In single-molecule stretching experiments by AFM, one end of the DNA is attached to a substrate (such as mica) and the other end is attached to the tip of an AFM cantilever (Figure 3C).

Figure 3.

(A) Schematic diagram of a dual-beam optical tweezers trapping a bead while a second bead is held by a micropipette tip. (B) Schematic diagram showing DNA stretching with magnetic tweezers. (C) Diagram of DNA stretching with an AFM instrument.

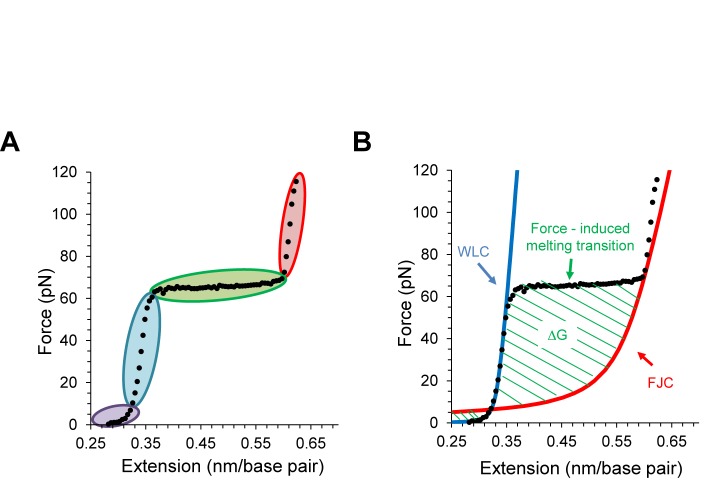
A DNA stretching curve (black data in Figure 4A) obtained with torsionally unconstrained DNA can be divided into four distinct regions (61,62). At low extensions (data shaded in violet) the DNA is stretched to its normal length with little change in the force. Since the force applied in this region is used to reduce the entropy of the DNA molecule, this region is known as the entropic stretching region. Further stretching beyond the normal DNA contour length (0.34 nm/bp at F = 30 pN) shows that the double helix behaves elastically (data shaded in blue), where a small extension results in a rapid force increase, which is known as the elastic region. Once the force reaches around F = 65 pN, the force remains almost constant while the extension is almost doubled (data shaded in green) indicating a clear phase transition. Recent experiments have confirmed that the cooperative and progressive DNA elongation during this transition is due to force induced double helix unwinding and base pair melting under many solution conditions, including low to moderate salt concentrations (73–80). At the end of the overstretching transition, most of the dsDNA is converted into ssDNA but a few GC rich regions may hold the two strands together (73–75). Stretching beyond the transition exhibits again distinct elastic properties (data in red shade). Releasing the DNA back slowly recovers the original elasticity of dsDNA, indicating that this is a reversible process, except in very low salt when melting is not reversible (76–79).

Figure 4.

(A) A typical dsDNA stretching curve showing the entropic stretching region (gray), the first elastic region (light blue), the overstretching transition (green) and the second elastic region (red). (B) Illustration of the free energy of the DNA melting transition.

Elastic properties from single-molecule DNA stretching

The dsDNA elasticity can be modeled as a homogeneous elastic rod with a smooth distribution of bending angles. The polymer model that describes dsDNA well is known as the worm-like chain (WLC) model, which effectively characterizes the end to end distance of dsDNA (L_ds) based on the contour length (L_ds,c) and persistence length (P_ds). The force dependence of the dsDNA length at high force (F) is given by an approximate solution

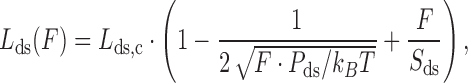(1)

where, S_ds is a stretch modulus of backbone extensibility, k_B is Boltzmann's constant and T is the temperature.

On the other hand, ssDNA is best modeled by the freely jointed chain (FJC) model. The FJC model describes a one dimensional polymer as a collection of independent segments with a characteristic length (Kuhn length) connected via freely rotating hinges with varying bond angles (81). The end to end distance of the ssDNA (L_ss) at force F can be characterized by the persistence length (P_ss) and the contour length (L_ss,c)

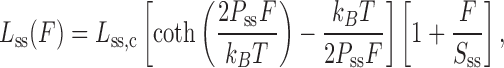(2)

where, S_ss is stretch modulus added to account for the backbone extensibility of ssDNA. Figure 4B illustrates that the dsDNA stretching data fits the WLC model (blue solid curve) before reaching the force-induced melting transition, and fits the FJC model (red solid curve) beyond the melting transition. The DNA F-L curves also provide information about the melting free energy associated with converting dsDNA to ssDNA. The area confined between the experimental data and the FJC polymer model (green striped area in Figure 4B) yields this melting free energy (76).

DNA binding modes of small molecules

Studies of small molecules, including current and potential drugs, showed that they can be classified as groove binders, intercalators, single-strand binders and multi-mode binders (4,5,9,22). The driving binding interactions can include electrostatic, hydrophobic, allosteric, hydrogen bonding and/or van der Waals interactions (4,5). Positively charged small molecules are likely to bind to DNA grooves either in the initial or final state. Most small molecules are characterized as minor groove binders, yet major groove binders have also been reported (82). In DNA stretching experiments, groove binders are found to increase the DNA overstretching transition force. For example, both distamycin-A and Methyl Green, minor and major groove binders respectively, raised the transition force, which indicates stabilization of the DNA double helix (83). In addition, major groove binders decreased DNA melting cooperativity, as indicated by a broadening of the overstretching transition force range (84). However, groove binding is often an intermediate state that leads to further binding modes in the final state, such as intercalation. For instance, Berenil is a drug that binds DNA in the minor groove at low concentration, but reportedly intercalates at higher concentrations (85). Some small molecules have even higher orders of DNA binding complexity, such as threading between the DNA base pairs before intercalation (46), or cross-linking after intercalation (86). While single-stranded DNA (ssDNA) binding is the least common binding mode, such as reported for DNA-glyoxal binding (87,88) there is an abundance of small molecule DNA intercalators. For the purpose of presenting a cohesive treatment, the following sections exclusively lay out measurements and analysis of DNA intercalation at different levels of binding complexity.

CONVENTIONAL DNA INTERCALATORS

Studies of conventional DNA mono- and bis-intercalators in bulk showed that equilibrium binding is reached on a timescale ranging from milliseconds to seconds (48,49). This fast kinetics relative to the typical timescale of DNA stretching experiments (∼10–100 s) provided the basis for examining DNA–ligand assembly in equilibrium for the first set of single-molecule observations of DNA interaction with conventional intercalators in 1996 using AFM and OT. Coury et al. used AFM (also known as scanning force microscopy SFM) images to measure single DNA molecule lengthening upon binding to ethidium, daunomycin and 2,5-bis (4-amidinophenyl) furan (APF) (64). Cluzel et al. utilized intercalators to investigate the overstretching transition observed during single molecule DNA stretching with OT (89). A saturated concentration of ethidium (∼25 μM) was used to show that the overstretching transition disappears, in an attempt to explain the overstretching transition, which was then believed to be from B form DNA to S-DNA. In 2000, Krautbauer et al. used AFM to explain how force spectroscopy can be used distinguish conventional intercalators from other binding modes like minor groove binding and cross-linking (90). Since then, measuring the extension of DNA upon binding to the intercalator has become a standard practice to quantify the binding properties of an intercalator in force spectroscopy studies. The first complete characterization of conventional intercalators using force spectroscopy was proposed by Vladescu et al. (91) by analyzing the effects on DNA stretching curves in the presence of ethidium as a function of force and concentration. This study later led to the novel quantitative method of measuring force-dependent binding properties using OT and extrapolating them to the zero-force values (22,92). In 2010, Lipfert et al. brought MT into studying intercalators under applied force. By examining torsionally constrained DNA, they characterized the double helix twist due to DNA unwinding upon binding to intercalators by measuring the rotation angles between the successive base pairs upon binding to ethidium (21).

Qualitative effects observed with conventional intercalators

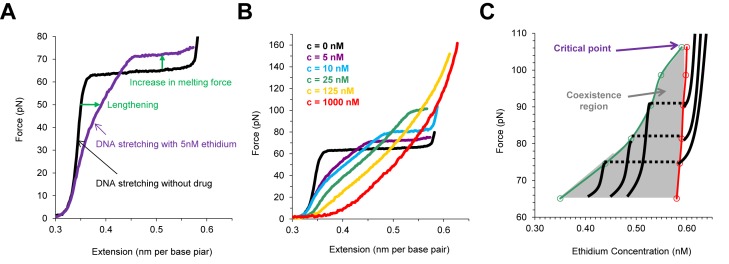
In all force spectroscopy experiments DNA lengthening is observed upon intercalator binding to dsDNA. In addition, stabilization of dsDNA structure upon intercalation is represented in the force extension curves by an increase in the melting force in the presence of the intercalator (Figure 5A). Combining the above two effects as we progressively increase intercalator concentration, the melting transition plateau progressively becomes shorter and disappears (Figure 5B). Beyond some critical concentration, the lengthening of dsDNA upon binding to intercalator makes the dsDNA–drug complex indistinguishable from ssDNA (Figure 5B). In comparison to the classical thermodynamic example of a liquid to gas phase transition at constant temperature, a critical point is observed in the dsDNA to ssDNA phase transition at a particular ligand concentration. As we increase the intercalator concentration, at some critical concentration we do not observe a phase transition, and we cannot distinguish between the intercalator-bound dsDNA and ssDNA, the same way we cannot distinguish between gas and liquid beyond the critical temperature. The phase diagram for ethidium (Figure 5C) can be mapped to show the similarity with the classical PVT phase diagrams of gaseous systems (91).

Figure 5.

Characterizing DNA melting transition in the presence of ethidium, adapted from (78). (A) dsDNA elongation and stabilization due to intercalation by ethidium. (B) The DNA overstretching transition plateau becomes shorter and vanishes at high concentrations of ethidium. (C) The phase diagram due to DNA intercalation by ethidium.

Quantifying the DNA binding properties of intercalators

The binding of intercalators to DNA at a particular force can be quantified by the fractional lengthening observed. The fractional lengthening directly corresponds to the fractional ligand binding 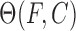associated with that concentration at a particular force, and is given by the ratio between the lengthening observed due to the binding of the intercalator at that concentration ΔL_eq(F,C) compared to the lengthening observed at saturated concentration :

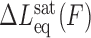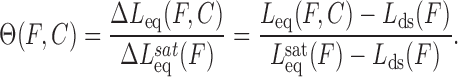(3)

Here L_eq(F,C) is the equilibrium extension observed with the drug-DNA complex at drug concentration C and at a particular force F, 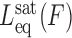is the extension of the drug-DNA complex at saturated drug concentration, and L_ds(F) is the extension of the dsDNA in the absence of drug. The experimentally obtained fractional binding measurements described above can be fit to a simple binding isotherm, an approximate binding isotherm model, or the McGhee–von Hippel (MH) binding isotherm (23,45,91). The MH non-cooperative binding isotherm accounts for the effect of neighbor exclusion and has been used as a standard binding isotherm in single-molecule DNA intercalation studies. By fitting to the MH binding isotherm (as shown in Figure 6A for DNA intercalation by ethidium), we obtain the equilibrium binding constant K(F) (or alternatively the equilibrium dissociation constant K_d(F) = 1/ K(F)) and the binding site size (n). The MH isotherm is described by:

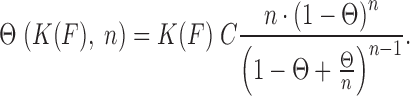(4)

Figure 6.

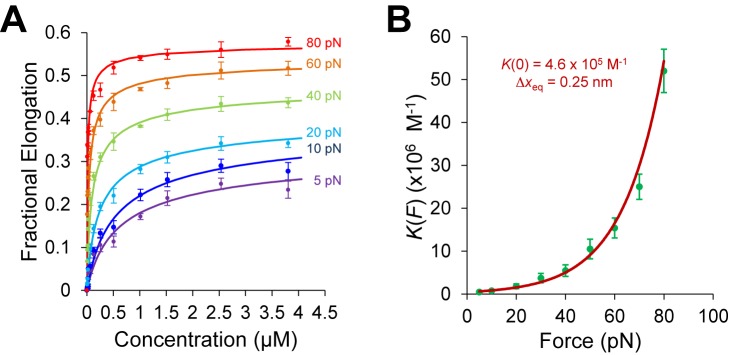
Determining DNA intercalation affinity and binding site size for ethidium, adapted from (19). (A) McGhee–von Hippel (MH) binding isotherm fits (Equation (4)) for the fractional DNA elongation as a function of ethidium concentration at each stretching force. (B) Fit of the ethidium binding constant K(F) to the exponential dependence on force (Equation (5)).

Although the binding constant obtained using this isotherm agreed well with bulk experiments, the binding site size of ethidium at high force appears to violate nearest neighbor exclusion expected for DNA intercalation (see Table 1). Due to the sugar puckering of the backbone that occurs with intercalation of ethidium, it was found to bind every other site and was reported to have a binding site size of 2 in the absence of applied force. This constraint seems to be relieved by high forces in single-molecule experiments. Stretching the backbone of DNA to nearly twice its length may enable the ethidium to bind to every available binding site, yielding n <2. This method was also used to find the binding constants and the binding site sizes (Table 1) for ruthenium complexes [Ru(phen)₃]²⁺, [Ru(bpy)₂dppz]²⁺ [Ru(phen)₂dppz]²⁺ and [Ru(phen)₂dppx]²⁺ using with AFM and OT (92). Note that the fractional ligand binding per binding site υ = Θ/n is sometimes alternatively used in fitting the MH isotherm (22).

Table 1. Binding constant (K), binding site size (n), lengthening upon single intercalation (x_eq) and twist between successive base pairs upon intercalation obtained from various force spectroscopy experiments (atomic force microscopy (or scanning force microscopy), magnetic tweezers, optical tweezers).

Intercalator	Binding constant K (x 10−6 M−1)	Binding site size n (base pairs)	Binding equilibrium elongation Δxeq (nm/bp)
Ethidium	0.036 ± 0.005a	2.01a
	10b	2b
	0.46 ± 0.05d	2.3 ± 0.1d	0.25 ± 0.03d
	0.13 ± 0.04f	1.9 ± 0.1f
	0.145g
Daunomycin	0.066 ± 0.024a	3.04a	-
AFP	2.48a	2a	-
[Ru(phen)3]2+	0.0088 ± 0.0003c	3.0 ± 0.2c
	e0.0016 ± 0.0002	e3.0 ± 0.1	0.28 ± 0.01d
[Ru(phen)2dppz]2+	0.15 ± 0.07c	2.2 ± 0.4c
	3.2 ± 0.1 (10 pN)c	3.0 ± 0.5 (10 pN)c
	0.90 ± 0.10d	e2.9 ± 0.1d	0.38 ± 0.02d
[Ru(bpy)2dppz]2+	0.15 ± 0.07c	2.2 ± 0.4c	-
	3.2 ± 0.1 (10 pN)c	3.0 ± 0.5 (10 pN)c
Oxazole Yellow (YO)	0.578 ± 0.080e		0.233 ± 0.013e
	0.29 ± 0.09i	3.8 ± 1.0i	0.31 ± 0.03i
Psoralen	0.088 ± 0.024h	1.43 ± 0.13h	-
SYTOX Orange (SxO)	2.4 ± 0.5i	3.0 ± 0.4i	0.30 ± 0.02i
SYTOX Green (SxG)	14 ± 3i	2.6 ± 0.6i	0.27 ± 0.02i
SGold (SbG)	7.8 ± 3.3i	3.2 ± 0.5i	0.30 ± 0.01i

^a(64)

^b(5)

^c(92)

^d(22)

^e(93)

^f(21)

^g(94)

^h(112)

ⁱ(23)

The determined binding constant K(F) and binding site size n are force-dependent and further analysis is required to obtain the zero-force binding properties (Figure 6B). The binding constant at various forces for ethidium- and ruthenium-based intercalators [Ru(phen)₃]²⁺ and [Ru(phen)₂dppz]²⁺ showed a clear exponential dependence on force (22). Vladescu et al. demonstrated that the binding constant in the absence of the force K(F) can be determined from the exponential dependence on force

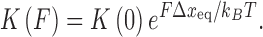(5)

The term FΔx_eq in the exponential component is the shift in the zero-force free energy of DNA intercalation as the force facilitates the required double helix equilibrium elongation Δx_eq for each ligand to reach the intercalation equilibrium state. A complete analysis using this method to determine the zero force binding constant K(0) and the lengthening upon forming a DNA–ligand intercalation complex, Δx_eq, for the intercalators ethidium (22), [Ru (phen)₃]²⁺ (22), [Ru (phen)₂dppz]²⁺ (22) and YO (93), are shown in Table 1. The measurements of the zero force binding constant as a function of salt concentration showed a significant decrease in the binding affinity with increased salt concentration (23). A similar approach was made with MT by Celedon et al. to quantify the torque dependence of ethidium binding constant (94). The torque or twisting of the DNA disfavors the binding of an Intercalator and it is given by,

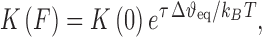(6)

where τ is the applied torque and 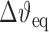is the change in twist upon intercalation.

Elastic properties of saturated DNA-intercalator complexes

Fitting the F-L curves obtained in the presence of intercalators to the WLC model yields the contour length , the effective persistence length P and elastic modulus S of the DNA-intercalator complex:

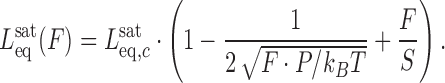(7)

All experimental measurements of the DNA contour length in the presence of the intercalators have supported the monotonic increase in contour length with intercalator concentration until it reaches the saturation value (22,93,95).The contour length from the saturated DNA-intercalator complex 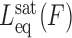and the equilibrium elongation per ligand Δx_eq provides a complementary estimate of the binding site size n:

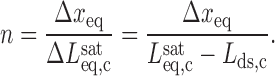(8)

By combining Equations ((3)) and ((4)), we obtain the DNA-intercalator complex extension as a function of the applied stretching force at each ligand concentration,

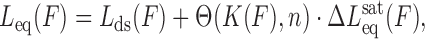(9)

Then we substitute Equations ((7)) and ((8)) to obtain:

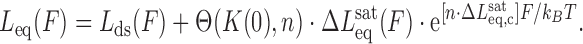(10)

This alternative approach allows fitting the force-dependent DNA equilibrium extension at each constant ligand concentration to estimate the zero-force binding constant and binding site size. The general trend for the effective persistence length in saturated concentrations of intercalators is that P decreased compared to the dsDNA value (22,93–95). OT experiments showed that the elastic modulus is reduced to almost one fourth of bare DNA upon binding to intercalators (22,93) and MT experiments showed that the twist stiffness is also reduced to almost one third of the bare DNA twist stiffness (94). Some OT experiments at low force (<2 pN) showed that the persistence length increases upon binding to intercalators and increases with concentration until a critical value and then drops below the DNA persistence length to give the general trend seen in other studies, but only above the critical concentration (95).

Studying the binding kinetics of conventional intercalators

In regard to the binding kinetics, many conventional intercalators have rapid association rates that can be as fast as microseconds, which is challenging to measure in single molecule force spectroscopy experiments. However, recent experiments by Biebricher et.al examined the kinetics of conventional mono- and bis-intercalators by employing OT aided by detection of fluorescence upon DNA intercalation (23). The investigated ligands yielded fast association rates for the mono-intercalators ranging from ∼2 × 10⁵ M^-1s^-1 for SYTOX Orange to ∼3 × 10⁷ M^-1s^-1 for YO-PRO-1 (YO), at different salt concentrations. The bis-intercalators such as POPO-3 (POPO) exhibited slower association rates (∼10⁴-10⁵ M^-1s^-1) (23). As single-molecule techniques are steadily improving in time resolution, it is expected that these experiments will be able to explore the kinetics from elongation measurements with a sub-second association timescale. Meanwhile, the kinetics investigations for slower unconventional intercalators are providing a general analysis framework, which can be in principle used for fast intercalating ligands. The additional ability to monitor intercalation optically may also provide significant new information of binding modes, given that fluorescence may be used to also detect modes that do not lengthen the DNA. Such studies may also be able to identify sequence-specific binding events.

UNCONVENTIONAL DNA INTERCALATORS

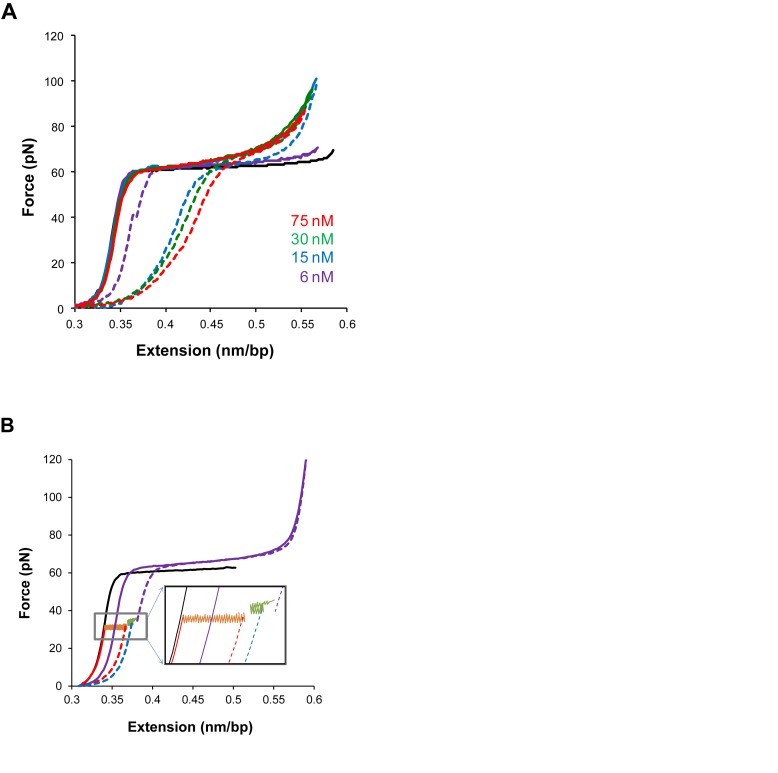
In experimental terms, unconventional intercalators often exhibit DNA–ligand kinetics slower than typical single DNA molecule stretching rates (42,45–47,52,96). The slow association/dissociation kinetics results in considerable hysteresis between the F-L curves in a cycle of stretching the DNA molecule to a higher force and then releasing the DNA back to the initial extension (45,46,96). The irreversible F-L curves indicate non-equilibrium measurements and can be explained based on force-facilitated DNA intercalation. The observed hysteresis may indicate that the DNA-intercalator complex extension is first underestimated as stretching forward to higher forces due to the ligand associating slower than the pulling rate, then overestimated as receding to lower forces due to the ligand dissociating slower than the relaxation rates (Figure 7A) (46). Paramanathan et al. demonstrated for ActD that the DNA–ligand equilibrium elongation is indeed larger than the stretching extension and smaller than relaxation extension (45). First, the DNA stretching proceeded until an assigned force, then a force-feedback maintained the applied force while tracing DNA elongation. Similar force-clamp experiments are done but initiated when the DNA–ActD complex extensions are relaxed from higher forces to the assigned lower force. The data showed that the DNA-intercalator elongation converged to similar equilibrium extension values (Figure 7B). In principle, a DNA pulling rate slower than the intercalation kinetics would produce a reversible stretching-releasing cycle. In this regard, Kleimann et al, investigating DNA-Triostin A intercalation, showed slowing the pulling rate reduced the hysteresis in the stretching-releasing cycle (96).

Figure 7.

The slow kinetics of unconventional DNA intercalation, from (45). (A) Stretch-release cycles of the DNA–ActD complex show considerable hysteresis between the stretch (solid lines) and release (dashed lines) parts of the cycle, indicating non-equilibrium measurements. (B) Measurements illustrating the slow kinetics of unconventional DNA intercalation and showing how constant force measurements ensure that DNA equilibrium elongation is reached.

The slow kinetics observed for unconventional DNA intercalators may arise from DNA structural accommodation of a non-intercalative moiety required for reaching the intercalative equilibrium state. For instance, some naturally derived antibiotics such as ActD, Triostin A and Thiocoraline, which are all neutral polypeptides, have been demonstrated by single-molecule force spectroscopy to unconventionally intercalate DNA (42,45,96). Crystal structures showed strong DNA unwinding in order to fit their linked/separate bicyclic peptide chains into the DNA groove before inserting the intercalating moieties (7,97,98). Further structural deformations such as DNA bending and base pair flipping are also reported (45). Another category of unconventional DNA intercalators is composed of complexes that have intercalating moieties engulfed in between non-intercalating moieties. This molecular design requires the non-intercalating moiety to thread through the DNA helix in order to bring the planar intercalating moiety in proximity of the base pairs (46). One of the early examples for such unusual molecular assembly was first reported for Nogalamycin, an anthracycline antibiotic, which has a dumbbell molecular structure composed of the intercalating chromophore in the middle between two bulky sugar substituents (99). Later, synthetic complexes of mono, bis and mullti-threading intercalators were demonstrated (50,51,53). In particular, DNA threading intercalation was recently characterized by single-molecule force spectroscopy for binuclear ruthenium complexes such as the mono-intercalator Δ,Δ-[μ-bidppz(phen)⁴Ru₂]⁴⁺ (Δ,Δ-P), and the bis-intercalator Δ,Δ-[μ-C4(cpdppz)₂(phen)₄Ru₂]⁴⁺ (Δ,Δ-Pc) (46,47).

Equilibrium elongation measurements

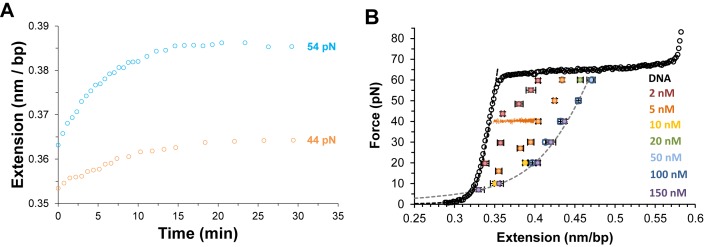
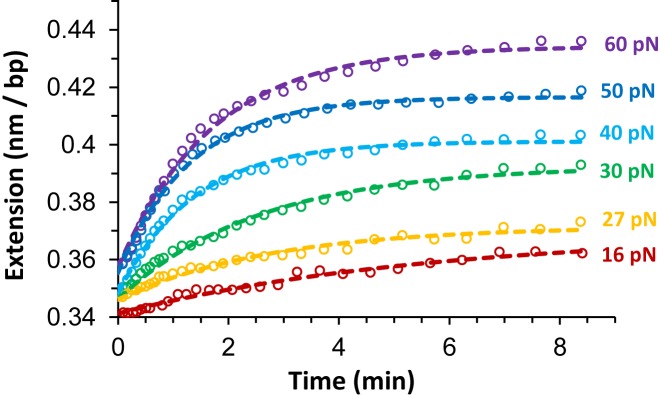
In essence, equivalent equilibrium binding isotherm analyses are used for all DNA intercalators. However, the slowly equilibrating DNA elongation of unconventional intercalators requires a revised experimental approach rather than a typical single-molecule stretch and release cycle. In order to apply the equilibrium analysis, each F-L data point is obtained at a given ligand concentration by conducting force clamp measurements on a single DNA molecule. In the typical single-molecule force clamp approach, the applied DNA stretching force (F) is maintained constant by force feedback control within a force resolution of ±1 pN, while the single DNA molecule elongates from the ligand-free DNA extension L_ds (F) until reaching an equilibrium extension L_eq(F,C), where the DNA–ligand complex extension becomes essentially time-invariant (see Figure 8A). The average data points for force clamp measurements at a range of constant forces and ligand concentrations is shown for DNA threading intercalation by Δ,Δ-P in Figure 8B (46). For each force, measurements are obtained at higher concentrations until no additional elongation is observed, demonstrating saturated extension .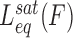

Figure 8.

(A) The time-dependent DNA extension as a function of time (open circles) for DNA in the presence of 2 nM Δ,Δ-P at constant applied forces as color coded, adapted from (49). (B) Average measurements of at least three DNA–ΔΔ-P complex equilibrium extensions for a range of constant forces between 7 and 60 pN at ligand concentrations of 2–150 nM as color coded. Dashed lines are fits of the DNA–ligand complex equilibrium extensions to the WLC model. Experiments were conducted at 21°C (10 mM Tris buffer, 100 mM NaCl, pH 8), adapted from (43).

Once the equilibrium intercalated DNA extension measurements are obtained, the equilibrium analysis proceeds in the same manner as was established for the conventional intercalators. All equilibrium properties are similarly provided from fitting 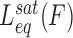data points to the WLC model (Equation (7)) to determine the DNA–ligand complex elasticity and fitting L_eq(F,C) for each applied force to a binding isotherm, such as the MH model (Equation (4)). This yields the force-dependent affinity and allows determination of the zero-force affinity and the equilibrium DNA deformation in the intercalative state from the exponential dependence on force (Equation (5)). Alternative to the force clamp approach detailed here, equilibrium F-L data points can be also acquired by force decay measurements. In this experimental approach, the tethered DNA molecule is stretched to an assigned extension and the applied tension is allowed to relax back by intercalated DNA elongation to an equilibrium force at a given ligand concentration (49). Furthermore, a force-jump approach is also used, in which a force-clamp is initially used to obtain at force F1 the equilibrium extension L_eq(F1,C), then jumping to a higher force F2 determines L_eq(F2,C). Note that in this last approach, only the first measured L_eq(F1,C) starts from the free DNA extension, which may be needed for investigating the kinetics of the approach to equilibrium.

One-step DNA intercalation kinetics

Measuring time-dependent non-equilibrium DNA elongation reveals significant characteristics of DNA intercalation complex assembly. The dynamic structural deformations and the governing energy landscape of DNA–ligand formation are derived from the force-dependent kinetics. In the force clamp experimental approach, most unconventional mono-intercalators show single-rate exponential dependence during DNA–ligand association. The single exponential time-dependence is indicative of a two-state molecular transition, from the non-intercalative DNA state (NI) to the intercalated DNA state (I):

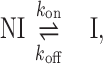(11)

Note that k_on is the forward rate resulting from the product k_aC, where k_a is the bimolecular association rate constant and k_off is the unimolecular reverse rate. At constant DNA stretching force and ligand concentration, the time dependent non-equilibrium DNA extension L(t) is fitted by:

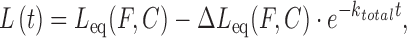(12)

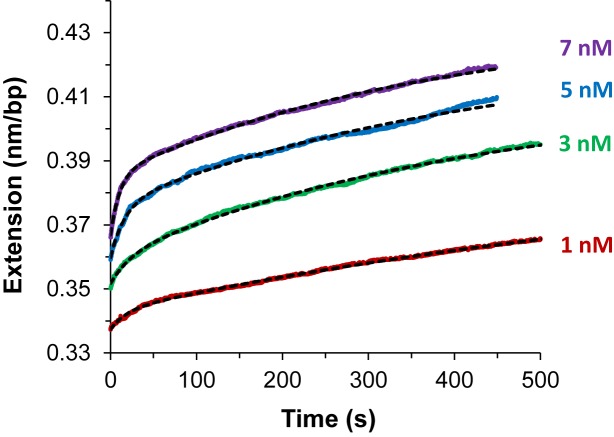
yielding L_eq(F,C), which is used in the previous equilibrium analysis, the net relaxation rate and 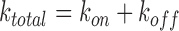, which provides the following kinetics analysis. Figure 9 shows fits for DNA threading intercalation by Δ,Δ-P for applied forces 16–60 pN at 5 nM ligand concentration (46).

Figure 9.

The time-dependent extension as a function of time (open circles) for DNA in the presence of 5 nM Δ,Δ-P at several constant forces. The dashed lines are fits to the single exponential dependence shown in Equation ((12)). Experiments were conducted at 21°C (10 mM Tris buffer, 100 mM NaCl, pH 8), from (43).

Introduced by Paramanathan et al, the force-dependent k_total (F) from fits to Equation (12) and K_d(F) from fits to Equation ((4)), provide the force-dependent forward rate k_on(F) and reverse rate k_off(F):

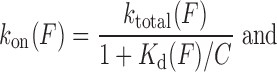(13)

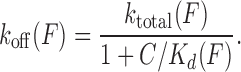(14)

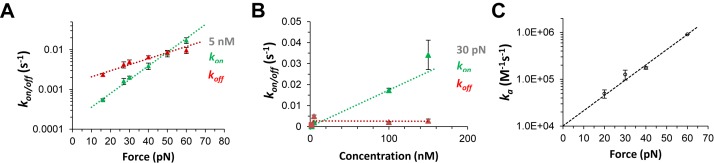
Following the established exponential dependence on force, k_on(F) and k_off(F) values are determined at each concentration, as shown in Figure 10A, to obtain the zero-force rates, k_on/off(0) and the dynamic DNA deformations for the forward intercalative transition x_on and the reverse intercalative transition x_off, respectively:

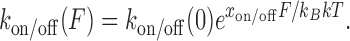(15)

The forward rates at each force k_on(F, C) = k_a(F)C, are fit to a linear concentration dependence (see Figure 10B) to determine the force-dependent k_a(F), and the exponential force dependence provides the zero-force bimolecular association rate k_a(0) (Figure 10C) (45,46).

Figure 10.

Kinetics analysis for single transition DNA threading intercalation, from (43). (A) The on rates (k_on, green data points) and off rates (k_off, red data points) at Δ,Δ-P concentration of 5 nM fitted to a single exponential dependence on force (dotted lines) to obtain the distances related to the on and off transitions. (B) The on rates (k_on) and off rates (k_off) as a function of concentration at 30 pN force, and the dotted lines are linear fits. (C) The association rates k_a(F) (data points) for forces from 20 to 60 pN fitted to the exponential force-dependence (dashed line), yielding the zero-force association rate and the length change required for ligand association.

The kinetics analysis is useful only after determining at least two of the following quantities K_eq(F), k_total(F) and k_off(F). The reverse intercalative rate k_off(F) is found to be measureable for some single-transition DNA intercalation complexes by rinsing the ligand out after initially allowing it to bind, as long as the intercalator dissociates into the ligand-free solution from the NI state significantly faster than k_a(F). For the ‘wash off’ experiments, a force clamp is applied while tracing the DNA-intercalator complex extension back to the ligand-free DNA extension. The traced extension at constant stretching force is fit to a single exponential time dependence by replacing (L_eq, −ΔL_eq, k_total) in Equation ((12)) with (L_ds, +ΔL_eq, k_off). The single transition rate that is consistently measured by single-molecule force spectroscopy for most DNA intercalators is in contrast to multiple rates reported in bulk measurements (33). This is possibly attributed in part to significant constraining of DNA–DNA contacts in single molecule experiments, which prevents competitive non-intercalative molecular transitions such as DNA–ligand aggregation. Some bulk methods may also measure rates that involve external biding kinetics and non-intercalative ligand accommodation in the DNA grooves. However, single molecule experiments are only sensitive to intercalative binding, which increases DNA length, allowing isolation of intercalation from other effects.

Two-step DNA intercalation kinetics

In contrast to the single-step DNA intercalation model, two distinctive fast and slow rates are observed by single-molecule studies for some unconventional bis-intercalators, such as the polypeptide bis-intercalator Thiocoraline and the threading bis-intercalator Δ,Δ-Pc (42,47). In a recent study of the threading bis-intercalator Δ,Δ-Pc, Bahira et al. (47) provided a comprehensive characterization of two intercalative molecular transitions, a fast first transition from the non-intercalative state NI to an intermediate intercalative state I^‡, then a slow second transition to the final intercalative state I:

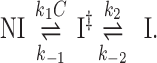(16)

The first molecular transition has rapid forward (k₁C) and reverse (k_-1) rates, and the second transition involves a slow unimolecular threading intercalation step with forward (k₂) and reverse (k_-2) rates. Based on the assumption that the NI and I^‡ states rapidly equilibrate before the second transition is initiated (k₁C + k_-1>> k₂+ k_-2), we can relate the measured fast and slow rates to the elementary association rates.

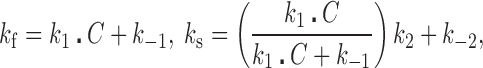(17)

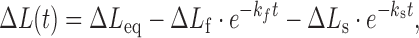(18)

The fast and slow rates are experimentally obtained from fitting the time-dependent DNA elongation ΔL(t) to Equation ((18)) (see Figure 11), where the DNA elongation due to the fast, slow and total binding are ΔL_f, ΔL_s and ΔL_eq respectively. The elementary association rates k₁ and k₂, as well as the reverse rates k-₁ and k-₂, are determined by fits to the concentration dependence in (Equation (17)) for k_f and k_s values at each applied force, as illustrated in Figure 12A (47). The obtained elementary rates for Δ,Δ-Pc validate the kinetics assumption discussed above, with the first rate at least an order of magnitude faster than the second rate. Once the force-dependent elementary rates are obtained, the exponential force dependence provides the zero-force fundamental rates and the dynamic DNA deformations (x_+i, x-_i) for each intercalative transition (see Figure 12B) (47).

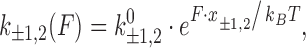(19)

Figure 11.

Δ,Δ-Pc intercalation kinetics for increasing ligand concentrations of 1, 3, 5 and 7 nM (red, green, blue and purple) when held at a force of 20 pN, adapted from (44). Fits (dashed black lines) are to Equation (18).

Figure 12.

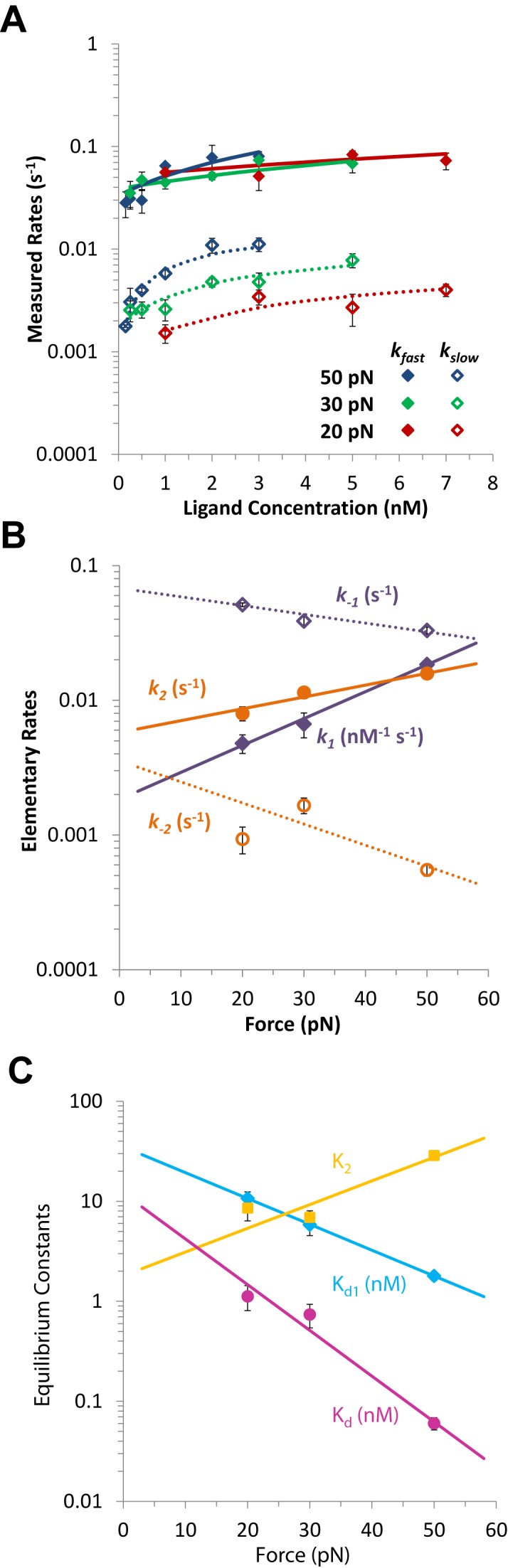
Kinetics of Δ,Δ-Pc binding to dsDNA, from (44). (A) Measured fast and slow rates versus concentration of Δ,Δ-Pc at three forces: 20, 30 and 50 pN (red, green and blue). Data points are rates k_f and k_s obtained by fitting the length versus time for the Δ,Δ-Pc/DNA complex to Equation ((18)). Lines are the results of fits to Equation ((17)) (solid line fits for k_f and dotted lines fits for k_s) which determine the elementary rates of the two-step reaction. (B) Fitted values of elementary rates for two-step intercalation, giving the forward rates k₁ and k₂ (solid purple and orange symbols) and reverse rates k_-1 and k_-2 (open purple and orange symbols). Lines represent fits to Equation ((19)), and give the force-independent elementary rates and transition distances. Fitted parameters are shown in Table 3. (C) Force-dependent binding constants for each step K_d1 (cyan) and K₂ (gold) and for overall binding K_d (magenta), determined from the elementary rates. Lines denote fits to the exponential force dependence, which give the zero-force binding constants and equilibrium length changes.

From (x_+i, x-_i), the net DNA deformation can be determined for each transition x_i = x_+i - x-_i, then the total DNA deformation Δx_total= x₁+ x₂ resulting from both molecular transitions. Furthermore, the elementary rates determine the equilibrium dissociation constant K_d(F) as well as the dissociation constants of the first transition K_d1(F) and the second transition K₂(F). The force-dependent dissociation constants are fitted similar to the exponential dependence on force to estimate the zero-force dissociation constants and the related DNA deformations, as shown in Figure 12C (47).

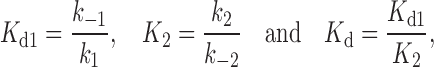(20)

After reaching the threading intercalation equilibrium state, Δ,Δ-Pc showed no significant dissociation by rinsing the ligand out of solution in force clamp measurements conducted over tens of minutes. It is possible that the flexible molecular structure of Δ,Δ-Pc and the strong positive charge may still enable stable electrostatic binding, as observed for some dsDNA binding proteins (100,101). Alternatively, this effect may also be due to the fact that simultaneous dissociation from both states is quite improbable in ligand-free solution (102). For the polypeptide bis-intercalator Thiocoraline, Camunas-Soler et al. obtained the dissociation rates from force clamp measurements in scavenger DNA solution (42). The measured time-dependent dissociation ΔL(t) also exhibited fast and slow rates indicative of a three-state model. Instead of the four elementary rates, the DNA-Thiocoraline double-transition intercalation is approximated to have three elementary rates, assuming identical reverse rates k_-1 = k_-2 for both intercalative transitions (42). This simplification holds as long that the second intercalation event is not exclusively coupled with DNA structural accommodation of the non-intercalating bicyclic polypeptide.

Equilibrium characteristics, kinetics and structural dynamics for unconventional intercalators

There are a few examples of unconventional intercalators investigated by single-molecule force spectroscopy (42,45–47,52,96). The available studies confirm distinct DNA intercalation properties in comparison with conventional intercalators. Table 2 shows the equilibrium parameters for all reported unconventional intercalators, including three neutral polypeptide intercalators and two cationic binuclear ruthenium threading intercalators. The ligands exhibit high DNA intercalation affinity, with K_d(F) ranging from ∼2 μM to ∼0.1 μM for polypeptide intercalators (42,45,96), and from 50 nM to 15 nM for binuclear ruthenium threading intercalators (46,47). The DNA–ligand complex persistence length is substantially reduced to values between 2 nm for Δ,Δ-P to 10 nm for ActD, indicating strongly enhanced stacking interactions with base pairs relative to conventional intercalators. Furthermore, the intercalative site size at F ≤ 10 pN is reported to be between 3 and 4 bp per ligand, consistent with an excluded neighboring base pair. It is also notable that the DNA equilibrium deformation Δx_eq is minimized for unconventional intercalators, with DNA elongation per ligand less than 0.5 nm for bis-intercalators and ∼0.2 nm for mono-intercalators. For ActD and Δ,Δ-P, this Δx_eq is coupled with base pair flipping in reported crystal structures (45,51).

Table 2. DNA intercalation equilibrium parameters for unconventional intercalators investigated by single-molecule force spectroscopy.

Equilibrium parameter	(Δ,Δ-Pc)4+	(Δ,Δ-P)4+	Thiocoraline	ActD	Triostin A
Kd(0) (nM)	15 ± 6	44 ± 2	77 ± 14a	1200 ± 500	1700 ± 0.002
Δxeq (nm)	0.44 ± 0.04	0.19 ± 0.01	0.41 ± 0.01	0.20 ± 0.01	0.32 ± 0.01
Persistence length, P (nm)	3 ± 1	2 ± 0.2	8 ± 1	10 ± 3
Elastic modulus, S (pN)	800 ± 50	598 ± 30	745 ± 320	320 ± 20
Intercalative site size n (bp)	3.2 ± 0.3b	3.7 ± 0.1, (10 pN)	3.8 ± 0.1, (2 pN)	3.8 ± 0.1	3.8 ± 0.1, (10 pN)

Non-zero force values are specified, where value (a) is K_d(F = 2 pN) and value (b) is determined by Equation (8) from reported quantities.

However, the major distinct characteristic of unconventional intercalation is the slow kinetics due to the strong dynamic DNA deformation required for assembly and/or disassembly of the DNA–ligand complex. Table 3 shows kinetic parameters obtained by the outlined analysis for single and double-transition DNA intercalation. It shows typical ∼10⁻³ s⁻¹ dissociation rates from the final equilibrium state, which is at least three orders of magnitude slower than conventional intercalators. The association rates from the non-intercalative state range over three orders of magnitude from 10³ M⁻¹s⁻¹ to 10⁶ M⁻¹s⁻¹. The single-step DNA intercalation by ActD and Δ,Δ-P show DNA deformation is relaxed to significantly smaller elongation in the equilibrium after larger x_on, referred to as a lock mechanism. For double-step DNA intercalation by Δ,Δ-Pc, the threading transition from the intermediate intercalative state does not show a lock mechanism but rather gradual DNA deformation, leading to minimal DNA deformation required for the forward transition from the intermediate state to the final equilibrium state (Table 3) (47). Furthermore, the dissociation rates are slowed by force, as indicated by the negative sign of the DNA deformation lengths x_-1 and x_-2, in contrast to force-facilitated dissociation in the intercalative lock mechanism. It is important to note that while the forward intercalative transitions are strongly or mildly facilitated by force for the examined DNA intercalators, the force-dependence of the reverse transitions are reportedly diverse, including strong to nominal facilitation as well as strong to nominal inhibition of dissociation rates.

Table 3. DNA intercalation kinetics parameters for unconventional intercalators investigated by single-molecule force spectroscopy.

Complex	Single-step DNA intercalation
	xon (nm)		xoff (nm)		ka(0) (M−1s−1) × 104		koff(0) (s−1) × 10−3
ActD	0.33 ± 0.02		0.11 ± 0.01		0.1(±0.02)		1.0(±0.2)
(Δ,Δ-P)4+	0.33 ± 0.02		0.14 ± 0.01		1 (±0.01)		1.4(±0.1)
	Double-step DNA intercalation
	x+1 (nm)	x+2 (nm)	x−1 (nm)	x−2 (nm)	k+1(0) (M−1s−1) × 106	k+2(0) (s−1) × 10−3	k−1(0) (s−1) × 10−3	k−2(0) (s−1) × 10−3
(Δ,Δ-Pc)4+	0.19 ± 0.02	0.08 ± 0.01	−0.06 ± 0.01	−0.15 ± 0.03	1.8 ± 0.4	5.8 ± 1.0	68 ± 4	3.6 ± 1.0

The dynamic DNA deformations can be coupled with the corresponding transition free energy to approximate the energy landscape of DNA–ligand intercalation. The free energy barriers can be determined by the association rates relative to a reference free energy ΔG₀ ∼ k_BT·ln(1 M⁻¹s⁻¹/k₀), where k₀ is a reference attempt rate. At C = K_d, the probability of the forward and reverse transitions are equal and the non-intercalative state and the final intercalative state are at the equal free energy of ΔG₀. In the case of the three state model, the difference in free energy between the intermediate and final states is k_BT^.ln(K₂) (see Equation (20) for K₂). From the forward transition rates 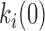, each transition free energy barrier is given by 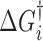∼ k_BT^.ln(k₀/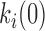.C). Setting the reference attempt rate to 1 M⁻¹s⁻¹ conveniently gives ΔG₀ ∼ 0. DNA intercalation energy landscapes are illustrated for single-step intercalation (Δ,Δ-P and ActD) in Figure 13A and for double-step intercalation (Δ,Δ-Pc) in Figure 13B utilizing this simplification.

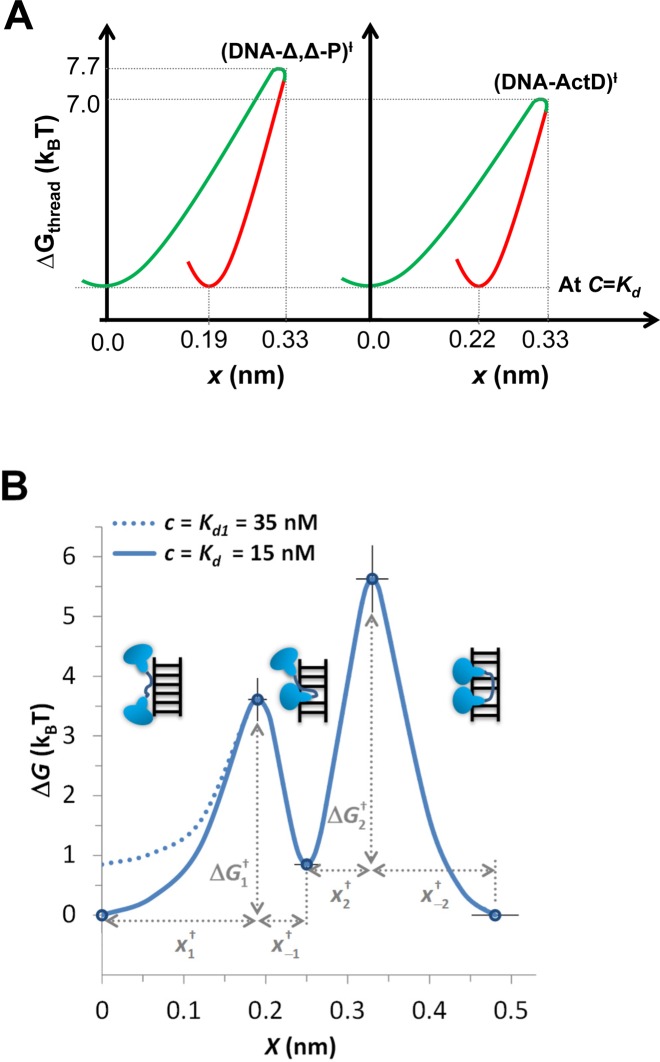
Figure 13.

(A) Comparing the free energy landscape of Δ,Δ-P and ActD upon intercalating DNA at C = K_d(0) (K_d(0) = 44 nM for Δ,Δ-P, and K_d(0)∼1 μM for ActD). The diagram illustrates the shared lock mechanism, in which the DNA helix deformation relaxes to smaller elongation in the equilibrium state. (B) Zero-force free energy profile of the DNA/Δ,Δ-Pc complex versus elongation, from (44). The three free-energy minima on this diagram correspond to the non-intercalated, mono-intercalated and bis-intercalated states illustrated in the figure. At the Δ,Δ-Pc concentration of C = K_d= 15 nM, the free energy of the non-intercalated and bis-intercalated states are the same and are taken here as the zero free energy reference state. At higher C = K_d1 = 35 nM the free energies of the non-intercalated and the mono-intercalated states are the same, and equal to k_BT^.ln(K₂) = k_BT^.ln(35/15) = 0.85 k_BT. Only the non-intercalated state free energy is affected by C, as illustrated by the two lines (solid line for 15 nM and dashed line for 35 nM).

The advantage of the energy landscape representation is the ability to illustrate the essential dynamic properties that govern the intercalative transition pathways. For example, even though ActD has an order of magnitude slower association rate than Δ,Δ-P, Figure 13A shows that the heights of the transition barriers are almost equivalent as determined at C = K_d of each ligand. Similarly, the DNA–ligand complexes relax from the transition DNA deformation to a smaller equilibrium DNA deformation. Note that the observed DNA deformations may have multidimensional dependence beyond merely double helix unwinding, and this may possibly include base pair melting, exclusion and/or re-annealing. The represented DNA deformation serves as a generalized DNA intercalation coordinate projected from the contributing DNA deforming molecular processes. This multidimensional nature is evident in the unusual energy landscape of the DNA–ligand intercalative lock mechanism in Figure 13A. The double-transition representation in Figure 10C for Δ,Δ-Pc shows that the first transition has a lower free energy barrier that can be linked to semi-conventional intercalation by the first moiety. Then the rate-limiting step has a higher barrier, which involves threading the linker to insert the second intercalating moiety into the final equilibrium state. The intermediate state serves as a gradual approach toward the equilibrium DNA deformation. Once the flexible linker is completely threaded to the opposite DNA groove, complete dissociation from the final state to the non-intercalative state becomes increasingly less probable.

COMPARING THE MECHANISMS OF FAST AND SLOW DNA INTERCALATION

We can now compare the DNA intercalation mechanisms of unconventional and conventional intercalators as obtained from kinetics studies. The kinetics of some conventional intercalators such as YO and POPO were investigated recently by the combination of OT aided by detection of fluorescence quenching upon DNA intercalation in Biebricher et al. (23). The bis-intercalation of POPO occurs in a single step, as is the case for the mono-intercalation of YO, in contrast to the two-step threading bis-intercalation by Δ,Δ-Pc, discussed above. The kinetics and the mechanism of intercalation for these conventional intercalators appear to be completely different. The association rates of the mono-intercalator YO (∼10⁷ M⁻¹ s⁻¹) and the bis-intercalator POPO (∼10⁶ M⁻¹ s⁻¹) (23) are two to four orders of magnitude higher than the rates of transition to the final equilibrium state for the unconventional intercalators discussed here. Even more dramatic is the difference in off rates, which are ∼100 s⁻¹ for YO and ∼10 s⁻¹ for POPO, compared to ∼10⁻³ s⁻¹ for the unconventional intercalators.

Moreover, nominal values for x_on were reported for YO and POPO (0.02–0.03 nm) (23), which differs significantly from the x_on values for the unconventional intercalators ActD, Δ,Δ-P and Δ,Δ-Pc (Table 3). This suggests that the transition state for the fast ligands is located much closer to the non-intercalated state compared to the slow ligands, such that most of the DNA extension occurs after the rate limiting event. In addition, for the fast ligands, the dissociation rate is strongly inhibited by force, while the association rate is almost force-independent. These kinetic characteristics are common to all investigated cyanine dye intercalators. The intercalation of these ligands involves primarily stacking of their aromatic rings in between the DNA base pairs, which is not kinetically constrained by the requirement of threading bulky side groups through the DNA duplex (such as for Δ,Δ-P), or fitting non-intercalating moieties into its grooves (such as for ActD). Therefore, one can hypothesize that the kinetics of these fast cyanine intercalators is typical for all other simple intercalators such as ethidium. These distinct intercalation mechanisms are governed by two different types of free energy landscapes determined by the DNA deformation required for association and dissociation. In fact, the much higher transition barrier for unconventional intercalators is proportional to the free energy cost of DNA structural distortion, which includes breaking base pair hydrogen bonds, in contrast to merely waiting for DNA breathing fluctuations to initiate insertion of the aromatic moieties of conventional intercalators.

OPTIMIZING DNA INTERCALATION PROPERTIES

There are many different extrinsic means of modulating DNA–ligand intercalation in vitro, such as controlling the temperature and buffer ionic strength (23). However, intrinsic optimization considers structural modifications that improve the affinity, kinetics, intercalation mechanism and the cellular uptake of DNA intercalators. In synthesizing DNA-targeted drugs, high DNA binding affinity and slow DNA binding kinetics enhance their therapeutic capability (19,61,103–105). Higher affinities lead to efficient dose exposure, lower association rates enable selective sequence binding, and advanced structural recognition and lower dissociation rates ensure disruption of DNA physiological functions (13,61,103,105–108). Traditionally, higher affinities are sought by converting mono-intercalators to bis-intercalators or even higher orders of intercalation. For imaging applications, this approach can also provide better optical signal, such as is observed for the bis-intercalator YOYO-1 (23,41). However, for therapeutic applications it is important that the intercalation kinetics is significantly slower than typical DNA replication and transcription processes.

As highlighted in this review, unconventional DNA intercalation can provide a combination of higher affinity and slow binding kinetics. It was found in recent studies that the binuclear ruthenium threading intercalator Δ,Δ-P has ∼20-fold higher affinity than its monomer Δ-P, and at least three order of magnitude slower kinetics (46). When the semi-rigid bond connecting the two Δ-P in Δ,Δ-P is replaced with a flexible longer linker in Δ,Δ-Pc, the affinity of the threading bis-intercalator is further increased by ∼5-fold relative to Δ,Δ-P (47), bringing the equilibrium dissociation constant to 15 nM, one of the highest affinities reported for a DNA intercalator. The effective dissociation rate Δ,Δ-Pc is extremely slow; in fact, no significant dissociation is observed in the single-molecule wash off experiment. Still, the dynamic DNA deformation of Δ,Δ-Pc does not show the lock mechanism found for the Δ,Δ-P and ActD. It is proposed that combining the ligand flexibility in Δ,Δ-Pc with the locking assembly of Δ,Δ-P may result in further increase in DNA intercalation affinity (47).

The cellular uptake efficiency for synthetic DNA intercalators is essential for therapeutic and imaging applications in vivo (31,38). Although the monomer Δ-P was demonstrated recently to exhibit in vivo antibiotic activity in treating bacterial infection of soil nematode (109), the binuclear ruthenium complexes Δ,Δ-P and Δ,Δ-Pc had less definite cellular uptake in vitro (38). In the absence of an effective drug delivery scheme, the high DNA binding affinity of these unconventional intercalators is insufficient to qualify them as DNA-targeting drug candidates. One of the solutions to cellular uptake deficiency is increasing the molecular hydrophobicity to enhance passive diffusion through the cellular membrane. This can be achieved by functionalizing ligands with lipid-like attachment such as alkyl chains (31). Another binuclear ruthenium complex that shares some of the Δ,Δ-P structural characteristics, [(Ru(phen)2)2(tpphz)]4+, has proven more successful in penetrating the membrane of breast cancer cells even without hydrophobic attachments (31). The binding mode of this light-switching ligand is surprisingly yet to be resolved, and bulk studies were not conclusive in determining whether it intercalates DNA or binds to the minor groove (36,110).

Nevertheless, the variability in cellular uptake for seemingly related ligands (110) highlights possible advanced molecular recognition that can be sensitive to fine structural alteration. Indeed, robust stereoselectivity is reported for threading intercalators for which multiple chiral units are accommodated in DNA minor and major groves (51,105). This extensive steric interaction is examined as a potential approach in developing DNA sequence-targeted drugs (107). Furthermore, bulk and single molecule studies have demonstrated that switching the chirality of intercalators may result in almost complete termination of their ability to intercalate DNA (97,105,107,111). It was also recently demonstrated that minimized equilibrium and dynamic DNA deformations required for DNA–ligand intercalation is significantly coupled with optimized affinity (111). This demonstrates that more single-molecule studies are needed to reveal the governing assembly mechanisms that help guide and optimize rational design of a new generation of antibiotic and anti-cancer drugs. The urgent quest for synthesizing new therapeutic small molecules and optimizing currently used agents is fueled by a fierce race to surpass the molecular evolution of drug resistance. Studies showed that combining drugs that have different binding modes to DNA, such as intercalation and cross linking, lowers the chance of cancer reoccurrence (19,109). Aside from the important applications of DNA intercalators, these small molecules serve as basic models that may improve our capacity to examine and understand much bigger and more complicated biological systems. We hope that the outlined single-molecule nanomechanical measurements and analysis may help advance the interest in revealing both the equilibrium and dynamic characteristics of diverse DNA assemblies.

FUNDING

National Science Foundation [MCB-1243883 to M.C.W.]; National Institutes of Health [GM072462 to M.C.W.]; King Abdulaziz University Scholarship (to A.A.A.). The open access publication charge for this paper has been waived by Oxford University Press - NAR.

Conflict of interest statement. None declared.