Long-timescale dynamics of the Drew–Dickerson dodecamer

Abstract

We present a systematic study of the long-timescale dynamics of the Drew–Dickerson dodecamer (DDD: d(CGCGAATTGCGC)₂) a prototypical B-DNA duplex. Using our newly parameterized PARMBSC1 force field, we describe the conformational landscape of DDD in a variety of ionic environments from minimal salt to 2 M Na⁺Cl⁻ or K⁺Cl⁻. The sensitivity of the simulations to the use of different solvent and ion models is analyzed in detail using multi-microsecond simulations. Finally, an extended (10 μs) simulation is used to characterize slow and infrequent conformational changes in DDD, leading to the identification of previously uncharacterized conformational states of this duplex which can explain biologically relevant conformational transitions. With a total of more than 43 μs of unrestrained molecular dynamics simulation, this study is the most extensive investigation of the dynamics of the most prototypical DNA duplex.

INTRODUCTION

The static picture of DNA derived from the early X-Ray studies is now challenged by a myriad of experimental and theoretical studies which show DNA to be a highly flexible entity, undergoing many conformational alterations and even modifications of its covalent structure. Simple inspection of the Protein Data Bank (PDB) illustrates how different sequences adopt different conformations, but also how identical sequences can be found in different conformations to due to the presence of ligands or of changes in the environment (1). Clearly, DNA structure should be explained in terms of conformational ensembles rather than in terms of individual structures.

Recently experimental techniques (2–5) are providing invaluable information on DNA dynamics, however most of what we know about the sequence-dependent flexibility of DNA comes from atomistic molecular dynamics (MD) simulations (6–10). As computer power increases and the reliability of force fields improve, more reliable information is derived from atomistic MD simulations (11). Such simulations have revealed the extent, and the complexity, of DNA movements and their tight coupling to the nature and dynamics of the environment (8,12–14). Unfortunately, MD simulations are extremely dependent on the quality of the force field (11,15–17) and, as simulations become longer, errors induced by force fields accumulate, generating erroneous patterns of flexibility (18–20). Continuous refinement of the force field is therefore required in order to profit from computational improvements and to gain better insight into the structure and dynamics of DNA. With this aim in mind, we have recently developed the PARMBSC1 force field, a new functional with an excellent ability to describe a variety of DNA structures on the microsecond timescale (20).

Here we use PARMBSC1 (20) to make a detailed exploration the dynamics of the best known fragment of DNA: the Drew–Dickerson dodecamer (DDD, (21)). DDD is an ideal model system: (i) it contains a biologically relevant sequence that fits well into the canonical B-form of DNA, (ii) it has been extensively studied experimentally (135 structures with the DDD sequence are available in the PDB, some of them solved at very high resolution) and (iii) it has also been widely studied by means of nanosecond-to-microsecond MD simulations (7,22,23). In summary, DDD is the best-known model system of DNA, and its analysis is likely to produce results that can be extrapolated to any canonical B-DNA.

In a first step, we evaluate the impact on DNA of a wide variety of solvent and ion models. In a second step, we analyze the impact that changes in ionic strength can have on the collected conformational samples. Finally, we explore in detail the long-timescale dynamics of DNA by using many multi-microsecond trajectories and one extended (10 μs) single trajectory. Our study reveals that the main conformational characteristics of DNA are quite insensitive to the nature of the models used to describe the solvent and ion environment. Changes due to the nature of the salt (Na⁺Cl⁻ or K⁺Cl⁻), or to the ionic strength, are also quite modest. PARMBSC1 provides very stable conformational samplings, which agree well with experimental information on this duplex, but also highlight unusual anharmonic deformations of DNA that can explain some biologically relevant transitions. Overall, in the framework of fixed-charge all-atom force fields, we present here the broadest and conceivably the most accurate study of the multi-microsecond timescale dynamics of duplex B-DNA to date.

MATERIALS AND METHODS

System set-up

Starting geometries for all systems used either Arnott-B DNA canonical values (24) or the high resolution X-Ray structure of DDD with PDB ID: 1JGR (25). The systems were then solvated by adding TIP3P or SPC/E waters to a truncated octahedral box and neutralized by adding 22 Na⁺ or K⁺. Both Smith-Dang (S&D; (26)) and Joung-Cheatham (J&C; (27)) ion models were considered and extra salt (Na⁺Cl⁻ or K⁺Cl⁻) was added up to a chosen ionic strength (0.15, 0.5 and 2.0 M added salt). Counterions were initially placed randomly, at a minimum distance of 5 Å from the solute and 3.5 Å from one another. For simulations involving potassium, two extra ion parameterizations were tested: Jensen-Jorgensen (J&J; (28)) and Beglov-Roux (B&R; (29)). All the systems were energy minimized, thermalized and pre-equilibrated using our standard multi-step protocol (22,30) followed by 50 ns of equilibration. All the systems were then simulated (production runs) on the microsecond timescale (see Table 1).

Table 1. Overall simulation information for the systems studied.

System name	Initial structure	Solvent model	Number of waters	Ion type	Ion model	Number of ions	Total time	Sample
PARMBSC1
J&C Na neutral	fiber	SPC/E	4968	Na+	J&C	22	2 μs	1 ps
S&D Na neutral	fiber	SPC/E	4968	Na+	S&D	22	2 μs	1 ps
S&D Na neutral	fiber	TIP3P	4998	Na+	S&D	22	2/10 μs	1/20 ps
J&C Na neutral	fiber	TIP3P	4970	Na+	J&C	22	2 μs	1 ps
S&D NaCl 0.15M	fiber	TIP3P	5324	Na+/Cl−	S&D	36/14	2 μs	1 ps
S&D NaCl 0.5M	fiber	TIP3P	5118	Na+/Cl−	S&D	64/42	3 μs	1 ps
S&D NaCl 2.0M	fiber	TIP3P	5095	Na+/Cl−	S&D	162/140	2 μs	1 ps
J&C neutral	1JGR	SPC/E	5037	K+	J&C	22	3 μs	1 ps
S&D neutral	1JGR	SPC/E	5187	K+	S&D	22	3 μs	1 ps
S&D neutral TIP	1JGR	TIP3P	5187	K+	S&D	22	2 μs	1 ps
S&D 0.15M	1JGR	SPC/E	5159	K+/Cl−	S&D	36/14	5 μs	1 ps
S&D 0.5M	1JGR	SPC/E	5118	K+/Cl−	S&D	64/42	3 μs	1 ps
S&D 2.0M	1JGR	SPC/E	5095	K+/Cl−	S&D	162/140	2 μs	1 ps
J&J neutral	1JGR	SPC/E	8609	K+	J&J	22	1 μs	1 ps
B&R neutral	1JGR	SPC/E	4993	K+	B&R	22	1 μs	1 ps
PARMBSC0
S&D neutral TIP	1BNA	TIP3P	4998	Na+	S&D	22	4 μs	1 ps
S&D 0.15M	fiber	SPCE	5044	K+/Cl−	S&D	36/14	2.4 μs	10 ps
J&C 0.15M	fiber	SPCE	5046	K+/Cl−	J&C	36/14	0.6 μs	10 ps
S&D NaCl 0.15M	fiber	SPCE	5044	Na+/Cl−	S&D	36/14	0.6 μs	10 ps
J&C NaCl 0.15M	fiber	SPCE	5049	Na+/Cl−	J&C	36/14	0.6 μs	10 ps

Simulation details

All systems were simulated in the isothermal-isobaric ensemble (P = 1 atm; T = 298 K) using the Berendsen algorithm (31) to control the temperature and the pressure, with a coupling constant of 5 ps. Although this has been the standard protocol adopted by the ABC consortium (8), and many others, for the simulation of short B-DNA sequences, readers should be aware that the Berendsen thermostat may produce a non-uniform temperature distribution. While this was demonstrated for proteins (32), the compact structure of the DDD dodecamer and the weak coupling of the thermostat (5 ps) are likely to minimize such effects in our simulations. In a previous work, the Nosé–Hoover (33) thermostat was also used in combination with PARMBSC1, giving results without perceptible differences (20) (data not shown). Center of mass motion was removed every 10 ps to limit build up of the translational kinetic energy of the solute. SHAKE (34) was used to keep all bonds involving hydrogen at their equilibrium values, which allowed us to use a 2 fs step for the integration of Newton equations of motion. Long-range electrostatic interactions were accounted for by using the Particle Mesh Ewald method (35) with standard defaults and a real-space cutoff of 10 Å. The PARMBSC1 force field (20) was used to represent DNA interactions. All simulations were carried out using the PMEMD CUDA code module (36) of AMBER 14 (37).

Analysis

During production runs, data was typically collected every 1 ps, which allowed us to study infrequent, but fast movements. All the trajectories were pre-processed with the CPPTRAJ (38) module of the AMBERTOOLS 15 package (37), the NAFlex server (39) and tools developed in the group (http://mmb.irbbarcelona.org/www/tools). DNA helical parameters and backbone torsion angles associated with the each base pair (bp) and base pair step (bps) were measured with the CURVES+ and CANAL programs (40). The substates of the torsion angles of the backbone (α, γ, ϵ and ζ) were categorized following the standard definition: gauche positive (g+) = 60 ± 40 degrees; trans (t) = 180 ± 40 degrees; and gauche negative (g−) = 300 ± 40 degrees. For the analysis of the vast majority of helical parameters we took advantage of the palindromic nature of the DDD sequence considering both strands independently, or as an average between the Watson and Crick strands. For comparison with the data available in the experimental databases, which were obtained in different environments, we built a single theoretical conformational space containing almost 40 million structures taken from all the independent trajectories and constituting an aggregated simulation time of 43 μs.

Experimental structures of the Drew–Dickerson docecamer

The experimental conformational space of DDD was defined as a set of experimental structures in the PDB with the sequence: d(CpGpCpGpApApTpTpCpGpCpG)₂; see Supplementary Table S1 for a detailed list. The final ensemble contained structures of DDD either isolated or in complex with small organic compounds (Supplementary Table S1). Both ligands and those sequences containing non-canonical covalent modifications were removed. After this selection procedure, the remaining 93 structures were analyzed with CURVES+ (40) and used as a reference conformational ensemble.

Solution X-ray scattering profiles from MD simulations

We computed SAXS/WAXS spectra from MD, with PARMBSC1, by taking 1000 structures from the last microsecond of the simulation with 0.15 M Na⁺Cl⁻ in TIP3P water, and generating 100 spectra, each being the average of 10 snapshots. The conditions in that simulation are the closest to the experimental ones, obtained in 0.10 M of added Na⁺Cl⁻ plus 0.05 M of Tris·HCl (41). With an estimated resolution of 2 Å, this experimental WAXS spectrum is, as far as we know, the most accurate available for the DDD sequence (41). To measure the intensities we used the method developed by Park et al. (42), which was implemented in AmberTools by Case group. Conceptually, X-ray scattering compares the scattering intensity from the sample of interest, in this case the full solvated DNA, to a ‘blank’ with just solvent present, and reports the difference, or ‘excess’ intensity. Consequently, we simulated a water box with 0.15 M of added Na⁺Cl⁻ (50 ns of production run), with the same settings mentioned above, and used it as the ‘blank’ sample. Only waters and ions within 10 Å distance from the nearest DNA atom were considered to build the spectra, and hydrogen atoms from the DNA were explicitly considered. In addition, we used the recent RISM model (43) to compute the WAXS spectra of the experimental structures 1BNA (X-ray), 1GIP (nuclear magnetic resonance; NMR) and the average structure from the MD. 1GIP is known to be the experimental structure that best matches the experimental solution scattering profile (44). The distribution function of waters and ions computed with RISM also considered a TIP3P solution with 0.15 of added Na⁺Cl⁻.

Analysis of the cations

The new CANION module from CURVES+ (45–47) was used to determine the position of each cation in curvilinear helicoidal coordinates for each snapshot of the simulations with respect to the instantaneous helical axis. Given a distance D along the helical axis, ion distributions were computed for each bps (defined here as N-0.2 ≤ D ≤ N+1.2 for a generic bps N_ipN_{i + 1}) inside the grooves (distance from the axis R ≤ 10.25 Å), dividing the contribution between the minor groove (A = 33–147°) and the major groove (polar angle A = 33° to 0° to 147°), as shown in Supplementary Figure S1. We analyzed the ion distribution in one-dimensional (R, D or A) and two-dimensional (RA, DA, DR) curvilinear helicoidal coordinates. Three-dimensional distributions were also reconstructed in Cartesian coordinates using an average structure for the DNA oligomers obtained with CPPTRAJ (38) from the full-length simulations. Ion densities were obtained in units of molarity as detailed elsewhere (45). Special attention was paid to the convergence of the ion population both inside and outside the DNA major and minor grooves for each bps as previously described (47).

Similarities, global and local flexibility in Cartesian and Helical spaces

Deformation modes were determined from a principal component analysis of the collected simulations using PCASUITE (http://mmb.pcb.ub.es/software/pcasuite/pcasuite.html). DNA entropy values were obtained from trajectories using the Schlitter (48) and the Andricioaei–Karplus (49) methods for all heavy atoms (excluding terminal base-pairs). Similarity indices were calculated using Hess metrics (50), and energy-weighted similarities (9). Eigenvalues (in Ų) were computed by diagonalizing the covariance matrix and were ordered according to their contribution to the total variance. Self-similarities of the first 10 eigenvalues were computed by comparing the first and second halves of a given trajectory. Relative similarities were computed as described in our previous work (6,51,52). Stiffness constants were determined using base pair step helical stiffness matrices, and base-resolution stiffness matrices, always obtained from the inversion of covariance matrices derived from the atomistic simulations (10). Persistence lengths (in nm) were obtained according to (53), considering all possible DNA sub-fragments. The sequence used to calculate the persistence lengths was artificially extended by taking the inner 8 bp of the DDD sequence and multiplying this segment by 20 to create a 160 bp oligomer: (CGAATTCG)₂₀. The calculations were executed on ensembles of 10⁴ structures generated by an in-house implementation of Olson's Monte Carlo procedure (54). As discussed elsewhere (53,54), persistence length is a macroscopic descriptor of the polymeric flexibility of duplex DNA that can be compared with experimental measures.

Sampling of extreme cases and anharmonic distortions

Certain fluctuations in the global structure of the DNA cannot be reasonably explained in the harmonic regime. Others, while harmonic, represent extreme cases found at the margins of the distribution of sampled conformations. The latter were detected by looking at the distribution of deformation energies, calculated for a reduced set of DNA conformations taken from each MD simulation (one structure every 2 ns), with respect to a reference state defined by the MD-derived basepair step stiffness matrix (6) and the average DNA conformation. We approximate the distribution of deformation energies to a normal distribution, and consider extreme deformations to be those structures with energies above either two or three standard deviations from the average. Anharmonicity was evaluated by applying the Shapiro–Wilk test (55), since none of the reduced sets of deformation energies obtained for each trajectory had more than 5000 values. Furthermore, the complete ensemble of deformation energies (combining all the trajectories) was analyzed graphically by means of Q-Q and box plots, characterizing the structures sampled by the force field beyond the harmonic approximation. In these analyses the terminal base pairs were not considered.

Statistics, graphics and molecular plots

The statistical analysis, including the Bayesian Information Criterion (BIC) and linear correlations, as well as associated graphics, were obtained with the R 3.0.1 statistical package (56) and the ggplot2 library (57). The molecular plots were generated using either VMD 1.9 (58), or the UCSF Chimera package version 1.8.1 (59).

RESULTS AND DISCUSSION

Environmental impacts on DNA

MD trajectories are dependent on the solvent and ion environment in two different ways: one legitimate, since changes in solvent, ionic strength or the nature of the ions should impact simulations, sometimes in a dramatic way (13,60), and one illegitimate, linked to the uncertainties in the force fields used to represent water or ions. Before analyzing the detailed dynamics of DNA, it is therefore necessary to evaluate the uncertainties introduced into simulations by the ion and/or solvent models used. For water, we considered the two most popular three-point models: TIP3P (61) and SPC/E (62), while for salt (Na⁺Cl⁻ or K⁺Cl⁻) we considered models by Joung-Cheatham (J&C), Smith-Dang (S&D), Jensen-Jorgensen (J&J) and Beglov-Roux (B&R) (the last two only for K⁺Cl⁻, see ‘Materials and Methods’ section). All trajectories involved at least 2–3 μs of simulation and were extended up to 5 μs when ion convergence was not clear.

Consistent with the general article describing the parameterization and validation of the PARMBSC1 force field (20), all the simulations yielded average RMSDs in the range 1.9–2.3 Å with respect to Arnott B-DNA values (1.6–2.0 Å if terminal base pairs were excluded), ∼2.2 Å with respect to the X-Ray structures (PDB IDs: 1BNA, 2BNA, 7BNA and 9BNA) and ∼1.8 Å with respect to the ensemble of NMR structures in the PDB ID: 1NAJ. About 91–98% of the Watson–Crick hydrogen bonds were maintained during the multi-microsecond simulations explored in this work (see Supplementary Table S2). Helical parameters, groove dimensions and torsion angles sampled in the simulations in all cases matched the values expected from experimental structures. A more detailed comparison with a large number of high resolution X-ray and solution NMR structures is carried out below.

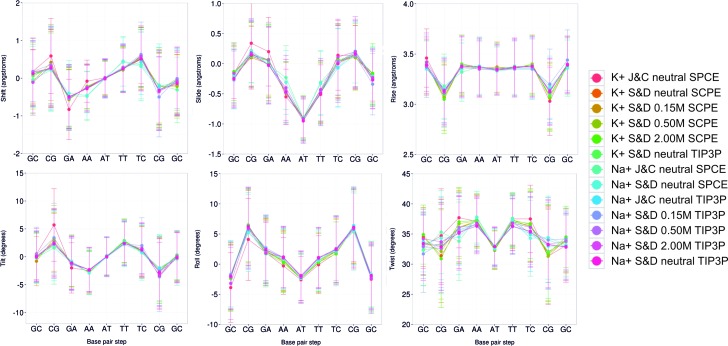
As already suggested by previous studies (7), the impact of using two different solvent models (SPC/E and TIP3P) is negligible in terms of the structural properties of DNA. We analyzed in detail the six helical base pair step parameters along the DDD sequence (Figure 1), and the complete set of 16 helical parameters and 8 torsion angles (see Supplementary Table S3 (Na⁺Cl⁻) and S4 (K⁺Cl⁻)). The impact of changing the ion force-field parameters also led to very small differences in terms of the global properties of DNA (see Figure 1 and supplementary Tables S3 and 4), in good agreement with previous PARMBSC0 (19) results (7,63). The use of Na⁺Cl⁻ or K⁺Cl⁻ has also little impact on the DNA structure, again in good agreement with previous simulations (46,63). Finally, increasing the ionic strength (here we tested ∼0.15, ∼0.5 and ∼2 M), also seemed to produce little effect (see Figure 1) on the average structure of DNA (for local effects linked to ionic strength see the discussion below).

Figure 1.

Averaged base pair step helical parameters along sequence for all the simulation performed with PARMBSC1. See Table 1 for a detailed description of the simulated systems. Translational parameters (shift, slide and rise) are reported in Å, and rotational ones (tilt, roll and twist) in degrees. The terminal base pairs were removed from the analysis.

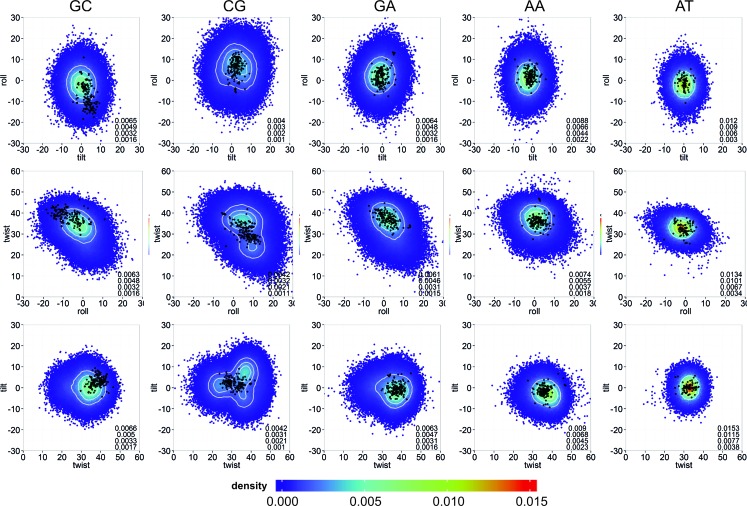
As the MD conformational ensembles appeared to be quite robust to changes in the solvent or ionic atmosphere, we combined all the trajectories to create a 43 μs meta-trajectory from which a ‘theoretical’ conformational space of B-DNA can be defined and compared with that derived from experimental structures (see ‘Materials and Methods’ section and Supplementary Table S1), which were also solved in different environments (93 structures, which thanks to the palindromic nature of DDD sequence provide 186 experimental estimates of helical parameters for each type of base pair step in the sequence: CpG, GpC, GpA, ApA, ApT and TpT). As shown in Figure 2, no experimental conformation lies outside the ‘theoretical’ conformational space derived from our simulations. Furthermore, experimentally observed conformations lie in the regions of higher density in the MD-derived sampling (see Figure 2 for a comparison of the rotational space, and Supplementary Figure S2 for the translational space). DDD actually covers quite a wide conformational space, as reflected by the variety of experimental structures, well reproduced by the MD simulations.

Figure 2.

Comparison at the bps level between the theoretical and experimental rotational spaces. Rotational parameters (tilt, roll and twist) are reported in degrees. All distinct bps found in DDD are shown (removing the ends): GC (first column), CG (second column), GA (third column), AA (fourth column) and AT (fifth column). Smoothed 2D densities, estimated by fitting the observed distributions to a bivariated normal kernel (evaluated on a square grid of 90 × 90 bins), are depicted by coloring the points coming from the MD simulations with a color gradient from low (blue) to high (red) density. Four iso-density curves are shown in white, and are quantified on the bottom right side of each plot. Experimental conformations are shown as black dots (supplementary Table S1).

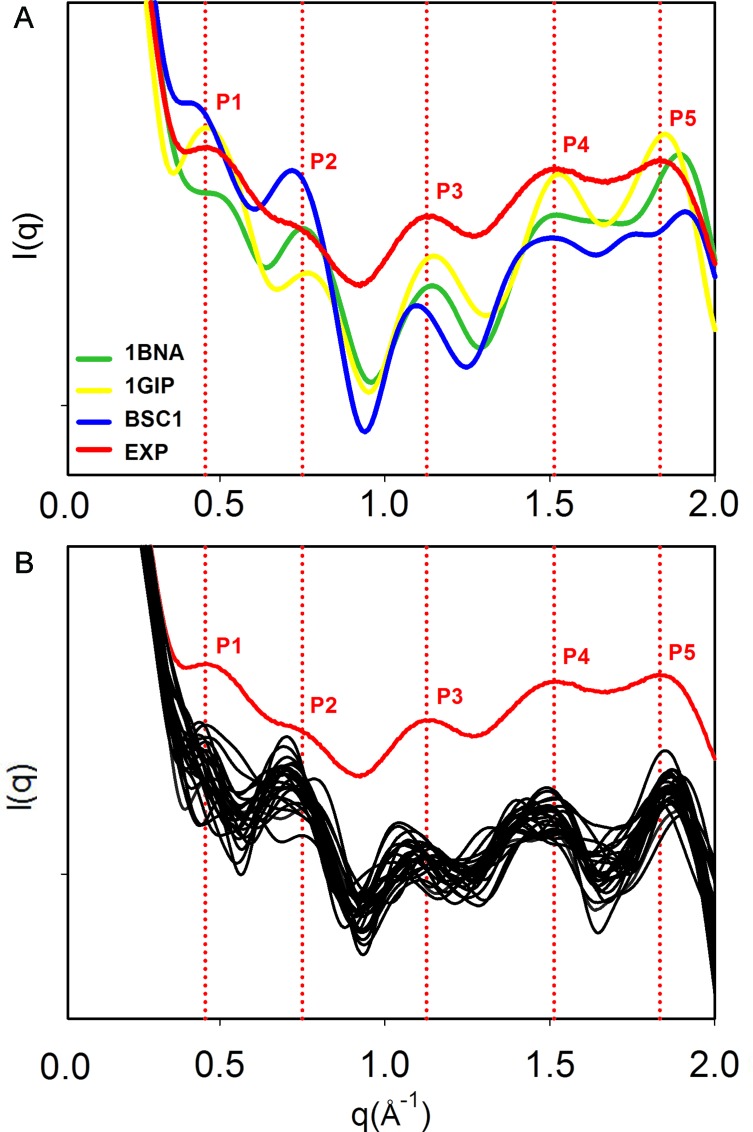
Although X-ray and NMR derived structures have been considered for the last 20 years the gold-standard for force field comparison (64), they both suffer from some limitations when it comes to represent the structure of the DNA in solution (65). Crystal packing and crystallization artifacts in X-ray techniques, or user-biased integration of the peaks and refinements based on all-atom force fields in NMR experiments, are just some of the known limitations. To complement this data, Small-Angle X-ray Scattering (SAXS) and Wide-Angle X-ray Scattering (WAXS) are able to deliver information about the shape and size of the molecules in solution. At high resolution, structural polymorphism such as the B-DNA/B’-DNA can be detected (41), although the spatial averaging carried out to derive the profiles also leads to a loss of information in SAXS/WAXS compared to crystallography. To complement our findings, we compared our simulations to the high-resolution (2 Å) WAXS spectrum obtained for DDD by Zuo and Tiede (41). Nevertheless, the reader should be aware that comparisons between theoretically-derived and experimental spectra have to be made with caution, due to the problems in generating profiles from structural models (specially related to the different way to treat the solvent; see ‘Materials and Methods’ section), the different conditions in the simulation and experiments, and the lack of definition in certain regions of the spectra. With these cautions in mind, it seems clear from Figure 3 that PARMBSC1 is able to overcome some of the deviations from experiment described previously using PARMBSC0 (60), and provide spectra that fit well the experimental ones. Quantitative comparison of peak location reveals that PARMBSC1 recovers the first peak (P1) near q ≈ 0.45 Å⁻¹, which was reported to be absent in PARMBSC0 simulation (65). The major deviation from experiment was found at wide angles (P5), where PARMBSC1 is slightly shifted respect to the experimental value, but where the resolution of both theory (43) and experiment is also lower and peak location is not so clear. It is worth noting that in general PARMBSC1 fits the experimental profiles with a quality similar or better than the best experimentally derived structures (by NMR or X-Ray), even in the most complicated region (P1–P3) that reflects the structure of the sugar-phosphate backbone (see Supplementary Table S5).

Figure 3.

Solution scattering profiles. (A) Solution interference patterns computed with the RISM approach (43) for the DDD crystal (PDB ID: 1BNA, green), the NMR (PDB ID:1GIP, yellow) and the average structure from the MD simulation (PARMBSC1, blue), compared to the experimental profile (red). Vertical dotted lines in red represent the peaks determined experimentally. (B) Scattering profiles obtained from the MD simulation with PARMBSC1 using the method from Park et al. (42) (see ‘Materials and Methods’ section), compared to the experimental result. The positions of the peaks are reported in Supplementary Table S5. Note that the absolute intensities were accordingly shifted to a common origin to maximize the overlap. The data to produce the experimental curve was a courtesy of Prof David Tiede (41).

In summary, PARMBSC1 trajectories reproduce experimental observables accurately and seem robust with respect to the (somewhat arbitrary) selection of ion and solvent force fields. In terms of general DNA structure, the trajectories are also quite insensitive to ionic strength (over a ‘physiological’ range) and to the nature of the salt (Na⁺Cl⁻ or K⁺Cl⁻). These results suggest that globally, despite the use of simple additive potentials (66,67) PARMBSC1 is performing very well. Further improvements are likely to require the inclusion of new factors such as polarization.

Similarities, global and local flexibility

Processing of the covariance matrix obtained from atomistic MD simulations provides a direct measure of DNA flexibility in Cartesian space, which can be described in terms of essential deformation movements and quasi-harmonic entropies (see ‘Materials and Methods’ section and reference (51)). These estimates cannot be directly compared with experimental observables, but are very useful in determining the similarity between deformation patterns and stiffnesses derived from different force fields (6). As shown in Supplementary Figure S3, the dynamics of the central 10 bp of DDD obtained with PARMBSC1 have a very high (>75%) similarity with respect to a reference simulation using PARMBSC0. This similarity increases to more than 90% if Boltzmann indices are considered (Supplementary Figure S3D). We can conclude that the nature and the magnitude of the principal deformations of DNA are very similar with both force fields. This is confirmed by an analysis of the Cartesian entropies and the stiffnesses associated with the main deformation movements (Supplementary Table S6). Helical stiffness analysis provides an alternative picture of DNA dynamics by considering local perturbations of helical parameters (10). Results at the base pair level (Supplementary Figure S4) and at the base pair step level (Supplementary Figure S5) show the expected sequence dependence (6) and confirm the similarity between PARMBSC0 and PARMBSC1 results. Finally, polymeric MD-stiffnesses derived from the extension of DDD to a very long duplex (see ‘Materials and Methods’ section) demonstrate that PARMBSC1 also reproduces the persistence length of duplex DNA with values ranging from 48 to 57 nm depending on simulation conditions (Supplementary Table S6), compared to experimental estimates of around 50 nm (68).

To further investigate the capacity of MD to sample extreme conformations and also structural distortions beyond the harmonic regime, we fitted the deformation energies (see ‘Materials and Methods’ section) with a normal distribution obtaining an average (α) of 1.8 kcal mol⁻¹ with a standard deviation (σ) of 0.4 for the meta-trajectory (note that we obtained the same α and σ for the single 10 μs trajectory). If the movements of the DNA could indeed be described by the harmonic regime, one would expect that the tails of the distribution beyond α ± 2σ would account for 4.56% of the total probability distribution. Following the same reasoning, the probability that a normal deviate would lie beyond α ± 3σ is at most 0.27%. Counting the number of times these extreme regions are sampled in the 10 μs long trajectory led to 5.64 and 1.32% beyond the α ± 2σ and α ± 3σ limits respectively. Using the complete meta-trajectory that describes 43 μs of DDD in different environments we obtained 8.91% (α ± 2σ) and 2.41% (α ± 3σ), clearly showing that PARMBSC1 simulations significantly sample extreme conformations, more frequently than expected from the harmonic regime. Furthermore, we applied the Shapiro–Wilk test to check whether the sets of distortion energies could be drawn from a normally distributed population. For all the trajectories, we rejected the null hypothesis with P < 0.05, supporting the deviation from normality. We also analyzed the complete space of deformation energies (combining the results obtained separately for each trajectory), using a graphical approximation. The distribution, Q-Q plot, and boxplot presented in Supplementary Figure S6, clearly supports the presence of anharmonic distortions related with highly bent structures.

We saw above that solvent and ion force-field models, including both Na⁺Cl⁻ or K⁺Cl⁻, had little impact on the global structure or flexibility of DDD. This may seem reasonable given the ‘physiological’ conditions range used in this work (see Noy and Golestanian (69)). However, while simulations carried out with minimal (neutralizing) ionic strength seem to lead to shorter persistence lengths (Supplementary Table S6), there is no systematic trend relating flexibility and ionic strength. Note that the use of the AMBER implementation of PME to treat long-range electrostatics precludes performing simulations at very low ionic strength (net-charged systems), where the connection between global flexibility and ionic strength could become significant. The reason is the implicit presence of a net-neutralizing plasma that appears due to the omission of the zeroeth-order term in the reciprocal Ewald sum (70,71).

Ion atmosphere

Previous sections have shown that the global structure and dynamics of DNA is not dramatically dependent on the solvent or ion force field, the nature of the monovalent cations (Na⁺ or K⁺), or the ionic strength (within the range studied). However, this robustness of DNA to environmental conditions does not preclude local changes linked to the solvent or ionic atmosphere. We investigated this possibility in more detail by looking at the interactions of DNA with ions. The first point that becomes evident when looking at the trajectories is that while DNA structure is reasonably well converged in several hundred ns (46), the ionic environment may require significantly more time to converge, as suggested from earlier simulations (47). This is indeed what the analysis of ion population at the base pair step level (see ‘Materials and Methods’ section) shows (see Supplementary Figures S7–10 for the analysis of K⁺Cl⁻. Similar profiles were obtained for Na⁺Cl⁻). It is also clear that the convergence of the ion distribution depends on the ion force field (Supplementary Figures S7 and 8) and also on the region of DNA that is analyzed. As an example, ions represented with the J&J model converge quickly (200 ns) inside the grooves and around the DNA, whereas the J&C ion atmosphere is not fully converged in the 3 μs studied here (Supplementary Figures S7 and 8). It is also clear that convergence is in general faster in external regions (around the phosphates, Supplementary Figures S7 and 9), than within the grooves and notably within the narrow minor groove where saw tooth-like curves can be observed (Supplementary Figures S8 and 10). In these cases, convergence is not fully guaranteed even after 5 μs (see the 150 mM S&D simulation in Supplementary Figure S10). It is worth noting that convergence problems do not decrease when ionic strength is increased, despite the fact that more ions are available in the DNA environment, indicating that it is not a simple statistical problem. Indeed, the saw tooth-like population curves of S&D ions inside the minor groove (especially at the central AT step) in the minimal salt simulations are present, and sometimes even amplified, in simulations at higher ionic strength (see Supplementary Figure S10). This suggests that ions visiting some narrow regions in the grooves may be frustrated (47), trapped in an oscillatory regime between two different substates. Ions with long residence times inside the grooves, could also explain part of the oscillatory regime. Thus, using the S&D 0.15 M simulation we compared the volume of the groove, the time evolution of K⁺ ions visiting the minor groove and the average residence at A₆T₇ and C₃G₄, which are the two most populated bps at physiological concentration (Supplementary Table S7). The average volume of the minor groove is significantly narrower for AT (193 ų) than for GC (239 ų) as previously reported (7,22). We also found that the average residence time of K⁺ inside the minor groove was 108 ps for AT versus 50 ps for CG (if we consider an ion to be present when it stays at least 20 consecutive ps inside the groove (46)). Indeed, K⁺ ions are able to remain within the AT step for several hundreds of ns (Supplementary Figure S11). During these long periods there is a higher probability of simultaneously finding two cations inside the narrow groove of AT, compared to CG. Based on the visual inspection of a single extended trajectory, this double occupancy seems to produce an imbalance that triggers the release of both ions from the groove within a few ps. This could explain the oscillatory ion population at the AT step, as it indeed occurs at each of the sawtooth-like peak we observed in the AT time series (Supplementary Figure S11). Nevertheless, a more systematic approach with statistical support should be undertaken to confirm these findings. Similar events are not seen in the minor groove of CG steps (Supplementary Figure S12).

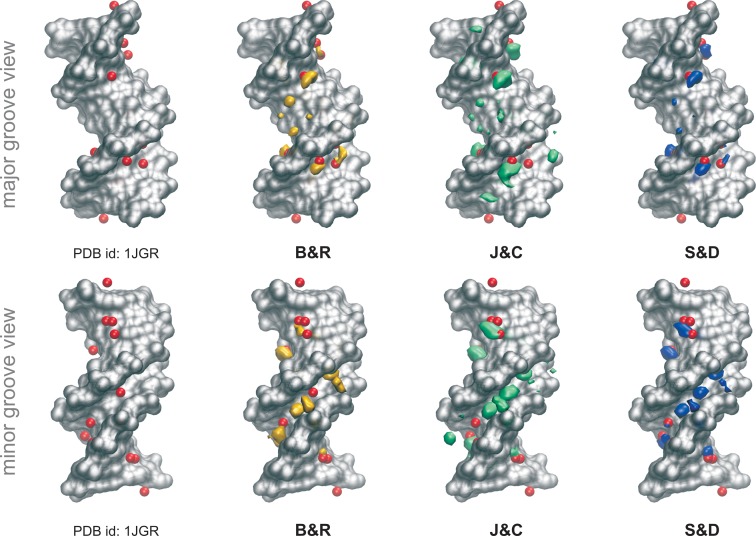
While remaining cautious with respect to convergence problems, we can reach some general conclusions on the impact of the ion force field on ion populations around DNA. Of the four K⁺ models tested, the Lorentz-Berthelot (LB) implementation of J&J is the one showing the weakest affinity for DNA (Figure 4 and Supplementary Figure S8), leading to very low ion populations inside the grooves and failing to explain the regions of high cation density found experimentally (25,72,73) in the minor groove of the AATT segment (note that this different behavior could be due to the conversion from geometric to LB combination rules used to build the Lennard-Jones potential in AMBER (37,63), since these parameters were created to work with another van der Waals functional (28)). J&C is the one with the strongest DNA affinity, possibly explaining its severe convergence problems in regions with narrow grooves. Finally, the S&D and B&R models (the two most used in DNA simulations), at a first glance, give similar ion distributions (see Figure 4 and Supplementary Figure S8). A more detailed picture of ion environment can be obtained by looking at 3D density plots (see ‘Materials and Methods’ section) such as those shown for B&R, J&C and S&D in Figure 5.

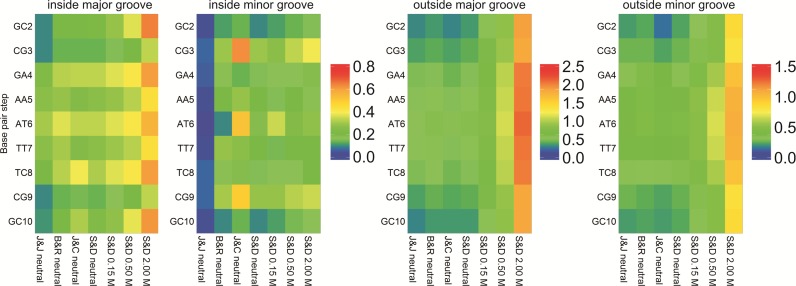
Figure 4.

Average K⁺ populations inside and outside the DNA grooves. Populations inside the major and the minor groove (left two panels), and outside both grooves (right two panels). The populations were measured for each bps removing the terminal ones (see ‘Materials and Methods’ section). See Supplementary Figure S1 for the CHC partitioning scheme used to divide the grooves.

Figure 5.

Potassium distributions along the helix. Cartesian K⁺ isomolarity surfaces at 5.0 M reconstructed from the CHC histograms with respect to the average structure (shown as a silver surface). For comparison purposes, neutral systems have been overlapped with the Tl⁺ cations (red spheres) that co-crystallized with the DNA (PDB ID: 1JGR). Note that thallium cations are used as a replacement of potassium in diffraction experiments (1). The distribution with the J&J parameters are not shown since any visible density was observed at 5.0 M concentration.

Looking at the minimal salt trajectories, differences in ionic atmosphere are especially visible at the edges of the groove, around the phosphate groups (where only the J&C model generates ion density when analyzing the 1.5 M isomolarity surface, Supplementary Figure S13) and in the central minor groove region, where the J&C model tends to concentrate all ion density in the AT and CG steps. In contrast the J&J model predicts a low ion concentration of ions anywhere in the groove, while S&D and B&R models show a more homogeneous distribution of ions along the groove (Figure 4, see Supplementary Tables S7–10). Looking at high isomolarity surfaces (5 M) shows that not all the parameterizations are able to reproduce the location of the K⁺ ions that co-crystallized with the DNA in the high-resolution X-ray experiment (25). It could be argued that those co-crystallized cations reached their final location in the crystal cell due to packing or crystallization effects. Nevertheless, the cations are found buried inside the grooves of the DNA in close interaction with the bases. The analysis of their precise location as been the subject of several studies, where the position of cations is correlated with changes in the groove widths, being part of a complex structured network involving cations, water and DNA interactions (22,73). While J&C and S&D models correctly predict the position of K⁺ ions in both grooves (S&D being the more accurate), B&R only reproduces the cations found in the major groove, while a systematic shift of the density clouds is observed in the minor groove (Figure 5). When the ionic strength is increased (only studied for the S&D model), the general 3D distribution of K⁺ does not change dramatically (see Supplementary Figure S14), except for the overall increase in ion density that is particularly visible in the major groove and at the groove edges close to the phosphate groups where new sites are populated. The general good agreement between the densities coming from the free dynamics in solution and the co-crystallized cations ‘fixed’ in the crystal cell, and the high concentration at which the cations were found inside the grooves of some specific bps (up to two orders of magnitude higher respect to the physiological background), make us think that these cations reached their final position in the crystal following a clear sequence-dependent pattern.

As discussed below, differences in cation population or density do not lead to significant structural or dynamic differences in DNA. However, a detailed analysis does show local changes linked to ion populations in the grooves. As an example, the J&J model which showed the weaker affinity for DNA leads to wider grooves (very visible in the AATT segment, see Supplementary Figure S14), while the J&C model, with the strongest DNA affinity, leads to narrower minor grooves in the central AATT segment. A clear correlation is also observed between increasing ion concentration and the width of both DNA grooves (Supplementary Figure S16). With the S&D model, the average minor groove width changes from 4.06 Å (neutral system) to 3.88 Å (2.0 M system; standard error of 2 × 10⁻⁵ Å). The absolute difference between these two extreme conditions is small in absolute terms, but is enough to add extra structural frustration to K+ ions entering the minor groove. In general, an increased population of ions attached to DNA leads to an increase in the local stiffness associated to the central AATT tract, but the differences are evident only when the ‘extreme’ J&J and J&C models are compared (Supplementary Figure S15). In contrast to groove geometry, no noticeable changes were found in BI/BII populations. Overall, it is clear that B-DNA is more affected by the choice of ion force fields than by the bulk ion concentration (Supplementary Figures S15 and 16), but these effects remain relatively mild.

Long-timescale dynamics of DNA

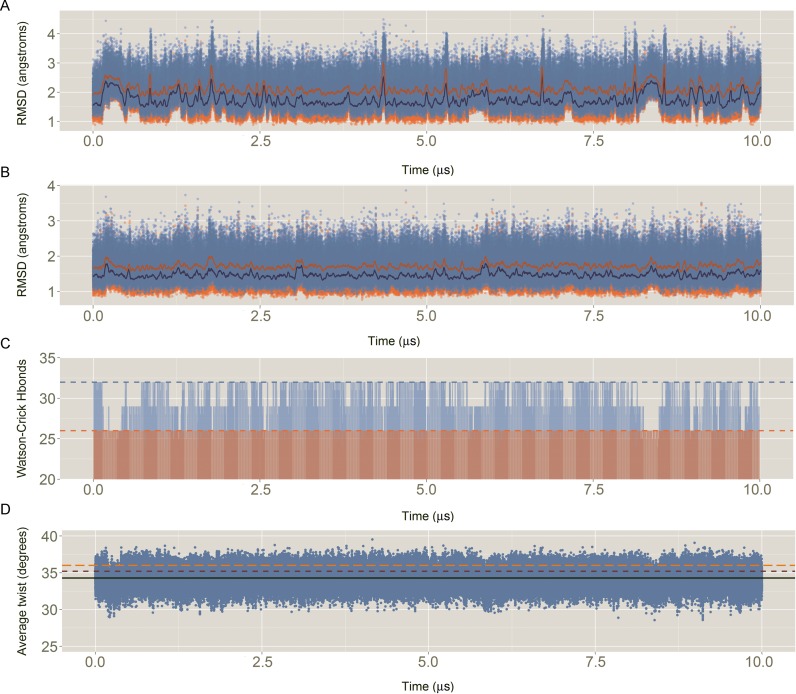
Results above demonstrate that, in general terms, the trajectories obtained from MD simulations are robust with respect to choices of water or ion force fields, the ionic strength or the nature of the salt. We next decided to extend one of our trajectories (S&D, minimal salt (22,46)) to 10 μs to explore slow conformational changes that might be not visible in shorter simulations. The entire 10 μs DDD trajectory samples canonical B-DNA conformations which are very close to both X-Ray (21,74–76) and NMR (77) structures (Figure 6). The average helical parameters (twist, roll, tilt, shift, slide, rise) derived from the MD simulation (including terminal bases) is (35.2, 2.8, 0.2, 0.0, −0.2, 3.3), which compares extremely well with the results derived from NMR ensembles (PDB ID: 1NAJ (35.9, 2.3, 0.0, 0.0, −0.2, 3.2)) or X-Ray crystallography (PDB IDs: 1BNA, 2BNA, 7BNA and 9BNA: (35.0, −0.3, −0.2, −0.1, −0.2, 3.3), confirming the ability of PARMBSC1 to reproduce the overall conformational properties of DNA (see Table 2 for more details) in simulations that are at least an order of magnitude longer than today's ‘state-of-the-art’.

Figure 6.

Descriptors of the quality of the simulation: (A) Root mean square deviation (RMSD) of all the heavy atoms of the Drew–Dickerson dodecamer (DDD) respect to the average experimental value. In blue, RMSD against an average of the X-ray structures (PDB IDs: 1BNA, 2BNA, 7BNA and 9BNA); In orange, RMSD against an average of the NMR ensemble with 5 structures (PDB ID: 1NAJ). For the sake of clarity, running averages every 20 ns are shown in dark orange and dark blue, for X-ray and NMR respectively. (B) Same than (A) but without considering the capping base pairs (i.e. removing all the heavy atoms of base pairs C1:G34 and G12:C13). (C) Evolution of the total number of Watson–Crick hydrogen bonds (Hbonds) with time. Considering a perfect interaction between the 12 bp would lead to a total of 32 Hbonds (light blue dashed line). Without considering the capping base pairs (light red), the ideal total number of Hbonds is 26 (light red dashed line). Hbonds were considered formed if the distance between the donor–acceptor atoms was ≤3.5 Å. (D) Sequence averaged twist for all the base pair steps (bps), excluding the terminals, with time. The average MD value is shown with a black line, while the experimental references are shown in dark red and orange dashed lines, for X-ray and NMR respectively.

Table 2. Sequence-averaged conformational parameters obtained from the 10 μs Drew–Dickerson dodecamer simulation^a.

Parameter	Average	SD	Range	Minimum	Maximum	NMRb	Xrayc
Shear	0.00	0.30	6.43	−3.62	2.81	0.00	0.03
Stretch	0.02	0.12	3.27	−0.78	2.48	−0.29	0.19
Stagger	0.10	0.38	4.79	−2.15	2.66	0.02	0.21
Buckle	0.0	9.7	92.9	−48.3	48.0	0.0	−0.5
Propeller	−9.2	8.4	81.6	−49.6	39.2	−17.4	−14.4
Opening	1.3	4.0	71.1	−29.4	56.8	1.1	1.6
Xdisp	−0.58	1.05	10.42	−6.05	4.36	−0.01	−0.15
Ydisp	0.00	0.84	9.16	−4.59	4.58	0.02	0.52
Inclination	2.2	5.7	56.0	−26.1	31.0	1.7	−0.6
Tip	0.1	6.9	58.6	−41.7	41.2	0.0	−2.6
Shift	−0.01	0.81	7.31	−3.71	3.63	0.00	−0.07
Slide	−0.24	0.53	5.50	−3.17	2.34	−0.22	0.14
Rise	3.32	0.29	3.32	1.96	5.30	3.20	3.35
Tilt	−0.1	4.7	44.6	−22.6	23.0	0.0	−0.4
Roll	1.5	5.5	60.1	−31.8	31.7	2.3	−0.7
Twist	34.3	5.5	52.3	3.4	57.1	36.0	35.2
αd	−72.6	18.2	314.4			−60.2	−57.5
β	166.8	21.7	251.1			171.0	166.4
γ	55.6	23.2	243.6			49.6	48.3
δ	135.2	14.5	119.7			125.7	126.3
ϵ	−159.9	23.5	169.1			−170.8	−164.3
ζ	−111.4	36.1	203.1			−103.5	−112.1
χ	−111.7	16.2	138.6			−111.5	−113.5
Phase	152.0	27.2	267.3			135.0	135.7
Amplitude	41.3	6.5	61.4			34.0	41.1

^aCapping base pairs were removed from the analysis.

^bComputed from the ensemble of structures (PDB ID: 1NAJ).

^cComputed from the X-ray structures with PDB IDs: 1BNA, 2BNA, 7BNA and 9BNA.

^dFor the dihedral angles only the Watson strand was considered.

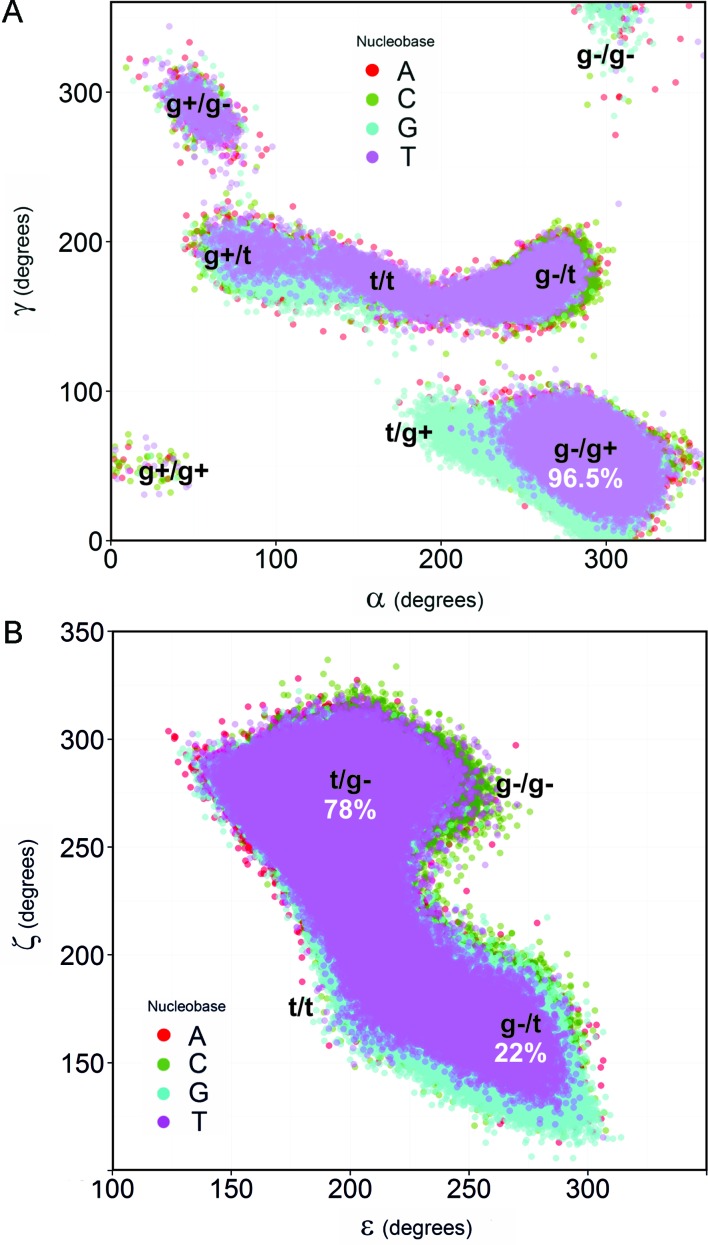
This long trajectory is also able to capture some subtle details, such as the lower χ values sampled by guanosines compared with the other nucleotides, sugar phase angle distributions sampling the correct South–South East regions (Supplementary Table S11), the sequence variability of helical twist (7,51) and BI/BII populations (Supplementary Figure S17). Backbone torsions follow the expected behavior for a duplex B-DNA, preferentially exploring the canonical B-DNA substate characterize by α in gauche− (g−) and γ in gauche+ (g+) (Supplementary Figure S18 and Supplementary Table S12), with ϵ in trans (t) and ζ in g− (i.e. the BI state).

Very interestingly, despite the canonical αγ state being the most populated (in agreement with previous PARMBSC0 simulations (10,22)), all the non-canonical conformations found in experimental protein–DNA complexes (78) are also detected here (Figure 7), thus improving on PARMBSC0 behavior. As shown in Supplementary Figure S18, αγ transitions are common (on average 460 transitions per μs per nucleotide) and fast (average residence times being around 3 ps); although only 0.01% of the non-canonical αγ states have non-negligible survival times of up to 1.2 ns (averaging across the four nucleotide types). Long-lived γ-flips of around 100 ns from the g+ to the non-canonical t state where not observed. Note that these flips were recently suggested to be a source of convergence problems when using PARMBSC0 (10). As expected (7,22), C and G nucleotides show longer-lived and more frequent αγ transitions than A or T (Supplementary Figures S18). However, the occurrence of non-canonical αγ states is not cooperative and does not lead to the destructuring of the double helix that was found with older force fields (18). On average, at any given moment, less than one (0.86) of the 24 nucleotides is in an unusual αγ state. Extrapolating to polymeric DNA implies that 3.6% of nucleotides will exhibit an unusual αγ conformation. This could be a factor favoring recognition by specific proteins, given that crystal structures of protein-DNA complexes show a significant percentage of such states (10%, (67)).

Figure 7.

Major substates of the backbone observed during the simulation of DDD. (A) Scatter plot of α and γ angles grouped by nucleobase. To obtain the distribution of A in the αγ-plane the dynamics of the nucleobases A5 and A6 were considered together (similarly: C3/C9, G4/G10 and T7/T8 were used to build the C, G and T ensembles respectively). (B) Same as (A), but for ϵ and ζ angles. The global percentages (considering both strands) of the major canonical states are shown in white.

As expected from previous experimental and theoretical studies (7,8,22,79,80), C·G base pairs show a significant propensity for BI/BII transitions (Figure 7), as evidenced by the concerted changes in ϵ and ζ from t to g− and from g− to t respectively (Supplementary Figure S19). BI/BII relative populations are notably improved with respect to PARMBSC0, and now reproduce more accurately NMR experiments (Table 3 and Supplementary Figure S17). As previously suggested (8,46,81), BI/BII polymorphism is directly connected to two sources of structural polymorphism, namely, the twist bimodality found for CG steps and the slide polymorphism observed for RpR steps. Concerted movements of the backbone and the bases allow the formation of an intra-molecular hydrogen bond of the type C8H8-O3′ between RpR steps, that was proved to be casually connected to BII populations (8,46). These concerted movements seems to be linked to twist polymorphism, the low twist state being driven by the presence of cations specifically binding in the minor groove of CG steps (46). Indeed, a systematic increase in the low twist state is observed upon increasing the amount of added K+Cl− from 0.15 to 2.0M (Supplementary Table S13). Note also that the weighted-average twist obtained with the BIC method (82) is higher with PARMBSC1 as a consequence of the higher population of the high twist state (0.66 versus 0.52 in PARMBSC0; Supplementary Table S13). PARMBSC1 is able to correctly reproduce this complex choreography: twist is correlated with ζ, with BI/BII, with the formation of the CH-O interaction and with the slide polymorphism in the neighboring step (Supplementary Figure S20). This is expected to be particularly important in understanding indirect recognition of DNA by proteins (83,84,85), and also the mechanism of DNA intercalation by small organic compounds (46,86).

Table 3. Percentage of BI substates obtained with PARMBSC1 compared with PARMBSC0 and NMR experiments^a.

Bps	PARMBSC0	PARMBSC1	NMR1	NMR2
GC	48	73	75	53
CG	87	78	75	66
GA	53	45	53	44
AA	91	82	75	63
AT	99	98	100	78
TT	100	99	99	93
TC	98	93	89	92
CG	79	62	75	77
GC	71	61	79	35

^aBI percentage for the bps in the DD dodecamer, obtained by averaging the difference between ϵ and ζ angles at the 3′-junction of the Watson strand of each base pair. NMR1 and NMR2 are values obtained using phosphorus chemical shifts as detailed in the works of Schwieters et al. (NMR1 (80)) and Tian et al. (NMR2, (79)), respectively.

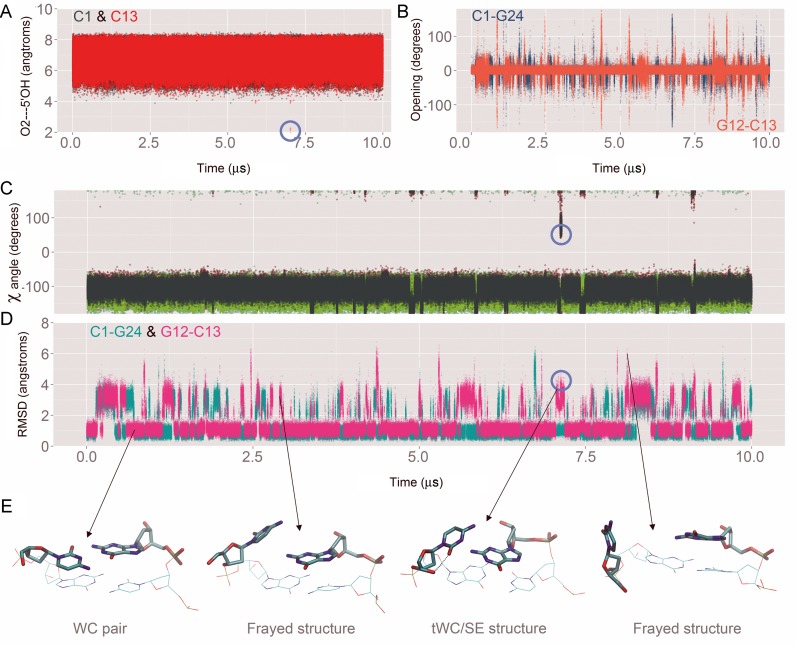
We have also used our long (10 μs) DDD simulation to investigate base opening events. It is experimentally known that base opening (understood as conformational states where bases are unpaired for significant periods of time) happens on the millisecond timescale (87), at least for coding nucleobases (88), and thus far beyond our simulation window. Terminal base pairs, where stacking interactions are weaker should show slightly higher opening frequencies, but available experimental data do not support the presence of long-lived open states for terminal base pairs (20) and strongly warn against long-lived non-canonical conformations of terminal base pairs stabilized by interactions with the DNA grooves, as found in previous simulations with other force fields (20,89). The PARMBSC1 10 μs trajectory shows that, as expected, the terminal C·G pairs are more labile that the central ones and it is not rare to lose some of the hydrogen bonds for short periods of time (see Figure 6). Fraying events are common, and unusual arrangements of the terminal bases are visited, but they quickly revert to canonical Watson–Crick pairing (see Figure 8) as experimentally expected (20). The tWC/SE state (where cytosine is turned around the glycosidic bond from the anti to syn conformation to form a non-WC pair resembling the trans Watson–Crick/Sugar Edge C·G pair well-known in RNA structures (90)), now occurs very rarely (probability <10⁻⁵ and with ps lifetimes), in line with NMR experiments, but in contrast to earlier simulations (7,89). The time evolution of the base pair opening parameter shows that most of the fraying is due to transient sampling of large opening angles (Figure 8). We observe very few events where the glycosidic torsion (χ) goes from anti to syn in the terminal cytosine (one such event is highlighted by the blue circle in Figure 8). These rare and reversible events are connected with the formation of aO2···5′OH intra-cytosine hydrogen bond, which in turn stabilizes the anomalous tWC/SE conformation. Our simulations suggest that rare and short-lived tWC/SE conformations do not affect neighboring base steps and have no impact on DNA structure and dynamics on multi-microsecond timescales. In addition, no through-the-groove interactions between terminal and inner bases are observed in our long trajectory.

Figure 8.

Analysis of the base-pair fraying at the ends of the dodecamer. Note that we used the same metrics described elsewhere (78) to analyze the fraying of DDD simulated with previous force fields. (A) Formation of an anomalous intra-cytosine hydrogen bond observed with PARMBSC0 and PARMBSC0-χOL4 (one formation event is highlighted by a blue circle). (B) Time evolution of the opening parameter. (C) χ angle during simulation is shown in red, light blue, dark green and light green for C1, G12, C13 and G24 respectively. (D) Mass-weighted RMSD of the capping base pairs respect to the first structure of the simulation. (E) Representative structures of the four mayor conformations found are depicted bellow. A similar behavior was observed in the other simulations performed changing the environment conditions (data not shown).

Finally, the 10 μs trajectory allowed us to analyze convergence issues in unprecedented detail; significantly extending previous studies (10,91,92). For this reason, we performed principle component analysis on segments of 1, 2 and 5 μs extracted from the 10 μs trajectory. Visual inspection of Supplementary Figure S21 (supplementary material) shows slight divergence between 1 μs segments, but no significant differences are observed between the 2 and 5 μs segments. The smoothed histograms of the main principal components clearly overlap, suggesting that DNA is sampling the same conformational space. Similarly, differences in entropy values for segments of 2 μs are smaller than 2% with respect to the entropy of the whole 10 μs trajectory, independently of the method used to calculate the entropy (see Supplementary Figure S22 in the supplementary material). This analysis suggest that PARMBSC1 is able to sample in 2 μs, what the user can expect to see in terms of conformational ensembles in 10 μs (91), and for most purposes (ion distribution being an exception) 2 μs trajectories can be considered to be converged.

CONCLUSIONS

The availability of PARMBSC1, a new and accurate force field for DNA, has allowed us to explore the long timescale dynamics of the DDD, a prototypical B-DNA duplex, in aqueous solution. An unprecedented degree of sampling (involving more than 43 μs of simulation, including a single 10 μs trajectory) has allowed us to test the impact of different solvent and ion models, and of different salts, on DNA and to characterize the ion atmosphere around the double helix. We have also analyzed the detailed interplay between ions and local and global conformational changes, the prevalence of non-harmonic distortions and we have obtained reliable estimates for conformational jumps that can be important in explaining the specific binding of proteins or ligands to DNA. Lastly, the simulations of the DDD with PARMBSC1 are shown to accurately reproduce experimental data and to represent a clear improvement over the results obtained with earlier force fields.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

MINECO Severo Ochoa Award of Excellence (Government of Spain) (to IRB Barcelona); Spanish Ministry of Science [BIO2012-32868, BFU2014-61670-EXP to M.O.]; Catalan SGR (to M.O.); Instituto Nacional de Bioinformática (to M.O.); European Research Council (ERC SimDNA) (to M.O.); H2020 program (MuG and BioExcel projects) (to M.O.); Czech Republic Grant Agency [14-21893S to T.D., F.L.]; ANR grant CHROME [ANR-12-BSV5-0017-01 to R.L.]. Funding for open access charge: European Research Council (ERC SimDNA).

Conflict of interest statement. None declared.