Ab Initio Values of the Thermophysical Properties of Helium as Standards

Abstract

Recent quantum mechanical calculations of the interaction energy of pairs of helium atoms are accurate and some include reliable estimates of their uncertainty. We combined these ab initio results with earlier published results to obtain a helium-helium interatomic potential that includes relativistic retardation effects over all ranges of interaction. From this potential, we calculated the thermophysical properties of helium, i.e., the second virial coefficients, the dilute-gas viscosities, and the dilute-gas thermal conductivities of ³He, ⁴He, and their equimolar mixture from 1 K to 10⁴ K. We also calculated the diffusion and thermal diffusion coefficients of mixtures of ³He and ⁴He. For the pure fluids, the uncertainties of the calculated values are dominated by the uncertainties of the potential; for the mixtures, the uncertainties of the transport properties also include contributions from approximations in the transport theory. In all cases, the uncertainties are smaller than the corresponding experimental uncertainties; therefore, we recommend the ab initio results be used as standards for calibrating instruments relying on these thermophysical properties. We present the calculated thermophysical properties in easy-to-use tabular form.

1. Introduction

Today, the most accurate values of the thermophysical properties of helium at low densities can be obtained from two, very lengthy, calculations. The first calculation uses quantum mechanics and the fundamental constants to obtain, ab initio, a potential energy φ(r) for the helium-helium (He₂) interaction at discrete values of the interatomic separation r and also limiting forms of φ(r) at large r (see Fig. 1). The second calculation uses standard formulae from quantum-statistical mechanics and the kinetic theory of gases to obtain the thermophysical properties of low-density helium from φ(r). Here, we report the results of the second calculation spanning the temperature range 1 K to 10⁴ K for the second virial coefficient B(T), the viscosity η(T), the thermal conductivity λ(T), the mass diffusion coefficient D(T), and the thermal diffusion factor α_T(T) for ³He, ⁴He, and their equimolar mixture. Our results, together with estimates of their uncertainties, are presented in easy-to-use tabular form in Appendix A. For the pure fluids, the statistical-mechanics calculations make negligible contributions to the uncertainties of the tabulated properties; therefore, we estimated the uncertainties of the results by varying φ(r) within its uncertainty and examining the consequences. For the equimolar mixture, the results from different orders of approximation in the transport theory are compared to estimate their contribution to the uncertainties.

Fig. 1.

Top: the helium-helium pair potential φ₀₀(r). Note: a logarithmic scale is used for positive values of φ₀₀(r) and a linear scale is used for negative values of φ₀₀(r). Bottom: the uncertainties of the ab initio results and their fractional deviations from φ₀₀(r). Also shown are the fractional deviations of the considered potentials fit to the various ab initio values. The fractional deviations diverge near r = 5.0 bohr where φ₀₀(r) passes through zero. Key: (— —) φ_A; (• • • • • •) φ_SAPT; (— • •) φ_B; □ Ceperley and Partridge [15]; ■ Komasa [24]; ● Korona et al. [18]; ○ van Mourik and Dunning [21]; ◇ van de Bovenkamp and van Duijneveldt [20]; △ Gdanitz [19].

The present results can be applied to many problems in metrology; here we mention a few. Low-density helium is used in primary, constant-volume, gas thermometry [1]; primary, dielectric-constant gas thermometry [2]; and in interpolating gas thermometry (required by ITS-90 in the temperature range 3 K to 24.6 K) [3]. These applications require the extrapolation of measurements to zero pressure. If the present values of B(T) are used for such extrapolations, the results may be more accurate and the probability of detecting systematic errors in the measurements will be increased. Low-density helium can be used to calibrate acoustic resonators for acoustic thermometry and for measuring the speed of sound in diverse gases. Spherical acoustic resonators [4] may be calibrated using the present values of λ(T), B(T), and temperature derivatives dB/dT and d²B/dT². The same properties together with η(T) may be used to calibrate cylindrical acoustic resonators [5]. Other instruments that might be calibrated with the help of the present results include the vibrating wire viscometer [6], the Greenspan acoustic viscometer [7], and the Burnett apparatus [8] for making very accurate measurements of the equation of state of moderately dense fluids.

The present work contrasts with a long tradition of using semi-empirical models for φ(r) to correlate the thermophysical property data for helium and the other monatomic gases [9, 10, 11]. These semi-empirical models combined limited ab initio results with critically evaluated and judiciously selected experimental data to determine the function φ(r) that correlates as much data as possible. In this work, we did not consider experimental results until all of the calculations were completed as in [12, 13]. The ab initio results were then compared to the sets of data that others had selected as inputs to semi-empirical models. In every case that we examined, the ab initio values of the thermophysical properties agreed with the data within plausible estimates of their combined uncertainties.

This manuscript is organized as follows: Sec. 2 reviews the ab initio results for φ(r) and our analytic representation of them. Section 3 outlines the steps in calculating the thermophysical properties of helium from φ(r). Each step includes a description of the precautions that were taken to insure that imperfections of the numerical methods did not adversely affect the results. Section 4 estimates the uncertainty of the ab initio helium pair potential and how it propagates into the uncertainties of the calculated properties. Section 5 describes the tabulated results and methods for their use. Section 6 compares the calculated properties with selected measurements. Section 7 summarizes the present results and the prospects for future refinements.

2. Ab Initio Values for the He₂ Potential Energy Functions φ(r)

Table 1 lists recent ab initio values of φ(r) at selected values of r (3.0 bohr, 4.0 bohr, and 5.6 bohr, where 1 bohr = 0.052917721 nm) and, where available, the uncertainties estimated by the original authors. As is conventional in this field, the potential energy is divided by k_B K and thus has the unit K (k_B is the Boltzmann constant [14] and K is the unit symbol for the kelvin). The various calculations almost, but not quite, agree within their uncertainties. The discrepancies near 4.0 bohr are particularly significant in determining the uncertainties of thermophysical properties of helium near ambient temperatures. A detailed evaluation of each calculation in Table 1 is beyond the scope of this paper. Here, we mention the observations that guided our selection among the sources cited in Table 1 to obtain φ₀₀(r), the function that we used to calculate the thermophysical properties of helium.

Table 1.

Selected ab initio values of φ(r). (1 bohr = 0.052 917 721 nm)

	φ(3.0 bohr)/K	φ(4.0 bohr)/K	φ(5.6 bohr)/K	Remarks
Ceperley and Partridge [15]	3800 ± 100			“exact” QMC
Anderson et al. [16]	3812 ± 96.0		−11.01 ± 0.10	“exact” QMC
Klopper and Noga [17]		294.5 292.6	−10.68 −11.00	corrected to FCI
Korona et al. [18]	3759.959 ± 11.3	291.64 ± 0.9	−11.06 ± 0.03	SAPT
Komasa [24]	3768.469	292.784	−10.947 −10.978	(1200 term) (2048 term) upper bound
Gdanitz [19]	3768.813 3768.0 ± 0.8	293.025 292.7 ± 0.4	−10.947 −11.05 ± 0.10	extrapolated to ∞ basis set
van de Bovenkamp and Duijneveldt [20]		293.48 292.72 ± 0.02	−10.95 −10.99 ± 0.02	corrected to FCI
van Mourik and Dunning [21]		293.498 292.578	−11.00 ± 0.03 −10.99	corrected to FCI

2.1 Long-Ranges: r ≳ 8 bohr

The asymptotic long-range attractive behavior of our preferred potential φ₀₀(r) is represented by the two-body dispersion coefficients C_n (n = 6, 8, …) in the multipole expansion. These coefficients have been calculated, ab initio, by two independent groups [22, 23] using a sum-over-states formalism with explicitly electron-correlated wave functions to describe the states. The independent calculations [22, 23] differed by less than 1 in the fourth digit. This small difference makes a negligible contribution to the uncertainties of the thermophysical properties calculated from φ₀₀(r).

2.2 Short-Ranges: r ≲ 3 bohr

Ceperley and Partridge [15] obtained values of φ(r) at small r using a quantum Monte Carlo (QMC) method. The QMC method is exact insofar as it requires no mathematical or physical approximations beyond those in the Schrödinger equation and the method yields estimates of the uncertainties of φ(r). Komasa [24] used a variational method to obtain rigorous upper bounds to φ(r) in the range 0.01 bohr ≤ r ≤ 15 bohr. At some values of r, the variational values of φ(r) are less than the QMC values; however the differences between the values are usually within twice the QMC uncertainties. Thus, we used the variational values to determine φ₀₀(r) and we have evidence that the QMC uncertainties are reasonable. At smaller values of r the variational and QMC results are inconsistent. For example, at r = 1 bohr (not plotted), Komasa reports φ(1 bohr) = (286.44 ± 0.03) × 10³ K, and Ceperley and Partridge report φ(1 bohr) = (291.9 ± 0.6) × 10³ K. We are unable to resolve this inconsistency; however, the inconsistency does not affect the thermophysical properties in the temperature range 1 K to 10⁴ K.

Komasa provides two values for the well depth at 5.6 bohr, ε/k_B = −10.947 K using a 1200-term basis set and ε/k_B = −10.978 K using a 2048 term basis set. The second value is 0.3 % lower. Komasa’s calculations at other values of r used the 1200-term basis set. We speculate that comparable reductions in φ(r) would occur if Komasa’s variational calculation were repeated with the larger basis set at all values of r.

2.3 Intermediate Ranges: 3 ≳ r ≳ 8 bohr

At intermediate ranges, we considered the seven relevant publications cited in Table 1. Anderson et al. [16] report exact QMC results that have relatively large uncertainties. Klopper and Noga [17] used an explicitly correlated coupled cluster [CCSD(T)] method that resulted in the limiting value for the well depth of ε/k_B = −10.68 K at 5.6 bohr. Then, they estimated the effects of quadruple substitutions to be −0.32 K at 5.6 bohr (and −1.9 K at 4.0 bohr) by comparing their results to the full configuration interaction (FCI) calculation of van Mourik and van Lenthe [25]. This extrapolation to a complete basis set resulted in ε/k_B = −(11.0 ± 0.03) K, which agrees with the QMC results of Anderson [16].

Korona et al. [18] used symmetry-adapted perturbation theory (SAPT) to calculate values for φ(r) with uncertainties that they estimated to be the larger of 0.3 % or 0.03 K in the range 3 bohr ≤ r ≤ 7 bohr. The SAPT well-depth is ε/k_B = −(11.06 ± 0.03) K, the lowest of all ab initio results; however, it also agrees with the QMC result [16] within the latter’s uncertainty.

While this project was in progress, two groups extended the CCSD(T) calculations of Klopper and Noga [17]. These groups (de Bovenkamp and Duijneveldt [20]; and van Mourik and Dunning [21]) used different techniques to extrapolate the results of Klopper and Noga [17] to an infinite basis set. Gdanitz [19] also published calculations labeled r12-MRACPF in which he extrapolated his results to an infinite basis set by yet another method. These three recent publications and the variational results of Komasa [24] indicate that the SAPT [18] results in the region around r = 4.0 bohr are too attractive by approximately 0.05 K (Fig. 1, lower panel). Nevertheless, we used the SAPT intermediate-range results in determining the potential φ₀₀(r) and we used the differences between the SAPT and the other results to determine alternative potentials that were used to estimate the uncertainties of the thermophysical properties. Our decisions are based on three observations. First, we recalled that Komasa’s [24] variational result at 5.6 bohr decreased 0.3 % upon increasing the basis set from 1200 terms to 2048 terms. If Komasa’s result at 4.0 bohr (292.784 K) were decreased by 0.3 %, it would be 291.906 K, in agreement with the SAPT value of 291.64 K. Gdanitz suggested that the decrease at 4.0 bohr might be less than 0.3 % because the variation method is more accurate at smaller separations [26]. Second, we noted that the two extensions of Klopper and Noga’ work [17] are not independent. The two decompose φ(r) in several components, the largest of which were calculated best by Klopper and Noga. Thus, the uncertainties of these results may be dominated by those of Klopper and Noga. (van Mourik and Dunning [21] state, “It is likely that the corrected curve is the most accurate available to date for He₂ interactions”. In effect, they asserted that Klopper and Noga’s interaction energies are more accurate than their own complete basis set extrapolated energies.) Third, Bukowski et al. [27] argue that their own Gaussian-type geminals (GTG) computation bounds the larger components of Klopper and Noga’s CCSD(T) computations and they suggest that Klopper and Noga’s results may be too high by approximately 0.3 K at 4 bohr and by approximately 0.04 K at 5.6 bohr. If Bukowski et al.’s suggestion is correct and if one decreases the CCSD(T) values of φ(r) accordingly, then they all would agree with the SAPT results. Ultimately, additional calculations will resolve these issues.

2.4 Algebraic Representations of ab initio Values of φ(r)

We calculated the thermophysical properties of helium six times, each using a different function to represent ab initio values of φ(r). We fitted two of these six functions, φ00 and φ_B, to our own selections among the published ab initio values. The third function, φ_SAPT, had already been fitted by others to ab initio results and used to calculate thermophysical properties. [18] We fitted the fourth, φ_A, to the same ab initio results used to obtain φ_SAPT; however, we added one additional fitting parameter. Thus, differences between the thermophysical properties computed from φ_SAPT and φ_A provide one indication of the sensitivity of the properties to the algebraic representation of the ab initio “data”. The last two functions are denoted, ${\phi }_{\mathrm{A}}^{-}$, and ${\phi }_{\mathrm{A}}^{+}$. To obtain ${\phi }_{\mathrm{A}}^{-}$, we decreased the ab initio short-range results [15] by their claimed uncertainties and decreased the intermediate-range SAPT results by 0.1 % and re-fitted them. Then, we increased the ab initio results by their claimed uncertainties and the SAPT results by 0.1 % and fitted them to obtain ${\phi }_{\mathrm{A}}^{+}$. The differences between the thermophysical properties calculated using φ_A, ${\phi }_{\mathrm{A}}^{-}$, ${\phi }_{\mathrm{A}}^{+}$ and φ_SAPT are analogous to the uncertainties of measured values of thermophysical properties conducted in a single laboratory and analyzed using different methods. In the present case, the differences between the thermophysical properties calculated from φ_A, ${\phi }_{\mathrm{A}}^{-}$, ${\phi }_{\mathrm{A}}^{+}$, and φ_SAPT are much smaller than the differences between those calculated from φ₀₀, φ_A, and φ_B.

2.4.1 φ₀₀

We used φ₀₀ to calculate the thermophysical properties tabulated in Appendix A. In our judgement, φ₀₀ is the best representation of the ab initio results available at the time of this writing. The subscript “00” identifies φ₀₀ by the year in which we began using it. The ab initio results fitted by φ₀₀(r) come from three sources: (1) at small r (1 < r < 2.5 bohr), the results of the variational calculation from Komasa [24], (2) at intermediate r (3 bohr < r < 7 bohr), the SAPT results from Korona et al. [18], (3) at large r, the asymptotic constants from the “exact” dispersion coefficients of Bishop and Pipin [22] and the higher order dispersion coefficients determined from the approximate relations presented by Thakkar [29]. The algebraic representation of φ₀₀(r) is a modification of the form given by Tang and Toennies [9]. The representation is the sum of repulsive (φ_rep) and attractive (φ_att) terms:

$$\begin{array}{l}{\phi }_{00}\left(r\right)=\{\begin{array}{ll}{\phi }_{\text{rep}}\left(r\right)+{\phi }_{\text{att}}\left(r\right),& 0.3\le r/\text{bohr}<\infty \\ {\phi }_{\text{rep}}\left(0.3\text{bohr}\right)+{\phi }_{\text{att}}\left(0.3\text{bohr}\right),& 0\le r/\text{bohr}<0.3\end{array}\\ {\phi }_{\text{rep}}\left(r\right)=A\exp \left(a_{1}r+a_2{r}^2+a_{-1}{r}^{-1}+a_{-2}{r}^{-2}\right),\\ {\phi }_{\text{att}}\left(r\right)=-{\displaystyle \sum _{n=3}^8\frac{f_{2n}\left(r\right)C_{2n}}{r^{2n}}}\left[1-\left({\displaystyle \sum _{k=0}^{2n}\frac{{\left(\delta r\right)}^k}{k!}}\right)\exp \left(-\delta r\right)\right].\end{array}$$ (1)

Equation (1) includes the factor f_2n(r) that accounts for the relativistic retardation of the dipole-dipole (n = 3) term applied over all r. This factor changes the behavior of the dipole-dipole term from r⁻⁶ to r⁻⁷ at very large r, and it was taken from Jamieson et al. [30]. When the expressions for the retardation of the higher dispersion terms C₈ and C₁₀ given by Chen and Chung [23] were applied to φ₀₀, the well depth changed by only 0.0014 K out of 11 K. The resulting changes in the calculated thermophysical properties were much smaller than their uncertainties; thus, we used the approximation f_2n(r) ≡ 1 for n > 3. (Note: retardation is included when calculating the thermophysical properties; however, by convention, it is not included when comparing Eq. (1) to the ab initio results.) We also considered the adiabatic correction of the helium dimer given by Komasa et al. [28]. The effects of this correction were also much smaller than those from the uncertainties in φ(r); thus, we omitted this correction.

The definition of φ₀₀(r) in Eq. (1) is broken into two ranges. If this were not done, φ₀₀(r) would have a spurious maximum at very small values of r. As indicated in Eq. (1), the break-point was set at 0.3 bohr.

The dispersion coefficients (C₆, C₈, … C₁₆) in Eq. (1) and Table 1 were held fixed [22, 29]. The values of the remaining parameters in Table 1 (a₋₂, a₋₁, a₁, a₂, and δ) were determined by fitting φ₀₀(r) to the ab initio results. When fitting φ₀₀ the ab initio results were weighted in proportion to the reciprocal of the uncertainty squared, where the uncertainties were taken (when available) from the publications that presented the results. [15, 18, 20, 21, 24].

2.4.2 φ_SAPT

Korona et al. fitted their SAPT results and the QMC values of Ceperley and Partridge [15] to the algebraic expression of Tang and Toennies [9] while holding constant the asymptotic dispersion coefficients of Bishop and Pipin [22]. They included higher order dispersion coefficient determined with combining rules of Thakkar [29] and retardation effects of the C₆ dispersion coefficient as given by Jamieson et al. [30]. Janzen and Aziz [11] calculated the thermophysical properties of helium using φ_SAPT and they “judged it to be the most accurate characterization of the helium interaction yet proposed.” We believe that φ₀₀ is more accurate than φ_SAPT because it uses the recent, accurate variational results of Komasa [24] instead of the earlier short range QMC values of Ceperley and Partridge [15].

2.4.3 φ_A ${\phi }_{\mathrm{A}}^{-}$, and ${\phi }_{\mathrm{A}}^{+}$

In an attempt to ascertain how uncertainties in the interaction energies propagate into the thermophysical properties we constructed alternative potentials which differed in the choice of ab initio results, and in the form of the algebraic expression. The first alternative, denoted φ_A, was obtained by fitting the exact same ab initio results from [18, 22, 24, 29] as φ_SAPT. The algebraic expression of Tang and Toennies [9] was modified by adding a a₃r³ to the exponent of the repulsive term, such that φ_rep = A exp(a₁r + a₂r² + a₃r³). The additional a₃r³ term enables φ_A to fit the φ_SAPT ab initio results within 0.1 % in two regions r = 3 bohr and at r > 6 bohr where φ_SAPT [18] deviates from the ab initio results slightly greater than 0.1 %.

To obtain ${\phi }_{\mathrm{A}}^{-}$, we decreased the ab initio short-range [15] and long-range [22] results by their claimed uncertainties and decreased the intermediate-range SAPT results by 0.1 % and the long-range dispersion coefficients by 0.08 %. Equation (1) was then re-fitted to obtain ${\phi }_{\mathrm{A}}^{-}$. We then increased the ab initio results by their claimed uncertainties and the intermediate-range SAPT results by 0.1 % and again fitted them to obtain ${\phi }_{\mathrm{A}}^{+}$.

2.4.4 φ_B

The potential φ_B, uses the CCSD(T) results of van Mourik and Dunning [21] and of van de Bovenkamp and van Duijneveldt [20] instead of the SAPT results of Korona et al. [18] in the intermediate range of 3 bohr < r < 7 bohr. To fit these values the algebraic expression of Tang and Toennies [9] was modified again by adding a a₋₁r⁻¹ and a₋₂r⁻² to the exponent of the repulsive term, such that φ_rep. = A exp(a₁r + a₂r² + a₋₁r⁻¹ + a₋₂r⁻²).

2.5 Comparison of φ₀₀, φ_SAPT, φ_A, and φ_B

Table 2 and the lower panel of Fig. 1 display the changes in φ(r) resulting from alternate choices among the ab initio results. The differences between the thermophysical properties calculated using φ₀₀, φ_SAPT, φ_A, and φ_B are analogous to the differences between measurements of thermophysical properties conducted in different laboratories using different methods and they are used to estimate the uncertainties of the results for pure ³He and pure ⁴He.

Table 2.

Parameters for Eq. (1) in atomic units (1 bohr = 1 Bo = 0.052 917 721 nm, 1 hartree = 1 Ha = 3.157 746 5 × 10⁵ K)

Property (unit)	φ00	φA	${\phi }_{\mathrm{A}}^{+}$	${\phi }_{\mathrm{A}}^{-}$	φB	φSAPT
10−6 A (K)	2.83379199	2.02311	2.03130	2.01529	3.12631	2.07436426
a1 (Bo−1)	−1.986231822	−1.84827	−1.85059	−1.84616	−2.01639	−1.88648251
102 a2 (Bo−2)	−5.034284240	−7.55879	−7.50314	−7.60470	−4.67475	6.20013490
103 a3 (Bo−3)	0.0	1.82924	1.71078	1.93491	0.0	0.0
a−1 (Bo)	−0.3514929118	0.0	0.0	0.0	−0.47972	0.0
a−2 (Bo2)	0.1101468439	0.0	0.0	0.0	0.16755	0.0
δ (Bo−1)	2.00788607	2.03451	2.02137	2.04780	2.01997	1.94861295
C6 (Ha·Bo−6)	1.46097780	1.46098	1.45981	1.46215	1.46098	1.46097780
10−1 C8 (Ha·Bo−8)	1.4117855	1.41179	1.41066	1.41291	1.41179	1.4117855
10−2 C10 (Ha·Bo−10)	1.83691250	1.83691	1.83544	1.83838	1.83691	1.83691250
a10−3 C12 (Ha·Bo−12)	3.265	3.265	3.262	3.268	3.265	3.265
a10−4 C14 (Ha·Bo−14)	7.644	7.644	7.638	7.650	7.644	7.644
a10−6 C16 (Ha·Bo−16)	2.275	2.275	2.273	2.277	2.275	2.275

^aCalculated using combining rules of Thakkar [29]

Table 3 lists some characteristic properties of the potentials that we have used. They include the well depth ε/k_B, the locations of the zero (σ) and of the minimum (r_m) of the potential, and the energy of the bound state (E_b) of a pair of ⁴He atoms. Following Janzen and Aziz [31], we estimated the number of Efimov states N_E from the scattering length and the effective range with the result N_E = 0.77 ± 0.01 for φ₀₀. Because N_E < 1 for all potentials in Table 2, Efimov states are unlikely to exist. A discussion of these properties of the interatomic potential for helium can be found in Ref. [31].

Table 3.

Properties of the fitted helium potentials. (1 Å = 10⁻¹⁰ m)

Property (unit)	φ00	φA	φB	${\phi }_{\mathrm{A}}^{-}$	${\phi }_{\mathrm{A}}^{+}$
ε/kB (K)	11.054	11.063	10.974	11.074	11.052
rm (bohr)	5.6039	5.6034	5.6097	5.6034	5.6034
rm (Å)	2.9654	2.9652	2.9685	2.9625	2.9652
σ (bohr)	4.9873	4.9870	4.9922	4.9868	4.9873
scattering length (Å)	83.68	82.00	96.91	85.30	78.90
effective range (Å)	7.24	7.24	7.30	7.26	7.22
bound state/kB (mK)	1.90	1.98	1.39	1.83	2.51

3. Numerical Calculations and Their Uncertainties

Here, we outline the steps required to calculate the thermophysical properties of helium from the interatomic potential. We also describe the precautions that were taken to insure that the uncertainties in the results from approximations in statistical mechanics and in the numerical methods were both smaller than the uncertainties results from different choices for φ(r).

The initial steps of calculating the thermophysical properties that depend upon pairs of helium atoms are all the same. (1) The Schrödinger equation for the scattering of a helium atom at the energy E in the potential φ(r) is separated in spherical coordinates, (2) the radial part of the wave function is expanded in partial waves ψ_ℓ(r) of angular momentum ℓ, (3) several nodes of the scattered wave are located far from the scattering atom, and (4) the phase shifts δ_ℓ of the scattered wave are determined and (5) summed with appropriate statistics to obtain cross sections. The summations account for large symmetry effects at low temperatures [32]. Thus, separate summations are required for ³He and ⁴He and their mixtures when calculating the second virial coefficient and the transport properties. The final step (6) is an integration over energy that is appropriate to the thermophysical property under consideration.

3.1 Integration of the Radial Schrödinger Equation

The Schrödinger equation is separated in spherical coordinates and decomposed into angular momentum states to obtain

$$\left(\frac{{\mathrm{d}}^2}{\mathrm{d}{r}^2}+k^2-\frac{\ell \left(\ell +1\right)}{r^2}-\frac{2\mu }{\hslash }\phi \left(r\right)\right){\psi }_{\ell }\left(r\right)=0$$ (2)

where ħ is Planck’s constant [14] divided by 2π, µ is the reduced mass µ= (m₁ + m₂)/m₁m₂, k = (2µE)^1/2/ħ is the wave number, and E is the energy of the incoming wave. Equation (2) is integrated to obtain the perturbed wave functions ψ_ℓ(k, r). The location r_n of the nth zero (or node) of the wave function ψ_ℓ(k, r) was found using a five point Aiken interpolation formula with values of ψ_ℓ(k, r) near the nth node. The integration was performed using Numerov’s method [33] as implemented in [34] and [35]. At each energy, r_n was recalculated using successively smaller step sizes. The calculation was terminated when halving the step size changed r_n less than 10⁻⁹ × r_n. We verified that the tolerance 10⁻⁹ × r_n was sufficiently small that further reductions of the step-size did not change the thermophysical properties beyond the tolerances given in Table 6. The final sizes of the integration steps are listed in Table 4.

Table 6.

Relative uncertainty of thermophysical properties of pure ⁴He and ³He propagated from the differences between potentials

2000	ΔB/B × 104	Δη/η × 104	Δλ/λ × 104	ΔD12/D12 ×104	ΔαT/αT × 104
2	80	40	40	56	301
5	89	17	17	15	84
10	125	6.3	6.5	5.8	32
20	559	5.4	5.2	4.5	10
50	91	8	8	6.6	7.5
100	43	7.7	7.7	6.4	4.4
200	29	6.7	6.8	5.8	4.5
300	22	6.1	6.2	5.4	4.1
400	19	5.7	5.8	5.1	7.1
500	17	5.5	5.5	4.9	9.8
1000	14	4.8	4.8	4.6	19.9
2000	11	4.6	4.6	5.6	33

Table 4.

Integration step sizes used in a given energy range to locate the nth zero of ψ_ℓ(k, r)

Integration step size (cm−1)	Applicable range (cm−1)
0.0001	0.0 ≤ k ≤ 0.01
0.001	0.01 ≤ k ≤ 0.4
0.01	0.4 ≤ k ≤ 10.0
0.05	10.0 ≤ k ≤ 100.0
0.1	100.0 ≤ k

3.2 Calculation of Phase Shifts, δ_ℓ(k,n)

The relative phase shifts, δ_ℓ(k,n) of the outgoing partial wave were evaluated from the relation

$${\delta }_{\ell }\left(k,n\right)=\arctan \frac{{\mathrm{j}}_{\ell }\left(k,r_n\right)}{{\mathrm{n}}_{\ell }\left(k,r_n\right)}$$ (3)

where j_ℓ(k,r_n) and n_ℓ(k,r_n) are the Bessel and Neuman functions for angular momentum quantum number ℓ and wave number k. In practice, the phase shifts were evaluated at groups of three consecutive nodes. If the phase shift did not change by more than 10⁻⁸ × δ_ℓ(k,n) between the first and last of the three nodes, it was assumed that n (and r_n) were sufficiently large that additional effects of the potential were negligible, and the calculation was terminated. Otherwise, the calculation was continued to larger values of r, and the test was repeated. We verified that the tolerance 10⁻⁸ × δ_ℓ(k,n) is consistent with the uncertainties of the thermophysical properties listed in Table 6.

3.3 Calculation of the Second Virial Coefficient, B(T)

The second virial coefficient was obtained by adding two or three terms; the first term is a thermal average B_th(T), the second term is that of an ideal gas B_ideal(T), and the third term is the bound state term B_bound(T), which applies to ⁴He, but not to ³He because a bound state exists only for ⁴He.

3.3.1 The Thermal Average Term B_th(T)

The thermal average term B_th(T) is

$$B_{\text{th}}={\displaystyle \underset{0}{\overset{\infty }{\int }}k\exp \left(-\frac{k^2}{k_{\mathrm{B}}T}\right)}{\displaystyle \sum _{\ell =0}^{\infty }\left(2\ell +1\right){\delta }_{\ell }\left(k,n\simeq \infty \right)\mathrm{d}k}$$ (4)

where k_B is the Boltzmann constant, and δ_ℓ(k,n ≃ ∞) is the phase shift at large enough separation that the potential no longer perturbs the outgoing wave function [32, 36].

Equation (4) contains both a sum and an integral with the limits 0 and ∞. Truncating the sum and the integral at a finite upper bound is a potential source of error. At each value of k, the sum was computed until the addition of six phase shifts did not change the sum by more than 10⁻⁸ of its value. At the lowest energies, this condition was met after adding seven phase shifts; at the highest energies, hundreds of phase shifts were added.

At this step of the calculation, symmetry effects are incorporated. The unweighted sum [Eq. (4)] is carried out over all values of ℓ only when calculating the interaction virial coefficient for mixtures of ³He and ⁴He, because these atoms are distinguishable and follow Boltzmann statistics. For pure ³He and ⁴He, weighted sums are performed over the even and odd values of ℓ using the formulas

$$\begin{array}{c}{\displaystyle {\sum }_{\text{BE}}}=\left[\frac{s+1}{2s+1}\right]{\displaystyle \sum _{\text{even}}+\left[\frac{s}{2s+1}\right]}{\displaystyle \sum _{\text{odd}} }\\ {\displaystyle {\sum }_{\text{FD}}}=\left[\frac{s+1}{2s+1}\right]{\displaystyle \sum _{\text{odd}}+\left[\frac{s}{2s+1}\right]}{\displaystyle \sum _{\text{even}} }\end{array}$$ (5)

where s is the spin quantum number (0 for ⁴He; ½ for ³He), BE stands for Bose-Einstein statistics for bosons (⁴He), and FD stands for Fermi-Dirac statistics for fermions (³He). Details on this calculation can be found in Ref. [32].

The integral in Eq. (4) was evaluated using a standard integration routine, DQAGI [37]. This routine is designed for semi-infinite or infinite intervals and automatically uses nonlinear transformation and extrapolation to achieve user-specified absolute and relative tolerances for a user-specified function. The relative error was set to 10⁻⁸. If the integrator could not achieve this accuracy, an error message would have been reported the problem.

3.3.2 The Ideal-Gas and Bound State Terms B_ideal(T) and B_bound(T)

The ideal-gas contribution B_ideal(T) is negative for BE and positive for FD, and zero for Boltzmann statistics as given by

$$B_{\text{ideal}}=\pm N_{\mathrm{A}}{2}^{-5/2}{\lambda }^3$$ (6)

where N_A is the Avagodro constant and λ ≡ [ħ/(µk_BT)]^1/2 is the “thermal wavelength.” The ideal-gas term is important only at low temperatures; it is 1/10 of B(T) at 5 K and 1/100 of B(T) at 75 K. The ideal-gas term is a function of fundamental physical constants and the resulting standard uncertainty is on the order of 10⁻⁶.

For ⁴He, the bound state term B_bound(T) is

$$B_{\text{bound}}=-N_{\mathrm{A}}{2}^{-3/2}{\lambda }^3\left({\mathrm{e}}^{E_{\mathrm{b}}/k_{\mathrm{B}}T}-1\right)$$ (7)

where E_b is the energy of the bound state. The bound state term is 1/1000 of B(T) at 3 K and 1/100 of B(T) at 0.4 K. E_b was determined from integrating the Schrödinger equation; thus, it depended upon the integration step size. Decreasing step sizes were used until consecutive values of E_b differed by less than 10⁻⁶ × E_b. This numerical uncertainty is much smaller than the 18 % difference between E_b determined from ${\phi }_{\mathrm{A}}^{-}$ and that determined from ${\phi }_{\mathrm{A}}^{+}$ (Table 3).

The sum of the numerical uncertainties in the calculation of B(T) is at most 10⁻⁵ × B(T). This is insignificant compared with the uncertainty of B(T) which arises from the uncertainty of the potential φ(r). For example, the uncertainty of B(T) resulting from the uncertainty of φ(r) is 0.0022 × B(T) at 300 K; the relative uncertainties at other temperatures are listed in Table 6.

3.4 Calculation of the Transport Properties

In order to calculate the transport properties, we used the numerical methods outlined above to obtain the phase shifts as functions of the wave number and angular momentum quantum number. Then we computed the sums over the phase shift that determine the quantum cross sections, Q⁽¹⁾, Q⁽²⁾, Q⁽³⁾….Q⁽ⁿ⁾, etc. [38]. The cross sections were integrated with respect to energy to obtain the temperature-dependent collision integrals. Finally, the transport properties were calculated using the appropriate combinations of the collision integrals.

3.4.1 Calculation of the Quantum Cross Sections Q⁽ⁿ⁾

The quantum cross sections are functions involving the sums of the phase shifts that depend upon the symmetry of the interacting atoms. The sums over the even and the odd values of ℓ are needed separately:

$$\begin{array}{c}{Q}_{\text{odd}}^{\left(1\right)}=\frac{4\mathrm{\pi }}{k}{\displaystyle \sum _{\ell =1,3,5\dots }^{\infty }\left(2\ell +1\right){\sin }^2{\delta }_{\ell }}\\ Q_{\text{even}}^{\left(1\right)}=\frac{4\mathrm{\pi }}{k}{\displaystyle \sum _{\ell =0,2,4\dots }^{\infty }\left(2\ell +1\right){\sin }^2{\delta }_{\ell }}\end{array}$$ (8)

and then weighted sums are computed. To evaluate Q⁽¹⁾ for Bose-Einstein (BE) or Fermi-Dirac (FD) statistics the sums are weighted with the spin-dependent quotients, as shown in Eq. (5). As for the case of the second virial coefficient, the sums in Eq. (8) extend to ℓ = ∞. The sum was continued until the addition of six more phase shifts changed the cross section by less than 10⁻⁸ of its value. Cross sections with moments up to n = 6 are required to calculate the collision or omega integrals used in the higher order approximations for the transport properties. The equations for these calculations are given by Ref. [38].

3.4.2 Calculation of the Collision Integrals Ω^(n,s)

The reduced collision integrals were evaluated from the equation

$$\begin{array}{r}{\Omega }^{\left(n,s\right)★}\left(T^{★}\right)={\left\{\left(s+1\right)!T^{★\left(s+2\right)}\right\}}^{-1}\\ \times {\displaystyle \underset{0}{\overset{\infty }{\int }}{Q}^{\left(n\right)★}\left(E^{★}\right){\mathrm{e}}^{-E^{★}/T^{★}}{E}^{★\left(s+1\right)}\mathrm{d}{E}^{★}}\end{array}$$ (9)

where the superscript ^★ indicates that both the energy and the temperature were scaled by the well-depth of φ₀₀ and Q^(n)★ was scaled by the value Q^(n)★ for a rigid sphere of radius r_m, the location of the minimum of φ₀₀ (Table 3; See Ref. [32]).

In order to evaluate of Eq. (9), the quantum cross sections Q^(n)★ must be calculated at each energy E used for the quadrature. We calculated a table of Q^(n)★ as a function of E^★ and used a 5 point Aiken interpolation to determine values of Q^(n)★ between tabulated values. The intervals in the table were determined such that the interpolated values had a uncertainty of less that 10⁻⁶ × Q^(n)★. Equation (9) was integrated using the automated quadrature routine DQAGI [37], discussed in Sec. 3.1.3, with the tolerance set to 10⁻⁸. The numerical methods used to calculate the collision integrals yielded results with a relative uncertainty of less than 10⁻⁵.

3.4.3 Calculation of the Transport Properties From the Collision Integrals

The transport properties of dilute gases are calculated using combinations of the collision integrals in approximations of increasing complexity and accuracy. The viscosity and thermal conductivity of pure ³He and ⁴He were calculated to the 5th order approximation [39]. The equimolar mixture thermal conductivity [40] and thermal diffusion factors [41] were calculate to the 3rd order, and the diffusion coefficient and mixture viscosity were calculated to 2nd order. Figure 2 shows the effects of truncating the order of the calculation. The changes in η and λ for ⁴He and equimolar mixtures of ⁴He and ³He are compared at four temperatures upon increasing order of the approximation. The calculations converge very well; 2nd to 3rd order results in less than a 0.1 % change, 3rd to 4th order results in less than a 0.01 % change, and 4th to the 5th order less than 0.001 %. The behavior of the other transport properties (η and λ for pure ³He, D₁₂, and α_T) is similar to that shown in Fig. 2. Figure 2 shows that the change in η and λ of the equimolar mixture from 1st to 2nd order, is very close to that of pure ⁴He. These results show that only calculations of the 2nd order contribute any significant uncertainty to the calculated properties. From these observations, we conclude that the relative uncertainty of η and D₁₂ for the equimolar mixture ranges from 0.01 % to 0.04 % in the temperature range 10 K ≤ T ≤ 10⁴ K. Figure 2, together with the equivalent figure for pure ³He, suggest that, at T > 100 K, the accuracy of the calculated η and D₁₂ for the equimolar mixture might be improved if one extrapolated from 2nd order to 5th order by following the curves for pure ⁴He and ³He.

Fig. 2.

Asymptotic approach of viscosity and thermal conductivity of ⁴He as a function of increasing order of approximation along the four indicated isotherms. The open symbols are for the equimolar mixture of ³He and ⁴He.

The rapid reduction of the uncertainty of the calculated viscosity with increasing order of approximation is not sensitive to φ(r); Viehland et al. [39] obtained similar results for the viscosity of rigid atoms that interact via (12-6) Lennard-Jones potentials.

3.5 Interpolation as a Function of Temperature

The tables in Appendix A list values of the second virial coefficient, the transport properties, and their first derivatives as functions of temperature. The temperature intervals were chosen so that the errors from linear interpolation would be smaller than the uncertainties propagated from the uncertainties of the interatomic potential. Table 5 lists bounds of the interpolation errors, and the unweighted average over the entire temperature range. Below 10 K, the interpolation errors increase because the temperature derivatives of the properties increase.

Table 5.

Relative uncertainties from interpolating between tabulated temperatures

	Max (1 K to 10 K)	Max (10 K to 104 K)	Average (1 K to 104 K)
ΔB/B × 106	187	95.3	18.0
Δη/η × 106	107	3.23	3.01
Δλ/λ × 106	85.5	3.24	3.05
ΔD12/D12 × 106	1.95	1.93	0.38
ΔαT/αT × 106	288	6.55	6.43

3.6 Classical Calculation

We made an important check of the entire calculation of each thermophysical property. To do so, we performed the relatively simple classical calculation [32] which is valid at high temperatures where the ratio of the de Broglie wavelength h(2πmkT)^−1/2 to atomic diameter σ is much less than 1. Figures 3 and 4 show that the classical calculations of the viscosity and of the second virial coefficient asymptotically approach the quantum results.

Fig. 3.

Fractional deviation of the calculated viscosity using the considered potentials. The base line is the viscosity calculated to the 5th approximation for ⁴He from φ₀₀. The other curves are identified in the figure. The shaded region around the curve for φ_A shows how ${\phi }_{\mathrm{A}}^{-}$ and ${\phi }_{\mathrm{A}}^{+}$ vary the predicted viscosity. Also shown is the classically calculated viscosity asymptotically approaching the quantum values with increasing temperature.

Fig. 4.

Fractional deviation of the calculated second virial coefficient using the considered potentials. The base line is B₀₀ calculated for ⁴He using φ₀₀. The other curves are as identified in the figure. The shaded region around the curve for B_A shows how ${\phi }_{\mathrm{A}}^{-}$ and ${\phi }_{\mathrm{A}}^{+}$ influence the predicted B. Also shown is the classically calculated value for B(T) asymptotically approaching the quantum values with increasing temperature.

4. Uncertainties of the Thermophysical Properties From the Uncertainty of the Potential

We now evaluate how the uncertainty of the ab initio values of φ(r) propagates into the uncertainty of calculated thermophysical properties. To do so, we calculated the properties with each of the potentials discussed in Sec. 2 and we plotted the results as deviations from the results obtained for φ₀₀(r). Figure 3 shows these deviations for the viscosity of ⁴He. In Fig. 3, the width of the shaded band surrounding the curve φ_A spans the range of results obtained with ${\phi }_{\mathrm{A}}^{-}$ to those obtained with ${\phi }_{\mathrm{A}}^{+}$. Similar bands could have been placed about the results from those obtained with φ₀₀, φ_B, and φ_SAPT; they were omitted for clarity.

We took the differences in the alternative potentials as an accurate estimate of the uncertainty in φ₀₀. By comparing the properties calculated from each alternative potential, we estimated the actual uncertainty propagated into each reported thermophysical property. Figure 3 shows that as the temperature is increased from 1 K to 10 K, the relative uncertainty of the viscosity u_r(η) of ⁴He decreases from 0.4 % to 0.1 %. In this temperature range, the discrepancies among the potentials are comparable to the uncertainty of each potential, as indicated by the width of the shaded band. In the range 10 K < T < 1000 K, the difference between the results obtained using φ₀₀ and the results obtained with φ_B and φ_SAPT lead us to conclude that u_r(η) is approximately 0.08 %. If the discrepancies between the ab initio results around 4.0 bohr could be resolved, then u_r(η) would be reduced by nearly a factor of three in this temperature range. In the range 1000 K < T < 10⁴ K, we also conclude u_r(η) ≈ 0.08 %. In this temperature range, the results from φ₀₀ and φ_B are more reliable than the results from φ_A and φ_SAPT having been fit to the short-range variational calculations of Komasa [5] as discussed in Sec. 2, above.

The relative uncertainty of the second virial coefficient u_r(B) of ⁴He can be judged from Fig. 4. In the range 1 K < T < 10 K, u_r(B) ≈ 1 %. At T ≈ 23.4 K, B(T) passes through zero. There, u_r(B) diverges; however, the uncertainty of B, u(B) ≈ 0.3 cm³·mol⁻¹. In the range 100 K < T < 10⁴ K, u_r(B) of ⁴He gradually declines from 0.4 % to 0.1 %.

The uncertainties for each property are summarized in Table 6 from comparisons similar to those provided in Figs. 3 and 4 and described in the preceding paragraphs. These uncertainties are much lower than those from measurements; thus, the corresponding values of the properties listed in the Appendices can be used as standards.

5. Results

The results of the present calculations for ⁴He, ³He, and their equimolar mixture are listed in Tables A1, A2, and A3 in Appendix A. These tables contain the second virial coefficient B for the pure species and the interaction second virial B₁₂ where $B_{\text{mix}}=x_1^2{B}_{11}+2x_1{x}_2{B}_{12}+x_2^2{B}_{22}$. The zero-density viscosity, thermal conductivity and their equimolar mixture. The diffusion coefficient at 101.325 kPa (one atmosphere), and the thermal diffusion factor. Derivatives with respect to temperature are provided to facilitate interpolation and for use in calculating acoustic virial coefficients. The tables for pure ⁴He and ³He contain the self-diffusion coefficient calculated without symmetry effects (Boltzmann statistics), and the thermal diffusion factor of a mixture of 99.999 % ⁴He or ³He respectively. The tables span the temperature interval 1 K ≤ T ≤ 10⁴ K. The highest temperature is well below the first excited state of helium (2 × 10⁵ K) and well below 2.91 × 10⁵ K, the highest value of the ab initio results used to determine φ_A. In order to calculate the thermophysical properties between the tabulated temperatures, we recommend interpolation using the cubic polynomial f(T) such that

$$\begin{array}{l}f\left(T\right)=a\left(T-T_1\right)+b\left(T-T_2\right)+\left\{c\left(T-T_1\right)+d\left(T-T_2\right)\right\}\left(T-T_1\right)\left(T-T_2\right)\\ \begin{array}{cc}a=f\left(T_2\right)/\mathrm{\Delta }T& c=\left\{f^{\prime }\left(T_2\right)/\left(\mathrm{\Delta }T\right)\right\}-\left\{\left(a+b\right)/{\left(\mathrm{\Delta }T\right)}^2\right\}\\ b=f\left(T_1\right)/\mathrm{\Delta }T& d=\left\{f^{\prime }\left(T_2\right)/{\left(\mathrm{\Delta }T\right)}^2\right\}-\left\{\left(a+b\right)/{\left(\mathrm{\Delta }T\right)}^2\right\},\end{array}\end{array}$$ (10)

where f′ = df/dT and ΔT = T₂ − T₁. The calculated values listed in the Tables are accurate to the uncertainties discussed in Sec. 4. Equation (10) contributes an additional uncertainty from the interpolation discussed as in Sec. 3.

6. Comparison With Measurements

In this section we compare the values of the thermophysical properties calculated using φ₀₀ with the best experimental values. In nearly every case, the experimental values agree with the calculated values within their combined uncertainties, and the calculated properties have the smaller uncertainties.

6.1 Second Virial Coefficient

Figure 5 displays the deviations of various experimental values of B(T) for ⁴He from B₀₀(T) calculated using φ₀₀. The dashed curves in Fig. 5 represent the values of B_A(T), calculated using φ_A, and the dash-dot-dot curves the values of B_B(T), calculated from φ_B. Also shown in Fig. 5 and summarized in Table 7, are measured values of B(T) along with their reported uncertainties. In nearly every case, B₀₀(T) agrees with the experimental values within the uncertainties of the experimental values. The maximum uncertainties of B₀₀(T) are estimated by comparing the variances with B_A(T) and B_B(T). These uncertainties are much smaller than the experimental uncertainties (see the dash-dot-dot curve in Fig. 5.).

Fig. 5.

Deviations of B_exp of ⁴He from B₀₀ calculated using φ₀₀. Key: ● Ref. [42]; ○ Ref. [42] adjusted by Ref. [43]; ■ Ref. [43]; ▲ Ref. [43]; ▼ Ref. [44]; ♦ Ref [45]; □ Ref. [46]; △ Ref. [8] Eqs. (37) and (38); — — Values of B_A(T) calculated using φ_A; — • • — B_B(T) calculated using φ_B.

Table 7.

Deviations of B_exp from B₀₀ calculated using φ₀₀

Authors [reference]	Temp. range	<|Bexp − B00|>	Range (Bexp − B00)	Reported uncertainties
	(K)	(cm3·mol−1)	(cm3·mol−1)	(cm3·mol−1)
Berry [42]	2.60 to 27.10	0.41	0.14 to 0.83	0.20 to 1.00
Gugan and Michel [43] [corrected for C(T)]	4.22 to 27.10	0.13	0.04 to 0.20	0.20 to 0.70
Gugan and Michel [43]	4.23 to 27.17	0.15	0.03 to 0.33	0.01 to 0.07
Kemp et al. [44]	27.10 to 172.01	0.06	−0.05 to 0.11	0.13 to 0.16
Gammon [45]	98.15 to 1474.85	0.05	−0.07 to 0.07	0.05 to 0.06
Kell et al. [46]	273.15 to 623.15	0.03	−0.05 to 0.05	0.01 to 0.15
Waxman and Davis [8]	298.15	0.08	0.08	0.01
Matacotta et al. [47]	1.47 to 20.30	0.42	−0.14 to 0.96	0.20 to 1.00

At very low temperatures B(T) is sensitive to the shape of the potential well. Figure 5 shows that the lower well depth of φ₀₀ predicted by Korona et al. [18] reproduces the low temperature measurements better than the shallower well depth predicted by Van de Bovenkamp and van Duijneveldt [20] and by Van Mourik and Dunning [21]. To further strengthen this argument, it is known that the low temperature second virial measurements have not been corrected for contributions from the third virial coefficient C(T). For ⁴He [42], the size of this “third virial correction” can be seen in the top panel of Figure 5. In that panel, the solid circles show the values B(T) before they were corrected in Ref. [43], and the open circles show the values after the correction. The correction for C(T) lowers the second virial values bringing them further in line with B₀₀(T) and away from B_B(T) indicating a preference for the lower well depth.

Table 7 provides two numerical measures of the differences between experimental values of B(T) and those calculated using φ₀₀. One measure is the mean of the absolute values of the differences B_exp − B₀₀ and the second is the range of these differences. The final column of Table 7 lists the range of the uncertainties reported by the experimenters. In nearly all cases the experimental uncertainties exceed the differences B_exp − B₀₀.

Figure 6 compares B_exp(T) of ³He, deduced from the measurements of Matacotta et al. [47], with B₀₀(T). There is an obvious trend in the deviations which is larger than the experimental uncertainties below 5 K. Probably, the trend would be removed if B_exp(T) was corrected for the for effects of the third virial coefficient of ³He [48] as discussed above for ⁴He [42].

Fig. 6.

Deviation of B_exp of ³He from B₀₀ calculated using φ₀₀(r). ■ Ref. [47]; — — Values of B_A calculated using φ_A; — • • — B_B calculated using φ_B.

6.2 Viscosity

Figures 7 and 8 and Table 8 compare the zero-density viscosity η₀₀, calculated using φ₀₀, with measured values from many sources. The experimental results are typically reported at 101.325 kPa where the density dependence is negligible in comparison with experimental uncertainties. Figure 7 shows the viscosity of ³He and ⁴He at low temperatures where the large quantum effects lead to important differences between the isotopes. The η₀₀(T) values are in good agreement with the measurements of Becker et al. [49].

Fig. 7.

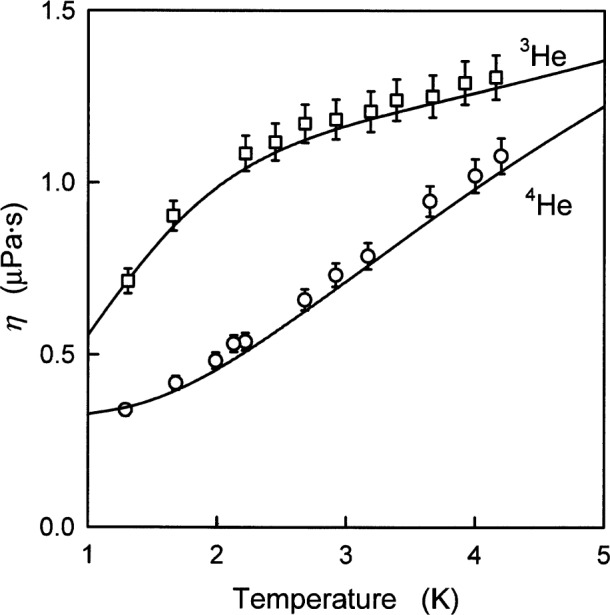
The viscosity of ³He and ⁴He at low temperature. Experimental values: □ for ³He and ○ for ⁴He from Ref. [49], ±5 % uncertainty bars are shown. The curves are η₀₀ calculated using φ₀₀.

Fig. 8.

Relative deviations of η_exp of ⁴He from η₀₀ calculated using φ₀₀(r). Experimental values: ● Ref. [51]; ■ Ref. [58]; Δ Ref. [54]; ▲ Ref [56] (smoothed); ○ Ref. [52]; □ Ref. [50]; ∇ Ref. [61]; — — Values of η_A calculated using φ_A; — • • — η_B calculated using φ_B.

Table 8.

Relative deviations of η_exp from η₀₀ calculated using φ₀₀

	Temperature range (K)	100× (Δη/η00)rms	Range of 100 × Δη/η00	Reported uncertainties (%)
Wakeham et al. [50]	298 to 793	0.22	0.12 to 0.32	0.2 to 0.5
Maitland and Smith [51]	80 to 2000	−0.51	−2.27 to −0.51	1.5
Vogel [52]	294.5 to 647.9	0.06	0.02 to 0.12	0.3
Kestin et al. [53]	298 to 973	0.20	0.08 to 0.30	0.1 to 0.3
Clark and Smith [54]	77.5 to 373	0.58	0.18 to 1.21	0.5
Dawe and Smith [55]	293 to 1600	−1.16	−2.43 to 0.45	1.0
Coremans et al. [56]	20.4 to 77.8	4.03	1.77 to 6.33	3.0
Kestin and Wakeham [57]	298 to 473	0.16	0.10 to 0.22	0.3
Johnston and Grilly [58]	79 to 296	−0.96	−1.60 to −0.18	3.0
Kalelkar and Kestin [59]	298 to 1121	−0.31	−2.16 to 0.46	0.5
Becker et al. [49] 4He	1.3 to 4.2	5.15	−1.65 to 9.57	5.0
Becker et al. [49] 3He	1.3 to 4.2	2.73	−0.13 to 4.37	5.0
Kestin et al. [60]	298 to 778	0.35	0.08 to 0.57	0.1 to 0.3
Guevara et al. [61]	1100 to 2150	−0.90	−3.93 to 0.31	0.65

Figure 8 displays the fractional deviations of various values of η_exp of ⁴He from η₀₀. In nearly every case they are smaller than the uncertainties provided by the experimenters. In Fig. 8, the barely visible dashed curve represents η_A calculated using φ_A, and the dash-dot-dot curve η_B, calculated from φ_B. The differences between these curves are a measure of the ab initio uncertainties which are much smaller than the reported experimental uncertainties.

6.3 Thermal Conductivity

Figure 9 and Table 9 compare the values of the zero-density thermal conductivity of ⁴He calculated using φ₀₀ with measured values from several sources. The experimental thermal conductivities are typically reported at 101.325 kPa, however the density dependence is negligible compared to the experimental uncertainties. As it was the case for B and η, most of the values of λ_exp differ from λ₀₀ by an amount comparable to the uncertainty of the measurements. The differences between the values λ₀₀, λ_A, and λ_B calculated using φ₀₀, φ_A, and φ_B are much smaller than the uncertainties of the measurements. Table 9 lists the root mean square of the relative differences Δλ/λ₀₀ ≡ (λ_exp − λ₀₀)/λ₀₀ and the range of these relative differences. The final column of Table 9 lists the range of the uncertainties reported by the experimenters.

Fig. 9.

Deviations of λ_exp from λ₀₀ calculated using φ₀₀ for ⁴He. Key: ○ Ref. [50]; □ Ref. [62]; Δ Ref. [65]; ∇ Ref. [64]; ◇ Ref [66]; — — λ_A calculated using φ_A; — • • — λ_B calculated using φ_B.

Table 9.

Relative deviations of λ_exp from λ₀₀

	Temperature range (K)	100 × (Δλ/λ00)rms	Range of 100 × Δλ/λ00	Reported uncertainties (%)
Wakeham et al. [50]	298.15 to 973.15	0.23	0.07 to 0.36	0.2 to 0.5
Haarman [62]	328.15 to 468.15	0.43	−0.54 to −0.32	0.3
Jody et al. [63]	400 to 2500	2.34	−4.67 to −0.41	2.0 to 4.7
Assael et al. [64]	308.15	0.20	−0.20	0.2
Acton and Kellner [65]	3.3 to 20.0	0.66	−0.34 to −1.30	1.0
Kestin et al. [66]	300.65	0.13	−0.13	0.3

6.4 Diffusion Coefficient D₁₂(T)

Figure 10 and Table 10 compare the values of the mutual diffusion coefficient for an equimolar mixture of ³He and ⁴He at one atmosphere (101325 Pa). Figure 10 shows the deviations of D_12,exp taken from three sources, from D_12,00, where D_12,00 was calculated using φ₀₀. Because the diffusion coefficient is difficult to measure, the uncertainties of the experimental values are comparatively large; therefore, the relative deviations of the values calculated using φ_A and φ_B are not visible in Fig. 10. The difference in D₁₂ on going from the first to the second order approximation is practically the same as seen for the viscosity in Fig. 2. Table 10 lists the root-mean-square of the relative differences ΔD/D₀₀ ≡ (D_exp − D₀₀)/D₀₀ and the range of these relative differences as well as the range of the uncertainties reported by the experimenters.

Fig. 10.

Fractional deviations of D_12,exp from D_12,00 calculated using φ₀₀, for an equimolar mixture of ³He and ⁴He. Key: ○ Ref. [67]; □ Ref. [68]; Δ Ref. [69]; — — Values of D_12,A calculated using φ_A; — • • — D_12,B calculated using φ_B.

Table 10.

Deviations of the D_12,exp from D_12,00 calculated using φ₀₀

	Temperature range (K)	100 × (ΔD/D00)rms	Range of 100 × ΔD/D00	Reported uncertainties (%)
Liner and Weissman [67]	303 to 806	1.613	−4.4 to 0.55	1.3 to 4.7
Bendt [68]	14.4 to 296.0	3.876	−6.9 to 5.6	2.0 to 4.0
DuBro and Weissman [69]	76.5 to 888.3	4.142	−6.7 to −1.1	5.0

6.4 Thermal Diffusion Factor α_T

The thermal diffusion factor α_T is a complicated function of temperature and concentration and only a few, relatively inaccurate measurements are available. Figure 11 compares α_T,exp for an equimolar mixture of ³He and ⁴He to the α_T,00 values calculated from φ₀₀. The values of α_T,A and α_T,B calculated from φ_A and φ_B are also shown, only differing at low temperatures. In the first-order approximate calculation of the transport properties, α_T is identically zero; thus, we compared the second-order transport-theory results to the third-order results to estimate the uncertainties of the ab initio results from truncating the transport theory. Going from the second to third order increased α_T by 0.56 % at 10 K and by 0.36 % at 10,000 K. The thermal diffusion factor is very difficult to measure the typical relative uncertainties are 4 % to 8 %. Owing to the experimental difficulties, the calculated values would be more accurate than any experimentally determined value.

Fig. 11.

Thermal diffusion factor α_T as a function of temperature for an equimolar mixture of ³He and ⁴He. The solid curve represents α_T,00 calculated using φ₀₀. Key: ○ Ref. [71]; □ Ref. [72]; Δ Ref. [73]; Δ Ref. [74]; ◇ Ref [75]; — — Values of α_T,A calculated using φ_A; — • • — α_T,B calculated using φ_B.

7. Conclusion

We have reviewed the recent ab initio calculations of φ(r) for helium. We represented one of the most accurate ab initio values of φ(r) by the algebraic expression φ₀₀(r) and we estimated its uncertainty by comparing the various ab initio calculations. For the thermophysical properties, the most significant uncertainties occur near 4.0 bohr. Using φ₀₀(r), we calculated B, η, λ, D₁₂, and α_T. The numerical methods used in these calculations contributed negligible uncertainty to the results. In all cases, the uncertainties of the calculated thermophysical properties propagated from the uncertainties in φ₀₀(r) were much less than the uncertainties of published measurements. Therefore, the calculated values should be used as standard reference values.

The large number of recent ab initio calculations of φ(r) demonstrate that this is an active field of research. In the near future, ab initio calculations will surely reduce the uncertainty of φ(r) near 4.0 bohr, further reducing the uncertainties in the calculated properties. Improved ab initio calculations of the molar polarizability of helium and of the dielectric virial coefficients are also under way. These may well lead to an ab initio standard of pressure based on measurements of the dielectric constant of helium near 273.16 K [70].

Biography

About the authors: John J. Hurly is a Research Chemist in the Fluid Science Group of the NIST Chemical and Science Technology Laboratory. Michael R. Moldover leads the Fluid Science Group and is a NIST Fellow. The National Institute of Standards and Technology is an agency of the Technology Administration, U.S. Department of Commerce.

8. Appendix A. Calculations

The results of the present calculations for ⁴He, ³He, and their equimolar mixture are listed in Tables A1, A2, and A3, respectively. These tables contain the second virial coefficient for the pure species, the interaction second virial coefficient B₁₂, the zero-density viscosity and thermal conductivity, the diffusion coefficient, and the thermal diffusion coefficient. Derivatives with respect to temperature are provided to facilitate interpolation and for use in calculating acoustic virial coefficients. The tables for pure ⁴He and ³He contain the self-diffusion coefficient, and the thermal diffusion factor of binary mixtures of ⁴He and ³He with mole fractions of 0.99999 and 0.00001, respectively.

Table A1.

Thermophysical properties of ⁴He as a function of temperature, where (−2) is × 10⁻²

T	B	dB/dT	d2B/dT2	η	dη/dT	λ	dλ/dT	D(101.3 kPa)	αT
(K)	(cm3·mol−1)	(cm3·mol−1·K−1)	(cm3·mol−1·K−2)	(μ Pa·s)	(μ Pa·K−1)	(mW·m−1·K−1)	(mW·m−1·K−2)	(10−4·m2·s−1)
1.0	−474.449	664.861	−1771.941	3.279(−1)	5.296(−2)	2.624	4.512(−1)	7.154(−5)	4.147(−2)
1.2	−369.743	411.102	−891.823	3.395(−1)	6.980(−2)	2.713	5.030(−1)	9.622(−5)	5.098(−2)
1.4	−302.255	276.706	−500.007	3.573(−1)	1.096(−1)	2.839	7.759(−1)	1.240(−4)	5.716(−2)
1.6	−255.395	198.357	−304.265	3.834(−1)	1.504(−1)	3.026	1.097	1.560(−4)	6.162(−2)
1.8	−220.996	149.180	−197.490	4.171(−1)	1.860(−1)	3.276	1.395	1.927(−4)	6.501(−2)
2.0	−194.640	116.448	−135.022	4.573(−1)	2.149(−1)	3.581	1.642	2.345(−4)	6.764(−2)
2.25	−169.200	88.972	−89.028	5.146(−1)	2.419(−1)	4.022	1.872	2.943(−4)	7.011(−2)
2.5	−149.421	70.388	−61.860	5.775(−1)	2.600(−1)	4.510	2.023	3.624(−4)	7.190(−2)
2.75	−133.560	57.209	−44.818	6.440(−1)	2.705(−1)	5.028	2.108	4.386(−4)	7.318(−2)
3.0	−120.530	47.499	−33.586	7.123(−1)	2.749(−1)	5.560	2.143	5.228(−4)	7.409(−2)
3.5	−100.334	34.377	−20.391	8.492(−1)	2.708(−1)	6.628	2.110	7.138(−4)	7.525(−2)
4.0	−85.360	26.103	−13.372	9.815(−1)	2.573(−1)	7.658	2.005	9.328(−4)	7.594(−2)
4.5	−73.788	20.526	−9.272	1.106	2.407(−1)	8.630	1.878	1.178(−3)	7.646(−2)
5	−64.566	16.578	−6.706	1.222	2.244(−1)	9.537	1.754	1.446(−3)	7.693(−2)
6	−50.774	11.477	−3.849	1.433	1.974(−1)	11.180	1.547	2.050(−3)	7.784(−2)
7	−40.944	8.419	−2.415	1.620	1.783(−1)	12.650	1.400	2.735(−3)	7.871(−2)
8	−33.581	6.440	−1.615	1.791	1.649(−1)	14.000	1.295	3.495(−3)	7.949(−2)
9	−27.859	5.084	−1.134	1.951	1.551(−1)	15.250	1.218	4.326(−3)	8.014(−2)
10	−23.285	4.114	−8.269(−1)	2.102	1.474(−1)	16.440	1.157	5.226(−3)	8.068(−2)
11	−19.547	3.397	−6.215(−1)	2.246	1.412(−1)	17.570	1.108	6.190(−3)	8.110(−2)
12	−16.435	2.850	−4.790(−1)	2.385	1.359(−1)	18.660	1.066	7.217(−3)	8.143(−2)
14	−11.556	2.087	−3.021(−1)	2.648	1.274(−1)	20.720	9.990(−1)	9.451(−3)	8.186(−2)
16	−7.910	1.591	−2.026(−1)	2.895	1.206(−1)	22.660	9.458(−1)	1.191(−2)	8.208(−2)
18	−5.088	1.251	−1.425(−1)	3.131	1.151(−1)	24.510	9.021(−1)	1.459(−2)	8.216(−2)
20	−2.842	1.007	−1.039(−1)	3.356	1.104(−1)	26.270	8.654(−1)	1.749(−2)	8.214(−2)
22	−1.017	8.27(−1)	−7.81(−2)	3.573	1.064(−1)	27.970	8.338(−1)	2.058(−2)	8.206(−2)
23	−0.227	7.54(−1)	−6.84(−2)	3.678	1.046(−1)	28.800	8.196(−1)	2.220(−2)	8.200(−2)
24	0.494	6.90(−1)	−6.02(−2)	3.782	1.029(−1)	29.610	8.063(−1)	2.387(−2)	8.193(−2)
25	1.155	6.33(−1)	−5.32(−2)	3.884	1.013(−1)	30.410	7.938(−1)	2.558(−2)	8.185(−2)
26	1.762	5.83(−1)	−4.73(−2)	3.985	9.980(−2)	31.200	7.821(−1)	2.734(−2)	8.177(−2)
28	2.840	4.98(−1)	−3.78(−2)	4.181	9.706(−2)	32.740	7.606(−1)	3.101(−2)	8.159(−2)
30	3.766	4.30(−1)	−3.07(−2)	4.373	9.460(−2)	34.240	7.412(−1)	3.485(−2)	8.140(−2)
35	5.587	3.08(−1)	−1.93(−2)	4.833	8.941(−2)	37.840	7.004(−1)	4.522(−2)	8.087(−2)
40	6.917	2.29(−1)	−1.28(−2)	5.269	8.523(−2)	41.260	6.675(−1)	5.664(−2)	8.034(−2)
45	7.921	1.76(−1)	−8.94(−3)	5.686	8.176(−2)	44.530	6.402(−1)	6.907(−2)	7.980(−2)
50	8.698	1.38(−1)	−6.46(−3)	6.087	7.882(−2)	47.670	6.171(−1)	8.246(−2)	7.928(−2)
60	9.806	8.86(−2)	−3.66(−3)	6.851	7.406(−2)	53.650	5.798(−1)	1.120(−1)	7.831(−2)
70	10.537	5.98(−2)	−2.25(−3)	7.572	7.035(−2)	59.290	5.507(−1)	1.452(−1)	7.741(−2)
80	11.038	4.16(−2)	−1.47(−3)	8.260	6.734(−2)	64.680	5.270(−1)	1.818(−1)	7.659(−2)
90	11.389	2.95(−2)	−9.98(−4)	8.920	6.483(−2)	69.846	5.073(−1)	2.216(−1)	7.584(−2)
100	11.640	2.11(−2)	−7.03(−4)	9.558	6.270(−2)	74.833	4.906(−1)	2.646(−1)	7.514(−2)
120	11.947	1.07(−2)	−3.78(−4)	10.775	5.923(−2)	84.360	4.633(−1)	3.597(−1)	7.390(−2)
140	12.098	4.92(−3)	−2.18(−4)	11.932	5.650(−2)	93.405	4.419(−1)	4.666(−1)	7.281(−2)
160	12.160	1.50(−3)	−1.32(−4)	13.039	5.428(−2)	102.063	4.245(−1)	5.847(−1)	7.184(−2)
180	12.167	−6.18(−4)	−8.32(−5)	14.105	5.242(−2)	110.403	4.099(−1)	7.137(−1)	7.097(−2)
200	12.140	−1.96(−3)	−5.34(−5)	15.137	5.083(−2)	118.474	3.975(−1)	8.532(−1)	7.017(−2)
225	12.077	−2.99(−3)	−3.10(−5)	16.386	4.914(−2)	128.241	3.842(−1)	1.042	6.927(−2)
250	11.994	−3.59(−3)	−1.78(−5)	17.596	4.769(−2)	137.701	3.729(−1)	1.246	6.845(−2)
275	11.900	−3.93(−3)	−9.74(−6)	18.772	4.644(−2)	146.897	3.630(−1)	1.466	6.769(−2)
300	11.799	−4.10(−3)	−4.69(−6)	19.919	4.534(−2)	155.863	3.544(−1)	1.700	6.699(−2)
325	11.695	−4.18(−3)	−1.46(−6)	21.040	4.436(−2)	164.625	3.467(−1)	1.949	6.634(−2)
350	11.591	−4.19(−3)	6.15(−7)	22.138	4.348(−2)	173.205	3.398(−1)	2.212	6.573(−2)
375	11.486	−4.15(−3)	1.95(−6)	23.215	4.268(−2)	181.621	3.336(−1)	2.489	6.516(−2)
400	11.383	−4.09(−3)	2.81(−6)	24.272	4.196(−2)	189.889	3.279(−1)	2.780	6.462(−2)
450	11.183	−3.93(−3)	3.66(−6)	26.338	4.069(−2)	206.028	3.179(−1)	3.403	6.361(−2)
500	10.991	−3.74(−3)	3.88(−6)	28.344	3.960(−2)	221.707	3.094(−1)	4.078	6.270(−2)
600	10.637	−3.36(−3)	3.66(−6)	32.211	3.783(−2)	251.926	2.955(−1)	5.584	6.108(−2)
700	10.319	−3.01(−3)	3.19(−6)	35.922	3.643(−2)	280.913	2.846(−1)	7.290	5.968(−2)
800	10.033	−2.72(−3)	2.72(−6)	39.506	3.529(−2)	308.912	2.757(−1)	9.189	5.843(−2)
900	9.774	−2.47(−3)	2.32(−6)	42.986	3.434(−2)	336.095	2.682(−1)	11.278	5.731(−2)
1000	9.538	−2.25(−3)	1.99(−6)	46.378	3.353(−2)	362.590	2.618(−1)	13.551	5.628(−2)
1200	9.124	−1.91(−3)	1.48(−6)	52.946	3.221(−2)	413.878	2.515(−1)	18.639	5.445(−2)
1400	8.770	−1.65(−3)	1.14(−6)	59.280	3.117(−2)	463.334	2.434(−1)	24.430	5.286(−2)
1600	8.462	−1.44(−3)	9.01(−7)	65.427	3.033(−2)	511.329	2.368(−1)	30.909	5.144(−2)
1800	8.190	−1.28(−3)	7.27(−7)	71.421	2.963(−2)	558.122	2.313(−1)	38.060	5.015(−2)
2000	7.947	−1.15(−3)	5.97(−7)	77.286	2.904(−2)	603.905	2.267(−1)	45.872	4.897(−2)
2500	7.437	−9.08(−4)	3.90(−7)	91.499	2.904(−2)	714.835	2.267(−1)	68.240	4.637(−2)
3000	7.026	−7.45(−4)	2.73(−7)	105.216	2.904(−2)	821.876	2.267(−1)	94.577	4.415(−2)
3500	6.684	−6.28(−4)	2.00(−7)	118.560	2.904(−2)	925.992	2.267(−1)	124.803	4.219(−2)
4000	6.393	−5.41(−4)	1.53(−7)	131.612	2.904(−2)	1027.819	2.267(−1)	158.862	4.043(−2)
4500	6.141	−4.73(−4)	1.20(−7)	144.429	2.904(−2)	1127.805	2.267(−1)	196.713	3.882(−2)
5000	5.918	−4.19(−4)	9.68(−8)	157.054	2.904(−2)	1226.279	2.267(−1)	238.324	3.734(−2)
6000	5.542	−3.39(−4)	6.62(−8)	181.847	2.904(−2)	1419.639	2.267(−1)	332.735	3.466(−2)
7000	5.232	−2.83(−4)	4.79(−8)	206.173	2.904(−2)	1609.339	2.267(−1)	441.969	3.229(−2)
8000	4.972	−2.41(−4)	3.61(−8)	230.154	2.904(−2)	1796.322	2.267(−1)	565.960	3.014(−2)
9000	4.747	−2.09(−4)	2.81(−8)	253.873	2.904(−2)	1981.249	2.267(−1)	704.683	2.816(−2)
10000	4.551	−1.84(−4)	2.24(−8)	277.393	2.904(−2)	2164.607	2.267(−1)	858.143	2.633(−2)

Table A2.

Thermophysical properties of ³He as a function of temperature, where (−2) is × 10⁻²

T	B	dB/dT	d2B/dT2	η	dη/dT	λ	dλ/dT	D(101.3 kPa)	αT
(K)	(cm3·mol−1)	(cm3·mol−1·K−1)	(cm3·mol−1·K−1)	(μ Pa·s)	(μ Pa·K−1)	(mW·m−1·K−1)	(mW·m−1·K−2)	(10−4·m2·s−1)
1.0	−237.503	174.583	−218.592	5.561(−1)	5.280(−1)	5.756	5.459	1.910(−4)	6.797(−2)
1.2	−206.501	137.501	−156.563	6.608(−1)	5.126(−1)	6.839	5.317	2.706(−4)	8.532(−2)
1.4	−181.829	110.586	−115.265	7.593(−1)	4.688(−1)	7.864	4.893	3.629(−4)	9.794(−2)
1.6	−161.811	90.544	−86.881	8.472(−1)	4.086(−1)	8.786	4.309	4.654(−4)	1.077(−1)
1.8	−145.295	75.286	−66.837	9.224(−1)	3.439(−1)	9.585	3.677	5.756(−4)	1.150(−1)
2.0	−131.470	63.444	−52.348	9.850(−1)	2.830(−1)	10.259	3.073	6.913(−4)	1.200(−1)
2.25	−117.097	52.073	−39.409	1.047	2.187(−1)	10.942	2.421	8.412(−4)	1.235(−1)
2.5	−105.208	43.422	−30.305	1.096	1.701(−1)	11.481	1.909	9.952(−4)	1.247(−1)
2.75	−95.226	36.710	−23.736	1.134	1.360(−1)	11.909	1.535	1.152(−3)	1.242(−1)
3.0	−86.736	31.410	−18.897	1.165	1.136(−1)	12.258	1.275	1.312(−3)	1.224(−1)
3.5	−73.089	23.709	−12.431	1.215	9.298(−2)	12.816	1.004	1.639(−3)	1.171(−1)
4.0	−62.616	18.504	−8.637	1.261	9.003(−2)	13.294	9.302(−1)	1.980(−3)	1.112(−1)
4.5	−54.332	14.836	−6.209	1.306	9.430(−2)	13.762	9.487(−1)	2.338(−3)	1.057(−1)
5	−47.616	12.159	−4.605	1.355	1.006(−1)	14.249	1.002	2.715(−3)	1.012(−1)
6	−37.392	8.599	−2.732	1.461	1.114(−1)	15.310	1.116	3.531(−3)	9.498(−2)
7	−29.972	6.405	−1.752	1.576	1.172(−1)	16.466	1.187	4.431(−3)	9.149(−2)
8	−24.336	4.958	−1.191	1.695	1.191(−1)	17.671	1.217	5.413(−3)	8.964(−2)
9	−19.909	3.953	−8.465(−1)	1.814	1.185(−1)	18.890	1.218	6.475(−3)	8.868(−2)
10	−16.338	3.226	−6.238(−1)	1.931	1.166(−1)	20.102	1.204	7.612(−3)	8.819(−2)
11	−13.397	2.682	−4.732(−1)	2.047	1.141(−1)	21.295	1.181	8.822(−3)	8.795(−2)
12	−10.933	2.264	−3.676(−1)	2.159	1.115(−1)	22.463	1.155	1.010(−2)	8.782(−2)
14	−7.038	1.675	−2.350(−1)	2.377	1.062(−1)	24.720	1.102	1.287(−2)	8.769(−2)
16	−4.101	1.287	−1.593(−1)	2.584	1.014(−1)	26.876	1.054	1.589(−2)	8.757(−2)
18	−1.811	1.018	−1.130(−1)	2.783	9.726(−2)	28.939	1.011	1.916(−2)	8.743(−2)
20	0.022	8.242(−1)	−8.309(−2)	2.974	9.365(−2)	30.923	9.735(−1)	2.266(−2)	8.724(−2)
22	1.519	6.795(−1)	−6.286(−2)	3.158	9.049(−2)	32.837	9.407(−1)	2.639(−2)	8.702(−2)
23	2.168	6.206(−1)	−5.517(−2)	3.248	8.906(−2)	33.770	9.258(−1)	2.834(−2)	8.690(−2)
24	2.762	5.688(−1)	−4.870(−2)	3.336	8.771(−2)	34.688	9.117(−1)	3.035(−2)	8.678(−2)
25	3.308	5.229(−1)	−4.318(−2)	3.423	8.643(−2)	35.593	8.985(−1)	3.240(−2)	8.665(−2)
26	3.810	4.822(−1)	−3.847(−2)	3.509	8.523(−2)	36.486	8.859(−1)	3.451(−2)	8.652(−2)
28	4.703	4.132(−1)	−3.091(−2)	3.677	8.301(−2)	38.234	8.628(−1)	3.889(−2)	8.626(−2)
30	5.471	3.573(−1)	−2.520(−2)	3.841	8.101(−2)	39.939	8.420(−1)	4.348(−2)	8.599(−2)
35	6.987	2.568(−1)	−1.593(−2)	4.235	7.674(−2)	44.033	7.976(−1)	5.580(−2)	8.531(−2)
40	8.097	1.915(−1)	−1.067(−2)	4.610	7.328(−2)	47.928	7.615(−1)	6.933(−2)	8.464(−2)
45	8.936	1.467(−1)	−7.476(−3)	4.969	7.038(−2)	51.658	7.313(−1)	8.400(−2)	8.400(−2)
50	9.586	1.148(−1)	−5.423(−3)	5.314	6.792(−2)	55.249	7.057(−1)	9.978(−2)	8.339(−2)
60	10.509	7.365(−2)	−3.091(−3)	5.973	6.392(−2)	62.088	6.640(−1)	1.345(−1)	8.226(−2)
70	11.114	4.929(−2)	−1.905(−3)	6.596	6.078(−2)	68.559	6.313(−1)	1.734(−1)	8.125(−2)
80	11.524	3.384(−2)	−1.243(−3)	7.190	5.823(−2)	74.735	6.047(−1)	2.161(−1)	8.033(−2)
90	11.808	2.355(−2)	−8.470(−4)	7.762	5.609(−2)	80.667	5.825(−1)	2.627(−1)	7.949(−2)
100	12.005	1.642(−2)	−5.961(−4)	8.313	5.427(−2)	86.394	5.635(−1)	3.128(−1)	7.872(−2)
120	12.237	7.620(−3)	−3.186(−4)	9.367	5.130(−2)	97.341	5.326(−1)	4.236(−1)	7.735(−2)
140	12.336	2.752(−3)	−1.826(−4)	10.369	4.896(−2)	107.740	5.082(−1)	5.479(−1)	7.616(−2)
160	12.360	−1.030(−4)	−1.096(−4)	11.328	4.705(−2)	117.698	4.883(−1)	6.852(−1)	7.510(−2)
180	12.339	−1.842(−3)	−6.771(−5)	12.253	4.545(−2)	127.293	4.717(−1)	8.349(−1)	7.415(−2)
200	12.291	−2.924(−3)	−4.241(−5)	13.148	4.408(−2)	136.581	4.574(−1)	9.968(−1)	7.329(−2)
225	12.206	−3.728(−3)	−2.354(−5)	14.231	4.262(−2)	147.821	4.422(−1)	1.216	7.231(−2)
250	12.107	−4.168(−3)	−1.253(−5)	15.280	4.137(−2)	158.711	4.293(−1)	1.452	7.142(−2)
275	12.000	−4.392(−3)	−5.884(−6)	16.301	4.029(−2)	169.298	4.180(−1)	1.707	7.060(−2)
300	11.889	−4.485(−3)	−1.787(−6)	17.296	3.933(−2)	179.621	4.081(−1)	1.978	6.985(−2)
325	11.776	−4.495(−3)	7.679(−7)	18.268	3.848(−2)	189.710	3.992(−1)	2.266	6.915(−2)
350	11.664	−4.455(−3)	2.364(−6)	19.220	3.772(−2)	199.590	3.913(−1)	2.571	6.849(−2)
375	11.554	−4.383(−3)	3.350(−6)	20.155	3.703(−2)	209.283	3.842(−1)	2.891	6.787(−2)
400	11.445	−4.291(−3)	3.939(−6)	21.073	3.641(−2)	218.804	3.777(−1)	3.228	6.729(−2)
450	11.236	−4.080(−3)	4.413(−6)	22.865	3.531(−2)	237.392	3.662(−1)	3.948	6.621(−2)
500	11.038	−3.857(−3)	4.428(−6)	24.606	3.437(−2)	255.451	3.564(−1)	4.729	6.524(−2)
600	10.673	−3.434(−3)	3.961(−6)	27.962	3.283(−2)	290.258	3.404(−1)	6.469	6.351(−2)
700	10.349	−3.068(−3)	3.370(−6)	31.183	3.162(−2)	323.649	3.278(−1)	8.439	6.201(−2)
800	10.058	−2.758(−3)	2.842(−6)	34.294	3.063(−2)	355.903	3.176(−1)	10.633	6.068(−2)
900	9.796	−2.496(−3)	2.400(−6)	37.314	2.981(−2)	387.217	3.090(−1)	13.044	5.948(−2)
1000	9.557	−2.275(−3)	2.042(−6)	40.259	2.910(−2)	417.739	3.016(−1)	15.669	5.839(−2)
1200	9.139	−1.923(−3)	1.515(−6)	45.959	2.796(−2)	476.824	2.897(−1)	21.541	5.645(−2)
1400	8.782	−1.658(−3)	1.160(−6)	51.457	2.706(−2)	533.800	2.804(−1)	28.225	5.476(−2)
1600	8.472	−1.452(−3)	9.133(−7)	56.793	2.633(−2)	589.092	2.728(−1)	35.699	5.325(−2)
1800	8.199	−1.288(−3)	7.355(−7)	61.996	2.572(−2)	643.000	2.665(−1)	43.949	5.189(−2)
2000	7.955	−1.155(−3)	6.031(−7)	67.087	2.521(−2)	695.745	2.611(−1)	52.961	5.064(−2)
2500	7.443	−9.112(−4)	3.926(−7)	79.424	2.521(−2)	823.544	2.611(−1)	78.760	4.790(−2)
3000	7.031	−7.471(−4)	2.741(−7)	91.331	2.521(−2)	946.864	2.611(−1)	109.131	4.556(−2)
3500	6.688	−6.296(−4)	2.013(−7)	102.913	2.521(−2)	1066.813	2.611(−1)	143.985	4.349(−2)
4000	6.396	−5.417(−4)	1.535(−7)	114.243	2.521(−2)	1184.125	2.611(−1)	183.256	4.164(−2)
4500	6.143	−4.737(−4)	1.206(−7)	125.369	2.521(−2)	1299.316	2.611(−1)	226.896	3.996(−2)
5000	5.920	−4.196(−4)	9.704(−8)	136.328	2.521(−2)	1412.766	2.611(−1)	274.868	3.841(−2)
6000	5.543	−3.393(−4)	6.638(−8)	157.849	2.521(−2)	1635.532	2.611(−1)	383.707	3.561(−2)
7000	5.234	−2.829(−4)	4.799(−8)	178.965	2.521(−2)	1854.081	2.611(−1)	509.625	3.314(−2)
8000	4.973	−2.412(−4)	3.616(−8)	199.781	2.521(−2)	2069.499	2.611(−1)	652.548	3.090(−2)
9000	4.748	−2.093(−4)	2.813(−8)	220.370	2.521(−2)	2282.550	2.611(−1)	812.447	2.885(−2)
10000	4.552	−1.842(−4)	2.243(−8)	240.786	2.521(−2)	2493.792	2.611(−1)	989.327	2.695(−2)

Table A3.

Thermophysical properties of an equimolar binary mixture of ³He ⁴He as a function of temperature, where (−2) is × 10⁻²

T	B	dB/dT	d2B/dT2	η	dη/dT	λ	dλ/dT	D(101.3 kPa)	αT
(K)	(cm3·mol−1)	(cm3·mol−1·K−1)	(cm3·mol−1·K−2)	(μPa·s)	(μPa·K−1)	(mW·m−1·K−1)	(mW·m−1·K−2)	(10−4·m2·s−1)
1.0	−338.460	362.783	−761.653	4.147(−1)	2.503(−1)	3.802	2.449	1.152(−4)	5.168(−2)
1.2	−278.477	248.027	−428.348	4.629(−1)	2.363(−1)	4.260	2.185	1.616(−4)	6.401(−2)
1.4	−236.166	180.498	−264.495	5.102(−1)	2.378(−1)	4.690	2.129	2.143(−4)	7.237(−2)
1.6	−204.675	137.383	−174.857	5.582(−1)	2.416(−1)	5.117	2.149	2.732(−4)	7.859(−2)
1.8	−180.297	108.166	−121.639	6.067(−1)	2.437(−1)	5.550	2.175	3.379(−4)	8.327(−2)
2.0	−160.849	87.440	−88.058	6.555(−1)	2.433(−1)	5.986	2.183	4.081(−4)	8.672(−2)
2.25	−141.430	69.017	−61.471	7.159(−1)	2.397(−1)	6.529	2.160	5.032(−4)	8.962(−2)
2.5	−125.902	55.906	−44.632	7.751(−1)	2.338(−1)	7.063	2.108	6.063(−4)	9.129(−2)
2.75	−113.192	46.238	−33.437	8.327(−1)	2.267(−1)	7.582	2.039	7.168(−4)	9.206(−2)
3.0	−102.590	38.900	−25.720	8.884(−1)	2.191(−1)	8.082	1.961	8.346(−4)	9.219(−2)
3.5	−85.895	28.672	−16.178	9.943(−1)	2.046(−1)	9.024	1.810	1.091(−3)	9.134(−2)
4.0	−73.329	22.034	−10.848	1.093	1.921(−1)	9.896	1.685	1.372(−3)	8.988(−2)
4.5	−63.518	17.477	−7.632	1.187	1.820(−1)	10.714	1.589	1.679(−3)	8.838(−2)
5	−55.638	14.211	−5.579	1.276	1.737(−1)	11.490	1.517	2.008(−3)	8.708(−2)
6	−43.756	9.939	−3.248	1.443	1.612(−1)	12.952	1.415	2.734(−3)	8.531(−2)
7	−35.212	7.347	−2.058	1.599	1.519(−1)	14.328	1.341	3.542(−3)	8.444(−2)
8	−28.767	5.654	−1.387	1.747	1.446(−1)	15.639	1.282	4.428(−3)	8.412(−2)
9	−23.731	4.486	−9.800(−1)	1.889	1.384(−1)	16.894	1.230	5.389(−3)	8.407(−2)
10	−19.687	3.646	−7.184(−1)	2.024	1.331(−1)	18.101	1.185	6.420(−3)	8.415(−2)
11	−16.369	3.021	−5.425(−1)	2.155	1.284(−1)	19.265	1.144	7.520(−3)	8.427(−2)
12	−13.597	2.543	−4.199(−1)	2.281	1.242(−1)	20.391	1.108	8.686(−3)	8.439(−2)
14	−9.233	1.872	−2.667(−1)	2.522	1.171(−1)	22.541	1.045	1.121(−2)	8.456(−2)
16	−5.957	1.433	−1.799(−1)	2.751	1.113(−1)	24.578	9.932(−1)	1.397(−2)	8.462(−2)
18	−3.411	1.130	−1.270(−1)	2.968	1.064(−1)	26.519	9.498(−1)	1.697(−2)	8.458(−2)
20	−1.380	9.125(− 1)	−9.303(−2)	3.177	1.022(−1)	28.381	9.127(−1)	2.019(−2)	8.448(−2)
22	0.276	7.508(−1)	−7.015(−2)	3.377	9.863(−2)	30.174	8.807(−1)	2.362(−2)	8.433(−2)
23	0.993	6.851(−1)	−6.148(−2)	3.475	9.701(−2)	31.047	8.663(−1)	2.542(−2)	8.425(−2)
24	1.649	6.273(−1)	−5.418(−2)	3.571	9.549(−2)	31.906	8.527(−1)	2.726(−2)	8.415(−2)
25	2.250	5.763(−1)	−4.799(−2)	3.666	9.406(−2)	32.753	8.399(−1)	2.916(−2)	8.405(−2)
26	2.803	5.311(−1)	−4.271(−2)	3.760	9.271(−2)	33.587	8.279(−1)	3.111(−2)	8.394(−2)
28	3.786	4.545(−1)	−3.424(−2)	3.942	9.024(−2)	35.220	8.058(−1)	3.515(−2)	8.372(−2)
30	4.631	3.927(−1)	−2.786(−2)	4.121	8.800(−2)	36.811	7.858(−1)	3.939(−2)	8.349(−2)
35	6.296	2.818(−1)	−1.754(−2)	4.548	8.328(−2)	40.631	7.436(−1)	5.080(−2)	8.290(−2)
40	7.514	2.100(−1)	−1.172(−2)	4.955	7.945(−2)	44.260	7.094(−1)	6.333(−2)	8.230(−2)
45	8.433	1.609(−1)	−8.188(−3)	5.344	7.627(−2)	47.734	6.810(−1)	7.694(−2)	8.171(−2)
50	9.146	1.260(−1)	−5.929(−3)	5.718	7.357(−2)	51.077	6.569(−1)	9.160(−2)	8.115(−2)
60	10.160	8.104(−2)	−3.370(−3)	6.431	6.919(−2)	57.442	6.177(−1)	1.239(−1)	8.010(−2)
70	10.827	5.450(−2)	−2.074(−3)	7.105	6.576(−2)	63.460	5.871(−1)	1.601(−1)	7.915(−2)
80	11.282	3.769(−2)	−1.353(−3)	7.748	6.297(−2)	69.202	5.622(−1)	1.999(−1)	7.829(−2)
90	11.599	2.650(−2)	−9.213(−4)	8.366	6.065(−2)	74.717	5.414(−1)	2.432(−1)	7.749(−2)
100	11.823	1.874(−2)	−6.493(−4)	8.963	5.866(−2)	80.039	5.237(−1)	2.900(−1)	7.677(−2)
120	12.092	9.153(−3)	−3.476(−4)	10.102	5.544(−2)	90.212	4.948(−1)	3.934(−1)	7.547(−2)
140	12.217	3.832(−3)	−2.001(−4)	11.185	5.290(−2)	99.873	4.722(−1)	5.094(−1)	7.433(−2)
160	12.260	6.941(−4)	−1.209(−4)	12.221	5.083(−2)	109.125	4.537(−1)	6.375(−1)	7.332(−2)
180	12.253	−1.232(−3)	−7.540(−5)	13.220	4.909(−2)	118.039	4.382(−1)	7.774(−1)	7.241(−2)
200	12.215	−2.444(−3)	−4.786(−5)	14.187	4.761(−2)	126.667	4.249(−1)	9.286(−1)	7.159(−2)
225	12.142	−3.361(−3)	−2.725(−5)	15.357	4.603(−2)	137.109	4.108(−1)	1.133	7.065(−2)
250	12.051	−3.879(−3)	−1.515(−5)	16.490	4.468(−2)	147.224	3.988(−1)	1.354	6.980(−2)
275	11.950	−4.159(−3)	−7.805(−6)	17.592	4.351(−2)	157.059	3.883(−1)	1.592	6.901(−2)
300	11.844	−4.294(−3)	−3.233(−6)	18.667	4.248(−2)	166.649	3.791(−1)	1.846	6.829(−2)
325	11.736	−4.336(−3)	−3.446(−7)	19.717	4.156(−2)	176.022	3.709(−1)	2.115	6.762(−2)
350	11.628	−4.320(−3)	1.491(−6)	20.746	4.074(−2)	185.200	3.635(−1)	2.400	6.699(−2)
375	11.520	−4.268(−3)	2.653(−6)	21.755	4.000(−2)	194.204	3.569(−1)	2.700	6.639(−2)
400	11.414	−4.192(−3)	3.375(−6)	22.746	3.932(−2)	203.050	3.509(−1)	3.015	6.583(−2)
450	11.209	−4.004(−3)	4.043(−6)	24.681	3.813(−2)	220.320	3.402(−1)	3.688	6.480(−2)
500	11.014	−3.797(−3)	4.155(−6)	26.562	3.711(−2)	237.099	3.312(−1)	4.419	6.385(−2)
600	10.655	−3.395(−3)	3.811(−6)	30.186	3.545(−2)	269.441	3.163(−1)	6.047	6.219(−2)
700	10.334	−3.040(−3)	3.286(−6)	33.664	3.415(−2)	300.470	3.047(−1)	7.891	6.074(−2)
800	10.045	−2.737(−3)	2.784(−6)	37.023	3.308(−2)	330.444	2.951(−1)	9.943	5.945(−2)
900	9.785	−2.481(−3)	2.361(−6)	40.285	3.219(−2)	359.549	2.872(−1)	12.200	5.830(−2)
1000	9.548	−2.263(−3)	2.014(−6)	43.465	3.143(−2)	387.918	2.804(−1)	14.656	5.724(−2)
1200	9.132	−1.915(−3)	1.499(−6)	49.621	3.019(−2)	442.843	2.693(−1)	20.153	5.536(−2)
1400	8.776	−1.652(−3)	1.150(−6)	55.558	2.922(−2)	495.813	2.607(−1)	26.409	5.373(−2)
1600	8.467	−1.448(−3)	9.072(−7)	61.320	2.843(−2)	547.223	2.537(−1)	33.405	5.227(−2)
1800	8.194	−1.285(−3)	7.313(−7)	66.938	2.778(−2)	597.352	2.478(−1)	41.128	5.094(−2)
2000	7.951	−1.152(−3)	6.002(−7)	72.436	2.722(−2)	646.403	2.428(−1)	49.565	4.973(−2)
2500	7.440	−9.097(−4)	3.913(−7)	85.759	2.613(−2)	765.270	2.332(−1)	73.716	4.707(−2)
3000	7.029	−7.461(−4)	2.734(−7)	98.617	2.534(−2)	879.990	2.261(−1)	102.149	4.479(−2)
3500	6.686	−6.289(−4)	2.008(−7)	111.126	2.472(−2)	991.593	2.206(−1)	134.778	4.279(−2)
4000	6.395	−5.412(−4)	1.532(−7)	123.361	2.424(−2)	1100.756	2.162(−1)	171.543	4.098(−2)
4500	6.142	−4.733(−4)	1.204(−7)	135.376	2.384(−2)	1207.960	2.127(−1)	212.399	3.934(−2)
5000	5.919	−4.193(−4)	9.690(−8)	147.211	2.351(−2)	1313.554	2.098(−1)	257.310	3.783(−2)
6000	5.542	−3.391(−4)	6.630(−8)	170.451	2.300(−2)	1520.927	2.052(−1)	359.205	3.510(−2)
7000	5.233	−2.827(−4)	4.795(−8)	193.255	2.263(−2)	1724.410	2.019(−1)	477.089	3.268(−2)
8000	4.972	−2.411(−4)	3.613(−8)	215.734	2.235(−2)	1925.011	1.994(−1)	610.893	3.049(−2)
9000	4.748	−2.092(−4)	2.811(−8)	237.969	2.213(−2)	2123.436	1.975(−1)	760.589	2.848(−2)
10000	4.551	−1.841(−4)	2.242(−8)	260.016	2.197(−2)	2320.201	1.961(−1)	926.183	2.661(−2)