Quantitative comparison of errors in ¹⁵N transverse relaxation rates measured using various CPMG phasing schemes

Abstract

Nitrogen-15 Carr-Purcell-Meiboom-Gill (CPMG) transverse relaxation experiment are widely used to characterize protein backbone dynamics and chemical exchange parameters. Although an accurate value of the transverse relaxation rate, R₂, is needed for accurate characterization of dynamics, the uncertainty in the R₂ value depends on the experimental settings and the details of the data analysis itself. Here, we present an analysis of the impact of CPMG pulse phase alternation on the accuracy of the ¹⁵N CPMG R₂. Our simulations show that R₂ can be obtained accurately for a relatively wide spectral width, either using the conventional phase cycle or using phase alternation when the r.f. pulse power is accurately calibrated. However, when the r.f. pulse is miscalibrated, the conventional CPMG experiment exhibits more significant uncertainties in R₂ caused by the off-resonance effect than does the phase alternation experiment. Our experiments show that this effect becomes manifest under the circumstance that the systematic error exceeds that arising from experimental noise. Furthermore, our results provide the means to estimate practical parameter settings that yield accurate values of ¹⁵N transverse relaxation rates in the both CPMG experiments.

Introduction

NMR relaxation is one of powerful methods to characterize internal motion of individual sites of proteins (Bruschweiler 2003; Dayie et al. 1996; Farrow et al. 1995; Fushman & Cowburn 2001; Igumenova et al. 2006; Ishima & Torchia 2000; Jarymowycz & Stone 2006; Kay 2005; Palmer 2001; Peng & Wagner 1995; Redfield 2004). Several relaxation rates, including the transverse relaxation rate (R₂), are typically used to characterize the degree of internal motion in biomolecules (Kay et al. 1989; Lipari & Szabo 1982a; Lipari & Szabo 1982b; Nirmala & Wagner 1988). R₂ is also used to detect slow conformational changes in biomolecules (Carver & Richards 1972; Davis et al. 1994; Ishima et al. 1998; Loria et al. 1999; Mulder et al. 1999; Orekhov et al. 1994). In biomolecular relaxation experiments, accurate error estimation is important in order to compare with NMR-derived dynamics parameters with those obtained by other methods, such as Gibbs free energy estimated from chemical exchange (Farrow et al. 1995; Huang & Oas 1995; Szyperski et al. 1993), molecular dynamics simulation data (Chandrasekhar et al. 1992; Eriksson et al. 1993; Horita et al. 2000; Smith et al. 1995; Wrabl et al. 2000; Yamasaki et al. 1995), and conformational entropy estimated from generalized order parameters (Akke & Palmer 1996; Li et al. 1996; Yang & Kay 1996). The accuracy and precision of R₂ measurements, have been carefully analyzed (Bain et al. 2010; Bain et al. 2011; Bretthorst et al. 2005; Czisch et al. 1997; Ishima & Torchia 2005; Istratov & Vyvenko 1999; Korzhnev et al. 2000; Long et al. 2008; Myint et al. 2009; Palmer et al. 1991; Ross et al. 1997; Skelton et al. 1993; Viles et al. 2001; Yip & Zuiderweg 2004). However, some of the R₂ measurements remain unclear, yet.

One approach to improve the accuracy of R₂ measurements, by reducing cumulative pulse error, is an alternative phase scheme that applies pairs of orthogonal 180° pulses (XXYȲ) rather than the conventional CPMG (XXXX) (Bain et al. 2010; Bain et al. 2011; Gullion et al. 1990; Long et al. 2008; Yip & Zuiderweg 2004). The alternative phase scheme with a correction factor given to account for longitudinal relaxation during the pulsing was found to provide more accurate transverse relaxation rates covering a wider off-resonance frequency range than the conventional scheme (Bain et al. 2011; Yip & Zuiderweg 2004). This conclusion was supported by simulation results as well as experimental results. However, the studies assumed relatively low power radio-frequency (r.f.) pulses (~2.5 kHz), which is far smaller than in typical applications (Bain et al. 2011; Yip & Zuiderweg 2004). Although we and others have studied off-resonance errors (Bain et al. 2011; Czisch et al. 1997; Ishima & Torchia 2005; Korzhnev et al. 2000; Myint et al. 2009; Ross et al. 1997), quantitative analysis of the uncertainty of R₂ determine using the alternative CPMG phase scheme has not been studied. Most ¹⁵N CPMG relaxation experiments applied to protein backbone dynamics studies have been performed using the conventional CPMG sequence (Meiboom & Gill 1958), and the practical advantage of the alternative phase scheme method has not yet been established.

The purpose of this article is to establish the condition under which the alternative phase scheme provides a practical advantage to the conventional CPMG scheme in measuring accurate R₂ values. In particular, we aim to identify whether it is advantageous or not when a relatively strong r.f. is employed for CPMG pulse train. In order to achieve this goal, we simulated ¹⁵N CPMG relaxation data using three different phase schemes, and determined R₂ and its uncertainty for each as a function of off-resonance frequencies. The R₂ uncertainty was estimated by Monte Carlo error estimations in which a Gaussian distribution was assumed to generate synthetic datasets for the samplings. We generated the synthetic dataset by employing two different standard deviations (a) given by a rmsd deviation of the noise of the NMR spectra and (b) by a rmsd deviation of the residuals (I_i − I^fit) in the fit. Both have been used for ¹⁵N relaxation data analysis (Nicholson et al. 1992; Palmer et al. 1991; Skelton et al. 1993). The former sampling reflects only the statistical noise uncertainties of R₂ but not any additional error. The later reflects overall fit-uncertainties that include both experimental statistical noise and systematic errors. By comparing the R₂ uncertainties, magnitudes of the uncertainties other than those due to the experimental noise are estimated (Ishima & Torchia 2005). Our results show that in CPMG experiments performed by employing a radio-frequency of B₁ > 5 kHz, R₂ obtained using the conventional CPMG (XXXX) phase scheme is close to the one obtained using the alternative phase scheme (XXYȲ) at the off-resonance frequency, ω_off/2π, up to 1400 Hz. However, the conventional CPMG is expected to introduce higher systematic error even with ω_off/2π < 1400 Hz presumably due to non-exponential behavior of magnetization decay. We conducted ¹⁵N CPMG relaxation experiments to verify the results of the calculations. Experimental results further showed that the differences in R₂ uncertainties in the two schemes are manifest only when the noise-to-signal ratio is significantly smaller than the fractional systematic error on R₂.

Methods

NMR Experiments

¹⁵N transverse relaxation experiments were conducted using a 0.8 mM ¹⁵N labeled ubiquitin at pH 4.5 on a Bruker Avance 900 NMR instrument. Ubiquitin sample was purchased and prepared as described previously (Myint et al. 2009). Three transverse relaxation experiments were performed with a conventional CPMG phase scheme (XX – XX, here noted 00-00), an alternative phase scheme (XX –YȲ, here noted as 00-13), and a long alternative phase scheme (XXYȲ – XXYȲ, here noted as 0013-0013). Here, X and Y indicate pulse phases, and a hyphen indicates the timing applied to the ¹H 180° pulses to suppress cross-correlation by ¹H-¹⁵N dipolar interaction and ¹⁵N chemical shift anisotropy (CSA) (Kay et al. 1992; Palmer et al. 1992). We used the same CPMG pulse sequence that was applied previously ((Freedberg et al. 2002), except for an additional semi-constant time for the t₁ evolution, not in the original sequence (Kay et al. 1992). The total phase cycle is 8 with a phase inversion for the CPMG period. All the ¹⁵N pulses are applied even number of times at each pulse scheme. Delays for the 00-00 and 00-13 experiments were varied: 0, 8, 16, 24, 32, 40, and 48 ms for the 00-00 and 00-13. Delays for the 0013-0013 experiments were varied: 0, 16, 32, and 48 ms. The maximum delay is set shorter than the expected 1/R₂ because of the high sensitivity of an instrument equipped with a cryogenic probe and to avoid significant sample heating (Myint et al. 2009). Radio-frequency power for the ¹⁵N pulses was 5.56 kHz (90 μs as a 180° pulse), and a half duration between ¹⁵N CPMG pulses, τ_CP, was 0.5 ms. Here, 2τ_CP is the time between the centers of two adjacent CPMG pulses. ¹⁵N pulses were applied at 130 ppm as a carrier frequency to investigate off-resonance effects. The number of scans was 8. Using the same pulse powers, ¹⁵N longitudinal relaxation was recorded for the analysis of the 00-13 type relaxation data. The delays applied for the longitudinal relaxation measurements were: 0, 0.05, 0.1, 0.25, and 0.5 s.

¹⁵N transverse relaxation experiments were also performed using a 250 μM Human Immunodeficiency virus-1 (HIV-1) protease at pH 5.8 on a Bruker Avance 600 MHz NMR instrument. The protease was over-expressed and purified mainly using the previous protocol (Nalam et al. 2007). Data was recorded using a conventional CPMG phase scheme (XX – XX) with delays of 0, 8, 16, 24, 32, 48, and 64 ms. Data were recorded by employing the same r.f. field strength for the ¹⁵N pulses, 5.56 kHz, as the same that of 900 MHz. However, the carrier frequency of the pulse was placed at 117 ppm that is approximately the center of the amide ¹⁵N chemical shifts of the protease sample. 64 scans were accumulated for each free induction decay.

Data analysis

Free induction decay signals were zero-filled four times, apodized with a sine window function with 40% offset, and Fourier transformed in both dimensions using NMRpipe software (Delaglio et al. 1995). Signal intensities at individual positions were taken instead of peak volumes using the NMRdraw software (Delaglio et al. 1995). Line-shape fitting algorithm was not used to estimate peak heights. Experimental noise was obtained for each two-dimensional spectrum, but assumed to be the same in each CPMG experiments.

For each time-course of magnetization decay, a transverse relaxation rate, R₂, was optimized assuming a mono-exponential decay function, I(t) = I₀exp(−t·R₂). In theory, if the initial intensity is correct, there is only one unknown parameter in this equation. However, since there is small loss of intensity at time zero, both I₀ and R₂ are typically optimized. Note that the same equation is used for R₁ determination as well as R₂ in protein ¹⁵N NMR relaxation since the Freeman-Hill method is used (Freeman & Hill 1971).

Once R₂ values were optimized, Monte Carlo error estimation was performed to estimate uncertainty of R₂. In this method, first unknown parameters, R₂ and the initial intensity, were optimized using the experimental data, and the set of the fit “ideal” intensities were back-calculated using the optimized parameters. Second, a hundred number of sets of synthetic intensity data were generated to allow a Gaussian distribution with the ideal intensities as the mean. Finally, optimization was repeated for these synthesized data sets to calculate the standard deviation of R₂ and the initial intensity. The Gaussian distribution to generate synthetic intensities was defined in two ways:

1. a root-mean-square deviation (rmsd) of the NMR spectral noise (Palmer et al. 1991; Skelton et al. 1993)

2. a standard deviation of the residual (I_i − I^fit) of the fit (Nicholson et al. 1992). In this article, R₂ errors that were calculated using the experimental noise are denoted R₂^noise_err, and those were calculated using the residual of the fit are denoted R₂^fit_err. The former reflects only experimental noise error and the later reflects overall fit-uncertainties that include both experimental statistic noise and systematic noise. By comparing the two types of R₂ uncertainties the uncertainties other than those due the experimental noise are estimated (Ishima & Torchia 2005).

The error in the R₂ value, measured using the 00-13 and 0013-0013 sequences, caused by R₁ relaxation during the r.f. pulses is recommended to be corrected using the equation introduced by Zuiderweg’s group (Yip & Zuiderweg 2004):

$${R_{\mathit{2}}}^{\mathit{obs}}=R_{\mathit{2}}+d(R_{\mathit{1}}-R_{\mathit{2}})/\mathit{4}=R_{\mathit{2}}(\mathit{1}-d/\mathit{4})+{dR}_{\mathit{1}}/\mathit{4}$$ (1)

Here, d indicates a duty cycle of the r.f. pulse: total duration of the r.f. pulses divided by the entire CPMG delay. However, in the following analysis, no correction was made because the correction factor is calculated to be small. When pulse power γ_NB₁/2π = 5.6 kHz is applied with a reasonable delay (τ_CP = 0.45 ms and 0.5 ms for simulation and experiments, respectively), the observed R₂ will be only 2.5% and 2.25% smaller than the correct R₂, respectively when R₁ = 0 (equation (1)). When 0 < R₁ < R₂, the difference becomes less than 2.5% and 2.25%, respectively. This is in contrast to the condition that was used by Yip and Zuiderweg in which ca. 8% correction of R₂ was needed (Yip & Zuiderweg 2004). Note that since this equation does not contain any off-resonance frequency, some of the error caused by the combination of the effects of pulse imperfection and off-resonance is not corrected by this equation. We did not use the 00130031 sequence (Yip & Zuiderweg 2004) because the minimum cycle, each CPMG loop (n=1) of (00130031-00130031)₂, needed to suppress cross correlation between ¹⁵N CSA and ¹H-¹⁵N dipolar interactions is long, i.e., 32 ms when τ_CP = 0.5 ms.

Simulation

The time evolution of bulk nuclear magnetization of a scalar-coupled ¹⁵N-¹H spin system was calculated to determine transverse relaxation rates. For this, we used a relaxation matrix that contains 16 Cartesian product operators as the base set, as described previously (Allard et al. 1997; Allard et al. 1998; Myint et al. 2009; Myint & Ishima 2009).

E/2	NX	NY	NZ	HX	HY	HZ	2NXHX
2NYHX	2NZHX	2NXHY	2NYHY	2NZHY	2NXHZ	2NYHZ	2NZHZ

Time dependence of the relaxation was calculated step by step for each time increment, t₁, by solving the M(t₀+ t₁)=exp(R₂*t₁)M(t₀). τ_CP is 0.45 ms, and each CPMG loop of (τ′_CP −180_N − τ′_CP − τ′_CP −180_N − τ″_CP −180_H − τ″_CP −180_N − τ′_CP − τ′_CP −180_N − τ′_CP)₂ was set to be a 7.2 ms, and incremented to a total 72 ms. Here, τ′_CP and τ″_CP satisfy τ_CP = τ′_CP + 90_N and τ_CP = τ″_CP + 90_N + 90_H. Simulation was done twice with the starting ¹⁵N transverse magnetization at X and −X and detection at X and −X, respectively, for the phase cycle. The output is the average time course of the two phase cycles. In the relaxation matrix, ¹H and ¹⁵N chemical shift and the 90-Hz ¹H-¹⁵N J-coupling evolution, r.f. pulse effects, auto and cross relaxation terms, and cross-correlation terms were included (Allard et al. 1997; Allard et al. 1998; Myint et al. 2009; Myint & Ishima 2009). In the calculation, ¹⁵N and ¹H r.f. pulses were applied at field strengths of 5.56 kHz and 25 kHz, respectively, and ¹⁵N signal off-resonance frequency, ω_off/2π, was varied from −3000 to 3000 Hz in 200 Hz steps. Off-resonance frequency of the ¹H signal was set at 2250 Hz, which corresponds to 7.5 ppm at 900 MHz NMR. Relaxation terms in the matrix were calculated assuming a simple Lorentzen spectral density function with a 5 ns rotational correlation time, 170 ppm ¹⁵N CSA, and 1.02 Å N-H distance. Additional ¹H longitudinal and transverse relaxation rates of 10 s⁻¹ and 20 s⁻¹ were added, in addition to the ¹H-¹⁵N dipolar term, to the ¹H relaxation (Myint et al. 2009).

Once the time dependence was calculated, R₂ and its uncertainty, R₂^fit_err, were determined by Monte-Carlo error estimation using the standard deviation of the residual (I_i − I^fit) of the fit as the uncertainty in I_i (Nicholson et al. 1992). However, R₂^noise_err was not calculated because experimental noise itself was not assumed in the simulation. The effect of the inhomogeneity of the B₁ field was simulated by assuming that relative magnetization intensities of 0.375, 0.5, and 0.125 experienced respective r,f, field strengths of 1.0B₁, 1.05B₁ and 1.1B₁, respectively, where B₁ is the correctly calibrated field strength. Then, R₂ and R₂^fit_err were determined from simulations of the weighted time course of the average magnetization. The simulation analysis for B₁ inhomogeneity was performed for the [00-00] and the [00-13] schemes individually. Calculations were performed using MATLAB software (The Mathworks Inc., Natick, MA).

Results and Discussions

The purposes of this study are to further identify systematic errors, that persist even when experiments are repeated (Bevington & Robinson 1992; Heinrich & Lyons 2007), in ¹⁵N transverse relaxation rates, which are used to characterize protein backbone dynamics. In particular, uncertainties in CPMG R₂ values caused by systematic errors present when using phase schemes, [00-00], [00-13], and [0013-0013] are compared. For this purpose, we will firstly compare values of R₂ and R₂^fit_err derived from simulations of measurments obtained using phase-schemes, [00-00] and [00-13]. Next, we will compare experimental results obtained using the [00-00], [00-13], and [0013-0013] schemes. In the evaluation of the experimental results, R₂ errors estimated from two sets of Monte-Carlo methods, R₂^fit_err and R₂^noise_err, are compared as well as the R₂ values to idenity systematic errors.

Simulated off-resonance frequency dependence of [00-00] and [00-13] at a practical r.f. power level

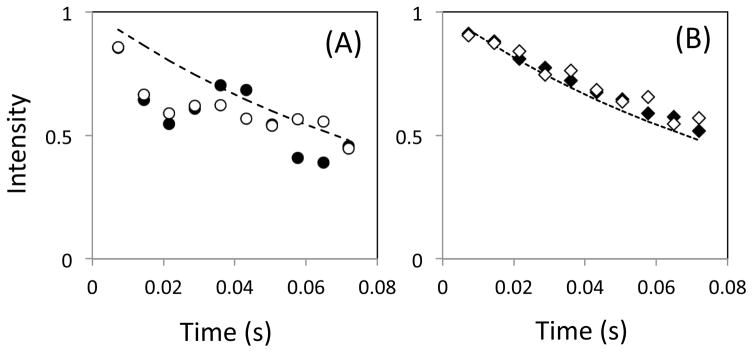
The time course of magnetization in a scalar-coupled two-spin system was calculated for the conventional phase [00-00] and the alternative phase [00-13], using r.f. pulse power of γ_NB₁/2π = 5.6 kHz (i.e., 90 μs, 180° pulse) at varying off-resonance frequency, ω_off/2π. Time courses of magnetization obtained by employing the [00-00] scheme at ω_off/2π = ±2400 Hz exhibit non single-exponential decay profiles (Figure 1A). The profiles are basically consistent to the previous results (For example, Fig. 4 of the reference, (Yip & Zuiderweg 2004)). In contrast, the time course of magnetization obtained by employing the [00-13] scheme under the same conditions exhibited profiles that are closer to a single-exponential decay (Figure 1B). This result is consistent with previous observations (Bain et al. 2011; Yip & Zuiderweg 2004). Note that our simulation shows slightly different profiles at positive and negative ω_off/2π. Such a different is not observed in the simulation for a single spin system, or when ¹H signal is located at the r.f. carrier frequency in the two-spin system (data not shown). Thus, although an even number of ¹H pulses is applied in each CPMG cycle, the difference in profiles is most likely due to an asymmetry caused by an ¹H off-resonance effect. The effect of the coupled spin was not taken into account in the previous CPMG simulations for the alternative phase schemes (Bain et al. 2011; Yip & Zuiderweg 2004).

Figure 1.

Simulated time course of transverse magnetization simulated using (A) the [00-00] sequence (circles) and (B) the [00-13] sequences (diamonds). In each figure, calculations were performed with ω_off/2π set equal to +2400 Hz (open circles) and −2400 Hz (closed circles).

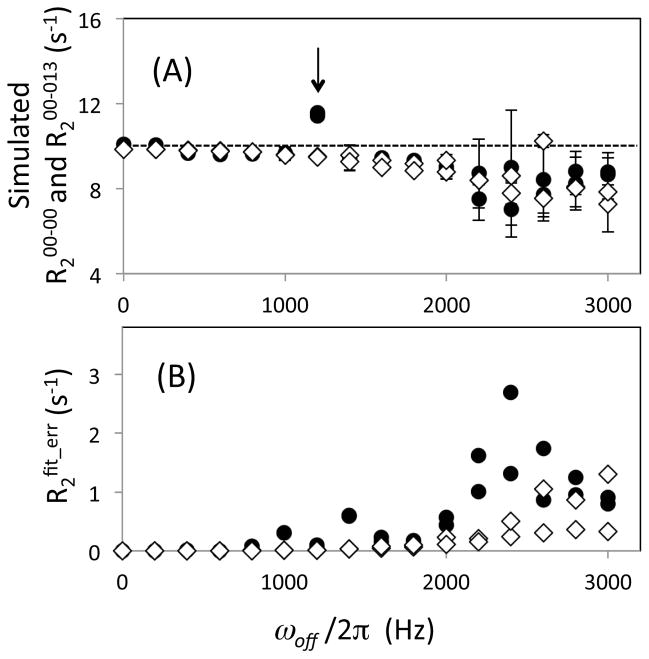
Once the time course of magnetization was simulated, R₂ was determined by assuming that each time course decayed as a single-exponential function. The resultant R₂ values are shown as a function of the absolute value of ω_off/2π in Figure 2A. R₂ values were determined using both [00-00] and [00-13] schemes and are denoted as R₂^00-00 and R₂^00-13, respectively. Both R₂ values were quite similar up to an off-resonance frequency, ω_off/2π = 1400 Hz (i.e., ω_off/(γ_NB₁) = 0.25), with average difference in R₂ 1.2% and with the maximum difference in R₂ of 2.2% (Figure 2A). Within each individual scheme, the fractional root-mean square deviations of R₂ values in the range from ω_off/2π 0 to 1400 Hz were 0.20% and 0.17% for R₂^00-00 and R₂^00-13, respectively. These results were obtained including all data except for the R₂^00-00 point at 1200 Hz. As shown by an arrow in Figure 2A, the R₂^00-00 at 1200 Hz was significantly higher than others. When the magnetization along X-axis starts CPMG duration and the pulses are applied from the X-axis, the Y-component of the transverse magnetization vector rotates through the Y-Z plane during the pulsing whereas the X-component stays mostly in the transverse plane. Thus, pulse imperfection effect caused by chemical shift precession during the pulsing becomes largest when a magnetization vector undergoes almost 360° precession between the adjacent CPMG pulses, as has been shown in other simulation and experimental results (Bain et al. 2011; Yip & Zuiderweg 2004).

Figure 2.

(A) Transverse relaxation rate, R₂, and (B) its error, R₂^fit_err, determined by simulation using the [00-00] (filled circles) and the [00-13] (open diamonds) sequences, plotted as a function of the absolute off-resonance frequency, ω_off/2π. Simulation of the time dependence of magnetization was performed varying ω_off/2π from −3000 to 3000 Hz at a 200 Hz step. Note that there are two data points determined using each pulse scheme at each ω_off/2π point, i.e., at the positive and the negative frequencies (Here, the two data points are shown by the same symbols). The arrow in (A) indicates a data point at a frequency that is close to the inverse of the CPMG pulse duration, a condition in which magnetization undergoes almost 360° precession during the period between the two adjacent CPMG pulses (see text). In (A), the dashed line indicates the original R₂ determined only by the auto relaxation. R₂ values are all plotted with R₂^fit_err as the error bars, while some of the error bars may not be notably large. R₂^fit_errs were estimated from the residual of the fits (see Methods section).

At ω_off/2π > 1400 Hz, deviations of R₂ by the off-resonance effects are observable in both R₂^00-00 and R₂^00-13 (Figure 2). In previous results, R₂^00-13 profiles were reported to exhibit a smaller and smoother change than those of R₂^00-00 (Bain et al. 2011; Yip & Zuiderweg 2004). This discrepancy between these results and ours is mostly caused by differences in experimental and simulation parameter: their applied B₁ field strength (γ_NB₁/2π ≤ 2.5 kHz) was smaller than that of ours (γ_NB₁/2π = 5.6 kHz), and their τ_CP (0.35 ms) was shorter than ours (0.45 ms and 0.5 ms). The latter set of the parameters make the [00-00] profile unfavorable. In addition, even in the previous experimental results, reduced but clear deviations of R₂ caused by off-resonance effects were shown even in R₂^00-13 (Bain et al. 2011; Yip & Zuiderweg 2004). Errors in R₂^00-13 found at a large ω_off/2π values are not corrected by equation (1) because equation (1) does not contain off-resonance frequency as one of calibration parameters. Overall, using our practical conditions for ¹⁵N relaxation measurements, R₂^00-00 and R₂^00-13 exhibit similar profiles almost within the entire experimentally required ω_off/2π range.

Uncertainty of each R₂ value, R₂^fit_err, was estimated from the Monte-Carlo method by assuming an average residual of the simulated intensities from the fit-intensities as a standard deviation for the normal distribution (Figure 2B). This R₂^fit_err solely reflects a discrepancy from a single-exponential decay model. R₂^fit_err for R₂^00-13 exhibits very small uncertainties (<0.1 s⁻¹ that correspond to <1% of R₂^00-13) in the entire ω_off/2π range. In contrast, R₂^fit_err obtained for R₂^00-00 exhibited large uncertainties at ω_off/2π > 1800 Hz, reflecting non-exponential behavior of magnetization simulated using the [00-00] scheme (Figure 2B). Nevertheless, R₂^fit_err values for R₂^00-00 (< 2%) remained small for ω_off/2π < 1800 Hz. Again this frequency range covers nearly all ¹⁵N signals of backbone amides in diamagnetic proteins up to 20 ppm at a 91 MHz ¹⁵N resonance frequency (Figure 2B). Overall, application of the practical B₁ field strength (γ_NB₁/2π = 5.6 kHz) provides similar R₂ values in both R₂^00-00 and R₂^00-13 schemes, within the spectral range of ±1400 Hz.

Effects of pulse strength miscalibration on R₂ error, determined by simulation

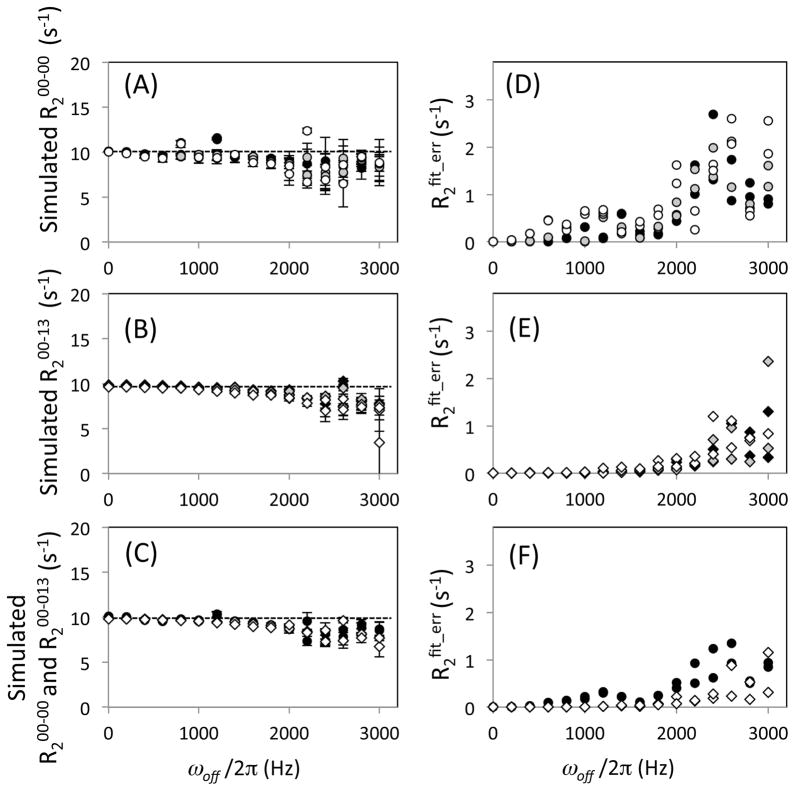
Similar simulations of magnetization and the determinations of R₂ were performed varying the B₁ field strength keeping the pulse width constant (i.e., power miscalibration). At a 5% or 10% increase (miscalibration) of the B₁ field strength, R₂^00-00 exhibits more variation of R₂ values at ω_off/2π < 1400 Hz (Figure 3A), which is larger than the variation of R₂^00-13 (Figure 3B). Similar to these observations, but more significantly, R₂^fit_err for R₂^00-00 (Figure 3D) became larger than that of R₂^00-13 at the miscalibrated B₁ field strength (Figure 3E). In particular, the R₂^fit_err for R₂^00-00 increased in proportion to the power miscalibration (Figure 3D). Such differences between R₂^00-00 and R₂^00-13, and between R₂^fit_err for R₂^00-00 and R₂^fit_err for R₂^00-13 are reduced when B₁ inhomogeneity is taken into account in the simulations (Figures 3C and F). Overall, the simulations demonstrate that the difference between R₂ obtained using R₂^00-00 and R₂^00-13 is insignificant for a relatively wide spectral width, provided that r.f. pulses are properly calibrated (Figure 2). However, the difference becames significant when r.f. pulses are miscalibrated (Figure 3). In particular, the [00-13] scheme is more tolerant to miscalibration errors than the [00-00] scheme.

Figure 3.

(A, B, C) Transverse relaxation rate, R₂, and (D, E, F) its error, R₂^fit_err, determined by simulation, plotted as a function of the off-resonance frequency, ω_off/2π. Simulation was performed (A, D) using the [00-00] scheme, (B, E) using the [00-13] scheme, and (C, F) assuming the B₁ inhomogeneity for both. In all figures, circle and diamond symbols indicate for R₂ obtained using the [00-00] and the [00-13] schemes, respectively. In (A–E), simulation of the time dependence of magnetization was done at a correctly calibrated B₁ field strength of 5.56 kHz CPMG 180° pulse of 90 μs (filled symbols), at a 5% stronger B₁ field strength (gray symbols), and at a 10% stronger B₁ field strength (open symbols). In (C) and (D), R₂ and R₂^fit_err determination assuming B₁ inhomogeneity was performed for both of the [00-00] and the [00-13] schemes (see Methods section). In the calculation, ω_off/2π was varied from −3000 to 3000 Hz at a 200 Hz step. There are two data points determined using each condition at each ω_off/2π, i.e., at the positive and the negative frequencies. In (A–C), R₂ values are all plotted with R₂^fit_err as the error bars while some of the error bars may not be notably large.

Experimental R₂ determined using [00-00], [00-13], and [0013-0013] sequences

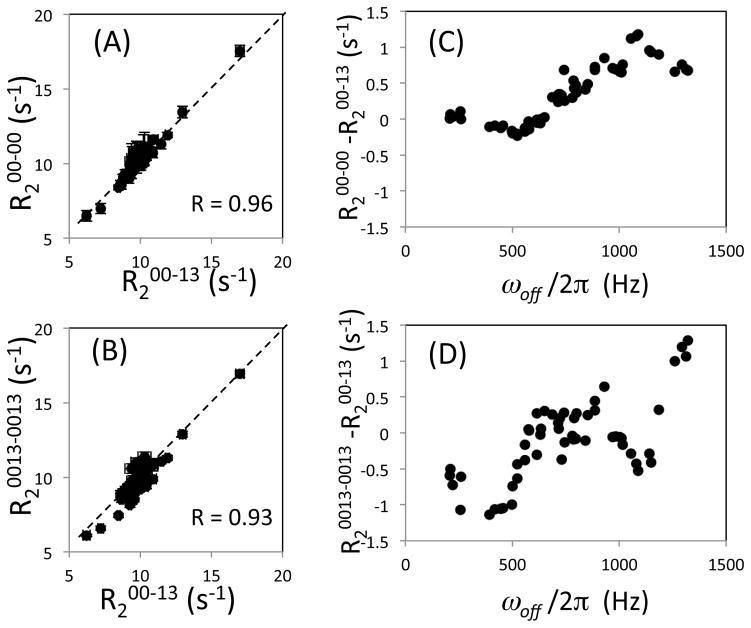
To verify the predictions of these simulations, we conducted ¹⁵N R₂ experiments for ubiquitin using a 900 MHz NMR instrument, and evaluated experimental results only for signals that were fit by an single-exponential decay function with R₂^err < 1 s⁻¹ (Figure 4). Most of the R₂^00-00 values were very similar to R₂^00-13 values (Figure 4A). As shown in Figure 4C, R₂^00-00 and R₂^00-13 did not exhibit significant difference for signals at ω_off/2π < 500 Hz, but the R₂ values increaslingly differ as ω_off/2π (off-resonance) increases. In contrast, although the effect of resonance off-set for R₂^0013-0013 is basically similar to that of R₂^00-13 (Figure 4B), R₂^0013-0013 exhibits differences from R₂^00-13 even when, ω_off/2π < 500 Hz (Figure 4D). Since the [0013-0013] scheme is more symmetric with respect to the ¹H 180° pulses than the [00-13] scheme, a possible explanation of the poor performance of the [0013-0013] scheme when ω_off/2π is small may be incomplete suppression of CSA-dipolar cross correlation. In the [0013-0013] scheme the period between ¹H 180° pulses is twice that of [00-13] scheme. As shown previously (Kay et al. 1992; Palmer et al. 1992), the cross correlation is suppressed in a two-spin system. However, artifacts in R₂ measurements may become significant because of the interactions with external protons that have been neglected in our simulations.

Figure 4.

Transverse relaxation rate, R₂, for ubiquitin experimentally determined using the [00-13] sequence was compared with (A) those obtained using the conventional [00-00] sequence and (B) those obtained using the [0013-0013] sequence using a 900 MHz NMR instrument. Difference of (C) the rates determined between the [00-00] and the [00-13] schemes, and (D) between the [0013-0013] and the [00-13] schemes are shown as a function of the off-resonance frequency, ω_off/2π. Note that the number of relaxation data points corrected for the [0013-0013] sequence were smaller than those of [00-00] and [00-13] due to the longer cycle length. For this reason, a [00130031-00130031] sequence (Yip & Zuiderweg 2004) was not applied. Only the data points at ω_off/2π < 1500 Hz were include because large error bars at larger resonance off-sets make it difficult to view the correlation plots. In (A) and (B), R₂ values are all plotted with R₂^fit_err error bars but may not be notable when the errors are small.

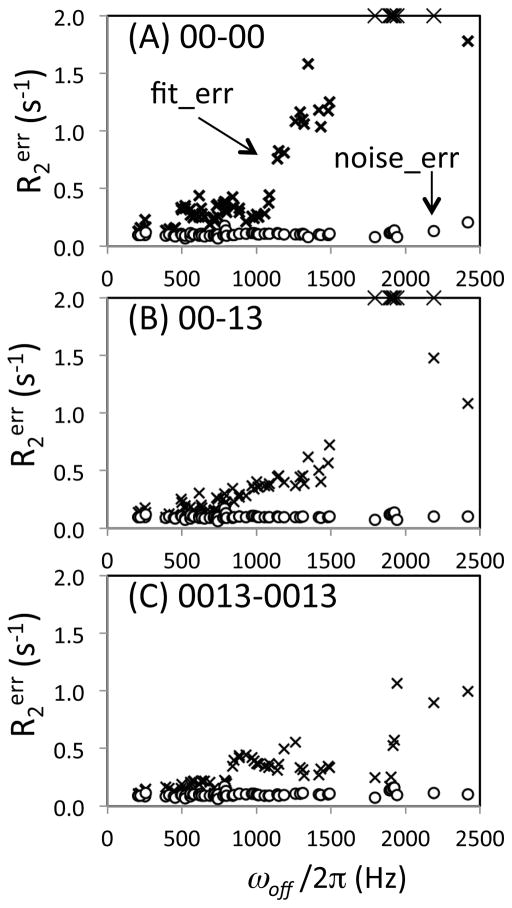
Monte-Carlo error estimation was calculated for ubiquitin R₂ values in two ways: using the spectral noise (R₂^noise_err) and using the residual of the fits (R₂^fit_err), to generate the synthetic data. Since ubiquitin is a rigid, small protein, amide signal heights were quite uniform (except for E24 that undergoes chemical exchange and exhibits severe line broadening at 900 MHz) as is evident in the R₂ correlations plotted in Figure 4. Therefore, R₂^noise_err was approximately the same for all three datasets (Figure 5, circles). In contrast, R₂^fit_err exhibits quite different profiles for R₂^00-00 (Figure 5A, ×-symbols) compared with R₂^00-13 and R₂^0013-0013 (Figures 5B and 5C, ×-symbols). R₂^fit_err for R₂^00-00 begins to increase at ω_off/2π ca. 1000 Hz, and becomes over 2 s⁻¹ at ω_off/2π > 1800 Hz (Figure 5A, ×-symbols). This profile is consistent with the simulations that incorporate the effect of pulse miscalibration, Figure 3F, demonstrating the excellent performance of the calculations. R₂^fit_err for R₂^00-13 and R₂^0013-0013 exhibits a more gradual increases as a function of ω_off/2π, and stays smaller than R₂^fit_err for R₂^00-00 even at ω_off/2π ~1500 Hz. This small gradual increase of R₂^err for the phase alternation experiments is also consistent with the simulation results, Figure 3F. Overall, in both R₂^00-00 and R₂^00-13, R₂^fit_err almost equals R₂^noise_err when ω_off/2π is small, and increases as ω_off/2π increases. This increasing discrepancy between the R₂^fit_err and R₂^noise_err as ω_off/2π increases is clear evidence of the off-resonance related systematic error.

Figure 5.

Uncertainties, R₂^err, of the transverse relaxation rates for ubiquitin experimentally determined using (A) [00-00], (B) [00-13], and (C) [0013-0013] sequences on a 900 MHz NMR instrument, shown as a function of the off-resonance frequency, ω_off/2π. R₂ values that are shown in Figure 4 are used. An additional 16 sets of data that exhibited R₂^err > 1 s⁻¹ were also included in the graphs in order to show how the uncertainty increases as a function of ω_off/2π. R₂^err values were determined by two different Monte-Carlo error estimations in which the standard deviations of a Gaussian distribution function that generates synthetic data sets were given by rmsd of spectral noise, R₂^noise_err (circle), and by rmsd of residuals of the initial fit intensities, R₂^fit_err (×-symbols). Difference of the two uncertainties indicates errors other than experimental noise. R₂^err values above 2 s⁻¹ are shown as the ceiling values.

Off-resonance systematic error is not observed in large proteins

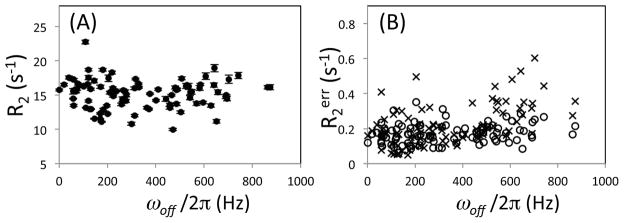
To test if off-resonance effects are observable in the case of a larger protein with less spectra sensitivity than ubiquition, the CPMG experiments were also performed for HIV-1 protease using a 600 MHz instrument. In this experiment, the ¹⁵N pulse carrier was placed at 117 ppm which is almost the center of the ¹⁵N chemical shifts of the protease backbone amides. R₂^00-00 for the 92 residues are on average 15.22 s⁻¹ (±2.1 s⁻¹), which is approximately 1.5 times larger than that of ubiquitin and consistent with previous protease measurements (Freedberg et al. 2002). R₂^00-00 values are relatively uniform in this ω_off/2π range (Figure 6A). R₂^noise_err is 0.17 s⁻¹ whereas R₂^fit_err is 0.22 s⁻¹ (Figure 6B). The R₂^noise_err values are approximately 2% of R₂^00-00. Although some R₂^fit_err are higher at ω_off/2π > 500 Hz, the differences between R₂^noise_err and R₂^fit_err are not significant. Thus, differences in R₂^err estimated by two methods are not observed because the noise error is larger than the off-resonance error. This result is in contrast to that obtained for ubiquitin.

Figure 6.

(A) Transverse relaxation rate, R₂, and (B) its uncertainty, R₂^err, for HIV-1 protease experimentally determined using the [00-00] sequence on a 600 MHz NMR instrument with 117 ppm as ¹⁵N pulse carrier frequency. In (A), R₂ values are all plotted with R₂^fit_err error bars but may not be notable when the errors are small. In (B), R₂^err values were determined by two different Monte-Carlo error estimations in which the standard deviations of a Gaussian distribution function that generates synthetic data sets were given by rmsd of spectral noise, R₂^noise_err (circle), and by rmsd of residuals of the initial fit intensities, R₂^fit_err (×-symbols).

Summary

In this study, ¹⁵N CPMG experiments with and without the phase alternation were investigated at the practical high pulse power (γ_NB₁/2π = 5.6 kHz) and also with ¹H 180° pulses that are applied to suppress dipolar/CSA cross correlation. Since CPMG performance is determined by the field strength of the r.f. pulse (γ_NB₁/2π), the delay between the CPMG pulses (τ_CP), the off-resonance frequency (ω_off/2π), and relaxation rates and scalar couplings, it is important to investigate the performance at optimal parameter settings. First, our results showed that, in the high power condition, both pulse phase schemes yield similar results unless resonance off-sets are very large. Our simulations reproduced the reduction of the measurement accuracy as ω_off/2π increases even with the phase alternation method, which is consistent with the experimental results. Second, when the pulse power is miscalibrated, the fit error becomes larger in the conventional CPMG than the phase alternation approach, even when the resonance off-set is small. Third, although the full (longer) phase alternation cycle has a better performance in theory, our experimental results show that the actual performance of the longer cycle was not improved in the ¹⁵N experiments with ¹H 180° pulses.

Abbreviations

CPMG

Carr-Purcell-Meiboom-Gill

R₂

transverse relaxation rate

R₂^err

uncertainty of transverse relaxation rate

ω_off/2π

off-resonance frequency

r.f

radio frequency