VARIABLE SELECTION AND PREDICTION WITH INCOMPLETE HIGH-DIMENSIONAL DATA

Abstract

We propose a Multiple Imputation Random Lasso (mirl) method to select important variables and to predict the outcome for an epidemiological study of Eating and Activity in Teens. In this study 80% of individuals have at least one variable missing. Therefore, using variable selection methods developed for complete data after listwise deletion substantially reduces prediction power. Recent work on prediction models in the presence of incomplete data cannot adequately account for large numbers of variables with arbitrary missing patterns. We propose MIRL to combine penalized regression techniques with multiple imputation and stability selection. Extensive simulation studies are conducted to compare MIRL with several alternatives. MIRL outperforms other methods in high-dimensional scenarios in terms of both reduced prediction error and improved variable selection performance, and it has greater advantage when the correlation among variables is high and missing proportion is high. MIRL is shown to have improved performance when comparing with other applicable methods when applied to the study of Eating and Activity in Teens for the boys and girls separately, and to a subgroup of low social economic status (ses) Asian boys who are at high risk of developing obesity.

1. Motivating example

In large epidemiological studies, accurately predicting outcomes and selecting variables important for explaining the outcomes are two main research goals. One commonly encountered complication in these studies is missing data due to subjects’ loss to follow up or nonresponses. It is not straightforward to handle missing data when performing variable selection since most existing variable selection approaches require complete data.

Our motivating study is the Eating and Activity in Teens (Project EAT) with a focus of identifying risk and protective factors for adolescent obesity [Larson et al. (2013), Neumark-Sztainer et al. (2012)]. A primary research goal is to identify the most important household, family, peer, school and neighborhood environmental characteristics predicting a teenagers’ weight status in order to provide recommendations for potential prevention strategies. A strength of Project EAT is the breadth of potential predictors of weight status collected on 2793 7th and 10th grade teens from 20 schools in Minneapolis/St. Paul school districts. Weight status was obtained by direct measurements of height and weight. Predictors were obtained from self-reported questionnaires from teens themselves as well as from peers (i.e., derived from friendship nominations) and parents (i.e., from a separate questionnaire sent home to parents). School administrators were surveyed to obtain variables about food and physical activity policies at schools. Potential predictors describing the neighborhood built environment (e.g., density of fast food restaurants) were measured using information from the Geographic Information System (GIS) centered at the home residence of each teen. In total there are 62 predictor variables across the different contexts which are of interest to examine in terms of their relationship with weight status. This multi-contextual source design is consistent with recent research paradigms for obesity which view it as impacted by not only individual behaviors but also social and physical contexts [Frerichs, Perin and Huang (2012)].

Several risk factors for teenagers’ body mass index (b.m.i.) z-score, including higher parental weight status and peer weight status and lack of neighborhood safety, were identified in Neumark-Sztainer et al. (2012) and Larson et al. (2013). High social economic status has been found consistently to be a protective factor as well as frequency of family meals. Some factors found to be protective, such as having more unhealthy food at home, may be more likely to be reactive to weight status rather than preventing it. For example, when the b.m.i. of a teenager is high, parents may apply higher restrictions of unhealthy high-calorie food and impose less pressure to eat.

One challenge in analyzing the Project EAT data is that since many measures were collected with different instruments, 81% of individuals have at least one variable missing data (only 523 of 2793 teenagers had all 62 predictors). We present some of the most frequent missing patterns in Table 1 for 9 variables shown to be important from the analyses by various methods. The proportion of missing for each data source is different (e.g., 15–20% missing from the parent survey, 40–44% missing from peer surveys, 2–10% missing from GIS variables). The missingness is nonmonotone, that is, does not satisfy monotone missingness: for variables (X₁, … , X_p), X_j on an individual is missing implies all subsequent variables X_k are missing for k > j; and there are a total of 247 distinct complex patterns for all 46 variables with missing entries, which makes it complicated to model the missingness. Another challenge is that many predictors are moderately or highly correlated, which makes it difficult to separate their effects. The candidate predictors in Project EAT are naturally classified into family, peer, school, and neighborhood measures. The variables within each class can be highly correlated because students in the same neighborhood tend to go to the same school and share the same peer groups.

Table 1.

Most frequent (≥ 1%) missing patterns of some important variables in Project EAT data (“X” indicates nonmissing and “·” indicates missing)

Variables	% missing*	Missing patterns
Parental pressure to eat	18	X	X	·	·	X	X	X	X	X
Parental restriction of high-calorie food	18	X	X	·	·	X	X	X	X	·
Asian	0	X	X	X	X	X	X	X	X	X
Parental weight status	21	X	X	·	·	·	·	X	X	X
Home unhealthy food availability	0	X	X	X	X	X	X	X	X	X
Hispanic	0	X	X	X	X	X	X	X	X	X
Social economical status	5	X	X	X	X	X	X	·	·	X
Weight status male friends	36	X	·	X	·	X	·	X	·	X
Native american	0	X	X	X	X	X	X	X	X	X
Missing pattern percentage (%)		48	26	9	5	2	2	1	1	1

^*Marginal missing proportion for each variable.

Our goal is to develop a method to perform variable selection for studies similar to Project EAT where the number of predictors is large (possibly larger than the sample size), some predictors are highly correlated, and there is substantial missingness with complicated arbitrary missing data patterns.

2. Review of variable selection methods in the presence of missing data

The most common practice for dealing with missing data is listwise deletion where any observation missing at least one variable is removed from the analysis and variable selection is applied to complete data. However, complete case analysis may cause bias when the missing completely at random (MCAR) assumption is not satisfied and will often cause severe loss of information particularly for high-dimensional data involving nonmonotone missing data patterns. There are three main types of methods to handle missing data. The first group of methods specify the joint distribution of the variables with and without missing data and compute the observed data marginal likelihood by integrating over the missing data distribution and performing variable selection by adapting likelihood-based information criteria developed for complete data [Claeskens and Consentino (2008), Garcia, Ibrahim and Zhu (2010a, 2010b), Ibrahim et al. (2011), Laird and Ware (1982), Shen and Chen (2012)]. However, none of these methods are easily applicable to our motivating example, Project EAT, where the number of variables with missing data is large and missing data patterns are complicated. It may be computationally intractable to specify a forty-six-dimensional missing data distribution (both continuous and categorical variables with missing entries) and integrate with respect to this distribution. In addition, these methods are not applicable when the number of variables p exceeds the number of observations n, which is the case for the subgroup analysis of Project EAT data.

A second approach to handle missing data in a variable selection setting is through inverse probability weighting. Johnson, Lin and Zeng (2008) introduced a general variable selection method based on penalized weighted estimating equations. However, this approach is only applicable to the monotone missing pattern, whereas the Project EAT data has a large number of missing data patterns that are nonmonotone and the probability of complete data for some subgroup of subjects is close to zero. Thus, the inverse probability weighting methods are not applicable.

A third group of methods based on multiple imputation is flexible to deal with nonmonotone and complex missing patterns, thus applicable to our motivating example. A traditional way of conducting multiple imputation analysis is to conduct linear regression for each imputation and combine inferences by Rubin’s Rule [Rubin (1987)]. Wood, White and Royston (2008) recommended applying classical variable selection methods such as stepwise selection where, at each step, the inclusion and exclusion criteria for a variable were based on overall least square estimators with standard errors computed from Rubin’s Rule [Rubin (1987)]. Chen and Wang (2013) proposed to apply the group lasso penalty to merged data sets of all imputations, treating the same variable from different imputations as a group. The advantages of techniques based on multiple imputation include the convenience of implementation by using standard software modules and the feasibility for high-dimensional data with complex missing patterns. There are limitations for the classical variable selection method such as stepwise selection including overfitting, difficulties to deal with collinearity and relying on p-value based statistics which do not have the claimed F-distribution [Hurvich and Tsai (1990), Tibshirani (1996), Derksen and Keselman (1992)]. Chen and Wang (2013) (CW) made the first attempt to combine multiple imputation and penalized predicting models. It is feasible for high-dimensional cases with a complex missing structure, however, the group lasso may be vulnerable to high correlation between variables, therefore, we aim at developing an alternative way to combine the two.

3. Multiple imputation random lasso (MIRL)

3.1. Rationale and algorithm

Here we develop a new method, Multiple Imputation Random Lasso (MIRL), which combines multiple imputation and random lasso [Wang et al. (2011)]. Random Lasso is shown to have advantages dealing with highly correlated predicting variables in variable selection and prediction [Wang et al. (2011)]. In a nutshell, MIRL performs simultaneous parameter estimation and variable selection across bootstrap samples of multiply imputed data sets. The final parameter estimates are aggregated across samples and important variables are chosen and ranked according to stability selection criteria [Meinshausen and Bühlmann (2010)]. To accommodate highly correlated variables, we incorporate a similar strategy as random lasso [Wang et al. (2011)], where for each bootstrap sample, half of the variables are used for variable selection. The developed approach can handle an arbitrary nonmonotone missing pattern under the missing at random (MAR) assumption and accommodate the p > n case. There are a few new features of MIRL. First, MIRL extends the random lasso to deal with data with missing entries by multiple imputation. Second, it improves the hard thresholding in random lasso by stability selection to yield higher prediction accuracy, better variable selection performance, and producing an importance ranking of the variables. The procedure shares some similarities with random forest regression [Breiman (2001)], where multiple models are fitted and a final model is obtained through aggregation.

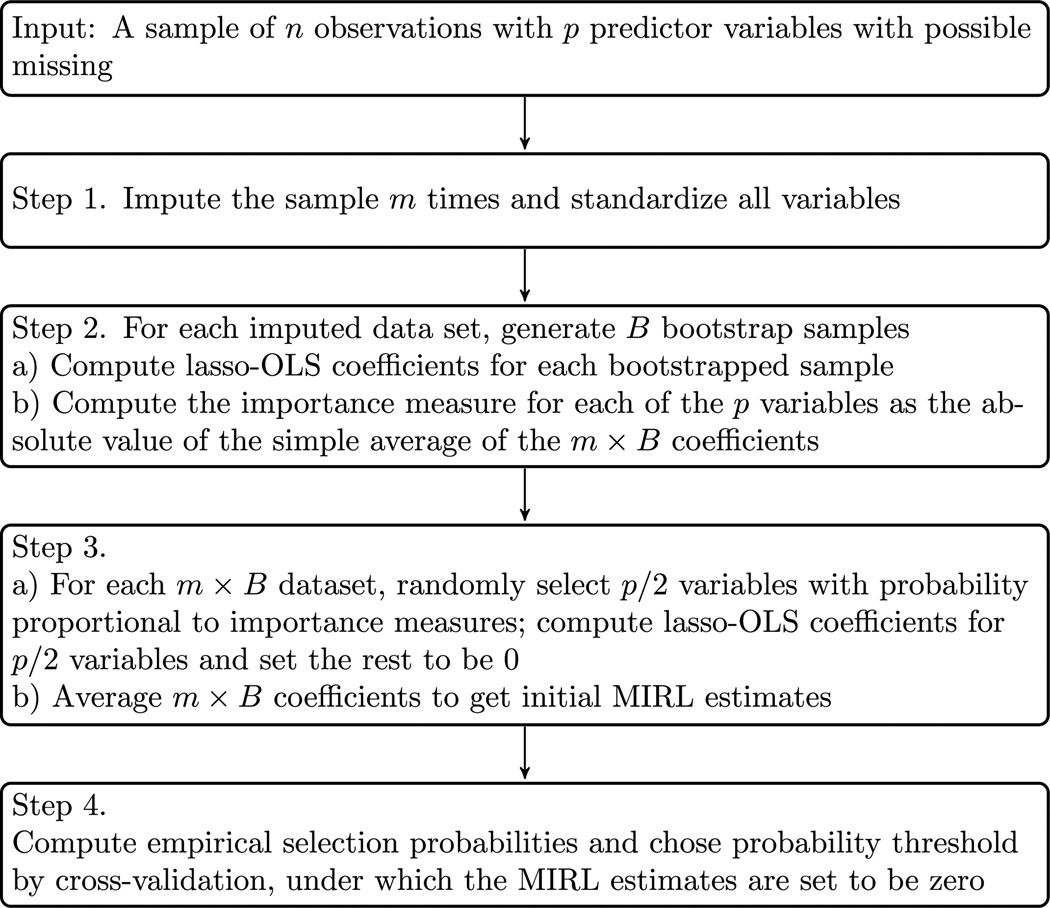
MIRL has four steps. In the first step, multiple imputation is performed to generate several sets of imputed data. In the second step, bootstrap samples are obtained for each imputed data set and an importance measure is created for each variable. In the third step, lasso-OLS estimates are produced for bootstrapped data sets where variables are sampled from importance measures. In the fourth step, final estimators are obtained through aggregation and use stability selection to get a final sparse model. The MIRL algorithm is presented below and illustrated by a flowchart in Figure 1, with implementation details of each step described in Section 3.2.

Fig. 1.

A flowchart of the MIRL algorithm as described in Section 3.

MIRL algorithm

Start with a sample of n observations and p predictors with missing entries. As an example, we consider the linear model Y = β₀ + Xβ + ε, where Y denotes a continuous response variable, X is a n × p design matrix, and ε is the random error. The parameter of interest is β = (β₁, β₂,…, β_p).

1. Let m denote the number of imputations. Impute the sample m times by chained equations [Azur et al. (2011)]. And standardize all variables to have mean 0 and variance 1.

2. For each imputed data set, generate B bootstrap samples and compute importance measures of predictors as follows:

   • (a)For the bth bootstrap sample in the ith imputation, b ∈ {1,…, B}, apply lasso-OLS to obtain estimates ${\widehat{\beta }}_{\mathit{\text{ij}}}^{(b)}$ for β_j, where i = 1,…, m and j = 1,…, p.
   • (b)
     Compute the importance measure of variable x_j by

     $$I_j={(\mathit{\text{mB}})}^{-1}\left|\sum _{i=1}^m\sum _{b=1}^B{\widehat{\beta }}_{\mathit{\text{ij}}}^{(b)}\right|.$$

3. Compute the initial MIRL estimates:

   • (a)For the bth bootstrap sample, randomly select [p/2] candidate variables with selection probability of x_j proportional to its importance measure I_j. Let Λ be a grid of K exponential decaying sequence of tuning parameters λ’s, apply lasso-OLS to obtain estimates ${\widehat{\beta }}_{\mathit{\text{ij}}\lambda }^{(b)}$ for β_j, j = 1,…, p and λ ∈ Λ.
   • (b)
     Average the m × B coefficients to get the initial MIRL estimate

     $${\widehat{\beta }}_j^{\text{init}}={(\mathit{\text{mB}})}^{-1}\sum _{i=1}^m\sum _{b=1}^B{\widehat{\beta }}_{\mathit{\text{ij}}{\lambda }_{\mathit{\text{ib}}}}^{(b)},$$

     where λ_ib is the tuning parameter chosen by cross-validation and ${\beta }_{\mathit{\text{ij}}{\lambda }_{i}b}^{(b)}=0$ if variable j is not sampled.

4. Compute selection probability and MIRL estimates with stability selection:

   • (a)
     Calculate the empirical probability

     $${\widehat{\prod }}_j^{\lambda }={(\mathit{\text{mB}})}^{-1}\sum _{i=1}^m\sum _{b=1}^{B}I\{{\widehat{\beta }}_{\mathit{\text{ij}}\lambda }^{(b)}\ne 0\}.$$
   • (b)Selection probability is given by ${\text{max}}_{\lambda \in \wedge }{\widehat{\prod }}_j^{\lambda }.$.
   • (c)
     The important variables are those in the stable variable set:

     $${\widehat{S}}^{\text{stable}}=\{j:\underset{\lambda \in \wedge }{\text{max}}{\widehat{\prod }}_j^{\lambda }\ge {\pi }_{\text{thr}}\},$$

     and the probability threshold π_thr is chosen by cross-validation with the one-standard error rule [Hastie et al. (2005)].
   • (d)
     The final MIRL estimates are defined as

     $${\widehat{\beta }}_j={\widehat{\beta }}_j^{\text{init}}\times I\{j\in {\widehat{S}}^{\text{stable}}\}.$$

The lasso-OLS estimator [Efron et al. (2004), Belloni and Chernozhukov (2013)] in the second and third step of the algorithm is a two-step procedure. First, we compute the lasso estimator $\widehat{\beta }=\text{arg min}{\Vert y-X\beta \Vert }_2^2+\lambda {\Vert \beta \Vert }_1,$, where the tuning parameter λ is chosen from cross-validation. Next, the lasso-OLS estimator is the ordinary least squares (OLS) estimator obtained by regressing the outcome on the subset of variables chosen by lasso. Belloni and Chernozhukov (2013) showed that lasso-OLS has the advantage of smaller bias compared to the original lasso.

3.2. Implementation details

We now describe some details on the implementation of the algorithm in each step. In step 1, multiple imputation is performed. Under the MAR assumption, we impute data through the multivariate imputation by chained equations (MICE) [Azur et al. (2011)]. As initial values, MICE imputes every missing value of a variable by the mean of observed values or a simple random draw from the data. Next, missing values on one particular variable are imputed by the predicted values from a suitable regression where the predictors are all other variables (penalized regressions can be applied for high-dimensional cases). Cycling through each of the variables with missing constitutes one cycle. Several cycles are repeated and the final imputations are retained as one imputed data set. A low number of cycles (say 10 to 20) is often sufficient [Buuren and Groothuis-Oudshoorn (2011)]. Last, the entire imputation process is repeated to generate multiple imputed data sets. The imputation regression models are provided for continuous data (predictive mean matching, normal), binary data (logistic regression), unordered categorical data (polytomous logistic regression) and ordered categorical data (proportional odds). For nonignorable missing data, there are also some procedures for multiple imputation. We refer the readers to Glynn, Laird and Rubin (1993) and Siddique and Belin (2008) for details.

In step 2, bootstrap samples are generated for each imputed data and an importance measure is created for each predictor variable. Specifically, for each bootstrap sample, lasso-OLS is applied where the tuning parameter is selected by cross-validation. A measure of importance for each covariate is calculated as the absolute value of the average of coefficients across bootstrap samples and imputations.

In step 3, for each imputed data, MIRL applies lasso-OLS where half of the variables are randomly selected with probability proportional to the importance measures obtained from step 2, and lasso-OLS is applied. We explored other choices of the number of variables to sample in the numerical study and found the result was insensitive to choices p/2 or p/3. Next, the initial MIRL estimators are obtained by averaging random lasso coefficients across bootstrap samples and imputations.

The initial MIRL estimators, however, are not sparse. As long as a predictor is selected at least once in a bootstrap sample, the corresponding coefficient will not be zero. A natural approach to yield the sparse model is through thresholding. The original random lasso algorithm [Wang et al. (2011)] introduced a threshold of t_n = 1/n, that is, consider a variable x_j to be selected in the final model only when the corresponding averaged coefficient satisfies $|{\hat{\beta }}_j|>t_n$. This threshold may produce a sparse model for situations where p ≫ n. However, for some epidemiological applications where p < n, it sets only a few coefficients to zero. For incomplete data, it is also difficult to determine whether n should be the sample size of the complete case data or the original data, or some value in between. In contrast, MIRL provides a systematic way to choose the threshold.

In step 4, MIRL ranks the variables and determines the informative ones by stability selection [Meinshausen and Bühlmann (2010)]. The central idea of stability selection is to refit the model on bootstrap sampled data sets and choose variables that are most frequently selected across the refitted models. It is sufficiently general to be applicable to many selection algorithms and shown to achieve consistent variable selection using the lasso penalty under weak assumptions on the design matrix [Meinshausen and Bühlmann (2010)]. Note the empirical selection probabilities in (1) involve π_thr as a predetermined threshold probability to be selected. Here, we use 4-fold cross-validation with a one-standard-error rule to choose selection probability threshold π_thr. That is, we obtain the threshold that minimizes the mean squared prediction error (MSPE) and set π_thr as the largest threshold whose MSPE does not exceed one standard deviation band of the minimizer. The empirical selection probabilities, ${\text{max}}_{\lambda \in \wedge }{\widehat{\prod }}_j^{\lambda },$, are natural measures of the importance of variables. For example, if determining the top 10 most important variables is desirable, instead of calculating π_thr, one can choose the top 10 variables with the highest selection probabilities.

4. Simulation studies

4.1. Simulation design

We conduct extensive simulations to compare MIRL with alternatives, including listwise deletion least squares regression (LDLS), listwise deletion lasso (LDlasso), multiple imputation with least squares regression (MILS) combined by Rubin’s Rule and MIRL without stability selection (MIRL⁻). LDLS is the least squares estimation for listwise deleted data after setting the coefficients not significant at the 5% level to be 0; MILS is the least squares estimation for multiply imputed data setting the combined coefficients not significant at the 5% level by Rubin’s rule to be 0; LDlasso is applying lasso to listwise deleted data with tuning parameter chosen by cross-validation; MIRL⁻ is the multiple imputed random lasso without stability selection, that is, MIRL⁻ uses a hard threshold and sets the coefficients to be 0 if the absolute values of coefficients are less than $\frac{1}{n}$ where n is the total sample size.

We simulated 100 data sets of size 400 from the linear model, Y = Xβ + ε, where X is a n by p matrix of multivariate normal random variables with a pair-wise correlation of ρ and ε ~ 𝒩(0, I_n). The first 10 variables have nonzero coefficients as (0.1, 0.2,0.3, 0.4,0.5, −0.1, −0.2, −0.3, −0.4, −0.5), and the others are noise variables. Each data set is separated into a training set and a testing set with 200 observations each.

We consider 24 scenarios, including 2 missing data schemes (MCAR or MAR), 2 missing proportions (50% or 75%), 3 sizes of noninformative variables (p = 25, 50, 100) and 2 pairwise correlations (ρ = 0.2, 0.6). Specifically, MAR data are generated as follows: covariates X₁ and X₆ are complete, outcome Y, and covariates X₅, X₁₀ are missing with probabilities {1 + exp(−X₆ + 2.5)}⁻¹, {1 + exp(−X₁ − X₆ + 2)}⁻¹ and {1 + exp(X₁ + 0.5X₆ + 2)}⁻¹, respectively. The other variables are missing completely at random and the missing probability is set such that overall the proportion of samples with missing entries on at least one variable is approximately 50% or 75%.

The goal is to evaluate MIRL’s ability in predicting the outcome and its variable selection properties. The MSPE is used as a measure of prediction ability and Matthews Correlation Coefficient (MCC) proposed in Matthews (1975), defined as the following,

$$\mathit{\text{MCC}}=\frac{\mathit{\text{TP}}*\mathit{\text{TN}}-\mathit{\text{FP}}*\mathit{\text{FN}}}{\sqrt{(\mathit{\text{TP}}+\mathit{\text{FP}})*(\mathit{\text{TP}}+\mathit{\text{FN}})*(\mathit{\text{TN}}+\mathit{\text{FP}})*(\mathit{\text{TN}}+\mathit{\text{FN}})}},$$

is considered as a measure of overall variable selection performance. Here TP, TN, FP and FN stand for true positive, true negative, false positive and false negative, respectively.

4.2. Simulation results

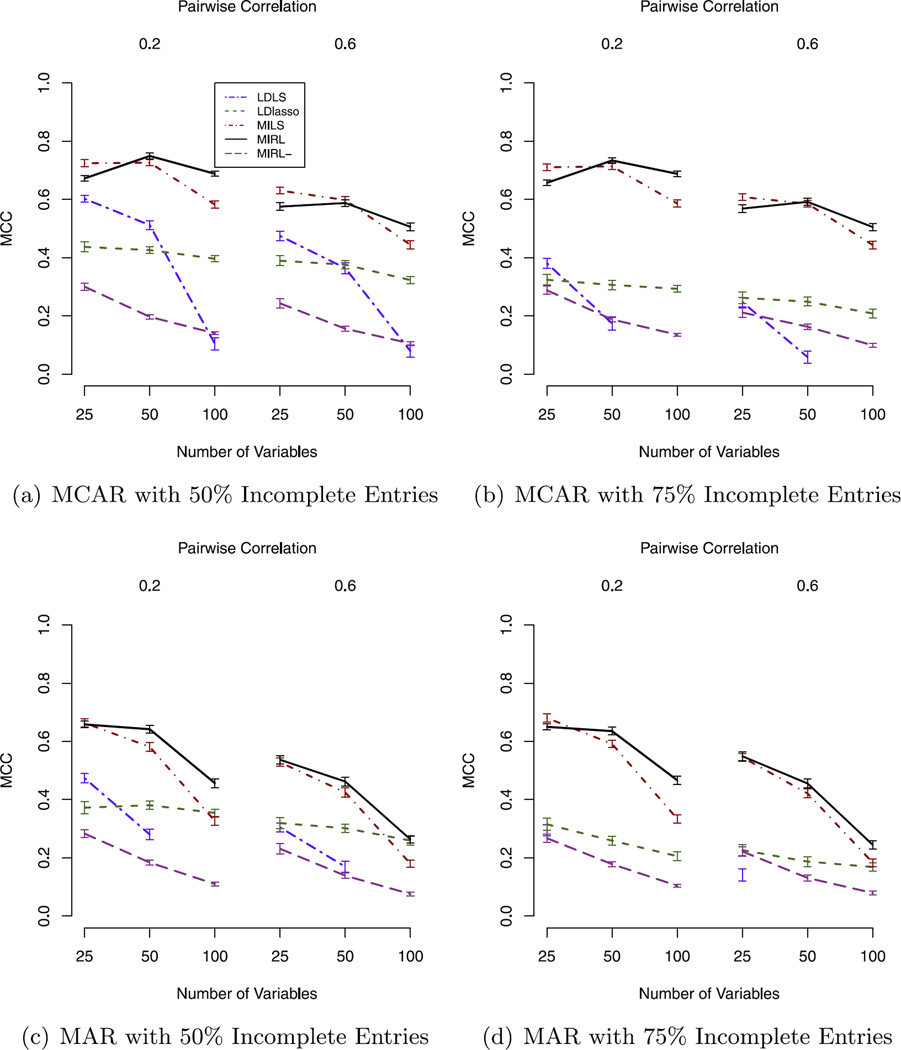
We present simulation results in Figures 2 and 3. First, the simulations demonstrate that stability selection enhances MIRL’s ability in variable selection. MIRL⁻ selects many noise variables, which may decrease the prediction accuracy. The MCC of MIRL⁻ is much smaller than that of MIRL in almost all scenarios, which shows that the stability selection step substantially improves the variable selection ability of MIRL compared to the hard threshold used in the random lasso. As for the prediction performance, MIRL has slightly larger MSPE than MIRL⁻ for some scenarios with p = 25, although these differences are within the one-standard error band. As the number of noise variable increases, MIRL shows more significant advantages. For MCAR 50% and 75% with pairwise correlation 0.2 and p = 100 scenario, MIRL has significantly smaller MSPE than MIRL⁻ as presented in Figures 2(a) and (b).

Fig. 2.

Prediction performance comparisons of MIRL with other methods under 4 missing schemes with varying number of variables and 2 pairwise correlations. (There are some missing or off-chart points for LDLS because when the number of variables is large and missing proportion is big, LDLS fails to give a reasonable estimator. Tables of exact numbers are omitted due to the page number limit; these tables can be provided upon request.)

Fig. 3.

Variable selection performance comparisons of MIRL with other methods under 4 missing schemes with varying number of variables and 2 pairwise correlations. (Tables of exact numbers are omitted due to the page number limit; they can be provided upon request.)

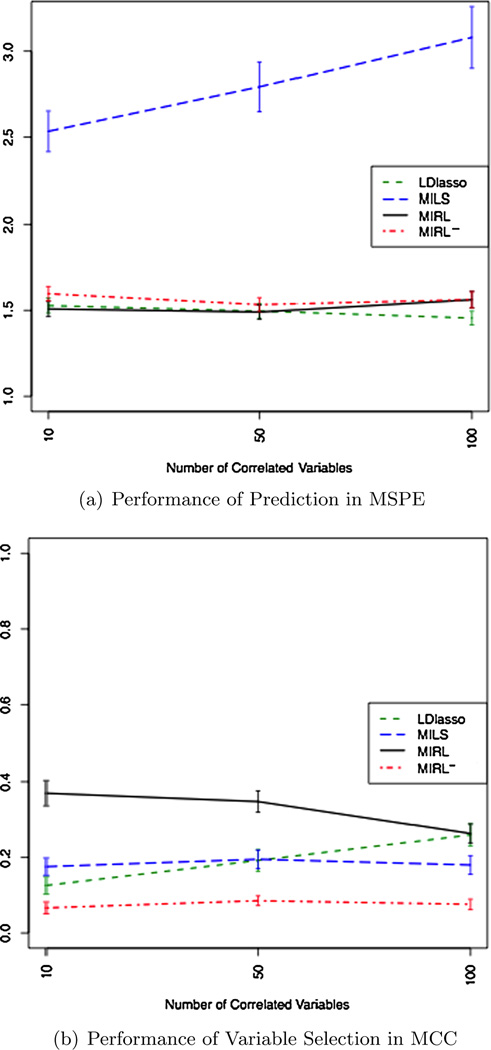
Second, the simulations show that the multiple imputation step makes better use of the available information than listwise deletion. MILS and MIRL are much better than LDLS in both MSPE and MCC in all scenarios. LDLS is not feasible when p is large and missing proportion is large because the sample size after list-wise deletion is less than the number of variables. LDlasso outperforms MIRL in the MAR scenario when p = 100, pairwise correlation 0.6 and missing proportion 50%. In this scenario, there is high correlation between all the informative variables and noise variables. MIRL selects more noise variables than LDlasso due to their correlation with important variables. When none or not all of the noise variables are highly correlated with influential variables, MIRL is expected to show a clear advantage. To demonstrate this, we run additional simulation and present results in Figure 4. The three scenarios are all MAR and the common missing proportion is 50%, and the common pairwise correlation is 0.6. The number of variables is fixed to be 100 with different numbers of noise variables correlated with informative ones, 0, 40, 90, respectively. We observe that when decreasing the number of noise variables correlated with informative ones, MCC increases for MIRL and decreases for LDlasso. For example, when there is no noise variable correlated with informative variables, the MCC of LDlasso is 0.126, which is 34.1% for MIRL. In the new scenarios, the MSPE of the two methods are not significantly different.

Fig. 4.

Performance comparison for varying number of correlated variables for a MAR scenario with 50% incomplete entries,p = 100 and pairwise correlation 0.6.

Third, MILS is MIRL’s closest competitor, and MIRL has comparative advantage over MILS when the number of variables is large and the correlation between variables is large. MIRL is significantly better than MILS in both MSPE and MCC when p = 100. For a smaller number of variables, that is, p = 50, MSPE of MIRL and MILS are not significantly different when pairwise correlation is 0.2, but MIRL has significantly smaller MSPE than MILS when the pairwise correlation is 0.6. Moreover, the increase of pairwise correlation does not affect the predictive ability of MIRL much, but it increases MSPE for MILS. For example, in Figure 2(a), for MCAR 50% scenario with p = 50 and pairwise correlation 0.2, MSPE is 1.208 for MIRL and 1.205 for MILS; when pairwise correlation is 0.6, MSPE is 1.226 for MIRL and 1.372 for MILS. In addition, for multiple imputation-based methods, MSPE and MCC are not significantly different between two missing proportions 50% and 75% with the other parameters fixed. Changing the missing data scheme from MCAR to MAR increases MSPE and decreases MCC, but this does not affect the ranking of methods.

4.3. Simulation summary

Compared with other existing methods, MIRL shows advantages when the data have a high proportion of missing and highly correlated influential variables. In addition, in contrast to alternative choices, MIRL has the advantage in scaling up to high-dimensional data with large n and p: MIRL uses a parallel algorithm such that it can be easily distributed in parallel to multiple computing cores and the results are summarized in the end. Additional simulation results of comparisons with other existing methods [Garcia, Ibrahim and Zhu (2010a), Johnson, Lin and Zeng (2008)] and a scenario where p > n are provided in Appendix A.

5. Data analyses of Project EAT

5.1. Main analyses

Here we present analyses of the proposed MIRL and other methods identifying risk and protective factors for adolescent obesity in Project EAT. Because of the nonmonotone and complicated missing structure, a large number of missing variables, and diverse types of variables, the application of Johnson, Lin and Zeng (2008) and Garcia, Ibrahim and Zhu (2010a) is difficult. Hence, we compared MIRL with LDLS, MILS and CW. The analysis of Project EAT data were stratified by gender for comparability with prior work [Larson et al. (2013)]. Our proposed method and competitors were applied to select the most important of the 62 multi-contextual environmental predictors of BMI z-score among 1307 teenage boys and 1486 teenage girls separately. The estimated coefficients are provided in Table 2 for boys and Table 3 for girls.

Table 2.

Comparison of MIRL with MILS, LDLS and CW for Project EAT data (Boys)

	MIRL			MILS			LDLS
Variables	refit	raw est.	prob.†	refit	raw est.	p-value	refit	raw est.	p-value	CW
Parental pressure to eat	−0.2664	−0.1779	1.0000	−0.2604	−0.2676	<0.0001	−0.1830	−0.1108	<0.0001	−0.2633
Parental restriction of high-calorie food	0.2166	0.2301	0.9980	0.2044	0.2001	<0.0001	0	0.0303	0.0613	0.1804
Asian	0.1765	0.0843	0.9970	0.1727	0.1903	0.0001	0	0.2753	0.3189	0.1713
Parental weight status	0.2117	0.1662	0.9960	0.2044	0.1925	<0.0001	0.2175	0.0269	0.0341	0.1922
Home unhealthy food availability	−0.1058	−0.1313	0.9610	−0.1017	−0.0875	0.0115	0	−0.0229	0.4993	−0.0981
Hispanic	0.1361	0.0118	0.9595	0.1408	0.1312	0.0033	0	−0.1621	0.5623	0.1225
Social economical status	−0.1090	−0.0787	0.9580	−0.1032	−0.0928	0.0187	0	−0.0200	0.7636	−0.0784
Weight status male friends	0.0861	0.0985	0.9470	0.0861	0.0844	0.0258	0.1116	0.5116	0.0106	0.0862
Native american	0.0911	0.0383	0.9180	0.0825	0.1021	0.0092	0	0.5176	0.2762	0.0813
Neighborhood unsafeness during the night and day	0	0.0567	0.8605	0	0.0559	0.0968	0	−0.0211	0.9227	0.0690
Age	0	−0.0773	0.8230	−0.0774	−0.1281	0.0147	0	−0.0448	0.5384	−0.0753
Presence of convenience store in 800 m	0	−0.0539	0.8080	0	−0.1668	0.0503	0	−0.6854	0.1605	−0.0769
Family meal frequency	0	−0.0143	0.8065	−0.0589	−0.0701	0.0411	0	0.0117	0.7446	−0.0559
Park/recreation space (% of area)	0	−0.0373	0.7925	0	−0.0518	0.1471	0	−0.3328	0.0523	−0.0458
Encouragement to eat healthy foods	0	0.0144	0.7715	0	0.0721	0.0583	0	0.1106	0.2884	0
Presence of convenience store in 1200 m	0	0.0116	0.7640	0	0.0578	0.1062	0	−0.1481	0.6209	0.0563
Number of male friends in sample	0	0.0161	0.7310	0	0.0497	0.2322	0	0.1559	0.1703	0.0407
Sedentary behavior female friends	0	0.0043	0.6460	0	−0.0337	0.3895	0	0.0025	0.5103	0
Neighborhood unsafeness during the night	0	−0.0167	0.6430	0	−0.0459	0.1724	0	−0.2547	0.1777	0
Moderate-to-vigorous PA female friends	0	−0.0087	0.6360	0	−0.0196	0.6340	0	−0.0133	0.4987	−0.0459
Parental time spent watching TV with	0	0.0305	0.6315	0	0.0352	0.3346	0	−0.0121	0.7611	0
Healthy food served at family meals	0	−0.0013	0.6045	0	−0.0447	0.2206	0	−0.0141	0.6569	0
Fast-food frequency male friends	0	0.0101	0.5815	0	0.0696	0.1346	0	0.0447	0.1848	0
Household food insecurity	0	0.0405	0.5500	0	0.0207	0.5901	0	0.2160	0.2115	0.0349
Limited variety of fruits and veges	0	−0.0425	0.5435	0	−0.0598	0.1744	0	−0.1286	0.3444	0
Black	0	−0.0210	0.5370	0	−0.0069	0.8864	0	−0.1754	0.5081	−0.0071
Weight status female friends	0	0.0167	0.5200	0	0.0309	0.4901	0	0.1742	0.3890	0
Friends’ support for PA	0	−0.0069	0.5095	0	−0.0265	0.4385	0	−0.0050	0.9018	0
Friends’ attitudes of eating healthy foods	0	0.0191	0.5080	0	0.0461	0.1860	0	0.0119	0.8967	0
Number of female friends in sample	0.0065	0.4645	0	0.0326	0.4601	0	0.0729	0.5432	0
	…
Parental role modeling of food choices	0	0.0015	0.3110	0	−0.0225	0.5766	−0.0392	−0.0542	0.0487	0
	…

^†Selection probability provided by MIRL. Note: Top 30 (based on MIRL) of the 62 predictors are shown plus any other predictors selected by other methods.

Table 3.

Comparison of MIRL with MILS, LDLS and CW for Project EAT data (Girls)

	MIRL			MILS			LDLS
Variables	refit	raw est.	prob.†	refit	raw est.	p-value	refit	raw est.	p-value	CW
Social Economic Status	−0.1037	−0.1206	1.0000	−0.1147	−0.0900	0.0022	0	−0.0700	0.1790	−0.0889
Parental pressure to eat	−0.2079	−0.2528	1.0000	−0.2068	−0.2150	<0.0001	−0.1830	−0.1023	<0.0001	−0.2065
Parental restriction of high-calorie food	0.2191	0.2679	1.0000	0.2165	0.2317	<0.0001	0.2313	0.0443	0.0004	0.2160
Parental weight status	0.1855	0.1646	1.0000	0.1987	0.1714	<0.0001	0.1994	0.0296	0.0065	0.1811
Home unhealthy food availability	−0.1005	−0.1001	0.9960	−0.0888	−0.1060	0.0001	0	−0.0071	0.7479	−0.1007
Family meal frequency	−0.0776	−0.0814	0.9880	−0.0882	−0.0843	0.0011	0	−0.0364	0.1480	−0.0802
Weight status female friends	0.0735	0.0183	0.9360	0	0.0534	0.1434	0.0799	0.3500	0.0282	0.0540
Neighborhood unsafeness during	0.0557	0.0470	0.9240	0.0518	0.0642	0.0161	0	0.2550	0.0922	0.0553
the night and day
Parental role modeling of food choices	−0.0410	−0.0211	0.9200	−0.0742	−0.0659	0.0311	0	−0.0105	0.6068	−0.0720
Hispanic	0	0.0338	0.8960	0	0.0478	0.1748	0	0.2774	0.2258	0.0497
Encouragement to eat healthy foods	0	0.0043	0.8960	0.0787	0.0822	0.0066	0	0.0964	0.2165	0.0818
Schools commitment to promoting PA	0	−0.0243	0.8960	0	−0.0299	0.7120	0	−0.1069	0.6960	−0.0605
Asian	0	−0.0458	0.8680	0	−0.0482	0.2300	0	0.1633	0.4959	−0.0507
Parental fast food intake	0	0.0280	0.8560	0	0.0414	0.1976	0	0.0242	0.6410	0.0372
Presence of convenience store in 1200 m	0	0.0306	0.8560	0	0.0520	0.0592	0	0.2049	0.3285	0.0314
Moderate-to-vigorous PA female friends	0	−0.0327	0.8440	0	−0.0522	0.0683	0	−0.0236	0.1632	−0.0383
Parental time spent supporting PA	0	0.0195	0.8080	0	0.0599	0.1410	0	0.0130	0.6853	0.0525
Weight status male friends	0	0.0276	0.8080	0	0.0368	0.2137	0	0.1555	0.3021	0.0447
Park/recreation space (% of area)	0	−0.0516	0.7960	0	−0.0360	0.1927	0	−0.0467	0.7186	−0.0356
Schools commitment to promoting healthy eating	0	−0.0143	0.7480	0	−0.1173	0.1330	0	0.0784	0.7962	0
TV during dinner	0	−0.0015	0.6760	0	0.0224	0.3769	0	0.0005	0.9931	0
Limited variety of available fruits and vegetables	0	−0.0129	0.6480	0	−0.0375	0.2462	0	0.0589	0.5608	0
Students allowed to drink during class	0	0.0182	0.6440	0	0.0244	0.7891	0	−0.1200	0.8501	0
Indoor campus PA facilities	0	−0.0042	0.6240	0	−0.0434	0.4623	0	−0.0819	0.4320	0
Home healthy food availability	0	−0.0141	0.6000	0	−0.0137	0.6533	0	−0.0299	0.2173	0
Distance to nearest gym/fitness center (m)	0	−0.0055	0.5880	0	0.0288	0.2899	0	0.0870	0.4931	0
Poor quality of fruits or vegetables	0	−0.0205	0.5520	0	−0.0237	0.4762	0	−0.0704	0.5297	0
Age	0	−0.0009	0.4520	0	−0.0516	0.2040	0	−0.0112	0.8407	0
Density of total crime incidents	0	0.0107	0.4440	0	0.0083	0.7629	0	0.0634	0.6367	0
Native American …	0	0.0068	0.4240	0	0.0207	0.4669	0	−0.0210	0.9548	0

^†Selection probability provided by MIRL. Note: Top 30 (based on MIRL) of the 62 predictors are shown.

The MSPE are based on 500 replications with training and testing sets of equal sizes. The MSPEs of LDLS, MILS, CW and MIRL are 1.2762 (se = 0.0015), 1.2274 (se = 0.0021), 1.2291 (se = 0.0022) and 1.2248 (se = 0.0021) for boys; and 0.8447 (se = 0.0015), 0.8422 (se = 0.0015), 0.8354 (se = 0.0015) and 0.8393 (se = 0.0015) for girls. LDLS yields the largest MSPE, and MILS is the second largest for both genders. MIRL has smaller MSPE than CW for boys and slightly larger for girls. The empirical selection probability of MIRL naturally provides a ranking of the variable importance as shown in Table 2. The ranking does not rely on a single tuning parameter from one model fit and, thus, it reduces sensitivity of the model selection to the tuning parameter. The chosen variable set is therefore more stable than those selected based on a single model. Cross-validation with the one-standard-error rule chose selection probability threshold as 0.9 for both genders.

MIRL selected 9 variables for boys. In addition to Hispanic, Native American and Asian boys having significantly higher BMI z-score, it showed that high social economic status is a protective factor, and higher parental weight status and weight of same gender friends were risk factors. As shown in the original Project EAT investigation [Larson et al. (2013), Neumark-Sztainer et al. (2012)], we found some reactive factors, such as more unhealthy food at home and higher parental pressure to eat, are associated with lower BMI z-score, and higher parental restriction of high-calorie food is associated with higher BMI z-score.

MIRL also selected 9 variables for girls with 6 overlapping those found for boys and 3 new ones included more frequent family meals as a protective factor, and lack of neighborhood safety for day and night and poorer parental role modeling for food choice as risk factors for higher BMI. The common influential risk factors chosen by MIRL for both genders include social economic status, parental weight status, parental pressure to eat, parental restriction of high-calorie food, home unhealthy food availability and weight status of same gender friend. The estimated effect directions and magnitudes are similar for these between boys and girls.

MILS identified most of the influential variables that MIRL selected and includes two additional variables for boys which are age and family meal frequency; and it identified one additional variable for girls which is encouragement to eat healthy foods. This finding strengthened the conclusion that more frequent family meals can be a common protective factor for girls and boys, since it has high selection probability by MIRL (80.7% for boys and 98.8% for girls) and was selected by MILS in both genders. Encouragement to eat healthy foods is a reactive factors for girls, as it has large selection probability by MIRL (89.6%) and also was picked by MILS. Last, MIRL was able to identify weight status of same gender friends for both boys and girls while MILS would have missed it for girls. Consistent with the simulation results, MILS performed similarly with MIRL since p = 62 is only a small fraction of the sample size (1307 boys and 1486 girls respectively).

For both genders, CW selected larger sets of variables. For girls, it chose the top 19 ranked by MIRL with the lowest selection probability 79.6%. For boys, the chosen set consists of the top 14 variables ranked by MIRL, as well as a few variables with lower selection probabilities, such as household food insecurity (55%) and black ethnicity group (53.7%). These larger sets of variables include two possible common influential variables with lower ranks by MIRL than the previous mentioned variables. Lack of neighborhood safety during night and day was picked for boys by CW. It is a common risk factor for both genders since CW agrees with MIRL, which provided high selection probability (86.1% for boys and 92.4% for girls), although MILS did not select it. Park/recreational space area is a common protective factor which is picked by CW for both genders and has selection probability (79.3% for boys and 79.6% for girls).

LDLS (based on n = 252 boys and n = 271 girls with complete entries) identified fewer variables than other methods. It identified 3 common variables for both genders, including parental pressure to eat, parental weight status and weight status of same sex friends which are also selected by MIRL. It missed the other variables chosen by MIRL, MILS and CW, and selected parental role modeling of food choices for boys, which is not picked by any other method and with low-selection probability from MIRL (31.1%). Parental restriction of high-calorie food was chosen as a risk factor for girls by LDLS as in other methods. These analyses suggested that loss of information due to listwise deletion reduced the power to identify some potentially important variables.

The magnitudes of the coefficients obtained directly from MIRL, MILS and CW were found to be different for some variables. One reason is that MIRL’s coefficients are averaged across bootstrapped samples including zero for the variables either not sampled in step 3 or shrunk to 0 when applying lasso regression. Thus, although we expect these coefficients to be consistent asymptotically, for finite samples, the shrinkage effect for the magnitude of covariates might be evident. The same phenomenon was observed for the random lasso [Wang et al. (2011)]. One way to mitigate the difference is to refit the model using the selected variables as suggested in CW. We present the refitted coefficients in Tables 2 and 3 for MIRL, MILS and LDLS, where we can see that the coefficients for the chosen variables have the same signs, and MIRL and MILS coefficient estimates are similar since they chose similar sets of variables. Because the LDLS chose many less variables, the difference of the magnitudes for the refitted variables is large due to collinearity of covariates.

5.2. Subgroup analyses

Next, we compare the methods in a targeted subsample previously identified as at high risk of being overweight [Larson et al. (2013)]. One strength of Project EAT is its ethnically diverse sample including the following: 19% non-Hispanic White, 29% Black, 17% Hispanic, 20% Asian, 4% Native Americans and 11% Mixed/Other as well as a large proportion of low-income adolescents. Hence, in addition to identifying risk and protective factors for the whole population, it is feasible to identify risk factors among specific at-risk subpopulations so that interventions can be targeted. Asian teenage boys in Minneapolis/St. Paul were found to have the largest secular increases in overweight status, going from 30% overweight in 1999 to 50% in 2010 [Neumark-Sztainer et al. (2012)]. Thus, it is of interest to consider specifically risk and protective factors within the subsample of n = 99 low-social economic status (SES) Asian boys.

In this subgroup, there were only 20 subjects with complete data which is less than the number of predictors. We excluded SES and race, which are degenerated in this analysis. We compared MIRL, MILS and CW where only MIRL identified an important predictor. For MIRL, cross-validation chose 90% as the threshold, and parental weight status was identified with selection probability 91.2%. All other variables have selection probability lower than 80%. Parental weight status is a strong predictor from a behavioral genetics perspective [Kral and Faith (2009)] and it is also picked in the larger sample analysis by all available methods. For MILS, the p-value of parental weight status is 0.5188. Table C1 in the Appendix presents coefficients from MIRL and MILS for the top 10 variables with highest ranking in MIRL. The analysis for this subgroup demonstrates MIRL’s advantages when the variable number p is relatively large compared to the sample size n: MIRL detected some influential variables while MILS and CW detected none. These results are consistent with our simulation results where MIRL shows greater comparative advantages over MILS and other methods in the cases with larger p and smaller n.

6. Conclusion and discussion

In conclusion, we recommend MIRL for the analysis of Project EAT data. MIRL selected 9 variables for boys and girls, respectively. High weight status of parents and same gender friends are common risk factors. High social economical status is a common protective factor. Parental pressure to eat, parental restriction of high-calorie food and home unhealthy food availability are common reactive factors. In addition, Asian, Hispanic and Native American ethnicity groups are associated with higher BMI in boys. For girls, neighborhood unsafeness and poor parental role modeling of food choice are risk factors; and more frequent family meal is a protective factor.

MIRL is proposed as a procedure to address the missing data issue in variable selection for high-dimensional data through multiple imputation. When the number of variables with missing is large, alternative methods to adjust for missingness (e.g., likelihood-based methods through the EM algorithm or inverse probability weighting) become difficult or infeasible. Our simulation results show that for the low-dimensional case (e.g., p = 25, n = 200), the least squares regression for multiply imputed data (MILS) can outperform more sophisticated lasso-based variable selection methods. However, when the number of predictor variables increases, the advantage of lasso-based methods can be substantial. Regarding the influence of missing, the efficiency loss in terms of MSPE for a complete data analysis is considerable even when missing proportion is moderate (e.g., 50% complete data left after listwise deletion).

MIRL is especially suitable for cases where the informative variables are likely to be correlated and it performs adequately when the noise variables are correlated with the informative ones. In this case, the bootstrap samples and random draw of variables according to the importance measure enable variables highly correlated with the outcome to have high selection probability and other noise variables to have low selection probability despite their correlation with the informative ones. Another advantage of MIRL lies in its flexibility in dealing with many missing data structures and variable selection techniques. In the imputation step, other imputation approaches such as MCMC can replace MICE. In the second step where penalized regression for each bootstrap sample is performed, other methods such as regression with SCAD penalty [Fan and Li (2001)] and elastic net penalty [Zou and Hastie (2005)] can be used instead of lasso. In addition, although we focus on MIRL using the linear model for continuous outcomes, it can be easily extended to generalized linear models for categorical outcomes, the Cox regression model for censored outcomes and mixed effects models for longitudinal outcomes.

One extension of MIRL is to consider mixed effects models to allow random effects (e.g., school-specific random effects in Project EAT). Groll and Tutz (2014) proposed the variable selection method to introduce the L₁ penalty in the mixed effects model. A possible solution is to conduct variable selection with random effects for each bootstrapped sample of imputed data, and combine coefficients from imputed data sets by taking the average. Further investigations are needed to draw inference for combining the multiply imputed correlated data or bootstrapped sample.

Last, since MIRL combines random lasso [Wang et al. (2011)] and stability selection [Meinshausen and Bühlmann (2010)] to analyze multiply imputed data, it is of interest to consider whether theorems developed for stability selection can be applied. Since the imputation is performed for the covariates in the design matrix, the random errors are independent when treating design matrix X as fixed in a regression problem. It is conjectured that an adapted version of Theorem 2 in Meinshausen and Bühlmann (2010) can be used to provide some insights for variable selection consistency of MIRL when the imputed design matrices satisfy sparse eigenvalue Assumption 1 in Meinshausen and Bühlmann (2010). However, rigorous theoretical investigation of MIRL is beyond the scope of this work.

APPENDIX A: FURTHER COMPARISONS WITH EXISTING LITERATURE

We compare MIRL with methods in Johnson, Lin and Zeng (2008), Garcia, Ibrahim and Zhu (2010a), Chen and Wang (2013) (CW), and RRstep under Rubin’s rule (e.g., stepwise regression with p-value computed based on Rubin’s rule standard error). We follow the same simulation settings reported in Johnson, Lin and Zeng (2008) and Garcia, Ibrahim and Zhu (2010a). The results for the scenario in Section 5.2 of Johnson, Lin and Zeng (2008) are presented in Table B7. We can see that MIRL, RRstep and MILS show good performance in variable selection and prediction in all four cases, and they outperform Johnson, Lin and Zeng (2008). MILS and RRstep perform similarly in this scenario and using stepwise selection does not lead to better results than one-step backward selection (MILS). The simulation results from Section 4.1 in Garcia, Ibrahim and Zhu (2010a) are shown in Table B8. MIRL outperforms all its competitors in terms of variable selection. RRstep and MILS also have high MCC for scenario 1 and 3. CW gives good MSPE for scenario 2 but the MCC is small. In these simulation settings, CW tends to select more variables, where gains are larger true positives at the cost of selecting more noise variables.

Table B9 presents simulation results comparing MIRL with RRstep and CW for p > n cases. The simulation settings contain two pairs of n and p: n = 50, p = 100 and n = 100, p = 200. The coefficients for x₁, x₂, …, x_p are β = (3, 1.5, 0, 0, 2, 0, …, 0), σ = 3, X₁ and X₂ missing at random depending on X₃ to X₈ and outcome, and about 30% of subjects remain after listwise deletion. In this case, MIRL outperforms the other two methods in terms of smaller prediction error and has similar performance in terms of MCC.

APPENDIX B: SIMULATION RESULTS

Table B1.

Simulation results for the setting described in Section 4.1 with p = 25 and pairwise correlation 0.2

	Approx.% left after listwise deletion		L1	L2	MSPE	TP	TN	MCC
MCAR	50%	LDLS	1.705 (0.044)	0.371 (0.016)	1.363 (0.021)	5.97 (0.119)	14.16 (0.097)	0.603 (0.012)
		MILS	1.069 (0.031)	0.154 (0.008)	1.138 (0.013)	7.38 (0.095)	14.25 (0.098)	0.725 (0.012)
		LD lasso cv	1.75 (0.041)	0.289 (0.014)	1.242 (0.015)	8.4 (0.147)	8.69 (0.292)	0.437 (0.017)
		MIRLnoSS	1.489 (0.03)	0.21 (0.009)	1.18 (0.014)	9.51 (0.063)	4.37 (0.157)	0.301 (0.013)
		MIRL	1.407 (0.03)	0.262 (0.011)	1.227 (0.016)	6.02 (0.122)	14.82 (0.061)	0.673 (0.01)
	25%	LDLS	3.086 (0.073)	1.105 (0.049)	1.969 (0.044)	3.14 (0.186)	14.3 (0.104)	0.381 (0.018)
		MILS	1.119 (0.032)	0.169 (0.008)	1.153 (0.012)	7.13 (0.105)	14.32 (0.091)	0.711 (0.012)
		LD lasso cv	2.576 (0.067)	0.64 (0.027)	1.518 (0.026)	6.35 (0.263)	9.76 (0.367)	0.324 (0.019)
		MIRLnoSS	1.541 (0.032)	0.223 (0.009)	1.188 (0.014)	9.45 (0.067)	4.33 (0.171)	0.288 (0.014)
		MIRL	1.473 (0.035)	0.288 (0.012)	1.243 (0.015)	5.83 (0.134)	14.82 (0.052)	0.658 (0.01)
MAR	50%	LDLS	2.376 (0.064)	0.701 (0.032)	1.651 (0.036)	4.4 (0.16)	14.21 (0.105)	0.474 (0.016)
		MILS	1.431 (0.035)	0.241 (0.01)	1.229 (0.015)	7.39 (0.121)	13.54 (0.115)	0.663 (0.015)
		LD lasso cv	2.192 (0.052)	0.434 (0.019)	1.373 (0.02)	7.63 (0.171)	8.92 (0.352)	0.372 (0.021)
		MIRLnoSS	1.784 (0.033)	0.302 (0.011)	1.266 (0.015)	9.41 (0.065)	4.28 (0.168)	0.283 (0.014)
		MIRL	1.654 (0.036)	0.35 (0.014)	1.31 (0.016)	6.06 (0.147)	14.62 (0.09)	0.658 (0.011)
	25%	LDLS	3.747 (0.151)	1.716 (0.168)	2.53 (0.143)	2.37 (0.166)	14.1 (0.138)	0.294 (0.021)
		MILS	1.385 (0.034)	0.234 (0.01)	1.207 (0.016)	7.33 (0.129)	13.82 (0.098)	0.681 (0.015)
		LD lasso cv	2.792 (0.074)	0.773 (0.034)	1.669 (0.036)	5.76 (0.279)	10.51 (0.357)	0.315 (0.022)
		MIRLnoSS	1.805 (0.033)	0.31 (0.011)	1.263 (0.016)	9.32 (0.072)	4.27 (0.167)	0.268 (0.014)
		MIRL	1.67 (0.034)	0.358 (0.013)	1.304 (0.017)	5.84 (0.143)	14.73 (0.066)	0.65 (0.01)

Table B2.

Simulation results for the setting described in Section 4.1 with p = 25 and pairwise correlation 0.6

	Approx.% left after listwise deletion		L1	L2	MSPE	TP	TN	MCC
MCAR	50%	LDLS	2.418 (0.06)	0.724 (0.03)	1.514 (0.037)	4.28 (0.156)	14.31 (0.088)	0.475 (0.016)
		MILS	1.536 (0.037)	0.307 (0.013)	1.203 (0.017)	6.05 (0.123)	14.38 (0.089)	0.631 (0.011)
		LD lasso cv	2.27 (0.052)	0.493 (0.021)	1.224 (0.015)	7.25 (0.198)	9.72 (0.313)	0.39 (0.017)
		MIRLnoSS	2.032 (0.036)	0.39 (0.014)	1.175 (0.013)	9.34 (0.076)	3.88 (0.174)	0.243 (0.016)
		MIRL	1.912 (0.04)	0.46 (0.018)	1.219 (0.014)	5.21 (0.171)	14.46 (0.123)	0.576 (0.013)
	25%	LDLS	3.79 (0.097)	1.694 (0.09)	2.224 (0.097)	1.87 (0.147)	14.25 (0.105)	0.248 (0.017)
		MILS	1.593 (0.039)	0.337 (0.014)	1.231 (0.019)	5.8 (0.123)	14.37 (0.085)	0.609 (0.012)
		LD lasso cv	3.02 (0.071)	0.928 (0.033)	1.407 (0.019)	4.47 (0.296)	11.4 (0.326)	0.262 (0.022)
		MIRLnoSS	2.104 (0.038)	0.414 (0.015)	1.186 (0.012)	9.27 (0.074)	3.58 (0.161)	0.212 (0.016)
		MIRL	1.956 (0.044)	0.483 (0.02)	1.23 (0.013)	4.97 (0.181)	14.55 (0.091)	0.569 (0.014)
MAR	50%	LDLS	3.207 (0.065)	1.2 (0.045)	1.942 (0.076)	2.46 (0.144)	14.32 (0.089)	0.305 (0.016)
		MILS	2.056 (0.047)	0.487 (0.018)	1.308 (0.02)	6.07 (0.128)	13.28 (0.121)	0.528 (0.014)
		LD lasso cv	2.741 (0.064)	0.752 (0.029)	1.365 (0.017)	5.51 (0.276)	10.77 (0.36)	0.319 (0.019)
		MIRLnoSS	2.227 (0.037)	0.454 (0.015)	1.222 (0.013)	9.21 (0.087)	3.95 (0.19)	0.231 (0.017)
		MIRL	2.073 (0.039)	0.517 (0.018)	1.264 (0.015)	5.38 (0.171)	13.97 (0.118)	0.537 (0.014)
	25%	LDLS	4.125 (0.176)	2.233 (0.303)	2.735 (0.402)	1.14 (0.121)	14.23 (0.114)	0.142 (0.024)
		MILS	2.003 (0.044)	0.476 (0.017)	1.328 (0.024)	5.96 (0.133)	13.57 (0.112)	0.545 (0.013)
		LD lasso cv	3.176 (0.113)	1.057 (0.098)	1.539 (0.075)	4.03 (0.283)	11.44 (0.337)	0.227 (0.02)
		MIRLnoSS	2.222 (0.038)	0.453 (0.015)	1.229 (0.014)	9.18 (0.086)	3.84 (0.163)	0.222 (0.016)
		MIRL	2.06 (0.04)	0.513 (0.018)	1.272 (0.016)	5.47 (0.177)	14.02 (0.114)	0.549 (0.015)

Table B3.

Simulation results for the setting described in Section 4.1 with p = 50 and pairwise correlation 0.2

	Approx.% left after listwise deletion		L1	L2	MSPE	TP	TN	MCC
MCAR	50%	LDLS	2.742 (0.087)	0.796 (0.036)	1.721 (0.039)	4.87 (0.166)	37.83 (0.206)	0.512 (0.016)
		MILS	1.403 (0.036)	0.234 (0.01)	1.205 (0.015)	7.43 (0.102)	38.22 (0.135)	0.726 (0.011)
		LD lasso cv	2.408 (0.07)	0.405 (0.015)	1.332 (0.021)	8.17 (0.13)	27.39 (0.626)	0.426 (0.012)
		MIRLnoSS	2.333 (0.034)	0.293 (0.009)	1.239 (0.016)	9.6 (0.053)	9.5 (0.282)	0.197 (0.008)
		MIRL	1.424 (0.031)	0.253 (0.01)	1.208 (0.016)	6.83 (0.105)	39.29 (0.13)	0.75 (0.01)
	25%	LDLS	5.946 (0.624)	6.475 (1.443)	6.637 (1.181)	0.875 (0.215)	38.286 (0.507)	0.175 (0.042)
		MILS	1.428 (0.037)	0.245 (0.011)	1.218 (0.017)	7.16 (0.104)	38.36 (0.133)	0.714 (0.011)
		LD lasso cv	3.539 (0.186)	0.985 (0.082)	1.799 (0.066)	5.38 (0.261)	30.56 (0.845)	0.307 (0.017)
		MIRLnoSS	2.366 (0.034)	0.299 (0.009)	1.238 (0.015)	9.59 (0.057)	9.01 (0.263)	0.188 (0.008)
		MIRL	1.458 (0.03)	0.266 (0.01)	1.223 (0.016)	6.59 (0.114)	39.34 (0.109)	0.734 (0.01)
MAR	50%	LDLS	4.179 (0.238)	2.021 (0.32)	2.837 (0.258)	2.152 (0.171)	38.152 (0.239)	0.28 (0.019)
		MILS	2.203 (0.07)	0.446 (0.019)	1.424 (0.021)	7.14 (0.119)	35.49 (0.267)	0.581 (0.015)
		LD lasso cv	2.879 (0.091)	0.632 (0.031)	1.536 (0.028)	6.85 (0.213)	29.41 (0.677)	0.381 (0.015)
		MIRLnoSS	2.799 (0.041)	0.411 (0.012)	1.37 (0.016)	9.7 (0.05)	8.16 (0.269)	0.184 (0.008)
		MIRL	1.891 (0.043)	0.382 (0.013)	1.35 (0.017)	6.67 (0.144)	37.24 (0.351)	0.642 (0.013)
	25%	LDLS	5.303 (1.752)	9.472 (8.068)	10.149 (7.689)	0 (0)	40 (0)	NaN (NA)
		MILS	2.087 (0.057)	0.428 (0.017)	1.366 (0.019)	6.89 (0.117)	36.28 (0.206)	0.591 (0.013)
		LD lasso cv	3.63 (0.113)	1.085 (0.044)	1.916 (0.041)	4.05 (0.263)	32.29 (0.737)	0.259 (0.016)
		MIRLnoSS	2.781 (0.04)	0.409 (0.012)	1.34 (0.016)	9.71 (0.054)	7.85 (0.333)	0.178 (0.009)
		MIRL	1.893 (0.041)	0.384 (0.013)	1.321 (0.016)	6.59 (0.133)	37.28 (0.344)	0.635 (0.013)

Table B4.

Simulation results for the setting described in Section 4.1 with p = 50 and pairwise correlation 0.6

	Approx.% left after listwise deletion		L1	L2	MSPE	TP	TN	MCC
MCAR	50%	LDLS	3.746 (0.119)	1.44 (0.067)	2.072 (0.084)	3.39 (0.16)	37.71 (0.211)	0.365 (0.019)
		MILS	2.043 (0.055)	0.478 (0.019)	1.372 (0.031)	5.87 (0.104)	37.99 (0.162)	0.598 (0.012)
		LD lasso cv	2.843 (0.069)	0.66 (0.025)	1.269 (0.016)	6.05 (0.236)	31.07 (0.616)	0.376 (0.015)
		MIRLnoSS	3.046 (0.043)	0.504 (0.015)	1.213 (0.014)	9.45 (0.066)	8.1 (0.27)	0.156 (0.008)
		MIRL	2.13 (0.044)	0.472 (0.016)	1.226 (0.015)	6.07 (0.146)	37.14 (0.316)	0.588 (0.011)
	25%	LDLS	6.986 (0.962)	9.495 (2.528)	7.595 (1.885)	0.607 (0.178)	38.071 (0.571)	0.059 (0.035)
		MILS	2.064 (0.056)	0.496 (0.02)	1.422 (0.035)	5.62 (0.099)	38.12 (0.153)	0.586 (0.011)
		LD lasso cv	3.782 (0.183)	1.245 (0.103)	1.521 (0.044)	3.65 (0.274)	32.97 (0.742)	0.249 (0.017)
		MIRLnoSS	3.099 (0.045)	0.517 (0.015)	1.218 (0.014)	9.54 (0.063)	8.01 (0.281)	0.163 (0.009)
		MIRL	2.158 (0.045)	0.48 (0.015)	1.243 (0.014)	6.09 (0.141)	37.05 (0.384)	0.592 (0.013)
MAR	50%	LDLS	5.375 (0.316)	3.631 (0.422)	3.238 (0.278)	1.273 (0.129)	38.071 (0.277)	0.169 (0.022)
		MILS	3.287 (0.094)	0.921 (0.035)	1.667 (0.042)	5.53 (0.142)	34.92 (0.242)	0.425 (0.016)
		LD lasso cv	3.298 (0.089)	0.928 (0.03)	1.409 (0.017)	4.21 (0.267)	33.23 (0.625)	0.302 (0.016)
		MIRLnoSS	3.609 (0.05)	0.677 (0.018)	1.307 (0.014)	9.42 (0.074)	7.36 (0.272)	0.139 (0.009)
		MIRL	2.778 (0.067)	0.651 (0.021)	1.324 (0.016)	6.32 (0.169)	33.3 (0.564)	0.462 (0.015)
	25%	LDLS	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)
		MILS	3.248 (0.088)	0.914 (0.034)	1.704 (0.046)	5.36 (0.138)	35.24 (0.217)	0.421 (0.015)
		LD lasso cv	3.645 (0.119)	1.22 (0.052)	1.559 (0.026)	2.26 (0.253)	35.43 (0.619)	0.187 (0.021)
		MIRLnoSS	3.594 (0.052)	0.665 (0.018)	1.296 (0.015)	9.5 (0.067)	6.7 (0.313)	0.131 (0.01)
		MIRL	2.757 (0.064)	0.645 (0.021)	1.326 (0.016)	6.22 (0.174)	33.36 (0.564)	0.455 (0.015)

Table B5.

Simulation results for the setting described in Section 4.1 with p = 100 and pairwise correlation 0.2

	Approx.% left after listwise deletion		L1	L2	MSPE	TP	TN	MCC
MCAR	50%	LDLS	6.662 (0.946)	5.162 (1.031)	6.018 (1.106)	0.739 (0.212)	86.283 (1.332)	0.104 (0.033)
		MILS	2.466 (0.078)	0.544 (0.021)	1.526 (0.029)	6.43 (0.111)	85.39 (0.307)	0.583 (0.012)
		LD lasso cv	2.754 (0.077)	0.529 (0.02)	1.428 (0.021)	6.59 (0.176)	75.89 (0.864)	0.397 (0.011)
		MIRLnoSS	3.682 (0.049)	0.418 (0.011)	1.346 (0.016)	9.49 (0.063)	22.16 (0.466)	0.141 (0.005)
		MIRL	1.745 (0.041)	0.311 (0.011)	1.273 (0.015)	7.1 (0.095)	87 (0.302)	0.689 (0.009)
	25%	LDLS	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)
		MILS	2.374 (0.075)	0.533 (0.021)	1.517 (0.028)	6.18 (0.111)	86.05 (0.282)	0.586 (0.012)
		LD lasso cv	3.551 (0.105)	0.946 (0.028)	1.794 (0.032)	4.01 (0.24)	79.11 (1.04)	0.294 (0.013)
		MIRLnoSS	3.712 (0.049)	0.429 (0.012)	1.376 (0.016)	9.49 (0.064)	21.4 (0.476)	0.136 (0.005)
		MIRL	1.761 (0.044)	0.325 (0.012)	1.299 (0.016)	6.92 (0.099)	87.23 (0.373)	0.688 (0.009)
MAR	50%	LDLS	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)
		MILS	6.023 (0.204)	1.737 (0.072)	2.535 (0.071)	5.87 (0.134)	75.02 (0.645)	0.326 (0.014)
		LD lasso cv	3.239 (0.112)	0.715 (0.028)	1.582 (0.03)	5.78 (0.213)	76.11 (1.118)	0.355 (0.012)
		MIRLnoSS	5.026 (0.066)	0.759 (0.019)	1.602 (0.02)	9.53 (0.07)	16.78 (0.443)	0.11 (0.007)
		MIRL	3.134 (0.089)	0.683 (0.021)	1.552 (0.021)	6.32 (0.17)	79.25 (0.955)	0.456 (0.015)
	25%	LDLS	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)
		MILS	5.362 (0.178)	1.596 (0.065)	2.465 (0.06)	5.35 (0.14)	78.16 (0.542)	0.334 (0.014)
		LD lasso cv	3.823 (0.105)	1.195 (0.032)	2.02 (0.035)	2.6 (0.244)	82.17 (0.855)	0.206 (0.017)
		MIRLnoSS	4.958 (0.061)	0.737 (0.018)	1.64 (0.022)	9.48 (0.063)	16.41 (0.407)	0.104 (0.005)
		MIRL	3.015 (0.082)	0.664 (0.02)	1.579 (0.023)	6.26 (0.163)	80.18 (0.848)	0.467 (0.014)

Table B6.

Simulation results for the setting described in Section 4.1 with p = 100 and pairwise correlation 0.6

	Approx.% left after listwise deletion		L1	L2	MSPE	TP	TN	MCC
MCAR	50%	LDLS	8.317 (1.357)	8.944 (1.951)	7.478 (1.716)	0.63 (0.187)	86.261 (1.273)	0.079 (0.032)
		MILS	3.576 (0.11)	1.136 (0.044)	1.959 (0.077)	4.64 (0.128)	85.5 (0.292)	0.444 (0.013)
		LD lasso cv	3.451 (0.117)	0.836 (0.028)	1.349 (0.017)	4.74 (0.256)	77.33 (1.201)	0.323 (0.014)
		MIRLnoSS	4.814 (0.063)	0.707 (0.019)	1.299 (0.015)	9.34 (0.082)	18.38 (0.43)	0.106 (0.007)
		MIRL	2.633 (0.077)	0.571 (0.019)	1.303 (0.018)	6.02 (0.146)	82.37 (0.912)	0.506 (0.013)
	25%	LDLS	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)
		MILS	3.404 (0.101)	1.095 (0.043)	1.927 (0.059)	4.34 (0.124)	86.21 (0.258)	0.444 (0.013)
		LD lasso cv	3.829 (0.148)	1.193 (0.048)	1.509 (0.025)	2.29 (0.241)	82.56 (1.03)	0.209 (0.018)
		MIRLnoSS	4.827 (0.063)	0.715 (0.02)	1.316 (0.016)	9.31 (0.072)	17.86 (0.439)	0.099 (0.007)
		MIRL	2.639 (0.071)	0.587 (0.02)	1.338 (0.018)	5.97 (0.138)	82.93 (0.796)	0.505 (0.013)
MAR	50%	LDLS	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)
		MILS	9.291 (0.248)	3.574 (0.122)	3.08 (0.092)	4.4 (0.162)	72.09 (0.597)	0.18 (0.013)
		LD lasso cv	3.565 (0.116)	0.991 (0.032)	1.455 (0.02)	3.39 (0.266)	80.62 (1.029)	0.259 (0.016)
		MIRLnoSS	6.717 (0.101)	1.243 (0.033)	1.562 (0.024)	9.5 (0.064)	12.32 (0.366)	0.076 (0.007)
		MIRL	4.969 (0.119)	1.171 (0.034)	1.562 (0.025)	6.21 (0.196)	66.46 (1.295)	0.263 (0.013)
	25%	LDLS	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)	NaN (NA)
		MILS	8.231 (0.235)	3.273 (0.119)	3.177 (0.161)	3.84 (0.152)	75.92 (0.527)	0.183 (0.013)
		LD lasso cv	4.046 (0.165)	1.373 (0.06)	1.625 (0.033)	1.63 (0.195)	83.52 (0.927)	0.169 (0.019)
		MIRLnoSS	6.625 (0.104)	1.22 (0.034)	1.518 (0.022)	9.51 (0.063)	12.58 (0.373)	0.079 (0.007)
		MIRL	4.957 (0.137)	1.16 (0.036)	1.531 (0.025)	6.11 (0.21)	64.59 (1.637)	0.245 (0.014)

Table B7.

Comparison for the scenario in Johnson, Lin and Zeng (2008), Section 5.2

		L1	L2	MPSE	TP	TN	MCC
Setting 1	MILS	0.52	0.07	1.07	5.65	3.81	0.90
σ = 1	LDlasso	0.97	0.16	1.15	5.98	1.73	0.62
	MIRL	0.65	0.11	1.09	5.30	3.84	0.85
	CW	0.59	0.07	1.06	5.99	2.75	0.75
	RRstep	0.56	0.08	1.06	5.63	3.85	0.90
	JohnLas				5.91	2.42	0.67
	JohnALas				5.77	3.55	0.86
Setting 1	MILS	1.08	0.30	1.25	4.92	3.81	0.76
σ = 2	LDlasso	2.37	1.02	2.08	5.67	2.01	0.57
	MIRL	1.28	0.40	1.31	4.75	3.87	0.76
	CW	1.10	0.23	1.17	5.70	2.89	0.71
	RRstep	1.13	0.28	1.19	5.07	3.79	0.78
	JohnLas				4.88	3.70	0.72
	JohnALas				5.60	2.54	0.61
Setting 2	MILS	0.29	0.04	1.03	3.00	6.67	0.94
σ = 1	LDlasso	0.87	0.16	1.14	3.00	3.48	0.52
	MIRL	0.27	0.03	1.02	3.00	6.60	0.95
	CW	0.48	0.06	1.04	3.00	4.95	0.66
	RRstep	0.31	0.04	1.03	3.00	6.63	0.93
	JohnLas				3.00	4.11	0.55
	JohnALas				3.00	6.25	0.85
Setting 2	MILS	0.56	0.15	1.15	3.00	6.64	0.93
σ = 2	LDlasso	2.14	0.99	2.01	3.00	3.79	0.55
	MIRL	0.50	0.10	1.12	3.00	6.69	0.95
	CW	0.85	0.19	1.18	3.00	5.02	0.67
	RRstep	0.54	0.12	1.13	3.00	6.72	0.95
	JohnLas				2.98	4.56	0.59
	JohnALas				2.98	6.08	0.81

Table B8.

Comparison for scenario in Garcia, Ibrahim and Zhu (2010a), Section 4.1

		L1	L2	MPSE	TP	TN	MCC
n =40	MILS	1.04	0.58	1.67	2.98	4.87	0.97
σ = 1	LDlasso	1.57	0.59	1.56	3.00	2.24	0.54
	MIRL	1.21	0.65	1.77	2.98	4.83	0.98
	CW	1.72	0.77	1.81	3.00	3.09	0.64
	RRstep	1.31	0.72	1.75	2.96	4.80	0.95
	GarciaAlasso				3.00	4.64	0.91
	GarciaSCAD				3.00	4.64	0.91
n = 40	MILS	3.75	6.26	6.67	2.07	4.76	0.73
σ = 3	LDlasso	5.20	6.32	7.31	2.74	2.65	0.50
	MIRL	3.82	5.55	6.31	2.24	4.71	0.80
	CW	3.77	3.94	4.40	2.93	3.49	0.68
	RRstep	4.26	6.60	5.53	2.24	4.65	0.71
	GarciaAlasso				2.72	4.31	0.75
	GarciaSCAD				2.67	4.53	0.79
n = 60	MILS	0.87	0.38	1.33	2.99	4.76	0.95
σ = 1	LDlasso	1.30	0.39	1.34	3.00	2.48	0.62
	MIRL	0.86	0.31	1.29	2.99	4.98	0.99
	CW	1.31	0.45	1.40	3.00	3.24	0.65
	RRstep	1.00	0.40	1.33	2.99	4.76	0.94
	GarciaAlasso				3.00	4.83	0.96
	GarciaSCAD				3.00	4.86	0.96

Table B9.

Comparison of MIRL with CW and RRstep for high-dimensional scenarios with p > n

Settings		L1	L2	MPSE	TP	TN	MCC
n =50	MIRL	9.55	16.51	19.50	1.12	92.93	0.27
p = 100	RRstep	14.01	25.78	26.23	1.23	91.22	0.27
	CW	35.94	42.04	42.15	2.65	43.32	0.13
n =100	MIRL	10.03	13.59	15.67	1.74	187.48	0.31
p = 200	RRstep	18.36	25.04	24.71	1.62	182.22	0.25
	CW	24.96	28.15	27.95	2.26	153.72	0.35

APPENDIX C: SUBGROUP ANALYSIS

Table C1.

MIRL selected sequence of important variables compared with MILS selection for low-income boys

	MIRL		MILS
Variables	raw est.	Prob	raw est.	p-value
Parental weight status	0.0689	0.9115	0.2347	0.5188
Distance to nearest recreation center (m)	−0.1039	0.7950	−0.2779	0.3471
Competitive food with policies	−0.1286	0.7590	−0.3597	0.5438
Park/recreation space (% of area)	−0.0035	0.7160	−0.0437	0.8842
Poor quality of fruits/vegetables	0.0386	0.7060	0.0038	0.9904
Friends’ attitudes of eating healthy foods	0.0359	0.7030	0.4056	0.1383
During the night	−0.1511	0.6985	−0.2100	0.6564
TV during dinner	−0.1696	0.6715	−0.4001	0.0751
Fast-food frequency male friends	−0.0719	0.6630	−0.3674	0.3973
Number of male friends in sample	0.0344	0.6255	−0.0505	0.8755
Parental fast food intake	0.0382	0.5975	−0.0226	0.9333