Abstract
The rheological properties of fibrin networks have been of long-standing interest. As such there is a wealth of studies of their shear and tensile responses, but their compressive behavior remains unexplored. Here, by characterization of the network structure with synchronous measurement of the fibrin storage and loss moduli at increasing degrees of compression, we show that the compressive behavior of fibrin networks is similar to that of cellular solids. A non-linear stress-strain response of fibrin consists of three regimes: 1) an initial linear regime, in which most fibers are straight, 2) a plateau regime, in which more and more fibers buckle and collapse, and 3) a markedly non-linear regime, in which network densification occurs by bending of buck-led fibers and inter-fiber contacts. Importantly, the spatially non-uniform network deformation included formation of a moving “compression front” along the axis of strain, which segregated the fibrin network into compartments with different fiber densities and structure. The Young’s modulus of the linear phase depends quadratically on the fibrin volume fraction while that in the densified phase depends cubically on it. The viscoelastic plateau regime corresponds to a mixture of these two phases in which the fractions of the two phases change during compression. We model this regime using a continuum theory of phase transitions and analytically predict the storage and loss moduli which are in good agreement with the experimental data. Our work shows that fibrin networks are a member of a broad class of natural cellular materials which includes cancellous bone, wood and cork.
1 Introduction
Fibrin is a polymer made from the blood plasma precursor protein fibrinogen. Fibrin forms a porous network of branching fibers that provides the scaffold of protective hemostatic blood clots and pathological obstructive thrombi. The structure and properties of the fibrin, including mechanical resilience to forces of blood flow and clot contraction, determine the course of pathological conditions, such as coronary heart disease, ischemic stroke, or bleeding (1; 2). Hence, the tensile and shear behaviors of fibrin networks have been studied for a long time (3; 1). Recent experimental studies have also focused on the tensile properties of a single fibrin fiber including the molecular unfolding of fibrin molecules at large deformations (4; 5; 6; 7; 8). The tensile behavior of single fibrin fibers can be used as an input to network models to predict the tensile behavior of the networks. We did this recently using the eight-chain model and were able to predict the mechanics of fibrin networks under tension (9; 10; 14; 15; 16). The shear behavior of fibrin networks has also been studied both experimentally and theoretically (13; 14; 15; 16; 17). For networks with thin fibrin fibers the shear behavior can also be explained in terms of the entropic elasticity of single fibrin fibers (14; 16).
Even though tension and shear behaviors of fibrin networks have been studied in detail, compression of these networks remains largely unexplored. Recently, Kim et. al. (18) found that the non-linear stress-strain curves of fibrin networks in compression have three distinct regimes, similar to the curves observed in networks of carbon nanotubes (19). There is an initial linear response which is expected of any elastic solid for small strains, followed by a stress plateau that begins when fibers in the network start to buckle and continues until a majority of them have done so. Then, network densification occurs creating a large number of contacts between the fibers as the stress increases steeply. This tri-phasic mechanical behavior could presumably be modeled using the theory of foams and other cellular solids (20) as shown schematically in Figure 1b. The initial shear and compression moduli of foams in the linear regime can be computed in terms of the Young’s modulus of the foam material and the geometric parameters of the foam (20). These moduli can also be connected to the moduli of fiber networks as has been done by (24; 25; 26). But, for large compressions these moduli are no longer sufficient and we must use more sophisticated theories.
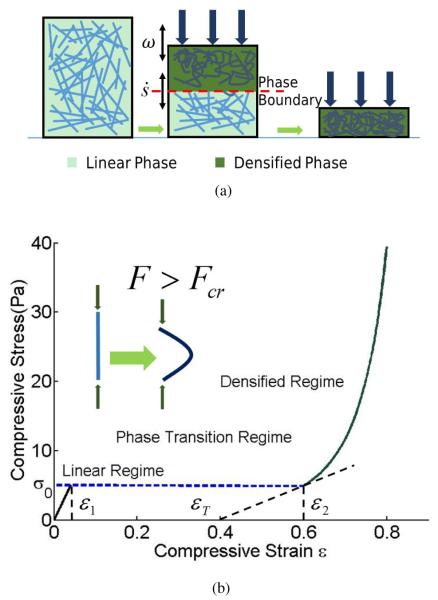
Fig. 1.
A fiber network under compression. (a) The top panel is a cartoon, schematically showing the high strain phase with a densified network on the right, the low strain phase with straight fibers on the left and a mixture of these two phases in the middle. Here ω indicates the frequency of applied oscillation and is the rate of change of phase fraction due to this oscillation. In the middle figure a sharp phase boundary separates the linear phase in the bottom from the densified phase on the top. The fraction of densified phase increases with increasing compressive strain. (b) The bottom panel quantitatively shows the tri-phasic stress-strain response of such a material assuming quasi-static loading. Theoretical curves are plotted according to Eqns. (3) and (8). We have used l = 1.32μm, d = 0.22μm, ν = 0.1μm−3, and the two coefficients n = 3, k = 0.5 corresponding to a fibrin network.
Our goal in this paper is to further study the mechanical and structural responses of fibrin to compression by a combination of experiment and theory. In particular, from precise dynamic rheological and microscopic measurements we have developed a model for the compression behavior of fibrin networks based on the theory of foams and other cellular solids. First, the compression stress-strain curve was measured in experiment along with the loss and storage moduli at various strains with simultaneous 3D visualization of the fibrin network during the deformation. In addition to the non-linear behavior of storage and loss moduli, we were able to reveal the non-uniformity of the compressive deformation with formation of a “compression front” or “phase boundary” along the axis of compressive strain (see Figure 1a) (27; 28). Next, we described how the non-linear rheological behavior could be explained by viewing the fibrin network as a “cellular” solid that could exist in two phases – the low-strain phase in which the fibers are mostly straight, and a high-strain phase in which the fibers are mostly buckled. In displacement-controlled experiments such a solid has a stress plateau when there is a mixture of both phases. The fraction of each phase at equilibrium is determined by a lever rule (29). However, the storage and loss moduli at various degrees of compression in our fibrin networks were obtained in the experiments by performing small oscillations around a certain strain. These oscillations changed the fractions of the two phases but they were not necessarily quasistatic. We treated these two phases using a continuum theory of phase transitions in which a kinetic equation relates the rate of change of the fraction of the phases to the stress (30). In this way we explained the storage and loss moduli of the networks while accounting for the contributions of the moving phase boundary as well as the viscoelasticity of each phase.
In this paper we first provide the details of the experimental procedures and present a description of the obtained data on controlled fibrin compression followed by a comprehensive theoretical analysis. After a short summary of the well-known results for cellular solids we show how this approach can be applied to fiber networks. We also describe the constitutive laws for fiber networks under large compression that have been studied using experiments and theory for several decades (32; 33). We finally show how these results can be generalized and combined with a continuum theory for phase transitions to obtain the storage and loss moduli of networks under compression. The novelties of this paper are (a) experimental visualization of a propagating phase boundary in compressed fibrin networks, (b) an explanation for the trends in storage and loss moduli of the compressed networks in terms of a theory of phase transitions, and (c) first application of foam theory to a bio-polymer network. Our analysis leads to some new experimentally testable predictions about the dependence of the mechanical properties of the clot on network parameters that have been summarized in the discussion section.
2 EXPERIMENTAL PROCEDURES
2.1 Fibrin Clot Formation
Fibrin clots were formed by adding human α-thrombin (1 U/mL final concentration) to pooled human citrated plateletpoor plasma in the presence of CaCl2 (40 mM final concentration). Before clotting, Alexa-Fluor 488-labeled human fibrinogen (Molecular Probes, Grand Island, NY) was added to the plasma samples (5% of total volume, 0.08 mg/mL final concentration) to visualize fibrin network structure in a fluorescence confocal microscope. The clots were allowed to form at room temperature for 90-100 minutes to ensure covalent cross-linking by factor XIIIa. Ten fibrin clots from different plasma samples were prepared as described and used for compression studies with combined structural and rheological examination.
2.2 Visualization of Fibrin Networks and Image Analysis
The fluorescent confocal microscopy and strain-controlled oscillatory measurements were performed synchronously using a home-built “confocal rheoscope” which combined Bohlin Gemini rheometer with Nikon Eclipse 200/Confocal VT Eye microscope (18; 34). The plasma clots were allowed to form between horizontal rheometer plates separated by a distance of 650-750 μm. The sample volume was 300-375 μl. The upper moving acrylic plate had a 20-mm diameter and the base motionless plate was made of a 22-mm-diameter round transparent microscope glass cover slip to perform confocal imaging of the network during rheological measurements.
To improve the image quality, in a separate series of experiments uncompressed and compressed fibrin clots were analyzed using the Zeiss LSM510 META NLO laser scanning confocal microscope to get higher resolution images with z-stacks spanning the entire clot thickness. We used Plan Apo 40x water immersion objective lens (NA 1.2). A laser beam with wave length of 488 nm was used for fluorescent imaging. The distance between slices in each zstack was 0.5 μm. The image resolution of each slice was 1024x1024 pixels.
The samples were subsequently processed and analyzed quantitatively using the automated program as described in (36). Briefly, a new two-stage method was used to extract the structure of the network in the 3D confocal microscopy images and to characterize the structure by vertices (end points and branch points of the network) and edges (fiber network segments) in a 3D graph. A detailed description of the algorithm can be found elsewhere (36).
2.3 Controlled Compression of Fibrin Clots
For confocal microscopy there were two types of fibrin clots compressed using a computerized AR-G2 Rheometer (TA Instruments, New Castle, DE). First, the 650-750-μm-thick fresh hydrated fibrin clots were formed directly between the rheometer plates and compressed vertically down to 1/10 of their initial thickness. 12 clots from various plasma samples were tested. The stepwise compression of the clots was performed in 25-μm and 50-μm steps at the rate of 30 μm/s, as the downward force was applied by the upper rheometer plate on the top surface of the clot. In the other type of compression experiments the 150-μm-thick fibrin clots were formed in a flow chamber built of a microscope glass slide (bottom) and a glass cover slip (top) separated by an adhesive and highly plastic putty, which permitted irreversible compression of the clot samples within the chamber placed between the rheometer plates. In both types of experiments the fully polymerized and cross-linked plasma clots were compressed to a different degree followed by confocal microscopy. We typically waited 2 minutes after each step before performing confocal microscopy. A compressive strain (or degree of compression), ε was defined as the absolute fractional decrease in fibrin clot thickness ε = |ΔL/L0|, where ΔL = L − L0, and L0 and L are the initial and reduced thickness dimensions of the uncompressed and compressed clots, respectively.
2.4 Oscillatory Shear Rheometry of Compressed Fibrin Clots
Changes of viscoelastic properties of fibrin clots during compression were measured by oscillating rheometry using a Bohlin Gemini rheometer (Malvern Instruments, Westborough, MA) with parallel plate geometry. Measurements were performed with a fixed oscillating 0.5% strain amplitude at a frequency of 1 Hz to produce a linear stress-strain response to imposed shear. The oscillations were initiated immediately after each subsequent step of compression and lasted for 300 s. In each test, the storage (G′) and loss (G″) moduli were measured in combination with confocal microscopy of the fibrin clot structure. The elastic response of the deformed clot to applied shear was characterized by the storage modulus, G′, which represents the stored energy and is defined as G′ = (τ0/γ0) cos(δ). Here, γ0 is a (small) strain amplitude, τ0 is a shear stress amplitude, and δ is a phase shift in the shear stress with respect to applied oscillatory strain. The viscous response of the deformed clot to applied shear was measured by the shear loss modulus, G″, corresponding to the energy dissipated as heat, and calculated as G″ = (τ0/γ0) sin(δ).
3 EXPERIMENTAL RESULTS
3.1 Compression-Induced Non-Uniformity of the Fibrin Network Structure
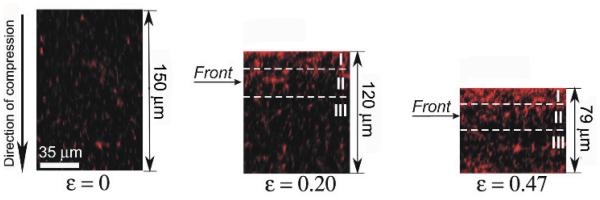
Visual examination of the fluorescent confocal images of the fibrin clots during compression revealed marked nonuniformity of the network structure. Here we define the XYZcoordinate system as Z-axis along the vertical direction that is opposed to the applied compression. The XZ-plane sections of the fibrin networks clearly showed the appearance and progression of a gradient in the fluorescence intensity in the direction of compression with a more or less sharp boundary between the areas with different intensities (Figure 2). To precisely quantify the non-uniformity of the network density, we computationally reconstructed and analyzed the 3D images of a 150-μm-thick uncompressed fibrin clot and the same clot after 20% and 50% compression by segregating each image into 14 equal horizontal sublayers spanning the entire height of the network. The thickness of the sublayers at various degrees of compression was different depending on the height of the clot. We quantified the uniformity of network densification as the node density in each layer and plotted it against the distance from the bottom of the clot compressed from above (Figure 3a). Our results showed that during vertical compression of a fibrin network a much higher degree of node densification was observed closer to the top of a clot, while the node and network density decreased towards the bottom. The top, middle and bottom layers of the compressed clots are indicated in Figure 2 and Figure 3a. As the degree of compression increased from ε = 0 to ε = 0.2 and ε = 0.47, the node density of the upper network layers increased by a factor of 1.8 and 2.3, respectively. At the same degrees of compression (ε = 0.2 and ε = 0.47) the node density of the middle layers of the network increased by only 1.1 and 1.2, respectively. The density of the bottom portion of the network did not change at ε = 0.2, but increased by 1.2 for ε = 0.47 as is apparent from the diffuse region near the bottom of the clot in Figure 2 (right panel). However, this does not contradict the presence of a moving compression front from the top of the clot. Since the width of the front given by the parameter c in Eqn. (1) is about 30μm and its center is located at Z0 = 42μm, the bottom portions of the network likely experience a non-zero strain that pushes them against the glass surface causing a moderate increase in fluorescence intensity.
Fig. 2.
The “compression front” or “phase boundary” is formed in response to vertical deformation of a fibrin clot. To provide visual examination of the changing clot structure, the distribution of fluorescence intensity in the XZ plane is shown in the same fibrin clot, uncompressed (left), about 20% compressed (center), and about 50% compressed (right). As the degree of compression increases, the fluorescence intensity (reflecting the network density) displays a gradient along the direction of compression. Here the compressive strain ε is a degree of compression defined as ε = |ΔL/L0|, where ΔL = L − L0, and L0 and L are the initial and reduced thickness dimensions of the uncompressed and compressed clots, respectively. The dashed lines outline the top (I), middle (II) and bottom (III) layers of the compressed clot, respectively. A horizontal arrow indicates the position of the compression front.
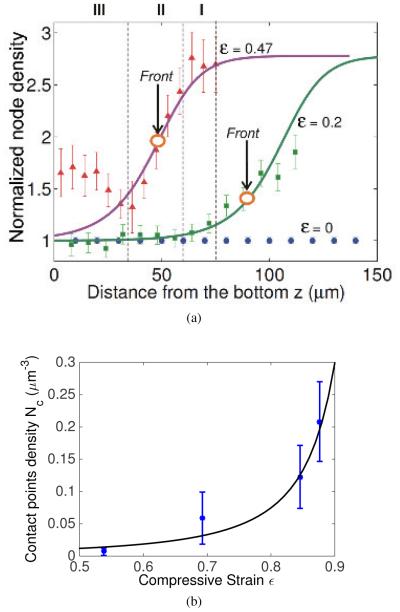
Fig. 3.
(a)The node density of the fibrin network as a function of height from the bottom of the sample based on 3D reconstruction of the network, uncompressed (ε = 0) and compressed to different degrees (ε = 0.2 and ε = 0.47). The node density was normalized with respect to the node density of the uncompressed clot. Note that the node density increases from bottom to top. The curve is flatter near the top and bottom of the sample and has a larger gradient near the middle. This suggests that the fibers are buckled near the top and straight near the bottom. The symbols represent experimental data (MSD, n=4) and we have modeled the regime of high gradient as a compression front or phase boundary. The lines represent fitting curves made using Eqns. (1) and (2) together with the experimental data with fitting parameters a = b = 0.2, c = 30, and Z0 = 42 for red curve, Z0 = 100 for green curve respectively. Z0 represents the center of the phase boundary in the reference configuration. The decrease of Z0 shows that the front moves downwards in response to increased compression. The top (I), middle (II) and bottom (III) layers of the compressed clot (ε = 0.47) are separated by the vertical dashed lines that correspond to the layers shown in Fig. 2. Large circles with vertical arrows indicate the position of the compression front. (b) Experimental data of node density under large compression is fitted by Eqn. (7). This justifies our use of Eqn. (8) for the densified network. We have used l = 1.32μm, d = 0.22μm, ν = 0.1μm−3.
To confirm the structural non-uniformities in fibrin clots produced by compressive loads, we also complemented the 3D structural analysis of compressed fibrin networks with an experiment to follow the displacement of microscopic fluorescent beads embedded into the network in response to clot compression. 2-μm polystyrene fluorescent beads were tracked during the compressive deformation in a clot volume of 35.8 × 35.8 × 25.5μm in the bottom portion of the clot. The compression was applied in 25μm steps. After each step we waited 2 minutes before measuring the displacements of the beads. We found that the beads’ position changed non-linearly in the Z-direction as a function of compressive strain (Figure 4), indicating the non-uniform compression of the network. In the case of spatially uniform compression, one would expect to observe a linear displacement of beads with compression irrespective of their initial position and the distance from the bottom of a clot. However, in our experiments the beads exhibited less than 20% relative displacements when the clot was exposed to compressive strains from ε = 0 to ε = 0.6, but revealed a rapid descent toward the bottom of the clot at ε > 0.6. To be more specific, when the compressive strain reached 0.6, the absolute distances changed by 2, 1.5 and 0.6μm for the beads initially located at 14.7, 11.1 and 2.7μm over the bottom, respectively. At a compressive strain of 0.7 the bead, which was the closest to the bottom of the clot, stopped moving because it had reached the surface. As the strain increased, other beads moved downwards until they also reached the bottom of the clot. The trajectory of all the beads turned downward at a similar compressive strain because they are all located within 15μm of the bottom while compression is applied in 25μm steps and the width of the front is about 30μm (see Figure 2 and Figure 3a). The nonlinear response of bead displacement to network compression indicated that the deformation of the network occurred non-uniformly with the top layers being compressed earlier and stronger than the lower network portions. As a result, the beads did not undergo large displacements at low strains but their vertical position started to change drastically at about ε > 0.6 as the boundary between the relatively compact (upper) and loose (lower) portions of the network approached the bottom of the clot.
Fig. 4.

The absolute vertical distance from the bead to the bottom of the clot along the direction of network compression for various locations in the same clot compressed from ε = 0 − 0.9. The network is characterized by z the bead distance from the bottom at a certain degree of compression and z0 the bead initial distance from the bottom of the network. 2μm polystyrene fluorescent beads were tracked during the compressive deformation in a clot volume of 35.8 × 35.8 × 25.5μm in the bottom portion of the clot. Densification occurs at the bottom of the clot only at high compressive strain, likely coinciding with the arrival of the compression front at the bottom. Before the arrival of the compression front the density in the bottom of the clot remains almost independent of strain. This is what we expect in the plateau regime when the network consists of a mixture of two phases that accommodate the increasing compressive strain simply by advancing the compression front.
Thus, both the structural analysis and bead tracking provide evidence for the formation and propagation of a “compression front” inside the network as more dense upper layers overtake the less dense bottom portions of the fibrin clot during progressive compression. Such a front can be represented by a strain profile given as:
| (1) |
| (2) |
where Z is the original height of a material point in the unstressed (reference) configuration, Z0 is the location of the center of the front in the unstressed configuration, and z is the deformed height that is measured in the experiment. We got Eqn. (2) by integrating dz/dZ = 1 − ε with boundary condition z(0) = 0, as in our experiments. Capital Z0 cannot be measured in our experiment but using Eqn. (2) the change in Z0 can be obtained from the experimentally measured changes in the location of the phase boundary as a function of z as explained below. The network density is proportional to 1/(1 − ε) as discussed in section 4.1. Thus, we can plot the network or node density as a function of z. Since the minimum and maximum values of the strain in Eqn. (1) are a ± b, we expect that 2b should approximately equal the transformation strain or the difference in strains between the high-strain and low-strain phases at the plateau stress σ0 (see Figure 1). a should be the strain at the center of the front, c should be a measure of the width of the front, and d is obtained by enforcing z(0) = 0 (see analysis in Appendix. Keeping this in mind we chose reasonable values of a, b and c to fit the experimental data. The data and the fits are shown in Figure 3a. We found that 2b ≈ 0.4, as expected to be the transformation strain shown in Figure 1. Furthermore, Z0 comes closer to the bottom of the sample when higher compression is applied, confirming that the “compression front” moves downward in response to the loading.
3.2 Non-linear Mechanical and Structual Response of Fibrin Networks to Compression
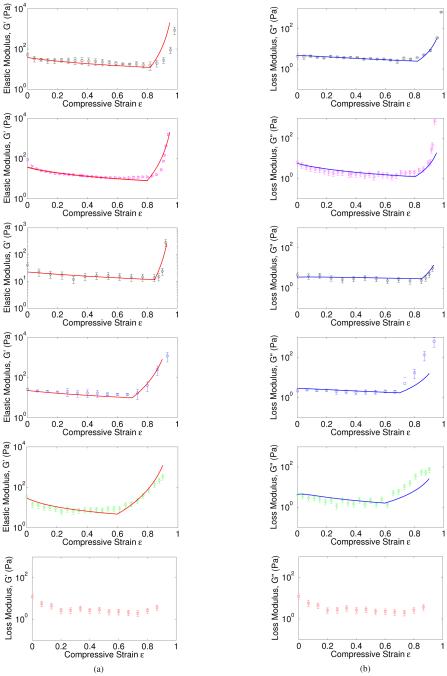
Structural alterations of fibrin network during compression underlie changes of shear viscoelasticity studied with rotational rheometry. The rheological measurements of fibrin clots with various initial shear storage and loss moduli were performed with two different compression steps (10 μm and 25 μm ) and at different degrees of compression. The experimental results are shown in Figures 5 and 6 in combination with the theoretical curves. The normal stress, calculated as the force distributed over the area of the smaller rheometer plate was measured for each degree of compression, and presented as the plots of normal stress, σ, versus compressive strain, ε (Figure 5). The curves were almost linear at lower degrees of compression with a steep increase of the normal stress at higher degrees of compression (ε > 0.5). The evolution of the shear viscoelastic properties of fibrin networks in response to compressive deformation displayed a typical tri-phasic behavior (Figure 6a). In the beginning of compression (ε < 0.05), the shear elastic modulus of a fibrin network was almost constant followed by a long relative plateau up to about ε = 0.7 − 0.8 compressive strain and finally dramatic increase at the highest compressive strains. The loss modulus followed the same trend (Figure 6b). If the current rheological measurements are correlated with the structural analysis of the network dynamics performed earlier in (18), the results could be described as follows. First, a linear viscoelastic response to compression was observed, in which most fibers are straight. Then, a plateau regime follows, accompanied by an increasing number of buckled fibers while the stress remains nearly constant as strain increases. Finally, we see a regime in which network densification occurs with a stress-strain response that is markedly non-linear and dominated by bending of fibers after buckling and inter-fiber contact. In the next section we will quantify these observations using a model for foams. We emphasize that the experimental results reported here are substantially distinct from those reported earlier (18) because in addition to the confirmed non-linear response, we were able to reveal the non-uniformity of the compressive deformation with formation of a “compression front” or “phase boundary” along the axis of compressive strain (see Figure 1a) (27; 28).
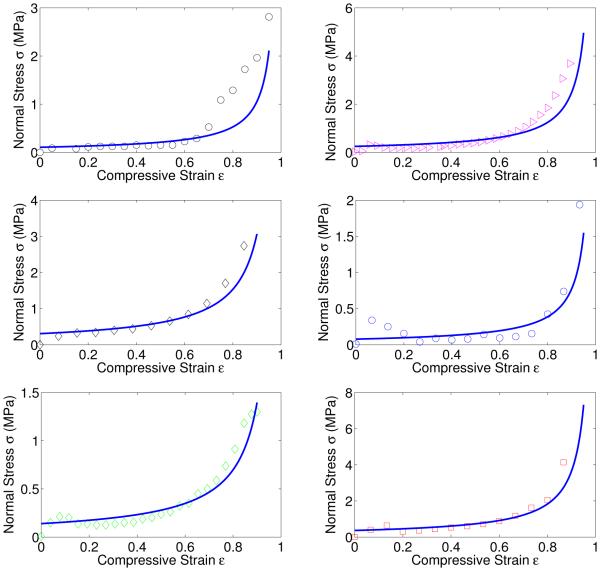
Fig. 5.
Fitting of the experimental data of normal stress according to Eqn. (14). Different symbols and colors are experimental data corresponding to different clot samples of varying height as shown in Table 1a. Since the rate at which they are compressed is 30μm/s for all samples the strain rate for each of them is different. Lines show model fits with parameters as given in Table 1a. Most of the normal stress measured in the compression experiments on our fibrin gels is due to the escape of water in response to compression. For this reason we cannot extract the storage and loss modulus of the networks from these stress-strain curves.
Fig. 6.
Fitting of the storage moduli and loss moduli according to Eqns. (4), (9), (32), (16), (18), and (32). We have used fitting parameters for each individual experimental group as given in Table 1b. Note that there is no densification regime in the last group. One possible reason could be the failure or damage of the network under large compression. However, the data for strains smaller than 0.8 in the last group are consistent with the other data sets.
4 THEORETICAL ANALYSIS OF THE EXPERIMENTAL DATA
4.1 Short Review of Cellular Solids
A foam is a porous low density structure consisting of cells or fibers made of a viscoelastic material. In our case these fibers are made of fibrin. If Es is Young’s modulus of a single fibrin fiber, then the Young’s modulus and shear modulus of the network or foam consisting of these fibers is given by (20):
| (3) |
| (4) |
where the important non-dimensional quantity φ = πνd2l/4 is the volume fraction of fibrin in the network, ν, d, and l are respectively the number of fiber segments per unit volume, fiber diameter and fiber segment length between branch points. φ0 is the initial fiber volume fraction before compression. These expressions are derived under the assumption of small strains so that the stress-strain relation of the foam can be approximated as linear. We will designate this phase of our fibrin network as the linear phase or the low-strain phase.
When this network is loaded in compression fibers will buckle (20) when a critical force is reached. From Euler’s formula, the critical axial load that causes fiber buckling is
| (5) |
where Es, I and l are the Young’s modulus, area moment of inertia, and the length of the fiber between branch points, respectively. The coefficient n is close to one and is determined by boundary conditions at the fiber ends. According to the analysis given in (20), n is taken to be 1 because the fiber lengh l varies over a range in random networks. We can use this expression for the critical load to estimate the stress σ0 at which buckling of fibers begins in the network. According to (20), since, σ0 ∝ Fcr /l2 ∝ EsI/l4, we could write it as
| (6) |
where the coefficient c is assumed to be 0.04 in (20). The strain corresponding to the critical stress in the low-strain phase is easily computed as ε1 = σ0/E1. Another way to estimate ε1 is to use Eqn. (5) – ε1 ≈ Fcr /(AEs) where A is fiber cross-sectional area. Both these methods give an estimate of ε1 around 0.05 and σ0 around 5 P a as shown in Figure 1 for the parameters in the experiments shown in Figures 5 and 6. These ideas for estimating σ0 can only be justified if the fibers in the network are not undulating due to thermal motion. The extent of thermal undulations depends on the persistence length of the fibers and their length between branch-points. The persistence length of fibrin varies over a wide range depending on the conditions (thrombin concentration, pH, calcilum concentration, etc.,(17)) under which a clot is made (21; 22). In fact, (16) summarizes several reasons in addition to fibrin assembly conditions (such as, protein packing density, lateral binding between protofibrils. etc.) that result in the variation of fibrin persistence length. For our fibrin networks, which have been derived from plasma clots, the average diameter of the fibers is about 220nm (18), which together with a Young’s modulus E = 5MPa (23) gives a persistence length EI/kB T at room temperature about 1m. The length l between branch points is about 1 − 2μm, on average. Thus, thermal fluctuations of the fibers are negligible, consistent with the assumption for foams.
When large compressive strain is applied to a fibrin network the total volume decreases considerably and the interfiber space is reduced. In this configuration a linear stressstrain relation is not applicable any more. The fibers are mostly buckled and forced to touch each other. We call this kind of configuration the “densified phase” or the high-strain phase. This sort of densified network has been studied by Toll (33) who showed that the number of contact points Nc per unit volume is an increasing function of fiber volume fraction φ and was given by
| (7) |
where f is a scalar invariant of the fiber orientation distribution function and is equal to π/4 for three dimensional isotropic networks (33). Following (20), in the densified phase we assume the fiber volume fraction φ = φ0/(1 − ε). In other words, all the volume change is due to the reduction in the thickness of the network in the direction of the compressive force with no change in the cross-sectional area. Our experiments indicate that this is a good approximation. We compared Eqn. (7) to the experimental data on contact point density Nc from (18) and found that it indeed varied quadratically with the fiber volume fraction φ as shown in Figure 3b. The stress-strain relation for such a network was proposed by van-Wyk (32) and Toll (33) in the following form:
| (8) |
where the coefficient k is determined by the material and loading conditions. It is found to be less than 1, as in (35). The exponent n was analytically derived to be 3 from Eqn. (7) for three-dimensional random networks in (33). This has been confirmed by several experiments (35; 38; 39; 40). From Eqn. (8), we can compute the local tangent moduli of the network in the densified regime. The tangent modulus at any strain in the densified regime is directly proportional to the storage modulus in the rotational rheometer oscillation experiments. Following the linear theory for foams at small strains we assume that the ratio between this storage modulus and the local tangent modulus in the densified regime is 3/8 (see Eqns. (3) and (4)) and get the following expression for the shear modulus of the densified network at strain ε:.
| (9) |
Any contributions due to the Poisson effect in the densified regime are absorbed into the constant k that has been treated as a fitting parameter in the literature. This is also consistent with our experimentally motivated assumption above that vertical compression of the fibrin network does not change its cross-sectional area. For the plateau stress σ = σ0, we find that the Young’s and shear moduli are
| (10) |
| (11) |
where ε2 is the strain at which .
We will use a linearized version of the stress-strain relations (in the neighborhood of σ = σ0) in our subsequent analysis. These are summarized for the low- and high-strain phases as follows.
| (12) |
where σ0 is the critical stress for buckling, as discussed previously. At this stress the straight and densified phases coexist. E1, E2 are Young’s moduli in the straight and densified phases respectively from Eqns (3) and (10). εT is the transformation strain which can be estimated by constructing the tangent to the stress-strain curve at ε = ε2 and reading off the intercept on the ε axis as shown in Figure 1. If we assume that the process of loading is quasi-static so that the sample stays in equilibrium during the compression process, then the compressive strain ε in the plateau corresponding to the stress σ0 is obtained simply by changing the fraction of fibers buckled. If we denote the fraction of fibrin in the high strain phase as s ∈ [0, 1], then total strain can be estimated from the insight that the sample consists of two ‘springs’ in series consisting of the straight and densified network respectively as observed in Figure 2.
| (13) |
This completes the description of the stress-strain curve for a fibrin network under compression. As an example we have plotted this stress-strain curve for a fibrin network with network parameters experimentally measured in Kim et al. (18) in Figure 1b. We have used values of the fiber Young’s modulus Es = 5 MPa (9; 10; 41). The stresses in Figure 1b are of the same magnitude as the measured storage moduli in Figure 6. However, the stress strain curve in Figure 5 does not have an initial linear regime for small strains even though it seems to have a flat plateau regime for intermediate strains and a regime with steeply increasing stress for high strains. Furthermore, the shear moduli measured in Figure 6 are at least three orders of magnitude lower than those seen in the normal stress data plotted in Figure 5. This indicates that Figure 5 is not a true reflection of the stress strain response of the network; rather it is the result of water squeezing out of the network in response to compression. To understand why this is the case we must account for the strain-rate dependence of the mechanical response of these fibrin gels.
4.2 Strain Rate Dependence
The fibrin networks that have been tested in our experiments really are gels that contain a large amount of water. As the gel is compressed, water is squeezed out. However, as it is sheared, water is not squeezed out because the total volume does not change. Hence, it is expected that the measured normal stresses in compression will depend on the applied strain rates. This effect is well-known as poro-viscoelasticity in foams and other cellular solids (20). An analytic relation for the stress as a function of the applied strain rate is given as (20)
| (14) |
where μ is dynamic viscosity of the fluid, ε and are the compressive strain and its rate, D is horizontal dimension of the foam sample, and l is the cell edge-length of the foam. The coefficient C is about unity. As shown in Figure 5, the measured normal stress during compression can be captured by Eqn. (14) with the parameters μ = 0.001 Pa·s (for water), D = 22 mm (known from our experimental set-up) and l as the only fitting parameter for each experiment. The strain rate for each experiment is different because the height of the samples varies while the rate of compression (30μm/s, see section 2.3) remains fixed for each experiment. The fitted values of l appear in Table 1a. They are within the range of variation of fiber lengths between branch points seen in experiments (18). We see that most of the normal stress measured in the experiments is due to the expulsion of water from the fibrin gel. Hence, the storage and loss moduli measured in our rheometer experiments and shown in Figure 6 cannot be extracted from the stress-strain curves shown in Figure 5.
Table 1.
Fitting parameters for each experiment.
| (a) Normal stress |
| Individual group | Sample height(mm) |
strain rate(s−1) |
Fiber length(μm) |
|---|---|---|---|
| Black circle | 550 | 0.055 | 0.5 |
| Magenta triangle | 650 | 0.046 | 0.3 |
| Black diamond | 650 | 0.046 | 0.27 |
| Blue circle | 750 | 0.04 | 0.5 |
| Green diamond | 650 | 0.046 | 0.4 |
| Red square | 750 | 0.04 | 0.3 |
| (b) Oscillatory shear |
| Individual group | ϕ 0 | k | ε 20 | M (Pa−1s−1) | wτon(10−18J · s) |
|---|---|---|---|---|---|
| Black circle | 0.0045 | 0.025 | 0.82 | 0.004 | 2 |
| Magenta triangle | 0.0045 | 0.0025 | 0.8 | 0.005 | 1.2 |
| Black diamond | 0.0035 | 0.0025 | 0.85 | 0.008 | 1.7 |
| Blue circle | 0.0035 | 0.333 | 0.7 | 0.008 | 4 |
| Green diamond | 0.004 | 0.333 | 0.6 | 0.008 | 6.5 |
| Red square | Densification not observerd | ||||
From Eqn (14), we can approximate the viscosity of the gel for small strains (infinitesimal values of ε) as
| (15) |
However, the viscous losses due to this term cannot be measured in the rotational rheometer experiments because the derivation of this expression assumes that the volume of the network is changing while the oscillatory experiments are performed in shear which involves no change in volume. Therefore, the loss modulus in the low strain phase should only come from the liquid viscosity itself. For water, this is merely μ = 0.001 Pa·s, which is much smaller than the value obtained from (15). Therefore, we treat the fibrin network in the low strain phase as a purely elastic solid with constant modulus.
Another important network property that is related to the strain rate is the inter-fiber friction. This is particularly important in the densified phase in which a large number of contacts are created between fibers. Fibers sliding against each other while in contact will cause dissipation in the network. In order to estimate the viscosity associated with this process we appeal to an elegant calculation in (43). This book gives an explanation for the molecular basis of “viscosity” due to the forming and breaking of bonds as molecules slide past each other. The expression is:
| (16) |
where w is the inter-molecular bond energy and τon the average life-time of a bond. An expression for Nc as a function of fibrin volume fraction is already given in Eqn. (7). However, w and τon are difficult to determine for fibrin fibers. Some work along this direction has been done for estimating the viscous losses in microtubule networks (42), but here we treat the product wτon as a fitting parameter. In summary, we model the densified network at σ = σ0 (for small strains) as a Kelvin-Voigt solid (44) in which the stress-strain relation is given as:
| (17) |
where the parameters E2 and η are taken from Eqns (10) and (16). In the rotational rheometer experiments the loss modulus is related to this viscosity as:
| (18) |
where ω is frequency of oscillation. The loss modulus for both the lowand high-strain phases can be determined using this formula if we use η = μ = 0.001Pa·s (of water) for the low-strain phase and Eqn.(16) for the high-strain phase. In order to estimate the loss modulus in the plateau regime of the stress-strain curve we need to account for the rate at which the fractions of the two phases evolve. This is explained in the next section.
4.3 Phase Boundary Mobility
In the oscillation experiments, the fraction of each phase depends on both applied strain and strain rate. As shown in Figure 1, the phase boundary is expected to oscillate as the applied loading oscillates. We treat this process in a onedimensional model as follows. After pre-compressing the sample, we assume that the oscillation is also in the axial direction. This is different from the experiments in which an oscillating shear strain is applied on the pre-compressed networks. However, since the oscillating shear strains applied in the experiments are small, we can assume that they will give storage and loss moduli that are proportional to those obtained in our calculations.
During the oscillation process the sample may not be in equilibrium and thus the stress may not be σ0. There will be oscillation in stress, phase fractions, as well as strain. We assume that the fraction s is determined by the kinetics of transformation as in (30). This means that the rate of change of each fraction is given as a function of stress σ. To simplify the problem we consider the particular kinetic equation (31):
| (109) |
or,
| (20) |
where M is a time-independent mobility parameter determined by the network that could be regarded as a fitting parameter in our theory and s0 is the fraction of high strain phase before oscillation is applied. In the experiment we apply a harmonic oscillating strain to the pre-compressed network as:
| (21) |
where ε0 is an initial strain in the plateau regime of phase transition before oscillation is applied. Taking account of the strain rate dependence we rewrite Eqn. (13) as:
| (22) |
Now, recall that the expression for equilibrium stress σ0 and strain ε0 are given by:
| (23) |
where the subscript 0 denotes the quantity in initial compression equilibrium before oscillation. Subtracting Eqns. (23) from (22) we get:
| (24) |
| (25) |
where x = ε1 −ε10 and y = ε2 −ε20 are the small oscillating components of strain in each phase. Since the oscillation in strain is small, we make an approximation in Eqn. (24) by replacing ε2 − ε1 with ε20 − ε10. Then, plugging Eqn. (20) and (25) in (24) we get:
| (26) |
Carrying out the integral of and rearranging terms, we find that
| (27) |
where the three dimensionless quantities A, B, and C are given by:
| (28) |
Let us assume that this equation has the solution:
| (29) |
where U and V are at present unknown. Plugging this into Eqn. (27) and solving for the two coefficients U and V gives:
| (30) |
Plugging this back into Eqn. (22) we get the expression for stress as:
| (31) |
Therefore, the storage and loss modulus in the plateau regime (i.e. σ = σ0) are respectively
| (32) |
In order to confirm that the above framework predicts the correct storage and loss moduli, we compared quantitatively our theory with the experimental data. The input parameters of the network in the above computations were taken from the experiments shown in Figure 6. Combining Eqns. (4), (9) and (32) together, we obtain the theoretical curve in each individual experiment in Figure 6. We take the value of branch point density and fiber density exactly as measured in experiment as 0.04μm−3 and 0.1μm−3 respectively. The other fitting parameters for each experiment are reported in Table 1b. The trends in storage and loss moduli are captured quite well with this model. Note that the experimentally measured average fiber length and average fiber diameter are 1.32 μm and 220 nm respectively (18), which result in a fiber volume fraction of φ0 = πνd2l/4 = 0.005. The φ0 values obtained by our fits are slightly below this value but well within the range of variation of φ0 in the experiments (18). Also note that the value of constant k in the densifed phase varies inversely with the strain ε20 where the phase transition finished. We have not yet been able to rationalize this.
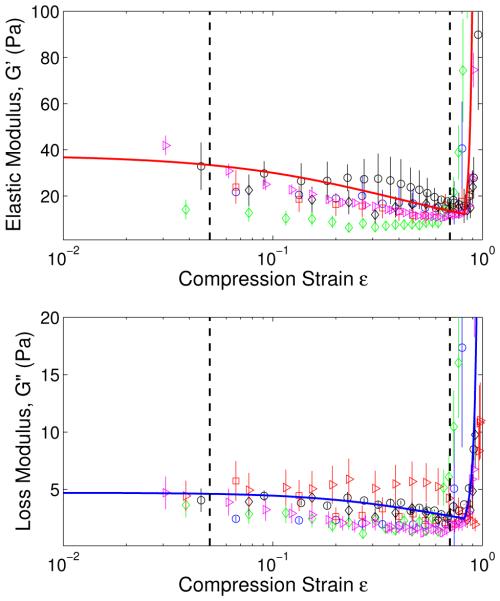
We will now connect our results for the variation in moduli to Figure 1 which schematically shows three distinct regimes in the stress-strain curve. To this end we have replotted all the data for storage and loss moduli in Figure 7 against the logarithm of the strain ε. The red and blue curves in the upper and lower panels are fits to the average of all the storage and loss moduli, respectively. The strains ε1 and ε2 have been indicated by dashed lines to demarcate the three regimes. In the initial linear regime, ε < ε1, the moduli G′ and G″ are constant. In the plateau regime, ε1 ≤ ε ≤ ε2 the network accommodates more strain by changing the fractions of the straight and densified phases of the networks through the motion of the phase boundary. G′ decreases with increasing strain in the plateau regime because the slope of the stress-strain curve of the densified phase at ε = ε2 is smaller than the slope for the straight phase at ε = ε1. For ε > ε2 densification occurs and both moduli increase steeply.
Fig. 7.
Experimental data of storage moduli and loss moduli versus logarithm of strain, showing three different regimes of fibrin network mechanics as indicated schematically in Figure 1. In the linear regime(0 < ε < 0.05), the moduli are constant; in the phase transition regime(0.05 < ε < 0.7), they are decreasing due to progressive fiber buckling; in the desification regime (0.7 < ε < 1), they are steeply increasing due to bending of the buckled fibers and increased interfiber contact. The theoretical curves passing through the experimental data are plotted using Eqns. (4), (9), (32), (16), (18), and (32) with φ0 = 0.0045, k = 0.025, ε20 = 0.7, M = 0.004Pa−1s−1, ωτon = 2 × 10−18J · s.
DISCUSSION
We have shown in this paper that fibrin networks are natural cellular materials. The theoretical description of the fibrin mechanical behavior is novel and treats fibrin networks in the context of a broad class of natural and synthetic foamlike materials which share some key features. Among these is the tri-phasic stress-strain response with a rarefied lowstrain phase, a densified high-strain phase, and a plateau phase consisting of a mixture of these two. Like most foams we also see a moving phase boundary separating the two phases when fibrin networks are compressed (27; 28). The phase boundary and several other features quantifying the structural non-uniformity of fibrin networks under compression were revealed by our 3D microscopy studies. Because of the complexity of the analysis, non-uniform fibrin networks under loads have not been previously quantified. However, it is clear that under physiological conditions fibrin networks are frequently exposed to dynamic forces, which would result in non-isotropy and structural heterogeneities. Since in many cases, fibrin networks participate in the permeation of blood clotting factors (45), variations in fibrin matrix density can affect the spatial-temporal distribution of factors and hence, alter their biochemical interaction. Our results indicate that even a uniform compression can produce structural gradients in fibrin networks, therefore, suggesting a non-uniform alteration of fibrin matrix transport properties with compression.
It is also worth noting that the mechanical response of fibrin networks under compression is dominated by fiber buckling and subsequent bending and is therefore non-affine. This is in contrast to the stress-strain response in tension and shear where the assumption of affine deformations worked quite well (9; 10) . This assumption is particularly good for rubbers and other polymeric materials (11; 12), and it works for fibrin networks under tension because the unfolding of the proteins results in cross-linked polymer chains much like those in rubber. It works well for shear of a network of thin fibrin fibers because such a network is not very different from cross-linked fluctuating polymer chains (14; 16). However, in compression the initial linear regime is governed by fiber bending instead of fiber stretching. Thus, we can no longer assume affine deformations. This is apparent in the non-linear dependence of the initial Young’s modulus in compression E1 on the fibrin volume fraction φ (see Eqn. (3)). The dependence would be linear if the deformations were affine as in tension and shear. Since φ2 = ν2d4l2 our model predicts that E1 ∝ ν2d4l2 where ν is fiber density, d is average fiber diameter and l is average fiber length. Our prediction can be tested in experiments since ν, d and l can be controlled by changing the polymerization conditions of the fibrin networks. In the densified network buckled fibers are in contact, so the assumption of affine deformations is not expected to work. Indeed, the stress-strain response depends on φ in a complex way that has been quantified both with experiments and theory in the textile literature (32; 33). We have shown in this paper that the same ideas can quantitatively capture the compression response of densified fibrin networks with an appropriate choice of fiber geometrical and material parameters. For example, at large compressive strains our model predicts that the tangent modulus in the densified phase where φ0 is the initial fiber volume fraction. This prediction can be tested since ν, d, l and ε can all be controlled in experiments. Similarly, our physically motivated constitutive law Eqns. (16) and (7) that accounts for the inter-fiber friction and captures the viscous response of densified fibrin networks can also be tested in experiments. We have already demonstrated the importance of the strain-rate dependence in the compressive response of fibrin networks by using poroelastic constitutive laws that govern the flow of water in cellular solids.
In this work the structural alterations in response to compression were studied at the microscopic level of a network. We have shown that structural non-uniformity manifests itself as a “compression front” or “phase boundary” separating regions in the network where fibers are straight from another regime where the fibers are buckled. While such a front has been visualized in many macroscopic (27; 28) and microscopic foams (19) we are not aware of attempts where its motion is treated using a theory of phase transitions (31) to obtain the storage and loss moduli. We have demonstrated in this work that a continuum theory of phase transitions can predict the rheological properties of fibrin networks under large deformations if we properly account for the dissipative motion of the phase boundary. It is likely that a similar model can be applied to other foams or foam-like materials since propagating interfaces have been visualized in them. The idea of a phase transition was also used in our earlier work on the tensile behavior of fibrin networks (9; 10). The difference here is that we have no evidence of forced molecular unfolding of the protein. However, fibrin has a complex multidimensional structure and it has been shown that compression of a hydrated fibrin clot is accompanied by changes in the α-helical coiled-coils, namely the transition of α-helix to β-sheet revealed using FTIR spectroscopy (46). However, a comparative analysis shows that the changes in the secondary structure of fibrin were observed at compressive stresses (≥ 25M P a) that are orders of magnitude higher than those applied in our work (Figure 5). It is likely that molecular structural transitions observed in a protein at very high degrees of compression results from its mechanical destruction, not reached in our present experiments. The aggregate of data suggests that at the degrees of deformation, not leading to complete disorganization of a filamentous network, compressive load is accommodated mainly by the structural changes in fiber arrangements at the network level. These changes include buckling, stretching, and formation of oblique contacts of individual fibers as well as overall network densification. It is noteworthy that the structural changes underlying compressive deformation of the networks are spatially non-uniform and form a stepped gradient along the axis of compression. Although we observed a single compressive front in our experiments that originated at the boundary of our sample, this is by no means necessary. Fronts can be nucleated in the interior of the network at a site of stress concentration or low network density. This prediction can also be tested since it is possible to visualize moving fronts as we show in our experiments.
Fibrin deformability has become a rapidly developing area not only in the study of the mechanics of filamentous networks, but also in various practical biomedical applications. First, studies of compression of fibrin networks provide a basis for understanding what happens to salutary hemostatic clots and pathological obstructive thrombi in vivo, when they are subject to natural deformations. There is a number of conceivable patho-physiological conditions, in which fibrin networks can experience compressive loads: vasoconstriction, arterial hydrodynamic blood flow, clot contraction, pulsation of a vessel wall or aneurism, muscular pressure, cardiac beats for intracardiac thrombi, lung motion during breathing, etc. Next, fibrin has been widely used as a sealant in surgery and its hemostatic efficiency strongly depends on the ability to withstand mechanical loads, including compression. Finally, fibrin has been well-known for various tissue engineering applications in combination with cells and with other materials to replace damaged or diseased organs and tissues (47). Mechanical and structural insights into fibrin deformability in combination with a theoretical framework of studying fibrin mechanics provide a foundation for developing new treatment modalities. In particular, modeling of fibrin compressibility using the theory of foam mechanics opens an avenue for physically treating fibrin clots and thrombi as well as for developing new fibrin-based biomaterials with predictable properties.
6 ACKNOWLEDGMENTS
We would like to thank Professor Paul A. Janmey for fruitful discussion and providing access to the rheometer and confocal microscope and Anne van Oosten for valuable technical assistance. We also thank Jianxu Chen and Professor Danny Chen for helping with image analysis. We acknowledge partial support from the National Science Foundation through grants NSF CMMI 09535448 and NSF CMMI 1066787 (PKP and XL), National Institute of Health grant NIH R01GM095959 (OVK and MSA), NIH 1U01HL116330 (OVK, RIL, JWW, and MSA), NIH HL090774 (JWW) and Walther Cancer Foundation (OVK).
Appendix. Structure of the Compression Front
In our analysis above we assumed that the compression front is sharp. However, our experiments reveal that it has a thickness over which there is a large gradient in the strain profile. Fortunately, these descriptions are connected and have been discussed at length in the literature (30). Recall that we fitted the strain profile in our compressed sample using Eqn. (1). In the following, we briefly describe why we use the strain profile given by Eqn. (1). We follow the analysis in (30). Our network can exist in multiple phases at the same stress. Such materials have an up-down-up type stress-strain curve that can be described using
| (33) |
where σ is the stress, ε is the strain, and α, β, σ0 and E∗ are ma terial parameters. If we remember that , where W (ε) is a stored energy function, then it is not difficult to see that W is a quartic function of ε with two wells. The well at low strains corresponds to a network in which the fibers are straight, while the well at high strains corresponds to a densified network with buckled fibers. Without loss of generality we will now refer to σ − σ0 as σ and to ε − ε∗ as ε. As an example, σ0 = 5 Pa, E∗ = 0.32, α = 51 Pa and β = 651 Pa captures the compression curve for Es = 5 MPa in Figure 1b. In Figure 8 we have plotted the Gibbs free energy density (Ψ = W − σε) landscape using the above parameters for three different values of σ to show which phase has lower energy at each stress. Since the motion of the compression front causes energy dissipation we augment this constitutive equation with a linear viscosity term and since interfaces cost energy we add a linear strain gradient term as follows (30):
| (34) |
where ρ is the density of the material, ν is a viscosity and λ accounts for the energy required to create an interface. We assume that the compression front travels at velocity v and define a new variable ξ = Z − vt. Since the stress σ in our sample is constant we wish to find a profile for ε(z, t) that satisfies
| (35) |
with remote conditions ε → ε+ as ξ → ∞ and ε → ε− as ξ → −∞. It is easy to show that
| (36) |
gives such a profile for a particular choice of a, b, c and v that depend nonlinearly on α, β, ν, λ, ρ and σ. In particular, a is a solution to the cubic . We recover Eqn. (1) by setting v = 0, justifying its use to fit the strain profile in our compressed samples. Note that in accordance with our assumption in Eqn. (19) the front velocity v in this augmented theory depends on σ. A sharp front corresponds to the limit as c → 0. In this limit the dissipation caused by the motion of the front can be captured by a kinetic equation like Eqn. (19) as in (30).
Fig. 8.
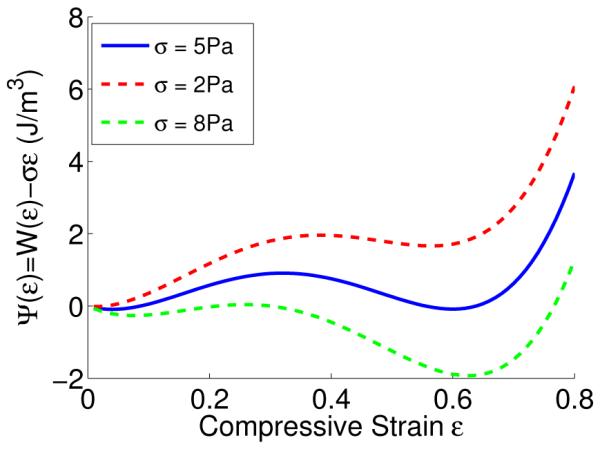
Multi-well Gibbs free energy landscape for various stresses. At the plateau stress σ = 5Pa both wells are at equal height, meaning that the straight and densified phases of the network can co-exist. For lower σ the straight phase has lower energy and for higher σ the densified phase has lower energy.
Contributor Information
Oleg V. Kim, Department of Applied and Computational Mathematics and Statistics, University of Notre Dame, Notre Dame, Indiana
Xiaojun Liang, Department of Mechanical Engineering and Applied Mechanics, University of Pennsylvania, Philadelphia, PA.
Rustem I. Litvinov, Department of Cell and Developmental Biology, Perelman School of Medicine, University of Pennsylvania, Philadelphia, Pennsylvania
John W. Weisel, Department of Cell and Developmental Biology, Perelman School of Medicine, University of Pennsylvania, Philadelphia, Pennsylvania
Mark S. Alber, Department of Applied and Computational Mathematics and Statistics, University of Notre Dame, Notre Dame, Indiana Department of Medicine, Indiana University School of Medicine, Indianapolis.
Prashant K. Purohit, Department of Mechanical Engineering and Applied Mechanics, University of Pennsylvania, Philadelphia, PA.
References
- 1.Weisel JW. The mechanical properties of fibrin for basic scientists and clinicians. Biophysical chemistry. 2004;112(2):267–276. doi: 10.1016/j.bpc.2004.07.029. [DOI] [PubMed] [Google Scholar]
- 2.Weisel JW, Litvinov RI. Mechanisms of fibrin polymerization and clinical implications. Blood. 2013;121(10):1712–1719. doi: 10.1182/blood-2012-09-306639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ferry JD. Viscoelastic properties of polymers. John Wiley Sons; 1980. [Google Scholar]
- 4.Liu WJLM, Jawerth LM, Sparks EA, Falvo M, Hantgan RR, Superfine R, Guthold M. Fibrin fibers have extraordinary extensibility and elasticity. Science. 2006;313(5787):634–634. doi: 10.1126/science.1127317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Falvo MR, Gorkun OV, Lord ST. The molecular origins of the mechanical properties of fibrin. Biophysical chemistry. 2010;152(1):15–20. doi: 10.1016/j.bpc.2010.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Houser JR, Hudson NE, Ping L, O’Brien ET, III, Superfine R, Lord ST, Falvo MR. Evidence that αC Region Is Origin of Low Modulus, High Extensibility, and Strain Stiffening in Fibrin Fibers. Biophysical journal. 2010;99(9):3038–3047. doi: 10.1016/j.bpj.2010.08.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hudson NE, Houser JR, O’Brien ET, III, Taylor RM, II, Superfine R, Lord ST, Falvo MR. Stiffening of individual fibrin fibers equitably distributes strain and strengthens networks. Biophysical journal. 2010;98(8):1632–1640. doi: 10.1016/j.bpj.2009.12.4312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hudson NE, Ding F, Bucay I, OBrien III ET, Gorkun OV, Superfine R, Falvo MR. Submillisecond Elastic Recoil Reveals Molecular Origins of Fibrin Fiber Mechanics. Biophysical journal. 2013;104(12):2671–2680. doi: 10.1016/j.bpj.2013.04.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brown AE, Litvinov RI, Discher DE, Purohit PK, Weisel JW. Multiscale mechanics of fibrin polymer: gel stretching with protein unfolding and loss of water. Science. 2009;325(5941):741–744. doi: 10.1126/science.1172484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Purohit PK, Litvinov RI, Brown AE, Discher DE, Weisel JW. Protein unfolding accounts for the unusual mechanical behavior of fibrin networks. Acta biomaterialia. 2011;7(6):2374–2383. doi: 10.1016/j.actbio.2011.02.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Arruda EM, Boyce MC. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. Journal of the Mechanics and Physics of Solids. 1993;41(2):389412. [Google Scholar]
- 12.Flory PJ. Principles of polymer chemistry. Cornell University Press; 1953. [Google Scholar]
- 13.Janmey PA, Euteneuer U, Traub P, Schliwa M. Viscoelastic properties of vimentin compared with other filamentous biopolymer networks. The Journal of cell biology. 1991;113(1):155160. doi: 10.1083/jcb.113.1.155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Storm C, Pastore JJ, MacKintosh FC, Lubensky TC, Janmey PA. Nonlinear elasticity in biological gels. Nature. 2005;435(7039):191–194. doi: 10.1038/nature03521. [DOI] [PubMed] [Google Scholar]
- 15.Kang H, Wen Q, Janmey PA, Tang JX, Conti E, MacKintosh FC. Nonlinear elasticity of stiff filament networks: Strain stiffening, negative normal stress, and filament alignment in fibrin gels. The Journal of Physical Chemistry B. 2009;113(12):37993805. doi: 10.1021/jp807749f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Piechocka IK, Bacabac RG, Potters M, MacKintosh FC, Koenderink GH. Structural hierarchy governs fibrin gel mechanics. Biophysical journal. 2010;98(10):2281–2289. doi: 10.1016/j.bpj.2010.01.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ryan EA, Mockros LF, Weisel JW, Lorand L. Structural origins of fibrin clot rheology. Biophysical journal. 1999;77(5):2813–2826. doi: 10.1016/S0006-3495(99)77113-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kim OV, Litvinov RI, Weisel JW, Alber MS. Structural basis for the nonlinear mechanics of fibrin networks under compression. Biomaterials. 2014;35(25):6739–6749. doi: 10.1016/j.biomaterials.2014.04.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hutchens SB, Needleman A, Greer JR. Analysis of uniaxial compression of vertically aligned carbon nanotubes. Journal of the Mechanics and Physics of Solids. 2011;59(10):2227–2237. [Google Scholar]
- 20.Gibson LJ, Ashby MF. Cellular solids: structure and properties. Cambridge university press; 1999. [Google Scholar]
- 21.Sharma RC, Papagiannopoulos A, Waigh TA. Optical coherence tomography picorheology of biopolymer solutions. Applied Physics Letters. 2008;92(17):173903. [Google Scholar]
- 22.Jahnel M, Waigh TA, Lu JR. Thermal fluctuations of fibrin fibres at short time scales. Soft Matter. 2008;4(7):1438–1442. doi: 10.1039/b802555j. [DOI] [PubMed] [Google Scholar]
- 23.Collet JP, Shuman H, Ledger RE, Lee S, Weisel JW. The elasticity of an individual fibrin fiber in a clot. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(26):9133–9137. doi: 10.1073/pnas.0504120102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Onck PR, Koeman T, Van Dillen T, Van der Giessen E. Alternative explanation of stiffening in cross-linked semiflexible networks. Physical review letters. 2005;95(17):178102. doi: 10.1103/PhysRevLett.95.178102. [DOI] [PubMed] [Google Scholar]
- 25.Broedersz CP, Sheinman M, MacKintosh FC. Filament-length-controlled elasticity in 3D fiber networks. Physical review letters. 2012;108(7):078102. doi: 10.1103/PhysRevLett.108.078102. [DOI] [PubMed] [Google Scholar]
- 26.Shahsavari A, Picu RC. Model selection for athermal cross-linked fiber networks. Physical Review E. 2012;86(1):011923. doi: 10.1103/PhysRevE.86.011923. [DOI] [PubMed] [Google Scholar]
- 27.Gaitanaros S, Kyriakides S, Kraynik AM. On the crushing response of random open-cell foams. International Journal of Solids and Structures. 2012;49(19):2733–2743. [Google Scholar]
- 28.Jang WY, Kyriakides S. On the crushing of aluminum open-cell foams: Part I. Experiments. International Journal of Solids and Structures. 2009;46(3):617–634. [Google Scholar]
- 29.Landau LD, Lifshitz EM, Pitaevskii LP. Statistical Physics (Course of Theoretical Physics. (3rd) 1984;5 [Google Scholar]
- 30.Abeyaratne R, Knowles JK. Evolution of phase transitions: a continuum theory. Cambridge University Press; 2006. [Google Scholar]
- 31.Raj R, Purohit PK. Phase boundaries as agents of structural change in macromolecules. Journal of the Mechanics and Physics of Solids. 2011;59(10):2044–2069. [Google Scholar]
- 32.Van Wyk CM. Note on the compressibility of wool. Journal of the Textile Institute Transactions. 1946;37(12):T285–T292. [Google Scholar]
- 33.Toll S. Packing mechanics of fiber reinforcements. Polymer Engineering and Science. 1998;38(8):1337–1350. [Google Scholar]
- 34.Wen Q, Basu A, Winer JP, Yodh A, Janmey PA. Local and global deformations in a strain-stiffening fibrin gel. New Journal of Physics. 2007;9(11):428. [Google Scholar]
- 35.Mezeix L, Bouvet C, Huez J, Poquillon D. Mechanical behavior of entangled fibers and entangled cross-linked fibers during compression. Journal of materials science. 2009;44(14):36523661. [Google Scholar]
- 36.Chen J, Kim OV, Litvinov RI, Weisel JW, Alber MS, Chen DZ. An Automated Approach for Fibrin Network Segmentation and Structure Identification in 3D Confocal Microscopy Images; Computer-Based Medical Systems (CBMS), 2014 IEEE 27th International Symposium on; May, 2014. p. 173178. IEEE. [Google Scholar]
- 37.Lee TC, Kashyap RL, Chu CN. Building skeleton models via 3-D medial surface axis thinning algorithms. CVGIP: Graphical Models and Image Processing. 1994;56(6):462–478. [Google Scholar]
- 38.Choong LT, Mannarino MM, Basu S, Rutledge GC. Compressibility of electrospun fiber mats. Journal of Materials Science. 2013;48(22):7827–7836. [Google Scholar]
- 39.Bouaziz O, Masse JP, Allain S, Orgas L, Latil P. Compression of crumpled aluminum thin foils and comparison with other cellular materials. Materials Science and Engineering: A. 2013;570:1–7. [Google Scholar]
- 40.Masse JP, Poquillon D. Mechanical behavior of entangled materials with or without cross-linked fibers. Scripta Materialia. 2013;68(1):39–43. [Google Scholar]
- 41.Collet JP, Shuman H, Ledger RE, Lee S, Weisel JW. The elasticity of an individual fibrin fiber in a clot. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(26):9133–9137. doi: 10.1073/pnas.0504120102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Yang Y, Bai M, Klug WS, Levine AJ, Valentine MT. Microrheology of highly crosslinked microtubule networks is dominated by force-induced crosslinker unbinding. Soft matter. 2013;9(2):383–393. doi: 10.1039/C2SM26934A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Howard J. Mechanics of motor proteins and the cytoskeleton. Sinauer Associates, Inc.; 2001. [Google Scholar]
- 44.Fung YC. Foundations of solid mechanics. Upper Saddle River; New Jersey, USA: 1965. [Google Scholar]
- 45.Kim OV, Xu Z, Rosen ED, Alber MS. Fibrin networks regulate protein transport during thrombus development. PLoS computational biology. 2013;9(6):e1003095. doi: 10.1371/journal.pcbi.1003095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lin SY, Wei YS, Hsieh TF, Li MJ. Pressure dependence of human fibrinogen correlated to the conformational α-helix to β-sheet transition: An Fourier transform infrared study microspectroscopic study. Biopolymers. 2004;75(5):393–402. doi: 10.1002/bip.20012. [DOI] [PubMed] [Google Scholar]
- 47.Ahmed TA, Dare EV, Hincke M. Fibrin: a versatile scaffold for tissue engineering applications. Tissue Engineering Part B: Reviews. 2008;14(2):199–215. doi: 10.1089/ten.teb.2007.0435. [DOI] [PubMed] [Google Scholar]