Direct neural current imaging in an intact cerebellum with magnetic resonance imaging

Abstract

The ability to detect neuronal currents with high spatiotemporal resolution using magnetic resonance imaging (MRI) is important for studying human brain function in both health and disease. While significant progress has been made, we still lack evidence showing that it is possible to measure an MR signal time-locked to neuronal currents with a temporal waveform matching concurrently recorded local field potentials (LFPs). Also lacking is evidence that such MR data can be used to image current distribution in active tissue. Since these two results are lacking even in vitro, we obtained these data in an intact isolated whole cerebellum of turtle during slow neuronal activity mediated by metabotropic glutamate receptors using a gradient-echo EPI sequence (TR = 100 ms) at 4.7 T. Our results show that it is possible (1) to reliably detect an MR phase shift time course matching that of the concurrently measured LFP evoked by stimulation of a cerebellar peduncle, (2) to detect the signal in single voxels of 0.1 mm³, (3) to determine the spatial phase map matching the magnetic field distribution predicted by the LFP map, (4) to estimate the distribution of neuronal current in the active tissue from a group-average phase map, and (5) to provide a quantitatively accurate theoretical account of the measured phase shifts. The peak values of the detected MR phase shifts were 0.27–0.37°, corresponding to local magnetic field changes of 0.67–0.93 nT (for TE = 26 ms). Our work provides an empirical basis for future extensions to in vivo imaging of neuronal currents.

Introduction

Functional study of the human brain has become possible with advances in non-invasive neuroimaging methods. The most widely used technique is blood oxygenation level-dependent functional MRI (BOLD-fMRI) (Ogawa et al., 1990; Kwong et al., 1992). Although BOLD-fMRI is a powerful tool for human brain activity mapping, it does not measure neuronal signals directly. Rather, it images slow local hemodynamic changes correlated with neuronal activity through a complex neurovascular coupling (Logothetis, 2003). At present, only electroencephalography (EEG) and magnetoencephalography (MEG) detect signals directly related to neuronal currents with a millisecond resolution. However, they estimate neuronal current sources from electrical potentials on the scalp or from magnetic fields outside the head, respectively. Measurement of these signals outside the brain leads to relatively poor spatial resolution due to ambiguity in inverse source estimation (Hämäläinen et al., 1993).

Our understanding of human brain function would significantly accelerate if it were possible to noninvasively detect neuronal currents inside the brain with superior spatiotemporal resolution. This possibility has led researchers to look for a method to detect neuronal currents with MRI. Many MRI approaches have been explored in the literature (Joy et al., 1989; Kraus et al., 2008; Witzel et al., 2008; Buračas et al., 2008; Höfner et al., 2011; Cassara and Maraviglia, 2008; Darquié et al., 2001; Le Bihan et al., 2006; Balasubramanian et al., 2014; Song and Takahashi, 2001). Of these, the mechanism most commonly used is based on local changes in MR phase caused by neuronal magnetic fields. Electrical currents in active neurons produce magnetic fields (ΔB) locally within the tissue. The component of this field (ΔB_z) along the main field (B_o) of the MR scanner alters the precession frequency of local water protons. This leads to a phase shift ΔΦ of the MR signal. For a gradient-echo (GE) sequence,

$$\mathrm{\Delta }\mathrm{\Phi }=\mathrm{\gamma }\mathrm{\Delta }{\mathrm{B}}_{\mathrm{z}}\text{TE}$$ (1)

where γ is the gyromagnetic ratio for hydrogen (2π × 42.58 MHz/T for protons) and TE is the echo time. According to Biot-Savart’s law, ΔB_z(t) is proportional to the current density J(t) produced by a population of neurons in the local region of the tissue (Murakami et al., 2003; Blagoev et al., 2007). Thus, measurements of the phase shift ΔΦ can be used to directly estimate neuronal currents in the brain.

Many attempts have been made to detect neuronal currents in human subjects in vivo, but the results so far are inconclusive (Bandettini et al., 2005; Hagberg et al., 2006). The literature contains several reports of positive results (Kamei et al., 1999; Xiong et al., 2003; Bianciardi et al., 2004; Liston et al., 2004; Konn et al., 2004; Petridou et al., 2006; Truong and Song, 2006; Chow et al., 2006a; Chow et al., 2006b; Chow et al., 2007; Chow et al., 2008; Xue et al., 2009) which conflict with reports of negative results (Chu et al., 2004; Parkes et al., 2007; Mandelkow et al., 2007; Tang et al., 2008; Luo et al., 2009; Rodionov et al., 2010; Luo, Jiang & Gao 2011; Huang, 2014).

This difficulty is presumably due to confounding factors such as blood flow, respiration and motion (Hagberg et al., 2012; Hagberg et al., 2008; Bandettini et al., 2005). Theoretical models, phantoms and cell culture studies indicate that it should be possible to detect neuronal currents with MRI in the absence of physiological noise sources (theoretical models: (Hatada et al., 2003; Hatada et al., 2005; Park and Lee, 2007; Blagoev et al., 2007; Cassara et al., 2008; Heller et al., 2009; Huang et al., 2010; Luo and Gao, 2010; Luo, Jiang, Chen, et al. 2011); current phantoms: (Joy et al., 1989; Scott et al., 1992; Bodurka et al., 1999; Bodurka and Bandettini, 2002; Pell et al., 2006; Blagoev et al., 2007; Truong et al., 2008; Witzel et al., 2008; Balasubramanian et al., 2014); cell cultures: (Petridou et al., 2006)).

Although these studies indicate that MRI technology should have enough sensitivity to detect neural currents, two types of key evidence are still lacking for demonstrating how MRI can be useful for neural current imaging: (1) there are no data showing that the phase shift is time-locked to some measure of population activity and that the phase shift time course matches that of a concurrently recorded local field potential (LFP), and (2) there is still no report showing how the phase shift data can be used to estimate the neuronal current distribution in the brain tissue, even though this should be the goal for neural current imaging.

Our work demonstrates that it is possible to measure an MR phase shift time course matching that of the simultaneously recorded evoked LFP in an isolated, intact whole cerebellum of turtle, free of physiological noise sources. We show how these MR phase maps can be used to estimate the neuronal current distribution in the active region in the tissue. We show that this estimated current distribution matches the distribution predicted based on spatial LFP maps. We discuss how these results can provide an empirical anchor for future development of techniques for in vivo neural current imaging.

Materials and methods

Choice of the preparation

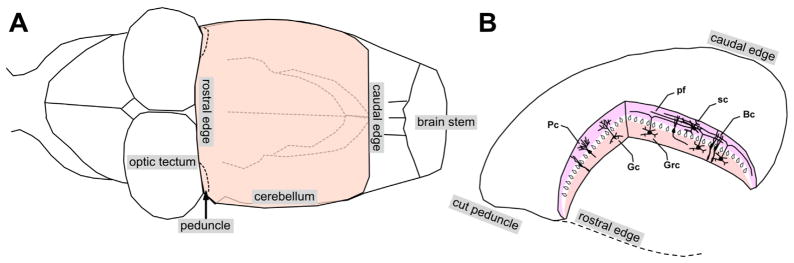
We used an isolated, intact whole cerebellum of turtle submerged in physiological saline. Fig. 1A shows the caudal region of the turtle brain based on a photograph of our preparation. The cerebellum is attached to the brain stem by a pair of cerebellar peduncles located behind the large optic tectum. The cerebellum is a lissencephalic cup-like structure in vivo that can be nearly flattened into an oblate spheroid in vitro. Fig. 1B schematically shows the cerebellum detached from the brain at the level of cerebellar peduncles. Even though it is not foliated as in mammals, its basic local cellular organization is same as in mammals (Ito, 2011). The turtle cerebellum is a 3-layer structure with a thickness of ~1 mm and a width of 4–5 mm both rostro-caudally and medio-laterally. It consists of the molecular layer in the dorsal half, where dendrites of the Purkinje cells are located, the granular layer in the ventral half, where granule cells are located, and the Purkinje cell layer in the middle (Fig. 1B). Peduncular stimulation activates the climbing and mossy fibers. The climbing fibers make focal synaptic contacts onto the dendritic shafts of the Purkinje cells on the ipsilateral side. The mossy fibers make synaptic contacts onto the granule cells. The axons of the granule cells project onto the superficial region of the molecular layer and bifurcate to produce parallel fibers, which run medio-laterally in the two hemispheres. The parallel fibers make excitatory synaptic contacts with the Purkinje cells along the beam of the parallel fibers.

Fig. 1.

Turtle cerebellum. (A) Schematic illustration of the caudal portion of a turtle brain with an intact cerebellum. (B) Cerebellum detached from the rest of the brain at the level of the cerebellar peduncles. Climbing fibers in the peduncle project to the Purkinje cells (Pc). Mossy fibers in the peduncle project to the granule cells (Grc). Grc axons ascend dorsally and bifurcate to form parallel fibers (pf), which make synaptic contacts with the Pc. Bergman cells (BC), stellate cells (sc), Golgi cells (Gc). Dorsal side up.

This preparation is ideal for this study for several reasons. (1) The entire cerebellum in vitro can be kept physiologically functional for extended periods since it can withstand hypoxia (Lutz and Milton, 2004). (2) Unlike brain slice preparations, the normal cellular circuit is completely intact. (3) MRI signals can be measured without any contamination from blood flow, respiration, and motion. (4) The flat geometry of the cerebellum facilitates detection of the spatial pattern of the local magnetic field and phase shift produced by an active neuronal tissue.

Tissue preparation

The surgical procedure involved in the preparation of the turtle cerebellum was approved by our institution’s Subcommittee on Research Animal Care. The brain of the red-eared turtle (Pseudemys scripta elegans) was removed rapidly after decapitation and craniotomy and placed in cold artificial cerebrospinal fluid (aCSF) (100 mM NaCl, 5 mM KCl, 40 mM NaHCO₃, 2.5 mM CaCl₂, 1.25 mM MgCl₂, 20 mM D-glucose). The whole cerebellum including the peduncles was dissected away from the brainstem and the optic tectum under a microscope.

Recording chamber and cerebellar placement

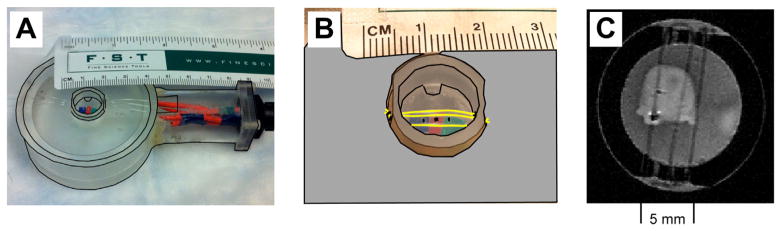
The cerebellum was placed in an acrylic chamber (Fig. 2A) filled with aCSF modified with addition of 1 mM picrotoxin (PTX) and 10 mM tetraethylammonium (TEA). PTX blocks fast inhibition while TEA blocks repolarizing calcium- and voltage-dependent potassium currents. The cerebellum was held in place by three nylon filaments (Fig. 2B, yellow) fixed to an acrylic insert. The stimulating, recording and ground electrodes entered the chamber from below. The stimulating electrodes (254 μm bare diameter) were twisted pair Teflon-coated silver wires (A-M Systems) with their exposed tips located approximately halfway in the tissue. One recording electrode (127 μm bare diameter) was placed in the tissue approximately 200 μm from the ventral surface while the other recording electrode was in the aCSF and served as the signal reference for differential recording. Fig. 2C shows an inversion-recovery T2-weighted structural MR image of the cerebellum held by three nylon monofilaments in the chamber with a bipolar electrode next to the cut peduncle and a recording electrode in the middle of the cerebellum on the ipsilateral side next to a monofilament.

Fig. 2.

Experimental chamber and preparation. (A) The acrylic chamber used for electrophysiology measurements outside the MR scanner and for the MRI-LFP measurements in the MR scanner. (B) Close-up of the chamber. Stimulating and recording electrodes enter the chamber from below. The cerebellum is placed flat on the acrylic platform and is held in place by an inner ring with 3 nylon monofilaments placed from above. (C) Inversion recovery T2-weighted structural image of the cerebellum in the chamber.

Electrophysiology outside the MRI

The cerebellum was placed on the plastic platform with the ventral surface up for ease of penetrating the tissue with an extracellular sharp-tip glass micropipette (filled with 1 M NaCl, 2–5 μm tip), since there is no pial membrane unlike the dorsal surface. The LFP was elicited with a single 100 μs current pulse (5 mA) with an inter-stimulus interval (ISI) of 20 s, using a pulse generator (Accupulser A310, World Precision Instruments) and a constant current stimulus isolator (A365, World Precision Instruments). The recording electrode was connected to one channel of a 32-channel MR-compatible EEG amplifier (BrainAmp MR Plus, BrainProducts) with an input impedance of 10 GΩ modified to function as a single-channel MR-compatible differential amplifier. This amplifier was used both inside and outside the MRI scanner. All the measurements outside the MRI were performed inside an electromagnetically shielded room.

Laminar extracellular potential profile

Previous work by Larson-Prior et al. (Larson-Prior and Slater, 1989; Larson-Prior et al., 1990) has shown that the LFP elicited with the long ISI of 20 s contains a fast, short-latency (within 100 ms) LFP mediated by ionotropic receptors followed by a slow response which reaches its maximum around 0.5–2 s after stimulation and returns to the baseline level in 2–10 s. This slow LFP is mediated by metabotropic glutamate receptors (mGluRs). The slow LFP disappears with shorter ISIs. In this work, we focused on this slow LFP, which we simply refer to here as LFP. In order to determine the generator of this LFP, we determined its laminar potential profile in 5 cerebelli. In each case, we recorded the LFP in the tissue with an extracellular sharp-tip glass micropipette at 100-μm depth increments along a single track ipsilateral to stimulation near the location on the cerebellum where the LFP was maximum.

Spatial map of the LFP

The spatial distribution of the LFP across the cerebellum was determined in 5 animals. The positive LFP was maximum at 200 μm below the ventral surface in the granular layer (see Results). Thus, the spatial distribution of the LFP over the entire cerebellum was determined at this depth by recording the response at multiple locations on a grid with 0.5 × 1 mm spacing. At each position, we recorded at least 5 responses. These responses were averaged to determine the representative response at each position.

Neural and receptor origins of the LFP

The neural origin of the LFP was demonstrated with kynurenic acid (KYNA, 2 mM), a non-specific blocker of excitatory amino acid (EAA) receptors, in 5 animals. We recorded the LFP in the tissue 200 μm from the ventral surface in (i) the response medium (modified aCSF with 1 mM PTX, 10 mM TEA), (ii) 30 min after application of 2 mM KYNA, and (iii) 30 min after the washout of the blocker to demonstrate the recovery of the LFP. Care was taken not to move the glass electrode and the chamber between medium changes to record the potential at the same location for the response, block, and the wash conditions.

The receptor origin of this slow LFP was demonstrated using mGluR blockers in 5 animals. We recorded the LFP in the tissue 200 μm from the ventral surface in (i) the response medium (the modified aCSF with 1 mM PTX, 10 mM TEA), (ii) 30 min after application of a non-specific mGluR blocker (LY341495, 100 μM) or a specific mGluR1 blocker (LY367385, 50 μM), and (iii) 30 min after the washout of the blocker.

Ionic current phantom study

Prior to imaging the cerebellum, an ionic current phantom was imaged in the same 4.7 T MRI scanner used for imaging the cerebellum (similar imaging setup to Fig. 4) to determine the polarity of the phase for each direction of the current in the phantom and the noise in phase measurements. The current phantom chamber was identical in dimension to the chamber used to image the cerebellum (Fig. 2). Fig. 3 shows the artificial current source in which a 100 μA square wave (1 Hz) ionic current was passed through a U-shaped capillary tube. The entire chamber and the capillary tube were filled with 0.9% saline containing 5 mM CuSO₄. A 1.5 cm-diameter transmit/receive surface coil (shown in Fig. 4) was placed on top of the chamber. GE EPI images were acquired with TR = 100 ms, TE = 26 ms, in-plane voxel size = 0.33 × 0.33 mm, 1 mm slice thickness, flip angle 25°. These imaging parameters are the same as those used in the cerebellar study (see the section “Simultaneous LFP and MRI measurements”). We computed the correlation of the current profile with the MR phase time course. The direction of current in the tube was reversed to verify that the imaging protocol was sensitive to the current direction, noting the direction of current with respect to B_o in each case. The phase was measured 10 times in the same imaging slice to estimate the temporal standard deviation of the phase measurements.

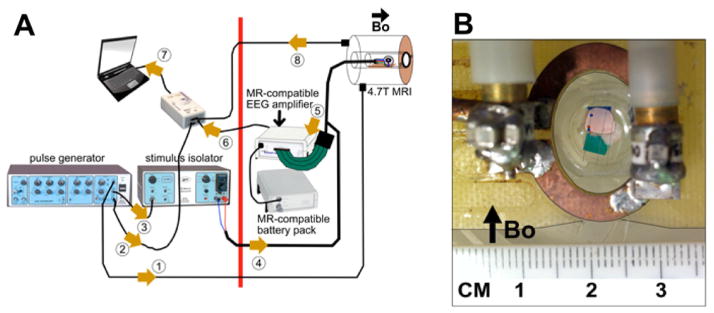
Fig. 4.

(A) MRI-LFP recording apparatus: The magnetic field of the scanner is active to the right of the thick red line. All non-MR-compatible hardware is placed to the left of the red line. The cerebellum is placed in the cradle/tray and is positioned at the scanner isocenter. A surface coil is placed on top of the chamber. The chamber tray has a faceplate that is bolted to the scanner bore using nylon screws. This keeps the chamber level and parallel to the floor. The numbered arrows show the signal flow in this setup: 1 = SYNC pulse, 2 = stimulus timing marker, 3 = trigger pulse to isolator, 4 = current stimulus (delivered to the stimulating electrodes in Cb), 5 = analog LFP signals (from recording electrodes in tissue to amplifier), 6 = digitized LFP signals (fiberoptic cable from amplifier to usb/laptop), 7 = usb input to laptop, 8 = “per-scan” MRI trigger markers. (B) Closeup of tissue submerged in aCSF placed in the chamber. Surface coil is placed on top of the chamber.

Fig. 3.

Ionic current phantom used to estimate temporal standard deviation in the phase data. Cyan-colored areas are filled with 0.9% saline containing 5 mM CuSO₄. The 100 μ_A current was restricted to the glass capillary tube. Dimensions of chamber are same as in the cerebellum study.

Simultaneous LFP and MRI measurements

After completing the measurements in the ionic current phantom, the MR signals were measured simultaneously with the LFP in a 4.7 T Bruker scanner with a 33 cm horizontal bore (Bruker Biospin, Billerica, MA) (Fig. 4A). The chamber was placed so that the tissue was at the isocenter. The cerebellum was placed with the ventral surface down (instead of up as in the outside-MRI electrophysiology studies) in order to place the recording electrode in the granular layer without having to penetrate the pial membrane, which can distort the recording position. A 1.5 cm transmit-receive surface coil tuned and matched to the resonance frequency (200 MHz) was placed flat directly on the top circular rim of the acrylic chamber, approximately 3 mm from the cerebellum (Fig. 4B). The tray carrying the chamber was anchored to the faceplate of the scanner so that the cerebellar surface was horizontal and parallel to the floor. The RF power was automatically calibrated and B_o was shimmed. We used a Fast Low Angle Shot (FLASH) sequence (TR 100 ms, TE 6 ms, flip angle 30°) to acquire orthogonal (3-plane localizer) images of the cerebellum. To locate the exact position of the tissue and the plastic platform, we acquired a cross-sectional image of the cerebellum and the chamber using an inversion-recovery (IR) T2-weighted rapid acquisition relaxation enhancement (RARE) sequence with TR 10,000 ms, TE 12 ms, TI 2000 ms, 256 × 256 matrix, 3.2 × 3.2 cm fov. We measured T1 using an IR-True-FISP (inversion recovery–true-fast imaging using steady state precession) sequence with a TR 4.4 ms, TE 2.2 ms, scan repetition time 18 s, 4 averages, 60 frames, 128 × 128 matrix, and T2* using a multiple gradient echo (MGE) sequence with TR 1.5 s, 12 echoes with TE = 4.5–81.5 s with inter-echo time of 7 ms and 256 × 256 matrix. With a 1 mm-thick imaging slice prescribed to contain as much of the cerebellum as possible, we imaged the tissue with a GE-EPI sequence (TR 100 ms, TE 26 ms, flip angle 25°, 96 × 96 matrix, 3.2 cm fov, 1 mm slice, 1024 time points/ scan, 40 scans).

The peduncular stimulation was done exactly as outside the scanner. The evoked response was elicited every 20 s with a single pulse applied near the cut end of a peduncle. The MR phase data were reconstructed using the on-site reconstruction program provided by Bruker. The first 10 s of each scan were discarded in order to reach steady state. For the data corresponding to each stimulus, we computed phase difference images by subtracting from each phase image a reference phase image corresponding to the 2-s pre-stimulus period. We filtered the ΔΦ time course with a 0.15 Hz high-pass filter to remove slow drifts in the time courses. The magnitude time courses were filtered with a 0.175 Hz high-pass filter as the magnitude time courses demonstrated more drift than the phase.

The LFPs were sampled at 5000 Hz during scanning. We recorded LFPs at a single location in the tissue ipsilateral to the stimulation site continuously during MR scanning. We recorded time markers corresponding to the slice acquisition times (from the MR scanner) and to the stimulus times (from the pulse generator). Both the slice time markers and the stimulus time markers were fed into the auxiliary input of the MR-compatible amplifier and were handled using in-house hardware and software.

For each condition (response, block, wash), we stimulated the tissue 5 times/scan with an inter-stimulus time of 20 s. Since there were 40 scans/ condition, this implied that we stimulated the tissue 200 times in each condition. Since we discarded the first 10 s of each of the 40 scans, we had 4 usable stimuli/scan, giving us 160 responses for analysis in each of the response, block, and wash conditions. The gradient artifacts in the LFP recording were removed using a template-based artifact removal method implemented in the BrainProducts Analyzer software (Allen et al., 2000).

In n = 7 animals, we acquired concurrent LFP recordings and GE EPI in the “RESPONSE” condition with modified aCSF (1 mM PTX, 10 mM TEA added). In n = 5/7 animals, we repeated the measurements in two additional conditions: the “BLOCK” condition with 2 mM kynurenic acid added and the “WASH” condition with the kynurenate removed. We used kynurenic acid to block the response for the MRI experiments as it remains potent in stock solution form for longer periods of time than the mGluR blocker (LY341495). Kynurenate as well as other antagonists of excitatory amino acid receptors are known to block the mGluR-mediated evoked response of the Purkinje cells (Larson-Prior and Slater, 1989; Larson-Prior et al., 1995; Yuan et al., 2007). The solution was exchanged outside the scanner without disturbing the preparation. We waited 30 min between solution changes before imaging.

Prediction of the local magnetic field and MR phase shift

Prior to the MR measurements, the strength and spatial distribution of the local magnetic field ΔB and corresponding ΔΦ expected for this preparation were computed for a distribution of currents determined from the spatial map of LFP. The chamber containing saline (Fig. 2) was modeled as a volume conductor (conductivity 1.33 S/m) using the boundary element method (BEM) (Hämäläinen et al., 1993) as implemented in the BEM MATLAB Toolbox of Stenroos et al. (2007). The flat cerebellum lying on the acrylic platform was modeled using the BEM based on the structural image (Fig. 2C); the platform itself was not modeled. We created triangular mesh surface representations of the tissue (~5200 vertices) and the aCSF medium (~4700 vertices). The conductivity of the cerebellum was 0.2 S/m (Okada et al., 1994). The generator of the ΔB was modeled by an ensemble of current dipoles oriented perpendicular to the cerebellar surface directed from the dorsal to the ventral side in a focal region corresponding to the 250 μV isocontour in the map in Fig. 6B. Current dipoles were placed in the middle layer displaced by 0.125 μm toward the dorsal surface. The current dipole moment (Q) was set to have a maximum value of 1 nA.m/mm² consistent with the values of 1–2 nA.m/mm² found empirically in this preparation (Okada et al., 1989). The ΔB was computed in the MR imaging slice with a 0.125 × 0.125 mm grid, by solving the forward problem using the method described in (Stenroos et al., 2007). The computation was carried out in six planes within the imaging slice (±0.125 mm, ±0.250 mm, and ±0.375 mm) and these values were averaged to compute the value of ΔB at each grid voxel on the x–z plane. The details of the BEM method including the equations used are described in the Appendix. The ΔΦ was computed using Eq. (1): ΔΦ = γΔB_z TE, where γ is gyromagnetic ratio of hydrogen, TE (=26 ms) is the echo time used in our study and ΔB_z is the B_o-component of ΔB.

Fig. 6.

Electrophysiological characteristics of the slow local field potential (LFP). (A) LFP 200 μm below the ventral surface of the cerebellum (in the granular layer) elicited by peduncular stimulation in a modified aCSF with 1 mM picrotoxin and 10 mM tetraethyammonium. (B) Isopotential pattern of the LFP in (A) at the peak of the response. Tissue shown dorsal side up.

Data analysis of MRI-LFP studies

Temporal waveform of ΔΦ

The temporal waveform of ΔΦ was first calculated for each voxel by averaging the ΔΦ relative to the prestimulus baseline across 160 epochs. The phase changes in single voxels were analyzed in some experiments to assess the sensitivity of our measurements. This analysis showed that the phase shift can be observed in single voxels in some cases, but averaging across pixels was necessary for increasing the signal to noise ratio. Thus, voxel-wise ΔΦ time courses were averaged across a ROI over the cerebellum. Only voxels with mean |ΔΦ| > 6 SEM (standard error of mean) within a time window around the peak of the LFP were used for the average. To avoid cancellation, the polarity was reversed for those voxels in which the mean ΔΦ within the time window was negative.

Spatial maps of ΔΦ

For each animal, we reconstructed the spatial map of the ΔΦ in the imaging slice, which was parallel to the cerebellar surface (see Fig. 2C). In order to reduce the noise in the data, for each voxel, we averaged the measured values of ΔΦ within a time window around the peak of the LFP and across all 160 responses. The time window was defined to start at least 400 ms after the stimulus and typically ended ~1.2 s after the peak of the response. The duration of the time window depended on the time course of the LFP as shown in Results. Again, as in all the analysis of the phase data, ΔΦ at any given time in each voxel was computed relative to the reference phase during the 2-s pre-stimulus period. We smoothed the average phase change maps with a Gaussian filter (σ = 0.65, i.e., 1.5 mm full-width-half-maximum). The average ΔΦ maps during the LFP for the different animals were registered by aligning the coordinates of the stimulating electrodes, which were fixed in the imaging chamber. In order to verify that any spatial signal changes seen in the ΔΦ maps for the RESPONSE condition were truly due to neuronal current effects, we also constructed similar ΔΦ maps for the BLOCK condition. As we performed the BLOCK study in n = 5 animals, this comparison was done for those 5 animals. Identical time windows were used to construct the average ΔΦ in the RESPONSE and in the BLOCK case.

Estimation of neural current distribution from the MR phase data

After obtaining the spatial map of the phase shift, we used these data to estimate the current distribution in the active tissue. All computations were performed using in-house software in MATLAB (Mathworks, Natick, MA). For all BEM calculations, we used the BEM MATLAB Tool-box of Stenroos et al. (2007). As mentioned in the Introduction, the neural current density J can be estimated by first calculating the local magnetic field ΔB from the measured phase shift ΔΦ using the Eq. (1). The spatial phase map in the imaging slice leads to a spatial map of ΔB_z (B_o-component of ΔB) in the slice. Given the ΔB_z map, the estimation of J in the imaging slice is analogous to the inverse estimation problem in the field of MEG. In MEG, the magnetic field measured around the head (just above the scalp) is used to estimate the neural current J in the brain. In our case, the magnetic field determined inside the cerebellum is used to estimate the J in the cerebellum. Thus, neural current imaging based on MR phase data can be carried out using tools developed for MEG (Hämäläinen et al., 1993; Dale and Sereno, 1993).

The forward solution relating the measured local magnetic field to the current sources has a linear form and can be written as

$$\mathbf{x}(\mathrm{t})=\mathbf{Aj}(\mathrm{t})+\mathbf{n}(\mathrm{t})$$ (2)

Here, x is the vector of instantaneous magnetic field measurements along the z-direction aligned with the main field B_o of the scanner (obtained from ΔΦ (t) using Eq. (1)), j is a vector of dipole strengths, n is a vector specifying the noise at each voxel, and A is the linear forward matrix operator, also known as the gain matrix, which can be computed using the BEM with a triangular meshing of the cerebellar surface. The neural current j can be estimated by solving Eq. (2).

$$\widehat{\mathbf{j}}(\mathrm{t})=\mathbf{W}\mathbf{x}(t),$$ (3)

where the linear inverse operator W=RA^T(ARA^T+C)⁻¹. C=〈n(t)n(t)^T〉 is the spatial noise covariance matrix and R=〈j(t)j(t)^T〉 is the spatial source covariance matrix. For each animal, we restricted the current sources to be within the cerebellum by setting the diagonal elements of R corresponding to voxels lying outside the cerebellum to be zero. Except for these elements, R is an identity matrix. We also assumed that the source currents were perpendicular to the imaging plane, a reasonable assumption given the geometry of the cerebellum (Fig 1B). Since the a priori variance of the currents is unknown, we use a regularization parameter λ². This results in W=R A^T(ARA^T+ λ²C)⁻¹. Larger λ² results in more regular current estimates and smaller current amplitudes. The purpose of regularization is to prevent noise amplification in the solution. The optimal selection of λ² depends on the SNR. We used λ² ≈10⁶ since this was observed to produce stable solutions while fitting the data adequately within the limits of the experimental noise. The noise covariance matrix C was a diagonal matrix containing the variance of the noise at different voxels during a 2-s pre-stimulus period. The inverse operator W was applied to the measured data x to estimate activity time courses ĵ(t) for every location inside the cerebellum. We then averaged the current source density estimate over the time window containing the LFP response.

Statistical parametric map of estimated source distribution

The method described above provides an estimate ĵ averaged over a particular time window at every voxel in the imaging plane. By normalizing these estimates by the predicted estimator noise, we can obtain noise normalized statistical parametric maps (SPMs) (Dale et al., 2000). Using this approach, we computed z-score spatial maps for each of the 7 animals used in the analysis. We combined these z-score maps into a χ-squared statistic by taking the sum of z². From this χ-squared statistic, we obtained p-values for the current source distribution. The p-values were Bonferroni corrected to account for multiple comparisons.

Results

Electrophysiology outside the MRI

Laminar extracellular potential profile

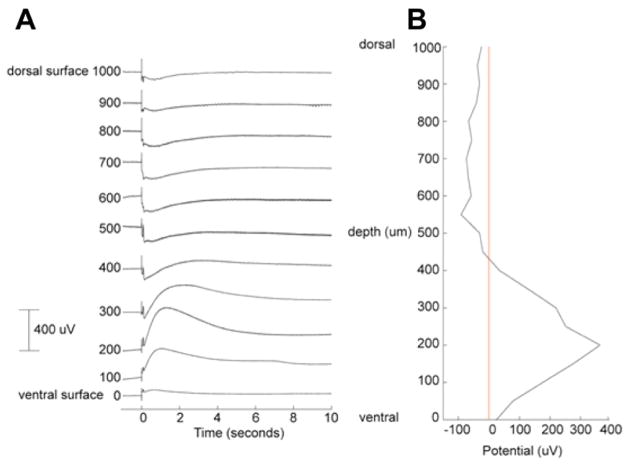
The LFP contained a fast component within 100 ms of stimulation, followed by a slow response. Fig. 5A shows the laminar profile of the LFP from the dorsal surface to the ventral surface of the cerebellum. The fast LFP has a sharp negative spike in the molecular layer and the corresponding positive component in the granular layer with the polarity reversal just above the Purkinje cell layer as in previous studies (Okada et al., 1989). The slow LFP was negative in the molecular and Purkinje cell layers and positive in the granular layer with the peak around 200 μm from the ventral surface. The peak latency of the positive component is at around 1 s post-stimulus. The slow LFP lasted a few seconds, returning to the baseline in about 5 s in this example.

Fig. 5.

Laminar extracellular potential profile along the depth of the cerebellum at a single location ipsilateral to the stimulation. (A) Measured LFPs at 100 μm increments. (B) Depth profile at the peak of the LFP. The profile suggests an extracellular current source in the granular layer and an extracellular current sink in the molecular layer and in the Purkinje cell layer. Measurement made using a glass micropipette outside the MRI in a magnetically shielded room.

Fig. 5B shows the depth profile at the time of positive peak at 200 μm. This profile differs from those measured earlier for the fast response (Okada et al., 1989). The profile of this slow LFP indicates that the extracellular current sink was in the molecular layer and the current source was in the granular layer with polarity reversal around the Purkinje cell layer. The intracellular current responsible for this laminar profile is directed from the dorsal to ventral surface.

Spatial map of the LFP

Fig. 6A shows the spatial distribution of the slow LFP. The maximum response at depth of 200 μm from the ventral surface was located on the side ipsilateral to the stimulation site. The isopotential map at this depth (Fig. 6B) is focal. The isopotential maps in the molecular layer (not shown) extended across the cerebellum from the ipsilateral to the contralateral side. The peduncular stimulation activates both the climbing and mossy fibers. This difference in the spatial distributions may reflect the difference in the projection of the climbing and mossy fibers. The climbing fibers are well known to make focal contacts on the ipsilateral Purkinje cells, whereas the mossy fibers activate Purkinje cells connected to the parallel fibers, which run laterally. In interpreting the MRI results, we considered the generators of the focal LFP with the maximum in the granular layer since the positive potential was several times stronger than the negative potential in the molecular layer (Fig. 5B).

Neural and receptor origins of the LFP

In all cases, we found that the fast and slow LFPs were blocked by 2 mM KYNA and they partially recovered after the washout indicating that both types of response were neural in origin and synaptically mediated (Fig. 11B). The slow LFP was mediated by mGluRs. Fig. 7 (red trace) shows the temporal waveform of the LFP in the response medium in the granular layer at a depth of 200 μm from the ventral surface. The LFP in the response medium (red trace) was abolished (green trace) by a non-specific mGluR antagonist (LY341495, 100 μM) in the bath. This response was recovered (blue trace) after washing out the blocker, showing that the response reduction was not due to some recording problems. The specific mGluR1 blocker (LY367385, 50 μM) also blocked the LFP.

Fig. 11.

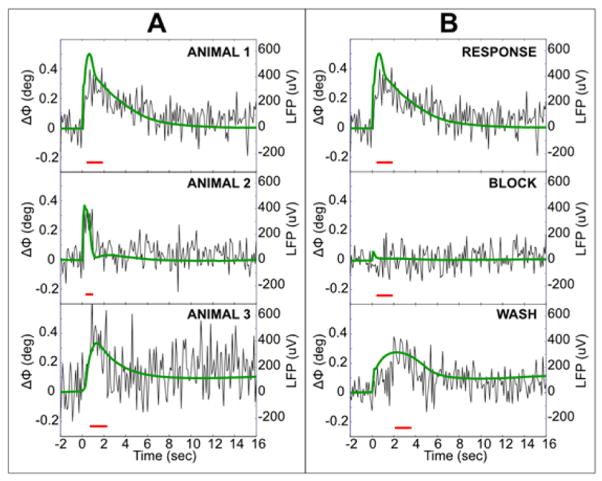
(A) Time course of the ΔΦ superimposed on simultaneously measured LFP (green). Examples from 3 animals in response medium. Correlation of LFP with ΔΦ for (i–iii) are 0.64, 0.46, 0.36, averaged over 160 trials and over 37, 49, 17 voxels with | ΔΦ | > 6*SEM in the red time window, respectively. (B) Neural origin of the signals. Both ΔΦ and LFP are abolished by 2 mM kynurenate added to modified aCSF, but recover after the washout. RESPONSE and BLOCK data were processed identically (same time window, sign correction, and 37 voxels in average). Correlation of ΔΦ with the RESPONSE LFP was 0.64 (p = 10⁻²³) and WASH LFP was 0.53 (p = 1.8 × 10⁻¹⁵). Correlation of the BLOCK-ΔΦ with the RESPONSE LFP was −0.04 (p = 0.5).

Fig. 7.

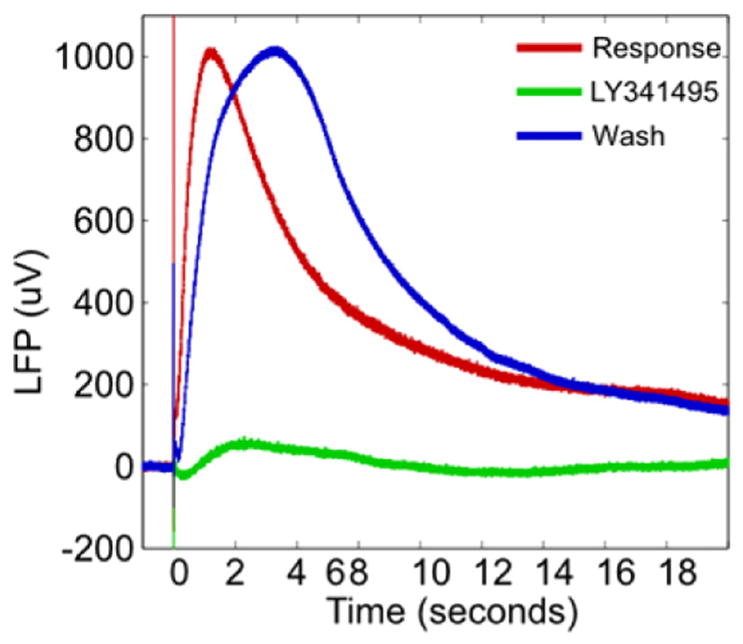
Neuronal and metabotropic origin of LFP. The LFP response recorded 200 μm from the ventral surface (red) is blocked (green) by a metabotropic glutamate receptor antagonist (LY341495, 100 μM) antagonist and is recovered with washout (blue). Measurement made using a glass micropipette outside the MRI in a magnetically shielded room.

Ionic current phantom

Fig. 8 shows an example of the spatial distribution of the ΔΦ obtained in the phantom study. The ionic current was directed into the plane of the page, orthogonal to the main field B_o, at the center of the phase map. As expected, the phase map was bipolar with the positive phase change on the left and the negative phase change on the right of the current phantom since the magnetic field produced by this phantom is clockwise and thus the field is parallel to the main field B_o of the magnet on the left and antiparallel on the right.

Fig. 8.

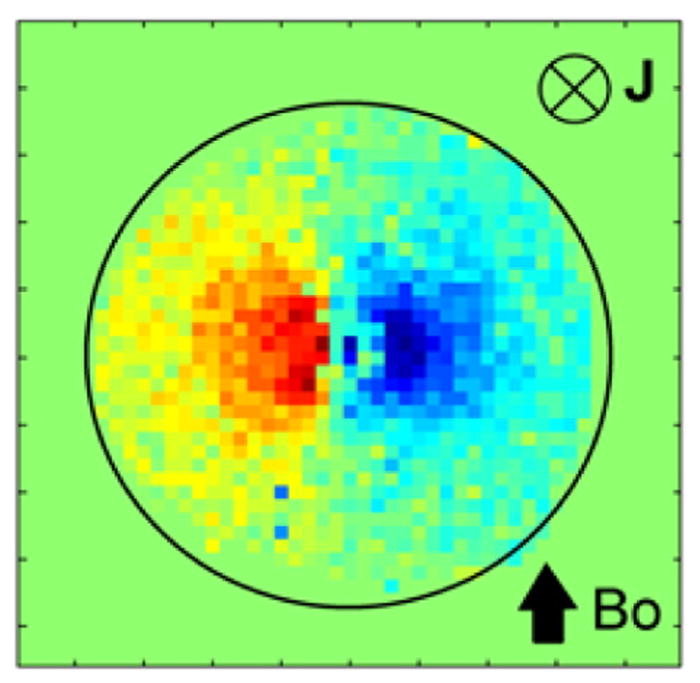
Correlation of MR phase with current in the ionic current phantom with current pointed into the plane of the page. B_o orientation same as in the animal study.

The temporal standard deviation of the phase time courses was 3.9° in this phantom study. This was used to calculate the number of LFPs required for averaging in order to detect the neural current signal with our MRI setup. As described below, the peak of the local magnetic field ΔB was 0.49 nT in our simulation study, corresponding to ΔΦ = 0.20°. Based on this, we determined that 1521 responses would need to be averaged to obtain a temporal SNR of 2:1.

Predicted local magnetic field and phase shift

After the initial electrophysiological studies outside the MR scanner, we computed the local magnetic field ΔB and phase shift ΔΦ in order to assess the feasibility of experimentally detecting the phase shift from this cerebellar preparation. Fig. 9 shows the source distribution used in the simulation study. This corresponds to the isopotential map shown in Fig. 6B, defined by the contour with the potential of 250 μV. The population current in this region was represented by an ensemble of current dipoles oriented ventrally with a maximum current dipole moment density of 1 nA.m/mm², based on our earlier work reviewed in (Murakami and Okada, 2015). The strengths of the current dipoles in the active area were distributed according to the isopotential map in Fig. 6B.

Fig. 9.

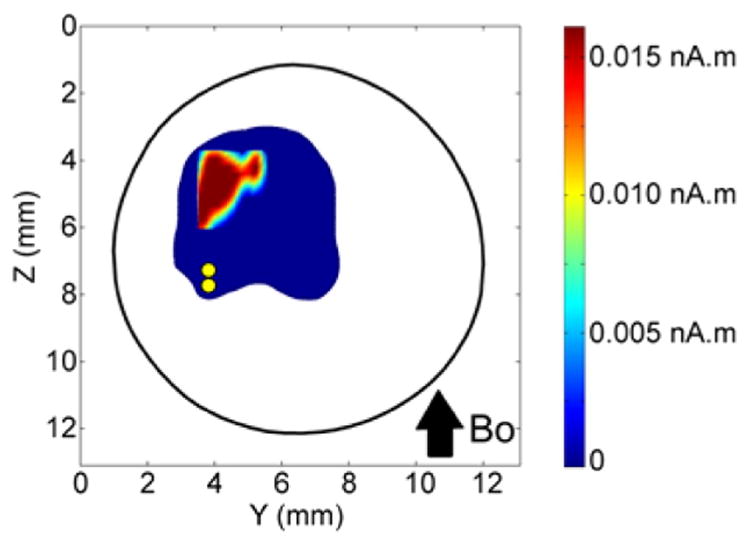
Distribution of current dipole moment (nA.m) based on the 250 μV isopotential contour in the map in Fig. 6B. Dipoles were located in the middle layer of the cerebellum in a 0.125 × 0.125 mm grid. At each grid location in the active area, a single current dipole was placed (pointing into plane of the image). The maximal current dipole moment was 0.0156 nA.m corresponding to a peak current dipole moment density of 1 nA.m/mm² assumed in this calculation. The pair of yellow dots shows location of the twisted pair of stimulating electrodes.

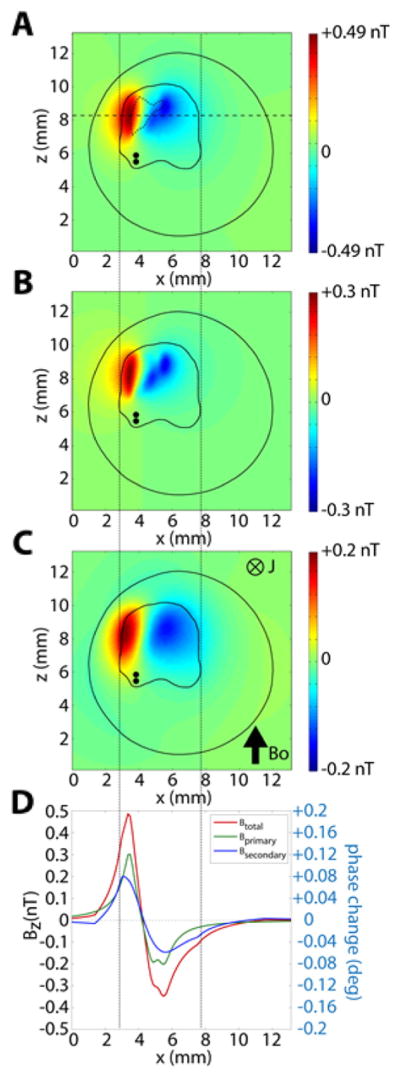
Fig. 10A shows the predicted values of ΔB in the imaging slice. As in the phantom study, the local field is bipolar. The model calculation for the cerebellum in the chamber showed that the ΔB in each voxel of the imaging slice is a vector sum of two types of ΔB: (1) ΔB_primary due to the current dipoles representing the intracellular currents in the Purkinje cells and (2) ΔB_secondary due to the secondary current sources at the cerebellum-saline boundary and at the saline-air boundary. The dipole moment of each secondary source is given by ΔσV, where Δσ is the difference in electrical conductivity across each boundary and V is the potential at the boundary (Huang et al., 1990). Figs. 10B and C show the ΔB_primary and ΔB_secondary, respectively. The distribution of ΔB_primary is focal compared to that of ΔB_secondary which is more diffuse due to the spread of the potential V at the conductivity boundaries away from the primary current sources. Fig. 10D shows that the peak value for the ΔB_primary is slightly larger than that of ΔB_secondary along the axis shown by a dashed line in Fig. 10A. Due to the slightly asymmetrical source geometry, there is an asymmetry between the positive and negative lobes of all three types of fields. The maximum ΔB was 0.49 nT and the minimum −0.39 nT. The peak values (max, min) of the primary field and the secondary fields were (0.3 nT, −0.25 nT) and (0.2 nT, −0.15 nT), respectively. The peak positive field was stronger than the peak negative field by 20% (primary), by 33.3% (secondary), and by 25.6% (total field). Fig. 10D also shows the profile of the predicted local magnetic fields (total, primary, secondary) and the corresponding predicted phase shift along the horizontal dotted line in Fig. 10A. We expect the peak phase change to co-localize with the peak magnetic field change. In this case, the +ΔB is located very close to the ipsilateral edge of the cerebellum due to the location of the peak LFP in Fig. 9. The −ΔB spreads to the contralateral side of the cerebellum.

Fig. 10.

z-component of the predicted local magnetic field ΔB, parallel to the axial B_{o fi}eld, for the distributed current dipole source in the model cerebellum. (A) Total ΔB_z (sum of primary and secondary magnetic fields). Active area is shown (dotted line). (B) Primary magnetic field ΔB_z,primary due to the dipoles. (C) Secondary field ΔB_z,secondary due to the boundary effect. (D) Magnitude of the ΔB_z, ΔB_z,primary, and ΔB_z,secondary along the line in A. In (A–C), the pair of black dots shows the location of the twisted pair of stimulating electrodes.

MRI data

Tissue relaxation times and structural image

We found T1 to be 2.1 s and T2* to be 25 ms. Our selected TE of 26 ms was close to T2*, giving us optimal SNR for the phase measurements. According to the phase change equation, ΔΦ is proportional to TE, thus the phase shift should be larger with larger values of TE. However, the SNR of the phase data decreased significantly when TE was increased to 36 ms due to T2* decay. There was very little anatomical contrast in the T1-weighted RARE images (Fig. 2C) because there is no variation in the cellular organization across the cerebellum. It has a uniform 3-layer structure throughout with the molecular layer on the dorsal side, the granular layer on the ventral side, and a thin layer of Purkinje cells midway.

Temporal waveform of ΔΦ

A single pulse of electrical stimulation was applied to the peduncle every 20 s (Fig. 11). This elicited a slow LFP mediated by mGluRs shown by a green trace in 3 animals in Fig. 11A. The time course of the concurrently recorded evoked phase shift ΔΦ is shown superimposed on the LFP. Each trace is average of phase shifts across 160 stimulus repetitions. For each stimulus, the ΔΦ time course was averaged across voxels located in the cerebellum for which | ΔΦ | > 6*SEM in the red time window. For animals 1–3, this meant averaging over 37, 49, and 17 voxels, respectively. Since we had 160 stimuli in each case, the average traces in Fig. 11A are based on 5920, 7840, and 2720 averages for these three animals, respectively. The phase waveform was highly correlated with the LFP waveform: r = 0.64, 0.46, and 0.36, respectively, for animals 1–3.

Fig. 11B shows that the phase shift as well as the LFP were neuronal in origin. These data were obtained for animal 1 in Fig. 11A in the response medium, followed by measurements after adding kynurenic acid (2 mM), and washing out the kynurenate. All data were processed identically (same time window, sign correction, and 37 voxels in average). Both the LFP and the MR phase shift responses were abolished by kynurenic acid but recovered after washout of the KYNA. Correlation of ΔΦ with the RESPONSE, BLOCK, and WASH LFPs were 0.64 (p < 10⁻²³), 0.04 (p > 0.5), and 0.53 (p < 10⁻¹⁵), respectively.

The peak values of ΔΦ during the LFP response in the RESPONSE were 0.27–0.37°. For TE of 26 ms, these ΔΦ values correspond to ΔB = 0.67–0.93 nT. These values are consistent with the BEM-predicted values of 0.2° and 0.49 nT (from Fig. 10A) based on the data from a single animal, assuming the maximum current dipole moment density q of 1 nA.m/mm². These predicted values suggest that the value of q was likely close to 1–2 nA.m/mm² across the preparations, consistent with previously reported current densities in this tissue (Murakami and Okada, 2015). Our values are also consistent with the values (0.2–3.9 nT) found in cell cultures (Petridou et al., 2006).

Sensitivity of ΔΦ measurements

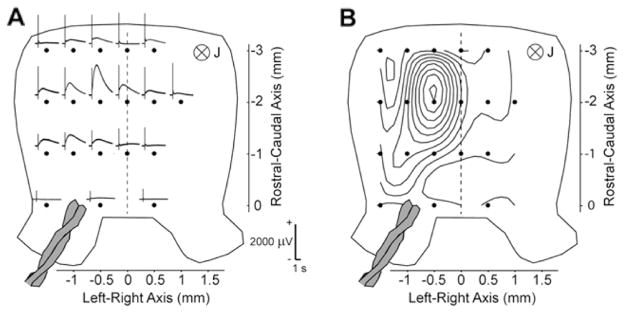
The sensitivity of our phase measurements was sufficiently high to detect the ΔΦ time course in single voxels. The top panels in Fig. 12 show the ΔΦ time courses from individual voxels in the red and blue patches, respectively, in one animal (averaged over 160 trials, but no further processing). The concurrently recorded LFP, shown by a green trace, is superimposed on the phase waveform. The lower panels show the ΔΦ’s from two single voxels (red and blue spots at right). The ΔΦwith opposite polarity can be clearly seen even in individual voxels.

Fig. 12.

Single-voxel detection of the ΔΦ. A(i) and B(i) show superimposed single-voxel ΔΦ time courses in all the voxels in the red and blue ROIs in C(i), respectively. Averaged across the 160 trials. Red and blue time courses in A(i) and in B(i)—average of all the single-voxel time courses in the red and blue regions in C(i). Concurrently recorded LFP shown in green. A(ii) and B(ii) show single-voxel ΔΦ time courses in the red and blue voxels labeled in C(ii). ROI in C(i) was selected from a single animal. In C(i–ii), the solid dots show location of the stimulating electrodes while the open dots show location of the recording electrodes.

Spatial maps of ΔΦ

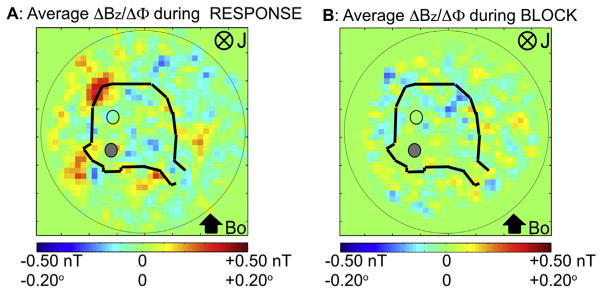
For n = 5 animals, we compared the average ΔΦ map during the RESPONSE and the BLOCK conditions (Fig. 13). The spatial signal changes in and near the tissue and the peduncles disappeared in the BLOCK condition. The standard deviation of ΔΦ in the tissue region in Fig. 13B was ~0.013°, which was ~1/20 of the peak values of the phase shift in RESPONSE.

Fig. 13.

Spatial map of ΔΦ during (A) the RESPONSE condition and during the same time window during (B) the BLOCK. Average phase change maps are over n = 5 animals. Phase changes seen in the RESPONSE are not visible in the BLOCK condition. In both A, B, the solid dots are the stimulating electrodes and the open dots are the recording electrodes, respectively.

Fig. 14A shows the ΔΦ/ΔBz map averaged across 7 animals during the peak period of evoked response across 160 stimulus repetitions. The map has a strong red region with a peak value of 0.15° in the caudal region of the cerebellum ipsilateral to the stimulation site on the peduncle. There is a broad blue region to the right of this peak area with a peak value of −0.10°. This bipolar pattern resembles the predicted spatial distribution of ΔΦ (Fig. 10A). The associated ΔB is directed clockwise, indicating that the underlying current was directed into the plane of the figure, which corresponds to an intracellular current directed from the dorsal to ventral surface of the cerebellum consistent with the measured laminar profile of LFP (Fig 5). There are unpredicted red and blue regions near the peduncles. We hypothesize that these phase changes are due to currents in the cut Purkinje axons near the peduncles. Consistent with this hypothesis, the phase shift disappeared around the peduncles in the BLOCK condition with kynurenic acid (Fig. 13B). The polarity of the ΔΦ was reversed when the cerebellum was turned upside down as expected.

Fig. 14.

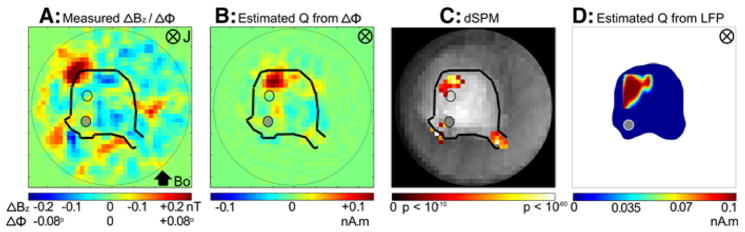
Spatial map of ΔΦ and current density matching the active tissue determined with LFPs. (A) Spatial map of ΔΦ during the peak of the LFP averaged across n = 7 animals. (B) Minimum norm estimate of current dipole moment Q (nA.m in each voxel) with a maximum of 1.013 nA.m/mm² (directed into the page ⊗), based on the ΔΦ map in A. (C) Statistical significance map of the density estimate in (B). Areas shown are (p < 10⁻⁵, log scale), after Bonferroni correction. (D) The density map of the active tissue determined with LFP. B_o is rostral to caudal. In (A–C), the solid dots are the stimulating electrodes (bottom) and the open dots are the recording electrodes (top), respectively. In (D), only the stimulating electrodes are shown (as a single solid dot).

Estimation of neural current distribution from MR phase data

Using the procedures described in the section “Estimation of neural current distribution from the MR phase data” under “Data analysis of MRI-LFP studies,” we estimated the active region giving rise to the phase map in Fig. 14A. Fig. 14B shows the current dipole moment (Q in nA.m) in each voxel (0.33 × 0.33 × 1.00 mm) in the imaging slice averaged across n = 7 animals. The map of Q for each animal was averaged across the animals by coregistering the maps using the location of the stimulating electrodes as the fiducial marker. This averaged estimate of current distribution shows a focal region in the caudal region ipsilateral to the peduncular stimulation site. Q is oriented downward, normal to cerebellar surface, in the entire active region. The peak estimated current dipole moment density was 1 nA.m/mm² (Q_peak of 0.1 nA.m in 0.33 × 0.33 mm² voxel). Fig. 14C shows the dynamic statistical parametric map (dSPM) with the areas significant at p < 10⁻⁵ after Bonferroni correction. The values of Q in the active tissue in the cerebellum are statistically significant. The active areas at the cut end of both peduncles are also significant, consistent with our hypothesis that the activity was produced by the cut axons of the Purkinje cells. The active region in the caudal area of the cerebellum is similar in spatial distribution to the active region estimated from LFP (Fig. 9), reproduced in Fig. 14D. If we assume the origin to be located at the stimulating electrode, the location of the peak response is at (0.33 mm, 3.3 mm) in Fig. 14B and at (0 mm, 2.8 mm) in Fig. 14D. The two peak locations are therefore only 0.6 mm apart.

The measured values of ΔΦ and the associated values of ΔB in the group-averaged data in Fig. 13A were close to, but slightly less than, the predicted values in Fig. 10. The average of the peak absolute phase change values (0.15°, −0.10°) is 0.12°, corresponding to a local magnetic field ΔB of 0.30 nT, as compared to the predicted values of 0.2° and 0.49 nT, respectively (Fig. 10). The predicted values of ΔΦ and ΔB in Fig. 10 have a closer fit to the individual animal data in Fig. 11A compared to the group-average data. This discrepancy is most likely due to the fact that the group-averaged spatial phase map tends to underestimate the maximum possible values, due to variability in spatial distribution and response strengths in some preparations.

Discussion

Main findings

We demonstrated that the ΔΦ can be detected reliably in individual cerebelli and that this phase shift is time-locked to the concurrently recorded LFP (Figs. 11A, 12). The temporal waveform of the ΔΦ matched that of the LFP. Both the MR signal and LFP were produced by neuronal currents mediated by mGluRs (Fig. 11B). The measured values of ΔΦ in the individual time traces (Fig. 11) corresponded to local magnetic fields of 0.67–0.93 nT for TE = 26 ms. According to our forward solutions (Fig. 10), these values correspond to a current dipole moment density q of 1–2 nA.m/mm², which agrees with the reported current density of 1–2 nA.m/mm² determined on the basis of MEG signals measured 2 cm above the cerebellum (Murakami and Okada, 2015).

We also show that the MR phase data can be used to estimate the active neuronal tissue (Fig. 13). This second step is important if MRI were to be used for imaging neuronal current distributions in the brain. We were able to use the minimum norm estimation technique developed in the field of MEG to estimate the current distribution in the cerebellum responsible for the measured phase shift (Hämäläinen and Ilmoniemi, 1984). The peak values of ΔΦ in the phase map averaged across 7 animals were 0.15° and −0.10°, corresponding to peak ΔB values of +0.37 nT and −0.25 nT, respectively (Fig. 13A). The empirically obtained group-average ΔΦ of 0.12° and ΔB of 0.30 nT (Fig. 13A) are close to the predicted values of 0.2° and 0.49 nT assuming q = 1 nA.m/mm² (Fig. 10A). The slightly smaller group-average ΔΦ and ΔB may be due to variability in the spatial phase map and responses across animals.

Alternative explanations of the main results

The pharmacological manipulation (Fig. 11B) demonstrates that the MR and LFP signals were mediated by neuronal currents. However, other potential sources of MR signal change must also be considered. MR phase is temperature sensitive as the proton resonant frequency decreases with temperature (−0.01 ppm/°C). At 4.7 T, this implies a frequency shift of 2 Hz/°C or a ΔΦ of 18.72°/°C change in temperature. Temperature changes around ~0.02 °C associated with neuronal firing could therefore produce phase variations of the order observed. However, temperature changes are unlikely to generate the observed dipolar pattern consisting of both positive and negative phase changes. Also, the ΔΦs were tightly coupled to the LFP. Our experimental setup may be sensitive to Lorentz forces since the stimulating and recording wires as well as the intracellular currents were perpendicular to B_o. However, this does not explain our data since the stimulating wires were a twisted pair cancelling opposing Lorentz forces and any vibration should cease after the brief 100-μs stimulus is terminated, especially because the wires were rigidly held by silicone glue in the plastic platform. The current in the recording electrode should have been minimal (<100 fA) since the preamplifier used for the recording had an input impedance of 10 GΩ. Based on prior work by Roth and Basser (Roth et al., 2014; Roth and Basser, 2009), we expect the displacement of the tissue itself due to the neuronal currents being subjected to Lorentz forces to be very small (on the order of 10 nm). Additionally, Lorentz forces would cause phase dispersion resulting in a magnitude signal loss rather than the observed phase shifts. Cell swelling due to neuronal activation and motion of water related to the flux of ions across the cell membrane could also be factors in the signal changes. But they both would cause signal dispersion and therefore magnitude signal loss rather than coherent phase shifts (Le Bihan et al., 2006; Darquié et al., 2001). An increase in intracellular water content due to water diffusion related to neuronal firing could decrease the T1 relaxation time. However, this would cause a magnitude signal change. We predominantly observed coherent phase shifts, which make this mechanism unlikely.

Relationship to previous in vitro and in vivo MRI studies of currents in biological tissue

Early work in this area was by Joy et al. who injected 2 mA/40 ms current pulses in the forearm of a healthy subject and acquired phase images using multishot spin-echo (Joy et al., 1989). While localized signal changes were observed in the phase maps in response to the applied currents, these currents were several orders of magnitude larger than neuronal currents and were not biological.

Detection of neuronal current related signals in humans in vivo remains controversial (Bandettini et al., 2005; Hagberg et al., 2006). In (Xiong et al., 2003), the authors reported a 1% magnitude decrease primarily in the motor cortex of 6 healthy subjects during a visuomotor task. The authors also concluded that magnitude changes showed the largest effect and were far more sensitive than phase. While Kim et al. (Kim et al., 2005) reported reproducibility of the work of Xiong et al., Chu et al. (Chu et al., 2004) reported inability to do so. In (Konn et al., 2004), the authors imaged alpha activity in healthy subjects using GE EPI with TR 40 ms and reported a smallest detected phase change of 0.13°, equivalent to a local magnetic field change of 0.34 nT. However, a subsequent study by Mandelkow et al. (2007) to image alpha activity was unable to detect such a signal and concluded that the instrumentation lacked both sensitivity and specificity to detect an alpha-related signal. Chow et al. (2006b) reported detection of evoked activity (0.15–0.3% magnitude changes) from the optic nerve and visual cortex corresponding to local magnetic field changes of 0.4–2.1 nT.

While interpretation of results from in vivo studies is confounded by physiological noise, in vitro studies allow measurement in the absence of physiological noise sources. In Luo et al. (2009), the authors imaged a bloodless turtle brain/eye preparation with GE-EPI at 9.4 T but reported an inability to detect any significant MR signal changes (magnitude or phase) related to visually evoked LFPs. Park et al. (2006) used dissected snail ganglia because the oxygen-carrying proteins in snails are non-magnetic hemocyanins. They detected large magnitude signal decreases (5.53%) in a single 2 × 2 × 2 mm³ voxel with an effective TR of 2 min. However, they did not report any phase changes. This contradicts the finding by Petridou et al. (2006) in rat brain cultures and by Konn et al. (2003) in a phantom suggesting that MR phase is much more sensitive than magnitude to local neuronal magnetic field changes. In Petridou et al. (2006), the authors used an in vitro epileptic fetal rat brain tissue culture preparation that displayed bursts of spontaneous neuronal activity at less than 2 Hz. They obtained single-voxel MR measurements at 7 T using an FID technique. All electrophysiological recording was performed outside the MRI and not during imaging. They found power increases in MR phase spectra within the frequency range corresponding to burst activity measured with EEG in the same cultures before and after the MR measurements. The phase shifts were 0.15°–3°, equivalent to magnetic field changes of 0.2–3.9 nT. The spectral power increases were abolished in the presence of tetrodotoxin (TTX), which blocks sodium channels. Since the MR phase and EEG signals were not recorded concurrently, the relationship between the time courses of these two signals is not known. While spin-echo imaging (TR = 1 s) of the cultures was performed at 3 T to localize the MR signal changes to the tissue, the spatial resolution (2.8 × 2.8 × 3 mm³) of the image was insufficient to resolve the spatial distribution of magnetic field inside the culture.

Petridou et al. did observe power increases corresponding to the burst frequencies in the MR magnitude spectra as in the phase, but the effect was much smaller (0.01–0.4%) and only observed at 7 T. In our study, we also observed ~0.4% magnitude changes during the period of LFP, but the changes were not consistent across 9 animals with approximately half showing a magnitude increase and the others showing a magnitude decrease. In contrast the phase shifts were consistently observed across the animals. Our observations therefore suggest that for this preparation and imaging protocol, the dominant source of the MR contrast is due to coherent shifts in MR phase, in agreement with Petridou et al. (2006).

Importance of secondary sources

The concepts underlying “secondary sources” are well developed (Hämäläinen et al., 1993). The total magnetic field can be represented in terms of the magnetic field produced by the so-called primary current sources (intracellular currents in active neurons) and those that arise from the influence of conductivity boundaries, for example the tissue–cerebrospinal fluid boundary or the air–scalp boundary. The magnetic field effectively produced by each conductivity boundary surface can be mathematically represented as being produced by fictitious secondary sources, which are current dipoles distributed over the surface of each such boundary. Each current dipole Q is oriented normal to the boundary surface S_ij between two regions of conductivity σ_i and σ_j, with the dipole oriented from region j to region i. The moment of Q is given as

$$Q=({\sigma }_i-{\sigma }_j)V(r^{\prime })n_{ij}(r^{\prime }),$$

where V is the potential on the boundary surface and n_ij is the normal to the surface. As the primary source moves closer to the conductivity boundary, the contribution of the secondary sources relative to the primary source increases since their strength is proportional to the potential V produced by the primary source on the boundary surface.

In this paper, we found that the magnetic field originating from volume currents amounted to about 1/3–2/3 of the field from the primary currents (Fig. 10). This deviates from that observed by Konn et al. in a simulation study where they found that the field contributions from volume currents were negligible (Konn et al., 2003). This discrepancy is due to the difference in the distance between the primary source and the boundaries. In our case, the primary source was within the cerebellum that was immersed in a bath of saline. There was a conductivity boundary between the cerebellum and the bath because of the difference in their conductivities. This conductivity boundary was only ~0.5 mm from the primary source. In addition, there was a conductivity boundary between the bath and the air. The tissue–saline boundary produced a relatively strong magnetic field inside the cerebellum compared to the saline–air boundary because the former was quite close to the primary source. Our findings are in agreement with theoretical calculations for the turtle cerebellum (Huang et al., 1990). In the case of Konn et al. (2003), the tissue–saline boundary was not present since the primary source was placed in a homogeneous spherical conductor and the authors considered the effect of the saline–air boundary on the local magnetic field. As this distance was >10 mm, the secondary sources did not contribute significantly to the field inside the conductor. Their observations would have been different if an inhomogeneous conductor model with boundary surfaces close to active neurons had been used.

In in vivo situations, one needs to realistically model the entire head as an inhomogeneous volume conductor and compute the magnetic field from each boundary surface. The modeling should take into account the actual experimental situation. For example, if the skull is removed with craniotomy, that needs to be represented in the model since the absence of skull will significantly alter the volume conduction. Similarly, presence or absence of the compartment containing cerebro-spinal fluid in epi- or subdural recording should be taken into account.

Development of MR-based in vivo neural current imaging methods

Our in vitro study provides an important empirical guidance for developing MR-based neural current imaging methods for the whole brain. The forward and inverse analyses showed that the MR phase shifts observed in this preparation are due to neuronal currents with q of 1–2 nA.m/mm². This value of q agrees with the value estimated for the fast LFP mediated by ionotropic receptors (Okada and Nicholson, 1988). Values of q are empirically uniform across brain structures and species (turtle cerebellum, guinea pig hippocampus, pig primary somatosensory cortex, rat barrel cortex, monkey visual cortex, and human epileptiform cortex) (Murakami and Okada, 2015). The maximum value of q agrees quantitatively with the values based on a mathematical network model of the hippocampus that has been empirically validated against electric and magnetic data in an hippocampal slice preparation (Murakami and Okada, 2015). In Murakami and Okada (2015), the authors hypothesize that this invariance is due to the well-known invariance in extracellular volume fraction of neurons (Syková and Nicholson, 2008) and in passive and active membrane parameters (Traub et al., 1994, 2008, 2005; Traub and Miles, 2008). Thus, it is possible that the phase shift (corresponding to 0.25–0.97 nT) during a synchronized population activity may be comparable in turtle cerebellum and in mammalian neocortices such as rat barrel cortex and human neocortex. This prediction could serve as the foundation for developing MR-based neural current imaging in intact brains in vivo.

It should be possible to obtain neural current images with a high spatial resolution. Our work shows that it is possible to detect phase shifts related to evoked neuronal activity in single voxels of 0.1 mm³ with a cross-sectional surface area of 0.1 mm² containing about 500 Purkinje cells. Voxels with a cross-sectional surface area of 0.1 mm² are comparable to single cortical columns. This spatial resolution is also comparable to the resolution for LFP measurements with intracortical electrodes with a blunt tip of 2–10 μm (Buzsáki, 2004). By imaging with thinner slices (~300–400 μm), we expect that it should be possible to resolve laminar differences in activity and localize the sources to individual cell layers.

The work in this study shows that the neural currents can be imaged with a time resolution of 100 ms. This temporal resolution is faster than typical BOLD-fMRI sampling times (~1 s). This temporal resolution is, however, too slow to detect evoked population responses mediated by ionotropic receptors, which have durations of 10–100 ms. While shorter TRs (~50 ms) can be used with the present protocol, it will be necessary to develop protocols that can image faster responses (Witzel et al., 2008).

The two large challenges facing neuronal current MRI in vivo are the relatively small signal change and the presence of respiratory, cardiac, and hemodynamic changes which may be spatially variant and not easily filterable. We expect that the first of these two challenges can be solved with higher sensitivity and improved spatial resolution by using higher field strengths, stronger imaging gradients, multichannel acquisition, and better pulse sequence development (Dale, 1999; Bodurka and Bandettini, 2002; Witzel et al., 2008; Feinberg and Setsompop, 2013). The second challenge, physiological noise, will cause spatially varying fluctuations in the phase data making it difficult to establish a temporally stable baseline. Removing this noise from the data will most likely require a combination of methods such as physiological monitoring during imaging, spatial high-pass filters, noise regression, and other retrospective methods for elimination of this noise from the data (Glover et al., 2000; Hagberg et al., 2008; Särkkä et al., 2012). Creating subject-specific volume conductor models accounting for the different conductivity boundaries and using realistic source geometries similar to the calculations done in this paper will also be useful in designing in vivo studies. Though the results presented in this study were measured in the absence of physiological noise sources, we expect the methodology presented here will form an empirical basis for the development of future techniques to detect these signals in vivo.

Conclusions

Our results for metabotropic receptor mediated evoked neuronal activity in an isolated whole turtle cerebellum demonstrate that MRI can be used to detect neuronal currents with a time resolution of 100 ms, approximately ten times greater than for BOLD-fMRI, and with a sensitivity sufficiently high for near single-voxel detection. We have shown that it is possible to detect the MR phase shift with a time course matching that of the concurrently measured local field potential in the tissue. Furthermore, we showed how these MR phase data can be used to accurately estimate the spatial distribution of the current dipole moment density in the tissue.

Appendix A

Here we provide a brief overview of the method as the principles of the BEM are well known and described in detail elsewhere (Hämäläinen et al., 1993). In our case, the forward problem involves calculation of the total magnetic field B at all locations r in the imaging plane given a quasi-static primary current distribution J^p within the tissue. The primary current distribution gives rise to an Ohmic volume (or return) current −σ∇V, so that the total current is J=J^p−σ∇V. The potential V is determined by the primary current J^p via the quasi-static condition: ∇ · J= 0 or ∇ J^p= ∇ · (σ∇V). The magnetic field is related to the total current density by the Biot-Savart’s law:

$$\mathbf{B}(\mathbf{r})=\frac{{\mu }_0}{4\pi }\int (\mathbf{J}({\mathbf{r}}^{\prime })\times \mathbf{R})/{\mid \mathbf{R}\mid }^3\mathrm{d}{\mathrm{v}}^{\prime },$$

where r is the point where the field is computed, R = r – r′, and the primed symbols refer to the region containing the current sources. When the volume conductor consists of inhomogeneous isotropic compartments, ∇σ is non-zero only on the boundaries and we can express the total magnetic field as (Hämäläinen et al., 1993; Huang et al., 1990)

$$\mathbf{B}(\mathbf{r})={\mathbf{B}}_{\mathbf{p}}(\mathbf{r})+\frac{{\mu }_0}{4\pi }\sum _{ij}({\sigma }_i-{\sigma }_j)\underset{\mathit{Sij}}{\int }\mathbf{V}({\mathbf{r}}^{\prime })\left(\mathbf{R}/{\mid \mathbf{R}\mid }^3\right)\times {{\mathbf{dS}}_{\mathbf{ij}}}^{\prime },$$ (4)

where

$${\mathbf{B}}_{\mathbf{p}}(\mathbf{r})=\frac{{\mu }_0}{4\pi }\int ({\mathbf{J}}^{\mathbf{p}}({\mathbf{r}}^{\prime })\times \mathbf{R})/{\mid \mathbf{R}\mid }^{3}d{v}^{\prime },$$

is the magnetic field from the primary source, and σ_i and σ_j are the conductivities of homogeneous regions G_i and G_j that are separated by the boundary surface S_ij. The surface integral term is the contribution to the total field B(r) from the secondary sources (σ_i–σ_j)V(r′)n_ij(r′) where n_ij(r′) is the unit vector normal to the surface S_ij at r′. The secondary magnetic field thus depends on the potential on the conductivity boundaries generated by the primary source. We would like to stress here that the secondary sources are not physical current sources but a mathematical representation of the effects of the conductivity boundaries. The potential on the boundary surfaces can be obtained by solving a Fredholm integral equation. For numerical computation of the primary and secondary fields, we utilized the routines from the BEM toolbox for MATLAB (Stenroos et al., 2007).