On the acquisition and analysis of microscale thermophoresis data

Abstract

A comprehensive understanding of the molecular mechanisms underpinning cellular functions is dependent on a detailed characterization of the energetics of macromolecular binding, often quantified by the equilibrium dissociation constant, K_D. While many biophysical methods may be used to obtain K_D, the focus of this report is a relatively new method called “microscale thermophoresis” (MST). In an MST experiment, a capillary tube filled with a solution containing a dye-labeled solute is illuminated with an infrared laser, rapidly creating a temperature gradient. Molecules will migrate along this gradient, causing changes in the observed fluorescence. Because the net migration of the labeled molecules will depend on their liganded state, a binding curve can be constructed as a function of ligand concentration from MST data and analyzed to determine K_D. Herein, simulations demonstrate the limits of K_D that can be measured in current instrumentation. They also show that binding kinetics are a major concern when planning and executing MST experiments. Additionally, studies of two protein-protein interactions illustrate challenges encountered in acquiring and analyzing MST data. Combined, these approaches indicate a set of best practices for performing and analyzing MST experiments. Software for rigorous data analysis is also introduced.

1 Introduction

The characterization of molecular interactions has become a major theme of modern molecular science, with applications across mechanism-oriented biology. Elucidating the molecular mechanisms of these complexes and assemblies often requires a detailed knowledge of the energetics of the respective interactions, which can be quantified by the equilibrium dissociation constant, K_D, or, equivalently, the equilibrium association constant, termed K_A (where K_D = 1/K_A). The contemporary researcher enjoys access to a host of techniques for the elucidation or estimation of K_D. For example, isothermal titration calorimetry (ITC), analytical ultracentrifugation (AUC), surface plasmon resonance (SPR), fluorescence spectroscopy, and nuclear magnetic resonance (NMR) experiments may be used to derive this quantity. These techniques all have their own sets of advantages and disadvantages [1–7]. In general, however, ITC, AUC, and NMR can have significant time and sample demands, while SPR requires substantial experimental design efforts and proper treatment of surface effects during data analysis.

A relative newcomer to this stable of techniques is microscale thermophoresis (MST) [8–10]. The method has modest sample requirements, it is quickly performed, and it does not occur on a surface; it therefore avoids some of the disadvantages of the techniques enumerated above. In a typical MST experiment, a population of one of the interacting partners is covalently labeled with a fluorescent dye (or protein). A solution of these molecules is placed in a transparent capillary tube, and a portion of the tube is illuminated with an infrared (IR) laser, thus establishing a stable temperature gradient. Due to a phenomenon commonly called “thermophoresis” [11], the molecules will migrate along this gradient, and their net movement can be monitored as a function of time using a fluorescence microscope focused on the IR-illuminated region, resulting in characteristically shaped time-traces (Fig. 1). In most cases, thermophoresis is “positive”, meaning that there is a net movement of molecules from hotter regions of the capillary to cooler ones; this manifests as a net decrease in the observed fluorescence at the point of IR illumination. Negative thermophoresis may also occur, however, depending on the properties of the solute(s).

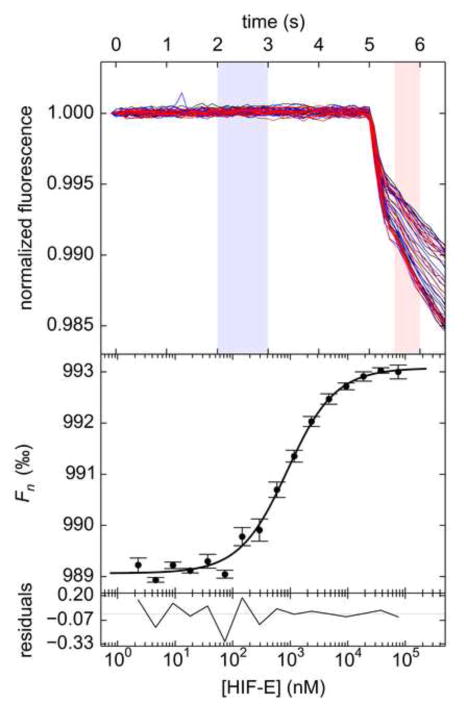
Figure 1. An MST example.

Shown are MST data and analyzed binding curves for the interaction between HIF-E and ARNT-R*. The top panel shows the thermophoretic time-traces from one sixteen-sample experiment, all normalized to a starting value of 1.0. Zones A, B, and C, are shown in gold, purple, and green, respectively, and respectively represent the regions before the activation of the IR laser, just after its activation, and just prior to its deactivation. These zones are used to calculate the quantity F_n (Eq. 1) in three different modes; the combinations used for these modes are labeled with arrows. TA, TJ and T + TJ stand for Thermophoresis Alone, T-Jump, and Thermophoresis + T-Jump, respectively. The F_n values obtained from these calculations are displayed as a function of [HIF-E] in the middle part (respectively colored markers). Parts of the curves that report on F_n,B* and F_n,AB* are marked. These data have been adjusted such that the smallest fitted value of F_n,B* has been subtracted from all F_n values. The lines represent fits to the data using a 1:1 binding model. The bottom panel shows the respectively colored residuals between the data and the fit line.

Many molecular characteristics govern the magnitude of thermophoresis for a given molecule. They include the effective charge, the surface area, and the hydration entropy at the interface of the molecule and solution [11]. It is therefore easy to conceive that binding to an interaction partner could alter the observed thermophoretic properties of a molecule. In a typical MST experiment to determine K_D, sixteen solutions are evaluated, with the concentration of the labeled partner held low and constant (usually 10–500 nM), and the concentrations of the unlabeled partner varied through a large range (the lowest and highest concentrations can differ by a factor greater than 10⁴). Thermophoresis of the labeled partner is calculated for all sixteen samples, and can then be evaluated as a function of unlabeled-partner concentration, with K_D being a fitted parameter in the analysis of this “binding curve”. Notably, MST can be used to determine other properties of biological macromolecules as well [9].

Currently, there is one commercial manufacturer of MST instrumentation: NanoTemper, LLC [9]. From this source are available numerous resources regarding the planning and execution of MST experiments [8,9,12]. Also, software is provided by the manufacturer for the evaluation and simulation of MST experiments.

Despite the wealth of information available from commercial and literature sources, we find that there are substantial information gaps regarding the performance and analysis of MST data. For example, our experience has demonstrated that thermophoresis can be drastically and unpredictably affected by the presence of high concentrations of a protein titrant (Section 3.5). Further, current experimental recommendations [8,9] neglect the potential effects of association and dissociation kinetics on the execution of MST experiments. Also, contemporary analytical software programs, both from the manufacturer and from third parties, report parametric confidence limits that may not be realistic.

To address these and other shortcomings, we have thoroughly examined MST experiments from planning through analysis. MST data simulations demonstrated the importance of kinetic considerations on MST experimental planning and revealed the best-case lower limit of K_D’s determined by the method. Additionally, we conducted a series of experiments featuring two small protein domains from the hypoxia-inducible factor 2 (HIF-2) transcription factor: the C-terminal Per-ARNT-Sim (PAS) domains from the hypoxia-inducible factor 2 alpha subunit (HIF-2α PAS-B) and the aryl hydrocarbon receptor nuclear translocator subunit (ARNT PAS-B). These studies highlighted some of the experimental pitfalls inherent to some MST experiments and correspondingly identified their solutions. Parallel studies of a peptide/protein interaction involving a peptide from Wiskott-Aldrich Syndrome Protein binding to actin exemplified the high-concentrations challenges mentioned above. A titration schedule was devised to minimize the effects of this problem, resulting in an excellent estimate of K_D. Finally, we have incorporated many of our empirical insights, simulation protocols, and analytical strategies into a new software program called PALMIST, the features of which are briefly outlined herein.

2 Materials and Methods

2.1 Theory and computation

2.1.1 MST

In this paper, we are mainly concerned with bimolecular binding, i.e. A + B* ↔ AB*. A and B can be almost any combination of interacting species [8,9,12,13], but for the purposes of this discussion, B* is labeled with a fluorophore that allows it to be monitored in the MST instrument. The data acquisition follows a strict sequence: first, an excitation LED is actuated, and the fluorescence of B* and AB* in a small area of the capillary tube is monitored as a function of time (Fig. 1, top panel; the resulting plot is called a “time-trace”). A short time (usually 5 s) later, the IR laser is activated. This temperature change first results in an immediate reduction in fluorescence, termed the “temperature jump”. This feature is not caused by thermophoresis; rather, it is likely due to the enhanced collisional quenching of the fluorophore at the elevated temperature. Next, thermophoresis commences, usually resulting in the net migration of the monitored B* and AB* complexes out of the field of observation (“positive thermophoresis”). A new, steady-state fluorescence is eventually achieved, often taking 30 – 60 s. After the IR-laser illumination is terminated, the fluorescence signal recovers as the labeled molecules diffuse back into the monitored area.

Relating thermophoresis to the free- and bound-state populations of a biomolecule is dependent on two observations: the mean steady-state fluorescence at an early time (“cold fluorescence”, or F_c) and the mean steady-state fluorescence at a later time (“hot fluorescence”, F_h). These two values must be compared to one another to arrive at the quantity termed “thermophoresis”, F_n. At least two distinct strategies have been employed to calculate F_n. One quantifies the difference between F_c and F_h and normalizes by F_c [14]. With the current commercial instrumentation, we find that this approach appears to introduce significant noise into the binding curve (not shown). Instead, we take the second approach [8], defining the observed thermophoresis as:

$$F_n=\frac{F_h}{F_c}\times 1,000,$$ Eq. 1

where the factor of 1,000 serves to put F_n on a per mille scale.

To ensure common frames of reference for all MST experiments, we recommend that the experimenter adhere to one of three combinations of time periods used to obtain F_c and F_h based on the identification of three time zones in the time-trace (Fig. 1). In this report, the start of Zone A is defined as 3 s before application of the temperature gradient, and lasts for 1 s; Zone B starts 0.5 s after the IR laser is actuated, and the zone’s duration is 0.5 s; and Zone C is the new steady-state region of the time trace, starting 2.1 s prior to the cessation of the IR-laser illumination, with a duration of 2 s. To some extent, these choices are arbitrary, but we have found that they faithfully capture the required information in the vast majority of thermophoretic time-traces that we have examined. In the temperature-jump (TJ) scheme, F_c is taken from Zone A, and F_h is from Zone B. As intimated above, the TJ method does not actually monitor thermophoresis per se. Instead, it focuses on the immediate diminution of fluorescence signal induced by the temperature change. To effect TJ changes, A must bind in a way that affects the physical properties of fluorophore attached to B*, and thus not all interaction pairs will exhibit changing TJ signals as a function of A (we use italicized letters to denote the concentrations of respective components in this report). The thermophoresis alone (TA) strategy obtains F_c from Zone B and F_h from Zone C, presumably eliminating contributions from the temperature jump in the analysis. Finally, the thermophoresis and temperature jump (T+TJ) method takes F_c from Zone A and F_h from Zone C. Because free dye would evidence both temperature-jump and thermophoresis, it is critically important to purify labeled proteins away from the labeling dye, an expedient that is easily accomplished through the use of desalting or gel-filtration chromatography. Which strategy is most appropriate depends on the interaction system under study. This choice has consequences that will be discussed in detail (Section 3.3).

In a typical MST experiment to determine K_D, B^* is held constant and low, usually 10–500 nM, while A is varied from a value well below K_D to one 10–100X above K_D. When F_n is plotted versus A (with the abscissa scaled logarithmically), a characteristic sigmoidal binding curve is obtained (Fig. 1, lower panel). Of course, achieving such an appearance is utterly dependent on there being significant differences in F_n between B^* and AB^*; otherwise, the binding curve would appear to be a flat line. To relate the observed F_n to B^* and AB^*, the following equation is used:

$$F_n=\left(\frac{B^{\ast }}{B_{\text{tot}}^{\ast }}·F_{n,{\mathrm{B}}^{\ast }}\right)+\left(\frac{A{B}^{\ast }}{B_{\text{tot}}^{\ast }}·F_{n,{\text{AB}}^{\ast }}\right),$$ Eq. 2

with F_n,B^* representing the F_n of free B^*, F_n,AB^* standing for the F_n of the AB^* complex, and $B_{\text{tot}}^{\ast }$ denoting the total concentration of B^* [8]. Both F_n,B^* and F_n,AB^* are unknown to the experimenter prior to the experiment. Together with equations of mass action and mass conservation (see Supplemental Methods), the binding curve may be evaluated with three fitted parameters: F_n,B^*, F_n,AB^*, and K_D.

A trimolecular competition framework in which B^* and C compete for a single binding site on A was also applied herein as described in the Supplemental Methods and elsewhere [15]. In such a case, the fitted parameters are F_n,B^*, F_n,AB^*, and the dissociation constants of the AB^* complex (K_D(AB^*)) and the AC complex (K_D(AC)).

2.1.2 Parametric Confidence Intervals

We and others [3,16–18] have used a method termed the “error-surface projection” (ESP) to estimate parametric confidence intervals. ESP is a post hoc procedure in that it is performed after a set of parameters {Π₁, Π₂, …, Π_n} is optimized by non-linear least squares minimization (NLSM). The observed residuals between the fitted line and the data points give rise to the best weighted sum of squared residuals, termed here ${\chi }_b^2$:

$${\chi }_b^2=\sum _{i=1}^m\frac{{\left(F_{n,i}-f_{n,i}\right)}^2}{e_i},$$ Eq. 3

where m is the number of data points, F_n,i is the i^th observed thermophoresis, f_n,i is the i^th thermophoresis obtained from the set of best fitted parameters {Π_b}, and e_i is the estimated error for F_n,i. Note that this is not a “reduced” χ², in that the value has not been normalized by the degrees of freedom. By the application of F-statistics and a confidence criterion, a new, critical χ², ${\chi }_c^2$, can be defined

$${\chi }_c^2={\chi }_b^2\left[1+\left(\frac{{\nu }_1}{{\nu }_2}·F\left([1-P],{\nu }_1,{\nu }_2\right)\right)\right],$$ Eq. 4

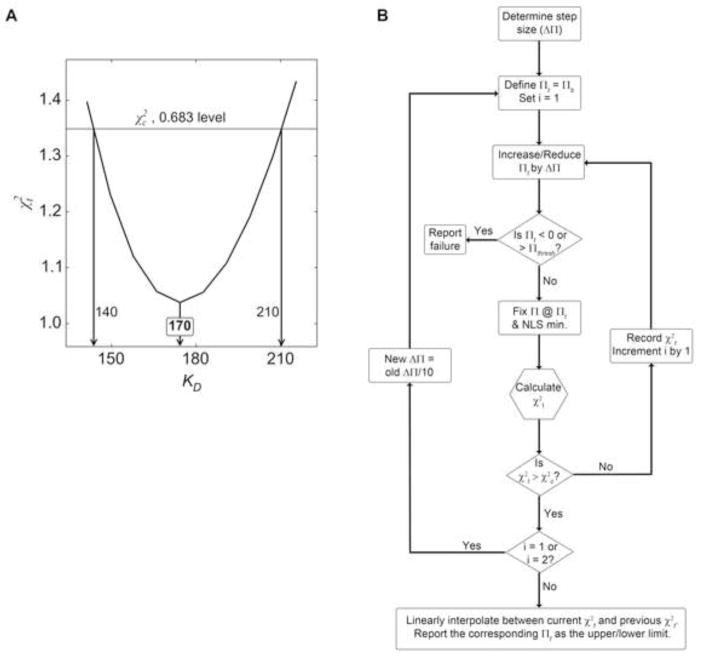
where P is the specified level of confidence (typically 0.683 or 0.95; we use 0.683 herein, and refer to this interval as the “68.3% confidence interval” hereafter), ν₁ is the first degree of freedom (the number of fitted parameters, μ), ν₂ is the second degree of freedom (m – μ), and the F term is the upper quantile of the Fisher distribution with the specified probability level and degrees of freedom [18]. The ${\chi }_c^2$ value thus provides a boundary for χ² during a systematic, one-dimensional exploration of parameter space; if an investigated set of parameters results in a χ² higher than ${\chi }_c^2$, it is outside the desired confidence interval [17,18]. We have developed an automated, adaptive algorithm for ESP (Fig. 2). First, the parameter of interest, Π, is decremented from its best, optimized value (Π_b), resulting in Π_t, the parameter’s test value. With Π fixed at the non-optimal value Π_t, the NLSM is repeated with all other parameters fitted in the original analysis allowed to refine, with the resulting χ² termed the “test” ${\chi }^2({\chi }_t^2)$. Π_t is systematically decremented until ${\chi }_t^2={\chi }_c^2$. This defines one end of the confidence interval (the lower one, Π_L in this example). The procedure would be repeated to define the opposite interval (Π_U) by fixing Π_t at non-optimal values in the opposite direction (+ΔΠ in this example). The result of this methodology can be visualized as an “error surface”, i.e. a plot of ${\chi }_t^2$ versus Π_t (Fig. 2A). The limits of the confidence interval can be read as the parameter values (on the x-axis) at which ${\chi }_t^2={\chi }_c^2$. Thus, the confidence interval [Π_L, Π_U] was discovered and reported subsequent to all parameter optimizations for all fitted parameters. We note that this algorithm (Fig. 2B) is well suited to the smooth, parabolic error surfaces (Fig. 2A) encountered in MST data analysis. Irregularly shaped error surfaces, such as those that might be encountered in the evaluation of interacting proteins by sedimentation equilibrium AUC [19], are best treated with interactive, user-guided explorations like those implemented in SEDPHAT [3,20]. The adaptive nature of the algorithm described here ensured that the sampling of parameter space is not too sparse. Yet, the step sizes were large enough that the algorithm was quick (usually consuming < 1 s of CPU time), and defining the boundaries was augmented by the interpolation described in Fig. 2.

Figure 2. The error-surface projection (ESP) method employed herein.

(A) An exemplary ESP plot. The x-axis shows the varied parameter of interest, K_D in this case. The y-axis shows ${\chi }_t^2$, i.e. the χ² resulting from holding K_D constant at the corresponding x-value and performing the fitting. The horizontal line shows ${\chi }_c^2$ (Eq. 4). An annotation at the curve’s minimum shows the best value of the parameter, Π_b. Annotations at the intersection of the curve and the horizontal line define the confidence interval. (B) Flow chart of automated ESP method used in this report. Presented as a flow chart is the procedure for defining the limits of confidence intervals reported in this paper and by the software PALMIST. Rounded rectangles represent general steps; diamonds denote branch points in which a yes/no determination is made; the hexagon shows a step in which only a calculation for the next step is performed. Π_t is the test value of the parameter. The procedure is performed twice: once to obtain the lower limit (decrements) and once to find the upper limit (increments). The first step, “Determine ΔΠ”, is usually accomplished by simply dividing the σ from the variance-covariance matrix for that parameter by 2. The threshold value of Π for the upper limit, Π_thresh, is typically chosen to be ten times the difference between Π_b and the lower limit, Π_l.

This automated method relied on the ability of the NLSM algorithm to arrive at the best set of parameters in every iteration. To increase the probability that this occurred, we always used two minimization techniques: the Nelder-Mead simplex (NMS) algorithm [21] and the minimization method of Levenberg and Marquardt (LM) [22,23]. During any given minimization, NMS was first applied, and the resulting optimized parameters were used as starting parameters in LM. If the parameters derived from the two minimizations did not agree to within a tolerance level (0.1% in all investigated parameters), the cycle began again; a maximum of five cycles were allowed.

Monte Carlo and bootstrap protocols, also commonly used to estimate confidence intervals [24,25], are only briefly described here. In the Monte Carlo method, random noise sampled from a Gaussian distribution with the same variance as that of the fit was added to the noiseless best-fit line at the same discrete points as the experimental data. The NLS minimization was performed, and new values of the parameter set were recorded. This process was repeated j times, where j ≥ 1,000. At the end of the procedure, the parameters were tabulated and ordered from low to high. The lower and higher limits of the confidence interval were defined by result number [(1 − P) · j/2] and result number [j − (1− P)(j/2)], respectively. The same strategy was used for the bootstrap method, except that random noise was not added; instead, the noise came from a table of the residuals from the actual fit, and this table was randomly sampled with replacement [26]. Thus, instead of assuming Gaussian-distributed errors, the bootstrap used the present residuals as the error model. Alternating cycles of NMS and LM were also used to ensure fit convergence in these methods.

2.1.3 Outlier detection

Outliers in raw MST data (“spikes” in the electronic noise) were detected by first fitting a straight line or a quadratic curve to data flanking the region of interest, i.e. the area used to determine F_h or F_c. The root-mean-square deviations (r.m.s.d.’s) between the fitted line and these data were calculated, and then the fitted line was interpolated into the region of interest. In this region, any deviation greater than 7 × r.m.s.d. was considered a spike. These data points were automatically removed to avoid their skewing the values of F_h or F_c.

A model-free, unbiased means of detecting outliers in the thermophoresis binding curves was also devised. This method was based solely on the expectation that the binding curve should be smooth, i.e. it should not be spiky. To initiate this process, a third-degree polynomial was fitted to the thermophoresis data. The r.m.s.d. between the data and the polynomial line was then calculated, and any data point with a deviation that was 3-fold or more higher than the r.m.s.d. was identified as a potential outlier. These putative outliers were not automatically removed; instead, the user must initiate outlier removal. This strategy is similar (but not identical) to one employed in NITPIC [27] for the estimation of local errors in ITC isotherms.

2.1.4 Kinetic simulations

The effects of association and dissociation kinetics on the approach to equilibrium in a bimolecular interaction were explored by using a generalized integrated rate equation [28]:

$$A{B}^{\ast }(t)=\frac{A{B}_{eq}^{\ast }·\left(1-e^{-\eta t}\right)}{1+\omega e^{-\eta t}},$$ Eq. 5

where $A{B}_{eq}^{\ast }$ is the final equilibrium concentration of AB^*, t is the time in seconds after mixing the constituents, and

$$\begin{array}{l}\eta =\sqrt{k_{\text{on}}^2·{\left(A_{\text{tot}}-B_{\text{tot}}^{\ast }\right)}^2+k_{\text{off}}^2+2k_{\text{on}}{k}_{\text{off}}\left(A_{\text{tot}}+B_{\text{tot}}^{\ast }\right)}\\ \omega =\frac{\eta -\beta }{\eta +\beta }\\ \beta =k_{\text{off}}+k_{\text{on}}·\left(A_{\text{tot}}+B_{\text{tot}}^{\ast }\right)\end{array},$$ Eq. 6

where k_on is the kinetic on rate (in M⁻¹s⁻¹) and k_off is the kinetic off rate (in s⁻¹). Thus, given AB*(t), A_tot, and B_tot, the terms A(t) and B*(t) may be calculated for any t with the initial assumption that AB*(0) = 0. These were transformed into thermophoresis space using mass-conservation/mass action equations and Eq. 2.

2.2 Protein Preparation

The HIF-2α PAS-B R247E (HIF-E) and aryl hydrocarbon receptor nuclear translocator PAS-B E362R (ARNT-R) domains were obtained as detailed elsewhere [29,30]. In brief, the two domains were expressed in Escherichia coli with an N-terminal His6X-Gβ1 tag and purified from the bacterial lysate by nickel affinity chromatography. The fusion protein was treated with tobacco etch virus (TEV) protease followed by a second round of nickel chromatography to remove the N-terminal affinity/solubility-enhancement tag. After exchanging these proteins into storage buffer (50 mM Tris, pH 7.5, 20 mM NaCl and 5 mM 2-mercaptoethanol (βME)) by size-exclusion chromatography, aliquots were flash frozen with liquid nitrogen and stored at −80°C.

Before MST experiments, both proteins were individually dialyzed against four exchanges of Buffer HA (10 mM NaPO₄, pH 7.5, 20 mM NaCl, and 5 mM βME) in the same vessel. Immediately prior to the labeling reaction, a portion of ARNT-R was exchanged into a similar buffer lacking βME using a gravity-flow PD-10 G25 column (GE Healthcare BioSciences, Piscataway, NJ). The labeling reaction consisted of 1 μL of 40 mM Alexa-Fluor 488-N-hydroxysuccinimide ester (Molecular Probes/Life Technologies, Grand Island, NY) dissolved in 100% anhydrous dimethyl sulfoxide (DMSO) incubated with 200 μL of 20 μM ARNT-R for 30 minutes at room temperature in the dark. The fluorophore-conjugated protein (ARNT-R*) was resolved from free dye and buffer-exchanged by passing it over a G25 column that had been equilibrated with Buffer HA. Finally, the post-reaction protein concentration (ε₂₈₀ = 15,470 M⁻¹cm⁻¹) and extent of fluorophore labeling (ε₄₉₄ = 73,000 M⁻¹cm⁻¹) were determined by spectrophotometry.

Fluorescently labeled, mutant verprolin-homology-central-acidic (VCA′*) [31] domain was produced from human neuronal Wiskott-Aldrich Syndrome protein (N-WASP) amino acid residues 430–505, with mutations S430C, C431A. This sequence was generated by PCR and cloned into a plasmid derived from pGEX2T (GE Healthcare) with an in-frame TEV protease site added between the sequences for glutathione S-transferase (GST) and the multiple cloning site (which was modified to include a 5′ NdeI site and 3′ BamHI site). Following verification by sequencing, E. coli strain BL21(DE3) T1R (Sigma-Aldrich, St. Louis, MO) were transformed with the construct, and grown in Luria-Bertani medium (LB) [32] supplemented with ampicillin. Expression was induced by adding 1 mM isopropyl β-D-1-thiogalactopyranoside (IPTG) to the culture medium and was allowed to proceed for 3 hours at 37°C. Cells were lysed using a C5 Emulsiflex (Avestin, Ottawa, ON) cell disruptor, and clarified by centrifugation. The VCA′ protein was purified using glutathione sepharose 4B (GE Healthcare) affinity chromatography, cleaved with TEV protease, and then the cleaved peptide was isolated using SOURCE 15Q (GE Healthcare) ion-exchange chromatography. An additional SOURCE 15Q ion-exchange step was used to concentrate the material and stringently remove reducing agents. At this point, 40 μM VCA′ was labeled with 150 μM AlexaFluor488 maleimide (Molecular Probes/Life Technologies, 40 mM stock in anhydrous DMSO). Following 2 hr of labeling at room temperature in the dark, 2 mM DTT was added and modified protein (VCA′*) was purified by SOURCE15Q and Superdex 75 chromatography in KMEI buffer (10 mM Imidazole pH 7.0, 50 mM KCl, 1 mM EGTA, 1 mM MgCl₂, 0.5 mM DTT). The absorbance at 492 nm was used to determine concentration (extinction coefficient of 71,000 M⁻¹·cm⁻¹) and the peptide was flash frozen in small aliquots. VCA′* was stored at −80°C.

Unlabeled VCA competitor was produced from wild-type human N-WASP amino acid residues 432–505, cloned, expressed, and lysed as above. The GST-VCA fusion was purified using glutathione sepharose followed by SOURCE 15Q ion-exchange chromatography. Following cleavage with TEV protease, the VCA was purified using another round of SOURCE 15Q ion exchange and also using a Superdex 75 gel-filtration column that had been equilibrated with KMEI buffer. Concentration was measured using absorbance at 280 nm.

Non-polymerizable actin (DVD-Actin) was prepared by a previously described method [33], with substantial modifications [34]. Briefly, non-polymerizable D. melanogaster 5C actin, with barbed-end blocking mutations D287A, V288A, and D289A, was produced as a TEV-protease-cleavable His6 fusion in Sf9 cells. This was accomplished using a recombinant baculovirus produced using the Bac-to-Bac system and a pFastBacHT expression vector (Invitrogen) modified to include an L21 enhancer sequence [35]. After expression, the protein was purified by Ni-NTA agarose affinity chromatography (Qiagen) and cleaved with TEV protease to remove the His6-tag. SOURCE15Q anion-exchange chromatography and Superdex200 gel-filtration chromatography completed the purification. Materials were concentrated using ultrafiltration, and then dialyzed against 2 mM Tris pH 8.0, 0.2 mM CaCl₂, 0.5 mM DTT, 0.1 mM ATP, quantified using absorbance at 290 nm (which minimizes interference from nucleotide), flash frozen in small aliquots, and stored at −80°C until needed.

2.3 Microscale Thermophoresis

For all thermophoretic experiments, standard treated capillary tubes were used (NanoTemper, LLC, Munich, Germany) unless otherwise noted. All data sets were collected at ambient temperature, i.e. ca. 24° C. For the study of the interaction between HIF-E and the labeled ARNT-R*, usually a concentration series of HIF-E was prepared using a 1:1 serial dilution of the protein into buffer HA, with the top [HIF-E] = 150 μM; sixteen 10-μL samples were thus prepared ranging in concentration from 150 μM to 4.6 nM. The association was initiated by the addition of an equal volume of 300 nM ARNT-R* to each reaction mixture, resulting in a final [ARNT-R*] of 150 nM and also halving all of the HIF-E concentrations. The mixtures were incubated in the dark at room temperature for 40 min before being loaded into capillary tubes and inserted into the apparatus for data acquisition. In kinetic-testing experiments, the incubation times were 10, 30, and 105 min. For the competition experiment, a serial-dilution series (sixteen 15-μL samples) was prepared having 200 nM ARNT-R* and varying the concentration of unlabeled ARNT-R from 100 μM to 3 nM; 5 μL of 2 μM HIF-E was added to initiate the association. Thus, the final concentrations were 150 nM ARNT-R*, 500 nM HIF-E, and varying ARNT-R from 2.3 nM to 75 μM. In cases that included Tween-20, it was added as a supplement to all buffers from a 10%(v/v) stock (NanoTemper, LLC); the final concentration was 0.05%. The LED power (i.e. the power supplied to the excitation LED) was 15% and the MST power (i.e. the power supplied to the IR laser) was 40%. The pre-MST period was 5 s, the MST-acquisition period was 30 s, and the post-MST period was 5 s.

For most of the DVD-Actin/VCA′* interaction studies, a strategy was followed that resulted in a final association buffer (Buffer VA) containing 10 mM imidazole pH 7.1, 50 mM KCl, 2 mM MgCl₂, 1 mM EDTA, 0.05% Tween-20, 0.5 mM DTT, and 100 μM ATP. For binary associations between DVD-Actin and VCA′*, sixteen samples of 22.5 μL were prepared containing a linear dilution of DVD-Actin starting at a concentration 666.7 nM and ending at 0 nM. To each of these samples, 7.5 μL of 100 nM VCA′* were added, resulting in a final [VCA′*] = 25 nM and a linear dilution series starting at 500 nM and ending at 0 nM DVD-Actin. The association mixtures were incubated for 75 min in the dark before being loaded into capillary tubes. The LED power was set to 50%, and the MST power was 40%. The pre-MST period was 5 s, the MST-acquisition period was 45 s, and the post-MST period was 5 s. For competition experiments, sixteen 28-μL samples were prepared by first mixing 7 μL 100 nM VCA′* and 14 μL of a solution with concentrations of the competitor (VCA) at varying concentrations (1.4 μM to 0 nM). To initiate the interaction, 7 μL of 400 nM DVD-Actin were added to each solution, resulting in final concentrations of 25 nM VCA′*, 100 nM DVD-Actin, and the linear dilution series of VCA from 700 nM to 0 nM (an extra concentration was added to this series such that the final three samples had 50, 25, and 0 nM VCA). The incubation periods and data-acquisition protocol were the identical to those for the binary interaction of DVD-Actin/VCA′* described above.

2.4 Isothermal titration calorimetry

HIF-E and ARNT-R were exhaustively dialyzed against a buffer containing 25 mM Tris pH 7.5, 50 mM NaCl, 5 mM βME prior to experimentation using a VP-ITC calorimeter (Malvern Instruments, Malvern, UK). The syringe contents were 175 μM HIF-E, and the 1.4 mL stirred reaction cell contained 25 μM ARNT-R. Two data sets were collected at 25° C; one had thirty-four 8-μl injections and the second featured twenty-three 12-μl injections. Initial injections of 2 μl were included in both experiments; they were excluded from the analyses.

2.5 Data analysis

Time-traces were loaded into PALMIST (http://biophysics.swmed.edu/MBR/software.html). They were evaluated using the appropriate model (i.e. either “1:1” or “1:1 Comp.”). All parameters except for species concentrations were allowed to refine. When replicates were present, they were averaged, but the data points were not weighted. For confidence intervals, the program’s default 68.3% interval was used. Analyses were carried out on a computer equipped with an Intel Xeon E5-1620 CPU with a clock-speed of 3.6 GHz.

For ITC data, the baseline and integrated heat of each injection were accessed with NITPIC v1.1.2 [27], and best-fit parameters values were extracted by global analysis of both experiments using SEDPHAT v12.1 [36]. Exothermic heats of dilution for HIF-E were treated as a single baseline parameter in SEDPHAT. For both data types, the plots were rendered with GUSSI v1.1.0 [37].

3 Results

3.1 What is the dynamic range of MST?

We first investigated the question of the dynamic range of K_D’s that can be determined with MST. There is no hypothetical upper limit for K_D’s determined by this technology. Instead, this limit will be practical. The experimenter must be able to explore titrant concentrations high enough to approach saturation of the complex, i.e. at least 10 × K_D. Even if the titrant is amenable to very high concentrations, the thermophoretic behavior must also be good under such conditions. This latter condition is not always met, as high ligand concentrations can cause aberrant MST traces, perhaps due to aggregation or other non-ideal transport phenomena (Section 3.5).

To determine the lower limits of K_D estimation in MST, we utilized simulations. Critical parameters in the simulations were: concentration of the fluorophore (B*), amplitude of the term |F_B* − F_AB*|, and magnitude of the noise. We have observed that the lowest practical B* in our NanoTemper NT.115 equipped with a blue/green filter set is about 10 nM under ideal conditions. In an excellent MST experiment with replicates, the signal/noise ratio is about 50. Thus, in our simulations, we set B* to 10 nM, the amplitude of |F_B* − F_AB*| to 50, and the noise to about 1.0. The simulated titrant concentrations (A) belonged to a 1:1 dilution series that varied from 0.03 nM to 1 μM. We simulated data sets in which the experiments were performed in triplicate. The noise was sampled with replacement from the residuals of a mock thermophoresis experiment designed to examine the experimental noise in MST (see Supplementary Methods and Fig. S1). The data points from each triplicate trial were averaged and subjected to NLSM, followed by ESP confidence interval discovery (Section 2.1.2, Fig. 2). Ten thousand trials were performed, with the resulting K_D’s and confidence intervals accumulated; the means are reported in Table 1. The success of each trial was assessed as whether (a) NLSM could converge on a rational solution and (b) ESP could determine the confidence interval of K_D under the simulated conditions.

Table 1.

Dynamic range calculations for MST data.

	B* = 10 nM; signal/noise = 50
	KD (nM)
	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
successful trialsa	8,301	9,566	9,898	9,975	9,998	10,000	10,000	10,000
mean value	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
C.I.b	[0.2, 0.4]	[0.3, 0.5]	[0.4, 0.7]	[0.5, 0.8]	[0.5, 0.9]	[0.6, 1.0]	[0.7, 1.1]	[0.8, 1.2]
C.I. (ESP)c	[0.1, 0.6]	[0.2, 0.7]	[0.3, 0.8]	[0.3, 1.0]	[0.4, 1.1]	[0.5, 1.2]	[0.6, 1.3]	[0.7, 1.4]
B* = 2 nM; signal/noise = 10
successful trials	N.D.	N.D.	7,206	8,155	8,742	9,051	9,368	9,621
mean value	-	-	0.6	0.7	0.8	0.9	1.0	1.1
C.I.b	-	-	[0.2, 0.9]	[0.3, 1.1]	[0.4, 1.2]	[0.4, 1.4]	[0.5, 1.5]	[0.6, 1.6]
C.I. (ESP)c	-	-	[0.2, 1.8]	[0.2, 2.0]	[0.3, 2.2]	[0.3, 2.4]	[0.3, 2.6]	[0.4, 2.8]

^aout of 10,000 total trials

^bConfidence interval calculated from the histogram of fitted values

^cConfidence interval calculated as the respective means of ESP limits for all successful trials

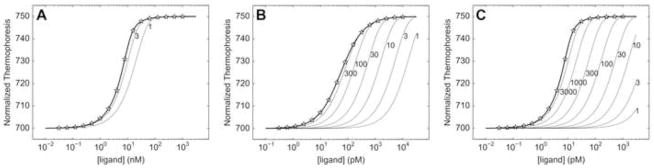
We systematically varied K_D from 1 nM to 300 pM using this simulation method. At a K_D value of 1 nM, the fitting and ESP algorithms succeeded in 100% of the trials, although the mean ESP limits suggested a wide confidence interval (Table 1). At K_D = 700 pM, the width of the mean confidence interval was the same magnitude as the K_D, and 2 of the 10,000 trials failed. At a K_D value of 400 pM, only 96% of the trials reached successful conclusions, and the confidence interval was wider than the simulated K_D value. Below this value, the simulations performed poorly, with drastically increasing failures in the 300 pM trial (Table 1).

One of the reasons for the generally wide error intervals in these simulations (Table 1) is that the concentration of B* is at least 10X higher than K_D. This results in a suboptimal shape of the binding curve, with fewer data points in its transition region (compare the optimal curve (thick, solid line) in Fig. 3B to the suboptimal one in Fig. 3C). In principle, this problem could be relieved by using a lower B*, but this would also likely degrade the quality of the signal. To explore this possibility, we simulated the same experiment with a lower B* (2 nM) and a correspondingly lower signal/noise ratio (10). These simulations performed poorly in all instances studied (Table 1), displaying many failures and wide error intervals with systematically skewed average K_D’s.

Figure 3. The effect of kinetics on MST data.

Shown are typical MST experiments, with the final equilibrium binding curves depicted as thick lines. Stars show discrete points along a typical concentration-sampling scheme. The pseudo-binding curves derived from kinetic calculations are shown as thin lines, with their respective times in minutes noted to their immediate right. Times ranging from 1 to 30,000 min. were tested; only those pseudo-binding curves whose r.m.s.d. from the equilibrium (thick) lines was greater than 0.1 thermophoresis units are shown. (A) K_D = 1 nM, k_off = 10⁻³ s⁻¹, B* = 10 nM. (B) K_D = 50 pM, k_off = 5 × 10⁻⁵ s⁻¹, B* = 10 pM. (C) K_D = 1 pM, k_off = 10⁻⁶ s⁻¹, B* = 10 pM.

We conclude that K_D values of about one-tenth the value of B* can be determined with passable confidence intervals and a high probability of success, as long as the signal-to-noise ratio is excellent. Thus, specifically in the case of MST performed in our commercial instrument, the lower limit of K_D is about 1.0 nM under ideal circumstances. Notably, these simulations were conducted with no concentration errors. Thus the practical limitation may be significantly higher than stated unless the concentrations of the components are very accurate. Another commercial MST instrument that can detect B* = 10 pM has been introduced [9]. We expect that a lower limit of K_D = 1 pM could be realized in this instrument, provided that the total input concentrations are known very accurately (this requires the avoidance of adsorption of the components at such low concentrations) and that the signal-to-noise ratio is high. The confidence interval is likely to be wide in such experiments.

3.2 MST and association/dissociation kinetics

In preparing samples for any binding assay, it is essential that enough time be allotted after the mixing of the components for equilibrium to be apparently achieved. Many protocols [8–10] for MST call for incubation times of about 30 min to 1 hr prior to the beginning of the experiment. This raises the question: given the concentrations that are typically used in MST, is this long enough?

The answer to this question was again probed by employing simulations, an approach that has been systematically explored elsewhere [38]. In this case, a kinetic rate equation (Eq. 5) was used to examine the appearances of noiseless MST binding curves at various times after mixing A and B*. These kinetically derived pseudo-binding curves were compared with the true equilibrium binding curve calculated using mass-conservation/mass-action equations and Eq. 2. In the binding curves shown in Fig. 3, only pseudo-binding curves that deviate from the true curve by a root-mean-square deviation of more than 0.1 thermophoresis units are marked with their respective times in min. Thus, importantly, the equilibration times cited below do not necessarily reflect the times to equilibrium for all samples; rather, they reflect the times necessary for the observed binding curve to be indistinguishable from the true, equilibrium curve.

All of our simulations (Table 2) centered on a protein-protein binding system in which the k_on was 10⁶ M⁻¹s⁻¹, which may be considered a fast on-rate for an interaction in which there are no strong attractive forces [39]. In our first simulation (Simulation 1; Table 2), the K_D was set to 1 nM (k_off = 10⁻³ s⁻¹), the lower limit examined above, with B* = 10 nM. In such an interaction, 10 min were enough for the pseudo-binding curves to closely resemble the equilibrium curve (Fig. 3A). In the next simulation (Simulation 2; Fig. 3B; Table 2), a higher affinity (50 pM), slower k_off (5 × 10⁻⁵ s⁻¹), and lower B* (10 pM) were input. This scenario demonstrated an experiment that might realistically be explored in the high-affinity instrument described above. These conditions would require more than 5 hr after mixing for the resulting binding curve to suitably resemble the equilibrium binding curve. The final simulation (Simulation 3; Fig. 3C; Table 2) featured the same B* as Simulation 2 and a very low K_D (1 pM) resulting in k_off of 10⁻⁶ s⁻¹. Under these conditions, it would take in excess of 50 hr for the binding curve to meet our suitability criterion.

Table 2.

Parameters for kinetics simulations

	Simulation No.
	1	2	3
KD (pM)	1,000	50	1
kon (M−1s−1)	1.0 × 106	1.0 × 106	1.0 × 106
koff (s−1)	1.0 × 10−3	5.0 × 10−5	1.0 × 10−6
B*(pM)	10,000	10	10

These simulations reinforce the fact that MST experimenters must take kinetics into account. Unless there is specific knowledge of on- and off-rates prior to the experiment, it seems prudent to carry out a control experiment at several time points to establish that the resulting binding curve does not vary with time, thus ensuring that equilibrium has been achieved.

Another critical result of these simulations was that the pre-equilibrium pseudo-binding curves strongly resembled true binding curves (Fig. 3). In some cases, they appeared to be slightly steeper than the true binding curves, but an unwary experimenter may fit such data and obtain a seemingly reliable result. Although a systematic mismatch between the data and the fitted line may betray the presence of a kinetic effect, this criterion by itself is not sufficient to diagnose this problem. Only the observation of signal over time can rule out kinetic effects such as these.

3.3 MST of the HIF-ARNT PAS-B Interaction

To illustrate some of the pitfalls and opportunities afforded by the characterization of protein-protein associations by MST, we studied two such interactions. The first was binding of the PAS-B domains of the hypoxia-inducible factor HIF-2α and the ARNT subunits of the HIF-2 transcription factor. HIF proteins play key roles in the cellular responses to variable, local oxygen levels and, when misregulated, promote cancer progression [40]. These two small protein domains (about 13.5 and 14.2 kDa, respectively) form contacts essential to the heterodimerization and transcriptional activity of the full-length proteins in cells [41,42]. Recently described small-molecule antagonists of HIF-1 and HIF-2 target intermolecular PAS-B contacts [43–46], representing promising avenues for novel cancer therapies. Characterized here is the interaction between mutant PAS-B domains that were designed to have a higher affinity than the wild-type pair: the HIF-2α R247E and the ARNT E362R mutants. Hereafter, we therefore refer to these proteins as “HIF-E” and “ARNT-R”, respectively.

Our experimental strategy was a typical one for MST experiments. The concentration of labeled ARNT-R (ARNT-R*, produced by covalently modifying ARNT-R with AlexaFluor488) was held constant in all 16 interaction mixtures at 150 nM. The concentration of HIF-E, on the other hand, was varied in a sixteen-sample, 1:1 serial dilution series from 2.3 nM to 75 μM. The experiment displayed a robust thermophoretic signal (not shown). We also observed a very strong trend in the overall fluorescence in Zone A (“raw fluorescence”) with respect to [HIF-E] (Fig. 4). The latter feature was not intrinsically problematic; indeed, such a signal may also be analyzed with a 1:1 binding model as in a traditional fluorescence quenching experiment [47]. However, we observed an essentially identical trend in the raw fluorescence signal when the study was conducted in a competition mode. In this experiment, ARNT-R* and HIF-E were held at constant respective concentrations, and unlabeled ARNT-R was the titrant. Under such conditions, high ARNT-R concentrations should effectively compete for HIF-E binding, resulting in greater free ARNT-R* concentrations. This configuration should have resulted in a raw fluorescence trend that was opposite to that noted above. Instead, the trend was nearly identical (Fig. 4). We concluded that the raw-fluorescence phenomenon was not due to HIF-E/ARNT-R binding. Rather, it likely was the result of ARNT-R* adhering to the plasticware used to dispense the proteins. Thus HIF-E (or ARNT-R in the competition experiment) was acting to diminish the adherence at high concentrations, preventing the labeled protein’s loss and generating a concentration-dependent, positive trend in raw fluorescence.

Figure 4. Raw fluorescence values for the HIF-E/ARNT-R interaction under various conditions.

The graph shows the “raw fluorescence”, i.e. the fluorescence reading prior to the actuation of the IR laser, for experiments noted in the inset legend.

A potential solution to this problem is to include at moderate concentration a so-called carrier protein such as bovine serum albumin (BSA) [8] to saturate non-specific protein-binding surfaces on plasticware and capillary tubes. We attempted to employ this measure in the HIF-E/ARNT-R* experiments. However, we found that the inclusion of 0.1 mg/mL BSA in the interaction mixtures severely impacted the thermophoresis of the proteins, resulting in negative thermophoresis and a contrary trend at high [HIF-E] (Fig. S2). It also resulted in a strong, reversed trend in raw fluorescence at greater titrant concentrations (Fig. 4). We therefore abandoned this approach, as it seemed likely that the BSA was directly interacting with the proteins and not behaving as a passive carrier. We note generally that BSA may be a suboptimal choice as a carrier protein in MST experiments because it can be intrinsically fluorescent at wavelengths relevant to the observation of MST signals, presumably due to contamination of the commercial preparations of the protein with fluorescent pigments [48].

Another means to eliminate the adhesion of proteins to apparatus is the inclusion of a mild detergent. Addition of 0.05% (v/v) Tween-20 in all interaction mixtures greatly reduced the raw fluorescence trend (Fig. 4), yet the samples retained a robust thermophoretic signal (Fig. 1, upper panel). We thus adopted this practice for all subsequent experiments featuring the HIF-E/ARNT-R* pair.

Given the kinetic result simulated above (Fig. 3), we devised a strategy to examine whether there were changes in the thermophoresis binding curve as a function of time. If observed, these changes would indicate that the time of incubation was not long enough to allow the mixtures to achieve equilibrium. A sufficient quantity of the interaction mixtures was prepared (30 μL for each titration point) such that the titrations could be sampled at three discrete time points (10, 30, and 105 min) and their respective thermophoresis binding curves obtained. Superposition of these binding curves (Fig. S3) resulted in almost perfect overlap, indicating that even the shortest incubation time was suitable for this interaction. A systematic exploration of the association kinetics for this interaction suggested that the k_off for this association could be about 3 × 10⁻³ s⁻¹ or faster (not shown).

As a final control experiment, we wished to establish the specificity of the interaction. To this end, we used a different protein as the titrant: the soybean trypsin inhibitor (SBTI). Titrating this protein against a constant concentration of ARNT-R* (150 nM) resulted in only a very weak trend in thermophoresis (amplitude = 1.5 thermophoresis units) (Fig. S3). This result effectively rules out the notion that the observed association between HIF-E and ARNT-R* was due solely to non-specific interactions.

Having successfully devised a strategy to obtain interpretable, reliable, and specific MST data, the data acquisition could proceed in earnest. Data from three titrations were collected and averaged; they appeared to be of excellent quality (Figs. 1 & 5).

Figure 5. TJ data for the HIF-E/ARNT-R* interaction.

The upper panel shows the time-traces, with the pink and blue areas depicting time-spans used to obtain F_h and F_c, respectively, for insertion into Eq. 1. Three trials are shown superposed, with the fluorescence normalized to a starting value of 1.0. Each trial is color-coded, with the first being black, the second blue, and the third red. The resulting binding curve data are shown in the middle panel, with each circle representing the average of F_n, and error bars show the standard deviation. The line is the best fit of the data to the 1:1 binding model. Residuals between the fit and the data are depicted in the bottom panel.

With interpretable data in hand, a new challenge was encountered: data analysis. Specifically, the extracted K_D was strongly dependent on which zones of the time-traces were compared in the thermophoretic quotient (Eq. 1), i.e. on the mode of analysis chosen (TA, TJ, or T+TJ; see Fig. 1 and Section 2.1.1). The K_D’s obtained using each of these modes varied from each other as much as five-fold (Table 3), raising the unsettling prospect that a researcher could choose the K_D that most closely fits a favored hypothesis through the choice of analysis mode.

Table 3.

Variation in calculated K_D’s for the HIF-E/ARNT-R* interaction

	Fn Definition
	TA	TJ	T+TJ
KD (nM)	170 [140, 210]a	820 [670, 990]	250 [220, 290]

^aNumbers in brackets represent the 68.3% confidence interval calculated by ESP

To resolve this conflict, we examined ITC data for HIF-E/ARNT-R obtained under similar conditions. These data (Fig. S4) indicated that the ΔH of the interaction was endothermic (+4.4 [4.2, 4.6] kcal/mol), and that the K_D was approximately 560 [440, 710] nM (68.3% confidence intervals are presented in brackets throughout this report). This K_D was close to the one obtained from MST in the TJ mode, i.e. 820 [670, 990] nM (Table 3). We note that other researchers have obtained a K_D of about 1.4 μM for the interaction of similar protein constructs [44]. Another point arguing in favor of the TJ analytical mode is that it presumably measures the effect of binding before temperature-induced changes in K_D can fully manifest (see Section 4.2).

Therefore, in the end, we chose the TJ mode for the final analysis of the HIF-E/ARNT-R* data (Fig. 5), yielding a K_D of 820 nM. While the fluorescence differences that were used in this analytical mode were small (Fig. 5, upper panel), they exceeded the noise of the instrument and they were very reproducible, yielding a precise, interpretable binding curve (Fig. 5, lower panel). Also, the width of the 68.3% error interval on K_D was similar to that obtained from the ITC experiment (Section 3.4; Table 3). As an additional measure of the consistency in the three individual titrations, we analyzed them all separately. This approach yielded an average K_D of 820 nM with a standard deviation of 150 nM.

3.4 Comparisons of confidence-interval calculations

The excellent data procured from the HIF-E/ARNT-R* interaction afforded the opportunity to assess the performance of several methods to determine the confidence intervals for the refined parameters. We examined four methods of calculating the confidence intervals for K_D, the most thermodynamically relevant parameter refined in these analyses: (1) the variance-covariance matrix; (2) ESP; (3) Monte Carlo; and (4) bootstrap. The 68.3% confidence interval is reported in the following discussion, but it is possible to calculate other intervals; the 95% interval is routinely used in many disciplines.

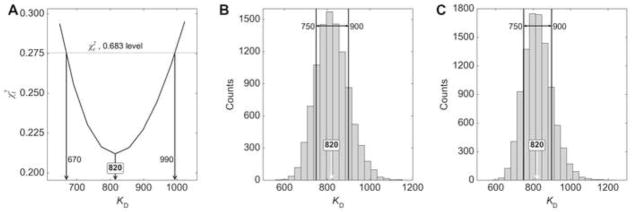
In the fitting procedure employed above, the variance-covariance matrix was calculated as a by-product. Thus, there was almost no computational cost to obtaining confidence intervals from this source. The diagonal elements of this matrix are the estimated variances of the respective fitted parameters, and therefore an approximate 1-σ interval for the parameters (equivalent to the 68.3% confidence level) may be calculated from the square roots of these elements (i.e., this interval is ± σ). For the HIF-E/ARNT-R* data, we found that the confidence interval for K_D calculated in this way was [740, 900] nM.

The other three methods are post-hoc procedures dependent on the residuals between the fitted line and the data points. The ESP method employed herein (section 2.1.2, Fig. 2B) efficiently arrives at error intervals, and thus we have automatically incorporated it at the conclusion of all fitting sessions. The ESP plot (Fig. 6A) shows that the confidence interval for HIF-E/ARNT-R* was [670, 990] nM. This interval was wider than that estimated by the variance-covariance method, but was likely to be more accurate because it was based on a systematic exploration of the error surface [17]. The Monte Carlo error-sampling method (Section 2.1.1; 10,000 iterations) was slower (about 2.5 min on our trial computer systems) and yielded a confidence interval of [750, 900] nM (Fig. 6B), very similar to that obtained from the variance-covariance matrix. Finally, the bootstrap method was also employed (Section 2.1.1). Again using 10,000 iterations and taking about 2.5 min, the confidence interval was estimated to be the same as for the Monte Carlo method, i.e., [750, 900] nM (Fig. 6C).

Figure 6. Results of three confidence-interval calculations for the HIF-E/ARNT-R* TJ data.

(A) An error-surface projection. The format is the same as in Fig. 2A. (B) A Monte-Carlo histogram. As in part A, the best fitted K_D is shown annotated on the X-axis, which shows the binned K_D; the ordinate shows how many counts from 10,000 trials fit into the given bin. The bounds of the central 68.3% of the results are shown with vertical lines. (C) A bootstrap histogram. The format is the same as that for part B.

Which confidence interval should be used, then? We routinely report the interval reported using the ESP method, because it represents a rigorous exploration of the error surface, accounting for the ability of other parameters to compensate for defects in the parameter of interest. It is also quicker. The variance-covariance interval is usually quite small and is based on assumptions of local error-surface behavior that may not be true, while those derived from the Monte Carlo and bootstrap methods are slower and can neglect parameter correlations [49]. Thus, the final, reported K_D for the HIF-E/ARNT-R* interaction was 820 [670, 990] nM.

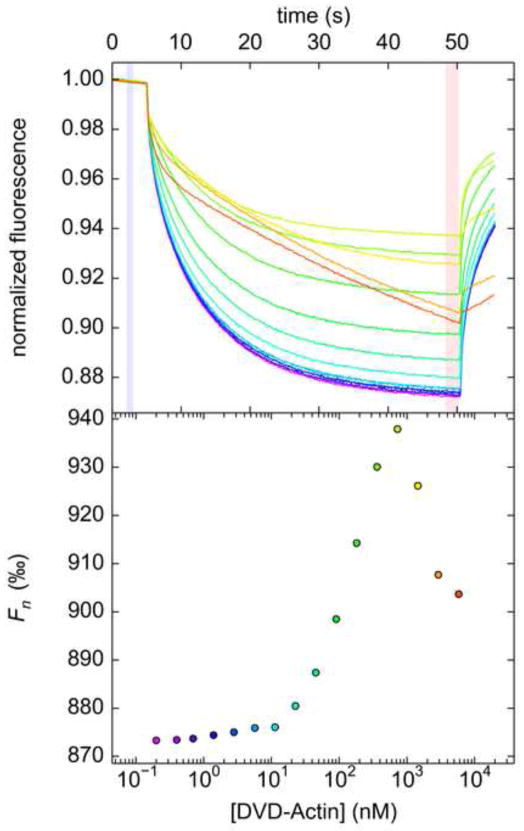
3.5 High-concentration aberrations in thermophoresis: the VCA/actin interaction

Occasionally and unpredictably, we have observed that thermophoresis can exhibit a strong contrary trend at high A. An example of this behavior can be observed (Fig. 7) in the interaction of two proteins implicated in the dynamics of actin filament assembly [50]: 5C actin from D. melanogaster (in this case, a non-polymerizable mutant called “DVD-Actin”) and the human neuronal Wiskott-Aldrich syndrome protein (N-WASP; we used a mutated, labeled peptide (VCA′*) from N-WASP; see Section 2.2). In this titration, a strong upward trend in thermophoresis was abruptly reversed at high [DVD-Actin] (Fig. 7). Although such behavior is conceivable if there were a second site on DVD-Actin for VCA′*, AUC data strongly imply that the two species interact with a 1:1 stoichiometry [51]. We therefore attributed the contrary trend in thermophoresis to aberrant behavior of the proteins under the conditions of the MST assay. This determination was corroborated by the very unusual (i.e. linear) appearance of the thermophoresis time-traces at high [DVD-Actin] (Fig. 7, upper panel). The cause of this phenomenon is unknown, but the fact that it appears only at high titrant concentrations suggests that it could be caused by hydrodynamic non-ideality (see [52–54] for treatments in the context of AUC) or concentration-dependent, heat-induced aggregation of the titrant. Thus, it is perhaps valid to exclude the high [DVD-Actin] data points from the analysis. However, doing so can introduce significant uncertainty in the fitted F_AB* and K_D parameters.

Figure 7. Concentration-dependent aberrations in DVD-Actin/VCA′*.

The top panel shows the color-coded time traces, with purple representing the time-trace with the lowest [DVD-Actin] and red denoting that with the highest. The areas used to calculate F_n are shaded blue and pink. The resulting binding curve is shown in the lower panel, with data points colored according to their respective time-trace.

In our experience, there is an alternative strategy that may be employed in systems such as DVD-Actin/VCA′*. Traditionally, information on the best values of F_B* and F_AB* is gathered by sampling the binding curve at very low and very high A, respectively (Fig. 1, lower panel). However, the curvature of the binding curve near to its inflection point is sufficiently information-rich such that, if well defined, it supplies a restraint on F_AB*. Thus the combination of knowing F_B*, which is easily probed experimentally, and choosing concentrations in the titration such that the curved region of the binding curve is well sampled allows for an adequate estimate of F_AB* and an excellent estimate of K_D.

We put this strategy into practice in the actin/VCA interaction. Operationally, a good way to oversample the curved region of the binding curve is to choose a linear titration mode rather than a logarithmic one; the latter has been accomplished thus far in this study by using 1:1 serial dilutions of A. In the case at hand, a linear titration was achieved by choosing a 16-point titration in which the highest [DVD-Actin] was 500 nM and lowering this concentration by 33.3 nM in each successive sample, ending with 0 nM actin in the sixteenth sample. When plotting such data, we choose to scale the x-axis linearly; thus, the binding curves will assume a square hyperbolic appearance, not the sigmoid shape of earlier examples. As with the HIF-E/ARNT-R* experiments (Section 3.3), the data points represent the averages of three independent replicates.

The data procured from this titration series allowed for a reasonable fit of the one-site K_D model for DVD-Actin/VCA′* (Fig. 8A). As with the HIF-E/ARNT-R* interaction, we found that analyzing data from the TJ and TA modes led to different values for K_D. The K_D for TA was 220 [180, 270] nM, but 62 [44, 86] nM for TJ. This trend in K_D was opposite that for the HIF-E/ARNT-R* system. Given our experience with HIF-E/ARNT-R*, we chose to analyze the TJ data. Indeed, in fluorescence polarization studies with similar materials [31], the measured K_D was 70 ± 10 nM, in excellent agreement with our TJ data.

Figure 8. Binding curves from the linear VCA′*/DVD-Actin titrations.

Circular markers are the averaged F_n values for the direct titration, and squares represent the data from the triplicated competition experiment. The black, dotted line represents the fit using only the direct data, resulting in a K_D of 62 [44, 86] nM. The gray, solid lines depict the results of a global fitting of the direct and competition data (i.e. the PALMIST “1:1 Comp.” model). Residuals are shown in the bottom panel in respective shades.

MST should be well-suited to competition experiments. However, these experiments must be carefully planned. The best experimental setting is to have a constant concentration of B* and A in all samples, with the titrant being a molecule C that competitively binds to A. At high C in the presence of moderate A, the observed F_n should approach F_B*, as B* will be unable to bind to A. The goal of such experiments is the simultaneous, global determination of K_D(AB*) and K_D(AC). This experimental mode is advantageous to the user because it allows the labeling of only one species (B); K_D’s of mutants or homologs of B (termed C here) can then be characterized without the labeling step.

To test the performance of competition experiments in MST and to examine the utility of our fitting algorithm (see Supplemental Methods), we conducted a competition experiment in which A and B* were DVD-Actin and VCA′*, and C was an unlabeled, wild-type version of the peptide (termed “VCA”). The [DVD-Actin] and [VCA′*] were held constant at 100 nM and 25 nM, respectively, and VCA was titrated linearly from 0 nM to 700 nM. In analyzing the data (Fig. 8B), we prefer to globally analyze both the direct and competitive titrations because both contain information on K_D(AB*) (Fig. 8B). The fitting algorithm performed admirably, yielding K_D(DVD-Actin/VCA′*) = 65 [52, 81] nM and K_D(DVD-Actin/VCA) = 110 [80, 140] nM. Importantly, the K_D(DVD-Actin/VCA′*) obtained here was extremely close to that obtained using only the direct binding curve (Fig. 8A). Another interesting conclusion to be drawn from these data was that the wild-type, unlabeled VCA appeared to have a slightly higher K_D for DVD-Actin. Whether this was a consequence of labeling, mutation, concentration errors, or a combination of these factors is unknown.

4 Discussion

The results presented in this study demonstrate that MST can be an accurate and robust method for determining K_D’s of biologically relevant interactions. However, our extensive simulations and our empirical observations suggest that there are several considerations—both experimental and analytical— that must be taken into account when planning, executing, and analyzing MST studies. These are presented below with the intention of supplying MST users with a rigorous set of best experimental practices.

4.1 Experimental considerations and controls

General experimental parameters for MST have been covered in other publications [8–10, 14]; we briefly present the most germane ones here. The three most critical instrumental parameters to explore are the power supplied to the excitation LED (LED power), the power supplied to the IR laser (MST power), and the time of observation for thermophoresis (t_t). LED power should be chosen such that there is enough fluorescence signal to provide a reasonable signal-to-noise ratio, as our simulations show that this is more important than having many points in the transition region of the binding curve (Table 2). In our Nanotemper NT.115 instrument, fluorescence readings between 200 – 1500 counts are desirable. However, the LED power should be low enough to avoid significant photobleaching of the fluorophore. This can be discerned by observing the fluorescence time-trace prior to the activation of the IR laser; if it exhibits a substantial slope, the LED power should be attenuated. Alternatively, other methods (such as scavenging free O₂) can be employed to ameliorate this problem [9]. A similar balance must be struck with the MST power: it should be high enough to induce significant thermophoresis in the sample, but not so high that it causes precipitation or aggregation of the solutes. The latter phenomenon often manifests itself in the fluorescence time-traces as an irregular, non-smooth appearance. We have also observed visible, concentration-dependent precipitation of large protein titrants in MST experiments. It is therefore important that experimenters visually inspect the capillary tubes immediately after an MST experiment to rule out this possibility, and capillary scans following the experiment are recommended to rule out heat-induced adhesion of the protein to the capillary walls. The final parameter, t_t, should be chosen to be long enough to allow thermophoresis to achieve a new steady state. This may be difficult to judge by eye, but at the very least, t_t should be chosen such that fluorescence time-traces exhibit very little slope prior to the extinguishment of the IR laser.

Inherent to the MST experiment is a change in temperature. This has a bearing on experiment planning because it can lead to a change in pH. Most buffering agents will manifest a change in pK_a upon a temperature change (d(pK_a)/dT). For instance, the widely used biological buffer Tris has one of the largest such effects, with d(pK_a)/dT ≈ −0.03 K⁻¹ [55–57]. Literature reports suggest that the change in temperature in a typical MST experiment ranges from 2 – 8 K. A temperature-induced change in the solution’s pH could effect a substantial change in the apparent K_D if proton uptake or release is implicated in the association under study and the experimental pH is near to the pK_a of the ionizable group [58]. The experimenter’s ability to observe such changes will be dependent on the association kinetics. To avoid this potential difficulty, we recommend that experimenters use a buffer with a small d(pK_a)/dT, such as phosphate (−0.0028 K⁻¹), acetate (0.0002 K⁻¹), or carbonate (−0.009 K⁻¹ for pK_a(2)) [55–57].

There are several control experiments for MST that should be conducted based on our findings. First, the time of incubation should be investigated to be certain that the interaction mixtures have achieved equilibrium before the MST data acquisition is initiated. We suggest that this be accomplished by preparing a single experiment with sufficient volume to accommodate three data acquisitions (i.e. each interaction mixture should be about 30 μL for the standard-volume capillary tubes). Three separate data sets using samples drawn from these mixtures should be collected at appropriately spaced points in time; we suggest 10, 30, and 100 min for interactions in which nothing is known about the association kinetics. If the observed K_D is dependent on time, longer incubation times are indicated. If these control experiments are not feasible, based on a lowest observable K_D of 1 nM and likely slowest k_on of 10⁴ M⁻¹s⁻¹, an overnight (ca.16-hr) incubation should suffice for most interactions that are practicable in a normal MST instrument.

It is also prudent to perform control experiments that support the specificity of the observed interaction. For example, for a protein-protein (A + B* ↔ AB*) interaction, an alternative hypothesis for any trend in the thermophoretic signal is that it is due solely to non-specific adherence of the labeled protein to any other protein. Specificity can be explored by replacing the titrant with a molecule that should not bind to the labeled species. Upon titrating the replacement molecule, one would expect to see no trend in thermophoresis, thus negating the alternative hypothesis. We successfully used this strategy in the HIF-E/ARNT-R* experiments, substituting SBTI for HIF-E (Fig. S3). Another strong indicator of specificity is the ability of an unlabeled competitor (C) to disallow the formation of the AB* complex at high C; thus the observed thermophoresis would trend to that of free B*. This was observed in the VCA′*/actin interaction (Fig. 8B).

A final set of experimental considerations pertains to aspects that MST has in common with other methods. For example, in many cases, extrinsic labeling of one binding partner (B, in our parlance) with a fluorescent dye is necessary (resulting in B*). MST shares this necessity with fluorescence quenching and fluorescence anisotropy experiments in which the native binding partners are not fluorescent. The dye adduct may affect the interaction between the modified molecule and its partner unpredictably. This potential problem may be addressed by competition experiments in which unmodified B is titrated into mixtures of B* and A. An additional experimental factor that may influence K_D is the presence of non-denaturing detergents; for example, we used Tween-20 in all of our assays to minimize the adherence of the labeled proteins to the capillary surface and to the plasticware used to measure and contain the solutions (Sections 2.3 & 3.3). Of course, it is possible that detergents may populate hydrophobic surfaces on proteins and interfere with the interaction. However, it is expected that the protein/detergent interactions are weak and non-specific [59], and thus the stronger, specific protein-protein interactions will dominate MST observations. Nonetheless, if it is known that two proteins interact via the burial of a large, hydrophobic surface area, it may be worthwhile to discover a combination of solution conditions, non-adhering plasticware, and capillary tubes that does not require the addition of surfactants.

4.2 Analytic considerations

Our results also highlight a set of best analytic practices. We recommend the ESP method of confidence-interval determination unless the user has a specific and valid reason to suspect that another method will perform better. If very small confidence intervals are necessary, the experimenter may wish to turn to other methodologies, e.g. fluorescence polarization. However, the most accurate approach to analyzing binding energetics may be a global analysis of data from several techniques [60,62].

While the ability of MST data to describe high K_D’s appears to be limited only by the concentration limits of the species, the lower limits are defined by the signal-to-noise level and the experimenters’ confidence in the concentrations of the components and in their pipetting technique. Under ideal conditions and using currently available commercial MST instrumentation, the lowest achievable K_D appears to be about 1 nM in a standard commercial instrument and 1 pM in an instrument designed for the detection of very low concentrations of fluorophores. However, these low K_D’s will come with wide confidence intervals, and thus the ability to discriminate between very low values will be eroded at these limits. Unlike ITC experiments [61], the lower limit of K_D in MST experiments is not effectively extended in competition experiments.

In both of the MST experimental systems detailed above (Sections 3.3 & 3.5), the refined K_D depended on the analysis mode, i.e. TA, TJ, or T + TJ. One potential explanation for this phenomenon was that the increase in temperature perturbed the value of K_D. Coupled with rapid dissociation kinetics, this could account for small changes in K_D during the time course of the MST experiment (conversely, slow dissociation kinetics should result in K_D’s that do not vary with the mode choice and that reflect the K_D at the pre-TJ temperature). We examined the feasibility of this hypothesis in the case of the HIF-E/ARNT-R* interaction. By employing the van’t Hoff equation in conjunction with the change in K_D (ca. 5X) and a guess of the change in temperature (+4 K), we estimated that ΔH would have to be about +70 kcal/mol for the variable K_D phenomenon to be solely attributable to the temperature change. The measured ΔH for this interaction was +4.4 kcal/mol; it was therefore unlikely that the temperature change alone was responsible for this phenomenon. Plausibly, this observation could be due to a complex interplay of dissociation kinetics, enthalpy, entropy, changes in heat capacity, detergent effects (if present), and temperature-induced pH changes. Further investigation is required to uncover the origins of this apparent change in K_D with respect to IR-irradiation time. Our experiences imply that TJ data, which ostensibly measure K_D before temperature effects become dominant, are most reliable under these circumstances. For this reason, we suggest that the TJ method be used preferentially to TA or T + TJ; the latter two may be useful when analyzing data traces in which no TJ changes are evident.

The choice of analytic mode also has implications on the reported temperature of the experiment. In the currently marketed MST instruments, the experimental temperature can be held between 22° and 45° C. If the TJ mode is used, we suggest that the pre-TJ temperature (i.e. the temperature in the instrument) be reported. However, the TA and T + TJ modes imply a rise in temperature to an unknown value. It is thus vital that the experimenter report both the pre-IR temperature as well as the MST power. Although this will not provide an exact temperature reading, at least it establishes a basis for the replication of experiment and for comparison to other, similar experiments.

We have observed on several occasions a reversal in the trend of the F_n vs. A curve at high A (e.g. see Fig. 7). Although the cause of this phenomenon is obscure, we have explored means to mitigate its impact on data analysis. One approach is to remove data points that are putatively affected by this aberration. We find that this strategy can work, but can also raise questions regarding which data points should be discarded and how accurate the resulting parameters are. The alternative approach used above for the DVD-Actin/VCA′* interaction is to sample the A space very thoroughly near to the curve’s inflection point, which allows for a good estimate of the parameter that would normally be observed at high A, F_AB*. This is often best accomplished using a linear rather than logarithmic titration series (Fig. 8). Linear sampling of A may also be useful in situations featuring poor ligand solubility or limited ligand availability.

4.3 PALMIST: software for MST analysis

We have designed new software called “PALMIST” (Python-based AnaLyzer of MIcroScale Thermophoresis) that aids in the experimental planning, troubleshooting, analysis, and documentation of MST data. Overall, the program features a user-friendly, intuitive interface with a large graphing window and easily accessed controls (Fig. S5), and is freely distributed with an instantly accessible manual.

For planning purposes, PALMIST features a simulation module that enables the user to anticipate the concentrations of components needed to arrive at a reliable K_D given a set of experimental parameters. This module also allows the user to test the effect of association kinetics on the appearance of the MST binding curve. Moreover, the user can check the likely robustness of the parameters derived from data similar to the simulated data by performing a Monte Carlo or pseudo-bootstrap analysis on the simulation. Simulated data can be written out as pseudo-time-trace data and analyzed, if desired. Also, at the user’s request, the program will write a text file that details an experimental protocol for preparing the titration. All of these features render PALMIST a very powerful tool for the experimental planning purposes, and we note that such experimental design concepts are not limited to MST data; thus, this module can be used by researchers to plan experiments from diverse technologies. Notably, all of the Monte Carlo (Table 1) and kinetic approach-to-equilibrium (Fig. 3) experimental simulations carried out in this study were performed in PALMIST.

The kinetics of the interaction plays an important role in MST binding assays (Fig. 3). We have recommended a control experiment in which MST binding curves from identical samples are studied as a function of time. PALMIST has a feature that can analyze these binding curves and report when a time-dependent change in K_D is encountered. This represents a fast and objective way to discover kinetic effects in the binding curves.

PALMIST also has many features that enable the rigorous and reliable estimation of the thermodynamic parameter K_D and its confidence interval. Importantly, the definitions of Zones A, B, and C (Fig. 1) are defined based on information supplied from the data file, and thus will be defined consistently even for multiple experiments that were not carried out identically. User intervention in the definition of the zones is allowed, but discouraged. During the optimization of parameters, PALMIST uses alternating NMS and LM NLSM algorithms (Section 2.1.2) to rapidly converge on best values. Potential outlier F_n data points are automatically detected and identified to the user upon request. Additionally, the ESP algorithm detailed in Fig. 2B is used automatically immediately after every converged optimization. ESP is the default confidence-interval calculation protocol in PALMIST, and because of the protocol delineated above, the results are immediately available to the user with no further action. The program can produce ESP plots like those shown in Figs. 2A & 6A upon request. Confidence intervals from the variance-covariance matrix, Monte Carlo simulation, or bootstrap simulation are also available; using our test data, 10,000 Monte-Carlo or bootstrap iterations can be completed in ca. 3 min. The user can choose to report either 68.3% or 95% confidence intervals. Three analysis models are currently available: 1:1, Hill (EC₅₀), and Competition.

An important feature of PALMIST is its advanced documentation capabilities. A log of all analysis steps is kept by the program, and this can be outputted or annotated at any time. Post-analysis, the user may write a report in the Portable Document Format (.pdf); this report includes a snapshot of the analysis window, text of the entire analysis log, and graphs depicting the confidence intervals (ESP plots or Monte Carlo/bootstrap histograms, depending on the user’s choice of confidence-interval determination). A similar report can be written in the Office Open XML Presentation Format (.pptx), which can be read by presentation software such as PowerPoint. Uniquely for MST data, the analysis session may be saved in a binary format (.palmpkl) that can be read later by PALMIST, enabling the quick recall and amendment of analyses. This file format contains everything about the MST analysis, including the data and session log, making it fully portable and thus enabling collaborative data sharing. Also, the program can interface with the graph-making software GUSSI [37] to enable the flexible creation of publication-quality graphs of the data (see Figs. 5, 7, & 8).

PALMIST is available for download free-of-charge at http://biophysiscs.swmed.edu/MBR/software.html. It is compiled to run under the Microsoft Windows operating system, but various emulation and non-emulation solutions are available, enabling operation of the program under the Apple Macintosh operating system.

On a final note, the analytical approaches incorporated into PALMIST should be applicable to other binding-assay techniques. Both SPR and biolayer interferometry seem particularly well suited to these methods: the time-traces produced by these methods can be converted to Langmuir isotherms [62,63], which may then be analyzed to yield K_D. Future development of the program is planned to expand its capabilities in this regard.

Abbreviations

βME

2-mercaptoethanol

ARNT

aryl hydrocarbon receptor nuclear translocator

ARNT-R

PAS-B domain of ARNT with E362R mutation

AUC

analytical ultracentrifugation

DMSO

dimethyl sulfoxide

DVD-Actin

triple-mutant, non-polymerizable actin

ESP

error-surface projection

GST

glutathione S-transferase

HIF

hypoxia inducible factor

HIF-E

PAS-B domain of HIF2α with R247E mutation

ITC

isothermal titration calorimetry

IPTG

isopropyl β-D-1-thiogalactopyranoside

LB

Luria-Bertani

LM

Levenberg-Marquardt

MST

microscale thermophoresis

NLSM

non-linear least-squares minimization

NMs

Nelder-Mead simplex

NMR

nuclear magnetic resonance

N-WASP

neuronal Wiskott-Aldrich Syndrome protein

PAS

Per-Arnt-Sim

r.m.s.d

root-mean-square deviation

SBTI

soybean trypsin inhibitor

SPR

surface plasmon resonance

TA

thermophoresis alone

TEV

tobacco etch virus

TJ

temperature jump

T+TJ

thermophoresis and temperature jump

VCA

verprolin-homology-central-acidic

WASP

Wiskott-Aldrich Syndrome protein