Application of the Multistate Tuberculosis Pharmacometric Model in Patients With Rifampicin‐Treated Pulmonary Tuberculosis

Abstract

This is the first clinical implementation of the Multistate Tuberculosis Pharmacometric (MTP) model describing fast‐, slow‐, and nonmultiplying bacterial states of Mycobacterium tuberculosis. Colony forming unit data from 19 patients treated with rifampicin were analyzed. A previously developed rifampicin population pharmacokinetic (PK) model was linked to the MTP model previously developed using in vitro data. Drug effect was implemented as exposure‐response relationships tested at several effect sites, both alone and in combination. All MTP model parameters were fixed to in vitro estimates except B_max. Drug effect was described by an on/off effect inhibiting growth of fast‐multiplying bacteria in addition to linear increase of the stimulation of the death rate of slow‐ and nonmultiplying bacteria with increasing drug exposure. Clinical trial simulations predicted well three retrospective clinical trials using the final model that confirmed the potential utility of the MTP model in antitubercular drug development.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC? ☑ There is a lack of semimechanistic PK/PD models within TB. The MTP model has been applied to in vitro and animal data in which natural growth and rifampicin drug effect were successfully described. • WHAT QUESTION DID THIS STUDY ADDRESS? ☑ Can the MTP model be applied to clinical CFU data after rifampicin monotherapy? Can the approach predict retrospective clinical data using clinical trial simulations? • WHAT THIS STUDY ADDS TO OUR KNOWLEDGE ☑ The MTP model was successfully applied, which indicates that the MTP model can be used for clinical and preclinical trial simulation. In addition, this study adds to the evidence concerning rifampicin mechanism of action. • HOW THIS MIGHT CHANGE CLINICAL PHARMACOLOGY AND THERAPEUTICS ☑ The MTP model can potentially aid in decision support for trial designs and program design evaluations within the field of TB drug development.

Rifampicin is a recommended first‐line antitubercular drug used in patients with drug‐susceptible pulmonary tuberculosis (TB)1 partly because rifampicin is efficient in avoiding relapse.2 Rifampicin inhibits bacterial DNA‐dependent RNA polymerase,3, 4 which is essential for bacterial metabolism, leading to activity against multiplying and nonmultiplying bacteria.5

Clinical symptoms appear late in the infection6 when infections are at a stationary phase in which no change in the colony forming unit (CFU) over time in untreated patients is seen.7 Studies on clinical sputum samples with resuscitation‐promoting factors revealed that only 0.01–20% of Mycobacterium tuberculosis (M. tuberculosis) cells are quantified as CFU,8 suggesting existence of a large portion of noncultivable nonmultiplying bacteria.

In short‐term clinical data, a biexponential pattern of decline in CFU can be seen.9 This is thought to be due to subpopulations with different drug susceptibility giving rise to an initial rapid and a late slower decline, respectively. The CFU readout is widely used within TB drug development to quantify treatment progression10 in which the rate of decline in CFU is associated with treatment outcome.11 In vitro, at least three different subpopulations exist within a M. tuberculosis culture.12 Susceptibility relates to in vitro conditions; log‐phase and oxygen‐rich cultures are susceptible to drugs, whereas stationary phase and oxygen‐poor cultures are not. Subpopulations surviving drug exposure are by definition phenotypically tolerant13 and are slow‐ or nonmultiplying.14

The Multistate Tuberculosis Pharmacometric (MTP) model is a semimechanistic model describing fast‐, slow‐, and nonmultiplying bacteria. It has been successfully applied to describe in vitro 15 and mouse data16 but not until now to clinical data.

The objective of the analysis was to apply the MTP model, linked to rifampicin pharmacokinetics (PKs), to clinical phase IIa CFU data in patients with drug‐susceptible pulmonary TB. In addition, we performed clinical trial simulations using the developed final model in order to predict retrospective clinical data as external validation.

METHODS

Patients and study design

Data included individual sputum CFU counts from 23 patients with treatment‐naive Kenyan drug‐susceptible pulmonary TB divided into four arms: (1) no treatment (negative control, n = 4); (2) 5 mg/kg (n = 3); (3) 10 mg/kg (n = 8); or (4) 20 mg/kg (n = 8) rifampicin daily at 8 am. Patients were treated for 14 days with sputum collected during 12 hours overnight (between 8 pm and 8 am) every second day, including two baseline measurements. Sputum samples were cultivated on agar plates for CFU counting. For more details, the reader is referred to the original publication.17 No formal ethical review boards or written consent process existed at the time of the conduct of the study (1966–1977). However, the principal investigator has confirmed that no restrictions relating to reuse of data were envisaged and reuse of the irreversibly anonymized data by the PreDiCT‐TB consortium was approved by the UK National Research Ethics Service.

Overall modeling strategy

The first step was to adapt the MTP model15 for the clinical TB setting. This was done by fixing all parameters except B_max to estimates from the in vitro MTP setting.15 The second step was to include a human rifampicin PK model in order to describe rifampicin exposure. Finally, drug effect was quantified by developing exposure‐response relationships linking the PK model to the MTP (disease) model. All observed CFU data were modeled simultaneously as the natural logarithm of CFU in ml⁻¹ and log‐transformation both sides. Data analysis was performed with the nonlinear mixed effects modeling software NONMEM version 7.3 (Icon Development Solutions [http://www.iconplc.com/technology/products/nonmem], Ellicott City, MD)18 using the first‐order conditional estimation with interaction. Data handling was performed in R version 3.1.1 (R Foundation for Statistical Computing [http://www.R-project.org], Vienna, Austria).

Population pharmacokinetic model

As previously described, the PK‐enzyme turnover model for rifampicin19 was used as the PK model. Because the data contained no observed rifampicin concentrations, a population PK parameter approach20 was used. Random variability parameters were removed with the remaining structural parameters fixed to reported estimates of fixed effects. As no covariate information was available, covariates were set to most common or median values. Each patient was assumed to be human immunodeficiency virus (HIV) negative with a body weight of 56 kg and a fat free mass of 45 kg, which were the mean observed demographics in the study used for developing the PK model.19 These patients originated from South Africa, Senegal, Benin, and Guinea.

The Multistate Tuberculosis Pharmacometric model

The structure of the MTP model15 developed using in vitro time‐kill data was used as the disease model. The structure included fast‐multiplying, slow‐multiplying, and nonmultiplying bacterial states. Only the bacterial numbers in the fast‐ and slow‐multiplying states were visible as CFU, the nonmultiplying state was considered nonculturable. Growth of the fast‐multiplying state was described by a Gompertz function. The MTP model does not include growth of slow‐multiplying bacteria but only increase of slow‐multiplying bacteria because of transfer of bacteria from the fast‐multiplying state.15 Each bacterial substate was allowed to transfer between all states, except from non‐ to fast‐multiplying state. This transfer was judged scientifically negligible in vitro because of hypoxia.15 The transfer rate from fast‐ to slow‐multiplying state increased linearly with time.

The differential equations were written as:

$$\frac{dF}{dt}=k_G·\log \left(\frac{B_{\mathrm{m}\mathrm{a}\mathrm{x}}}{F+S+N}\right)·F+k_{SF}·S-k_{FS}·F-k_{FN}·F$$

$$\frac{dS}{dt}=k_{FS}·F+k_{NS}·N‐k_{SF}·S-k_{SN}·S$$

$$\frac{dN}{dt}={k_{FN}·F+k}_{SN}·S$$

where $k_{FS}=k_{F{S}_{lin}}·t$ where F, S, and N are the model predicted bacterial number (ml⁻¹) in fast‐, slow‐, and nonmultiplying states, respectively. Various k with two‐letter subscripts are transfer rates between substates. The first letter describes the transfer origin and the second letter describes the direction. The parameter k_FSlin multiplied by time (t) in days after infection describes the time‐dependent transfer rate from fast‐ to slow‐multiplying state. The parameter k_G is the fast‐multiplying bacterial growth rate and B _max is the system carrying capacity, constraining the growth in the stationary phase.

In order to evaluate the importance of the nonmultiplying substate in the MTP model, an alternative two‐state model not including a nonmultiplying state was developed. The differential equations for the two‐state model were written as:

$$\frac{dF}{dt}=k_G·\log \left(\frac{B_{\mathrm{m}\mathrm{a}\mathrm{x}}}{F+S}\right)·F+k_{SF}·S-k_{FS}·F-k_D·F$$

$$\frac{dS}{dt}=k_{FS}·F-k_{SF}·S-k_D·S$$

where $k_{FS}=k_{F{S}_{lin}}·t$ where k_D is the natural death rate in days⁻¹, needed to adequately describe the CFU in vitro data when assuming no nonmultiplying state.15 The CFU declines at ∼70 days, which is correctly described as a shift into the nonmultiplying state in the MTP model but is described as natural death in the alternative two‐state model. The parameters of the two‐state model were estimated using the same in vitro data as was used to develop the structure of the MTP model.15 All model fitting and assumptions were otherwise similar as for the MTP model.

All patients were assumed to have stationary phase infections. Time from inoculum (i.e., infection) to stationary phase for the in vitro MTP model15 was investigated through simulations in Berkeley Madonna version 8.3.18 (Department of Molecular and Cellular Biology, University of California [http://www.berkeleymadonna.com], Berkeley, CA). Simulations in Berkeley Madonna were also used to assess identifiability of parameters suitable for estimation and corresponding impact on CFU vs. time.

Drug effect using the clinical data was investigated in four sequential steps. The first step investigated drug effect on different effect sites as univariate (i.e., single effect site) models. Effect site refers to either inhibition of fast‐multiplying growth or stimulation of fast‐, slow‐, or nonmultiplying death in the MTP model. Included models were on/off (constant maximal drug effect at drug concentrations above 0 mg/L), linear, E_max, and sigmoidal E_max models. Drug effects were incorporated as:

$$\frac{dF}{dt}=k_G·\log \left(\frac{B_{\text{max}}}{F+S+N}\right)·F·\left(1-EF{F}_{FG}\right)+k_{SF}·S-k_{FS}·F-k_{FN}·F-EF{F}_{FD}·F$$

$$\frac{dS}{dt} =k_{FS}·F+k_{NS}·N-k_{SF}·S-k_{SN}·S-EF{F}_{SD}·S$$

$$\frac{dN}{dt} ={k_{FN}·F+k}_{SN}·S-k_{NS}·N-EF{F}_{ND}·N$$

where EFF_FG, EFF_FD, EFF_SD, and EFF_ND are the drug effects as inhibition of fast‐multiplying growth and death of fast‐, slow‐, and nonmultiplying, respectively. Models were statistically significant at 5% significance level if the objective function value (OFV) decreased by at least 3.84 (χ² distribution) for nested models with addition of one parameter. The second step investigated effect sites in combination. To not exclude effect sites that were apparent only in combination, all effect sites were included. In addition, to not exclude any exposure‐response relationships, all effect sites included at least linear models. All combinations of effect sites were tested. The statistically significant combination that fitted the data best (i.e., lowest OFV) was selected. The third step reevaluated the exposure‐response relationship at each effect site. All drug effect models were retested at each effect site. If an alternative drug effect model was statistically significant on one effect site, that model was kept. If multiple effect sites had statistically significant alternative drug effect models, the model with the best model fit (i.e., lowest OFV) was kept and tested for statistical significance in combination with the model with the second best model fit until no alternative model was supported. The fourth step was a backward elimination step at 1% significance level (ΔOFV ≥6.63 for removal of one parameter). Each effect site was removed to exclude nonsignificant effect sites at 1% significance level, resulting in a full model.

Three approaches to handle predictions of CFU were evaluated. For the last time point method, predictions were defined as the bacterial number in the fast‐ and slow‐multiplying states per milliliter sputum at the last time point of the sputum sampling interval, which was at 8 am because all samples were collected between 8 pm and 8 am. For the mid‐time point method, predictions were defined as the bacterial number in the fast‐ and slow‐multiplying states in mL⁻¹ at the mid‐point in the sputum sampling period (2 am). The time for each observation was for both methods specified in the dataset. Predictions of CFU were defined as:

$$PRED=\log \left(F+S\right)$$

where PRED is the prediction of the natural logarithm of F and S in mL⁻¹.

For the sputum sampling compartment method, predictions were defined as the average bacterial number in the fast‐ and slow‐multiplying states (mL⁻¹) in the sputum sampling interval (between 8 pm and 8 am). This was implemented by inclusion of a sputum sample compartment described by:

$$\frac{dSample}{dt}=k_{prod}·\left(F+S\right)$$

where $k_{prod}=\frac{V_{sputum}}{D_{sample}}$ Sample is the bacterial number in the fast‐ and slow‐multiplying states in the specified sputum volume over the sampling interval. The sputum production rate is k_prod (mL/h). Sputum volume is V_sputum (mL) and the sampling duration is D_sample (hours). The amount in the sample compartment was set to 0 at the start of each collection period. Predictions of CFU were defined as:

$$PRED=log\left(\frac{Sample}{V_{sputum}}\right)$$

where PRED is the natural logarithm of the average bacterial number in the fast‐ and slow‐multiplying states (mL⁻¹) over the sampling interval. The true sample volume was unavailable in this study and was assumed to be 10 mL for all samples, a realistic value based on reported sputum volumes.21 Start and duration of sputum sample collection and sample volume were specified in the dataset (Supplementary Material S1).

Attempts were made to model immune response implemented as specific zero‐ and first‐order death rates on the fast‐, slow‐, and nonmultiplying states. Furthermore, effect delay models, implemented as effect compartment models, were tested on all effect sites.

Random effects were tested in B_max. Interindividual variability (IIV) was parameterized as:

$$P=TV{P\times e}^{\eta }$$

where P is the parameter, TVP is the typical value of the parameter, and η is a normally distributed parameter. Error models implemented as additive error on log scale (approximates proportional error on normal scale) and combined errors (including two additive errors; one on normal scale and one on log scale) were tested.

Observed CFU values were reported in replicate and analyzed without averaging. To avoid bias because of correlation between replicates a residual error model with two components, one where the error was similar for all replicates and one where the error was the same for replicates from the same sputum sample, were tested. This was implemented using the L2 data item in NONMEM. No data were below the limit of quantification.

Model selection and evaluation

Models were evaluated by comparing the difference in OFV together with parameter precision and diagnostic plots generated with the R package Xpose version 4.5.2 (Department of Pharmaceutical Biosciences, Uppsala University [http://xpose.sourceforge.net], Uppsala, Sweden).22, 23 In addition, prediction‐corrected visual predictive checks24 were generated using PsN version 4.3.2 (Department of Pharmaceutical Biosciences [http://psn.sourceforge.net])22, 25 using 1,000 simulations. A prediction‐corrected visual predictive check normalizes the observed and simulated dependent variable to the median typical prediction within each bin, allowing visual interpretation of several doses in one plot, which is not always the case with a traditional visual predictive check.22, 25 A 1,000 sample bootstrap was performed in PsN^22,25 on the final model in order to obtain the nonparametric 95% confidence interval for all estimated parameters.

Clinical trial simulations

External validation was performed by comparing model predicted 95% prediction intervals (PIs) of the typical change in CFU from baseline vs. time to the mean ± SE of four datasets not used for model building. The datasets consisted of rifampicin in monotherapy with different doses and study lengths,26, 27, 28 summarized in Table 1. The PI of the typical predictions was generated from 1,000 samples simulated with uncertainty in parameter estimates.

Table 1.

Overview of trials included in external validation

Dose arm	Location	Ethnicities	Age	Comorbidities	Study arm size	Study length	Sputum sampling	Publication year	Reference
600 mg	South Africa	57% blacka	Median 34 y, range 18–61 ya	31% HIV‐positivea	15	7 d	Baseline and d 1, 2, 3, 4, 5, 6, and 7	2008	26
20 mg/kg	South Africa	No information available in publication	Mean 27 y, SD 9 y	23% HIV‐positive	13	5 d	Baseline and d 1, 2, 3, 4, and 5	2007	27
300 mg	South Africa	No information available in publication	No information available in publication	24% HIV‐positivea	16	5 d	Baseline and d 2 and 5	2005	28
600 mg	South Africa	No information available in publication	No information available in publication	24% HIV‐positivea	14	5 d	Baseline and d 2 and 5	2005	28

HIV, human immunodeficiency virus.

^aFor the whole trial and not the rifampicin arm specifically.

RESULTS

The final MTP model had the same structure as the final MTP model developed using in vitro data,15 as shown in Figure 1. An example dataset and final model code are found in Supplementary Material S1 and S2, respectively. Simulations from the MTP model developed using in vitro data15 revealed that stationary phase was apparent beyond 130 days after infection. Because all patients were assumed to have stationary phase infections, time for start of treatment was set to 150 days after infection for all patients.

Figure 1.

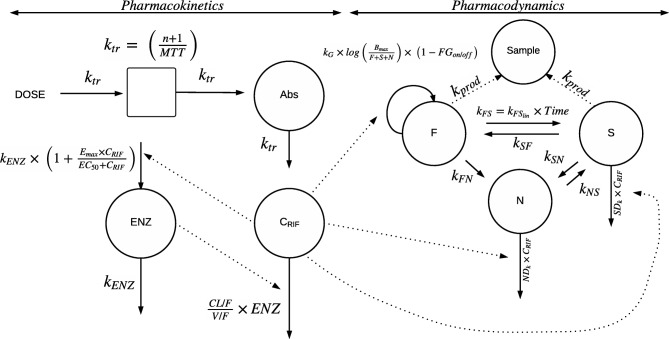
Schematic describing the final model. The dose (DOSE) is transferred from the absorption site (Abs) to the central compartment by a transit rate constant k_tr, which is described by the number of compartments (n) +1 divided by the mean transit time (MTT). Drug is eliminated linearly as described by rifampicin oral clearance (CL/F) divided by the apparent volume of distribution (V/F), at the preinduced stage. The pharmacokinetic (PK) model includes an enzyme turnover model, in which plasma concentrations of rifampicin (C_RIF) increase the rate constant for first‐order degradation of the enzyme pool (k_ENZ), which leads to an increase in the enzyme pool (ENZ) with an E_max model leading to increased elimination of rifampicin. The parameter EC₅₀ is the rifampicin concentration (C_RIF) at which half the E_max is reached. E_max is the maximal increase in the enzyme production rate. C_RIF drives the effect implemented in the Multistate Tuberculosis Pharmacometric (MTP) model. The MTP model consists of three bacterial compartments; the fast‐multiplying state (F), the slow‐multiplying state (S), and the nonmultiplying state (N). Growth is present for F described by a fast‐multiplying bacterial growth rate (k_G) multiplied by the natural logarithm of the system carrying capacity per milliliter sputum (B_max) divided by the number of F, S, and N. F can transfer to N described by the transfer rate from fast‐ to nonmultiplying state (k_FN). Transfer between F and S is described by a time‐dependent transfer rate from fast‐ to slow‐multiplying state (k_FSlin). S can transfer to F and N described by the transfer rate from slow‐ to fast‐multiplying state (k_SF) and transfer rate from slow‐ to nonmultiplying state (k_SN), respectively. N can transfer to S described by the transfer rate from non‐ to slow‐multiplying state (k_NS). Drug effect enters the model as fractional inhibition of growth of fast‐multiplying state (FG_on/off) in presence of drug according to the PK model, as second‐order nonmultiplying death rate (ND_k) and as second‐order slow‐multiplying death rate (SD_k). The bacterial number of F and S together with the sputum production rate (k_prod) describes the amount of bacteria that is present in the sputum sample compartment (Sample).

The OFV was lower (ΔOFV = −4.19) for the final MTP model compared to the two‐state model without nonmultiplying state, which indicates a better fit.

All MTP model parameters were fixed to in vitro estimates,15 except for B_max, which was estimated. Using the in vitro B_max value resulted in an increase in OFV by 53.2 and predicted typical log‐10 CFU at day 150 of 6.23 mL⁻¹, whereas the mean observed baseline value in the clinical dataset was 7.64 mL⁻¹. Simulations with different values for B_max yielded identical relative amounts of bacterial states at stationary phase because transfer rates between states were fixed. Parameters k_G, k_FSlin, k_SF, k_SN, k_NS, and k_FN were unidentifiable. This was probably because of the short study duration and that data were obtained at a stationary phase of infection. Regardless, fixing these parameters to in vitro estimates provided a good fit to the observed data (Figure 2).

Figure 2.

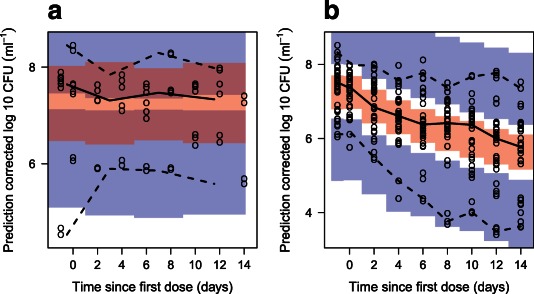
Prediction‐corrected visual predictive check of the final model stratified on presence of drug in which (a) is the group that received no drug and (b) is all groups that received drug. The solid and dashed lines are the median, 2.5th, and 97.5th percentiles of the observed data, respectively. The shaded areas (top to bottom) are the 95% confidence intervals of the 97.5th (blue), median (red), and 2.5th (blue) percentiles of the simulated data. Open circles are prediction‐corrected observations.

Statistically significant exposure‐response relationships were found between drug exposure and inhibition of the growth rate of the fast‐multiplying state and stimulation of the death rates of the slow‐ and nonmultiplying states (Figure 1). The data did not support any statistically significant exposure‐response relationship concerning death of the fast‐multiplying state. Inhibition of the growth rate of the fast‐multiplying state was described by an on/off effect. Drug effects on the slow‐ and nonmultiplying states were described by second‐order death rates, denoted SD_k and ND_k, respectively. The second‐order rates were dependent on the plasma concentration of rifampicin and amount of bacteria (slow‐ or nonmultiplying).

The sputum sampling compartment method was chosen to handle CFU predictions. The last time point and mid‐time point methods provided similar OFV, but was regarded to not resemble the actual sample collection procedure. The data did not support any statistically significant effect delay or immune response.

The data supported IIV in B_max, which allowed for prediction of different baseline levels in CFU between individuals. The residual variability was described by two additive components (on log‐scale), one shared by all replicates and one shared between replicates from the same sputum sample. Final parameter estimates are listed in Table 2.

Table 2.

Parameter estimates based on the final model

Parameter	Description	Typical estimate	RSE%a	95% CIb
Drug PK parametersc
CL/F (L · h−1)	Oral clearance at the preinduced state in a patient weighing 70 kg	10.0 FIX	‐	‐
V/F (L)	Apparent volume of distribution in a patient weighing 70 kg	86.7 FIX	‐	‐
MTT (h)	Mean transit time	0.713 FIX	‐	‐
NN	Number of transit compartments	1.00 FIX	‐	‐
Emax	Maximal increase in the enzyme production rate	1.04 FIX	‐	‐
EC50 (mg · L−1)	Rifampicin concentration at which half the Emax is reached	0.0705 FIX	‐	‐
kENZ (h−1)	Rate constant for first‐order degradation of the enzyme pool	0.00369 FIX	‐	‐
F	Bioavailability	1.00 FIX	‐	‐
(Ffat)CL/F	Contribution of fat‐free mass and body weight to CL/F	0.311 FIX	‐	‐
(Ffat)V/F	Contribution of fat‐free mass and body weight to V/F	0.188 FIX	‐	‐
Multistate Tuberculosis Pharmacometric modeld
kG (days−1)e	Fast‐multiplying bacterial growth rate	0.206 FIX	‐	‐
kFN (days−1)	Transfer rate from fast‐ to nonmultiplying state	8.97·10−7 FIX	‐	‐
kSN (days−1)	Transfer rate from slow‐ to nonmultiplying state	0.186 FIX	‐	‐
kSF (days−1)	Transfer rate from slow‐ to fast‐multiplying state	0.0145 FIX	‐	‐
kNS (days−1)	Transfer rate from non‐ to slow‐multiplying state	0.00123 FIX	‐	‐
kFSlin (days−2)f	Time‐dependent transfer rate from fast‐ to slow‐multiplying state	0.00166 FIX	‐	‐
F0 (mL−1)	Initial bacterial number of fast‐multiplying state	4.10 FIX	‐	‐
S0 (mL−1)	Initial bacterial number of slow‐multiplying state	9770 FIX	‐	‐
Bmax (mL−1)d	System carrying capacity per mL sputum	2.61·109	30.5	1.51·109−4.52·109
IIV Bmax (%)g	Interindividual variability in Bmax	152	15.9	97.8–191
Exposure‐response parameters
FGon/off	Fractional inhibition of growth of fast‐multiplying state	1.00 FIX	‐	‐
SDk (L·mg−1·days−1)	Second‐order slow‐multiplying state death rate	0.200	41.6	0.0854–0.390
NDk (L·mg−1·days−1)	Second‐order nonmultiplying state death rate	0.106	19.0	0.0643–0.188
Residual error parameters
ε (CV%)	Additive residual error on log scale (approximates a proportional error on normal scale) for all replicates	110	12.0	83.7–133
εrepl (CV%)	Additive residual error on log scale (approximates a proportional error on normal scale) between replicates	23.1	10.2	18.4–27.2

CI, confidence interval; FIX, parameter was fixed during estimation; PK, pharmacokinetic; RSE, relative standard error.

^aRelative standard error from the covariance step in NONMEM18 reported on the approximate SD scale.

^b95% CI is the 95% percentile confidence interval from a nonparametric bootstrap (1,000 samples).

^cAll drug PK model parameters were fixed to estimates reported by Smythe et al.19

^dAll Multistate Tuberculosis Pharmacometric Model parameters except B_max were fixed to estimates reported by Clewe et al.15

$\frac{dF}{dt}=k_G·\left(\frac{B_{\mathrm{m}\mathrm{a}\mathrm{x}}}{F+S+N}\right)·F$

^e

$k_{FS}={k_{FS}}_{lin}·t$

^fIIV is the inter‐individual variability expressed as coefficient of variation (CV).

The final model described the patient data well, according to the prediction‐corrected visual predictive checks (Figure 2). The estimated second‐order death rates were 0.200 and 0.106 L·mg⁻¹·days⁻¹ for the slow‐ and nonmultiplying states, respectively. The inhibition of fast‐multiplying growth was estimated close to 1 (100%) and was therefore be fixed to 1 in the final model with no change in OFV. The model predicted a gradient of decline in CFU with dose (Figure 3 a). In Figure 3 b, the typical model predicted bacterial number over time is seen for different states. External validation revealed the ability of the final MTP model to predict data from other sources well without any re‐estimation (Figure 4). Simulations using the alternative two‐state model without a nonmultiplying state did not predict external data well (Figure 5).

Figure 3.

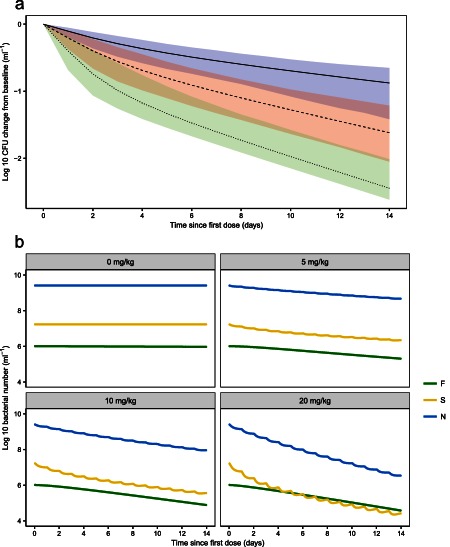
Typical model predictions from the final Multistate Tuberculosis Pharmacometric model of (a) log‐10 change from baseline in colony forming unit (CFU) after daily rifampicin doses of 5 mg/kg body weight (solid black line, blue shaded area is the 95% prediction interval [PI], including model uncertainty), 10 mg/kg body weight (dashed black line, red shaded area is the 95% PI, including model uncertainty), and 20 mg/kg body weight (dotted black line, green shaded area is the 95% PI, including model uncertainty) and (b) model predicted typical bacterial number of the fast‐ (green), slow‐ (yellow), and nonmultiplying (blue) states, denoted F, S, and N, respectively, following different daily doses of rifampicin per kg body weight.

Figure 4.

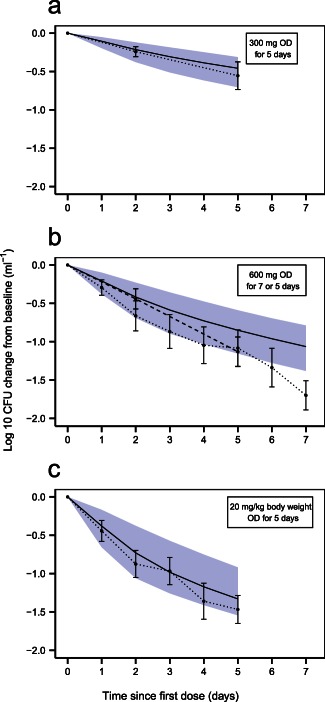
Clinical trial simulations using the final Multistate Tuberculosis Pharmacometric model. Log‐10 colony forming unit (CFU) in mL^{− 1} change from baseline vs. time since first dose of rifampicin for (a) 300 mg of rifampicin given once daily (OD) for 5 days²⁸; (b) 600 mg rifampicin given OD for 5 (dashed line) and 7 (dotted line) days^26,27; (c) 20 mg rifampicin per kg body weight given OD for 5 days.27 Shaded areas are the 95% confidence interval for the typical prediction of log‐10 CFU (mL^{− 1}) change from baseline vs. time since first dose from 1,000 samples simulated with parameter uncertainty. Solid lines are the typical predictions from the final model for the study design indicated in the top right box in each graph. Dots are the mean values at each designated time point with SEs shown as error bars. The dots are connected with dotted and/or dashed lines.

Figure 5.

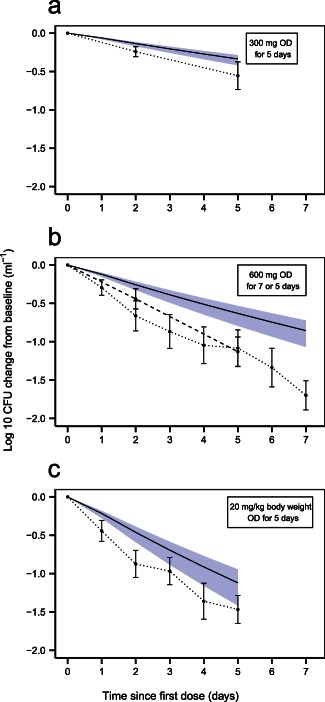
Clinical trial simulations using an alternative two‐state model without inclusion of a nonmultiplying state. Log‐10 colony forming unit (CFU) in mL^{− 1} change from baseline vs. time since first dose of rifampicin for (a) 300 mg of rifampicin given once daily (OD) for 5 days²⁸; (b) 600 mg rifampicin given OD for 5 (dashed line) and 7 (dotted line) days^26,27; (c) 20 mg rifampicin per kg body weight given OD for 5 days.27 Shaded areas are the 95% confidence interval for the typical prediction of log‐10 CFU (mL^{− 1}) change from baseline vs. time since first dose from 1,000 samples simulated with parameter uncertainty. Solid lines are the typical predictions from the model without a nonmultiplying state for the study design indicated in the top right box in each graph. Dots are the mean values at each designated time point with SEs shown as error bars. The dots are connected with dotted and/or dashed lines.

DISCUSSION

The MTP model can be applied to clinical data with only re‐estimation of the B _max parameter and estimation of the exposure‐response relationships for rifampicin. Other MTP model parameters can be fixed to estimates obtained from fitting the model to in vitro data.15 The external validation showed the ability of the final model to predict change in CFU after different rifampicin doses (Figure 4).

All patients were assumed to have stationary phase infections. Time of onset of symptoms and trial entry were unknown. A suggested incubation period is 1.26 years.29 However, at that time, patients are in the stationary phase with negligible change in CFU with respect to time. For computational simplicity, the time of entering trial was assumed to 150 days, a time point at which the model predicts negligible change in CFU in the stationary phase.

In order to account for different baseline sputum CFU values in the in vitro and clinical settings, B_max was re‐estimated. Re‐estimation of B_max did not affect the relative amounts of bacterial states. The relative amounts are determined by the rates between states that were fixed to in vitro estimates.15 In the in vitro system, transfer from non‐ to fast‐multiplying state was excluded because of hypoxia. In contrast, clinical lesions might have partial access to oxygen. However, the transfer might be suppressed clinically by the immune system. In the in vitro model, there is a time‐dependent transfer between fast‐ and slow‐multiplying bacteria,15 which has not been validated in vivo because of clinical data not being informative enough. There might be strain differences between the in vitro H37Rv strain data used to develop the MTP model and clinical strains. The most important difference would be the drug susceptibility. However, all exposure‐response parameters were estimated in this work using the clinical data. Growth‐ and transfer rates between substates were fixed to estimates from the in vitro model, which might deviate from clinical strains, but did not seem to affect the overall ability to predict external data as such (Figure 4).

A limitation of this analysis was that no PK information was available. However, a population PK parameter approach20 was used, which does not require PK information but is reusing a previously developed population PK model.19 As no IIV or covariate information were included in the PK model, IIV in exposure‐response parameters was not evaluated as it would most likely represent a sum of PK and pharmacodynamic (PD) variability. Only IIV in B_max was estimated, which allowed for prediction of different CFU baseline levels. One assumption in the population PK parameter approach is that the typical patient in the dataset used for developing the population PK model is representative for a typical patient in the PD dataset. Because covariates for the PD dataset were unknown, it is difficult to judge the impact of this assumption. The PK model applied was developed using patient data from South Africa, Benin, Senegal, and Guinea,19 whereas the patients included in this analysis originated from Kenya. Rifampicin exposure has been shown to be slightly higher in eastern Africa.30 Our analysis relies on a small historical dataset, which may not reflect current TB trials. However, the final model predicted recent trials (Figure 4) justifying the approach and data used despite these discrepancies.

We investigated the immune system as a bactericidal process but no immune effect was supported that might be due to the limited study duration. Most information regarding this parameter was available in the negative control group.

The final model predicted a gradient of reduction in CFU with increasing dose (Figure 3 a). Bowness et al.31 compared matched CFU counts with time to positivity in mycobacterial growth incubator tube in rifampicin‐treated patients in which mycobacterial growth incubator tube quantifies a subpopulation unable to grow on solid media. Rifampicin had a dose‐dependent activity against this subpopulation that we believe coincides with the drug effect on the nonmultiplying state seen here. The predicted potency was higher toward slow‐ than nonmultiplying bacteria (Table 2). No drug effect was supported regarding death of fast‐multiplying state, contradicting that fast‐multiplying subpopulations are more susceptible to drug exposure.14 However, the fast‐multiplying bacteria might have been too few in the stationary phase patients in order to find any significant drug effect or there was an indistinguishable balance between kill and inhibition of growth.

In Figure 3 b, the typical model predicted bacterial number over time is seen for the different subpopulations. The change in slow‐ and nonmultiplying states is circadian because of the direct effect by the drug through the link to plasma concentration. As the model included no concentration‐dependent effect on fast‐multiplying bacteria, but only complete inhibition of the growth of fast‐multiplying bacteria, no circadian change is seen for this state.

The model predicted high numbers of unquantifiable bacteria (i.e., nonmultiplying state), as inherited from the in vitro model.15 In vitro, animal and clinical studies support M. tuberculosis subpopulation(s) that are culture‐negative on solid media but can grow in liquid media.32, 33, 34

The final MTP model was compared to a two‐state model, not including a nonmultiplying state. The OFV was lower (ΔOFV = −4.19) for the final MTP model compared to the two‐state model without a nonmultiplying state. The latter model predicted a net decline in CFU in the stationary phase that did not agree with the negative control group. Noncultivable subpopulations have been described in PK/PD models for malaria35, 36 and Escherichia coli.37 There are several empirical CFU models for TB,9, 11, 38, 39 but none are semimechanistic like the MTP model, which links PK to multiple mycobacterial states.

The sputum sampling compartment method was chosen to handle predictions of CFU that best resembled the sample collection procedure compared with the other methods investigated. Sampling intervals, time points for sampling, and sample volumes can deviate within and between studies, which can be accounted for using our approach (Supplementary Material S1 and S2). Patients produce less sputum as treatment progresses, which could be important to account for in future analyses.21 Variability in CFU is also affected, as it increases at smaller sample volumes. Larger sputum volumes can be obtained (e.g., by increasing the sampling interval),40 which could be accounted for using our approach. The assumed volume of 10 mL will not affect the predictions because the model predicts the average bacterial number over the sampling interval. Assuming higher volumes would be compensated by a higher sputum production rate.

In addition to the clinical application presented here, the MTP model has been successfully applied to in vitro 15 and mouse data.16 As such, the MTP model can be used for analysis and simulation of clinical and preclinical trials within TB drug development to optimize the development of drugs against TB.

In summary, the MTP model was successfully applied to clinical data with rifampicin‐treated patients. Retrospective data were successfully predicted using this approach.

CONFLICT OF INTEREST

The authors declared no conflict of interest.

AUTHOR CONTRIBUTIONS

R.J.S. and U.S.H.S. wrote the manuscript. R.J.S. and U.S.H.S. designed the research. R.J.S. and U.S.H.S. analyzed the data.

Supporting information

Supporting Information

Supporting Information