Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 May 20;6:25639. doi: 10.1038/srep25639

Independent modulations of the transmission amplitudes and phases by using Huygens metasurfaces

Xiang Wan 1,2,*, Sheng Li Jia 1,3,*, Tie Jun Cui 1,4,a, Yong Jiu Zhao 3,b
PMCID: PMC4873753  PMID: 27197759

Abstract

We propose ultrathin Huygens metasurfaces to control transmission amplitudes and phases of electromagnetic waves independently, in which each unit cell is comprised of an electric dipole and a magnetic dipole. By altering the electric and magnetic responses of unit cells, arbitrary complex transmission coefficients with modulus values smaller than 0.85 are obtained. Two Huygens metasurfaces capable of controlling the diffraction orders are designed and fabricated by modulating the distributions of the complex transmission coefficients. More complicated functions such as holographic imaging can also be accomplished by using the proposed Huygens metasurfaces.

As a kind of two-dimensional metamaterials, metasurfaces have attracted a lot of attentions in both engineering and science societies1,2,3,4,5,6,7,8,9,10,11. The geometrical features of metasurfaces alleviate the difficulties in engineering realizations, and bring new concepts and methods, such as the holography12,13,14,15 and generalized Snell’s law8,16,17 in designing functional devices2,8,11. Independent controls of amplitudes and phases are important requirements in practical applications such as beam shaping and synthesizes, which have been realized using different metasurfaces18,19,20,21,22,23,24,25,26, most of which, however, only manipulate the electric responses, thus leading to low efficiencies and limited abilities in fully controlling the electromagnetic waves. Huygens principle provides a method to design both of the electric and magnetic responses. Several functional metasurfaces have been proposed by using the Huygens principle27,28,29,30,31, and the ability of Huygens metasurfaces to control reflection amplitudes and phases independently has been confirmed in the optical region32, in which the maximum efficiency is 45%. Nevertheless, the transmission-type Huygens metasurfaces with capability to control both amplitudes and phases have not been reported.

Here, we propose high-efficiency and independent controls of the transmission amplitudes and phases by engineering both electric and magnetic responses of the proposed Huygens particles. Full-wave simulations show that arbitrarily complex transmission coefficients with modulus values less than 0.85 are available. Based on these efficient particles, two Huygens metasurfaces are designed and fabricated, which are capable of controlling the diffraction beams. The measurement results show very well agreements with numerical simulations. We remark that more complicated functions can be designed by modulating the distributions of transmission amplitudes and phases on the metasurfaces.

Theories and analyses

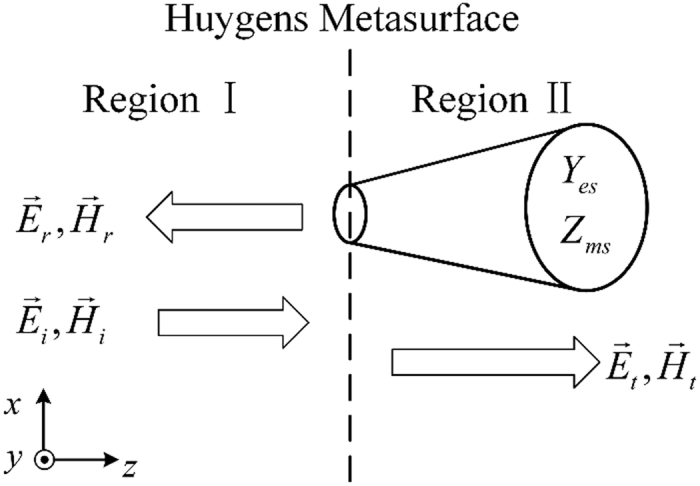
Figure 1 gives the schematic of a Huygens metasurface under the normal incidence. The Huygens metasurface can be characterized by the electric surface admittance 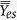Inline graphic and magnetic surface impedance 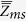Inline graphic. For a predetermined field distribution in Region Ι, arbitrary electromagnetic fields in Region ΙΙ can be produced by altering the electric surface admittance and magnetic surface impedance. According to the equivalence principle and the boundary condition, the electromagnetic fields in such two regions satisfy the following equations24,33.

Figure 1. The schematic of a Huygens metasurface under normal incidence.

Figure 1

Open in a new tab
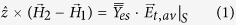graphic file with name srep25639-m3.jpg
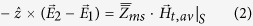graphic file with name srep25639-m4.jpg

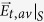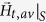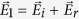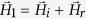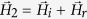where Inline graphic and Inline graphic are the averaged tangential electric and magnetic fields on the surface, respectively24. Inline graphic, Inline graphic and Inline graphic, Inline graphic are the total fields in Regions Ι and ΙΙ, respectively. The transmission and reflection coefficients can be represented by the electric and magnetic surface impedances as34,35

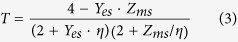graphic file with name srep25639-m11.jpg
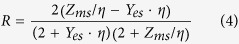graphic file with name srep25639-m12.jpg

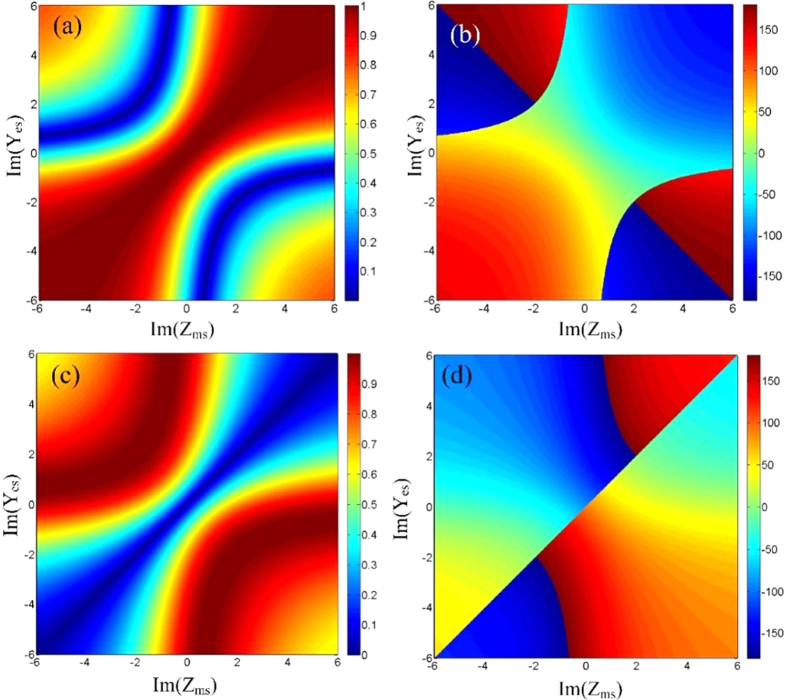
in where η is the wave impedance in free space. For simplicity, the electric and magnetic surface impedances are assumed to be isotropic (Yes and Zms) when the polarization of the incident wave is determined. Figure 2 gives the amplitudes and phases of the calculated transmission and reflection coefficients as functions of the surface electrics and magnetic impedances. The Huygens metasurface is assumed to be passive and lossless. It is observed that the phases tend to be unchanged when the amplitudes vary, and vice versa. This property indicates that the amplitudes and phases can be controlled independently.

Figure 2. The amplitudes and phases of calculated transmission and reflection coefficients as functions of the surface electrics and magnetic impedances.

Figure 2

Open in a new tab

(a) The transmission amplitudes. (b) The transmission phases. (c) The reflection amplitudes. (d) The reflection phases.

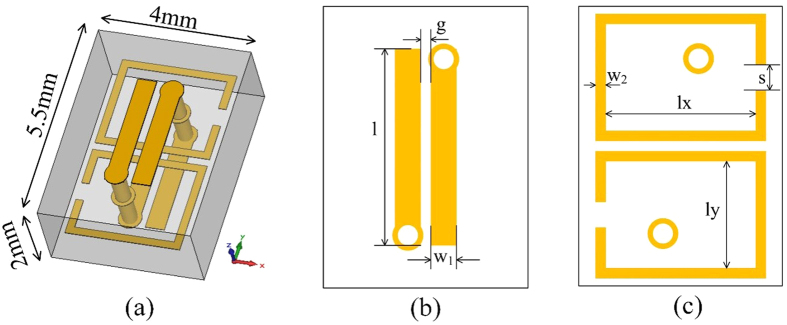
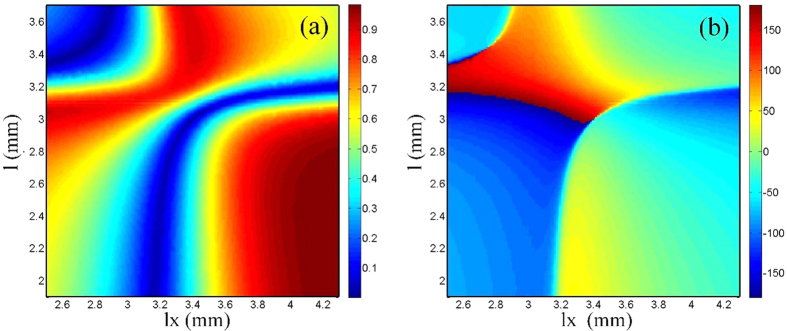
Figure 3 illustrates a subwavelength-scale Huygens particle, which is composed of two horizontal split-ring resonators (SRRs) and a vertical double-SRR, integrated on a dielectric substrate (εr = 2.65, tan δ = 0.009). The electric response is contributed by the horizontal SRRs in the middle layer, and the magnetic response is contributed by the vertical double-SRR. The independent controls of electric and magnetic responses are realized by adjusting the size of horizontal SRRs and vertical double-SRR. Full-wave simulations of the particle are executed in the commercial software, CST Microwave Studio (CST). In the procedures of designing unit cells, we found that magnetic responses mainly relate to l and electric responses mainly relate to lx, hence a database mapping transmission and reflection coefficients to the values of l and lx is established with the aids of CST. The other parameters are optimized by CST and finally are fixed as w1 = 0.5 mm, w2 = 0.2 mm, g = 0.2 mm, s = 2 mm and ly = 2.5 mm. When designing functional metasurfaces, we can search from the database for different sizes of the unit cells corresponding to different values of transmission and reflection coefficients. The transmission and reflection coefficients as functions of l (relating to magnetic responses) and lx (relating to electric responses) are given in Fig. 4, from which similar variation trends of amplitudes and phases are observed to those shown in Fig. 2. Figure 5 displays the available range in the Cartesian system. It is clearly demonstrated that arbitrary complex transmission coefficients with modulus values smaller than 0.85 is obtained. The transmission efficiency is much higher than that in previous works. In addition, the independent controls of transmission amplitudes and phases are not performed by rotating the particles, and hence little cross polarizations are introduced in the procedures.

Figure 3. Detailed geometries of a Huygens particle.

Figure 3

Open in a new tab

(a) Perspective view. (b) The geometries of the outer layer. (c) The geometries of the middle layer.

Figure 4. Parametric analyses when change the values of l and lx, other parameters are fixed at: w1 = 0.5 mm, w2 = 0.2 mm, g = 0.2 mm, s = 2 mm and ly = 2.5 mm.

Figure 4

Open in a new tab

(a) Transmission amplitudes. (b) Transmission phases.

Figure 5. Value range of complex transmission coefficients.

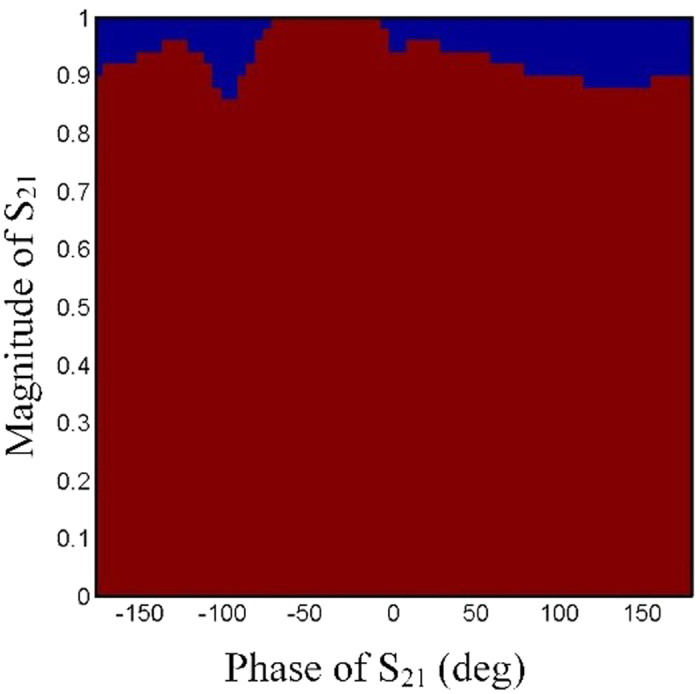
Figure 5

Open in a new tab

The red area shows the obtainable range, while the blue area shows the unobtainable range.

Designs and experiments

Two Huygens metasurface gratings that are able to produce multiple diffraction orders are designed using the Huygens particle. The general expression of transmission coefficient for the gratings are written as

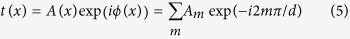graphic file with name srep25639-m13.jpg

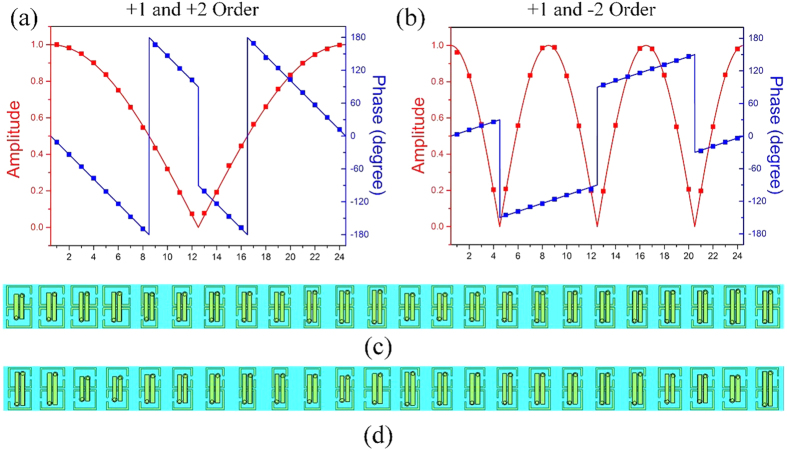
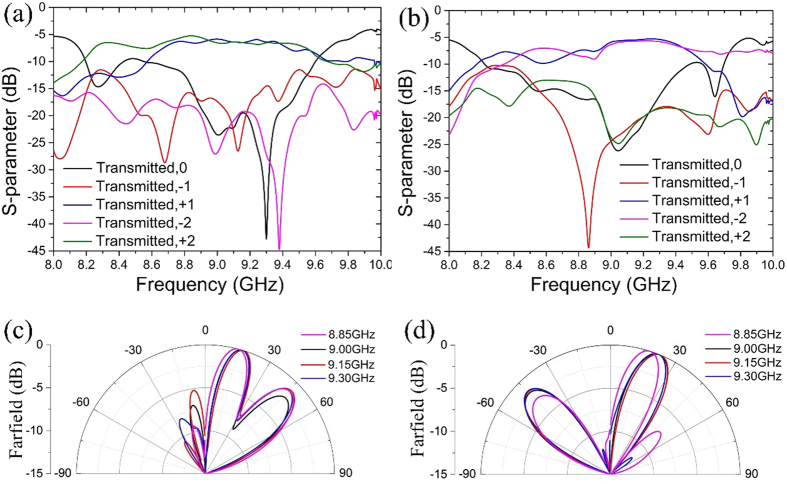
where d is the grating period and m is an integer denoting the diffraction order, Am is amplitude of desired diffraction order. The first metasurface produce two diffraction orders corresponding to m = +1 and m = +2; the second metasurface produce two diffraction orders corresponding to m = +1 and m = −2. The amplitudes of all the diffraction orders are set to be identical. The period of the designed metasurface is 96 mm, and each period contains 24 particles. In Fig. 6, solid lines give the required profiles of transmission amplitudes and phases according to Eq. (5), while symbols show the designed values corresponding to different particles. Full-wave simulations are performed with the aids of commercial software (CST microwave studio). Floquet ports and unit-cell boundaries are applied to mimic the infinite metasurface gratings. Simulated Floquet harmonics in Fig. 7(a,b) verify that the desired diffraction orders are excited by the proposed metasurfaces at around 9 GHz. The normalized far-field patterns in Fig. 7(c,d) display the directions of the diffraction beams. The higher orders tends to away from the normal direction. The gain decreases of the higher-order diffraction beams is resulted from the fact that the scatted fields of Huygens particles are not uniform in free space.

Figure 6. Amplitude and phase profiles of the metasurface gratings.

Figure 6

Open in a new tab

Solid lines represent the calculated values, and symbols represent the designed values by using different particles. (a) Metasurface grating with m = +1 and m = +2; (b) Metasurface grating with m = +1 and m = −2; (c) One period of the simulation model of the metasurface grating with m = +1 and m = +2; (d) One period of the simulation model of the metasurface grating with m = +1 and m = −2.

Figure 7. The simulated results of two metasurface gratings.

Figure 7

Open in a new tab

(a) Floquet harmonics and (c) normalized farfield patterns of the metasurface grating with m = +1 and m = +2. (b) Floquet harmonics and (d) normalized farfield patterns of the metasurface grating with m = +1 and m = −2.

The two designed metasurfaces are fabricated with the size of 288 mm × 297 mm. The experiments are taken in an anechoic chamber. The measuring environment is illustrated in Fig. 8(a). A metamaterial lens antenna36, which transforms the quasi-spherical waves into plane waves, serves as the source antenna in experiments. The diameter of antenna’s aperture is 100 mm. The lens antenna and the fabricated metasurface grating are separated by foams, and both of them are mounted on an antenna turntable. A standard horn antenna serves as the receiving antenna. The lens antenna and the standard horn are connected to two ports of an Agilent N5245A network analyzer. The measured far-field patterns of the diffraction beams are shown in Fig. 8(b) (for m = +1 and m = +2) and 8(c) (for m = +1 and m = −2). According to the measurements, the working frequencies are higher than those in simulations, and small deviations of the elevations angles are observed. These inconsistences mainly resulted from the reason that the incident plane waves are produced in near-field region by using metamaterials lens antenna. Multiple reflections between samples and source antenna destroy the uniformity of the plane waves. These problem can be alleviated by integrating the design of Huygens samples and source antennas. Nevertheless, reasonable agreements between simulations and measurements are observed.

Figure 8. Measuring environment and measured far-field patterns.

Figure 8

Open in a new tab

(a) The experimental platform. (b) The measured far-field patterns of the metasurface grating with m = +1 and m = +2. (c) The measured far-field patterns of the metasurface grating with m = +1 and m = −2.

Conclusion

High-efficiency and independent controls of transmission amplitudes and phases are realized by using Huygens metasurfaces. Two metasurface gratings are combined with a metamaterials lens to control multiple diffractions beams. The proposed Huygens metasurfaces can be applied in synthesizing complex field patterns such as computer generated holography. The highly efficient and independent controls of transmission amplitudes and phases can also be used in designing low-sidelobe antennas. Compared with conventional metasurfaces, the proposed metasurface takes the advantages of arbitrarily designing multiple diffraction beams, hence can be used in multi-object monitorings and multi-channel communications.

Additional Information

How to cite this article: Wan, X. et al. Independent modulations of the transmission amplitudes and phases by using Huygens metasurfaces. Sci. Rep. 6, 25639; doi: 10.1038/srep25639 (2016).

Acknowledgments

This work was supported in part from the National Science Foundation of China (61171024, 61171026, 61302018, 61401089, 61571117, 61501112, 61501117 and 61138001), in part from the 111 Project (111- 2-05), in part from the National Instrumentation Program (2013YQ200647), and in part from the Natural Science Foundation of the Jiangsu Province (BK20150620).

Footnotes

Author Contributions X.W., S.L.J., T.J.C. and Y.J.Z. conceived the idea, did the theoretical calculations, and wrote the manuscript. X.W. and S.L.J. designed the samples and performed the measurements.

References

  1. Zhao Y. & Alu A. Manipulating light polarization with ultrathin plasmonic metasurfaces. Phys. Rev. B 84, 205428 (2011). [Google Scholar]
  2. Yu N. F. et al. A Broadband, Background-Free Quarter-Wave Plate Based on Plasmonic Metasurfaces. Nano. Lett. 12, 6328–6333 (2012). [DOI] [PubMed] [Google Scholar]
  3. Ma H. F., Wang G. Z., Jiang W. X. & Cui T. J. Independent control of differently-polarized waves using anisotropic gradient-index metamaterials. Sci. Rep. 4, 6337 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Zhu B. O., Zhao J. M. & Feng Y. J. Active impedance metasurface with full 360 degrees reflection phase tuning. Sci. Rep. 3, 3059 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Sun S. L. et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat. Mater. 11, 426–431 (2012). [DOI] [PubMed] [Google Scholar]
  6. Ni X. J., Ishii S., Kildishev A. V. & Shalaev V. M. Ultra-thin, planar, Babinet-inverted plasmonic metalenses. Light-Sci. Appl. 2, e27 (2013). [Google Scholar]
  7. Ni X. J., Emani N. K., Kildishev A. V., Boltasseva A. & Shalaev V. M. Broadband Light Bending with Plasmonic Nanoantennas. Science 335, 427 (2012). [DOI] [PubMed] [Google Scholar]
  8. Yu N. F. et al. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 334, 333–337 (2011). [DOI] [PubMed] [Google Scholar]
  9. Yin X. B., Ye Z. L., Rho J., Wang Y. & Zhang X. Photonic Spin Hall Effect at Metasurfaces. Science 339, 1405–1407 (2013). [DOI] [PubMed] [Google Scholar]
  10. Yang Y. M. et al. Dielectric Meta-Reflectarray for Broadband Linear Polarization Conversion and Optical Vortex Generation. Nano. Lett. 14, 1394–1399 (2014). [DOI] [PubMed] [Google Scholar]
  11. Yu N. F. & Capasso F. Flat Optics: Controlling Wavefronts with Optical Antenna Metasurfaces (invited paper). 2013 IEEE Antennas And Propagation Society International Symposium (Apsursi), 2341–2342 (2013).
  12. Lin J., Genevet P., Kats M. A., Antoniou N. & Capasso F. Nanostructured Holograms for Broadband Manipulation of Vector Beams. Nano. Lett. 13, 4269–4274 (2013). [DOI] [PubMed] [Google Scholar]
  13. Zheng J. et al. Highly anisotropic metasurface: a polarized beam splitter and hologram. Sci. Rep. 4, 6491 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Huang L. L. et al. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun. 4, 2808 (2013). [Google Scholar]
  15. Ni X. J., Kildishev A. V. & Shalaev V. M. Metasurface holograms for visible light. Nat. Commun. 4, 2807 (2013). [Google Scholar]
  16. Belardini A. et al. Asymmetric transmission and anomalous refraction in metal nanowires metasurface. J. Eur. Opt. Soc-Rapid 7, 12051 (2012). [Google Scholar]
  17. Li Z. W., Huang L. R., Lu K., Sun Y. L. & Min L. Continuous metasurface for high-performance anomalous reflection. Appl. Phys. Express 7, 112001 (2014). [Google Scholar]
  18. Pors A., Nielsen M. G., Roberts A. S. & Bozhevolnyi S. I. Gap plasmon-based metasurfaces: from amplitude to phase control of reflected light. Paper presented at 2014 8th International Congress on Advanced Electromagnetic Materials In Microwaves And Optics (Metamaterials), Lyngby. Piscataway, N.J.:IEEE. (10.1109/MetaMaterials.2014.6948612)(25–28 Aug. 2014).
  19. Pors A. & Bozhevolnyi S. I. Gap plasmon-based phase-amplitude metasurfaces: material constraints. Opt. Mater. Express 5, 2448–2458 (2015). [Google Scholar]
  20. Pors A., Albrektsen O., Radko I. P. & Bozhevolnyi S. I. Gap plasmon-based metasurfaces for total control of reflected light. Sci. Rep. 3, 2155 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Liu L. X. et al. Broadband Metasurfaces with Simultaneous Control of Phase and Amplitude. Adv. Mater. 26, 5031–5036 (2014). [DOI] [PubMed] [Google Scholar]
  22. Zhang X. Q. et al. Broadband Terahertz Wave Deflection Based on C-shape Complex Metamaterials with Phase Discontinuities. Adv. Mater. 25, 4567–4572 (2013). [DOI] [PubMed] [Google Scholar]
  23. Farmahini-Farahani M., Cheng J. R. & Mosallaei H. Metasurfaces nanoantennas for light processing. J. Opt. Soc. Am. B 30, 2365–2370 (2013). [Google Scholar]
  24. Pfeiffer C. & Grbic A. Bianisotropic metasurface for optimal polarization control: analysis and synthesis. Phys. Rev. Appl. 2, 044011 (2014). [Google Scholar]
  25. Elek F., Tierney B. B. & Grbic A. Synthesis of Tensor Impedance Surfaces to Control Phase and Power Flow of Guided Waves. IEEE Trans. Antenn. Propag. 63, 3956–3962 (2015). [Google Scholar]
  26. Zhu B. O. et al. Dynamic control of electromagnetic wave propagation with the equivalent principle inspired tunable metasurface. Sci. Rep. 4, 4971 (2014). [Google Scholar]
  27. Pfeiffer C. & Grbic A. Metamaterial Huygens’ Surfaces: Tailoring Wave Fronts with Reflectionless Sheets. Phys. Rev. Lett. 110, 197401 (2013). [DOI] [PubMed] [Google Scholar]
  28. Pfeiffer C. et al. Efficient Light Bending with Isotropic Metamaterial Huygens’ Surfaces. Nano. Lett. 14, 2491–2497, (2014). [DOI] [PubMed] [Google Scholar]
  29. Epstein A. & Eleftheriades G. V. Passive Lossless Huygens Metasurfaces for Conversion of Arbitrary Source Field to Directive Radiation. IEEE Trans. Antenn. Propag. 62, 5680–5695 (2014). [Google Scholar]
  30. Jia S. L., Wan X., Fu X. J., Zhao Y. J. & Cui T. J. Low-reflection beam refractions by ultrathin Huygens metasurface. AIP Adv. 5, 067102 (2015). [Google Scholar]
  31. Jia S. L., Wan X., Bao D., Zhao Y. J. & Cui T. J. Independent controls of orthogonally polarized transmitted waves using a Huygens metasurface. Laser Photon. Rev. 9, 545–553 (2015). [Google Scholar]
  32. Kim M., Wong A. M. H. & Eleftheriades G. V. Optical Huygens’ Metasurfaces with Independent Control of the Magnitude and Phase of the Local Reflection Coefficients. Phys. Rev. X 4, 041042 (2014). [Google Scholar]
  33. Selvanayagam M. & Eleftheriades G. V. Discontinuous electromagnetic fields using orthogonal electric and magnetic currents for wavefront Manipulation. Opt. Express 21, 14409–14429 (2013). [DOI] [PubMed] [Google Scholar]
  34. Holloway C. L., Mohamed M. A., Kuester E. F. & Dienstfrey A. Reflection and transmission properties of a metafilm: With an application to a controllable surface composed of resonant particles. IEEE Trans. Electromag. Comp. 47, 853–865 (2005). [Google Scholar]
  35. Holloway C. L. et al. An Overview of the Theory and Applications of Metasurfaces: The Two-Dimensional Equivalents of Metamaterials. IEEE Antenn. Propag. M 54, 10–35 (2012). [Google Scholar]
  36. Chen X., Ma H. F., Zou X. Y., Jiang W. X. & Cui T. J. Three-dimensional broadband and high-directivity lens antenna made of metamaterials. J. Appl. Phys. 110, 044904 (2011). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES