Predicting Electrostatic Forces in RNA Folding

Abstract

Metal ion-mediated electrostatic interactions are critical to RNA folding. Although considerable progress has been made in mechanistic studies, the problem of accurate predictions for the ion effects in RNA folding remains unsolved, mainly due to the complexity of several potentially important issues such as ion correlation and dehydration effects. In this chapter, after giving a brief overview of the experimental findings and theoretical approaches, we focus on a recently developed new model, the tightly bound ion (TBI) model, for ion electrostatics in RNA folding. The model is unique because it can treat ion correlation and fluctuation effects for realistic RNA 3D structures. For monovalent ion (such as Na⁺) solutions, where ion correlation is weak, TBI and the Poisson–Boltzmann (PB) theory give the same results and the results agree with the experimental data. For multivalent ion (such as Mg²⁺) solutions, where ion correlation can be strong, however, TBI gives much improved predictions than the PB. Moreover, the model suggests an ion correlation- induced mechanism for the unusual efficiency of Mg²⁺ ions in the stabilization of RNA tertiary folds. In this chapter, after introducing the theoretical framework of the TBI model, we will describe how to apply the model to predict ion-binding properties and ion-dependent folding stabilities.

1. Introduction

Because RNA backbone is highly charged, the formation of a compact RNA structure is accompanied by massive charge build-up. How does an RNA molecule overcome the strong charge–charge repulsion to form a stable structure? How do metal ions facilitate the folding process via electrostatic interactions? How to accurately predict the electrostatic forces for different ions and ion concentrations? The answers to these questions are essential for understanding and predicting the stability, cooperativity, and kinetics for RNA folding (Chen, 2008; Chu and Herschlag, 2008; Draper, 2008; Walter et al., 2009).

Mechanistic studies for RNA folding have revealed many important features of the ion-dependence of RNA folding. Adding metal ions into the solution would cause an increased ion binding and a reduction in backbone charge repulsion, which would lead to a higher flexibility of the RNA chain and a higher stability of RNA helices. An important consequence of the reduced charge repulsion is that it allows more frequent close approaches between the different RNA segments, causing the tertiary contacts to be kinetically accessible and thermodynamically stable. Further experimental and theoretical studies for specific systems have pointed to the importance of ion charge density (ion charge/ion size), in addition to the ion concentration, as a determinant for the ion effects in RNA stability (Heilman-Miller et al., 2001; Koculi et al., 2007; Takamoto et al., 2002; Weixlbaumer et al., 2004).

Mg²⁺ ions play an essential role in RNA tertiary structure folding (Chen, 2008; Chu et al., 2007; Draper, 2008; Walter et al., 2009). Extensive experimental studies have led to the conclusion that Mg²⁺ ions are unusually efficient than Na⁺ in stabilizing RNA tertiary folds. The effect of Mg²⁺ ions is unusual because it cannot be explained simply by the larger ionic strength of Mg²⁺ than Na⁺. Although considerable progress has been made in mechanistic studies for the Mg²⁺ effect, owing to the complexity of the electrostatic interactions involving Mg²⁺ ions, many problems about quantitative predictions for the Mg²⁺ ion-mediated electrostatic interactions in RNA folding remain unsolved. For instance, how does [Mg²⁺] modulate the stability of specific intermediate structures? How do the ion size, charge, and charge density determine the ion-specific folding energy landscape? How to quantify the ion dehydration and ion correlation effects in Mg²⁺–RNA interactions? In this chapter, we describe a recently developed theory, namely, the tightly bound ion (TBI) theory (Tan and Chen, 2005), that aims to tackle these effects.

In parallel to the investigations on the ion-dependence of RNA folding, systematic thermodynamic measurements for simple RNA folding systems at a fixed ionic condition (1 M NaCl) have led to quantitative insights into RNA folding energetics (Mathews and Turner, 2006; Serra and Turner, 1995). However, using the thermodynamic data at 1 M NaCl to predict RNA folding at a general ionic condition, such as the physiological solution condition, requires a theory for the ion effects, such as the TBI theory to be described in this chapter.

In this chapter, we will give a brief overview for the experimental findings and the main theoretical approaches for the ion effects in RNA and DNA thermal stabilities. We will then describe the TBI theory. We will focus on both the theoretical formalism and the practical applications of the theory. Our aim here is to provide sufficient detail so that all the major issues in the theoretical derivations and numerical computations can be clearly understood and readily followed.

2. Overview of Experimental Results for the Ion-Dependence of RNA Thermal Stability

Extensive experimental studies (see Table 22.1 for a brief summary) on the ion effects for a broad range of nucleic acids, from small hairpins and pseudoknots to large tetrahymena group I intron, have led to several important conclusions as well as quantitative estimations for the ion-mediated electrostatic forces in RNA folding, as described below.

Table 22.1.

Measurements for the nucleic acids thermodynamics in ionic solutions^a

Nucleic acids	References	Ionic conditions	Thermodynamic quantities
24-bp DNA duplex	Bai et al. (2007)	Mixed Na+/Mg2+	fNa+, fMg2+
	Bai et al. (2007)	Mixed monovalent ions	f’s
	Bai et al. (2007)	Mixed divalent ions	f’s
24-bp DNA triplex	Bai et al. (2007)	Mixed Na+/Mg2+	fNa+, fMg2+
Poly(AU)	Krakauer (1971)	Mixed Na+/Mg2+	fMg2+
Calf thymus DNA	Clement et al. (1973)	Mixed Na+/Mg2+	fMg2+
RNA duplexesb	Tan and Chen (2007)	Na+, Mg2+	ΔG, Tm
DNA duplexesb	Tan and Chen (2006a)	Na+, Mg2+	ΔG, Tm
DNA and RNA hairpinsb	Tan and Chen (2008b)	Na+, Mg2+	ΔG, Tm
DNA duplexes (10–30 bp)	Owczarzy et al. (2004)	Na+	Tm
RNA hairpins (49–124 nt)	Vieregg et al. (2007)	K+, Na+	ΔG
BWYV pseudoknotc	Soto et al. (2007)	Na+, mixed Na+/Mg2+	ΔH, ΔS, fMg2+
58-nt rRNA	Bukhman and Draper (1997)	Mixed NH+/Mg2+	ΔG
	Grilley et al. (2007)	Mixed K+/Mg2+	fMg2+
Yeast tRNAphe	Romer and Hach (1975)	Mixed Na+/Mg2+	ΔG, fMg2+
	Rialdi et al. (1972)	Mixed Na+/Mg2+	fMg2+
HIV-1type kiss complex 1	Weixlbaumer et al. (2004)	Na+, mixed Na+/Mg+	Tm
HIV-1type kiss complex 2	Lorenz et al. (2006)	Na+, mixed Na+/Mg2+	Tm
T2 pseudoknot	Nixon and Giedroc (1998)	K+, mixed K+/Mg2+	ΔG
MMTV pseudoknotd	Theimer and Giedroc (2000)	Na+, mixed K+/Mg2+	Tm
T4-35 pseudoknot	Qiu et al. (1996)	Mixed Na+/Mg2+	ΔG, Tm
T4-32 pseudoknot	Qiu et al. (1996)	Mixed Na+/Mg2+	ΔG, Tm
T4-28 pseudoknot	Qiu et al. (1996)	Mixed Na+/Mg2+	ΔG, Tm
Tetrahymena ribozyme	Heilman-Miller et al. (2001)	K+, Na+, Mg2+, spermidine	Fraction folded
	Takamoto et al. (2002)	Na+, Mg2+	RH
	Koculi et al. (2007)	Mg2+, Ca2+, Sr2+, Ba2+	Fraction folded
Hairpin ribozyme	Walter et al. (1999)	Mg2+, Na+	Fraction folded
	Pljevaljcic et al. (2004)	Mg2+	Fraction folded
	Bokinsky et al. (2003)	Na+, Mg2+	Fold and unfold rates
A RNA three-way junction	Kim et al. (2002)	Na+, Mg2+	Fold and unfold rates

^aThe table summarizes the ion-dependent thermodynamics of nucleic acid secondary and tertiary structures, including ion-binding numbers f, folding free energy ΔG, melting temperature T_m, Stokes radius R_H, fraction folded, and other folding properties.

^bThe ion-dependent thermodynamic data and corresponding experimental references for the various DNA duplexes, RNA duplexes, and DNA and RNA hairpins are collected/summarized in (Tan and Chen, 2006a, 2007, 2008b and references therein).

^cBWYV: beet western yellow virus.

^dMMTV: mouse mammary tumor virus.

2.1. General properties of ion binding

Multivalent ions such as Mg²⁺ ions are much more efficient than monovalent ions to neutralize RNA backbone charges and to screen the Coulombic repulsions (Draper, 2008). For example, 10 mM Mg²⁺ is approximately equivalent to 1 M Na⁺ in stabilizing short DNA and RNA oligomers (Tan and Chen, 2006a, 2007, 2008b; and references therein). Such unusually high efficiency of Mg²⁺ ions goes beyond the mean-field ionic strength effect.

Furthermore, the high efficiency of Mg²⁺ is more pronounced for more compact/complex structures. For example, for a simple 24-bp DNA duplex, 0.4 mM Mg²⁺ is equivalent to ~20 mM Na⁺ in ionic neutralization, that is, 0.4 mM Mg²⁺ and 20 mM Na⁺ can cause the same neutralization for the phosphate charges. In contrast, the 76-nt yeast tRNA^phe, a more complex structure, 0.4 mM Mg²⁺ is equivalent to ~32 mM, a much higher Na⁺ concentration (Bai et al., 2007; Romer and Hach, 1975).

2.2. Helix–helix assembly

Ions can mediate nucleic acid helix–helix interactions and consequently affect the structure and stability of the helix assembly. Osmotic pressure-based experiments (Rau and Parsegian, 1992a,b) show that multivalent ions such as Co³⁺ can cause attraction between DNA helices (Rau and Parsegian, 1992a), while monovalent ions such as Na⁺ can only modulate the strength of helix–helix repulsion. For divalent ions, the experiments show that some ions such as Mn²⁺ can induce helix–helix attractive force, while others such as Ca²⁺ cannot. Mg²⁺ ions, with the addition of methanol in the solution, can cause attraction between DNA helices (Rau and Parsegian, 1992a). The different effects of the divalent ions may be attributed to the (solvent-mediated) ion-binding affinity to different groups of DNA.

Small angle X-ray scattering (SAXS) experiments for a system with two short helices tethered by a neutral loop indicate that high-concentration ions (including 1+, 2+, and 3+ ions) cause a random conformational state (Bai et al., 2005), where Coulomb repulsion between the helices is relaxed. Furthermore, quantitative measurements suggest that the attraction is ≤0.21 k_BT/bp between two 24-bp helices in a 0.6 M Mg²⁺ solution (Bai et al., 2005). Further measurements on the Mg²⁺-induced folding of the system show that [Mg²⁺] at the transition point is over 10 times lower than that predicted from the Poisson–Boltzmann theory (PB) (Bai et al., 2008). Because PB neglects ion correlation effect, the experimental finding suggests the possibility for ion correlation to be responsible for the unusually high efficiency of the Mg²⁺ ions.

2.3. RNA tertiary structures and RNA–RNA complexes

One of the central issues for the ion effects in RNA tertiary structure folding is the unusually efficient role of Mg²⁺ ions. For example, for a short DNA/RNA helix, 10 mM Mg²⁺ and 1 M Na⁺ can cause similar folding stabilities (Tan and Chen, 2007), while for a complex RNA tertiary structure such as tetrahymena ribozyme, a much lower concentration 0.5 mM of Mg²⁺ would be sufficient to induce folding transition as 0.5 M Na⁺ (Heilman-Miller et al., 2001). Even with high-concentration monovalent ion background, Mg²⁺ ions can make significant contribution to the folding stability of RNA tertiary structures. For example, for a 58-nt ribosomal RNA fragment, in the background of 1.6 M monovalent ions, 0.05 M Mg²⁺ can contribute about −5 kcal/mol to the global tertiary folding stability (Bukhman and Draper, 1997).

Thermodynamic measurements for HIV-1 dimerization initiation signal (DIS) kissing complexes (Lorenz et al., 2006; Weixlbaumer et al., 2004) show that, compared to the corresponding duplex of the same sequence at the kissing interface, (a) the melting temperature T_m for kissing complexes increases with ion (Na⁺ and Mg²⁺) concentrations much more rapidly and (b) the high efficiency of Mg²⁺ over Na⁺ is much more pronounced. Depending on the sequence, for a kissing complex, Mg²⁺ may bind to the specific site at the kissing interface. The specific binding can affect the [Mg²⁺]-dependence of stability of the kissing complex (Lorenz et al., 2006).

3. Overview of Theoretical Methods for Predicting Ion Electrostatics for RNA Folding

3.1. Counterion condensation theory

The counterion condensation (CC) theory was originally developed to treat an infinitely long line-charge system in an infinitely dilute ionic solution (Manning, 1978). The theory has led to several widely used conclusions such as the linear dependence of melting temperature T_m of nucleic helix on the logarithm of salt concentration (Manning, 1978). However, application of the CC theory to the interactions between two DNA helices predicts an attractive force between the helices even in a monovalent ion solution. This prediction as well as the predicted dependence of the attractive force on the ion charge (Ray and Manning, 2000) are not consistent with the experimental measurements (Qiu et al., 2007; Rau and Parsegian, 1992a,b) and computer simulations (Luan and Aksimentiev, 2008; Lyubartsev and Nordenskiold, 1995).

3.2. Poisson–Boltzmann theory

The history of PB theory can be traced back to the Gouy–Chapmann theory and Debye–Huchel theory in the early of 1900s (e.g., see Carnie and Torrie, 1984). These two theories represent special simplified forms of the PB theory: Gouy–Chapmann theory is a one-dimensional simplification for electric double-layer, while the Debye–Huchel theory is a special solution for spherical symmetric system. The PB equation can be derived based on the Poisson equation with a self-consistent mean electric potential ψ and a Boltzmann distribution for the ions

$$\nabla ·{\epsilon }_0\epsilon \nabla \psi (\mathbf{r})=-4\pi \{{\rho }_f+\sum _{\alpha }{z}_{\alpha }e{c}_{\alpha }^0{\mathrm{e}}^{-z_{\alpha }e\psi (\mathbf{r})/k_{\mathrm{B}}T}\},$$ (22.1)

where z_αeψ is the electrostatic energy for an ion of species α with ionic charge z_ce in the mean electric potential ψ. ε is the dielectric constant, ρ_f is the charge density of fixed charges, and $c_{\alpha }^0$ is the bulk concentration of ion species α. With proper boundary conditions, the solution of the PB equation gives the electric potential and the ion distribution for realistic nucleic acid structures (Baker et al., 2000; Gilson and Zhou, 2007; Gilson et al., 1987).

PB equation is based on the mean-field approximation, where ions are treated as continuous fluid-like particles moving independently in a mean electric potential. The theory ignores the discrete ion properties such as ion size, ion–ion correlation and ion fluctuations. Fail to consider these properties can cause inaccurate predictions for RNA folding, especially in the presence of multivalent ions which are prone to ion correlation due to the strong, long-range Coulomb interactions. For example, PB cannot predict the experimentally observed attractive force between DNA helices in multivalent ion solutions.

3.3. Modified Poisson–Boltzmann theories

Several attempts have been made to improve the PB by accounting for the effects of ion size, ion correlation, and fluctuations of ion distributions. The resultant modified models have led to improved predictions for the ion effects in RNA/DNA folding stability.

3.3.1. Size-modified Poisson–Boltzmann theory

Motivated by the need to consider finite size of ions in the PB model, Chu et al. employed a lattice gas model for the ionic system, where ions of finite sizes are placed on the grid cells. In this way, the ion size can be conveniently represented by the cell size and the system can be treated with the lattice gas approximation (Chu et al., 2007). The modified PB theory gives notable improvements in predictions for ion-binding properties of monovalent counterions, especially at high salt concentration, which involves saturation effect for ion binding. However, for nucleic acid solution containing multivalent ions, the model may not be accurate because the model, like PB, does not treat long-range interion correlations (Chu et al., 2007).

3.3.2. Modified PB based on Kirkwood/BBGY hierarchy

Based on the Kirkwood/BBGY hierarchy, a fluctuation potential and an ion-size-exclusion term in the potential of mean force are used to represent the effect of ion correlations (Carnie and Torrie, 1984; Grochowski and Trylska, 2008). The fluctuation potential is associated with the energy for charging an ion, therefore, it implicitly takes into account the interion Coulomb correlations. The theory gives improved predictions for multivalent ion distributions near macroions of ideal shapes such as cylinder, sphere or plane (Carnie and Torrie, 1984). However, for realistic nucleic acids structures, the three-dimensional numerical solution requires exceedingly large computational cost. This is because the effective fluctuation potential itself is coupled to the electrostatic potential. As a result, the theory is computationally impractical for applications to realistic nucleic acid structures (Gavryushov, 2008).

3.3.3. Correlation-corrected Poisson–Boltzmann model

Recently, Forsman developed a correlation-corrected PB model by introducing an effective potential between like-charge ions (Forsman, 2007). The effective potential at large ion–ion separation approaches the classical Coulomb potential and becomes a reduced effective repulsive Coulomb potential for small ion–ion separation. Such an effective potential represents liquid-like correlation behavior between the ions. For electric double layer with multivalent ions, the model makes improved predictions for the ion distribution and predicts an attractive force between two planes in the presence of multivalent ions (Forsman, 2007). However, for realistic nucleic acid structures, the model is computationally expensive. In addition, the ad hoc effective potential lacks validation for realistic nucleic acid structures.

In addition to the above modified PB models, theories based on other approaches such as the density functional theory (e.g., Wu and Li, 2007) and the integral equation theory (e.g., Vlachy, 1999) have been developed to account for the interion correlation effects. However, the computational complexity for these approaches prohibits efficient applications to realistic RNA 3D structures.

Recently, inspired by the experimental findings for the significance of ion size, ion correlation and fluctuations, the TBI model (Tan and Chen, 2005, 2008a) was developed. Comparisons between the TBI theory predictions and the experimental data on ion-binding properties (Stellwagen et al., 2007; Tan and Chen, 2005), thermal stabilities of DNA and RNA helices and hairpins in Na⁺ and Mg²⁺ solutions (Tan and Chen, 2006a, 2007, 2008b), and electrostatic energy landscapes for helix bending (Tan and Chen, 2008a) and helix assemblies (Tan and Chen, 2006b,c) indicate that the TBI model gives much improved predictions than previous models such as PB. In the following, we will focus on the TBI model and describe the theoretical framework as well as the details in numerical computations and applications of the model.

4. Tightly Bound Ion Model

4.1. General formalism of the theory

Ion binding around a (polyanionic) nucleic acid structure causes counterion accumulation on the molecular surface. The strong, long-range Coulomb force between the ions cause the ions to become correlated (networked). Mathematically, the strong correlation can be characterized by the large correlation parameter Γ

$$\mathrm{\Gamma }=\frac{{(ze)}^2}{\epsilon a{k}_{B}T}\ge {\mathrm{\Gamma }}_{\mathrm{c}},$$ (22.2)

where z is the valency of the ion, e is the electronic charge, ε is the dielectric constant of the solvent (≃78 for aqueous solvent), a is the Wigner–Seitz distance between the ions, and k_B = 1.99 cal/mol K is the Boltzmann constant and T is the temperature. Γ_c = 2.6 is the critical value for the gas–liquid transition for an ionic system (e.g., Ichimaru et al., 1987). Control tests for different Γ_c values suggest that the model is quite robust against small variations of Γ_c.

The correlation strength distinguishes two types of ions: the tightly bound ions (TBIs) (Γ ≥ Γ_c, strong correlation) and the diffusive ions (Γ < Γ_c, weak correlation). The tightly bound and the diffusive ions are distributed in the vicinity of the nucleic acid (tightly bound region) and in the outer region (diffusive region), respectively. A central point in the TBI model is to treat the diffusive ions using the PB method while treating the TBIs with discrete ion distributions.

A direct implication of the ion correlation is that the likelihood of finding an ion at a location is sensitive to the locations of other ions. Therefore, to treat the ion correlation effect, we must consider an ensemble of discrete ion distributions (i.e., fluctuations) (Ha and Thirumalai, 2003). In order to enumerate the different distributions for the TBIs, we divide the tightly bound region into discrete phosphate cells, each around a phosphate group. We generate the ensemble of distributions for the TBIs by enumerating the different ways of partitioning the TBI among the different cells. We call each such distribution of the TBIs as a mode.

The total partition function Z of the system is the sum of the partition function Z_M for each mode M

$$Z=\sum _M{Z}_M.$$ (22.3)

A mode is defined by a set of numbers (not the coordinates) of the TBIs in the different cells. The partition function Z_M is given by the average over all the different spatial coordinates of the ions for a given mode M:

$$Z_M=Z^{(id)}{(c_z)}^{N_{\mathrm{b}}}(\int \prod _{i=1}^{N_{\mathrm{b}}}\mathrm{d}{R}_i){\mathrm{e}}^{-(\mathrm{\Delta }{G}_{\mathrm{b}}+\mathrm{\Delta }{G}_{\mathrm{d}}+\mathrm{\Delta }{G}_{\mathrm{b}}^{\text{pol}})/k_{\mathrm{B}}T},$$ (22.4)

where Z^(id) is the partition function for the uniform ion solution (without the nucleic acid), N_b is the total number of the TBIs, c_z is the bulk concentration of the z-valent counterions, and R_i denotes the coordinate of the ith TBI. $\int {\prod }_{i=1}^{N_{\mathrm{b}}}\mathrm{d}{\mathbf{R}}_i$ is the volume integral over the tightly bound region for the TBIs. ΔG_b and $\mathrm{\Delta }{G}_{\mathrm{b}}^{\text{pol}}$ are the Coulombic free energy and the (Born) self-polarization energy for the charges in the tightly bound region and ΔG_d is the free energy for the interaction between the diffusive ions and between the diffusive and the TBIs (Tan and Chen, 2008a).

From the partition function, we can predict the ion distribution from the probability distribution

$$p_M=\frac{Z_M}{Z}$$

of the ion-binding modes and the electrostatic free energy of the system:

$$G^E=-k_{\mathrm{B}}T\text{ ln }\left(\frac{Z}{Z^{(id)}}\right)=-k_{\mathrm{B}}T\text{ ln }\sum _M\left(\frac{Z_M}{Z^{(id)}}\right).$$ (22.5)

4.2. Free energy of the tightly bound ions

Consider a TBI in a phosphate cell. Averaging over the possible positions in the respective phosphate cells for the TBIs (Tan and Chen, 2005, 2006c, 2008a) gives two useful potentials of mean forces: Φ_l(i) for the interactions between charges within the cell i and Φ₂(i, j) for the interactions between different cells i and j:

$${\mathrm{\Phi }}_1(i)=-k_{\mathrm{B}}T\text{ ln}\langle {\mathrm{e}}^{-u_{ii}(R_i)/k_{\mathrm{B}}T}\rangle ; {\mathrm{\Phi }}_2(i,j)=-k_{\mathrm{B}}T\text{ ln}\langle {\mathrm{e}}^{-u_{ij}(R_i,R_j)/k_{\mathrm{B}}T}\rangle .$$ (22.6)

Here u_ii and u_ij are the Coulomb (generalized Born) potentials (Liu and Zou, 2006; Still et al., 1990) for the charges in cell i and between the charges in two different cells i and j, respectively. 〈…〉 denotes averaging over all the possible positions R_i (R_j) of the TBIs within the respective phosphate cells.

For a give mode, we can readily compute ΔG_b, the free energy for the charges inside the tightly bound region, as the sum of the potentials of mean force:

$$\mathrm{\Delta }{G}_{\mathrm{b}}\simeq \sum _i{\mathrm{\Phi }}_1(i)+\sum _{ij}{\mathrm{\Phi }}_2(i,j).$$ (22.7)

Because we can pretabulate the potentials of mean force before enumerating the modes, the computation of ΔG_b for a give mode is efficient.

4.3. Free energy of the diffusive ions

With the mean-field approximation for the diffusive ions, we compute ΔG_d from the following equation (Tan and Chen, 2005):

$$\mathrm{\Delta }{G}_{\mathrm{d}}=\frac{1}{2}\int \sum _{\alpha }{c}_{\alpha }(\mathbf{r})z_{\alpha }q[\psi (\mathbf{r})+\psi \prime (\mathbf{r})]{\mathrm{d}}^3\mathbf{r}+k_{\mathrm{B}}T\int \sum _{\alpha }[c_{\alpha }(\mathbf{r})\text{ ln}\frac{c_{\alpha }(\mathbf{r})}{c_{\alpha }^0}-c_{\alpha }(\mathbf{r})+c_{\alpha }^0]{\mathrm{d}}^3\mathbf{r},$$ (22.8)

where ψ(r) and ψ′(r) are the electric potentials at position r for the system with and without the diffusive ions, respectively. c_α(r) and $c_{\alpha }^0$ are the concentrations of ion species α at position r and in the bulk solvent, respectively. We use ψ′(r) here because ψ(r) − ψ′(r) gives the contribution to the electrostatic potential from the diffusive ions. With the given charge distribution of the TBIs, we calculate ψ(r) and ψ′(r) from the nonlinear PB (with salt) and the Poisson equation (without salt), respectively.

4.4. Polarization energy of charges inside the tightly bound region

The free energy $\mathrm{\Delta }{G}_{\mathrm{b}}^{\text{pol}}$ in Eq. (22.4) is the change in Born energies for the charges transferred from the bulk solvent to the tightly bound region. We compute $\mathrm{\Delta }{G}_{\mathrm{b}}^{\text{pol}}$ as a sum for all the charges, including the phosphates and the TBIs, inside the tightly bound region:

$$\mathrm{\Delta }{G}_{\mathrm{b}}^{\text{pol}}=\sum _i{\mathrm{\Phi }}_0(i),$$ (22.9)

where Φ₀(i) is the Born energy for the charges inside the ith tightly bound cell. Assuming there is a TBI in the ith cell, we compute Φ₀(i) by averaging over all the possible positions R_i of the ion (Tan and Chen, 2008a):

$${\mathrm{\Phi }}_0(i)=-k_{\mathrm{B}}T\text{ ln}\langle {\mathrm{e}}^{-(\mathrm{\Delta }{U}_{\mathrm{P}}^{\text{pol}}+\mathrm{\Delta }{U}_{\mathrm{I}}^{\text{pol}})/k_{\mathrm{B}}T}\rangle ,$$ (22.10)

where $\mathrm{\Delta }{U}_{\mathrm{P}}^{\text{pol}}=\mathrm{\Delta }{U}_{\mathrm{P}}^{\text{pol}}(i,{\mathbf{R}}_i)$ and $\mathrm{\Delta }{U}_{\mathrm{I}}^{\text{pol}}=\mathrm{\Delta }{U}_{\mathrm{I}}^{\text{pol}}(i,{\mathbf{R}}_i)$ are the (generalized Born) self-energies of the phosphate i and of the ion (at position R_i), respectively. 〈…〉 denotes averaging over all the possible ion positions R_i within the cell.

5. Enhancing the Computational Efficiency for the Numerical Calculations of the TBI Model

5.1. A hybrid treatment for the tightly bound modes

The computational efficiency of the TBI model is limited by the enumeration of the large number of the binding modes, which scales with the number N of nucleotides as ~2^N, assuming each phosphate cell contains 0 or 1 tightly bound (multivalent) ions. Therefore, an exhaustive enumeration of all the modes for a large nucleic acid molecule is extremely computationally expensive. To improve the computational efficiency, we developed a hybrid method. The strategy of the hybrid method is to consider the complete ensemble of the low-energy modes and treat the vast number of the high-energy modes through a computationally efficient random sampling algorithm.

The partition function is calculated from the following equation (Tan and Chen, 2006b):

$$Z=\sum _{N_{\mathrm{b}}}(\sum ^{M_l}{Z}_M+\frac{M_0-M_l}{M_r}\sum ^{M_r}{Z}_M)$$ (22.11)

where N_b is the number of TBIs, M₀ and M_l are the total number of the modes and the number of the low-energy modes for a given N_b, respectively, and M_r is the number of the high-energy modes that are selected for random sampling.

The method is reliable because the most important modes, namely, the low-energy modes, are treated exactly. Because the low-energy modes form only a small fraction of the total ensemble of the modes, this approach leads to drastic improvements in the computational efficiency.

5.2. Computation of the free energy ΔG_d for the diffusive ions

Strictly speaking, the free energy of the diffusive ions is dependent on the TBI mode. For each mode, the computation of ΔG_d requires the result for the electric potentials solved from the nonlinear PB and Poisson equations (see Eq. 22.8). Given the large number of the modes, the computation of ΔG_d can be time-consuming. To improve the computational efficiency, we use a coarse grained method for the computation of ΔG_d. The basic strategy of the method is to precalculate ΔG_d for several typical number of the TBIs N_b (averaging over the different modes with the same N_b), then use the results to fit ΔG_d as a polynomial function of N_b (Tan and Chen, 2005, 2007). For any given mode with N_b TBIs, we can efficiently compute ΔG_d from the polynomial.

6. Applications of the TBI Model

In this section, we show how to apply the TBI model to predict the ion-dependent thermodynamic properties, such as ion-binding numbers and electrostatic free energies for realistic RNAs and DNAs. For illustrative purpose, we choose a short DNA duplex as a paradigmatic system.

6.1. General procedure for the numerical computations for the partition function

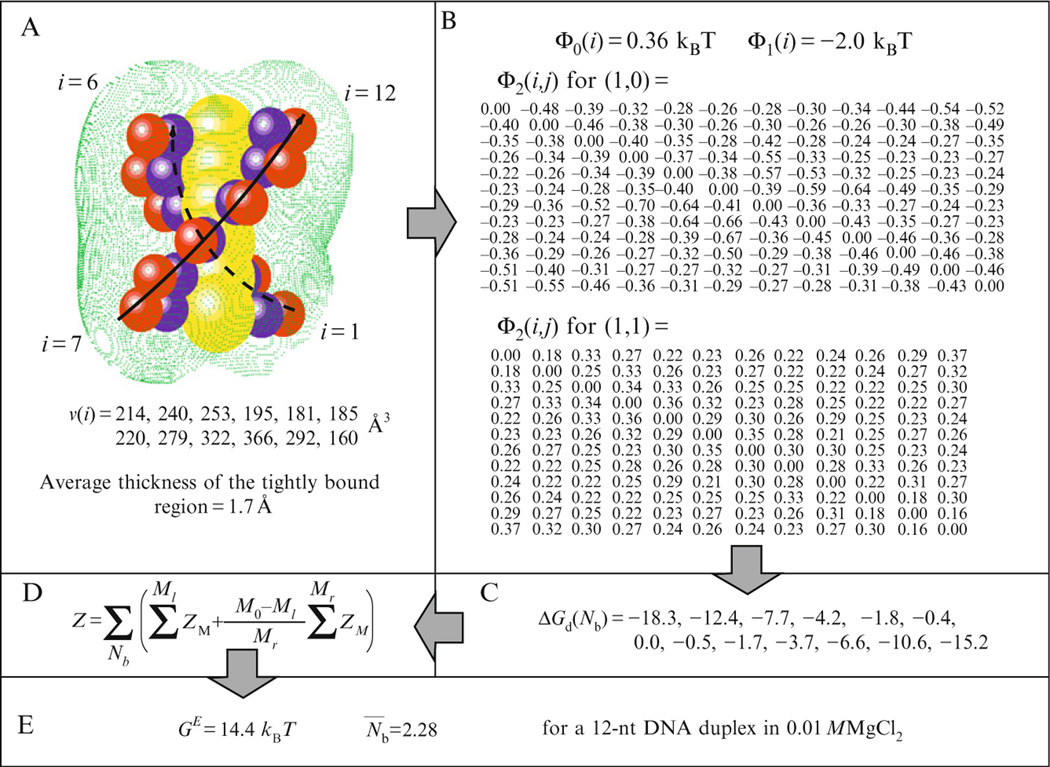
The computational procedures for the numerical calculations of the TBI model for specific systems were described in several previous publications (Tan and Chen, 2005, 2008a). Here, we summarize the general computational procedure using a 12-nt DNA duplex as an example. We assume temperature T = 25 ° C, dielectric constant ε = 78 for solvent and 20 for the nucleic acid interior, and the radii of the (hydrated) ions 4.5 Å for Mg²⁺ and 3.5 Å for Na⁺. The numerical calculations of the TBI model involve the following five steps:

1. To construct the 3D structural model. We construct a 3D structure for the 12-nt DNA duplex. The current form of the TBI model is base on a coarse-grained structural model—grooved primitive model (Montoro and Abascal, 1995; Tan and Chen, 2005), where each nucleotide consists of two “united atoms” (spheres), representing the electrically neutral group and the charged phosphate group, respectively (see Fig. 22.1A).

2. To identify the tightly bound region. For the nucleic acid structure immersed in a given ionic solution, we solve the nonlinear PB equation for the spatial distribution of the ion concentration, from which we calculate the spatial distribution of the ion–ion distance (a in Eq. (22.2)). From the criteria for strong correlation (Eq. (22.2)), we determine the tightly bound region. For a 12-nt DNA helix immersed in a 0.01 M Mg²⁺ solution, we find that the tightly bound region is a thin layer of average thickness ~1.7 Å surrounding the helix (Fig. 22.1A).

3. To calculate and tabulate the pair-wise potentials of mean force Φ₁(i), Φ₂(i, j) (Eq.(22.6)) and the Born energy Φ₀(i) (Eq.(22.10)). A key issue in the calculations for the average over ion positions inside the respective phosphate cells is to take into account the finite size (excluded volume) of the ions and the detailed shape of the molecular surface. For the 12-nt helix in 0.01 M Mg²⁺ solution, Φ₁(i) is ~−2.0k_BT, Φ₀(i) is ~0.36k_BT, and Φ₂(i, j) for the interaction between phosphate cells i and j varies with i and j; see Fig. 22.1B. Φ₂(i, j) < 0 (attractive interaction) if one of the cells is vacant and the other is occupied by a tightly bound (Mg²⁺) ion (denoted as (1, 0) in Fig. 22.1B). Φ₂(i, j) < 0 (repulsive interaction) if both cells are occupied (denoted as (1, 1) in Fig. 22.1B).

4. To calculate the free energy ΔG_d for the diffusive ions (Fig. 22.1C). In order to fit a polynomial for ΔG_d as a function of the number of the TBIs N_b, for a general structure of N nucleotides (phosphates), we evaluate ΔG_d for a set of N_b’s, such as N_b = 0, N/8, N/4, 3N/8, N/2, 2N/3, 5N/6, and N. From such an eight-point dataset, we can readily calculate ΔG_d for an arbitrary N_b through either polynomial-fitting or interpolation.

5. To compute the partition function. Using the above hybrid treatment for the ensemble of ion-binding modes, we calculate the partition function from the sum of the modes (Eq. (22.11)). For each mode, the free energies ΔG_b and $\mathrm{\Delta }{G}_{\mathrm{b}}^{\text{pol}}$ for the TBIs are directly given by the pretabulated potentials of the mean force (Eqs. (22.7) and (22.9)).

Figure 22.1.

A 12-nt DNA duplex in 0.01 M MgCl₂ is used to illustrate the computational procedure of the TBI model. (A) The 3D structure and the tightly bound region (green region). The two strands are labeled from i = 1 to 6 and from i = 7 to 12, respectively. The molecule contains totally N = 12 nucleotides (phosphate groups). The red and blue spheres surrounding the central cylinder represent the charged and neutral groups of the nucleotides, respectively. v(i) denotes the volume of each tightly bound cell i (1 ≤ i ≤ 12). (B) The results for the potentials of mean force (in k_BT). For Φ₂(i, j) (i, j = 1, 2, …, N = 12), the row and column correspond to i and j, respectively. (C) The results for the free energy ΔG_d.

From the partition function, we can predict a variety of ion-dependent folding properties such as the ion-binding properties and the ion-dependence of the folding stability.

6.2. Ion-binding properties

From the partition function Z, we can predict any experimentally measurable property A from the statistical average Ā:

$$Z=\sum _M{Z}_M;\hspace{1em}Ā=\frac{1}{Z}\sum _M{A}_M{Z}_M,$$ (22.12)

where A_M is the result of property A for mode M. An important application of the above general equation is the computation of the mean number of the TBIs N_b from the partition function Z. The experimentally measured number of bound ions includes both the TBIs and the diffusively bound ions:

$$N_{\mathrm{M}{\mathrm{g}}^{2+}}={\overline{N}}_{\mathrm{b}}+\int [c_{\mathrm{M}{\mathrm{g}}^{2+}}(\mathbf{r})-c_{\mathrm{M}{\mathrm{g}}^{2+}}^0]{\mathrm{d}}^3\mathbf{r};$$ (22.13)

$$N_{\mathrm{N}{\mathrm{a}}^{+}}=\int [c_{\mathrm{N}{\mathrm{a}}^{+}}(\mathbf{r})-c_{\mathrm{N}{\mathrm{a}}^{+}}^0]{\mathrm{d}}^3\mathbf{r}.$$ (22.14)

here c(r) and c⁰ are the local concentration at position r and the bulk concentration, respectively. c(r) is solved from the PB equation for the diffusive ions. The integrals account for the contributions from the diffusive ions. Because the correlation effect is weak and negligible for monovalent ions, N_b ≃ 0 for Na⁺.

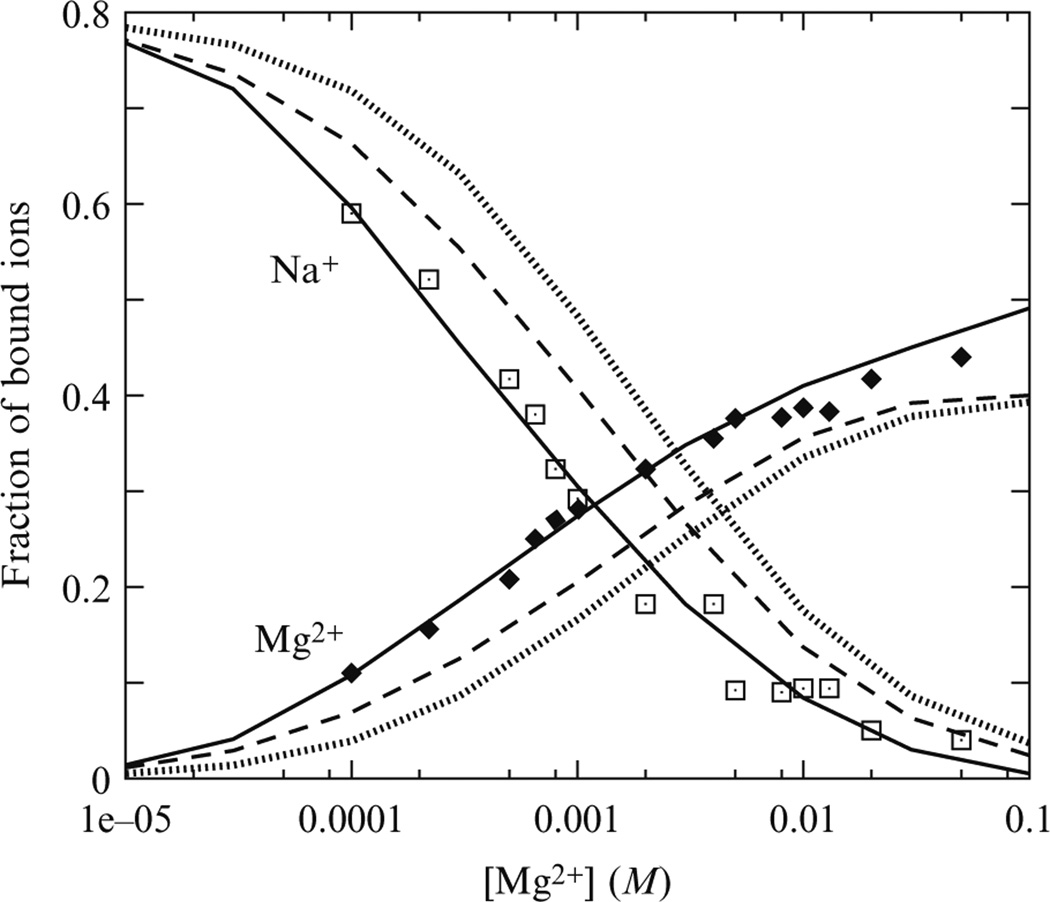
For an illustrative calculation, we apply the TBI model to predict the number of bound ions (Eq. (22.14)) for a 24-bp DNA duplex immersed in an ionic solution with fixed 2 mM [Na⁺] and different [Mg²⁺]. As shown in Fig. 22.2, comparison with the experimental data (Bai et al., 2007; Chu et al., 2007) shows that the predictions from the TBI model are more accurate than the results from PB. For example, for 2 mM [Mg²⁺], the improvement for Mg²⁺-binding number is ~20%.

Figure 22.2.

The mean number of the bound Mg²⁺ and Na⁺ ions per nucleotide for a 24-bp DNA duplex, as functions of Mg²⁺ concentration in the presence of 20 mMNa⁺. Symbols, the experimental data (Bai et al., 2007; Chu et al., 2007); solid lines, the TBI theory predictions; dotted lines, the PB predictions with exclusion layer of width 4.5 Å (=radii of hydrated Mg²⁺); dashed lines, the PB predictions with exclusion layer of width 3.5 Å. In the calculation, the radii of hydrated Na⁺ is taken as 3.5 Å. The mean number of the bound ions per nucleotide is calculated as the total number.

6.3. Folding stability

Folding stability, as quantified by the free energy difference between the folded state and the ensemble of the unfolded states, is determined by the free energy landscape—the distribution of the free energy for different structures. To predict the ion-dependent free energy landscape, we need to generate all the possible conformations, including all the folded and unfolded conformations, and compute the free energy, including the electrostatic free energy (Eq. (22.5)), for each conformation. For example, for a system of two helices tethered by a loop, we need to enumerate all the conformations with different helix orientations and interhelix distances as well as the different loop conformations (Bai et al., 2008; Tan and Chen, 2006c). From the ion dependence of the free energy landscape, we can predict how ions change the conformational distribution and folding stability to cause the structural transitions.

To predict the ion-dependent folding stability for a short DNA helix, we use a two-state model. Specifically, we assume that the conformational ensemble of the system consists of two states: double-stranded (ds) helix as the folded state and single-stranded (ss) helices (stabilized by the single-stranded self-stacking) as the unfolded state. For a given ionic condition (Na⁺, Mg²⁺) and temperature T, using the TBI model (Fig. 22.1), we compute the electrostatic free energies for the duplex $G_{\mathrm{d}\mathrm{s}}^{\mathrm{E}}$ and the unfolded state $G_{\mathrm{s}\mathrm{s}}^{\mathrm{E}}$, respectively. The electrostatic contribution to the folding stability is

$$\mathrm{\Delta }{G}^{\mathrm{E}}=G_{\mathrm{d}\mathrm{s}}^{\mathrm{E}}-G_{\mathrm{s}\mathrm{s}}^{\mathrm{E}}.$$ (22.15)

The ion-dependence of ΔG^E shows how the ionic condition affects the folding stability and how the changes in ionic conditions induce the folding/unfolding transition.

To predict the total folding stability also requires the result for the nonelectric part of the free energy difference ΔG^NE. Assuming the ion-independence of ΔG^NE, we can estimate ΔG^NE from the empirical parameters measured at 1 M Na⁺ (SantaLucia, 1998):

$$\mathrm{\Delta }{G}_{\mathrm{T}}(\mathrm{N}{\mathrm{a}}^{+}/\mathrm{M}{\mathrm{g}}^{2+})=\mathrm{\Delta }{G}_{\mathrm{T}}^{\mathrm{E}}(\mathrm{N}{\mathrm{a}}^{+}/\mathrm{M}{\mathrm{g}}^{2+})+\mathrm{\Delta }{G}^{\mathrm{N}\mathrm{E}}=\mathrm{\Delta }{G}_{\mathrm{T}}^{\mathrm{E}}(\mathrm{N}{\mathrm{a}}^{+}/\mathrm{M}{\mathrm{g}}^{2+})+[\mathrm{\Delta }{G}_{\mathrm{T}}(1\mathrm{M}\mathrm{N}{\mathrm{a}}^{+})-\mathrm{\Delta }{G}^{\mathrm{E}}(1\mathrm{M}\mathrm{N}{\mathrm{a}}^{+})].$$ (22.16)

Here ΔG_T is the total folding free energy, including the electric and nonelectric free energies.

From the folding free energy ΔG_T(Na⁺/Mg²⁺), we can predict the ion-dependent melting temperature T_m from the following equation:

$$\mathrm{\Delta }{G}_{\mathrm{T}}-RT\text{ ln }{C}_{\mathrm{S}}=0,$$ (22.17)

where R (=1.987 cal/K mol) is the gas constant, C_S is the strand concentration. C_S is replaced with C_S/4 for noncomplementary sequences.

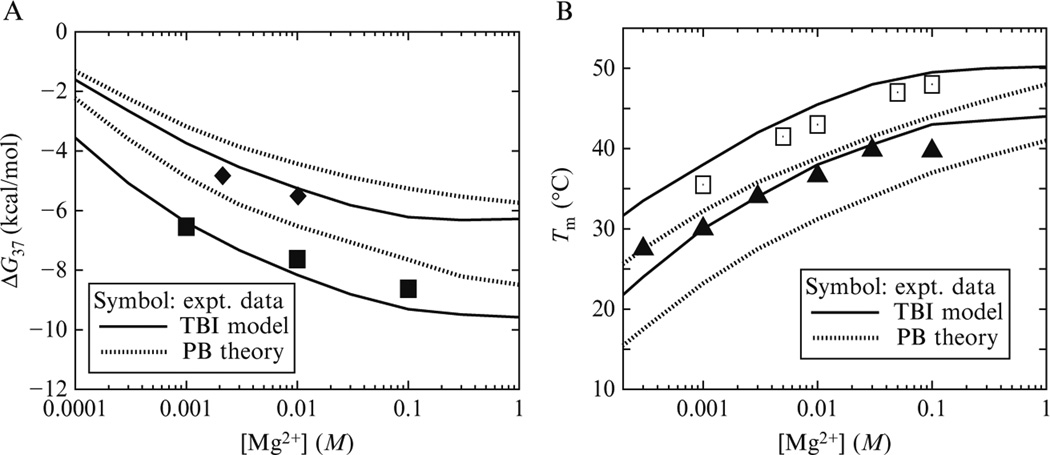
Figure 22.2 shows the TBI-predicted folding free energy ΔG_T and melting temperature T_m for short DNA duplexes as functions of [Mg²⁺] (Tan and Chen, 2006a). Comparisons with the experimental data indicate that the TBI model gives much improved predictions than the PB theory (Fig. 22.3).

Figure 22.3.

The folding free energy ΔG₃₇ at 37 ° C (A) and the melting temperature T_m (B) as functions of [Mg²⁺]. (A) The upper lines are for sequence GCATGC, and the bottom lines are for sequence GCCAGTTAA (Tan and Chen, 2006a; and references therein). (B) The upper lines are for sequence AGAAAGAGAAGA with total strand concentration C_S = 6 µm, and the bottom lines are for sequence GCCAGTTAA with strand concentration C_S = 8 µm (Tan and Chen, 2006a; and references therein). Here, the data for AGAAAGAGAAGA are taken from the duplex melting in the study of the triplex melting in Mg²⁺ and C_S = 6 µm is the total strand concentration for triplex formation. T_m is calculated from ΔG − RT ln C_S/6 = 0 (Tan and Chen, 2006a).

7. Summary

Ion correlation can be potentially important for RNA folding. Because correlated states can reach energies much lower than the mean-field energy, correlation can significantly enhance stability. Neglecting correlation (such as in the PB theory) can cause notable under-estimation of the folding stability (Chen, 2008). Furthermore, the correlation effect may make significant contributions to the unusually high efficiency of the multivalent Mg²⁺ ions in RNA stability, especially for tertiary structures. In RNA tertiary structure folding process, the close approach of the helices and other structural units causes significant build-up of the phosphate charges, inducing a strong correlation for the multivalent counterions. The strong correlation results in a further correlation-enhanced stabilizing force for tertiary folds. Such a correlation-induced enhancement in RNA stability goes beyond the classical charge neutralization/screening effects predicted by the mean-field theories. Therefore, multivalent ions can have much higher efficiency in stabilizing RNA structures than that predicted from the PB theory, and the high efficiency is more pronounced for tertiary structures. This causes a correlation-induced force from the multivalent ions to promote the formation of the tertiary folds.

The TBI model tackles ion correlation/fluctuation effects by evaluating the energetics based on the discrete all-ion distributions for the TBIs. This is contrastingly different from the mean-field (correlation-free) approaches which are based on an average distribution for a system of independent ions. The TBI model also accounts for the volume exclusion effects due to the finite sizes of the ions. Control tests indicate that the excluded volume correlation is weak as compared with the Coulomb correlation. For systems with weak correlation, such as RNAs in monovalent ion solutions, the TBI gives nearly identical results as the PB and both the TBI and PB results agree with the experiment. But for RNAs/DNAs in Mg²⁺ solutions, where correlation can be strong, the TBI theory gives much improved predictions than the PB as shown by the experimental comparisons.

The TBI model is not based on any of such preassumptions, while other models such as the PB are based on a priori assumptions about the nonexistence of the ion correlation/fluctuation effect. If the ion correlation and fluctuation effects are strong, the TBI model will capture them, otherwise, the model gives identical predictions as other (PB-based) models. Therefore, the TBI model can effectively complement the PB-based methods.

Ion dehydration effects can be responsible for a variety of ion-dependent RNA folding properties, especially for the tertiary structure folding (Draper, 2008). Refinement of the TBI model should include a more accurate treatment for the possible ion dehydration effect. Further development of the model should also consider the all-atom details of the RNA structure and the improvements of computational efficiency.