Emergence of proto-organisms from bistable stochastic differentiation and adhesion

Abstract

The rise of multicellularity in the early evolution of life represents a major challenge for evolutionary biology. Guidance for finding answers has emerged from disparate fields, from phylogenetics to modelling and synthetic biology, but little is known about the potential origins of multicellular aggregates before genetic programmes took full control of developmental processes. Such aggregates should involve spatial organization of differentiated cells and the modification of flows and concentrations of metabolites within well-defined boundaries. Here, we show that, in an environment where limited nutrients and toxic metabolites are introduced, a population of cells capable of stochastic differentiation and differential adhesion can develop into multicellular aggregates with conflict mediation mechanisms and a complex internal structure. The morphospace of possible patterns is shown to be very rich, including proto-organisms that display a high degree of organizational complexity, far beyond simple heterogeneous populations of cells. Our findings reveal that there is a potentially enormous richness of organismal complexity between simple mixed cooperators and embodied living organisms.

1. Introduction

Multicellularity has evolved multiple times through the history of our planet, leading to a wide array of spatially organized living structures such as aggregates, sheets, clusters or filaments [1]. The transition to multicellularity required the emergence of alternative cellular states along with stable, physical interactions among previously isolated cells [2–5]. In our present-day biosphere, multicellular systems display intricate spatial and temporal patterns implemented by developmental programmes, which are tightly controlled by genetic networks [6,7]. However, an early stage might have involved non-inherited stochastic phenotypic switches and physical aggregation phenomena that could have given rise to some class of cooperating multicellular assemblies [8,9]. This is supported by the well-known observation that single-celled organisms can behave as multicellular systems using precisely these processes [10] particularly in the face of high-stress events [11–13]. Simple multicellular systems, such as Anabaena, where cell differentiation is induced under nitrogen deprivation, or myxobacteria [10] are examples of the minimal types of multicellular organization [14,15]. A minimal form of multicellularity is provided by persister cells and phase variation phenomena, i.e. slow-growing cell subpopulations that can spontaneously switch back and forth among multiple resistant phenotypes, as a bet-hedging strategy in the face of potential catastrophe [16,17].

In this paper, we aim to explore the potential for organismality [18] emerging from a minimal set of assumptions, including (i) multistability [19], incorporated as a stochastic bistable phenotype [20], allowing for two cell types (1 and 2), (ii) differential adhesion, which can lead to spatial segregation of different proto-tissues and pervades several key processes of development [5,21] and (iii) a selective environment where the presence of external nutrients and toxic waste forces the selection of genotypes with higher fitness. Both types of cells can survive only in presence of nutrients, which are transformed into internal energy, and die if exposed to high concentrations of waste. Cells of type 2 have the additional capability of degrading waste in the medium, at the expense of their capability of elaborating nutrients. Previous models involving the evolution of undifferentiated multicellularity [22,23] have shown that appropriate metabolic trade-offs might pervade the coexistence of cell clusters. Our model goes a step further by allowing alternative cell states to organize in space. We find that if the system is allowed to exploit spatial organization, its evolution gives rise not only to cell heterogeneity, but also to nested substructures and to the creation of an internal environment, thus suggesting that combining differential adhesion and multistability provides the necessary toolkit for evolving proto-organisms in a robust manner. The results reported here indicate that the generative potential which is typical of the morphological landscape can also be obtained by a simple, previously unexplored set of pattern-forming rules, where cell–cell communication or genetic networks are not taken in account. It contains the three key components of evolved MC [24] namely (i) fitness-coupled spatial patterning, (ii) cooperation and specialization, and (iii) a transition from ‘simple’ to ‘complex’ multicellular forms.

2. Model specifications

Our hypothesis is that aggregative organisms involving multiple cell states present a better fitness than single-state organisms in a habitat with limited resources and toxic molecules. In order to explore this hypothesis, we consider a model in which cells are able to stochastically switch between two different metabolic states, and present differential cell–cell adhesion (figure 1). If a cell is able to survive the habitat's conditions, then it can generate offspring, starting an evolutionary process by means of mutation occurring in the genotype parameters upon reproduction.

Figure 1.

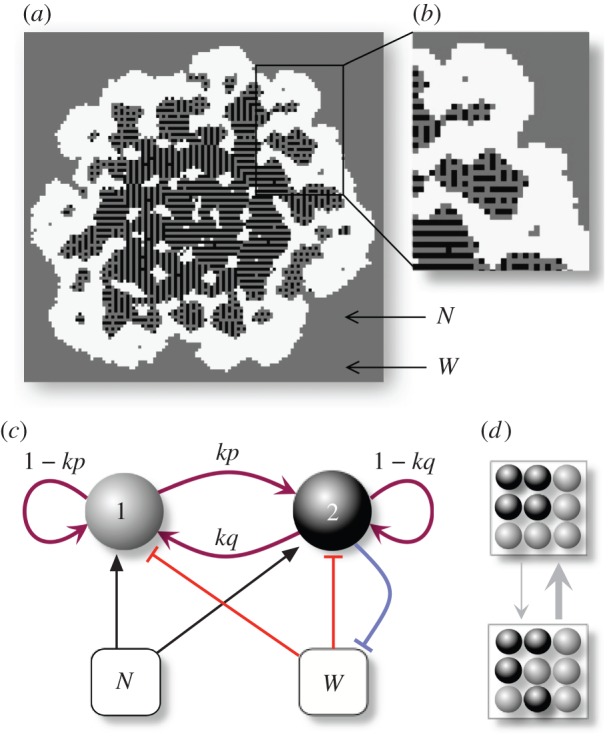
Minimal description of our model for the emergence of proto-organisms. The world is defined as a regular two-dimensional lattice continuously seeded with nutrients and toxic metabolites in the empty space (white), where two types of cells (grey and black) can coexist. In (a), we show the example of an evolved proto-organisms displaying complex nested structures (b). (c) Cells can stochastically switch between the two available phenotypes, which can have different adhesive and metabolic properties. Phenotypic switching in both directions may occur with a certain probability (kp, kq), whereas (1−kp, 1−kq) are the probabilities that no change occurs for grey or black cells, respectively. Cells also interact with the local fields of a nurturing substance (N) and a toxic metabolite (W), which are involved in cell duplication, survival and death. The metabolism of black cell includes the ability to degrade waste (blue arrow). (d) In our model, cells move by swapping locations with a neighbouring cell, provided that the final energy is reduced, in accordance with their (evolved) adhesion properties. (Online version in colour.)

2.1. Metabolism and competition

A selective environment is introduced including both an incoming external nutrients (N) and a toxic waste (W) as well as an internal currency molecule (E). A regular L × L square lattice (Ω) is used. Each site 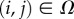is characterized by a state, indicated as S_ij. This state can be 0 if the site is empty and either 1 or 2 if the site is occupied by cells. These two values indicate two different cell types with different adhesion and metabolic properties. Both N and W are added continuously to the empty lattice sites and passively diffuse through the external medium and across nearest cells. Cells of type 1 and 2 process nutrients (N) into energy (E), the accumulation of which leads to cell division. Cells of type 2 can allocate resources for waste degradation, at the cost of reduced nutrient elaboration, following a linear trade-off (ɛ > 0) consistent with a maximum metabolic load and shared resources between tasks. For type 1 cells, we have ε = 0. All three molecules experience linear degradation.

The spatial dynamics are described by a discrete set of coupled differential equations. For each site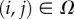

Here, 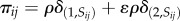and 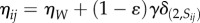include decay and active removal of N and W, respectively. We have used Dirac's delta function δ_kl = 1 if k = l and zero otherwise. Similarly, the input terms 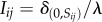for each site are effective provided that the site is empty. The normalization factor λ (the fraction of sites occupied by cells) ensures a constant flux of N and W throughout the lattice. A cell divides when its E-value increases beyond a fixed threshold (Θ_div), and there is an empty site in the vicinity. This new cell inherits the genotype and the phenotypic state of the progenitor with a small chance of mutations (see electronic supplementary material), and the energy is equally split among the two (i.e. no asymmetric divisions are considered). Conversely, cells die if the W value surpasses another fixed threshold (Θ_tox), if E falls below a critical value (Θ_starv), or with a small random probability (ξ), releasing their contents (N, W and E as nutrients) to the surrounding medium. Following this formulation, there is a natural competition for resources that can promote selection of different multicellular communities.

2.2. Stochastic switching genetics

We introduce genetics into our model in the form of a stochastic transition between phenotypes (figure 1c) relevant for cell sorting and metabolism, as it is assumed in phase and antigenic variation in certain microbial populations [16,25,26]. Specifically, cells can switch between states with evolvable probabilities 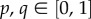, i.e.

where κ is a fixed scaling factor, introduced to account for the timescale separation between adhesion kinetics and genetic processes. Therefore, the phenotypic transitions are not dependent on any molecular cue nor cellular memory beyond their current state.

2.3. Minimal model for cell adhesion

The physics of cell sorting can be introduced considering the arrangement of cells constrained by their local preferences [27,28]. Following Steinberg's differential adhesion model, we assume that cell movement is driven by the minimization of adhesion energy with cells being more or less prone to remain together, avoiding the external medium, or maximizing contact with it [5,28–30]. An adhesion (or interaction) matrix weights the strength of pairwise interactions among neighbouring sites

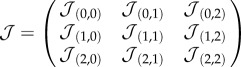which is symmetric, i.e. 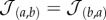, and has 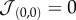. Other approaches [31] consider each cell as formed by a number of sites, thus allowing for a better matching with the underlying physics of cells. For the sake of simplicity, we keep our model confined to a one cell–one site scheme. Because cell–cell (and cell–medium) interactions are necessarily local (figure 1c), a given cell can only interact with a set Γ_ij of eight nearest neighbours. The model allows cell movement between neighbouring positions by switching the two local states provided that the final state is more likely to happen, i.e. consistent with the optimization of both cell adhesion energies. This is given by an energy function

which averages the interaction matrix of both cells. The superindexes denote the adhesion matrix of a particular site and normalize the effect of interacting with empty medium.

At each step, we choose a random neighbour for each site, compute the new energy 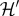and compare it with the original one . If the difference 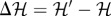is negative, a decrease in the global energy would occur, and thus the state swap is always applied. Instead, when 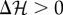, the larger the difference, the less likely the change is assumed to happen, with a probability following the Boltzmann rule (for more details, see electronic supplementary material, S1):

As defined, the transition is likely to occur if an energy reduction takes place, with a noise factor introduced by T, acting as an effective ‘temperature’. A small stochasticity prevents the system from getting trapped into local energy minima.

3. Results

3.1. Resource and waste levels influence selection for complex multicellularity

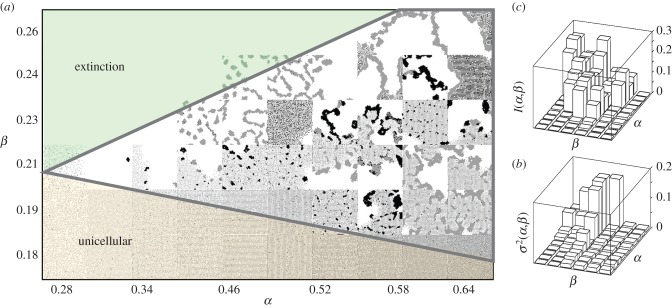
In order to analyse the prevalence of multicellular traits, we have explored the role played by nutrient and waste inputs in selecting different phenotypes by evolving the different parameters. The results are shown in figure 2a. Simulations are started with type 1 cells only with no adhesion (i.e. 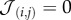for all adhesion strengths) thus behaving as random walkers (because 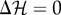and thus 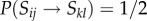). This parameter space displays three main phases, including a cell-free (extinction) phase, a second phase with sparse distribution of unicellular populations (lower domain) and an intermediate phase (marked by a thick line) associated with organismal structures. Moreover, different measures were applied to these endpoint states of evolutionary processes (figure 2b,c), showing an overall increase in complexity for the multicellular region of this phase space in terms of structural organization and genetic diversity (see electronic supplementary material). In particular, the increase in genetic diversity is due to the existence of multiple distinguishable strains that create different, complex spatial arrangements, as measured by the spatial mutual information measure.

Figure 2.

Impact of energy availability and waste input on the selected phenotypes. Here, we show a representative region of the system for different nutrient (α) and waste (β) input values after 5 × 10⁵ iterations of the genetic algorithm (a). The multicellular region of this phase space is confined by a minimum energy density below which aggregates cannot grow, but is otherwise expanded by increasing fluxes of both N and W. Mutual information (b) of the cellular states for neighbourhoods of size 3 (see electronic supplementary material). Genetic diversity (c), calculated from the final normalized genotypes (see electronic supplementary material). As α and β become larger, more spatial structure is observed and increasingly diverse genotypes are established, eventually settling to more than one strain coexisting (see below). (Online version in colour.)

3.2. Cellular embodiment enables niche construction

Within the multicellular region of this phase space, proto-organisms display consistent spatial and temporal structures of remarkable complexity. Typically, an outer layer of cells that develops aggregative features in order to withstand the mounting levels of toxic waste, and which surrounds and protects an internal environment with lower W and N levels, which is suitable for colonization by cells that are preferentially exposed to the environment. Within these ‘containers’, other cell types (not viable outside these boundaries) can coexist (figure 1a). These nested structures can regenerate the protective layer in case it breaks or even create a whole new proto-organism, thus acting as a propagule (see electronic supplementary material, S1) and effectively defining a rudimentary life cycle. Moreover, given the spatial constraints to the local concentration and flows of metabolites caused by the organization of cell types, ecosystem engineering is also present [32,33].

3.3. Convergent evolution towards multicellularity

Beyond the small-scale dynamics of the system, the particular paths taken by each population in the evolutionary process were also analysed. In figure 3, we display the evolutionary dynamics of three different scenarios using a reduced genotype space. In particular, we find that the tendency to form homo-aggregates of each cell type and the waste degradation potential yield a functional clustering of individuals into discrete subpopulations or strains (see electronic supplementary material for a principal component analysis of the population genotypes). These populations will generate aggregates of a particular type if 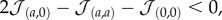and will display unicellular traits—i.e. will tend to attach to the external medium—otherwise. In addition, cells will process more waste at the expense of efficiency in nutrient absorption the lower the ɛ values.

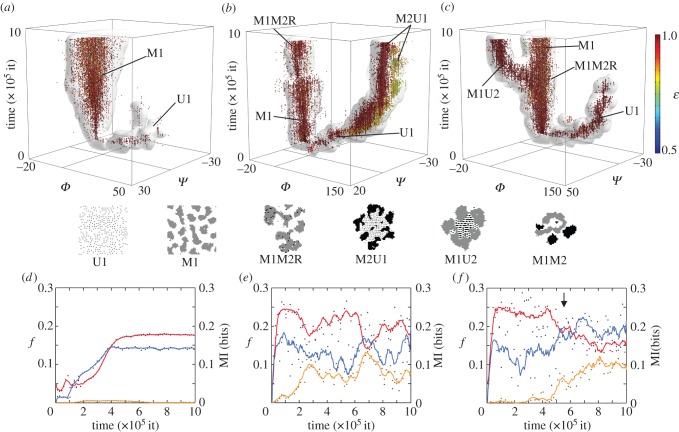
Figure 3.

Speciation process in our GA. The plots on the first row (a–c) show the evolutionary dynamics of populations of cells in different parameter sets (α,β), forming distinct branches or ‘species'. Here, individuals are represented as dots in time coordinates (z-axis) as well as a reduced genotype space (x, y and colour). More precisely, we use the tendency of grey cells to adhere to other grey cells Φ (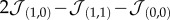), the tendency of black cells to adhere to other black cells Ψ (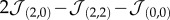) and the ability to process waste ɛ. An isosurface of genotype density is also shown (see electronic supplementary material). The lines on the bottom face of each cube mark axes origin and the starting population genotype at Φ = Ψ = 0. As a guide for the eye, we provide a representation of each of the main lineages at the bottom of the figure. On the second row (d–f), for each run, we show the population dynamics of each cell type in fraction of lattice occupied f (red and yellow for types 1 and 2, respectively) as well as the mutual information evolution in bits, right axis (blue). Points represent actual values, whereas lines are moving averages (binning window: nine data points). (Online version in colour.)

The first example shows the evolution of a ‘simple’, undifferentiating aggregative strain (M1) under medium energetic conditions and high inputs of waste. The other two—different runs of the same parameter set—display coexisting strains, giving rise to complex multicellular phenotypes with differentiation and division of labour. Interestingly, all three cases share the same lineages for a short period at the beginning of the simulation yet soon diverge into different evolutionary histories. For instance, in the second scenario, the type 1 unicellular lineage (U1) acquires a protective aggregative layer that is also proficient in processing waste (thus becoming M2U1), whereas in the third case, it is the aggregative strain M1 that fills the U1 niche once this strain disappears, evolving into M1U2 (see also electronic supplementary material, S2–S4). The evolution of these mirror multicellular proto-organisms M2U1 (figure 3b) and M1U2 (figure 3c)—which are essentially the same phenotype with switched adhesion properties between the two cell types, yet coming from different lineages—is a clear example of convergent evolution and path-dependence in our system. Figure 3e,f shows the population dynamics and the evolution of the mutual information of the system in each simulation. In the first case, the population follows a classic logistic growth and has a fixed, stable MI. The other two, instead, display heavy fluctuations in both the population levels and the mutual information, even showing signs of quasi-periodic dynamics (b). It can also be clearly observed the emergence of a new strain and its impact in the mutual information in the third dataset (arrow marks the branching of the main strain M1 into M1U2 at approx. 6 × 10⁵ iterations).

3.4. Collective fitness, cheating and green beard traits

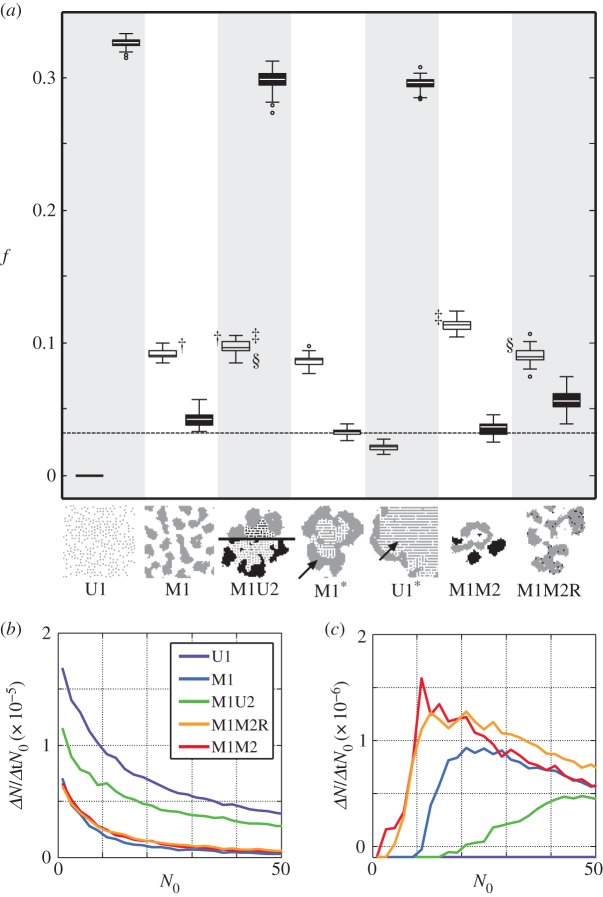
In previous examples, some strains are shown to coexist, whereas others appear to be mutually exclusive, implying a rich repertoire of underlying ecological interactions. In order to better understand the fitness dependencies and evolution of multicellular traits in our model, we performed controlled experiments with some of the most commonly observed genotypes and two different environments: one with abundance of nutrients and waste, and a more stringent one with lower levels of nutrient and toxic metabolites. In each simulation, the lattice was inoculated with a few cells of one or two genotypes, namely U1, M1, M1U2/M2U1, M1 and U1 together, M1M2 and M1M2R. Figure 4a shows the normalized population size in each scenario attained after 10³ iterations. Some genotypes appear to be viable in only one of the two environments, whereas some (especially M1U2/M2U1) provide efficient growth in both, possibly being the most fit genotype in fluctuating environments.

Figure 4.

Fitness characterization of the most commonly observed strains in the GA. In (a), we show the occupied fraction of the lattice (f) after 10³ algorithm iterations of growth without mutation by different genotypes or combinations of them. For two environments (α = 0.36, β = 0.193 in filled boxes and α = 0.56, β = 0.247 in white boxes), an empty lattice was inoculated with a few cells (basal dotted line) of one or two genotypes, from left to right: U1, M1, M1U2/M2U1, M1 and U1 together (M1 shown), M1 and U1 together (U1 shown), M1M2 and M1M2R. Boxes represent the limits of the first and the third quartile of the data, the central line is the median value and bars stand for the most extreme values not considered outliers, which are plotted individually as circles (50 simulations for each condition). §, † and ‡ link datasets that were found to have different mean values (t-test, significance p < 10⁻⁴). In (b,c), we show the impact of the initial cell number (N₀) on growth rates (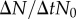) for the same environments and genotypes previously used (25 simulations of each condition). In the high W environment (c), a cooperative domain is found below a finite population size, in which adding cells to the propagule nonlinearly increases growth rates. Beyond this fitness peak, cells compete for resources and space, leading to a cumulative decrease in fitness similar to the results obtained in the low W environment (b). (Online version in colour.)

Interestingly, the nature of the ecological interaction among genotypes U1 and M1 is shown to switch from straight competition in the low W and N scenario to parasitism in the high W and N scenario. In fact, in the first scenario, both genotypes survive when alone but they compete for scarce resources when together, marking a decrease in the fitness of both genotypes. On the contrary, in the latter scenario, only M1 survives when the genotypes are alone, but creates a protective layer for U1 when the genotypes live together, so that U1 can survive at the expenses of M1, which receives less N and sees its fitness decrease. As commented previously, this is mainly caused by the capacity of multicellular entities to create an internal environment, which can be colonized by a unicellular strain, similarly to a parasitic microbiome–host relation. Figure 4b,c, on the other hand, characterizes the interactions between cells of the same genotype by varying the initial population size (N₀) in the same environments. Using the initial population and the growth after 10³ iterations, we approximate the specific growth rate following

We observe that regardless of the genotype, cells compete for resources and space in the low energy input scenario (b), meaning that each cell added to the initial population decreases the growth rate of the whole. A very different set of interactions appears to be in place in the high waste environment (c), giving rise to a cooperation domain in which increasing the propagule size increases the growth rate of the whole, resorting afterwards to competition between cells. This suggests that, under these simple rules, an optimum propagule size exists and a fitness beyond the individual has emerged.

Moreover, one of the reported strains displayed evolved division of labour: phenotypic switching and investment in waste management (yellow branch in figure 3b). This combination of features was accompanied by increased self-adhesion, which enables cells to manipulate who do they stand next to and thus, mitigate the effects of cheating (see electronic supplementary material). The evolution of this adhesive property is a clear example of a green beard trait: a feature of cells that can be readily recognized by other cells and which facilitates the spreading of cooperative strategies, in this case division of labour and fitness transfer between cell types.

4. Discussion

Emerging multicellularity can be described as cooperative groups of cells assembled from independent replicators [18]. This transition might have involved different paths, from mixed aggregates to clonal organisms with simple developmental plans and life cycles. The existing literature usually deals with cooperators achieving some kind of selective advantage as a consequence of mutualism, including spatial clustering or structured communities, as occurs in biofilms [34–36]. However, true organismality, with a diverse set of cellular phenotypes arranged in space as a functional structure, has not been previously described as emerging from evolved interactions among simple virtual cells embodied as Darwinian entities.

Here, we have provided a minimal set of rules grounded in biological processes that shift the selective pressures towards aggregative behaviour and division of labour. Morphological complexity [37] increased throughout our simulations and a fitness transfer was shown to be in place with the evolution of ɛ. Interestingly, those cells with lower values of ɛ, also displayed stronger attachment between them (lower Ψ). This suggests that from a game-theoretical perspective cells become ‘intelligent’ players and try to surround themselves with other players whose strategy is the most mutually beneficial (see electronic supplementary material). Although our cells live in a non-clonal environment [38], they can manipulate who they stand next to, potentially shaping local genetic relatedness. This would ensure that the investment in W reduction mostly benefits cells with a similar genotype, paving the way for the evolution of cooperative and altruistic behaviour [39].

As a premise for this model, we have assumed the existence of death-promoting agents in the environment, of which there are several naturally occurring candidates, such as oxygen [40,41], secreted antibiotics [42] or exoenzymes and toxins [43,44]. We think that a particularly interesting scenario is the one given by niche construction [45], in which the efforts to exclude extant microorganisms from the population by other ecological players might drive the evolution of multicellularity. This relation would entail a coupling between ecological and organismal complexity, a link that has eluded previous efforts in artificial life research (see [46] and references therein).

By allowing our virtual cells to evolve through mutation of parameters affecting interactions with the external fields as well as with other cells, we provide a clear framework to evolve complexity under selection. The result of this is a system that spontaneously evolves, under many parametric conditions, to a complex, spatially organized multicellular state. The embodied structures emerging from the interplay of cell sorting and stochastic phenotypic switching display interesting and relevant features, including spatial modification of concentrations and flows of resources as well as temporal dynamics resembling proto-life cycles. In these spatial communities, pattern formation is enforced by the optimization of nutrient uptake along with an efficient removal of waste. In doing so, our cell assemblies arrange themselves in fitness-coupled collectives, indicating that organismality might be an inevitable outcome while solving the conflict associated with simultaneously dealing with both requirements.

Our analysis also suggests that in the context of the evolution of organismality proposed in [18], our proto-organisms would fit in the high cooperation–reduced conflict category. This class of entities harbours species of disparate complexity, yet all showing a fitness-relevant division of labour and differentiation, which stands at the core of our model. Specifically, some artificial organisms have been shown to include an exclusively cooperative domain and specialization in terms of a metabolic trade-off, producing a fitness transfer from one cell type to the other. Differentiation into terminal lineages (i.e. generating a soma), although not contemplated in our current formulation, would be an interesting addition because it would provide new grounds for conflict and interaction between cell types.

The model presented here can be improved by incorporating more realistic physics allowing for movement of aggregates [47] as well as heterogeneous media [48] where resources and waste might be generated in a non-homogeneous fashion. Similarly, we have limited ourselves to a binary switch, therefore confining the functional cell diversity to two main classes. We also assume that cell types are always alive, excluding the possibility of having material scaffolds formed through the differentiation processes, as it occurs with many solitary and colony-forming microorganisms in shallow waters. No less relevant in this context is the potential of creating multicellular systems by means of artificial evolution experiments [49–51] or synthetic biology approaches [52–55]. There is great potential associated with the use of existing genetic components to engineer pattern-forming modules. Our proposed minimal system might help to define feasible paths to implement proto-organisms.

Authors' contributions

S.D.N., A.B., R.S. conceived the research. S.D.N., A.B., R.M., R.S. performed research. S.D.N., A.B., R.M., S.V. analysed data. S.D.N., A.B., R.M., R.S. wrote the paper.

Funding

This work has been supported by the European Research Council Advanced Grant, the Botín Foundation, Banco Santander through its Santander Universities Global Division, BES-2010-038940 MINECO fellowship and by the Santa Fe Institute.

Competing interests

We declare we have no competing interests.