Notions of synergy for combinations of interventions against infectious diseases in heterogeneously mixing populations

Abstract

In public health programmes interventions are frequently combined with hoped for ‘synergies’ [22]. However, there is not yet a precise definition for synergy between interventions that captures the idea that there is added benefit at the population level in using them together. To explore the synergy between interventions in the context of endemic disease, we consider a general model of infection spread in a heterogeneously mixing population. We consider interventions which may alter individuals’ infectiousness, susceptibility, profile of infectiousness through time and survival while infected. Allowing general patterns of overlap and targeting in those receiving the interventions, we show how to compute changes to epidemiological indices such as R₀, and introduce a simple technique for calculating equilibrium prevalences and incidences via an iterated map. We argue for a particular definition of synergy and investigate its behaviour, both analytically and numerically, concluding that it is easiest to achieve synergy between interventions which perform poorly in isolation; implementation strategies that minimize the overlap of different interventions in the population tend to achieve more synergy; and that in populations with heterogeneous risk, interventions that are redundant when universally targeted can regain substantial synergy when applied in a targeted manner.

1. Introduction

It is often the case that there is a range of possible interventions against an infectious disease to chose from, each of them being only partially effective on their own. This raises questions about choices of intervention combinations and the patterns of their distribution. It is also often the case that populations are not homogeneous, with some individuals being more at risk of disease, or contributing more to its spread. This raises questions about targeting interventions towards higher-risk groups¹. It is always the case that resources are limited. This means that combinations of interventions and strategies for targeting and distributing them should be chosen so as to maximise public health benefit. Practical and ethical complexities rarely lend themselves to a precise notion of utility or constraints, allowing a formal optimization problem to be defined, but general understanding and ‘rules of thumb’ are still useful for policy-makers. The goal of this paper is therefore to study the interactions of interventions in structured populations, and to give a precise meaning to the notion of synergy - two interventions combining to give more than additional benefit at the population-level - and investigate its behaviour.

Each of these considerations applies particularly to the case of HIV. Apart from condoms, and changes in risk behaviour, the prevention toolbox for HIV is painfully limited. Most optimistically, male circumcision (MC) has been shown to be around 60% effective at preventing acquisition of the infection in men (but is not thought to affect infectiousness upon acquisition) [5, 6, 14, 28]. Increasing roll-out of (early) anti-retroviral therapy (ART) holds some promise for prevention [13, 21] since it likely reduces infectiousness of those on treatment [4, 29], although in extending life, it provides more opportunities for transmission. Future prospects include microbicides (for use by women) [27], pre- and post-exposure prophylaxis [8, 1, 26], and yet more distant, vaccines [3]. All of these will almost certainly be of only partial efficacy. Heterogeneities in sexual behaviour are known to be important to the epidemiology of sexually transmitted infections (STIs) like HIV [2, 16], which means that in addition to only being able to apply interventions like MC to portions of the population (men), targeting those at higher risk is likely to yield greater dividends.

The aim in the rest of this paper is then to consider a model of infectious disease spread which includes enough features to describe the case of HIV, while remaining as general and simple as possible. We derive techniques to handle multiple, overlapping, and targeted interventions in heterogeneously mixing populations, and for computing their effect on epidemiological indices such as R₀ and equilibrium prevalence. We then investigate under what circumstances interventions combine synergistically, both analytically and numerically, trying here to draw out a general picture and understanding rather than focusing on particular cases.

The rest of this paper is set out as follows. In Section 2 we introduce the general model class that we analyse, and explain how its features are motivated by properties of HIV and its interventions. In Section 3 we show how to compute R₀ and equilibrium prevalence and incidence for this class of models. Equilibrium quantities can be efficiently obtained by iterating a discrete map. This, and its consequences, are proved in the Appendix. In Section 4 we set out how to calculate changes in these quantities under interventions. In Section 5, we define a metric of synergy between interventions and show that combined interventions do not have an immediate synergistic effect on incidence because the synergistic effect is mediated through reductions in prevalence. In Section 5.2, we show that synergy does not occur for perfect vaccines in homogeneous populations, and then, in Section 6, go on to consider more general interventions and populations numerically. Finally, in Section 7 we summarize and discuss our results, including mention of some of the short-comings of our analysis.

2. General model considered

Both the hazard of dying, and infectiousness are known to vary substantially during the course of a typical HIV infection [17, 25]. ART is typically commenced when the CD4-positive lymphocyte count has dropped below a threshold, which is equivalent, on average, to starting ART at a certain time after infection. The effect of ART is both to prolong life, and to reduce infectiousness [5, 6, 14, 28]. Thus, to realistically model this, one needs to explicitly include time-since-infection for HIV. We will keep track of the number of individuals N_k(t) in class k, the number in class k who are susceptible S_k(t), and the number who have been infected for a length of time τ by introducing the density I_k(t, τ). The normalised infectiousness after this length of infection will be denoted ϕ(τ); and the excess death rate, ν(τ), over the constant background mortality rate µ. Given that some interventions against HIV apply to only one sex, it will be necessary to model genders explicitly. Further, differences in contact rates across a population are important for HIV and other STIs, heterogeneity that is most simply included by stratifying the population into two activity groups. To include 2 genders and high- and low-sexual activity groups, we need 4 groups. Specifying the potential for different groups to infect one another in this context or more generally, requires a mixing matrix, which we will denote K. For a heterosexual population along these lines, with i = 1 … 4 corresponding to high-activity women, low-activity women, high-activity men, and low-activity men respectively, K takes the form:

$$K=\left(\begin{array}{cc}0& M\\ W& 0\end{array}\right)$$ (1)

where M and W are 2 × 2 matrices. Generally, K will be a square matrix with non-negative entries at least some of which are positive.

Combining all these features leads us to a system of partial differential equations:

$${\dot{S}}_j(t)=B_j(t)-S_j(t)F_j(t)-\mu S_j(t)$$ (2)

$$({\partial }_t+{\partial }_{\tau })I_k(t,\tau )=-(\nu (\tau )+\mu )I_k(t,\tau )$$ (3)

$$I_j(t,0)=S_j(t)F_j(t)$$ (4)

$$F_j(t)={\displaystyle \sum _k{\displaystyle \int d\tau K_{jk}\varphi (\tau )}}\frac{I_k(t,\tau )}{N_k(t)}$$ (5)

where ∂_x denotes partial differentiation with respect to a variable x. The quantity B_j(t) here denotes the recruitment rate into group j determined by the number of people beginning sexual activity in this group at time t. More generally, this might be group recruitment of any kind, including the standard example of birth.

We have not included a recovered class as clearance of HIV infection is not possible. Treatment of an infectious agent conforming to the SIR paradigm is possible within this framework if one is prepared to consider those with τ > T as ‘recovered’ for some T after which ϕ ≡ 0. However, one must take care of the meaning of prevalence in this case, which would measure the fraction no longer susceptible (i.e. lump both infectious and recovered individuals together).

3. Epidemiological indices

In this section, we show how to compute 3 epidemiological indices relating to an infection described with a model given by Eqns.5, namely: the reproductive number R₀; the prevalence of infection at equilibrium; the incidence of infection at equilibrium.

3.1. R ₀

The next generation matrix (NGM) [10, 9, 11], contains as its ij-th element the expected number of type i individuals infected by a single type j individual over their infectious period, in the limit of a large population. For this model then,

$${\overline{K}}_{NGM}=P^{-1}\overline{K}P$$ (6)

$$\overline{K}={\displaystyle {\int }_0^{\infty }d\tau \varphi (\tau )e^{-H(\tau )}K}$$ (7)

where

$$H(\tau )={\displaystyle {\int }_0^{\tau }ds(\nu (s)+\mu )}$$ (8)

is the cumulative hazard of death, and where P is a diagonal matrix whose elements are the proportions of the total population in each class. The matrix P derives from the factors 1/N_j in the force of infection Eqn.5, and P⁻¹ from the factor of S_j → N_j in Eqn.4. Eqn.7 has the interpretation as the sum of an individual’s infectiousness at different stages of infection, discounted by their probability of surviving to that stage.

R₀ is defined as the largest eigenvalue of the next generation matrix [10, 9, 11]. Thanks to Eqn.6, R₀ can equally be computed as the largest eigenvalue of $\overline{K}$. In the sequel, we will prefer to work with $\overline{K}$.

For the special case of a heterosexual population, with classes specified as men or women with high- or low-levels of sexual activity, K is 4 × 4 block off-diagonal, as in Eqn.1. If the block representing transmission from women-to-men is denoted W, and the block representing transmission from men-to-women M, one can compute:

$$R_0=\frac{h}{\sqrt{2}}{\left[u+\sqrt{u^2-4v}\right]}^{1/2}$$ (9)

$$u=\text{tr}(MW)$$ (10)

$$v=\text{det}(MW)$$ (11)

where $h={\displaystyle \int d\tau \varphi (\tau )e^{-H}.}$

3.2. Equilibrium prevalence

In this section, we show how to obtain the prevalence in each group at equilibrium.

Eqn 3 can be solved by characteristics, however we will restrict out attention to the long time limit t → ∞. In this limit

$$I_j(\infty ,\tau )=I_j(\infty ,0)e^{-H(\tau )}$$ (12)

and since each class comprises infected and susceptible individuals

$$S_j(\infty )+c{I}_j(\infty ,0)=N_j(\infty )$$ (13)

where $c={\int }_0^{\infty }d\tau e^{-H(\tau )}.$ If we use this, and write x_j for the equilibrium prevalence as a proportion of group j:

$$x_j=\underset{t\to \infty }{\lim }\left(1-\frac{S_j(t)}{N_j(t)}\right)$$ (14)

it follows straightforwardly that

$$x_i=(1-x_i){\displaystyle \sum _k{\overline{K}}_{ik}{x}_k}$$ (15)

$$b_j(\infty )=(1-x_j)\left({\displaystyle \sum _k{\overline{K}}_{jk}\frac{x_k}{c}+\mu }\right)$$ (16)

where b_j (∞) = B_j (∞)/N_j(∞) is the asymptotic per-capita recruitment-rate into group j. This could be a birth-rate, or in the case of sexually transmitted infections, a rate representing sexual debut in a given class. Intuitively, Eqn.15 says that as generations pass at equilibrium, the number of infections (x) is maintained by the force-of-infection $(\overline{K}x)$ acting on those still susceptible (1 − x).

In the Appendix, we show that the equations Eqn.15 have the following properties:

1. The equilibrium prevalence equations 15 always admit the disease-free solution x = 0, and if R₀ < 1 this is the only solution.

2. If R₀ > 1, there is precisely one non-zero solution, and the prevalences satisfy

   $$x_i\ge \left(1-\frac{1}{R_0}\right)v_i$$ (17)

   where υ is the dominant eigenvector of $\overline{K}$ normalised such that max_i υ_i = 1.
3. If υ > 0 (true if, as here, $\overline{K}$ is irreducible), we can obtain the solution by iterating the map

   $$ℳ(x){|}_i=\frac{\overline{K}x{|}_i}{1+\overline{K}x{|}_i}$$ (18)

   on x⁽⁰⁾ = (1, …, 1)^T.

The fixed-point condition for the map ℳ of Eqn.18 is a simple rearrangement of the equilibrium equations Eqn.15. Iterating Eqn.18 is akin to generating a continued fraction expression for the fixed point. The Appendix shows that this procedure does in fact converge.

3.3. Equilibrium incidence

Incidence to class j at time t is simply I_j (t, 0). Denote the per-capita incidence in class j in the long-time limit lim_t→∞ I_j (t, 0)/N_j(t) = y_j. By Eqns. 13,14:

$$y_j=\frac{x_j}{c}$$ (19)

4. Intervention categories

In this section, we show how the NGM changes under general combinations of interventions, and how to compute the changes in each of the epidemiological quantities described above.

Similarly to [23, 15], we will separate interventions into two broad categories: ‘U-control’ interventions which are applied to the whole population regardless of infection status; and ‘I-control’ interventions which are applied only to a subset of the infected individuals (for example treatment or behavioural interventions targeted at those HIV infected). We will allow interventions to affect the susceptibility to infection and the infectiousness when infected separately (as, e.g. in [30]), and for them to have different effects when applied in combination to the same individuals. Each intervention can have its own coverage, which may be different in each group of the population, and which may overlap with the other interventions in a specified way.

4.1. U-control interventions

4.1.1. Homogeneous populations

To fix notation and introduce concepts, we first consider the case of a homogeneous population. There is assumed to be only one class, so that the mixing matrix K, the NGM, and $\overline{K}$ are simply numbers (1 × 1 matrices). We will consider two interventions (1 and 2) applied to the population so that a proportion p₀ will receive no intervention, a fraction p₁ intervention 1 only, p₂ intervention 2 only, and p₃ will receive both 1&2.

In common with, e.g. [30, 18], we allow U-control interventions to be only partially effective at reducing both susceptibility to infection, and infectiousness if infected (reflecting the properties of existing interventions such as MC). Denote by f_i the factor reduction in infectiousness for those in group i, and the multiplicative reduction in susceptibility by g_i for those in group i. We will generally assume that multiple interventions compound multiplicatively for f and g separately, but this is not necessary. Under the above scenario, the new NGM, ${\overline{K}}_{NGM}^{\prime },$ becomes:

$${\overline{K}}_{NGM}^{\prime }=\overline{K}\left(\begin{array}{c}{p}_0\\ p_1{g}_1\\ p_2{g}_2\\ p_3{g}_3\end{array}\right)\left(\begin{array}{cccc}1& f_1& f_2& f_3\end{array}\right)$$ (20)

capturing the reduced infectiousness of intervention and non-intervention individuals, and the proportion of contacts which are expected to be with one class or the other. This is defined in a standard way, and records the expected number of infections in the new classes produced over the infectious period of a single individual in some new class. The new R₀ is defined as the largest eigenvalue of this matrix.

To calculate the new equilibrium quantities, we will need the change in $\overline{K}$ . The force of infection splits as:

$$\begin{array}{l}{\displaystyle \int d\tau \varphi (\tau )\frac{I(t,\tau )}{N}}\to \\ {\displaystyle \int d\tau \varphi (\tau ){\displaystyle \sum _i\frac{I_i(t,\tau )}{N_i}\frac{N_i}{N}}}\end{array}$$ (21)

so that upon assigning these forked groups different infectious and susceptibility properties, the new version of Eqn.15 replaces $\overline{K}$ with

$${\overline{K}}^{\prime }=\overline{K}\left(\begin{array}{c}1\\ g_1\\ g_2\\ g_3\end{array}\right)\left(\begin{array}{cccc}{p}_0& p_1{f}_1& p_2{f}_2& p_3{f}_3\end{array}\right)$$ (22)

4.1.2. Take and degree

To clarify the role of the quantities f and g capturing the reduced infectiousness and susceptibility of intervention individuals respectively, consider the case with only one intervention applied to a fraction p of the population. Our efficacies (1 − f) and (1 − g) for preventing transmission and infection, respectively, are then related to the notions of ‘take’ and ‘degree’ for a vaccine [19, 12, 24]. If x̄ is the mean equilibrium prevalence across the vaccinated and unvaccinated groups, we can distinguish between three possible scenarios: 1) vaccinating everyone with a vaccine of efficacy (1 − g) at preventing infection (‘degree’); 2) vaccinating a proportion p of the population which is perfectly efficacious at preventing infection (‘take’, g = 0); 3) vaccinating a proportion p of the population with a vaccine which is perfectly efficacious at preventing transmission (‘take’, f = 0). Writing x̄_deg(g) for the degree case prevalence of case 1), and x̄_g=0(p) and x̄_f=0(p) for cases 2) and 3) respectively, we can use

$${\overline{K}}^{\prime }=\overline{K}\left(\begin{array}{c}1\\ g\end{array}\right)\left(\begin{array}{cc}1-\mathit{\text{p}}& pf\end{array}\right)$$ (23)

Using this in Eqn.15, and writing x and y for the prevalences in the unvaccinated and vaccinated groups respectively, the relevant equations in the three cases become:

$$1):\frac{y}{1-y}=g\overline{K}y$$ (24)

$$2):\frac{x}{1-x}=\overline{K}(1-p)x$$ (25)

$$3):\frac{x}{1-x}=\overline{K}(1-p)x,$$ (26)

$$\frac{y}{1-y}=g(1-p)\overline{K}x$$ (27)

One can solve these and average as x̄ = (1 − p)x + py in the three cases to calculate that, where positive, the mean prevalences are:

$${\overline{x}}_{\mathrm{deg}}(g)=1-\frac{1}{\overline{K}g}$$ (28)

$${\overline{x}}_{g=0}(p)=1-\frac{1}{\overline{K}}-p$$ (29)

$${\overline{x}}_{f=0}(p)={\overline{x}}_{g=0}(p)+\frac{\overline{K}{p}^2{\overline{x}}_{\mathit{deg}}(p)}{1+\overline{K}p{\overline{x}}_{\mathit{deg}}(p)}$$ (30)

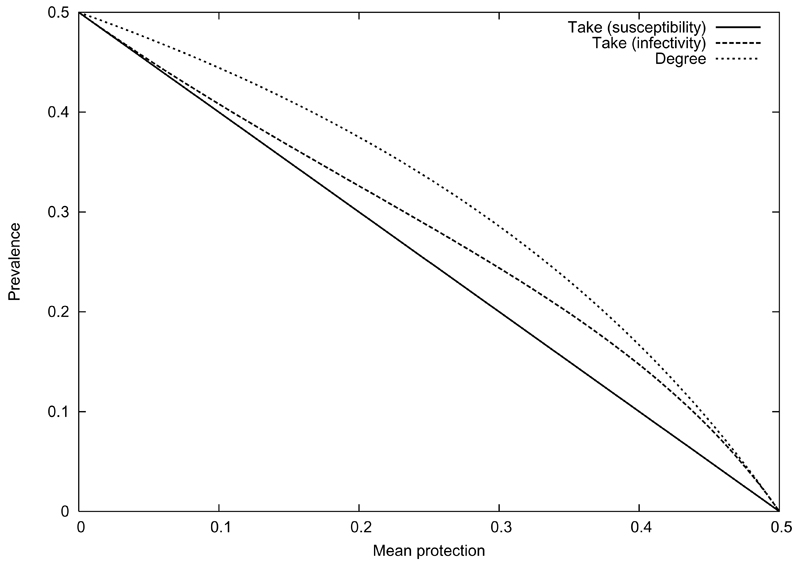
(zero when a right-hand side is negative). These prevalences are compared in Fig. 4.1.2, for $\overline{K}=R_0=2,$ and for the same mean level of protection in the population (i.e. coverage for the take scenarios; efficacy = 1 − g for the degree scenario). They share the same elimination threshold, but have rather different forms. In particular, the g = 0 case is linear, the degree scenario convex, and the f = 0 case has regions where it is convex and regions where it is concave. These differences in convexity represent the difference between local super- or sub-additivity of response, and are thus important to our later discussion of synergy.

4.1.3. Heterogeneous populations

To arrive at ${\overline{K}}^{\prime }$ for the case of a heterogeneous population, where $\overline{K}$ is now an n × n matrix with n > 1, one must replace each element ${\overline{K}}_{ij}$ by:

$${\overline{K}}_{ij}\to {\overline{K}}_{ij}{a}_i{b}_j^T$$ (31)

$$a_i^T=(p_0^i,p_1^i{g}_1^i,\dots ,p_{n_i}^i{g}_{n_i}^i)$$ (32)

$$b_j^T=(1,f_1^j,\dots ,f_{n_j}^j)$$ (33)

Here, $p_l^i$ denotes the proportion of group i who are subject to the combination of interventions indexed by l in this group, and $f_l^i$ and $g_l^i$ are the corresponding reductions in infectiousness and susceptibility respectively. There are n_j non-trivial combinations of interventions applied to group j. If N_j interventions are applied to group j and all possible combinations arise, this would mean n_j = 2^N_j.

Similarly, the new NGM ${\overline{K}}_{NGM}^{\prime }$ is found by replacing each ij-th element of ${\overline{K}}_{NGM}$ by:

$${({\overline{K}}_{NGM})}_{ij}\to {({\overline{K}}_{NGM})}_{ij}{\widehat{a}}_i{\widehat{b}}_j^T$$ (34)

$${\widehat{a}}_i^T=(1,g_1^i,\dots ,g_{n_i}^i)$$ (35)

$${\widehat{b}}_j^T=(p_0^j,p_1^j{f}_1^j,\dots ,p_{n_j}^j{f}_{n_j}^j)$$ (36)

For our specific example of a two-activity level heterosexual population, with K of the form Eqn. 1, applying n intervention combinations to men and n to women would yield

$${\overline{K}}^{\prime }=\left(\begin{array}{cc}0& w_g\overline{M}mf\\ m_g\overline{W}{w}_f& 0\end{array}\right)$$ (37)

where m_f and w_f are 2 × (n + 1) matrices encoding the changes in men and women’s infectiousness respectively, and similarly m_g and w_g are (n + 1) × 2 matrices enforcing the changes in susceptibility for men and women.

Remarkably, one can still calculate R₀ in closed form. The characteristic equation, χ(λ), for the new $\overline{K}$ obeys

$$\chi (\lambda )={\lambda }^{2(n+1)}\text{det}\left(\begin{array}{cc}1& -w_g\overline{M}{m}_f/\lambda \\ -m_g\overline{W}{w}_f/\lambda & 1\end{array}\right)={\lambda }^{2(n+1)}\text{det}(1-m_g(\overline{W}{w}_f{w}_g\overline{M}{m}_f)/\lambda )={\lambda }^{2n}\det (\lambda 1_{2\times 2}-\overline{W}(w_f{w}_g)\overline{M}(m_f{m}_g))$$ (38)

where we have used Leibniz’s identity for determinants and the standard result that det(1 + CD^T) = det(1 + D^TC) (see, e.g., [20]). This brings the problem into the form for a 2 × 2 matrix, no matter how many interventions we apply. Generally then, applying $n_X^Y$ interventions to each group of gender X and activity-level Y, we have

$$R_0^{new}=\frac{1}{\sqrt{2}}{\left[u^{\prime }+\sqrt{{u^{\prime }}^2-4.v^{\prime }}\right]}^{1/2}$$ (39)

$$u^{\prime }=\text{tr}(C)$$ (40)

$$v^{\prime }=\det (C)$$ (41)

$$C=\overline{W}{\Gamma }_W\overline{M}{\Gamma }_M$$ (42)

$${\Gamma }_X=\text{diag}({\gamma }_X^H,{\gamma }_X^L)$$ (43)

$${\gamma }_X^Y={\displaystyle \sum _{i=1}^{n_X^Y}{(f_X^Y)}_i{(g_X^Y)}_i{(p_X^Y)}_i}$$ (44)

where ${(f_X^Y)}_i$ is the reduction in infectiousness for the ith intervention in gender X, activity Y, etc.

This is similar to [7]. Note that, unlike equilibrium prevalence and incidence, R₀ is only affected by the group means of the product of susceptibility and infectiousness.

Another possible quantity of interest is the instantaneous incidence at the moment the interventions are introduced. Without interventions, this is given by

$$S^{T}KF$$ (45)

where F is the force of infection from each group (given as the population mean value of ϕ in each group), and S the vector of susceptible counts in each group. Under a general intervention in a population with N groups,

$$S^{T}KF\to S^T𝓖K𝓕F$$ (46)

$$𝓖=\text{diag}({\overline{g}}_1,\dots ,{\overline{g}}_N)$$ (47)

$$𝓕=\text{diag}({\overline{f}}_1,\dots {\overline{f}}_N)$$ (48)

$${\overline{f}}_i={\displaystyle \sum _{l=0}^{n_i}{(f_l)}_i{(p_l)}_i}$$ (49)

$${\overline{g}}_i={\displaystyle \sum _{l=0}^{n_i}{(g_l)}_i{(p_l)}_i}$$ (50)

Note that this is depends only on the means of the fs and gs, unlike R₀, and incidence and prevalence at equilibrium.

4.2. I-control interventions

We will assume that, upon infection, a proportion π_j of the S_j move onto an unbarred I_j time-course corresponding to no treatment, and a proportion ${\overline{\pi }}_j$ onto the ${\overline{I}}_j$ time-course (with its treatment-modified $\overline{\varphi }$ and $\overline{\nu }$). That is, a proportion $\overline{\pi }$ are destined at infection to undergo treatment, possible at some later stage, in which case $\overline{\varphi }(\tau )$ and $\overline{\nu }(\tau )$ would only depart from the untreated values ϕ(τ) and ν(τ) only once τ reaches the average treatment start time. Then, instead of Eqn.5, we have

$${\dot{S}}_j=B_j(t)-S_j(t)F_j(t)-\mu S_j(t)$$ (51)

$$({\partial }_t+{\partial }_{\tau })I_j(t,\tau )=-(\mu +\nu (\tau ))I_j(t,\tau )$$ (52)

$$({\partial }_t+{\partial }_{\tau }){\overline{I}}_j(t,\tau )=-(\mu +\overline{\nu }(\tau )){\overline{I}}_j(t,\tau )$$ (53)

$$I_j(t,0)={\pi }_j{S}_j(t)F_j(t)$$ (54)

$${\overline{I}}_j(t,0)={\overline{\pi }}_j{S}_j(t)F_j(t)$$ (55)

$$F_j(t)={\displaystyle \sum _k{K}_{jk}}\times {\displaystyle \int d\tau \left(\varphi (\tau )\frac{I_k(t,\tau )}{N_k(t)}+\overline{\varphi }(\tau )\frac{{\overline{I}}_k(t,\tau )}{N_k(t)}\right)}$$ (56)

write

$$\overline{h}={\displaystyle \int d\tau .\overline{\varphi }(\tau )e^{-\overline{H}(\tau )}}$$ (57)

$$\overline{c}={\displaystyle \int d\tau .e^{-\overline{H}(\tau )}}$$ (58)

and denote the fraction of group j infected and destined for treatment as x̄_j, and the fraction of group j infected and destined for no treatment as x_j. Then we can proceed with the t → ∞ analysis as in Section 3.2 to obtain:

$$x_j={\pi }_j\frac{S_j(\infty )}{N_j(\infty )}{\displaystyle \sum _k{K}_{jk}(x_{k}h+{\overline{x}}_k\overline{h})}$$ (59)

$${\overline{x}}_j={\overline{\pi }}_j\frac{S_j(\infty )}{N_j(\infty )}{\displaystyle \sum _k{K}_{jk}(x_{k}h+{\overline{x}}_k\overline{h})}$$ (60)

implying that ${\overline{x}}_j/x_j={\overline{\pi }}_j/{\pi }_j.$ Conservation of people implies that

$$S_j(\infty )+c{I}_j(\infty ,0)+\overline{c}{\overline{I}}_j(\infty ,0)=N_j(\infty )$$ (61)

and therefore, introducing the total fraction infected in group j

$${\tilde{x}}_j=\underset{t\to \infty }{\lim }\left(1-\frac{S_j(t)}{N_j(t)}\right)$$ (62)

we have

$${\tilde{x}}_j=\frac{{\pi }_{j}c+{\overline{\pi }}_j\overline{c}}{{\pi }_{j}c}{x}_j$$ (63)

$${\tilde{x}}_j=\frac{{\pi }_{j}c+{\overline{\pi }}_j\overline{c}}{{\overline{\pi }}_j\overline{c}}{\overline{x}}_j$$ (64)

Bringing all this together, the equations for equilibrium prevalence become

$$\begin{array}{c}{\tilde{x}}_i=(1-{\tilde{x}}_i){\displaystyle \sum _k{\tilde{K}}_{ik}{\tilde{x}}_k}\\ b_j(\infty )=(1-{\tilde{x}}_j)\left({\displaystyle \sum _k{K}_{jk}{L}_k{\tilde{x}}_k+\mu }\right)\end{array}$$ (65)

with

$$L_k=\left(\frac{{\pi }_{k}h+{\overline{\pi }}_k\overline{h}}{{\pi }_{k}c+{\overline{\pi }}_k\overline{c}}\right)$$ (66)

$${\tilde{K}}_{jk}=({\pi }_{j}c+{\overline{\pi }}_j\overline{c})K_{jk}\left(\frac{{\pi }_{k}h+{\overline{\pi }}_k\overline{h}}{{\pi }_{k}c+{\overline{\pi }}_k\overline{c}}\right)$$ (67)

For given π_j and ${\overline{\pi }}_j,\tilde{K}$ can be obtained from $\overline{K}$ by knowing the average survival times c and c̄, and the ratio h̄/h. Note that if the intervention is randomly targeted, the ratio h̄/h alone suffices.

To calculate the incidence in group j at equilibrium, inc_j, one uses Eqns. 63 and 64 to obtain

$$\begin{array}{l}in{c}_j=\frac{x_j}{c}+\frac{{\overline{x}}_j}{\overline{c}}\\ =\frac{{\tilde{x}}_j}{{\pi }_{j}c+{\overline{\pi }}_j\overline{c}}\end{array}$$ (68)

4.3. Mixed interventions

Cases combining both U- and I-control interventions are a simple extension of the above. Note that I-control interventions do not result in a proliferation of groups. The modifications for I-control are simply made to each separate population group with a particular combination of U-control interventions applied to it.

4.4. Targeting and Overlaps

Later, we will consider targeted interventions. This means preferentially directing resources towards groups in the population who are contributing more to transmission. In a two-group population, group 1 making up proportion ρ₁ of the whole population and group 2 making up a proportion ρ₂, this means that a total coverage c preferentially applied to group 1 will result in the following coverages c₁ and c₂ in each group:

$$c_1=\frac{\min ({\rho }_1,c)}{{\rho }_1}$$ (69)

$$c_2=\frac{\max (c-{\rho }_1,0)}{{\rho }_2}$$ (70)

Within each group, we will consider three possible distribution scenarios for multiple interventions, representing different levels of overlap: 1) random overlap - the overlap that results from uncoordinated distribution of each intervention within a group, i.e. independently and at random; 2) minimum overlap - the two interventions are applied avoiding each other, so as to minimize the number of people in each group who receive both interventions; 3) maximum overlap - the number of individuals receiving both interventions is maximized, with the smallest intervention nested inside the larger. These situations are caricatured by Venn diagrams resembling a butterfly, two separate circles, and concentric circles respectively. For given coverages c₁, and c₂, this means the coverages (p₀, p₁, p₂, p₃) are given in each scenario by

$$\begin{array}{l}1):\\ p_0=(1-c_1)(1-c_2)\\ p_3=c_1{c}_2\end{array}$$ (71)

$$\begin{array}{l}2):\\ p_0=\text{max}(0,1-c_1-c_2)\\ p_3=\text{max}(0,c_1+c_2-1)\end{array}$$ (72)

$$\begin{array}{l}3):\\ p_0=1-\text{max}(c_1,c_2)\\ p_3=\text{min}(c_1,c_2)\end{array}$$ (73)

with p₁ = c₁ − p₃ and p₂ = c₂ − p₃ in all the cases.

5. Synergy

There are many senses in which one could take two interventions 1 and 2 to be synergistic in improving some measure of performance. We will call two interventions synergistic if the reduction of some index of disease burden, Q, under both interventions (1&2) is greater than the sum of the reductions in Q for each intervention separately. More particularly, we will measure the level of synergy by the quantity

$$\sigma =\frac{Q(\varnothing )-Q(1\&2)}{(Q(\varnothing )-Q(1))+(Q(\varnothing )-Q(2))}-1$$ (74)

where Q(∅) is the value of Q without interventions; Q(1), Q(2), Q(1&2) the values under intervention 1, 2 or 1&2 combined, respectively. This is chosen so that σ > 0 if the reductions in the index Q are super-additive, i.e. ∆₁ + ∆₂ > ∆₁₂ where ∆_s = (Q(∅)−Q(s)) is improvement in Q under intervention set s. It also has the advantage of being dimensionless, so that it is independent of any choice of units and depends only on relative changes.

Additivity is perhaps the most natural null model with which to compare combined interventions, as resource use is usually additive. However, one might consider other null models, e.g. that the factor (F₁₂ = Q(1&2)/Q(∅)) by which combined interventions reduce the index Q is the product of the reduction factors for each intervention separately (F₁F₂). This leads to a definition of synergy as satisfaction of the condition F₁₂ < F₁F₂. This multiplicative criterion for synergy is a weaker condition than the additive condition we favour. This can been seen since F_s = (1−∆_s/Q(∅)) implies the condition F₁₂ < F₁F₂ is equivalent to ∆₁₂ > ∆₁ + ∆₂ − ∆₁∆₂/Q(∅).

Although multiplicative synergy may seem a mathematically appealing null model for combining proportional changes, the additive definition more closely corresponds to intuitive notions of the benefits synergy confers. As an illustration of this, consider a situation with a linear response. In this case, subsequent improvements in coverage are considered synergistic in the multiplicative definition, but not the additive definition. Specifically, consider two increments of size δ in the coverage of a take vaccine. As shown in Eqn.29 and illustrated in Figure.4.1.2, the response of prevalence is a linear decline (above eradication). The additive definition of synergy would not register subsequent improvements in coverage as synergistic (σ = 0), whereas the multiplicative definition would regard these subsequent increments as synergistic, since (1 − 2δ) < (1 − δ)².

5.1. Population-level effects

In this section we show that there is no ‘population-level’ synergy for instantaneous incidence, as opposed to equilibrium incidence. By this, we mean that unless two interventions applied to the same individual synergize (i.e. produce a superadditive reduction in the product of infectivity and susceptibility), the two interventions cannot synergize for the population as a whole (i.e. the reduction in incidence cannot be superadditive). This is in contradistinction with equilibrium quantities, where ‘herd immunity’ allows non-linear gains as one reduces R₀.

Remembering that $𝓕$ and $𝓖$ are diagonal, one can use Eqn.46 to cast the instantaneous incidence under interventions as:

$$S^T𝒢KℱF={\displaystyle \sum _{ijkl}{P}_{ijkl}{\gamma }_{ijkl}}$$ (75)

where P_ijkl = S_iK_ijF_l depends on the baseline population structure and disease transmission, and γ_ijkl = $𝒢$_ij$𝓕$_kl depends on the interventions. Since P_ijkl ≥ 0 and it has a non zero sum, one can regard this as proportional to a probability distribution over i, j, k and l, so that

$${\displaystyle \sum _{ijkl}{P}_{ijkl}{\gamma }_{ijkl}}\propto \mathbb{E}\left[\gamma \right]$$ (76)

Note that γ(∅)_ijkl = δ_ijδ_kl. The combined effect of interventions 1 and 2 is superadditive if

$$0\le \mathbb{\text{E}}[(\gamma (\mathrm{\varnothing })-\gamma (1\&2))]-\mathbb{\text{E}}[(\gamma (\varnothing )-\gamma (1))]-\mathbb{\text{E}}[(\gamma (\varnothing )-\gamma (2))]=\mathbb{\text{E}}[\gamma (1)\gamma (2)-\gamma (1\&2)]-\mathbb{\text{E}}[(\gamma (\varnothing )-\gamma (1))(\gamma (\varnothing )-\gamma (2))]$$ (77)

which is therefore possible only if $𝔼$[γ(1)γ(2) − γ(1&2)] ≥ 0, which is to say, if the infection-weighted average across genders and activity classes of the reductions for individuals is more than multiplicative when interventions are combined. The average cannot be greater than zero without some synergy at the individual level in the above sense.This is in line with the incidence being linear in the product of infectiousness and susceptibility. The inequality Eqn.77 is harder to satisfy the more effective interventions 1 and 2 are by themselves.

5.2. An example without synergy

One last generality before considering a specific case, is that for interventions against infection in homogeneous populations, which are perfectly efficacious (‘take’, g = 0), there is never any synergy. The mean prevalence in this case takes the particularly simple form

$$\overline{x}=p_0-\frac{1}{\overline{K}}$$ (78)

(and zero where the right-hand side is negative) and it is easy to show from this that for any coverages and any of the overlap scenarios of Section 4.4 σ ≤ 0, with the minimum overlap strategy performing best. Although this is a very simple example, two aspects remain true more generally: synergy is hard when interventions are individually very effective, and minimum overlap distribution strategies tend to perform best.

6. Numerical examples

In this section we present the results of numerical investigations into the population-level interactions between interventions. While R₀ has proved spectacularly useful in infectious disease epidemiology, we will not pursue its behaviour here as it is only an indirect metric of the burden of disease - for example, if R₀ < 1 the endemic prevalence is zero whatever the value of R₀. Moreover, it is less useful as a descriptor of heterogeneously mixing populations, e.g. the equilibrium prevalence need not be a monotone function of R₀. In view of the results of Section 5.1, the best candidate performance metrics for investigating interactions between interventions are the equilibrium prevalence and incidence. In the below, we will concentrate on the incidence, though the results for equilibrium prevalence would be extremely similar.

6.1. Homogeneous populations

Typical results for interventions in a homogeneous population are presented in Fig.6.1 and discussed in Section 7.

6.2. Heterogeneous populations

Rather than try to consider all possible types of heterogeneity, we will in this section focus on our example of HIV with K given by Eqn.1. We will parametrize M and W in the standard way: if ρH and ρL are the proportion of men (and women) who are categorized high-activity and low-activity respectively, and the ratio of high:low activity is H, then

$$M=W=\beta \left(\begin{array}{cc}H\alpha +\frac{(1-\alpha )H^2{\rho }_H}{H{\rho }_H+{\rho }_L}& \frac{(1-\alpha )H_{{\rho }_H}}{H{\rho }_H+{\rho }_L}\\ \frac{(1-\alpha )H_{{\rho }_L}}{H{\rho }_H+{\rho }_L}& \alpha +\frac{(1-\alpha ){\rho }_L}{H{\rho }_H+{\rho }_L}\end{array}\right)$$ (79)

where α is an parameter between 0 and 1 quantifying assortativity, and β is an infection rate which can be specified by choosing $R_0^L$ - the value R₀ would take if the population were low-activity only.

Typical results for interventions in a heterogeneous population are presented in Fig.6.2 and discussed in Section 7.

7. Discussion

The behaviour of multiple interventions in structured populations is difficult to investigate, to a large part because the number of variants one could consider grows exponentially with the number of interventions. It is therefore important to use models and tools which are as simple as possible, but which are still able to include pertinent features of interventions. This means being able to model interventions which: are applied only to infected individuals (I-control); are targeted by membership of population sub-group; may overlap with each other in different patterns; differentially effect susceptibility to infection and infectiousness if infected; modify any of these effects at the individual level when applied together; alter the level and course of infectiousness through time; change the distribution of survival times as infectious. By concentrating on equilibrium prevalence and incidence, we show above how this wealth of complexity can be encoded in changes to the next-generation matrix (NGM) following certain rules, and that the equilibrium quantities can then be simply calculated by iteration. This makes exploring many possibilities more feasible, and a certain amount of analytical insight possible. The fact that Eqn. 15 for per-capita quantities do not depend on recruitment rates avoids unnecessary assumptions, and means that in effect, we are considering equivalence classes of model which share the same NGM.

In considering whether two (or more) interventions achieve an additional effect that one might term synergistic, one must choose a measure of effect or performance, and a precise sense in which ‘synergy’ means a combination is particularly beneficial. The simplest choice for a definition of synergy is that the improvement in some performance index when interventions are combined, is more than the sum of improvements for each intervention separately (super-additive). Additivity is natural since the resources used to affect interventions are additive (unless cost savings are achieved by coordinating combined interventions). Our chosen definition of Eqn.74, satisfies these requirements with σ being positive or negative according to whether combinations achieve super- or only sub-additivity.

Evident candidates for a performance measure include: instantaneous incidence; equilibrium incidence; equilibrium prevalence; and R₀. We have not considered R₀ because it is not directly related to disease burden, and less useful in structured populations. Instantaneous incidence has the advantages of being concrete, immediate, and depending on fewer model assumptions that the other measures. However, population-level interactions due to the non-linearity of the dynamics are invisible in this quantity. We show in Section 5.1 that any synergy for the population in this measure is simply a sum of the individual-level synergy for each pairing, weighted by the intensity of each pairing as a route of infection. This is because instantaneous incidence is bilinear in the current state of the system and, as in the simple SIR model, fails to capture herd- or threshold-effects. Theory indicates that equilibrium incidence and prevalence should behave very similarly (identically, unless interventions alter infectious lifespan). We chose to focus on equilibrium incidence because, in the case of HIV, increases in lifespan due to ART make prevalence a more removed measure of an intervention’s impact.

In Section 5.2, we point out that synergy does not occur for any coverage or combination of U-control interventions in homogeneous populations that have perfect take in eliminating susceptibility to infection, and that minimum overlap distributions do least badly in terms of σ. The messages from this observation which hold more generally are that:

1. synergy is hardest to achieve for interventions which are individually very efficacious

2. distribution strategies which minimize overlap tend to do best.

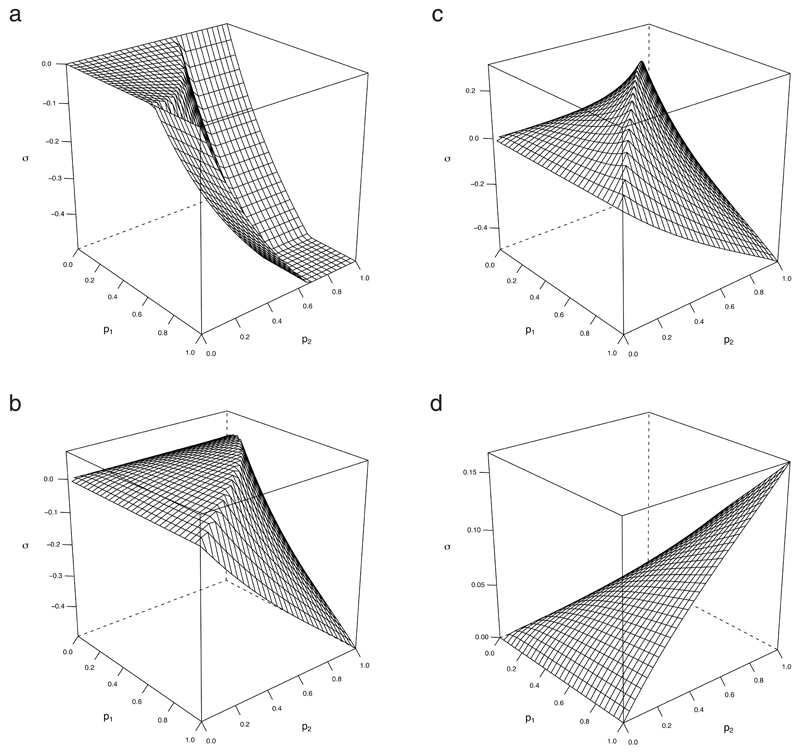
Neither of these features should be surprising: applying an intervention to someone who is already well protected from infection is usually redundant, whereas reaching more people with at least one intervention can bring nonlinear benefits if the prevalence response curve steepens. The results of Fig. 2c are typical. Synergy increases as higher coverages begin to reach nonlinear regimes, with peak synergy occurring in a ridge after which it declines sharply due to redundancy, flattening out at σ = −0.5, which results if each intervention alone is enough to eliminate the infection. For poorer individual interventions therefore, the peak occurs at higher coverages (Fig. 2d), or may even achieve a maximum at complete coverage for particularly poor interventions. For asymmetric cases, areas with positive synergy are shifted towards the axis for the poorer intervention.

FIG 2.

Synergy for symmetric U-interventions in a homogeneous population. Efficacy is (1 − g), f = 1 and R₀ = 2.

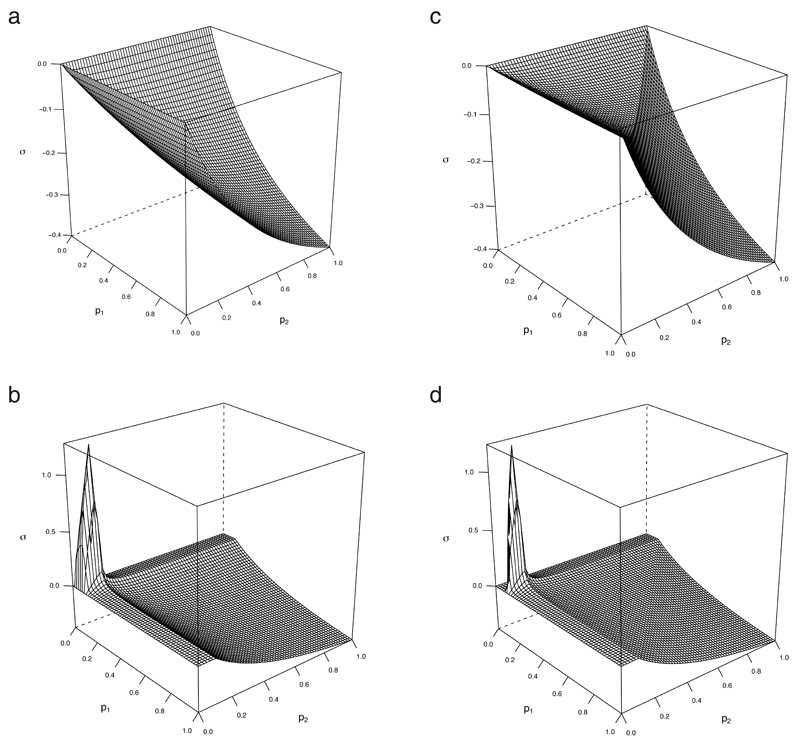
Heterogeneous populations introduce another dimension. If a small fraction of the population is responsible for much of the transmission, universal use of interventions can result in redundancy by widespread application amongst those unlikely to transmit. If interventions are targeted against high-risk portions of the population, they are vastly more effective at reducing prevalence; but they are also more likely to achieve synergy. Figs. 3a and 3b show an example where synergy is regained by targeting, and peaks along individual coverages a little larger than the proportion of the population who are high-risk. For individually less effective interventions that are less redundant without targeting, the effect can be much more marked as in Figs. 3c and 3d. Here, strong synergy is achieved for wide ranges of coverage, as long as a substantial fraction of the high-risk group has been reached. This represents the third general message to emerge from this work:

• 3.targeting interventions at high-risk groups can achieve synergy where there would otherwise be redundancy.

FIG 3.

Gains in synergy due to targeting: symmetric U-control with $R_0^L=0.5,$ ρ_H = 0:1, H = 200, α = 0.5, f = 1 and g = 0.25. (a) and (b): random overlap . (c) and (d): minimum overlap.

There are several shortcomings of our discussion which should be borne in mind. First, in considering equilibria, we have completely ignored the temporal aspect. It may be the case, for example, that interventions which are redundant in our sense because they each eliminate the infection, nevertheless have benefit when used in tandem because they shorten the time to elimination. Secondly, our treatment has been deterministic. Redundant interventions may have added benefits used in combination, in terms of reducing the probability or expected size of stochastic outbreaks. Thirdly, in considering overlaps, we have ignored distribution costs. If one is interested in synergies in cost-effectiveness, it may be that overlapping distribution strategies do better if costs are strongly determined by total coverage. Lastly, we have not considered changes in mixing patterns, which might be achieved through behavioural interventions. Each of these consideration carries with it substantial added complications, and here we have sought to keep an already complex system simple enough to allow some insight. However, we hope that this work has provided a sensible concrete definition of synergy for multiple interventions, at least a caricature of its behaviour in structured populations, and some tools for more specific further investigations.

FIG 1.

Degree and take vaccination (for preventing infection, and for preventing transmission) in a homogeneous population with R₀ = 2.

Appendix

A1.1 Solutions of equilibrium equations

We want to establish some results about the solutions of the final prevalence equations Eqn.15, where the next generation matrix $\overline{K}$ is assumed to be non-negative (i.e. K_ij ≥ 0 ∀i, j) and irreducible. We are only interested in solutions with 0 ≤ x_i ≤ 1, i.e. x ∈ [0, 1]ⁿ =: U. Notice that x = 0 is always a solution to Eqn.15.

A1.1.1 R₀ < 1

First, we establish

Theorem A1.1. If R₀ < 1, x = 0 is the only solution of Eqn.15 in U

It will be useful to define the map ℳ component-wise by

$$ℳ(x){|}_i=\frac{\overline{K}x{|}_i}{1+\overline{K}x{|}_i}$$ (80)

The relevance of this is that x* is a solution of Eqn.15 if and only if it is a fixed point of ℳ:

$$ℳ(x^{*})=x^{*}$$ (81)

Proof. Let $B_{\sqrt{n}}^{+}$ be the intersection of the closed Euclidean ball of radius $\sqrt{n}$ centred at the origin and ${[0,\sqrt{n}]}^n.$ Recall that R₀ is defined as the dominant eigenvalue of the matrix $\overline{K}.$

$$ℳ(x){|}_i-ℳ(y){|}_i=\frac{\overline{K}(x-y){|}_i}{(1+\overline{K}x{|}_i)(1+\overline{K}y{|}_i)}$$ (82)

Thus, if d(., .) denotes the Euclidean distance,

$$d(ℳ(x),ℳ(y))\le d(\overline{K}x,\overline{K}y)\le R_0.d(x,y)$$ (83)

Since R₀ < 1 by assumption, ℳ is a contraction mapping. Also, it maps $B_{\sqrt{n}}^{+}$ into itself. The situation therefore matches the requirements of the Banach fixed point theorem, which guarantees the existence of a unique fixed point in $B_{\sqrt{n}}^{+}.$ We know by inspection that this solution is x = 0. Since $U\subset B_{\sqrt{n}}^{+}$ and 0 ∈ U, 0 is the unique fixed point of ℳ in U.

A1.2 R₀ > 1

When R₀ > 1, ℳ is no longer a contraction mapping, and we must work a bit harder.

Theorem A1.2 (Existence). When R₀ > 1 there is at least one solution to Eqn.15 other than x = 0.

Let U_y = [y₁, 1] × ⋯ × [y_n, 1] for a vector y with all its components in [0, 1]; and let v be the maximal eigenvector of $\overline{K},$ normalised so that the largest component is 1.

Lemma A1.3. When R₀ > 1, there is an 0 < є < 1 such that ℳ maps U_єv into itself.

Proof of lemma.

$$ℳ(єv){|}_i=\frac{\overline{K}єv{|}_i}{1+\overline{K}єv{|}_i}=\frac{єR_0{v}_i}{1+єR_0{v}_i}$$ (84)

Can we choose an є > 0 so that

$$ℳ(єv){|}_i\ge єv_i,{\forall }_i?$$ (85)

For each i, this inequality rearranges as

$$єv_i\le 1-\frac{1}{R_0}$$ (86)

Since max_i v_i = 1, our question is answered in the affirmative by choosing $є=1-R_0^{-1}.$

Let w = єv + q, where q_i ≥ 0. Note that

$$ℳ(w){|}_i-ℳ(єv){|}_i=\frac{\overline{K}{q}_i}{(1+\overline{K}w{|}_i)(1+\overline{K}єv{|}_i)}\ge 0$$ (87)

Since also

$$ℳ(z){|}_i=\frac{\overline{K}z{|}_i}{1+\overline{K}z{|}_i}\le 1$$ (88)

for any z with z_i ≥ 0, any vector in U_єv is again mapped into U_єv under ℳ.

Proof of Theorem A1.2. The set U_єv and the map ℳ satisfy the requirements of the Schauder fixed point theorem, and so ℳ must have at least one fixed point in U_єv. Since 0 ∉ U_єv this is distinct from the trivial fixed point.

Theorem A1.4 (Uniqueness). When R₀ > 1 there is only one solution to Eqn.15 in U_єv.

Proof of Theorem A1.4. Suppose x and y are both fixed points of ℳ in U_єv. Then

$$x_i-y_i=\frac{\overline{K}(x-y){|}_i}{(1+\overline{K}x{|}_i)(1+\overline{K}y{|}_i)}=\frac{\overline{K}(x-y){|}_i}{(1+x_i/(1-x_i))(1+y_i/(1-y_i))}=(1-y_i)(1-x_i)\overline{K}(x-y){|}_i$$ (89)

using the fixed point property of x and y. It follows from this that

$$d(x,y)\le \underset{i}{\max }(1-y_i)(1-x_i).R_0.d(x,y)\le {(1-є)}^2{R}_0.d(x,y)=\frac{1}{R_0}.d(x,y)$$ (90)

Since R₀ > 1, this implies that d(x, y) = 0, and therefore x = y.

Remark A1.5. In fact we have also proved that the prevalences satisfy the bound

$$x_i\ge \left(1-\frac{1}{R_0}\right)v_i$$ (91)

where υ is the dominant eigenvector of $\overline{K}$ normalised such that max_i υ_i = 1

At this point, we will restrict to the the case where all the components of the maximal eigenvector of the next generation matrix are strictly positive. This is a fairly natural assumption, as a zero component of v would correspond to a group which does not become infected during the exponential growth phase of an epidemic. In most cases, the analysis could be rephrased so as to omit this inert group.

Theorem A1.6 (Convergence). Let x₀ be the vector with each x₀|_i = 1. If R₀ > 1, and each υ_i > 0 for the dominant eigenvector of $\overline{K},$ υ. Then x_n = ℳⁿ(x₀) converges to the non-trivial fixed point of ℳ.

Proof of Theorem A1.6. Let y be the non-trivial fixed point of M.

If y ≠ єυ, then since y ∈ U_єυ, there is a δ > 0 such that y|_i − єυ_i ≥ δ/R₀.

$$ℳ(x){|}_i-ℳ(y){|}_i=(1-y_i)\frac{\overline{K}(x-y){|}_i}{(1+\overline{K}x{|}_i)}$$ (92)

means that

$$d(M(x),y)\le \underset{i}{\max }(1-y_i)R_0.d(x,y)=(1-\delta ).d(x,y)$$ (93)

and therefore

$$d(x_n,y)\le {(1-\delta )}^n.d(x,y)\to 0$$ (94)

If instead y = єv, ℳ(y) = y implies that

$$y_i=єv_i=1-R_0^{-1}$$ (95)

and, in turn, that ${\displaystyle {\sum }_j{\overline{K}}_{ij}=R_0.}$ The symmetry of x₀ is preserved under ℳ, allowing us to reduce to a one dimensional problem:

$$x_n=m_n.x_0$$ (96)

$$m_n=\frac{R_0{m}_{n-1}}{1+R_0{m}_{n-1}}$$ (97)

The convergence of the map Eqn.97 to the fixed point $m=1-R_0^{-1}$ from m₀ = 1 is easy to see by considering the graphs of y = R₀x/(1 + R₀x) and y = x in the usual way.