The Phase Lag between Agonist-Induced Oscillatory Ca²⁺ and IP₃ Signals Does Not Imply Causality (December 2015)

Abstract

Activated phospholipase C (PLC*) generates 1,4,5-triphosphate (IP₃) and diacylglycerol (DAG) from phosphatidyl inositol (PIP₂). The DAG remains in the plasma membrane and co-activates conventional protein kinase C (PKC) with Ca²⁺. We have developed a mathematical model for the activation of the Ca²⁺-dependent PKC and its negative feedback on phospholipase C (PLC) and coupled it to the De Young-Keizer model for IP₃ mediated Ca²⁺ oscillations. The model describes the cascade of reactions for the translocation of PKC to plasma membrane, and simulates activation of Ca²⁺ and diacylglycerol (DAG) oscillations. The model demonstrates that oscillations in Ca²⁺ and DAG are possible with or without a positive Ca²⁺ feedback on phospholipase C consistent with experiment. In many experimental studies, the timing of the peaks of the Ca²⁺ and IP₃ oscillations have been used to suggest causality, i.e. that the IP₃ oscillations cause the Ca²⁺ oscillations. The model is used to explore this question. To this end, the positive and negative feedback between Ca²⁺ and IP₃ production are modulated, resulting in changes to the phase lag between the peaks in [Ca²⁺]_cyt and [IP]_cyt. The model simulates a possible experimental protocol that can be used to differentiate whether or not the positive feedback of Ca²⁺ on PLC is needed for the oscillations.

I. Introduction

In response to plasma membrane receptor-coupled G-protein activation, the specific proteins such as G_q (α and βγ subunits) activate phospholipase Cβ (PLCβ). PLCβ cleaves PIP₂ to form DAG and IP₃. In contrast, another isoform PLCγ is activated through phosphorylation by a tyrosine kinase to also produce DAG and IP₃. The newly produced DAG remains in the plasma membrane while IP₃ diffuses into the cytoplasm. The IP₃ binds to the IP₃ receptor in the endoplasmic reticulum (ER) to release Ca²⁺. The dynamics of Ca²⁺ often takes the form of oscillations that involve cycles of uptake and release from the ER.

These Ca²⁺ release events are thought to provide feedback on PLC by two mechanisms: 1) through protein kinase C (PKC) and 2) through calmodulin binding to PLC ^[5–9]. In the first mechanism, the increased cytosolic [Ca²⁺] binds to PKC, the PKC isoforms participate in a number of signaling transduction pathways in many cells. They are classified into three groups: conventional, novel, and atypical. The conventional PKCs have several isoforms (α, βI, βII, γ) and are regulated by Ca²⁺ and DAG. In contrast to conventional PKC, novel PKC isoforms (δ, ε, η, θ) are activated by DAG alone. Our computational study considers the role of a classic PKC. Before activation, PKC is found mainly in the cytosol. A conceptual “sequential model” has been proposed by others suggested that Ca²⁺ binding of C2 domain led to a conformational change and translocation to the cell membrane, which allows DAG binding of C1 domain ^{[10, 11]}. Many experiments have shown that PKC inhibits the activation of PLCβ ^{[6, 9]}. PKC inhibition of other isoforms of PLC has also been reported, for example PKC phosphorylates serine 1248 of PLCγ which may alter the interaction of PLCγ with protein tyrosine kinase and leads to a decrease in PLC activity ^[12]. The second proposed mechanism is based on more indirect evidence. Biden and co-workers observed in pancreatic β-cells that Ca²⁺ is necessary for IP₃ production from PIP₂^[7]. Codazzi and colleagues (2001) observed that oscillating translocations of PKC are accompanied by oscillations in the indicators reporting both Ca²⁺ and DAG binding domain (GFP-C1₂δ) in astrocytes. The observed that the oscillations of the translocation of DAG binding domain lagged in phase behind the oscillations in the Ca²⁺ indicator and that the Ca²⁺ signal reached a threshold triggering the translocation of GFP-C1₂δ. Based on these phase lags a conceptual model in which there is fast activation of PLCβ by Ca²⁺ has been proposed. More recently, Thore and co-workers observed in pancreatic β-cells, activation of PLC-β required elevation of cytosolic Ca²⁺ due to CRAC channels ^[8]. In support of this hypothesis, recent experimental findings have shown that the affinity of PLCβ for calmodulin increases with increasing calcium ^[5]. For PLCγ no evidence of direct activation by Ca²⁺ has been observed. In this study, we utilize computational models to explore how Ca²⁺, IP₃, DAG, PKC, and PLC interact to produce experimentally observed dynamics. It demonstrates that the phase lag between Ca²⁺ and IP₃ peaks during agonist-induced oscillations can vary greatly and therefore should not be used to imply that one peak triggers the other (causality). Specifically, we study how the negative feedback of Ca²⁺ on PLC activity though the activation of PKC by both Ca²⁺ and DAG affects Ca²⁺, IP₃, and DAG dynamics. The model first demonstrates that the experimentally observed oscillations in Ca²⁺ and DAG are possible both with and without fast positive feedback of Ca²⁺ on PLC. The model is also used to explore how the positive feedback of Ca²⁺ on PLC might affect Ca²⁺, IP₃ and DAG dynamics for cells that have PLCβ. Finally the model suggests a test that might be used to explore whether this positive feedback is playing an essential role in the oscillations.

II. Methods

THE MODEL

A computational model was developed to explore the dynamics and interactions of Ca²⁺, DAG, IP₃, PKC, and PLC during Ca²⁺ oscillations. The model includes the following features: 1) the model for intracellular Ca²⁺ dynamics used by De Young and Keizer ^[13]; 2) an IP₃ production formulation is based on the model by Swillens and Mercan ^[1]; and 3) a new experimentally constrained computational model of the interactions of PKC with DAG, Ca²⁺ and PLC; and 4) fast activation of PLC by Ca².

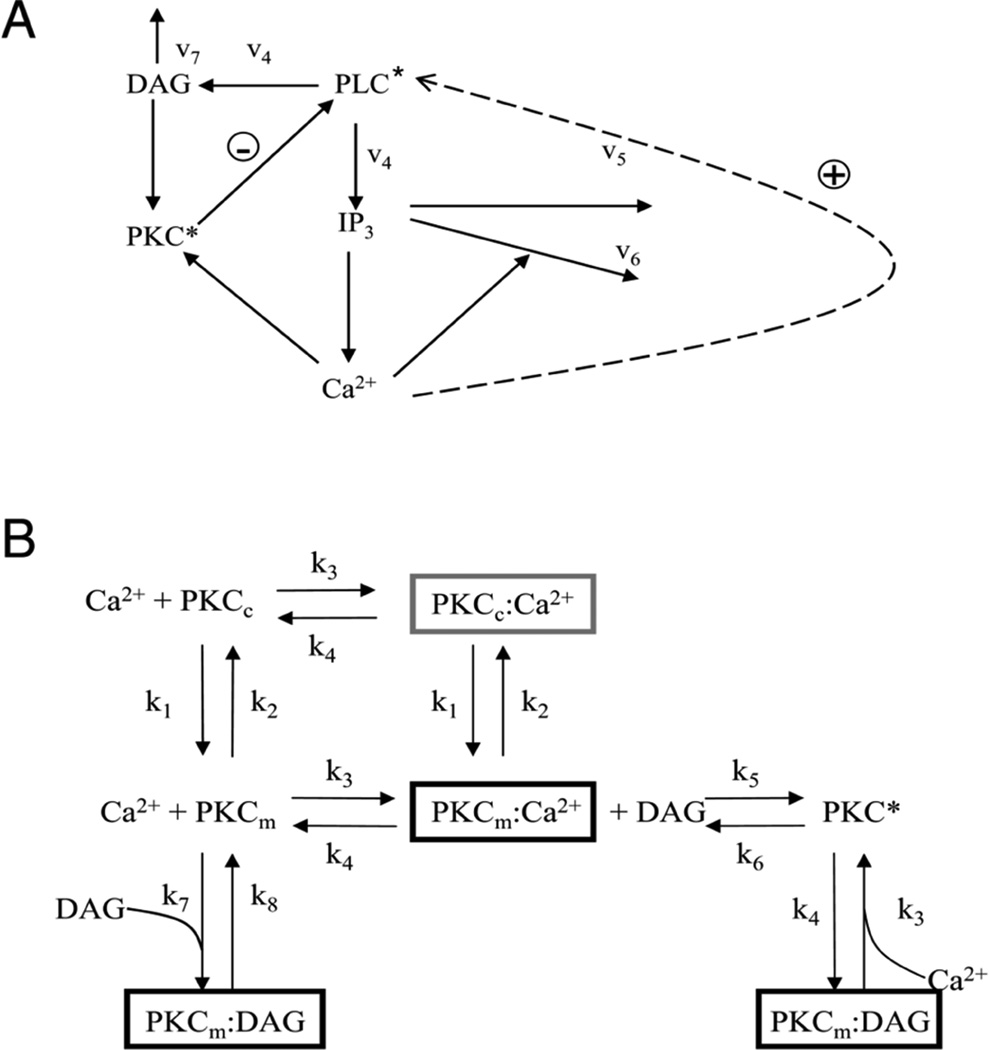
The De Young-Keizer model ^[6] was revised to include the dynamics of PKC activation, PLC activation, and IP₃ production. The mathematical model for the action of PKC describes the binding of Ca²⁺ to the C2 domain and translocation and activation of PKC triggered by the binding of DAG to the C1 domain. A schematic diagram of mechanism is shown in Fig. 1A. Activated PLC (PLC*) generates IP₃ and DAG (rate constant v₄ in Fig. 1A). Ca²⁺ is released from the ER by changes in IP₃ concentrations and positive feedback by Ca²⁺. The mechanism for IP₃ degradation is through dephosphorylation by a 5-phosphatase and by phosphorylation to inositol 1,3,4,5-tetrakisphosphate ^[1]. Ca²⁺ and DAG bind to C2 and C1 domains of PKC, respectively, which cause PKC translocation. PKC is known to reduce PLC activity via negative feedback on PLC in Fig. 1A ^{[6, 14]}. The activation of PLC by Ca²⁺ is added to the model shown by the dotted arrow (rate constant v₅ in Fig. 1A).

Fig. 1.

Model schematic. A. PLC activation pathway. (DAG – diacyl glycerol; PKC* - activated protein kinase C; PLC* – activated phospholipase C; IP₃ – inositol 1,4,5-trisphosphate; Ca²⁺ - calcium ion, v₁–v₆ – reaction rates). The dashed line indicates the positive feedback of Ca²⁺ on PLC which is explored further in this study. B. Reaction scheme for PKC activation. (PKC_c – cytoplasmic PKC; PKC_m – membrane associated PKC; k₁–k₈ reaction rates).

A detailed reaction scheme of PKC activation is demonstrated in Fig. 1B. Here cytosolic species are shown in the upper half of the figure and given the subscript c. Membrane species are shown in the lower half of the figure and given the subscript m. At rest, PKC is located primarily in the cytosol (PKC_c). Upon elevation of Ca²⁺, Ca²⁺ binds the C2 domain of PKC_c in the cytoplasm resulting in its activated form, designated PKC_c:Ca²⁺ (Fig. 1B - dark gray box). The activated C2 domain results in translocation of the entire complex to the plasma membrane and is designated PKC_m:Ca²⁺ (Fig. 1B – black). Once in the membrane DAG binds the C1 domain of PKC_m:Ca²⁺ resulting in fully activated PKC (PKC^*). The model treats cytosolic and plasma membrane entities as distinct, and thus includes the 7 separate chemical species shown in Fig. 1B. The arrows between species represent forward and reverse chemical reactions, or membrane translocation. The rates of reaction, and of translocation, are represented by the 8 rate constants, designated k₁ to k₈ (Table I).

TABLE I.

PKC Rate Constants

Rate Constant	Value	Reference
k1	0.0001 s−1	estimated
k2	0.0001 s−1	estimated
k3	0.1 s−1	estimated
k4	2.2 s−1	estimated
k5	0.261 s−1	[4]
k6	0.26 s−1	[4]
k7	0.00378 s−1	estimated
k8	0.2 s−1	estimated

The model consists of twelve differential equations: (1) the cytosolic Ca²⁺ concentration (2) the ER Ca²⁺ concentration (3) the cytosolic IP₃ concentration; (4) the fraction of cytosolic IP₃R subunit in the closed state with only IP₃ bound; and (5) the fraction of cytosolic IP₃R subunits in the open state with both IP₃ and an activating Ca²⁺ bound, and (6)–(12) the system of 7 first order differential equations describing the mass action kinetics of the 7 states of PKC shown in the reaction scheme (Fig. 1B) (Appendix). The parameters in the equations include the 8 rate constants.

Two processes of the cytosolic calcium cycling from the ER in De Young-Keizer model is used in the model. The first is Ca²⁺ influx through the IP₃ receptor (IP₃R), and leak flux across the ER membrane (J_IP3R) can be described by

$$J_{I{P}_{3}R}=c_1(v_1{X}_{110}^3+v_2)({[C{a}^{2+}]}_{ER}-{[C{a}^{2+}]}_{\mathit{\text{cyt}}})$$ (1)

where v₁ is the maximal Ca²⁺ flux rate through the IP₃R, X₁₁₀ is fraction of IP₃R subunits in the permissive state (both activating Ca²⁺ and IP₃) bound, v₂ is the leak flux rate, and c₁ is the ER to cytosol volume ratio. The ER and cytosolic Ca²⁺ concentrations are represented by [Ca²⁺]_ER and [Ca²⁺]_cyt, respectively, and their difference describes the Ca²⁺ concentration gradient. The fraction X₁₁₀ is cubed to reflect that three subunits need to be in the permissive state in order for the channel to be open. In the second process, Ca²⁺ is removed from the cytosol and sequestered into the ER via Ca²⁺ uptake by the SERCA pump (J_SERCA), described by

$$J_{SERCA}=\frac{v_3{[C{a}^{2+}]}_{\mathit{\text{cyt}}}^2}{{[C{a}^{2+}]}_{\mathit{\text{cyt}}}^2+K_3^2}$$ (2)

Here v₃ is the maximal SERCA pump rate and K₃ is the affinity of SERCA for cytosolic Ca²⁺. The balance equations for [Ca²⁺]_cyt is

$$\frac{d{[C{a}^{2+}]}_{\mathit{\text{cyt}}}}{dt}={\beta }_{\mathit{\text{cyt}}}(J_{I{P}_{3}R}-J_{SERCA})$$ (3)

where β_cyt is a constant describing the fraction of Ca²⁺ flux not bound to Ca²⁺ buffers in the cytosol. The balance equations for ER Ca²⁺ concentration is given by

$$\frac{d{[C{a}^{2+}]}_{ER}}{dt}={\beta }_{ER}\left(\frac{J_{SERCA}-J_{I{P}_{3}R}}{c_1}\right)$$ (4)

where the fluxes are described above and β_ER is the fraction of ER Ca²⁺ flux not bound to ER Ca²⁺ buffers.

The activation and inactivation states of cytosolic IP₃ receptors by Ca²⁺ are given by following equations:

$$\frac{d{X}_{100}}{dt}=-a_2{[C{a}^{2+}]}_{\mathit{\text{cyt}}}{X}_{100}-a_5{[C{a}^{2+}]}_i{X}_{100}+b_5{X}_{110}$$ (5)

$$\frac{d{X}_{110}}{dt}=-a_2{[C{a}^{2+}]}_{\mathit{\text{cyt}}}{X}_{110}+b_2{c}_2[I{P}_3]+a_5{[C{a}^{2+}]}_i{X}_{100}-b_5{X}_{110}$$ (6)

where X₁₀₀ is the fraction of channels with the IP3 bound that is not in the activated state and X₁₁₀ is the fraction of activated channels with both IP₃ and activating Ca²⁺ bound ^[2]. The three subscripts indicate IP₃ bound, activating Ca²⁺ bound, and inactivating Ca²⁺ bound by a “1” moving from left to right. A “0” indicated that the site is available (i.e. nothing is bound to it).

The formulation of IP₃ production and degradation dynamics in the cytosol are based on Swillens-Mercan model ^[1]. The equation of free cytosolic concentration of IP₃ ([IP₃]_cyt) is given by

$$\frac{d{[I{P}_3]}_{\mathit{\text{cyt}}}}{dt}=v_4[PL{C}^{*}]-\frac{v_5}{[1+{\left(\frac{K_5}{{[I{P}_3]}_{\mathit{\text{cyt}}}}\right)}^h]}-\frac{v_6}{[1+{\left(\frac{K_6}{{[I{P}_3]}_{\mathit{\text{cyt}}}}\right)}^h]}\times \frac{1}{[1+(\frac{K_7}{{[C{a}^{2+}]}_{\mathit{\text{cyt}}}}\left)\right]}$$ (7)

where v₄ is the rate of formation of IP₃ from PLC. In the second term, v₅ is the maximal rate of dephosphorylation IP₃ by a 5-phosphatase governed by the binding constant K₅. The third term represents that the rate of IP₃ phosphorylation to inositol 1,3,4,5-tetrakisphosphate by a 3-kinase with maximal rate v₆ and binding constant K₆ that is increased by Ca²⁺ with binding constant K₇ (Fig. 1A) ^[1].

In the model, there is a direct activation of PLC ([PLC*]) by Ca²⁺. It describes the Ca²⁺ activated PLC via positive feedback though inclusion of an additional factor in the first term in the equation for PLC activation and K_Ca describes the affinity of PLC for Ca²⁺.

$$\frac{d[PL{C}^{*}]}{dt}=k_{\mathit{\text{plcon}}}[PLC]\frac{{[C{a}^{2+}]}_{\mathit{\text{cyt}}}}{(K_{ca}+{[C{a}^{2+}]}_{\mathit{\text{cyt}}})}-k_{\mathit{\text{plcoff}}}[PL{C}^{*}]\frac{[PK{C}^{*}]}{(K_{pkc}+[PK{C}^{*}])}$$ (8)

Here, K_pkc is the dissociation constant for PKC inhibition. The parameter values and definitions are given in Tables II–III.

TABLE II.

Ca²⁺ Regulatory Mechanism Parameters

Parameter	Definition	Value	Reference
c1	Ratio of ER volume to cytosolic volume	0.185	[2]
c2	Proportionary constant of X111 to [IP3]	0.2 µM	[3]
v1	Maximum IP3 receptor flux	10.0 s−1	[2]
v2	Ca2+ leak rate constant	2.0 s−1	Rescaled from [2]
v3	SERCA maximal pump rate	80.0 µM s−1	[2]
K3	SERCA dissociation rate	0.1 µM	Rescaled from [2]
a2	Inhibitory receptor binding constant	0.03 µM−1 s−1	[2]
a5	Activation receptor binding constant	20.0 µM−1 s−1	[2]
d2	Inhibitory receptor binding constant	1.049 µM	[2]
d5	Activation receptor binding constant	82.34 nM	[2]
βcyt	Ca2+ buffers in the cytosol	0.01	estimated
βER	ER Ca2+ buffers	0.01	estimated

TABLE III.

IP₃ Production Parameters

Parameter	Definition	Value	Reference
v4	PIP2 turnover rate by PLC	0.12 µM s−1	Scaled from[1]
v5	IP3 dephosphorylation rate	0.625 µM s−1	Scaled from[1]
v6	IP3 dissociation rate	0.75 µM s−1	Scaled from[1]
K5	IP3 dissociation constant	25.0 µM	Scaled from[1]
K6	IP3 dissociation constant	0.2 µM	Scaled from[1]
K7	Ca2+ dissociation constant	1 µM	Scaled from[1]
h	Hill coefficient	1	[1]
Kpkc	Dissociation constant for PKC inhibition	0.1 µM	estimated
KCa	Dissociation constant for calmodulin/PLCβ1 interaction	0.2 µM	(Mccullar et al 2007)
kdag	Degradation rate	0.1 s−1	estimated
kplcon	Positive feedback	0.2 s−1	estimated

The time course for the concentrations of each of the chemical species from a given initial condition is determined by numerical solution of the system using Euler’s Method. Table I lists the rate constants used in the model. Those rate constants were estimated from published data so that model variables and time courses conformed to experimental data. Parameter definitions and all values are given in Table I–IV. These are used in all the simulations unless otherwise specified in the text. The computer program was written in FORTRAN and run on an HP-UX workstation, and the results were visualized and graphs were made using MATLAB 7.0.1 by the Mathworks, Inc.

TABLE IV.

Resting State Concentrations

Variable	Concentration (µM)
[Ca2+]cyt	0.1
[Ca2+]ER	100.6
X100	0.24
X110	0.32
[IP3]cyt	0.25
DAG	1.0
PKCm:DAG	0.57
PKCc:Ca2+	0.1
PKCm:Ca2+	0.078
PKC*	0.01
PKCc	18
PKCm	17

III. Results

Using the parameter values in Tables I–III, the model is allowed to come to steady state at rest. The resting state concentrations are shown in Table IV. Codazzi and co-workers ^[14] have studied how conventional PKC isoforms affect Ca²⁺ oscillations in astrocytes using total internal reflection fluorescence (TIRF) microscopy. They observed oscillations in PKC translocation to the plasma membrane using GFP-PKCγ. They also observed that oscillations in DAG lagged behind Ca²⁺ oscillations in phase by measuring fluorescence of GFP-C1 bound to DAG and Ca²⁺ bound to the Ca²⁺ indicator Ca²⁺ crimson. They suggested that the phase lag might indicate that during the Ca²⁺ oscillations when Ca²⁺ concentration increased it activates PLC, which in turn generates more DAG.

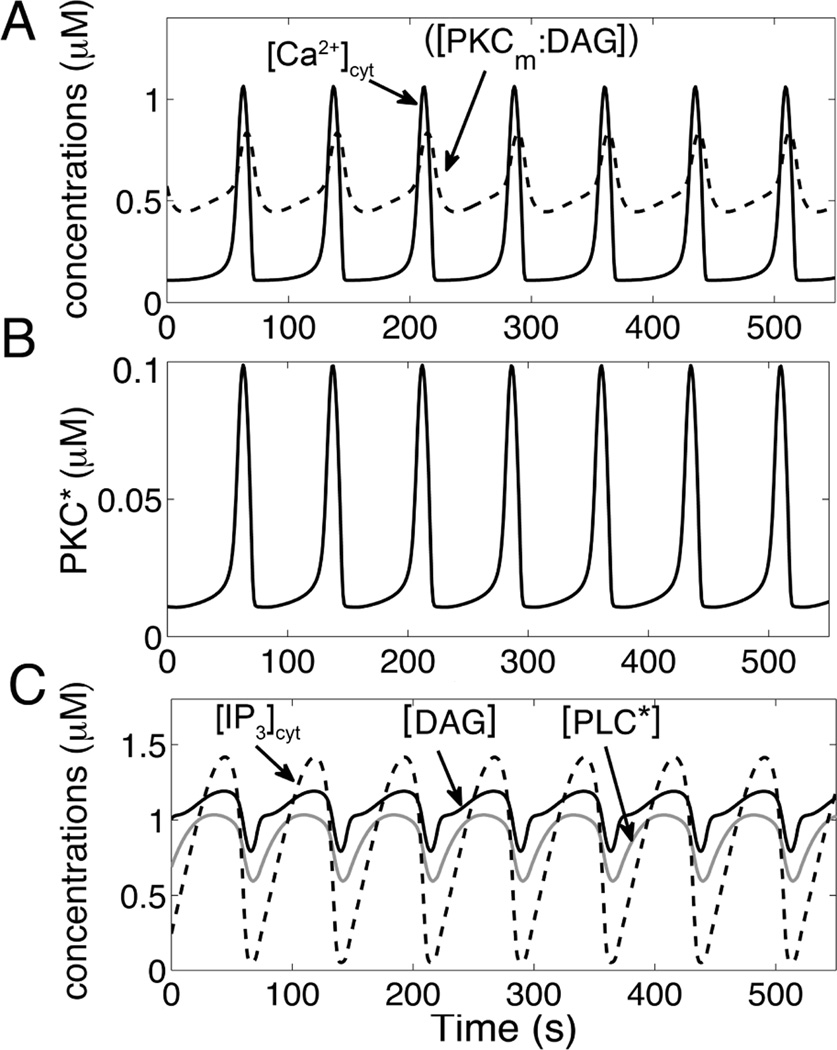
To this end, the model is used to simulate the experimental results. In order to simulate agonist stimulation and PLC activation v₄ was increased to 0.15 µM s⁻¹ causing production of IP₃ and DAG and the ensuing Ca²⁺ oscillations. Fig. 2A shows our simulated train of Ca²⁺ oscillations. In these simulations, [Ca²⁺] is released from ER stores caused by fast activation of IP₃R and with termination by depletion of the ER. Fig. 2B shows the activated PKC (PKC*) concentrations plotted as a function of time that seem to be almost in-phase with the Ca²⁺ oscillations with only a slight lag. The simulated PKC* is delayed by a few seconds compares to cytosolic Ca²⁺ oscillation similar to the experiments by Codazzi and co-workers (2001) measuring the C1 domain of PKC (GFP-C1). In addition, Matsu-ura and co-workers observed IP₃ oscillations during agonist stimulation in HeLa cells ^[15]. Our results show the accompanying oscillations in IP₃, DAG, and PLC in Fig. 2C. The IP₃ concentration (dashed line) rises prior to the Ca²⁺ oscillations along with DAG (solid black line). The results show that the DAG and IP₃ produced at the same rate from PLC as one would expect.

Fig. 2.

Simulated time courses of concentrations. A. Simulated intracellular Ca²⁺, DAG binding domains of PKC-C1 (PKC_m:DAG) oscillations when PLC is active (top panel). The translocation of C1 is delayed by a few seconds. B. Activated PKC (PKC^*) oscillations are almost in-phase with Ca²⁺ transit. C. Activated PLC ([PLC*]), DAG and IP₃ show in-phase oscillations.

Fig. 3A shows free PKC concentrations in cytosol [PKC_c] and plasma membrane [PKC_m] behave in a similar manner; [PKC_m] increases seconds after elevation of [PKCc]. The concentration of PKC binding of Ca²⁺ ([PKC_c:Ca²⁺]) follows the reverse trend, increasing rapidly after [PKC_c] reaches a certain level as shown in Fig. 3B. The translocation of PKC-C1 (Fig. 3C) appears to start seconds later after Ca²⁺ concentrations reached a threshold. These simulations suggest that binding process of PKC caused the delayed translocation of PKC-C1 because elevation of the cytosolic Ca²⁺ concentration is needed for Ca²⁺ to bind to PKC-C2 domains. The binding of Ca²⁺ to PKC-C2 results in its translocation to the plasma membrane, which then allows DAG to bind to PKC-C1 domains. This indicates that Ca²⁺ activation of PLC is not necessary to see the phase lag observed experimentally.

Fig. 3.

Simulated time courses of concentrations. A. Free PKC concentrations in the cytosol [PKC_c] and PKC concentrations associated with the plasma membrane [PKC_m] oscillate during PLC activation pathway. B. PKC bound to Ca²⁺ in cytoplasm ([PKC_c:Ca²⁺]), and C. Ca²⁺ binding of PKC-C2 domains translocate to plasma membrane ([PKC_m:Ca²⁺]) both oscillate during Ca²⁺ oscillations.

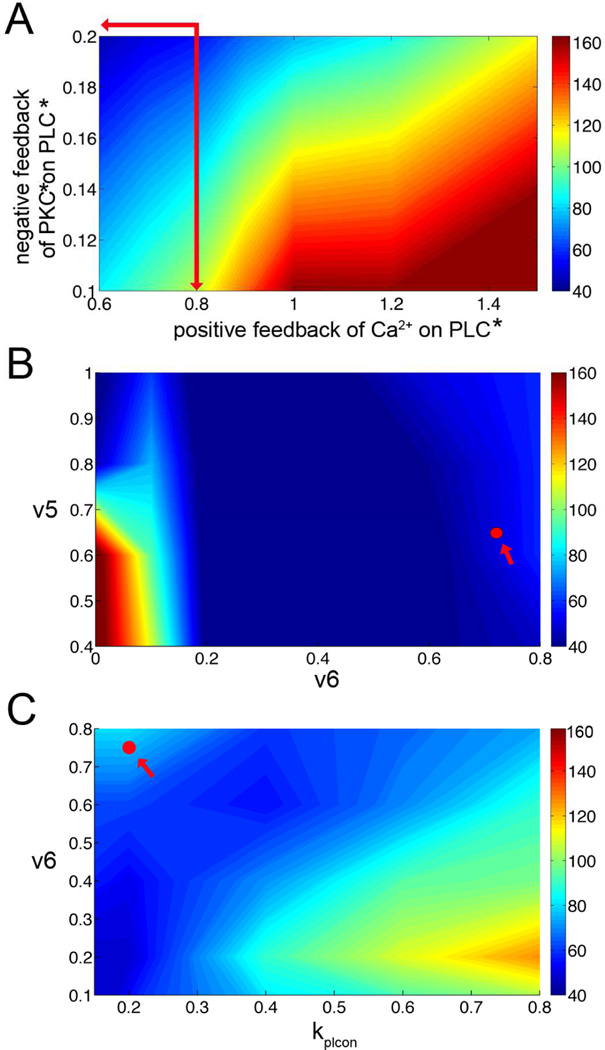
The next set of simulations tested how the phase lag between Ca²⁺ and IP₃ oscillations is modulated by PLC dynamics. In order to do this, the positive feedback of Ca²⁺ on PLC and the negative feedback on PLC by Ca²⁺ through PKC were varied (Fig. 4A). Here the DAG peak is used as it corresponds with the IP₃ peak and it is often used in experiments as an indicator of IP₃. Depending upon the relative contributions of each feedback mechanism, the phase lag varies greatly. When the positive feedback is strong, the Ca²⁺ and IP₃ oscillations can be 160° out of phase. However, when the negative feedback dominates, the phase lag is minimal. Note that the oscillations are never completely in phase. The default model values for these parameters are indicated at the intersection of the red arrows. Varying individual parameters such as the degradation rate of IP₃ (v₅) and the positive feedback of Ca²⁺ on PLC (v₆) also can affect the phase lag (Fig. 4B). A reduction of both parameters promotes out of phase oscillations. The default model parameters are indicated by the solid red circle. In Fig. 4C the effect of v₆ and the Ca²⁺ dependent rate k_plcon of positive feedback is studied. The interplay between these two parameters shows once again that the phase lag can vary depending upon parameter choices. The default model parameters are indicated by the solid red circle. In summary, the phase lag between the Ca²⁺ and IP₃ oscillations can vary depending upon the signaling strength of various components of the signaling network. Biologically, this might simply depend upon gene expression levels or the phosphorylation state of the system.

Fig. 4.

Phase maps. A. The effects of positive feedback of Ca²⁺ and negative feedback of PKC* on Ca²⁺ and DAG oscillations. These plots show the phase difference between the [Ca²⁺]_cyt and [IP₃]_cyt oscillation peaks. The phase difference is calculate as 360*((time of Ca²⁺ peak) - (time of DAG peak))/(oscillation period), In this way when the periods are aligned the value is 0, when they are opposite in phase it is 180. The synchronization between Ca²⁺ and DAG oscillations varies with feedback strength. B. The changing of the degradation rate of IP₃ (v₅) affects the phase differences of Ca²⁺ and IP₃. When v₆ (Ca²⁺ dependent rate of PLC activation) large, the oscillations of calcium and IP₃ are in phase. The default model parameter is shown by the red circle. C. The Ca²⁺ dependent rate of PLC activation (v₆) and Ca²⁺ dependent rate k_plcon for positive feedback affect the phase differences of Ca²⁺ and IP₃. The default model parameter is shown by the red circle.

In earlier modeling work by Meyer and Stryer ^[16], there was an important interplay between the Ca²⁺ and IP₃ concentrations that produced oscillations. In our model, when Ca²⁺ concentration is held fixed, the IP₃ oscillations cease consistent with this idea (Fig. 5A). In the model when Ca²⁺ oscillations are present, there are oscillations in the amount of activated PLC ([PLC*]) (Fig. 5B – solid line). When DAG degradation is blocked the oscillations cease (Fig. 6B – dashed line).

Fig. 5.

Ca²⁺ oscillations affect IP₃ and activated PLC ([PLC*]) oscillations. A. There is no IP₃ oscillation when Ca²⁺ is set to a constant level (1.0 µM). B. Blocking DAG degradation eliminates [PLC*] oscillation (dashed line), whereas DAG degradation results in PLC oscillations (solid line).

Fig. 6.

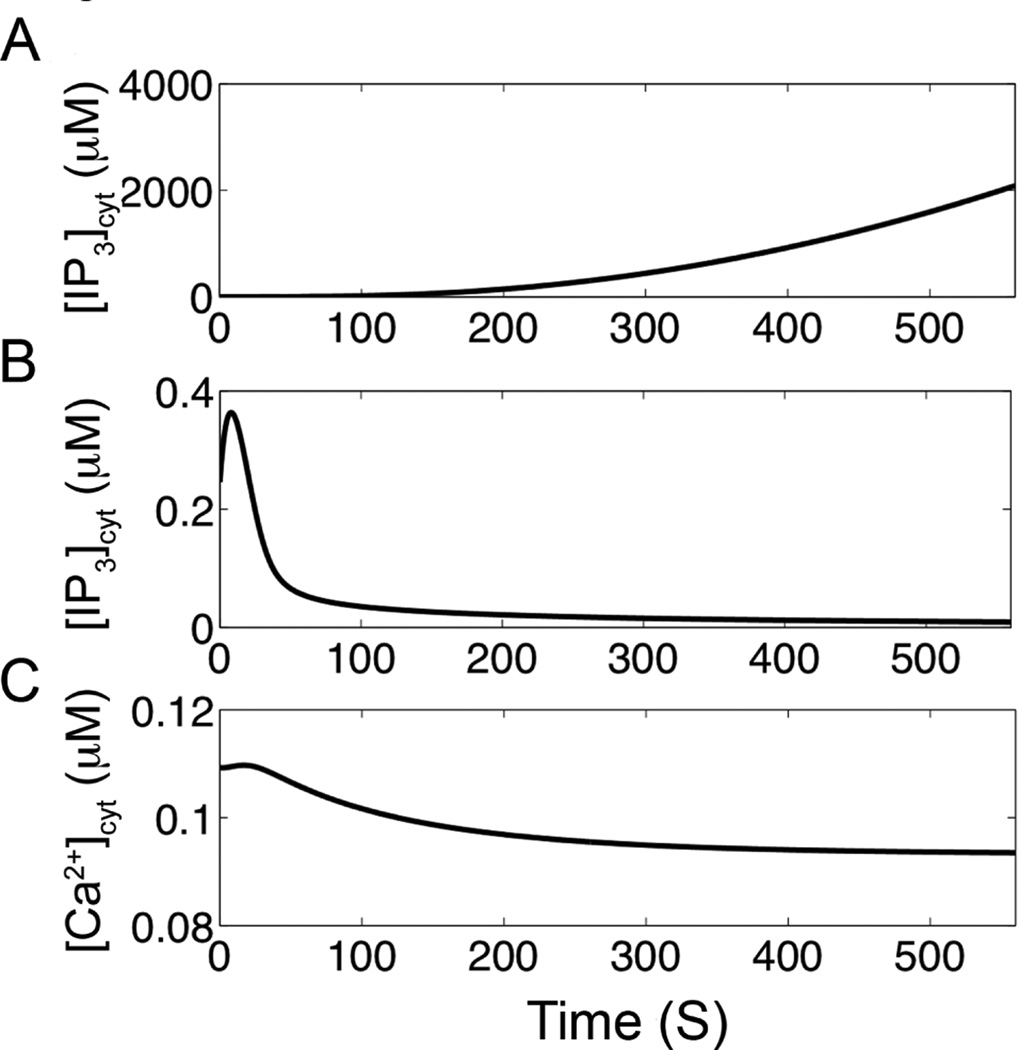
Blocking the feedbacks on PLC affect Ca²⁺ dynamics. A. There are no Ca²⁺ oscillations and the IP₃ rise by blocking PKC. Furthermore, the IP₃ concentration rises as there is no negative feedback on PLC. B. When the positive feedback of Ca²⁺ on PLC is eliminated the IP₃ concentration returns to steady state. C. When the positive feedback of Ca²⁺ on PLC is eliminated the Ca²⁺ concentration also returns to steady-state level. However, if the mean [IP₃]_cyt is raised, [Ca²⁺]_cyt oscillations can occur in the absence of positive feedback of Ca²⁺ on PLC (see Figure 8).

Additional simulations were performed to understand the interacting components on Ca²⁺ dynamics during agonist-induced signaling. To further understand the role of PKC, the action of PKC on PLC is blocked which terminated the oscillations (Fig. 6A). The IP₃ concentration rises as the negative feedback on the production of IP₃ by PLC has been removed. Similarly, the [DAG] concentration will also rise. The positive feedback of Ca²⁺ on PLC activation is blocked to assess its role in Ca²⁺ oscillations (Figs. 6B and 6C). In this case, the oscillations cease and the IP₃ concentration (Fig. 6B) and the Ca²⁺ concentration (Fig. 6C) both return to baseline. However, it would be incorrect to conclude that this means that the positive feedback is needed for oscillations. The oscillations can be restored by adjusting parameters to increase the IP₃ concentration slightly as shown in Fig. 7.

Fig. 7.

Test to see if positive feedback of Ca²⁺ on PLC is involved with [Ca²⁺]_cyt oscillations. An applied IP₃ pulse as shown results in different behaviors in the models with and without positive feedback of Ca²⁺ on PLC. In both cases the [Ca²⁺]_cyt oscillation frequency increases with the increased [IP₃]_cyt. A. In the model with positive feedback of Ca²⁺ on PLC, the oscillations resume similar to those before the pulse. B. In the model without positive feedback of Ca²⁺ on PLC, the [Ca²⁺]_cyt oscillations do not resume. C. The time course for activated [PLC] shows differing dynamics in the system with Ca²⁺ feedback on PLC (black) and without Ca²⁺ feedback on PLC (red).

The modeling results suggest that the phase lag between the [Ca²⁺]_cyt and [IP₃]_cyt oscillations is not a good indicator of the presence of the positive feedback of Ca²⁺ on PLC. To provide a simple test that could be implemented in experiment, a pulse of IP₃ was applied with a gradual decay back to baseline in as shown in Fig. 7. In the model that included the positive feedback of Ca²⁺ on PLC, the frequency and amplitude of the [Ca²⁺]_cyt oscillations increase during the pulse and return to pre-pulse amplitude and frequency afterward (Fig. 7A). On the other hand, in the model that excluded the positive feedback of Ca²⁺ on PLC*, the increase in the [Ca²⁺]_cyt oscillations is followed by oscillations of low amplitude after the IP₃ pulse ended (Fig. 7B). Fig. 7C shows that in both cases the system with the positive feedback of Ca²⁺ on PLC, the amount of PLC activation is higher than in the case without positive feedback of Ca²⁺ on PLC. It is important to note that the only difference between the two models is that in the case without Ca²⁺ feedback on PLC, the term for [Ca²⁺]_cyt is set to its resting level of 0.1 µM to eliminate the positive feedback. Therefore the pulse of IP₃ provides a possible test for the role of the positive feedback of Ca²⁺ on PLC.

In order to understand the differing dynamics of the Ca²⁺ oscillations in the two systems shown in Fig. 7, a number of simulations were determined to construct bifurcation diagrams. Fig. 8 shows bifurcation diagrams for the concentrations of activated PLC, IP₃, and DAG, in panels A, B, and C, respectively. In these diagrams the solid lines show the steady-state [Ca²⁺]_cyt and the dotted lines show the maximum and minimal [Ca²⁺]_cyt values during oscillations. This behavior is consistent with experiments and other models ^{[16, 17]}. However, the dynamics are significantly more complex as these quantities are not simple parameters. Instead, they are variables whose values are determined by the dynamics. This would be similar to the case found in living cells. In the system with the positive feedback of Ca²⁺ on PLC, the level of activated PLC after the pulse of IP₃ rises to cross the bifurcation point for the advent of oscillation (Fig. 8A). On the other hand, in the case without feedback, the levels of activated PLC are too low to allow for oscillations. The reason that the former reaches higher level is that there is a positive feedback loop where Ca²⁺ activates PLC, which increases IP₃ production resulting in further mobilization of Ca²⁺. On the other hand if Ca²⁺ does not activate PLC, then only the inhibiting effect of Ca²⁺ through PKC activation remains effectively attenuating the levels of activated PLC. Fig. 8B shows oscillations within a finite range similar to previous studies. Fig. 8C demonstrates that as [DAG] rises above a certain range oscillations terminate. Figs. 8B–C provide an explanation why the block of PKC in Fig. 6A results in the termination of oscillations, i.e. the [IP₃] or [DAG] levels could rise out of the oscillatory regime with the block of the negative feedback of PKC on PLC.

Fig. 8.

Bifurcation diagrams for Ca²⁺ oscillations (——) indicates stable steady states and (-------) gives maximum and minimum [Ca²⁺]_cyt during oscillations. A. The model generates oscillations in Ca²⁺ while [PLC*] between 1 and 4.2 µM. B. The constant IP₃ ([IP₃] + [IP₃β]) between 0.8 and 4.4 µM can produce Ca²⁺ oscillations. C. [DAG] can affect Ca²⁺ oscillations when set [DAG] to a constant in between 0.0 and 2.0 µM.

IV. Discussion

In the past several models of agonist-induced Ca²⁺ oscillations have been proposed. Meyer and Stryer ^[18] proposed a model in which the Ca²⁺ positively activates PLCβ to increase IP₃ concentrations and IP₃ cause Ca²⁺ release that generates the next calcium transients. Swillens and Mercan ^[1] developed a model that suggested negative control of Ca²⁺ efflux through IP₃ receptor contribute to Ca²⁺ oscillations, and also the activation of 3-kinase positively co-operates with the calcium for oscillating IP₃. DeYoung and Keizer ^[2] presented a model that described the kinetics of the IP₃ receptor along with ER sequestration of Ca²⁺ and found that its dynamics was sufficient to produce Ca²⁺ oscillations. While all these models have modeled different pieces of the Ca²⁺ signaling pathway, this is the first to model integrate the different parts into one model. As a result it shows how the different pieces modulate Ca²⁺ oscillations.

The Ca²⁺ and DAG dependent conventional PKC activation (PKC*) model presented here incorporates experimentally determined reaction pathways. The model reproduces experimentally observed behaviors of translocation of PKC to plasma membrane. Several parameter values were estimated to fit the experimental observations. The model simulates the PKC oscillations consistent with experimental results ^{[10, 14]}. Similar to their experiments, we observed oscillations in both DAG and IP₃ in the model. The model presents a classic type of Ca²⁺ oscillations induced by IP₃ leads to Ca²⁺ release and uptake of Ca²⁺ from intracellular ER stores, with a negative feedback of PKC on PLC in this manuscript. It suggests that the translocation of PKC to plasma membrane is delayed by a few second without a positive feedback of Ca²⁺ on PLC. A previous model by Pollitti and co-workers (2006) explored the effects of positive and negative feedback on Ca²⁺ oscillations^[19]. They concluded that the model with coupled IP₃ and Ca²⁺ oscillations displayed a greater frequency range than simpler models. Furthermore, they suggested that positive feedback of Ca²⁺ on PLC required fast degradation of IP₃ and negative feedback requires slow degradation IP₃ turnover.

The model demonstrates that the apparent lag of peak values of [Ca²⁺]_cyt and [IP₃]_cyt oscillations is not a sufficient criterion to determine causality, that is, which process is triggering the other in the oscillatory regime. Moreover, the model suggests a test that can be used to determine whether or not Ca²⁺ feedback on PLC is playing a role in the oscillations. Another work by Sneyd and co-workers (2006) addressed a similar question with a combined modeling and experimental study ^{[20, 21]}. They sought to determine if Ca²⁺ oscillations depend upon IP₃ oscillations. They considered class I models where the [Ca²⁺]_cyt oscillation frequency is an increasing function of the parameter [IP₃]_cyt and class II models where [IP₃]_cyt is a variable that oscillates. Perturbation of the oscillations by IP₃ injections in class I models results in a transient increase in oscillation frequency. On the other hand, injection of IP₃ in class II models results in a delay in the oscillation phase, i.e. the next peak in [Ca²⁺]_cyt is delayed. The model presents here is a class II model as IP₃ concentration is a variable that can oscillate. Here, we demonstrate that the presence or absence of Ca²⁺ feedback on PLC is does not absolutely determine phase lag between [Ca²⁺]_cyt and [IP₃]_cyt oscillations.

V. Conclusions

The model presented here integrates experimentally observed IP₃ receptor and PLC dynamics to demonstrate their interplay during agonist induced Ca²⁺ signaling. It demonstrates that Ca²⁺ occurs through a complex interplay of factors. Furthermore, it suggests that the phase lag between Ca²⁺ and IP₃ oscillations is not a good indicator of causality because the phase lag can be changed dramatically depending upon the strength of positive feedback of Ca²⁺ on PLC as well as the strength of the negative feedback of Ca²⁺ through PKC.

Biographies

Pei-Chi Yang received her PhD degree from George Mason University in 2007 from the Program in Bioinformatics and Computational Biology. She is currently an Assistant Project Scientist working with Colleen Clancy in the Department of Pharmacology, University of California, Davis, CA, USA. Her research interests include calcium signaling, cardiac electrophysiology, arrhythmia susceptibility, and pharmacology.

M. Saleet Jafri received the PhD degree from the Mount Sinai School of Medicine/City University of New York University, New York, NY, USA, in 1993 from the Department of Biomathematical Sciences. He is currently Professor and Chair of the Molecular Neuroscience Department at George Mason University, Fairfax, VA USA. He is an Adjunct Professor at the Center for Biomedical Engineering and Technology, University of Maryland, Baltimore, MD, USA. From 1999 to 2002 to 2009, he was Assistant Professor at the Department of Mathematical Sciences, The University of Texas at Dallas, Richardson, TX, USA. Prior to that he was a Research Associate at the Department of Biomedical Engineering, The Johns Hopkins University, Baltimore, MD, USA. He did his Postdoctoral work with Joel Keizer at the Institute for Theoretical Dynamics, University of California, Davis, CA, USA. His research interest includes the use of computational model to understand the cellular mechanism of normal and pathophysiology. His areas of expertise include calcium signaling, cardiac excitation-contraction coupling, mitochondrial physiology, and t-cell signaling.

APPENDIX

PKC Model Equations

$$\frac{\mathrm{d}[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{c}}]}{dt}=k_2[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}]-k_1[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{c}}]-k_3[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{c}}][\mathrm{C}{\mathrm{a}}^{2+}]+k_4[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{c}}:\mathrm{C}{\mathrm{a}}^{2+}]$$

$$\frac{\mathrm{d}[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{c}}:\mathrm{C}{\mathrm{a}}^{2+}]}{dt}=k_3[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{c}}][\mathrm{C}{\mathrm{a}}^{2+}]-k_4[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{c}}:\mathrm{C}{\mathrm{a}}^{2+}]+k_2[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}:\mathrm{C}{\mathrm{a}}^{2+}]-k_1[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{c}}:\mathrm{C}{\mathrm{a}}^{2+}]$$

$$\frac{\mathrm{d}[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}:\mathrm{C}{\mathrm{a}}^{2+}]}{dt}=k_3[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}][\mathrm{C}{\mathrm{a}}^{2+}]-k_4[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}:\mathrm{C}{\mathrm{a}}^{2+}]+k_1[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{c}}:\mathrm{C}{\mathrm{a}}^{2+}]-k_2[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}:\mathrm{C}{\mathrm{a}}^{2+}]-k_5[DAG][PK{C}_m:C{a}^{2+}]+k_6[PK{C}^{*}]$$

$$\frac{\mathrm{d}[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}]}{dt}=k_1[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{c}}]-k_2[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}]-k_3[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}][\mathrm{C}{\mathrm{a}}^{2+}]+k_4[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}:\mathrm{C}{\mathrm{a}}^{2+}]-k_7[DAG][PK{C}_m]+k_8[PK{C}_m:DAG]$$

$$\frac{\mathrm{d}[\mathrm{P}\mathrm{K}{\mathrm{C}}^{*}]}{dt}=k_3[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}:DAG][\mathrm{C}{\mathrm{a}}^{2+}]-k_4[\mathrm{P}\mathrm{K}{\mathrm{C}}^{*}]+k_5[PK{C}_m:C{a}^{2+}][DAG]-k_6[PK{C}^{*}]$$

$$\frac{\mathrm{d}[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}:\mathrm{D}\mathrm{A}\mathrm{G}]}{dt}=k_7[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}][DAG]-k_8[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}:DAG]-k_3[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}:DAG][\mathrm{C}{\mathrm{a}}^{2+}]+k_4[\mathrm{P}\mathrm{K}{\mathrm{C}}^{*}]$$

$$\frac{\mathrm{d}[\mathrm{D}\mathrm{A}\mathrm{G}]}{dt}=v_4[PL{C}^{*}]-k_{dag}[DAG]-k_5[\mathrm{P}\mathrm{K}{\mathrm{C}}_{\mathrm{m}}:C{a}^{2+}][\mathrm{D}\mathrm{A}\mathrm{G}]+k_6[\mathrm{P}\mathrm{K}{\mathrm{C}}^{*}]-k_7[DAG][PK{C}_m]+k_8[PK{C}_m:DAG]$$