Variable Selection with Prior Information for Generalized Linear Models via the Prior LASSO Method

Abstract

LASSO is a popular statistical tool often used in conjunction with generalized linear models that can simultaneously select variables and estimate parameters. When there are many variables of interest, as in current biological and biomedical studies, the power of LASSO can be limited. Fortunately, so much biological and biomedical data have been collected and they may contain useful information about the importance of certain variables. This paper proposes an extension of LASSO, namely, prior LASSO (pLASSO), to incorporate that prior information into penalized generalized linear models. The goal is achieved by adding in the LASSO criterion function an additional measure of the discrepancy between the prior information and the model. For linear regression, the whole solution path of the pLASSO estimator can be found with a procedure similar to the Least Angle Regression (LARS). Asymptotic theories and simulation results show that pLASSO provides significant improvement over LASSO when the prior information is relatively accurate. When the prior information is less reliable, pLASSO shows great robustness to the misspecification. We illustrate the application of pLASSO using a real data set from a genome-wide association study.

1 INTRODUCTION

In many scientific areas, it is common that experiments with similar goals are performed simultaneously or repetitively to establish a replicable conclusion. A typical example arises from the genome-wide association studies (GWAS). GWAS have become a common practice in exploring the genetic factors underlying complex diseases with the rapid advancement in high-throughput sequencing technology. It usually happens that multiple studies investigating the same question of interest (e.g., looking for the genetic variants associated with a particular human disease) have been carried out repetitively. This brings in the “prior” information for a current study. For example, previous studies provide us with some knowledge about possible effects of certain genes and/or single nucleotide polymorphisms (SNPs) on a disease, although the existing information may include both true and false positives.

Meanwhile, the massive data collected from current research are challenging the statistical analysis. Taking GWAS as an example again, it is well documented that the large number of genetic markers and the generally small size of their effects make it very unlikely for researchers to detect important genetic factors with a desired statistical significance in a single study. For example, hundreds of thousands of SNPs are typically genotyped, and yet their individual effect sizes are usually small. Therefore, it is imperative for us to utilize the existent biological and biomedical information. This prior information, if used appropriately, can alleviate the “curse of dimensionality” and hence improve the power of a study to discover important genetic factors.

Meta-analysis has actually provided effective means to combine different studies or their results to improve the statistical power, especially for genetic studies as well as biomedical studies broadly (Zeggini and Ioannidis, 2009 ; Cantor et al., 2010). Although meta-analysis has been proven successful in many studies (Zeggini et al., 2008), its applicability is restrictive for the present application. For example, the studies in a meta-analysis have to be similar in certain aspects such as the design of the experiments and the analytical methods. In addition, in genome-wide association studies, data are often collected using different genotyping platforms. As a consequence, the SNPs are different across studies, which makes it difficult to combine the results. While there exist methods to impute SNPs across platforms, the implication is not well understood between the results for genotyped and imputed SNPs. Most analytic methods treat the imputed SNPs naively as if they are genotyped SNPs.

We consider the situation where the data from the current study are analyzed using LASSO (Tibshirani, 1996) in conjunction with generalized linear models (McCullagh and Nelder, 1989). LASSO simultaneously selects a subset of explanatory variables and estimates their effects on the response. The goals of LASSO are achieved by balancing the model fitting and model complexity through a penalized likelihood approach. In general, LASSO considers all explanatory variables equally in terms of penalization. Suppose previous studies offered the plausible information about the importance of explanatory variables (e.g., genes or SNPs in GWAS). To incorporate the prior information, a seemingly natural method is to make use of the adaptive LASSO (Zou, 2006 ; Zhang and Lu, 2007), by assigning different weights of penalization to different variables to reflect various levels of prior evidence for significance. For example, variables with smaller p-values (or larger effect sizes) from previous studies should be penalized less such that they have a greater chance to be selected than the variables with larger p-values (or smaller effect sizes). However, this approach suffers from similar difficulties to those that we mentioned for meta-analysis methods. Moreover, this approach will perform poorly when the prior information contains a lot of false positives.

In this paper we propose a new solution named prior LASSO (pLASSO) to incorporate prior information into a LASSO problem. To utilize pLASSO, we only need to assume that the prior information can make certain prediction of the response. Then, pLASSO imposes an extra term using these predictive response values on the criterion function of LASSO to incorporate the prior information. In addition to the balance between model fitting and complexity in LASSO, pLASSO further balances the trade-off between the data and the prior information. It is noteworthy that pLASSO is a very flexible framework that can handle different types of prior information, including information presented as a set of significant explanatory variables (genes/SNPs), the effect sizes of some explanatory variables (genes/SNPs), or even the response values (disease status) given a set of explanatory variables (gene/SNP conditions).

Computationally, we investigate the solution path of pLASSO where the path reflects the change of belief in the prior information. Compared to the piecewise linear paths in the Least Angle Regression (LARS) of Efron et al. (2004) and in the similar work by Rosset and Zhu (2007), our path is piecewise smooth but not linear. Similar to the relationship between LARS and LASSO, our solution path fully characterizes the local effect of incorporating the prior information into a LASSO problem.

Theoretically, we compare the asymptotic properties of the LASSO and pLASSO estimators in three aspects: the asymptotic distribution in the low-dimensional setting, the weak oracle property in the high-dimensional setting, and the oracle inequalities for excess risk and estimation error in the high-dimensional setting. All three comparisons show that pLASSO results in a more efficient estimator than LASSO when the prior information is reasonably reliable. They also illustrate the trade-off between the variance reduction by incorporating the correct prior information and the additive bias due to the prior error.

Finally, numerically, the simulation results verify that pLASSO provides significant improvement over LASSO when the prior information is accurate. We will also see that when the prior information is less reliable, pLASSO shows great robustness to the misspecification. To illustrate the applicability of pLASSO to real data, we re-analyze a genetic data set on bipolar disorder using both LASSO and pLASSO and compare their results.

2 PRIOR LASSO

2.1 LASSO

Assume that we have a collection of independent observations ${\{({\mathbf{X}}_i,Y_i)\}}_{i=1}^n$, where Y_i’s are independently observed response values given the p-dimensional predictor vector X_i. Let Y = (Y₁, …, Y_n)^T and be the design matrix with X_i as its i-th row. Assume that, with a canonical link, the conditional distribution of Y_i given X_i belongs to the canonical exponential family with the following density function (ignoring a multiplier that depends on Y_i only):

$$f(Y_i\mid {\theta }_i)\propto exp[Y_i{\theta }_i-b({\theta }_i)],$$ (1)

where ${\theta }_i={\mathbf{Z}}_i^T\mathit{\beta }$ with ${\mathbf{Z}}_i={(1,{\mathbf{X}}_i^T)}^T$. As is common in generalized linear models, b(θ) is assumed to be twice continuously differentiable with positive b″(θ). The loss function (the negative log-likelihood function) of a generalized linear model is given by

$$L(\mathit{\beta };\mathbb{X},\mathbf{Y})=-\frac{1}{n}\sum _{i=1}^n[Y_i{\theta }_i-b({\theta }_i)]=-\frac{1}{n}\sum _{i=1}^n[Y_i{\mathbf{Z}}_i^T\mathit{\beta }-b({\mathbf{Z}}_i^T\mathit{\beta })],$$ (2)

where β = (β₀, β₁, …, β_p)^T.

Traditionally, the maximum likelihood estimator (MLE) of β, denoted by β̂, is obtained by minimizing L(β; , Y). To select a subset of predictors, LASSO adds an L₁-norm penalty term of (β₁, …, β_p)^T to L(β; , Y). Thus, the LASSO estimator β̂^λ is calculated by minimizing the following L₁-norm penalized loss function:

$$L_{\lambda }(\mathit{\beta };\mathbb{X},\mathbf{Y})=L(\mathit{\beta };\mathbb{X},\mathbf{Y})+\lambda \sum _{j=1}^p\mid {\beta }_j\mid ,$$ (3)

where λ is a tuning parameter.

The following well-known observation about a generalized linear model provides a good intuition on how LASSO works. Note that the term $-[Y_i{\mathbf{Z}}_i^T\mathit{\beta }-b({\mathbf{Z}}_i^T\mathit{\beta })]$ in (2) is proportional to the Kullback-Leibler (KL) distance between the distribution in (1) and the following distribution:

$$f(Y_i\mid {\theta }_{i1})\propto exp[Y_i{\theta }_{i1}-b({\theta }_{i1})],\text{where}{\theta }_{i1}\text{is}\text{determined}\text{by}{b}^{\prime }({\theta }_{i1})=Y_i.$$ (4)

Model (4) is the so-called saturated model which often serves as the reference model for evaluating the performance of a fitted model (Collett, 2003). In other words, a generalized linear model is a model reduction tool to approximate the saturated model. The idea of LASSO is to balance the trade-off between the approximation accuracy and the model complexity.

2.2 Prior LASSO

As discussed in the Introduction, we focus on the prior information about possible effects of certain predictors on the response. It can be a set of significant predictors, their effect sizes, or the predictive values given a set of predictors. Mathematically, these can be presented as some existing knowledge about the support of β, the values of β, or the predicted values of the response, etc. For the time being, let us assume that a preprocessing step can summarize the prior information into the predicted responses denoted by ${\widehat{\mathbf{Y}}}^{\mathrm{p}}={({\widehat{Y}}_1^{\mathrm{p}},\dots ,{\widehat{Y}}_n^{\mathrm{p}})}^T$. Depending on the nature of the prior information, different methods may be used in this step, and we shall revisit this issue below.

To incorporate the prior information, we need to weigh between the prior information and the presently observed data. Then, in the same spirit of the loss function L(β; , Y), it is natural to add the KL distance between the distribution in (1) and the following distribution in L_λ(β; , Y):

$$f(Y_i\mid {\theta }_{i2})\propto exp[Y_i{\theta }_{i2}-b({\theta }_{i2})],\text{where}{\theta }_{i2}\text{is}\text{determined}\text{by}{b}^{\prime }({\theta }_{i2})={\widehat{Y}}_i^{\mathrm{p}}.$$ (5)

Consequently, the pLASSO estimator β̂^λ,η is defined to be the minimizer of the following criterion function:

$$L_{\lambda ,\eta }(\mathit{\beta };\mathbb{X},\mathbf{Y},{\widehat{\mathbf{Y}}}^{\mathrm{p}})=L(\mathit{\beta };\mathbb{X},\mathbf{Y})+\eta L(\mathit{\beta };\mathbb{X},{\widehat{\mathbf{Y}}}^{\mathrm{p}})+\lambda \sum _{j=1}^p\mid {\beta }_j\mid ,$$ (6)

where η is another tuning parameter playing in a similar role to λ. The parameter η balances the relative importance of the data themselves and the prior information. In the extreme case of η = 0, pLASSO is reduced to LASSO. If η = ∞, pLASSO will solely rely on the prior information to fit the model. Furthermore, the tuning parameter η has another appealing interpretation: it controls the variance of β in its prior distribution from a Bayesian viewpoint (see Section 2.3.1).

We can simplify L_λ,η(β; , Y, Ŷ^p) as follows:

$$\begin{array}{l}{L}_{\lambda ,\eta }(\mathit{\beta };\mathbb{X},\mathbf{Y},{\widehat{\mathbf{Y}}}^{\mathrm{p}})=-\frac{1}{n}\sum _{i=1}^n[(Y_i+\eta {\widehat{Y}}_i^{\mathrm{p}}){\mathbf{Z}}_i^T\mathit{\beta }-(1+\eta )b({\mathbf{Z}}_i^T\mathit{\beta })]+\lambda \sum _{j=1}^p\mid {\beta }_j\mid \\ \propto -\frac{1}{n}\sum _{i=1}^n\left[\frac{Y_i+\eta {\widehat{Y}}_i^{\mathrm{p}}}{1+\eta }{\mathbf{Z}}_i^T\mathit{\beta }-b({\mathbf{Z}}_i^T\mathit{\beta })\right]+\frac{\lambda }{1+\eta }\sum _{j=1}^p\mid {\beta }_j\mid \\ =L_{\lambda /(1+\eta )}(\mathit{\beta };\mathbb{X},\stackrel{\sim }{\mathbf{Y}}),\end{array}$$ (7)

where Ỹ = (Y + ηŶ^p)/(1 + η) is the adjusted response values using the prior information. The pLASSO criterion function is in exactly the same form as the LASSO criterion function in (3). Essentially any LASSO fitting algorithm can be used to solve pLASSO.

As discussed above, a preprocessing step is needed to summarize the prior information into predictions Ŷ^p. For generalized linear models, we can obtain the predicted values of the response by plugging in a prior estimator β̂^p of β and then calculate ${\widehat{Y}}_i^{\mathrm{p}}=b^{\prime }({\mathbf{Z}}_i^T{\widehat{\mathit{\beta }}}^{\mathrm{p}})$, i.e., the expectation of Y_i given X_i and β̂^p.

A common type of prior information is about the support of β: A subset of predictors, denoted by , have been identified to be associated with the response by previous studies. The following simple version of weighted LASSO can be employed to force the predictors to stay in the model,

$$L_{\kappa ,{\mathcal{S}}^{\mathrm{p}}}(\mathit{\beta };\mathbb{X},\mathbf{Y})=-\frac{1}{n}\sum _{i=1}^n[Y_i{\mathbf{Z}}_i^T\mathit{\beta }-b({\mathbf{Z}}_i^T\mathit{\beta })]+\kappa \sum _{j=1}^p\mid {\beta }_j\mid I(X_j\notin {\mathcal{S}}^{\mathrm{p}}).$$ (8)

The resultant estimator from (8) can be used as the prior estimator β̂^p. In fact, minimizing (8) is to compute the predictions Ŷ^p given that we fully trust the previously identified signals in . Certainly, we also consider the variables not in but impose a L₁ penalty on them. By doing so, both β̂^p and Ŷ^p depend directly on the reliability of the prior information. Therefore, the pLASSO criterion function in (6) further balances the trade-off between the data and the prior information summarized in Ŷ^p from (8).

2.3 Special Cases

In this subsection, we consider the application of pLASSO to linear regression and logistic regression—two simplest, yet most frequently used generalized linear models.

2.3.1 Linear regression

Assume both Y and are centralized, so we can set β₀ = 0 and let β = (β₁, …, β_p)^T without ambiguity. Setting b(θ) = θ ²/2 in (2) leads to the loss function for linear regression

$$L(\mathit{\beta };\mathbb{X},\mathbf{Y})=\frac{1}{2n}{(\mathbf{Y}-\mathbb{X}\mathit{\beta })}^T(\mathbf{Y}-\mathbb{X}\mathit{\beta }).$$ (9)

Then the pLASSO criterion function for linear regression can be written as

$$L_{\lambda ,\eta }(\mathit{\beta };\mathbb{X},\mathbf{Y},{\widehat{\mathbf{Y}}}^{\mathrm{p}})=L(\mathit{\beta };\mathbb{X},\mathbf{Y})+\eta L(\mathit{\beta };\mathbb{X},{\widehat{\mathbf{Y}}}^{\mathrm{p}})+\lambda \sum _{j=1}^p\mid {\beta }_j\mid$$ (10)

$$\propto \frac{1}{2n}{(\stackrel{\sim }{\mathbf{Y}}-\mathbb{X}\mathit{\beta })}^T(\stackrel{\sim }{\mathbf{Y}}-\mathbb{X}\mathit{\beta })+\frac{\lambda }{1+\eta }\sum _{j=1}^p\mid {\beta }_j\mid ,$$ (11)

where L is defined in (9). It is noteworthy that {Ỹ_i : i = 1, …, n} in Ỹ are usually not statistically independent, as { ${\widehat{Y}}_i^{\mathrm{p}}$: i = 1, …, n} are in general not statistically independent.

It is also interesting to interpret the above criterion function from the Bayesian viewpoint. The middle term in (10) can be considered from a prior distribution of the parameters β as p(β) ∝ exp{−η(Ŷ^p − β)^T(Ŷ^p − β)/(2n)}, provided that Ŷ^p is known. Assume that Ŷ^p is obtained from an estimator β̂^p of β by Ŷ^p = β̂^p. Then p(β) ∝ exp{−(β − β̂^p)^T(η )(β − β̂^p)/(2n)} is the density of a normal distribution with mean β̂^p and a variance inversely proportional to η. Hence, the weight of the prior information increases as η increases. We shall revisit this observation in Section 3 when we investigate the pLASSO solution path with respect to η.

2.3.2 Logistic regression

Logistic regression fits each observation (X_i, Y_i) by a Bernoulli distribution with probability p(X_i) = P(Y_i = 1|X_i), where

$$p({\mathbf{X}}_i)=\frac{exp({\mathbf{Z}}_i^T\mathit{\beta })}{1+exp({\mathbf{Z}}_i^T\mathit{\beta })}.$$ (12)

The corresponding loss function is

$$L(\mathit{\beta };\mathbb{X},\mathbf{Y})=-\frac{1}{n}\sum _{i=1}^n[Y_{i}log\{p({\mathbf{X}}_i)\}+(1-Y_i)log\{1-p({\mathbf{X}}_i)\}],$$ (13)

which is obtained by setting b(θ) = log[1+exp(θ)] in (2). The prediction ${\widehat{Y}}_i^{\mathrm{p}}$ can be computed as ${\widehat{Y}}_i^{\mathrm{p}}=b^{\prime }({\mathbf{Z}}_i^T{\widehat{\mathit{\beta }}}^{\mathrm{p}})=exp({\mathbf{Z}}_i^T{\widehat{\beta }}^{\mathrm{p}})/[1+exp({\mathbf{Z}}_i^T{\widehat{\mathit{\beta }}}^{\mathrm{p}})]$. Following (7), the pLASSO criterion function for logistic regression is:

$$\begin{array}{l}{L}_{\lambda ,\eta }(\mathit{\beta };\mathbb{X},\mathbf{Y},{\widehat{\mathbf{Y}}}^{\mathrm{p}})=L(\mathit{\beta };\mathbb{X},\mathbf{Y})+\eta L(\mathit{\beta };\mathbb{X},{\widehat{\mathbf{Y}}}^{\mathrm{p}})+\lambda \sum _{j=1}^p\mid {\beta }_j\mid \\ \propto -\frac{1}{n}\sum _{i=1}^n[{\stackrel{\sim }{Y}}_{i}log\{p({\mathbf{X}}_i)\}+(1-{\stackrel{\sim }{Y}}_i)log\{1-p({\mathbf{X}}_i)\}]+\frac{\lambda }{1+\eta }\sum _{j=1}^p\mid {\beta }_j\mid ,\end{array}$$ (14)

where L is defined in (13) and Ỹ = (Ỹ₁, …, Ỹ_n)^T.

Note that each term Y_i log{p(X_i)} + (1 − Y_i) log{1 − p(X_i)} in L(β; , Y) is the KL distance between two Bernoulli distributions—Bernoulli(Y_i) and Bernoulli{p(X_i)}. Each term ${\widehat{Y}}_i^{\mathrm{p}}log\{p({\mathbf{X}}_i)\}+(1-{\widehat{Y}}_i^{\mathrm{p}})log\{1-p({\mathbf{X}}_i)\}$ in L(β; , Ŷ^p) is the KL distance between $\text{Bernoulli}({\widehat{Y}}_i^{\mathrm{p}})$ and Bernoulli{p(Xi)}. Alternatively, we can view the pLASSO criterion function as a LASSO criterion function with observations ${\{({\mathbf{X}}_i,{\stackrel{\sim }{Y}}_i)\}}_{i=1}^n$. Here, Ỹ_i ∈ [0, 1] can be regarded as the probability of Y_i = 1 obtained after adjusting the distribution Bernoulli(Y_i) using the prior information.

We note that the same KL distance has been used in Schapire et al. (2005) to incorporate prior information into the boosting classification algorithm. It is not surprising that it also works for logistic regression given the close connection between logistic regression and boosting as shown in Friedman et al. (2000). However, the goal and development of our method are obviously different from those in Schapire et al. (2005).

3 SOLUTION PATH

For linear regression, the geometric interpretation of the LASSO estimator provides a useful insight into the mechanism of LASSO, leading to the development of the LARS algorithm (Efron et al., 2004 ). The pLASSO solution would enjoy the same property of the LASSO solution regarding the change of λ for a given η. In this section, we show that the pLASSO estimator of (10) has a similar solution path with respect to the change of η for a given λ. This result allows us to fully characterize the local effect of incorporating the prior information into a LASSO problem.

Let G^λ,η = n⁻¹(1 + η) β̂^λ,η − n⁻¹ (Y + ηŶ^p) be the gradient evaluated at β = β̂^λ,η of the pLASSO criterion function in (10) excluding the L₁ penalty. Similar to Efron et al. (2004), β̂^λ,η and G^λ,η are continuous of both λ and η. Let be the current active set, i.e., ${\mathcal{A}}^{\lambda ,\eta }=\{j:{\widehat{\mathit{\beta }}}_j^{\lambda ,\eta }\ne 0\}$. The points of discontinuity of are denoted by {η₁, η₂, η₃, …} where 0 < η₁ < ··· < η_k < η_k+1 < ··· < ∞. Therefore, within the interval of η ∈ (η_k, η_k+1), = is a constant set. Finally, define = to be the submatrix of consisting of the columns in , and similarly ${\mathit{\beta }}_{{\mathcal{A}}_k}={(\cdots ,{\beta }_j,\cdots )}_{j\in {\mathcal{A}}_k}^T$ to be the subvector of β consisting of the elements in .

The necessary and sufficient conditions for β̂^λ,η to be a pLASSO estimator are that

$$\{\begin{array}{lllll}(\mathrm{C}1):\hfill & G_j^{\lambda ,\eta }\hfill & =\hfill & -\lambda \text{sign}({\widehat{\beta }}_j^{\lambda ,\eta }),\hfill & j\in {\mathcal{A}}^{\lambda ,\eta },\hfill \\ (\mathrm{C}2):\hfill & \mid G_j^{\lambda ,\eta }\mid \hfill & \le \hfill & \lambda ,\hfill & j\notin {\mathcal{A}}^{\lambda ,\eta }.\hfill \end{array}$$ (15)

From condition (C1) in (15), we have that

$$n^{-1}(1+\eta ){\mathbb{X}}_{{\mathcal{A}}_k}^T{\mathbb{X}}_{{\mathcal{A}}_k}{\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{\lambda ,\eta }-n^{-1}{\mathbb{X}}_{{\mathcal{A}}_k}^T(\mathbf{Y}+\eta {\widehat{\mathbf{Y}}}^{\mathrm{p}})=-\lambda \text{sign}({\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{\lambda ,\eta }),\eta \in ({\eta }_k,{\eta }_{k+1}).$$ (16)

Choose any η and η′ such that η_k < η′ < η < η_k+1. It follows that $\text{sign}({\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{\lambda ,\eta })=\text{sign}({\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{\lambda ,{\eta }^{\prime }})$ from the continuity of β̂^λ,η and the fact that does not change for η ∈ (η_k, η_k+1). Plugging η and η′ into (16) and then subtracting, we can solve the linear equation and obtain

$${\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{\lambda ,\eta }=\frac{1+{\eta }^{\prime }}{1+\eta }{\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{\lambda ,{\eta }^{\prime }}+\frac{\eta -{\eta }^{\prime }}{1+\eta }{({\mathbb{X}}_{{\mathcal{A}}_k}^T{\mathbb{X}}_{{\mathcal{A}}_k})}^{-1}{\mathbb{X}}_{{\mathcal{A}}_k}^T{\widehat{\mathbf{Y}}}^{\mathrm{p}}.$$

Let us define as the vector that satisfies ${\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{{\mathcal{A}}_k,\mathrm{p}}={({\mathbb{X}}_{{\mathcal{A}}_k}^T{\mathbb{X}}_{{\mathcal{A}}_k})}^{-1}{\mathbb{X}}_{{\mathcal{A}}_k}^T{\widehat{\mathbf{Y}}}^{\mathrm{p}}$ and ${\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k^c}^{{\mathcal{A}}_k,\mathrm{p}}=\mathbf{0}$. In fact, is the restricted least squares estimator with the response Ŷ^p and the design matrix restricted to the columns . By the continuity of β̂^λ,η, setting η′ → η_k leads to

$${\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{\lambda ,\eta }=\frac{1+{\eta }_k}{1+\eta }{\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{\lambda ,{\eta }_k}+\frac{\eta -{\eta }_k}{1+\eta }{\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{{\mathcal{A}}_k,\mathrm{p}},\eta \in ({\eta }_k,{\eta }_{k+1}).$$ (17)

Also note that ${\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k^c}^{\lambda ,{\eta }_k}={\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k^c}^{{\mathcal{A}}_k,\mathrm{p}}=\mathbf{0}$. We have proved the following theorem.

Theorem 1

For η ∈ (η_k, η_k+1), the pLASSO solution of (10) satisfies that

$${\widehat{\mathit{\beta }}}^{\lambda ,\eta }=\frac{1+{\eta }_k}{1+\eta }{\widehat{\mathit{\beta }}}^{\lambda ,{\eta }_k}+\frac{\eta -{\eta }_k}{1+\eta }{\widehat{\mathit{\beta }}}^{{\mathcal{A}}_k,\mathrm{p}}.$$

Theorem 1 implies that the pLASSO solution follows a piecewise smooth path with respect to the change of η. A similar solution path can be found in the proof of Lemma 4 in Meinshausen and Yu (2009). Their solution path was obtained by moving the response variable along the direction to the noise, which modifies only the linear term of β in the loss function. In our case, the change to the loss function with respect to η is slightly more complicated than their situation because both linear and quadratic terms of β are involved. As a consequence, the path of pLASSO in Theorem 1 is smooth, but not linear as in Meinshausen and Yu (2009).

To understand the pLASSO solution path better, we need to derive how the active set evolves with respect to the change of η. In light of the conditions in (15), for any given λ and η, the elements of an estimator β̂^λ,η can be partitioned into the following three non-overlapping groups,

$${\mathcal{J}}_1^{\lambda ,\eta }=\{j:{\widehat{\beta }}_j^{\lambda ,\eta }\ne 0,G_j^{\lambda ,\eta }=-\lambda \text{sign}({\widehat{\beta }}_j^{\lambda ,\eta })\},$$ (18)

$${\mathcal{J}}_2^{\lambda ,\eta }=\{j:{\widehat{\beta }}_j^{\lambda ,\eta }=0,\mid G_j^{\lambda ,\eta }\mid =\lambda \},$$ (19)

$${\mathcal{J}}_3^{\lambda ,\eta }=\{j:{\beta }_j^{\lambda ,\eta }=0,\mid G_j^{\lambda ,\eta }\mid <\lambda \}.$$ (20)

Obviously, ${\mathcal{J}}_1^{\lambda ,\eta }={\mathcal{A}}^{\lambda ,\eta }$. The following theorem fully characterizes the evolvement of the active set with the change of η.

Theorem 2

Assume the “one at a time” condition in Efron et al. (2004). Given λ > 0 and the current active set ,

1. η_k+1 = η and = \ {j} if and only if j enters ${\mathcal{J}}_2^{\lambda ,\eta }$ from ${\mathcal{J}}_1^{\lambda ,\eta }$ at η;

2. η_k+1 = η and = ∪ {j} if and only if j enters ${\mathcal{J}}_2^{\lambda ,\eta }$ from ${\mathcal{J}}_3^{\lambda ,\eta }$ at η.

The active set can increase or decrease as η increases. “One at a time” means that the increases and decreases never involve more than a single index j. The proof of Theorem 2 can be found in the Appendix. Theorems 1 and 2 present the whole picture of the solution path of the pLASSO estimator. This piecewise smooth path is different from the piecewise linear path as in LARS or the similar work by Rosset and Zhu (2007). It is also different from the differential equation-based solution path in Wu (2011). This unique solution path deepens our understanding of how the prior information is incorporated into the original LASSO problem locally.

Figure 1 shows an example of what the pLASSO solution path looks like. It is noteworthy that this solution path is limited to the linear regression setting. Also importantly, it is known that LARS, which is again a solution path algorithm, is not as efficient as some other algorithms such as the coordinate descent algorithm (Wu and Lange, 2008; Friedman et al., 2010). Hence, our presentation of the pLASSO solution path is purely to gain insight into how and why pLASSO works. In simulation and real data analysis, however, we use other algorithms that are more convenient.

Figure 1.

An Example of pLASSO Solution Path. This path is illustrated using the diabetes data in Efron et al. (2004), with η on the horizontal axis and coefficient estimates on the vertical axis. There are 10 predictors in the diabetes data, each of which is standardized to have a unit norm. We choose a prior set = {X₅, X₆, X₇, X₈}. λ is fixed at 316.07 with an initial set = {3, 4, 9}. Each vertical line in the plot represents a change of the active set, with the inclusion/deletion of a variable noted at the top of the plot, and the corresponding η value noted at the bottom. The last vertical line is hypothetical to show the limit of coefficients when η → ∞.

4 THEORETICAL PROPERTIES

This section mainly deals with the theoretical properties of pLASSO. In Section 4.1, we compare the asymptotic distributions of the LASSO and pLASSO estimators when p is fixed. In Section 4.2, we study the weak oracle property of pLASSO when p → ∞ and compare it with LASSO. In Section 4.3, we establish the oracle inequalities for excess risk and estimation error of pLASSO, and again compare them with existing results of LASSO.

4.1 Low-Dimensional Asymptotic Distribution

Assuming that the dimension p is fixed, we derive the asymptotic distribution of the pLASSO estimator and compare it with that of the LASSO estimator. The asymptotic distribution of the LASSO estimator is studied thoroughly by Knight and Fu (2000) in the linear regression setting. A similar result can be obtained in the framework of generalized linear models.

Without loss of generality, let ${\mathit{\beta }}_0={({\mathit{\beta }}_{1,0}^T,{\mathit{\beta }}_{2,0}^T)}^T$ be the true values of the parameters β with nonzero parameters β_1,0 = (β_0,0, β_1,0, …, β_s,0)^T and zero parameters β_2,0 = (β_s+1,0, …, β_p,0)^T = 0. Accordingly, write $\mathit{\beta }={({\mathit{\beta }}_1^T,{\mathit{\beta }}_2^T)}^T$, where β₁ = (β₀, β₁, …, β_s)^T and β₂ = (β_s+1, …, β_p)^T. Define

$$\begin{array}{l}\mathit{\mu }(\mathit{\beta })={[b^{\prime }({\mathbf{Z}}_1^T\mathit{\beta }),\dots ,b^{\prime }({\mathbf{Z}}_n^T\mathit{\beta })]}^T,\\ \mathbf{\sum }(\mathit{\beta })=\text{diag}[b^{″}({\mathbf{Z}}_1^T\mathit{\beta }),\dots ,b^{″}({\mathbf{Z}}_n^T\mathit{\beta })],\end{array}$$

and F(β) = Σ(β) with = (Z₁, …, Z_n)^T. In the definition of μ(β) and Σ(β), for linear regression (9), b′(θ) = θ and b″(θ) ≡ 1; for logistic regression (13), b′(θ) = exp(θ)/[1 + exp(θ)] and b″(θ) = exp(θ)/[1 + exp(θ)]².

Theorem 3 provides the asymptotic distribution of the LASSO estimator β̂^λ. This result is well known in the linear regression setting (Knight and Fu, 2000).

Theorem 3

Suppose $\sqrt{n}\lambda \to {\lambda }_0\ge 0$, F(β₀)/n → Ω with a positive definite matrix Ω, and $sup\{{\Vert \mathbf{F}(\mathit{\beta })/n-\mathbf{F}({\mathit{\beta }}_0)/n\Vert }_2:\sqrt{n}{\Vert \mathit{\beta }-{\mathit{\beta }}_0\Vert }_2\le \delta \}\to 0$ for any δ > 0. Let u ~ N(0, Ω), then the LASSO estimator β̂^λ follows that $\sqrt{n}({\widehat{\mathit{\beta }}}^{\lambda }-{\mathit{\beta }}_0){\to }_{d}argmin(V)$, where

$$V(\mathit{\varphi })=Q(\mathit{\varphi })+P_{{\lambda }_0}(\mathit{\varphi }).$$ (21)

In (21), Q and P_λ0 are defined as

$$\begin{array}{l}Q(\mathit{\varphi })={\mathit{\varphi }}^T\mathbf{\Omega }\mathit{\varphi }/2-{\mathbf{u}}^T\mathit{\varphi },\\ P_{{\lambda }_0}(\mathit{\varphi })={\lambda }_0\sum _{j=1}^p[{\varphi }_j\text{sign}({\beta }_{j,0})I({\beta }_{j,0}\ne 0)+\mid {\varphi }_j\mid I({\beta }_{j,0}=0)].\end{array}$$

In parallel, we will show that a similar result to the above theorem exists for pLASSO. To proceed, we need to be slightly more specific about how the prior information is summarized. As in Section 2.2, we use a prior set to indicate the set of those identified variables of potential importance. Then, a prior estimator β̂^p is obtained using (8), and the prior information is summarized into ${\widehat{Y}}_i^{\mathrm{p}}=b^{\prime }({\mathbf{Z}}_i^T{\widehat{\mathit{\beta }}}^{\mathrm{p}})$. Theorem 4 provides the asymptotic distribution of the pLASSO estimator β̂^λ,η when n → ∞.

Theorem 4

Suppose $\sqrt{n}\lambda \to {\lambda }_0\ge 0,\sqrt{n}\kappa \to {\kappa }_0\ge 0$, F(β₀)/n → Ω with a positive definite matrix Ω, and $sup\{{\Vert \mathbf{F}(\mathit{\beta })/n-\mathbf{F}({\mathit{\beta }}_0)/n\Vert }_2:\sqrt{n}{\Vert \mathit{\beta }-{\mathit{\beta }}_0\Vert }_2\le \delta \}\to 0$ for any δ > 0. Then, the pLASSO estimator β̂^λ,η follows that $\sqrt{n}({\widehat{\mathit{\beta }}}^{\lambda ,\eta }-{\mathit{\beta }}_0){\to }_{d}argmin(V)$, where

$$V(\mathit{\varphi })=(1+{\eta }_0){\mathit{\varphi }}^T\mathrm{\Omega }\mathit{\varphi }/2-{[argmin(Q)+{\eta }_{0}argmin(Q+P_{{\kappa }_0,{\mathcal{S}}^{\mathrm{p}}})]}^T\mathbf{\Omega }\mathit{\varphi }+P_{{\lambda }_0}(\mathit{\varphi })$$ (22)

when η → η₀ ≥ 0, and

$$V(\mathit{\varphi })=Q(\mathit{\varphi })+P_{{\kappa }_0,{\mathcal{S}}^{\mathrm{p}}}(\mathit{\varphi })$$ (23)

when η → ∞. In (22) and (23), Q and P_λ0 are defined as in Theorem 3, and is defined as

$$P_{{\kappa }_0,{\mathcal{S}}^{\mathrm{p}}}(\mathit{\varphi })={\kappa }_0\sum _{j=1}^p[{\varphi }_j\text{sign(}{\beta }_{j,0}\text{)}I({\beta }_{j,0}\ne 0)+\mid {\varphi }_j\mid I({\beta }_{j,0}=0)]I(X_j\notin {\mathcal{S}}^{\mathrm{p}}).$$

The influence of incorporating the prior information can be revealed by comparing the asymptotic distributions of the LASSO and pLASSO estimators. In the extreme case when η → ∞, the prior information dominates, and it is not surprising to observe that the asymptotic distribution of the pLASSO estimator is the same as the prior estimator as in (23). In the other extreme case when η → 0, the contribution of the prior information vanishes eventually so that the asymptotic distribution of the pLASSO estimator simplifies to that of the LASSO estimator.

The non-trivial situation arises when η → η₀ > 0. For simplicity, let’s assume λ₀ = 0, which implies that the L₁ penalization has a negligible effect asymptotically. This is a fair assumption as both (21) and (22) have the same term P_λ0(ϕ), which leads to

$$\sqrt{n}({\widehat{\mathit{\beta }}}^{\lambda }-{\mathit{\beta }}_0){\to }_{d}argmin(Q)={\mathbf{\Omega }}^{-1}\mathbf{u},$$ (24)

$$\sqrt{n}({\widehat{\mathit{\beta }}}^{\lambda ,\eta }-{\mathit{\beta }}_0){\to }_d\frac{1}{1+{\eta }_0}[argmin(Q)+{\eta }_{0}argmin(Q+P_{{\kappa }_0,{\mathcal{S}}^{\mathrm{p}}})].$$ (25)

Compared with the asymptotic form arg min(Q) of the LASSO estimator, the pLASSO estimator yields a sum of arg min(Q) and argmin(Q + ) weighted by the tuning parameter η₀. Certainly, whether arg min(Q + ) is an improvement or a degradation of arg min(Q) depends on the quality of the prior set as well as the extent (reflected by the parameter κ₀) to which we penalize the variables in ( )^c when constructing Ŷ^p.

Writing $\mathbf{\Omega }=\left[\begin{array}{cc}{\mathbf{\Omega }}_{11}& {\mathbf{\Omega }}_{12}\\ {\mathbf{\Omega }}_{21}& {\mathbf{\Omega }}_{22}\end{array}\right]$ by splitting the subscripts {0, 1, …, p} into {0, 1 …, s} and {s + 1, …, p}, we use the following two extreme cases for illustration. On the one hand, suppose that we happen to have the best prior set = {X₁, …, X_s} and we believe they are the only nonzero parameters by setting κ₀ large enough. It leads to that $argmin(Q+P_{{\kappa }_0,{\mathcal{S}}^{\mathrm{p}}})={[{({\mathbf{\Omega }}_{11}^{-1}{\mathbf{u}}_1)}^T,{\mathbf{0}}^T]}^T$ with $\mathbf{u}={({\mathbf{u}}_1^T,{\mathbf{u}}_2^T)}^T~N(\mathbf{0},\mathbf{\Omega })$. On the other hand, suppose that we have the worst prior set = {X_s+1, …, X_p}. This yields arg min(Q + ) = Ω⁻¹[u − κ₀sign(b)] with b = (0, β_1,0, …, β_s,0, 0, …, 0)^T and sign(0) = 0. These are the best and worst cases when we incorporate the prior information, while it is common to have an intermediate case in practice.

In the above two cases, the asymptotic distribution in (25) is respectively simplified into

$$\frac{1}{1+{\eta }_0}\left[{\mathbf{\Omega }}^{-1}\mathbf{u}+{\eta }_0\left(\begin{array}{c}{\mathbf{\Omega }}_{11}^{-1}{\mathbf{u}}_1\\ \mathbf{0}\end{array}\right)\right]~N\left[\mathbf{0},\frac{1}{{(1+{\eta }_0)}^2}{\mathbf{\Omega }}^{-1}\left\{\mathbf{\Omega }+(2{\eta }_0+{\eta }_0^2)\stackrel{\sim }{\mathbf{\Omega }}\right\}{\mathbf{\Omega }}^{-1}\right],$$ (26)

$$\frac{1}{1+{\eta }_0}[{\mathbf{\Omega }}^{-1}\mathbf{u}+{\eta }_0{\mathbf{\Omega }}^{-1}\{\mathbf{u}-{\kappa }_0\text{sign}(\mathbf{b})\}]~N\left[-\frac{{\eta }_0{\kappa }_0}{1+{\eta }_0}{\mathbf{\Omega }}^{-1}\text{sign}(\mathbf{b}),{\mathbf{\Omega }}^{-1}\right],$$ (27)

with $\stackrel{\sim }{\mathbf{\Omega }}=\left[\begin{array}{cc}{\mathbf{\Omega }}_{11}& {\mathbf{\Omega }}_{12}\\ {\mathbf{\Omega }}_{21}& {\mathbf{\Omega }}_{21}{\mathbf{\Omega }}_{11}^{-1}{\mathbf{\Omega }}_{12}\end{array}\right]$. In the best case (26), Ω − Ω̃ is non-negative definite because ${\mathbf{\Omega }}_{22}-{\mathbf{\Omega }}_{21}{\mathbf{\Omega }}_{11}^{-1}{\mathbf{\Omega }}_{12}$ is non-negative definite. Thus, the pLASSO estimator has a smaller asymptotic variance than the LASSO estimator by comparing (26) and (24). Both estimators are asymptotically unbiased. In the worst case (27), the LASSO and pLASSO estimators have the same asymptotic variance Ω⁻¹ but the pLASSO estimator becomes asymptotically biased. This result clearly illustrates the trade-off between variance reduction and increased bias depending on the quality of the prior information. It is also apparent from the asymptotic distributions in (26)–(27) that the theoretical choice of η depends on the quality of the prior information.

4.2 High-Dimensional Weak Oracle Property

Statistical properties of LASSO for high-dimensional data (p ≫ n) have been studied by many works, including Zhao and Yu (2006) for variable selection consistency, Meinshausen and Yu (2009) for estimation consistency, and Fan and Lv (2011) for weak oracle property. We focus on the weak oracle property of pLASSO in this subsection.

To provide a coherent comparison with the existing results, we adopt the same notation as in Fan and Lv (2011). Therefore, we do not include the intercept β₀ and set β = (β₁, …, β_p)^T as in Fan and Lv (2011). Slightly different from Section 4.1, β₁ = (β₁, …, β_s)^T and β₂ = (β_s+1, …, β_p)^T. This setting results in the following LASSO and pLASSO criterion functions:

$$L_{\lambda }(\mathit{\beta };\mathbb{X},\mathbf{Y})=-\frac{1}{n}\sum _{i=1}^n[Y_i{\mathbf{X}}_i^T\mathit{\beta }-b({\mathbf{X}}_i^T\mathit{\beta })]+\lambda {\Vert \mathit{\beta }\Vert }_1,$$ (28)

$$L_{\lambda ,\eta }(\mathit{\beta };\mathbb{X},\mathbf{Y},{\widehat{\mathbf{Y}}}^{\mathrm{p}})=-\frac{1}{n}\sum _{i=1}^n[Y_i{\mathbf{X}}_i^T\mathit{\beta }-b({\mathbf{X}}_i^T\mathit{\beta })]-\frac{\eta }{n}\sum _{i=1}^n[{\widehat{Y}}_i^{\mathrm{p}}{\mathbf{X}}_i^T\mathit{\beta }-b({\mathbf{X}}_i^T\mathit{\beta })]+\lambda {\Vert \mathit{\beta }\Vert }_1.$$ (29)

We review in the following the weak oracle property of LASSO in Fan and Lv (2011). Let and respectively be the submatrices of the design matrix = (x₁, …, x_p) formed by columns in the nonzero positions of β₀ and the complement. Without loss of generality we assume that each covariate x_j has been standardized so that ${\Vert {\mathbf{x}}_j\Vert }_2=\sqrt{n}$. Let d_n = 2⁻¹ min{|β_j,0| : β_j,0 ≠ 0}. Similar to Section 4.1, define

$$\begin{array}{l}\mathit{\mu }(\mathit{\beta })={[b^{\prime }({\mathbf{X}}_1^T\mathit{\beta }),\dots ,b^{\prime }({\mathbf{X}}_n^T\mathit{\beta })]}^T,\\ \mathbf{\sum }(\mathit{\beta })=\text{diag}[b^{″}({\mathbf{X}}_1^T\mathit{\beta }),\dots ,b^{″}({\mathbf{X}}_n^T\mathit{\beta })].\end{array}$$

Condition A: The design matrix satisfies that

$$\begin{array}{l}{\Vert {[{\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1]}^{-1}\Vert }_{\infty }=O(b_s{n}^{-1}),\\ {\Vert {\mathbb{X}}_2^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1{[{\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1]}^{-1}\Vert }_{\infty }\le C\in (0,1),\\ \underset{{\mathit{\beta }}_1\in {\mathcal{N}}_0}{max}\underset{1\le j\le p}{max}{\lambda }_{max}[{\mathbb{X}}_1^T\text{diag}\{\mid {\mathbf{x}}_j\mid \circ \mid {\mathit{\mu }}^{″}({({\mathit{\beta }}_1^T,{\mathbf{0}}^T)}^T)\mid \}{\mathbb{X}}_1]=O(n),\end{array}$$

where the L_∞ norm of a matrix is the maximum of the L₁ norm of each row, b_s is a diverging sequence of positive numbers depending on s, = {β₁ ∈ ℝ^s : ||β₁ − β_1,0||_∞ ≤ d_n}, and ∘ denotes the Hadamard product.

Condition B: Assume that d_n ≥ n^−γ log n and $b_s=o\{min(n^{1/2-\gamma }\sqrt{logn},s^{-1}{n}^{\gamma }/logn)\}$, for some γ ∈ (0, 1/2]. In addition, assume that λ satisfies $\lambda =o(b_s^{-1}{n}^{-\gamma }logn)$ and λ ≫ n^−α(log n)² with $\alpha =min(\frac{1}{2},2\gamma -{\alpha }_0)$, s = O(n^α₀), and α₀ < 1, and that ${max}_{1\le j\le p}{\Vert {\mathbf{x}}_j\Vert }_{\infty }=o(n^{\alpha }/\sqrt{logn})$ if the responses are unbounded.

Condition C: With a constant c₁ > 0, P(|a^TY − a^T μ(β₀)| > ||a||₂ε) ≤ 2e^−c₁ε2 where ε ∈ (0, ∞) if the responses are bounded and ε ∈ (0, ||a||₂/||a||_∞] if the responses are unbounded.

Conditions A–C are rewritten from Conditions 1–3 and the exponential bound (22) in Fan and Lv (2011), specifically for the LASSO situation. The following theorem is rewritten from Theorem 2 in that paper for the LASSO estimator.

Theorem 5

Assume that Conditions A–C are satisfied and log p = O(n^1−2α). Then, there exists a LASSO estimator β̂^λ such that with probability tending to one,

1. ${\widehat{\mathit{\beta }}}_2^{\lambda }=0$;

2. ${\Vert {\widehat{\mathit{\beta }}}_1^{\lambda }-{\mathit{\beta }}_{1,0}\Vert }_{\infty }\le n^{-\gamma }logn$, with γ defined in Condition B.

In comparison, we present a parallel result of the pLASSO estimator. Similar to the previous subsection, we assume that the prior information in pLASSO is captured by a prior estimator β̂^p so that ${\widehat{Y}}_i^{\mathrm{p}}=b^{\prime }({\mathbf{X}}_i^T{\widehat{\mathit{\beta }}}^{\mathrm{p}})$. We show that the weak oracle property can be achieved by imposing some extra conditions on the prior estimator (information).

Condition D: The prior estimator β̂^p satisfies that

$$\begin{array}{l}{\Vert {\widehat{\mathit{\beta }}}_1^{\mathrm{p}}-{\mathit{\beta }}_{1,0}\Vert }_{\infty }=o_P({\eta }^{-1}{n}^{-\gamma }logn),\\ {\Vert {\mathbb{X}}^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1({\widehat{\mathit{\beta }}}_1^{\mathrm{p}}-{\mathit{\beta }}_{1,0})\Vert }_{\infty }=o_P(n\lambda {\eta }^{-1}),\\ {\Vert {\mathbb{X}}^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_2{\widehat{\mathit{\beta }}}_2^{\mathrm{p}}\Vert }_{\infty }=o_P(n\lambda {\eta }^{-1}),\\ {\Vert {\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_2{\widehat{\mathit{\beta }}}_2^{\mathrm{p}}\Vert }_{\infty }=o_P(b_s^{-1}{\eta }^{-1}{n}^{1-\gamma }logn),\\ {\Vert {\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0\Vert }_2^2=o_P[min(\lambda {\eta }^{-1},b_s^{-1}{\eta }^{-1}{n}^{-\gamma }logn)],\end{array}$$

and that

$$\underset{\mathit{\beta }\in {\mathcal{N}}_0^{\mathrm{p}}}{max}\underset{1\le j\le p}{max}{\lambda }_{max}[{\mathbb{X}}^T\text{diag}\{\mid {\mathbf{x}}_j\mid \circ \mid {\mathit{\mu }}^{″}(\mathit{\beta })\mid \}\mathbb{X}]=O_P(n),$$

where ${\mathcal{N}}_0^{\mathrm{p}}$ is the line segment between β₀ and β̂^p.

Theorem 6

Assume that Conditions A–D are satisfied and log p = O(n^1−2α). Then, there exists a pLASSO estimator β̂^λ,η such that with probability tending to one,

1. ${\widehat{\mathit{\beta }}}_2^{\lambda ,\eta }=0$;

2. ${\Vert {\widehat{\mathit{\beta }}}_1^{\lambda ,\eta }-{\mathit{\beta }}_{1,0}\Vert }_{\infty }\le n^{-\gamma }logn/(1+\eta )$, with γ defined in Condition B.

It is obvious that η plays an important role in Condition D. All the conditions involved with η in Condition D have the same explanation: how much we should believe in the prior information (measured by η) depends on how well the prior estimator β̂^p performs. When η = 0, those conditions are automatically satisfied and the conclusion of Theorem 6 becomes identical to that of Theorem 5.

Theorem 6 implies that, if the prior information is reasonably reliable, the pLASSO estimator can achieve the same property of variable selection consistency as the LASSO estimator. In addition, the pLASSO possesses a lower L_∞-norm loss for the nonzero coefficients compared to the LASSO estimator, similar to what we concluded in Section 4.1 when the dimension p is fixed and low. Both theoretical conclusions show the improvement of efficiency of pLASSO over LASSO with reliable prior information.

4.3 Oracle Inequalities

In addition to statistical properties on variable selection and asymptotic distribution, a great deal of attention has been devoted to the oracle inequalities for the excess risk (prediction error) and/or estimation error of the LASSO estimator. In linear models, these results include Bunea et al. (2007) for prediction error of LASSO, Bickel et al. (2009) for prediction error of both LASSO and Dantzig selector as well as bounds on estimation error, and Koltchinskii et al. (2011) for a sharp oracle inequality of prediction error. Some parallel results have been developed for generalized linear models, including but not limited to, Van de Geer (2008), Bach (2010) and Kwemou (2012). In this subsection, we establish the oracle inequalities for pLASSO in the framework of generalized linear models, including its excess risk and estimation error.

We utilize the same notation as in Section 4.2. Specifically, the intercept β₀ is omitted, β₀ denotes the true values of the parameters β, and the pLASSO estimator β̂^λ,η is defined to be the minimizer of the criterion function (29). J(β) = {j ∈ {1, …, p} : β_j ≠ 0} denotes the subscript set of nonzero components of β and |J(β)| denotes the cardinality of J(β). Thus, from Section 4.2, J(β₀) = {1, …, s} and |J(β₀)| = s. In addition, we introduce the following notation:

$$\mathit{\epsilon }={({\epsilon }_1,\dots ,{\epsilon }_n)}^T=\mathbf{Y}-\mathit{\mu }({\mathit{\beta }}_0)\text{and}{\widehat{\mathit{\epsilon }}}^{\mathrm{p}}={({\widehat{\epsilon }}_1^{\mathrm{p}},\dots ,{\widehat{\epsilon }}_n^{\mathrm{p}})}^T={\widehat{\mathbf{Y}}}^{\mathrm{p}}-\mathit{\mu }({\mathit{\beta }}_0),$$ (30)

where $\mathit{\mu }({\mathit{\beta }}_0)={[b^{\prime }({\mathbf{X}}_1^T{\mathit{\beta }}_0),\dots ,b^{\prime }({\mathbf{X}}_n^T{\mathit{\beta }}_0)]}^T$ as in Sections 4.1–4.2.

Following Van de Geer (2008), the excess risk of an estimator β̂ in a generalized linear model is defined as

$$\mathcal{E}(\widehat{\mathit{\beta }})=R(\widehat{\mathit{\beta }})-R({\mathit{\beta }}_0)=L[\widehat{\mathit{\beta }};\mathbb{X},\mathit{\mu }({\mathit{\beta }}_0)]-L[{\mathit{\beta }}_0;\mathbb{X},\mathit{\mu }({\mathit{\beta }}_0)].$$ (31)

Before presenting the main result, let us review the restricted eigenvalue condition in Bickel et al. (2009) as follows.

Condition RE(r, c₀): For some integer r such that 1 ≤ r ≤ p and a positive number c₀, the following condition holds:

$$\kappa (r,c_0)=\underset{\begin{array}{c}J\subseteq \{1,\dots ,p\},\\ \mid J\mid \le r\end{array}}{min}\underset{\begin{array}{l}\mathit{\delta }\in {ℝ}^p,\mathit{\delta }\ne 0,\\ {\Vert {\mathit{\delta }}_{J^c}\Vert }_1\le c_0{\Vert {\mathit{\delta }}_J\Vert }_1\end{array}}{min}\frac{{\Vert \mathbb{X}\mathit{\delta }\Vert }_2}{\sqrt{n}{\Vert {\mathit{\delta }}_J\Vert }_2}>0.$$

Moreover, we impose two other regularity conditions.

Condition E: Assume that sup_{n≥1,1≤i≤n} ||X_i||_∞ < ∞. Moreover, there exists a constant M > 0 such that sup_{n≥1,1≤i≤n} E(|ε_i|^m) ≤ m!M^m for m = 2, 3, 4, ….

Condition F: The parameter space under consideration is restricted to ${\mathbb{B}}_{\delta }=\{\mathit{\beta }\in {ℝ}^p:{min}_{1\le i\le n}{min}_{0\le t\le 1}{b}^{″}({\mathbf{X}}_i^T[(1-t){\mathit{\beta }}_0+t\mathit{\beta }])\ge 2\delta \}$ for a constant δ > 0.

The first part of Condition E was employed by Kwemou (2012) when they derived oracle inequalities for LASSO. The second part of Condition E, justified by Jiang and Zhang (2013), is used here to control the probability with which the oracle inequalities hold, by applying Bernstein’s inequality [e.g., Lemma 2.2.11 in van der Vaart and Wellner (1996)]. It is noteworthy that this condition is automatically satisfied in logistic regression. Condition F essentially imposes a uniform lower bound on the function b″(·), and it depends on the function b. For linear regression, the lower bound is automatically satisfied as b″(·) ≡ 1 so = ℝ^p when we choose any δ ≤ 1/2. For logistic regression, b″(θ) = exp(θ)/[1 + exp(θ)]². Intuitively, Condition F enforces that the probabilities of the Bernoulli variables are uniformly bounded away from 0 and 1. Rigorously speaking, Condition F requires that δ < 1/8, and ${\mathbf{X}}_i^T{\mathit{\beta }}_0$ and ${\mathbf{X}}_i^T\mathit{\beta }$ are uniformly bounded by the interval $[log\{(1-\sqrt{1-8\delta })/(4\delta )-1\},log\{(1+\sqrt{1-8\delta })/(4\delta )-1\}]$ for 1 ≤ i ≤ n. When δ → 0, this interval tends to ℝ so → ℝ^p. For Poisson regression, b″(θ) = exp(θ), and Condition F is satisfied as long as ${\mathbf{X}}_i^T{\mathit{\beta }}_0\ge log(2\delta )$ and ${\mathbf{X}}_i^T\mathit{\beta }\ge log(2\delta )$ for 1 ≤ i ≤ n. Again, when δ → 0, log(2δ) → − ∞ and thus → ℝ^p.

Theorem 7

Fix a constant φ > 0 and an integer 1 ≤ r ≤ p. Let Condition RE(r, 3+4/φ) be satisfied. Assume that log p = o(n). Suppose b(·) in (29) is twice continuously differentiable with b″(·) > 0. Let $\lambda =A{n}^{-1/2}(\sqrt{logp}+\eta B_{{\widehat{\mathit{\epsilon }}}^{\mathrm{p}}})$ for a large enough constant A > 0 and B_ε̂^p = n^−1/2|| ε̂^p||_∞. Under Conditions E and F, with probability tending to one, the pLASSO estimator β̂^λ,η satisfies

$$\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })\le (1+\phi )\underset{\begin{array}{l}\mathit{\beta }\in {\mathbb{B}}_{\delta }\\ J(\mathit{\beta })\le r\end{array}}{inf}\left\{\mathcal{E}(\mathit{\beta })+\frac{2C(\phi )A^2}{\delta {\kappa }^2(r,3+4/\phi )}\mid J(\mathit{\beta })\mid \left[\frac{1}{(1+{\eta }^2)}\frac{logp}{n}+\frac{{\eta }^2}{{(1+\eta )}^2}\frac{B_{{\widehat{\mathit{\epsilon }}}^{\mathrm{p}}}^2}{n}\right]\right\},$$ (32)

with δ defined in Condition F and C(φ) = (2 + φ)²/[φ(1 + φ)].

Theorem 7 provides a general oracle inequality for the excess risk of the pLASSO estimator. This result is parallel to those for LASSO, such as Theorem 2.1 in Van de Geer (2008). Compared to the well known oracle rate r_LASSO = |J(β)|log p/n for the LASSO estimator (Van de Geer, 2008; Bickel et al., 2009 ), the rate of pLASSO’s excess risk has two components (by omitting the foregoing constants):

$$r_{\text{pLASSO},1}=\frac{1}{{(1+\eta )}^2}\frac{\mid J(\mathit{\beta })\mid logp}{n}\text{and}{r}_{\text{pLASSO},2}=\frac{{\eta }^2}{{(1+\eta )}^2}\frac{\mid J(\mathit{\beta })\mid B_{{\widehat{\mathit{\epsilon }}}^{\mathrm{p}}}^2}{n}.$$

r_pLASSO,1 is a fraction of r_LASSO, and r_pLASSO,2 depends on the prediction error of the prior estimator ε̂^p = Ŷ^p − μ(β₀).

Clearly, the result illustrates the trade-off between the variance reduction by incorporating the correct prior information and the additive bias due to the prior error, exactly in the same spirit as in Sections 4.1–4.2. On the one hand, let’s consider the situation when the prior information has a high quality. Take linear regression as an example where ε₁, …, ε_n independently follow an identical normal distribution. Suppose we know the support of β₀, then the best prior estimator is the oracle estimator ${\widehat{\mathit{\beta }}}^{\mathrm{p}}={[{({\widehat{\mathit{\beta }}}_1^{\mathrm{p}})}^T,{\mathbf{0}}^T]}^T$ with ${\widehat{\mathit{\beta }}}_1^{\mathrm{p}}={({\mathbb{X}}_1^T{\mathbb{X}}_1)}^{-1}{\mathbb{X}}_1^T\mathbf{Y}$. In this case, ${\widehat{\mathit{\epsilon }}}^{\mathrm{p}}={\mathbb{X}}_1{({\mathbb{X}}_1^T{\mathbb{X}}_1)}^{-1}{\mathbb{X}}_1^T\mathit{\epsilon }$, so we have

$$B_{{\widehat{\mathit{\epsilon }}}^{\mathrm{p}}}=n^{-1/2}{\Vert {\mathbb{X}}^T{\mathbb{X}}_1{({\mathbb{X}}_1^T{\mathbb{X}}_1)}^{-1}{\mathbb{X}}_1^T\mathit{\epsilon }\Vert }_{\infty }=n^{-1/2}max({\Vert {\mathbb{X}}_1^T\mathit{\epsilon }\Vert }_{\infty },{\Vert {\mathbb{X}}_2^T{\mathbb{X}}_1{({\mathbb{X}}_1^T{\mathbb{X}}_1)}^{-1}{\mathbb{X}}_1^T\mathit{\epsilon }\Vert }_{\infty }).$$

Firstly, the Bernstein’s inequality [Lemma 2.2.11 in van der Vaart and Wellner (1996)] leads to $n^{-1/2}{\Vert {\mathbb{X}}_1^T\mathit{\epsilon }\Vert }_{\infty }=O_P(\sqrt{logs})$. Secondly, noticing that a^Tε follows a normal distribution for any vector a satisfying ||a||₂ = 1, it is easy to verify that

$$n^{-1/2}{\Vert {\mathbb{X}}_2^T{\mathbb{X}}_1{({\mathbb{X}}_1^T{\mathbb{X}}_1)}^{-1}{\mathbb{X}}_1^T\mathit{\epsilon }\Vert }_{\infty }=n^{-1/2}\underset{j\notin J({\mathit{\beta }}_0)}{max}{\Vert {\mathbf{\Pi }}_1{\mathbf{x}}_j\Vert }_2{O}_P[\sqrt{log(p-s)}],$$

where ${\mathbf{\Pi }}_1={\mathbb{X}}_1{({\mathbb{X}}_1^T{\mathbb{X}}_1)}^{-1}{\mathbb{X}}_1^T$. Therefore, $B_{{\widehat{\mathit{\epsilon }}}^{\mathrm{p}}}^2$ can have a much smaller order than log p with a large probability [depending on the maximum L₂ norm of the projections of x_j, j ∉ ∈ J(β₀), on the space spanned by ], then the pLASSO excess risk rate is only a fraction of the LASSO rate. On the other hand, if the prior information is not reliable, a small choice of η will control the additional excess risk caused by the wrong information.

Following Theorem 7, Corollary 1 provides some specific oracle inequalities for excess risk and estimation bias for the pLASSO estimator. Except the constants in the bounds, the rates are essentially the same as in (32). Therefore, Corollary 1 provides the same insight for us to better understand the pLASSO method.

Corollary 1

Assume the same conditions as in Theorem 7, except that Condition RE(r, 3+ 4/φ) is replaced by Condition RE(s, 3). Then, with probability tending to one, the pLASSO estimator β̂^λ,η satisfies

$$\begin{array}{r}\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })\le \frac{8A^2}{\delta {\kappa }^2(s,3)}s\left[\frac{1}{{(1+\eta )}^2}\frac{logp}{n}+\frac{{\eta }^2}{{(1+\eta )}^2}\frac{B_{{\widehat{\mathit{\epsilon }}}^{\mathrm{p}}}^2}{n}\right],\\ \frac{1}{n}{\Vert \mathbb{X}{\widehat{\mathit{\beta }}}^{\lambda ,\eta }-\mathbb{X}{\mathit{\beta }}_0\Vert }_2^2\le \frac{8A^2}{{\delta }^2{\kappa }^2(s,3)}s\left[\frac{1}{{(1+\eta )}^2}\frac{logp}{n}+\frac{{\eta }^2}{{(1+\eta )}^2}\frac{B_{{\widehat{\mathit{\epsilon }}}^{\mathrm{p}}}^2}{n}\right],\\ {\Vert {\widehat{\mathit{\beta }}}^{\lambda ,\eta }-{\mathit{\beta }}_0\Vert }_1^2\le \frac{128A^2}{{\delta }^2{\kappa }^4(s,3)}{s}^2\left[\frac{1}{{(1+\eta )}^2}\frac{logp}{n}+\frac{{\eta }^2}{{(1+\eta )}^2}\frac{B_{{\widehat{\mathit{\epsilon }}}^{\mathrm{p}}}^2}{n}\right].\end{array}$$

5 SIMULATION

5.1 Unweighted Penalization Methods

In this subsection, we perform simulation studies to compare the following three estimators: the LASSO estimator β̂^λ without using any prior information as in (3), the prior estimator β̂^p which fully trusts the prior information, and our proposed pLASSO estimator β̂^λ,η which incorporates the prior information into LASSO as in (6). All three methods use L₁-norm penalty, so we refer to them as unweighted penalization methods in contrast to those in Section 5.2.

As in Section 2.3, we utilize both linear regression and logistic regression in our simulations. For linear regression, the training data are generated from the following model:

$$\mathbf{X}~N(\mathbf{0},\mathbf{\sum }),Y~N({\mathbf{X}}^T{\mathit{\beta }}_0,{\sigma }^2),$$ (33)

where Σ = (σ_ij) with σ_ij = ρ^|i−j|, i, j = 1, …, p. In (33), we fix ρ = 0.5, σ = 1, and β₀ = (−0.5, −2, 0.5, 2, −1.5, 1, 2, −1.5, 2, −2, 1, 1.5, −2, 1, 1.5, 0, …, 0)^T, with X₁, …, X₁₅ relevant to the response.

With the same β₀ and Σ, the training data are generated from the following model for logistic regression:

$$\mathbf{X}~N(\mathbf{0},\mathbf{\sum }),Y~\text{Bernoulli}[{\text{logit}}^{-1}({\mathbf{X}}^T{\mathit{\beta }}_0)].$$ (34)

It is noteworthy that the above design matrix X has the so-called “power decay correlation.” It has been shown in Corollary 3 of Zhao and Yu (2006) that X satisfies the strong irrepresentable condition in linear regression, which is our main condition for the weak oracle property (the second condition of Condition A in Section 4.2). Moreover, X also satisfies the restricted eigenvalue condition in Bickel et al. (2009) with a large probability, which is our main condition for the oracle inequalities [Condition RE(r, c₀) in Section 4.3 ]. For details, we refer to Example 1 in Raskutti et al. (2010).

In the above models, we set n = 200, p = 1000 in (33), and n = 200, p = 400 in (34). We adopt the form of prior information introduced in Section 2.2. A subset of explanatory variables is provided and the criterion function in (8) is used to estimate β̂^p. In our computation, twelve different sets are used for comparison, classified in four groups:

$$\begin{array}{l}{\mathcal{G}}_1:{\mathcal{S}}_1^{\mathrm{p}}=\{X_1,\dots ,X_5\},{\mathcal{S}}_2^{\mathrm{p}}=\{X_1,\dots ,X_{10}\},{\mathcal{S}}_3^{\mathrm{p}}=\{X_1,\dots ,X_{15}\};\\ {\mathcal{G}}_2:{\mathcal{S}}_4^{\mathrm{p}}=\{X_{16},\dots ,X_{20}\},{\mathcal{S}}_5^{\mathrm{p}}=\{X_{16},\dots ,X_{40}\},{\mathcal{S}}_6^{\mathrm{p}}=\{X_{16},\dots ,X_{60}\};\\ {\mathcal{G}}_3:{\mathcal{S}}_7^{\mathrm{p}}={\mathcal{S}}_2^{\mathrm{p}}\cup \{X_{16},\dots ,X_{18}\},{\mathcal{S}}_8^{\mathrm{p}}={\mathcal{S}}_2^{\mathrm{p}}\cup \{X_{16},\dots ,X_{20}\},{\mathcal{S}}_9^{\mathrm{p}}={\mathcal{S}}_2^{\mathrm{p}}\cup \{X_{16},\dots ,X_{22}\};\\ {\mathcal{G}}_4:{\mathcal{S}}_{10}^{\mathrm{p}}=\{X_1,\dots ,X_3\}\cup {\mathcal{S}}_6^{\mathrm{p}},{\mathcal{S}}_{11}^{\mathrm{p}}=\{X_1,\dots ,X_5\}\cup {\mathcal{S}}_6^{\mathrm{p}},{\mathcal{S}}_{12}^{\mathrm{p}}=\{X_1,\dots ,X_7\}\cup {\mathcal{S}}_6^{\mathrm{p}}.\end{array}$$

The sets in the first and second groups ( and ) respectively consist of all relevant and irrelevant predictors only. The sets in the third and fourth groups ( and ) are mixed with relevant and irrelevant variables. The relevant predictors dominate the sets in the third group while the irrelevant predictors dominate the sets in the fourth group .

We use the coordinate descent algorithm developed by Friedman et al. (2010) and the algorithm from Meier et al. (2008) for our linear regression setting and logistic regression setting, respectively. After an estimator is obtained, it is further refitted using only those selected predictors to improve the estimation/prediction accuracy. The tuning parameters λ and η are selected by a 3-fold cross validation to maximize the average empirical likelihood. Specifically, for the selection of λ, we adopt the “one standard error rule” (Breiman et al., 1984) to achieve a more parsimonious model. That is, the parameter λ is selected to be the largest possible which gives an average empirical likelihood within one standard error from the highest average empirical likelihood. The standard error is estimated from the three folds in cross validation. With an independently simulated test set of the same size as the training set, the following criteria are used to assess the performance of an estimator in the setting of linear regression:

1. #CNZ, #INZ: the number of variables that are correctly and incorrectly selected, respectively;

2. Bias: the L₁ norm bias of an estimator for the nonzero coefficients;

3. MSR: the mean squared residuals of an estimator evaluated on the test data.

   In addition to (a) and (b), the following criteria are used to assess the performance of an estimator in the setting of logistic regression:

4. ME: the model error defined as E_X[{logit⁻¹(X^Tβ̂) − logit⁻¹(X^Tβ₀)}²]. RME: the relative model error as the ratio of the model error to that of the LASSO estimator. In our simulation, the model error is approximated by the empirical average using the test set;

5. MR: the misclassification rate of the classifier induced by an estimator, evaluated on the test data.

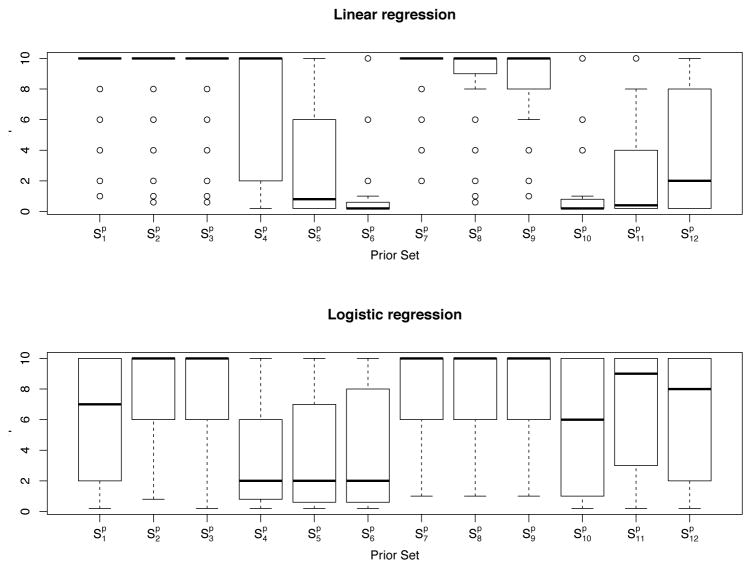
Therefore, criteria (a)–(c) apply to linear regression, while criteria (a), (b), (d) and (e) apply to logistic regression. In summary, the criteria in (a) consider the variable selection property of an estimator; criteria (b) and (d) take into account its estimation property; and criteria (c) and (e) evaluate its prediction performance on the test data. For each choice of , 100 training/test data sets are generated from each model. Figures 2–3 provide the boxplots of the criteria (a)–(c) for linear regression from the 100 runs; Figures 4–5 provide the boxplots of the criteria (a), (b), (d) and (e) for logistic regression. In the figures, we denote the three methods by LASSO, p, and pLASSO, respectively. In addition, we report the optimal selection of η by pLASSO from the 100 runs in Figure 6.

Figure 2.

Simulation results of unweighted penalization methods for linear regression. Rows 1–3 correspond to prior sets ${\mathcal{S}}_1^{\mathrm{p}}-{\mathcal{S}}_3^{\mathrm{p}}$ in respectively, and rows 4–6 correspond to prior sets ${\mathcal{S}}_4^{\mathrm{p}}-{\mathcal{S}}_6^{\mathrm{p}}$ in respectively. Columns 1–4 correspond to #CNZ, #INZ, Bias and MSR, respectively.

Figure 3.

Simulation results of unweighted penalization methods for linear regression. Rows 1–3 correspond to prior sets ${\mathcal{S}}_7^{\mathrm{p}}-{\mathcal{S}}_9^{\mathrm{p}}$ in respectively, and rows 4–6 correspond to prior sets ${\mathcal{S}}_{10}^{\mathrm{p}}-{\mathcal{S}}_{12}^{\mathrm{p}}$ in respectively. Columns 1–4 correspond to #CNZ, #INZ, Bias and MSR, respectively.

Figure 4.

Simulation results of unweighted penalization methods for logistic regression. Rows 1–3 correspond to prior sets ${\mathcal{S}}_1^{\mathrm{p}}-{\mathcal{S}}_3^{\mathrm{p}}$ in respectively, and rows 4–6 correspond to prior sets ${\mathcal{S}}_4^{\mathrm{p}}-{\mathcal{S}}_6^{\mathrm{p}}$ in respectively. Columns 1–5 correspond to #CNZ, #INZ, Bias, RME and MR, respectively.

Figure 5.

Simulation results of unweighted penalization methods for logistic regression. Rows 1–3 correspond to prior sets ${\mathcal{S}}_7^{\mathrm{p}}-{\mathcal{S}}_9^{\mathrm{p}}$ in respectively, and rows 4–6 correspond to prior sets ${\mathcal{S}}_{10}^{\mathrm{p}}-{\mathcal{S}}_{12}^{\mathrm{p}}$ in respectively. Columns 1–5 correspond to #CNZ, #INZ, Bias, RME and MR, respectively.

Figure 6.

Optimal selection of the tuning parameter η by pLASSO in linear regression (upper panel) and logistic regression (lower panel).

In the case where includes only the relevant variables (group ), the prior estimator performs the best among the three methods: it selects the most variables correctly and the fewest variables incorrectly; it also yields the lowest estimation bias (and/or smallest model error) and the smallest mean squared residuals (or misclassification rate). Moreover, pLASSO behaves better than LASSO in most criteria we have examined. However, pLASSO includes a similar (or even a larger) number of irrelevant variables to LASSO. For more discussion about this, we refer to Section 5.2 and the Discussion section.

In the other case where includes only irrelevant variables (group ), the prior estimator performs the worst, especially since it selects all those wrong variables in the prior set. pLASSO and LASSO are also better in identifying relevant variables. In terms of estimation bias and prediction accuracy, pLASSO performs comparably with LASSO, with a clear advantage over the prior estimator.

When the prior set includes a mixture of relevant variables and irrelevant variables (groups and ), the numerical performance depends on the “quality” of the prior set. On the one hand, benefitted from the higher-quality prior information in , the prior estimator and pLASSO reduce the estimation bias (and/or model error) and yield a better prediction on the test data. They also correctly include more relevant variables in the model. On the other hand, the lower-quality prior information in forces the prior estimator to select all irrelevant variables in the prior set, not as appealing as LASSO or pLASSO. LASSO and pLASSO perform similarly with a lower estimation bias and more accurate prediction than the prior estimator.

In terms of the tuning parameter η, it is clearly seen from Figure 6 that the optimal selection of η conform with our intuition. In group , the tuning parameter η is usually selected at the highest value we set; while the optimal η is much smaller in group . For groups that have both relevant and irrelevant variables, η is selected at higher values in than in , since there are more relevant variables in and more irrelevant variables in .

In summary, the prior and LASSO estimators are the preferred choices when the prior information is of high and low quality, respectively. However, they are not very robust and can perform poorly in some other situations. The pLASSO method is a more robust choice regardless of the quality of the prior information.

5.2 Weighted Penalization Methods

Now, we include the adaptive LASSO method (Zou, 2006) in our simulation studies. Adaptive LASSO is a weighted penalization method which uses an initial estimator β^initial to weight the L₁ penalties. In our context, the adaptive LASSO estimator minimizes the following criterion function:

$$-\frac{1}{n}\sum _{i=1}^n[Y_i{\mathbf{Z}}_i^T\mathit{\beta }-b({\mathbf{Z}}_i^T\mathit{\beta })]+\lambda \sum _{j=1}^p\frac{\mid {\beta }_j\mid }{1+\tau \mid {\beta }_j^{\text{initial}}\mid },$$ (35)

where λ and τ are tuning parameters. A referee suggested we investigate the case where the initial estimator is the prior estimator β̂^p.

For a more comprehensive and fair comparison, we also include the cases where the initial estimator is chosen to be the LASSO and pLASSO estimator. Altogether, we have three weighted penalization methods to compare, which respectively use β̂^λ, β̂^p and β̂^λ,η as initial estimators. For convenience, we refer to them as LASSO-A, p-A and pLASSO-A.

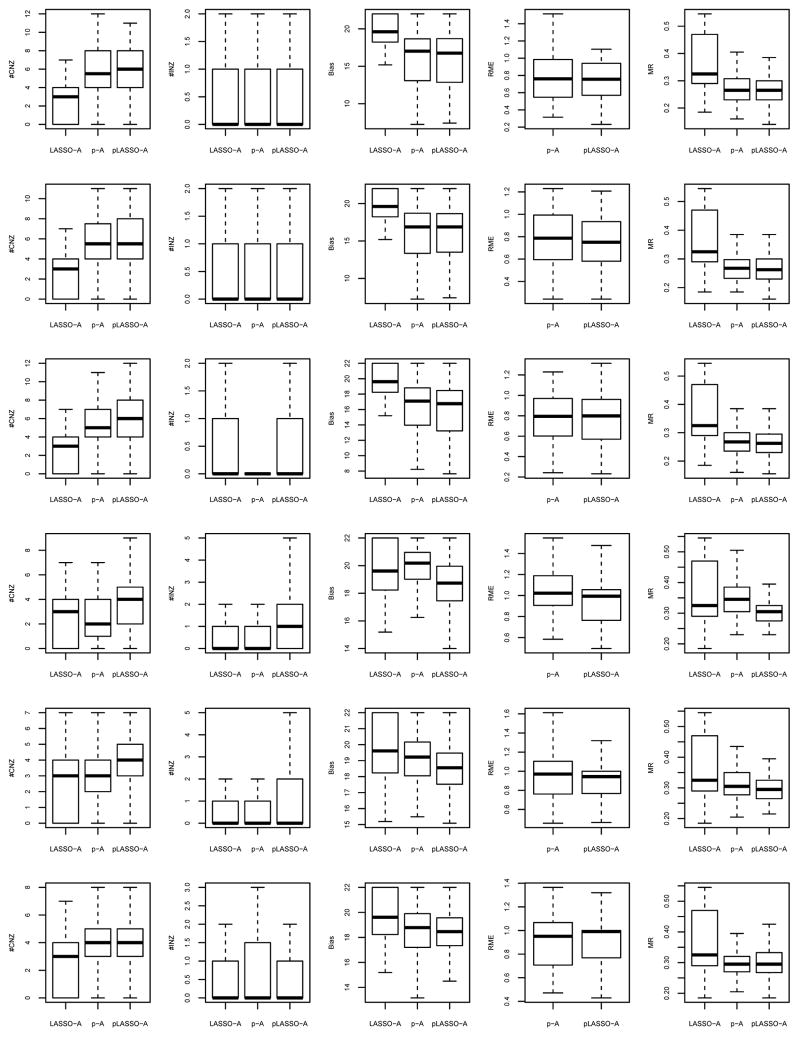
The simulation settings and computational algorithms utilized in this subsection are almost the same as in Section 5.1. Thus, we only point out the differences here. The tuning parameters (including λ and τ) are still optimized using 3-fold cross validation. The relative model error (RME) of the p-A/pLASSO-A estimator is defined to be the ratio of the model error to that of the LASSO-A estimator. Except this minor difference, the criteria used to compare among methods are exactly the same as those in Section 5.1. Figures 7–8 provide the boxplots of the criteria (a) – (c) for linear regression from the 100 runs; Figures 9–10 provide the boxplots of the criteria (a), (b), (d) and (e) for logistic regression.

Figure 7.

Simulation results of weighted penalization methods for linear regression. Rows 1–3 correspond to prior sets ${\mathcal{S}}_1^{\mathrm{p}}-{\mathcal{S}}_3^{\mathrm{p}}$ in respectively, and rows 4–6 correspond to prior sets ${\mathcal{S}}_4^{\mathrm{p}}-{\mathcal{S}}_6^{\mathrm{p}}$ in respectively. Columns 1–4 correspond to #CNZ, #INZ, Bias and MSR, respectively.

Figure 8.

Simulation results of weighted penalization methods for linear regression. Rows 1–3 correspond to prior sets ${\mathcal{S}}_7^{\mathrm{p}}-{\mathcal{S}}_9^{\mathrm{p}}$ in respectively, and rows 4–6 correspond to prior sets ${\mathcal{S}}_{10}^{\mathrm{p}}-{\mathcal{S}}_{12}^{\mathrm{p}}$ in respectively. Columns 1–4 correspond to #CNZ, #INZ, Bias and MSR, respectively.

Figure 9.

Simulation results of weighted penalization methods for logistic regression. Rows 1–3 correspond to prior sets ${\mathcal{S}}_1^{\mathrm{p}}-{\mathcal{S}}_3^{\mathrm{p}}$ in respectively, and rows 4–6 correspond to prior sets ${\mathcal{S}}_4^{\mathrm{p}}-{\mathcal{S}}_6^{\mathrm{p}}$ in respectively. Columns 1–5 correspond to #CNZ, #INZ, Bias, RME and MR, respectively.

Figure 10.

Simulation results of weighted penalization methods for logistic regression. Rows 1–3 correspond to prior sets ${\mathcal{S}}_7^{\mathrm{p}}-{\mathcal{S}}_9^{\mathrm{p}}$ in respectively, and rows 4–6 correspond to prior sets ${\mathcal{S}}_{10}^{\mathrm{p}}-{\mathcal{S}}_{12}^{\mathrm{p}}$ in respectively. Columns 1–5 correspond to #CNZ, #INZ, Bias, RME and MR, respectively.

Overall, the weighted penalization methods perform better than the unweighted penalization methods in the corresponding settings. The weighted L₁ penalty improves all unweighted penalization methods in terms of variable selection, as well as estimation and prediction. It is noteworthy that pLASSO-A performs much better than pLASSO for eliminating irrelevant variables. As follows, we focus on the comparison within three weighted penalization methods. Their relative performance follows similar trends to their unweighted counterparts, although the differences are less obvious.

When includes only the relevant variables (group ), p-A and pLASSO-A outperform LASSO-A in all criteria including variable selection, estimation and prediction. The difference gets larger when the prior set size gets larger.

When includes only the irrelevant variables (group ), p-A is not forced to include all the irrelevant variables in . However, its performance can still be affected by the wrong information, especially when there are many irrelevant variables in (e.g., rows 5–6 in Figure 7). In linear regression, LASSO-A and pLASSO-A exclude more irrelevant variables than p-A (e.g., rows 5–6 in Figure 7); while in logistic regression, the difference is not obvious (rows 4–6 in Figure 9). pLASSO-A also identifies more relevant variables than p-A. Moreover, LASSO-A and pLASSO-A outperform p-A in terms of the precision of the estimation and prediction.

When includes a mixture of relevant variables and irrelevant variables (groups and ), the numerical performance depends again on the quality of the prior set. The results from prior set groups and are similar to those from groups and , respectively. This is consistent to our observation in Section 5.1 for unweighted penalization methods.

6 REAL DATA ANALYSIS

In this section, we re-analyze the data from a study of bipolar disorder to illustrate how to carry out a real data analysis with pLASSO. Bipolar disorder is a serious and potentially life-threatening mood disorder (Merikangas et al., 2007). It is known that bipolar disorder has a substantial genetic component (Craddock and Forty, 2006). However, the underlying genetic mechanism of bipolar disorder remains elusive, despite significant research effort. There have been at least six genome-wide association studies reported in the literature so far (WTCCC, 2007; Baum et al., 2007; Ferreira et al., 2008; Scott et al., 2009; Sklar et al., 2008; Smith et al., 2009). While these studies revealed promising association signals, top findings from various studies do not show obvious overlap (Baum et al., 2008; Ollila et al., 2009).

In this work, we use the data collected in the Wellcome Trust Case Control Consortium (WTCCC) study as the primary data set. Then we choose the top findings from the other studies as prior information. Among the five prior studies, both Ferreira et al. (2008) and Scott et al. (2009) used meta-analysis by jointly analyzing an independently collected data set and the WTCCC data. Another study, Smith et al. (2009), focused on analyzing the data from two independent populations—individuals of European ancestry and individuals of African ancestry. Since we use the WTCCC data as the primary data and this data set includes only individuals of European ancestry, we do not utilize the results from the above three studies. Therefore, the other two studies—Baum et al. (2007) and Sklar et al. (2008)— serve as “previous” studies which provide us with prior information of potentially important variants for bipolar disorder. The following genes have been reported as top findings in these two studies: MYO5B, TSPAN8, EGFR, SORCS2, DFNB31, DGKH, VGCNL1, and NXN. In our context, we regard the SNPs in those genes as a previously identified set of variants whose information we can borrow in our current study. GeneALaCart (http://www.genecards.org/BatchQueries/index.php), the batch-querying platform of the GeneCards database, is used to extract the SNPs within these eight genes.

Certain quality control and prescreening procedures are performed before we carry out the association study for the WTCCC data. All SNPs with Minor Allele Frequency (MAF) less than 0.05 or failing the Hardy-Weinberg equilibrium test at p-value 0.0001 are excluded from further analysis. To reduce the computational burden, a univariate SNP analysis was performed to select a smaller set of SNPs that we are going to analyze with a regression model. Specifically, a covariate-adjusted (adjusted by age and gender) regression model using bipolar disorder as the response variable is run separately for each SNP after quality control. A SNP is included in the final analysis if either of the following two conditions is satisfied: (a) the p-value of the SNP from the logistic regression is smaller than 0.0001; (b) the SNP belongs to one of the eight previously identified genes and its logistic regression p-value is smaller than 0.1. With these selection criteria, the final data set in our analysis includes 916 SNPs in total, among which 174 SNPs compose the prior set as in Section 2.2. The tuning parameters λ and η in both LASSO and pLASSO are selected by a 3-fold cross validation, together with the “one standard error rule” for λ. The final model is fitted using the optimal choice of tuning parameters. The algorithm in Meier et al. (2008) is employed in this example.

From our final results, the optimal choice of η is selected to be 0.2 in pLASSO. Compared with the weight of 1 for the data part in (6), it indicates that pLASSO imposes a mild belief on the prior information by balancing the trade-off between the data and the prior information. The relatively small value of η partially supports the findings that various studies might not agree with each other in detecting the genetic factors underlying bipolar disorder (Baum et al., 2008; Ollila et al., 2009). However, it also gives us some evidence that the data can be better fitted by incorporating prior information to some extent. Therefore, compared with LASSO based on the data themselves, pLASSO has the flexibility of deciding whether or not and to what extent we should incorporate the previous findings in a current study. In addition, both pLASSO and LASSO select a small value of λ, resulting in a large final model for this data set. This observation supports the common belief that bipolar disorder is a complex disease with multiple genetic variants of small effect sizes.

In GWAS, researchers are often looking for a list of top SNPs ranked by statistical significance, which deserves further investigation. With penalized regression, researchers are using different criteria to rank the SNPs, including effect size (Cho et al., 2009), self-developed significance (Wu et al., 2009), etc. To keep our situation simple, we provide a list of top SNPs sorted by effect size from pLASSO and LASSO separately. We will compare how two methods affect the list. Table 1 provides the top twenty SNPs with the largest effect sizes, along with the gene in which each SNP is located or its nearest gene within a distance of 60 kb (Johnson and O’Donnell, 2009).

Table 1.

Real Data Results. Top 20 SNPs with the largest effect size from LASSO and pLASSO separately.

LASSO				pLASSO
SNP	Chr.	Gene	OR	SNP	Chr.	Gene	OR
Matched
rs2226284	1	LRRC7	1.51	rs2226284	1	LRRC7	1.30
rs6691577*	1	LRRC7	0.67	rs6691577*	1	LRRC7	0.77
rs4407218*	2	-	1.25	rs4407218*	2	-	1.18
rs10496366	2	-	0.81	rs10496366	2	-	0.85
rs12640371	4	-	1.26	rs12640371	4	-	1.20
rs4451017	5	-	1.28	rs4451017	5	-	1.22
rs10041150	5	-	1.24	rs10041150	5	-	1.17
rs2609653*	8	-	1.24	rs2609653*	8	-	1.17
rs884672	10	SORCS3	0.78	rs884672	10	SORCS3	0.84
rs10994548	10	RHOBTB1	0.81	rs10994548	10	RHOBTB1	0.85
rs659991	13	DGKH	1.28	rs659991	13	DGKH	1.32
rs7159947	14	PARP2	1.22	rs7159947	14	PARP2	1.17
rs7176592	15	C15orf23	1.24	rs7176592	15	C15orf23	1.18
rs12938916	17	MRPS23	1.36	rs12938916	17	MRPS23	1.28
rs2837588	21	DSCAM	1.24	rs2837588	21	DSCAM	1.18
Unmatched
rs6668411	1	DAB1	0.82	rs12472797	2	-	0.86
rs6895541	5	FBXL21	1.22	rs11103407	9	COL5A1	1.17
rs17053171	6	-	0.81	rs10982246*	9	DFNB31	0.86
rs6987445	8	-	1.22	rs17600642	10	ADAMTS14	1.17
rs4984405	15	-	1.22	rs6574988	14	-	1.17

The SNPs/genes in the prior set are in bold characters. Chr.: chromosome; Gene: within or nearby gene; OR: odds ratio estimate;

^*identified in WTCCC (2007) with a strong or moderate association with bipolar disorder.

It is seen that 15 SNPs are overlapping between these two lists, and they possess similar odds ratio estimates. This is due to the small choice of η from our calculation. In other words, two methods partially agree with each other when they are applied to the WTCCC data. It is also noteworthy that rs659991, a SNP in both two top lists, belongs to the gene DGKH which is one of the potential gene associated with bipolar disorder by Baum et al. (2007). This provides us with some evidence for the common genetic variants from the two studies (Baum et al., 2007; WTCCC, 2007).

There are 5 SNPs, however, in each list that are not matched between the two lists. This illustrates the effect of pLASSO compared with LASSO. In particular, one of the 5 unmatched SNPs selected by pLASSO, rs10982246, belongs to the gene DFNB31 as the previously identified information (Baum et al., 2007). Without considering the prior information, we would have missed this gene in the top findings solely by LASSO. Therefore, pLASSO provides a flexible framework to make analysis using information from multiple data sets.

It is also interesting to compare the results from multivariate analysis (LASSO/pLASSO) with univariate analysis in the original paper WTCCC (2007). As indicated in Table 1, some of our top SNPs/genes were identified to possess a strong or moderate association with bipolar disorder in WTCCC (2007). In summary, this example illustrates the applicability of pLASSO to, but not limited to, genetic studies. Certainly, our findings warrant further investigation, but we will leave this to our future work.

7 DISCUSSION

7.1 Summary

This paper presents pLASSO to incorporate prior information into penalized generalized linear models. pLASSO summarizes the prior information into an additional loss function term to achieve a balance between the prior information and the data, where the balance is controlled by a tuning parameter η. Notice that this is different from the elastic net method where the balance is between the L₁ and L₂ penalties (Zou and Hastie, 2005; Bunea, 2008). However, a shared feature is that neither the L₂ penalty nor our additional loss is meant to be standalone. Instead, they provide additional balance to improve the overall performance of the estimation process. Specifically, the L₂ penalty stabilizes the estimator and our additional loss increases its efficiency if the prior information is reliable.

Although we keep the settings simple, this represents the first attempt to examine such a scenario, to the best of our knowledge. A few comments are noteworthy. Firstly, the generalized linear models under consideration are coupled with the canonical link functions. Secondly, we keep the L₁ penalty as in LASSO and mainly compare pLASSO to LASSO but not other variable selection methods. We study both theoretically and empirically the effect of incorporating prior information by altering the loss function part. Both theoretical and numerical results show that pLASSO is more efficient when the prior information is of high quality, and is robust to the low quality prior information with a good choice of the tuning parameter η.

7.2 Tuning Parameters

For the choice of the tuning parameter η, we mainly investigate the performance of cross validation in our simulations. If incorporating the prior information improves the estimator’s performance, cross validation will pick a relatively large tuning parameter η to improve the efficiency of the resultant estimator. Otherwise, cross validation will select a small tuning parameter to maintain the estimator’s robustness. Simulation results support the effectiveness of cross validation for our purpose. Depending on the quality, pLASSO automatically incorporates the prior information to a proper extent and achieves estimation efficiency and prediction accuracy.

We should note that practical tuning methods, such as the cross validation used in our numerical studies, may not satisfy the conditions imposed on λ or η in our theory. Theoretical justification of practical tuning methods is known to be very challenging and remains to be an open problem, especially for high-dimensional data. We utilize a commonly-used practical tuning approach, and recognize that it is important to investigate this problem and pursue alternative approaches to selecting the tuning parameters. Methods that are computationally more efficient than cross-validation grid search are preferred and need to be pursued, e.g., the bisection method in Bunea and Barbu (2009).

7.3 pLASSO, LASSO, and adaptive LASSO

The distinction between pLASSO and LASSO is the additional loss function which measures the goodness of fit to the prior information (instead of the fit to the data in the usual loss function). Incorporating high-quality prior information will result in a more efficient estimator than LASSO, which is theoretically supported by a smaller asymptotic variance (Section 4.1), a smaller L_∞ loss (Section 4.2), and a lower excess risk rate (Section 4.3). It is also practically verified by simulations (Section 5.1). However, incorporating low-quality prior information will lead to the asymptotic bias (Section 4.1) or a higher excess risk rate (Section 4.3). Fortunately, we can adaptively select the tuning parameter η, making pLASSO robust to the low-quality prior information (Section 5.1).

Here, pLASSO only alters the loss function part but keeps the L₁ penalty exactly the same as in LASSO. In our numerical studies, pLASSO and adaptive LASSO does not dominate each other and have different advantages under different settings, and hence complement each other. Adaptive LASSO can incorporate the prior information into the penalty part through its adaptive weights, e.g., as in (35). It is interesting to explore in the future whether we can incorporate prior information into both loss and penalty so that estimation efficiency and variable selection advantage can be simultaneously achieved. We have made preliminary progress in investigating the combination of pLASSO and adaptive LASSO (i.e., pLASSOA) in our simulation studies (Section 5.2), and demonstrated its advantage over adaptive LASSO. However, this issue warrants further studies.

8 APPENDIX

8.1 Proof of Theorem 2

By the continuity of β̂^λ,η and G^λ,ηof η, it is impossible for the two groups ${\mathcal{J}}_1^{\lambda ,\eta }$ and ${\mathcal{J}}_3^{\lambda ,\eta }$ to exchange elements directly. Hence, any change of can only happen if ${\mathcal{J}}_2^{\lambda ,\eta }$ is not empty, and that single element in ${\mathcal{J}}_2^{\lambda ,\eta }$ will be the one either entering or deleted from . Therefore, the “only if” parts for (a) and (b) are straightforward. We focus on the “if” parts as follows.

For (a), it is seen from (17) that

$${\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{\lambda ,\eta }=\frac{1+{\eta }_k}{1+\eta }({\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{\lambda ,{\eta }_k}-{\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{{\mathcal{A}}_k,\mathrm{p}})+{\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{{\mathcal{A}}_k,\mathrm{p}},\eta \in ({\eta }_k,{\eta }_{k+1}).$$

So ${\widehat{\beta }}_j^{\lambda ,\eta }$ is a monotone function of η ∈ (η_k, η_k+1) for any j ∈ . Then if some j enters ${\mathcal{J}}_2^{\lambda ,\eta }$ from ${\mathcal{J}}_1^{\lambda ,\eta }$ at η, i.e., ${\widehat{\beta }}_j^{\lambda ,\eta }$ becomes 0 at η for some j ∈ , η must be a discontinuity point of . That is, η_k+1 = η. If not, η < η_k+1 and stays as . By the monotonicity, ${\widehat{\beta }}_j^{\lambda ,\eta }$ will change its sign, which is contradictive to the continuity of G^λ,η and the fact that $G_j^{\lambda ,\eta }=-\lambda \text{sign}({\widehat{\beta }}_j^{\lambda ,\eta })$ for any j ∈ . Moreover, since η_k+1 = η is proved, = \{j} is the only allowed change of .

For (b), by Theorem 1, we have that when η ∈ (η_k, η_k+1),

$$\begin{array}{l}{G}_{{\mathcal{A}}_k^c}^{\lambda ,\eta }=n^{-1}(1+{\eta }_k){\mathbb{X}}_{{\mathcal{A}}_k^c}^T{\mathbb{X}}_{{\mathcal{A}}_k}{\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{\lambda ,{\eta }_k}+n^{-1}(\eta -{\eta }_k){\mathbb{X}}_{{\mathcal{A}}_k^c}^T{\mathbb{X}}_{{\mathcal{A}}_k}{\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{{\mathcal{A}}_k,\mathrm{p}}-n^{-1}{\mathbb{X}}_{{\mathcal{A}}_k^c}^T(\mathbf{Y}+\eta {\widehat{\mathbf{Y}}}^{\mathrm{p}})\\ =G_{{\mathcal{A}}_k^c}^{\lambda ,{\eta }_k}+n^{-1}(\eta -{\eta }_k){\mathbb{X}}_{{\mathcal{A}}_k^c}^T({\mathbb{X}}_{{\mathcal{A}}_k}{\widehat{\mathit{\beta }}}_{{\mathcal{A}}_k}^{{\mathcal{A}}_k,\mathrm{p}}-{\widehat{\mathbf{Y}}}^{\mathrm{p}}).\end{array}$$

Hence $G_j^{\lambda ,\eta }$ is a monotone function of η ∈ (η_k, η_k+1) for any $j\in {\mathcal{A}}_k^c$. Then if j enters ${\mathcal{J}}_2^{\lambda ,\eta }$ from ${\mathcal{J}}_3^{\lambda ,\eta }$ at η, i.e., | $G_j^{\lambda ,\eta }$| becomes λ for some $j\in {\mathcal{A}}_k^c$, η must be a discontinuity point of . That is, η_k+1 = η. If not, η <η_k+1 and stays as . By the monotonicity, | $G_j^{\lambda ,\eta }$| will be larger than λ which is impossible. Moreover, since η_k+1 = η is proved, = ∪ {j} is the only allowed change of .

8.2 Proof of Theorem 3

Let $\mathit{\varphi }=\sqrt{n}(\mathit{\beta }-{\mathit{\beta }}_0)$. In the LASSO criterion function (3), using Taylor’s expansion,

$$\begin{array}{l}nL(\mathit{\beta };\mathbb{X},\mathbf{Y})=nL({\mathit{\beta }}_0+n^{-1/2}\mathit{\varphi };\mathbb{X},\mathbf{Y})\\ \simeq -\frac{1}{\sqrt{n}}\sum _{i=1}^n{Y}_i{\mathbf{Z}}_i^T\mathit{\varphi }+\sum _{i=1}^{n}b({\mathbf{Z}}_i^T{\mathit{\beta }}_0+n^{-1/2}{\mathbf{Z}}_i^T\mathit{\varphi })\\ \simeq -\frac{1}{\sqrt{n}}\sum _{i=1}^n[Y_i-b^{\prime }({\mathbf{Z}}_i^T{\mathit{\beta }}_0)]{\mathbf{Z}}_i^T\mathit{\varphi }+\frac{1}{2n}\sum _{i=1}^n{b}^{″}({\mathbf{Z}}_i^T{\mathit{\beta }}_0){({\mathbf{Z}}_i^T\mathit{\varphi })}^2+o_P(1)\end{array}$$ (A.1)

$${\to }_d-{\mathbf{u}}^T\mathit{\varphi }+\frac{1}{2}{\mathit{\varphi }}^T\mathbf{\Omega }\mathit{\varphi }=Q(\mathit{\varphi }),$$ (A.2)

where ≃ stands for the equality if ignoring an additive term independent with ϕ. (A.2) follows from Lemma 1 in Fahrmeir and Kaufmann (1985) by verifying their conditions (D) and (N). Furthermore, since $\sqrt{n}\lambda \to {\lambda }_0$,

$$n\lambda \sum _{j=1}^p(\mid {\beta }_j\mid -\mid {\beta }_{j,0}\mid )\to {\lambda }_0\sum _{j=1}^p[{\varphi }_j\text{sign}({\beta }_{j,0})I({\beta }_{j,0}\ne 0)+\mid {\varphi }_j\mid I({\beta }_{j,0}=0)]=P_{{\lambda }_0}(\mathit{\varphi }).$$

Thus, the proof is finished using the same argument as in the proof of Theorem 2 in Knight and Fu (2000).

8.3 Proof of Theorem 4

We briefly outline the proof. As the pLASSO criterion function (6) includes the two loss functions L(β; , Y) and L(β; , Ŷ^p), we need to evaluate them jointly. To do so, we first write L(β; , Y) in terms of β̂, the maximum likelihood estimator of β, i.e., the minimizer of the criterion function (2); and also write L(β; , Ŷ^p) in terms of β̂^p, the prior estimator of β. Then, the two loss functions can be jointly evaluated by studying the joint distribution of β̂ and β̂^p. In another word, the relationship between the observed response Y and the prior response Ŷ^p can be investigated through jointly studying β̂ and β̂^p, which is feasible because the two estimators minimize (2) and (8) separately but based on the same data set. This is a key step in the proof. The detailed proof follows.

8.3.1 Case 1: η → η₀ ≥ 0

Let $\mathit{\varphi }=\sqrt{n}(\mathit{\beta }-{\mathit{\beta }}_0)$. In the pLASSO criterion function (6), similar to (A.1),

$$nL(\mathit{\beta };\mathbb{X},{\widehat{\mathbf{Y}}}^{\mathrm{p}})\simeq -\frac{1}{\sqrt{n}}\sum _{i=1}^n[{\widehat{Y}}_i^{\mathrm{p}}-b^{\prime }({\mathbf{Z}}_i^T{\mathit{\beta }}_0)]{\mathbf{Z}}_i^T\mathit{\varphi }+\frac{1}{2n}\sum _{i=1}^n{b}^{″}({\mathbf{Z}}_i^T{\mathit{\beta }}_0){({\mathbf{Z}}_i^T\mathit{\varphi })}^2+o_P(1).$$ (A.3)

First, we write the first terms in (A.1) and (A.3) in terms of β̂ and β̂^p respectively as follows:

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n[Y_i-b^{\prime }({\mathbf{Z}}_i^T{\mathit{\beta }}_0)]{\mathbf{Z}}_i^T\mathit{\varphi }=\sqrt{n}{(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)}^T\mathbf{\Omega }\mathit{\varphi }+o_P(1),$$ (A.4)

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n[{\widehat{Y}}_i^{\mathrm{p}}-b^{\prime }({\mathbf{Z}}_i^T{\mathit{\beta }}_0)]{\mathbf{Z}}_i^T\mathit{\varphi }=\sqrt{n}{({\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0)}^T\mathbf{\Omega }\mathit{\varphi }+o_P(1).$$ (A.5)

By verifying conditions (D) and (N) in Fahrmeir and Kaufmann (1985), (A.4) is a direct conclusion from Theorems 3 therein and also (3.13) in its proof. For (A.5),

$$\begin{array}{l}\frac{1}{\sqrt{n}}\sum _{i=1}^n[{\widehat{Y}}_i^{\mathrm{p}}-b^{\prime }({\mathbf{Z}}_i^T{\mathit{\beta }}_0)]{\mathbf{Z}}_i^T\mathit{\varphi }=\frac{1}{\sqrt{n}}\sum _{i=1}^n{b}^{″}({\mathbf{Z}}_i^T\stackrel{\sim }{\mathit{\beta }}){\mathbf{Z}}_i^T({\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0){\mathbf{Z}}_i^T\mathit{\varphi }\\ =\sqrt{n}{({\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0)}^T\frac{1}{n}\sum _{i=1}^n{b}^{″}({\mathbf{Z}}_i^T{\mathit{\beta }}_0){\mathbf{Z}}_i{\mathbf{Z}}_i^T\mathit{\varphi }+o_P(1)\\ =\sqrt{n}{({\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0)}^T\mathbf{\Omega }\mathit{\varphi }+o_P(1).\end{array}$$

with β̃ between β₀ and β̂^p. The above equalities hold due to the fact that $\sqrt{n}({\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0)=O_P(1)$, which can be proved similarly to Theorem 3 since $\sqrt{n}\kappa \to {\kappa }_0\ge 0$.

Next, we evaluate the asymptotic joint distribution of β̂ and β̂^p. It is observed that

$$\begin{array}{l}{\left[\sqrt{n}{(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)}^T,\sqrt{n}{({\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0)}^T\right]}^T\\ =arg\underset{{\mathit{\varphi }}_1,{\mathit{\varphi }}_2}{min}[L({\mathit{\beta }}_0+n^{-1/2}{\mathit{\varphi }}_1;\mathbb{X},\mathbf{Y})+L_{\kappa ,{\mathcal{S}}^{\mathrm{p}}}({\mathit{\beta }}_0+n^{-1/2}{\mathit{\varphi }}_2;\mathbb{X},\mathbf{Y})],\end{array}$$

and a similar argument to (A.1) and (A.2) leads to

$$nL({\mathit{\beta }}_0+n^{-1/2}{\mathit{\varphi }}_1;\mathbb{X},\mathbf{Y})+n{L}_{\kappa ,{\mathcal{S}}^{\mathrm{p}}}({\mathit{\beta }}_0+n^{-1/2}{\mathit{\varphi }}_2;\mathbb{X},\mathbf{Y}){\to }_{d}Q({\mathit{\varphi }}_1)+Q({\mathit{\varphi }}_2)+P_{{\kappa }_0,{\mathcal{S}}^{\mathrm{p}}}({\mathit{\varphi }}_2).$$

Similar to Theorem 2 in Knight and Fu (2000), the above observations imply that

$$\begin{array}{r}{\left[\sqrt{n}{(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)}^T,\sqrt{n}{({\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0)}^T\right]}^T{\to }_{d}argmin[Q({\mathit{\varphi }}_1)+Q({\mathit{\varphi }}_2)+P_{{\kappa }_0,{\mathcal{S}}^{\mathrm{p}}}({\mathit{\varphi }}_2)]\\ ={[argmin{(Q)}^T,argmin{(Q+P_{{\kappa }_0,{\mathcal{S}}^{\mathrm{p}}})}^T]}^T.\end{array}$$

Finally, from (A.1), (A.3)–(A.5), and the above asymptotic joint distribution,

$$\begin{array}{l}nL({\mathit{\beta }}_0+n^{-1/2}\mathit{\varphi };\mathbb{X},\mathbf{Y})+n\eta L({\mathit{\beta }}_0+n^{-1/2}\mathit{\varphi };\mathbb{X},{\widehat{\mathbf{Y}}}^{\mathrm{p}})\\ =-{\left[\sqrt{n}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)+n\sqrt{n}({\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0)\right]}^T\mathbf{\Omega }\mathit{\varphi }+\frac{1+\eta }{2n}\sum _{i=1}^n{b}^{″}({\mathbf{Z}}_i^T{\mathit{\beta }}_0){({\mathbf{Z}}_i^T\mathit{\varphi })}^2+o_P(1)\\ {\to }_d(1+{\eta }_0){\mathit{\varphi }}^T\mathbf{\Omega }\mathit{\varphi }/2-{[argmin(Q)+{\eta }_{0}argmin(Q+P_{{\kappa }_0,{\mathcal{S}}^{\mathrm{p}}})]}^T\mathbf{\Omega }\mathit{\varphi }.\end{array}$$

Then the proof is finished similar to that of Theorem 3. F

8.3.2 Case 2: η → ∞

Let $\mathit{\varphi }=\sqrt{n}(\mathit{\beta }-{\mathit{\beta }}_0)$. Similar to the proof in Case 1,

$$\begin{array}{c}n{\eta }^{-1}{L}_{\lambda ,\eta }(\mathit{\beta };\mathbb{X},\mathbf{Y},{\widehat{\mathbf{Y}}}^{\mathrm{p}})=n{\eta }^{-1}L(\mathit{\beta };\mathbb{X},\mathbf{Y})+nL(\mathit{\beta };\mathbb{X},{\widehat{\mathbf{Y}}}^{\mathrm{p}})+n{\eta }^{-1}\lambda \sum _{j=1}^p\mid {\beta }_j\mid \\ {\to }_d{\mathit{\varphi }}^T\mathbf{\Omega }\mathit{\varphi }/2-{[argmin(Q+P_{{\kappa }_0,{\mathcal{S}}^{\mathrm{p}}})]}^T\mathbf{\Omega }\mathit{\varphi },\end{array}$$

ignoring an additive term independent with ϕ. So the conclusion is proved.

8.4 Proof of Theorem 6

Similar to Theorem 1 in Fan and Lv (2011), the Karush-Kuhn-Tucker (KKT) sufficient conditions for (29) are

$${\mathbb{X}}_1^T[\mathbf{Y}-b^{\prime }({\mathbb{X}}_1{\widehat{\mathit{\beta }}}_1)]+\eta {\mathbb{X}}_1^T[{\widehat{\mathbf{Y}}}^{\mathrm{p}}-b^{\prime }({\mathbb{X}}_1{\widehat{\mathit{\beta }}}_1)]-n\lambda \text{sign}({\widehat{\mathit{\beta }}}_1)=0,$$ (A.6)

$${\Vert {\mathbb{X}}_2^T[\mathbf{Y}-b^{\prime }({\mathbb{X}}_1{\widehat{\mathit{\beta }}}_1)]+\eta {\mathbb{X}}_2^T[{\widehat{\mathbf{Y}}}^{\mathrm{p}}-b^{\prime }({\mathbb{X}}_1{\widehat{\mathit{\beta }}}_1)]\Vert }_{\infty }<n\lambda ,$$ (A.7)

where f(u) = [f(u₁), …, f(u_n)]^T for any univariate function f and vector u = (u₁, …, u_n)^T for simplicity of notation hereafter. (A.6) and (A.7) imply that $\widehat{\mathit{\beta }}={({\widehat{\mathit{\beta }}}_1^T,{\mathbf{0}}^T)}^T$ is a pLASSO estimator.

8.4.1 Step 1: Existence of a solution to (A.6)

We prove that (A.6) has a solution β̂₁ inside the hypercube

$$\mathcal{N}=\{{\mathit{\beta }}_1\in {ℝ}^s:{\Vert {\mathit{\beta }}_1-{\mathit{\beta }}_{1,0}\Vert }_{\infty }=n^{-\gamma }logn/(1+\eta )\}.$$

For any β₁ ∈ , since d_n ≥ n^−γ log n, we have sign(β₁) = sign(β_1,0) and

$$\underset{1\le j\le s}{min}\mid {\beta }_j\mid \ge \underset{1\le j\le s}{min}\mid {\beta }_{j,0}\mid -n^{-\gamma }logn/(1+\eta )\ge \frac{1+2\eta }{1+\eta }{n}^{-\gamma }logn.$$

With a slight abuse of notation, let γ(β) = b′( β), γ(β₁) = b′( β₁), ξ = [Y − b′( β₀)] and ξ^p = [Ŷ^p − b′( β₀)], then (A.6) is equivalent to Ψ₁(β̂₁) = 0 where

$${\mathbf{\Psi }}_1({\mathit{\beta }}_1)=(1+\eta )[{\mathit{\gamma }}_1({\mathit{\beta }}_1)-{\mathit{\gamma }}_1({\mathit{\beta }}_{1,0})]-{\mathit{\xi }}_1-\eta {\mathit{\xi }}_1^{\mathrm{p}}+n\lambda \text{sign}({\mathit{\beta }}_{1,0}).$$

Similar to the proof of Theorem 2 in Fan and Lv (2011), ${\Vert {\mathit{\xi }}_1\Vert }_{\infty }=O_P(\sqrt{\mathit{n}logn})$, and

$${\mathit{\gamma }}_1({\mathit{\beta }}_1)-{\mathit{\gamma }}_1({\mathit{\beta }}_{1,0})={\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1({\mathit{\beta }}_1-{\mathit{\beta }}_{1,0})+{\mathbf{r}}_1,$$

where r₁ = (r₁, …, r_s)^T and for each j = 1, …, s,

$$r_j=\frac{1}{2}{({\mathit{\beta }}_1-{\mathit{\beta }}_{1,0})}^T\frac{{\partial }^2}{\partial {\mathit{\beta }}_1\partial {\mathit{\beta }}_1^T}{\gamma }_j({\stackrel{\sim }{\mathit{\beta }}}_{1j})({\mathit{\beta }}_1-{\mathit{\beta }}_{1,0}),$$

with β̃_1j lying on the line segment between β₁ and β_1,0. Therefore,

$${[{\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1]}^{-1}{\mathbf{\Psi }}_1({\mathit{\beta }}_1)=(1+\eta )({\mathit{\beta }}_1-{\mathit{\beta }}_{1,0})+\mathbf{u},$$

where

$$\mathbf{u}={[{\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1]}^{-1}[(1+\eta ){\mathbf{r}}_1-{\mathit{\xi }}_1-\eta {\mathit{\xi }}_1^{\mathrm{p}}+n\lambda \text{sign}({\mathit{\beta }}_{1,0})].$$

In addition, we have similarly that

$${\mathit{\xi }}_1^{\mathrm{p}}={\mathit{\gamma }}_1({\widehat{\mathit{\beta }}}^{\mathrm{p}})-{\mathit{\gamma }}_1({\mathit{\beta }}_0)={\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0)[{\mathbb{X}}_1({\widehat{\mathit{\beta }}}_1^{\mathrm{p}}-{\mathit{\beta }}_{1,0})+{\mathbb{X}}_2{\widehat{\mathit{\beta }}}_2^{\mathrm{p}}]+{\mathbf{r}}_1^{\mathrm{p}},$$

where ${\mathbf{r}}_1^{\mathrm{p}}={(r_1^{\mathrm{p}},\dots ,r_s^{\mathrm{p}})}^T$ and for each j = 1, …, s,

$$r_j^{\mathrm{p}}=\frac{1}{2}{({\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0)}^T\frac{{\partial }^2}{\partial \mathit{\beta }\partial {\mathit{\beta }}^T}{\gamma }_j({\stackrel{\sim }{\mathit{\beta }}}_j)({\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0),$$

with β̃_j lying between β̂^p and β₀.

This leads to u = u₁ + u₂ + u₃ with

$$\begin{array}{l}{\mathbf{u}}_1={[{\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1]}^{-1}[(1+\eta ){\mathbf{r}}_1-{\mathit{\xi }}_1+n\lambda \text{sign}({\mathit{\beta }}_{1,0})],\\ {\mathbf{u}}_2=-\eta ({\widehat{\mathit{\beta }}}_1^{\mathrm{p}}-{\mathit{\beta }}_{1,0})-\eta {[{\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1]}^{-1}{\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_2{\widehat{\mathit{\beta }}}_2^{\mathrm{p}},\\ {\mathbf{u}}_3=-\eta {[{\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1]}^{-1}{\mathbf{r}}_1^{\mathrm{p}}.\end{array}$$

Using the similar arguments as in the proof of Theorem 2 in Fan and Lv (2011),

$${\Vert {\mathbf{u}}_1\Vert }_{\infty }=O(b_s{n}^{-1})O_P[s{n}^{1-2\gamma }{(logn)}^2/(1+\eta )+\sqrt{\mathit{n}logn}+n\lambda ].$$

It is also seen that

$$\begin{array}{l}{\Vert {\mathbf{u}}_2\Vert }_{\infty }\le \eta {\Vert {\widehat{\mathit{\beta }}}_1^{\mathrm{p}}-{\mathit{\beta }}_{1,0}\Vert }_{\infty }+\eta {\Vert {[{\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1]}^{-1}\Vert }_{\infty }{\Vert {\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_2{\widehat{\mathit{\beta }}}_2^{\mathrm{p}}\Vert }_{\infty },\\ {\Vert {\mathbf{u}}_3\Vert }_{\infty }=O(\eta b_s{n}^{-1})\underset{\mathit{\beta }\in {\mathcal{N}}_0^{\mathrm{p}}}{max}\underset{1\le j\le s}{max}{\lambda }_{max}[{\mathbb{X}}^T\text{diag}\{\mid {\mathbf{x}}_j\mid \circ \mid b^{‴}(\mathbb{X}\mathit{\beta })\mid \}\mathbb{X}]{\Vert {\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0\Vert }_2^2\\ =O_P(\eta b_s){\Vert {\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0\Vert }_2^2.\end{array}$$

As ||β₁ − β_1,0||_∞ = n^−γ log n/(1 + η) for β₁ ∈ , it is already proved that ||u₁||_∞ = o_P [(1 + η)||β₁ − β_1,0||_∞] by Condition B. In addition, under Condition D, it is verified that ||u₂||_∞ = o_P [(1 + η)||β₁ − β_1,0||_∞] and ||u₃||_∞ = o_P [(1 + η)||β₁ − β_1,0||_∞] for β₁ ∈ . Therefore, the existence of β̂₁ inside satisfying Ψ₁(β̂₁) = 0 is implied by the Miranda’s existence theorem as similarly argued by Fan and Lv (2011).

8.4.2 Step 2: Verification of condition (A.7)

Let β̂₁ be the solution of (A.6). Note that (A.7) is equivalent to ||Ψ₂||_∞ < nλ, where

$$\begin{array}{l}{\mathbf{\Psi }}_2={\mathbb{X}}_2^T[\mathbf{Y}-b^{\prime }({\mathbb{X}}_1{\widehat{\mathit{\beta }}}_1)]+\eta {\mathbb{X}}_2^T[{\widehat{\mathbf{Y}}}^{\mathrm{p}}-b^{\prime }({\mathbb{X}}_1{\widehat{\mathit{\beta }}}_1)]\\ ={\mathit{\xi }}_2+\eta {\mathit{\xi }}_2^{\mathrm{p}}-(1+\eta )[{\mathit{\gamma }}_2({\widehat{\mathit{\beta }}}_1)-{\mathit{\gamma }}_2({\mathit{\beta }}_{1,0})].\end{array}$$

Similar to Fan and Lv (2011), ${\Vert {\mathit{\xi }}_2\Vert }_{\infty }=O_P(n^{1-\alpha }\sqrt{logn})$, and

$${\mathit{\gamma }}_2({\widehat{\mathit{\beta }}}_1)-{\mathit{\gamma }}_2({\mathit{\beta }}_{1,0})={\mathbb{X}}_2^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1({\widehat{\mathit{\beta }}}_1-{\mathit{\beta }}_{1,0})+{\mathbf{r}}_2,$$

where r₂ = (r_s+1, …, r_p)^T and for each j = s + 1, …, p,

$$r_j=\frac{1}{2}{({\widehat{\mathit{\beta }}}_1-{\mathit{\beta }}_{1,0})}^T\frac{{\partial }^2}{\partial {\mathit{\beta }}_1\partial {\mathit{\beta }}_1^T}{\gamma }_j({\stackrel{\sim }{\mathit{\beta }}}_{1j})({\widehat{\mathit{\beta }}}_1-{\mathit{\beta }}_{1,0}),$$

with β̃_1j lying between β̂₁ and β̂_1,0. It follows from Fan and Lv (2011) that

$$\begin{array}{l}{\Vert {\mathbf{r}}_2\Vert }_{\infty }\le \frac{1}{2}\underset{{\mathit{\beta }}_1\in {\mathcal{N}}_0}{max}\underset{s+1\le j\le p}{max}{\lambda }_{max}[{\mathbb{X}}_1^T\text{diag}\{\mid {\mathbf{x}}_j\mid \circ \mid b^{‴}({\mathbb{X}}_1{\mathit{\beta }}_1)\mid \}{\mathbb{X}}_1]{\Vert {\widehat{\mathit{\beta }}}_1-{\mathit{\beta }}_{1,0}\Vert }_2^2\\ =O[s{n}^{1-2\gamma }{(logn)}^2/{(1+\eta )}^2].\end{array}$$

In addition, by Step 1,

$${\widehat{\mathit{\beta }}}_1-{\mathit{\beta }}_{1,0}={(1+\eta )}^{-1}{[{\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1]}^{-1}[{\mathit{\xi }}_1+\eta {\mathit{\xi }}_1^{\mathrm{p}}-(1+\eta ){\mathbf{r}}_1-n\lambda \text{sign}({\mathit{\beta }}_{1,0})],$$

where ${\Vert {\mathit{\xi }}_1\Vert }_{\infty }=O_P(\sqrt{\mathit{n}logn})$ and ||r₁||_∞ = O[sn^1−2γ(log n)²/(1+η)²] from Step 1. Moreover,

$${\Vert {\mathit{\xi }}_1^{\mathrm{p}}\Vert }_{\infty }\le {\Vert {\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1({\widehat{\mathit{\beta }}}_1^{\mathrm{p}}-{\mathit{\beta }}_{1,0})\Vert }_{\infty }+{\Vert {\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_2{\widehat{\mathit{\beta }}}_2^{\mathrm{p}}\Vert }_{\infty }+{\Vert {\mathbf{r}}_1^{\mathrm{p}}\Vert }_{\infty },$$

with ${\Vert {\mathbf{r}}_1^{\mathrm{p}}\Vert }_{\infty }=O_P(n){\Vert {\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0\Vert }_2^2$ from Step 1. Therefore,

$$\begin{array}{l}{\Vert {\mathbb{X}}_2^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1({\widehat{\mathit{\beta }}}_1-{\mathit{\beta }}_{1,0})\Vert }_{\infty }\\ ={(1+\eta )}^{-1}{\Vert {\mathbb{X}}_2^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1{[{\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1]}^{-1}\Vert }_{\infty }[{\Vert {\mathit{\xi }}_1\Vert }_{\infty }+\eta {\Vert {\mathit{\xi }}_1^{\mathrm{p}}\Vert }_{\infty }+(1+\eta ){\Vert {\mathbf{r}}_1\Vert }_{\infty }+n\lambda ]\\ ={(1+\eta )}^{-1}C[O_P(\sqrt{\mathit{n}logn})+O[s{n}^{1-2\gamma }{(logn)}^2/(1+\eta )]+\eta {\Vert {\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1({\widehat{\mathit{\beta }}}_1^{\mathrm{p}}-{\mathit{\beta }}_{1,0})\Vert }_{\infty }\\ +\eta {\Vert {\mathbb{X}}_1^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_2{\widehat{\mathit{\beta }}}_2^{\mathrm{p}}\Vert }_{\infty }+O_P(\eta n){\Vert {\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0\Vert }_2^2+n\lambda ].\end{array}$$

Similar to ${\mathit{\xi }}_1^{\mathrm{p}}$ in Step 1,

$${\mathit{\xi }}_2^{\mathrm{p}}={\mathit{\gamma }}_2({\widehat{\mathit{\beta }}}^{\mathrm{p}})-{\mathit{\gamma }}_2({\mathit{\beta }}_0)={\mathbb{X}}_2^T\mathbf{\sum }({\mathit{\beta }}_0)[{\mathbb{X}}_1({\widehat{\mathit{\beta }}}_1^{\mathrm{p}}-{\mathit{\beta }}_{1,0})+{\mathbb{X}}_2{\widehat{\mathit{\beta }}}_2^{\mathrm{p}}]+{\mathbf{r}}_2^{\mathrm{p}},$$

where ${\mathbf{r}}_2^{\mathrm{p}}={(r_{s+1}^{\mathrm{p}},\dots ,r_p^{\mathrm{p}})}^T$ and for each j = s + 1, …, p,

$$r_j^{\mathrm{p}}=\frac{1}{2}{({\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0)}^T\frac{{\partial }^2}{\partial \mathit{\beta }\partial {\mathit{\beta }}^T}{\gamma }_j({\stackrel{\sim }{\mathit{\beta }}}_j)({\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0),$$

with β̃_j lying between β̂^p and β₀. Thus,

$${\Vert {\mathit{\xi }}_2^{\mathrm{p}}\Vert }_{\infty }\le {\Vert {\mathbb{X}}_2^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_1({\widehat{\mathit{\beta }}}_1-{\mathit{\beta }}_{1,0})\Vert }_{\infty }+{\Vert {\mathbb{X}}_2^T\mathbf{\sum }({\mathit{\beta }}_0){\mathbb{X}}_2{\widehat{\mathit{\beta }}}_2^{\mathrm{p}}\Vert }_{\infty }+O_P(n){\Vert {\widehat{\mathit{\beta }}}^{\mathrm{p}}-{\mathit{\beta }}_0\Vert }_2^2.$$

It is implied that ||ξ₂||_∞ = o(nλ) from Condition B and $\eta {\Vert {\mathit{\xi }}_2^{\mathrm{p}}\Vert }_{\infty }=o_P(n\lambda )$ from Condition D. In addition, ||(1 + η)[γ₂(β̂₁) − γ₂(β_1,0)]||_∞ ≤ Cnλ + o_P (nλ) from Conditions B and D. Therefore, with probability tending to one, (A.7) holds with the solution β̂₁ in Step 1.

8.5 Proof of Theorem 7

Recall from Condition F that the parameter space under consideration is restricted to . As β̂^λ,η minimizes (29) for β ∈ , the following inequality holds for any β ∈ ,

$$L({\widehat{\mathit{\beta }}}^{\lambda ,\eta };\mathbb{X},\mathbf{Y})+\eta L({\widehat{\mathit{\beta }}}^{\lambda ,\eta };\mathbb{X},{\widehat{\mathbf{Y}}}^{\mathrm{p}})+\lambda \sum _{j=1}^p\mid {\widehat{\beta }}_j^{\lambda ,\eta }\mid \le L(\mathit{\beta };\mathbb{X},\mathbf{Y})+\eta L(\mathit{\beta };\mathbb{X},{\widehat{\mathbf{Y}}}^{\mathrm{p}})+\lambda \sum _{j=1}^p\mid {\beta }_j\mid .$$ (A.8)

With R(β) defined in (31), by noticing that

$$\begin{array}{c}L(\mathit{\beta };\mathbb{X},\mathbf{Y})-R(\mathit{\beta })=-\frac{1}{n}\sum _{i=1}^n[Y_i-b^{\prime }({\mathbf{X}}_i^T{\mathit{\beta }}_0)]{\mathbf{X}}_i^T\mathit{\beta },\\ L(\mathit{\beta };\mathbb{X},{\widehat{\mathbf{Y}}}^{\mathrm{p}})-R(\mathit{\beta })=-\frac{1}{n}\sum _{i=1}^n[{\widehat{Y}}_i^{\mathrm{p}}-b^{\prime }({\mathbf{X}}_i^T{\mathit{\beta }}_0)]{\mathbf{X}}_i^T\mathit{\beta },\end{array}$$

(A.8) can be rewritten as

$$(1+\eta )\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })\le (1+\eta )\mathcal{E}(\mathit{\beta })+I_1+I_2+I_3,$$ (A.9)

where

$$I_1=\frac{1}{n}\sum _{i=1}^n{\epsilon }_i{\mathbf{X}}_i^T({\widehat{\mathit{\beta }}}^{\lambda ,\eta }-\mathit{\beta }),I_2=\frac{\eta }{n}\sum _{i=1}^n{\widehat{\epsilon }}_i^{\mathrm{p}}{\mathbf{X}}_i^T({\widehat{\mathit{\beta }}}^{\lambda ,\eta }-\mathit{\beta }),I_3=\lambda \sum _{j=1}^p(\mid {\beta }_j\mid -\mid {\widehat{\beta }}_j^{\lambda ,\eta }\mid ),$$

with ε_i and ${\widehat{\epsilon }}_i^{\mathrm{p}}$ defined in (30). By direct calculations,

$$\begin{array}{l}\mid I_1\mid =\left|\sum _{j=1}^p\frac{1}{n}\sum _{i=1}^n{\epsilon }_i{X}_{ij}({\widehat{\beta }}_j^{\lambda ,\eta }-{\beta }_j)\right|\le \sum _{j=1}^p\mid {\widehat{\beta }}_j^{\lambda ,\eta }-{\beta }_j\mid \underset{1\le j\le p}{max}\left|\frac{1}{n}\sum _{i=1}^n{\epsilon }_i{X}_{ij}\right|,\\ \mid I_2\mid =\left|\sum _{j=1}^p\frac{\eta }{n}\sum _{i=1}^n{\widehat{\epsilon }}_i^{\mathrm{p}}{X}_{ij}({\widehat{\beta }}_j^{\lambda ,\eta }-{\beta }_j)\right|\le \sum _{j=1}^p\mid {\widehat{\beta }}_j^{\lambda ,\eta }-{\beta }_j\mid \underset{1\le j\le p}{max}\left|\frac{\eta }{n}\sum _{i=1}^n{\widehat{\epsilon }}_i^{\mathrm{p}}{X}_{ij}\right|.\end{array}$$

Recall that $\lambda =A{n}^{-1/2}(\sqrt{logp}+\eta B_{{\widehat{\mathit{\epsilon }}}^{\mathrm{p}}})$ where B_ε̂^p = n^−1/2|| ε̂^p||_∞. Consider the following two events,

$${\mathcal{A}}_1=\left\{\underset{1\le j\le p}{max}\left|\frac{1}{n}\sum _{i=1}^n{\epsilon }_i{X}_{ij}\right|\le \frac{\lambda }{4}\right\},{\mathcal{A}}_2=\left\{\underset{1\le j\le p}{max}\left|\frac{\eta }{n}\sum _{i=1}^n{\widehat{\epsilon }}_i^{\mathrm{p}}{X}_{ij}\right|\le \frac{\lambda }{4}\right\}.$$

Our derivation will be restricted on ∩ hereafter, and we will bound the probability of ( ∩ )^c at the end of the proof. On ∩ ,

$$\mid I_1\mid \le \frac{\lambda }{4}\sum _{j=1}^p\mid {\widehat{\beta }}_j^{\lambda ,\eta }-{\beta }_j\mid ,\mid I_2\mid \le \frac{\lambda }{4}\sum _{j=1}^p\mid {\widehat{\beta }}_j^{\lambda ,\eta }-{\beta }_j\mid .$$

Then (A.9) leads to

$$(1+\eta )\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })+\frac{\lambda }{2}\sum _{j=1}^p\mid {\widehat{\beta }}_j^{\lambda ,\eta }-{\beta }_j\mid \le (1+\eta )\mathcal{E}(\mathit{\beta })+\lambda \sum _{j=1}^p(\mid {\beta }_j\mid -\mid {\widehat{\beta }}_j^{\lambda ,\eta }\mid +\mid {\widehat{\beta }}_j^{\lambda ,\eta }-{\beta }_j\mid ).$$ (A.10)

When j ∉ J(β), β_j = 0, then $\mid {\beta }_j\mid -\mid {\widehat{\beta }}_j^{\lambda ,\eta }\mid +\mid {\widehat{\beta }}_j^{\lambda ,\eta }-{\beta }_j\mid =0$. Then, (A.10) leads to

$$(1+\eta )\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })+\frac{\lambda }{2}\sum _{j=1}^p\mid {\widehat{\beta }}_j^{\lambda ,\eta }-{\beta }_j\mid \le (1+\eta )\mathcal{E}(\mathit{\beta })+2\lambda \sum _{j\in J(\mathit{\beta })}\mid {\widehat{\beta }}_j^{\lambda ,\eta }-{\beta }_j\mid .$$ (A.11)

Define another event $ℬ=\{2\lambda {\sum }_{j\in J(\mathit{\beta })}\mid {\widehat{\beta }}_j^{\lambda ,\eta }-{\beta }_j\mid \le \phi (1+\eta )\mathcal{E}(\mathit{\beta })\}$ for the constant φ > 0 defined in Theorem 7. On the one hand, on event , (A.11) implies that

$$\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })\le (1+\phi )\mathcal{E}(\mathit{\beta }),\text{for}\text{any}\mathit{\beta }\in {\mathbb{B}}_{\delta }.$$

Thus, the inequality (32) in Theorem 7 is proved on event .

On the other hand, on event , (A.11) leads to

$$\frac{\lambda }{2}\sum _{j=1}^p\mid {\widehat{\beta }}_j^{\lambda ,\eta }-{\beta }_j\mid \le 2\lambda (1+1/\phi )\sum _{j\in J(\mathit{\beta })}\mid {\widehat{\beta }}_j^{\lambda ,\eta }-{\beta }_j\mid .$$ (A.12)

Denoted by δ = β̂^λ,η − β, (A.12) implies that

$$\frac{1}{2}{\Vert {\mathit{\delta }}_{J{(\mathit{\beta })}^c}\Vert }_1+\frac{1}{2}{\Vert {\delta }_{J(\mathit{\beta })}\Vert }_1\le 2(1+1/\phi ){\Vert {\mathit{\delta }}_{J(\mathit{\beta })}\Vert }_1,\mathrm{i}.\mathrm{e}.,{\Vert {\mathit{\delta }}_{J{(\mathit{\beta })}^c}\Vert }_1\le (3+4/\phi ){\Vert {\mathit{\delta }}_{J(\mathit{\beta })}\Vert }_1.$$

Under Condition RE(r, 3 + 4/φ), for any β satisfying |J(β)| ≤ r,

$${\kappa }^2(r,3+4/\phi ){\Vert {\mathit{\delta }}_{J(\mathit{\beta })}\Vert }_2^2\le \frac{1}{n}{\Vert \mathbb{X}\mathit{\delta }\Vert }_2^2=\frac{1}{n}{\Vert \mathbb{X}{\widehat{\mathit{\beta }}}^{\lambda ,\eta }-\mathbb{X}\mathit{\beta }\Vert }_2^2.$$ (A.13)

From (A.11) and (A.13), we have that

$$\begin{array}{l}(1+\eta )\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })\le (1+\eta )\mathcal{E}(\mathit{\beta })+2\lambda \sqrt{\mid J(\mathit{\beta })\mid }{\Vert {\mathit{\delta }}_{J(\mathit{\beta })}\Vert }_2\\ \le (1+\eta )\mathcal{E}(\mathit{\beta })+\frac{2\lambda \sqrt{\mid J(\mathit{\beta })\mid }}{\sqrt{n}\kappa (r,3+4/\phi )}{\Vert \mathbb{X}{\widehat{\mathit{\beta }}}^{\lambda ,\eta }-\mathbb{X}\mathit{\beta }\Vert }_2.\end{array}$$ (A.14)

Furthermore, Lemma 1 shows that, for β ∈ ,

$$\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })\ge \frac{1}{n}\delta {\Vert \mathbb{X}{\widehat{\mathit{\beta }}}^{\lambda ,\eta }-\mathbb{X}{\mathit{\beta }}_0\Vert }_2^2\text{and}\mathcal{E}(\mathit{\beta })\ge \frac{1}{n}\delta {\Vert \mathbb{X}\mathit{\beta }-\mathbb{X}{\mathit{\beta }}_0\Vert }_2^2,$$

Then, (A.14) becomes

$$\begin{array}{l}(1+\eta )\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })\le (1+\eta )\mathcal{E}(\mathit{\beta })+\frac{2\lambda \sqrt{\mid J(\mathit{\beta })\mid }}{\sqrt{\delta }\kappa (r,3+4/\phi )}[\sqrt{\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })}+\sqrt{\mathcal{E}(\mathit{\beta })}]\\ \le (1+\eta )\mathcal{E}(\mathit{\beta })+2b\frac{{\lambda }^2\mid J(\mathit{\beta })\mid }{\delta {\kappa }^2(r,3+4/\phi )}+\frac{1}{b}\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })+\frac{1}{b}\mathcal{E}(\mathit{\beta }),\end{array}$$ (A.15)

where we have applied the inequality 2uv ≤ bu² + v²/b for b > 0. With b > 1/(1 + η), (A.15) implies

$$\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })\le \frac{b+b\eta +1}{b+b\eta -1}\mathcal{E}(\mathit{\beta })+\frac{2b^2{\lambda }^2\mid J(\mathit{\beta })\mid }{(b+b\eta -1)\delta {\kappa }^2(r,3+4/\phi )}.$$

Setting (b + bη + 1)/(b + bη − 1) = 1 + φ leads to b = (2 + φ)/[φ (1 + η)] and therefore,

$$\begin{array}{l}\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })\le (1+\phi )\left[\mathcal{E}(\mathit{\beta })+\frac{{(2+\phi )}^2{\lambda }^2\mid J(\mathit{\beta })\mid }{\phi (1+\phi )\delta {(1+\eta )}^2{\kappa }^2(r,3+4/\phi )}\right]\\ \le (1+\phi )\left(\mathcal{E}(\mathit{\beta })+\frac{2C(\phi )A^2\mid J(\mathit{\beta })\mid }{\delta {\kappa }^2(r,3+4/\phi )}\left[\frac{1}{{(1+\eta )}^2}\frac{logp}{n}+\frac{{\eta }^2}{{(1+\eta )}^2}\frac{B_{{\widehat{\mathit{\epsilon }}}^{\mathrm{p}}}^2}{n}\right]\right),\end{array}$$

for any β ∈ satisfying that J(β) ≤ r. Therefore, the inequality (32) in Theorem 7 is proved on event .

The last part of the proof is to bound the probability of ( ∩ )^c. Recall that $\lambda =A{n}^{-1/2}(\sqrt{logp}+\eta B_{{\widehat{\mathit{\epsilon }}}^{\mathrm{p}}})$. With the same notation as in Condition E, define M′ = max[M sup_n,i ||X_i||_∞, 2(M sup_n,i ||X_i||_∞)²] < ∞. For , applying Bernstein’s inequality (Lemma 2.2.11 in van der Vaart and Wellner (1996)) leads to

$$\begin{array}{l}P({\mathcal{A}}_1^c)\le \sum _{j=1}^{p}P\left(\left|\sum _{i=1}^n{\epsilon }_i{X}_{ij}\right|>\frac{A}{4}\sqrt{\mathit{n}logp}\right)\\ \le 2pexp\left\{-\frac{1}{2}\frac{(A^2/16)\mathit{n}logp}{M^{\prime }[n+(A/4)\sqrt{\mathit{n}logp}]}\right\}\\ \le 2exp\left\{-\frac{1}{2}\frac{(A^2/16-2M^{\prime })\mathit{n}logp-2M^{\prime }(A/4)\sqrt{n}{(logp)}^{3/2}}{M^{\prime }[n+(A/4)\sqrt{\mathit{n}logp}]}\right\}.\end{array}$$

It is seen that $P({\mathcal{A}}_1^c)\to 0$ when A > 0 is large enough and log p = o(n). In addition, for ,

$$\underset{1\le j\le p}{max}\left|\frac{\eta }{n}\sum _{i=1}^n{\widehat{\epsilon }}_i^{\mathrm{p}}{X}_{ij}\right|=n^{-1/2}\eta B_{{\widehat{\mathit{\epsilon }}}^{\mathrm{p}}}\le \frac{\lambda }{4},$$

as long as A ≥ 4. Then $P({\mathcal{A}}_2^c)=0$. Therefore, P[( ∩ )^c] → 0.

8.6 Proof of Corollary 1

In the proof of Theorem 7, setting β = β₀ in (A.11) leads to

$${\Vert {\mathit{\delta }}_{0,J_0^c}\Vert }_1\le 3{\Vert {\mathit{\delta }}_{0,J_0}\Vert }_1,$$ (A.16)

where δ₀ = β̂^λ,η − β₀, J₀ = J(β₀) with |J₀| = s. Thus, Condition RE(r, 3 + 4/φ) becomes RE(s, 3) and κ(r, 3+4/φ) becomes κ(s, 3) in the proof. Also = ∅ when β = β₀. Meanwhile, setting β = β₀ in (A.14) we have that

$$\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })\le \frac{4{\lambda }^2\mid J_0\mid }{\delta {(1+\eta )}^2{\kappa }^2(s,3)}.$$

In addition, by Lemma 1,

$$\frac{1}{n}{\Vert \mathbb{X}{\widehat{\mathit{\beta }}}^{\lambda ,\eta }-\mathbb{X}{\mathit{\beta }}_0\Vert }_2^2\le \frac{1}{\delta }\mathcal{E}({\widehat{\mathit{\beta }}}^{\lambda ,\eta })\le \frac{4{\lambda }^2\mid J_0\mid }{{\delta }^2{(1+\eta )}^2{\kappa }^2(s,3)}.$$

Furthermore, (A.16) implies that ${\Vert {\mathit{\delta }}_0\Vert }_1\le 4{\Vert {\mathit{\delta }}_{0,J_0}\Vert }_1\le 4\sqrt{\mid J_0\mid }{\Vert {\mathit{\delta }}_{0,J_0}\Vert }_2$. Therefore, under Condition RE(s, 3),

$${\Vert {\widehat{\mathit{\beta }}}^{\lambda ,\eta }-{\mathit{\beta }}_0\Vert }_1^2\le \frac{16\mid J_0\mid }{n{\kappa }^2(s,3)}{\Vert \mathbb{X}{\widehat{\mathit{\beta }}}^{\lambda ,\eta }-\mathbb{X}{\mathit{\beta }}_0\Vert }_2^2\le \frac{64{\lambda }^2\mid J_0{\mid }^2}{{\delta }^2{(1+\eta )}^2{\kappa }^4(s,3)}.$$

Therefore, all results in Corollary 1 are proved by noticing that

$${\lambda }^2\le 2A^2\left(\frac{logp}{n}+{\eta }^2\frac{B_{{\widehat{\mathit{\epsilon }}}^{\mathrm{p}}}^2}{n}\right).$$

8.7 A Lemma

Lemma 1

Under Condition F, for any β ∈ ,

$$\mathcal{E}(\mathit{\beta })\ge \frac{1}{n}\delta {\Vert \mathbb{X}\mathit{\beta }-\mathbb{X}{\mathit{\beta }}_0\Vert }_2^2.$$

Proof

For t ∈ [0, 1], consider the following function

$$g(t)=\frac{1}{n}\sum _{i=1}^{n}b({\mathbf{X}}_i^T[t\mathit{\beta }+(1-t){\mathit{\beta }}_0]).$$

Clearly, g is twice continuously differentiable. By Taylor’s expansion,

$$g(1)-g(0)-g^{\prime }(0)={\int }_0^1{g}^{″}(t)(1-t)\mathrm{d}t.$$

Note that the left-hand side of the above equation is just (β), and the right-hand side is

$$\frac{1}{n}\sum _{i=1}^n{[{\mathbf{X}}_i^T(\mathit{\beta }-{\mathit{\beta }}_0)]}^2{\int }_0^1{b}^{″}({\mathbf{X}}_i^T[t\mathit{\beta }+(1-t){\mathit{\beta }}_0])(1-t)\mathrm{d}t\ge \frac{1}{n}\delta \sum _{i=1}^n{[{\mathbf{X}}_i^T(\mathit{\beta }-{\mathit{\beta }}_0)]}^2,$$

under Condition F. The proof is completed.