Abstract
The prefrontal cortex is centrally involved in a wide range of cognitive functions and their impairment in psychiatric disorders. Yet, the computational principles that govern the dynamics of prefrontal neural networks, and link their physiological, biochemical and anatomical properties to cognitive functions, are not well understood. Computational models can help to bridge the gap between these different levels of description, provided they are sufficiently constrained by experimental data and capable of predicting key properties of the intact cortex. Here, we present a detailed network model of the prefrontal cortex, based on a simple computationally efficient single neuron model (simpAdEx), with all parameters derived from in vitro electrophysiological and anatomical data. Without additional tuning, this model could be shown to quantitatively reproduce a wide range of measures from in vivo electrophysiological recordings, to a degree where simulated and experimentally observed activities were statistically indistinguishable. These measures include spike train statistics, membrane potential fluctuations, local field potentials, and the transmission of transient stimulus information across layers. We further demonstrate that model predictions are robust against moderate changes in key parameters, and that synaptic heterogeneity is a crucial ingredient to the quantitative reproduction of in vivo-like electrophysiological behavior. Thus, we have produced a physiologically highly valid, in a quantitative sense, yet computationally efficient PFC network model, which helped to identify key properties underlying spike time dynamics as observed in vivo, and can be harvested for in-depth investigation of the links between physiology and cognition.
Author Summary
Computational network models are an important tool for linking physiological and neuro-dynamical processes to cognition. However, harvesting network models for this purpose may less depend on how much biophysical detail is included, but more on how well the model can capture the functional network physiology. Here, we present the first network model of the prefrontal cortex which has not only its single neuron properties and anatomical layout tightly constrained by experimental data, but is also able to quantitatively reproduce a large range of spiking, field potential, and membrane voltage statistics obtained from in vivo data, without need of specific parameter tuning. It thus represents a novel computational tool for addressing questions about the neuro-dynamics of cognition in health and disease.
Introduction
The prefrontal cortex (PFC) is a key structure in higher-level cognitive functions, including working memory, rule and concept representation and behavioral flexibility [1–6], and has been linked to impairments of these functions in psychiatric disorders like schizophrenia [7–10] or attention-deficit/hyperactivity disorder [11]. Our understanding of the computational and dynamic mechanisms underlying these cognitive functions, their neuromodulation, and their aberrations in psychiatric disorders, is still very limited, however.
Computational network models are a highly valuable tool for driving forward such an understanding, as data from many different levels of experimental analysis can be integrated into a coherent picture. With respect to psychiatric conditions, it is of particular importance that models incorporate sufficient biological detail and exhibit physiological validity in order to serve as explanatory tools. Psychiatric conditions like schizophrenia are characterized by a multitude of abnormalities in diverse cellular and synaptic properties, transmitter systems, and neuromodulatory input [7–10]. Moreover, pharmacological treatment options target the neurochemical and physiological level, yet they are supposed to change functionality at the behavioral and cognitive level. It is thus crucial to gain insight into the explanatory links between behavioral functions and the underlying neurobiological “hardware”, a task that requires sufficient physiological detail in the model specification, in particular realistic assumptions about anatomical structure and cell type diversity.
Ultimately, the physiological validity of a computational model ought to be reflected in the degree to which it can reproduce and predict detailed aspects of the neural activity observed in vivo. That is, from a statistical perspective, one may define a good, physiologically valid model as one that accurately (i.e., quantitatively) captures distributions compiled from the electrophysiological activity (spiking, field potentials, membrane voltages) produced by networks in vivo, but not necessarily as one that captures every detail of membrane biophysics or receptor kinetics. In our perception, such requirements are currently not met even by sophisticated cortical network models which do include a lot of biophysical detail [12–14], as these are often only loosely compared to in vivo data or test only specific aspects of those.
In this work, we present a computational network model of the PFC which has high physiological validity and predictivity both at the single-neuron- (in vitro) and at the network- (in vivo) level, yet is still simple enough to be computationally tractable. Its anatomical structure, neural, and synaptic properties are completely derived from the experimental literature and our own experimental data. The activity of the network is compared with a range of statistics derived from in vivo data, including spike trains, local field potentials, and membrane potential fluctuations. The model turns out to reproduce these data quantitatively, and also exhibits robustness with respect to moderate changes in parameters.
Results
Key features of the prefrontal cortex model
The network model introduced in Materials and Methods aims to combine computational tractability with physiological validity. This balance is achieved by embedding a simple, reduced two-dimensional single neuron model into a realistic network architecture that is derived from the experimental literature. All model parameters were directly estimated from our own in vitro data and the experimental literature (see Materials and Methods for details), and no specific parameter tuning was necessary to bring the network model closer to in vivo-like behavior.
At the single-cell level, the network is based on an approximation (simpAdEx [15]) to the adaptive exponential integrate-and-fire model (AdEx [16]) which yields closed-form expressions for instantaneous and steady-state firing rates, thus allowing for fast and fully automatized fitting to f-I and V-I curves from physiologically recorded cells (Fig 1A). We had shown previously that this cell model is able to accurately predict spike times of recorded neurons driven by in vivo-like fluctuating currents not used for model fitting [15] (Fig 1B) and, like the full AdEx [17], can generate a wide range of spike patterns. In vitro recordings from ∼200 L2/3 and L5 pyramidal cells, fast-spiking and bitufted interneurons from the medial PFC of adult rodents were used to generate a distribution of model cells that reflects the diversity of neurons in the real PFC (see Materials and Methods for details). The resulting model parameters (Table 1) follow broad distributions (Fig 1C), mostly of Gaussian shape, with the exception of ΔT and τw which are best described by a Gamma distribution, and b which follows an exponential distribution (red curves in Fig 1C indicate distributions from which model parameters were drawn).
Fig 1. Single neuron recordings and model fitting.
(A) Example of the initial (upper curve) and steady-state (lower curve) input-output relation (f-I curve) of a single neuron. Black and gray curves show experimental data, red and blue curves indicate the simpAdEx model fits. (B) Voltage trace from a slice recording of a prefrontal cortical layer 5 pyramidal cell (black) and from the corresponding model cell (red) in response to the same fluctuating input current. The same neuron model and parameters as in Panel A were used [15]. (C) Examples of parameter distributions obtained from fitting model neurons to electrophysiologically recorded cells. Histograms (black) and derived parameter distributions used for network specification (red) illustrating parameters with an approximately Gaussian (gL, left), Gamma (τw, middle), and exponential distributional form (b, right).
Table 1. Neuron parameters.
| parameter | PC L2/3 | FS | BT | MC | PC L5 |
|---|---|---|---|---|---|
| C (pF) | 164.96 (59.11) | 59.58 (10.59) | 79.36 (14.83) | 81.12 (28.96) | 251.81 (82.61) |
| gL (nS) | 7.04 (1.72) | 5.34 (0.91) | 3.99 (0.51) | 2.98 (0.55) | 7.62 (2.09) |
| EL (mV) | -85.00 (5.40) | -85.15 (5.81) | -84.63 (4.71) | -72.20 (7.64) | -80.57 (6.71) |
| ΔT (mV) | 21.44 (6.42) | 19.58 (8.50) | 19.02 (4.08) | 22.30 (10.44) | 24.47 (5.96) |
| τw (ms) | 121.78 (41.19) | 15.15 (2.71) | 43.56 (21.89) | 60.13 (15.05) | 107.48 (64.08) |
| b (pA) | 7.29 (6.80) | 34.87 (37.88) | 6.65 (7.19) | 5.37 (5.78) | 8.27 (12.66) |
| Vr (mV) | -118.20 (38.14) | -90.16 (15.16) | -152.67 (49.15) | -55.89 (9.65) | -69.98 (14.45) |
| Vth (mV) | -52.40 (5.43) | -58.79 (9.82) | -59.95 (4.67) | -38.01 (6.03) | -48.69 (7.18) |
| Vup (mV) | -45.91 (7.22) | -51.01 (5.59) | -55.46 (4.39) | -36.94 (2.55) | -44.12 (7.28) |
Mean and standard deviation of the parameters of the simpAdEx model for the five different neuron types used in the network (PC: Pyramidal cell, FS: Fast-spiking interneuron, BT: Bitufted interneuron, MC: Martinotti cell)
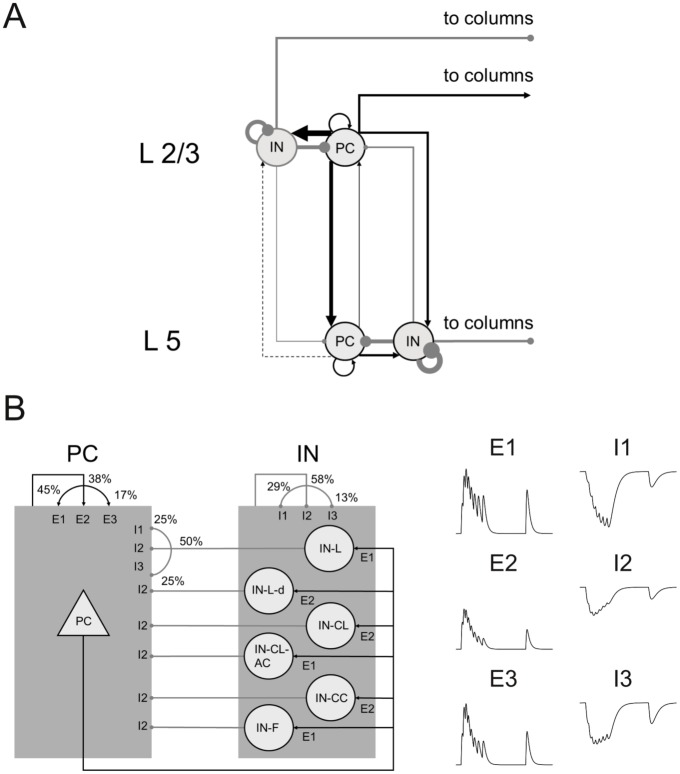
Anatomically, the network is divided into two laminar components, representing the superficial layers L2/3 and deep layer L5 (Fig 2A). Neurons are distributed over the five cell types in each layer based on estimates from the literature (Table 2). The neurons are randomly connected with different connection probabilities pcon for each pair of cell types according to the literature [18–27], including local clusters of higher connectivity [28, 29]. The neurons are assumed to be organized in a single column and horizontal spatial distance is not taken into account. However, all neurons receive a constant background current (i.e., without fluctuations) that represents synaptic connections from outside the network, both within and outside the same column (see section “Admissable and realistic range of input currents” below). Since these currents were constant, all irregularity was produced intrinsically within the simulated network.
Fig 2. Anatomical and synaptic properties.
(A) Laminar structure of a single network column. Arrow widths represent relative strength of connections (black: excitatory, gray: inhibitory), i.e. the product of connection probability and synaptic peak conductance. (B) Left panel: Distribution of three different short-term plasticity types over different combinations of pre- and postsynaptic neuron types. Arrows from or to one of the shaded blocks (rather than from or to a single neuron type) denote connection types that are identical for all excitatory (PC) or inhibitory (IN) neurons. Where all three types are drawn, they are randomly distributed over all synapses between these two neuron types according to the probabilities given in the figure. Right panel: Illustration of the postsynaptic potential in response to a series of presynaptic spikes for three types of short-term synaptic plasticity for excitatory (E1 to E3) and inhibitory synapses (I1 to I3).
Table 2. Cell numbers.
| Layer | PC | IN-L | IN-CL | IN-CC | IN-F |
|---|---|---|---|---|---|
| L2/3 | 47% | 3.1% | 2.6% | 2.6% | 2.1% |
| L5 | 38% | 0.5% | 0.5% | 1.8% | 1.8% |
Relative numbers of cells for each type. PC: pyramidal cell, IN: interneuron, see Materials and Methods for interneuron subtypes.
Neurons are connected by conductance-based synapses (AMPA, GABAA and NMDA) with kinetics estimated from electrophysiological data, short-term synaptic plasticity [30] that is matched to the types of the connected neurons [31, 32], synaptic delays and random failure of synaptic transmission [33–36]. Distributions of synaptic weights (log-normal [37]) and delays (Gaussian) were extracted from the literature (Table 3). The average connection strength (connectivity pcon times synaptic peak conductance gmax) between pyramidal cells and interneurons in the different columns and layers is indicated by the width of the arrows in Fig 2A.
Table 3. Synaptic parameters.
| pre | post | pcon | gmax [mV] | τD [ms] |
|---|---|---|---|---|
| PC L2/3 | PC L2/3 | 0.139 | 0.84 (0.49) | 1.55 (0.31) |
| PC L2/3 | PC L5 | 0.233 | 0.95 (0.39) | 1.91 (0.17) |
| PC L5 | PC L2/3 | 0.045 | 0.84 (0.28) | 2.75 (0.18) |
| PC L5 | PC L5 | 0.081 | 0.88 (0.67) | 1.56 (0.44) |
| PC L2/3 | IN-L L2/3 | 0.325 | 1.34 (1.09) | 0.96 (0.25) |
| PC L2/3 | IN-CL L2/3 | 0.159 | 0.47 (0.20) | 0.96 (0.25) |
| PC L2/3 | IN-F L2/3 | 0.290 | 0.25 (0.20) | 0.96 (0.25) |
| PC L2/3 | IN-L L5 | 0.087 | 0.77 (0.86) | 1.18 (0.13) |
| PC L2/3 | IN-CL L5 | 0.080 | 0.27 (0.16) | 1.18 (0.13) |
| PC L2/3 | IN-F L5 | 0.150 | 0.14 (0.16) | 1.18 (0.13) |
| PC L5 | IN-K L2/3 | 0.188 | 1.52 (0.63) | 1.05 (0.08) |
| PC L5 | IN-CL L2/3 | 0.092 | 0.53 (0.12) | 1.05 (0.08) |
| PC L5 | IN-F L2/3 | 0.168 | 0.28 (0.12) | 1.05 (0.08) |
| PC L5 | IN-L L5 | 0.333 | 1.74 (1.12) | 0.60 (0.20) |
| PC L5 | IN-CL L5 | 0.080 | 0.88 (0.70) | 0.60 (0.20) |
| PC L5 | IN-F L5 | 0.362 | 0.28 (0.30) | 0.60 (0.20) |
| IN-L L2/3 | PC L2/3 | 0.466 | 2.30 (1.98) | 1.25 (0.18) |
| IN-CL L2/3 | PC L2/3 | 0.301 | 0.13 (0.48) | 1.25 (0.18) |
| IN-F L2/3 | PC L2/3 | 0.710 | 1.91 (3.83) | 1.25 (0.18) |
| IN-L L2/3 | PC L5 | 0.217 | 1.07 (0.92) | 1.54 (0.10) |
| IN-CL L2/3 | PC L5 | 0.140 | 0.06 (0.22) | 1.54 (0.10) |
| IN-F L2/3 | PC L5 | 0.330 | 0.89 (1.78) | 1.54 (0.10) |
| IN-L L5 | PC L2/3 | 0.039 | 0.10 (0.01) | 1.44 (0.04) |
| IN-CL L5 | PC L2/3 | 0.027 | 0.04 (0.01) | 1.44 (0.04) |
| IN-F L5 | PC L2/3 | 0.040 | 0.07 (0.06) | 1.44 (0.04) |
| IN-L L5 | PC L5 | 0.274 | 0.69 (0.10) | 0.82 (0.09) |
| IN-CL L5 | PC L5 | 0.173 | 0.30 (0.05) | 0.82 (0.09) |
| IN-F L5 | PC L5 | 0.282 | 0.50 (0.40) | 0.82 (0.09) |
| IN L2/3 | IN L2/3 | 0.250 | 1.35 (0.35) | 1.10 (0.40) |
| IN L5 | IN L5 | 0.600 | 1.35 (0.35) | 1.11 (0.40) |
Mean and standard deviation of the parameters of the synapses connecting the different pre- and postsynaptic neuron types (pcon: connection probability, gmax: peak conductance, τD: transmission delay. Cross-column interneurons (IN-CC) have the same parameters as local interneurons (IN-L), as they are both basket cells).
Wherever possible, we used data from the rodent prefrontal cortex, or at least agranular cortices such as the motor cortex, which in rodents shows a similar layered anatomy as the PFC. Apart from the missing granular layer 4, specific features of the rodent PFC that are modeled here include an increased fraction of reciprocal compared to unidirectional connections [32], longer NMDA time constants than in other areas [38, 39], and a uniquely prefrontal distribution of short-term synaptic plasticity properties for connections among pyramidal cells [32].
Reproduction of in vivo activity
To assess whether the network model can reproduce the dynamics of real prefrontal neurons in vivo, we compared measures computed from the model with those from electrophysiological data, as well as with a number of findings from the literature. Unless otherwise stated, we simulate a single column with 1000 neurons and apply a constant DC current of 250 pA to all pyramidal cells and 200 pA to all interneurons. These currents are the only parameters that are not directly obtained from experimental data. As discussed below, appropriate values for these currents were derived by inferring from lumped-population input simulations the amount of current produced by a network of realistic size, set up with the very same structure as the explicitly modeled network.
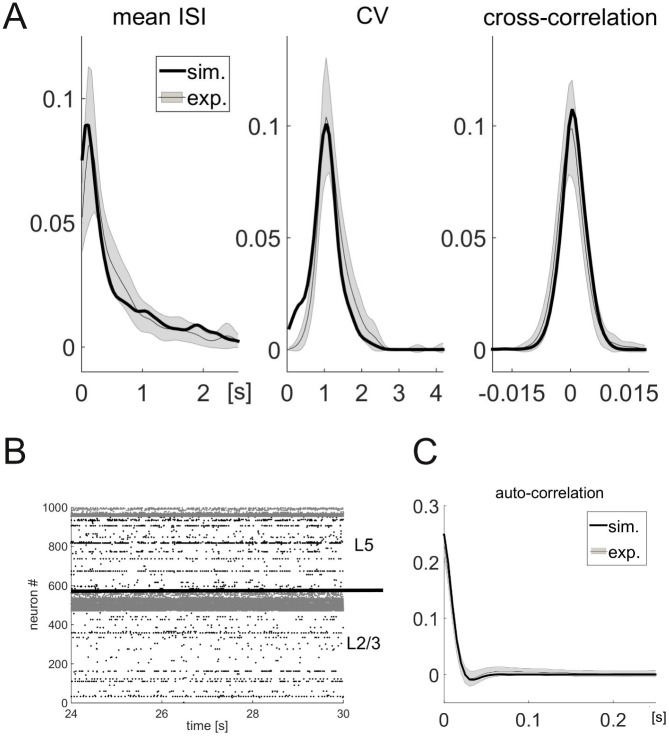
Spike-train statistics. All experimentally recorded spike trains (kindly provided by Dr. Christopher Lapish, Indiana University Purdue University, Indianapolis, see [40] for details) were first segregated into statistically stationary segments to yield estimates of spike train statistics that reflect in vivo baseline activity, free from task-related responses (not modeled here) or other potential confounds [41]. For consistency, the same procedure was applied to the simulated spike trains, although, strictly, these were stationary by simulation setup. From all jointly stationary segments, the mean 〈ISI〉, coefficient of variation CV, and autocorrelation function of the inter-spike intervals (ISIs) were computed for each individual spike train, as well as the zero-lag cross-correlation CC(0) between pairs of neurons (Fig 3).
Fig 3. Spiking statistics of simulated PFC model networks.
(A) Comparison of relative frequency histograms for three different spike time statistics between recordings from an in vivo experiment (gray, see text for details) and from the simulation with input currents Iex = 250 pA, Iinh = 200 pA (black). The shaded region represents the mean ± the SEM at each point of the experimental distribution. (B) Raster plot of the spike times over the last six seconds of the simulation. The two layers (L2/3 and L5) are separated by a black line, pyramidal cells (PC) are in black, interneurons (IN) in gray. (C) Auto-correlation function of the inter-spike intervals of the experimental recordings (gray) and the network simulations (black).
The in vivo data show very low zero-lag cross-correlations between neuron pairs (2.4 ⋅ 10−4 ± 2.5, mean ± SD) and CV s near one (1.04 ± 0.33), consistent with the proposal of an “asynchronous-irregular” (AI) state of cortical dynamics (although the correlations theoretically proposed for the AI state are usually even at least one order of magnitude larger than obtained here [42]). The average single-cell ISIs follow a monotonically decreasing distribution with a mean comparable in size to the standard deviation (570 ± 610 ms), but with a heavy tail that is better described by a log-normal or beta-2 distribution [43] rather than an exponential distribution. The autocorrelation function shows a rapid decay with small negative flanks (half-width at half maximum: 10.1 ± 1.1 ms, minimum: 64.6 ± 69.9 ms, mean ± SD).
Without further tuning of network parameters beyond their derivation from slice-physiological and anatomical data, all these in vivo statistics are well reproduced by the model (Fig 3). Two-sample Kolmogorov-Smirnov tests did not find notable differences between experimental and simulated distributions in any of the statistics (CV : p = 0.26, KS(29) = 0.28; mean ISI: p = 0.4, KS(29) = 0.23; CC: p = 0.4, KS(29) = 0.24), indicating that simulated distributions were not statistically distinguishable from the experimental ones. The asynchronous- irregular firing with low rates is also seen in the raster plot of spike times (Fig 3B).
Low fraction of spiking neurons and layer-dependent firing rates. Fig 3B reveals a relatively low fraction of spiking pyramidal cells in both layers—only 22% of the cells emitted more than 10 spikes during the 30s of simulated time, which will be used as the definition of “spiking neurons” throughout the paper, in line with [44–46]. Comparing the neural and synaptic parameters of those neurons which fire at a sufficiently high rate (> 0.33 Hz) and those which do not (≤ 0.33 Hz), we find that only the rheobase (and the cell parameters that contribute to it) differs between the two populations: Spiking neurons have rheobases at the lower end of the distribution (42.9 ± 2.1 pA), compared to 69.0 ± 1.6 pA for non-spiking neurons (mean ± SEM; p = 3.5 ⋅ 10−20, t(997) = 9.4, two-sided t-test), some of them even firing spontaneously (called “generator neurons” [47]).
While neurons firing at very low rates may go undetected using extracellular single-unit recordings, recording techniques that are less biased toward spiking neurons, such as calcium imaging or in vivo patch-clamp, often reveal a large fraction of neurons that are mostly silent (“dark matter theory” of neuroscience, [44–46]). Consistent with these results, the fraction of neurons with more than 10 spikes rarely exceeded 40% in simulations with in vivo-like firing patterns (see section “Admissible and realistic range of input currents” below). This can be explained by the way the neurons are activated: While most neurons receive a background current above their rheobase, the high firing rates of the interneurons (Fig 3B) lead to an average membrane potential in the pyramidal cells below the firing threshold (mean difference: -17.3mV, range: -37.2 to -2.2mV for the example shown in Fig 3) that is occasionally kicked above threshold by random fluctuations. This means that the firing rate is mostly determined by the amplitude of the fluctuations of the membrane potential (see below for statistics). These results are qualitatively conserved across the range of input currents for which the overlap between experimental and simulated distributions is reasonably high.
Membrane potential and local field potential statistics. In addition to the spike data, we also compared the membrane potential statistics and LFP signals between simulation and experiments. For the simulated network, we observed a broad range of membrane potential fluctuations (after removing spike events; Fig 4A; 3.28 ± 0.72 mV, mean ± SD; range between 0.72 mV and 11.23 mV). We compared this distribution of standard deviations with those from in vivo patch-clamp recordings from 10 putative pyramidal cells during up-states in anesthetized adult rodent PFC (kindly provided by Dr. Thomas Hahn, Central Institute of Mental Health and BCCN Heidelberg-Mannheim). The simulated distribution is less than one SEM away from the average of the experimental distribution (pooled over all data sets) for most bins, and a Kolmogorov-Smirnov test (see Materials and Methods) does not show a significant difference (p = 0.45, KS(29) = 0.23). The range of membrane potential fluctuations in the model and in the recordings used here is also consistent with values found in the literature [48, 49].
Fig 4. Comparison of simulated membrane and local field potentials with experiments.
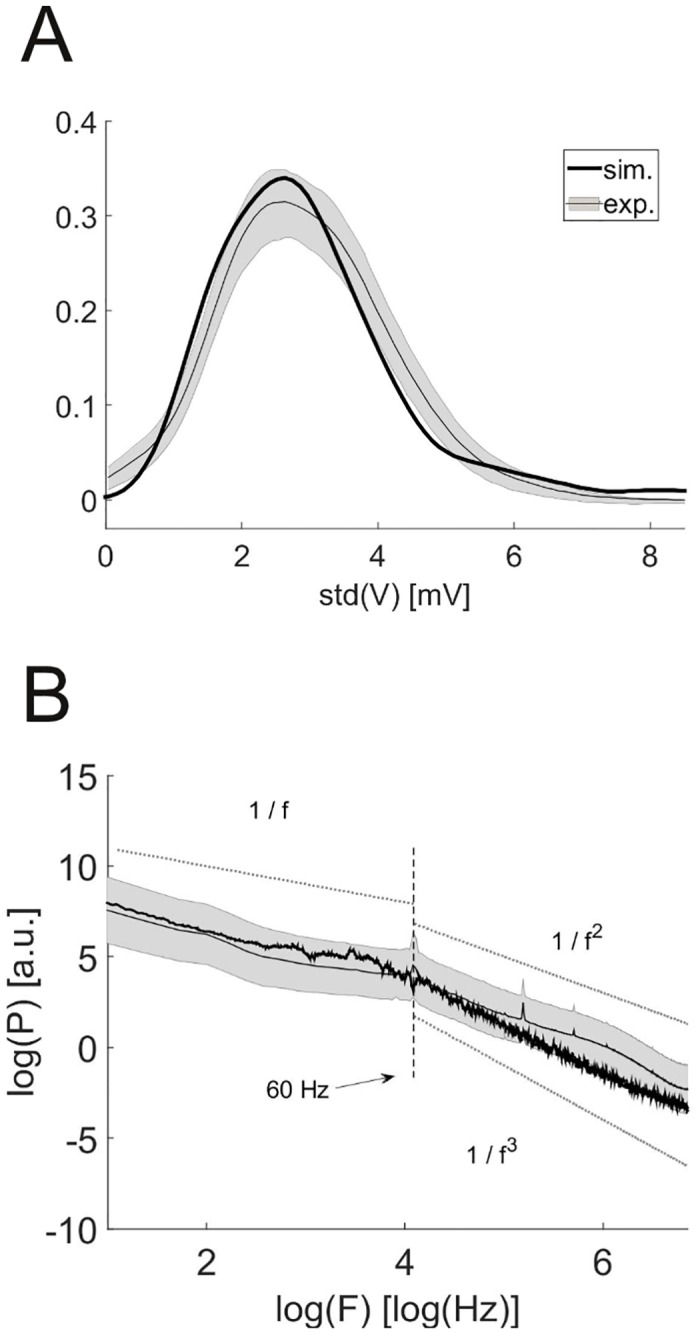
(A) Estimated distribution of the standard deviation of the membrane potential from anaesthetized rats (gray) and simulated neurons (black) with non-zero firing rates. (B) Power spectrum of the local field potential obtained from experiments (gray) and simulations (black). The dotted lines illustrate the three power laws. The shaded region represents the mean ± the SEM at each point of the experimental distribution, as in Fig 3.
The local field potential (LFP) in the model was estimated as the sum of all synaptic currents (allowing excitatory and inhibitory currents to partially cancel). This is a reasonable approximation to the standard model of the LFP [50] under the assumption that all neurons are confined in a small volume of cortical space. We computed the power spectral density of this model-derived signal and of the LFP signals obtained from the in vivo recordings (Fig 4B). Up to a constant offset (that has been removed in the figure), the spectrum of the simulated LFP is less than one SEM away from the average estimated from the experimental recordings (from awake, behaving animals, also provided by Dr. Christopher Lapish [40]) at most of the frequencies. Both spectra follow a 1/f power law for frequencies below 60 Hz and change their scaling behavior for higher frequencies, consistent with LFP spectra described in the literature [51–53] (the fluctuations in the simulated curve are stochastic in nature, i.e. there is no systematic deviation from the 1/f behavior across different simulations). For frequencies beyond 60 Hz, the experimental spectrum is well described by a 1/f2 power law, while the simulated one rather follows a 1/f3 relation. Both scaling behaviors have been reported in the literature (1/f2 [52, 54], 1/f3 [51]), and the difference may result from the simplifications made in the computation of the simulated LFP, e.g. neglecting the spatial integration of currents in extracellular space or the contribution of active currents [14].
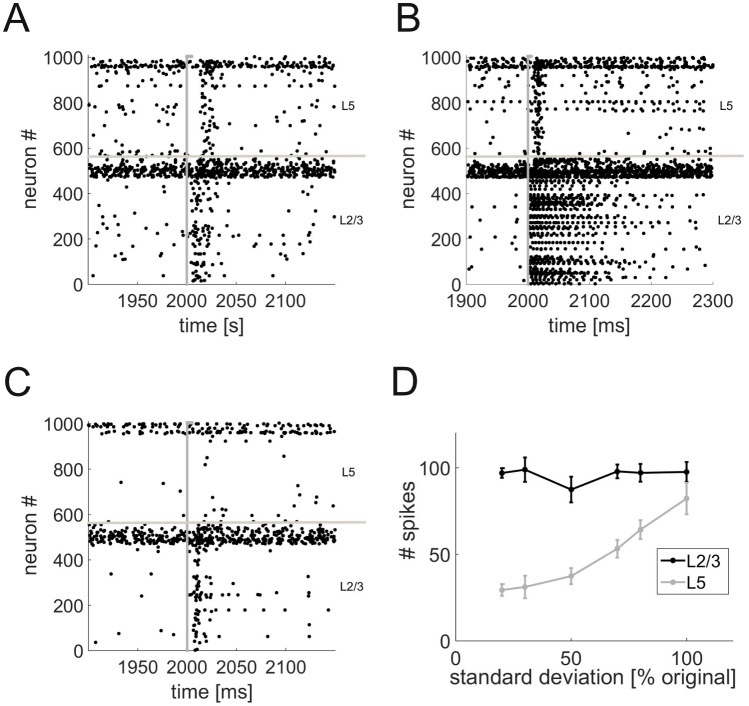
Transient information transfer and the role of neuronal heterogeneity. We next examined how neurons in L2/3 and L5 would respond to a simple stimulus simulated by a brief series of spikes at high rate (250 spikes within 5 ms) from a virtual (not explicitly simulated) “input population” connected to 10% of the pyramidal cells in L2/3 (cf. Table 3). The stimulus induces a number of spikes in L2/3, and with a short delay also in L5 (Fig 5A). The delays (L2/3: 8.9 ± 1.1 ms; L5: 17.7 ± 1.2 ms, mean ± SD) are similar to values that have been reported in the literature (e.g. 3.4 ± 0.5 ms in L2/3 and 16.6 ± 1.2 ms in L5 [55]). Note that these delays are significantly longer than the fixed synaptic delays (below 2 ms, see Materials and Methods) and arise from the dynamics of the neurons and the kinetics of the synapses (c.f. [56]). For a sufficiently strong stimulus (e.g. 500 spikes within 5 ms), the neurons in L2/3 show a brief period (100–150 ms) of persistent activity (Fig 5B).
Fig 5. Propagation of transient input.
(A) Raster plot of the spike times in the network in response to an external input (gray line) to 10% of the L2/3 pyramidal cells. The input currents are Iex = 250 pA, Iinh = 200 pA. (B) Same as Panel A, but with a stronger (higher rate) external stimulus (see text for details). (C) Same as Panel A, but with neuron parameter variability reduced by 80% (standard deviation set to 20% of its original value). (D) Number of spikes in response to the input as a function of neuron parameter variability. Each data point is the mean ± SEM over a number of repetitions.
The transmission of transient stimuli between layers crucially depends on the heterogeneity of the neuronal parameters. With a 80% reduction in the variance of all parameter distributions (but no change in the means), the stimulus only elicits a response in L2/3, but is not transmitted to the output layer L5 anymore (Fig 5C). Indeed, L2/3 activity is almost independent of neuronal variability, whereas the number of spikes in L5 systematically decreases as the standard deviation of neuronal parameters is reduced (Fig 5D).
To further examine the transmission dynamics, we reproduced an in vitro experiment with suppressed inhibition [57] which showed that input in L2/3 resulted in an epileptiform spread of activation across the whole network under this condition, whereas the same input in L5 did not. We mimicked this setup by reducing the inhibitory synaptic weights in the network to 30% of their original values and inducing a strong stimulus (see above) in each of the two layers, while varying the peak conductance gmax of the synaptic connection between the mimicked Poisson input population and the network. For moderate connection strengths (gmax = 2), only a fraction of the network responds, and the number of spikes elicited by the network is much larger if the stimulus is injected in L2/3 (404 ± 116, mean ± SD) compared to a stimulus in L5 (118 ± 33). Higher connection strengths (gmax = 20) reliably drive the network into an “epileptic state” (transient high-rate response from all neurons in the network) for a stimulus in L2/3. In contrast, this state was never reached for an input in L5, consistent with the experimental results in [57].
Conditions for in vivo-like dynamics
In the previous section we showed that the model can reproduce a wide range of characteristics of neural activity in vivo. Here, we assess how the reproduction quality of in vivo-like behavior depends on those parameters of the model which were only loosely constrained by experimental data. We restrict this analysis to the spike series statistics 〈ISI〉, CV and CC(0).
Admissible and realistic range of input currents. The background currents have so far been treated as free parameters, as such estimates are difficult to obtain or at least have not been reported experimentally. We address this in two ways: First, we systematically vary these four currents and assess the similarity between experimental and simulated spike time distributions using Kolmogorov-Smirnov statistics as before. Second, we estimate the required background currents from the simulation itself, using the assumption that the simulated network is embedded in a larger, but structurally identical network from which these currents originate.
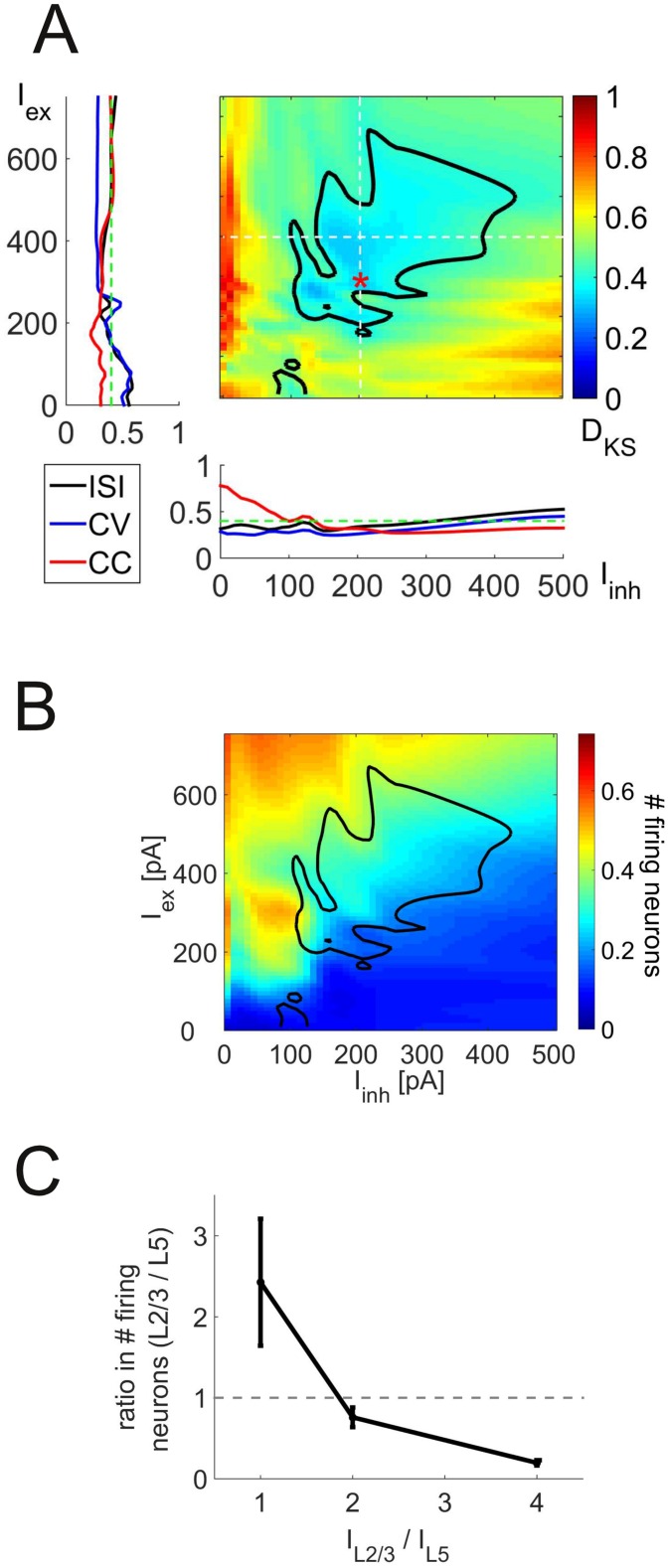
Fig 6A shows the Kolmorgorv-Smirnov test statistic DKS as a function of Iex and Iinh, where and (see below for a discussion of laminar differences in the input currents). The figure reveals that the overlap between experimental and simulated distributions is acceptable (p > 0.05 for the two-sample Kolmogorov-Smirnov test, i.e. failure to reject the null hypothesis H0 of equal distributions for the two samples, see Materials and Methods) for a wide region of Iex and Iinh values (delimited by the black isocline in Fig 6A, associated with DKS values below 0.4). More specifically, simulated CV and mean ISI distributions become indistinguishable from their experimental counterparts as Iex increases, while the overlap with the ISI distribution decreases again for very high Iex values (Fig 6A, left inset). Both CV and mean ISI deviate from the experimental distributions as Iinh increases. CC, on the other hand, matches well with the experiments for high Iinh values (Fig 6A, lower inset). As mentioned above, the fraction of firing neurons is quite low in most networks showing in vivo-like firing patterns, typically between 20 and 30%, as shown in Fig 6B (blackly delimited region gives the empirically acceptable parameter regime copied from Fig 6A).
Fig 6. Dependence of network behavior on the magnitude of synaptic background inputs.
(A) Maximum of the Kolmogorov-Smirnov test statistic (DKS) comparing the experimental and respective simulated distributions for the mean ISI, CV, and cross-correlation as a function of input currents into excitatory (Iex) and inhibitory (Iinh) neurons in layer 2/3. DKS values within the blackly delineated area have p values larger than 0.05 for each of the three tests. The insets show the three individual DKS values as a function of one of these input currents alone (for Iinh = 200 pA in the left and Iex = 400 pA in the lower inset, indicated by the white dotted lines). DKS values above 0.4 (green lines) correspond to significant (p = 0.05) deviations from experiments in the given distribution. The red asterisk indicates the parameter set used for the simulations presented in the previous figures. (B) Fraction of neurons emitting at least 10 spikes during a 30 sec simulation period for the same currents used in Panel A. The blackly delineated area was copied from Panel A and superimposed on the current graph. (C) Ratio of the number of spiking pyramidal cells between layers 5 and 2/3 as a function of the input current ratio into pyramidal cells in layers 2/3 and 5. Each data point represents the mean ± SEM over three different ratios of input currents into interneurons in layers 2/3 and 5 and a number of and values.
The ratio of inputs into the two layers, and , does not have a strong influence on these results within the tested range (mean DKS ± SEM: 0.31 ± 0.05, 0.32 ± 0.05 and 0.35 ± 0.06 for ratios of 1, 2 and 4, respectively), but does of course affect the relative firing rate between the two layers. In vivo experiments found that firing rates are considerably higher in L5 compared to L2/3 pyramidal cells (3–20 times [27]). This condition is fulfilled in our model as long as L2/3 receives less or the same input as L5 (Fig 6C).
To estimate which range of I values could be realistically assumed, we tested whether a substantially larger network than the 1000-neuron-network simulated here would produce mean synaptic currents that are large enough to self-sustain in vivo-like activity (i.e. within the blackly circumscribed regions in Fig 6A). In this case, the activity in the large network and the small network (the latter driven by the currents from the larger one) would be indistinguishable, and the in vivo-like activity would be supported by the larger network. We increased the size of the network either by changing the density of neurons or by adding input from nearby columns (see “Estimation of background currents” in Materials and Methods).
Fig 7 shows the mean synaptic current into pyramidal cells and interneurons in L2/3 and L5 that would result from the reduced equivalent-population input models described in Materials and Methods if the network size was varied through the number of columns (Fig 7A) or the density of neurons within columns (Fig 7B, both figures showing currents averaged over the values of the other independent variable, i.e. neural density or number of columns, respectively). The shaded areas show the ranges for Iex (blue) and Iinh (red) within which these currents would produce in vivo-like activity (DKS < 0.4). Note that it is sufficient that one of the two layers receives a current above the lower bound, as it will push the other layer into the right regime by cross-layer synaptic connections. The upper bound, on the other hand, may not be exceeded by either of the two layers, as this would push the other layer beyond its upper bound as well. It is apparent that these conditions are fulfilled already for (spatially) relatively small networks (∼ 5 columns), and currents saturate as network size grows further (Fig 7A). By increasing the neuron density, on the other hand, the input currents increase monotonically over a wide range (Fig 7B, averaged over all column numbers ≥ 5). Mean synaptic currents sufficient to drive the network into the experimentally observed regime arise for densities between 19,000 and 44,000 neurons per mm3. This range overlaps with densities found in anatomical studies (30,000 to 90,000 neurons per mm3 [58–60]; horizontal dotted lines).
Fig 7. Scaling of total synaptic input current with network size.
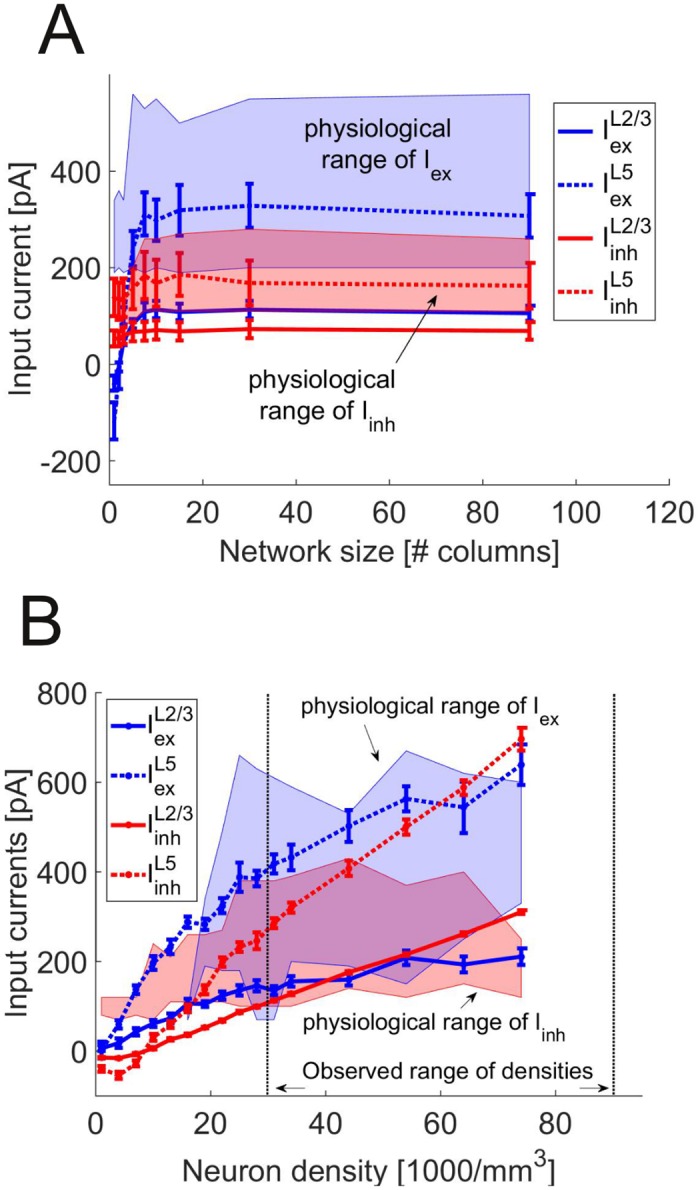
(A) Synaptic input current as a function of the number of columns. Shown are the averaged values over different neuron densities (mean ± SEM) as a function of column number for the inputs into L2/3 pyramidal cells (solid blue), L2/3 interneurons (solid red), L5 pyramidal cells (dotted blue) and L5 interneurons (dotted red). The region of currents which yield in vivo-like behavior (cf. black region in Fig 6A, DKS < 0.4) is marked in blue for Iex and in red for Iinh. (B) Same as in A, but synaptic input as a function of total cell density, averaged over column numbers ≥ 5. The dotted horizontal lines show the upper and lower bound of densities found in anatomical studies.
Variation of synaptic parameters. We attempted to estimate all synaptic parameters from data reported in the literature. Given that these come with some uncertainty and variation, however, we explored how sensitive the network behavior is with respect to changes in mean synaptic peak conductances and their distribution, synaptic time constants, and the GABAA reversal potential. All these parameter variations were performed for a range of different background currents and averaged results are reported.
The GABAA reversal potential was initially set to -70mV, which is well within the range of the values reported in the literature [19, 24, 55, 61]. Within the physiologically reasonable range from -90 to -60mV [62], the divergence between simulated and experimental distributions (as assessed by the KS test statistic) increases with (Fig 8A). At the same time, the standard deviation of the membrane potential decreases. The time constants of the synaptic kinetics also turned out to be important for the agreement with in vivo data: While small changes are acceptable, both very fast and very slow GABAA kinetics strongly diminish the agreement with the experimental data (DKS = 0.99 for τon = 0.6 ms and τoff = 8 ms and DKS = 0.85 for τon = 12 ms and τoff = 160 ms). The NMDA time constants have less effect, unless they are very strongly increased (DKS = 1.0 for τon = 17.2 ms and τoff = 300 ms, compared to values of τon ≤7 ms and τoff ≤ 100 ms reported in the literature [38, 39]). The effects of the mean synaptic peak conductances are shown in Fig 8B. While small to moderate changes ( ± 50%) have no significant effect, a strong decrease in the inhibitory synaptic efficiencies leads to a significant mismatch with the in vivo statistics.
Fig 8. Effect of synaptic parameter changes on network activity.
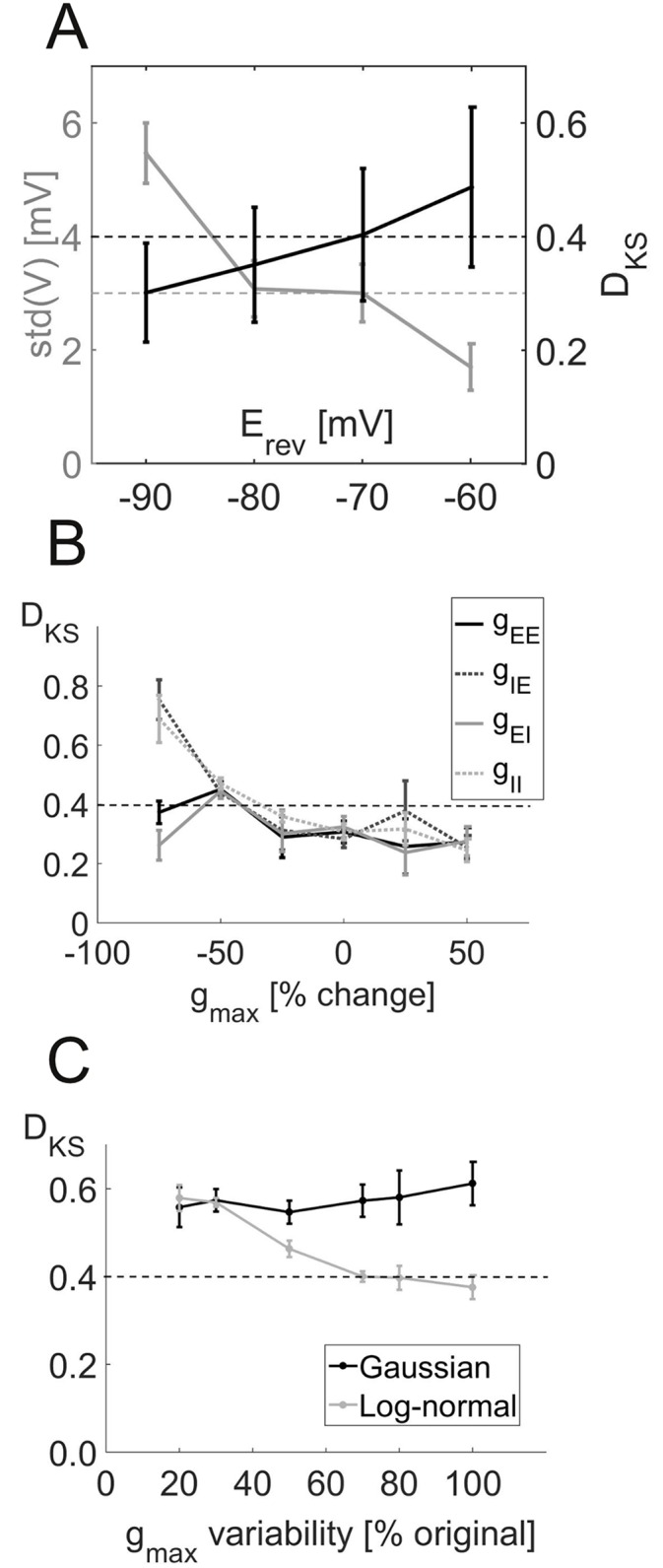
(A) Maximum of the Kolmorov-Smirnov test statistics (DKS) comparing the three experimental and simulated distributions (black) and standard deviation of the simulated membrane potential (gray) for different GABAA reversal potentials. Each data point is the mean ± SEM over several values of input currents. The black line denotes the DKS limit of 0.4 above which differences become significant (p ≤ 0.05), and the gray line marks the average of the experimentally observed standard deviations (cf. Fig 4A). (B) DKS values as a function of percent change in overall synaptic peak conductances between pyramidal cells (E) and interneurons (I). The dotted line denotes the critical DKS value of 0.4 (see above). (C) DKS values for different values of the standard deviation of the synaptic peak conductances using either the original log-normal distribution (gray curve) or a Gaussian distribution with the same mean and standard deviation (black curve). As above, the dotted line marks the critical DKS value of 0.4. In all figures, each data point shows the mean ± SEM over the DKS values for a number of different input currents.
Apart from the mean, we also analyzed how the distribution of the synaptic peak conductances affected in vivo-like behavior by either reducing the variability or drawing them from a normal rather than a log-normal distribution (conserving mean and standard deviation). Reducing the variability of the synaptic weights increased the mismatch between empirical and simulated distributions (Fig 8C, gray line). Surprisingly, just changing the form of the underlying distribution from log-normal to normal, without changing its mean or standard deviation, had a similarly strong effect as a pronounced reduction in standard deviation (Fig 8C, black line), so both the variability as well as the functional form of the synaptic conductance distribution are crucial for reproducing spiking dynamics as observed in vivo. Without the long tail of the log-normal distribution, the network activity becomes much more synchronized (CC(0): 0.017 ± 0.006, mean ± SD) and exhibits strong bursts (CV : 1.81 ± 0.09, mean ± SD), while mean firing rates are not much affected (〈ISI〉: 420 ± 558 ms, mean ± SD).
Discussion
We presented a model of the prefrontal cortex which is entirely defined by electrophysiological and anatomical data, and is capable of reproducing a wide range of in vivo statistics, including properties of single spike trains and pairwise correlations, the power spectrum of the local field potential and the variability of the membrane potential. Importantly, this reproduction did not require specific tuning of model parameters towards in vivo behavior. In fact, variation of the synaptic parameters shows that the ability of the network to show in vivo-like behavior is robust against considerable changes. In particular, it is possible to increase or decrease the synaptic weights by up to 50% of their original value without significant changes in the prediction performance (Fig 8B). This keeps the model flexible to synaptic plasticity, i.e. the weights can be modified by task-related learning rules without changing the global activity of the network. The only variable that was not tightly constrained by in vitro data, the external input currents, showed a wide range of admissible values, within a range that would be produced by a network supposedly large enough to self-sustain activity. Despite the high biological validity, the model remains simple enough to allow for efficient simulation, due to the combination of a simple, but versatile neuron model and a complex network structure. To our knowledge, no other biophysical model currently exists that is as tightly constrained by the specific neuronal and synaptic properties of the prefrontal cortex and systematically compared to in vivo data as the one presented here.
Relation to other network models
The current model has a strong focus on its tight connection to data. Many existing network models of the neocortex are based on neurobiological findings as well [13, 14, 63–65], but the present model differs from them in two respects: The strict way in which the in vitro data is used to fix or systematically infer every detail of the model, and, more importantly, the quantitative test of the model’s validity on a wide range of in vivo findings. Recently, a few studies have also moved in this direction. Fisher et al. [66] proposed a model for the short-term memory circuit in the oculo-motor system of the adult goldfish. They fitted the model simultaneously to a range of anatomical, physiological and behavioral data. This approach gives a coherent picture of this particularly well-defined non-cortical system. Furthermore, Potjans and Diesmann [27] proposed a model of a sensory cortex network where the connection probabilities are thoroughly derived from in vitro studies. While the neuron parameters are generic and homogeneous, their focus is on the precise laminar and horizontal organization of the synaptic connections. They compare the results of their simulations with the baseline firing rates and flow of transient information through the different layers in vivo. These comparisons to experimental data are qualitative in character, as it is the case for most existing large-scale models of cortical networks [12–14, 67]. However, a few recent studies also made statistical comparisons on partial aspects of physiological data [68, 69]. It would be interesting to assess these models on a wider range of in vivo data as we proposed here, to see which degree of biological detail is sufficient to predict their key properties.
An important simplification made in the present model is the reduction to two laminar components, leaving out layer 4 and 6 as well as the long-range fiber bundles and interneurons in layer 1. While layer 4 is missing in rodent PFC, layer 6 is only weakly connected to the other layers in our reference connectivity maps, which are based on the motor cortex [57, 70, 71]. Thus, its inclusion in the network should not have a major impact on the results shown here. This is probably different in sensory networks, where layer 6 strongly interacts with both pyramidal cells and interneurons in layer 4 [72].
The relevance of synaptic and cellular heterogeneity
The model exhibits a low fraction of spiking neurons, consistent with results from recording methods such as calcium imaging, which are not biased towards high firing rates (“dark matter theory” of neuroscience [44–46]). As described above, this may partly result from the variance-driven firing of the neurons: The membrane potential is on average well below the spiking threshold, but large fluctuations still lead to occasional spiking. The size of the fluctuations and the low-rate, Poisson-like firing (CV ≈ 1) of the neurons is consistent with the high-conductance state theory [48] and balanced-state theory [42, 73]. We note that the irregular and highly asynchronous firing of the neurons [74] observed here is a generic property of the network that simply emerged from its parametrization through in vitro and anatomical findings.
There are two main determinants of the high-fluctuation regime of the model: First, variability in the membrane potential requires variability in the synaptic parameters and in particular, the fat tail of the log-normal distribution of the synaptic weights. Second, the range between the firing threshold Vup and the GABAA reversal potential must be sufficiently large, because below , all synaptic currents depolarize the cell, so the dynamical range for a balanced, variance-driven state is constrained between these two values.
Using the multivariate distributions of neuron parameters obtained from our in vitro recordings, we also observed that decreased cellular heterogeneity has a profound effect on the processing of transient stimuli. It prevents the transmission of stimulus-induced activity from L2/3 to L5. This phenomenon can be understood if one considers the rheobase distribution: Reduced heterogeneity removes those neurons that originally had a very low or even negative rheobase. These are the ones which are highly susceptible to even small inputs and form a small but significant fraction of L5 neurons that were activated by the transient synaptic input from the L2/3 cells. Given that L5 provides the majority of output to other brain areas, impaired transfer of stimuli to this layer may lead to major impairments in information processing.
Thus, apparently quite subtle changes in the distributional properties of synaptic and cellular parameters (not affecting their means) may lead to major changes in network dynamics and functional connectivity among columns or areas, effects that have been proposed to underlie major psychiatric conditions like schizophrenia [8, 9].
Self-sustained activity of the PFC
By varying the total input from a virtual population designed according to the same principles as the actually simulated network, we provided evidence that a larger network than the one actually simulated with anatomically realistic neuron densities should be capable of self-sustaining in vivo-like spiking modes. Although we did not demonstrate self-consistency in a strict sense, we have shown that the background currents into the smaller, simulated network needed to yield in vivo-like behavior are consistent with the range produced by a much larger network of anatomically reasonable size. For currents within the blackly delimited region of Fig 6A, the spike train distributions are statistically indistinguishable from the in vivo statistics, and the background currents that would result from scaling up the simulated network to anatomically realistic size lie exactly within this regime. This analysis implies that in vivo-like activity can be self-sustained in a larger network with the same anatomical layout as explicitly simulated here, as it has been observed for instance in deafferented cortical slabs [75], while e.g. the thalamus or other sub-cortical structures may provide transient, stimulus-related input or modulate the overall activity of the network [76].
Interestingly, the currents produced by this procedure are much higher in L5 compared to L2/3 (Fig 7), as required for the much higher firing rates observed in vivo [27]. At first glance, this seems counterintuitive, as L2/3 neurons receive input from neighboring columns, while L5 neurons do not (see “Estimation of background currents” in Materials and Methods). However, L5 also receives strong inputs from L2/3, while the inverse projections are much weaker (Fig 2A). Thus, once L2/3 neurons receive enough input from other columns to spike, they drive L5 much stronger than themselves.
In terms of space, input from just a few columns is sufficient to drive the network, as connectivity rapidly decays over the cortical extent. Nevertheless, a single column is not sufficient for driving the network because of the higher fraction of excitatory synapses in long-range connections and the more local connectivity of interneurons. This is consistent with recent experimental studies [60, 77] and earlier results from deafferented cortical slabs [75] (but see [78]).
Possible applications
In this study, we have focused on the resting state of the network. However, it may also be used as a foundation for more functional investigations of cognition. For instance, the clusters of increased synaptic connectivity may serve as building blocks for cell assemblies [29] which can be used to represent behavioral rules [3, 40] or transient stimuli that need to be kept in working memory [64]. Moreover, the fast and fully automatized framework for fitting the neuron model to in vitro data [15] opens a convenient way to test the network effects of genetic or pharmacological manipulations: Recordings from neurons that underwent such a manipulation can be used by the very same fitting procedure as employed for wildtype or control cells, resulting in different parameter sets that can be plugged into the network to assess their implications for network behavior. Likewise, this could be done for the synaptic parameters using paired recordings and recent methods to fit the parameters of short-term synaptic plasticity models to these data [79].
In summary, we have provided a prefrontal cortex network model here with single cells and synapses strictly parametrized through in vitro electrophysiological findings (no specific tuning or adjustment of synaptic currents to compensate for simulated network size), with realistic cellular and synaptic heterogeneity, and with a structural layout derived from anatomical data. We have then systematically compared the full network activity to a number of spiking and correlation statistics from in vivo multiple single cell recordings in awake rodents, as well as LFP data from these animals, and estimates of membrane potential fluctuations from in vivo patch-clamping. Our model is therefore highly validated at the in vivo physiological level, yet it is computationally efficient by virtue of its computationally comparatively simple single unit design. We therefore hope that this network model can serve as a valuable tool in the further study of how physiological and anatomical properties relate to cortical network dynamics, and ultimately cognition, and how alterations of these properties may give rise to symptoms observed in various psychiatric conditions.
Materials and Methods
Model specification
Neuron model. Single neurons were modeled by the simplified adaptive exponential integrate-and-fire neuron (simpAdEx) introduced in [15]:
| (1) |
| (2) |
where C is the membrane capacitance, gL a leak conductance (with reversal potential EL), τm and τw are the membrane and adaptation time constants, respectively, Θ denotes the heavy-side function, and wV is the V-nullcline of the system as defined in Eq 1. Like the full AdEx [80], this model consists of one differential equation for the membrane potential V (including an exponential term with slope parameter ΔT, which causes a strong upswing of the membrane potential once it exceeds VT), and one for an adaptation variable w, and can reproduce a whole variety of different spiking patterns [15]. A spike is recorded whenever V crosses Vup, at which point the voltage is reset to Vr and spike-triggered adaptation is simulated by increasing w by a fixed amount b. The simpAdEx was derived from the full AdEx based on phase-plane considerations, effectively dissecting the dynamics into three different regimes (defined through their distance from the V-nullcline, see Eq 2), each of them approximated in a way that allows for closed-form expressions for the instantaneous and steady-state firing rates. This enables fast and efficient fitting of the model to f-I and I-V curves as commonly used to characterize the electrophysiological behavior of cells in vitro [15] (Fig 1A).
We had shown previously that this model, although estimated from f-I and I-V curves only, can predict spike times under in vivo-like conditions with high accuracy from physiological recordings not used for model fitting [15]. Different from [15], the upper voltage limit Vup was initially estimated from the inflection point of the voltage traces. This makes Vup an absolute firing threshold (as in the leaky integrate-and-fire neuron) and leaves Vth as a free parameter for the subthreshold dynamics, resulting in a shallower exponential rise to the spike, more akin to what would be expected from the action of persistent sodium channels [81] or L-type calcium channels [82].
We estimated neuron models for a large number of in vitro recordings from different cell types from the prefrontal cortex of rats and mice, namely layer 3 (n = 34) and layer 5 pyramidal cells (n = 108), fast-spiking (n = 32), and bitufted (n = 22) interneurons. Additionally, we extracted statistics (means and variances) about f-I curves and subthreshold dynamics of Martinotti cells from the literature [26, 83–88], and used these to construct 100 sets of f-I and I-V curves drawn from Gaussian distributions instantiated by the empirically estimated parameters. For each data set drawn from these distributions, Martinotti cell models were estimated. The pool of estimated models for each cell type defines a multivariate parameter distribution for each type of neuron, from which the final parameter sets for the 1000 neurons used in the network simulations were drawn. This joint parameter distribution for each cell type was initially modeled as a multivariate Gaussian, where marginal distributions not of Gaussian shape (as estimated from the empirical data) were first Box-Cox-transformed to adhere with the Gaussian assumptions. In a second step, the Box-Cox transform was inverted to regain the non-Gaussian shape of the marginal distributions (red curves in Fig 1C). The mean values and standard deviations of all model parameters for the different cell types are given in Table 1.
Network anatomy and connectivity. The network is divided into two laminar components, representing the superficial layers L2/3 and the deep layer L5 (Fig 2A). The network also includes a horizontal organization into distinct columns which are typically about 300μm wide [89], so the model is in principle suited to study information transfer between columns. For most part, however, the present analyses focuses on a single column which was found to be sufficient to reproduce in vivo-like resting-state activity, provided a source of constant external input (see below). The relative numbers of pyramidal cells and interneurons in each layer were taken from [58] who studied the rat motor cortex, as such data are not available for the PFC. Following [58], 47% of all cells were modeled as L2/3 pyramidal cells (L2/3-E), 10.4% as L2/3 interneurons (L2/3-I), 38% as L5 pyramidal cells, and 4.6% as L5 interneurons. With regards to the specific types of interneurons and their distribution across layers, we followed [90] and [91] and defined local interneurons (IN-L) with projections within the same layer and column as fast-spiking cells, cross-layer interneurons (IN-CL) as bitufted cells, and far-reaching interneurons (IN-F) with projections both outside of their column and layer of origin as Martinotti cells [90] (Table 1). The cross-column cells (IN-CC) have been classified as large basket cells [90, 92, 93], with electrophysiological properties resembling those of pyramidal cells [94]. Therefore, we used the same parameter distributions as for the pyramidal cells in the respective layer for this cell class. Markram et al. [90] also estimated the relative numbers of different types of interneurons within each cortical layer. Together with the classification above, these data result in the full distribution of cell types summarized in Table 2.
Neurons were randomly connected with distinct connection probabilities pcon for each pair of cell types as derived from a survey of about 40 studies, e.g. [95–99], most of which are reviewed in [22] and [27], except [18–21, 23–25] and [26]. Most of them performed whole cell or dual sharp electrode recordings in vitro in various neocortical regions of rats and mice. We also included a few studies using monkeys, ferrets and cats, as there are more studies from PFC in these species and some parameters were not available in rodents. Connection probabilities were further adjusted jointly with the connection weights to match data from photostimulation experiments as explained in detail below [57, 70, 71, 100, 101]. Pyramidal cells within the same layer form clusters of increased connection probability as defined by the “common neighbor rule” [28, 29] which states that the connection probability of two neurons increases linearly with the number of neurons they are both connected to. Furthermore, a fraction of 47% of the connections was specified as reciprocal [32], since the proportion of reciprocal connections was experimentally observed to be significantly higher than chance [32, 37]. For cross-column projections, connection probabilities exponentially decay with the distance from the column of origin. Data from rodent studies [29, 60, 77, 102, 103] suggest a wide range of spatial decay constants. We use the median from these studies, which is 114μm for pyramidal cells and 95μm for interneurons.
Apart from the recurrent synaptic connections within the network, we also introduced constant background currents that are fed into all neurons and which differ in strength for pyramidal cells and interneurons in layer 2/3 and 5. Appropriate values for these four streams of background inputs were determined using reduced equivalent-population input models (see below). It is emphasized that there was no source of external noise fed into the network, i.e. the external inputs consisted of just constant (DC) currents. Thus, all variability observed in the network arises from its internal dynamics.
Synaptic properties. Neurons were connected through conductance-based AMPA-, GABAA-, and NMDA-type synapses, with kinetics modeled by double exponential functions [104]
| (3) |
where X ∈ {AMPA, GABAA, NMDA}. The reversal potential Erev is set to zero for AMPA and NMDA, and to −70 mV for GABAA [19, 24, 55, 61]. The onset and offset time constants τon and τoff are set to 1.4 ms and 10 ms, respectively, for AMPA [39, 94], 3 ms and 40 ms for GABAA and 4.3 ms [105] and 75 ms [38, 39] for NMDA. NMDA conductances exhibit a nonlinear voltage-dependency s(V) due to their magnesium block at lower voltages [106]. Synaptic transmission delays τD were drawn from Gaussian distributions with means and standard deviations depending on the pair of connected cell types, with parameters derived from the same electrophysiological literature as the connection probabilities (see below; Table 3). Synaptic delays were chosen to increase linearly with distance from the target column [107], τD(d) = τD(1 + d), where d is the number of columns separating the connected neurons.
Synapses were also equipped with short-term plasticity dynamics implemented by the corrected version [108] of the Tsodyks and Markram model [30]
| (4) |
| (5) |
| (6) |
These recursive equations describe the dynamics of the relative efficiency a(tspk) across series of spikes, with initial conditions u1 = U and R1 = 1, where tspk is the interval between the (k − 1)th and the kth spike. Model parameters U, τrec and τfac were specified according to [31] and [32] who differentiated between facilitating (E1/I1), depressing (E2/I2) or combined (E3/I3) short-term dynamics, for both excitatory (E) and inhibitory (I) connections (Fig 2B, right panel; Table 4). The cell types of the pre- and postsynaptic neurons determine which of these classes is used for each individual combination (Fig 2B, left panel). Synaptic inputs were further subject to release failures with a probability of 30% [33–36].
Table 4. Short-term synaptic plasticity.
| parameter | U | τrec [ms] | τfac [ms] |
|---|---|---|---|
| E1 | 0.28 (0.02) | 194 (18) | 507 (37) |
| E2 | 0.25 (0.02) | 671 (17) | 17 (5) |
| E3 | 0.29 (0.03) | 329 (53) | 326 (66) |
| I1 | 0.16 (0.10) | 45 (21) | 376 (253) |
| I2 | 0.25 (0.13) | 706 (405) | 21 (9) |
| I3 | 0.32 (0.14) | 144 (80) | 62 (31) |
Mean and standard deviation of the parameters of the six types of short-term synaptic plasticity.
Distributions of peak conductances (“synaptic weights”) gmax for each cell population were derived in two steps. As the first step, initial estimates were obtained from the anatomical and electrophysiological literature (see above). Generally, peak conductances were adjusted such that they reproduced log-normal distributions of postsynaptic potential (PSP) amplitudes as reported in [37] (means and standard deviations given in Table 3). For excitatory synapses, only the AMPA conductances are specified this way, while NMDA conductances are given by 1.09 times the respective AMPA peak conductance [38, 39], with both AMPA and NMDA synapses activating after the same delay. For synaptic connections where peak conductances were not directly available from the surveyed literature, estimates were obtained in one of the following ways: 1) Missing estimates for specific interneuron types were replaced by estimates from other interneuron types where possible. 2) Missing estimates for inhibitory connections within one layer were replaced by those from another layer, rescaled such that they followed the same between-layer ratio as the excitatory inputs. 3) If only means but no standard deviations for the distribution of synaptic parameters were available, we used standard deviations from another layer scaled according to the ratio of the means between layers (missing values of connection probabilities or synaptic delays were estimated in the same way). Finally, for cross-column projections, synaptic weights were assumed to decay with the same exponential course (space constant of 114μm for pyramidal cells and 95μm for interneurons) as taken for the connection probabilities themselves (see above).
In a second step, since by far most of the studies cited above have been performed in sensory areas, data from laser scanning photostimulation (LSPS) [57, 70, 100, 101] and genetically targeted photostimulation [71] studies from motor cortex were used to obtain values closer to PFC. Specifically, all connection probabilities and synaptic weights were scaled such that the total input to each cell type would match the one observed experimentally in these studies. To compute this scaling factor , the product pcon ⋅ gmax of connection probability and synaptic weight was assumed to be proportional to the quantity ILSPS obtained in the experimental studies [70], yielding
| (7) |
where |⋅| denotes the sum over all matrix elements. pcon and gmax are then multiplied element-wise by , such that pcon ⋅ gmax agrees with ILSPS. The scaled values of all parameters are given in Table 3. The average connection strength (as defined by pcon ⋅ gmax) between pyramidal cells and interneurons in the different stripes and layers is coded by the arrow width in Fig 2A.
Simulation details. All simulations were performed in customized C code written by the authors. Differential equations were numerically integrated using a 2nd-order Runge-Kutta method with a maximum time step of 0.05 ms, and all spikes, synaptic, and external events were exactly timed by adjusting the time steps accordingly. More specifically, whenever an incoming spike or a change in external currents occurs within the default time step, the time step is reduced accordingly and all equations are updated at the precise time of that event. Neurons were initialized with and wi(0) = 0 for all i. MATLAB-based routines were used for parameter estimation and network analysis. All software is publicly available at https://www.zi-mannheim.de/index.php?id=626 and on the freely available repository ModelDB (http://senselab.med.yale.edu/ModelDB/).
Estimation of background currents
The constant background currents I used in the simulations are assumed to replace missing synaptic input from the surrounding network not explicitly simulated. A network of sufficient size should be able to produce these amounts of current inherently (with physiologically realistic synaptic efficacies as used here) and thus self-sustain its in vivo-like activity. To test this idea, we computed the amount of current that is produced by a larger network N that is set up and connected exactly the same way as the actually simulated network n and compared it to the range of background currents that are required for in vivo-like activity. The currents IN were modeled as the time-averaged synaptic currents that are elicited in a single neuron for each cell type (with the averaged cellular and synaptic parameters of all neurons of that type) in response to a bombardment of spikes drawn from a Poisson distribution that mimics a large number of input neurons, reflecting its input connectivity. For a Poisson input spike train with the same firing rate as in the original network, this yields the same synaptic current In as in the full simulation. Larger networks N are simulated by using a higher number of inputs, resulting in higher overall input spike rates. Because connection probabilities decay with distance between neurons [89], we independently tested two ways to increase the number of input neurons in the network: By increasing its spatial size L (measured in number of columns NC, each LC = 300μm in diameter) or its within-column neuron density D. For cross-column input, we assumed a radial distribution of inputs [60, 89] and an exponential decay of connection probabilities with distance (lE = 114μm, lI = 95μm, see above). Only pyramidal cells in L2/3 as well as cross-column (IN-CC) and far-reaching (IN-F) interneurons project across columns. Specifically, the number of input neurons projecting onto a neuron of cell type i is given by
| (8) |
is the fraction of neurons that connects to cell type i. denotes the number of neurons within a hollow cylinder defined by the inner radius L1 and the outer radius L2 and the height of 1 mm [60] that are connected to a neuron of cell type i at the center of this cylinder, given a neuron density D. Thus, the two terms represent input from within the same column (up to LC) and from outside that column (up to the full radius L). The ratio of pyramidal cells and interneurons that project beyond a single column (Table 2) is reflected in different scaling factors for excitatory and inhibitory connectivity for input from within (fC) and from outside the same column (fN). The resulting background currents IN are then computed independently for the four main cell types—pyramidal cells and interneurons in layer 2/3 and 5.
Analysis of simulated and in vivo data
Two in vivo data sets were used for comparison with simulation results (kindly provided by Dr. Christopher Lapish, Indiana University Purdue University, Indianapolis and Dr. Thomas Hahn, Central Institute of Mental Health and BCCN Heidelberg-Mannheim). For spike trains and local field potentials, extracellular multiple single-unit recordings were obtained from the rat’s anterior cingulate cortex (ACC) while they were performing an eight-arm radial maze task [40]. Stationary periods (largely free from motor or sensory responses) were obtained from 381 units using a previously described stationarity-segmentation method [41]. For the voltage traces, we used patch-clamp recordings from anaesthetized rodents (see [109, 110] for details).
Spike trains, voltage traces and local field potentials from the network simulation and the in vivo data were analyzed the same way. For each model cell or recorded unit, mean and coefficient of variation (CV) of the interspike interval (ISI) distributions were computed. Autocorrelations of ISI series and the zero-lag cross-correlation CC(0) between ISIs from pairs of spike trains were computed as well according to the procedures described in [41] to correct for non-stationarities. All analyses were restricted to spike trains of at least 10 spikes to yield sensible estimates of single-cell statistics without cutting off too much of the low-rate tail from the distributions (see Results section for a more empirical justification).
Similarity among simulated and experimentally obtained distributions was assessed by two-sample Kolmogorov-Smirnov (KS) tests, where test statistic DKS is bounded between zero (complete overlap) and one (maximally dissimilar distributions). Underlying distributions were inferred through kernel-density estimation [111] (implemented by the function “ksdensity” in MATLAB’s statistics toolbox). As KS test statistics may depend on sample size but different simulations vary in number of spikes, we limited the number of data points to a sufficiently low, common value (30), repeated KS tests with 100 random drawings, and report averages across obtained p values and KS statistics. The overall similarity of a simulation data set with the experimental spike data is quantified by conducting the test for the mean ISI, the CV and the CC(0) distributions, and reporting the minimal p or the maximal DKS value of those three (i.e., the value associated with the largest difference between the compared distributions).
Finally, we visualize the statistical overlap of distributions by plotting shaded areas representing the SEM around the mean at each value of the experimental distributions, which are computed from the 100 bootstrap samples as indicated above.
Acknowledgments
We are very grateful to Dr. Christopher Lapish, (Indiana University, Purdue University, Indianapolis) and Dr. Thomas Hahn (Central Institute of Mental Health, Medical Faculty Mannheim of Heidelberg University) for providing physiological recordings from rodent PFC for comparison with the model.
Data Availability
All relevant data are within the paper. All software is publicly available at https://www.zi-mannheim.de/index.php?id=626 and on the freely available repository ModelDB (https://senselab.med.yale.edu/ModelDB/ShowModel.cshtml?model=189160).
Funding Statement
This work was funded by grants from the German ministry for education and research (BMBF) through the Bernstein Center for Computational Neuroscience (01GQ1003B) and the e:Med program (01ZX1314G), and the Deutsche Forschungsgemeinschaft to DD (Du354/6-1 & 7-2). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Fuster JM. Prefrontal cortex. New York: Springer; 1988. [Google Scholar]
- 2. Fuster JM. The Prefrontal Cortex—An Update: Time is of the essence. Neuron. 2001;30:319–333. 10.1016/S0896-6273(01)00285-9 [DOI] [PubMed] [Google Scholar]
- 3. Durstewitz D, Vittoz NM, Floresco SB, Seamans JK. Abrupt transitions between prefrontal neural ensemble states accompany behavioral transitions during rule learning. Neuron. 2010;66(3):438–448. 10.1016/j.neuron.2010.03.029 [DOI] [PubMed] [Google Scholar]
- 4. Kesner RP, Churchwell JC. An analysis of rat prefrontal cortex in mediating executive function. Neurobiol Learn Mem. 2011;96:417–431. 10.1016/j.nlm.2011.07.002 [DOI] [PubMed] [Google Scholar]
- 5. Passingham RE, Wise SP. The Neurobiology of the Prefrontal Cortex. Oxford University Press; 2012. [Google Scholar]
- 6. Stuss DT, Knight RT. Principles of Frontal Lobe Function. Oxford University Press; 2013. [Google Scholar]
- 7. Manoach DS. Prefrontal cortex dysfunction during working memory performance in schizophrenia: reconciling discrepant findings. Schizophr Res. 2003;60(2–3):285–298. 10.1016/S0920-9964(02)00294-3 [DOI] [PubMed] [Google Scholar]
- 8. Meyer-Lindenberg A, Weinberger DR. Intermediate phenotypes and genetic mechanisms of psychiatric disorders. Nature Rev Neurosci. 2006;7:818–827. 10.1038/nrn1993 [DOI] [PubMed] [Google Scholar]
- 9. Durstewitz D, Seamans JK. The dual-state theory of prefrontal cortex dopamine function with relevance to catechol-o-methyltransferase genotypes and schizophrenia. Biol Psychiatry. 2008;64(9):739–749. 10.1016/j.biopsych.2008.05.015 [DOI] [PubMed] [Google Scholar]
- 10. Meyer-Lindenberg A. From maps to mechanisms through neuroimaging of schizophrenia. Nature. 2010;468:194–202. 10.1038/nature09569 [DOI] [PubMed] [Google Scholar]
- 11. Castellanos FX, Tannock R. Neuroscience of Attention-Deficit/Hyperactivity Disorder: The Search for Endophenotypes. Nature Rev Neurosci. 2002;3:617–628. 10.1038/nrn896 [DOI] [PubMed] [Google Scholar]
- 12. Cattell R, Parker A. Challenges for brain emulation: why is building a brain so difficult. Natural intelligence. 2012;1(3). [Google Scholar]
- 13. deGaris H, Shuo C, Goertzel B, Ruiting L. A world survey of artificial brain projects, Part I: Large-scale brain simulations. Neurocomputing. 2010;74:3–29. 10.1016/j.neucom.2010.08.004 [DOI] [Google Scholar]
- 14. Reimann MW, Anastassiou CA, Perin R, Hill SL, Markram H, Koch C. A Biophysically Detailed Model of Neocortical Local Field Potentials Predicts the Critical Role of Active Membrane Currents. Neuron. 2013;79:375–390. 10.1016/j.neuron.2013.05.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Hertäg L, Hass J, Golovko T, Durstewitz D. An Approximation to the Adaptive Exponential Integrate-and-Fire Neuron Model Allows Fast and Predictive Fitting to Physiological Data. Front Comput Neurosci. 2012. September;6 10.3389/fncom.2012.00062 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Brette R, Gerstner W. Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J Neurophysiol. 2005;94:3637–3642. 10.1152/jn.00686.2005 [DOI] [PubMed] [Google Scholar]
- 17. Naud R, Marcille N, Clopath C, Gerstner W. Firing patterns in the adaptive exponential integrate-and-fire model. Biol Cybern. 2008;99:335–347. 10.1007/s00422-008-0264-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Gibson JR, Beierlein M, Connors BW. Two networks of electrically coupled inhibitory neurons in neocortex. Nature. 1999. November;402(6757):75–79. 10.1038/47035 [DOI] [PubMed] [Google Scholar]
- 19. Gao WJ, Wang Y, Goldman-Rakic PS. Dopamine Modulation of Perisomatic and Peridendritic Inhibition in Prefrontal Cortex. J Neurosci. 2003. January;23(5):1622–1630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. González-Burgos G, Krimer LS, Povysheva NV, Barrionuevo G, Lewis DA. Functional Properties of Fast Spiking Interneurons and Their Synaptic Connections With Pyramidal Cells in Primate Dorsolateral Prefrontal Cortex. J Neurophysiol. 2005. January;93(2):942–953. 10.1152/jn.00787.2004 [DOI] [PubMed] [Google Scholar]
- 21. Koester HJ, Johnston D. Target Cell-Dependent Normalization of Transmitter Release at Neocortical Synapses. Science. 2005. June;308(5723):863–866. 10.1126/science.1100815 [DOI] [PubMed] [Google Scholar]
- 22. Thomson AM, Lamy C. Functional maps of neocortical local circuitry. Front Neurosci. 2007;1(1):19 10.3389/neuro.01.1.1.002.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Frick A, Feldmeyer D, Helmstaedter M, Sakmann B. Monosynaptic Connections between Pairs of L5A Pyramidal Neurons in Columns of Juvenile Rat Somatosensory Cortex. Cereb Cortex. 2008. February;18(2):397–406. 10.1093/cercor/bhm074 [DOI] [PubMed] [Google Scholar]
- 24. Berger TK, Perin R, Silberberg G, Markram H. Frequency-dependent disynaptic inhibition in the pyramidal network: a ubiquitous pathway in the developing rat neocortex. J Physiol. 2009;587(22):5411–5425. 10.1113/jphysiol.2009.176552 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Otsuka T, Kawaguchi Y. Cortical Inhibitory Cell Types Differentially Form Intralaminar and Interlaminar Subnetworks withExcitatory Neurons. J Neurosci. 2009. August;29(34):10533–10540. 10.1523/JNEUROSCI.2219-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Fino E, Yuste R. Dense Inhibitory Connectivity in Neocortex. Neuron. 2011. March;69(6):1188–1203. 10.1016/j.neuron.2011.02.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Potjans TC, Diesmann M. The cell-type specific cortical microcircuit: relating structure and activity in a full-scale spiking network model. Cereb Cortex. 2014;24(3):785–806. 10.1093/cercor/bhs358 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Yoshimura Y, Dantzker JLM, Callaway EM. Excitatory cortical neurons form fine-scale functional networks. Nature. 2005. February;433(7028):868–873. 10.1038/nature03252 [DOI] [PubMed] [Google Scholar]
- 29. Perin R, Berger TK, Markram H. A synaptic organizing principle for cortical neuronal groups. Proc Natl Acad Sci. 2011. March;108(13):5419–5424. 10.1073/pnas.1016051108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Markram H, Wang Y, Tsodyks M. Differential signaling via the same axon of neocortical pyramidal neurons. Proc Natl Acad Sci. 1998. April;95(9):5323–5328. 10.1073/pnas.95.9.5323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Gupta A, Wang Y, Markram H. Organizing Principles for a Diversity of GABAergic Interneurons and Synapses in the Neocortex. Science. 2000. January;287(5451):273–278. 10.1126/science.287.5451.273 [DOI] [PubMed] [Google Scholar]
- 32. Wang Y, Markram H, Goodman PH, Berger TK, Ma J, Goldman-Rakic PS. Heterogeneity in the pyramidal network of the medial prefrontal cortex. Nat Neurosci. 2006. April;9(4):534–542. 10.1038/nn1670 [DOI] [PubMed] [Google Scholar]
- 33. Allen C, Stevens CF. An evaluation of causes for unreliability of synaptic transmission. Proc Natl Acad Sci. 1994. October;91(22):10380–10383. Available from: http://www.pnas.org/content/91/22/10380. 10.1073/pnas.91.22.10380 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Gao WJ, Krimer LS, Goldman-Rakic PS. Presynaptic regulation of recurrent excitation by D1 receptors in prefrontal circuits. Proc Natl Acad Sci. 2001. February;98(1):295–300. 10.1073/pnas.98.1.295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Huang CC, Hsu KS. Presynaptic Mechanism Underlying cAMP-Induced Synaptic Potentiation in Medial Prefrontal Cortex Pyramidal Neurons. Mol Pharmacol. 2006. January;69(3):846–856. [DOI] [PubMed] [Google Scholar]
- 36. Loebel A, Silberberg G, Helbig D, Markram H, Tsodyks M, Richardson MJE. Multiquantal Release Underlies the Distribution of Synaptic Efficacies in the Neocortex. Front Comput Neurosci. 2009. November;3 10.3389/neuro.10.027.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Song S, Sjöström PJ, Reigl M, Nelson S, Chklovskii DB. Highly Nonrandom Features of Synaptic Connectivity in Local Cortical Circuits. PLoS Biol. 2005. March;3(3):e68 10.1371/journal.pbio.0030068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Myme CIO, Sugino K, Turrigiano GG, Nelson SB. The NMDA-to-AMPA Ratio at Synapses Onto Layer 2/3 Pyramidal Neurons Is Conserved Across Prefrontal and Visual Cortices. J Neurophysiol. 2003. January;90(2):771–779. 10.1152/jn.00070.2003 [DOI] [PubMed] [Google Scholar]
- 39. Wang H, Stradtman GG, Wang XJ, Gao WJ. A specialized NMDA receptor function in layer 5 recurrent microcircuitry of the adult rat prefrontal cortex. Proc Natl Acad Sci. 2008. October;105(43):16791–16796. 10.1073/pnas.0804318105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Lapish CC, Durstewitz D, Chandler LJ, Seamans JK. Successful choice behavior is associated with distinct and coherent network states in anterior cingulate cortex. Proc Natl Acad Sci. 2008. August;105(33):11963–11968. 10.1073/pnas.0804045105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Quiroga-Lombard CS, Hass J, Durstewitz D. Method for Stationarity-Segmentation of Spike Train Data with Application to the Pearson Cross-Correlation. J Neurophysiol. 2013;110(2):562–572. 10.1152/jn.00186.2013 [DOI] [PubMed] [Google Scholar]
- 42. Renart A, de la Rocha J, Bartho P, Hollender L, Parga N, Reyes A, et al. The Asynchronous State in Cortical Circuits. Science. 2010;327(5965):587–590. 10.1126/science.1179850 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Tsubo Y, Isomura Y, Fukai T. Power-law inter-spike interval distributions infer a conditional maximization of entropy in cortical neurons. PLoS Comput Biol. 2012;8(4):e1002461 10.1371/journal.pcbi.1002461 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Brecht M, Sakmann B. Dynamic representation of whisker deflection by synaptic potentials in spiny stellate and pyramidal cells in the barrels and septa of layer 4 rat somatosensory cortex. J Physiol. 2002;543:49–70. 10.1113/jphysiol.2002.018465 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Shoham S, O’Connor DH, Segev R. How silent is the brain: is there a “dark matter” problem in neuroscience? J Comp Physiol [A]. 2006;192:777–784. 10.1007/s00359-006-0117-6 [DOI] [PubMed] [Google Scholar]
- 46. Barth AL, Poulet JFA. Experimental evidence for sparse firing in the neocortex. Trends Neurosci. 2012;35(6):345–355. 10.1016/j.tins.2012.03.008 [DOI] [PubMed] [Google Scholar]
- 47. Latham PE, Richmond BJ, Nirenberg S, Nelson PG. Intrinsic dynamics in neuronal networks. II. Experiment. J Neurophysiol. 2000;83:828–835. [DOI] [PubMed] [Google Scholar]
- 48. Destexhe A, Rudolph M, Pare D. The high-conductance state of neocortical neurons in vivo. Nature Rev Neurosci. 2003;4:739–751. 10.1038/nrn1198 [DOI] [PubMed] [Google Scholar]
- 49. London M, Roth A, Beeren L, Häusser M, Latham PE. Sensitivity to perturbations in vivo implies high noise and suggests rate coding in cortex. Nature. 2010;466(7302):123–127. 10.1038/nature09086 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Pettersen KH, Einevoll GT. Amplitude Variability and Extracellular Low-Pass Filtering of Neuronal Spikes. Biophy J. 2008;94(3):784–802. 10.1529/biophysj.107.111179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Bedard C, Kroger H, Destexhe A. Does the 1/f frequency scaling of brain signals reflect self-organized critical states? Phys Rev Lett. 2006;97:118102 10.1103/PhysRevLett.97.118102 [DOI] [PubMed] [Google Scholar]
- 52. Miller KJ, Sorensen LB, Ojemann JG, den Nijs M. Power-law scaling in the brain surface electric potential. PLoS Comput Biol. 2009;5:e1000609 10.1371/journal.pcbi.1000609 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Dehghani N, Bedard C, Cash SS, Halgren E, Destexhe A. Comparative power spectral analysis of simultaneous elecroencephalographic and magnetoencephalographic recordings in humans suggests non-resistive extracellular media. J Comp Neurosci. 2010;29:405–421. 10.1007/s10827-010-0263-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Milstein J, Mormann F, Fried I, Koch C. Neuronal shot noise and Brownian 1/f2 behavior in the local field potential. PLoS ONE. 2009;4:e4338 10.1371/journal.pone.0004338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Apicella AJ, Wickersham IR, Seung HS, Shepherd GM. Laminarly orthogonal excitation of fast-spiking and low-threshold-spiking interneurons in mouse motor cortex. J Neurosci. 2012;32(20):7021–7033. 10.1523/JNEUROSCI.0011-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Hass J, Blaschke S, Rammsayer T, Herrmann JM. A neurocomputational model for optimal temporal processing. J Comput Neurosci. 2008;25(3):449–464. 10.1007/s10827-008-0088-4 [DOI] [PubMed] [Google Scholar]
- 57. Weiler N, Wood L, Yu J, Solla SA, Shepherd GMG. Top-down laminar organization of the excitatory network in motor cortex. Nat Neurosci. 2008. March;11(3):360–366. 10.1038/nn2049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Beaulieu C. Numerical data on neocortical neurons in adult rat, with special reference to the GABA population. Brain Res. 1993. April;609(1–2):284–292. 10.1016/0006-8993(93)90884-P [DOI] [PubMed] [Google Scholar]
- 59. Gabbott PL, Warner TA, Jays PR, Salway P, Busby SJ. Prefrontal cortex in the rat: projections to subcortical autonomic, motor, and limbic centers. J Comp Neurol. 2005;492(2):145–177. 10.1002/cne.20738 [DOI] [PubMed] [Google Scholar]
- 60. Boucsein C, Nawrot MP, Schnepel P, Aertsen A. Beyond the Cortical Column: Abundance and Physiology of Horizontal Connections Imply a Strong Role for Inputs from the Surround. Front Neurosci. 2011. April;5 10.3389/fnins.2011.00032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Tamás G, Somogyi P, Buhl EH. Differentially Interconnected Networks of GABAergic Interneurons in the Visual Cortex of the Cat. J Neurosci. 1998. January;18(11):4255–4270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Silberberg G, Markram H. Disynaptic Inhibition between Neocortical Pyramidal Cells Mediated by Martinotti Cells. Neuron. 2007. March;53(5):735–746. 10.1016/j.neuron.2007.02.012 [DOI] [PubMed] [Google Scholar]
- 63. Compte A, Brunel N, Goldman-Rakic PS, Wang XJ. Synaptic Mechanisms and Network Dynamics Underlying Spatial Working Memory in a Cortical Network Model. Cereb Cortex. 2000;10:910–923. 10.1093/cercor/10.9.910 [DOI] [PubMed] [Google Scholar]
- 64. Durstewitz D, Seamans JK, Sejnowski TJ. Dopamine-Mediated Stabilization of Delay-Period Activity in a Network Model of Prefrontal Cortex. J Neurophysiol. 2000;83:1733–1750. [DOI] [PubMed] [Google Scholar]
- 65. Lansner A. Associative memory models: from the cell-assembly theory to biophysically detailed cortex simulations. Trends Neurosci. 2009;32(2):178–186. 10.1016/j.tins.2008.12.002 [DOI] [PubMed] [Google Scholar]
- 66. Fisher D, Olasagasti I, Tank DW, Aksay ERF, Goldman MS. A Biophysically Detailed Model of Neocortical Local Field Potentials Predicts the Critical Role of Active Membrane Currents. Neuron. 2013;79:987–1000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Izhikevich EM, Edelman GM. Large-scale model of mammalian thalamocortical systems. Proc Natl Acad Sci. 2008;105(9):3593–3598. 10.1073/pnas.0712231105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Hay E, Hill S, Schürmann F, Markram H, Segev I. Models of neocortical layer 5b pyramidal cells capturing a wide range of dendritic and perisomatic active properties. PLoS Comput Biol. 2011;7(7):e1002107 10.1371/journal.pcbi.1002107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Hill SL, Wang Y, Riachi I, Schürmann F, Markram H. Statistical connectivity provides a sufficient foundation for specific functional connectivity in neocortical neural microcircuits. Proc Natl Acad Sci. 2012;109(42):E2885–E2894. 10.1073/pnas.1202128109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Hooks BM, Hires SA, Zhang YX, Huber D, Petreanu L, Svoboda K, et al. Laminar Analysis of Excitatory Local Circuits in Vibrissal Motor and Sensory Cortical Areas. PLoS Biol. 2011. January;9(1):e1000572 10.1371/journal.pbio.1000572 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Kätzel D, Zemelman BV, Buetfering C, Wölfel M, Miesenböck G. The columnar and laminar organization of inhibitory connections to neocortical excitatory cells. Nat Neurosci. 2011. January;14(1):100–107. 10.1038/nn.2687 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Thomson AM. Neocortical layer 6, a review. Front Neuroanat. 2010;4(13). 10.3389/fnana.2010.00013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Brunel N. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J Comp Neurosci. 2000;8(3):183–208. 10.1023/A:1008925309027 [DOI] [PubMed] [Google Scholar]
- 74. Ecker AS, Berens P, Keliris GA, Bethge M, Logothetis NK, Tolias AS. Decorrelated neuronal firing in cortical microcircuits. Science. 2010;327(5965):584–587. 10.1126/science.1179867 [DOI] [PubMed] [Google Scholar]
- 75. Timofeev I, Grenier F, Bazhenov M, Sejnowski T, Steriade M. Origin of slow cortical oscillations in deafferented cortical slabs. Cereb Cortex. 2000;10(12):1185–1199. 10.1093/cercor/10.12.1185 [DOI] [PubMed] [Google Scholar]
- 76. Reinhold K, Lien AD, Scanziani M. Distinct recurrent versus afferent dynamics in cortical visual processing. Nat Neurosci. 2015;18:1789–1797. 10.1038/nn.4153 [DOI] [PubMed] [Google Scholar]
- 77. Stepanyants A, Martinez LM, Ferecskó AS, Kisvárday ZF. The fractions of short-and long-range connections in the visual cortex. Proc Natl Acad Sci. 2009;106(9):3555–3560. 10.1073/pnas.0810390106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Sanchez-Vives MV, McCormick DA. Cellular and network mechanisms of rhythmic recurrent activity in neocortex. Nat Neurosci. 2000;3(10):1027–1034. 10.1038/79848 [DOI] [PubMed] [Google Scholar]
- 79. Costa RP, Sjostrom PJ, van Rossum MCW. Probabilistic Inference of Short-Term Synaptic Plasticity in Neocortical Microcircuits. Front Comput Neurosci. 2013;7(75). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Gerstner W, Kistler WM. Spiking Neuron Models: Single Neurons, Populations, Plasticity. Cambridge University Press; 2002. [Google Scholar]
- 81. Crill WE. Persistent Sodium Current in Mammalian Central Neurons. Annu Rev Physiol. 1996;58:34–62. 10.1146/annurev.ph.58.030196.002025 [DOI] [PubMed] [Google Scholar]
- 82. Lipscombe D, Helton TD, Xu W. L-Type Calcium Channels: The Low Down. J Neurophysiol. 2004;92:2633–2641. 10.1152/jn.00486.2004 [DOI] [PubMed] [Google Scholar]
- 83. Kawaguchi Y, Kubota Y. Physiological and morphological identification of somatostatin- or vasoactive intestinal polypeptide-containing cells among GABAergic cell subtypes in rat frontal cortex. J Neurosci. 1996. April;16(8):2701–2715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84. Kawaguchi Y. Physiological subgroups of nonpyramidal cells with specific morphological characteristics in layer II/III of rat frontal cortex. J Neurosci. 1995. January;15(4):2638–2655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Wang Y, Toledo-Rodriguez M, Gupta A, Wu C, Silberberg G, Luo J, et al. Anatomical, physiological and molecular properties of Martinotti cells in the somatosensory cortex of the juvenile rat. J Physiol. 2004;561(1):65–90. 10.1113/jphysiol.2004.073353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86. Ma Y, Hu H, Berrebi AS, Mathers PH, Agmon A. Distinct Subtypes of Somatostatin-Containing Neocortical Interneurons Revealed in Transgenic Mice. J Neurosci. 2006. October;26(19):5069–5082. 10.1523/JNEUROSCI.0661-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87. Fanselow EE, Richardson KA, Connors BW. Selective, State-Dependent Activation of Somatostatin-Expressing Inhibitory Interneurons in Mouse Neocortex. J Neurophysiol. 2008. January;100(5):2640–2652. 10.1152/jn.90691.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. Uematsu M, Hirai Y, Karube F, Ebihara S, Kato M, Abe K, et al. Quantitative Chemical Composition of Cortical GABAergic Neurons Revealed in Transgenic Venus-Expressing Rats. Cereb Cortex. 2008. February;18(2):315–330. 10.1093/cercor/bhm056 [DOI] [PubMed] [Google Scholar]
- 89. Voges N, Schüz A, Aertsen A, Rotter S. A modeler’s view on the spatial structure of intrinsic horizontal connectivity in the neocortex. Prog Neurobiol. 2010;92:277–292. 10.1016/j.pneurobio.2010.05.001 [DOI] [PubMed] [Google Scholar]
- 90. Markram H, Toledo-Rodriguez M, Wang Y, Gupta A, Silberberg G, Wu C. Interneurons of the neocortical inhibitory system. Nat Rev Neurosci. 2004. October;5(10):793–807. 10.1038/nrn1519 [DOI] [PubMed] [Google Scholar]
- 91. DeFelipe J, López-Cruz PL, Benavides-Piccione R, Bielza C, Larrañaga P, Anderson S, et al. New insights into the classification and nomenclature of cortical GABAergic interneurons. Nature Rev Neurosci. 2013;14(3):202–216. 10.1038/nrn3444 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92. Melchitzky DS, Sesack SR, Pucak ML, Lewis DA. Synaptic targets of pyramidal neurons providing intrinsic horizontal connections in monkey prefrontal cortex. J Comp Neurol. 1998;390(2):211–224. 10.1002/(SICI)1096-9861(19980112)390:2%3C211::AID-CNE4%3E3.0.CO;2-4 [DOI] [PubMed] [Google Scholar]
- 93. Lewis DA, González-Burgos G. Intrinsic excitatory connections in the prefrontal cortex and the pathophysiology of schizophrenia. Brain Res Bull. 2000. July;52(5):309–317. 10.1016/S0361-9230(99)00243-9 [DOI] [PubMed] [Google Scholar]
- 94. Krimer LS, Goldman-Rakic PS. Prefrontal Microcircuits: Membrane Properties and Excitatory Input of Local, Medium, and Wide Arbor Interneurons. J Neurosci. 2001. January;21(11):3788–3796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95. Reyes A, Sakmann B. Developmental Switch in the Short-Term Modification of Unitary EPSPs Evoked in Layer 2/3 and Layer 5 Pyramidal Neurons of Rat Neocortex. J Neurosci. 1999. May;19(10):3827–3835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96. Thomson AM, West DC, Wang Y, Bannister AP. Synaptic Connections and Small Circuits Involving Excitatory and Inhibitory Neurons in Layers 2–5 of Adult Rat and Cat Neocortex: Triple Intracellular Recordings and Biocytin Labelling In Vitro. Cereb Cortex. 2002. January;12(9):936–953. 10.1093/cercor/12.9.936 [DOI] [PubMed] [Google Scholar]
- 97. Yoshimura Y, Callaway EM. Fine-scale specificity of cortical networks depends on inhibitory cell type and connectivity. Nat Neurosci. 2005. November;8(11):1552–1559. 10.1038/nn1565 [DOI] [PubMed] [Google Scholar]
- 98. Bannister AP, Thomson AM. Dynamic Properties of Excitatory Synaptic Connections Involving Layer 4 Pyramidal Cells in Adult Rat and Cat Neocortex. Cereb Cortex. 2007. September;17(9):2190–2203. 10.1093/cercor/bhl126 [DOI] [PubMed] [Google Scholar]
- 99. Lefort S, Tomm C, Floyd Sarria JC, Petersen CC. The Excitatory Neuronal Network of the C2 Barrel Column in Mouse Primary Somatosensory Cortex. Neuron. 2009. January;61(2):301–316. 10.1016/j.neuron.2008.12.020 [DOI] [PubMed] [Google Scholar]
- 100. Dantzker JL, Callaway EM. Laminar sources of synaptic input to cortical inhibitory interneurons and pyramidal neurons. Nat Neurosci. 2000. July;3(7):701–707. 10.1038/76656 [DOI] [PubMed] [Google Scholar]
- 101. Xu X, Callaway EM. Laminar Specificity of Functional Input to Distinct Types of Inhibitory Cortical Neurons. J Neurosci. 2009. July;29(1):70–85. 10.1523/JNEUROSCI.4104-08.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102. Tomioka R, Okamoto K, Furuta T, Fujiyama F, Iwasato T, Yanagawa Y, et al. Demonstration of long-range GABAergic connections distributed throughout the mouse neocortex. Eur J Neurosci. 2005;21(6):1587–1600. 10.1111/j.1460-9568.2005.03989.x [DOI] [PubMed] [Google Scholar]
- 103. Levy RB, Reyes AD. Spatial profile of excitatory and inhibitory synaptic connectivity in mouse primary auditory cortex. J Neurosci. 2012;32(16):5609–5619. 10.1523/JNEUROSCI.5158-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104. Durstewitz D. Self-Organizing Neural Integrator Predicts Interval Times through Climbing Activity. J Neurosci. 2003;23(12):5342–5353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105. Zaitsev AV, Povysheva NV, Lewis DA, Krimer LS. P/Q-Type, But Not N-Type, Calcium Channels Mediate GABA Release From Fast-Spiking Interneurons to Pyramidal Cells in Rat Prefrontal Cortex. J Neurophysiol. 2007. January;97(5):3567–3573. 10.1152/jn.01293.2006 [DOI] [PubMed] [Google Scholar]
- 106. Jahr CE, Stevens CF. Voltage dependence of NMDA-activated macroscopic conductances predicted by single-channel kinetics. J Neurosci. 1990. January;10(9):3178–3182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107. González-Burgos G, Barrionuevo G, Lewis DA. Horizontal Synaptic Connections in Monkey Prefrontal Cortex: An In Vitro Electrophysiological Study. Cereb Cortex. 2000. January;10(1):82–92. 10.1093/cercor/10.1.82 [DOI] [PubMed] [Google Scholar]
- 108. Maass W, Markram H. Synapses as dynamic memory buffers. Neural Networks. 2002. March;15(2):155–161. 10.1016/S0893-6080(01)00144-7 [DOI] [PubMed] [Google Scholar]
- 109. Hahn TT, Sakmann B, Mehta MR. Phase-locking of hippocampal interneurons’ membrane potential to neocortical up-down states. Nat Neurosci. 2006;9(11):1359–1361. 10.1038/nn1788 [DOI] [PubMed] [Google Scholar]
- 110. Hahn TT, McFarland JM, Berberich S, Sakmann B, Mehta MR. Spontaneous persistent activity in entorhinal cortex modulates cortico-hippocampal interaction in vivo. Nat Neurosci. 2012;15(11):1531–1538. 10.1038/nn.3236 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111. Bowman AW, Azzalini A. Applied smoothing techniques for data analysis. Clarendon Press; 2004. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All relevant data are within the paper. All software is publicly available at https://www.zi-mannheim.de/index.php?id=626 and on the freely available repository ModelDB (https://senselab.med.yale.edu/ModelDB/ShowModel.cshtml?model=189160).