A Multistate Model Predicting Mortality, Length of Stay, and Readmission for Surgical Patients

Abstract

Objective

Simultaneously evaluate postoperative mortality, length of stay (LOS), and readmission.

Data Source

National Surgical Quality Improvement Program (NSQIP).

Design

Retrospective cohort.

Methods

Data from elective general surgical patients were obtained from the 2012 NSQIP Participant Use File. For each postoperative day, each patient's state was classified as index hospitalization, discharged home, discharged to long‐term care (LTC), readmitted, or dead. Transition rates were estimated using exponential regression, assuming constant rates for specified time periods. These estimates were combined into a multistate model, simulated results of which were compared to observed outcomes.

Findings

Age, comorbidities, more complex procedures, and longer index LOS were associated with lower rates of discharge home and higher rates of death, discharge to LTC, and readmission. The longer patients had been discharged, the less likely they were to die or be readmitted. The model predicted 30‐day mortality 0.38 percent (95 percent CI: 0.36–0.41), index LOS 2.85 days (95 percent CI: 2.83–2.86), LTC discharge 2.76 percent (95 percent CI: 2.69–2.82), and readmissions 5.53 percent (95 percent CI: 5.43–5.62); observed values were 0.39 percent, 2.82 days, 2.87 percent, and 5.70 percent, respectively.

Conclusions

Multistate models can simultaneously predict postoperative mortality, LOS, discharge destination, and readmissions, which allows multidimensional comparison of surgical outcomes.

The quality of hospital care is difficult to measure. Risk‐adjusted mortality during the index hospitalization is the outcome most frequently used, and a hospital's reputation may be affected if this result is publicized by payors or regulators. Hospital length of stay (LOS) is used rightly or wrongly as a rough measure of cost, and payment systems providing a fixed reimbursement for a given diagnosis give hospitals an incentive to avoid prolonged LOS (Taheri, Butz, and Greenfield 2000; Polverejan et al. 2003; Altman 2012). The Centers for Medicare & Medicaid Services have also decided to reduce payment for “avoidable” readmissions (Jencks, Williams, and Coleman 2009). Hospitals are thus expected to minimize three short‐term outcomes (mortality, LOS, and readmission) which are not independent and which may have different utilities for each patient, each institution, and society as a whole.

The American College of Surgeons (ACS) has developed a National Surgical Quality Improvement Program (NSQIP), which records mortality, LOS, readmissions, and other adverse events (including those after initial hospital discharge) up to 30 days after a surgical procedure. Using NSQIP data, we sought to develop a statistical approach that would allow for the interdependence of these short‐term outcomes for surgical patients. “Multistate” or “compartmental” models, like the one presented here, can simultaneously estimate the effects of covariates on each transition of a patient's postoperative status, and thus enable prediction of cumulative outcomes that reflect overall health and cost. Compared to separate analyses of mortality, LOS, and readmission, the multistate approach offers the potential for a more useful multidimensional comparison of surgical outcomes for different hospitals and/or regions.

Methods

Data Management

The NSQIP Participant Use File (PUF) for 2012 was obtained in accordance with its standard Data Use Agreement. A supplemental file containing the PUF identifying numbers for patients from our own hospital was provided by NSQIP upon request. PUF does not otherwise identify hospital characteristics or even which patients were in the same hospital, and we made no attempt to link PUF data to other patient data from our hospital. The use of these data for this project was judged exempt from further review by an Institutional Review Board at our hospital.

PUF data were imported into Stata (Version 12; StataCorp, College Station, TX, USA), and merged with the file identifying our own hospital patients. For this study, analysis was restricted to elective general surgical cases (surgspec = “General Surgery,” electsurg = “Yes”), admitted on the day of operation.

Indicator variables (1 if yes, 0 if no) were created for each category of “Targeted” elective general surgical procedures in NSQIP (ACS 2013a), namely pancreatectomy, colectomy, proctectomy, ventral herniorraphy, bariatric surgery, hepatectomy, thyroidectomy, and esophagectomy. Variables were created to indicate each of the abnormal preoperative symptoms or conditions recorded in the PUF. Variables were created to indicate laboratory values considered abnormal in standard NSQIP risk‐adjustment models (ACS 2013b), namely WBC>11.0, platelets<150, PTT>35, albumin<3, creatinine>1.2, SGOT>40, BUN>40, bilirubin>1.0, sodium>145, or alkaline phosphatase>125. Four age categories were also created (18–39, 40–64, 65–79, and 80+). Six categories for postoperative LOS (each approximately twice as long as the previous category) were created (1 day, 2 days, 3–4 days, 5–8 days, 9–16 days, 17–30 days).

A variable was created to indicate that a patient had died in the hospital if the date of death was the same as the date of discharge, and the discharge destination was given as “Expired.” A variable was created for discharge home if the discharge destination was “Home,” and a variable was created for discharge to long‐term care (LTC) if the discharge destination was not “Expired,” “Home,” or “NULL.” Variables indicating the occurrence of each of the 20 complications recorded in the PUF were created, separately indicating the complication as occurring prior to discharge if the day of occurrence was before the day of discharge, or occurring after discharge if the day of occurrence was on or after the day of discharge. A variable was created to indicate that the patient had been readmitted at least once if the “readmission1” variable was “Yes.” The postoperative day (POD) of readmission was taken as the value of “readmpoday1”; if this value was missing, the day of the first complication on or after the day of discharge was assumed to be the day of readmission; if this value was also missing, the day of readmission was imputed using predictive mean modeling.

Statistical Modeling

Using the Stata command “logit,” logistic regression (LR) models were fitted predicting LOS >6 days (excluding patients who died during the initial hospitalization), readmission (excluding patients who were not discharged alive in less than 30 days), and 30‐day mortality. Preliminary models included all of the procedure categories, age categories, abnormal symptoms, abnormal laboratory values, LOS categories, and discharge destination categories described above. Symptoms or laboratory values were assumed to be normal if missing. Individual variables found to be significant predictors of any outcome (p < .05) were combined to define indicator variables for any degree of obesity (BMI ≥ 30), smoking and/or COPD, any of several other abnormal symptoms (sepsis, SIRS, septic shock, dyspnea, weight loss, disseminated cancer, steroid use, or dialysis), and any abnormal laboratory value.

After exploration of covariate effects using LR models, the first step toward constructing a multi‐state model was to consider subjects on a given POD to be in one of several states: hospitalized for initial postoperative care, discharged home after hospitalization, discharged to LTC after hospitalization, readmitted to a hospital either from home or LTC, or dead. The Stata “stsplit” command was used to separate each subject's data into separate records corresponding to the number of days they were at risk for a subsequent transition while in each state.

An exponential model assumes that the baseline hazard for a given subject is constant, but if this is unrealistic, one can construct a “piecewise exponential” (PWE) model, which assumes only that the baseline hazard is constant for each of several specified time periods. We implemented PWE models for each state transition by adding variables indicating the length of time that subjects had been in their current state (1 day, 2 days, 3–4 days, 5–8 days, 9–16 days, 17–30 days). For each transition, the Stata “stsplit” command was used again to split each subject's data further, so that separate transition rates could be estimated for each of these time periods based on the number of days at risk in a given state.

Using the Stata command “streg, distribution (exponential),” PWE proportional hazards regression models were created to predict covariate effects on the rates (“hazards”) for each transition from one state to another, censoring subjects who experienced an outcome other than the transition being modeled. For posthospital transitions, the proportional hazards models also included the initial hospital LOS categories.

In a proportional hazards model,

$$\text{log}\text{hazard}(\text{event},t)={\mathit{\beta }}_0(t)+{\mathit{\beta }}_1{X}_1+\cdots +{\mathit{\beta }}_k{X}_k,$$

where the baseline hazard, exp(β ₀(t)), is the instantaneous probability for a subject still at risk to experience the event of interest at time t. If both sides of the equation are exponentiated, and the values of X ₁…X _n are restricted to 0 or 1, it can be seen that the hazard is equal to the baseline hazard multiplied by any coefficients β _k for which X _k = 1. Thus, for any subject on any day, the probability that the subject will transition from his/her current state to another state can be calculated from his/her current characteristics (including initial hospital LOS and time elapsed in the current state).

Construction of the multistate model was completed by combining the estimates obtained from PWE models for each state transition as depicted in Figure 1. Subjects transferred to LTC were assumed to remain there until POD 30, or until they were readmitted to a hospital or died. Subjects who were readmitted to a hospital from home or LTC were assumed to remain hospitalized until POD 30, or until they died.

Figure 1.

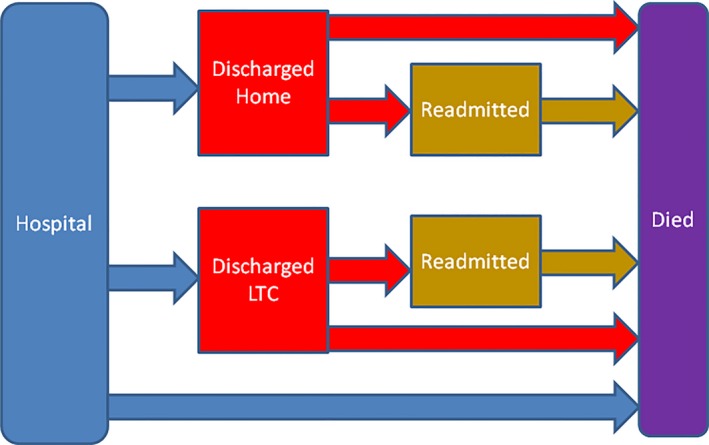
Components and Relationships of the Multistate Model. At any time, patients are considered to be in one of the following states: Initial hospitalization, discharged home, discharged to long‐term care (LTC), readmitted from home, readmitted from LTC, or dead. For a given patient on a given day, the transition rates from one state to another can be determined from Tables 3 and 4

Estimated outcomes for the entire sample or any desired subsample were obtained by simulating the experience of each subject based upon their states on each day, with randomly generated transitions to other states based upon the hazards predicted for each subject on each day. For the entire system, outcomes of these simulated “event histories” were used to generate summary statistics, including the number of subjects in each state at any time and the number of days each subject had spent in each state up to POD 30. In order to demonstrate the potential utility of multistate modeling for interhospital comparisons, we also simulated results for the subsample that had been admitted to our own hospital (MMC), which was the only hospital we could identify using the PUF.

For complex models, an estimate of the robustness of the predicted outcomes can be obtained by running the model multiple times with different random samples (with replacement) of the original dataset, a procedure known as “bootstrapping” and implemented using the Stata command “bsample.” Five hundred bootstrapped simulations of the multistate model were performed, and the results were used to estimate the mean of each 30‐day outcome, including a confidence interval based on the assumption of approximately normal distributions for these means. Model estimates were compared to the actual observed outcomes for the entire PUF sample and for the subsample from MMC.

Results

The 2012 NSQIP PUF contained 543,885 records submitted from 374 participating sites. A total of 206,937 records met our definition of elective general surgery. These patients were 60.2 percent female, and 94.2 percent under the age of 80 years. A total of 200,048 patients (96.7 percent) were discharged home after the initial hospitalization, and 6,280 (3.0 percent) were discharged to LTC. A total of 491 patients (0.24 percent) died during their initial hospitalization, and another 118 patients (0.06 percent) remained in the hospital after 30 days; overall, there were 816 deaths within 30 days (0.39 percent). The mean LOS for the initial hospitalization, excluding those who died in the hospital, was 2.82 days; the 90th percentile for LOS was 6 days. Among 205,437 patients discharged alive from the initial hospitalization within 30 days, 11,807 (5.8 percent) were readmitted. The day of readmission (or day of first postdischarge complication) was recorded for 99.5 percent of the readmitted patients, and it was imputed for the others. Further characteristics and outcomes of the PUF sample are shown in Table 1.

Table 1.

Characteristics, Procedures, and Outcomes for Elective General Surgical Patients in NSQIP PUF 2012

Characteristics (N = 206,937)	Number	Percent
Patient factors
Age 18–39	36,940	17.8
Age 40–64	108,836	52.6
Age 65–79	49,056	23.7
Age 80–99	12,105	5.8
Male	82,446	39.8
ASA 1	18,409	8.9
ASA 2	103,628	50.1
ASA 3	79,422	38.4
ASA 4–5	5,478	2.7
Obese	91,584	44.3
Smoker or COPD	37,794	18.3
Other abnormal symptoms	29,550	14.3
Abnormal laboratory values	60,101	29.0
Procedures
Pancreatectomy	4,879	2.4
Colectomy	22,248	10.8
Proctectomy	3,939	1.9
Ventral herniorraphy	31,585	15.3
Bariatric surgery	18,680	9.0
Hepatectomy	2,715	1.3
Thyroidectomy	9,120	4.4
Esophagectomy	453	0.2
Other procedure	113,318	54.8
Outcomes
Died in hospital	491	0.24
Discharged home	200,048	96.67
Discharged to LTC	6,280	3.03
Readmitted from home	10,998	5.31
Readmitted from LTC	809	0.39
Died within 30 days	816	0.39

Logistic regression models predicting LOS >6 days in the initial hospital, readmission after discharge from the initial hospital, and overall mortality are shown in Table 2. All of these outcomes were more likely with greater American Society of Anesthesiologists (ASA) preoperative classifications, abnormal symptoms or laboratory values, pancreatectomy, colectomy, proctectomy, hepatectomy, or esophagectomy. Ventral herniorraphy, bariatric surgery, or thyroidectomy were associated with lower incidence of prolonged LOS, readmission, or mortality. Increased age was associated with prolonged LOS and mortality, but a lower incidence of readmission.

Table 2.

Separate Logistic Regression Models Predicting the Odds of Prolonged Length of Stay (LOS >6 days), Readmission, and 30‐Day Mortality. LOS prediction does not include patients who died in the hospital; readmission prediction does not include patients who died in the hospital or never left the hospital. To predict outcomes for individual patients, the baseline odds are multiplied by odds ratios corresponding to factors known at the time of operation

	Long LOS	Readmission	Death
Number of subjects at risk	206,446	205,436	206,937
Baseline odds (constant)	.0137	.0203	.0000558
Odds ratios
Age 40–64 vs. <40	1.12a	0.90a	2.21a
Age 65–79 vs. <40	1.25a	0.87a	4.77a
Age 80–99 vs. <40	1.38a	0.96	9.51a
Male vs. female	1.14a	0.92a	1.34a
ASA 2 vs. 1	2.85a	1.94a	2.86
ASA 3 vs. 1	5.81a	3.18a	9.65a
ASA 4–5 vs. 1	9.15a	4.24a	32.17a
Obese	0.90a	1.04	1.00
Smoker or COPD	1.17a	1.11a	1.48a
Other abnormal symptoms	1.78a	1.44a	2.06a
Abnormal laboratory values	1.60a	1.35a	2.49a
Pancreatectomy	35.79a	2.94a	3.09a
Colectomy	6.89a	1.87a	2.02a
Proctectomy	14.07a	3.48a	2.13a
Ventral herniorraphy	0.71a	0.86a	0.78
Bariatric surgery	0.28a	0.87a	0.52a
Hepatectomy	8.57a	1.69a	2.76a
Thyroidectomy	0.13a	0.66a	0.13a
Esophagectomy	212.68a	2.18a	2.14

^a p < .01.

Results of the individual PWE models are shown in Tables 3 and 4. For a given patient on a given day, the rate for each transition to another state can be estimated as the baseline rate multiplied by the applicable hazard ratios shown in these tables. For example, consider a 75‐year‐old obese man with no other comorbidities or laboratory abnormalities, who is POD 10 from a colectomy, had been given an ASA score of 2, and had been discharged home from the hospital on POD 7. The probability that this subject would be readmitted to the hospital on POD 10 (i.e., the hazard for that day), can be calculated as:

$$\begin{array}{cc}\hfill h(t)& =0.00178[\text{baseline hazard}]\hfill \\ & \ast 0.83[\text{age}65-79]\hfill \\ & \ast 0.92[\text{male sex}]\hfill \\ & \ast 1.61[\text{ASA}2]\hfill \\ & \ast 1.07[\text{obese}]\hfill \\ & \ast 0.92[\text{colectomy}]\hfill \\ & \ast 3.78[\text{initial LOS}5-8\text{days}]\hfill \\ & \ast 0.66[\text{home for}3-4\text{days}]\hfill \\ & =0.00537.\hfill \end{array}$$

Table 3.

Exponential Regression Models Predicting Daily Transition Rates (Hazards) from Hospital to Home, from Hospital to Long‐Term Care (LTC), and from Home or LTC Back to Hospital (Readmission). To predict outcomes for individual patients, the baseline hazards are multiplied by hazard ratios corresponding to factors known at the time of operation, and those corresponding to the observed or simulated initial hospital length of stay (LOS) and duration of time in the current state

	Discharge from Hospital		Readmission to Hospital
	To Home	To LTC	From Home	From LTC
Number of subjects at risk	206,937	206,937	199,631	5,945
Baseline hazard (constant)	.909	.00554	.00178	.00131
Hazard ratios
Age 40–64 vs. <40	0.97**	1.00	0.88**	1.31
Age 65–79 vs. <40	0.93**	1.95**	0.83**	1.40
Age 80–99 vs. <40	0.83**	4.69**	0.95	1.19
Male vs. female	1.00	0.76**	0.92**	1.03
ASA 2 vs. 1	0.83**	0.66**	1.61**	3.22*
ASA 3 vs. 1	0.65**	0.95	2.26**	4.54*
ASA 4–5 vs. 1	0.46	1.33**	2.87**	4.35*
Obese	1.04**	1.11**	1.07**	1.02
Smoker or COPD	0.96**	1.14**	1.09**	1.20*
Other abnormal symptoms	0.81**	0.98	1.29**	1.10
Abnormal laboratory values	0.84**	1.10**	1.22**	1.21*
Pancreatectomy	0.30**	0.47**	1.32**	1.21
Colectomy	0.42**	0.60**	0.92**	1.02
Proctectomy	0.35**	0.72**	1.59**	1.58**
Ventral herniorraphy	1.05**	0.98	0.88**	0.87
Bariatric surgery	1.00	0.48**	0.76**	1.23
Hepatectomy	0.43**	0.41**	0.86*	0.84
Thyroidectomy	1.34**	0.97	0.86*	0.86
Esophagectomy	0.23**	0.56**	0.95	1.02
Initial LOS 2 vs. 1	0.57**	0.65**	1.78**	1.44
Initial LOS 3–4 vs. 1	0.58**	1.22**	2.60**	1.56**
Initial LOS 5–8 vs. 1	0.68**	2.66**	3.78**	2.29**
Initial LOS 9–16 vs. 1	0.41**	3.78**	4.73**	2.09**
Initial LOS 17–30 vs. 1	0.18**	3.91**	4.73**	2.09**
Days in current state 2 vs. 1			0.73**	0.69*
Days in current state 3–4 vs. 1			0.66**	0.61**
Days in current state 5–8 vs. 1			0.51**	0.50**
Days in current state 9–16 vs. 1			0.32**	0.37**
Days in current state 17–30 vs. 1			0.18**	0.17**

*p < .05, **p < .01.

Table 4.

Exponential Regression Models Predicting the Daily Probability of Death (Hazard) from the Initial Hospital, Home (without Readmission), Long‐Term Care (LTC), after Readmission from Home, and after Readmission from LTC. To predict mortality for individual patients, the baseline hazards are multiplied by hazard ratios corresponding to factors known at the time of operation, and those corresponding to the observed or simulated initial hospital length of stay (LOS) and duration of time in the current state

	Mortality from Other States
	Initial	After Discharge		After Readmission
	Hospital	To Home	To LTC	From Home	From LTC
Number of subjects at risk	206,937	199,631	5,945	10,992	809
Baseline hazard (constant)	.0000109	.00000457	.000173	.000184	.00559
Hazard ratios
Age 40–64 vs. <40	1.94*	3.24	1.07	2.92	0.28
Age 65–79 vs. <40	3.41**	7.36**	1.99	8.87**	1.10
Age 80–99 vs. <40	6.93**	11.50**	3.14	16.24**	1.25
Male vs. Female	1.40**	1.32	1.22	1.08	1.12
ASA 2 vs. 1	2.71
ASA 3 vs. 1	6.49
ASA 3 vs. 1–2		2.82**	2.11	1.86*	1.06
ASA 4–5 vs. 1	15.26**
ASA 4–5 vs. 1–2		8.23**	3.84*	2.83**	1.68
Obese	1.14	1.16	1.08	0.52**	0.56
Smoker or COPD	1.23*	1.65*	1.77*	1.25	2.29*
Other abnormal symptoms	1.60**	1.59*	1.88*	2.29**	0.59
Abnormal laboratory values	1.78**	2.10**	2.20*	1.64*	1.86
Pancreatectomy	1.04	1.31	0.41	0.49	0.29
Colectomy	0.92	0.85	0.65	1.06	1.93
Proctectomy	0.93	0.81	0.48	0.59	0.44
Ventral herniorraphy	1.09	1.20	<0.01	0.99	0.91
Bariatric surgery	0.77	1.04	<0.01	0.35	<0.01
Hepatectomy	1.24	1.46	1.88	1.33	1.65
Thyroidectomy	0.43	<0.01	<0.01	0.66	<0.01
Esophagectomy	0.56	1.19	<0.01	<0.01	<0.01
Initial LOS 2 vs. 1	0.92	1.55	<0.01	1.00	1.48
Initial LOS 3–4 vs. 1	1.40	2.01*	1.00	1.29	0.34
Initial LOS 5–8 vs. 1	2.73**	2.15**	1.31	0.97	0.85
Initial LOS 9–16 vs. 1	4.56**	5.28**	2.16	1.40	0.94
Initial LOS 17–30 vs. 1	7.42**	5.28**	2.16	1.40	0.94
Days in current state 2 vs. 1		0.36**	0.21*	0.25**	0.44
Days in current state 3–4 vs. 1		0.27**	0.28**	0.20**	0.45
Days in current state 5–8 vs. 1		0.17**	0.21**	0.19**	0.51
Days in current state 9–16 vs. 1		0.12**	0.14**	0.14**	0.17**
Days in current state 17–30 vs. 1		0.08**	0.14**	0.09**	0.10**

*p < .05, **p < .01.

Calculating all of the transition rates (hazards) for each patient for each POD was very rapid using a standard desktop computer. One simulation of the entire system took about 2 minutes; however, bootstrapping 500 simulations took several hours.

Tables 3 and 4 show that higher ASA classification, abnormal symptoms, and abnormal laboratory values were associated with increased daily rates of mortality and readmission, and increased daily rates of discharge to LTC, but decreased daily rates of discharge home. Increased age was associated with increased mortality, decreased daily rates of discharge home (but increased daily rates of discharge to LTC), and decreased daily rates of readmission from home (but not readmission from LTC). Pancreatectomy, colectomy, proctectomy, hepatectomy, and esophagectomy were associated with decreased daily rates of discharge from the initial hospitalization, while ventral herniorraphy and thyroidectomy were associated with increased daily rates of discharge home.

In the multistate model, longer initial LOS was generally associated with lower daily rates of discharge home and higher daily rates of discharge to LTC. The more days that patients had been hospitalized, the more likely they were to be readmitted; the more days that patients had been discharged, the less likely they were to be readmitted. Mortality increased with longer LOS, for both hospitalized and discharged patients; mortality decreased markedly the longer that patients had been discharged home, but mortality decreased only slightly the longer that patients had been discharged to LTC.

For any given subject or cohort, it was possible to construct curves depicting expected outcomes by graphing the simulated number in each state on each day. For example, Figure 2 graphically compares the overall outcomes for patients with selected “Targeted” procedures. In addition to showing the proportion of patients expected to be in any state at any time, the mean LOS in any state can be visualized (and calculated) as the area between two curves.

Figure 2.

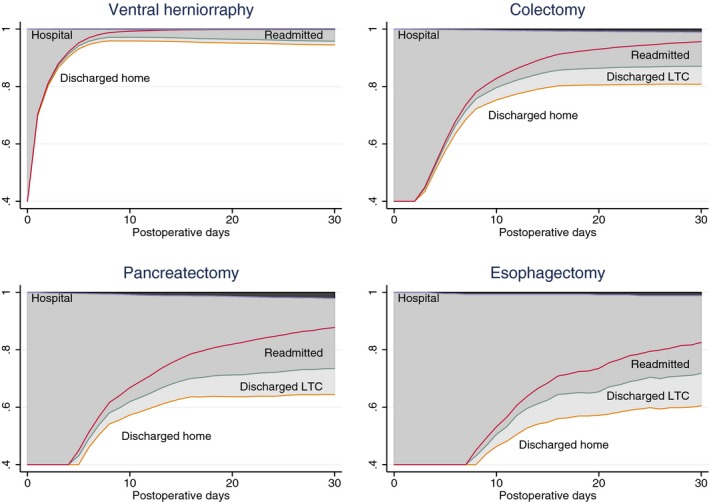
Depiction of Simulated Outcomes from the Multistate Model for Elective Surgical Patients after Ventral Herniorraphy, Colectomy, Pancreatectomy, or Esophagectomy. Mortality is shown by the dark shaded areas of the graphs. Length of stay in a hospital or in long‐term care (LTC) can be visualized as the lighter shaded areas of the graphs

When event histories were simulated for all subjects using the multistate model, results were similar to the outcomes that had actually been observed (Table 5, “All hospital” columns). Outcomes related to LTC or readmission were not quite as precisely reproduced by the model, but it should be recalled that NSQIP provides no information about hospitals, or even which patients were treated in the same hospital (other than a participant's own institution). When event histories were simulated for patients from our own hospital (MMC), under the assumption that patient‐level covariates had effects similar to those in the entire PUF, we found that the observed number of discharges to LTC and number of days spent in LTC were significantly lower than expected (Table 5, “MMC” columns). When separate simulations were carried out for each of the “Targeted” procedures, the simulated results were still similar to the observed outcomes for each procedure, and significantly lower LTC utilization by MMC was still apparent.

Table 5.

Outcomes Estimated by the Overall Multistate Model (Using Simulation), Compared to the Actual Observed Outcomes. Subjects not discharged to home were assumed to be in long‐term care (LTC) and to remain there until the end of the 30‐day period unless they died or were readmitted. Subjects readmitted to the hospital were assumed to remain there until the end of the 30‐day period unless they died

	Subjects from All Hospitals (N = 206,937)			Subjects from MMC (n = 1,079)
	Estimated	95% CI	Observed	Estimated	95% CI	Observed
Hospital mortality (%)	0.24	0.22, 0.26	0.24	0.28	0.00, 0.59	0.19
Discharge to LTC (%)	2.76	2.69, 2.82	2.87	3.05	2.04, 4.07	0.76
Readmissions (%)	5.53	5.43, 5.62	5.70	5.69	4.29, 7.10	5.62
30‐day mortality (%)	0.38	0.36, 0.41	0.39	0.42	0.02, 0.82	0.19
LOS initial hospital (mean days)	2.85	2.83, 2.86	2.82	3.33	3.02, 3.64	3.37
LOS LTC (mean days)	0.57	0.55, 0.58	0.64	0.59	0.37, 0.82	0.15
LOS readmitted (mean days)	0.94	0.92, 0.96	0.91	0.94	0.69, 1.19	0.91

CI = confidence interval; LOS = length of stay.

Discussion

Limitations of Binary Outcome Models

There have been many studies of hospital outcomes, especially mortality but more recently emphasizing LOS or readmission. Most outcome studies have been limited to a single binary dependent variable, such as hospital survival, long LOS or not, readmitted or not (Chen et al. 2010). However, there are several statistical and contextual limitations of looking at each of these outcomes in isolation.

LR models (including random‐effects models and other possible refinements) are fairly robust for predicting the odds of mortality (in the absence of censoring). However, a surprisingly large proportion of postoperative deaths occur after patients (especially older patients) have been discharged from their initial hospitalization, so that outcome studies based only on data from the index hospitalization are of limited value (Bilimoria et al. 2010). In this respect, NSQIP is an important advance because it records mortality up to POD 30 regardless of whether a subject is still hospitalized.

LOS can be minimized either by a desirable event (discharge alive) or by an undesirable event (death), a situation that may be described as “competing outcomes.” Often, a “long LOS” (longer than some arbitrary number of days) is modeled as a binary outcome; in the present study, a cutoff of LOS >6 was arbitrarily chosen to approximate the 90th percentile. LOS can only be considered a measure of quality if hospital deaths are infrequent or are accounted for in some way. Clark and Ryan have described PWE multistate models with time‐varying covariates to predict hospital LOS for acutely injured patients, and suggested the use of such models especially when a significant hospital mortality must also be anticipated (Clark and Ryan 2002). Because an increasing number of older patients are discharged to LTC rather than home, it is useful to extend this approach to accommodate more than one discharge destination (Clark, Lucas, and Ryan 2007; Clark, Ryan, and Lucas 2007).

Binary outcome models for readmission have not performed very well in practice (Kansagara et al. 2011) and have obvious theoretical problems. Readmission is the result of several time‐dependent intermediate outcomes: First, the patient must survive the initial hospitalization, then be discharged home or to one of several types of LTC facilities, and finally be readmitted alive to the original hospital or another hospital. Patient and/or hospital factors may affect these intermediate transitions in different ways, and at different times (Dharmarajan et al. 2013). Furthermore, the arguably undesirable event of readmission for a given subject is still generally preferable to death and may be preferable to prolonging the initial hospitalization (two simplistic ways to reduce the incidence of readmission).

Others have also reported difficulties in using simple binary modeling for NSQIP outcomes. Dimick and colleagues (Dimick et al. 2013) have proposed using “composite” measures, in which a weighted combination of morbidity, reoperation, LOS, and data from related procedures are combined. Lucas and colleagues (Lucas et al. 2013) recognized the “immortal person‐time bias” when evaluating the relationship of LOS and readmission, and restricted their analysis to subjects with shorter LOS. We believe our extension of proportional hazards modeling is a more natural approach to avoiding some of these difficulties, and we can demonstrate some practical results as evidence of its theoretical appropriateness.

Enhanced Analysis Using a Multistate Model

Older age appears to reduce the frequency of readmission in the binary outcome model (Table 2), whereas the PWE components of the multistate model (Table 3) make it easier to see that this is because older patients are not discharged as early as younger patients and are more often discharged to LTC. Thus, when older patients encounter postoperative problems, they are more likely to be still in the hospital or in a LTC institution. A naïve interpretation of the binary model might lead to complacency about the outcomes of older patients discharged home after surgery, when in fact they are at increased risk of death (Table 4), especially on the first day home and after a prolonged LOS.

The association of male gender and longer LOS seen in the binary model (Table 2) can be explained using the multistate model (Table 3) primarily by the much lower daily rates of discharge to LTC among males. Readmission to the hospital from LTC did not appear to be affected much by age or gender, but readmission to the hospital from home was also less likely for males. As with the older patients, males with postoperative problems may not need to be readmitted as often in part because they have not yet been discharged. Other reasons for the observed disparities are more likely to be affected by social or economic factors than by physiologic differences or the quality of hospital care, and they can more easily be hypothesized from the multistate model.

Although the individual PWE models can be useful, the greatest value of the multistate model comes from combining them to achieve a multidimensional perspective of mortality, LOS, and readmission. If binary outcomes alone are considered, our own hospital does not differ significantly from the rest of the NSQIP sample with respect to any of these individual outcomes. However, the multistate model (Table 5) demonstrates that discharge to LTC from our hospital (MMC) is much less frequent than expected from our patient mix, which may reflect our geographic region, our hospital type, or other characteristics of potential interest for health care efficiency. These comparisons are with respect to hospitals of all sizes and locations (the only comparison possible using the current NSQIP PUF), and might be different if MMC were compared to other hospitals of its own size and/or geographic region.

The “All Hospitals” columns of Table 5 suggest that the PWE multistate model described here reproduces the observed outcomes for the entire population with reasonable accuracy. The simulation approach shows that it is feasible to develop a bootstrap sample of cases with the characteristics of patients from one hospital, but following the predicted outcomes based on hazards derived from the entire sample. Indeed, the multistate model allows any desired composite outcome to be statistically compared among patients with any desired categorization. The example using our own institution suggests that there may be considerable variation in outcome patterns among US hospitals and regions.

The ability to incorporate a patient's “event history” as it develops over time, by using multistate models, is a powerful addition to any form of outcome analysis (Andersen and Keiding 2002; Putter, Fiocco, and Geskus 2007; Beyersmann et al. 2011; Sutradhar et al. 2012). The models proposed here envision subjects as spending predictable amounts of time in certain states and therefore not only allow predictions of the short‐term binary outcomes above, but also longer term outcomes (e.g., survival at 30 days), the time spent in various states (e.g., LOS in LTC as well as LOS in hospital), and the differing covariate effects on each transition. Figure 2 depicts the different event histories expected for different procedures, but a similar graphical comparison could be made for any categorization of patients by procedure type, demographic characteristics, comorbidities, hospitals, etc. A more complex but potentially interesting model could also be created by adding the occurrence of postoperative complications or other events as factors affecting subsequent state transitions.

Limitations of the Multistate Model

Any attempt at greater explanatory power, including the multistate model we propose, will still share some of the limitations of binary models, including unrecorded covariates or interactions. NSQIP does not include data on the LOS in LTC institutions, so assuming that the patients remained in LTC through POD 30 is an oversimplification; however, the standard Medicare Skilled Nursing coverage is for 21 days after an acute hospital stay of at least 3 days (Mor et al. 2010), so the assumption seems fairly reasonable. NSQIP does not include data on the LOS of readmissions, so assuming that a readmitted patient would stay hospitalized through POD 30 is also an oversimplification; the mean LOS for the second hospitalization in one study of readmitted colorectal surgery patients was 8.69 days (Keller et al. 2014). However, patients discharged a second time would theoretically not return to the same state as patients discharged the first time, and it does not seem wise to create a more complicated model with the limited data available.

The PWE assumption for baseline transition rates from one state to another is not too difficult to understand. If the number of “pieces” were the same as the number of days it would be equivalent to a nonparametric model, but by reducing the number of “pieces” to a relatively small number, this “loosely parametric” method is able to present the results more clearly, with little loss of generality (Friedman 1982). The starting and ending times for the time “pieces” can be selected using various practical and goodness‐of‐fit criteria: One practical point in time is clearly the 30‐day limit of NSQIP; a goodness‐of‐fit criterion might be to minimize the daily difference between modeled and observed incidence rates (Kooperberg and Clarkson 1997). It is possible to make other parametric assumptions about transition rates (Collett 1994; Sa, Dismuke, and Guimaraes 2007), but describing a baseline hazard function with a mathematical formula rather than piecewise constants would probably be more confusing than helpful to clinicians.

Limitations of NSQIP Data

The production of reliable outcome data for hospital evaluation has been a goal of the American College of Surgeons for more than a century (Codman 1914). In recent years, NSQIP has come closer than ever to achieving this ideal (ACS 2013a,b), although 30 days of postoperative follow‐up may still not be long enough to evaluate some outcomes such as readmission after complex procedures requiring prolonged LOS (Lucas et al. 2013). Comparisons with administrative sources of hospital outcomes have found that the hospitals identified as high or low performers may differ depending upon which data source is used (Simorov et al. 2014; Lawson et al. 2015). As with any large database, there are potential issues involving inclusion criteria, coding differences, and missing data (Hamilton et al. 2010; Parsons et al. 2011). Data issues are most likely to affect results when only a small subset of cases is examined; although computer‐intensive imputation methods can be employed, the purpose of our study was such that we only used imputation for one variable of direct interest (time until readmission).

Conclusion

This study demonstrates that a “multistate” or “compartmental” model can extend the useful aspects of PH regression, without undue complexity. The multistate modeling approach could be applied using other sources of data that include outcomes after patients leave an acute‐care hospital (e.g., Medicare data). The method accounts for the interdependence of short‐term outcomes, and it allows a more realistic multidimensional interpretation of the quality of care that could improve comparison of different hospitals and regions. While they are unlikely to replace completely the familiar binary outcome predictions, multistate models could at least be a useful adjunct to help explain interdependent outcomes and identify where potential interventions might be most effective.

Supporting information

Appendix SA1: Author Matrix.