Abstract
Neurons in the visual cortex are generally selective to direction of movement of a stimulus. Although models of this direction selectivity (DS) assume linearity, experimental data show stronger degrees of DS than those predicted by linear models. Our current study is intended to determine the degree of non-linearity of the DS mechanism for cells within different lamina of the cat’s primary visual cortex. To do this, we analyzed cells in our database using neurophysiological and histological approaches to quantify non-linear components of DS in four principal cortical laminae (layers 2/3, 4, 5, and 6). We use a direction selectivity index (DSI) to quantify degrees of DS in our sample. Our results show laminar differences. In layer 4, the main thalamic input region, most neurons are simple type and exhibit high DSI values. For complex cells in layer 4, there is a broad distribution of DSI values. Similar features are observed in layer 2/3, but complex cells are dominant. In deeper layers (5 and 6), DSI distributions are characterized by clear peaks at high values. Independent of specific lamina, high DSI values are accompanied by narrow orientation tuning widths. Differences of orientation tuning for non-preferred versus preferred directions are smallest in layer 4 and largest in layer 6. These results are consistent with a non-linear process of intra-cortical inhibition which enhances DS by selective suppression of neuronal firing for non-preferred directions of stimulus motion in a laminar dependent manner. Other potential mechanisms are also considered.
Keywords: cat’s visual cortex, direction selectivity, intra-cortical inhibition, non-linear process
Introduction
Most cells in the cat’s visual cortex respond selectively to the direction of movement of an optimally oriented visual stimulus (Hubel & Wiesel, 1959, 1962; Orban et al., 1981; Emerson et al., 1992; Jagadeesh et al., 1993). However, this property, direction selectivity (DS), is not generally observed for LGN cells, which provide major inputs to the cortex. Therefore, DS must be created by a specific organization of geniculo-cortical and intra-cortical connections. For the cortical DS property, models of DS have been proposed (Barlow et al., 1964; Adelson & Bergen, 1985; van Santen & Sperling, 1985; De Valois et al., 2000; Peterson et al., 2004). In most cases, linearity has been assumed at the first stage but the degree of DS predicted by linear stage only is generally weaker than that measured with drifting gratings indicating nonlinear contributions (Reid et al., 1987; Tolhurst & Dean, 1991; DeAngelis et al., 1993a, 1993b; Murthy et al., 1998; Peterson et al., 2004).
Several mechanisms may be involved in the non-linear contribution to DS. They include nonlinear transformations of membrane potentials to spiking activity (Carandini & Ferster, 2000; Mechler & Ringach, 2002) and non-linear lateral excitation & inhibition from other neurons in the visual cortex (Wielaard et al., 2001; Priebe & Ferster, 2005). Anatomical and physiological studies show that visual information from LGN arrives mainly at layer 4 in visual cortex, and then flows to layer 2/3 followed by deeper layers (layers 5 & 6) (Alonso, 2002; Thomson & Bannister, 2003). (But note that this is a simplified description and actual projection patterns are much more complicated). Note also that organizational patterns of thalamo-cortical and intra-cortical connections are different depending on cortical lamina (Gilbert & Kelly, 1975; Martin & Whitteridge, 1984; Douglas & Martin, 1991; Fitzpatrick, 1996; Callaway, 1998).
Based on these factors, we hypothesize here that the degree of non-linear components of DS may vary with cortical layers. To test this hypothesis, we have analyzed neuronal response patterns for cells in our substantial database of cortical neurons using a reverse correlation technique combined with standard histological reconstructions. Two-dimensional Fourier analysis of the spatiotemporal (space-time) RF profile enables prediction of DS to a grating stimulus of given spatial and temporal frequencies (DeAngelis et al., 1993a, 1993b). With an assumption that the input to simple cells is linear (Jagadeesh et al., 1997), we consider the difference between tested- and predicted DS values as the non-linear contribution to DS.
The granular layer (layer 4, the primary recipient of LGN input) is characterized by a dominant proportion of simple cells and lower spontaneous neural activity compared with upper and lower layers (Hubel & Wiesel, 1962; Sillito, 1975; Gilbert, 1977). Our physiological data and histological reconstructions are consistent with these observations. We find that in layer 4, DSI values are generally well matched to those predicted from spatiotemporal linear RFs. In contrast, for supra- and infra-granular layers, measured DSIs are substantially larger than those predicted. This shows a larger non-linear contribution to DS. In addition, our results show that DS cells have narrower orientation tuning widths for non-preferred directions of motion. Differences in orientation tuning widths between the two directions also differ depending on cortical layers. The smallest are in layer 4 and the largest in layer 6. Functional implications are considered in Results and Discussion sections.
Materials and Methods
Physiological preparation
Extracellular recordings from well-isolated single units were made from cells in the striate cortex of anesthetized and paralyzed cats. While electrocardiogram (ECG), heart rate, temperature, intra-tracheal pressure, and electroencephalogram (EEG) were being monitored, the amount of anesthetic drug (1mg/kg·hr of sodium thiamylal along with 10mg/kg·hr of gallamine triethiodide (muscle relaxant)) was systematically adjusted depending on body weight and depth of anesthesia. Electrode penetrations made along the medial bank of the post-lateral gyrus (P4L2, Horsley-Clarke coordinates) allowed us to measure spiking activity of neurons whose receptive field eccentricities were within the central 15 deg of the visual field (DeAngelis et al., 1993a, 1993b). Custom-made digital signal processing software was used to discriminate individual action potentials on the basis of shape as well as amplitude. Briefly, brief spike waveforms (about 2ms) that crossed the threshold (upper, lower or both, adjustable) were sampled at 25 kHz and overlapped one another in time-voltage space. On viewing the waveforms, multiple upward or downward arrows are additionally placed to specify regions that the waveforms must intersect. The arrows could be moved to any positions on the waveforms. Waveforms satisfying these requirements are assigned as a single unit. After discrimination, spike occurrence time was recorded with 1ms resolution for the off-line analysis. Once a single unit was identified by the spike waveform, optimal orientation, spatial frequency, and size were measured quantitatively with sinusoidal gratings drifting at 2Hz.
Detailed orientation tuning curves were made from presentation of drifting gratings at optimal spatial frequencies and sizes. Six to ten orientation values spanning 90 deg, with the pre-determined optimal orientation at the center, were drifted in either the preferred or non-preferred direction of motion. Then, individual tuning curves for each direction were fitted with a Gaussian function as follows.
| (1) |
where K is the maximum neural response, x is the orientation, μ is the preferred orientation, σ is the standard deviation of the Gaussian, and R0 represents the baseline neural response when there is no visual stimulation.
Histology
Histological reconstructions from our database were reviewed and information was selected from 41 animals to be used for analysis in the current study. We chose the data based on quality such that cells were not used if they were close to laminar borders. We also took into account that formaldehyde fixation and subsequent steps (e.g., dehydration and embedding processes) in brain processing produces about a 20% decrease in linear dimensions of neural tissue which we factored in for laminar identification (Fox et al., 1985). Reconstructions, which contained at least two clearly identifiable lesions, were evaluated to determine if the distance between the lesions corresponded to that between their specified depths within a 25% margin of error. Data that did not meet this criterion were excluded from the analysis.
As is standard, neurons were stained with cresyl violet and analyzed for Nissl substance. The amount and distribution of Nissl substance varies with different types of neurons and cortical layers (O’Leary, 1941; Peters & Yilmaz, 1993). After recording depths were corrected for brain shrinkage (20~25%), individual neurons were assigned to one of four laminar groups based on the following criteria as described in previous studies (O’Leary, 1941; Peters & Yilmaz, 1993).
Layer 2/3 (Supra-granular layer): Layer 2 and 3 are essentially indistinguishable. These layers are composed of approximately equal amounts of granular and small pyramidal cells.
Layer 4 (Granular layer): Layer 4 is wide relative to layer 2/3, and consists of small granular cells interspersed among large stellate cells.
Layer 5 (Infra-granular layer): Layer 5 is the smallest layer in area 17, consisting of pyramidal cells with no clear columnar organization.
Layer 6 (Infra-granular layer): Layer 6 is a relatively large layer consisting of multiform and fusiform cells organized into columns.
As noted above, to maximize reliability of laminar location, cells that were close to borders 4/5 or 5/6 were excluded from the database. No attempt was made to classify layers into various sub-laminae (e.g., layers 4A, 4B, 6A, 6B).
Cell classification and direction selectivity index
We classified cells in the visual cortex as simple or complex by a standard technique. We compared the first harmonic (F1) to the DC (F0) level of the peri-stimulus time histogram obtained with an optimal (spatial frequency & orientation) grating stimulus of 2 Hz. Simple cells have F1/F0 ratios greater than 1 (Skottun et al., 1991).
A direction selectivity index (DSI: 0 is non-DS and 1 is highly DS) was calculated for responses to preferred (p) and non-preferred (np) directions. Depending on cell types, F1 (for simple) or F0 (for complex) amplitude of response was used for the calculation (Peterson et al., 2004, 2006).
| (2) |
Predicted direction selectivity index
For simple cells, spatiotemporal linear RFs were measured with a reverse correlation procedure (Jones & Palmer, 1987). Detailed description of the procedure is available elsewhere (DeAngelis et al., 1993a, 1993b; Anzai et al., 1999). Briefly, individual bar stimuli of either bright (32 cd/m2) or dark (2 cd/m2) luminance were displayed against a gray background (17 cd/m2), one at a time at 2- dimensional random grid locations for 40 msec. A cross-correlation between the stimulus sequence and the cells’ spike response yields a linear spatiotemporal RF. Simple cells rarely exhibit much maintained discharge without a visual stimulus so it is difficult to measure directly the inhibitory receptive field with a dark or bright noise stimulus. To resolve this difficulty, in the current study, a linear spatiotemporal receptive field is created by taking the difference between responses to bright and dark noise stimuli (DeAngelis et al., 1993a, 1993b). This approach is based on the assumption that dark-induced excitation is equivalent to bright-induced inhibition, and vice versa. This assumption is reasonable in that ON sub-regions yield excitation when probed with bright stimuli and inhibition when activated with dark stimuli. Similarly, an OFF sub-region yields excitation for dark stimuli and inhibition for bright stimuli (Heggelund, 1981; Palmer & Davis, 1981; Ferster, 1988; Priebe & Ferster, 2005). Both excitation and inhibition follow the time course of response so that they are arranged in a push-pull fashion in space-time (Priebe & Ferster, 2005), although they may be spatially overlapped when temporal information is ignored. Therefore, the linear spatiotemporal receptive field can reflect substantial inhibitory as well as excitatory RF regions.
Given a linear spatiotemporal RF, a prediction of direction selectivity can be made by calculation of the spatiotemporal amplitude spectrum via Fourier analysis. The complete amplitude spectrum is composed of four quadrants, which are symmetrical about the origin. We consider only two quadrants with positive spatial frequencies. Neurons with spatiotemporally separable RFs have spectra that are identical in amplitude for positive and negative temporal frequencies, whereas those with inseparable RFs produce asymmetry between positive and negative values. Therefore, the relative amplitude of the positive and negative temporal frequency quadrants can be used for linear prediction of a cell’s direction selectivity (Adelson & Bergen, 1985; DeAngelis et al., 1993a, 1993b).
The amplitude spectrum in each of two quadrants is fitted with the following function to extract estimates of the cell’s spatial and temporal frequency tuning curves.
| (3) |
where A0, sf0, a, k, θ are free parameters.
This function is slightly modified from that used in our previous study (DeAngelis et al., 1993a, 1993b), and is expressed as the product of Gaussian (for spatial frequency) and Gamma (for temporal frequency) distributions. Specifically, A0 determines the height of the Gaussian curve sf0 is the preferred spatial frequency, a is the standard deviation of the Gaussian. k and θ represent the shape and scale parameters of the Gamma distribution, respectively. The amplitude values at a given spatial frequency and a 2 Hz temporal value are used as the predicted responses to a grating drifting in the preferred and non-preferred directions. The DSI values are computed from the predicted responses using Equation 2.
Results
Laminar distribution of simple and complex cells
We examined data from 899 cells in our database and quantified for each neuron the ratio of the amplitude of the first harmonic of the response to the mean spike rate at the preferred orientation. For 437 cells, this ratio was greater than 1 and they were classified as simple cells. The remaining 462 cells were classified as complex. These groups were further broken down depending on the analysis in order to provide the cell data needed for the specific questions.
A linear model successfully describes the receptive field of a simple cell as a result of combined inputs from multiple LGN cells whose receptive fields are positioned along the preferred orientation (Hubel & Wiesel, 1962; Alonso et al., 2001). This implies that simple cells reside mainly in cortical layers which receive extensive feed-forward projections from LGN cells.
Figure 1 compares the distributions of F1/F0 ratio values for four layer groups. Consistent with standard descriptions, layer 4 is predominantly comprised of simple cells (220 out of 281 cells or 79.29%). In contrast, complex cells are dominant in layers 2/3 & 5. Distributions of F1/F0 ratios in these layers resemble mirror images of those of layer 4, reflecting much higher proportions of complex cells (layer 2/3: 136 out of 191 cells or 71.2%; layer 5: 111 out of 128 cells or 86.72%) than simple types (Mann-Whitney U-test: p<10−23 for layer 4 vs. layer 2/3, p<10−32 for layer 4 vs. layer 5, p<0.01 for layer 2/3 vs. layer 5). In layer 6, however, the F1/F0 distribution is not strongly biased towards one direction but exhibits a balance between simple (146 out of 299 cells or 48.83%) and complex types (153 out of 299 cells or 51.17%) (Mann-Whitney U-test: p<10−14 for layer 4 vs. layer 6, p<0.01 for layer 2/3 vs. layer 6, p<10−8 for layer 5 vs. layer 6).
Figure 1. Comparisons of F1/F0 distributions & spontaneous activity among four laminar groups.
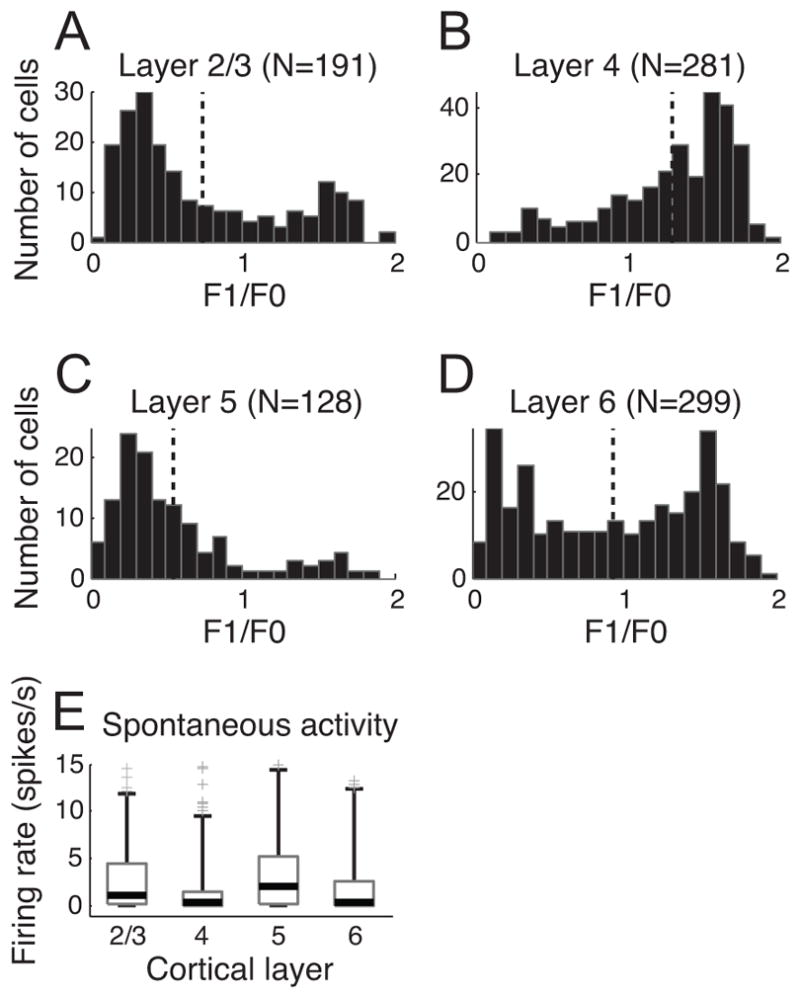
A total of 899 cells in our database were assigned to one of four layer categories based on histological reconstruction. We classified simple and complex cells based on F1/F0 ratio and quantified spontaneous activity from each neuron. Vertical dotted lines (A–D) indicate mean values of F1/F0 ratio distributions for four different layer groups. A. F1/F0 distribution in layer 2/3. 55 out of 191 cells were classified as simple type (F1/F0 ratio greater than 1). B. F1/F0 distribution in layer 4. 220 out of 281 cells were classified as simple type. C. F1/F0 distribution in layer 5. 17 out of 128 cells were classified as simple type. D. F1/F0 distribution in layer 6. 146 out of 299 cells were classified as simple type. E. Spontaneous activity is compared across layers 2/3, 4, 5, and 6. In each boxplot, the thick horizontal line within the box is the median (50th percentile), the top and bottom edges of the box are the 25th and 75th percentile of the data set, respectively. The upper and lower vertical lines extend to cover 95% of the entire data distribution. The gray cross marks outside the range indicate outliers. Extreme outliers (>15 spikes/s) are omitted in drawing.
Besides the dominance of simple cells, low spontaneous activity may be another factor that differentiates cells in layer 4 from those in adjacent layers. Previous studies have shown that spontaneous rates in layers 2/3 and 5, are relatively high compared to those in layers 4 and 6 (Gilbert, 1977; Sillito, 1977; Schwarz & Bolz, 1991). This probably reflects stronger spontaneous activity of special complex cells, those that do not show length summation within the RF. For our sample, consistent with previous findings, spontaneous activity of cells in layer 4 is generally weaker than those for layers 2/3 and 5 (Mann-Whitney U-test: p<10−4 for layer 4 vs. layer 2/3, p<10−6 for layer 4 vs. layer 5). However, there is no significant difference between layers 4 and 6.
Direction selectivity of simple and complex cells and their laminar relationships
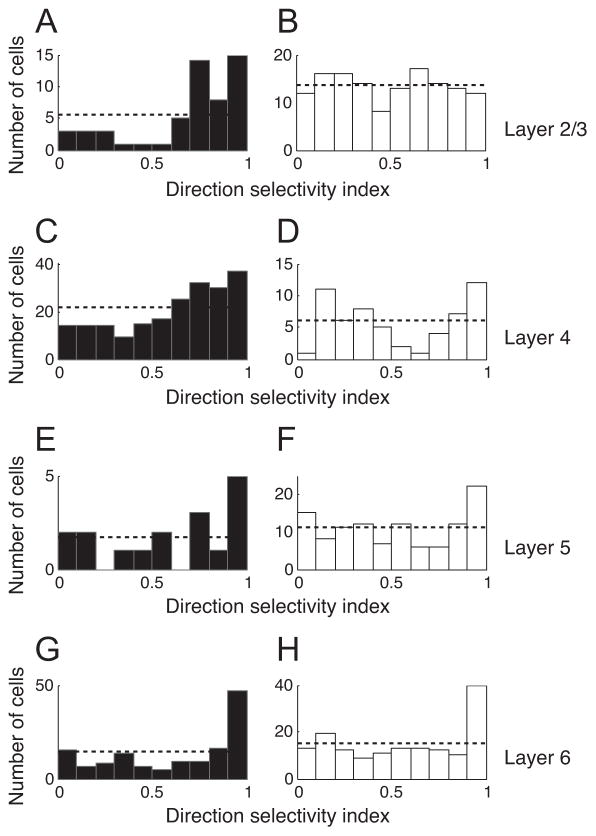
Our data show that there are substantial differences in direction selectivity depending on cell type and layer. Distributions of direction selectivity index (DSI) across layers, separated into populations of simple and complex cells are illustrated in Figure 2. In layer 4 (i.e., the main LGN input), 64.09% (141 out of 220) of simple cells are categorized as direction selective units (DSI≥0.5). In the range of DSI between 0.5 and 1, the number of simple cells increases gradually as DSI goes higher (Figure 2C). In contrast, DSI values of complex cells (about 20% of total cells in this layer) are not biased for one particular direction (Figure 2D).
Figure 2.
Direction selectivity index (DSI) distributions for four laminar groups. DSI is calculated using: , where p and np indicate neural responses for preferred and non-preferred (180deg away from the optimal value) directions, respectively. A, B. DSI distribution for layer 2/3. Filled and unfilled bars represent simple cells (F1/F0 ratios greater or less than 1, respectively). The horizontal dotted line designates a mean uniform DSI distribution. C, D. DSI distribution for layer 4. The same format is used as in A & B. E, F. DSI distribution for layer 5. G, H. DSI distribution for layer 6.
In layer 2/3, the relative proportions of simple and complex cells are reversed compared to layer 4. The DSI distribution of complex cells is almost uniform across the entire range of DSI values (0 to 1) (Figure 2B). Simple cells account for less than 30% of the total population in layer 2/3, but their DSI distribution shows a unique characteristic (Figure 2A). As for layer 4, simple cells in layer 2/3 tend to be more direction selective compared with complex cells. However, this tendency is more prominent in layer 2/3 with 78.2% of simple cells (43 out of 55) having DSI values higher than 0.5 (Note that 50.74% of complex cells have DSI >0.5).
In infra-granular layers (layers 5 & 6), the DSI histogram has a clear peak at the highest DSI value (DSI > 0.9) for both simple and complex cells. This feature is more pronounced in layer 6 (Figure 2G & H) compared to layer 5 (Figure 2E & F).
Non-linear components of direction selectivity
We measured space-time RFs for 158 simple cells. The numbers of simple cells from the supra-granular (layer 2/3), granular (layer 4) and infra-granular layers (layer 5 & 6) are 29, 61 and 68 (7 in layer 5, 61 in layer 6), respectively.
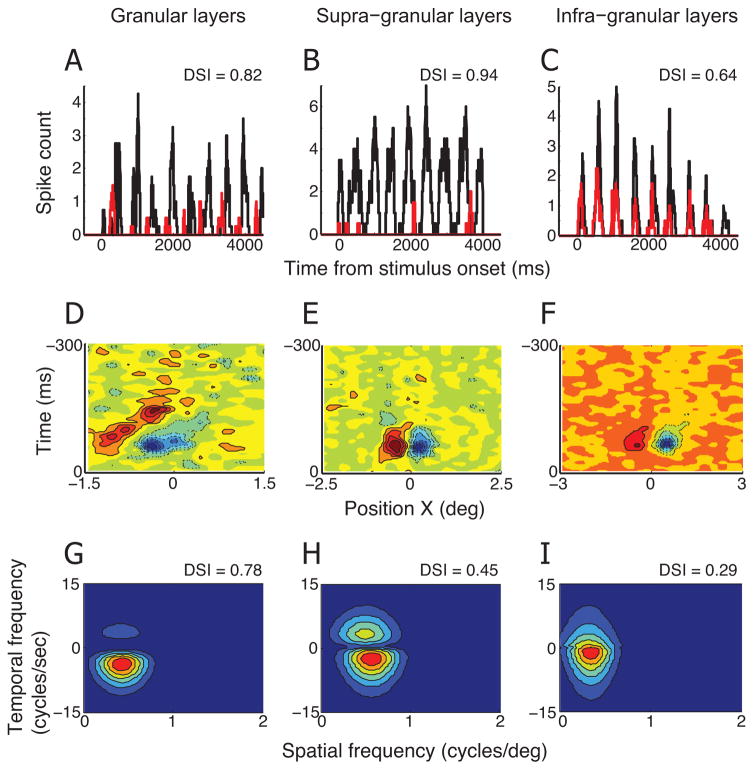
Figure 3A shows the neural activity of a direction selective simple cell recorded in the granular layer. Black and red curves represent peri-stimulus time histograms calculated for preferred and non-preferred (opposite to preferred) directions, respectively. A grating stimulus drifting in the non-preferred direction caused clear non-zero spike activity, but it is much weaker than the neural response for the preferred direction. The DSI calculated for this cell’s spike response is 0.82.
Figure 3. Linear predictions of DSIs made for three representative simple cells.
A. Peri-stimulus time histograms (PSTHs) for preferred (black) and non-preferred (red) directions of motion were calculated for a simple cell in the granular layer. The numbers of spikes were counted for a 50ms sliding window with 1ms steps. The DSI measured with moving grating stimuli for this cell is 0.82. D. X-T profile of spatiotemporal linear RF of the simple cell described in A. Red color with solid contour lines represents bright-excitatory (or ON) subregion of RF. Blue color with dashed contour lines represents dark-excitatory (or OFF) subregion of RF. G. A 2-dimensional Fourier transform is applied to X-T plot in D. The amplitude spectrum for positive temporal frequency reflects neural response for rightward direction of motion. Contour map shows the best fit of equation (2). DSI predicted from this amplitude spectrum is 0.78. B, E, H. Linear prediction of DSI is made for a simple cell in the supra-granular layer. The same conventions are used as in A, D, G. C, F, I. Linear prediction of DSI is made for a simple cell in the infra-granular layer. The same conventions are used as in A, D, G.
We compared the DSI measured with grating stimuli to that predicted from a linear model. First, we derived linear spatiotemporal RFs using a reverse correlation procedure. For most cells, the spatiotemporal linear RF was two-dimensional (spatially one-dimensional), because the recordings included only a long bar stimulus with a preferred orientation that varied in position along the X-axis. However, more extensive three-dimensional spatiotemporal RFs were also measured for a smaller number of cells. In these cases, we integrated the three-dimensional dataset along the Y-axis to reduce it to a two-dimensional RF (i.e., X-T plot).
The X-T plot for this representative cell has clearly defined sub-regions (Figure 3D). These sub-regions are slanted to the right, indicating that this cell is direction selective. Fourier analysis of the X-T plot yields a spatiotemporal amplitude spectrum (Figure 3G). Two quadrants of negative spatial frequencies are omitted because they have the same information as those of the positive data. From the spatiotemporal amplitude spectrum, we can predict direction selectivity of a neuron. The positive and negative temporal frequency quadrants provide relative neural response predictions for motion in the preferred and non-preferred directions, respectively. For this cell, predicted DSI is 0.78, which is closely similar to the DSI measured with grating stimuli (0.82).
The other two columns in Figure 3 illustrate two additional example cells for which the same analysis was conducted. One was collected from supra-granular layers, and the other from an infra-granular location. Both cells exhibit clear directional selectivity in spike response for grating stimuli (Figure 3B & C). However, unlike the previous example cell from the granular layer, sub-regions of their spatiotemporal linear RFs are not substantially tilted to the left or to the right (Figure 3E & F). Consequently, the spatiotemporal amplitude spectrum shows comparable power in positive and negative temporal quadrants, and predicted DSIs are much smaller compared with those measured with grating stimuli (Figure 3H & I).
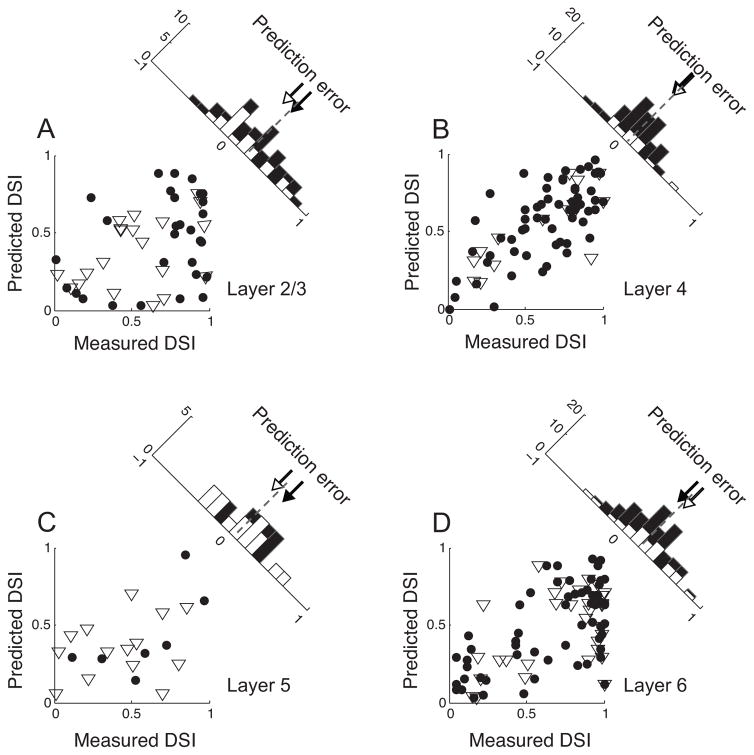
We assume that any difference between measured DSI and linearly predicted DSI reflects a non-linear component of direction selectivity. From population data, we identify how this non-linear component of direction selectivity differs in extent depending on cortical layers. For the granular layer (Figure 4B), measured and linearly predicted DSI values show a strong positive correlation (r = 0.7, p<10−9). A positive correlation is also evident for simple cells in layer 6 (Figure 4D), but its magnitude (r = 0.65, p<10−7) is slightly weaker than that for the granular layer.
Figure 4. Comparisons of measured and predicted DSIs.
A. Simple (N=61, filled circles) and complex (N=15, open triangles) cells in layer 4. The values plotted in the X- and Y-axes indicate DSIs measured with grating stimuli and those predicted from the spatiotemporal amplitude spectrum, respectively. The histogram in the upper-right shows the distribution of prediction errors (Measured DSI – Predicted DSI). Dashed line indicates the mean value of the distribution. Open and closed arrows indicate mean values of corresponding shaded sub-distributions. B. Simple (N=29) and complex (N=20) cells in layer 2/3. The same format is used as in A. C. Simple (N=7) and complex (N=14) cells in layer 5. The same format is used as in A. D. Simple (N=61) and complex (N=31) cells in layer 6. The same format is used as in A. Note that the distributions of prediction errors are centered at zero for layer 4, but clearly shifted to positive values for both supra- and infra-granular layers.
As shown in Figure 2A, nearly all simple cells in supra-granular layers of our data population are direction selective. However, the spatiotemporal linear RF doesn’t provide a reasonable prediction for measured DSIs (r = 0.34, p = 0.07), indicating a highly non-linear component of direction selectivity (Figure 4A).
The derivation of a linear spatiotemporal RF is not possible for most complex cells, which do not have well segregated On/Off sub-regions in their receptive fields. Here, we try to evaluate the degree of non-linearity for a sub-population of complex cells whose F1/F0 ratios are larger than 0.5 (open triangles in each panel of Figure 4, 15 (64% of complex cells, estimated from Figure 1, have F1/F0 ratios greater than 0.5) in layer 4, 20 (31% of complex cells) in layer 2/3, 14 (31% of complex cells) in layer 5, 31 (39% of complex cells) in layer 6). Consistent with the results from simple cells, measured and linearly predicted DSI values of complex cells are positively correlated in layer 4 (r = 0.79, p<10−3) and layer 6 (r = 0.48, p<0.01), but not in layer 2/3 (r = 0.39, p=0.08) and 5 (r=0.09, p=0.75).
The difference in the non-linear component of direction selectivity between laminae is not simply due to how cells in each layer are fitted by our model according to equation 3 (see Materials and Methods). The overall goodness-of-fit is better for simple cell data than complex response type (Mann-Whitney U-test, p<10−10; the mean of adjusted r-squared: 0.91 (simple cells), 0.84 (complex cells with F1/F0>0.5)). However, there is no meaningful difference depending on layers for each cell group (One-way ANOVA, p=0.98 (simple), 0.43 (complex); the mean of adjusted r-squared for simple cells: 0.906 (layer 2/3), 0.910 (layer 4), 0.904 (layer 5), 0.906 (layer 6); the mean of adjusted r-squared for complex cells: 0.827 (layer 2/3), 0.830 (layer 4), 0.878 (layer 5), 0.833 (layer 6)).
The histogram in each panel in Figure 4 shows a distribution of a non-linear component of direction selectivity (the difference between measured and predicted DSI). For the granular layer, the distribution of this non-linear component is centered at zero (Figure 4B), and there is no significant difference between measured and predicted DSIs (Wilcoxon signed rank test, p = 0.12). However, for supra-granular layers (Figure 4B), the mean of the distribution of the non-linear component of direction selectivity is positive, indicating that linearly predicted DSIs are substantially smaller than DSIs measured with grating stimuli (Wilcoxon signed rank test, p<10−3). The distribution of non-linear component values for layer 6 is similar to that for the supra-granular layers (Wilcoxon signed rank test, p<10−8).
Orientation selectivity for preferred and non-preferred directions of motion
Based on our linear assumption of input from the LGN, we find here that direction selectivity of visual neurons depends largely on intra-cortical processing. Differences between measured and linearly predicted DSIs are statistically significant for layers 2/3 & 6 but not for layer 4 (i.e., the major LGN input layer). Intra-cortical processing may provide visual neurons with enhanced direction selectivity by selectively exciting (or inhibiting) neural responses for preferred (or non-preferred) directions of motion.
Here, we examine the possibility of a selective intra-cortical inhibitory mechanism by analyzing orientation tuning widths for two opposite directions of motion. LGN cells are thought to provide only excitation to visual cortex (Freund et al., 1989; Kharazia & Weinberg, 1994). Therefore, a pure thalamo-cortical feedforward mechanism cannot produce the observed orientation tuning which is sharp and contrast-invariant. Numerous studies have shown that intra-cortical inhibition plays an essential role in shaping orientation selectivity of visual neurons (Hata et al., 1988; Shapley et al., 2003). Blocking of cortical inhibition causes a substantial broadening or loss of orientation tuning (Sillito, 1975; Crook et al., 1998), whereas administration of GABA (and its agonist) or activation of specific inhibitory interneurons sharpens orientation tuning and enhances direction selectivity (Leventhal et al., 2003; Lee et al., 2012). If intra-cortical inhibition selectively suppresses the neural response for non-preferred direction of motion, orientation tuning width for this condition may also be more affected than that for the opposite (i.e., preferred) direction of motion. Additional and alternative mechanisms are also considered (see Discussion).
In order to test this hypothesis, we created orientation tuning curves from neural responses for preferred and non-preferred directions of motion (see Materials and Methods). We take advantage of adjusted r-squared values as a standard of goodness of fit. Adjusted r-squared is the basic r-squared (i.e., the percentage of variance explained by the model) corrected by a number of free parameters to prevent over-fitting of the model. Only cells with adjusted r-squared values at or above 0.9 for both directions are included in the following analysis. Therefore, cells not showing orientation selectivity or those whose responses to non-preferred directions are too weak (e.g., DSI=1) are excluded.
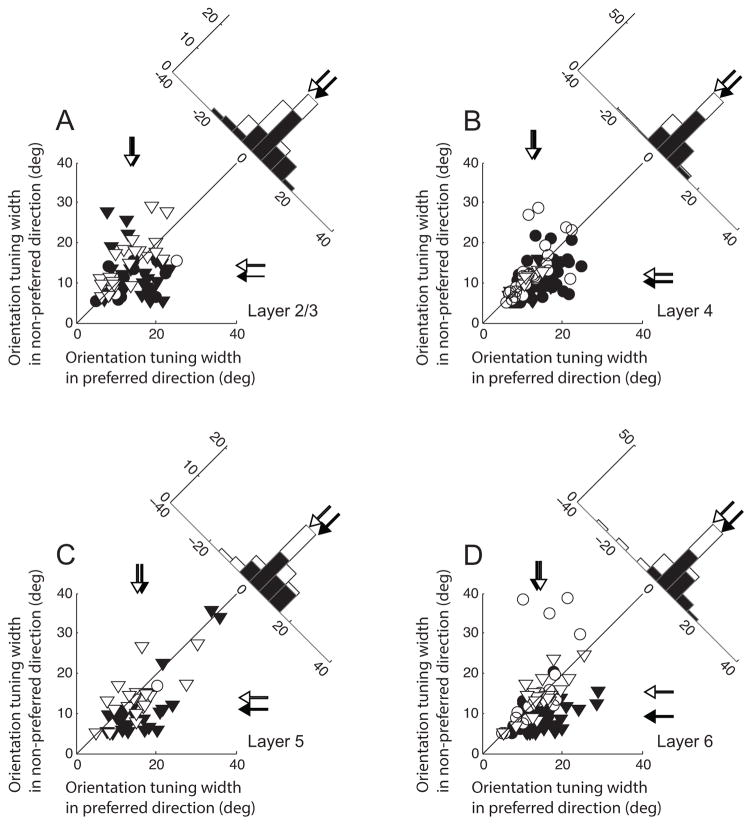
We compared the values of parameter σ between preferred and non-preferred directions across four different cortical layer groups (Figure 5). Filled and open symbols indicate direction selective (DS, DSI≥0.5) and non-selective (non-DS, DSI<0.5) units, respectively. For each axis, mean values of these two groups of cells are marked by corresponding filled and unfilled arrows. Circles and triangles represent simple and complex type neurons, respectively. DS cells in layer 2/3 tend to have broader orientation tuning widths for preferred compared with non-preferred directions of motion (Figure 5A). However, the orientation tuning widths of non-DS units show no difference concerning direction preference. The difference between DS and non-DS units may be derived from a decrease of orientation tuning width for the non-preferred direction (y-axis), not an increase of width in the preferred direction (x-axis). Results from the other three laminar groups are consistent with these observations. However, the amount of decrease of orientation tuning width in the non-preferred direction differs depending on cortical layers. It is smallest in layer 4 (Figure 5B) and largest in layer 6 (Figure 5D). To test the statistical significance of the laminar dependent difference, we first created 10,000 bootstrap samples from each DS and non-DS unit in our cell population and estimated the distributions of the differences between sample means in each of the 4 layers. Then, we defined one-sided p-values as the proportions of simulated differences in one distribution (e.g., layer 4) which are bigger than the observed difference in the layer of comparison (e.g., layer 6). The test results indicate that the amount of orientation tuning width difference between DS and non-DS units significantly differs between layer 4 and layer 6 (one-sided bootstrap test, p<10−3). The difference between layer 4 and layer 2/3 does not reach statistical significance (one-sided bootstrap test, p=0.22). However, the effect might be underestimated because the analysis does not include cells whose responses to non-preferred directions are too weak for the analysis of orientation selectivity.
Figure 5. Comparisons of orientation tuning widths between preferred and non-preferred directions of motion.
A. Data from 66 units in layer 2/3. X- and Y-axes indicate orientation tuning widths (parameter σ of Gaussian fitting curve) obtained for preferred and non-preferred directions of motion, respectively. Circles and triangles represent simple and complex cells, respectively. Direction selective units (filled symbols, DSI≥0.5) and non-selective cells (open symbols, DSI<0.5) are differentially indicated. Arrows for each axis indicate mean values of corresponding shaded units. The histogram in the upper-right shows the distribution of differences of orientation tuning widths between two opposite directions (preferred and non-preferred directions). For direction selective (but not non-selective) cells, orientation tuning curves for non-preferred directions tend to be narrower than those for preferred directions. B. Data from 110 cells in layer 4. The same format is used as in A. C. Data from 47 cells in layer 5. The same format is used as in A. D. Data from 98 cells in layer 6. The same format is used as in A. Note that the amount of decrease of orientation tuning width in the non-preferred direction differs depending on cortical layers. It increases gradually in the direction of visual information flow (layer 4 → layer 2/3 → layer 5 → layer 6).
Discussion
Previous studies have shown that a linear prediction of direction selectivity of simple cells is generally smaller than that measured with drifting sinusoidal grating stimuli (DeAngelis et al., 1993a, 1993b; Murthy et al., 1998; Peterson et al., 2004). We have posited here that differences between measured and linearly predicted DSIs (i.e., the non-linearity of DSI) is largely derived from intra-cortical connections. And based on this assumption, we hypothesize that the non-linearity of DSI varies in extent with cortical lamina.
This hypothesis has been examined previously for simple cells in layers 4 & 6 of area 17 in the cat. (Murthy et al., 1998). Stationary counter-phasing gratings were used in this previous study to characterize the linear spatiotemporal (S-T) structure of simple cell receptive fields. The main finding is that S-T structure is correlated with direction selectivity in layer 4 but not in layer 6, suggesting a larger involvement of intra-cortical signals in layer 6.
This previous study is important and our current work extends it in several ways. First, we have analyzed our very large database of cortical neurons (899 cells) which are distributed in the four cortical layer groups. This provides detailed data regarding various features of neural activity (e.g., F1/F0 ratio, spontaneous activity, direction selectivity, orientation tuning width, etc.) and differences in the path of visual information flow in the primary visual cortex (Layer 4 → 2/3 → 5 → 6). Second, we use a reverse correlation technique to derive linear spatiotemporal structures of receptive fields. Compared with counter-phasing gratings, white noise stimuli are advantageous because they reduce the influence of non-linearities (e.g., adaptation to strong or prolonged stimuli, recruitment of neighboring cortical neurons) and they provide a full characterization of a neuron’s spatial and temporal sensitivities (Chichilnisky, 2001). Third, we have evaluated the non-linearity of direction selectivity not only for simple cells but also for a sub-population of complex cells (F1/F0 ratio > 0.5) and the results show that laminar dependency of non-linearity is observed for both cell types. Non-linearity of DSI is largest in the supra-granular layer which is reported to contain well-developed horizontal connections (Callaway & Katz, 1990; Hirsch & Gilbert, 1991; Fitzpatrick, 1996). Finally, our analysis of orientation tuning width suggests a selective intra-cortical inhibition mechanism to refine direction selectivity.
Differences between supra-granular and infra-granular layers
We show here that neurons in supra- and infra-granular layers share several properties that are different from those in the granular layer. For example, they generally have stronger spontaneous activity. Consistent with this, complex cells are more common than the simple type. There is also a considerable amount of non-linearity in the DS process for cells within these layers.
Considerable experimental work has shown that neurons in the supra-granular layer (layer 2/3) receive their principal input from the granular layer (layer 4) (Gilbert & Wiesel, 1979; Callaway & Katz, 1992). A simplified projection pattern is that thalamo-cortical input arriving in layer 4 is relayed from layer 4 to 3 (and 2), then from layer 3 to layer 5, and from layer 5 to 6 (Alonso, 2002; Thomson & Bannister, 2003). Information processed in the primary visual cortex is transmitted to other cortical areas via layers 3 and 6. Neurons in layer 6 are more unique in that they receive direct LGN input and also provide feedback projections to LGN (Sillito et al., 2006; Wang et al., 2006). It is also reported that many neurons in layer 6 of the cat’s visual cortex can maintain their response properties (selectivity for orientation or direction) in the absence of input from layer 2/3 (Schwark et al., 1986).
Consistent with these connective pathways, our results show that the proportion of complex cells relative to simple cells is the smallest in layer 4 and increases gradually in the direction of visual information flow (20.71% in layer 4 → 71.2% in layer 2/3 → 86.72% in layer 5). In layer 6, simple and complex cells occupy comparable proportions of the total population. This is thought to be due to direct input from LGN cells (LeVay & Gilbert, 1976; Shatz & Luskin, 1986).
An interesting characteristic of our DSI distribution for the infra-granular layer is that there is a clear peak at the highest DSI value (DSI>0.9). It is most prominent in layer 6 but also observable in layer 5 regardless of cell type, although the number of simple cells in layer 5 is small. We note that this finding is consistent with results reported in previous work (Schiller et al., 1976; Hawken et al., 1988). For monkey V1, the majority of cells that are highly direction selective, are confined to the upper sub-layers of 4 and layer 6 (Hawken et al., 1988). In the cat’s visual cortex, a reasonably uniform distribution of directionally selective cells is reported for all cortical layers (Gilbert, 1977).
Intra-cortical connections and direction selectivity
In the supra-granular layers (layer 2/3), simple cells constitute less than 30% of the total population, and their DSI distribution is strongly biased toward high values. Simple cells in layer 4 are numerous and also exhibit high DSI values but lower than those in the supra-granular layers.
We have previously found that direction selective (DS) simple cells can be formed from excitatory non-DS simple cell inputs with variable temporal phase differences. Direct input from lagged LGN cells is not necessarily required (Peterson et al., 2004). This is consistent with our current finding that higher proportions of simple cells are categorized as DS units in layer 2/3 (43 out of 55) compared to layer 4 (the LGN main input layer, 141 out of 220).
The role of intra-cortical inhibition concerning direction selectivity has been tested by application of bicuculline methiodide (BMI), a selective antagonist for the GABAA receptor (Sato et al., 1995; Murthy & Humphrey, 1999). Blockage of intra-cortical inhibition caused a clear reduction of direction selectivity for most cells in layer 2/3 and layer 4b. This suggests that excitatory inputs to layer 2/3 are bi-directional but slightly biased for one direction and that extra non-selective inhibitory inputs determine the degree of directionality by raising the firing threshold. However, the direction selectivity of cells in layer 6 was minimally affected by BMI (Sato et al., 1995). If direction selectivity of layer 6 cells is largely dependent on directionally tuned excitatory inputs rather than inhibitory mechanisms, this could account for the layer 6 finding (Sato et al., 1995).
Intra-cortical inhibition has also been considered as an essential mechanism for sharpening of orientation tuning (Hata et al., 1988; Shapley et al., 2003; Chen et al., 2005). Administration of GABA (and its agonist) or activation of specific inhibitory interneurons is reported to cause the sharpening of orientation tuning and the enhancement of direction selectivity (Leventhal et al., 2003; Lee et al., 2012). This implies that there is a possible relationship between orientation tuning width and direction selectivity. Our current results show that orientation tuning width for the preferred direction is similar for DS (DSI≥0.5) and non-DS (DSI<0.5) cells. However, we also find that orientation tuning width for the non-preferred direction is significantly narrower in DS units. And the difference varies depending on cortical lamina (the smallest in layer 4, and the largest in layer 6), suggesting that selective suppression of the neural response to the non-preferred direction may be involved in stronger direction selectivity.
Several studies have reported that excitatory and inhibitory inputs may both be involved in establishing tuning preferences (Monier et al., 2003; Priebe & Ferster, 2005). If this is the case, narrower orientation tuning in the non-preferred direction of motion cannot be interpreted as a result of stronger suppression in that direction. Simple rectification of a weak response may explain a part of the result. The larger degree of non-linearity for cells of supra- or infra-granular layers may be explained as a result of multiple rectification processes (layer 4 → layer 2/3 → layer 5 → layer 6) compared with those in layer 4. However, a rectification only mechanism is not free from the contrast-invariance of orientation selectivity (Troyer et al., 1998). Both excitatory and inhibitory inputs, which have similar orientation tuning but different spatial & temporal phases, must be considered in the mechanism for the direction selectivity observed in the visual cortex (Murthy & Humphrey, 1999; Saul, 1999).
Other possible mechanisms may contribute to laminar orientation tuning width differences and refinement of direction selectivity (Sato et al., 1995; Vidyasagar et al., 1996; Sompolinsky & Shapley, 1997; Livingstone, 1998; Ferster & Miller, 2000). Previous studies have demonstrated that recurrent intra-cortical excitation (Somers et al., 1995; Carandini & Ringach, 1997; Han & Mrsic-Flogel, 2013; Li et al., 2013) or non-linear transformation of membrane potential to spiking activity (Wilent & Contreras, 2005; Priebe & Ferster, 2008) can generate sharp, contrast-invariant orientation tuning from broadly tuned or weakly biased excitatory inputs. Feedback connections from extra-striate cortex are also likely to influence direction selectivity of neurons in the primary visual cortex (Hupé et al., 1998). As supporting evidence, application of a cholinergic agonist, which is clearly linked with arousal and selective attention, caused enhancement of orientation and direction selectivity in the visual cortex of the cat (Sillito & Kemp, 1983; Murphy & Sillito, 1991). However, in anesthetized cats, the modulatory influence of feedback projections on direction selectivity may not be substantial (Wang et al., 2000), but also see (Galuske et al., 2002; Shen et al., 2006).
Limitations of the current study
We have identified features of direction selectivity of visual neurons for four different cortical laminar groups (layers 2/3, 4, 5 & 6). For a given layer, simple and complex cells exhibit different characteristics of direction selectivity. However, we note that there are nonuniformities in cell characteristics and sub-divisions of cortical lamina that may influence direction selectivity (Kelly & Van Essen, 1974; Gilbert & Wiesel, 1979; Katz, 1987).
In the cat, the primary visual cortex receives LGN inputs through at least three different pathways, characterized, respectively, by X, Y, and W types of LGN cells (Wilson et al., 1976; Alonso, 2002). These pathways have different response properties (e.g., conduction velocity, receptive field size, and linearity in spatial summation within the receptive field) and their main projection target cells are segregated in different cortical layers. Although it is reported that X- and Y-type LGN relay cells exhibit the same degree of direction selectivity (Thompson et al., 2009), our cell database does not provide enough information for a quantitative assessment.
Previous studies and our present investigation suggest that both excitatory and inhibitory intra-cortical inputs are involved in the direction selectivity of cortical neurons (Sillito, 1977; Sato et al., 1995; Peterson et al., 2004). Again, our database doesn’t contain the relevant information (e.g., action potential waveform, morphological features, etc.), to enable segregation of inhibitory and excitatory cells. It would be interesting to see how distributions of these two types vary across cortical layers and whether there is a relationship between nonlinearity of direction selectivity and excitatory-inhibitory balance.
Another potential limitation is sampling biases of neural recording using a microelectrode. It generally results in biased sampling of pyramidal neurons with large cell bodies and high firing rates (Olshausen & Field, 2005). This may be related to oversampling of excitatory neurons. Temporal frequency of a visual stimulus is also not experimentally determined as optimal and is always fixed at 2Hz because cortical cells are nearly all responsive at that value. These types of factors may contribute to sampling biases which could alter the distribution of DSI but effects like this are likely to be minimal.
Conclusion
Organizational patterns of thalamo-cortical and intra-cortical connections vary with cortical lamina. Accordingly, DS of visual neurons that incorporate both kinds of connections, also varies across cortical layers. Spatiotemporal linear RFs provide a reasonable prediction of measured DSIs in layer 4, but not in other layers due to a high degree of non-linear intra-cortical contribution. We find for DS cells, that orientation tuning width for non-preferred directions is significantly narrower than that for the preferred. And the difference of tuning width between the two opposite directions also depends on cortical lamina (the smallest is in layer 4, and the biggest in layer 6). Considered together, these results are consistent with previous reports which suggest that intra-cortical inhibition enhances direction selectivity of visual neurons by selectively suppressing neural activity for the non-preferred direction of motion.
Acknowledgments
This research is supported by NIH grant EY01175.
Footnotes
Conflict of Interest: None
References
- Adelson EH, Bergen JR. Spatiotemporal energy models for the perception of motion. J Opt Soc Am A. 1985;2:284–299. doi: 10.1364/josaa.2.000284. [DOI] [PubMed] [Google Scholar]
- Alonso JM. Neural connections and receptive field properties in the primary visual cortex. Neuroscientist. 2002;8:443–456. doi: 10.1177/107385802236967. [DOI] [PubMed] [Google Scholar]
- Alonso JM, Usrey WM, Reid RC. Rules of connectivity between geniculate cells and simple cells in cat primary visual cortex. J Neurosci. 2001;21:4002–4015. doi: 10.1523/JNEUROSCI.21-11-04002.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anzai A, Ohzawa I, Freeman RD. Neural mechanisms for encoding binocular disparity: receptive field position versus phase. J Neurophysiol. 1999;82:874–890. doi: 10.1152/jn.1999.82.2.874. [DOI] [PubMed] [Google Scholar]
- Barlow HB, Hill RM, Levick WR. Retinal ganglion cells responding selectively to direction and speed of image motion in the rabbit. J Physiol. 1964;173:377–407. doi: 10.1113/jphysiol.1964.sp007463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Callaway EM. Local circuits in primary visual cortex of the macaque monkey. Annu Rev Neurosci. 1998;21:47–74. doi: 10.1146/annurev.neuro.21.1.47. [DOI] [PubMed] [Google Scholar]
- Callaway EM, Katz LC. Emergence and refinement of clustered horizontal connections in cat striate cortex. J Neurosci. 1990;10:1134–1153. doi: 10.1523/JNEUROSCI.10-04-01134.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Callaway EM, Katz LC. Development of axonal arbors of layer 4 spiny neurons in cat striate cortex. J Neurosci. 1992;12:570–582. doi: 10.1523/JNEUROSCI.12-02-00570.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carandini M, Ferster D. Membrane potential and firing rate in cat primary visual cortex. J Neurosci. 2000;20:470–484. doi: 10.1523/JNEUROSCI.20-01-00470.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carandini M, Ringach DL. Predictions of a recurrent model of orientation selectivity. Vision Res. 1997;37:3061–3071. doi: 10.1016/s0042-6989(97)00100-4. [DOI] [PubMed] [Google Scholar]
- Chen G, Dan Y, Li C. Stimulation of non-classical receptive field enhances orientation selectivity in the cat. J Physiol. 2005;564:233–243. doi: 10.1113/jphysiol.2004.080051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chichilnisky EJ. A simple white noise analysis of neuronal light responses. Network. 2001;12:199–213. [PubMed] [Google Scholar]
- Crook JM, Kisvárday ZF, Eysel UT. Evidence for a contribution of lateral inhibition to orientation tuning and direction selectivity in cat visual cortex: reversible inactivation of functionally characterized sites combined with neuroanatomical tracing techniques. Eur J Neurosci. 1998;10:2056–2075. doi: 10.1046/j.1460-9568.1998.00218.x. [DOI] [PubMed] [Google Scholar]
- De Valois RL, Cottaris NP, Mahon LE, Elfar SD, Wilson JA. Spatial and temporal receptive fields of geniculate and cortical cells and directional selectivity. Vision Res. 2000;40:3685–3702. doi: 10.1016/s0042-6989(00)00210-8. [DOI] [PubMed] [Google Scholar]
- DeAngelis GC, Ohzawa I, Freeman RD. Spatiotemporal organization of simple-cell receptive fields in the cat’s striate cortex. II. Linearity of temporal and spatial summation. J Neurophysiol. 1993a;69:1118–1135. doi: 10.1152/jn.1993.69.4.1118. [DOI] [PubMed] [Google Scholar]
- DeAngelis GC, Ohzawa I, Freeman RD. Spatiotemporal organization of simple-cell receptive fields in the cat’s striate cortex. I. General characteristics and postnatal development. J Neurophysiol. 1993b;69:1091–1117. doi: 10.1152/jn.1993.69.4.1091. [DOI] [PubMed] [Google Scholar]
- Derrington AM, Fuchs AF. Spatial and temporal properties of X and Y cells in the cat lateral geniculate nucleus. J Physiol. 1979;293:347–364. doi: 10.1113/jphysiol.1979.sp012893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douglas RJ, Martin KA. A functional microcircuit for cat visual cortex. J Physiol. 1991;440:735–769. doi: 10.1113/jphysiol.1991.sp018733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emerson RC, Bergen JR, Adelson EH. Directionally selective complex cells and the computation of motion energy in cat visual cortex. Vision Res. 1992;32:203–218. doi: 10.1016/0042-6989(92)90130-b. [DOI] [PubMed] [Google Scholar]
- Ferster D. Spatially opponent excitation and inhibition in simple cells of the cat visual cortex. J Neurosci. 1988;8:1172–1180. doi: 10.1523/JNEUROSCI.08-04-01172.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferster D, Miller KD. Neural mechanisms of orientation selectivity in the visual cortex. Annu Rev Neurosci. 2000;23:441–471. doi: 10.1146/annurev.neuro.23.1.441. [DOI] [PubMed] [Google Scholar]
- Fitzpatrick D. The functional organization of local circuits in visual cortex: Insights from the study of tree shrew striate cortex. Cereb Cortex. 1996;6:329–341. doi: 10.1093/cercor/6.3.329. [DOI] [PubMed] [Google Scholar]
- Fox CH, Johnson FB, Whiting J, Roller PP. Formaldehyde fixation. J Histochem Cytochem. 1985;33:845–853. doi: 10.1177/33.8.3894502. [DOI] [PubMed] [Google Scholar]
- Freund TF, Martin KA, Soltesz I, Somogyi P, Whitteridge D. Arborisation pattern and postsynaptic targets of physiologically identified thalamocortical afferents in striate cortex of the macaque monkey. J Comp Neurol. 1989;289:315–336. doi: 10.1002/cne.902890211. [DOI] [PubMed] [Google Scholar]
- Galuske RAW, Schmidt KE, Goebel R, Lomber SG, Payne BR. The role of feedback in shaping neural representations in cat visual cortex. Proc Natl Acad Sci U S A. 2002;99:17083–17088. doi: 10.1073/pnas.242399199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert CD. Laminar differences in receptive field properties of cells in cat primary visual cortex. J Physiol. 1977;268:391–421. doi: 10.1113/jphysiol.1977.sp011863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert CD, Kelly JP. The projections of cells in different layers of the cat’s visual cortex. J Comp Neurol. 1975;163:81–105. doi: 10.1002/cne.901630106. [DOI] [PubMed] [Google Scholar]
- Gilbert CD, Wiesel TN. Morphology and intracortical projections of functionally characterised neurones in the cat visual cortex. Nature. 1979;280:120–125. doi: 10.1038/280120a0. [DOI] [PubMed] [Google Scholar]
- Han Y, Mrsic-Flogel T. A finely tuned cortical amplifier. Nat Neurosci. 2013;16:1166–1168. doi: 10.1038/nn.3507. [DOI] [PubMed] [Google Scholar]
- Hata Y, Tsumoto T, Sato H, Hagihara K, Tamura H. Inhibition contributes to orientation selectivity in visual cortex of cat. Nature. 1988;335:815–817. doi: 10.1038/335815a0. [DOI] [PubMed] [Google Scholar]
- Hawken MJ, Parker AJ, Lund JS. Laminar organization and contrast sensitivity of direction-selective cells in the striate cortex of the Old World monkey. J Neurosci. 1988;8:3541–3548. doi: 10.1523/JNEUROSCI.08-10-03541.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heggelund P. Receptive field organization of simple cells in cat striate cortex. Exp Brain Res. 1981;42:89–98. doi: 10.1007/BF00235733. [DOI] [PubMed] [Google Scholar]
- Hirsch JA, Gilbert CD. Synaptic physiology of horizontal connections in the cat’s visual cortex. J Neurosci. 1991;11:1800–1809. doi: 10.1523/JNEUROSCI.11-06-01800.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields of single neurones in the cat’s striate cortex. J Physiol. 1959;148:574–591. doi: 10.1113/jphysiol.1959.sp006308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J Physiol. 1962;160:106–154. doi: 10.1113/jphysiol.1962.sp006837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hupé JM, James AC, Payne BR, Lomber SG, Girard P, Bullier J. Cortical feedback improves discrimination between figure and background by V1, V2 and V3 neurons. Nature. 1998;394:784–787. doi: 10.1038/29537. [DOI] [PubMed] [Google Scholar]
- Jagadeesh B, Wheat HS, Ferster D. Linearity of summation of synaptic potentials underlying direction selectivity in simple cells of the cat visual cortex. Science. 1993;262:1901–1904. doi: 10.1126/science.8266083. [DOI] [PubMed] [Google Scholar]
- Jagadeesh B, Wheat HS, Kontsevich LL, Tyler CW, Ferster D. Direction selectivity of synaptic potentials in simple cells of the cat visual cortex. J Neurophysiol. 1997;78:2772–2789. doi: 10.1152/jn.1997.78.5.2772. [DOI] [PubMed] [Google Scholar]
- Jones JP, Palmer LA. The two-dimensional spatial structure of simple receptive fields in cat striate cortex. J Neurophysiol. 1987;58:1187–1211. doi: 10.1152/jn.1987.58.6.1187. [DOI] [PubMed] [Google Scholar]
- Katz LC. Local circuitry of identified projection neurons in cat visual cortex brain slices. J Neurosci. 1987;7:1223–1249. doi: 10.1523/JNEUROSCI.07-04-01223.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly JP, Van Essen DC. Cell structure and function in the visual cortex of the cat. J Physiol. 1974;238:515–547. doi: 10.1113/jphysiol.1974.sp010541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kharazia V, Weinberg R. Glutamate in thalamic fibers terminating in layer IV of primary sensory cortex. J Neurosci. 1994;14:6021–6032. doi: 10.1523/JNEUROSCI.14-10-06021.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Kwan AC, Zhang S, Phoumthipphavong V, Flannery JG, Masmanidis SC, Taniguchi H, Huang ZJ, Zhang F, Boyden ES, Deisseroth K, Dan Y. Activation of specific interneurons improves V1 feature selectivity and visual perception. Nature. 2012;488:379–383. doi: 10.1038/nature11312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeVay S, Gilbert CD. Laminar patterns of geniculocortical projection in the cat. Brain Res. 1976;113:1–19. doi: 10.1016/0006-8993(76)90002-0. [DOI] [PubMed] [Google Scholar]
- Leventhal AG, Wang Y, Pu M, Zhou Y, Ma Y. GABA and its agonists improved visual cortical function in senescent monkeys. Science. 2003;300:812–815. doi: 10.1126/science.1082874. [DOI] [PubMed] [Google Scholar]
- Li Y, Ibrahim La, Liu B, Zhang LI, Tao HW. Linear transformation of thalamocortical input by intracortical excitation. Nat Neurosci. 2013;16:1324–1330. doi: 10.1038/nn.3494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Livingstone MS. Mechanisms of direction selectivity in macaque V1. Neuron. 1998;20:509–526. doi: 10.1016/s0896-6273(00)80991-5. [DOI] [PubMed] [Google Scholar]
- Martin KA, Whitteridge D. Form, function and intracortical projections of spiny neurones in the striate visual cortex of the cat. J Physiol. 1984;353:463–504. doi: 10.1113/jphysiol.1984.sp015347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mechler F, Ringach DL. On the classification of simple and complex cells. Vision Res. 2002;42:1017–1033. doi: 10.1016/s0042-6989(02)00025-1. [DOI] [PubMed] [Google Scholar]
- Monier C, Chavane F, Baudot P, Graham LJ, Frégnac Y. Orientation and direction selectivity of synaptic inputs in visual cortical neurons: A diversity of combinations produces spike tuning. Neuron. 2003;37:663–680. doi: 10.1016/s0896-6273(03)00064-3. [DOI] [PubMed] [Google Scholar]
- Murphy PC, Sillito AM. Cholinergic enhancement of direction selectivity in the visual cortex of the cat. Neuroscience. 1991;40:13–20. doi: 10.1016/0306-4522(91)90170-s. [DOI] [PubMed] [Google Scholar]
- Murthy A, Humphrey AL. Inhibitory contributions to spatiotemporal receptive-field structure and direction selectivity in simple cells of cat area 17. J Neurophysiol. 1999;81:1212–1224. doi: 10.1152/jn.1999.81.3.1212. [DOI] [PubMed] [Google Scholar]
- Murthy A, Humphrey AL, Saul AB, Feidler JC. Laminar differences in the spatiotemporal structure of simple cell receptive fields in cat area 17. Vis Neurosci. 1998;15:239–256. doi: 10.1017/s0952523898152045. [DOI] [PubMed] [Google Scholar]
- O’Leary JL. Structure of the area striata of the cat. J Comp Neurol. 1941;75:131–164. [Google Scholar]
- Olshausen BA, Field DJ. How close are we to understanding v1? Neural Comput. 2005;17:1665–1699. doi: 10.1162/0899766054026639. [DOI] [PubMed] [Google Scholar]
- Orban GA, Kennedy H, Maes H. Response to movement of neurons in areas 17 and 18 of the cat: direction selectivity. J Neurophysiol. 1981;45:1059–1073. doi: 10.1152/jn.1981.45.6.1059. [DOI] [PubMed] [Google Scholar]
- Palmer LA, Davis TL. Receptive-field structure in cat striate cortex. J Neurophysiol. 1981;46:260–276. doi: 10.1152/jn.1981.46.2.260. [DOI] [PubMed] [Google Scholar]
- Peters A, Yilmaz E. Neuronal Organization in Area 17 of Cat Visual Cortex. Cereb Cortex. 1993;3:49–68. doi: 10.1093/cercor/3.1.49. [DOI] [PubMed] [Google Scholar]
- Peterson MR, Li B, Freeman RD. The derivation of direction selectivity in the striate cortex. J Neurosci. 2004;24:3583–3591. doi: 10.1523/JNEUROSCI.5398-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterson MR, Li B, Freeman RD. Direction selectivity of neurons in the striate cortex increases as stimulus contrast is decreased. J Neurophysiol. 2006;95:2705–2712. doi: 10.1152/jn.00885.2005. [DOI] [PubMed] [Google Scholar]
- Priebe NJ, Ferster D. Direction selectivity of excitation and inhibition in simple cells of the cat primary visual cortex. Neuron. 2005;45:133–145. doi: 10.1016/j.neuron.2004.12.024. [DOI] [PubMed] [Google Scholar]
- Priebe NJ, Ferster D. Inhibition, Spike Threshold, and Stimulus Selectivity in Primary Visual Cortex. Neuron. 2008;57:482–497. doi: 10.1016/j.neuron.2008.02.005. [DOI] [PubMed] [Google Scholar]
- Reid RC, Soodak RE, Shapley RM. Linear mechanisms of directional selectivity in simple cells of cat striate cortex. Proc Natl Acad Sci U S A. 1987;84:8740–8744. doi: 10.1073/pnas.84.23.8740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato H, Katsuyama N, Tamura H, Hata Y, Tsumoto T. Mechanisms underlying direction selectivity of neurons in the primary visual cortex of the macaque. J Neurophysiol. 1995;74:1382–1394. doi: 10.1152/jn.1995.74.4.1382. [DOI] [PubMed] [Google Scholar]
- Saul aB. Visual cortical simple cells: who inhibits whom. Vis Neurosci. 1999;16:667–673. doi: 10.1017/s095252389916406x. [DOI] [PubMed] [Google Scholar]
- Schiller PH, Finlay BL, Volman SF. Quantitative studies of single-cell properties in monkey striate cortex. I. Spatiotemporal organization of receptive fields. J Neurophysiol. 1976;39:1288–1319. doi: 10.1152/jn.1976.39.6.1288. [DOI] [PubMed] [Google Scholar]
- Schwark HD, Malpeli JG, Weyand TG, Lee C. Cat area 17. II. Response properties of infragranular layer neurons in the absence of supragranular layer activity. J Neurophysiol. 1986;56:1074–1087. doi: 10.1152/jn.1986.56.4.1074. [DOI] [PubMed] [Google Scholar]
- Schwarz C, Bolz J. Functional specificity of a long-range horizontal connection in cat visual cortex: a cross-correlation study. J Neurosci. 1991;11:2995–3007. doi: 10.1523/JNEUROSCI.11-10-02995.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapley R, Hawken M, Ringach DL. Dynamics of orientation selectivity in the primary visual cortex and the importance of cortical inhibition. Neuron. 2003;38:689–699. doi: 10.1016/s0896-6273(03)00332-5. [DOI] [PubMed] [Google Scholar]
- Shatz CJ, Luskin MB. The relationship between the geniculocortical afferents and their cortical target cells during development of the cat’s primary visual cortex. J Neurosci. 1986;6:3655–3668. doi: 10.1523/JNEUROSCI.06-12-03655.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen W, Liang Z, Chen X, Shou T. Posteromedial lateral suprasylvian motion area modulates direction but not orientation preference in area 17 of cats. Neuroscience. 2006;142:905–916. doi: 10.1016/j.neuroscience.2006.06.046. [DOI] [PubMed] [Google Scholar]
- Sillito A. The contribution of inhibitory mechanisms to the receptive field properties of neurones in the striate cortex of the cat. J Physiol. 1975;250:305–329. doi: 10.1113/jphysiol.1975.sp011056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sillito AM. Inhibitory processes underlying the directional specificity of simple, complex and hypercomplex cells in the cat’s visual cortex. J Physiol. 1977;271:699–720. doi: 10.1113/jphysiol.1977.sp012021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sillito AM, Cudeiro J, Jones HE. Always returning: feedback and sensory processing in visual cortex and thalamus. Trends Neurosci. 2006;29:307–316. doi: 10.1016/j.tins.2006.05.001. [DOI] [PubMed] [Google Scholar]
- Sillito AM, Kemp JA. Cholinergic modulation of the functional organization of the cat visual cortex. Brain Res. 1983;289:143–155. doi: 10.1016/0006-8993(83)90015-x. [DOI] [PubMed] [Google Scholar]
- Skottun BC, De Valois RL, Grosof DH, Movshon JA, Albrecht DG, Bonds AB. Classifying simple and complex cells on the basis of response modulation. Vision Res. 1991;31:1079–1086. doi: 10.1016/0042-6989(91)90033-2. [DOI] [PubMed] [Google Scholar]
- So Y, Shapley R. Spatial properties of X and Y cells in the lateral geniculate nucleus of the cat and conduction velocities of their inputs. Exp Brain Res. 1979;36:533–550. doi: 10.1007/BF00238521. [DOI] [PubMed] [Google Scholar]
- Somers DC, Nelson SB, Sur M. An emergent model of orientation selectivity in cat visual cortical simple cells. J Neurosci. 1995;15:5448–5465. doi: 10.1523/JNEUROSCI.15-08-05448.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sompolinsky H, Shapley R. New perspectives on the mechanisms for orientation selectivity. Curr Opin Neurobiol. 1997;7:514–522. doi: 10.1016/s0959-4388(97)80031-1. [DOI] [PubMed] [Google Scholar]
- Thompson KG, Zhou Y, Leventhal AG. Direction-sensitive X and Y cells within the A laminae of the cat’s LGNd. Vis Neurosci. 2009;11:927–938. doi: 10.1017/s0952523800003886. [DOI] [PubMed] [Google Scholar]
- Thomson AM, Bannister AP. Interlaminar connections in the neocortex. Cereb Cortex. 2003;13:5–14. doi: 10.1093/cercor/13.1.5. [DOI] [PubMed] [Google Scholar]
- Tolhurst DJ, Dean AF. Evaluation of a linear model of directional selectivity in simple cells of the cat’s striate cortex. Vis Neurosci. 1991;6:421–428. doi: 10.1017/s0952523800001280. [DOI] [PubMed] [Google Scholar]
- van Santen JP, Sperling G. Elaborated Reichardt detectors. J Opt Soc Am A. 1985;2:300–321. doi: 10.1364/josaa.2.000300. [DOI] [PubMed] [Google Scholar]
- Vidyasagar TR, Pei X, Volgushev M. Multiple mechanisms underlying the orientation selectivity of visual cortical neurones. Trends Neurosci. 1996;19:272–277. doi: 10.1016/S0166-2236(96)20027-X. [DOI] [PubMed] [Google Scholar]
- Wang C, Waleszczyk WJ, Burke W, Dreher B. Modulatory influence of feedback projections from area 21a on neuronal activities in striate cortex of the cat. Cereb Cortex. 2000;10:1217–1232. doi: 10.1093/cercor/10.12.1217. [DOI] [PubMed] [Google Scholar]
- Wang W, Jones HE, Andolina IM, Salt TE, Sillito AM. Functional alignment of feedback effects from visual cortex to thalamus. Nat Neurosci. 2006;9:1330–1336. doi: 10.1038/nn1768. [DOI] [PubMed] [Google Scholar]
- Wielaard DJ, Shelley M, McLaughlin D, Shapley R. How simple cells are made in a nonlinear network model of the visual cortex. J Neurosci. 2001;21:5203–5211. doi: 10.1523/JNEUROSCI.21-14-05203.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilent WB, Contreras D. Stimulus-dependent changes in spike threshold enhance feature selectivity in rat barrel cortex neurons. J Neurosci. 2005;25:2983–2991. doi: 10.1523/JNEUROSCI.4906-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson PD, Rowe MH, Stone J. Properties of relay cells in cat’s lateral geniculate nucleus: a comparison of W-cells with X- and Y-cells. J Neurophysiol. 1976;39:1193–1209. doi: 10.1152/jn.1976.39.6.1193. [DOI] [PubMed] [Google Scholar]