Microfluidics made easy: A robust low-cost constant pressure flow controller for engineers and cell biologists

Abstract

Over the last decade, microfluidics has become increasingly popular in biology and bioengineering. While lab-on-a-chip fabrication costs have continued to decrease, the hardware required for delivering controllable fluid flows to the microfluidic devices themselves remains expensive and often cost prohibitive for researchers interested in starting a microfluidics project. Typically, microfluidic experiments require precise and tunable flow rates from a system that is simple to operate. While many labs use commercial platforms or syringe pumps, these solutions can cost thousands of dollars and can be cost prohibitive. Here, we present an inexpensive and easy-to-use constant pressure system for delivering flows to microfluidic devices. The controller costs less than half the price of a single syringe pump but can independently switch and deliver fluid through up to four separate fluidic inlets at known flow rates with significantly faster fluid response times. It is constructed of readily available pressure regulators, gauges, plastic connectors and adapters, and tubing. Flow rate is easily predicted and calibrated using hydraulic circuit analysis and capillary tubing resistors. Finally, we demonstrate the capabilities of the flow system by performing well-known microfluidic experiments for chemical gradient generation and emulsion droplet production.

I. INTRODUCTION

The ability to route and control flows within microchannels is an essential requirement for many lab-on-a-chip applications.^1,2 Often this is accomplished with a flow controller, which can dispense fluid at a desired flow rate to a specific fluid inlet on a microfluidic chip. Precise and tunable flow rates are crucial in microfluidic applications involving droplets,³ cell manipulation,^4,5 chemical and biomolecular sensing,^6,7 and sample processing.⁸ One major barrier to making microfluidics more attractive for research in biology and bioengineering labs is that the hardware requirement for controlling this fluid flow is often cost prohibitive.⁹ Commercial solutions, for example, can provide controlled flow rates to multiple microchannels simultaneously, but cost upward of $20 000 USD. As an alternative, laboratories with less complicated microfluidic routing requirements use syringe pumps as a means to control fluid flow. While an adequate substitution, they are still expensive and can cost several thousand dollars. Cost aside, there are several inherent technical issues associated with using syringe pumps, including slow fluid response time, limitations on volume dispensed, unwanted pulsatile fluid flow, and no knowledge of the pressure applied to the device, which can lead to chip leakage and device debonding. Finally, microfluidic chips that use multiple inlets often require multiple syringe pumps, which can be costly and bulky.

One reason labs can often justify the purchase and use of expensive syringe pumps is because they are convenient to use. They allow a user to define a specific flow rate for a device, and the system delivers this by applying the appropriate pressure drop across the microchannel. Syringe pumps are therefore sources of constant flow rate, where it does not matter what the hydrodynamic resistance is within a device so long as a sufficient pressure can be applied to achieve the desired flow rate. Another way to control fluid flow is to use a constant pressure source. In this way, the user defines a particular pressure to deliver a corresponding flow rate. If the device geometry changes, the resulting flow rate will be different.^10,11 Engineering laboratories often use commercial constant pressure systems to deliver flow, but they are not easy to control because the flow rate often remains unknown and its relationship with pressure changes with device geometry. Microfluidic flow sensors are readily available to alleviate this problem, but they are expensive and can exceed $1000 per unit. Without a flow sensor, the user only knows the applied pressure. It is hard to control flows using this method, because the flow rate is proportional to the hydraulic resistance of the device and many parameters including the inlet and outlet tubing length, and the microchannel geometry, can influence this value. Without expensive flow sensors, users must apply pressure to the device and measure the flow rate manually. Since microfluidic flows are often on the order of microliters per minute, these measurements can be tedious and require significant time to obtain, and must be repeated when using a new type of device or a different length of inlet/outlet tubing. For these reasons, many labs utilizing basic microfluidics avoid constant pressure sources and opt for easy-to-use, but expensive, constant flow rate sources.

In this work, we seek to alleviate this problem and make accurate, but low cost, microfluidic flow control readily available to research labs interested in experimenting with microfluidics. Here, we present an inexpensive, easy-to-use constant pressure microfluidic flow controller as a low-cost alternative to commercial systems and syringe pumps. The flow controller is simple to setup and capable of independently regulating the flow of multiple microfluidic inlets for less than half the price of a single syringe pump. Our overall aim is to address the needs of both experienced and novice microfluidics labs that could benefit from a low-cost flow controller. In the first part of this paper, we introduce the flow system and develop a simple hydraulic circuit model that describes the relationship between the applied pressure drop across a microchannel and the resulting flow rate.¹² Using this flow model, we develop the necessary engineering design criteria to predict and control the fluid flow rate for an arbitrary microfluidic channel geometry. We then discuss the important features of our flow system, including a low cost switch to prevent fluid backflow and how to use inexpensive hydrodynamic capillary resistors (∼$30 per meter) to predictably control the fluid flow rate in a microfluidic device. We then compare the reliability and responsiveness of this to a commercially available syringe pump. Finally, to promote interest in experienced microfluidics labs, we demonstrate the capabilities of the flow controller using different microfluidic applications including generating laminar liquid interfaces, producing chemical gradients, and producing microfluidic water-in-oil emulsion droplets.

II. BACKGROUND

A. Controlling and measuring microfluidic flow

Fluid flow requires a source of momentum to impart hydrodynamic stress to a fluid volume and drive it into motion. In microfluidics, these forces can arise from many sources including gravity,¹³ electrical^14–16 and magnetic forces,^17,18 and buoyancy.¹⁹ One common method is to use a normal surface stress, commonly known as pressure, to drive fluid flow through a network of microchannels. For pressure-driven flow, a known pressure is applied to the inlet of a fluid-filled microchannel to create a pressure gradient along the channel length and drive fluid motion.

The volumetric rate of flow can be regulated using either constant pressure or constant flow rate sources. A syringe pump, for example, delivers flow using a constant flow rate source. In this manner, the user only cares about the flow rate and is not concerned with the pressure required to create this flow. If we increase a microchannel's hydrodynamic resistance by a factor of two, for example, the syringe pump automatically increases the necessary pressure to produce the desired flow rate. This approach is quite useful for microfluidic applications, in that flow rate can be easily controlled independently of channel geometry. However, syringe pumps can be expensive, suffer from flow oscillations or pulses at low flow rates and have slow response times.

Conversely, flow can be generated using a constant pressure source where one applies a fixed pressure drop across a microchannel to induce a net flow rate. While effective, constant pressure sources can be difficult to use in applications where the flow rate must be precisely controlled. Because the microchannel resistance influences the fluid flow, different device designs produce different flow rates for the same applied pressure. However, there are many benefits to using constant pressure sources, including fast response times, high stability and pulseless flow, and the ability to process large volumes of fluid.

One way to determine the flow rate from an applied pressure source is to use an inline flow meter. These devices are reliable and accurate, however, a single flow meter can often cost more than a syringe pump. Another less expensive method is to capture the fluid at the microchannel device outlet and calculate the volume collected as a function of time for varying pressure values. In this way, one can obtain a pressure-flow rate (P-Q) curve for a particular microfluidic device. This technique, however, is not robust because it must be repeated if the device geometry is modified.

B. A low-cost microfluidic flow controller

Our microfluidic flow controller drives fluid flow through microfluidic channels using a constant pressure source. Unlike commercial solutions, the entire system uses readily available plastic fittings, costs ∼$500.00 USD and requires less than 1 h to assemble. The system, illustrated in Figure 1, is capable of delivering flow to four independently addressable microfluidic channel inputs at a fraction of the cost of a single syringe pump. Pressurized house air (∼50 psi) powers the flow controller. As shown in Figure 1(a), blue airline tubing exits a pressure regulator and is split into four separate lines (labelled 1, 2, 3, and 4) using an aluminum pressure manifold. A 3-way air switch controls the flow of pressured air into each line. When each switch is turned, pressurized air is sent into a precision pressure regulator, which controls the output pressure and directs this into a fluid-filled cryogenic sample vial. The pressure inside the vial increases and drives fluid flow through the tubing and the microfluidic device. We control the flow rate by adjusting this pressure using the precision pressure regulator and monitoring the air pressure on the accompanying pressure gauge.

FIG. 1.

(a) Low-cost microfluidic flow controller for controlling flows through four fluidic inlets. (b) Schematic of pressurized sample vial. A pressure (P_o) is applied to a cryovial and fluid flows through a series of tubing resistors (R₁), a capillary resistor (R_cap), R₂, into the device (R_chip) and exiting through outlet tubing (R₃) at a flow rate Q. (c) Hydraulic circuit diagram of the fluidic system.

C. Hydraulic circuit analysis

To regulate the fluid flow rate and render it independent to varying device geometry, we place hydraulic resistors upstream of the microfluidic device. The resistors are short lengths of capillary tubing and have a much larger hydrodynamic resistance than the downstream microfluidic device. In this way, fluid flow through the micro device is dictated by the resistance of the upstream hydraulic resistor and not the microfluidic device. These hydraulic resistors are a useful feature of this system because changes in device design will not influence the pressure-flow relationship within the microfluidic chip. Therefore, the user only needs to measure the pressure-flow rate relationship once, and it will remain accurate for devices of related, but different geometry.

Constant pressure sources can be reliably engineered to produce well-controlled flows in microfluidic systems using hydraulic circuit analysis. This method treats a network of microchannels as a complex circuit of fluidic resistors. For low Reynolds number flow in microchannels, there is an approximately linear relationship between pressure and flow rate. For an infinitely long cylindrical microchannel with a uniform circular cross section area, A, channel radius R, aligned in the positive z-direction, the fluid velocity profile at any given radial point r in the channel cross-section is given by

$$u_z=-\frac{1}{4\mu }\frac{\partial P}{\partial z}\left(R^2-r^2\right),$$ (1)

where $\mu \hspace{0.17em}$ and $\partial p/\partial z$ are the fluid viscosity and axial channel pressure gradient, respectively. To calculate the flow rate, the fluid velocity profile can be integrated over the channel cross-sectional area

$$Q=-\frac{A{R}^2}{8\mu }\frac{\partial P}{\partial z}.$$ (2)

Assuming the channel length (L) is much larger than the channel radius (R), we can neglect entrance effects and treat each channel as an infinitely long tube. Replacing dP/dx with $\Delta P/L$, where $\Delta P=P_{\mathit{I}\mathit{N}}-P_{\mathit{O}\mathit{U}\mathit{T}}$, is the pressure drop across the channel (e.g., the difference between the pressure at the inlet and the outlet), we can write this relationship between pressure and flow rate as

$$Q=\frac{\Delta P\pi R^4}{8\mu L},$$ (3)

which is known as the Hagen-Poiseuille law. Based on Eq. (3), an applied pressure drop produces a flow rate Q that is proportional to the channel's hydraulic resistance (R_h): $8\mu L/\pi R^4$. The Hagen-Poiseuille law describes to a good approximation the relationship between applied pressure and flow rate. It is analogous to Ohm's law for electrical circuits, where the voltage (pressure) is proportional to the current (flow rate)

$$\Delta P=Q{R}_h.$$ (4)

This equation provides a good estimate for steady flow through long and narrow cylindrical microchannels, however, this relation can be extended to other channel shapes by replacing R with the hydraulic radius, $r_h=2A/P$, where A and P are the channel cross-sectional area and perimeter, respectively. Using Eq. (3), we can design hydraulic resistors that serve as a bottleneck for regulating flow rate within varying microfluidic device geometries.

D. Regulating flow rate

We used hydraulic circuit analysis to design fluidic resistor elements that can predictably restrict the flow rate through an arbitrary microfluidic device. To generate microfluidic flow, we apply a known air pressure (P_o) to a sealed fluid-filled vial and maintain the device outlet at 1 atm (P₁), as depicted in Figure 1(b). Each flow line has five fluidic circuit components that influence the flow rate in a microfluidic device (Figure 1(c)). When the flow controller delivers a pressure, P_o, to the sample vial, the pressure drives fluid flow into the submerged tubing and into the microfluidic device.

One way to control fluid flow to the microfluidic chip is to insert flow elements with a large hydraulic resistance such that it dominates the pressure-flow rate behavior of the entire fluidic circuit. Illustrated in Figure 1(c), fluid will flow through five hydraulic resistors—the submerged inlet tubing (R₁), the capillary resistor (R_cap), tubing at the microfluidic inlet (R₂), the microfluidic device (R_chip), and the outlet tubing (R₃). Modifications to any of these components directly influence the overall resistance of the entire fluidic circuit and resulting pressure-flow rate relationship. To design capillary circuit elements with sufficiently large enough hydraulic resistance to regulate flow, but not too large that flow is impeded, we measure the resistance of the microfluidic device (R_chip) and calculate the length of capillary tubing required such that R_cap ∼ 10 × (R_chip + R₁ + R₂ + R₃). If the capillary tubing has a resistance significantly larger than the remaining elements in the hydraulic circuit, it will serve as a predictable bottleneck for regulating fluid flow rate.

III. FLOW CONTROLLER ASSEMBLY AND TESTING METHOD

Here, we describe the assembly and operation of our microfluidic flow controller and the design of hydraulic resistors for flow rate regulation. For those interested in building their own system, a detailed list of all vendors and part numbers used in our controller is provided in the supplementary material.²¹

A. Essential components

Construction of the flow controller takes less than 1 h and requires three primary assemblies: a pressure manifold, a multi-line manifold, and a sample holder. The entire system is powered by pressurized air and uses a series of pressure regulators, pneumatic air switches, and manifolds to control gas pressure inside sealed liquid-filled cryotubes and direct flow to microfluidic channels. To regulate the air pressure, we direct house gas (50 psi) through an air filter and into a primary pressure regulator (SMC Pneumatics, IR2010-NO2), where it exits at a fixed pressure (20 psi). We use a pressure manifold with one inlet and four outputs (McMaster-Carr, 5469K121) to deliver this regulated air pressure to four separate fluid-filled cryovials. Each manifold output is fitted with a 3-way air switch (Pneumadyne, C030621) to control the gas flow to downstream precision pressure regulators with accompanying pressure gauges (McMaster-Carr, 3846K411). The precision regulators control the gas pressure delivered to each cryovial, and the corresponding pressure gauges provide an easy way to monitor regulator pressure. Each of the air lines then connect to a multi-line manifold, which holds fluid-filled cryotubes for sample holding and pressure-driven fluid delivery to the microfluidic device. To deliver flow, we use a precision regulator to increase the air pressure inside a desired cryovial, which then forces flow through the submerged tubing and out into the chip. We can control the flow rate in each sealed vial by increasing or decreasing the vial pressure using the appropriate precision pressure regulator.

B. Flow controller assembly

To make this system easy to setup and operate, we attached the pressure manifolds, air regulators, and gauges to an inexpensive wooden pegboard using plastic cable ties. Before assembly, all threaded fittings were wrapped with two layers of Teflon tape to ensure a proper seal and prevent gas leaks. All components were fitted with push-to-connect fittings and connected with 1/4″ PTFE tubing. The pressure manifold inline/outline was fitted 1/4–1/8 National Pipe Thread (NPT) male fittings (McMaster-Carr, 5779K108), and each gas outlet threaded to 3-way switches (Pneumadyne, C030621) with 1/4-10-32 UNF male connectors (McMaster Carr, 5779K246). Each switch controlled the airflow on/off to a precision pressure regulator (Airtrol, R-800-10) with 1/4-1/8 NPT male connectors. Regulator outlets were attached to pressure gauges (0–15 psi, McMaster-Carr, 3846K411) threaded into 1/8″ brass T's with 1/8″ NPT male fittings.

C. Sample holder assembly

We used sealed cryovials as inexpensive and readily available pressure vessels for delivering fluid flow to microfluidic channels. The cryovial assembly houses the necessary components to load the fluid samples and to pressurize and direct their flow. Tubing from the outlet of each pressure gauge was connected to the back end of a multi-line manifold with 1/8″ NPT connections and we connected male luer-lock fittings (7/16″ hex–1/8-27 NPT, Value Plastics) to the front of the manifold. To attach a sealed vial to each of these fittings, we modified the top cap of each cryovial by drilling a small 3 mm diameter hole in the cap of each cryotube and attaching it to a plastic male luer fitting (7/16″ hex–1/8-27 NPT, Value Plastics) using quick setting epoxy. After allowing the epoxy to cure for 15 min, we fitted the cap with the bottom of a male luer tee fitting.

D. Connecting the tubing

The final step in completing the sample assembly is to create an airtight connection that allows for the sample to flow from the pressurized cryotube, through submerged tubing and into the microfluidic device. To do this, we make use of a female luer lug tee fitting. This inexpensive fitting has two openings and a third centered and oriented perpendicular to each opening. We attached the cryovial to the bottom opening of the tee fitting. At the top opening, we pushed plastic tubing (Cole Palmer), through a fitted male lock ring (Value Plastics), leaving 4″ of exposed tubing within the cryovial. Epoxy was applied to the junction of the lock ring and tubing to make an airtight seal. The other end of the tubing is connected to a specific microfluidic device inlet. When pressurized, the fluid inside the vial will be driven into the tubing and the microfluidic device.

IV. MICROFLUIDIC DEVICE FABRICATION

A. Hydraulic resistance of microfluidic channels

We fabricated a series of single microfluidic channels (65 $\mu$m in height, 100 $\mu$m in width) of varying length (1, 1.5, and 2 cm) to experimentally validate the ability to predictably control flow rate using capillary resistors. All microfluidic devices were constructed from polydimethylsiloxane (PDMS) (Momentive, RTV 615A) and fabricated using standard soft lithographic techniques. A 1:10 mixture of PDMS elastomer and curing agent was poured atop a lithographically fabricated SU-8 (Microchem Corp.) polymer mold, cured for 50 min at 90 °C and gently peeled off. Fluid ports were punched into the PDMS using a 0.75 mm biopsy punch (Ted Pella, Inc.). A glass coverslip (50 × 30 mm - #1 Fisher Scientific) and the cured PDMS slab were exposed to oxygen plasma for 15 s using a handheld tesla coil (Electro-Technic Products, Inc., BD-20) and immediately aligned and bonded by baking at 100 °C for 10 min.

B. Microfluidic gradient generator

To demonstrate the applicability of our controller for applications in cell biology, we used a passive microfluidic gradient generator to produce a stable chemical gradient (Figure 5). The microfluidic design was similar to that developed previously by Skoge et al. to study chemotaxis under varying gradient steepness.²⁰ The device consists of two large 80 $\mu$m tall channels connected by a network of shallow 2 $\mu$m channels (Figure 5(a)). To establish a stable chemical gradient, two separate fluid flows were directed into each tall flow channel at equal flow rates and the stable linear gradients formed through molecular diffusion across the shallow channels (Figure 5(b)).

FIG. 5.

(a) Confocal image of the microfluidic gradient generator. (b) Enlarged image of channels forming a gradient.

C. Droplet microfluidics

Another popular microfluidic application requiring precise flow control is in the production of emulsions with highly uniform droplets. Microfluidics offers a useful route to fabricating these droplets and bubbles. Typically, this is accomplished using flow-focusing geometries where two or more immiscible liquids are driven into a fluidic constriction and forced to break up. The mechanism for droplet production is highly sensitive to the flow rate of each fluid stream. For this work, we used a flow-focusing microfluidic geometry similar to devices reported previously (Figure 6). Two immiscible liquids enter the device through three microchannels. Two outside channels contain the “continuous phase” with the “discontinuous phase” flowing through the center channel. Downstream, the three liquids merge at a restriction and the continuous phase hydrodynamically focuses the central stream into a thin liquid jet. The jet stretches as it flows through the restriction and break ups into discrete droplets. We use light mineral oil (Sigmal Aldrich, M5904) mixed with 5%_w/w non-ionic surfactant (Span 80, Sigma Aldrich) as the continuous outer liquid and deionized water as the discontinuous central stream.

FIG. 6.

Mineral oil and deionized water are flow focused at a microfluidic restriction to produce emulsion droplets. The controller is used to vary the oil flow rate and produces different droplet regimes: (a) squeezing, (b) liquid jetting, and (c) dripping.

V. RESULTS AND DISCUSSION

A. Hydraulic resistance measurements

We first used the flow controller to drive fluid flow at different applied pressures through microchannels of varying length. As shown in Figure 2, the flow rate was measured through microchannels 0.5, 1 and 1.5 cm in length and plotted as a function of applied pressure. All flow rate measurements were performed with microfluidic flow sensors (Elveflow MFS 2 and MFS 3). As expected and depicted in Figure 2(a), the Q-P relationship for each channel is significantly influenced by channel length and the slope of each dataset was used to determine each channel's experimental hydraulic resistance. Using Eq. (3), we determined the length of capillary tubing required to exceed the hydraulic resistance of the longest microchannel by a factor of 10. We then repeated these experiments with this length of capillary tubing (15.5 cm) inserted upstream the inlet of each microfluidic channel. Since the capillary tube had the largest hydraulic resistance in the system, the flow rate for the system was dictated by the capillary tube, therefore, the flow rate was seen to be largely independent of the channel length (Figure 2(b)).

FIG. 2.

(a) Pressure versus flow rate for three channel lengths without a capillary tube. (b) Pressure versus flow rate for three channels with an upstream capillary resistor and with a capillary tube. All three datasets collapse to single curve, with minor deviation ($0.5\hspace{0.17em}\mu \mathrm{l}/\text{min}$) at larger pressures.

B. Flow rate capabilities, stability and response time

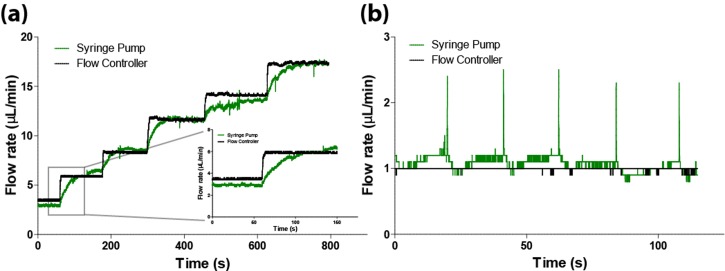
To demonstrate our system is a feasible low-cost alternative to commercial syringe pumps, we performed real-time flow response comparisons between the flow controller and a commercial syringe pump. Using a passive in-line flow sensor, flow rates were measured for both the flow controller and syringe pump in response to a step change in pressure. A time-response and stability comparison between the syringe pump and flow controller is shown in Figure 3(a). As illustrated, the flow controller has a significantly faster response time than the syringe pump, requiring less than 5 s to switch from a flow rate of 3 $\mu \mathrm{l}/\text{min}$ to 6 $\mu \mathrm{l}/\text{min}$. The syringe pump, however, took upwards of 60 s to reach steady state. The flow rate stability is approximately the same for both the syringe pump and flow controller with an approximate 0.2 $\mu \mathrm{l}/\text{min}$ variation. The syringe pump, however, becomes pulsatile and unstable at a low flow rate (1 $\mu \mathrm{l}/\text{min}$), shown in Figure 3(b). Comparing the stability of both the flow controller and syringe pump, one can see the syringe pump produced a pulsatile flow, while under the same conditions the flow controller produced a constant flow. Finally, it is important to note the operating range of the flow rates produced by the flow controller. We found the flow controller can provide reliable and steady flow rates from 0.5 to 35 $\hspace{0.17em}\mu \mathrm{l}/\text{min}$ with a 15.5 cm long capillary resistor. However, the user can alter this range by adjusting the length of the upstream capillary tubing. A longer capillary, for example, will produce a smaller flow rate, while a shorter capillary tube will allow for increased flow rate.

FIG. 3.

(a) Time response comparison of the presented flow controller and a commercial syringe pump. The syringe pump requires, on average, 20 s to stabilize while the flow controller requires less than five seconds. In some instances the syringe pump requires almost 60 s, as shown in the subplot. (b) Flow rate comparison between the flow controller and syringe pump at 1 μL/min. The syringe pump exhibits pulsatile flow at low flow rates while the flow controller offers stable flow rates.

C. Flow switches prevent fluid back flow

For many microfluidic applications, it is not sufficient to simply control when a single flow stream is on or off. Experiments in cell biology, for example, often require the ability to vary the fluid flow rate and switch between multiple streams. To accommodate these requirements, we also developed a simple and inexpensive switching solution to make our flow system suitable for a broader range of microfluidic applications. This is an important feature because switching flows on and off using pressurized fluid vials can be initially challenging because fluid flow follows the path of least resistance in a microfluidic network. It is important to have a method to prevent fluid backflow to sample vials: when fluid from one fluid-filled vial flows into the device and then unwantedly flows back out into a neighboring vial.

Backflow occurs when a pressure difference between two microfluidic inlets exist that is large enough to drive flow from one inlet, into the device, and out into a second inlet. Backflow is typically unwanted because it can contaminate neighboring vial samples and lead to longer setup times. To alleviate this problem, we designed a novel and inexpensive flow controller switches (Figure 4(a)) to prevent backflow.

FIG. 4.

(a) Low-cost fluidic switch for fluid routing. When the switch is turned “off,” it prevents the sample from flowing backward from one cryotube and into another. (b) Two laminar liquids flow side-by-side at equal flow rates in a microfluidic T-channel. (c) The switch for the “red” stream is turned off and the “green” stream follows the path of least resistance. (d) The switching is reversed. (e) Two samples with different cryotube volumes are delivered to a microfluidic T-channel. (f) Without a capillary the hydraulic head of the “green” stream is greater than the “red,” resulting in the “green” stream having a faster flow rate and the interface is not centered. (g) When the capillary is introduced to the same system both flow rates become equal and the interface becomes centered. The effect of the hydraulic head is eliminated as the flow rate is bottlenecked at the high resistive capillary.

To test the effectiveness of the flow controller switch, we used a microfluidic T-channel device with two inlets and one single outlet, shown in Figure 4(b). Two fluid streams were driven into the device at equal pressures to produce co-laminar streams that flow side-by-side. To aid in flow visualization, one fluid stream was dyed with Alexa Fluor 488 (green) and the adjacent stream is dyed with Alexa Fluor 594 (red). The applied pressures for both solutions were equal, producing a fluid interface centered in the main flow channel. Each fluid line was turned on or off using the appropriate flow controller switch. When the switch connected to the red solution was turned to the “off” position no backflow occurs (Figure 4(c)) Instead, the red solution stops in the T-channel junction. Conversely, when the red stream is turned “on” and the green stream turned “off,” the green stream stops before the junction (Figure 4(d)). While this is a simple application, this is an important technical ability done at a fraction of the cost of a single syringe pump. This tool is applicable to many applications including simple solution switching, chemical titrations, surface functionalization, and delivery of specific drugs, inhibitors or chemokines to downstream cells.

D. Flow contributions from hydrostatic pressure

In addition to backflow, it is important to note that gravitational forces can also influence the flow controller's fluid flow behavior. During flow experiments, we observed that when cryovial fluid volumes differed, a different pressure is required to produce equal flow rates. Because the sample volume exists over a height, h, several centimeters above the microfluidic device, a hydrostatic head pressure ($\Delta P_g=\rho gh)$ exists between the top of the fluid sample and the base of the microfluidic chip. While this may appear trivial to the advanced microfluidics researcher, this feature is often overlooked by beginners and so we address how to solve this problem here. To observe this gravitational influence, we used a T-channel device with a different fluid volume loaded in each cryovial, as shown in Figure 4(e). Each vial was filled with a different volume of DI water, one with a volume of 4 ml dyed with Alexa Fluor 488 (green) and the other with 1 ml and dyed with Alexa Fluor 561 (red). When equal pressure was applied to both cryovials, the liquid-liquid interface is not centered in the main channel, indicating that the flow rates in each fluid inlet are not equal. This occurs because the hydrostatic pressure is greater in one cryovial, and therefore, the overall pressure driving flow is also greater. Recall Eq. (4), flow rate is dependent on both the hydrodynamic resistance and pressure. The initial pressure has two components associated with its value, the applied pressure from the flow system and gravity, leading to the following equation:

$$\frac{\Delta P}{R_h}+\frac{\rho gh}{R_h}=Q.$$ (5)

For our flow controller with a sample volume ∼6 cm above the chip, $\Delta P_g=0.1\hspace{0.17em}\text{psi}$, and is large enough to impact the fluid flow rate (Figure 4(f)). However, if the hydraulic circuit resistance is large relative to the chip, the gravitational contribution becomes negligible compared to the applied term ($\Delta P/R_h=0.1\hspace{0.17em}\text{psi}$) and we observe no gravitational impact on fluid flow. This is illustrated in Figure 4(g), where a capillary was inserted upstream of each microfluidic inlet to produce perfectly centered liquid-liquid interface even when the sample volume heights were significantly different.

With the ability to regulate and control the flow rate for microfluidic devices with varying hydraulic resistance, we now demonstrate the applicability of our flow controller to regulate chemical gradients to study cell migration and to generate microfluidic water-in-oil emulsions for droplet studies.

E. Microfluidic applications: Gradient generator

Microfluidics offers a useful means to produce well-defined and stable chemical gradients. Using microfluidics to control these gradients can be technically challenging for laboratories not versed in flow control. Here, we demonstrate the ability to produce stable chemical gradients using the presented flow controller. The device consisted of two main flow channels connected to gradient chambers oriented perpendicular to the flow channels. A gradient of two different fluorescent dyes was generated by flowing phosphate buffered saline labelled with Alexa 488 and a second labelled with Alexa 561 through each main channel inlet at equal pressures (Figure 5(a)). When the flow rate is equal, a stable chemical gradient is produced by molecular diffusion across the two primary flow channels (Figure 5(b)).

F. Microfluidic applications: Droplet microfluidics

Another popular application that requires precise flow control is droplet-microfluidics. Droplet-based microfluidic systems have attracted extensive interest due to their potential uses in material synthesis, drug encapsulation, and protein crystallization. Conventionally, monodisperse droplets are created using flow-focusing microfluidics. A flow-focusing device uses laminar flow and elongational shear to controllably breakup immiscible fluid-fluid interfaces (Figure 6). The fluid phase to be dispersed as drops flow into a surrounding continuous phase where it is confined to a narrow region and pinched off into droplets. Precise flow control is needed to control droplet breakup, and drops can form under different processes depending on the flow rate ratio between the dispersed and continuous fluid phases.

We used our flow controller with a flow-focusing droplet device (Figure 6) to deliver a highly tunable and responsive flow rate to control droplet formation. We first determined the hydraulic resistance for both phases in respect to the respective inlets. For the oil phase, the two water inlets were blocked off, oil flowed from inlet to outlet and the flow rate was measured at varying pressures. Conversely, for the water phase, the oil inlets were blocked off, and a cryovial filled with DI water was pressurized and the flow rate was measured for varying applied pressures. The hydraulic resistance for the oil and water phase were 3.3 × 10¹³ and 2 × 10¹³, respectively. With the flow rate relationships known, pressure driven flow was then used to deliver oil into two parallel microchannels that surround a central stream containing a continuous aqueous phase. At the junction of the three channels, the liquid flows together into a downstream contraction. Here, viscous stresses and squeezing pressure from the outer phase draw the aqueous phase through and force it to break up into droplets. By varying the flow rate of the continuous oil phase, we were able to produce droplets under different regimes. As shown in Figure 6, the flow controller is capable of producing three different droplet generation modes, including drop production by squeezing (Figure 6(a)), liquid jetting (Figure 6(b)), and dripping (Figure 6(c)). Typically, the flow rate of the continuous phase has the greatest impact on droplet formation and size. These experiments demonstrate that our constant pressure flow controller is capable of producing droplets in all three of these regimes.

VI. CONCLUSIONS

Many types of microfluidic applications require precise and robust fluid control. While commercially available flow controllers and syringe pumps often satisfy this need, they are often expensive and beyond the scope of many biology and bioengineering laboratories. To lower the cost and technological barrier associated with microfluidics, we have presented a small, inexpensive flow controller capable of generating tunable chip-scale flows. The system uses external pressure to drive fluid flow. Such constant pressure sources, where the flow rate is dependent on the device hydraulic resistance, are often difficult to control and regulate. Using hydraulic circuit analysis, we determined the necessary capillary tube length to restrict the fluid flow to a predictable flow rate that was independent of microchannel geometry. Furthermore, we implemented an inexpensive switch to redirect fluid flows on and off without producing unwanted fluid backflow. Finally, we demonstrated the versatility and power of this novel microfluidic flow controller by generating chemical gradients and producing monodisperse water-in-oil droplets. The complete flow control system costs less than half of a single syringe pump and is easy to assemble and operate. With the ability to switch fluid flows on/off at predictable flow rate, this system offers a quick, simple, and affordable way to get involved with microfluidics.