Enhancement of continuous-flow separation of viable/nonviable yeast cells using a nonuniform alternating current electric field with complex spatial distribution

Abstract

The variability in cell response to AC electric fields is selective enough to separate not only the cell types but also the activation states of similar cells. In this work, we use dielectrophoresis (DEP), which exploits the differences in the dielectric properties of cells, to separate nonviable and viable cells. A parallel-plate DEP device consisting of a bottom face with an array of micro-fabricated interdigitated electrodes and a top face with a plane electrode was proposed to facilitate the separation of cells by creating a nonuniform electric field throughout the flow channel. The operation and performance of the device were evaluated using live and dead yeast cells as model biological particles. Further, numerical simulations were conducted for the cell suspensions flowing in a channel with a nonuniform AC electric field, modeled on the basis of the equation of motion of particles, to characterize the separation efficiency by changing the frequency of applied AC voltage. Results demonstrated that dead cells traveling through the channel were focused onto a site around the minimum electric field gradient in the middle of the flow stream, while live cells were trapped on the bottom face. Cells were thus successfully separated under the appropriately tuned frequency of 1 MHz. Predictions showed good agreement with the observation. The proposed DEP device provides a new approach to, for instance, hematological analysis or the separation of different cancer cells for application in circulating tumor cell identification.

I. INTRODUCTION

The ability to separate and isolate target cells from a diverse population is fundamental to many biomedical applications. For example, isolation of circulating tumor cells (CTCs) from a blood sample may allow reliable early detection and molecular characterization of cancer at diagnosis.¹ Collecting fetal cells in peripheral blood is essential for early detection of chromosomal diseases and abnormalities.²

Dielectrophoresis (DEP) is one of the most effective and widely used techniques for manipulating, separating, sorting, and identifying biological cells in microfluidic systems.^3–10 DEP is an electro-mechanical phenomenon in which polarizable but electrically uncharged particles move due to an applied nonuniform AC electric field. In such a field, a cell will polarize, and the polarizability of the cell is frequency-dependent. The polarized cell can be represented by a dipole, which experiences the DEP force proportional to the gradient of the electric field that will move the cell. Thus, the DEP force in turn is proportional to the strength of the electric field gradient; a reduction of the electrode size and/or spacing will markedly increase the DEP force. This advantageous scaling of the DEP force with electrode geometry makes DEP very suitable for manipulating cells in microfluidic systems.

The physical and electrical properties of the cell, conductivity and permittivity of the suspending medium, and strength and frequency of the applied AC electric field are the substantial parameters determining a cell's electro-mechanical DEP response. In particular, the most prominent advantage of DEP over the existing cell-separation methods is that the DEP force is strongly dependent on the cell viability. Several studies have demonstrated the effectiveness of DEP in separating viable and nonviable cells.^11–16 In recent years, studies of microelectrode-based DEP fluidic device for cell separation have rapidly become more popular and attracted much attention due to advanced micro-processing technologies.¹⁷ A cell sorting technique using a combination of platinum electrodes with a photo-patterned insulator was proposed to analyze and synchronize yeast cell division.¹⁸ Polymeric microfluidic device with integrated thick Carbon-Polydimethylsiloxane (C-PDMS) composite electrodes was proposed to carry out DEP trapping of low abundance biological cells.¹⁹ In this study, by using C-PDMS electrodes as thick as a channel height, it was possible to extend the DEP force influence in the whole volume of the channel and maintaining high trapping efficiency. The hybrid DEP system that integrated a chemical surface coating with a microfluidic device containing interdigitated microelectrodes was proposed to impart positive dielectrophoresis (pDEP) for enhanced trapping of the cells.²⁰ In this study, the trapping efficiency of Escherichia coli and Cryptosporidium parvum increased from 29.0% and 61.3% in an uncoated DEP system to 51.9% and 82.2% in the hybrid DEP system, respectively. Dielectrophoresis field-flow fractionation (DEP-FFF) is another kind of time-based separation method, and the advantage of this method is that more than two kinds of particles can be separated.²¹ As described above, advances in microfluidics have enabled the realization of miniaturized devices offering capabilities of high-efficiency cell separation. However, significant technical challenges arise in applying DEP for clinical applications when it is necessary to process extremely large numbers of cells with sufficient separation and isolation at sufficiently high throughput. Most previously, proposed DEP devices for cell separation and isolation continue to lack feasibility for scaling to clinical specimens.

In the present study, a novel parallel-plate flow-channel type DEP device is proposed to effectively separate nonviable cells from viable cells using their different DEP characteristics in response to a nonuniform AC electric field. A nonuniform AC electric field is established throughout the interior flow channel to enhance cell separation. The nonuniform electric field in the flow channel creates sites of minimum field gradient slightly above the bottom face, while simultaneously generating maximum regions at the bottom face. As a result, nonviable cells traveling along the flow stream are concentrated around the sites of minimum field gradient slightly above the bottom of the channel and are effectively separated from the viable cells that attach to the electrodes on the bottom face. We conduct numerical and experimental studies to examine the ability of the proposed DEP cell-separation device to effectively separate nonviable cells from a sample containing both viable and nonviable cells.

II. DEP CELL-SEPARATION DEVICE

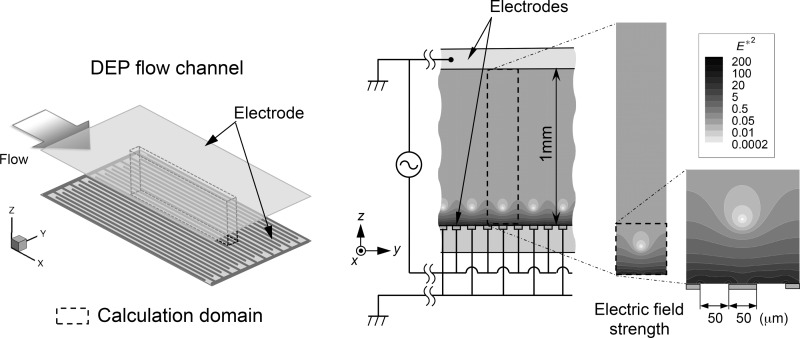
Figure 1 is a schematic illustration of the proposed cell-separation DEP device. The device was designed so that the flowing cell mixture was exposed to a nonuniform electric field under the conditions such that the electric field lines were arranged in the channel cross-section perpendicular to the streamlines of the flow. In the figure, a conceptual illustration of the proposed DEP device is shown on the left, an illustration of the cross-sectional view of the flow channel is in the middle, and the distribution of the AC electric field strength (E²) in a cross-section of the flow channel is shown on the right. The top face of the flow channel is a planar electrode. On the bottom face of the channel, 50-μm wide linear and flat interdigitated counter electrodes are installed in parallel at 50-μm intervals in the lateral (y) direction. The planar electrode at the top and one of the grounded electrodes on the bottom are electrically connected and grounded. When an AC electric voltage is applied across the channel height, the electrodes at the top and bottom create a nonuniform electric field throughout the flow channel, with extremely steep field gradients around the edges of the high-voltage electrodes on the bottom. Meanwhile, zones of minimum field gradient occur along the flow direction with vertical positions slightly above the centerline of each grounded electrode on the bottom face.

FIG. 1.

Schematic illustration of the cell-separation DEP device: (left) conceptual illustration of the DEP device; (middle) cross-sectional view of the flow channel; and (right) distribution of the square of non-dimensional AC electric field strength (E*²) in a cross-section of the flow channel.

Under AC electrical excitation, the electrode array will produce DEP forces on cells along the electric field gradient. The DEP force, h, acting on a cell of diameter d can be written as

$$\mathit{h}=2\pi {\epsilon }_0{\epsilon }_f{\left(\frac{d}{2}\right)}^3\mathrm{Re}(\beta )\nabla (\mathit{E}\cdot \mathit{E}),$$ (1)

where $\nabla$ is the Nabla operator, E is the electric field vector at the position of the cell, and Re(β) is the real component of the Clausius-Mossotti factor,²²

$$\beta =\frac{{\epsilon }_c^{*}-{\epsilon }_f^{*}}{{\epsilon }_c^{*}+2{\epsilon }_f^{*}},$$ (2)

between the cell and the suspension medium. The values ε₀, ε_f, and ε_c are the vacuum permittivity, the relative dielectric permittivity of the suspending medium, and the relative dielectric permittivity of the cell, respectively. The values ${\epsilon }_{\mathrm{c}}^{*}$ and ${\epsilon }_f^{*}$ are the frequency-dependent complex dielectric permittivities of the cell and its suspending medium, respectively. Because the DEP force is dependent on a cell's physical and electrical properties, DEP can be used as to separate cells by exploiting these differences in various cell types. The value Re(β) can take a positive or negative value depending on the relative magnitude relationship of dielectric properties between the cell and the suspending medium. When the cell is more polarizable than the suspending medium (Re(β) > 0), it will move toward regions containing the highest gradient of the inner product of the electric field ($\mathit{E}\cdot \mathit{E}$) (positive DEP; pDEP). If the medium is more polarizable than the cell (Re(β) < 0), the cell will be pushed away from regions of the highest gradient of the inner product (negative DEP; nDEP), in other words, focused onto the regions of the minimum field gradient.

Biological cells have very different electrical properties and exhibit large induced polarizations that are highly dependent on the applied AC electric field frequency. For instance, the cell membrane consists of a lipid bilayer and is highly insulated, while the cell interior contains many dissolved charged molecules and ions. Upon death, the cell membrane becomes permeable, and its conductivity can increase markedly due to free exchange of the cell contents and the external medium. Hence, there is a large difference in DEP responses (positive and negative for viable and nonviable cells, respectively) depending on the field frequency, and a selective separation is possible between viable and nonviable cells in the proposed system.

The idea is to use the spatially inhomogeneous DEP forces as a means of separating the cells according to their electrical properties. In the proposed flow channel, dead (nonviable) cells levitate at around equilibrium height, where the minimum electric field gradient is realized, while live (viable) cells are trapped at the electrode edges on the bottom face where the maximum electric field gradient exists, until the electrical forces are removed or made weak enough to release them. The height of the equilibrium is determined by the balance of the DEP and sedimentation forces acting on a cell, as well as by the width of the electrodes, the spacing between two adjacent electrodes, and the ratio of the width of the electrodes to the height of the flow channel. Thus, the zone of the minimum electric field gradient (zone of nonviable cells) always appears slightly above the grounded electrode on the bottom face, regardless of the height of the flow channel and size of the electrode array. In this regard, the design of the proposed configuration of electrodes in the flow channel is very advantageous, as they force nonviable cells to focus at the equilibrium height while viable cells are trapped or settled on the bottom of the flow channel. By increasing the channel height and operating the device at an optimized flow rate, applied voltage, and field frequency, we expect a throughput capacity over an order of magnitude higher than those of existing microfluidic systems with similar structures. This could broaden the clinical utility of the DEP devices for cell separation.

A. Numerical simulation model

Yeast cells were modeled as elastic spheres with uniform diameter d and density ρ_c. The motion of the cell i in a suspending medium of density ρ_f is described by the equation of motion

$$m\frac{d^2{\mathit{r}}_i}{d{t}^2}={\mathit{F}}_i-{\mathit{S}}_i+\frac{4}{3}\pi ({\rho }_c-{\rho }_f){\left(\frac{d}{2}\right)}^3\mathit{g},$$ (3)

where m is the mass of the cell, r_i is the positional vector of the cell i, F_i is the electro-mechanical force acting on cell i, and g is the vector of the acceleration of gravity. The cell density was ρ_c = 1.11 g/cm³.²³ The density ρ_f and viscosity μ of the suspending medium were ρ_f = 1.00 g/cm³ and μ = 8.94 $\times$ 10⁻⁴Pa s at room temperature, respectively. The second term on the RHS, S_i, is the Stokes drag force exhibited on cell i due to its motion relative to the suspension medium and is given by

$${\mathit{S}}_i=3\pi \mu d\left(\frac{d{\mathit{r}}_i}{\mathit{d}\mathit{t}}-{\mathit{u}}_i\right),$$ (4)

where u_i is the local fluid velocity of clear fluid evaluated at the center of cell i. The flow of suspension in the channel is laminar and fully developed,²⁴ and the cross section of the channel is rectangular with a high aspect ratio. Therefore, it can be assumed that the profile of the velocity vector, u_i, has only a single component, u, and the velocity in the flow (x-axis) direction. This is described as a two-dimensional Poiseuille flow of the function of the channel height (z coordinate) only

$$u=6\frac{Q}{A}{z}^{*}\left(1-z^{*}\right),$$ (5)

where Q, A, and z* are the volumetric flow rate of the suspension, the cross-sectional area of the unit volume, and the nondimensional z coordinate normalized to the channel height, respectively. The last term in Eq. (3) is the external force that arises due to the difference in densities between the cell i and the suspending medium. The electro-mechanical force, F_i, in Eq. (3) is given by the expression,

$${\mathit{F}}_i=\sum _{i\ne j}{\mathit{f}}_{\mathit{i}\mathit{j}}+{\mathit{h}}_i,$$ (6)

where f_ij is the long-range dipole-dipole interaction force between cells i and j, and h_i is the DEP force induced on cell i. Force f_ij is derived from the expression,

$${\mathit{f}}_{\mathit{i}\mathit{j}}=-\frac{\partial {\Phi }_{\mathit{i}\mathit{j}}}{\partial r}{\mathit{e}}_r-\frac{1}{r}\frac{\partial {\Phi }_{\mathit{i}\mathit{j}}}{\partial \theta }{\mathit{e}}_{\theta },$$ (7)

where θ is the azimuthal angle between the field direction and the line connecting the two centers of a pair of cells i and j, and e_r and e_θ are unit vectors parallel to the directions of the relative positional vectors r_i − r_j and θ, respectively. The value Φ_ij is the dipole-dipole interaction potential between cells i and j described as

$$\begin{array}{c}{\Phi }_{\mathit{i}\mathit{j}}=\frac{1}{4\pi {\epsilon }_0{\epsilon }_f}\left(\frac{{\mathit{p}}_i\cdot {\mathit{p}}_j}{r_{\mathit{i}\mathit{j}}^3}-\frac{3({\mathit{p}}_i\cdot {\mathit{r}}_{\mathit{i}\mathit{j}})({\mathit{p}}_j\cdot {\mathit{r}}_{\mathit{i}\mathit{j}})}{r_{\mathit{i}\mathit{j}}^5}\right),\\ {\mathit{r}}_{\mathit{i}\mathit{j}}={\mathit{r}}_i-{\mathit{r}}_j,\end{array}$$ (8)

where the dipole moment of cell i, p_i, is defined as

$${\mathit{p}}_i=4\pi {\epsilon }_0{\epsilon }_f{\left(\frac{d}{2}\right)}^3\mathrm{Re}(\beta )\mathit{E}\left({\mathit{r}}_i\right),$$ (9)

and the term of the DEP force, h_i, is expressed as follows:

$${\mathit{h}}_i=2\pi {\epsilon }_0{\epsilon }_f{\left(\frac{d}{2}\right)}^3\mathrm{Re}(\beta )\nabla \mathit{E}{\left({\mathit{r}}_i\right)}^2.$$ (10)

The relative dielectric permittivity of the medium used, ε_f, was ε_f = 80.0. The values of the Clausius-Mossotti factor, Re(β), for the live and dead cells were determined from the literature^25–27 so that they exhibited positive and/or negative DEP characteristics as functions of the field frequency. Thus, the following two couples of values of Re(β) for live and dead cells were determined: (i) when the live cells exhibited pDEP while the dead cells exhibited nDEP, the values were Re(β) = 0.25 for the live cells and Re(β) = −0.20 for the dead cells, corresponding to those at a frequency of 1 MHz; (ii) when both the live and dead cells exhibited nDEP, the values were Re(β) = −0.01 for the live cells and Re(β) = −0.18 for the dead cells, corresponding to those at a frequency of 100 MHz.

The force acting on a single cell was evaluated by summing the dipole-dipole interactions, f_ij, and DEP forces, h_i, acting on the corresponding cell. The dipole-dipole interaction was established by the surrounding polarized cells. When the terms of higher orders of multipolar expansions directly amenable to intercellular force determination are omitted, Equation (7) serves to approximate the total force of f_ij on cells, because the field polarity reversals of the AC electric field are too rapid for any cell's response. The frequency dependence of the higher-order force components is also a minor contribution, because the field frequency in the present study was high enough to allow us to ignore the effects of corresponding forces.

For the numerical integration of Eq. (3), we used the time step Δt = 2 $\times$ 10⁻⁶ s, which ensured that both the cell trajectory and the average kinematic energy of all the cells became independent of the size of the time step. The shifted-force version of the usual electrostatic potential was used for the wall-cell and intercellular force calculations to prevent cells from overlapping or running through each other or the channel walls. The shifted-force potential and its first derivative that go to zero continuously at the cutoff radii r_c = 0.6d and 1.1d were used for wall-cell and intercellular repulsive interactions, respectively. To evaluate the dipole-dipole interaction, the value of cutoff radius r_c = 6.0d, which ensured that the value of potential decreases to less than 1 $\times$ 10⁻⁸ of its value at the cell surface (r_c = d/2), was applied. To calculate the total electro-mechanical forces acting on a cell, the periodic boundary condition was applied to the cells located on the planes of the periodic boundary to eliminate the boundary's surface effect. The effect of the drag forces between the cells aggregating on the bottom face was not taken into account in the model. Because the flow velocity is quite low near the bottom face, drag forces between the cells are thought to have a secondary effect on their movement compared with the dominant driving forces, i.e., the DEP force and dipole-dipole interaction among cells.

B. Numerical simulation procedure

Numerical simulations were conducted for a fixed number of cells. To conserve computation resources, simulations were performed in the rectangular unit volume indicated in Fig. 1. The dimension of the unit volume was 1-mm (H) $\times$ 5-mm (L) $\times$ 0.2-mm (W). At the inlet boundary of the unit volume, a cell leaving the unit volume through the outlet boundary was simultaneously replaced by another cell entering through the inlet boundary at the same y and z coordinates as those of the departing cell. A periodic boundary condition was applied over the x-z planes on both lateral sides of the unit volume. Once a cell reached the edges of the high-voltage electrode on the bottom where the field gradient peaked, it was regarded as trapped, and its further displacement along and away from the bottom face was not allowed.

For calculation of the electric field in the unit volume, since there was no field variation along the flow direction, we adopted the approximation of a two-dimensional electric field in a y-z plane. The Laplace equation of the electric potential over a cross-section (y-z plane) of the unit volume was solved using a finite difference method to obtain the converged solution of the electric field distribution. The sizes of the finite difference mesh in the y and z directions were Δy = Δz = d/4. As the electric field was symmetric about the vertical plane of symmetry in the unit volume along the flow direction, we computed the electric potential in only half of the symmetry area under the boundary condition,

$$\frac{\partial \mathit{E}}{\partial \mathit{n}}=0,$$ (11)

on the corresponding plane of symmetry. An AC field with a peak-to-peak voltage of V_pp = 3.0 V was applied between the high-voltage and grounded electrodes. The converged solution of the distribution of the square of the non-dimensional electric field strength, E*², is shown in Fig. 1. The value of the electric field strength was normalized to that of the average value. The positions of the electrodes on the bottom face are also indicated. The gradient of the field strength peaked at the edges of the high-voltage electrodes on the bottom face, whereas the minimum gradient appeared at a height of ∼110 μm right above the center of the grounded electrode on the bottom face.

To prepare the configuration of cells used for the initial conditions of the numerical simulations, we performed a simulation of cells traveling along the flow stream without the electric field for 20 s, beginning with the initial state of random distribution of cells in the suspending medium. A modified Brünger-Brooks-Karplus (BBK) method^28,29 was used for the simulation. The computer program was parallelized, and computations were performed on clusters of the National Defense Academy.

III. EXPERIMENTS

A. Experimental setup

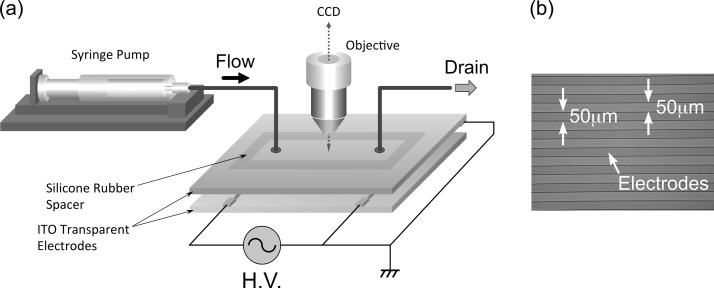
Figure 2 shows (a) the experimental set up of the parallel-plate DEP flow channel, and (b) a photograph of the fabricated interdigitated counter electrode used. The 1-mm (H) $\times$ 40-mm (L) $\times$ 10-mm (W) DEP flow channel was constructed of parallel top and bottom glass plates separated by a 1-mm thick silicon-rubber spacer. The top face of the flow channel was an Indium Tin Oxide (ITO) glass plate electrode, which allowed a clear view of the transient behavior of cells in the suspending medium. The arrays of parallel electrodes, shown in Fig. 1, were interdigitated with equal widths and gaps of 50 μm on the glass plate, forming the bottom face of the flow channel. Electrodes were fabricated by standard photolithography. In brief, 50-mm (W) $\times$ 90-mm (L) ITO coated glass blanks (GEOMATEC Co., Ltd., ITO thickness 0.33 μm, glass thickness 0.7 mm) were deposited with 300-nm thick SiN film by conventional parallel-plate plasma CVD (P-CVD). The positive photoresist (S1808, Rohm and Haas Electronic Materials) was then spin-coated at 4000 rpm and baked on hot plate at 90 °C for 3 min. The resist layer was exposed to UV light through a positive mask image of the electrode array, using a mask aligner. The exposed photoresist was developed with MF-319 (Rohm and Haas Electronic Materials) developer and baked on a hot plate at 130 °C for 5 min. The uncovered SiN region was then removed by means of reactive ion etching (RIE), and the photoresist was removed with AZ 100 remover (AZ Electronic Materials). The uncovered ITO region was etched in an etching solution (ITO-02, Kanto Chemical) at 40 °C for 10–15 min. Finally, the SiN film covering the un-etched regions of the electrodes was removed using RIE. Electrodes were fabricated in the Semiconductor Center of Kitakyushu Foundation for the Advancement of Industry, Science, and Technology. Silicon-rubber tubes (ID: 1 mm, OD: 3 mm), glued into flow-inlet and -outlet holes drilled through the top ITO glass plate with a diamond drill, allowed for the introduction and removal, respectively, of cell suspensions. A function generator (Tektronix, AFG3101) was connected to the electrode arrays to generate a nonuniform electric field in the flow channel. Sinusoidal AC voltages were applied to the electrodes through lead wires. Lead wires were bonded to the ITO glass plate on the top and electrodes on the bottom face of the flow channel using electrically conductive 2-part resins (ITW Chemtronics, CW2400). The input voltage was monitored by a digital oscilloscope (Tektronix, TDS2012B). A digital syringe pump (KD Scientific, KDS-100) was used to provide a continuous flow of cell suspension through the flow channel. Cell behaviors were monitored using a phase-contrast inverted microscope (Olympus, CKX41) equipped with a CCD camera (WATEC, WAT-231S2) and recorded on a digital camera capable of capturing video (Olympus PEN Lite E-PL6).

FIG. 2.

(a) The experimental set up of the parallel-plate DEP flow channel and (b) a photograph of the micro-fabricated array of parallel electrodes.

The DEP flow channel was constructed of parallel top and bottom glass plates separated by a silicon-rubber spacer. The top face of the flow channel was an Indium Tin Oxide (ITO) glass plate electrode, which provided a clear view of the transient behavior of cells in the suspending medium. Forming the bottom face of the flow channel, the arrays were interdigitated counter electrodes with equal widths and gaps of 50 μm.

B. Cell preparation

Yeast cells (Saccharomyces cerevisiae) were cultured in yeast extract peptone dextrose (YPD) medium (Sigma D6546, containing 1% yeast extract, 2% glucose, and 2% polypeptone) supplemented with 0.006% Adenine Hemisulfate (Sigma A9126) with constant shaking at 30 °C. The cells were harvested at the early stationary growth phase after a 30-h culture. Nonviable (dead) cells were prepared by exposing cultured cells to 80 °C for 15 min, determined to be an adequate time to kill the majority of the cells in a sample. Staining with methylene blue was used to distinguish dead cells from viable (live) cells; dead cells were stained blue and live cells were unstained. From stock suspensions of both live and dead cells, suitable volumes were pipetted and mixed together at a ratio of 4:1 in order to prepare samples for separation studies. Methylene blue (Sigma M4159) of 0.2% (w/v) solution was added to the mixtures. After the cells were stained, the volumes were diluted with Milli-Q water, the suspension was then centrifuged, and the supernatant liquid was drained off. The cells were resuspended in fresh Milli-Q water and again centrifuged. This process was repeated until the conductivity of the suspension, as measured with a conductivity meter (HORIBA, ES-51), was at or below the desired value (∼1 mS/m). Volumes were then resuspended in Milli-Q water to achieve a final cell concentration of ϕ = 1.5 $\times$ 10⁶ cells/ml, which was necessary to optimize the image quality for analysis.

C. Experimental method

The cell suspension was introduced into the flow channel mounted on the stage of the inverted microscope with a syringe pump at a constant volumetric flow rate of Q = 11.5 ml/h, corresponding to a mean velocity of 0.32 mm/s in the flow channel, through the silicon tube joined with a luer-lock connector. Before the suspension was introduced to the channel, the ITO glass plate on top was gently pressed down to ensure a tight seal between the spacer and the plates. After the cell sample was introduced into the flow channel inlet, cells were allowed to travel along the stream of the steady flow, and AC voltage was applied.

A sinusoidal AC voltage with a peak-to-peak value of V_pp = 3.0 V was imposed between the top and bottom faces of the flow channel. Applied voltage frequencies of 1 and 100 MHz were tested to examine the frequency dependence of the cell-separation performance. Electric fields can stress cells via an increase in temperature due to the Joule heating of the suspending medium or via reactive species formed at the electrode-electrolyte interface. The value of the applied voltage was therefore chosen with care to minimize such damage. An input voltage of less than 3.0 V has been demonstrated to be sufficient to create an electro-mechanical force to manipulate cells without excessive increase in temperature.³⁰

The effect of the presence of cells on the strength of the AC field in the flow channel was examined by keeping the voltage of the input power at V_pp = 3.0 V and using a digital oscilloscope to monitor the amplitude of the AC field in (1) the presence and (2) the absence of cells in the suspending medium. It was found that there was hardly any difference, less than 1%, in the amplitude of the AC field between these two cases. The movies of the cell-separation process were recorded from the onset of the AC electric field application and lasted several minutes. Snapshots of cell behaviors were extracted from the digitalized video sequences and converted into gray scale digital images.

IV. RESULTS AND DISCUSSION

In the numerical simulation, we adopted a cell concentration of ∼1500 cells in the unit volume. This was actually equivalent to the volume fraction of the cell in the unit volume ϕ = 1.5 $\times$ 10⁶ cells/ml, the same value as that used in the experiment. The ratio of the number of live cells to dead cells in the suspension was set to 4:1, which was also the same as that used in experiment. The mean velocity of the Poiseuille flow of the cell suspension in the unit volume,

$$u_m=\frac{1}{h}{\int }_0^{h}u\hspace{0.17em}dz,$$ (12)

was set to u_m = 0.32 mm/s, where h is the channel height. Thus, the Reynolds number, Re, was Re = 3.2 $\times$ 10⁻¹. The root mean square (rms) value of the applied peak-to-peak voltage was V_pp = 3.0 V.

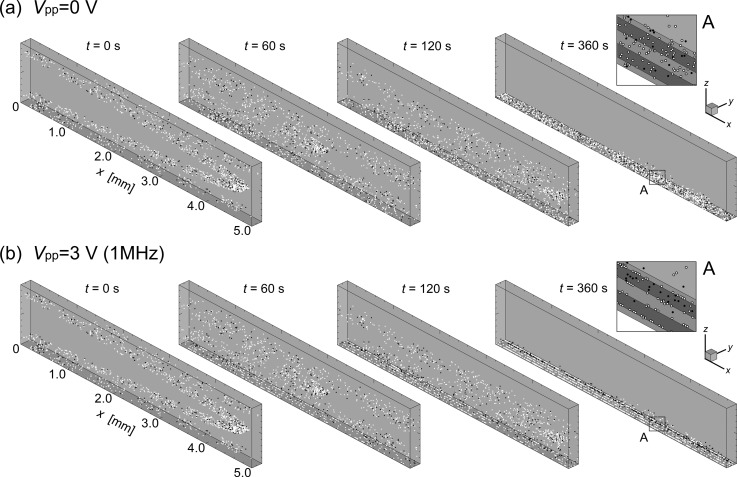
Figure 3 contains bird's-eye views of the transient distribution of cells traveling through the unit volume. Both the top (a) and bottom (b) panels present sequences of instantaneous snapshots of the cell distribution at times t = 0, 60, 120, and 360 s following the application of AC voltage of peak-to-peak values (a) V_pp = 0 V (no electric field) and (b) V_pp = 3.0 V at a frequency of 1 MHz. The open and closed circles in the figure indicate the live and dead cells, respectively. Insets on the RHS of each panel are enlargements of the unit volume at time t = 360 s, indicated with squares labeled “A” for visibility.

FIG. 3.

Sequences of instantaneous snapshots of cell distribution at times t = 0, 60, 120, and 360 s following the application of AC voltage of peak-to-peak values (a) V_pp = 0 V (no electric field) and (b) V_pp = 3.0 V with a frequency of 1 MHz. The open and closed circles in the figure indicate the live and dead cells, respectively. Insets on the RHS of each panel are enlargements of the unit volume at time t = 360 s indicated by squares labeled “A” for visibility.

When the AC electric field was absent (panel (a)), cells traveled through the unit volume along the stream of flow with the velocity distribution of a fully developed Poiseuille flow and gradually settled down by the bottom face due to gravitational force as they moved with the fluid flow. After a long period of time, both live and dead cells settled as sediment on the bottom face of the unit volume. However, when the AC electric field was applied (panel (b)), the live cells in the suspension, having a positive DEP property, migrated downward as they moved with the fluid flow and finally attached to the edges of electrodes on the bottom face due to the attractive DEP forces induced there. The dead cells, meanwhile, having a negative DEP property, migrated downward at first, but gradually began to concentrate slightly above the bottom face of the unit volume where the repulsive DEP force and gravitational force were balanced. Consequently, most of the live cells were trapped at the edges of electrodes on the bottom surface, where the attractive DEP force was at its maximum. Dead cells traveling in the direction of the flow concentrated further, and eventually formed a single thin layer lying slightly underneath the site where the minimum field gradient was exerted. They then maintained this thin layer in the stream of the flow. Results suggest that dead cells can be effectively separated from live cells by the proposed DEP channel device.

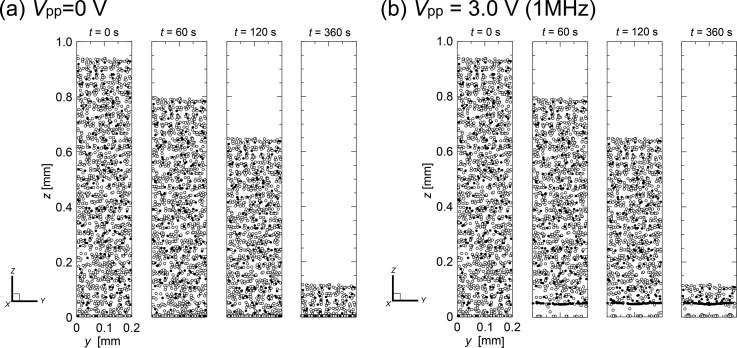
Figure 4 presents a different view of the same results shown in Fig. 3. Distributions of cells are shown from the downstream end looking toward the upstream of the unit volume to provide clear images of the transient cell separation kinetics. Both the left (a) and the right (b) panels of Fig. 4 present sequences of instantaneous snapshots of the cell distribution at times t = 0, 60, 120, and 360 s, following the application of AC voltage of peak-to-peak values (a) V_pp = 0 V (no voltage) and (b) V_pp = 3.0 V, respectively, with the frequency of 1 MHz. The open and closed circles in the figure indicate the live and dead cells, respectively. However, when the AC voltage was applied, in the first 10 s (not shown) the live cells that had initially distributed within the lower part of the unit volume moved down to the bottom face, where the strong attractive DEP forces were present at the edges of electrodes. The rest of the live cells that had initially distributed in the area higher than ∼50 μm from the bottom face gradually settled down due to the gravitational force. Because the magnitude of the electro-mechanical force within the corresponding area was negligibly small compared with the gravitational force, gravitational force alone caused the sedimentation of live cells. Subsequently, the live cells that moved close to the bottom face were attracted and finally attached to the edges of the electrodes. In contrast, dead cells exhibited the nDEP property. Cells that had begun to move close to the bottom face by sedimentation during the earlier stages of AC voltage application were soon lifted up by the repulsive DEP forces induced at the edges of electrodes on the bottom face. Consequently, dead cells traveling through the unit volume began to concentrate at the vertical equilibrium position where the repulsive upward-acting DEP force and the gravitational force were balanced, ∼50 μm above the bottom face. A significant time after AC field application, most of the live cells were captured at the edges of electrodes on the bottom face, while the dead cells gradually aggregated and before long formed a single thin layer slightly above the bottom face in the flow channel. The dead cells were finally separated from the live cells by time t ∼ 500 s (not shown).

FIG. 4.

Sequences of instantaneous snapshots of cell distribution viewed from the downstream end of the unit volume toward the upstream at times t = 0, 60, 120, and 360 s following the application of AC voltage of peak-to-peak values (a) V_pp = 0 V (no electric field) and (b) V_pp = 3.0 V; the frequency was 1 MHz. The open and closed circles in the figure indicate the live and dead cells, respectively.

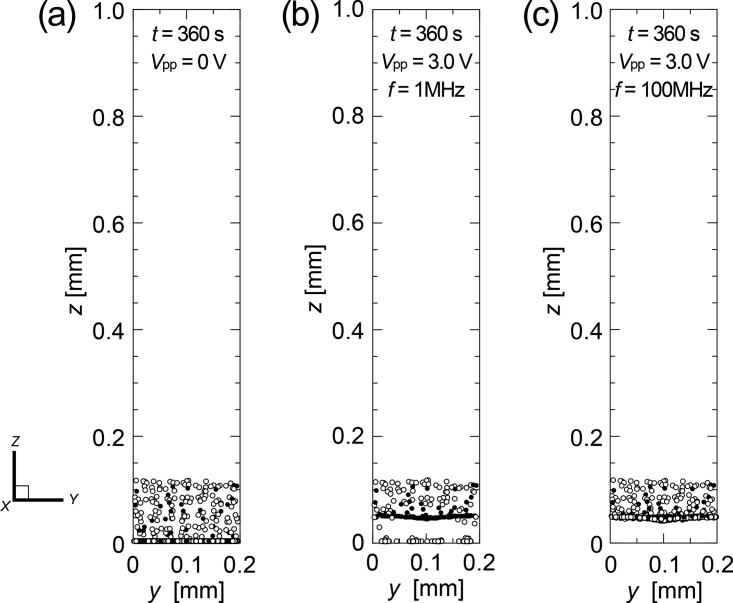
Figure 5 contains snapshots of the distribution of cells traveling through the unit volume viewed from the downstream end and looking upstream at t = 360 s with the voltage of peak-to-peak values (a) V_pp = 0 V (no electric field), (b) V_pp = 3.0 V with the frequency of 1 MHz, and (c) V_pp = 3.0 V with the frequency of 100 MHz. The figure reveals that the cell-separation ability of the proposed device depends simply on the DEP characteristics of live and dead cells and strongly on field frequency. The 1-MHz nonuniform electric field lifted the dead cells and sustained them in the unit volume slightly above the bottom face, while most of the live cells were captured at the bottom face. The dead cells concentrated in a narrower region as time evolved. It is interesting to note that the thin layer of dead cell aggregation was formed horizontally (y) across the width of the unit volume despite the fact that the gradient of the electric field was distributed across the width. This was because the Stokes drag force is another dominant force, driving up the dead cells traveling near both side boundaries (vertical planes along the centerlines of the high-voltage electrodes on both ends in the figure). When the AC electric field of frequency 100 MHz was applied, both the live and dead cells collected at the site are ∼50 μm above the bottom face because all cells exerted the nDEP property in this range of the field frequency.

FIG. 5.

Snapshots of the distribution of cells traveling through the unit volume viewed from the downstream end and looking toward the upstream at t = 360 s, following the application of AC voltage of peak-to-peak values (a) V_pp = 0 V (no electric field), (b) V_pp = 3.0 V with the frequency of 1 MHz, and (c) V_pp = 3.0 V with the frequency of 100 MHz.

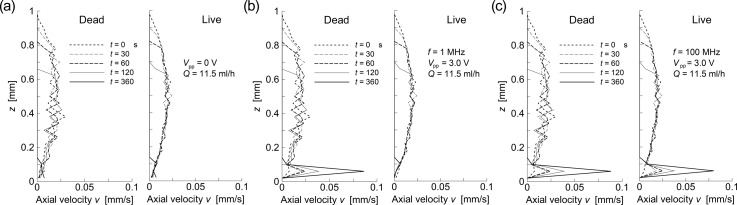
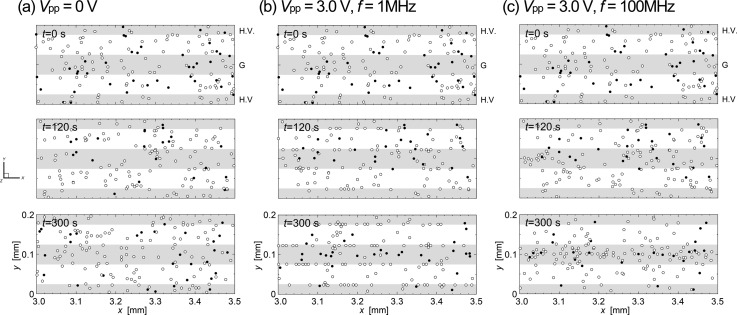
Figure 6 shows the relationship between the time evolution of the velocity of the flowing cells, v, and the distribution of the vertical positions of the live (right) and dead (left) cells in the unit volume, z, following the application of AC voltage of peak-to-peak values (a) V_pp = 0 V (no electric field), (b) V_pp = 3.0 V with the frequency of 1 MHz, and (c) V_pp = 3.0 V with the frequency of 100 MHz. When there was no electric field (panel (a)), both live and dead cells gradually settled at a constant sedimentation velocity while moving axially at a velocity of less than v ∼ 0.02 mm/s. This was about ∼1/16 of the local velocity of the pure fluid, associated with the parabolic axial flow profile. However, the time evolution of both the magnitude and the profile of the flow velocity of dead cells showed significantly different features from those of live cells when an AC voltage of V_pp = 3.0 V was applied (panel (b)). The dead cells were accelerated in the flow direction with time as they gradually concentrated at the site of the minimum field gradient. This acceleration of the axial velocity of a dead cell was caused by the elimination of forces acting on the dead cell in the vertical direction. The lift force due to the negative DEP effect cancelled the gravitational force acting on the dead cell. Therefore, most of the dead cells traveled faster through the unit volume with vertical positions maintained at ∼50 mm above the bottom face. The dead cells at this site were further accelerated, while those outside of the site decelerated due to the hydraulic drag force in the vertical direction during their downward migration (sedimentation) or an upward movement (lifting due to the repulsive DEP force) in the unit volume. When the AC voltage of V_pp = 3.0 V with the frequency of 100 MHz was applied (panel (c)), both the live and dead cells were accelerated in the flow direction over time as they gradually concentrated at the site of the minimum field gradient; this was because both exerted the nDEP property at the 100-MHz frequency. Figure 7 shows the snapshots of the time course of the distribution of cells traveling through the flow channel observed at times t = 0, 120, and 300 s following the application of AC voltage of peak-to-peak values (a) V_pp = 0 V (no electric field), (b) V_pp = 3.0 V with the frequency of 1 MHz, and (c) V_pp = 3.0 V with the frequency of 100 MHz. High-voltage (H.V.) electrodes appear on both the top and bottom ends in Fig. 7, while the electrode in the middle is grounded (G). The cell suspension flow of the mean velocity u_m = 0.32 mm/s is from left to right, as indicated by a white arrow. When no AC voltage was applied (panel (a)), both live and dead cells traveled through the flow channel without being trapped at the edges of electrodes. However, with an AC voltage of V_pp = 3.0 V at a frequency of 1 MHz (panel (b)), the number of live cells attached to the edges of electrodes gradually increased with time, whereas few dead cells attached to the electrodes. Most of the dead cells levitated in the flow stream, maintaining a height of ∼20 μm above the bottom face. The height of a levitating cell was estimated by readings on the focusing dial of the microscope when the focus was on the bottom face and on the corresponding cell.

FIG. 6.

Relationship between the time evolution of the velocity of the flowing cells, v, and the distribution of the vertical positions of the live (right) and dead (left) cells in the unit volume, z, following the application of AC voltage of peak-to-peak values (a) V_pp = 0 V (no electric field), (b) V_pp = 3.0 V with the frequency of 1 MHz, and (c) V_pp = 3.0 V with the frequency of 100 MHz.

FIG. 7.

Snapshots of the time course of the distribution of cells traveling through the flow channel observed at times t = 0, 120, and 300 s following the application of AC voltage of peak-to-peak values (a) V_pp = 0 V (no electric field), (b) V_pp = 3.0 V with the frequency of 1 MHz, and (c) V_pp = 3.0 V with the frequency of 100 MHz. High-voltage (H.V.) electrodes appear on both the top and bottom ends the figure, while the electrode in the middle is grounded (G). The cell suspension flow of the mean velocity u_m = 0.32 mm/s is from left to right, as indicated by the white arrow.

Experimental results were then compared with those of numerical simulations. Figure 8 shows numerical predictions of the transient distribution of cells traveling through the unit volume at times t = 0, 120, and 300 s following the application of AC voltage of peak-to-peak values (a) V_pp = 0 V (no electric field), (b) V_pp = 3.0 V with the frequency of 1 MHz, and (c) V_pp = 3.0 V with the frequency of 100 MHz. The open and closed circles in the figure indicate the live and dead cells, respectively. Predictions showed good agreement with the experimental results.

FIG. 8.

Numerical predictions of the transient distribution of cells traveling through the unit volume at times t = 0, 120, and 300 s following the application of AC voltage of peak-to-peak values (a) V_pp = 0 V (no electric field), (b) V_pp = 3.0 V with the frequency of 1 MHz, and (c) V_pp = 3.0 V with the frequency of 100 MHz. The open and closed circles in the figure indicate the live and dead cells, respectively.

However, the behaviors of cells were slightly different from those of the experiment when the field frequency was 100 MHz. In the prediction, cells traveling through the unit volume were focused onto somewhat narrower areas along the centerline of the grounded electrode, implying that the cells were likely to concentrate at the sites where the field gradient was minimum, right above the centerline of the grounded electrode. This was barely observed in the experiment. It can be considered that the real cells were not as sensitive to the electric field as those having idealized dielectric properties assumed in the present simulation model. In fact, in the experiment, it was observed that some of dead cells attached to the edges of electrodes even when an AC voltage of 1 MHz was applied. Recent studies showed that the DEP characteristic of yeast cells varies widely, depending on the cell size, shape, and electric properties of cell contents and membrane.^18,31 In particular, the reported values of the crossover frequency where the value of Re(β) of the cell changes its sign (e.g., from negative to positive) have a range that spans one order of magnitude of the field frequency. This situation may be prominent for cultured yeast cells because of the budding process, which leads to a change in shape and size during growth.

An important finding is that in the numerical predictions, it took about 500 s to completely separate the dead cells from the live cells as mentioned before (not shown). For example, all the dead cells experiencing negative DEP were elevated above the electrode into the flowing fluid, whereas all the live cells attached to the electrodes at the bottom in 500 s after the field application. This implies that the length of the flow channel L = 0.32 mm/s (mean flow velocity) $\times$ 500 s = 160 mm is necessary for the proposed DEP device to complete the separation of the cell suspension. A longer flow channel sometimes gives rise to the problem for existing micro DEP systems having shallow depth of parallel-plate flow channels. It causes temperature raise in the channel due to Joule heating and a remarkable increase in the hydrodynamic resistance to flow. However, the proposed DEP device can avoid these problems because it is possible to extend the depth of the channel, up to 1 mm in the present experiment, without a significant loss of DEP force influence in the entire space of the channel and thus being capable of performing high efficiency. Moreover, the strength of the applied voltage is also an important factor for cell separation DEP device because it majorly affects the cell viability. It was found that the cell separation was possible with the application of a relatively low voltage V_pp = 3.0 V in the proposed DEP device having a wide gap of 1 mm between the top and the bottom faces of the flow channel.

V. CONCLUSIONS

Numerical and experimental studies were conducted to evaluate the performance of a proposed dielectrophoretic (DEP) device to effectively concentrate on the specific cells from diverse populations through the separation of nonviable cells from a sample containing both viable and nonviable cells. The proposed parallel-plate DEP flow channel consists of a planar electrode on the top face and an array of narrow linear interdigitated electrodes on the bottom face. It thus creates a nonuniform AC electric field throughout the flow channel, enabling high-performance cell separation. Cultured yeast cells were used for the samples of viable (live) and nonviable (dead) cells. The results demonstrated that the use of the nonuniform AC electric field with a tuned frequency (∼1 MHz) selectively concentrated on the nonviable cells in the trapping site along the flow stream where the repulsive DEP force and the gravitational force were balanced, while the viable cells were captured at the edges of electrodes on the bottom face. The numerical predictions performed with the model based on the equations of motion of dispersed cells showed good agreement with the experimental results. The proposed device has the potential for use in cell sample separation, as well as in disease detection and treatment, along with other microfluidic applications.