Characterisation of Population Pharmacokinetics and Endogenous Follicle-Stimulating Hormone (FSH) Levels After Multiple Dosing of a Recombinant Human FSH (FE 999049) in Healthy Women

Abstract

Objective

The aim of this study was to characterise the population pharmacokinetics of FE 999049, a novel recombinant human follicle-stimulating hormone (FSH), after multiple dosing in healthy women, taking into account endogenous FSH levels and the reproductive hormone dynamics.

Methods

Longitudinal measurements of FSH, luteinising hormone, progesterone, estradiol, and inhibin B levels were collected after repeated subcutaneous dosing with 225 IU of FE 999049 in 24 gonadotropin downregulated healthy women. The FSH data were described using nonlinear mixed-effects modelling.

Results

The measured FSH levels were modelled as a sum of endogenous FSH and FE 999049. The FE 999049 population pharmacokinetics were best described using a one-compartment model with first-order absorption and elimination, and a transit model for delayed absorption. The apparent clearance and volume of distribution increased with body weight in accordance with an allometrically scaled power exponent of 0.75 and 1, respectively. Endogenous FSH levels were lower in individuals with higher progesterone levels at baseline and were further suppressed over time with increasing inhibin B levels.

Conclusions

This characterisation of FE 999049 population pharmacokinetics after repeated dosing is in line with previous findings after single-dose administration. The results provide a basis for study design and data evaluation in the future development of recombinant FSH products, and show it can be of importance to account for endogenous FSH levels and its variation over time for accurate estimation of exogenously administered FSH pharmacokinetic parameters. Thus, correcting FSH concentrations by the observed endogenous FSH baseline value at all time points may be incorrect.

Key Points

The multiple-dose pharmacokinetics of FE 999049 have been described, accounting for endogenous follicle-stimulating hormone (FSH) levels.

Exposure to FE 999049 was influenced by body weight, which may be a potential factor for individualised dosing recommendations.

Endogenous FSH levels were influenced by progesterone and inhibin B levels. This time-varying contribution of endogenous FSH may be important to consider when characterising the pharmacokinetics of recombinant FSH products.

Introduction

Follicle-stimulating hormone (FSH) is a gonadotropin that is synthesised and secreted by the anterior pituitary gland. The major function of FSH is to regulate the reproductive processes by stimulating the gonads. In females, FSH stimulates follicular development in the ovaries and production of inhibin B, progesterone, and oestrogens by the ovarian follicular granulosa cells. Luteinising hormone (LH), another gonadotropin from the anterior pituitary, stimulates the theca cells of the follicles to deliver androgens to the granulosa cells for conversion to oestrogens. It is also responsible for ovulation of the dominant follicle that has reached a fully mature, pre-ovulatory stage. The ovarian hormones promote further follicular development as well as exerting negative and positive feedback loops to the hypothalamus and pituitary affecting the gonadotropin production and secretion. In addition, gonadotropin secretion is stimulated by gonadotropin-releasing hormone (GnRH) produced in the hypothalamus.

Female infertility can be caused by numerous factors at any level, from the hypothalamus to the ovaries and uterus. Gonadotropin therapy with either menotropins or recombinant FSH (rFSH) preparations can be used for infertility treatment when the cause is not primary ovarian failure, such that the ovaries are still responsive and contain primordial follicles. The purpose of controlled ovarian stimulation with daily administration of gonadotropins prior to assisted reproductive technologies such as in vitro fertilisation (IVF) or intracytoplasmic sperm injection (ICSI) is to obtain an adequate number of oocytes per retrieval, with minimum risks for the patient [1]. An appropriate ovarian response leading to the availability of several embryos makes it possible to select the best one(s) for transfer.

Recently, a novel recombinant human FSH (rhFSH; FE 999049, Ferring Pharmaceuticals A/S) was expressed for the first time in a human cell line (PER.C6^®; Crucell, Leiden, The Netherlands), while existing rFSH preparations in clinical use (e.g. follitropin-α and follitropin-β) are derived from Chinese hamster ovary cell lines (CHO). Previously, in a population pharmacokinetic analysis of first-in-human data after single ascending doses [2], body weight was identified as a factor that negatively correlates with serum FE 999049 concentration. In the present work, the FE 999049 population pharmacokinetics were characterised after multiple dosing. The influence of body weight on drug exposure was investigated in order to further explore its importance as a factor for individualised FE 999049 dosing. Moreover, endogenous FSH levels may vary over time across the target patient group of infertile women, which may be an important aspect to consider in rFSH drug development and when analysing hormone data. The endogenous FSH contribution to the total FSH levels, and the influence of other reproductive hormones on the endogenous FSH levels, were therefore also evaluated in this analysis.

Methods

Clinical Trial Design and Data

Data were generated in a randomised, double-blind, active control, multiple-dose trial with the aim of investigating the safety, tolerability, immunogenicity, pharmacokinetics, and pharmacodynamics of FE 999049 in healthy women. The trial was performed according to the Helsinki declaration and good clinical practice, and was approved by regulatory authorities and local Ethics Committees. All subjects gave written informed consent to participate. The trial has been described in more detail in a recent publication comparing the pharmacokinetic and pharmacodynamic properties of FE 999049 and GONAL-F (follitropin-α; EMD Serono, Inc., Rockland, USA) using non-compartmental analysis (NCA) [3]. Briefly, 49 healthy women were administered daily subcutaneous doses of 225 IU rFSH for 7 days; 24 of the 49 women were treated with FE 999049 and 25 women received GONAL-F as an active comparator. Prior to the trial (day −28 and −14), subjects were administered two doses of a GnRH agonist (LUPRON DEPOT, 1-month depot) to downregulate endogenous FSH.

Blood samples for FSH, inhibin B, estradiol, progesterone, and LH measurements were collected at 60 and 30 min prior to administration of FE 999049, immediately before administration, and once daily for 15 days. In addition, after administration of the last dose on day 6 and until day 8, the FSH concentration was measured every 4 h. Analysis of serum FSH concentrations was performed at Ferring Pharmaceuticals A/S using a validated immunoassay based on electrochemiluminescence (MSD sector™ Imager 2400) with a lower limit of quantification (LLOQ) of 0.075 µg/L.

The present analysis included data from the 24 women receiving FE 999049. Three of the 672 FSH measurements (0.4 %) were below the quantification limit and were excluded from further analysis. The personal demographics and baseline characteristics for the included subjects are listed in Table 1. Subjects with missing hormone baseline values were given the median population baseline value. Between days 6 and 8, FSH was measured every 4 h, and the other hormones were measured only once daily, leaving missing hormone values in between. To fill out the extra time points, the last measured hormone values were carried forward.

Table 1.

Summary of subject characteristics

	Mean	(Range)
Age (years)	31.1	(21.5–38.7)
Height (cm)	163.5	(149.0–175.3)
Weight (kg)	71.5	(46.1–86.6)
BMI (kg/m2)	26.6	(20.8–28.9)
FSH (µg/L)	0.211	(0.089–0.376)
E2 (pg/mL)	24.21	(7.0–55.0)
LH (IU/L)	0.719	(0.1–1.4)
Prog (µg/L)	0.652	(0.08–1.49)
InhB (pg/mL)	22.0	(4.0–89.0)

Demographics and measured baseline hormone levels for the 24 subjects receiving FE 999049

BMI body mass index, FSH follicle-stimulating hormone, E2 estradiol, LH luteinising hormone, Prog progesterone, InhB inhibin B

Pharmacokinetic Modelling

The pharmacokinetic model was developed using nonlinear mixed-effects modelling, where both the population parameters, interindividual variability (IIV), and residual errors are estimated. For parameters with IIV, the ith subject’s individual parameter (θ_i) is log-normally distributed:

$${\mathit{\theta }}_i=\mathit{\theta }exp\left({\mathit{\eta }}_i\right)$$ 1

where θ is the typical population parameter and η_i is the individual random effect from an approximately normal distribution with mean zero and variance ω² for describing the IIV of the parameter. In the model, potential influential factors can be tested for significance as a covariate to explain some of the IIV in a parameter. Thus, the set of individual parameters (Θ_i) is given as a function of the typical population parameters (Θ) individual values of the covariates (c_i) and random effects (η_i):

$${\mathit{\Theta }}_i=g\left(\mathit{\Theta },{\mathbf{c}}_i,{\mathit{\eta }}_i\right)$$ 2

The residual errors (ε) are assumed normally distributed with mean zero and variance σ², and are the unexplained deviations of model predictions from the observations:

$$y_{ij}=f\left(t_{ij},{\mathit{\Theta }}_i\right)+{\mathit{\epsilon }}_{ij}$$ 3

where y_ij is the observation at time t_ij and the subscript ij denotes the jth number for subject i. The individual model prediction f (·) at time t_ij is calculated from the individual parameters (Θ_i).

Model development was guided by changes in the NONMEM objective function value (OFV), precision of parameter estimates, and graphical model goodness-of-fit assessments, including visual predictive checks (VPC). In the VPC, the observed data are compared with model predictions based on 1000 simulated trial datasets using the final model. It displays the observations and the 2.5th, 50th, and 97.5th percentiles of observations, and the 95 % confidence intervals (CI) for the corresponding model predictions are plotted. The OFV is approximately proportional to −2log likelihood. The difference in OFV (dOFV) between two nested models is approximately Chi square-distributed, with degrees of freedom (df) equal to the difference in the number of parameters. Based on this, the statistical significance for inclusion/exclusion of a model parameter can be judged. A significance level of 0.05 was used for discrimination among nested models and covariate testing, corresponding to a 3.84 change in OFV for 1 df.

Measurable FSH levels before drug administration indicated that endogenous FSH was not fully suppressed in this trial. The total FSH amount at time t in the central compartment was therefore modelled as the sum of the endogenous FSH and the exogenously administered rhFSH (FE 999049):

$$\text{FSH}(t)={\text{FSH}}_{\text{en}}\left(t\right)\text{+ rhFSH}\left(t\right)$$ 4

The endogenous FSH was assumed to have the same elimination rate constant from the central compartment as FE 999049; thus, the total FSH is eliminated from the central compartment with rate constant k given by clearance (CL) divided by volume of distribution (V). Since data are obtained after subcutaneous dosing, the bioavailability (F) is not known. The CL and V estimated here are therefore the apparent CL (CL/F) and apparent V (V/F).

The change in endogenous FSH amount over time in the central compartment was described as a turnover model with a zero-order production rate k_in:

$$\frac{{\text{dFSH}}_{\text{en}}\left(t\right)}{\text{d}t}=k_{\text{in}}-k·{\text{FSH}}_{\text{en}}\left(t\right)$$ 5

At time zero, before rhFSH dosing, the measured concentration in the central compartment is purely endogenous FSH. The endogenous FSH baseline concentrations (FSH_bl) for each subject can therefore be estimated as the initial concentration in the central compartment and is the initial condition for the differential equation for the central compartment FSH_bl·V/F, i.e. the individual endogenous FSH amount at baseline. When assuming steady state and hence zero change in the total FSH concentration before dosing, individual values of k_in can be calculated from the other estimated parameters and baseline values.

One- and two-compartment models were tested for describing the distribution of FE 999049. A lag-time and transit compartments were investigated for modelling a potential delay in the absorption process. Body weight, age, and hormone (estradiol, inhibin B, progesterone) values at baseline were tested as potential covariates, explaining some of the IIV in parameter estimates. Inhibin B was also tested as a covariate over time since it has a purely inhibitory effect on FSH. The measured hormone levels were assumed to not affect the rhFSH concentration, but only tested as covariates on the endogenous FSH baseline parameter (FSH_bl). Besides a decrease in OFV, the significance of a covariate was also evaluated by looking at the reduction in the IIV, measured as a coefficient of variation (CV) for the parameter’s random effect.

Software

The models were implemented and parameters estimated in NONMEM 7.2.0 (Icon Development Solutions, Ellicott City, MD, USA) [4]. Data handling and graphical representations were performed in R version 2.11.1 [5]. VPCs were performed using PsN [6, 7] and plotted using Xpose [8].

Results

The best structural model was a one-compartment distribution model. The FE 999049 absorption was found to be delayed, and a one-compartment transit model best described the process. Endogenous FSH contributed significantly to the total FSH concentration in the central compartment. Observed inhibin B levels [InhB(t)] suppressed endogenous FSH production rate (k_in) over time when introduced in the model as a time-varying covariate. The relationship was found to be best described by an inhibitory E_max model, also know as an I_max function, expressed as a fractional inhibition with complete inhibition possible and a parameter InhB_ef as the inhibin B concentration giving 50 % inhibition [see Eq. (8)].

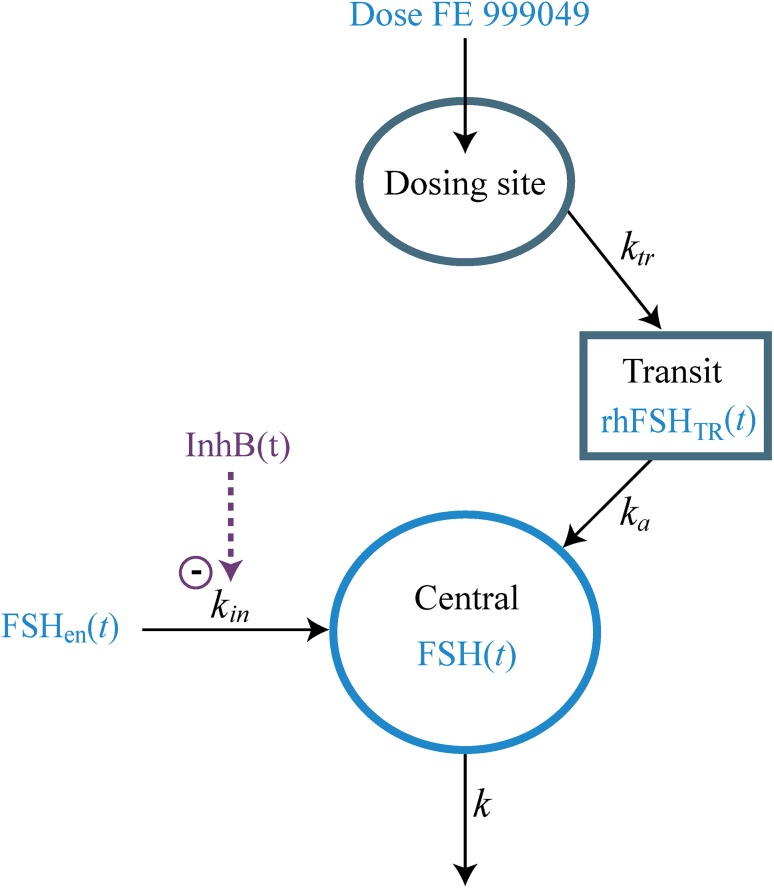
The full compartment model is illustrated in Fig. 1 and the corresponding differential equations are as follows:

$$\frac{{\text{drhFSH}}_{\text{DS}}\left(t\right)}{\text{d}t}=-k_{\text{tr}}·{\text{rhFSH}}_{\text{DS}}\left(t\right)$$ 6

$$\frac{{\text{drhFSH}}_{\text{TR}}\left(t\right)}{\text{d}t}=k_{\text{tr}}·{\text{rhFSH}}_{\text{DS}}\left(t\right)-k_a·{\text{rhFSH}}_{\text{TR}}\left(t\right)$$ 7

$$\frac{\text{dFSH}\left(t\right)}{\text{d}t}=k_{\text{in}}·\left(1-\frac{\text{InhB}(t)}{\text{InhB}(t)+{\text{InhB}}_{\text{ef}}}\right)+k_a·{\text{rhFSH}}_{\text{TR}}\left(t\right)-k·\text{FSH}\left(t\right)$$ 8

where rhFSH_DS(t) and rhFSH_TR(t) are the FE 999049 amounts at the dosing site and in the transit compartment, respectively, and k_tr is the absorption rate from the dosing site to the transit compartment. Equation (8) describes the change in total FSH amount in the central compartment, with the endogenous FSH contribution as the first term. The exogenously administered rhFSH enters the central compartment with rate constant k_a.

Fig. 1.

Compartment diagram illustrating the pharmacokinetic model for FE 999049 with a contribution of endogenous FSH to the central compartment. FSH follicle-stimulating hormone, rhFSH recombinant human FSH, FSH _en (t) endogenous FSH amount, InhB(t) inhibin B level, rhFSH _TR (t) rhFSH amount in the transit compartment, FSH(t) total FSH amount in the central compartment, k _in endogenous FSH production rate, k _tr absorption rate from the dosing site, k _a absorption rate from the transit compartment, k elimination rate

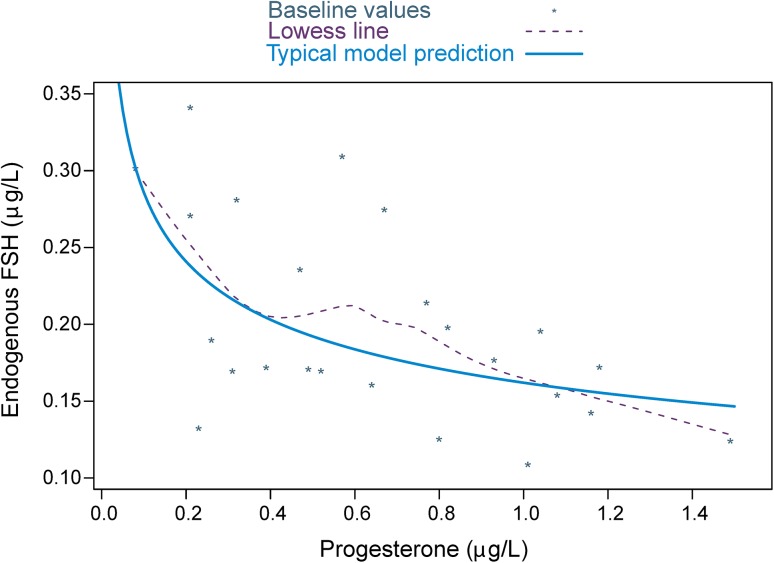
IIV was introduced for CL/F, V/F, k_tr, and FSH_bl. The variances of the IIV on CL/F and V/F were positively correlated. Body weight was an allometrically scaled covariate at CL/F and V/F, with the power exponents fixed to 0.75 and 1, respectively. Adding body weight as a covariate reduced CV for the unexplained IIV from 18.1 to 15.6 % CV for CL/F, and from 22.0 to 18.4 % CV for V/F. A trend towards lower estimated FSH baseline levels was seen in individuals with higher progesterone baseline levels (Fig. 2). The progesterone baseline effect was confirmed to be a statistically significant covariate when modelled as an inhibitory power function at the FSH_bl parameter. This decreased IIV in FSH_bl from 32.6 to 27.8 % CV.

Fig. 2.

The relationship between endogenous FSH and progesterone at baseline. Points are individual-predicted FSH_bl values and observed progesterone baseline values with a smooth LOWESS trend line (broken line). The solid line is the power function used in the model describing the typical population relationship for the effect of progesterone baseline at the parameter FSH_bl. FSH follicle-stimulating hormone, FSH _b1 endogenous FSH baseline

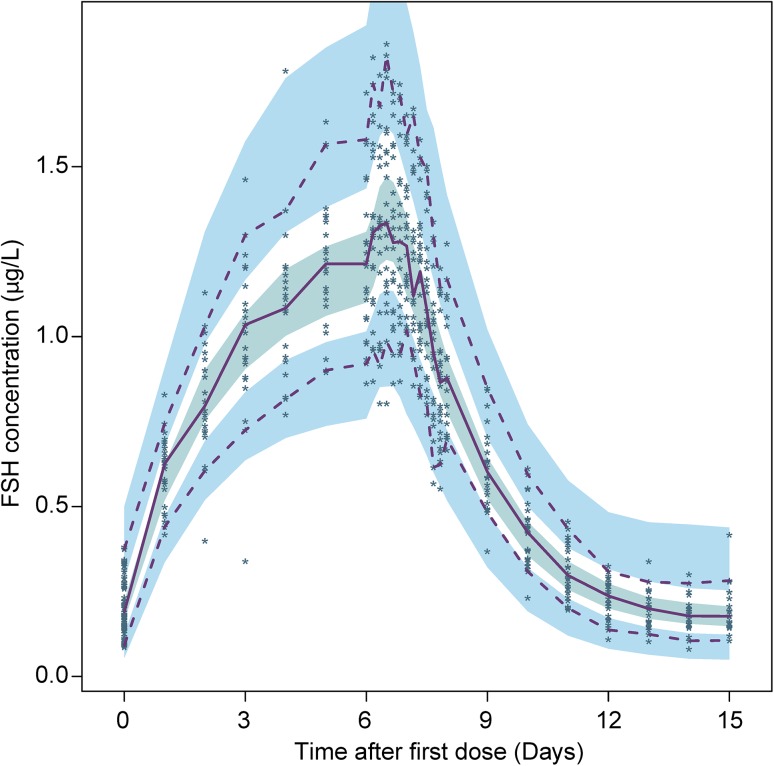
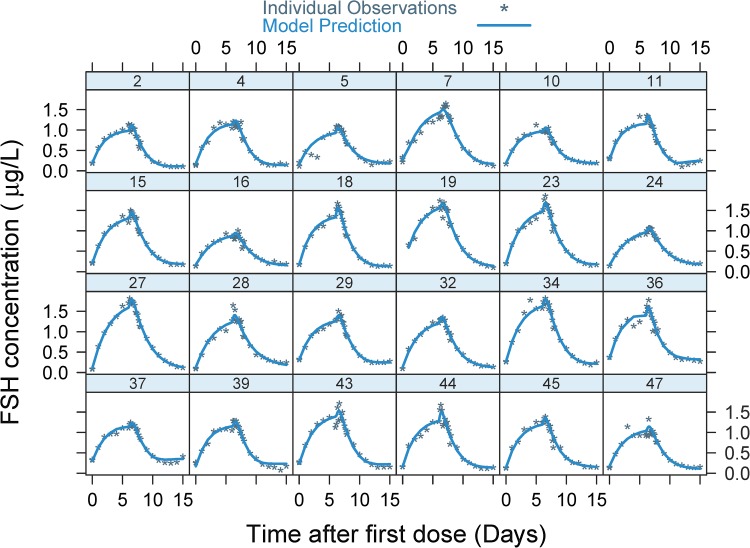
A combined additive and proportional error model was used to describe the residual error. The final model parameter estimates are displayed in Table 2. The VPC plot (Fig. 3) based on 1000 simulations, shows that the model overall adequately predicts the FSH concentrations over time, with appropriate variation. The model also satisfactorily predicted the individual pharmacokinetic profile for each subject in the trial (Fig. 4). The typical population CL/F and V/F for a 65-kg woman were 0.423 L/h and 24.3 L, respectively, giving an elimination rate of 0.017 h⁻¹ and a terminal half-life of 40 h. When the best model was found in a forward development process, it was checked to see if all the elements were still significant or if the model could be reduced. Table 3 describes the resulting increase in OFV after removing the elements. No reduction was possible since the dOFV was a minimum of 7 and up to 78.

Table 2.

Pharmacokinetic parameter estimates

Parameter	Estimate	(RSE%)	IIV CV%	(RSE%)	Shrinkage (%)
CL/F (L/h)	0.423	(3.9)	15.6	(12.7)	−1.05
V/F (L)	24.30	(4.6)	18.4	(14.4)	2.80
k tr (h−1)	0.329	(17.0)	83.4	(24.1)	24.6
k a (h−1)	0.148	(13.2)
FSHbl (µg/L)	0.162	(9.1)	27.8	(16.5)	5.51
Progblef	−0.246	(34.7)
InhBef	100	(37.2)

Typical population parameter estimates obtained from modelling

For CL/F and V/F the value is the typical value for a woman weighing 65 kg

RSE relative standard error, IIV interindividual variability, CV coefficient of variation, F bioavailability, CL/F apparent clearance, V/F apparent volume of distribution, k _tr absorption rate from the dosing site, k _a absorption rate from the transit compartment, FSH _bl endogenous follicle-stimulating hormone baseline, Progbl _ef power exponent for progesterone baseline covariate effect, InhB _ef inhibin B time-varying covariate effect

Fig. 3.

Visual predictive check for the final model, showing the individual observed FSH concentrations (points) and the 2.5th, 50th, and 97.5th percentiles of observations (lines). The shaded areas are the 95 % confidence intervals for the 2.5th, 50th, and 97.5th percentiles of the simulations. FSH follicle-stimulating hormone

Fig. 4.

Individual model fit with observed (points) and predicted (lines) total FSH concentrations versus time. The number at each subplot is the subject identification number. FSH follicle-stimulating hormone

Table 3.

Change in objective function value for reduced models

Removing	df	dOFV
WT at V/F	0	14.36
WT at CL/F	0	12.61
WT at CL/F and V/F	0	8.91
cov (CL/F, V/F)	1	11.77
Progesterone effect	1	7.01
Inhibin B effect	1	78.01

The resulting dOFV when removing covariates or the correlation between CL/F and V/F [cov(CL/F,V/F)]

F bioavailability, CL/F apparent clearance, V/F apparent volume of distribution, WT body weight, df degrees of freedom, dOFV difference in objective function value

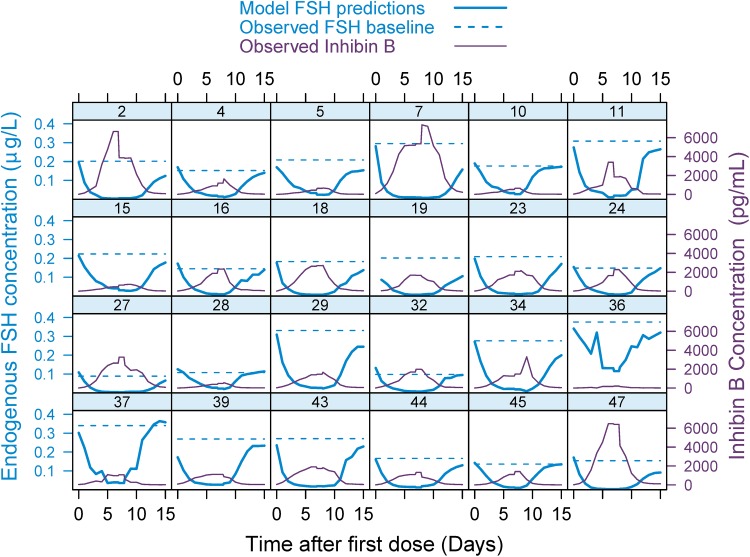
In order to see what difference accounting for endogenous FSH in the model makes, the individual concentration–time profiles for the model-predicted endogenous FSH level were compared with when the observed endogenous FSH baseline was assumed to be constant throughout the trial (Fig. 5). Due to the suppression by observed InhB(t) over time, the predicted endogenous FSH levels were lower than the observed baselines. Furthermore, accounting for inhibin B suppression of the endogenous FSH contribution over time increased the V/F estimate from 18.9 to 24.3 L. Not including inhibin B as a covariate in the final model resulted in an increase from 83.4 to 164.9 % CV at k_tr.

Fig. 5.

Individual hormone concentration profiles over time. The broken blue line indicates the observed endogenous FSH baseline level when assuming it to be constant throughout the trial, and the solid blue line is the model-predicted endogenous FSH level when accounting for the suppression caused by the observed inhibin B levels (purple line) over time, as identified by the model. The number at each subplot is the subject identification number. FSH follicle-stimulating hormone

Discussion

The FE 999049 population pharmacokinetics have previously been characterised after single-dose administration using a one-compartment model. The results were in agreement with modelling results from the literature [2]. In accordance with those results, the current analysis showed that after multiple FE 999049 dosing, the population pharmacokinetics were also best described by a one-compartment model with first-order elimination and absorption through a transit compartment. A correlation between CL/F and V/F was observed, and body weight was an allometrically scaled covariate for both CL/F and V/F. Hereby, it was confirmed that lower average steady-state drug exposure in females correlates with higher body weight after repeated doses, which is in agreement with single-dose FE 999049 results.

In contrast to the single-dose trial, FSH downregulation in this trial was not complete since a measurable endogenous FSH level was detected before any drug administration. The observed endogenous FSH contributes to total FSH measurements and thereby affects the evaluation of rhFSH concentrations in the trial; thus, it had to be accounted for in the model. To adjust the model accordingly, it was necessary to add an endogenous supply of FSH to the central compartment for proper prediction of the total FSH concentration.

When evaluating the pharmacokinetics of drugs that are naturally occurring substances, data are often baseline corrected in order to get values representing only the exogenously administered drug. However, when dealing with hormones, fluctuations from the endogenous baseline value over time may be observed due to various feedback control systems. Even with gonadotropin downregulation, the endogenous FSH level will most likely change over time as progesterone, inhibin B, and estradiol exert inhibitory and stimulatory feedback loops at the production and release of gonadotropins. The potential impact of varying endogenous FSH levels at the pharmacokinetic assessment of FE 999049 was tested by incorporating different covariate relationships in the model. Before any drug was administered, there was a tendency towards a decreased endogenous FSH baseline with increasing progesterone baseline. A power function for the relation between progesterone baseline and FSH_bl was shown to be significantly better than using a linear, an exponential, or an I_max function. When introduced as a time-varying covariate, inhibin B was found to suppress the endogenous FSH production rate over time, with an I_max function being the most significant relationship. When accounting for the inhibitory effect of inhibin B over time, the resulting model-predicted endogenous FSH concentration profiles indicated that the observed FSH baseline is an overestimate of the endogenous FSH level at all time points other than zero (Fig. 5). As a consequence, the drug concentration would be underestimated if the data were baseline corrected. When multiple covariates and correlations have been added to the model, it is possible that initial significant relations have become redundant and hence can be removed from the model. It was therefore checked whether the model could be reduced. Removing any relations resulted in an increase in OFV, and thus all relations were still significant. Removing body weight from both CL/F and V/F increased OFV less than removing body weight from only one of these parameters, which could be due to the fact that there is a correlation between the two parameters.

The population pharmacokinetic parameters estimated with nonlinear mixed-effect modelling for single and multiple doses of FE 999049 are similar. In the modelling of single-dose data, CL/F and V/F for a 65 kg woman were found to be 0.430 L/h and 28.0 L, respectively [2], with a resulting terminal half-life of 45 h. In this trial, CL/F was 0.423 L/h and V/F was 24.3 L. By incorporating the inhibin B dynamics into the model, and suppressing the endogenous FSH contribution instead of letting the FSH baseline be constant throughout the trial, V/F increased from 18.9 to 24.3 L, suggesting that without proper estimation of endogenous FSH levels over time a bias in V/F may be obtained. The terminal half-life in the current analysis was estimated to be 40 h, thus slightly shorter than the 45 h reported after single-dose administration. The phenomenon of shorter half-life after repeated subcutaneous dosing compared with single administration was also observed using NCA-based methods for analysing different FE 999049 datasets, but could not be further explained [3].

The CL/F for other rFSH products has been found to be 0.99 L/h [3] and 0.71 L/h [9]; thus, our estimated CL/F for FE 999049 is consistently lower. Furthermore, the terminal half-life of FE 999049 is longer than reported values in the literature for repeated subcutaneous dosing of rFSH products, which is approximately 24 h [3, 10]. In the same studies, a longer terminal half-life has been reported after single subcutaneous dosing (34.5 [3] and 27 h [10]). One study [11] found a terminal half-life of 59 h after single subcutaneous dosing of 115 IU rFSH; however, they noted that the estimate was not reliable since the low dose only gave a concentration slightly over baseline.

This work shows that when subjects have measurable endogenous FSH levels, total FSH concentration is affected, and the endogenous FSH level varies over time as a consequence of the feedback from ovarian hormones. If not accounting for this in the model, the pharmacokinetic parameter estimates can be biased. The inclusion of endogenous hormones in the model might be even more important in the target patient group since they are likely to have higher endogenous FSH baseline levels as they will not be pituitary downregulated or suppressed. In addition, the variation in endogenous FSH levels over time could be very different between patients due to their different types of infertility, which might affect the reproductive hormone dynamics differently. Characterising the endogenous FSH level and considering the hormone dynamics is therefore important as it could have clinical relevance for the dose needed.

In summary, this early characterisation of FE 999049 population pharmacokinetics after repeated dosing is in line with previously reported findings of rhFSH population pharmacokinetics after single-dose administration. The results provide a basis for study design and data evaluation considerations in the future development of rFSH products. The standard method of baseline-correcting data for rFSH products has been questioned since the model indicates that endogenous FSH significantly affects the total FSH concentration and varies over time.

Conclusions

The multiple-dose FE 999049 population pharmacokinetics were in agreement with results obtained after single-dose administration [2]. It was confirmed that after repeated drug administration, FE 999049 exposure also appears lower in females with a higher body weight. These findings add to the evidence of body weight being an important factor in designing individualised dosing schemes.

This analysis indicates that the inclusion of endogenous FSH levels and quantifying the influence of the reproductive hormone dynamics at the endogenous FSH level over time may well be essential for proper estimation of the pharmacokinetic parameters for FSH preparations. The standard method of baseline-correcting data does not account for a variation during the trial and could potentially cause an underestimation of serum drug concentration and hence inaccurate parameter estimation.

To better explore and link the time-varying impact of inhibin B on endogenous FSH levels, a more mechanistic modelling approach may be warranted for including indirect delayed response and hormone feedback mechanisms in a pharmacokinetic–pharmacodynamic model, and simultaneously quantifying the inhibin B response to rhFSH stimulation. The relevance of endogenous hormone levels should also be related to other pharmacodynamic and clinical endpoints in order to establish its significance.

Compliance with Ethical Standards

Funding

This work was supported by Innovation Fund Denmark (Industrial PhD Case Number 11-117436).

Conflict of interest

Trine Høyer Rose, Daniel Röshammar, Lars Erichsen, and Lars Grundemar are all current or former employees of Ferring Pharmaceuticals A/S. Johnny T. Ottesen has no conflicts of interest to declare.

Ethical approval

All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.

Informed consent

Informed consent was obtained from all individual participants included in the study.