Population Pharmacokinetic Modelling of FE 999049, a Recombinant Human Follicle-Stimulating Hormone, in Healthy Women After Single Ascending Doses

Abstract

Objective

The purpose of this analysis was to develop a population pharmacokinetic model for a novel recombinant human follicle-stimulating hormone (FSH) (FE 999049) expressed from a human cell line of foetal retinal origin (PER.C6^®) developed for controlled ovarian stimulation prior to assisted reproductive technologies.

Methods

Serum FSH levels were measured following a single subcutaneous FE 999049 injection of 37.5, 75, 150, 225 or 450 IU in 27 pituitary-suppressed healthy female subjects participating in this first-in-human single ascending dose trial. Data was analysed by nonlinear mixed effects population pharmacokinetic modelling in NONMEM 7.2.0.

Results

A one-compartment model with first-order absorption and elimination rates was found to best describe the data. A transit model was introduced to describe a delay in the absorption process. The apparent clearance (CL/F) and apparent volume of distribution (V/F) estimates were found to increase with body weight. Body weight was included as an allometrically scaled covariate with a power exponent of 0.75 for CL/F and 1 for V/F.

Conclusions

The single-dose pharmacokinetics of FE 999049 were adequately described by a population pharmacokinetic model. The average drug concentration at steady state is expected to be reduced with increasing body weight.

Key Points

The population pharmacokinetics of the novel recombinant human follicle-stimulating hormone FE 999049 have been characterised in healthy females after single ascending dosing.

Follicle-stimulating hormone measurements below the quantification limit were accounted for by the model.

Body weight influences exposure to FE 999049 and may be an important factor for dosage considerations.

Introduction

The female reproductive function is controlled by periodically regulated production, secretion and interaction of hormones in the hypothalamic–pituitary–gonadal axis. Of particular importance are the two gonadotropins: follicle-stimulating hormone (FSH) and luteinising hormone (LH), both of which are released from the anterior pituitary gland upon stimulation by gonadotropin-releasing hormone (GnRH) from the hypothalamus. During the normal menstrual cycle, the combined actions of FSH and LH induce development of a single dominant follicle, ovarian hormone production, oocyte maturation and ovulation.

In the management of infertility, exogenous FSH administration is used to induce monofollicular development and ovulation in anovulatory women [1], or multiple follicular development to allow selection of embryos for transfer in women undergoing in vitro fertilisation (IVF)/intracytoplasmic sperm injection (ICSI) treatment [2].

Urinary menopausal gonadotropin preparations that contain both FSH and LH activity are being extensively used for controlled ovarian stimulation (COS) in IVF/ICSI treatment. In 1989, advances in DNA technologies enabled development of a recombinant FSH (rFSH) generated in Chinese Hamster Ovarian (CHO) cell lines which expressed the genes encoding human FSH [3]. Since then, several rFSH products have been marketed including two original rFSH compounds originating from CHO cell lines [4, 5] and a long-acting rFSH [6].

A novel recombinant human FSH (rhFSH, FE 999049) expressed from a human foetal retinal cell line (PER.C6^®, Crucell, Leiden, The Netherlands) is under development by Ferring Pharmaceuticals A/S for patients undergoing COS for IVF/ICSI. FE 999049 has a lower clearance compared with an rFSH from a CHO cell line, as would be expected since FE 999049 has higher sialic acid content and is thus more similar to natural FSH in the human body [7]. Dose proportionality has been shown for maximum concentration (C_max) and area under the concentration–time curve (AUC) by non-compartmental analysis (NCA) of data from both a single ascending dose phase 1 trial with Caucasian women and one with Japanese women [8]. The purpose of this analysis was to describe the population pharmacokinetics of FE 999049 based on the Caucasian trial in Olsson et al. [8]. When using a population modelling approach with nonlinear mixed effects models, as opposed to NCA, it is possible to investigate variation in the population and to identify potential covariates explaining some of the variability in drug exposure. Moreover, the development of a population pharmacokinetic (PK) model can be of importance for the design of subsequent clinical FE 999049 trials and provide a basis for further model development of emerging data.

Materials and Methods

Clinical Trial Design

The first-in-human trial with FE 999049 was a randomised, double-blind, placebo-controlled, sequential single-dose escalation trial investigating the safety, tolerability and pharmacokinetics. The trial was carried out in accordance with the Declaration of Helsinki and Good Clinical Practice. It was approved by regulatory authorities and local ethics committees. All subjects gave written informed consent to participate. The trial is the ‘Caucasian study’ described in Olsson et al. [8]. In summary, the trial population consisted of 40 healthy female volunteers aged 21–35 years with a body mass index (BMI) of 18–29 kg/m² (Table 1). Furthermore, the subjects had a menstrual cycle of 24–35 days, no history of ovarian dysfunction, nor any current clinically significant findings on the trans-vaginal ultrasound or gynaecological examination. They received a single subcutaneous abdominal injection of 37.5, 75, 150, 225 or 450 IU FE 999049 or placebo. In each dose group there were eight women, of whom two were given placebo.

Table 1.

Summary of subject characteristics

Dose (µg)	2.2 (n = 6)	4.4 (n = 6)	8.8 (n = 6)	13.1 (n = 6)	26.3 (n = 6)
Age (years)	30.2 (21–35)	29.5 (24–34)	26.2 (22–31)	30.2 (24–34)	27.3 (21–32)
Height (cm)	158.5 (154.9–166.0)	164.5 (157.5–175.3)	167.4 (154.9–182.9)	159.1 (152.4–162.6)	161.6 (152.4–170.2)
Weight (kg)	59.4 (51.6–75.4)	70.8 (65.9–80.3)	68.4 (51.8–90.0)	61.5 (54.5–69.1)	61.6 (52.5–68.6)
BMI (kg/m2)	23.5 (21.5–27.4)	26.2 (22.9–28.6)	24.3 (19.7–28.9)	24.3 (21.3–27.9)	23.7 (18.7–27.2)

Personal demographics for all the subjects in the five dosing groups. The values are mean with range in brackets

n Number of subjects in each group, BMI body mass index

To avoid any interference with endogenous FSH levels during the trial, all volunteers were pituitary down-regulated by means of a combined oral contraceptive (COC). To ensure similar down-regulation in all subjects, they were all switched from their COC to the same high-dose COC (OGESTREL 0.5/50, ethinyl estradiol 50 µg, norgestrel 0.5 mg, Watson Pharma Inc.) 14 days before drug administration.

Blood samples for measurement of serum FSH concentration were collected 60 and 30 min prior to administration, immediately before administration, every 4 h for the first 48 h and subsequently every day up to 9 days after administration. Determination of serum FSH concentrations was performed at Ferring Pharmaceuticals A/S with a validated immunoassay based on electrochemiluminescence (MSD sectorTM Imager 2400) with a lower limit of quantification (LLOQ) of 0.075 µg/L and an upper limit of quantification of 5.00 µg/L. The performance of the assay was within the validated specification with a bias of the quality control (QC) samples within ±7 % and an inter-assay precision ≤10 % coefficient of variation (CV).

Data

FE 999049 was dosed in IU and for this analysis converted to μg units (2.2, 4.4, 8.8, 13.1 and 26.3 μg) using the specific activity in order to estimate the serum concentrations of FE 999049 in µg/L units.

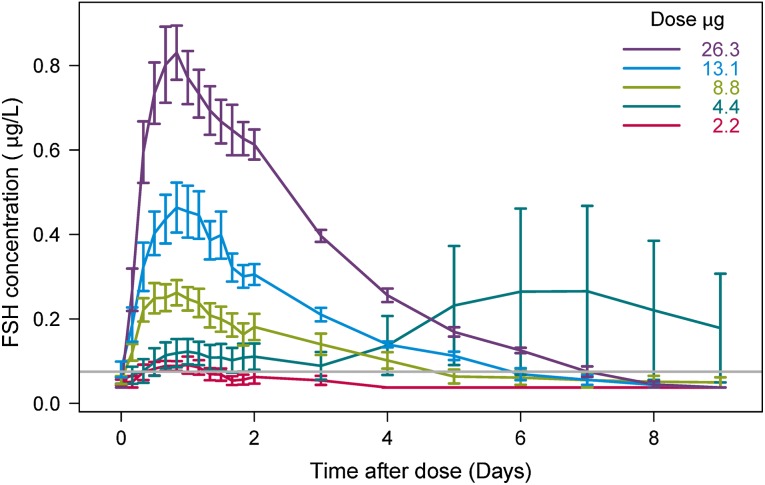
Prior to the modelling, mean serum FSH concentrations versus time were plotted for each of the five treatment groups including all subjects (Fig. 1). A second increase in FSH concentration starting at day 3 after administration was observed for the 4.4-μg dose group. From the individual concentration–time profiles (not shown), two subjects were identified to cause this increase. One subject in the 8.8-μg dose group had a second increase in FSH concentration at day 2. This late second peak indicated interference from endogenous FSH, thus their concentration–time profiles were considered not to reflect the PK profile for the exogenously administered rhFSH (FE 999049) and were excluded from the analysis. A total of 594 samples from 27 individuals were included in the analysis; 258 measurements, constituting over 40 % of the total data points, were below the quantification limit (BQL). In the 2.2, 4.4, 8.8, 13.1 and 26.3 μg dose groups, 67, 74, 39, 23 and 23 % of the measurements were BQL, respectively.

Fig. 1.

The observed FSH concentration shown as mean of all subjects with standard error (SE) bars for each treatment group. The grey line represents the LLOQ of 0.075 µg/L. Observed BQL measurements were plotted as LLOQ/2. BQL below the quantification limit, FSH follicule-stimulating hormone, LLOQ lower limit of quantification

Pharmacokinetic Modelling

A population PK model was developed using nonlinear mixed effects modelling. This included finding a structural model together with appropriate error models describing interindividual and residual variability. One- and two-compartment models were tested for the structural model. Both a lag time and transit compartments were tested for describing a potential delay in the absorption. To increase the predictive capability of the model, it was checked if part of the interindividual variability (IIV) in parameter estimates could be explained by covariates (body weight, age and dose).

Model development was guided by changes in the NONMEM objective function value (OFV), precision of parameter estimates and graphical model goodness-of-fit assessments including visual predictive checks (VPC). The OFV is approximately proportional to −2log likelihood. The difference in OFV between two nested models is approximately χ²-distributed, with degrees of freedom equal to the difference in the number of parameters. Based on this, the statistical significance for inclusion/exclusion of a model parameter can be judged. For this descriptive analysis a significance level of 0.05 was used for discrimination among nested models and covariate testing.

BQL measurements were accounted for in the analysis using the M3 method since for a high proportion of BQL it is the preferred method out of the seven existing methods [9–11]. With the M3 method, BQL data are censored observations and treated as categorical data. These are included in the likelihood function for the model parameter estimation as the likelihood that the observation is truly BQL. The sensitivity of the model parameter estimates to the BQL method used was evaluated by comparing the estimates from the final model to those estimated when the BQL measurements were ignored (M1), set to LLOQ/2 (M5), or set to zero (M7).

The final model was used for simulations to illustrate the FE 999049 concentration–time profile and steady-state exposure following repeated administration of 10 µg. The average steady-state exposure was calculated as

$$C_{\text{ss,av}}=\frac{10\mathrm{\mu }\text{g}}{\text{CL/}F\times 24\text{h}}$$ 1

Software

The models were implemented and parameters estimated in NONMEM 7.2.0 (Icon Development Solutions, USA) [12] using first-order conditional estimation with interaction. Data handling and graphical representations were performed in R version 2.11.1 [13]. VPCs were performed using PsN [14, 15] and plotted using Xpose [16].

Results

A one-compartment distribution model with first-order absorption and a transit model for adding a delay in the absorption was found to adequately describe data. The time course of serum FE 999049 concentration after dosing was described by the differential Eqs. (2)–(4), one for each of the three compartments representing the dosing site, the transit model and the central compartment, respectively.

$$\frac{\text{d}{A}_1(t)}{\text{d}t}=-k_{\text{tr}}{A}_1(t)$$ 2

$$\frac{\text{d}{A}_2(t)}{\text{d}t}=k_{\text{tr}}{A}_1\left(t\right)-k_{\text{a}}{A}_2(t)$$ 3

$$\frac{\text{d}{A}_3(t)}{\text{d}t}=k_{\text{a}}{A}_2\left(t\right)-k{A}_3(t)$$ 4

At time t, A_i(t) is the FE 999049 amount in the ith compartment. The absorption rates from the dosing site and the transit compartment are k_tr and k_a, respectively. The elimination rate of FE 999049, k, is clearance (CL) divided by the volume of distribution (V). Since it is the amount tracked in the equations, predicted serum FE 999049 concentrations are calculated as A₃(t)/V. Data is obtained after subcutaneous dosing so the bioavailability (F) is not known. The CL and V estimated here are therefore the apparent clearance (CL/F) and apparent volume of distribution (V/F). A combined additive and proportional error model was used to describe the residual error.

The parameters CL/F, V/F and k_a varied between subjects. A variation in k_tr was also observed, but given the current data it was not possible to include separate IIV on both parameters describing the absorption process. It was chosen to keep the variability on k_a because this model had the best OFV compared with the model with variability on only k_tr. For parameters with IIV, the ith subject’s individual parameter, P_i, is

$$P_i=P_{\text{tv}}exp\left({\mathit{\eta }}_i\right),$$ 5

where P_tv is the typical population parameter and η_i is the individual random effect from an approximately normal distribution with mean zero and variance ω_p² for the IIV. A positive correlation was identified between CL/F and V/F by a statistically significant improvement in OFV when adding a covariance between the two parameters.

Body weight was found to be a statistically significant covariate on CL/F and V/F and was included in the model parameters as

$$P_i=P_{\text{tv}}exp\left({\mathit{\eta }}_i\right){\left(\frac{{\text{WT}}_i}{65\text{kg}}\right)}^{{\text{AL}}_{\text{P}}}$$ 6

where WT_i is the ith subject’s body weight and AL_p is the allometric values: 0.75 for CL/F and 1 for V/F. Adding body weight as a covariate caused a drop of −2.94 in OFV which was considered significantly better since no extra parameters were added. In addition, the CV for the unexplained IIV was reduced from 31.4 to 28.2 % CV for CL/F and from 46.4 to 44.3 % CV for V/F. Not including body weight in the final model at either CL/F or V/F increased the OFV by 10.8 and 4.4, respectively. Subject’s age did not further explain any of the IIV. Neither was there any influence of dose at the parameters, indicating that the pharmacokinetics is linear.

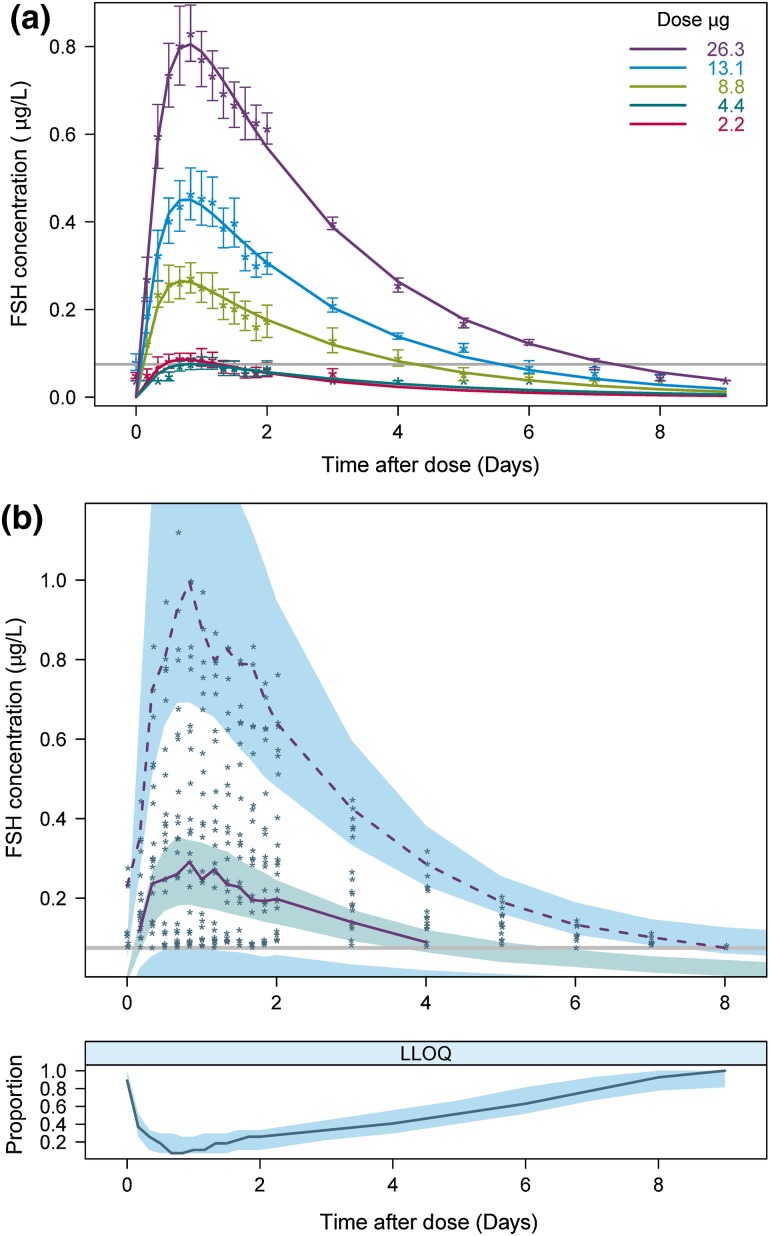
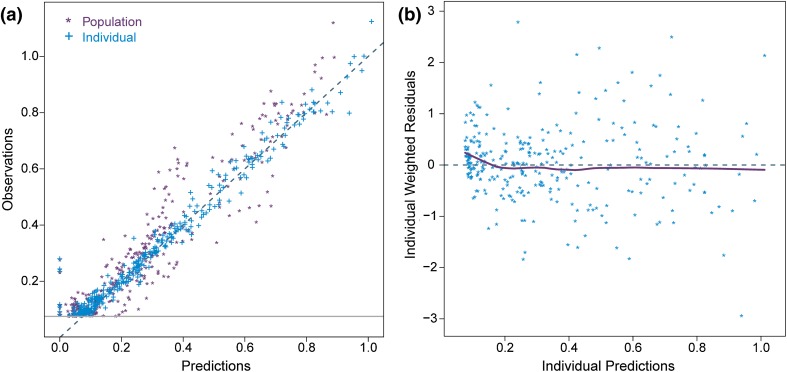
The final model had a successful estimation (3.6 significant digits) with a successful covariance step. The model parameters are listed in Table 2 with the relative standard error (RSE) calculated from the NONMEM covariance step. The mean observed FSH data and typical model predictions are shown for each dose level in Fig. 2a. In the diagnostic VPC plot (Fig. 2b), the observed data is compared with model predictions based on 1000 simulated trial datasets using the final model. Since the data consisted of more than 40 % BQL measurements that were included in the model by the M3 method, a two-panel VPC illustrating both continuous and categorical (BQL) data was used [11]. The top panel displays the observations above LLOQ. The 2.5th, 50th and 97.5th percentiles of observations and the 95 % confidence intervals (CI) for the corresponding model predictions are plotted. In the bottom panel, the observed and predicted proportions of BQL observations are visualised. Both the points for observations against individual and population predictions fall around the unity line and there is no trend observed in the model residuals (Fig. 3).

Table 2.

Pharmacokinetic parameter estimates

Parameter	Estimate	(RSE %)	IIV CV %	(RSE %)	Shrinkage (%)
CL/F (L/h)	0.430	(6.3)	28.2	(29.5)	5.31
V/F (L)	28.0	(9.1)	44.3	(20.7)	4.82
k tr (h−1)	0.517	(24.8)
k a (h−1)	0.160	(12.9)	23.3	(27.8)	31.8
Additive error (µg/L)	0.038	(26.1)
Proportional error (µg/L)	0.033	(64.9)

Typical population pharmacokinetic parameter estimates and residual error estimates obtained from modelling with the RSE calculated from the NONMEM covariance step in brackets

For CL/F and V/F, the value is the typical value for a woman weighing 65 kg

CL/F apparent clearance, CV coefficient of variation, F bioavailability, IIV interindividual variability, k _a absorption rate to the central compartment, k _tr absorption rate from the dosing site to the transit compartment, RSE relative standard error, V/F apparent volume of distribution

Fig. 2.

Model predictions compared with observations. a Points are mean of observations with standard error (SE) bars. Lines are typical model predictions for each treatment group. The grey line represents the LLOQ of 0.075 µg/L. Observed BQL measurements were plotted as LLOQ/2. b Two-panel visual predictive check for all dose groups together. The top panel shows the observations above LLOQ (points) and the 50th and 97.5th percentiles of observations (purple lines). The 2.5th percentile of observations is not shown since it solely consists of BQL points. The shaded areas are the simulated 95 % confidence intervals (CI) for the 2.5th, 50th and 97.5th percentiles. The grey line represents the LLOQ of 0.075 µg/L. In the bottom panel the blue line is the fraction of BQL observations with the 95 % CI for the median from simulations. BQL below the quantification limit, FSH follicule-stimulating hormone, LLOQ lower limit of quantification

Fig. 3.

Goodness of fit plots. a Observations against population predictions (purple points asterisks) and individual predictions (blue points plus symbol) with the unity line. The grey line represents the LLOQ of 0.075 µg/L. b Individual residuals against individual predictions (points) with a smooth lowess line. LLOQ lower limit of quantification

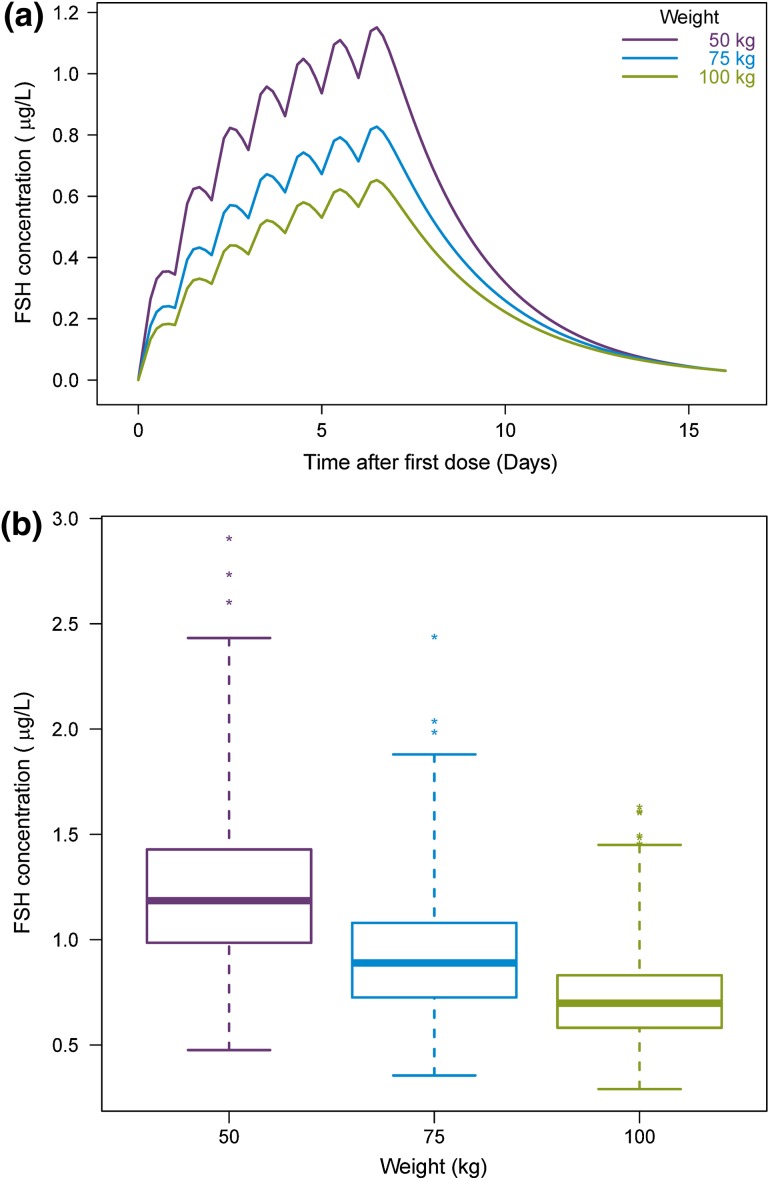
When re-estimating the final model parameters using a simpler method than M3 for handling BQL measurements, slight changes in the parameter estimates were observed. With the M1 or M5 method the PK parameters changed by <10 % from the parameters obtained with the M3 method. On the contrary, applying the M7 method instead of M3 caused greater parameter changes from the values in the final model and the RSEs increased. The largest change was an increase in the CL/F estimate by 22 % to 0.524 L and with a 4-fold increase in its RSE. Thus, M7 is the least precise method for this model. The impact of body weight on the expected FE 999049 concentration following multiple dose administration was investigated using the final model for simulations. In Fig. 4a, illustrating the time course of FE 999049 concentration in three subjects of different weights, it is shown how the concentration decreases with increasing body weight. Taking IIV into consideration, there are large overlaps in the average steady-state concentrations across the three weight groups as shown by the box plot in Fig. 4b which is based on 1000 simulations. The range for the box is the first and third quartile which are 0.99–1.43, 0.73–1.08 and 0.58–0.83 µg/L for the 50-, 75- and 100-kg weight groups, respectively. However, the FSH exposure appears to be lower in the majority of subjects with body weight of 100 kg compared with FSH levels in subjects with body weight of 50 kg. The mean average steady-state concentrations based on 1000 simulations were 1.23, 0.92 and 0.72 µg/L for the 50-, 75- and 100-kg weight groups, respectively.

Fig. 4.

Effect of body weight at the FSH concentration. a Simulation of the typical expected FSH concentration after multiple dosing of FE 999049 10 µg for three subjects with different body weights. b Boxplot of the average steady-state concentration obtained from 1000 simulations for each weight group. FSH follicule-stimulating hormone

Discussion

In the present study, population PK modelling was carried out to characterise the pharmacokinetics of FE 999049 after single ascending doses in healthy women. The objective was to get an initial understanding of the time course of drug exposure and the magnitude of IIV through a modelling approach. In addition, to optimise ovarian response to treatment with FE 999049, it was examined whether patient-specific variables can aid in the design of individualised dosing schemes.

The pharmacokinetics of FE 999049 were described by a one-compartment distribution model with first-order absorption and elimination. These findings are in accordance with previous results that have shown that FSH, either as a urinary or recombinant preparation, follows a one-compartment model after subcutaneous or intramuscular administration [17–21]. Some of these studies have found exogenous FSH pharmacokinetics to be best described by a two-compartment model if the data is ‘rich’ (i.e. with an extensive number of samples) or if doses are given intravenously [18–20]. A two-compartment distribution model was also tested here. As this was a first single-dose trial with few subjects, the limited data generated was not sufficient to give successful estimation of the extra parameters for the peripheral distribution compartment.

A transit model with one compartment was introduced to describe a somewhat prolonged absorption of FE 999049 causing an apparent delay for the measurable change in serum FE 999049 concentration. It is conceivable that this extra transit time in the absorption process could be attributed to the lymphatic system, since proteins given subcutaneously are usually absorbed through the lymphatic system [22]. It was tested whether the FE 999049 absorption could be described by alternative models. Adding an extra transit compartment in the final model increased the OFV by 0.002 and is thus worse. Using a lag time instead of a transit compartment decreased the OFV by 0.085, but these two models are not nested and the OFV cannot be compared with statistical significance. Since the models have the same number of parameters and basically no difference in either OFV or the model fit graphs, it was chosen to keep the transit model because it is more mechanistically correct than a lag time.

As part of the model development it was checked whether any covariates could be identified. Body weight was found to be the cause of some of the variation in FE 999049 concentration after treatment. It is consistent with previous analyses that have shown a relation between serum FSH and the PK parameters with body weight [17, 18, 23, 24]. In the current study, with the power exponent fixed to allometric values, body weight was a significant covariate and could explain some of the IIV in CL/F and V/F indicated by a reduction from 31.4 and 46.4 % CV to 28.2 and 44.3 % CV, respectively. The marginal effect of adding body weight as a covariate is likely due to the limited number of subjects in this first-in-human trial with a relatively narrow body-weight range. Among the potential covariates (age, body weight and dose), body weight was the only covariate identified.

Despite the high proportion of BQL points in the data, and hence the need for using the M3 method, the model was successfully estimated and appeared to be stable. When the correlation between CL/F and V/F was introduced, the model fit improved but the model became ill-conditioned. The model could be re-stabilised when the correlation between CL/F and V/F was slightly differently parameterised. The proportional error in the residual error model was low and associated with high uncertainty (RSE 64.9 %); however, the combined error model was significant better than only an additive error model, so it was kept for completeness.

In the article by Olsson et al. [8] presenting NCA results of the same data with FE 999049 as in the current work, PK parameters were calculated separately for only the three highest dosing groups. They found the mean CL/F to be 0.70, 0.50 and 0.39 L/h for the 150-, 225- and 450-IU dosing groups, respectively. From NCA of data from a repeated subcutaneous dosing trial, CL/F was significant lower for FE 999049 (0.58 L/h) compared with follitropin α (0.99 L/h) [7]. Our CL/F, estimated at 0.43 L/h for a typical female with body weight of 65 kg, falls within the range from these previous articles with FE 999049. It is also lower than CL/F for another rFSH product which has been reported from population modelling results to be 0.71 L/h [18]. Our results thus support the finding that FE 999049 may have a lower clearance than other rFSH products.

In order to avoid interference with endogenous FSH in the analysis of FE 999049 pharmacokinetics, all subjects in this trial were pituitary suppressed by means of COC. Since all pre-dose FSH measurements were BQL, the measured serum FSH concentrations were exclusively reflecting exogenous FSH from FE 999049. Nonetheless, three subjects showed an additional peak of FSH levels several days after administration of FE 999049, which could likely be due to endogenous FSH levels not being fully suppressed. These individuals were excluded from the analysis as their FSH levels were judged not to reflect the pharmacokinetics of the exogenously administered FE 999049. The initiation of the additional FSH peak occurred 3 days after FE 999049 administration, which was the day after the trial subjects were discharged from the residential stay in the clinic. A possible explanation for the later secondary increase in FSH levels could be poor compliance in taking OGESTREL after discharge from the clinic; however, such protocol deviation was not reported.

The primary utility of this model was to provide a first characterisation of rhFSH population pharmacokinetics in humans that will form a base for further model development of data from subsequent studies. In addition, the model can provide a basis for the design of future clinical studies and FE 999049 sampling schedules. It is important to note that the current findings are based on first-in-human data from a homogenous group of healthy female subjects who were pituitary suppressed. Since the range of demographic data was rather narrow compared with the target population, model adjustments are assumed to be needed for new emerging data and additional covariates explaining variability in FE99909 exposure must be screened for. In future studies where subjects are not pituitary suppressed or down-regulated, endogenous FSH levels have to be considered in the modelling, especially in phase 2 studies where patients could have varying and measurable endogenous FSH levels influencing the total FSH concentration. When available, the significance of other reproductive hormones such as inhibin B, estradiol and progesterone should also be studied. Since these hormones influence FSH levels over time, they could potentially further explain the observed variation in the FSH concentration profile between subjects. Modelling has previously been used to set two different rFSH dosage regimens for subjects weighing more or less than 60 kg [17, 25], but a higher treatment success rate could potentially be gained from further individualising dosing based on individual body weight. The identified lower drug exposure with higher body weight should be further quantified in future models from other clinical studies with repeated FE 999049 dosing and in the target patient population. It must also be related to any subsequent effects that possibly could add variability in clinical efficacy endpoints (e.g. number of oocytes retrieved, successful implantation rate and pregnancy rate) in order to judge if there is a therapeutic value in individualising dosing based on the patient’s body weight.

Conclusions

A population PK model was successfully developed for FE 999049 using data from a single ascending dosing trial in healthy female subjects. This work is of value for further PK model building of emerging PK data in subsequent clinical studies. It has provided some initial evidence for body weight potentially affecting FE 999049 exposure after single subcutaneous administration in healthy women as there were indications that FE 999049 exposure decreases with increasing body weight. When also considering findings from the literature, body weight can be an important factor to consider in efforts to develop individualised dosing regimens for optimised treatment outcomes. In order to confirm the influence of body weight at FE 999049 exposure, the model should be updated using data from subsequent clinical trials including multiple dose trials and trials involving patients where the body weight range is likely to be wider. In addition, the relationship between drug exposure and clinical efficacy/safety parameters must be established. With the increasing infertility prevalence it is important to keep improving therapies for infertility and to identify optimal strategies. This work shows the importance and usefulness of modelling and simulation in early characterisation of a drug’s pharmacokinetic properties in the clinical setting and in getting early knowledge of factors potentially influencing drug exposure.

Compliance with Ethical Standards

Funding

This work was supported by Innovation Fund Denmark (Industrial PhD case number 11-117436).

Conflicts of interest

Trine Høyer Rose, Daniel Röshammar, Lars Erichsen and Lars Grundemar are all current or former employees at Ferring Pharmaceuticals A/S. Johnny T. Ottesen has no conflicts of interest to declare.

Ethical approval

All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki Declaration and its later amendments or comparable ethical standards.

Informed consent

Informed consent was obtained from all individual participants included in the study.