Comparing Dynamic Treatment Regimes Using Repeated-Measures Outcomes: Modeling Considerations in SMART Studies

Abstract

A dynamic treatment regime (DTR) is a sequence of decision rules, each of which recommends a treatment based on a patient’s past and current health status. Sequential, multiple assignment, randomized trials (SMARTs) are multi-stage trial designs that yield data specifically for building effective DTRs. Modeling the marginal mean trajectories of a repeated-measures outcome arising from a SMART presents challenges, because traditional longitudinal models used for randomized clinical trials do not take into account the unique design features of SMART. We discuss modeling considerations for various forms of SMART designs, emphasizing the importance of considering the timing of repeated measures in relation to the treatment stages in a SMART. For illustration, we use data from three SMART case studies with increasing level of complexity, in autism, child attention deficit hyperactivity disorder (ADHD), and adult alcoholism. In all three SMARTs we illustrate how to accommodate the design features along with the timing of the repeated measures when comparing DTRs based on mean trajectories of the repeated-measures outcome.

1. Introduction

A dynamic treatment regime (DTR) [1–5] is a sequence of decision rules, each taking the current characteristics and past treatments of a patient as input, and outputting a recommended treatment. Also known as adaptive treatment strategies [6–10], treatment policies [11–13] or adaptive interventions [14], dynamic treatment regimes aim to provide treatments when patients need them; to do this, DTRs adapt the type or dosage of treatments to patients’ changing needs. DTRs are particularly useful for the treatment of chronic diseases, where the status of the individual is often waxing and waning, or in settings in which no one treatment is effective for most individuals, and thus a sequence of treatments that are adapted to the patients’ needs and conditions are often needed to achieve an improvement in health. An example DTR for improving spoken communication in children with autism spectrum disorder [15,16] is “Begin with a therapist-delivered behavioral language intervention (BLI) for 12 weeks. At the end of week 12, if a child is a slow responder, augment BLI with an augmentative or alternative communication (AAC) approach, most often a speech-generating device; otherwise, if the child shows early signs of response, continue with the first stage BLI for an additional 12 weeks.”

A vast literature is available on the methodology that can be used to inform the construction of effective DTRs with both observational data and experimental data. These methods include marginal structural models [17–21], inverse probability weighting [22], structural nested mean models [5, 23], likelihood-based methods [24], and statistical learning-based methods [25].

This manuscript focuses on statistical methods for comparing DTRs on the basis of a repeated-measures outcome observed across the multiple stages of treatment in a sequential, multiple assignment, randomized trial (SMART; [6,8,26]). In the context of the autism example, a researcher may be interested in comparing two DTRs, say, based on the trajectory of the number of socially communicative utterances collected at baseline and weeks 12, 24 and 36. Study features that are unique to SMARTs make repeated-measures modeling a challenge. In this setting, repeated-measures models must account appropriately for (i) the temporal ordering of treatments relative to outcome measurement occasions and (ii) the fact that participants may transition from one stage of treatment to the next at different time points. In this manuscript we discuss how to accommodate the features of various forms of SMART designs in modeling repeated-measures outcomes. For illustration, we use data from three SMART case studies in autism, child attention deficit hyperactivity disorder (ADHD), and adult alcohol dependence. We do this because each case study presents a progressively more complex SMART design. We generalize the weighted-and-replicated methods of Orellana and colleagues [17,19,21] to estimate the parameters in our repeated-measures models.

This paper is organized as follows. In Section 2, we describe SMART studies in more detail. In Section 3, we present and discuss general principles for modeling repeated-measures outcomes in SMART and illustrate these principles with the three SMART studies. A weighted-and-replicated estimator for the parameters in the repeated-measures marginal model is proposed in Section 4. In Section 5 we present the data analysis results for the three SMART studies. In Section 6 we report results of simulation studies illustrating the importance of modeling considerations. Finally, a discussion, including other possible ideas for modeling repeated-measures outcomes from a SMART, is presented in Section 7.

2. Sequential, Multiple Assignment, Randomized Trials

In a SMART participants proceed through multiple treatment stages, and at each treatment stage the participant may be randomized to one of several treatment options available at that stage. Each randomization is designed to address a scientific question concerning the type, dosage or intensity of the treatment at that decision point. Often, subsequent randomized treatment options in a SMART are restricted depending on the participant’s response to prior treatment. A variety of these trials have been conducted, with some of the earliest taking place in cancer research, for the purpose of developing medication algorithms for leukemia [10], or to develop adaptive treatments of prostate cancer [9]. A selection of SMART studies may be found at http://methodology.psu.edu/ra/adap-inter/projects.

In this section we present the three SMART studies that we use for illustration in this paper: the autism, ADHD and ExTENd studies. The review paper by Lei et al. [27] describes the design of each of the three studies in greater detail, including each study’s rationale, the interventions examined, and the primary and secondary aims. These designs vary in complexity, with the autism study being the least complex and the ExTENd study being the most complex of the three. The complexity in study design is in terms of the number of DTRs that are embedded in the design and the number of time points at which participants can transition from one treatment stage to another. In Section 3, we will discuss how these varying design features have implications on the choices of models for repeated measures arising from the SMART studies.

Figure 1 provides the design of the autism SMART (C. Kasari, P.I.; [16]), for the treatment of minimally verbal children with autism, aged 5 to 8 years. In this SMART, at the first stage children were randomized to BLI or BLI+AAC. Both BLI and BLI+AAC involves two one-hour long sessions per week with a language therapist. This stage lasted for 12 weeks for all children. After 12 weeks, children were classified as either early responders or slow responders to the initial treatment, according to pre-specified criterion, and made the transition to the second stage. In the second stage, early responders continued with the treatments that were assigned in the first stage. Slow responders to initial BLI+AAC received intensified BLI+AAC (increasing sessions from two to three per week). Slow responders to initial BLI were randomly assigned to either intensified BLI (increasing sessions from two to three per week) or to augmenting BLI with AAC (i.e., BLI+AAC). The second stage treatment lasted for 12 weeks.

Figure 1.

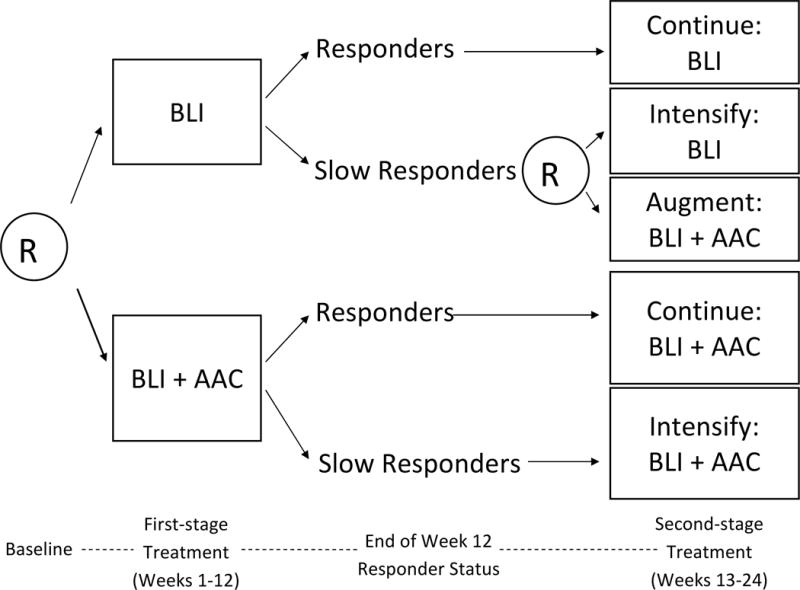
A SMART study for developing a DTR for children with autism who are minimally verbal. R = randomization. BLI = behavioral language intervention. AAC = augmentative or alternative communication approach.

SMARTs, such as the one shown in Figure 1, have a set of DTRs embedded within them. The variables that tailor the treatment assignment in these DTRs can only be the variables that are used to restrict (re-)randomization in the design of the SMARTs (e.g., the early response status in the autism SMART). In this SMART there are three embedded two-stage DTRs; they are listed in Table 1. These three embedded DTRs correspond to three different strategies of using AAC in the context of the BLI treatment: deferring the use of AAC (DTR (BLI, BLI+AAC)), withholding the use of AAC (DTR (BLI, INT)) and using AAC from the beginning (DTR (BLI+AAC, ·)). Note that some participants in SMART have treatment sequences that are consistent with more than one DTR. For example, early responders to BLI have a treatment sequence that is consistent with both (BLI, INT) and (BLI, BLI+AAC).

Table 1.

Embedded DTRs in the autism SMART.

	Label	Treatment decision rule
DTR (BLI, BLI+AAC)	(1, −1)	Begin treatment with BLI for 12 weeks. At the end of week 12, if the child does not show early signs of response, augment BLI with AAC for 12 weeks. Otherwise, continue with BLI for another 12 weeks.
DTR (BLI, INT)	(1, 1)	Begin treatment with BLI for 12 weeks. At the end of week 12, if the child does not show early signs of response, intensify BLI for 12 weeks. Otherwise, continue with BLI for another 12 weeks.
DTR (BLI+AAC, ·)	(−1, ·)	Begin treatment with BLI+AAC for 12 weeks. At the end of week 12, if the child does not show early signs of response, intensify BLI+AAC for 12 weeks. Otherwise, continue with BLI+AAC for another 12 weeks.

Figure 2 shows the design of the ADHD SMART for the treatment of children (aged 5 to 13 years with mean of 8 years) with ADHD (W. Pelham, P.I.). In this SMART, at the first stage children were randomly assigned to begin with low-intensity behavioral modification (BMOD) or with low-dose medication (MED; methylphenidate). Starting at the end of month two, children were assessed monthly for response/non-response to the initial treatment. See [27] and [28] for more details concerning the definition of response/non-response. Children who met the criteria for non-response were immediately re-randomized to either an intensified version of the initial treatment (INT) or to augmenting the initial treatment with the alternative treatment (MED+BMOD). Children who continued to respond remained on their initial treatment. Treatment duration was eight months in total for all children in the study.

Figure 2.

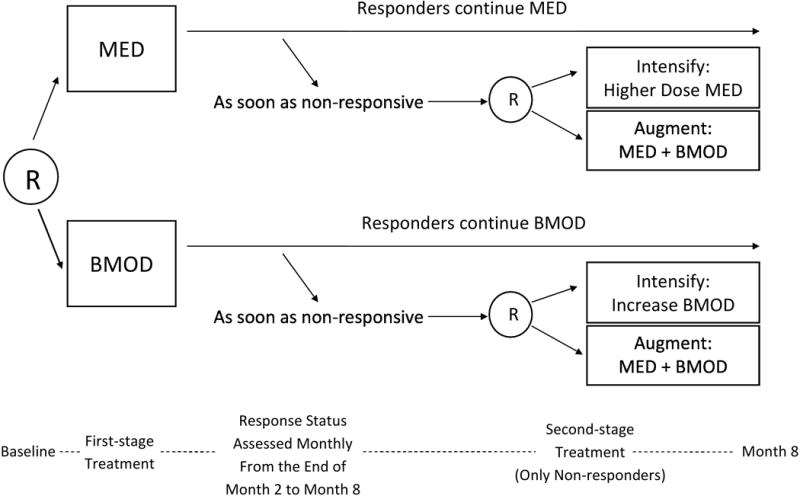
A SMART study for developing a DTR for children with attention deficit/hyperactivity disorder. R = randomization. MED = medication. BMOD = behavioral modification.

The ADHD SMART differs from the autism SMART in that the duration of stage one varied among participants. Those who met the non-response criteria at later time points transitioned to the second treatment stage later during the study, and the duration of the first treatment stage was an outcome of the initial treatment. Those who continued to respond to the initial treatment did not transition to the second stage. The ADHD SMART has four embedded DTRs, as a result of the initial randomization and re-randomization of non-responders.

Figure 3 shows the design of a third SMART study, the ExTENd SMART aiming to develop a DTR for individuals with alcohol dependence. At study entry, patients were randomized to either a stringent criterion for early non-response (two or more heavy drinking days within the first eight weeks) or a lenient criterion for early non-response (five or more heavy drinking days within the first eight weeks). All patients received open-label Naltrexone (NTX; medication, an opiate antagonist) as the initial treatment. Starting at the end of week two, patients’ early response status was assessed weekly; those who met their assigned criterion for early non-response immediately transitioned to the second stage and were re-randomized to either NTX+CBI+MM or Placebo+CBI+MM, where CBI stands for combined behavioral interventions and MM stands for medical management. Patients who did not meet their assigned non-response criterion by week eight were classified as responders and were re-randomized to either usual care (UC)+NTX prescription or telephone disease management (TDM)+NTX prescription. The second-stage treatment lasted four months.

Figure 3.

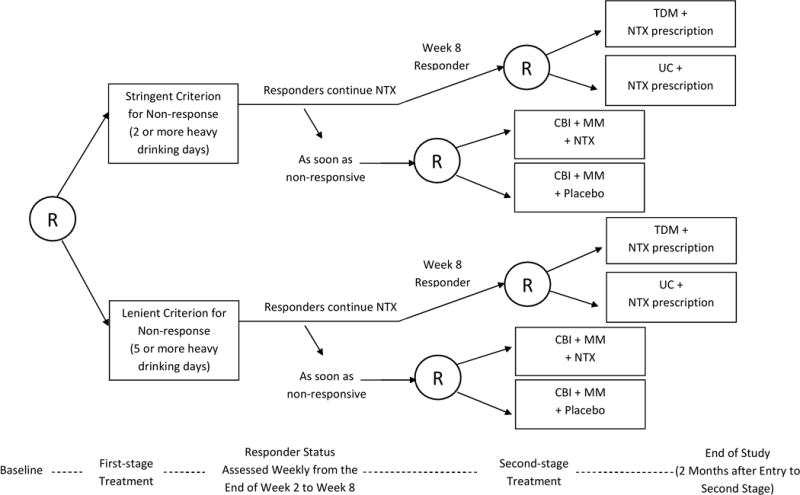
A SMART study for developing a DTR for adults with alcohol dependence. R = randomization. NTX = Naltrexone. TDM = telephone disease management. UC = usual care. CBI = combined behavioral interventions. MM = medical management.

The ExTENd SMART design is more complex than the autism and ADHD studies. Similar to the ADHD study, in ExTENd the duration of stage one varied among participants. Specifically, non-responders transitioned to stage two at any of a variety of weeks prior to week eight whereas all responders transitioned to stage two at week eight. However, in ExTENd both responders and non-responders to the initial treatment were re-randomized to subsequent treatment options. As a result, the ExTENd SMART has eight embedded DTRs.

Both responders and non-responders to the initial treatment were re-randomized to subsequent treatment options. The duration of stage one varied among participants: non-responders transitioned to stage two at any of a variety of weeks prior to week eight whereas all responders transitioned to stage two at week eight. The ExTENd SMART has eight embedded DTRs, as a result of the initial randomization and re-randomization of both responders and non-responders.

3. Repeated-Measures Marginal Model

In this section we develop marginal models for comparing the embedded DTRs in a SMART based on repeated measures. For simplicity, we focus on two-stage SMARTs; all ideas can be extended readily to SMARTs with more than two stages. By examining the three SMART studies introduced above, we will illustrate modeling considerations by varying degrees of complexity in SMART design. There has been work that compares DTRs by focusing on repeated measures that occur only after all the re-randomizations [29]; in this paper we will allow the repeated measures to span across multiple treatment stages.

For modeling and estimation purposes, we label each embedded DTR in a two-stage SMART by the pair (a₁, a₂), where a_j is used to denote a treatment option at stage j. We use contrast coding (i.e., {−1, 1}) for a_j [28, 30, 31]. For example, in the autism SMART, we let a₁ = 1 denote BLI and let a₁ = −1 denote BLI+AAC. We let a₂ = 1 denote assigning intensified BLI to slow responders to first stage BLI and let a₂ = −1 denote assigning BLI+AAC to slow responders to first stage BLI. Note that in the autism SMART, a₂ is nested within a₁ = 1 because only slow responders to BLI were re-randomized. See Table 1 for the labels of all three embedded DTRs in the autism study.

X denotes baseline, pre-randomization covariates, such as age, gender and ethnicity. In all models below, the variables in X are mean-centered to facilitate model interpretations. Y_t denotes the repeated-measures primary outcome that is of scientific interest, observed at time t, $t\in \mathcal{T}$. In the autism study, Y_t is the number of socially communicative utterances at week t = 0 (baseline), 12, 24, 36. For this outcome, higher values of Y_t are more favorable.

$E_{\left(a_1,a_2\right)}\left[Y_t|X\right]$ is the marginal mean of the repeated-measures outcome Y_t under the embedded DTR defined by (a₁, a₂), conditional on the baseline variable X. Note that under the potential outcome framework [32, 33], this is the mean of the repeated-measures outcomes had all participants been assigned DTR (a₁, a₂) at the outset. Thus a model μ_t(X, a₁, a₂; β) for $E_{\left(a_1,a_2\right)}\left[Y_t|X\right]$ is a repeated-measures marginal structural mean model [21, 34]; in this paper for conciseness we will call μ_t(X, a₁, a₂; β) a marginal mean model. The primary focus of this manuscript is on developing parametric models μ_t(X, a₁, a₂; β) for $E_{\left(a_1,a_2\right)}\left[Y_t|X\right]$ under various forms of SMART designs. Because it is important to make the distinction between modeling and estimation, in this section we discuss modeling and in Section 4 we discuss the estimation of the unknown parameter β using data from SMART studies.

3.1. A Traditional yet Naïve Approach to Modeling Repeated Measures in a SMART

To appreciate the need to accommodate the specific features of a SMART design in repeated-measures modeling, we first consider using a traditional approach to comparing the mean trajectories between two DTRs in the autism SMART. For simplicity, suppose we are interested in comparing DTR (BLI, BLI+AAC) (labeled (1, −1) in Table 1) versus DTR (BLI, INT) (labeled (1, 1) in Table 1) using only data from children who began with BLI (a₁ = 1). A traditional model in this case might be

$$E_{\left(a_1,a_2\right)}[Y_t|X]={\eta }^{T}X+{\beta }_0+{\beta }_{1}t+{\beta }_2{1}_{a_1=1,a_2=1}t.$$

This is a traditional approach in that it is often used in the analysis of 2-arm RCTs. In this model, the trajectories associated with the two DTRs are modeled as two straight lines that start with the same intercept at t = 0: averaging over the baseline covariate X, the marginal mean of Y_t under DTR (1, −1) is (β₀ + β₁t), whereas the marginal mean of Y_t under DTR (1, 1) is (β₀ + (β₁ + β₂)t). In this example of a traditional approach, therefore, the difference between the marginal mean trajectories is given by the single parameter β₂. This model will incur bias if either one of the two DTRs does not have a linear mean trajectory. However, in a study such as the autism SMART, it may be important to accommodate a possible deflection at week 12 in the mean trajectory because this is the point at which the treatment is modified for slow responders. Further, since neither participants nor staff were aware of the randomly assigned second-stage treatment during the first stage of treatment (this is a typical feature of SMART designs), these two DTRs should not differ, on average, from t = 0 to t = 12. In Section 6 we investigate, via simulations, the bias that occurs when adopting a traditional slope or quadratic model to analyze repeated measures from a SMART. An example of an improved model is presented in the next section.

In addition, when it is no longer reasonable to adopt simple models such as the slope model above, the comparison between DTRs based on a repeated-measures outcome would require alternative estimands. In the following subsections, we discuss (a) modeling considerations for μ_t(X, a₁, a₂; β) for various forms of SMART designs, and (b) options for estimands in the comparison of the embedded DTRs in a SMART.

3.2. Repeated-Measures Modeling Considerations: The Autism Example

As noted earlier, modeling of a repeated-measures outcome arising from a SMART should be guided by two key principles: (a) properly accommodate the timing of repeated measures in relation to the treatment stages in a SMART; and (b) properly accommodate the restrictions applied on the randomizations by design. The autism SMART provides a relatively simple example to illustrate these modeling principles.

In the autism SMART, all participants had the same duration of stage one treatment (12 weeks) and stage two treatment (12 weeks), and they all advanced to stage two after week 12. Additionally, only slow responders to BLI were re-randomized.

The primary outcome, the number of socially communicative utterances, was measured on four occasions. Baseline measurement Y₀ was pre-treatment; Y₁₂ was measured right before the second treatment stage (re-randomization, if applicable, happened right after Y₁₂); Y₂₄ was measured at the end of treatment; Y₃₆ was measured post treatment and treatment ended at the end of week 24. Since all participants transitioned at t = 12, one approach to modeling the repeated measures in the autism SMART is using a continuous, piecewise marginal model with a knot at week 12. For example, consider the following marginal model for Y_t:

$$\begin{array}{l}{E}_{(a_1,a_2)}\left[Y_t\right|X]={\eta }^{T}X+{\beta }_0+1_{t\le 12}\{{\beta }_{1}t+{\beta }_{2}t{a}_1\}\\ +1_{t>12}\{12{\beta }_1+12{\beta }_2{a}_1+{\beta }_3(t-12)+{\beta }_4(t-12)a_1+{\beta }_5(t-12\left)1_{a_1=1}{a}_2\right\},\end{array}$$ (1)

where the unknown parameters β = (β₀, β₁, β₂, β₃, β₄, β₅) model the effect of the three embedded DTRs over time. An advantage of using contrast coding (−1/1, as opposed to 0/1 coding) is that certain coefficients in the marginal mean model have an interpretation as “main effect”. For example, as a result of a₁ being coded as {−1, 1}, β₁ in (1) can be interpreted as the average slope for all participants (averaging all stage-one and stage-two treatment options) from baseline to t = 12. η captures the association between the time-varying outcome and baseline covariates X. β are of primary interest.

This example model entails two restrictions. The first restriction is that Y₀ is modeled to have the same marginal mean for all three embedded DTRs. This is a common restriction used in the analysis of longitudinal randomized trials [35] since, by design, treatment groups are not expected to differ at baseline (prior to randomization). The second restriction is that the marginal mean trajectory is assumed to be the same between embedded DTRs (BLI, INT) (labeled (1, 1)) and (BLI, BLI+AAC) (labeled (1, −1)) until week 12. This restriction is unique to SMARTs. It is consistent with the study design, in that (1) these two DTRs are identical up to week 12 and (2) re-randomization to second stage treatment does not occur until week 12 (i.e., there can be no expectancy or anticipatory effects due to knowledge of second stage treatments during stage one).

For simplicity, the example model above assumes a piecewise linear trend. In practice, a quadratic mean trajectory (or some other trend) may be more appropriate.

3.3. Repeated-Measures Modeling Considerations: The ADHD Example

In analyzing the ADHD SMART, we focus on comparing the four embedded DTRs based on the repeated measures of school performance measured on eight occasions – at the end of each month of the study (i.e., Y₁, …, Y₈). Note that unlike in the autism SMART, the repeated-measures outcome is unavailable at baseline. This outcome is coded so that higher values are more favorable. Each of the four embedded DTRs is labeled by a pair (a₁, a₂). Let a₁ = 1 denote starting with low-intensity BMOD and let a₁ = −1 denote starting with low-dose MED. Let a₂ = 1 denote intensifying the initial treatment for non-responders and let a₂ = −1 denote augmenting the initial treatment with the alternative treatment for non-responders.

As discussed previously, the SMART design in the ADHD study is more complex relative to the autism study. While the duration of the entire study was the same for all participants (i.e., eight months), the duration of the first and the second treatment stages varied across participants. More specifically, the duration of the first treatment stage could be as short as two months (for the children who became non-responders at the end of month two), or as long as eight months (for the children who continued to respond throughout the entire study). This has implications for modeling the marginal mean under a DTR in that, for a fixed t > 2, the marginal mean of Y_t is a weighted average of the mean for participants who have transitioned and the mean for participants who have yet to transition; as a result, there may be deflections in the marginal mean at any given month, starting at month 2 (t = 2) and ending at month 7 (t = 7).

Additionally, the initial treatment (BMOD versus MED) had an impact on participants’ performance, which determined whether or when the participants transitioned to the second stage as non-responders. For example, among the 75 participants who were assigned to MED initially, only 19 transitioned to stage two (as non-responders) at month two; whereas among the 75 participants who were assigned to BMOD initially, 36 transitioned to stage two (as non-responders) at month two. Therefore, we may allow the pattern of deflection in the mean trajectory to differ between DTRs that start with BMOD and those starting with MED (see the exploratory plot in the Web Appendix).

Based on the discussions above, as well as exploratory analysis aimed at refining the modeling assumptions, we propose to model the repeated measures from the ADHD study as shown below:

$$\begin{array}{l}{E}_{(a_1,a_2)}\left[Y_t\right|X]={\eta }^{T}X+{\beta }_0+{\beta }_1{a}_1+1_{a_1=1}{1}_{t\le 2}{\beta }_2(t-1)\\ +1_{a_1=1}{1}_{t>2}\left({\beta }_2+1_{a_2=1}\left({\beta }_3\left(t-2\right)+{\beta }_4{\left(t-2\right)}^2\right)+1_{a_2=-1}{\beta }_5\left(t-2\right)\right)\\ +1_{a_1=-1}{1}_{t\le 3}{\beta }_6\left(t-1\right)\\ +1_{a_1=-1}{1}_{t>3}\left(2{\beta }_6+1_{a_2=1}{\beta }_7\left(t-3\right)+1_{a_2=-1}{\beta }_8\left(t-3\right)\right).\end{array}$$ (2)

Here, the DTR (BMOD, BMOD+MED) (i.e., (a₁, a₂) = (1, −1)) is assumed to have a piecewise linear trajectory with a knot at t = 2, whereas (BMOD, INT) (i.e., (a₁, a₂) = (1, 1)) has the same mean trajectory as (BMOD, BMOD+MED) until t = 2 and then develops a quadratic trajectory. The two DTRs that begin with MED are assumed to have piecewise linear trajectories with a knot at t = 3 and they share the same mean trajectory until t = 3.

3.4. Repeated-Measures Modeling Considerations: The ExTENd Example

The greater complexity in the ExTENd SMART necessitates more careful modeling considerations. In analyzing the ExTENd SMART, we focus on comparing the eight embedded DTRs based on a repeated-measures outcome of alcohol craving. Alcohol craving was collected on 17 occasions: at baseline (Y₀) and the end of each week for 16 weeks (Y₁, …, Y₁₆). This outcome is re-coded so that higher values are more favorable. The eight DTRs are denoted by (a₁, a_2R, a_2NR), where a₁ is used to denote whether the stringent definition or the lenient definition of early non-response is adopted, a_2R is used to denote a treatment option for responders at stage two, and a_2NR is used to denote a treatment option for non-responders at stage two.

The transition time to the second treatment stage ranged from the end of week two to the end of week eight. As a result, similar to the ADHD study, for a fixed t, Y_t may come from different treatment stages for different participants. In addition, note that DTRs that begin with the same a₁ might differ only in a_2R (how responders are treated in the second stage), only in a_2NR (how non-responders are treated in the second stage), or both. The impact of differing a_2NR can take place from the end of week two (non-responders could start to transition to stage two as early as the end of week two); however the impact of differing a_2R can only take place from the end of week eight (responders could only transition to stage two at the end of week eight).

Because of the features illustrated above, and given the relatively frequent repeated measures, we do not model each of the mean trajectories by simple parametric form; instead, we adopt flexible spline-based models with constraints that are consistent with the SMART study design. First, we allow two DTRs that differ only in a_2NR to start to differ in the mean trajectories after t = 2, because participants could become non-responders and, therefore, receive salvage treatment options specified by a_2NR on or after week two. Second, we allow two DTRs that differ only in a_2R to start to differ in the mean trajectories after t = 8, because on week eight participants could become responders and, therefore, receive the maintenance treatment options specified by a_2R. Aside from forcing all DTRs to have the same mean of Y₀ and these two constraints, we allow the trajectories of the DTRs to be regression splines. In the appendix we provide additional details about incorporating these design features into the regression splines model.

3.5. Estimands

In repeated-measures analysis of SMARTs, a variety of interesting estimands are possible for the comparisons among embedded DTRs. Here, we present two that are clinically important and easy to communicate: change score comparisons and area under curve (AUC). The first approach, change score comparisons, measures the differences among embedded DTRs in terms of change in response from t₁ to t₂. A change score estimand is ${\mathrm{\Delta }}_{t_1,t_2}=E_{(a_1,a_2)}[Y_{t_2}-Y_{t_1}]-E_{(a_1^{\ast },a_2^{\ast })}[Y_{t_2}-Y_{t_1}]$, where (a₁, a₂) and $(a_1^{\ast },a_2^{\ast })$ are two embedded DTRs. In the autism example, a change score comparison from week 0 to week 36 compares the embedded DTRs in terms of the mean increase from baseline to the end of follow-up in the number of socially communicative utterances.

The second approach, AUC, summarizes the cumulative amount of Y_t within a time range (t₁, t₂) [36, 37]; it provides an alternative single number summary of the overall mean trajectory under each embedded DTR. In the autism study, the AUC of Y_t from t = 0 to t = 36 for a specific embedded DTR has a clinically relevant interpretation as the average total number of socially communicative utterances from t = 0 to t = 36 under this DTR.

Both of these two metrics are linear in the coefficients in the marginal model (in Web Appendix we represent each estimand, in the autism study, as a function of coefficients in (1)). The AUC is a more informative summary of the marginal mean trajectory than the change score, because it captures not only change from the start to the end point, but also captures characteristics of the progression in the mean outcome during the period. In the data analysis, we report the AUC for the embedded DTRs.

4. Estimator for Repeated-Measures Marginal Model

4.1. Observed Data

For simplicity, we present the proposed estimator for the repeated-measures marginal model with the autism example. Details about how this estimator is implemented to analyze the ADHD and ExTENd SMARTs can be found in the appendix.

The structure of the data is as follows. For individual i (i = 1, …, N), we observe X_i, A_1,i, R_i, A_2,i and $Y_{t,i},t\in \mathcal{T}$. X includes a set of mean-centered baseline covariates; A₁ denotes the first-stage treatment to which an individual is randomized; R is the indicator of early response; A₂ denotes the second-stage treatment to which the individual is re-randomized. Y_t is the observed value of the repeated-measures outcome at time t.

For example, in the autism SMART, we have (X_i, Y_0,i, A_1,i, Y_12,i, R_i, A_2,i, Y_24,i, Y_36,i). A₁ denotes whether the child was randomized to BLI (A₁ = 1) or BLI+AAC (A₁ = −1) during the first 12 weeks. For slow responders to BLI (A₁ = 1, R = 0), A₂ denotes whether the child was re-randomized to intensified BLI (A₂ = 1) or BLI+AAC (A₂ = −1).

4.2. A Review of the Weighted-and-Replicated Estimator with an End-of-study Outcome

This section is a review of a weighted-and-replicated (WR) estimator for comparing the DTRs with respect to an end-of-study outcome [17–19, 21, 28], illustrated with the autism example. In the following section, we extend this estimator to repeated-measures outcomes.

Suppose that one is interested in comparing the mean of Y₃₆ among the embedded DTRs, and assume that μ₃₆(X, a₁, a₂; β) is a parametric model for the marginal mean of Y₃₆ under embedded DTR (a₁, a₂), which takes a linear form in β and has derivative d(X, a₁, a₂) with respect to β. The WR estimator for β is obtained by solving the following estimating equation:

$$0={\displaystyle \sum _{i=1}^N{\displaystyle \sum _{\left(a_1,a_2\right)}I\left\{\text{treatment}\text{sequence}\text{of}\text{individual}i\text{consistent}\text{with}\text{DTR}\left(a_1,a_2\right)\right\}}\cdot d\left(X_i,a_1,a_2\right)W_i\cdot \left(Y_{36,i}-{\mu }_{36}\left(X_i,a_1,a_2;\beta \right)\right)},$$

where I{treatment sequence of individual i consistent with DTR (a₁, a₂)} is a binary indicator that the individual i was assigned to treatment sequence that would be observed under the DTR (a₁, a₂); and W_i is the product of stage-specific weights, each being the inverse probability of receiving the observed treatment, conditional on the observed covariate and treatment history. In a SMART, W is known, by design. For example in the autism study, W = 1/(Pr(A₁|X, Y₀) · Pr(A₂|X, Y₀, A₁, Y₁₂, R)). Slow responders to BLI receive a weight equal to 4; all the other participants receive a weight equal to 2.

To appreciate why weighting is necessary, note that by design, BLI slow responders are randomized twice, whereas other participants are randomized only once; thus, slow responders to BLI would have a 1/4 chance of following the sequence of treatments they were offered, whereas other participants would have a 1/2 chance of following the treatments they were offered. Therefore, slow responders to BLI are under-represented in the data. To account for this imbalance, weights inversely proportional to the probability of being assigned to a particular treatment sequence are employed in the estimating equation.

Next, note that this estimating equation is an aggregate of estimating equations for each of the embedded DTRs. In a SMART, each individual may be consistent with one or more embedded DTRs depending on the study design. For example, in the autism SMART, responders to initial BLI are consistent with DTRs (BLI, INT) and (BLI, BLI+AAC); that is, their treatment sequences are identical to the treatment sequences that would be recommended if embedded DTRs (BLI, INT) or (BLI, BLI+AAC) are followed. To account for this “sharing” of observations, those observations contribute to the estimating equations for multiple DTRs.

4.3. An Extension for Repeated Measures

For the estimation of the repeated-measures marginal model, we use a longitudinal version of the WR estimator reviewed above. This estimator builds on previous work by Robins and colleagues concerning the estimation of the effect of time-varying treatment on a repeated-measures outcome [38–42].

Let Y_i = (Y_0,i, Y_1,i, …, Y_T,i)^T denote the vector of repeated-measures outcome for individual i. Denote the vector of the model for the marginal mean as μ(X_i, a₁, a₂; β, η), where μ = (μ₀, μ₁, …, μ_T)^T. Recall μ_t(x, a₁, a₂; β, η) is a parametric model for the marginal mean of Y_t among participants that have pre-treatment baseline covariates equal to x, under the embedded DTR labeled (a₁, a₂). Denote the derivative of μ(X_i, a₁, a₂; β, η) with respect to (η, β) as D(X_i, a₁, a₂). D(X_i, a₁, a₂) is a (T + 1)-by-p matrix, where p is the dimension of (η, β).

An estimator for (η, β) for a general SMART design is

$$0={\displaystyle \sum _{i=1}^N{\displaystyle \sum _{\left(a_1,a_2\right)}I\left\{\text{treatment}\text{sequence}\text{of}\text{individual}i\text{consistent}\text{with}\text{DTR}\left(a_1,a_2\right)\right\}}\cdot D{\left(X_i,a_1,a_2\right)}^{T}V{\left(a_1,a_2\right)}^{-1}{W}_i\cdot \left(Y_i-\mu \left(X_i,a_1,a_2;\beta ,\eta \right)\right)}.$$ (3)

V (a₁, a₂) is a working variance-covariance matrix of (Y₀, Y₁, …, Y_T)^T conditional on the baseline X, under the embedded DTR labeled (a₁, a₂). The weight W is used to account for the fact that participants received the observed treatment sequences with different probabilities. In the autism example, W = 1/(Pr(A₁|X, Y₀) · Pr(A₂|X, Y₀, A₁, Y₁₂, R)). The choice of the working variance-covariance matrix V (a₁, a₂) does not have an impact on the unbiasedness of the estimating equation above, assuming that the marginal model μ(X, a₁, a₂; β, η) and the weight W are correctly specified. In the analysis of SMART studies, the weight W can be correctly specified because the treatments are assigned according to known probabilities.

The estimator in (3) is an extension of the WR estimator that accommodates a repeated-measures outcome; the observations of a participant contribute to the estimation of all the embedded DTRs that the treatment sequence of this participant is consistent with. Each patient now has a vector-valued outcome. Moreover, this estimator uses a working variance-covariance matrix for the vector of repeated measures, which is a strategy that is usually taken when performing longitudinal analysis, for the purpose of improving statistical efficiency [43]. Asymptotics of this estimator is provided in the Web Appendix; this includes the formula for the asymptotic standard error of $\widehat{\beta }$. In particular, calculation of the standard error accounts for the fact that some patients contribute to the estimation of multiple DTRs.

Pepe [44] and Lai and Small [45] note that the use of a non-independent working correlation structure in the analysis of longitudinal data may lead to bias when the estimated marginal regression model is conditional on time-dependent covariates. However, in the estimator described in Equation (3), the weights have the effect of creating a pseudo-population [38] where it is as if all participants had been assigned a specific DTR at the outset. Another way to think about this is that the marginal model being estimated is one that only conditions on pre-treatment baseline covariates X, not time-dependent covariates. Thus, in our estimator, using a non-independent working correlation does not create bias.

Furthermore, known weights W_i in (3) can be estimated, for example, using covariates thought to be correlated with the repeated-measures outcome [39, 46, 47]. This approach can asymptotically improve efficiency of the estimator. We take this approach in our analyses of the data arising from three SMART studies. In the Web Appendix, we describe the usage of R package geepack to implement the estimator (3) and to obtain valid standard errors.

5. Data Analysis

Here, we present the results of the data analysis of the three SMART studies. For all three SMARTs, prior to analysis, a sequential type of multiple imputation algorithm was used to replace missing values in the data set [48]. This was implemented using the mice package in R [49]. All estimates and standard errors reported are calculated using standard rules for combining identical analyses performed on each of the imputed data sets [50]. Data are analyzed using the approach outlined in Section 4.3, with an auto-regressive working correlation structure.

5.1. Analysis of the Autism SMART Data

We first present the analysis of data arising from the autism SMART (N = 61). The weight at the first stage is estimated using age, gender, indicator of African American, indicator of Caucasian, number of socially communicative utterances at baseline; the weight (for slow responders to the first-stage BLI) at the second stage is estimated using number of socially communicative utterances at baseline and number of socially communicative utterances at week 12. Figure 4 displays a plot of the estimated marginal mean trajectories of the number of socially communicative utterances for each of the three embedded DTRs. Estimates and standard errors for the parameters in the repeated-measures model and pairwise comparisons among the three embedded DTRs based on the AUCs are given in Table 3. To enhance interpretation we report estimates of AUC/36, which can be interpreted as the average number of socially communicative utterances over the entire course of the 36-week study.

Figure 4.

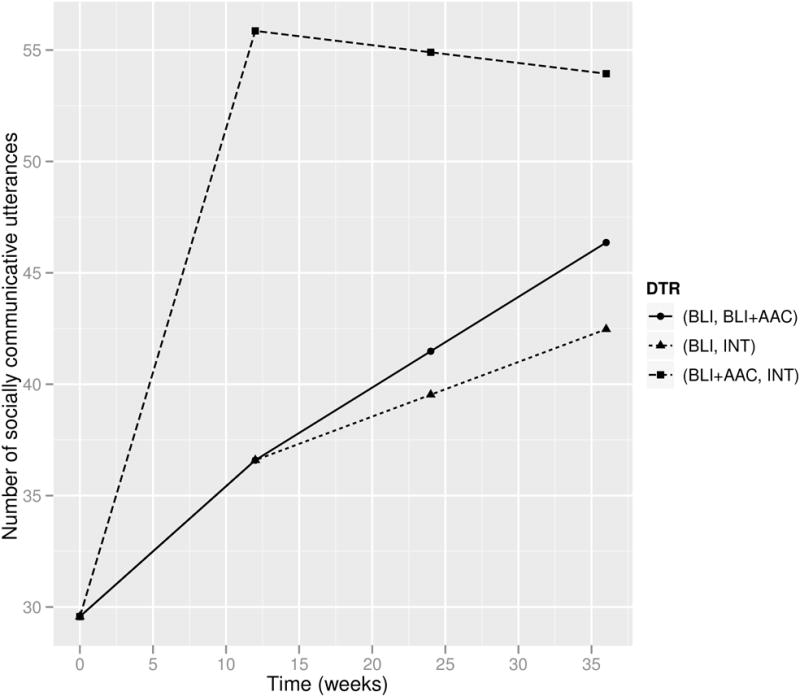
Estimated mean trajectories under the embedded DTRs of the autism SMART.

Table 3.

An analysis of the repeated-measures outcome from the autism SMART. The reported summary of each DTR and the comparison between DTRs is regarding AUC/36.

	Estimate	SE	p-value
β0 (Intercept)	29.57	3.30	<0.01
η1 (age)	−3.63	2.92	0.22
η2 (male)	−9.39	13.38	0.49
η3 (AfricanAmerican)	1.04	11.52	0.93
η4 (Caucasian)	1.09	8.17	0.89
β1 (time; stage one)	1.39	0.32	<0.01
β2 (time×A1; stage one)	−0.80	0.29	<0.01
β3 (time; stage two)	0.12	0.17	0.47
β4 (time×A1; stage two)	0.20	0.18	0.27
β5 (time×A1A2; stage two)	−0.08	0.23	0.73
(BLI, INT)	37.38	4.16	<0.01
(BLI, BLI+AAC)	38.68	4.99	<0.01
(BLI+AAC, ·)	50.84	4.27	<0.01
(BLI, INT) vs (BLI, BLI+AAC)	−1.30	3.72	0.73
(BLI+AAC, ·) vs (BLI, BLI+AAC)	12.16	5.43	0.03
(BLI+AAC, ·) vs (BLI, INT)	13.46	5.02	0.01

The DTR (BLI+AAC, ·) (labeled (−1, ·)) appears to outperform the other two embedded DTRs, in terms of the AUC (e.g., 95% CI of the contrast of (BLI+AAC, ·) versus (BLI, INT) is (3.50, 23.19)). Under this DTR, the average number of socially communicative utterances during the 36-week study is estimated to be 50.84 (95% CI (42.47, 59.20)), whereas it is smaller than 40 for the other two DTRs.

5.2. Analysis of the ADHD SMART Data

Analysis of the ADHD SMART data (N = 150) is based on the repeated-measures model proposed in (2). The repeated-measures outcome is the classroom performance rated by teachers; higher values indicate better classroom performance. The weight at the first stage is estimated using age, indicator of being previously medicated at home, indicator of being diagnosed with oppositional defiant disorder (ODD), baseline ADHD severity of symptoms, classroom performance rating at baseline; the weight (for non-responders) at the second stage is estimated using age, stage one treatment, time to re-randomization, classroom performance rating at baseline and immediately prior to re-randomization.

Table 4 presents the estimated AUCs for the four embedded DTRs and their comparisons. AUC/7 can now be interpreted as the average classroom performance rating from the end of month one until the end of month eight. The estimated mean trajectories of the classroom performance under the four embedded DTRs are shown in Figure 5.

Table 4.

An analysis of the repeated-measures outcome from the ADHD SMART. The reported summary of each DTR and the comparison between DTRs is regarding AUC/7.

	Estimate	SE	p-value
β0 (Average Intercept of BMOD and MED)	2.31	0.12	< 0.01
β1 (A1; baseline)	−0.25	0.11	0.03
β2 (time; t ≤ 2 under BMOD)	−0.01	0.16	0.93
β3 (time; t > 2 under (BMOD,INT))	0.34	0.13	0.01
β4 (time2; t > 2 under (BMOD,INT))	−0.04	0.02	0.03
β5 (time; t > 2 under (BMOD,BMOD+MED))	0.09	0.03	0.01
β6 (time; t ≤ 3 under MED)	0.11	0.07	0.13
β7 (time; t > 3 under (MED,INT))	−0.03	0.04	0.41
β8 (time; t > 3 under (MED,MED+BMOD))	−0.05	0.03	0.17
(BMOD, BMOD+MED)	2.29	0.14	< 0.01
(BMOD, INT)	2.48	0.13	< 0.01
(MED, MED+BMOD)	2.67	0.13	< 0.01
(MED, INT)	2.69	0.12	< 0.01
(BMOD, BMOD+MED) vs (BMOD, INT)	−0.19	0.13	0.15
(BMOD, BMOD+MED) vs (MED, MED+BMOD)	−0.38	0.19	0.05
(BMOD, BMOD+MED) vs (MED, INT)	−0.41	0.19	0.03
(BMOD, INT) vs (MED, MED+BMOD)	−0.19	0.18	0.30
(BMOD, INT) vs (MED, INT)	−0.21	0.18	0.24
(MED, MED+BMOD) vs (MED, INT)	−0.03	0.07	0.71

Figure 5.

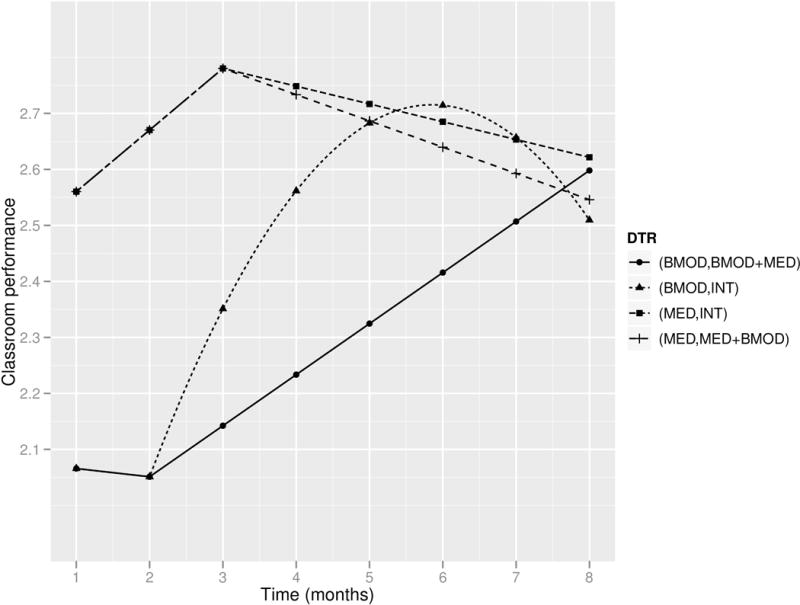
Estimated mean trajectories under the embedded DTRs of the ADHD SMART.

The DTR (BMOD, BMOD+MED) is estimated to have the smallest AUC among the four embedded DTRs, and it differs significantly from the two DTRs that start with MED. The two MED DTRs are identical in terms of AUC. However, the two DTRs starting with BMOD seem to differ. Specifically, as suggested by the estimated coefficients, the slope of DTR (BMOD, BMOD+MED) after t = 2 is significantly positive (0.09; 95%CI (0.03, 0.15)); on the other hand, (BMOD, INT) has a quadratic trajectory with the second-order coefficient significantly negative (−0.04; 95%CI (−0.08, 0)), and the two MED DTRs both have a slope not significantly different from zero after t = 3. The data suggest that (BMOD, BMOD+MED) is the only embedded DTR that maintains a trend of improvement after t = 2. In summary, assigning MED initially seems to yield a more positive outcome than assigning BMOD initially in the short term, but the performance of children who initially receive BMOD improves within a wider range of time. In addition, there is no evidence that the two DTRs starting with MED differ in terms of their second-stage trajectories, but the two DTRs beginning with BMOD differ markedly in terms of their second-stage trajectories.

5.3. Analysis of the ExTENd SMART Data

Our analysis of the ExTENd SMART data (N = 250) is based on the flexible regression splines model discussed in Section 3.4 (details are presented in the appendix). The repeated-measures outcome is alcohol craving, assessed using the Penn Alcohol Craving Scale (PACS; [51]); values of this variable are reverse coded (ranging from 0 to 30), such that higher values indicate less alcohol craving, which is more favorable. Recall that in this study there were two definitions of non-response: stringent and lenient definitions. The weight at the first stage is estimated using age, gender, pre-study percent days heavy drinking, alcohol craving at the screening visit and the first stage one visit; the weight at the second stage is estimated using age, alcohol craving at the first and the last stage one visits, the assigned non-response definition, indicator of response to the first stage treatment, duration of stage one.

The estimated mean trajectories for alcohol craving under the eight embedded DTRs are shown in Figure 6. The estimated AUCs for the eight embedded DTRs are reported in Table 5. AUC/16 can be interpreted as the average alcohol craving from entry to study to the end of week 16. The estimated trajectories imply that outcomes improve over time, on average across all eight embedded DTRs. DTRs that utilize the lenient definition for non-response were estimated to lead to less alcohol craving than DTRs that use the stringent definition. In particular, the DTR with the highest AUC (21.19; 95%CI (20.16, 22.23)) utilizes the lenient definition and assigns UC to responders and Placebo+CBI to non-responders. There were no significant differences between the eight DTRs in terms of the AUCs.

Figure 6.

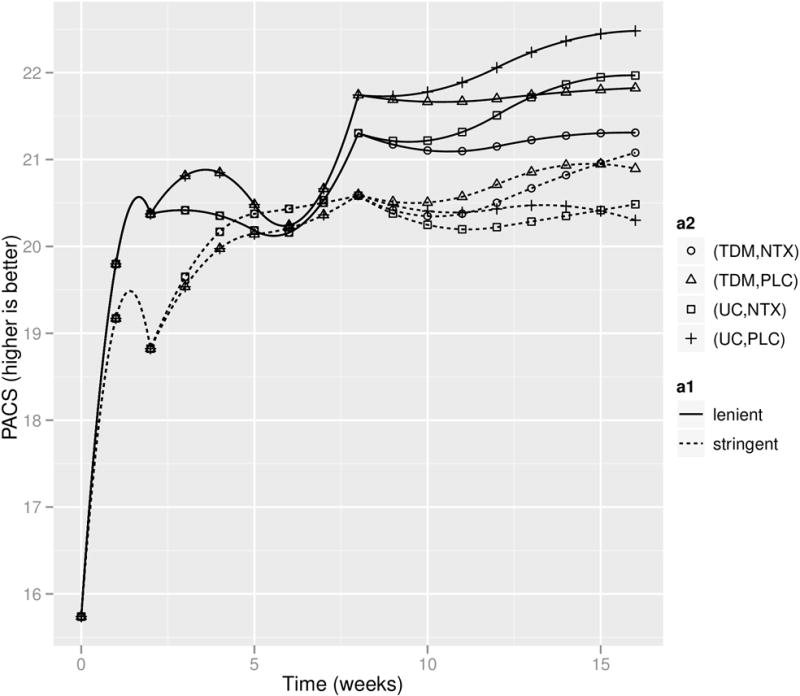
Estimated mean trajectories under the embedded DTRs of the ExTENd SMART. a1 (the definition for non-response) and a2 (stage two treatment regime) jointly specify the eight embedded DTRs.

Table 5.

An analysis of the repeated-measures outcome from the ExTENd SMART. LNT=lenient non-response definition. STRGT=stringent non-response definition. NTX=naltrexone+CBI. PLC=placebo+CBI.

Embedded DTR	Estimate of AUC/16	SE of AUC/16
(LNT, TDM, NTX)	20.65	0.54
(LNT, TDM, PLC)	21.02	0.52
(LNT, UC, NTX)	20.83	0.56
(LNT, UC, PLC)	21.19	0.53
(STRGT, TDM, NTX)	20.18	0.56
(STRGT, TDM, PLC)	20.18	0.52
(STRGT, UC, NTX)	20.04	0.54
(STRGT, UC, PLC)	20.03	0.54

6. Simulations

A small set of simulation experiments were conducted to investigate the importance of incorporating the unique features of a SMART in repeated-measures models comparing embedded DTRs. In particular, we compared the bias and relative efficiency of estimators from a repeated-measures model that incorporates the features of a SMART versus traditional repeated-measures models that ignore these features. Data (X, Y₀, A₁, Y₁₂, R, A₂, Y₂₄, Y₃₆) were generated to mimic the autism SMART study. Notation is the same as described in Section 4. In particular, X is a 4-dimensional pre-treatment covariate for age, gender, indicator of African American, indicator of Caucasian.

It is well known that bias in the estimated comparison between the DTRs is expected to occur under misspecified models [21]. Here we focus on a type of model misspecification that is specific to the analysis of repeated-measures data in a SMART. We adopt a series of data-generative models under which the mean trajectory of DTR (−1, ·) is maintained to be linear, and the average of the two mean trajectories of DTRs (1, 1) and (1, −1) is maintained to be linear. Recall that DTRs (1, 1) and (1, −1) ought to share trajectories up to t = 12. We create a series of models by varying the extent to which the trajectories of (1, 1) and (1, −1) deviate from the average between them, thus deviating from being linear. More specifically, we let the mean trajectories of (1, 1) and (1, −1) be two piecewise linear curves that share the path from t = 0 to t = 12. To quantify the magnitude of the deviation from linear, we conceptualize an effect size in terms of the comparison of AUCs between DTRs (1, 1) and (1, −1); this is operationalized as the true difference between the two AUCs divided by the pooled standard deviation in person-specific AUCs in each DTR group. Data sets with effect sizes equal to 0, 0.2, 0.5 and 0.8 and with sample sizes N = 100 and N = 300 are generated (details provided in the appendix). Note that a zero effect size corresponds to the case where the two DTRs (1, 1) and (1, −1) do not differ over the entire course of the study; thus in this case both DTRs have a linear mean trajectory.

For each data-generative scenario, we fit three models: (a) the model shown in Equation (1); (b) a linear slope model, in which the mean trajectory of each embedded DTR is assumed to be linear; (c) a quadratic model, in which the mean trajectory of each embedded DTR is assumed to be quadratic. The slope and quadratic models do not impose the constraint that DTRs (1, 1) and (1, −1) share the same trajectory until the end of the first treatment stage; in other words, the treatment stage transition is not explicitly accounted for in those two models. In all cases, the estimator for the repeated-measures models utilizes an independence working correlation.

We present results for two pairwise comparisons: ${\mathrm{\Delta }}_1^{\mathit{\text{AUG}}}$ (the difference in AUC between DTRs (1, 1) and (1, −1)) and ${\mathrm{\Delta }}_2^{\mathit{\text{AUG}}}$ (the difference in AUC between DTRs (−1, ·) and (1, −1)). We report the bias in the estimates when using the slope model and quadratic model, and the ratio of MSE of estimators arising from the slope and quadratic models over the MSE of estimators arising from the model (a). As the slope and quadratic models are correctly specified models only in the scenario with zero effect size, we expect to see bias in all scenarios except zero effect size. On the other hand, model (a) is a correctly specified model across all simulation scenarios. However, since the slope model is more parsimonious than model (a), for small effect sizes we expect the slope model to have smaller MSE than model (a).

Results are shown in Table 6. We notice that, as expected, the slope and quadratic models produce biased estimates when they are not correctly specified (i.e., effect size not equal to zero). However, the slope model has smaller MSE than model (a) in some non-zero effect size cases; in particular, when the sample size is small (N = 100), the slope model has smaller MSE than model (a) for the estimation of ${\mathrm{\Delta }}_2^{\mathit{\text{AUG}}}$ unless the effect size is large (this is when there is severe mis-specification when assuming the slope model). This is due to the bias-variance tradeoff; the slope model is more parsimonious thus may have smaller MSE when the induced bias is larger than model (a). This tradeoff can also be appreciated by noticing that, as the sample size increases, model (a) starts to outperform the slope model under conditions with small effect sizes. Interestingly, for the estimation of ${\mathrm{\Delta }}_1^{\mathit{\text{AUG}}}$, model (a) is better than the slope model uniformly under all simulation scenarios. This can be intuitively explained by the fact that, the information that DTRs (1, 1) and (1, −1) share trajectory from t = 0 to t = 12 is particularly useful for the estimation of the AUC contrast between these two DTRs; this information is explicitly imposed in model (a) but not in the slope model. We also notice that the quadratic model always leads to a larger MSE than model (a), for estimation of both contrasts and across sample sizes.

Table 6.

Bias and Relative MSE (in relation to model (a) that respects the design features of a SMART) of estimates from the slope model and the quadratic model. ${\mathrm{\Delta }}_1^{\mathit{\text{AUC}}}$ = the constrast in AUC between DTRs (1, 1) and (1, −1); ${\mathrm{\Delta }}_2^{\mathit{\text{AUC}}}$ = the contrast in AUC between DTRs (−1, ·) and (1, −1). Bias that significantly differs from zero is in bold.

Effect Size	N = 100
	${\mathrm{\Delta }}_1^{\mathit{\text{AUC}}}$				${\mathrm{\Delta }}_2^{\mathit{\text{AUC}}}$
	Bias × 100 Slope	Quad	RMSE Slope	Quad	Bias × 100 Slope	Quad	RMSE Slope	Quad
0	0.1	1.7	1.67	1.87	−5.2	−1.9	0.71	1.55
0.2	−35.4	13.5	1.89	1.73	−19.7	−0.7	0.77	1.48
0.5	−98.6	33.6	2.7	1.6	−50.1	14.9	0.98	1.49
0.8	−161.8	65.6	2.91	1.35	−79	33.9	1.32	1.37

Effect Size	N = 300
	Bias × 100 Slope	Quad	RMSE Slope	Quad	Bias × 100 Slope	Quad	RMSE Slope	Quad
0	0.1	0	1.71	1.71	3.4	5.4	0.72	1.43
0.2	−41	10.7	2.57	1.69	−20.9	6.2	0.85	1.45
0.5	−105.5	25.7	5.17	1.57	−54.5	10.7	1.53	1.44
0.8	−189.2	36	7.87	1.34	−96	17	2.97	1.38

These results suggest that it is important to account for the unique features of a SMART in the analysis of repeated-measures data. More traditional models such as the slope or quadratic model (these are the types of models often used in the analysis of three-arm RCTs) do not effectively utilize known information about the SMART study design and may result in bias and efficiency loss. The efficiency loss for certain estimands appears to occur even in settings where the true mean trajectories do not deviate much from the slope model or the quadratic model.

In Web Appendix, we provide additional simulations that examine (1) the extent to which efficiency is improved when adopting a non-independent working correlation structure in the estimation, for varying levels of true within-person correlations among Y_t; and (2) the performance of confidence intervals constructed based on the asymptotic standard error. The results show that using the non-independent working correlation is only notably more efficient when the true underlying correlation among repeated measures is at least moderately high. Additionally, the confidence intervals seem to have reasonably good coverage probability.

7. Discussion

This manuscript provides modeling guidelines for comparing DTRs based on a repeated-measures outcome arising from a SMART. Three distinct SMART study designs were used for illustration. The autism SMART has a relatively simple design, with only three embedded DTRs, and all patients transitioned to the second stage at the same time. In addition, there are only four measurement occasions during the entire study. Therefore, we suggested the piecewise linear model. In the ADHD SMART, non-responders transitioned to the second stage at different time points, and the transition times vary between two initial treatment groups. Thus we recommended a parametric model that accommodates these features. The ExTENd SMART differs from the other two SMARTs in that both responders and non-responders were re-randomized, but with different transition times to second stage. There are more DTRs embedded in this study (i.e., eight DTRs) and more measurement occasions. Thus we modeled the trajectories of all embedded DTRs using regression splines that are properly constrained to respect the relationship among the embedded DTRs. In practice, decisions about how to appropriately model repeated measures arising from SMARTs should be based on when patients transition between treatment stages, the timing of outcome measurement occasions relative to treatment stages, and any additional area specific knowledge about the developmental pattern of the repeated-measures outcome under the assigned treatments.

In additional simulations not reported here we discovered that including the repeated measures before re-randomization in the model for estimating the true known weight seems to play a similar role as specifying a non-independent working correlation structure in the GEE implementation, for the purpose of improving the efficiency of the estimator. However, this was in simulations mimicking the autism study with just two measurement occasions in the second stage. One advantage of the approach of using non-independent working correlation is that it allows scientists to capitalize on utilizing correlation among repeated measures that belong to the second treatment stage, which cannot be included in the model for estimating the weights.

In our data analysis, we report standard errors that are calculated from the asymptotics. In some experiments not presented in this paper, we have found that for a small sample size (such as N = 100), the true standard deviations of the parameter estimates can be under-estimated by the asymptotic standard errors, thus the resulting confidence intervals might have lower coverage than the nominal level. This phenomenon has been discovered and discussed in the GEE literature [52]. With the weighting and replication in our repeated-measures estimator for SMART data, it is more challenging to correct for the small-sample bias in the asymptotic standard error. We will investigate this correction in future work.

Model selection for modeling the repeated measures under the embedded DTRs in a SMART is a challenging task and a direction for future research. In this paper, we mainly focused on the general principles of a repeated-measures model that takes into account the specific design features of a SMART study. However, there might be multiple parametric models that are in accordance with the design features of a SMART study. Evaluation of the goodness of fit in the context of the weighted-and-replicated estimation procedure requires novel statistical methods.

The repeated-measures estimator we propose in this paper is built based on some moment equalities of the observed data that are derived from moment equalities in populations where each DTR is assigned upfront. In fact, due to the sequential randomization of the treatment, there might be more valid moment equalities of the observed data that we can write, especially regarding the repeated measures at earlier time points. Appropriately utilizing these valid equalities in proposing the estimator may further improve the efficiency. Lai and Small [45] propose similar idea, in the context of regression analysis of longitudinal data, that aims to construct more efficient estimators when the regression model is conditional on time-varying covariates. We will investigate more along this direction in future work.

The ExTENd SMART contains more subtle features that may have implications on modeling repeated measures, which are beyond the scope of this paper. For example, the initial randomization is between two distinct criteria for non-response, instead of between two distinct treatments, as in most other trials. This implies that two DTRs that differ in the criterion for non-response can only start to differ, after the participant meets the more stringent non-response criterion. In other words, there is a chance for all the embedded DTRs to share the same mean trajectory during the first few weeks of the study. In addition, non-responders were blinded to the re-randomization, but responders were not (due to the nature of the treatments); this might have implications for modeling repeated-measures data in ExTENd. In future work we will extend the guidelines provided here to accommodate other unique features of SMART designs like ExTENd.

This work can also be extended readily in a number of directions. One natural extension is to consider different link functions in the marginal model to examine how DTRs differ based on trajectories of categorical, count or ordinal outcomes. A second extension is to the analysis of cluster- (or group-) randomized SMARTs in which clusters are randomized sequentially, yet the primary outcome is measured at the level of individuals nested within clusters [53]; this is a setting where GEE methods are often used to account for clustering of individuals (patients) within clusters (groups).

Table 2.

Design features of ExTENd study and their implications on modeling.

Design features	Implications for repeated-measures modeling
Randomization is (or should be) stratified on baseline measurements; there is no difference in anticipatory effect among the eight DTRs.	Trajectories of all the eight DTRs have the same intercept.
Patients became responders only if they stayed in stage one for eight weeks without meeting the assigned criterion for non-response. There can be no expectancy effects due to knowledge of second stage treatments during stage one.	A pair of DTRs that only differ in a2R (the second-stage treatment for responders) should share the same trajectory until the end of week eight, and may differ from then on.
Patients transitioned to stage two as non-responders as early as week two. There can be no expectancy effects due to knowledge of second stage treatments during stage one.	A pair of DTRs that only differ in a2NR (the second-stage treatment for non-responders) should share the same trajectory until the end of week two, and may differ from then on.

APPENDIX A. Potential Outcome Framework

Here we briefly review the potential outcome framework and the required assumptions that make the marginal structural mean $E_{\left(a_1,a_2\right)}\left[Y_t|X\right]$ identifiable from the observed data. The potential outcome framework was introduced by [32, 33] for time-independent treatments and later extended by [1] for time-dependent treatments. Associated with DTR, potential outcomes for Y_t can be conceptualized for each subject if he/she had followed this particular DTR. Readers may refer to [21] for a more complete exposition. One of the key assumptions, the Consistency Assumption requires that, each observed outcome is equal to the potential outcome associated with the DTR the individual was consistent with (see pages 7–8 in [21] for more details).

The second identifying assumption is the Sequential Randomization, which states that the treatment assignment at each stage is independent of all potential outcomes given the observed history prior to that treatment. The third identifying assumption, Positivity Assumption, requires that if certain covariate history and treatment sequence can exist in the population where all the subjects follow the DTR (a₁, a₂), the pair of this covariate history and this treatment sequence must also exist with positive probability in the observed population. In a SMART study, these two assumptions are satisfied by design. Under these three assumptions, E[Y_t(a₁,a₂)|X], which is identical to $E_{\left(a_1,a_2\right)}\left[Y_t|X\right]$, can be identified from the observed data.

APPENDIX B. Details Concerning the Data-generative Models for the Simulation

In the simulation in Section 6, we illustrate the importance of considering the special features of SMART designs in the modeling of repeated measures from SMART trials, by comparing a repeated-measures model that incorporates SMART features with more traditional longitudinal models such as slopes and quadratic models. Here we provide additional details about the data-generative models used in this simulation. We adopted a series of data-generative models under which the mean trajectory of DTR (−1, ·) is maintained to be linear, and the average of the two mean trajectories of DTRs (1, 1) and (1, −1) is maintained to be linear; each data-generative model in the series is indexed by a parameter θ > 0, which quantifies the extent to which the trajectories of DTRs (1, 1) and (1, −1) deflect at t = 12.

We generate data (X, Y₀, A₁, Y₁₂, R, A₂, Y₂₄, Y₃₆) for each individual in a sample of size N.

• X includes six mean-centered baseline covariates: age, gender, indicator of African American, indicator of Caucasian, indicator of Hispanic, indicator of Asian. (Note that in the simulation experiments, the marginal model we fit for repeated measures only includes the first four covariates in X to avoid rank deficient problem in the estimation) X is sampled (with replacement) from the real autism SMART data. For notational simplicity, we let X below always contain intercept as the first coordinate.

• Generate $Y_0={\eta }_0^{T}X+{\epsilon }_0$, where ɛ₀~N (0, σ²)

• Generate A₁ to be −1 or 1 with equal probability.

• Generate $Y_{12}={\eta }_{11}^{T}X+{\eta }_{12}{Y}_0+{\beta }_{11}{A}_1+{\epsilon }_1$, where ɛ₁~N (0, σ²)

• Generate A₂ to be −1 or 1 with equal probability, among individuals with A₁ = 1 and R = 0; otherwise set A₂ = 0.

• Generate $Y_{24}={\eta }_{21}^{T}X+{\eta }_{22}{Y}_0+{\eta }_{23}^T{A}_1+{\eta }_{24}{Y}_{12}+{\beta }_{21}\left(1-R\right)\left(A_1+1\right)A_2+{\epsilon }_2$, where β₂₁ = −θ and ɛ₂~N (0, σ²).

• Generate $Y_{36}={\eta }_{31}^{T}X+{\eta }_{32}{Y}_0+{\eta }_{33}^T{A}_1+{\eta }_{34}{Y}_{12}+{\beta }_{31}\left(1-R\right)\left(A_1+1\right)A_2+{\epsilon }_3$, where η₃₁ = 2η₂₁, η₃₂ = 2η₂₂, η₃₃ = 2η₂₃, η₃₄ = 2η₂₄ − 1, β₃₁ = 2β₂₁ = −2θ and ɛ₃~N (0, σ²).

• The values of the coefficients mentioned above: η₀ = (29.5,−5.1, −16.3, 0, 14.3,−11.8, 0.5), σ = 10, η₁₁ = (23.46, 1.4,−3.0, 16.6, 11.1, 6.5, 22.5), η₁₂ = 0.3, β₁₁ = −1, η₂₁ = (22.758, 1.20, 4.33, 12.33, 4.00, 7.53, 7.47), η₂₂ = 0.2, η₂₃ = −1.8, η₂₄ = 0.2.

In order to have data-generative models that are reasonable, we conceptualize an effect size in terms of the contrast in AUC between two embedded DTRs. We define the effect size of the comparison between DTR (1, 1) and DTR (1, −1) as the ratio of the difference in their AUCs over the pooled standard deviation of “a person-specific AUC” between the two DTR groups. More specifically, we operationalize the person-specific AUC as 12(Y₀/2 + Y₁₂ + Y₂₄ + Y₃₆/2) for each individual. Let σ_(1,1) denote the standard deviation of this person-specific AUC under DTR (1, 1) and σ_(1,−1) denote the standard deviation of this person-specific AUC under DTR (1, −1). Then the effect size mentioned above can be written as $\left(AU{C}_{\left(1,1\right)}-AU{C}_{\left(1,-1\right)}\right)/\sqrt{\left({\sigma }_{\left(1,1\right)}^2+{\sigma }_{\left(1,-1\right)}^2\right)/2}$. This measure quantifies the extent to which DTRs (1, 1) and (1, −1) differ throughout the entire study period.

Figure 7 shows the true mean trajectories of the repeated measures under the three embedded DTRs, in each of the four data-generative models (with the effect size defined earlier equal to 0, 0.2, 0.5, 0.8) that we use in our simulation experiments. Across all of the four data-generative models, the effect size in terms of the comparison between DTR (−1, ·) and the average of DTRs (1, 1) and (1, −1) is kept at around 0.4.

Figure 7.

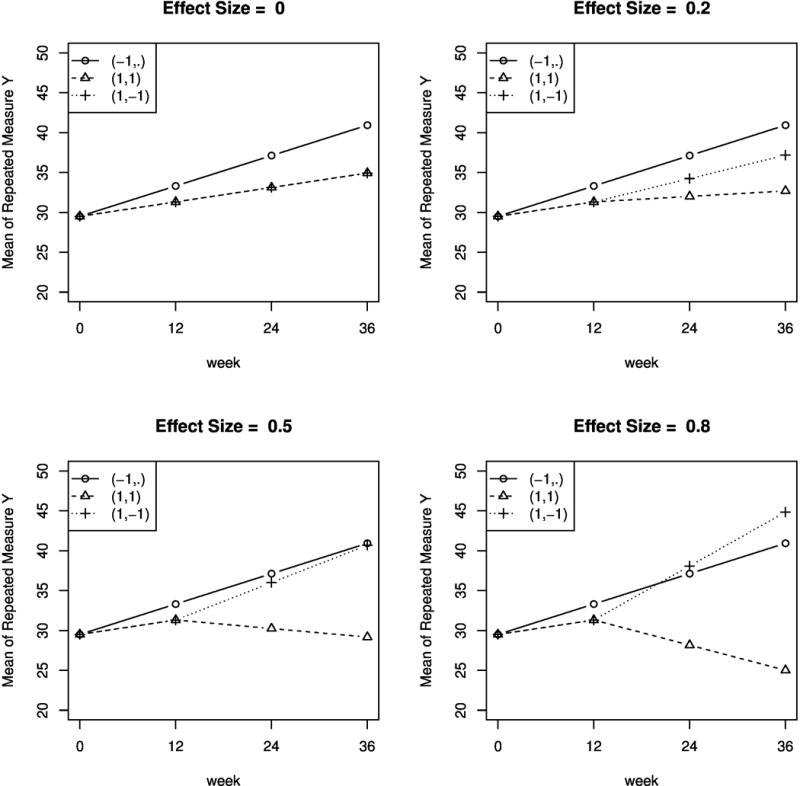
True mean trajectories of the repeated measures under the embedded DTRs, under four data-generative models corresponding to effect size (of the contrast in AUC between DTR (1, 1) and (1, −1)) = 0, 0.2, 0.5, 0.8.

APPENDIX C. Details Concerning the Analysis of Repeated-Measures Data in the ADHD Study

For individual i, we observe X_i, A_1,i, R_i, M_i, A_2,i and repeated measures Y_1,i, …, Y_8,i. A₁ = 1 denotes that the individual received low-intensity BMOD and A₁ = −1 denotes that the individual received low-dose MED. R indicates whether the individual continued to respond until the end of the study. When R = 0 (i.e., the individual became a non-responder during the study), M denotes the time (in months) of non-response and A₂ denotes whether (A₂ = 1) the initial treatment was intensified or (A₂ = −1) the initial treatment was augmented with the alternative treatment.

The repeated-measures model proposed in (2) was estimated using the estimator presented in (3). In particular, the treatment sequence of each individual is consistent with either one or two of the embedded DTRs. An individual’s treatment sequence is consistent with only one embedded DTR if this individual was a non-responder (e.g., a non-responder to BMOD who was later re-randomized to INT is only consistent with DTR (BMOD, INT)). An individual’s treatment sequence is consistent with two embedded DTRs if this individual was a responder (e.g., a responder to BMOD is consistent with both (BMOD, INT) and (BMOD, BMOD+MED)). The weight W in (3) is the inverse probability of an individual receiving the treatment sequence that was assigned to him/her. Therefore, responders receive a weight equal to 2 (they were randomized only once, to two options) and non-responders receive a weight equal to 4 (they were randomized twice, each time to two options). In our data analysis, however, we estimate these known weights using covariates specified in Section 5.2 to improve the statistical efficiency.

APPENDIX D. Details Concerning the Analysis of Repeated-Measures Data in the ExTENd Study

Given the many measurement occasions of the repeated-measures outcome, we adopted a piecewise splines model. Here we describe the details. From t = 0 to t = 2, we let the mean trajectory under DTR (a₁, a_2R, a_2NR) be a regression spline that can only vary with a₁ and has the identical intercept regardless of a₁. From t = 2 to t = 8, we let the mean trajectory under the DTR (a₁, a_2R, a_2NR) be a regression spline that continously connects to the trajectory before t = 2, which can vary with different values of (a₁, a_2NR). From t = 8 to t = 16, we let the mean trajectory under the DTR (a₁, a_2R, a_2NR) be a regression spline that continuously connects to the trajectory before t = 8, and the trajectory can vary with different values of (a₁, a_2R, a_2NR). For model simplicity, all the b-spline bases are of degree 2. We apply internal knots at t = 5 (midway from t = 2 to t = 8) and t = 12 (midway from t = 8 to t = 16).

A regression splines model can be viewed as a linear model, with properly chosen functions of b-spline bases as predictors. Therefore, the estimator presented in (3) can be readily applied. More specifically, in the ExTENd study, each individual’s treatment sequence is consistent with two embedded DTRs. For example, a patient who was assigned the lenient early non-response definition and later transitioned to stage two as a responder and received TDM was consistent with the following two DTRs: (a₁, a_2R, a_2NR)=(lenient, TDM, NTX+CBI) and (a₁, a_2R, a_2NR)=(lenient, TDM, Placebo+CBI). The weight in (3) is equal to 4 for every individual, because in the ExTENd study each individual was randomized twice, each time to one of two options. In our data analysis, we estimate these known weights using the covariates specified in Section 5.3 to improve the statistical efficiency.