Extent of Resection of Glioblastoma Revisited: Personalized Survival Modeling Facilitates More Accurate Survival Prediction and Supports a Maximum-Safe-Resection Approach to Surgery

Abstract

Purpose

Approximately 12,000 glioblastomas are diagnosed annually in the United States. The median survival rate for this disease is 12 months, but individual survival rates can vary with patient-specific factors, including extent of surgical resection (EOR). The goal of our investigation is to develop a reliable strategy for personalized survival prediction and for quantifying the relationship between survival, EOR, and adjuvant chemoradiotherapy.

Patients and Methods

We used accelerated failure time (AFT) modeling using data from 721 newly diagnosed patients with glioblastoma (from 1993 to 2010) to model the factors affecting individualized survival after surgical resection, and we used the model to construct probabilistic, patient-specific tools for survival prediction. We validated this model with independent data from 109 patients from a second institution.

Results

AFT modeling using age, Karnofsky performance score, EOR, and adjuvant chemoradiotherapy produced a continuous, nonlinear, multivariable survival model for glioblastoma. The median personalized predictive error was 4.37 months, representing a more than 20% improvement over current methods. Subsequent model-based calculations yield patient-specific predictions of the incremental effects of EOR and adjuvant therapy on survival.

Conclusion

Nonlinear, multivariable AFT modeling outperforms current methods for estimating individual survival after glioblastoma resection. The model produces personalized survival curves and quantifies the relationship between variables modulating patient-specific survival. This approach provides comprehensive, personalized, probabilistic, and clinically relevant information regarding the anticipated course of disease, the overall prognosis, and the patient-specific influence of EOR and adjuvant chemoradiotherapy. The continuous, nonlinear relationship identified between expected median survival and EOR argues against a surgical management strategy based on rigid EOR thresholds and instead provides the first explicit evidence supporting a maximum safe resection approach to glioblastoma surgery.

INTRODUCTION

Glioblastoma is the most common malignant brain tumor, with approximately 12,000 new cases diagnosed annually in the United States.¹ The current standard of care is surgical resection followed by adjuvant chemoradiotherapy.^2,3 Mortality is greater than 90% at 2 years,^1,4 and age, Karnofsky performance score (KPS), and the extent of surgical resection of enhancing tumor on T1-postgadolineum magnetic resonance imaging (EOR) modulate this estimate.^4–11

Several studies demonstrate the critical role of surgical resection in glioblastoma management and also suggest that some EOR thresholds (eg, 88% to 89% or 95% to 98%) distinguishes two subgroups of postresection patients with significant differences in median survival.^4–11 Although statistically valid, these discontinuous survival models ensue from categoric analyses that are fundamentally limited in their ability to describe the probabilistic nature of continuous-time processes but were initially necessary because limited data availability precludes more complex mathematical modeling. Also, using categoric models for individual, patient-level survival predictions requires secondary generalization of aggregate data,^4,7 and data from categoric models can be misinterpreted to suggest that subthreshold resections are not clinically indicated. The former risks inadequately informing clinicians and patients during medical decision-making; the latter may result in inappropriately withholding potentially beneficial surgical intervention.

We hypothesize that a continuous, probabilistic approach to survival modeling will provide a more accurate representation^4,7 of the relationship between the factors influencing the survival of patients with glioblastoma after surgical resection than is achievable with current, categoric models. High-level interpretation of a continuous, probabilistic survival model can provide additional insight into the general role of surgery in glioblastoma management and into the nature of the relationship between EOR and survival. Also, individualized application of the model using patient-specific covariate data allows clinicians to calculate personalized survival curves, to estimate individual median survival, and to predict the patient-specific, incremental survival effects of quantitative changes in EOR and of qualitative changes in adjuvant therapeutic strategy.

PATIENTS AND METHODS

Patient Selection

Our investigation was approved by the institutional review boards at The University of Texas MD Anderson Cancer Center (IRB No. DR07-0585) and at the Cleveland Clinic (IRB No. 2559). The MD Anderson Cancer Center Neuro-Oncology database was used to identify all patients who underwent initial surgical resection of histologically confirmed glioblastoma between June 1, 1993 and October 20, 2011. All patients at least 18 years old were eligible for inclusion (n = 933). Patients who were alive at the time of analysis (n = 165; 17.7%) were excluded so that all analyzed survival data were noncensored. Patients with incomplete preoperative and postoperative magnetic resonance imaging volumetric tumor data were also excluded (n = 47; 5.0%). A total of 721 patients met all criteria and comprised the study sample (Table 1). Identical inclusion criteria were used to identify 109 novel patients with glioblastoma treated at the Cleveland Clinic, and this data set (Cleveland Clinic validation data) was used for external validation purposes.

Table 1.

Patient Demographic Characteristics (N = 721)

Characteristic	No. of Patients	%
Sex
Male	430	59.6
Female	291	40.4
Age at diagnosis, years
Mean	59.4
SD	12.3
Median	60.1
Q1, Q3	51.6, 68.4
Range	18.6-87.8
KPS
< 60	39	5.4
60	26	3.6
70	95	13.2
80	213	29.5
90	284	39.4
100	64	8.9
Median	80
Q1, Q3	80, 90
Symptoms at presentation
Headache	302	41.9
Visual problems	154	21.4
Dizziness	47	6.5
Cranial neuropathy	31	4.3
Nausea or vomiting	101	14.0
Sensory symptoms	74	10.2
Speech problems	222	30.8
Seizure	185	25.7
Focal weakness	234	32.4
Memory deficits	183	25.4
Mental status changes	115	16.0
Confusion	85	11.8
Unsteady gait	98	13.6
Other	56	7.8
Tumor location
Brain stem, basal ganglia, or thalamus	18	2.5
Cerebellar	9	1.2
Frontal	234	32.5
Occipital	31	4.3
Parietal	88	12.2
Temporal	242	33.6
Intraventricular/pineal/suprasellar	6	0.8
Multifocal	93	12.9
Tumor side
Right	345	47.9
Left	353	49.0
Midline	7	1.0
Bilateral	16	2.2
Functional involvement
Eloquent	302	41.9
Near eloquent	356	49.4
Noneloquent	63	8.7
Imaging characteristics
Mass effect	513	71.2
T1 postgadolinium enhancement	721	100
Calcified	2	0.3
Hemorrhagic	77	10.7
Prior therapy
Prior biopsy	174	24.1
Corticosteroids before surgery	405	56.2
Antiepileptics before surgery	440	61.0
Postoperative adjuvant therapy
Postoperative XRT, any regimen	469	65.0
Adjuvant chemotherapy
Any regimen	406	56.3
Regimen containing temozolomide	354	49.1
Regimen not containing temozolomide	52	7.2
Volumetric data, mL
Preoperative
T1 hypointensity
Mean	4.0
SD	22.5
T1 postgadolinium enhancement
Mean	33.7
SD	25.6
T2/FLAIR hyperintensity
Mean	59.2
SD	61.5
Total volume
Mean	96.82
SD	79.5
Postoperative
T1 hypointensity
Mean	1.2
SD	9.2
T1 postgadolinium enhancement
Mean	1.8
SD	4.9
T2/FLAIR hyperintensity
Mean	24.9
SD	30.8
Total volume
Mean	27.9
SD	34.8
Extent of resection, % by volume
T1 hypointensity		85.1
T1 postgadolinium enhancement		94.7*
T2/FLAIR hyperintensity		60.0
Total volume		76.1

Abbreviations: EOR, extent of surgical resection; FLAIR, fluid-attenuated inversion recovery; KPS, Karnofsky performance score; Q1, first quartile; Q3, third quartile; SD, standard deviation; XRT, cranial radiotherapy.

^*More information on the distribution of the EOR variable is in the Data Supplement.

Summary of Analytic Methods

Forty patient-specific preoperative features were screened for potential inclusion in the survival model (Table 1) through a multistep statistical process involving correlation testing and univariable and multivariable analysis. The features selected using this reductive strategy were used as covariates for predictive survival modeling using the log-logistic accelerated failure time (AFT) method.^12,13 The applicability of this approach and the validity of the final model were tested through distribution analysis, proportional odds assessment, and residual analysis (Data Supplement).^12,13

Goodness-of-fit, explanatory ability, and model-based statistical significance were tested using standard metrics. Pseudoexternal validation was performed using 20% bootstrapping and leave-one-out crossvalidation. True external validation was performed by measuring the median absolute predictive error (APE; Data Supplement) that was observed when the study model was applied to the validation set of 109 novel patients with glioblastoma (Table 2).

Table 2.

Model Validation

Characteristic	Model MD Anderson AFT Model (median)	Pseudoexternal Validation						True External Validation Cleveland Clinic Glioblastoma Data
		Holdout Validation					Leave-One-Out Crossvalidation
		80% Training Set (median)	20% Test Set (median)	Full v Training (P)	Full v Test (P)	Training v Test (P)		Median	P
Actual survival, months	11.57	11.16	13.00	.78	.38	.28		12.17
				.56
Predicted survival, months	10.90	10.54	11.10	.57	.67	.93		14.60
				.82
SE of prediction	0.82	0.79	0.77					0.47
SE, %	7.30	0.22	0.23					3.53
Difference (actual-predicted, net)	−0.02	−0.21	0.49	.96	.17	.18		−0.43	.79
				.36
Difference (actual-predicted, absolute)	4.37	4.46	4.06	.69	.26	.16		4.42	.33
				.39
R2	0.31	0.30					0.31
C index		0.69					0.69

Characteristic	Comparison to Alternate Models
	Final Model	EOR > 98%	EOR > 95%	EOR > 90%	EOR > 85%	EOR > 80%	Berger RPA Category	EOR > 98% With XRT and TMZ As Factors
Median absolute predictive error, months*	4.37	5.57	5.77	5.83	5.80	5.90	5.60
Difference v model, %		21.5	24.2	25.1	24.7	25.9	21.9
P v final model		< .001	< .001	< .001	< .001	< .001	< .001
R2	0.307	0.054	0.040	0.027	0.023	0.014	0.067	0.278
Log-ratio test, χ2	264.2	40.1	29.8	19.6	16.8	9.9	49.6	234.6
Degrees of freedom	5	1	1	1	1	1	4	3
P v final model		< .001	< .001	< .001	< .001	< .001	< .001	< .001

NOTE. Multiple approaches were used to test the goodness-of-fit and the external validity of the survival model. The top section presents data from both pseudoexternal validity tests (20% bootstrap and leave-one-out crossvalidation) and from true external validation (using a novel sample from a different institution). The holdout (bootstrap) analysis shows that there is no statistically significant difference between the median estimated survival using the study model versus a novel model trained on 80% of the original data and tested against the remaining 20% (10.54 v 11.10 months; P = .57). Similarly, the median of the patient-level differences between actual and predicted survival is not significant between the study model and the 20% test model (4.37 v 4.06 months; P = .26). The remaining P values are included to illustrate that the complete, training, and test sets are fundamentally similar regarding relevant parameters. Model-fit testing of both the holdout and the leave-one-out crossvalidation suggest that the model fit and the explanatory ability of the study model is stable under holdout validation testing (r²; c index).

The true external validation tested the study model on 109 novel patients with glioblastoma collected at a different institution with a similar, tertiary care clinical brain tumor practice. Survival characteristics of both the primary (MD Anderson) and the validation (Cleveland Clinic) patient populations were similar, and model testing showed no significant difference in median individualized predictive error when the study model was applied to the novel, external dataset (4.37 v 4.42 months; P = .33). All P values were calculated nonparametrically using the Mann-Whitney U test.

The bottom section compares the median absolute predictive error of the study model with that of seven alternate methods for individual survival prediction, and the statistical significance of this difference is tested using the Mann-Whitney U test. The relative explanatory abilities of the models for survival are compared using Nagelkerke's Pseudo R² (larger values indicate superior explanatory ability). Finally, the overall statistical significance of each model is compared with that of the study model using the log-ratio test and the results are presented both in terms of absolute difference of the χ² statistic (with degrees of freedom) and as a P value. This analysis shows that the study model predicts individual survival more accurately (overall) than any of the EOR-threshold–based models, even when adjuvant XRT and TMZ are accounted for as covariates. Similarly, the model outperforms the recently proposed, four-class RPA model suggested by Sanai et al.⁴ The methods for calculating the APE are discussed in detail in the text and in the Data Supplement.

Abbreviations: AFT, accelerated failure time; APE, absolute predictive error; c index, concordance index; EOR, extent of surgical resection; RPA, recursive partitioning analysis; TMZ, temozolomide-based chemotherapy; XRT, cranial radiotherapy.

^*Distributions across all groups are tested with a one-way, three-class, independent samples Kurskal-Wallis test.

Accuracy of personalized survival prediction and comparative explanatory ability of the study model was tested against current EOR-threshold-only models and their derivatives using APE and Nagelkerke's pseudoR², respectively (Table 2).

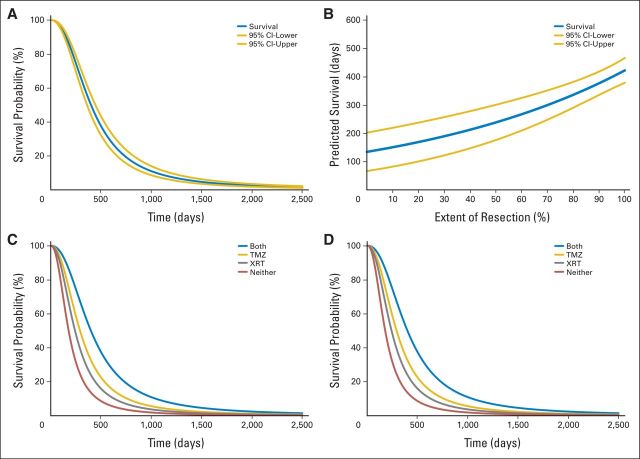
The final model was used to generate prototypic patient-specific survival profiles comprising four curves representations of the relationship between model parameters and survival (see Discussion; Fig 1). These curves can also be used to calculate the incremental survival effects of changes in EOR and adjuvant therapy regimens (Figs 2 and 3).

Fig 1.

Personalized survival profile for a hypothetical patient. This figure depicts the four primary curve sets that comprise a patient-specific survival profile constructed using this model. The specific curves used in this example are for a hypothetical 72-year-old patient with a Karnofsky performance score (KPS) of 80. (A) Survival curve. This curve depicts a patient's estimated probability of survival at any time in days (gold lines, 95% CIs). It can be used to calculate the estimated survival for any percentile (including the median, where p(x) = 0.5. It presents the most comprehensive survival information but requires that all covariates in the model be known. Here, extent of resection (EOR) of gadolinium-enhancing (T1) tumor is 98%, cranial radiotherapy (XRT) is positive, and temozolomide-based chemotherapy (TMZ) is positive. This curve is useful to determine survival rates either preoperatively (when the plan for adjuvant therapy is known and the surgeon can estimate the anticipated extent of resection) or postoperatively (when all values are known explicitly). (B) Survival versus EOR curve. This curve presents estimated median survival as a function of EOR (gold lines, 95% CIs). This curve is particularly useful preoperatively to a surgeon attempting to determine the incremental survival advantages associated with increases in EOR (Fig 2, application details). Here, XRT is positive and TMZ is positive. (C) Survival versus adjuvant therapy curves. This is the family of survival curves (similar to A) generated when all possible combinations of XRT and TMZ variables are simulated. It can be used to calculate the estimated survival for any percentile [including the median, where p(x) = 0.5] when various adjuvant therapy strategies are applied. Although adjuvant chemoradiotherapy is currently considered standard of care, individual circumstances or patient preferences may require assessment of the individualized survival advantages of alternate adjuvant strategies. This curve is useful for investigating these relationships and informing individualized treatment plans. Here EOR is 98%. (D) Survival, EOR, and adjuvant therapy curve. Combining the simulations used for (B) and (C) produces a family of curves stratified by adjuvant therapy strategy for which the survival estimate is a function of EOR. This family of curves provides a considerable amount of clinically relevant information using relatively little specified data; only the values of the invariant parameters in the model (age and KPS) are required and the rest are simulated using the model for all possible covariate values. This representation, which simulates and then summarizes the effects of all of the modifiable factors in the survival equation, is useful preoperatively to inform survival implications of various combinations of surgical resection strategies and adjuvant therapy modalities.

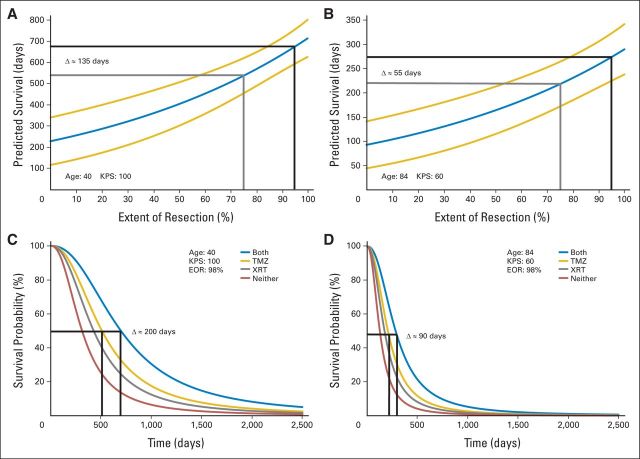
Fig 2.

Personalized survival effects of extent of resection (EOR) of gadolinium-enhancing (T1) tumor or adjuvant therapy as individual covariates. These figures illustrate how to use survival versus EOR curves (Fig 1B) or survival versus adjuvant therapy curves (Fig 1C) to estimate the personalized survival effects of changes in these modifiable covariates. (A and B) Survival implications of 75% (gray) versus 95% (black) EOR in two different patients. (A) The estimated incremental survival benefit of a more aggressive resection in a hypothetical young (age, 40 years), high-functioning (Karnofsky performance score [KPS], 100) patient is calculated at 135 days. (B) In contrast, a similar calculation in a hypothetical patient who is elderly (age 84 years) and debilitated (KPS, 60) has the same incremental survival benefit at only 55 days. These curves illustrate the importance of patient-specific covariates in the relationship between survival and EOR, and they can inform surgeons of the potential advantages of a more aggressive resection. This, in turn, provides better information on which patient-specific decisions regarding the risk/benefit balance of more aggressive surgical resections can be based. (C and D) Survival implications of alternative adjuvant therapy strategies in two different patients. (C) The estimated incremental survival benefit of adjuvant temozolomide alone (TMZ) versus adjuvant temozolomide plus radiotherapy (XRT) in a hypothetical young (age, 40 years), high-functioning (KPS, 100) patient is calculated at 200 days. (D) In contrast, a similar calculation in a hypothetical patient who is elderly (age 84 years) and debilitated (KPS, 60) results in an incremental survival benefit of only 90 days. These curves illustrate the importance of patient-specific covariates in the survival advantages of adjuvant therapy, and they can inform oncologists of the potential advantages of more aggressive adjuvant therapy. This, in turn, provides better information on which patient-specific decisions regarding the risk/benefit balance of the ideal, patient-specific adjuvant therapy strategy can be based. These curves also show that the survival effects of both EOR and adjuvant therapy vary with patient-specific covariates. This may have implications for the design, analysis, and interpretation of future trials that incorporate surgery, TMZ, or XRT as part of the glioblastoma management strategy being studied.

Fig 3.

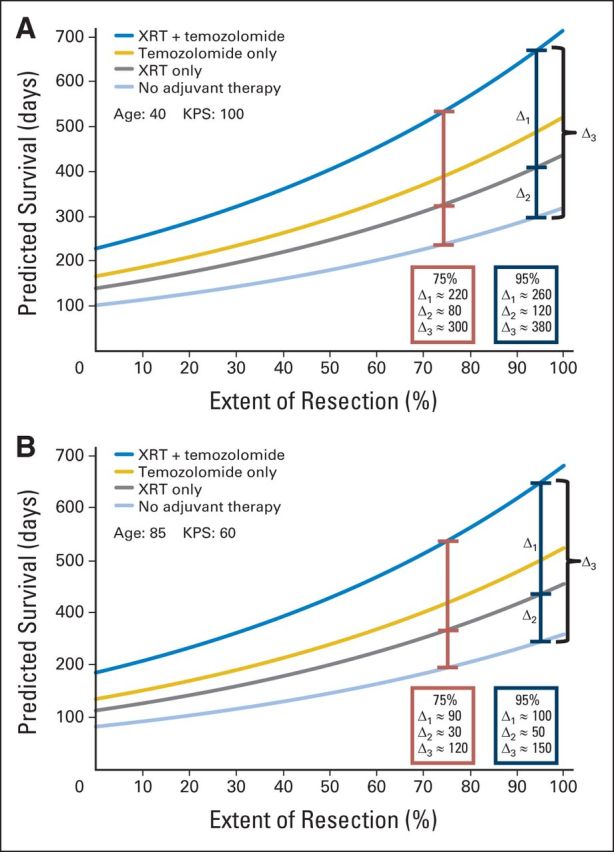
Personalized survival effects of extent of resection (EOR) of gadolinium enhancing (T1) tumor and adjuvant therapy as simultaneous covariates and how to use an integrated EOR and adjuvant therapy survival curve (Fig 1D) to estimate the personalized survival effects of simultaneous changes in these modifiable covariates. (A) The combined effects of EOR and adjuvant therapy on estimated survival in a hypothetical young (age 40 years), high-functioning (Karnofsky performance score [KPS], 100) patient is examined. When 95% resection is achieved (blue intervals), cranial radiotherapy (XRT) alone adds an estimated 120 days of survival (Δ₂) and concomitant temozolomide-based chemotherapy (TMZ) adds an additional 260 days (Δ₁) for a total of 380 days of estimated survival advantage versus no adjuvant therapy (680 days v 300 days total, Δ₃). When EOR is decreased from 95% to 75%, the absolute values of the intervals decrease, and the absolute survival advantage is reduced (relative to the estimated survival for 95% EOR) from 680 to 540 days. (B) The combined effects of EOR and adjuvant therapy on estimated survival in a hypothetical patient who is elderly (age 84 years) and debilitated (KPS, 60) is examined. When 95% resection is achieved (blue intervals), XRT alone adds an estimated 50 days of survival (Δ₂) and concomitant TMZ adds an additional 100 days (Δ₁) for a total of 150 days of estimated survival advantage versus no adjuvant therapy (270 days v 120 days total, Δ₃). When EOR is reduced from 95% to 75%, the absolute values of the intervals decrease and the absolute survival advantage is reduced (relative to the estimated survival for 95% EOR) from 270 to 220 days. Together, these observations may have implications for the interpretation of the incremental advantages of adjuvant therapy as well as for the design, analysis, and interpretation of future trials that incorporate surgery, TMZ, or XRT.

A detailed discussion of the statistical and mathematical methods is presented in the Data Supplement.

RESULTS

Final Model

The final survival model has an intercept and five variables (Table 3). This includes three continuous variables, age, the natural log of the preoperative KPS, and EOR, plus two categoric variables (0, absent; 1, present) describing adjuvant therapy, cranial radiotherapy (XRT; positive if the patient received any postoperative radiotherapy) and temozolomide (TMZ; positive if the patient received any postoperative chemotherapeutic regimen that included temozolomide). The rationale for these definitions is presented in the Data Supplement. Distribution, log-odds, and residual analyses confirmed the applicability of the log-logistic AFT model (Data Supplement).

Table 3.

Survival Model

Characteristic	Final Model
	Coefficient	SE	P
Intercept	1.1754	0.7072	.0965
Adjuvant XRT (1 = yes)	0.3157	0.0835	< .001
Adjuvant temozolomide (1 = yes)	0.492	0.0795	< .001
Age, years	−0.0104	0.0024	< .001
ln(KPS)	0.8391	0.1545	< .001
Extent of resection of enhancement, % as decimal	1.1399	0.2569	< .001
Model χ2	264.2
P			< .001
R2	0.307

NOTE. Covariates included in the accelerated failure time survival model. The log-logistic accelerated failure time model is a proportional odds model with multiplicative hazards. This differs from the more common additive, proportional hazards of the Cox model, and so care should be exercised when interpreting these model covariates.

Abbreviations: KPS, Karnofsky performance score; ln, natural log; XRT, cranial radiotherapy.

Model Validation

Model fit (internal validity) was confirmed by testing the statistical significance of the final model versus the null model (χ² = 262.4; P < .001) and the significance of each term in the model (all P < .001; Table 3). R² was calculated to investigate the degree to which the model explains the observed survival. The model's R² value of 0.307 suggests that the covariates explain approximately 30% of the variability seen in the estimated survival. Internal model accuracy for individualized survival estimation was assessed by calculating the median APE for the source data set (Data Supplement), which was 4.37 months with an SE percent of ± 7.3%. Pseudoexternal validity was assessed by examining pseudoR² and concordance indices (c index) from two holdout models: 20% bootstrapping and leave-one-out crossvalidation. The pseudoR²s were 0.30 and 0.31, respectively, which closely approximate that of the final model. Additionally, the c indices were 0.69 and 0.69, respectively, suggesting good model concordance with the underlying data. True external validity was assessed by determining the APE of the model when applied to a novel data set of 109 patients collected at a different institution. The median APE for that data set was 4.42 months with an SE percent of ± 3.53%. This suggests that the model performs at least as well on completely novel data as it does on the native training set (Table 2).

Comparison With Current Models

The pseudoR² for the five threshold-only models^4,7,8 and for the recursive partitioning model described by Sanai et al⁴ ranged from 0.014 to 0.067. This is markedly less than the study model's value of 0.307, suggesting that the study model has considerably more explanatory ability for survival than models based only on EOR thresholds or on recursive partitioning analysis classes.⁴ A model that combines an EOR greater than 98% with categoric data on adjuvant therapy had a pseudoR² of 0.278, which is still less than that of the final model. This suggests that the final model provides explanation beyond the simple combination of EOR threshold data plus knowledge of adjuvant therapy modulators. Also, the predictive performance of the final model was significantly better than any of the seven comparators (all P < .001).

The median APE of the final model was 4.37 months. This was better than any of the five threshold-only models or the Sanai et al⁴ recursive partitioning analysis model, which had APEs range from 5.57 to 5.90 months. This represents a 21.5% to 25.9% reduction in the APE of the final model relative to the threshold-only models (all P < .001; Table 2).

Individual Predictive Models

In addition to allowing calculation of point estimates for patient-specific median survival, the study model can also be used to generate at least four types of patient-specific data plots that convey additional, clinically relevant information. The first is a survival curve, which presents the probability of survival p(S) at any time [(t); Fig 1A]. The second depicts the relationship between the median estimated survival and extent of resection of enhancing tumor. This is generated by setting p(S) = 0.5 and solving for EOR over the interval (1,100%; Fig 1B). The third is a family of survival curves for all possible combinations of the categoric variables for XRT and/or TMZ while the remaining patient-specific parameters remain constant (Fig 1C). This plot demonstrates the patient-specific survival effects of each type of adjuvant therapy, alone or in combination. Finally, the fourth plot is a combination of the EOR curve and the adjuvant therapy curves. By again letting p(S) = 0.5 and varying both the EOR and the categoric values of the XRT and TMZ variables, a family of curves that depict the relationship between EOR and adjuvant therapy on median predicted survival can be plotted (Fig 1D).

DISCUSSION

Analysis of 40 potential clinical and imaging features (Table 1) identified five patient-level covariates that make significant contributions to a model for survival prediction: age, KPS, EOR, and adjuvant therapy with XRT and/or temozolomide. The covariate coefficients (Table 3) show that lower age, higher KPS, higher EOR, and positive XRT and TMZ are associated with increased survival. All of these factors have been previously demonstrated to have similar qualitative influence on survival,^2–8 which supports the results of our feature selection and modeling processes.

The study model has been specifically designed to be used clinically before surgery for the purpose of better informing the surgical decision-making and consent processes, so only factors whose values are available before surgery have been included in the model. Although the actual values of the EOR and adjuvant therapy variables are not precisely known preoperatively, they are commonly estimated by the surgeon and can be used on an intention-to-treat basis.

In contrast with the Cox proportional hazards model, log-logistic AFT modeling is particularly useful for applications that involve prospective prediction (in this case, survival) because the model is closed-form, involves a fixed intercept, and is associated with explicit hazard and survival functions.^12,13 This enables accurate point estimation of median survival and facilitates construction of probabilistic survival curves (Fig 1A) that are explicit and patient-specific, rather than being estimated by scaling the population median with semiquantitative hazards (as with the Cox proportional hazards model). Also, univariable and multivariable model-based simulation allow straightforward investigation and graphical representation of the patient-specific relationships between individual or combined covariates (eg, EOR, adjuvant therapy) and survival (Figs 1B to 1D).

The AFT modeling approach to the survival analysis (Table 3) yields at least five novel, clinically relevant results that were previously unavailable using categoric survival models. These are summarized herein and are subsequently discussed in additional detail.

Patient-specific median survival estimates calculated using this model are more accurate than patient-level secondary generalizations of categoric median survival data from previous investigations (Table 2). Patient-specific survival curves, which offer more information than point-estimates of median survival, and covariate-specific incremental survival curves can be computed (Fig 1) using this model. Survival versus EOR curves can inform personalized, preoperative surgical decision-making by estimating the individual, incremental survival benefits associated with more aggressive surgical resections (Fig 2). Survival versus adjuvant therapy curves can be used to quantify the patient-specific survival benefits of adjuvant therapy (Figs 1 to 3). EOR versus adjuvant therapy curves can depict the complex relationship between these variables and the survival effects associated with their simultaneous, multivariable manipulation (Fig 3 and Data Supplement).

The most basic survival statistic of interest to both clinicians and patients is the estimated median survival. Our results demonstrate that using a patient-specific AFT survival model improves predictive accuracy by 21.5% to 25.9% over current EOR-threshold-only models (Table 3). We believe that this can be attributed to a combination of the personalized predictive approach (as opposed to a secondary generalization of categoric survival data) facilitated by the study model and to the predictive advantages of the AFT over the more commonly applied Cox proportional hazards survival model.^12,13

Static median survival estimates present a limited view of the expected clinical course for a patient with glioblastoma. By using the study model to construct personalized survival curves, the patient and clinician are afforded a more comprehensive, probabilistic overview of the expectation of survival as a function of time (Fig 1A). Also, by simulating variations in the expected EOR and/or the course of adjuvant therapy, a comprehensive view of the influence of these parameters on survival as a function of time can be appreciated (Figs 1B and 1C). This provides the patient and clinician with much more information on which to base management decisions and the informed consent process.

During the preoperative surgical decision-making process, surgeons and patients must weigh the potential survival benefits of aggressive resection against the risks of postoperative neurologic deficits. This is particularly true of tumors that involve or are adjacent to eloquent areas, where extending the resection by only a few percent may significantly increase the risk of deficit. The prior neurosurgical literature, which has focused on EOR thresholds,^4–8 is of limited utility for informing these decisions. Although it shows that achieving a prescribed EOR threshold is likely to improve overall median survival, the patient-specific relationship of EOR and survival can neither be specified accurately nor estimated quantitatively using these data. In this context, increased risks may be unnecessarily accepted to achieve an EOR threshold perceived as critical for prolonged survival, or surgical resection may be withheld in favor of a biopsy-only strategy because the surgeon feels that an adequate EOR threshold cannot be safely achieved and that subthreshold resection is meaningless. In either circumstance, inadequate patient-specific information regarding the relationship of EOR and survival could lead to suboptimal surgical decision-making.

Using the study model, holding all patient-specific parameters constant and varying EOR from 1% to 100% produces a curve of estimated median survival as a function of EOR (Fig 1). This curve can then be used to calculate the incremental survival advantages associated with incremental changes in EOR (Figs 2A and 2B), and these data can be used in the context of patient-specific management priorities to more accurately inform the decision-making process regarding the intended EOR.

Because the estimated survival is a function of four additional patient-specific covariates, the magnitude of the incremental advantage of increasing EOR will vary between patients. Similarly, because the survival function is nonlinear, the absolute change in estimated median survival per unit EOR will not be constant over the entire EOR spectrum for a given patient (eg, the survival advantage of going from 93% to 98% may be different than the advantage of going from 40% to 45% in a given patient, despite the identical ΔEOR = 5%). These observations illustrate the importance of determining the personalized relationship between survival and EOR during the management decision-making process, and the AFT facilitates this determination.

Examining the general behavior of the median survival versus EOR curves calculated using the study model advocates for an important paradigm shift in the surgical management of glioblastoma; namely, it favors a maximum safe resection rather than a percent-EOR-threshold approach to glioblastoma surgery. Whereas the static, dichotomous nature of the analytics applied in previous investigations of the relationship between EOR and survival could only be interpreted as representing a critical resection threshold, the curves generated using the study model suggests a continuous relationship between EOR and median survival.

Clinically, this suggests that there is a survival advantage associated with any degree of resection and therefore provides the first explicit evidence supporting the practice of maximum safe resection for glioblastoma. Similarly, this model argues against the practice of withholding surgery based on the belief that failure to achieve some predefined EOR threshold will negate potential survival benefits of surgery. Conceptually, this brings glioblastoma surgery in line with many other forms of oncologic surgery, where cytoreductive procedures are performed for maximum safe reduction of tumor burden in preparation for adjuvant therapy.

Surgical resection of glioblastoma is currently undertaken as part of a comprehensive, multimodality approach to management that also includes adjuvant XRT and chemotherapy.^2,3 However, extenuating clinical circumstances or unique patient preferences may prompt the neurooncologist to consider management strategies that omit one or both adjuvant modalities. Previously, the effect of such decisions on estimated median survival could only be generalized from aggregate data that describe the incremental advantages of such therapies. However, using the AFT model, all four possible combinations of the adjuvant therapy options (± XRT and ± TMZ) can be simulated and a family of survival curves can be generated (Fig 1C). When EOR is known (eg, postoperatively), these curves can be used to estimate the incremental differences in survival of any percentile for each of the four alternate strategies of adjuvant therapy (Figs 2C and 2D). When EOR is not yet known (eg, preoperatively), the effect on median survival of alternate adjuvant therapy strategies can be examined in the context of variable EOR by combining the two simulation processes (Fig 1D). This allows the incremental effects on median survival for each adjuvant therapy to be calculated for any given EOR (Fig 3).

Analysis of these curve families also suggests that patient-specific covariates (including EOR) influence the magnitude of the incremental benefit of adjuvant XRT and temozolomide (Figs 1D and 3). This finding suggests that these factors may need to be considered when designing future adjuvant therapy trials and be accounted for during the analysis and interpretation of such data.

Age, preoperative KPS, EOR, and postoperative treatment with radiotherapy and with temozolomide-containing chemotherapy regimens affect the postresection survival rates of patients with glioblastoma. A nonlinear, multivariable AFT model incorporating these factors provides more accurate point-estimates of median survival than previous methods based on secondary generalizations of the median survival of categoric patient groups. Also, AFT modeling allows prospective, preoperative, patient-specific construction of probabilistic survival curves and allows the relationships between survival, EOR, and adjuvant therapies to be estimated quantitatively. These comprehensive predictive survival analyses provide significantly more information to patients and clinicians regarding the anticipated course of disease, the overall prognosis, and the influence of modulatory factors than do previous, static estimates of median survival, and this information can be used to improve the quality of surgical decision-making and of the informed consent process. A free, online tool for performing individual, patient-level predictive analyses using this model is available at http://www.neurosurgeryriskprofiles.com. The continuous nature of expected median survival as a function of EOR argues against a surgical management strategy based on EOR thresholds and instead provides the first explicit evidence supporting a maximum safe resection approach to glioblastoma surgery.

AUTHORS' DISCLOSURES OF POTENTIAL CONFLICTS OF INTEREST

The author(s) indicated no potential conflicts of interest.

AUTHOR CONTRIBUTIONS

Conception and design: Nicholas F. Marko, Robert J. Weil, Raymond E. Sawaya

Financial support: Nicholas F. Marko, Raymond E. Sawaya

Administrative support: Robert J. Weil, Dima Suki, Raymond E. Sawaya

Provision of study materials or patients: Robert J. Weil

Collection and assembly of data: Nicholas F. Marko, Robert J. Weil, Jason L. Schroeder, Dima Suki

Data analysis and interpretation: Nicholas F. Marko, Robert J. Weil, Frederick F. Lang

Manuscript writing: All authors

Final approval of manuscript: All authors