Decision-theoretic designs for small trials and pilot studies: A review

Abstract

Pilot studies and other small clinical trials are often conducted but serve a variety of purposes and there is little consensus on their design. One paradigm that has been suggested for the design of such studies is Bayesian decision theory. In this article, we review the literature with the aim of summarizing current methodological developments in this area. We find that decision-theoretic methods have been applied to the design of small clinical trials in a number of areas. We divide our discussion of published methods into those for trials conducted in a single stage, those for multi-stage trials in which decisions are made through the course of the trial at a number of interim analyses, and those that attempt to design a series of clinical trials or a drug development programme. In all three cases, a number of methods have been proposed, depending on the decision maker’s perspective being considered and the details of utility functions that are used to construct the optimal design.

1 Introduction

There is little consensus on the way in which pilot studies and other small exploratory clinical trials should be designed, with a relatively wide range of approaches proposed.^1–4 In part, this reflects the range of objectives for such studies. Pilot studies are usually designed to explore and evaluate the efficacy and safety of a new/experimental treatment or new combination/regime of treatments, perhaps to provide some evidence of response in order to justify the financial input required for larger-scale studies, though they may also address specific additional or alternative research questions. Generally, the sample size required in pilot studies is quite small, as they commonly precede a larger definitive clinical trial. The terminology of such small exploratory clinical studies reflects the range of objectives, with small trials that are conducted prior to a major definitive study referred to as ‘pilot studies’, ‘feasibility studies’ or – if the following study is a ‘phase III’ trial – ‘phase II clinical trials’. While a phase II clinical trial can be in some cases relatively large, it usually has key objectives to decide whether or not and how to conduct the following phase III trial(s). The different terminology depends sometimes on, often fairly subtle, differences in the aim of the study, but also on the setting in which the study is being conducted, with different names being used for trials with essentially the same purpose conducted by pharmaceutical companies and in the public sector, for example.

The variety in design approaches in pilot studies and other small early phase trials is in contrast to the setting of confirmatory or phase III clinical trials where almost all trials are designed using a frequentist paradigm so as to control probabilities of a type I error, corresponding in this setting to claiming an experimental treatment is better than the control treatment when it is not, and of a type II error, that is failing to claim that the experimental treatment is better when it is by some specified magnitude. The type I error rate is usually, although only by convention, set at a (two-sided) level of 0.05 and the type II error rate is conventionally set at 0.10 or 0.20, corresponding to a power of 0.9 or 0.8, respectively.^5,6

The frequentist approach with conventionally used error rates for a typical effect size may lead to the relatively large sample sizes associated with confirmatory studies, so may not be appropriate when the sample size is smaller. This is the case in pilot studies and early phase trials. Small trials may also be unavoidable, for example, in the setting of trials in small population groups such as patients suffering from a rare disease, patient groups where patient recruitment is difficult such as children and other vulnerable populations or in a specifically targeted subpopulation. In these settings, then, either the frequentist approach can be applied with error rates relaxed, or some other method must be used to design the trial.^7–10

A number of novel approaches have been proposed for pilot studies and other small clinical trials. As the sample sizes are small, often with recruitment occurring relatively slowly, sometimes in a single centre, multi-stage designs with decisions made at one or more interim analyses are often an attractive option, as are multi-arm trials, widening the range of design choices further. Alternatives to the frequentist paradigm that have been proposed for the design of such small clinical trials include the Bayesian approach and the decision-theoretic approach in which, as described in the next section, the consequences of decisions are explicitly modelled. The latter might seem particularly appropriate in pilot studies and early phase clinical trials as the outcome from such trials is often a relatively simple decision that is within the control of the clinical team conducting the trial, such as the decision whether or not to conduct further clinical research in the area, sometimes called ‘Go/No-Go’ decisions.

The aim of this article was to review methods for the design of small trials and pilot studies where the primary aim is to explore and evaluate treatment efficacy based on the Bayesian decision-theoretic framework. In order to provide as comprehensive as possible a review of the current literature in this area, we used systematic reviewing methodology to identify relevant published work in the area. In addition, human pharmacology studies that aim to assess toxicity, to explore drug metabolism and drug interactions, or to describe the pharmacokinetics and pharmacodynamics are usually designed as small studies. These studies are sometimes known as ‘phase I’ trials. Although the sizes of these studies tend to be small, their objectives are not to explore and evaluate the efficacy of a new/experimental or new combination/regime of treatments. As such, these studies are excluded from the review of this paper.

Pilot or feasibility studies may also be used to test practical aspects intended to be used in a later study such as drug supply, acceptability of randomization or visit schedules and so on. Such studies, which may closely resemble a larger study conducted in miniature are, however, outside the scope of this paper.

Following this introduction, the next section of the article gives a very brief overview of the decision-theoretic approach as it may be applied to clinical trial design. The third, and most substantial, section of the article then describes the review method used and gives details of publications found. Papers are classified into a number of groups according to the specific type of design being considered, the types of utility function proposed and the perspective of the decision-maker (commercial, regulatory/societal or patient). The aim is to allow the reader to rapidly identify key references in each particular area. The paper ends with a brief discussion of the scope of the review, suitability of the decision-theoretic paradigm for pilot study design and suggestion of areas where further research work might be most appropriate.

2 The decision-theoretic approach to clinical trial design

Decision theory is a statistical technique by which the problem of decision-making under uncertainty may be formalized. The method enables an optimal decision to be made between a number of possible actions on the basis of the consequences of each action under all possible scenarios.^11–13

In the setting of a clinical trial, we may wish to decide between a number of possible design options. Prior to the start of the trial, this might entail a choice of the clinical trial sample size. During the trial at an interim analysis, a decision might be taken as to whether or not to terminate the trial or to modify the trial conduct in some way. At the end of the trial, this might correspond to a decision of whether or not to proceed with further trials, or in a multi-arm study, to choose an experimental treatment for further evaluation.

Denote by Y the vector of responses from n patients in a clinical trial, with Y assumed to follow a distribution with density function of known form with some unknown parameter(s), θ. Having observed Y = (y₁, y₂, … , y_n), a decision, to choose one from a set of possible actions, 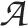 = {a₁, a₂, …} is made. Suppose that the consequences associated with each possible action can be expressed by some loss or gain. As the consequences may well depend on the true unknown state of nature, the loss or gain will be a function of parameter θ. This function is called a loss, gain or utility function. Therefore, the utility function for action a may be written as U_a(θ).

Uncertainty regarding the parameter θ may be expressed in terms of a Bayesian prior distribution, or, following observation of some data, by the corresponding posterior distribution. The expected utility from taking action a is then the expected value E(U_a(θ)), the expectation being taken over this prior (or posterior) distribution. Comparing expected utility values for different actions enables the optimal action to be determined.

The utility functions should express the values of the consequences of possible actions from the perspective of the decision-maker. These could be monetary loss or reward, which is measurable on an existing scale, or could also express consequences that have no immediately obvious numerical scale of measurement, such as treatment success (patient experienced a positive response) or treatment satisfaction. In the latter cases, it can be very difficult to assign the numerical values required to specify the utility function to the qualitative values, as considered in the discussion section below.

Similarly, the prior distribution should reflect prior belief regarding the parameters of the distribution of the responses. The source of information for the prior distribution may be obtained from data from previous similar trials, elicitation of expert opinion or, as a conjugate prior, for computational convenience.

Once utility functions have been specified for all possible actions, the optimal trial design can often be obtained by working in a reverse time order using a method known as ‘dynamic programming’ or ‘backward induction’. For example, suppose we wish to obtain the optimal sample size for a single stage trial with a number of possible actions available at the end of the trial. First, all possible actions at the end of the trial are considered and, for given possible observed data Y, their corresponding expected posterior utilities are computed and compared to obtain the optimal action a given Y. Second, since at the planning stage Y is unknown, the expected utility (assuming after the trial the optimal action is chosen) is obtained from the distribution of Y given n and θ. Finally, because also θ is unknown, the expectation of this expected utility is taken over the prior distribution for θ. Thus, overall the expected utility is computed, taking the expectation over the prior predictive distribution for Y given n. This gives the prior expected utility from a trial of sample size n if the optimal action is always taken at the end of the trial. This is a function of n alone, so maximizing this over n gives the optimal sample size, which is thus obtained by finding

$${\arg max}_n\{{\int }_y{max}_a\{\int U_a(\theta )p(\theta |y,n)\text{d}\theta \}f(y|n)\text{d}y\}$$ (1)

where f(y|n) is the density function for y before sampling and with only prior knowledge of θ, that is the prior predictive distribution of y.¹⁴ Note that for discrete responses, the expectation may be the summation for all possible values of y. This method can be extended to multi-stage trials with optimal decisions at the end of a given stage obtained by considering the consequences in terms of decisions taken later in the trial.

Although relatively easily described as aforesaid, the application of decision theory in a clinical trial setting can present a number of challenges: in specification of appropriate prior distributions and, perhaps more especially, in specification of utility functions. When considering decisions made during or prior to the start of a trial, calculations of how the utility functions should incorporate the impact of data as yet unobserved should also be taken into consideration. The required computation can also be challenging, particularly in the case of multi-stage trials.^15,16

3 Review of decision-theoretic approaches to pilot studies and small clinical trials

3.1 Literature review search strategy and results

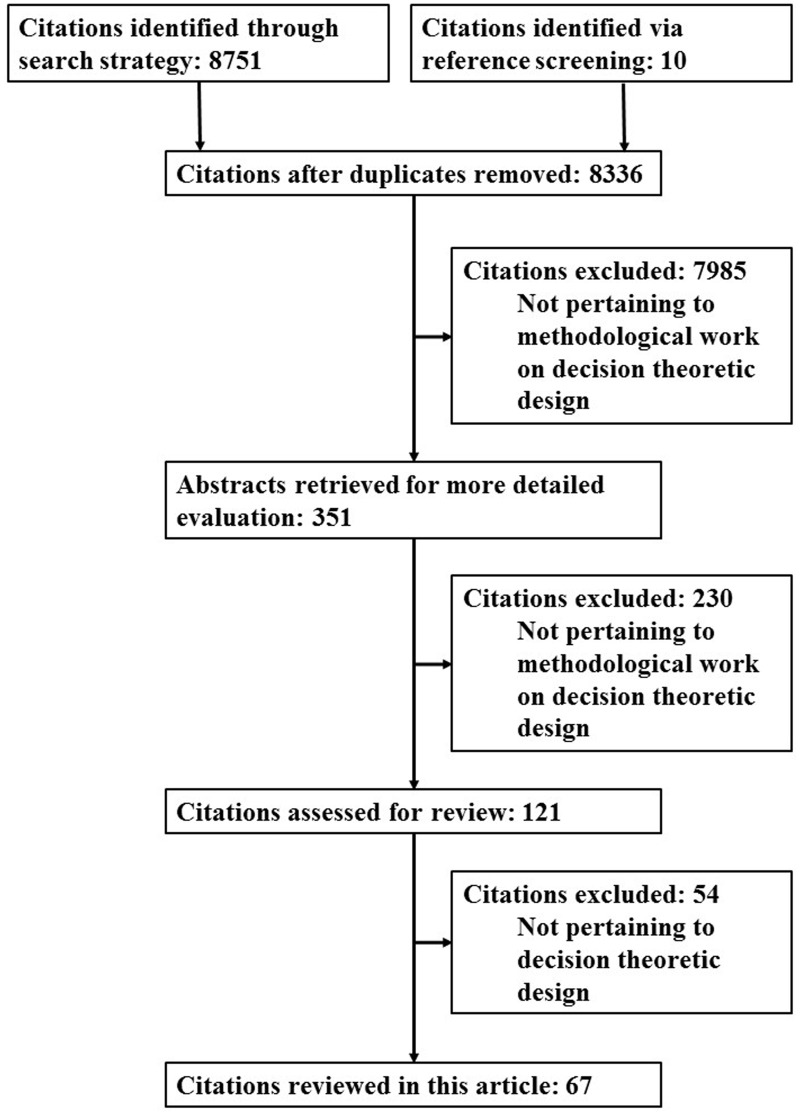
We undertook a systematic search in the electronic database Scopus for research articles published up to 10 October 2014 to identify work on decision-theoretic methods for the design of pilot studies and small clinical trials.¹⁷ The exact search terms used and number of hits from each of these terms are shown in Appendix 1. The searches were not limited by subject area. A total of 8751 articles were identified of which 425 were duplicates, leading to a total of 8326 unique articles. We also identified a further 10 articles via screening of references in relevant articles. Figure 1 shows the flow diagram of articles identified, excluded and included in this review. Articles were screened by title, abstract or whole paper for relevance to this review, leading to final inclusion of 67 articles which are discussed in detail later.^14,18–83 The details of the 67 articles are given in Table 1.

Figure 1.

Flow diagram of articles identified, excluded and included for review.

Table 1.

Articles by types of design, utility and perspective of decision-makers.^a

Types of design	Simple utility				More realistic utility
	Patient	Regulatory/ societal	Commercial	Not specified	Patient	Regulatory/societal	Commercial	Not specified
Single-stage
Single-arm	–	–	–	Lindley14 Staquet and Sylvester38 Sylvester39 Sylvester and Staquet40	–	–	–	Brunier and Whitehead19
Two-arm	–	–	Chen and Beckman20	–	Gittins and Pezeshk56,57 Pezeshk and Gittins73	Claxton and Posnett52 Claxton and Thompson53 Eckermann and Willan54 Gittins and Pezeshk56,57 Halpern et al.58 Hornberger and Eghtesady60 Kikuchi and Gittins63,64 Pezeshk and Gittins73 Pezeshk et al.74 Willan and Eckermann80 Willan and Pinto83	Chen et al.21 Claxton and Thompson53 Gittins and Pezeshk55–57 Kikuchi et al.65 Maroufy et al.68 Patel and Ankolekar71 Pezeshk and Gittins73 Pezeshk et al.75 Willan79 Willan and Eckermann80,81	–
Multi-stage
Single-arm	–	–	–	Banerjee and Tsiatis18 Jung et al.25 Cheng et al.50 Zhao et al.43 Zhao and Woodworth44	–	–	Chen and Smith22 Ding et al.23 Rossell et al.30 Stallard31,32 Stallard et al.37	Zhao et al.43
Two-arm	Heitjan et al.59	–	–	Cheng and Berry47 Cheng and Shen48, 49 Cheng et al.50 Chernoff and Petkau51 Jennison and Turnbull61 Jiang et al.62 Lewis and Berry66 Lewis et al.67 Nixon et al.27 Wang76 Wathen and Christen77 Wathen and Thall78	–	Willan and Kowgier82	Berry and Ho45 Chen and Willan46 Mehta and Patel69	Orawo and Christen70
Multi-arm	–	–	Chen and Beckman20 Lai et al.26	Palmer29 Stallard et al.35 Thall et al.41	–	–	Patel and Ankolekar71 Patel et al.72	–
Enrichment	–	–	–	–	–	–	–	Trippa et al.42
Series of trials	–	Stallard34	Chen and Beckman20 Stallard34	–	–	–	Hee and Stallard24 Pallay28 Stallard33 Stallard and Thall36	–

^aThe total number of articles in the cells exceed 67 as some described more than one design or perspective.

Twenty-seven articles^18–44 specifically described methods in pilot or phase II settings. The others^14,45–83 did not describe methods specific to small clinical trials or pilot studies, but would nevertheless be appropriate in this setting.

A study of the articles identified indicated that the design problems considered fell into three broad categories, with different approaches used for each. The simplest type of design considered was that for clinical trials conducted in a single stage so that decisions considered are those taken at the end of the trial and those taken regarding trial design prior to the start of the trial essentially using the method outlined above. The second type of design considered was that for multi-stage trials, so that decisions taken through the course of the trial, at a number of interim analyses, are also considered. The third type of design considered was that concerning multi-arm trials or the simultaneous optimal design of a series of clinical trials. Within each of these three design types, there was a variety of approaches corresponding to the viewpoint of the decision-maker and the complexity of the utility functions considered, ranging from approaches in which a relatively simple utility function aims to reflect the number of patients successfully treated, to more complex utility functions based on a detailed elicitation of the costs and consequences of a range of possible outcomes from the perspective of a particular decision-maker. Table 1 shows the identified articles classified by types of design, utility function and perspective of the decision-maker. The literature in each of the areas identified is described in the following subsections. One paper⁴² fell outside of the three categories just described, being concerned with the design of enrichment studies. This paper is also discussed further.

3.2 Single-stage designs

The simplest type of study design considered is the single-stage design in which no analysis of the data is conducted until the study is completed. For a trial comparing an experimental treatment with a control (a two-arm trial) or a historical control (a single-arm trial), the statistical design choices are relatively limited; the main one being the choice of sample size. Authors whose works considered this type of design include Brunier and Whitehead,¹⁹ Chen and Beckman,²⁰ Chen et al.,²¹ Claxton and Posnett,⁵² Claxton and Thompson,⁵³ Eckermann and Willan,⁵⁴ Gittins and Pezeshk,^55–57 Halpern et al.,⁵⁸ Hornberger and Eghtesady,⁶⁰ Kikuchi and Gittins,^63,64 Kikuchi et al.,⁶⁵ Lindley,¹⁴ Maroufy et al.,⁶⁸ Patel and Ankolekar,⁷¹ Pezeshk and Gittins,⁷³ Pezeshk et al.,^74,75 Staquet and Sylvester,³⁸ Sylvester,³⁹ Sylvester and Staquet,⁴⁰ Willan,⁷⁹ Willan and Eckermann^80,81 and Willan and Pinto.⁸³

At the end of such a trial, a decision is made from a possible set of actions which typically consists of whether or not to accept the experimental treatment for further study. The utility function may be written simply as a function of the cost of sampling, which is independent of θ, the benefit of treating patients with the experimental treatment and the cost of making an incorrect decision.^{14,20,38–40} The cost of sampling may reflect the costs, interpreted broadly, of recruiting, monitoring or treating patients in the trial, and can be expressed as a cost per patient, in some cases expressed in monetary units. If the experimental treatment is accepted for further study and it is indeed effective, then some expected number of future patients will benefit from it. In considering the cost of making an incorrect decision (i.e. accepting an ineffective experimental treatment or rejecting an effective experimental treatment), one may assign an absolute value to each of these consequences, but this is not as easy as assigning monetary rewards or loss. As the utility function expresses the consequences of actions in relation to each other, one approach is to order the actions in terms of seriousness and to assign the less serious consequence some arbitrary utility value, say 1, with the other more serious consequence assigned some multiple of this. Finally, both the benefit of health outcome of future patients and the cost of incorrect decisions are rescaled to monetary terms so that these can be combined in the same utility function. Alternatively, the cost of sampling may be rescaled to a health outcome. For example, in the health economic ‘Value of Information’ approach, costs and benefits in terms of quality of life are often expressed in Quality-adjusted Life Years. As the benefit and cost are in relation to each other, some authors have proposed a model that is a function of the benefit–cost ratio.²⁰ Alternatively, the utility function may encompass a more realistic setting with health outcome and economic criteria such as the profit from treating future patients, market share, the costs incurred from conducting the trial and the costs of sampling explicitly included.^{19,21,52–58,60,63–65,68,71,73–75,79–81,83}

Designs that considered simple utility functions did not generally specify the perspective of the decision-maker,^14,38–40 whereas more realistic utility functions are often explicitly based on a commercial,^{21,55–58,65,68,71,73,75,79–81} regulatory^{54,56,57,73,74,81} or societal perspective.^{52,53,55,60,63,64,83} Exceptions are the work of Chen and Beckman²⁰ where the utility function is a simple function based on a commercial perspective that controls for type I and II error rates under the constraint of limited sample size, and Brunier and Whitehead¹⁹ where the utility function is a more realistic one that incorporates costs that may be incurred during the trial but there was no specification of the perspective of the decision-maker.

Possible actions for designs based on a societal perspective include whether to delay the decision-making and start a new trial, to adopt the experimental treatment (granting licence or reimbursement of costs of the treatment in general clinical use) and start a new trial to gather more information or to adopt the experimental treatment without starting a new trial (i.e. requiring no further information).^54,74,81

3.3 Multi-stage designs

A more complex decision-making process arises in trials that are conducted in a number of stages with interim analyses conducted at the end of each. The majority of clinical trials’ design methods based on decision theory have considered this setting, usually with the possible actions at the end of each stage taken to be those corresponding to stopping the trial for futility, stopping with a positive result or continuing to further stage(s). Specific articles include Banerjee and Tsiatis,¹⁸ Berry and Ho,⁴⁵ Chen and Willan,⁴⁶ Chen and Smith,²² Cheng and Berry,⁴⁷ Cheng and Shen,^48,49 Cheng et al.,⁵⁰ Chernoff and Petkau,⁵¹ Ding et al.,²³ Heitjan et al.,⁵⁹ Jennison and Turnbull,⁶¹ Jiang et al.,⁶² Jung et al.,²⁵ Lewis and Berry,⁶⁶ Lewis et al.,⁶⁷ Mehta and Patel,⁶⁹ Nixon et al.,²⁷ Orawo and Christen,⁷⁰ Palmer,²⁹ Rossell et al.,³⁰ Stallard,^31,32 Stallard et al.,³⁷ Wang,⁷⁶ Wathen and Christen,⁷⁷ Wathen and Thall,⁷⁸ Willan and Kowgier,⁸² Zhao et al.⁴³ and Zhao and Woodworth.⁴⁴

A multi-stage trial may be designed based on consideration of a fixed and known maximum number of patients that can be included in the trial. In rare diseases settings, one may be able to estimate the number of cases eligible for clinical trials relatively easily, or it can be tied to budget allocation. In such scenarios, at the final stage when all patients have been recruited, there are two terminal actions to choose; stop and accept the treatment for further study or stop and reject the treatment from further study.

Some designs are aimed to optimize the patient allocation for a fixed and known number of future patients, known as the ‘patient horizon’, N, which may be estimated via the incidence rate for the disease of concern and an assumption regarding the life of any potential new treatment. The aim is to choose n, the number of patients that are allocated to the pilot or phase II trial assuming the remaining N – n are either included in the larger phase III trial or subsequently receive the recommended treatment.^{47,50,51,76,82} The expected utility for each terminal action (stop and accept treatment or stop and reject treatment) is given directly by the utility function specified, whereas the expected utility from continuing to the next stage depends on the observations and decisions made at a future stage. Thus, to estimate the expected utility function for each action at each stage, we begin by considering the terminal actions at the ultimate stage supposing that responses from all N patients have been observed. Having estimated the maximized utility function, we can go one step back and estimate the expected utility function for all possible actions prior to the penultimate stage. Following this manner of iteration, the expected utility function for each action at the first stage is computed, extending the method outlined above to a full backward induction approach.

The backward induction computation becomes very intensive as the number of stages increases. Orawo and Christen,⁷⁰ and Wathen and Christen⁷⁷ have considered using an approximation method rather than computing the exact value. For designs that do not assume a fixed known patient horizon, the optimal sequential design can sometimes be computed by forward simulation and constrained backward induction.^23,30,43,78 Heitjan et al. consider a two-stage design,⁵⁹ reducing the computational burden considerably, and use direct numerical optimization rather than the backward induction approach to obtain optimal designs in this case, while Jung et al.²⁵ adopt a similar approach for two-stage single-arm cancer trials, comparing their approach with the commonly used design due to Simon.⁸⁴

Just as we had a range of single stage designs considered above, authors have taken a number of approaches to the design of multi-stage trials. Some authors have considered simple utility functions (costs of making incorrect decisions and cost of sampling) in their designs.^{18,25,29,43,44,47–51,59,61,62,66,67,76–78} Cheng and Shen⁴⁹ related the utility function parameters to frequentist error rates, while Nixon et al.²⁷ related it to the expected prior probability of success which is sometimes known as assurance, a term introduced by O’Hagan and Stevens.⁸⁵ Frequentist error rates are also considered by Jennison and Turnbull⁶¹ who use backward induction to obtain group sequential designs that are optimal in that the expected sample size is minimized subject to the error rate requirements. Others have considered more realistic utility functions.^{22,23,30–32,37,43,45,46,69,70,82} In this latter case, the utility function is usually constructed from a commercial perspective.

3.4 Enrichment designs

Trippa et al. proposed a decision-theoretic approach to an enrichment design.⁴² In this two-stage design, all patients enrolled to stage 1 receive the same experimental treatment. The data from these patients are then used to optimally identify the population of patients to be used in the main, second, stage of the trial, in which patients are randomized to receive either the experimental or the control treatment. In the design proposed by Trippa et al., the utility function encompasses the benefit that will be received by future patients if the experimental treatment is recommended for further study in a phase III setting in the population identified, the costs incurred for conducting the phase II and III trials, and the duration of treatment in stage 1 which influences the population of patients for whom treatment is successful that will be used in the second stage.

Although represented by a single paper in our review, the area of enrichment designs is one of considerable recent statistical interest (see, for example, Graf et al.,⁸⁶ Simon and Simon⁸⁷ and Wang et al.⁸⁸), suggesting that this is an area in which new work on decision-theoretic approaches might be anticipated.

3.5 Designs for multi-arm trials, programmes of studies or a series of trials

Some articles extend the multi-stage designs for single-arm trials or two-arm comparative trials to seek optimal multi-arm designs. Such a problem is considered by Chen and Beckman,²⁰ Lai et al.,²⁶ Palmer,²⁹ Patel and Ankolekar,⁷¹ Patel et al.,⁷² Stallard et al.³⁵ and Thall et al.⁴¹ This introduces, in addition to possible actions corresponding to stopping or continuing the trial, the option of dropping one or more treatment arms at an interim analysis, so that the decision process can become increasingly complex.

In multi-arm trials, J doses of the experimental treatment or J different experimental treatments may be tested against the standard treatment or placebo. At each interim analysis, a decision is made to drop an inferior dose(s) or treatment(s), and to continue recruitment to the remaining dose(s) or treatment(s). At the final stage, a decision is made to either recommend the superior dose or experimental treatment for further study in a phase III trial setting, or to reject it from further study. Note that this type of study is different from dose-finding trials. The J doses are assumed to have been recommended from dose-finding trials.

In the designs considered earlier, patients are generally considered in groups, with decisions made at interim analyses once the data from each group of patients has been observed. If patients are considered one at a time, the problem becomes one of optimally allocating treatments to each patient. Such an approach is considered in a two-arm study by, for example, Jiang et al.⁶² This problem is closely related to the multi-arm bandit problem. In some settings, the different treatments being compared in a multi-arm design may be different doses of the same drug. In this case, a parametric dose–response model may be assumed. These two settings are considered briefly in the Discussion section.

The objective of the designs considered by Patel and Ankolekar⁷¹ and Patel et al.⁷² is to maximize the expected profit from a portfolio of treatments while incurring the costs of running the trials within the given budget. An optimal size is obtained for each treatment (each trial) and the trials may run concurrently.

Some articles use decision theory methods to design not a single study but a series of studies, which may themselves employ single stage or multi-stage designs. The problem of decision-making at the end of one trial in a series of potential trials is rather like that at an interim analysis in a multi-stage trial, so that the methods often build on those described above. In this setting, actions corresponding to moving on from one trial to another need to be considered. Articles considering designs for this setting include Chen and Beckman,²⁰ Hee and Stallard,²⁴ Pallay,²⁸ Stallard^33,34 and Stallard and Thall.³⁶ The trials, usually with one experimental treatment per trial (either a single-arm design or two-arm comparison with a control), run sequentially, so that a decision made in one trial can affect possible future trials. In a series of single stage trials, suppose n is the sample size of a trial and upon observing all the responses a decision is made either to accept the experimental treatment for further study or to reject it from further study and start a new trial with a different treatment. In a series of multi-stage trials, at each interim stage, a decision is made whether to continue recruitment to the current trial or to terminate the trial and recommend the experimental treatment for further study or to initiate a new trial with a different experimental treatment. Some designs may also have a possibility of terminating the current trial and abandoning the whole development plan.²⁴

The full backward induction approach can be very challenging in this case, so authors have generally either considered small sample sizes,³⁶ or sought simpler algorithms or asymptotic results to give approximately optimal designs.^47,50

The expected utility for a series of sequential trials may also be computed via a backward induction algorithm similar to that described above. For a series of multi-stage trials, the backward induction is used within each trial as well as for the series of sequential trials. Almost all assumed a commercial perspective with realistic utility functions.^24,28,33,36 Both Chen and Beckman²⁰ and Stallard,³⁴ on the other hand, assumed a commercial perspective with simple utility functions.

4 Discussion

The aim of this article was to review the literature on methods for pilot studies and small clinical trials that are based on the use of Bayesian decision theory. Methods have been published for single-stage and multi-stage clinical trials as well as for multi-arm trials or series of trials, with utility functions based on a number of different decision-makers’ perspectives. Most methods have focussed on a decision regarding the sample size of the trial, though in general other features of the design could be chosen in a similar way. Specific examples that have been considered include dropping of arms in a multi-arm trial and selection of the population in the enrichment design.

It is inevitable that when writing an article such as this, decisions must be made regarding the scope of the review. Within the limit of Bayesian decision-theoretic methods, our intention has been to keep the scope fairly wide, including discussion of methods for any clinical trial design that might be appropriate for a small trial or pilot study with an efficacy endpoint. One exclusion has been methods for phase I or dose-finding studies, where the main concern is usually a safety or toxicity endpoint. Although Bayesian and decision-theoretic methods are relatively common in this setting, the different endpoint, use of sequential designs with very small groups, often making decisions after each subject, and incorporation of dose–response information (so that data from one arm can lead to inference regarding other arms) mean that the methods proposed are rather different to those we have considered, and are less suited to other small trials. Readers interested in this area are directed to the work by Cheung⁸⁹ and Simes.⁹⁰ One of the few published applications of the decision-theoretic methodology is in the phase I oncology setting.⁹¹ Our choice of search terms also excluded literature on the multi-arm bandit problem, identifying one paper⁷⁶ applying this methodology specifically to clinical trial design with the intention of optimally allocating patients one at a time to treatments in a multi-arm study. There is a relatively large body of literature on this problem in applied probability journals which, although considered from a more generally viewpoint, might be relevant to clinical trials of this type.^92–94

A challenge, in any Bayesian methodology, is the specification of a prior distribution. Most of the papers identified in the review used conjugate prior distributions to facilitate mathematical derivation.^{14,22–24,26–28,30–37,41–51,54–58,60,62–70,73–83} In most cases, this involved using a beta prior distribution for a Bernoulli distribution, or in some cases taking a two-point prior corresponding to an experimental treatment that is either effective or ineffective.^{18,20,21,25,29,38–40,52,53,59,61,72} In some cases, the prior distribution may be for a vector of unknown parameters. Some examples are normal distribution with both unknown mean and variance^57,63,65 or a time-to-event endpoint where the hazard function is modelled with a three-parameter generalized gamma and the unknown priors follow a gamma and inverse gamma distributions.⁷⁸ Authors whose works consider more than one endpoint, for example, Bernoulli efficacy and Bernoulli toxicity, assume a Dirichlet distribution,^22,37,75 or for time-to-event and Bernoulli toxicity endpoints where the unknown parameters follow a bivariate gamma (regression) distribution⁴¹ or gamma and beta distributions.²⁶ Some papers used MCMC methods,^43,68 and one paper was based on a non-parametric approach.⁴³ When priors were specified, they were usually informative, sometimes with a number of alternative priors used and results compared. Although there is a considerable literature on elicitation of Bayesian prior distributions (see, for example, Chaloner et al.,⁹⁵ Kadane and Wolfson,⁹⁶ O’Hagan,⁹⁷ and case studies by Blanck et al.,⁹⁸ and Kinnersley and Day⁹⁹), only two articles identified in our review described the use of formal methods for prior elicitation methods.^42,52

As described above, one major challenge in the development and application of decision-theoretic methods in clinical trials is that of constructing utility functions that accurately reflect the consequences of possible actions. It is clear from the articles discussed above that approaches to this challenge have varied. Some researchers have focussed on monetary costs and rewards, whilst others have compared these with improvement or deterioration in health states using approaches from health economics. The utilities should reflect the preferences of consequences from the point of view of the decision-maker. This can be particularly challenging when more than one individual or group will make a decision based on the results of a clinical trial, or be otherwise affected by the results, or if the decision-maker and the trialist have different viewpoints. For example, decision-making by a societal decision-maker such as National Institute for Health and Care Excellence (NICE) in the UK may primarily be based on cost-effectiveness, whereas decision-making by a pharmaceutical company may be based more on whether or not the current information is sufficient to apply for licensing for the experimental treatment. In an attempt to reconcile this challenge, Willan and Eckermann⁸¹ proposed a design that combined both public health service and commercial perspectives where the utility function is made up of two thresholds, namely, a maximum price of the experimental treatment acceptable to the public health service for reimbursement and a minimum price to the pharmaceutical company that does not result in a loss of investment.

More general methods for construction of utility values based on direct consideration of consequences have been based on prioritizing preference, for example, using methods first proposed by Ramsey¹⁰⁰ or methods discussed by Lindley¹⁰¹ or Emrich and Sedransk.¹⁰² Although a variety of approaches have been taken, most researchers proposing single-stage designs have based utility functions on a patient or societal perspective, whereas commercial perspectives have been more common in development of multi-stage designs. In the description of the method aforesaid, we have taken the utility function to depend on the unknown parameters alone, as proposed by Lindley¹⁴ and Raiffa and Schlaifer.¹² Most authors proposing simple utility functions have followed this approach. Some authors have proposed more complex utility functions in which the utility depends also on the observed trial data, for example, with a gain if a trial indicates a significant treatment effect. In spite of the numerous approaches proposed, it seems likely that it is this difficulty with specification of an appropriate utility function, together with a lack of familiarity, both with Bayesian methods in general and with decision-theoretic methods in particular, that is responsible for the very limited use of decision-theoretic methods in practice.

In spite of the challenges, we consider the Bayesian decision-theoretic approach to be appropriate for the design of pilot studies and early phase trials given the clear role of these trials is to inform decisions regarding further future clinical research. However such trials are designed, these decisions will be made and the decision-theoretic approach formalizes this by considering the decisions and their consequences explicitly. Even when trials are designed based on other approaches, we believe that the decision-theoretic methodology is a useful tool for trialists and statisticians designing trials, enabling the properties of trial designs obtained under one paradigm to be evaluated based on another. This is, perhaps, particularly important in small trials when compromise is inevitable, as it leads to a careful consideration of the purpose of the trial and its required properties, thus ensuring that it is fit for purpose. One thing that we believe could increase the use of decision-theoretic designs is a greater familiarity and improved understanding through retrospective evaluation of such approaches.

This review has identified many decision-theoretic approaches. In any real application, it is important to consider the purpose of the trial and ensure that this is reflected in the formulation of the decision problem and utility function so that the trial design proposed is appropriate to match this purpose.

Appendix 1

Terms used in Scopus search with number of hits.^a

Search terms	Number of hits
(TITLE-ABS-KEY(“small trial”) OR TITLE-ABS-KEY(“phase II”) OR TITLE-ABS-KEY(pilot) OR TITLE-ABS-KEY(“serie* of trial”) AND TITLE-ABS-KEY(“decision theor*”) ) AND DOCTYPE(ar OR cp)	262
(TITLE-ABS-KEY(“small trial”) OR TITLE-ABS-KEY(“phase II”) OR TITLE-ABS-KEY(pilot) OR TITLE-ABS-KEY(“serie* of trial”) AND TITLE-ABS-KEY(sequential) ) AND DOCTYPE(ar) AND (PUBYEAR > 2004)	1189
(TITLE-ABS-KEY(“small trial”) OR TITLE-ABS-KEY(“phase II”) OR TITLE-ABS-KEY(pilot) OR TITLE-ABS-KEY(“serie* of trial”) AND TITLE-ABS-KEY(sequential) ) AND DOCTYPE(ar) AND (PUBYEAR < 2005)	1010
(TITLE-ABS-KEY(“small trial”) OR TITLE-ABS-KEY(“phase II”) OR TITLE-ABS-KEY(pilot) OR TITLE-ABS-KEY(“serie* of trial”) AND TITLE-ABS-KEY(sequential) ) AND DOCTYPE(cp)	336
(TITLE-ABS-KEY(“small trial”) OR TITLE-ABS-KEY(“phase II”) OR TITLE-ABS-KEY(pilot) OR TITLE-ABS-KEY(“serie* of trial”) AND TITLE-ABS-KEY(“decision mak*”) ) AND DOCTYPE(ar) AND (PUBYEAR > 2008)	1705
(TITLE-ABS-KEY(“small trial”) OR TITLE-ABS-KEY(“phase II”) OR TITLE-ABS-KEY(pilot) OR TITLE-ABS-KEY(“serie* of trial”) AND TITLE-ABS-KEY(“decision mak*”) ) AND DOCTYPE(ar) AND ( LIMIT-TO(PUBYEAR,2008) OR LIMIT-TO(PUBYEAR,2007) OR LIMIT-TO(PUBYEAR,2006) OR LIMIT-TO(PUBYEAR,2005) )	901
(TITLE-ABS-KEY(“small trial”) OR TITLE-ABS-KEY(“phase II”) OR TITLE-ABS-KEY(pilot) OR TITLE-ABS-KEY(“serie* of trial”) AND TITLE-ABS-KEY(“decision mak*”) ) AND DOCTYPE(ar) AND (PUBYEAR < 2005)	1446
(TITLE-ABS-KEY(“small trial”) OR TITLE-ABS-KEY(“phase II”) OR TITLE-ABS-KEY(pilot) OR TITLE-ABS-KEY(“serie* of trial”) AND TITLE-ABS-KEY(“decision mak*”) ) AND DOCTYPE(cp)	1130
(TITLE-ABS-KEY(“small trial”) OR TITLE-ABS-KEY(“phase II”) OR TITLE-ABS-KEY(pilot) OR TITLE-ABS-KEY(“serie* of trial”) AND TITLE-ABS-KEY(bayes* PRE/5 decision)) AND DOCTYPE(ar OR cp)	70
(TITLE-ABS-KEY(“small trial”) OR TITLE-ABS-KEY(“phase II”) OR TITLE-ABS-KEY(pilot) OR TITLE-ABS-KEY(“serie* of trial”) AND TITLE-ABS-KEY(“optimal* design”) ) AND DOCTYPE(ar OR cp)	222
(TITLE-ABS-KEY(“small trial”) OR TITLE-ABS-KEY(“phase II”) OR TITLE-ABS-KEY(pilot) OR TITLE-ABS-KEY(“serie* of trial”) AND TITLE-ABS-KEY(“optimal* decision”) ) AND DOCTYPE(ar OR cp)	16
(TITLE-ABS-KEY(“small trial”) OR TITLE-ABS-KEY(“phase II”) OR TITLE-ABS-KEY(pilot) OR TITLE-ABS-KEY(“serie* of trial”) AND TITLE-ABS-KEY(“optimal* sample siz*”) ) AND DOCTYPE(ar OR cp)	10
TITLE-ABS-KEY(“trial design”) AND TITLE-ABS-KEY(“decision theor*”) AND DOCTYPE(ar OR cp)	25
TITLE-ABS-KEY(“trial design”) AND TITLE-ABS-KEY(bayes* PRE/5 decision) AND DOCTYPE(ar OR cp)	32
TITLE-ABS-KEY(“trial design”) AND TITLE-ABS-KEY(“optimal* design”) AND DOCTYPE(ar or cp)	38
TITLE-ABS-KEY(“trial design”) AND TITLE-ABS-KEY(“optimal* decision”) AND DOCTYPE(ar or cp)	4
TITLE-ABS-KEY(“trial design”) AND TITLE-ABS-KEY(“optimal* sample size”) AND DOCTYPE(ar or cp)	9
TITLE-ABS-KEY(“trial design”) AND TITLE-ABS-KEY(sequential* PRE/5 decision*) AND DOCTYPE(ar or cp)	3
(TITLE-ABS-KEY(“clinical trial*”) AND TITLE-ABS-KEY(“decision theor*”)) AND DOCTYPE(ar or cp)	278
(TITLE-ABS-KEY(“clinical trial*”) AND TITLE-ABS-KEY(“optim* sample size*”)) AND DOCTYPE(ar or cp)	65

^aSome search terms led to more than 2000 hits and to circumvent Scopus citation export restriction, these terms were split by publication year.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was conducted as part of the InSPiRe (Innovative methodology for small populations research) project funded by the European Union’s Seventh Framework Programme for research, technological development and demonstration under grant agreement number FP HEALTH 2013 – 602144.