Skip to main content
NCBI home page
Journal of Computational Biology logoLink to Journal of Computational Biology
. 2016 May 1;23(5):300–310. doi: 10.1089/cmb.2015.0184

Constructing Structure Ensembles of Intrinsically Disordered Proteins from Chemical Shift Data

Huichao Gong 1, Sai Zhang 1, Jiangdian Wang 2, Haipeng Gong 3,,4, Jianyang Zeng 1,,4,✉
PMCID: PMC4876552  PMID: 27159632

Abstract

Modeling the structural ensemble of intrinsically disordered proteins (IDPs), which lack fixed structures, is essential in understanding their cellular functions and revealing their regulation mechanisms in signaling pathways of related diseases (e.g., cancers and neurodegenerative disorders). Though the ensemble concept has been widely believed to be the most accurate way to depict 3D structures of IDPs, few of the traditional ensemble-based approaches effectively address the degeneracy problem that occurs when multiple solutions are consistent with experimental data and is the main challenge in the IDP ensemble construction task. In this article, based on a predefined conformational library, we formalize the structure ensemble construction problem into a least squares framework, which provides the optimal solution when the data constraints outnumber unknown variables. To deal with the degeneracy problem, we further propose a regularized regression approach based on the elastic net technique with the assumption that the weights to be estimated for individual structures in the ensemble are sparse. We have validated our methods through a reference ensemble approach as well as by testing the real biological data of three proteins, including alpha-synuclein, the translocation domain of Colocin N, and the K18 domain of Tau protein.

Key words: : chemical shift, elastic net, intrinsically disordered proteins, least squares

1. Introduction

Unlike traditional ordered proteins, which generally take a well-defined 3D structure to perform their functions, intrinsically disordered proteins (IDPs) lack ordered or fixed 3D structures (Iakoucheva et al. 2002; Dunker et al. 2001; Dyson and Wright 2005). However, IDPs usually play important roles in essential biological processes and are generally associated with many diseases, such as cancers (Iakoucheva et al., 2002) and neurodegenerative disorders (Karres et al., 2007). Therefore, modeling the atomic structural details of IDPs is critical for understanding their cellular functions and revealing their regulation mechanisms in signaling pathways of related diseases.

Ensemble modeling has been believed to be the most accurate way to describe the 3D structures of IDPs (Choy and Forman-Kay, 2001; Fisher et al., 2010; Fisher and Stultz, 2011). In general, a structure ensemble consists of two parts: a set of 3D structures and the corresponding weights that describe the likelihoods of individual conformations. When experimental data (e.g., chemical shifts, nuclear Overhauser effect (NOE) distances, and residual dipolar couplings) are available, the 3D structures and their weights are often constructed to optimally match these experimental observations. In the literature, numerous approaches have been proposed to construct 3D structure ensembles of IDPs from experimental data (Jensen et al., 2010; Nodet et al., 2009; Marsh and Forman-Kay, 2009; Ganguly and Chen, 2009; Fisher et al., 2010). These approaches can be roughly divided into two categories (Fisher and Stultz, 2011). The first one is called the ensemble-restrained molecular dynamics (MD) simulation, which explicitly incorporates available data restraints in the potential function and enforces the whole ensemble to satisfy these experimental constraints during the simulation (Allison et al., 2009). In principle, these ensemble-restrained approaches require a large number of constraints to drive accurate MD simulation. On the other hand, in practice, such a large number of constraints are rarely available from experimental data for an IDP. As discussed in Ganguly and Chen (2009), such ensemble construction approaches usually fail when there is an insufficient number of constraints available for supporting the restrained MD simulation. The second group of ensemble construction approaches (Choy and Forman-Kay, 2001; Nodet et al., 2009; Fisher et al., 2010; Chen et al., 2007) applies a different strategy. They first generate an initial structure pool (which is also called the predefined conformational library) using MD simulation, and then select a subset of these structures to represent conformational space. After that, the corresponding weights of individual selected structures are computed to match experimental observations. In this strategy, when constructing the IDP ensemble, stochastic sampling algorithms—such as Monte Carlo, simulated annealing, and evolutionary algorithms—are often applied to stochastically assign random weights to the selected structures in order to achieve the best possible solutions (Fisher and Stultz, 2011). Unfortunately, these stochastic approaches cannot provide any theoretical guarantee to find the global optimal solutions within limited simulation time.

One main challenge in the IDP ensemble construction task lies in addressing the degeneracy problem (Fisher et al., 2010; Terakawa and Takada, 2011): Due to the large degrees of freedom in this problem, there can exist multiple ensemble solutions to satisfy experimental data. This problem remains a challenge even after the initial conformational library has been defined. The degeneracy problem in IDP ensemble construction has been well discussed in Fisher et al. (2010) and Fisher and Stultz (2011).

In this article, we propose two effective methods to accurately construct the structure ensembles of IDPs. Our approaches follow the strategy of constructing a predefined conformational library, but use more elegant algorithms to compute the optimal weights of the selected structures to satisfy experimental constraints. In particular, when the constraints derived from experimental data outnumber the unknown variables (i.e., the weights of individual structures that need to be estimated), we use a least squares method to compute the optimal solution. Note that a similar least squares method has been proposed to characterize RNA ensembles in a recent study (Fonseca et al., 2014). However, Fonseca et al. (2014) did not handle the situation in which the unknown variables outnumber the constraints derived from experimental data. In the second case (i.e., the number of experimental constraints is smaller than the number of the selected structures), the problem becomes ill-posed and underdetermined, which is the main cause of the degeneracy problem. To address this problem, we assume that the weights to be estimated are sparse, that is, most of them are with zero values. With this reasonable assumption, we propose a regularized regression approach based on the elastic net technique (Zou and Hastie, 2005) to derive the optimal weights that best interpret experimental data. In this article, we mainly use chemical shifts as experimental data to drive the ensemble construction process. Chemical shifts provide strong indicators about local chemical environment in a protein structure and have been widely used for protein structure modeling (Cavalli et al., 2007; Shen et al., 2008). Notably, our methods can be easily extended to incorporate other nuclear magnetic resonance (NMR) data, such as NOEs and RDCs.

Unlike other existing ensemble construction approaches, which stochastically compute the approximate weights of the structures in the predefined conformational library, our least squares method can find the global optimal solution in closed form. When only a small number of experimental restraints are available, our elastic net–based regression approach provides a new framework with reasonable sparsity assumption for addressing the degeneracy problem in the IDP ensemble construction process. To our knowledge, our work provides the first framework to estimate the best solution by applying the least squares method and the elastic net regression approach respectively, depending on whether the experimental data are sufficient or not. We have validated the performance of our algorithms using a reference ensemble approach (Kuriyan et al., 1986), in which simulated data are used to verify the ensemble construction results. In addition, we have tested our methods on real biological data of three proteins, including alpha-synuclein, the translocation domain of Colicin N, and the K18 domain of Tau protein. The test results have demonstrated that our methods can be effectively used to construct accurate structure ensembles of IDPs using chemical shift data.

2. Methods

2.1. Overview

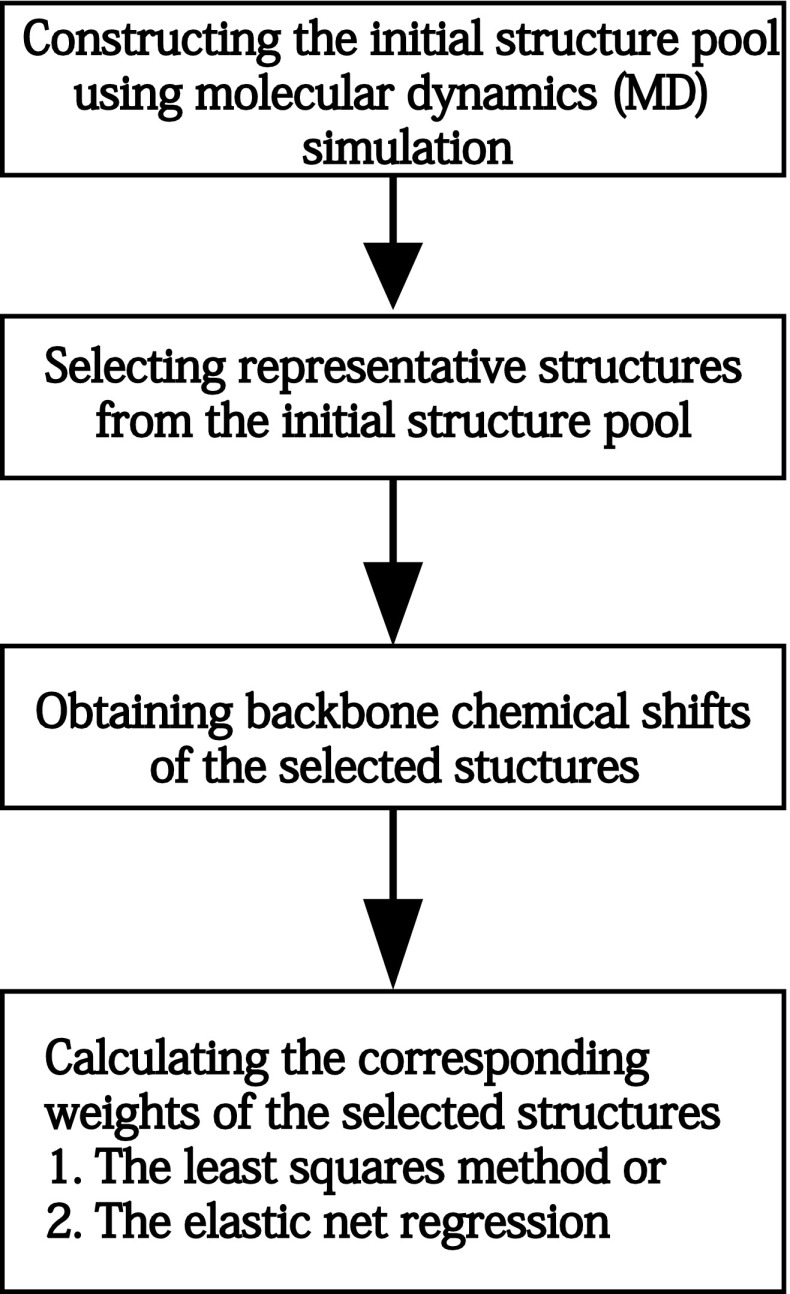
Our goal is to construct an ensemble of representative structures for a given IDP and to derive the accurate weights associated with individual conformations in this ensemble. As shown in Figure 1, our pipeline for constructing an IDP structure ensemble consists of four steps. In step 1, we use MD simulation to generate the lifetime trajectories of the target IDP, which yields a large number of different conformations. We call this initial set of different structures the initial structure pool. In step 2, we select a subset of conformations from the initial structure pool by applying a clustering algorithm (Hastie et al., 2001) to group structurally similar conformations, and picking the conformation with the lowest average root-mean-square deviation (RMSD) to all other conformations within the same cluster to represent each cluster. In step 3, we predict the backbone chemical shifts of the selected structures using software SHIFTX2 (Han et al., 2011). In Step 4, we compute the weights of the selected structures such that the ensemble average best fits the chemical shift data. In particular, this step is divided into two scenarios. When the number of constraints derived from chemical shift data is equal to or larger than the number of unknown variables that need to be estimated (which is equivalent to the number of the selected structures from the initial pool), we compute the weights of all representative structures using a least squares method to minimize the discrepancy between experimentally measured and computationally predicted chemical shifts. When the unknown variables outnumber the constraints derived from experimental observations, the problem becomes ill-posed and underdetermined such that there are an infinite number of solutions. In this case, we add a combination of L1- and L2-norm penalties to the objective function and apply an elastic net technique to solve the regression problem.

FIG. 1.

FIG. 1.

Open in a new tab

Our pipeline of intrinsically disordered proteins (IDP) ensemble construction.

2.2. Constructing the initial structure pool

We construct the initial structure pool of an IDP using the molecular dynamics (MD) simulation package NAMD2.8 (Phillips et al., 2005). In particular, we perform a 10ns MD simulation at the temperature 300K using the CHARMM27 force field (Brooks et al., 1983) and the generalized born implicit solvent model (Tanner et al., 2011). We use either available structures from the Protein Data Bank (PDB) (Berman et al., 2000) or random structures generated by Xplor-NIH (Schwieters et al., 2003, 2006) as the starting templates. The trajectory coordinates are saved per picosecond during the simulation, and in total 10,000 final structures are output as the initial structure pool, which is similar to the procedure used in Fisher et al. (2010). Here, we assume that the structures generated by the MD simulation can represent the diverse conformational space of the IDP. In principle, other softwares, such as Flexible-Meccano (Ozenne et al., 2012) and TraDES (Feldman and Hogue, 2000, 2002), can also be used to increase the efficiency of conformational sampling.

2.3. Selecting representative structures from the initial pool

Considering the difficulty to directly process a large number of conformations in the initial pool, we select a subset of representative structures using the following clustering scheme: (1) Pick a structure Si from the initial pool, and create a cluster Gi that only contains Si at the beginning. (2) Calculate the RMSD of backbone atoms between Si and every other structure Sj in the pool. If their RMSD is less than a cutoff (e.g., 2.1 Å, which was also used in Fisher et al., 2010), move Sj from the structure pool to cluster Gi. (3) When all structures in the initial pool have been compared with Si, remove Si from the initial pool. The above process is repeated until all structures in the initial pool have been clustered. After that, for each cluster, the structure with the lowest average RMSD to all other structures in the same cluster is chosen as a representative conformation.

2.4. Obtaining the chemical shifts of backbone atoms

In our approach, we use the chemical shifts of backbone atoms, such as HN, N, CA, and HA, to drive the construction of an IDP ensemble. The experimental values of chemical shifts are obtained from the Biological Magnetic Resonance Bank (BMRB) (Doreleijers et al., 2003), while the predicted chemical shifts of the selected conformations are produced by SHIFTX2 (Han et al., 2011) based on available structural information.

2.5. Calculating the corresponding weights of the selected structures

After selecting the representative conformations from the initial structure pool, we need to determine their corresponding weights. Depending on whether the number of constraints is less than the number of the representative structures in the ensemble, we use two different strategies to compute the optimal weights for the experimental data. Below we will describe the details of these two strategies.

2.5.1. The least squares method

When the number of unknown weights that need to be estimated is equal to or less than the number of constraints derived from chemical shifts, we apply a least squares approach to solve the regression problem. We first introduce notation before describing the details of this algorithm. Let Sj represent the jth conformation in the set of the selected structures. Let aij denote the predicted backbone chemical shift of the ith residue in structure Sj, and let bi denote the experimental chemical shift of the corresponding backbone atom in the ith residue in the protein, which is derived from the BMRB (Doreleijers et al., 2003) (here, for simplicity, we assume each residue has only one backbone atom with available chemical shift). 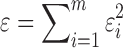The difference between predicted and experimental backbone chemical shifts of the ith residue, denoted by ɛi, can be defined as Inline graphic, where wj represents the weight of structure Sj and n stands for the total number of representative structures. Then the overall difference between predicted chemical shifts and experimental observations over all residues is defined as Inline graphic, where m stands for the number of residues whose backbone chemical shifts are available from experimental data. Then, our goal is to find the optimal weights for all representative structures that minimize ɛ.

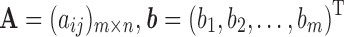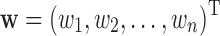We use A to denote a matrix that contains all backbone chemical shifts aij predicted from SHIFTX2, b to denote a vector that includes all experimental chemical shifts bi, and w to denote a vector that includes the weights of all representative structures, that is, Inline graphic, and Inline graphic. Then the difference between predicted and experimental chemical shifts can be expressed as:

graphic file with name eq5.gif

In addition, we need to consider the following two constraints:

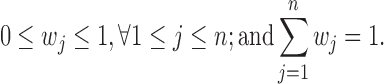graphic file with name eq6.gif

Overall, the regression problem can be described as:

graphic file with name eq7.gif
graphic file with name eq8.gif
graphic file with name eq9.gif

When m ≥ n, the above form is a typical data-fitting problem with an overdetermined linear system. Thus we can solve this problem using a least squares approach that guarantees to find the optimal weights that minimize ɛ. In principle, the restricted quadratic programming (Frank and Wolfe, 1956) can be used to solve the above least squares problem.

2.5.2. The elastic net method

The least squares method described previously can be used to efficiently solve the regression problem in overdetermined form. However, when the unknown weights associated with representative conformations outnumber the constraints derived from experimental data, the regression model described in the Section The Least Squares Method becomes underdetermined and cannot be solved by the least squares method. In this case, we need to resort to other techniques to effectively solve the problem. Here, we assume that only a small number of structures are truly present in the ensemble, that is the weights are sparse. According to this sparsity assumption, we introduce an elastic net method (i.e., adding a combination of L1- and L2-norm penalty terms) to solve the regression problem, which can address the deficiency caused by the insufficient number of experimental constraints, and thus handle the degeneracy problem well. In the new formalization of our regression problem, we relax the constraint in Equation (3), as we mainly focus on the relative weighting factors among structures in the ensemble. We can renormalize the calculated weights and obtain the updated weights of individual structures in the ensemble later. Overall, we aim to solve the following optimization problem:

graphic file with name eq10.gif
graphic file with name eq11.gif

where Inline graphic, while λ and α are regularization parameters. To enforce the sparsity on the solution, we set specific values of α and λ. Alternatively, we can use a cross-validation procedure (Friedman et al., 2010; Simon et al., 2011) to determine their values.

2.6. Implementation

We implement the above two methods in MATLAB. For the least square algorithm, we call the function lsqlin in MATLAB to calculate the optimal weights. For the elastic net-based method, we first call the corresponding elastic net function cvglmnet (Friedman et al., 2010; Simon et al., 2011) in MATLAB to solve the regression problem through a cross-validation procedure. After that, we normalize all calculated weights and use these updated weights as our final solution.

3. Results

3.1. Validation through a reference ensemble approach

We first evaluated the performance of our algorithms using the reference ensemble method (Kuriyan et al., 1986). More specifically, this method first constructs a set of “true” conformations and their corresponding weights, which are called the reference ensemble. Then “experimental” data are synthesized based on “true” information of this reference ensemble. The algorithm being evaluated takes these synthetic “experimental” data as input and computes a structure ensemble. By comparing the computed ensemble with the reference one, we can properly assess performance of the proposed algorithm.

Here, we validated our least squares method using alpha-synuclein protein, a 140-residue IDP that had been previously studied (Tamiola et al., 2010; Recchia et al., 2004; Vekrellis and Stefanis, 2012), and the elastic net method using the K18 domain of Tau protein. We illustrated the validation of these two approaches individually.

For alpha-synuclein, we first constructed a reference ensemble and synthesized their “experimental” data. Then, we used these data to back-compute the optimal weights with the least squares method. Finally, we compared the performance of our method with the Monte Carlo approach. As shown in Figure 2, our least squares method significantly outperformed the Monte Carlo approach. More details of the validation of the least squares method can be found in Supplementary Material Section S1 of Gong et al. (2015).

FIG. 2.

FIG. 2.

Open in a new tab

The validation results of the least squares method through the reference ensemble method. In each scenario, we compared the performance of our method with that of the Monte Carlo approach; MC stands for the Monte Carlo sampling method and LS stands for our least squares approach. In (a) and (c), the weights of individual conformations in the reference ensemble followed the Gaussian distribution, while in (b) and (d), the weights followed the uniform distribution. Both Ω (wC, wT) and the RMSD of HN chemical shift were calculated for each case. Each test was conducted 50 times with different random seeds.

In addition, to investigate the robustness of our method upon the types of experimental data, we tested different combinations of input chemical shift data. As shown in Figure 3, we tested the following four combinations of chemical shift data: (1) HN chemical shifts only; (2) HN and HA chemical shifts; (3) HN, HA, and CA chemical shifts; and (4) HN, HA, CA, and N chemical shifts. As Figure 2 had shown that the distribution of the synthesized weights did not affect the results, here we set wT to follow the Gaussian distribution and set standard deviation as 0.02 for noise in synthetized data. As shown in Figure 3, incorporating more chemical shift data yielded better results, that is, smaller Ω (wC, wT) values between computed and “true” weights as well as RMSD values between back-computed and experimental data. This trend was expected, as considering more data restraints usually alleviated the difficulty of constructing an IDP ensemble with the larger degrees of freedom and led to better modeling results. Though the accuracy seemed to only increase slightly when we added CA chemical shifts, we found that the interquartile range in the box plots became less, which implies the results became more stable.

FIG. 3.

FIG. 3.

Open in a new tab

Results on using different chemical shift data in our validation test. Here, Gaussian noise with standard deviation 0.02 ppm was used to synthesize the chemical shift data. Each test was repeated 50 times with different random seeds. A factor of 0.1 was multiplied to the chemical shifts of heavy atoms (i.e., CA and N) to combine with those of hydrogen atoms (i.e., HN and HA).

Next, we validated the elastic net method with the similar strategy. As shown in Figure 4, we found that the elastic net method significantly outperformed the Monte Carlo approach in this sparsity condition. In addition, compared to the previous nonsparsity situation (Fig. 2), a larger improvement over the Monte Carlo approach was observed for the elastic net method. More details of our validation of the elastic net method can be found in Supplementary Material Section S2 of Gong et al. (2015).

FIG. 4.

FIG. 4.

Open in a new tab

The validation results of the elastic net method through the reference ensemble method. We compared the performance of our method with that of the Monte Carlo approach; MC stands for the Monte Carlo sampling method and EN stands for our elastic net approach. Both Ω (wC, wT) and the RMSD of HN chemical shift were calculated. The test was conducted 50 times with different random seeds.

3.2. Tests on real data

In this section, we tested our ensemble construction methods on real data of three IDPs, including alpha-synuclein, the translocation domain of Colicin N, and the K18 domain of Tau protein, which contain 140, 90, and 130 residues, respectively. For the first two proteins (i.e., alpha-synuclein and Colicin N), in which the number of constraints derived from chemical shift data is larger than the number of representative structures, we applied the least squares algorithm to compute the optimal weights. While for the K18 domain of Tau protein, we used the elastic net method. For alpha-synuclein and the translocation domain of Colicin N, we ran a 10ns MD simulation and obtained a structure pool of 10,000 structures for each IDP. For the K18 domain of Tau protein, we ran a 30ns MD simulation and had a structure pool of 10,000 structures. After that, we clustered each structural pool using the procedure described in section 2.3 with the clustering cutoff 2.1 Å. In total, we obtained 133, 233, and 882 conformations in the initial pool for alpha-synuclein, the translocation domain of Colicin N and the K18 domain of Tau protein, respectively.

The experimental chemical shift data were obtained from the Biological Magnetic Resonance Bank (BMRB) (Doreleijers et al., 2003) and used as input data to our ensemble construction. In particular, we used HN, HA, CA, and N chemical shifts for alpha-synuclein, and HN, CA, and N chemical shifts for the translocation domain of Colicin N and the K18 domain of Tau protein (chemical shifts of HA for these two proteins are not available from the BMRB database). When chemical shifts of both hydrogen and heavy atoms (e.g., CA and N) were combined, we set 0.1 as the weighting factor for the chemical shifts of heavy atoms.

To evaluate the performance of our methods, we mainly focused on the RMSD and Pearson correlation between back-computed and experimental chemical shifts of the tested proteins. The back-computed chemical shifts were calculated based on the ensemble-averaged values, which were shown in Figure 5. We found that the back-computed chemical shifts of heavy atoms based on the constructed IDP ensembles agreed well with experimental values, with Pearson correlation above 0.89. On the other hand, the results on the back-computed chemical shifts of HN and HA (especially HN atoms) became worse. As stated in Wishart and Nip (1998), this phenomenon is probably because the chemical shifts of hydrogen can be predicted much less reliably than the heavy atoms using SHIFTX2. Theoretically, the hydrogen chemical shifts are often affected more significantly by the electric field effect, ring currents, and other local shielding phenomena, which raises the difficulty for their accurate prediction using the current chemical shift prediction programs (e.g., SHIFTX2) (Wishart and Nip, 1998; Han et al., 2011).

FIG. 5.

FIG. 5.

Open in a new tab

Correlation between back-computed and experimental chemical shifts for alpha-synuclein, the translocation domain of Colicin N, and K18 domain of Tau protein. Panels (a) to (d) are for alpha-synuclein, panels (e) to (g) are for the translocation domain of Colicin N, and panels (h) to (j) are for K18 domain of Tau protein. The x label stands for (ensemble-averaged) back-computed chemical shifts, while the y label represents experimental chemical shifts. The symbol r represents the Pearson correlation.

3.3. Case study

In this section, we focused on the IDP structure ensemble constructed by our elastic net method for the K18 domain of Tau protein and analyzed the structural details of long-range interactions between different residues. Overall, the structure ensemble of this protein constructed by our method contains only 58 structures with nonzero weights (i.e., whose weights are larger than the threshold 10−7), as compared to the 882 structures selected from the initial pool. For the constructed ensemble, the RMSD and correlation between back-computed and experimental chemical shifts of CA were 0.953 Å and 0.989, respectively, indicating that our elastic net algorithm computed a reasonably good structure ensemble for Tau protein that agreed with experimental data. In particular, we picked the 10 most probable structures (i.e., with the largest weights) from the ensemble and looked into the details of these conformations. Figure 6 shows the overlay of these 10 structures, where the fragments between residues 20–44 were used in structure alignment. The region in residues 20–44 has been believed to participate in interactions between two different regions divided by a turn motif, PGGG (Fisher et al., 2010). The visualization confirmed this finding, though our results are less obvious compared to those in Fisher et al. (2010).

FIG. 6.

FIG. 6.

Open in a new tab

The structure overlay of the 10 most probable structures (i.e., with the largest weights) in the ensemble of Tau protein computed by our elastic net based method. Panel (a) shows the view of these structures aligned using residues 20–44, and panel (b) shows the view of zooming into the fragment of residues 20–44.

Next, we examined the contact maps of the top 10 structures with the largest weights, which were produced based on the distance cutoff 25 Å between CA atoms. Though some contact maps may look similar, these structures are actually quite different. As shown in Figure 7, for most structures, the regions near residues 33–38 and 64–69 exhibited long-range interactions with the N-terminal residues that are at least 5 residues away along the sequence.

FIG. 7.

FIG. 7.

Open in a new tab

The contact maps for the top 10 structures in the ensemble of K18 domain of Tau protein calculated by our elastic net method. From (a) to (j), the weights of the corresponding structures are in decreasing order.

These observations were consistent with the previous studies in Marsh and Forman-Kay (2009). These two regions (i.e., residues 33–38 and 64–69) form the paired helical filament (PHF) and are supposed to play core functions in the transition state of the Tau aggregation process from normal/unfolded form to pathological states (von Bergen et al., 2005). Thus, the structures modeled by our computational method can provide useful molecular basis for further investigating the functional roles of Tau protein in the related diseases.

4. Conclusions

Constructing structure ensembles for IDPs is a challenging but important task for understanding their cellular functions. In this article, we proposed two novel approaches based on least squares and elastic net techniques to construct the structure ensemble of an IDP from chemical shift data. Validation via the reference ensemble approach and tests on real data have demonstrated the superiority of our methods over traditional stochastic sampling-based approaches. Our least squares method can find the global optimal solution, and the constructed ensemble can depict the structures of IDPs more accurately. Furthermore, our elastic net–based method can successfully address the degeneracy problem, which is the current main challenge of the IDP ensemble construction task.

There are several possible extensions to our IDP structure ensemble. In the current version of our ensemble construction pipeline, we assume that the life trajectories generated by the MD simulation can represent the whole conformational space. In the future, we will improve the current procedure of constructing the initial structure pool, such that it can be better integrated with the computation of optimal weights. In addition, for future work, we will incorporate more information to guide our ensemble construction, such as additional experimental data and available prior knowledge about IDP structures.

Acknowledgments

This work was supported in part by the National Basic Research Program of China Grant 2011CBA00300, 2011CBA00301; the National Natural Science Foundation of China Grant 61033001, 61361136003, and 61472205; and China's Youth 1000-Talent Program.

Author Disclosure Statement

The authors declare that no competing financial interests exist.

References

  1. Allison J.R., Varnai P., Dobson C.M., and Vendruscolo M., 2009. Determination of the free energy landscape of α-synuclein using spin label nuclear magnetic resonance measurements. J. Am. Chem. Soc. 131, 18314–18326 [DOI] [PubMed] [Google Scholar]
  2. Berman H.M., Westbrook J., Feng Z., et al. , 2000. The protein data bank. Nucleic Acids Res. 28, 235–242 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Brooks B.R., Bruccoleri R.E., Olafson B.D., et al. , 1983. Charmm: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4, 187–217 [Google Scholar]
  4. Cavalli A., Salvatella X., Dobson C.M., and Vendruscolo M., 2007. Protein structure determination from NMR chemical shifts. Proc. Natl. Acad. Sci. U. S. A. 104, 9615–9620 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chen Y., Campbell S.L., and Dokholyan N.V., 2007. Deciphering protein dynamics from NMR data using explicit structure sampling and selection. Biophys. J. 93, 2300–2306 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Choy W.-Y., and Forman-Kay J.D., 2001. Calculation of ensembles of structures representing the unfolded state of an SH3 domain. J. Mol. Biol. 308, 1011–1032 [DOI] [PubMed] [Google Scholar]
  7. Doreleijers J.F., Mading S., Maziuk D., et al. , 2003. BioMagResBank database with sets of experimental NMR constraints corresponding to the structures of over 1400 biomolecules deposited in the Protein Data Bank. J. Biomol. NMR 26, 139–146 [DOI] [PubMed] [Google Scholar]
  8. Dunker A., Lawson J., Brown C.J., et al. , 2001. Intrinsically disordered protein. J. Mol. Graph. Model. 19, 26–59 [DOI] [PubMed] [Google Scholar]
  9. Dyson H.J., and Wright P.E., 2005. Intrinsically unstructured proteins and their functions. Nat. Rev. Mol. Cell. Biol. 6, 197–208 [DOI] [PubMed] [Google Scholar]
  10. Feldman H.J., and Hogue C.W., 2000. A fast method to sample real protein conformational space. Proteins Struct. Funct. Bioinform. 39, 112–131 [PubMed] [Google Scholar]
  11. Feldman H.J., and Hogue C.W., 2002. Probabilistic sampling of protein conformations: New hope for brute force? Proteins Struct. Funct. Bioinform. 46, 8–23 [PubMed] [Google Scholar]
  12. Fisher C.K., and Stultz C.M., 2011. Constructing ensembles for intrinsically disordered proteins. Curr. Opin. Struct. Biol. 21, 426–431 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fisher C.K., Huang A., and Stultz C.M., 2010. Modeling intrinsically disordered proteins with bayesian statistics. J. Am. Chem. Soc. 132, 14919–14927 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Fonseca R., Pachov D.V., Bernauer J., and Van Den Bedem H., 2014. Characterizing RNA ensembles from NMR data with kinematic models. Nucleic Acids Res. 42, 9562–9572 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Frank M., and Wolfe P., 1956. An algorithm for quadratic programming. Nav. Res. Logistics Q. 3, 95–110 [Google Scholar]
  16. Friedman J.H., Hastie T., and Tibshirani R., 2010. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 33, 1–22 [PMC free article] [PubMed] [Google Scholar]
  17. Ganguly D., and Chen J., 2009. Structural interpretation of paramagnetic relaxation enhancementderived distances for disordered protein states. J. Mol. Biol. 390, 467–477 [DOI] [PubMed] [Google Scholar]
  18. Gong H., Zhang S., Wang J., et al. , 2015. Constructing structure ensembles of intrinsically disordered proteins from chemical shift data—supplementary material. http://iiis.tsinghua.edu.cn/%7ecompbio/papers/recomb15IDPSM.pdf [DOI] [PMC free article] [PubMed]
  19. Han B., Liu Y., Ginzinger S.W., and Wishart D.S., 2011. SHIFTX2: Significantly improved protein chemical shift prediction. J. Biomol. NMR 50, 43–57 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hastie T., Tibshirani R., and Friedman J., 2001. The Elements of Statistical Learning. Springer Series in Statistics. Springer New York Inc., New York [Google Scholar]
  21. Iakoucheva L.M., Brown C.J., Lawson J., et al. , 2002. Intrinsic disorder in cell-signaling and cancer-associated proteins. J. Mol. Biol. 323, 573–584 [DOI] [PubMed] [Google Scholar]
  22. Jensen M.R., Salmon L., Nodet G., and Blackledge M., 2010. Defining conformational ensembles of intrinsically disordered and partially folded proteins directly from chemical shifts. J. Am. Chem. Soc. 132, 1270–1272 [DOI] [PubMed] [Google Scholar]
  23. Karres J.S., Hilgers V., Carrera I., et al. , 2007. The conserved microrna mir-8 tunes atrophin levels to prevent neurodegeneration in drosophila. Cell 131, 136–145 [DOI] [PubMed] [Google Scholar]
  24. Kuriyan J., Petsko G.A., Levy R.M., and Karplus M., 1986. Effect of anisotropy and anharmonicity on protein crystallographic refinement. An evaluation by molecular dynamics. J. Mol. Biol. 190, 227–254 [DOI] [PubMed] [Google Scholar]
  25. Marsh J.A., and Forman-Kay J.D., 2009. Structure and disorder in an unfolded state under nondenaturing conditions from ensemble models consistent with a large number of experimental restraints. J. Mol. Biol. 391, 359–374 [DOI] [PubMed] [Google Scholar]
  26. Nodet G., Salmon L., Ozenne V., et al. , 2009. Quantitative description of backbone conformational sampling of unfolded proteins at amino acid resolution from NMR residual dipolar couplings. J. Am. Chem. Soc. 131, 17908–17918 [DOI] [PubMed] [Google Scholar]
  27. Ozenne V., Bauer F., Salmon L., et al. , 2012. Flexible-meccano: A tool for the generation of explicit ensemble descriptions of intrinsically disordered proteins and their associated experimental observables. Bioinformatics 28, 1463–1470 [DOI] [PubMed] [Google Scholar]
  28. Phillips J.C., Braun R., Wang W., et al. , 2005. Scalable molecular dynamics with NAMD. J. Comput. Chem. 26, 1781–1802 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Recchia A., Debetto P., Negro A., et al. , 2004. α-synuclein and parkinsons disease. FASEB J. 18, 617–626 [DOI] [PubMed] [Google Scholar]
  30. Schwieters C.D., Kuszewski J.J., and Clore G.M., 2006. Using Xplor-NIH for NMR molecular structure determination. Prog. Nucl. Magn. Reson. Spectrosc. 48, 47–62 [Google Scholar]
  31. Schwieters C.D., Kuszewski J.J., Tjandra N., and Clore G.M., 2003. The Xplor-NIH NMR molecular structure determination package. J. Magn. Reson. 160, 65–73 [DOI] [PubMed] [Google Scholar]
  32. Shen Y., Lange O., Delaglio F., et al. , 2008. Consistent blind protein structure generation from NMR chemical shift data. Proc. Natl. Acad. Sci. U. S. A. 105, 4685–4690 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Simon N., Friedman J.H., Hastie T., and Tibshirani R., 2011. Regularization paths for cox's proportional hazards model via coordinate descent. J. Stat. Softw. 39, 1–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Tamiola K., Acar B., and Mulder F.A.A., 2010. Sequence-specific random coil chemical shifts of intrinsically disordered proteins. J. Am. Chem. Soc. 132, 18000–18003 [DOI] [PubMed] [Google Scholar]
  35. Tanner D.E., Chan K.-Y., Phillips J.C., and Schulten K., 2011. Parallel generalized born implicit solvent calculations with NAMD. J. Chem. Theory Comput. 7, 3635–3642 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Terakawa T., and Takada S., 2011. Multiscale ensemble modeling of intrinsically disordered proteins: p53 n-terminal domain. Biophys. J. 101, 1450–1458 [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Vekrellis K., and Stefanis L., 2012. Targeting intracellular and extracellular alpha-synuclein as a therapeutic strategy in parkinson's disease and other synucleinopathies. Expert Opin. Ther. Targets 16, 421–432 [DOI] [PubMed] [Google Scholar]
  38. von Bergen M., Barghorn S., Biernat J., et al. , 2005. Tau aggregation is driven by a transition from random coil to beta sheet structure. Biochim. Biophys. Acta Mol. Basis Disease 1739, 158–166 [DOI] [PubMed] [Google Scholar]
  39. Wishart D.S., and Nip A.M., 1998. Protein chemical shift analysis: A practical guide. Biochem. Cell Biol. 76, 153–163 [DOI] [PubMed] [Google Scholar]
  40. Zou H., and Hastie T., 2005. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 67, 301–320 [Google Scholar]

Articles from Journal of Computational Biology are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES