Abstract
Introduction
Lumosity's Memory Match (LMM) is an online game requiring visual working memory. Change in LMM scores may be associated with individual differences in age-related changes in working memory.
Methods
Effects of age and time on LMM learning and forgetting rates were estimated using data from 1890 game sessions for users aged 40 to 79 years.
Results
There were significant effects of age on baseline LMM scores (β = −.31, standard error or SE = .02, P < .0001) and lower learning rates (β = −.0066, SE = .0008, P < .0001). A sample size of 202 subjects/arm was estimated for a 1-year study for subjects in the lower quartile of game performance.
Discussion
Online memory games have the potential to identify age-related decline in cognition and to identify subjects at risk for cognitive decline with smaller sample sizes and lower cost than traditional recruitment methods.
Keywords: Online games, Cognitive decline, Alzheimer's disease, Internet game, Internet registry, Online cognitive assessments, Memory
1. Background
In older individuals a number of neurodegenerative conditions are associated with cognitive decline, especially decline of memory function. These disorders include Alzheimer's disease [1], Lewy body disease [2], Parkinson's disease [2], [3], cerebrovascular disease [4], [5], [6], and other conditions [7] that have been associated with memory impairments [8], [9], [10]. Currently, there is no effective treatment for slowing the progression of these neurodegenerative disorders, despite numerous expensive clinical trials [11]. One of the major obstacles to developing effective therapies for Alzheimer's disease and other neurodegenerative disorders is the high cost of identifying, recruiting, and screening participants for clinical trials.
One approach toward reducing the cost of clinical trials is to develop Internet-based registries of prescreened subjects who meet specific criteria for eligibility [11], [12]. Recent studies using brief computerized cognitive tests have shown that intraindividual decline in cognitive performance predicts the presence of cortical amyloid in cognitively normal subjects [13], [14]. An Internet registry that administers computerized cognitive assessments could be used to longitudinally follow a large, diverse population and identify subjects who demonstrate progressive intraindividual decline. Furthermore, it has been suggested that the use of auxiliary baseline covariates can improve the efficiency of the estimators for treatment effects [15]. Therefore, measurements of rates of decline before subjects are enrolled in randomized studies may be useful as covariates to predict future rates of decline and increase the statistical power of the study. Furthermore, higher statistical power could facilitate clinical trial designs with smaller sample sizes and reduced length of monitoring.
Lumos Labs is the developer of Lumosity, which is a suite of mobile and web-based games designed to facilitate cognitive training. Over one million individuals have played a variety of these games longitudinally over multiple years. Although the validity of these games with respect to existing measures of working memory has not been established, many of the games have been adapted from standard cognitive tests. One popular game is Lumosity's Memory Match (LMM), which is a two-back visual working memory task. Although a previous cross-sectional analysis of LMM data suggested that older age was associated with reduced LMM game scores [16], to our knowledge, there has been no longitudinal analysis relating LMM game scores to age.
Similar to other measures of change in cognitive performance, the instantaneous slope of LMM game scores can be primarily determined by the two opposing forces of learning and forgetting [17], [18], [19], [20]. The learning rate imparts a positive component to the slope whereas the forgetting rate contributes the negative component. Cognitive decline may be associated with low learning rates or high forgetting rates, but cognitive decline may not necessarily exhibit declining scores if task engagement frequency is sufficiently high. Therefore, estimation of both learning and forgetting rates would be required to evaluate potential cognitive decline with LMM scores.
The first goal of this study was to determine the association between age and the learning rate, forgetting rate, and baseline LMM score. We hypothesize that learning rates, forgetting rates, and baseline scores would decline with age. If this hypothesis is correct, then progressive intraindividual decline in the learning rate over many years of observation may also indicate aging and cognitive decline, an assertion that could be tested in a future study. The second goal of this study was to develop a model that would explain much of the variation in the LMM data in terms of learning and forgetting effects. If a low learning rate is an indicator of memory impairment, then one would expect an improvement in learning rates for individuals who have completed an effective AD treatment in future studies. Therefore, a final goal was to estimate the sample size of a study that has 80% power to detect a 25% reduction in the gap between the average learning rate of the sample for a particular age and the average learning rate for subjects who had been identified as decliners of the same age.
2. Methods
2.1. Instrument
LMM is an online two-back visual working memory game developed by Lumos Labs (San Francisco, CA). LMM presents a randomly generated sequence of colorful geometric figures, and the user is tasked with indicating whether the current figure matches the one presented two figures prior. The user is given 45 seconds to match as many figures as possible. The session number, session date, number of attempted matches, and the number of correct matches (score) are recorded for each session. The validity of the LMM score as a measure of working memory has not yet been evaluated, and there was no possibility of comparing LMM performance to accepted measures of valid working memory for this study.
2.2. Sample
Deidentified LMM game session (at least one complete game) data for 1.3 million users was analyzed. The data included session numbers, the session dates, and the scores for each subject in the sample. Demographic data such as the age, gender, and education level for each subject were also included. Subjects played at least one session of LMM at some time between January 2007 and August 2013. Most subjects played dozens of sessions during that period, and some played several thousand sessions. The game sessions were unsupervised and the environments where the games were played may not have been free from distractions. No assessment of working memory or motor function before enrollment had been obtained for the subjects. Moreover, the sample is limited to people who have access to the Internet and play computer games.
One thousand eight hundred and ninety subjects were selected from the original data set based on the satisfaction of several criteria. First, those selected must have attained an age between 40 and 79 years by their first session. Second, selected subjects must have played 50 sessions of LMM over 1 or more years to allow for more robust estimates of forgetting. Third, selected subjects must have played on 4 or more separate days. This third criterion ensured that each individual had at least three intersession time gaps, which are necessary for estimating individual forgetting rates. Finally, the selected subjects must have played at least three consecutive sessions on 3 or more days. Because the forgetting effect is negligible when the intersession time gaps are less than one day, this final criterion ensured a good estimate of the learning rate, which was not confounded with the forgetting effect. The final sample consisted of older (mean age = 58.2, standard deviation or SD = 9.5, range = 40–79, 69.4% women) individuals who played 50 LMM sessions over one or more years.
2.3. Model and measurements
Using the nlme package for the R statistical computing environment, we estimated the individual LMM learning rates, forgetting rates, and the cross-sectional effects of age on learning rates, forgetting rates, and baseline scores with a linear mixed effects regression model. The first four sessions were discarded to allow users to become familiar with the game, and the last five sessions were set aside to test the forecast accuracy of the model. The fifth session was the baseline session, and changes in the LMM scores were measured with respect to this session. Equations (1), (2), (3) represent a model for the difference between the scores for the Sth session and the baseline session for the ith individual. In equation 1, the score for the ith individual on the Sth session is YS,i; the baseline score is Y5,i; and the total elapsed time, measured in days between the first and the Sth session, is TS,i, where S is an index between 6 and 45.
The random slope (ai) associated to the session number is the linear rate at which the ith individual's scores increase per session and is interpreted as the learning rate. Alternatively, the random slope (bi) for the time variable is the linear rate at which the ith individual's scores decline per year after adjustment for the accumulated practice and is interpreted as the forgetting rate. In equations (2), (3), the random slopes (ai, bi) are expressed in terms of the population averages (aμ, bμ) for the mean age (Aμ), adjustments for the individual baseline age (A5,i), and the individual random effects (εa,i, εb,i). Equation 4 relates the individual baseline score (Y5,i) to the population average (Y5,μ) for the mean age and an adjustment for baseline age. The parameters of interest are the age effects (α,β,γ) and the random effects (εa,i) associated to the individual differences in the learning rates with respect to the mean learning rate for other individuals in the same age group.
| (1) |
| (2) |
| (3) |
| (4) |
2.4. Sample size study with LMM pilot data
An Internet game may never be validated for use in a clinical trial for AD treatments. Nevertheless, to demonstrate the potential of an Internet registry of Internet game play data for screening and assessing subjects during a clinical trial, we computed the sample size of a putative randomized placebo-controlled study using the LMM sample as pilot data. We supposed that a group of decliners could be identified during the first 45 LMM sessions. After discarding the first four sessions, we estimated the learning rates for the sample with the mixed effects model specified by equations (1), (2), (3). Subjects with estimated learning rates lower than the 25th percentile for their ages were identified as decliners. Then we supposed that the decliners could be randomly allocated to two groups of equal size with one group given a placebo and the other an effective AD treatment. Subjects in both groups may be asked to play four sessions of LMM on 14 days spanning 1 year for a total of 56 sessions per subject. The intersession time gaps, measured in days, between the 14 testing days were assumed to be the following: 1, 28, 1, 56, 1, 84, 1, 28, 1, 56, 1, 84, 1. Consecutive days were separated by 1 day.
Each decliner's trajectory of scores deviated from the expected trajectory given by the fixed effects. If the treatment effectively increases the learning rate, then the deviations from the expected scores should shrink for the participants in the treatment group. Let CS,i = YS,i − YK,i denote the change in the score between the Kth and the Sth sessions for the ith subject, when session K occurs during the first day of the trial. Further define ĈS,i to be the expected change for a subject possessing average learning and forgetting rates, and beginning the study with the same age and baseline score as the ith subject, and playing LMM with the same frequency. Then the subject's deviation from the expected change is given by DS,i = CS,i − ĈS,i. If the placebo group is labeled with “A” and the treatment group is labeled with “B”, then the models for deviation after assignment to group A or B are given by equations (5), (6) with the random effects denoted by α and the fixed effects denoted by β.
| (5) |
| (6) |
The parameters of interest, β1A and β1B, are the average interactions between the treatment and the session numbers for the placebo and treatment groups, respectively. We assumed that a successful treatment will reduce the slope, β1B, for the treatment group by 25%, so that β1A − β1B ≥ .25 * β1A. Diggle et al. [21] provides a sample size formula, which requires estimates of the fixed effects and random effects in equation 5. The necessary parameter estimates were obtained by fitting a random effects model to the decliners' LMM data. Then we calculated the sample size to detect a 25% reduction in β1B with 80% power and 5% significance.
3. Results
3.1. Age effects
A likelihood ratio test comparing the full model specified by equations (1), (2), (3) to a restricted model that did not include age as a covariate was significant (χ2(2) = 104, P < .0001). Table 1 summarizes the parameter estimates for the entire sample of 1890 LMM players. Consistent with our hypotheses, older ages were associated with lower baseline scores (γ = −0.31, standard error or SE = 0.16, P < .0001) and lower learning rates (α = −.0066, SE = .0008, P < .0001). Older ages were not associated with more severe forgetting rates (β = .02, SE = .02, P < .27), a result that was contrary to our hypothesis.
Table 1.
Fixed effects game play data
| Estimate | Standard error | P-value | |
|---|---|---|---|
| Baseline score [YK,μ] | 18.95 | 0.16 | <.0001 |
| Baseline score* (age 58 years) [γ] | −0.31 | 0.02 | <.0001 |
| Learning rate [aμ] | 0.37 | 7.48E−003 | <.0001 |
| Learning rate* (age 58 years) [α] | −6.56E−003 | 7.87E−004 | <.0001 |
| Forgetting rate [bμ] | −2.12 | 0.19 | <.0001 |
| Forgetting rate* (age 58 years) [β] | 0.02 | 0.02 | .27 |
The age trends for the baseline scores and the learning rates are graphically shown in Fig. 1, Fig. 2 with age accounting for only 4% of the variation in the learning rates. The relatively large standard deviation (σ = 0.31; Table 2) in the learning rates, compared with the age-adjusted mean (aμ = .37), suggests a wide range in learning ability for all ages with some learning rates near zero.
Fig. 1.
Age trend for the baseline score with 95% prediction interval.
Fig. 2.
Age trend for the learning rate with 95% prediction interval.
Table 2.
Random effects standard deviations game play data
| Standard deviation | |
|---|---|
| Baseline score [εi] | 6.92 |
| Learning rate [εa,i] | 0.31 |
| Forgetting rate [εb,i] | 7.09 |
| Standard dev. [εS,i] | 5.05 |
Although participants played LMM at different times and with different frequencies, the usage patterns did not meaningfully differ by age group and, therefore, did not have an influence on reported age effects. The mean number of play days was 18.58 for ages 40 to 59 and 18.02 for ages 60 to 79 (pooled SD = 6.36). The difference of the mean play days between the two age groups was not statistically significant (F(1,1888) = 3.652, P > .05). The mean engagement period, measured in days, was 695 for ages 40 to 59 and 650 for ages 60 to 79 (pooled SD = 289). The difference of 45 days was statistically significant (F(1,1888) = 11.02, P < .01). The mean number of sessions per day was 2.15 for ages 40 to 59 and 2.22 for ages 60 to 79 (within subject SD = 1.84, between subject SD = .99). The difference of a small fraction of a session was significant (F(1,1888) = 6.17, P = .01). The mean number of days between sessions was 31.72 for ages 40 to 59 and 29.76 for ages 60 to 79 (within subject SD = 100.41, between subject SD < .01). The effect of age on the days between sessions was not significant (F(1,1888) = 3.161, P = .07).
3.2. Model fit
The marginal R2 (0.16) and the conditional R2 (0.75) for the full model were also estimated with r.squaredGLMM in the MuMIn package for R. The conditional R2 is the proportion of the total variation explained by the full model, including both the fixed and random effects, whereas the marginal R2 is the proportion explained by the fixed effects only. The high conditional R2 indicates a good fit for each individual's data series and validates the use of a random effects model. The relatively low marginal R2 indicates that the average does not fit the data very well and therefore also reinforces the need for random effects at the subject level.
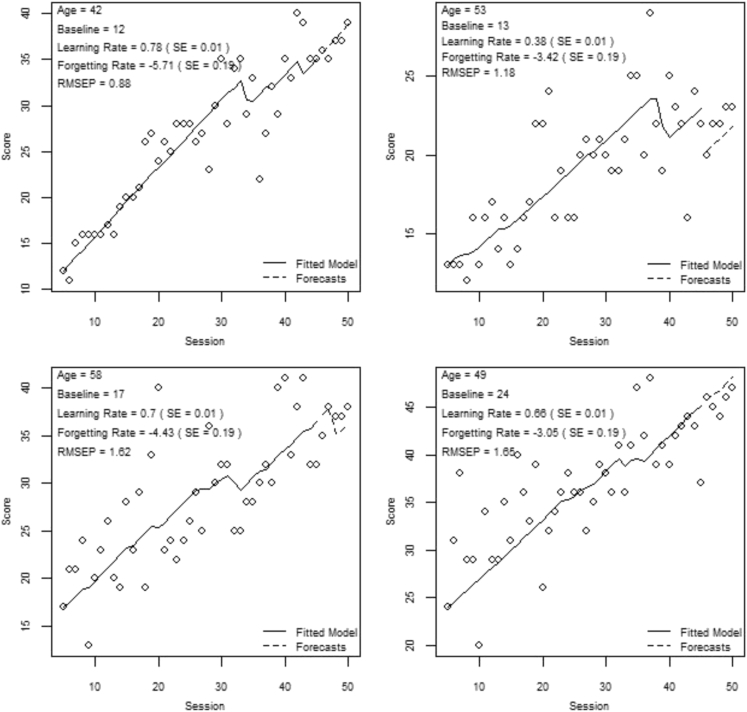
A measure of forecast accuracy is the root mean squared error of prediction (RMSEP) for the five forecasts for each participant. The average RMSEP was 5.27 (SD = 3.44). The fitted model and the forecasts are plotted with the actual scores for four individuals in Fig. 3. The forecast errors for these four examples are low relative to the average RMSEP. In Fig. 4, the scores and forecasts of four decliners are plotted. Contrasting against the first four examples, the trajectories in Fig. 4 are flat, showing no general improvement of the score over time. Another measure of forecast accuracy is the test-retest reliability, which was estimated by the sample correlation between the fifth and sixth sessions. The estimated test-retest reliability was 0.79.
Fig. 3.
Model fit and forecasts of four Lumosity's Memory Match (LMM) participants demonstrating large learning rates.
Fig. 4.
Model fit and forecasts of four Lumosity's Memory Match (LMM) decliners.
3.3. Sample size
Two hundred and two subjects per arm are required to detect a 25% reduction in the gap between the average age-adjusted learning rate of the entire sample and the average age-adjusted learning rate for subjects who had been identified as decliners with 80% power and 5% significance.
4. Discussion
There is considerable interest in developing computerized tests [22] that will identify subjects at risk for the development of cognitive impairment and dementia. Such tests could be used to screen subjects for clinical trials before prescribing treatments aimed at slowing cognitive decline. Longitudinal change in standard neuropsychological assessments could be used in this fashion, but the high cost of having subjects tested in-person by neuropsychologists prevents this approach on a large scale. The availability of online game data represents an additional, but untested, avenue to screen subjects for clinical trials.
This study is a retrospective analysis of online computer game scores with the objective of demonstrating the potential of web-based game data for identifying subjects at risk for cognitive decline. Computer games are not designed to be valid neuropsychological tests, and we emphasize that LMM has not been validated as a measure of working memory. Furthermore, games are performed in a completely unsupervised manner. Subjects may play online games in an environment with many distractions or under the influence of alcohol or other substances that may affect performance.
Our data suggest that LMM scores are very susceptible to the influences of practice and forgetting. A comparison of two scores is not meaningful without an adjustment for the engagement frequency, which has been modeled explicitly by the use of covariates for the number of completed sessions and the total elapsed time between sessions. As indicated by the generally positive estimates for the individual learning rates, frequent practice tends to improve game score. For example, the main effect for the learning rate (aμ = .37, SE = .007, P < .0001) suggests that the average subject, aged 58, improves by approximately 1 correct match for every three sessions when the intersession time gaps are sufficiently small. The generally negative estimates for forgetting rates indicate that long breaks cause declines in game performance. The main effect for the forgetting rate (bμ = −2.12, SE = .19, P < .0001) suggests that the average subject, aged 58, declines by approximately two correct matches per year when there is a long break in the sessions.
Although there has been much debate over the form of learning and forgetting curves [17], [18], [19], [20], the first 50 sessions of LMM were modeled successfully with simple lines that rise in response to practice and decline during long breaks. As measured by the conditional R2 for the mixed effects model, 75% of the variation in the LMM scores is explained by individual learning and forgetting rates. The good fit of the model suggests that learning and forgetting rates predict well the LMM scores. Moreover, the estimated test-retest reliability (0.79) is comparable with the estimates for standard neuropsychological tests. Therefore, the learning and forgetting rates appear to be stable measures of performance that identify genuine differences between individuals.
Among the factors that cause differences between individuals, age has been shown to affect the learning rate. Baseline scores and learning rates decline across ages, suggesting that some individual learning rates decline over time. Therefore, it is reasonable to conclude that a low LMM learning rate may serve as a measure of age-related decline in the working memory function of participating subjects, although a follow-up study demonstrating a correlation between LMM learning rates and the scores of valid tests for working memory would be necessary. Our data suggest that age did not affect the forgetting rate. It must be remembered that both the learning and forgetting rates are absolute measures of change with the learning rate expressed in units of correct matches per session, and the forgetting rate expressed in units of correct matches per year. If the forgetting rate had been expressed as the proportional change in the score per year, then a significant age interaction might have been observed.
If low LMM learning rates are shown to be valid screening measures of cognitive dysfunction, then it would be possible to identify declining individuals, invite them to complete valid tests, and potentially enroll them into clinical trials. In this study, decliners are defined as individuals whose estimated learning rates are lower than the 25th percentile for their age. A power analysis of a putative trial aimed at slowing cognitive decline in preselected decliners showed that sample sizes are extremely reasonable and possibly smaller than sample sizes currently used in AD clinical trials.
Research in context.
-
1.
Systematic review: The authors reviewed the literature obtained from PubMed and other traditional sources. Publications spanning the entire history of inquiry into the functional form of learning and forgetting curves were reviewed.
-
2.
Interpretation: Internet games may be used for identifying subjects at risk for cognitive decline.
-
3.
Future directions: Validation of Internet-based games and assessments for use in identifying individuals at risk for cognitive decline represents a significant priority for future research.
Acknowledgments
The authors gratefully acknowledge the following funding sources for the Brain Health Registry: The Rosenberg Alzheimer's Project, The Ray and Dagmar Dolby Family Fund, Connie, and Kevin Shanahan, General Electric, and The Drew Foundation. The authors would also like to acknowledge Diana Truran, Shannon Finley, Monica Comacho, Derek Flennikan, Rachel Nosheny, and Kevin Sweeney for their contributions to the development and facilitation of the Brain Health Registry which made this manuscript possible. Additionally, the authors would like to acknowledge the contributions of Dallas Veitch and Keifer Katovich at Lumos Labs for their assistance in preparing this manuscript.
References
- 1.Ballard C., Gauthier S., Corbett A., Brayne C., Aarsland D., Jones E. Alzheimer's disease. Lancet. 2011;377:1019–1031. doi: 10.1016/S0140-6736(10)61349-9. [DOI] [PubMed] [Google Scholar]
- 2.Selikhova M., Williams D.R., Kempster P.A., Holton J.L., Revesz T., Lees A.J. A clinico-pathological study of subtypes in Parkinson's disease. Brain. 2009;132(Pt 11):2947–2957. doi: 10.1093/brain/awp234. [DOI] [PubMed] [Google Scholar]
- 3.Williams-Gray C.H., Foltynie T., Brayne C.E., Robbins T.W., Barker R.A. Evolution of cognitive dysfunction in an incident Parkinson's disease cohort. Brain. 2007;130(Pt 7):1787–1798. doi: 10.1093/brain/awm111. [DOI] [PubMed] [Google Scholar]
- 4.Knopman D.S. Cerebrovascular disease and dementia. Br J Radiol. 2007;80 Spec No 2:S121–S127. doi: 10.1259/bjr/75681080. [DOI] [PubMed] [Google Scholar]
- 5.Knopman D.S., Roberts R.O., Geda Y.E., Boeve B.F., Pankratz V.S., Cha R.H. Association of prior stroke with cognitive function and cognitive impairment: a population-based study. Arch Neurol. 2009;66:614–619. doi: 10.1001/archneurol.2009.30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Edwards J.D., Jacova C., Sepehry A.A., Pratt B., Benavente O.R. A quantitative systematic review of domain-specific cognitive impairment in lacunar stroke. Neurology. 2013;80:315–322. doi: 10.1212/WNL.0b013e31827deb85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Walker F.O. Huntington's disease. Lancet. 2007;369:218–228. doi: 10.1016/S0140-6736(07)60111-1. [DOI] [PubMed] [Google Scholar]
- 8.Levy G., Jacobs D.M., Tang M.X., Cote L.J., Louis E.D., Alfaro B. Memory and executive function impairment predict dementia in Parkinson's disease. Mov Disord. 2002;17:1221–1226. doi: 10.1002/mds.10280. [DOI] [PubMed] [Google Scholar]
- 9.Schneider J.A., Arvanitakis Z., Yu L., Boyle P.A., Leurgans S.E., Bennett D.A. Cognitive impairment, decline and fluctuations in older community-dwelling subjects with Lewy bodies. Brain. 2012;135(Pt 10):3005–3014. doi: 10.1093/brain/aws234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.El Haj M., Caillaud M., Fasotti L., Verny C., Allain P. Episodic memory decline in Huntington's disease, a binding deficit? J Huntingtons Dis. 2013;2:305–313. doi: 10.3233/JHD-130056. [DOI] [PubMed] [Google Scholar]
- 11.Reiman E.M., Langbaum J.B., Fleisher A.S., Caselli R.J., Chen K., Ayutyanont N. Alzheimer's Prevention Initiative: a plan to accelerate the evaluation of presymptomatic treatments. J Alzheimers Dis. 2011;26(Suppl 3):321–329. doi: 10.3233/JAD-2011-0059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ayutyanont N., Langbaum J.B., Hendrix S.B., Chen K., Fleisher A.S., Friesenhahn M. The Alzheimer's prevention initiative composite cognitive test score: sample size estimates for the evaluation of preclinical Alzheimer's disease treatments in presenilin 1 E280A mutation carriers. J Clin Psychiatry. 2014;75:652–660. doi: 10.4088/JCP.13m08927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Darby D.G., Brodtmann A., Pietrzak R.H., Fredrickson J., Woodward M., Villemagne V.L. Episodic memory decline predicts cortical amyloid status in community-dwelling older adults. J Alzheimers Dis. 2011;27:627–637. doi: 10.3233/JAD-2011-110818. [DOI] [PubMed] [Google Scholar]
- 14.Darby D.G., Pietrzak R.H., Fredrickson J., Woodward M., Moore L., Fredrickson A. Intraindividual cognitive decline using a brief computerized cognitive screening test. Alzheimers Dement. 2012;8:95–104. doi: 10.1016/j.jalz.2010.12.009. [DOI] [PubMed] [Google Scholar]
- 15.Zhang M., Tsiatis A.A., Davidian M. Improving efficiency of inferences in randomized clinical trials using auxiliary covariates. Biometrics. 2008;64:707–715. doi: 10.1111/j.1541-0420.2007.00976.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sternberg D.A., Ballard K., Hardy J.L., Katz B., Doraiswamy P.M., Scanlon M. The largest human cognitive performance dataset reveals insights into the effects of lifestyle factors and aging. Front Hum Neurosci. 2013;7:292. doi: 10.3389/fnhum.2013.00292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Newell A., Rosenbloom P. Carnegie Mellon University; Hillsdale, NJ: 1980. Mechanisms of skill acquisition and the law of practice. Paper 2387. [Google Scholar]
- 18.Heathcote A., Brown S., Mewhort D.J. The power law repealed: the case for an exponential law of practice. Psychon Bull Rev. 2000;7:185–207. doi: 10.3758/bf03212979. [DOI] [PubMed] [Google Scholar]
- 19.Loftus G. Evaluating forgetting curves. J Exp Psychol. 1985;11:397–406. [Google Scholar]
- 20.Wixted J. On the form of forgetting. Pyschol Sci. 1991;2:409–415. [Google Scholar]
- 21.Diggle, P.J., Hagerty, P., Liang, K., Zeger, S.L., Analysis of longitudinal data. 2002.
- 22.Wild K., Howieson D., Webbe F., Seelye A., Kaye J. The status of computerized cognitive testing in aging: a systematic review. Alzheimers Dement. 2008;4:428–437. doi: 10.1016/j.jalz.2008.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]