Interface dynamics and crystal phase switching in GaAs nanowires

Summary

Controlled formation of non-equilibrium crystal structures is one of the most important challenges in crystal growth. Catalytically-grown nanowires provide an ideal system for studying the fundamental physics of phase selection, while also offering the potential for novel electronic applications based on crystal polytype engineering. Here we image GaAs nanowires during growth as they are switched between polytypes by varying growth conditions. We find striking differences between the growth dynamics of the polytypes, including differences in interface morphology, step flow, and catalyst geometry. We explain the differences, and the phase selection, through a model that relates the catalyst volume, contact angle at the trijunction, and nucleation site of each new layer. This allows us to predict the conditions under which each phase should be preferred, and use these predictions to design GaAs heterostructures. We suggest that these results may apply to phase selection in other nanowire systems.

Introduction

Many materials can grow in multiple (meta)stable crystal structures, and phase selection is one of the most fundamental problems in material science. However, the selection process can be difficult to access experimentally. For example, many metastable phases are only obtained by rapid quenching of a liquid into a polycrystalline multiphase solid. In contrast, nanowires provide an ideal system for studying phase selection. Typical zincblende-structure (ZB) III-V semiconductors can form nanowires in the wurtzite (WZ) structure as well as the ZB ^1–5. Nanowires can be easily switched between structures by varying the temperature, source-material flux, or impurities ^3,4,6–14; and their small diameter guarantees that they are single crystals, with phase switching occurring along the growth axis where it is easily observed. Since ZB and WZ have different bandstructures ¹⁵, this creates unique opportunities for designing modulated nanowire structures with new electronic properties. Crystal phase heterostructures are particularly interesting because they can access the electronic properties of heterostructure quantum dots for photonics and single electron transistor applications, but without the challenges of compositional control ^16–19.

In order to take full advantage of the possibilities offered by crystal structure control, a detailed understanding of the physics behind polytype formation is required. Based on post-growth observations, different models have been proposed for the phase selection. These emphasize the role of supersaturation, catalyst geometry and interfacial energies ^20–25. Experimental results are typically interpreted in terms of the dominant role of one of these factors ^{6–8,10,12,20,26–28}.

Here, we directly observe the dynamic processes that take place during nanowire growth for each polytype and during the switch between polytypes using in situ transmission electron microscopy. We find surprising differences in the structure and dynamics during growth of ZB vs WZ. Most importantly, the switching process itself, and the associated changes in geometry, offer unexpected clues that allow us to develop a new model identifying the underlying mechanism driving crystal phase selection. In this model, droplet geometry is the key parameter in determining structure, but indirectly – via its effect on the nanowire edge morphology. This understanding allows us to form crystal phase quantum dots with atomic layer precision.

Imaging interface and catalyst geometry

We observed the two GaAs nanowire polytypes during growth in situ using a Hitachi H-9000 ultra-high vacuum transmission electron microscope (UHV-TEM) ^29,30. Si substrates were first prepared with pre-grown GaAs nanowires using standard metal-organic vapor phase epitaxy (MOVPE) and Au aerosol particles with diameters of 30nm, 50nm and 70nm. Such samples can be heated resistively in situ, using a pyrometer to calibrate the temperature at each heating current (see Methods). Pure trimethylgallium (TMGa) and arsine (AsH₃) were used as precursor gases and were introduced close to the substrate using separate capillary tubes to a maximum total pressure during imaging of 2 × 10^-5 Torr. Details of how the growth parameters in situ compare to conventional MOVPE are provided in the Methods section. On heating to temperatures around 550°C, a liquid AuGa droplet formed at the nanowire tip and growth took place at the droplet/nanowire interface. Growth was recorded at 30 images per second. Dark-field imaging conditions, as used in Figure 1 below, allow the crystal structure to be distinguished, in other words the WZ polytype and the two twin variants of the ZB polytype (Extended Data Figure 1). Bright-field imaging conditions, as used in Figure 2, allow a more accurate determination of the droplet and nanowire dimensions.

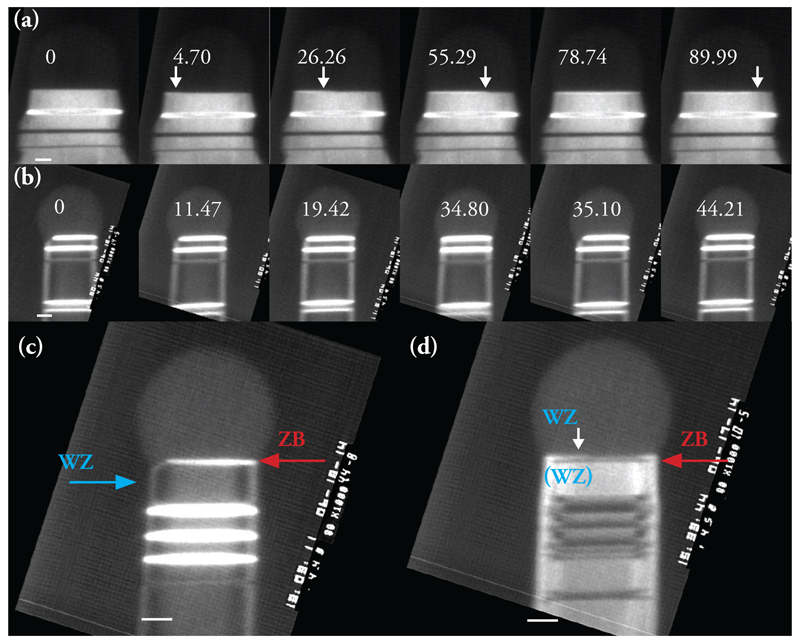
Figure 1.

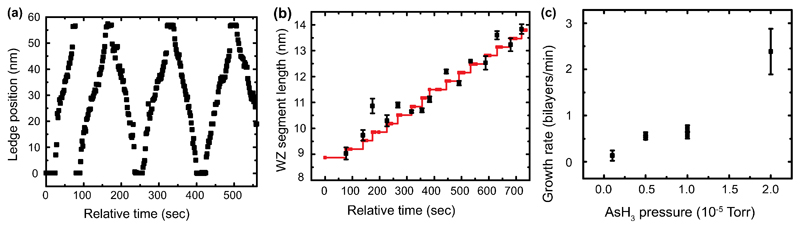
Interface dynamics during WZ and ZB growth of GaAs. (a) Images extracted from a dark-field movie recorded during WZ growth. A step flows across the top facet of a 60nm diameter nanowire, position arrowed. Also see Supplementary Video 1. Growth conditions: 550°C, AsH₃ = 1 × 10^-5 Torr, TMGa = 3.5 × 10^-8 Torr. The narrow stripes show previously grown ZB segments: ZB can occur in two twinned orientations, one appearing bright and the other dark in this imaging condition. (b) Images extracted from a dark-field movie recorded during ZB growth. The truncation slowly fills then jumps back to its maximum size (the simultaneous rapid step flow across the growth interface is not visible). Also see Supplementary Video 2. Growth conditions (not steady-state for this example): 550°C, AsH₃ just increased from 10^-7 to 1.4 × 10^-5 Torr, TMGa = 2.0 × 10^-8 Torr. ZB appears bright and WZ dark in this imaging condition. Note that the truncation shows strongly on one side of the nanowire; this was typical, see text, although some (5%) nanowires showed synchronized oscillation on both sides, as in Supplementary Video 5. (c) The first ZB bilayer growing on WZ, imaging conditions as in (b). The AsH₃ pressure was reduced; the droplet is in the process of growing larger past the critical volume; the first layer of ZB appears followed immediately by a truncation that cuts into the previously grown WZ. (d) The first WZ bilayer growing on a ZB segment. The AsH₃ pressure was increased; the droplet is in the process of growing smaller; the truncation fills in and the first layer of WZ appears via step flow. The truncation does not appear, and step flow is slow, even though ZB covers the top facet. Scale bars are 10nm in all images. The relative time of each image is shown is seconds.

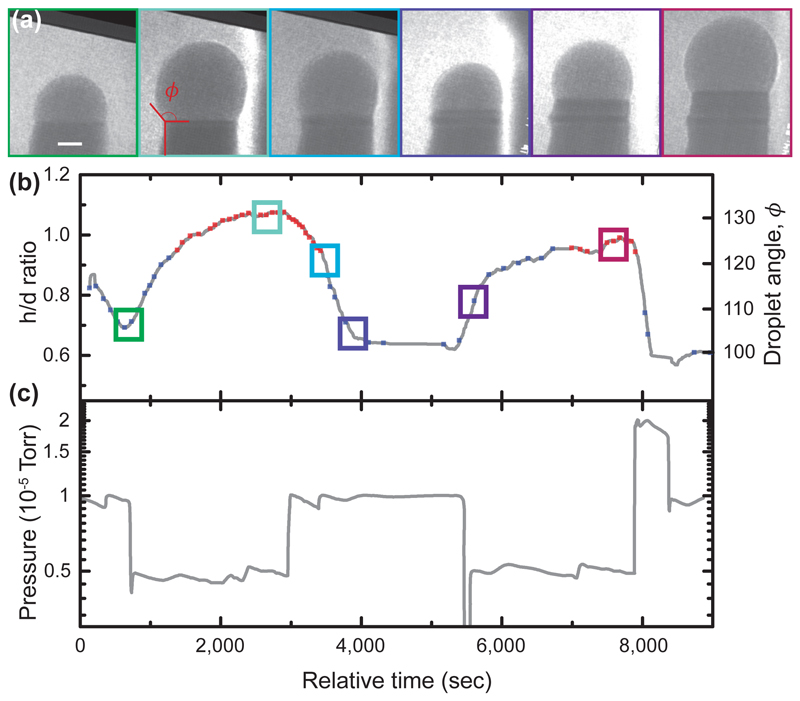
Figure 2.

Droplet volume changes during phase switching. (a) Series of bright field images obtained during growth of a GaAs nanowire at varying AsH₃ flow, constant TMGa flow (2 × 10^-8 Torr) and constant temperature (550°C). Scale bar is 10nm. (b) Droplet aspect ratio h/d and angle ϕ as defined in (a). The times of the images in (a) are indicated by colored boxes. The droplet volume takes several minutes to respond to the change in pressure. The crystal phase is indicated as blue (WZ) and red (ZB) squares. Each red square marks the occurrence of a truncation of the top facet and nucleation of a ZB bilayer. Each blue square marks the identification of WZ growth via step flow. (c) AsH₃ pressure vs. time.

We find that in situ, both ZB and WZ GaAs can be grown by varying the precursor pressures (the V/III ratio) while maintaining a constant temperature. Within the parameter range accessible in situ, WZ forms at higher V/III ratios and ZB at lower ratios at steady-state conditions; transient conditions are discussed below. The two polytypes show striking differences in terms of their growth dynamics. For WZ, growth proceeds by step flow across the droplet/nanowire interface (Figure 1a and Supplementary Video 1). Steps flow slowly with each one starting as soon as the previous one has finished its growth (Extended Data Figure 2a). By counting the number of step flow events and correlating with the length of the nanowire (Extended Data Figure 2b), as in Ref. 31, we find that each step flow represents the addition of one WZ GaAs (0001) bilayer, 0.3nm in height. The growth rates are low under the conditions accessible in situ, typically one bilayer per minute (see Supporting Information). Growth rates are proportional to AsH₃ pressure (Extended Data Figure 2c) suggesting that growth under these circumstances is limited by the arrival and incorporation of As (see Supporting Information). We can then understand the step flow dynamics through the solubility of As in AuGa. This is generally accepted to be low ³². When the droplet contains no reservoir of the rate-limiting species (in our case, As), the arriving atoms are incorporated immediately into the nanowire, leading to slow and gradual step flow ³³.

The growth of ZB appears quite different from that of WZ (Figure 1b, Supplementary Video 2). Growth also proceeds by addition of bilayers, but each bilayer flows across the growth interface too rapidly to observe. Furthermore, the droplet/nanowire interface shows an oscillating geometry at the trijunction (where solid, liquid and vapor meet) similar to that seen in Si, ZB GaP, Ge and Al₂O₃ ^30,31,34,35. The edge of the nanowire appears truncated (first panel, Fig. 1b). The three dimensional geometry of this “edge facet” is shown schematically in Extended Data Figure 1. Material gradually adds to the edge facet to fill in the corner (panels 2-3). The interface jumps forwards as one step flows quickly, and the edge facet reappears (panels 4-5). Each oscillation in trijunction geometry is correlated with the nucleation and flow of a new bilayer, as in Ref. 31. The step can move quickly, even with no reservoir of As, because it is supplied by material from the truncated volume. A rough estimate of the change in the truncated volume is consistent with it being the source for the 1 bilayer of growth.

In parallel with the observed changes in the interface dynamics, the droplet geometry also changes as we vary the V/III ratio to achieve growth of WZ and ZB. Figure 2 and Supplementary Video 3 shows the effect on the droplet of changing the arsine pressure between high values, to achieve WZ, and low values, to achieve ZB, at constant TMGa (2 × 10^-8 Torr). Temperature was kept constant throughout the experiments (540 - 560°C) to avoid introducing temperature dependencies that would obscure the observed trends (see Methods). Throughout the changes in arsine pressure, the nanowire continues to grow. The most striking aspect is the change in volume of the droplet. We quantify this in Fig. 2b via droplet aspect ratio h/d (droplet height divided by nanowire diameter at the growth interface), or, equivalently, via the droplet angle ϕ (angle between the basal plane and the tangent to the droplet at its edge, see Fig. 2a). On decreasing the AsH₃ pressure, the droplet rapidly increases in volume; increasing AsH₃ decreases the droplet volume. A quasi-steady state volume is reached, depending on the V/III ratio. These volume changes must be driven by the addition or subtraction of Ga: we do not expect Au to move in and out of the droplet, since its diffusion on GaAs can be assumed to be negligible at this temperature ³⁶, while As comprises only a small fraction of the volume due to its low solubility discussed above. An Au-Ga-As alloy with over 40% Ga forms a liquid at this temperature, with no upper limit for the Ga content ³², so droplets of a range of volumes are possible. Furthermore, since the volume changes occur more quickly than the rate at which Ga could be consumed by incorporation into the growing nanowire, the Ga must be supplied or removed by surface diffusion along the nanowire. In the simplest picture ³⁰, there is a surface reservoir of mobile Ga adatoms that equilibrate with the droplet over time whenever the chemical potentials of Ga in the droplet (and surface) are changed by altering the arsine pressure. This way, the V/III ratio controls the droplet size. (A more complete treatment would include diffusion and the effect of As flux on Ga diffusion, but this would not change the general picture. ²²)

We have shown above that crystal structure and droplet volume both change as the V/III ratio varies. We now explore how they correlate with each other. During a growth experiment, it is possible to measure crystal structure and droplet volume by alternating between dark- and bright-field imaging conditions. The crystal structure identified during the experiment in Figure 2 is shown as the red and blue data points in Figure 2b. It is clear that the switch between WZ and ZB crystal structure occurs as the droplet passes a certain aspect ratio, under these conditions at h/d ˜ 0.95 and ϕ ˜125°. (Other experiments show a small hysteresis not visible in this data, for example Fig. S3.) Since the droplet takes several minutes to respond to the pressure change, it is clear that WZ–ZB polytypic growth is correlated to the droplet h/d and ϕ rather than the instantaneous AsH₃ pressure. This direct correlation between crystal switch and droplet dimensions (volume, aspect ratio, angle), governed ultimately by the V/III ratio, is a key result that provides the basis for the model we develop below.

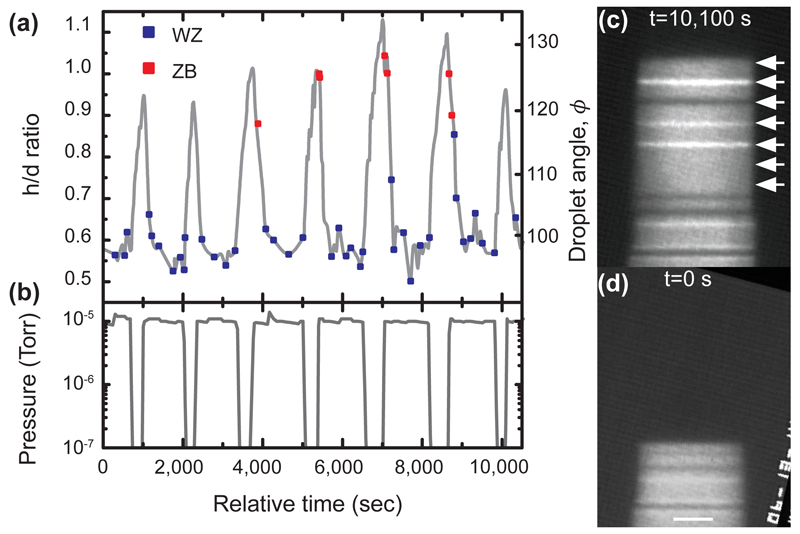
Understanding that the droplet geometry is the critical parameter, rather than the gas environment itself, provides valuable guidance in growing polytype heterostructures. The length of each polytype segment depends on the time over which the droplet has the appropriate geometry. The relatively slow kinetics of the droplet volume change mean that the V/III ratio must be designed with appropriate offsets in timing. An example is shown in Figure 3. Here, the V/III ratio was set initially at a value that formed WZ GaAs. The arsine pressure was then decreased, for short pulses, to a V/III ratio that would be expected to form ZB GaAs. The result is a series of ZB inclusions in a WZ nanowire with lengths that are repeatable but not directly proportional to the pulse duration. The shortest pulses did not form ZB at all. Longer pulses produced 1 or 2 bilayers of ZB stacking. The correlation between droplet volume and crystal phase in Figure 3 confirms that the droplet must reach a critical volume for the structural change to occur; the reduction of arsine in itself may not trigger a structure change. Designing a polytype heterostructure thus requires consideration of the kinetics of droplet volume change.

Figure 3.

Growth of a WZ nanowire containing multiple narrow ZB segments. TMGa was constant at 2 × 10^-8 Torr and the temperature was 550°C. (a) Droplet aspect ratio h/d and droplet angle ϕ vs. time (grey line), and crystal phase vs. time (squares). Each square indicates addition of a bilayer of WZ (blue) or ZB (red), as described in Fig. 1. ZB segments 0, 1 or 2 bilayers in thickness form each time h/d increases. (b) AsH₃ pressure vs. time. The pressure was held at 1 × 10^-5 Torr to grow WZ, but was pulsed downwards to below 10^-8 Torr for seven intervals of duration 5, 5, 7, 7, 9, 9, and 5 minutes respectively. (c, d) Image of the nanowire at the start and end of the experiment; scale bar 10nm. In (c) the position of the growth front at each of the seven intervals is indicated by arrows. The ZB segments grown in the 7 and 9 minute intervals are visible as narrow stripes. Three have one ZB twin orientation (bright contrast in this imaging condition) and one has the other ZB twin orientation (dark contrast).

A model for interface geometry

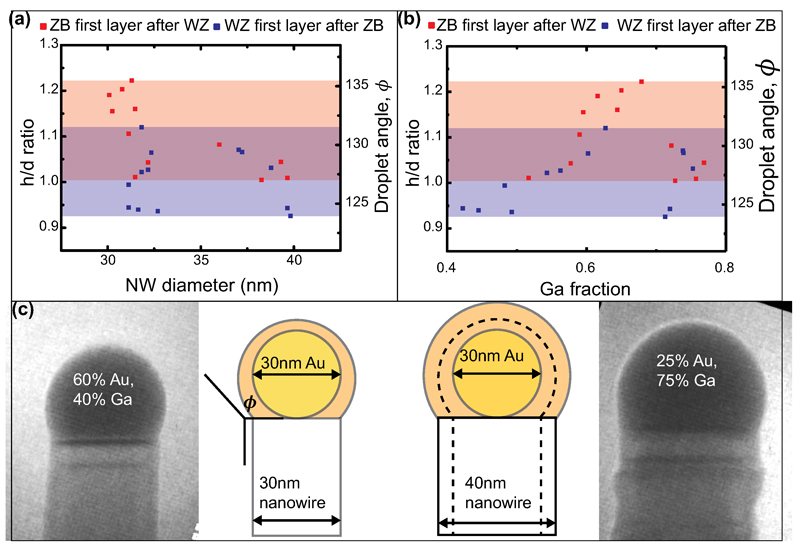
Developing a framework to understand the relationship observed above between droplet volume, interface growth dynamics and crystal structure requires two additional key observations. We first note that when the droplet changes volume, it changes composition too. This could in principle affect phase selection e.g. by changing the surface energy ²⁷. Which factor determines crystal structure, the Au:Ga ratio or the geometry (h/d and ϕ)? To establish this we measured the droplet h/d and ϕ at the switch for one particular nanowire, then allowed the nanowire to increase its diameter by conformal growth on the sidewalls, and again measured h/d and ϕ while inducing a switch (Extended Data Figure 3). As the nanowire widens, but the amount of Au present does not change, relatively more Ga is needed to achieve the same h/d and ϕ. We did not see any strong effect of diameter on the switch between crystal phases; h/d and ϕ appear to be the controlling parameters.

The second observation concerns the relationship between crystal phase and the dynamics at the growth front. In Figure 1(c, d) and Supplementary Videos 2, 4 we show the crystal switch in more detail, specifically the growth of the first ZB layer on WZ and the first WZ layer on ZB. Starting from a WZ nanowire, we reduce the As pressure (Fig. 3c); the droplet enlarges and the first ZB layer forms as the critical h/d and ϕ are reached. As the ZB step flows (too rapidly to see) across the growth interface, an edge facet appears (Supplementary Video 4). This facet cuts into the WZ beneath. Thus, even though steady state growth of WZ proceeds without an edge facet, it is possible to form an edge facet in WZ under appropriate conditions. Conversely, in Fig 1d, we start from a ZB nanowire and increase the As pressure; the droplet shrinks and the first WZ layer grows. It grows by slow step flow and without an edge facet appearing (Supplementary Video 2), even though ZB is exposed on the growth interface as it starts to grow.

These observations are particularly surprising. One might expect the presence of an edge facet to be controlled by the crystal structure at that facet; but instead, Figure 1(c, d) shows that it correlates with the crystal structure on the main [i.e. ZB (111) or WZ (0001)] growth facet, and thus with the droplet h/d and ϕ. To untangle cause and effect, we analyze how the droplet angle ϕ will affect the morphology of the growth interface. Equilibrium crystal shapes generally do not have edge angles as sharp as 90°, so one would expect an edge facet in a GaAs crystal. A sharp edge only exists during nanowire growth because the droplet is present, providing a capillary force that can pull on the edge facet and shrink it to zero. We can calculate the circumstances under which this occurs. We assume an ideal, symmetrical nanowire where the droplet angle ϕ is the same all around the edge (see Fig. 4a); the more realistic, asymmetrical case is discussed below. Comparing this ideal nanowire having an edge facet to the same geometry but with a sharp edge, the free energy differs by ³¹

$$\Delta E=c_{1}yL+\frac{1}{2}{y}^2(\cot \theta )({\mu }_{cat}-{\mu }_0)L+c_2{y}^{2}L$$ (1)

where L is the total length of the edge, y is the facet size and θ is the facet angle (see Fig. 4a), μ_cat-μ₀ reflects the supersaturation, and c₂ assembles various other second-order terms, as described in Ref. 31. For a sufficiently small facet size y, this energy is dominated by the linear term c₁, which reflects the capillary forces acting on the corner facet. Thus for c₁<0 it is always energetically favorable to have the edge facet (ΔE is negative), while for c₁>0 we expect the edge to be sharp everywhere and have no facet. Examining c₁ in more detail and including all the capillary terms as described in Ref. 37, we find

$$c_1={\gamma }_e\frac{1}{\sin \theta }-{\gamma }_{vs}-{\gamma }_{ls}\frac{\cos \theta }{\sin \theta }+{\gamma }_{vl}\sin \varphi$$ (2)

where γ_e is the liquid-solid interfacial energy at the edge facet, γ_vs is the vapor-solid interfacial energy on the sidewall, γ_ls is the liquid-solid interfacial energy at the main growth facet, γ_vl is the vapor-liquid interfacial energy, and ϕ is the droplet angle (defined in Fig. 2a and 4).

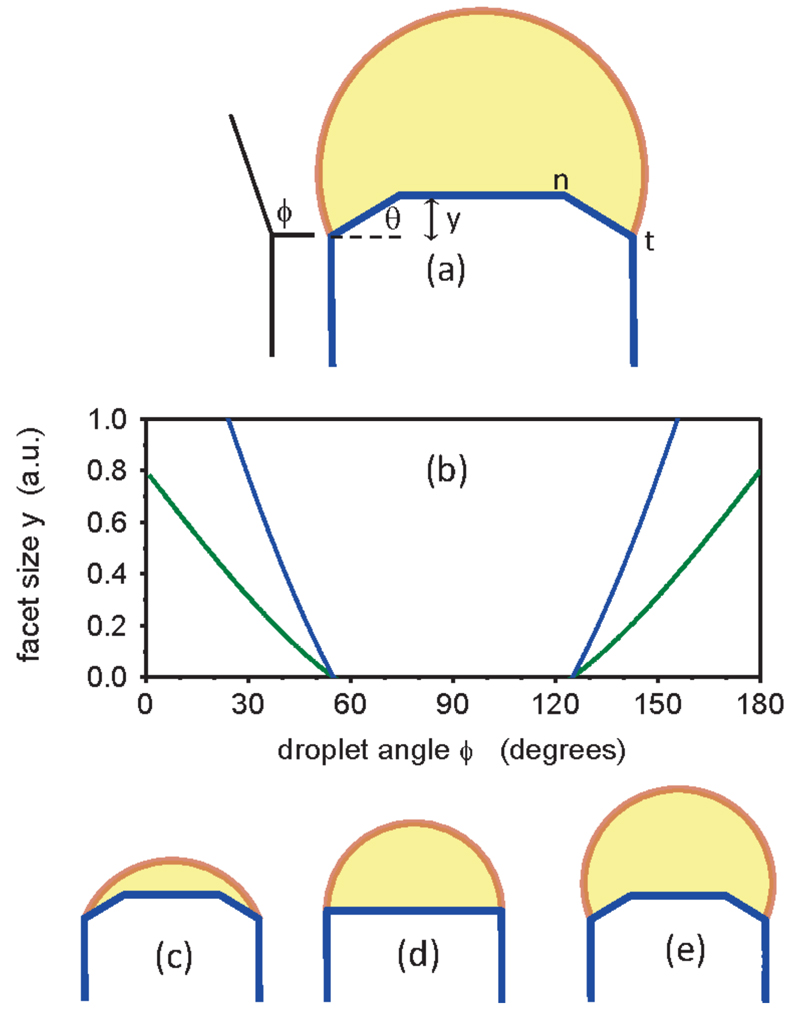
Figure 4.

Model relating droplet size to interface morphology. (a) Schematic diagram of a “quasi-2D” ideal, symmetrical nanowire to illustrate the droplet angle ϕ and edge facet angle θ and length (in growth direction) y. n marks the interior point where ZB nucleates. t marks the trijunction. (b) y vs. ϕ, calculated for two different values of supersaturation for the symmetrical situation. There is a range of ϕ in which y=0, i.e. c₁ changes sign and the edge facet goes out of existence. Note that supersaturation (low=blue, high=green) does not affect this range. (c-e) Schematic diagrams of the nanowire and droplet for ϕ>90°, ϕ=90°, and ϕ<90°. The possibility of depinning of the droplet from point t is not included in the model.

The key point here is the presence of angle ϕ in Eq. 2. This implies that the droplet angle can alter c₁ and hence change the lowest-energy state of the nanowire from one with an edge facet to one with a sharp corner. A hemispherical droplet (ϕ=90°) gives the maximum possible value of c₁, and so is the most favorable for eliminating the edge facet. This is shown in Figure 4(b), where we calculate the size y of the edge facet as a function of angle ϕ for a symmetrical but otherwise arbitrary illustrative case. In our experiments, the droplet is never less than a hemisphere during stable growth, so the analysis in Eqs. (1) and (2) predicts that a switch could occur from having an edge facet for large droplets to having a sharp edge for smaller droplets; that is indeed what we observe.

Connecting geometry to crystal phase

Why should the presence or absence of an edge facet control the crystal phase? Without attempting to develop a microscopic model, we can understand heuristically how this would occur by considering the analysis of Glas et al. ²⁰ and others. Several models have argued that the crystal structure should be determined by the location of the nucleation event on the main growth facet ^{6–8,10,13,20–23,26,38}. The argument is that metastable WZ can only grow if it has a lower nucleation barrier than ZB. With sharp edges, nucleation is expected to occur at the trijunction (rather than in the middle of the facet) so the solid-vapor interface plays a critical role. In particular, the solid-vapor interface energy is thought to be lower for WZ nanowires, reducing the nucleation barrier for WZ relative to ZB in this geometry ²⁰. However, when edge facets are present, nucleation on the main facet occurs away from the trijunction (presumably at position n in Figure 4c ³¹) and the liquid-vapor interface plays no role. If we adopt this argument, it is no surprise that the radical change in the trijunction geometry can result in easier nucleation of WZ than ZB in one case but not the other. This is also qualitatively consistent with in-situ X-ray diffraction studies which infer (indirectly) that crystal structure in GaAs nanowires is determined by geometry of the liquid-vapor interface^39,40. Here we have not considered effects of interlayer interactions on the nucleation barrier, which may lead to formation of higher-order polytypes under certain conditions⁴¹, since we do not observe such phases in our experiments.

In Figure 4b, it is intriguing to note that our analysis also suggests the possibility of an edge facet and hence ZB growth at very small h/d. Although we can not access such conditions in our experiments, they may occur transiently at the beginning of nanowire growth, since the droplet has much smaller h/d when sitting on a flat surface ⁴², and perhaps at the end of growth if material in the droplet is consumed. Indeed, ZB has been observed at the bases and tips of WZ nanowires ²⁰, although under growth conditions that are different enough that our model may not be applicable. Recent experiments have in fact shown two transitions, from ZB to WZ and then back to ZB, as V/III is increased⁹, consistent with the model in Fig. 4. However, since our experiments have only a limited V/III ratio range, we can not observe the second transition back to ZB so can not assess whether the transition is associated with interface dynamics in a way that is analogous to the switch at lower group V.

The discussion above is simplified in several respects. No difference in interfacial or surface energies between ZB and WZ structures is included. The small but real differences could lead to hysteresis in the switching angle as the droplet grows and shrinks. However, data such as Fig. 2, with no strong hysteresis, suggests that the droplet angle has a larger effect than the differences between ZB and WZ interfacial energies.

More importantly, our quasi-2D model treats the droplet angle ϕ as uniform all the way around the edge. For the true 3D geometry, in which the droplet sits on a hexagonal prism whose side lengths may not even be equal⁴³, it is clear that ϕ will vary around the trijunction. Suppose for a WZ nanowire we change the conditions to enlarge the droplet. At some point, ϕ will become large enough along one edge for that edge to become truncated, even though other edges remain sharp. As the droplet continues to grow, each other edge will progressively become truncated. We thus expect any nanowire with unequal edge lengths to show a mix of sharp and truncated edges over a range of droplet volumes. It is interesting to note that in the experiments, we observe ZB once the first truncated corner appears - as in Figure 1 and Supplementary Videos 2 and 4. Since we typically stabilize conditions as soon as we see the crystal switch, the majority of nanowires presented here show a mix of sharp and truncated edges. However, we also observe symmetrically oscillating nanowires, with examples shown in Supplementary Video 5, presumably because the wire is more symmetrical or the droplet has grown large enough to cause all edges to be truncated. The observation mentioned above that ZB grows if any edge is truncated, while WZ grows only when all edges are sharp, implies that nucleation of ZB at a truncated edge is actually easier than nucleation of either WZ or ZB at a sharp one. This somewhat unexpected result could provide guidance in refining model parameters in nucleation calculations.

Conclusions

Direct observation during growth has enabled us to probe the phenomena controlling crystal phase in nanowires. WZ and ZB polytypes in GaAs appear strikingly different during growth, in terms of the morphology of the nanowire/droplet interface, the flow of steps, and the droplet size. The step flow kinetics can be understood as a consequence of As-limited growth, low As solubility in the droplet, and the role of the edge truncation as an alternative reservoir. Examining the switch between polytypes suggests a scenario where the growth conditions (here, the V/III ratio) determine the volume of the droplet and hence its aspect ratio and angle ϕ; the value of ϕ determines whether an edge facet will be present; the presence or absence of the edge facet determines the nucleation site for a new layer; and the nucleation site determines which phase, WZ or ZB, is most likely to nucleate. Our interpretation differs markedly from previous models of phase selection. Since nanowire growth has been achieved over a wide range of parameters and growth techniques, it is possible that phase selection is controlled by different physics under different circumstances. However, the regime we analyze here, MOVPE under As-limited conditions, has advantages for atomic-level control and high-throughput manufacturing.

This understanding of the causal sequence, in particular the changes in droplet volume with conditions and the controlling role of the droplet angle ϕ, has practical consequences. First, the dramatic changes in droplet volume as a function of conditions may be relevant to aspects of nanowire growth other than crystal phase control¹³. For example, kinking can be caused by depinning of droplets from the nanowire tip ^37,44, and experiments such as those shown here can explore the range of conditions under which droplets attain sizes extreme enough to cause depinning. In terms of crystal phase control, since the Au:Ga ratio in the droplet appears not to be critical, the results may be applicable to self-catalyzed (Au-free) nanowire growth (although any small difference in liquid surface energies may lead to a slightly different critical angle). A second consequence is that any means of controlling the energy balance between a truncated and sharp edge should affect the crystal phase: we have used V/III ratio in this work, but temperature and surfactants are also possible ways to tune polytypism. We anticipate that similar behavior may occur in other III-V semiconductors that show polytypism, although it is not guaranteed because the various interfacial energy parameters are material-specific. Finally, understanding how crystal structure switching depends on the kinetics of group III motion into and out of the droplet helps us work towards precise control of individual polytype superlattices, to enable fabrication of new types of electronic devices that make full use of the possibilities for engineering band structure that are provided by polytypic nanowires.

Methods

The GaAs nanowires imaged in this study were grown on Si (111). The substrates were cut from a Si(111) wafer into strips 3mm × 350μm × 500μm, small enough to fit directly into the TEM heating holder. The strips were, however, too small to be handled in the GaAs growth system, so they were stacked in arrays, parallel to each other with the polished surface facing upwards, and mounted on a larger Si wafer. At Lund University, Au aerosol particles with diameters of 30nm, 50nm and 70nm were deposited onto the arrays of strips using a size-selected aerosol source at a total density of ˜1 particle per μm². Then GaAs nanowires of the order of 500nm in length were grown on the arrays using standard metal-organic vapor phase epitaxy in an Epiquip system, operating at 100mbar with AsH₃ and TMGa as precursor gases and H₂ as carrier gas. After growth, the arrays were glued to sample boxes using a small piece of SEM-type double-sided carbon tape, the sample boxes were placed in a plastic bag which was vacuum sealed, then the bag was sent through air to the UHV TEM at IBM. The individual strips were separated and each sample was degassed in UHV by resistive heating below 100°C for 30 minutes, flowing a direct current through the Si strip. The heating current required for a temperature of around 300 °C was then determined in a separate UHV chamber using an infrared pyrometer. All of the strips had a similar temperature-current calibration, so it was possible to estimate the current required to heat the sample to 500 or 550°C. The sample was transferred to the UHV TEM column to check that the nanowires and Au catalysts were still present after this process. Finally, TMGa was flowed to a chosen pressure around 5 × 10^-8 Torr as measured using a mass spectrometer, arsine was flowed to a chosen pressure around 2 × 10^-5 Torr as measured on the column ion gauge, the nanowires were heated to nominally 500-550°C and GaAs was grown at the nanowire tips. The crystal phase was generally controlled using arsine pressure, which was easier to measure and faster to change than TMGa. After experiments on one sample were completed, the full current-temperature calibration curve was obtained for that sample. The reason for this calibration procedure was to prevent any damage (e.g. etching) of the wires by accidental overheating before the growth experiment began. Due to drift of the temperature on continued heating, we estimate the temperature accuracy at +/-20°C. All observations of crystal switching occurred between 500 and 570°C. Approaching 500°C, the temperature range over which switching occurred became narrower and ZB grew for all accessible pressures. Above 600°C the nanowires etched slowly at the Au/GaAs interface, presumably due to the low group V pressure.

This growth in situ within the TEM is somewhat different from standard MOVPE. Even though the conventional MOVPE precursor gases are used, there is no H₂ carrier gas, as is typically used during MOVPE growth of GaAs. In addition, the absolute pressures of the two precursor species are lower than typical precursor partial pressures used in MOVPE. The much lower partial pressures can alone account for the low growth rates observed here compared to MOVPE. To compare the effects of V/III ratio, we need to consider the possible differences in more detail.

The growth in this study was observed to always be group V limited, as seen in Extended Data Figure 2(c). This is in contrast to standard MOVPE, where high group V flows and group III-limited regimes are typically used. Instead, one could argue that the in situ TEM conditions are more similar or relevant to CBE or possibly MBE, rather than MOVPE. The group V-limited regime is also highly relevant to catalyst-free growth from Ga droplets. One exception for MOVPE is a recent study ⁹ exploring group V-limited regimes in a standard MOVPE reactor to grow WZ and ZB GaAs. In this work, it was shown that at low enough V flow to give V-limited growth, WZ grows at “high” V/III ratio within this regime, while ZB grows when V/III is lowered. This is in contrast to the more well-known behavior in the III-limited regime, in which ZB forms at high V/III ratio. It is entirely in agreement with the results of this study. Where this work and Ref. 9 differ is in the absolute magnitude of the V/III ratio: here, V/III ratios of 100 or more were found to yield V-limited nanowire growth, while in Ref. 9, the V-limited regime occurred at V/III ratios below 2.

This comparison suggests that the effective As pressure at the growth front is significantly lower, relative to the Ga pressure, than in typical MOVPE. To understand this, we first note that AsH₃ pyrolysis in GaAs growth is generally considered to proceed heterogeneously on GaAs surfaces, without interaction with the carrier gas ⁴⁵. This starts with adsorption of AsH₃ onto the surface, followed by sequential dissociation of H atoms one by one, eventually leaving atomic As adsorbed on the surface ⁴⁶. When combined with trimethylgallium (TMGa), however, the two species decompose in concert via adduct formation on the surface; this decomposition pathway does not involve hydrogen and is more efficient than the decomposition of either species alone ⁴⁵. That the species decompose primarily on the surface is an important clue to the relatively inefficient supply of As in the UHV TEM. First, the nanowires are grown on Si substrates rather than GaAs; although there is also ample GaAs surface on the pre-grown nanowire stubs, this surface is clearly different from the typical GaAs substrates used for MOVPE nanowire growth. Second, the surfaces are likely to be passivated with H when growth occurs in a H₂ atmosphere; the absence of H₂ here may affect the supply in a number of ways, changing for example the decomposition process and precursor surface diffusion. Finally, it must be noted that the decomposition process relies on the desorption of gas-phase As species. This adsorption process naturally depends on the partial pressure; since As has a significantly higher vapor pressure than Ga, the adsorption process of As will be reduced relatively much more by the lower partial pressure.

Other minor differences are expected due to the experimental setup. Using needle valves rather than standard mass flow controllers to control the precursor flows, experimental parameters are less accurately controlled than in dedicated epitaxy growth systems. At the high V/III ratios used (V/III>100), the TMGa partial pressure is much lower than the AsH₃. A gauge reading the total pressure close to the sample is used to monitor the AsH₃ flow and provide fast feedback on the actual AsH₃ at the sample. To monitor TMGa, a mass spectrometer is used, with a controlled, steady pressure of TMGa set at the start of the experiment and generally held constant. The mass spectrometer is continuously used during the experiments to monitor any drift in the TMGa pressure.

Extended Data

Extended Data Figure 1.

Distinguishing polytypes using dark field imaging. (a) Dark field images recorded using three spots in the diffraction pattern showing how WZ and the two variants of ZB are distinguished in the <110> direction. The spots are indicated by arrows in (b). These are post growth images recorded in a JEOL 3000 TEM. (c) Image recorded during growth, also in the <110> direction, showing the dark field contrast and the measured angle of the truncated corner. (d) A schematic diagram showing the hexagonal cross section as seen from the side (beam direction) and from above. Seen from the side, the droplet contact angle, ϕ and corner-facet angle, θ, are shown. Seen from above, the electron beam direction is shown.

Extended Data Figure 2.

Kinetics of WZ growth. (a) Step flow kinetics measured for the WZ nanowire shown in Movie 1 and Figure 1(a). (b) Length of a WZ nanowire versus number of step flow events. The gradient of the graph confirms that each step is 0.33nm in height, i.e. a WZ (0001) bilayer. (c) Growth rate vs AsH₃ pressure, estimated by measuring length increase for the nanowire shown in Figure 2 during growth intervals at different AsH₃ pressures. The growth temperature was 550°C and TMGa was constant at 3.5×10^-8 Torr.

Extended Data Figure 3.

Data showing that the droplet angle at the transition does not change with Au composition in the droplet. (a-b) During growth, the crystal structure of a nanowire was switched back and forth several times by changing the As pressure, measuring the angles and absolute droplet volume at which the switch from WZ to ZB (red) and ZB to WZ (blue) occurred. During this time the wire also grew radially (c). (a) Switch angles versus nanowire diameter. Shading indicates the range of observed angles at which WZ switches to ZB (red) and ZB to WZ (blue). Some hysteresis in switching is visible, perhaps because the droplet continues to change angle in the time before the switched layer grows. The data is scattered, but there is no strong dependence of angle on diameter (especially for the blue data points). For example, ZB switches to WZ at angles between 123° and 132° at both large and small diameter, and WZ switches to ZB at angles between 127° and 136°. (b) Switch angle versus inferred composition, as calculated from the measured h/d assuming the amount of Au does not change. The data is scattered, but there is no strong dependence of angle on composition. For example, the first few data points, where the nanowire had 30nm diameter, ZB switched to WZ for Ga < 60%. Later, at 40nm diameter, the switch did not occur until Ga ˜ 75%. The fact that droplet angles are similar in spite of the diameter change suggests that droplet geometry controls the switch while droplet volume or composition do not appear to be important.

Supplementary Material

Supplementary Information is linked to the online version of the paper at www.nature.com/nature.