Abstract
An acoustically actuated, bubble-based technique is developed to investigate the deformability of cells suspended in microfluidic devices. A microsized bubble is generated by an optothermal effect near the targeted cells, which are suspended in a microfluidic chamber. Subsequently, acoustic actuation is employed to create localized acoustic streaming. In turn, the streaming flow results in hydrodynamic forces that deform the cells in situ. The deformability of the cells is indicative of their mechanical properties. The method in this study measures mechanical biomarkers from multiple cells in a single experiment, and it can be conveniently integrated with other bioanalysis and drug-screening platforms. Using this technique, the mean deformability of tens of HeLa, HEK, and HUVEC cells is measured to distinguish their mechanical properties. HeLa cells are deformed upon treatment with Cytochalasin. The technique also reveals the deformability of each subpopulation in a mixed, heterogeneous cell sample by the use of both fluorescent markers and mechanical biomarkers. The technique in this study, apart from being relevant to cell biology, will also enable biophysical cellular diagnosis.
1. Introduction
The characterization of cell deformability as a mechanical biomarker is valuable for both diagnostics as well as biological studies.[1–3] Changes in cell deformability have been used to identify diseases such as cancer, malaria, arthritis, atherosclerosis, hypertension, cerebral edema, stroke, and asthma.[4] In addition, identifying the cellular mechanical biomarkers with corresponding alterations in the cytoskeleton and gene expression aid the investigation of cellular processes, including metastasis, cytoskeleton development, cell differentiation, and the cell cycle.[5–8] Cell deformability may be measured by exposing adherent or suspended cells to a nonuniform external force field, which results in deformation on the cells. In contrast with the many cellular geometries observed upon contact with substrates, most mammalian cells are essentially spherical when suspended in a fluid environment, with a simple cortical actin cytoskeleton layer underneath the cell membrane to maintain mechanical integrity.[9] The characterization of mechanical biomarkers from cells in suspension, then, would offer both simple operation as well as improved repeatability of measurements.
Advances in micro-electro-mechanical systems[10,11] have yielded multiple approaches to measure cell deformability.[12–15] These approaches may be categorized as either flow-based or in situ methods. Among the plethora of cell-deforming methods, flow-based methods[15–19] are popular: suspended cells are delivered, focused, and stretched via hydrodynamic effects such as shear stress and inertial force.[20–24] Cell deformability,[18] velocity,[16] and pressure variations[19] are recorded as characteristic mechanical properties. On the contrary, the cells are often static during in situ methods such as atomic force microscopy,[25] microaspiration,[26,27] laser cavitation,[28,29] optical tweezers,[30–32] and methods using elelctro-deformation.[33,34] Both flow-based and in situ methods have pros and cons. For example, flow-based methods offer better throughput over in situ methods; however, the deformability of cells is measured when cells pass through a detection spot from the inlets to the outlets, providing only data on cellular shape. This limitation makes it difficult to accurately identify each individual cell before and after the cell-stretching process. By contrast, an in situ measurement can record more information from the measurement. They can also easily integrate with other techniques such as cell culture and drug treatment, albeit at lower throughput. Thus, there is a need for a technique to measure mechanical biomarkers which combines the advantages of both flow-based (i.e., high throughput) and in situ methods (i.e., the capability to record more information, and easy integration with other bioanalysis and drug-treatment units).
In this article, we describe an optothermally generated, acoustically actuated, bubble-based technique to deform cells. A bubble is generated by the optothermal effect[35,36] at any desired position within a microfluidic chamber. When this bubble is actuated by acoustic waves, the oscillation of the air–liquid interface perturbs the liquid nearby, resulting a localized acoustic streaming around the bubble.[37–42] Once a suspended cell is introduced to the flow field, the cell is stretched by hydrodynamic forces. Since the flow is essentially static except for the bubble-induced localized streaming, the cell deformability measurement is performed in situ, allowing for cell identification after bubble-based cell deformation. This article is structured as follows: first, the configuration and working mechanism of the bubble-based cell deformability measurement platform is outlined. Second, a numerical study is exhibited to identify the localized acoustic streaming responsible for deforming the cells. Third, the testing of three typical cell lines (HeLa, HEK 239, and HUVEC) demonstrates that our device distinguishes the mechanical properties of different cells, and that it analyzes multiple cells while achieving high throughput. Fourth, the cell-deforming technique is integrated with cell-culturing and drug-treatment platforms. HeLa cells are incubated with the Cytochalasin D, and their deformability is measured in situ. Finally, the capability of integrating deformability measurement with other biochemical markers is presented. Two different fluorescent markers stain the cell mixture, composed of protein-denatured and healthy HeLa cells. By simultaneously observing differences in deformability and biochemical markers, the mechanical properties of each subpopulation in the mixture are identified without needing a cell-separation procedure.
2. Theory
Streaming generated from acoustically oscillated bubbles has been studied extensively.[43,44] Dissipation in fluid is rapid and nonharmonic in response to a harmonic force, which may be generated by the acoustic oscillations of a microbubble. This response can be considered as a superposition of a time-harmonic acoustic response with the same frequency as the actuation frequency, and a slower, steady response known as “acoustic streaming.”[45–51] The nonlinear hydrodynamic coupling[52] results in transmission of acoustic energy to the fluid as steady momentum, manifested as acoustic streaming around the oscillating bubble. The fluid response is governed by the standard Navier–Stokes equations for a linear viscous compressible fluid[45,46]
| (1) |
| (2) |
where ρ is the mass density, ν is the fluid density, p is the fluid pressure, and μ and μb are the shear and the bulk dynamic viscosities, respectively. As is commonly done in simulations of acoustic streaming,[41] the relation between p and ρ is chosen to be linear, namely , where c0 is the speed of sound in the fluid at rest. Direct numerical simulation of this nonlinear system of equations is computationally challenging and expensive, due to discrepancy in space (characteristic wavelengths of acoustic waves vs the characteristic geometrical dimensions of the system) and time scales (characteristic oscillation periods vs characteristic times dictated by the streaming speed). However, in the case of small oscillations, the fluid response can be studied using a perturbation expansion of the flow variables in the Navier-Stokes equations. We employ Nyborg’s perturbation approach[53] where the fluid velocity, density, and pressure are assumed to be of the following form
| (3) |
where e is a nondimensional parameter defined as the ratio of oscillation amplitude to the bubble radius.[35] Substitution of Equation (3) into Equations (1) and (2) and segregation of first-order terms yield a first-order system
| (4) |
| (5) |
where μ and μb represent, respectively, the shear viscosity and the bulk viscosity. Repeating the same procedure for the second-order terms, followed by time averaging over a period of oscillation, yields a second-order system
| (6) |
| (7) |
where <A> indicates the time time average of the quantity A over a full oscillation time period. Equations (4)–(7), complemented with appropriate boundary conditions, were solved numerically using the commercial finite element software COMSOL Multiphysics 4.4 to characterize the patterns of acoustic streaming around the oscillating bubble. Here, we studied the streaming patterns generated by a single bubble in the microfluidic chamber of dimensions 600 × 600 μm2. A single bubble was simulated with diameter 60 μm, oscillating with amplitude 5 μm at frequency 100 kHz.
3. Results and Discussion
3.1. Generation and Actuation of Bubble
The microsized bubble (diameter: ≈60 μm) was formed with the optothermal effect.[36] In this process, a gold-coated glass slide was used to absorb the laser energy and heat the surrounding liquid to form bubbles. By controlling the position of laser-focusing spot, a bubble can be generated near any targeted cells (Figure 1d). The size of the bubble is adjustable by varying the illuminating time and power of the laser.[36,54] Furthermore, unlike optical tweezers[55,56] or direct laser cavitation[28,29] that typically requires high-cost focusing lens with large numerical aperture and lasers with high beam quality (TEM00), the technique shown in this paper does not have special requirements on the laser beam quality and focusing elements. A low-cost semiconductor laser with multimode output is sufficient to focus on the gold substrate and generate microsized bubbles. Our experimental setup is easy-to-assemble and convenient-to-operate. After the bubble is generated, acoustic waves are applied to actuate the microsized bubble. By tuning the frequency and amplitude of the acoustic waves, the bubble size, and the viscosity of medium, one can control the extent of cell deformation.
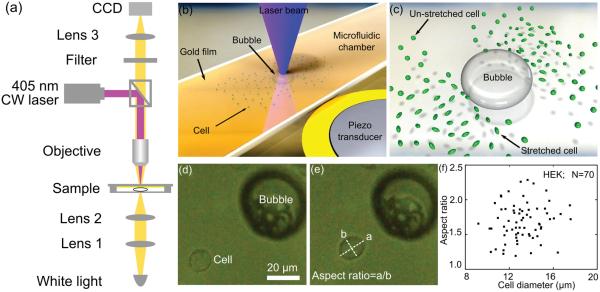
Figure 1.
a) Optical setup to generate bubbles by the optothermal effect; b) schematic for the configuration of microfluidic chamber and piezo transducer; c) schematic for cell stretching in the flow field around an acoustically activated oscillating bubble; d,e) a spherical-shaped suspended cell is stretched near an oscillating bubble, where the aspect ratio is used to characterize the cell’s deformability; f) the statistical analysis of deformability (i.e., aspect ratio) for HEK cells.
3.2. Mechanism for Cell Deformation
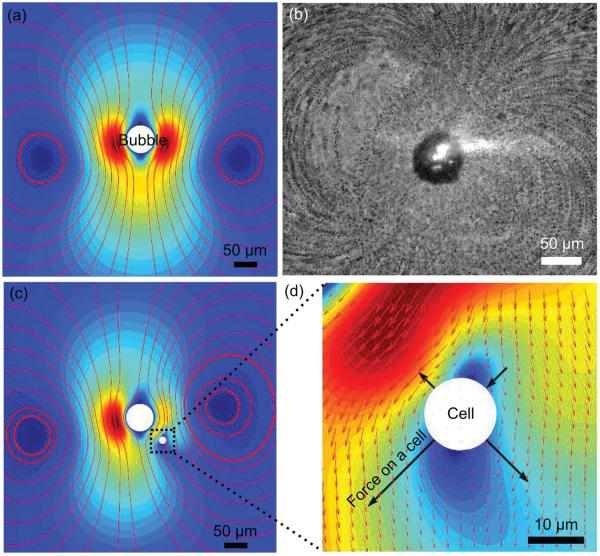
Acoustic streaming, which exerts shear force on cells, was investigated via both experiments and simulations. Figure 2a shows the numerical results of acoustic streaming patterns generated by the oscillating bubble; the presence of two vortices around the bubble is similar to those observed experimentally (Figure 2b). This streaming pattern was also observed previously by Tho et al.[57] and is associated with ellipsoidal motion of the bubble (i.e., the bubble oscillates both laterally and radically). Since the mode of the bubble’s vibration varies with both the applied frequency and the size of the bubble,[57] the acoustic streaming patterns for a different oscillation mode (i.e., lateral oscillations only) were also studied. The patterns revealed a quadrupole acoustic streaming pattern (Figure S4 in the Supporting Information). The numerical results reported here are instructive in determining the acoustic streaming through a perturbation approach, even when the oscillation amplitude of the bubble is difficult to observe.
Figure 2.
Working mechanism for deforming a cell by acoustic streaming. a) Simulation and b) experimental results for acoustic streaming flow patterns around an oscillating bubble; c) acoustic streaming patterns around the oscillating bubble in the presence of a particle positioned at (50 μm, −50 μm) relative to the bubble center; d) an enlarged picture of panel (c) showing the nonuniform flow field near the cell and the shear force on the cell. The color indicates the magnitude of the streaming velocity from min (blue) to max (red), while the arrows indicate the direction of the streaming velocity.
Once the acoustic streaming is identified by numerical simulation, validation of the shear force to deform a cell in the fluidic field becomes feasible. Since the presence of a cell near the bubble alters the streaming patterns around the bubble, a fully coupled fluid-structure interaction model is required to investigate the deformation of the cells inside the acoustic streaming field. However, we considerably simplified this problem to obtain qualitative understanding of our device’s working mechanism by considering a fixed particle (a cell) inside the domain and investigating the force that the particle experiences for different positions relative to the bubble. To study the force experienced by a particle due to acoustic streaming, we numerically simulated a spherical particle of diameter 15 μm at coordinates (50 μm, −50 μm) relative to the bubble center. The flow field was recalculated in the presence of this particle (Figure 2c); the hydrodynamic traction was integrated over the surface of the particle to calculate the force (Figure 2d) exerted on the particle in the acoustic streaming field. While the net force on the particle acts in the direction of the acoustic streaming flow, the nonuniform traction distribution observed on the particle’s surface would result in the deformation of the particle (Figure 2d). In addition, simulations with different positions of the particle (Figure S3 in the Supporting Information) to the bubble were conducted to study the force experienced by the particle for different positions in the microfluidic channels. Due to the nonuniform flow field, the force experienced by the particle is different for particles at different positions relative to the oscillating bubble. Thus, by tuning the operational parameters as well as the bubble’s position relative to the cell, the cell can be subjected to a wide range of force distributions that, in combination with the cell’s response, can be used to investigate the mechanical properties of the cell. The simulations confirm a powerful aspect of our technology, namely the ability to modify the flow field at will and thereby subject the cells to a wide range of force distributions.
3.3. Parallel Measurement of Deformability
Deformability, as a parameter of mechanical biomarker, is used to characterize cell properties. To realize a statistically meaningful value, multiple cells must be measured. Conventional in situ measurements, including optical tweezers and atomic force microscopy, have relatively low throughput (≈1 cell min−1). By contrast, our technique measures the deformability from multiple cells simultaneously, so statistically meaningful data can be conveniently obtained.
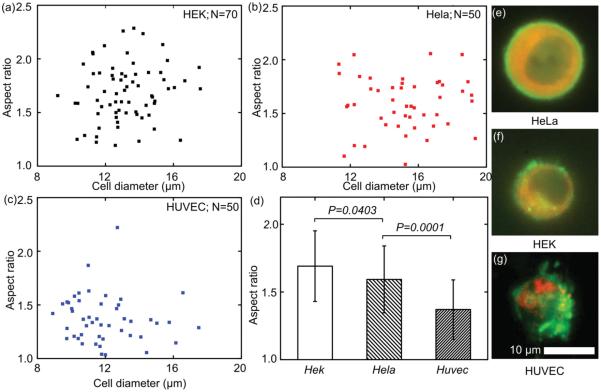
Here, the deformability of three cell lines, HeLa (N = 50), HEK (N = 70), and HUVEC (N = 50), was tested to demonstrate the capability of our devices. The results are shown in Figure 3, where the HEK cell has the most deformability (mean: 1.691; standard deviation: 0.2608), the HeLa cell has the medium deformability (mean: 1.592; standard deviation: 0.2473), and the HUVEC has the least deformability (mean: 1.370; standard deviation: 0.2192). The deformability of HEK cells is significantly greater than HeLa cells (P = 0.0403); while the deformability of HeLa cells is significantly greater than HUVEC cells (P = 0.0001). These results indicate that the HEK cell has the least mechanical strength, while the HUVEC cell has the greatest. Once a single bubble is actuated acoustically, it can deform tens of cells around it within seconds; sufficient data on cell deformability may thereby be obtained for statistical analysis.
Figure 3.
The deformability of a) HEK, b) HeLa, and c) HUVEC; d) statistical analysis indicated that the HEK cell has the largest deformability, while HUVEC has the least deformability; e–g) the deformability reflects differences in cytoskeleton structure.
The differences in the deformability of each cell line arise from cytoskeleton structures, which are visualized by fluorescent images of GFP-actin and RFP-microtubule. When cells are suspended, the F-actin forms a hollow-spherical-shaped, cortical actin layer to maintain the cell shape and mechanical properties, while the microtubule usually exists deeper under the cell membrane. Previous reports[9] revealed that most mammalian cells had cortical actin of thicknesses from 50 nm to 2 μm. For example, HEK 293 has a cortical actin thickness of 0.99 ± 0.38 um. The fluorescent images we presented here are in agreement with previous observations. Further, the structures of cortical actins in three cell lines are distinct. The HEK cell has the thinnest cortical actin layer under the cell membrane; the HeLa cell shows a thin but more-uniform cortical actin layers to maintain the suspended cells; the HUVEC shows much thicker cortical actin. As a consequence of cortical actin variations in their structures, the three cell lines deforms differently under nearly identical acoustic operating conditions. The HUVEC, with the most condensed cortical actin, exhibits the least deformability; while the HEK cells, with the thinnest cortical actin, exhibits the greatest deformability. The reason for a weaker cortical actin in the HEK and HeLa than HUVEC (i.e., larger deformability for HEK and HeLa), may relate to the origins of these cell lines. HeLa cells are from cervical cancer. HEK 293 cells are from human embryonic kidneys. HUVEC are derived from nonmalignant endothelial cells. This result suggests that tumor cell lines, HeLa and HEK, are similar in their immature nature of their cytoskletons. As a result, cancer cells are generally less stiff than nonmalignant cells. Our result is consistent with a previous report, which found stiffness changes of malignant cells compared with their healthy counterparts.[2]
3.4. In Situ Measurement of Deformability during Drug Treatment
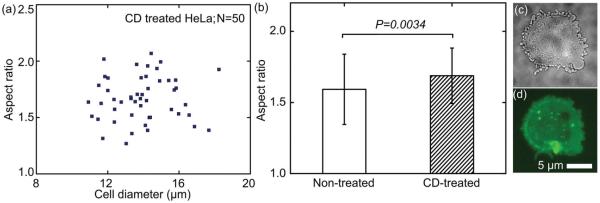
Our bubble-based cell deformability measurement can be conveniently integrated with other cell operation platforms due to its in situ operation. Hence, this technique enhances prognostic analyses in which the cells’ mechanical properties are characterized during therapeutic treatment. Here we demonstrate the effect of Cytochalasin D on the deformability of cells by incorporating cell deformability measurements with drug treatment. During incubation of the drug, the measurement of deformability, and the fluorescent visualization of cytoskeleton structure, the cells were kept in the same micro-fluidic chamber. Cytochalasin D was added to a suspension of HeLa cells (with sodium alginate to adjust viscosity) for incubation at 37 °C. After 20 min, a bubble was generated near a group of cells to measure the deformability of cells after Cytochalasin D treatment. Treatment with Cytochalasin D enhanced the cell deformability (mean: 1.688, standard deviation: 0.1951, N = 50) (Figure 4b). Compared with the untreated group, a significant increase in the cell deformability occurs (P = 0.0336). The increase reveals that Cytochalasin D undermined the F-actin, which maintains the cells’ stiffness. Their morphology was visualized in both bright-field and fluorescent microscopy. After the treatment of Cytochalasin D for 20 min, the Cytochalasin D was bound to F-actin polymer, which prevented further polymerization of actin monomers. Thus, F-actin must not be synthesized, in order to maintain the cells’ structure. A bright-field image (Figure 4c) shows that blebs emerge after the Cytochalasin D treatment: the attachment between actin and the membrane was destabilized by Cytochalasin D, promoting bleb nucleation.[5] Existing blebs did not assemble an actin rim and did not retract. The actin-GFP fluorescent images (Figure 4d) show that the fiber-shaped cortical actin became discrete actin fragments.
Figure 4.
a) The deformability of CD-treated HeLa cells; b) the CD-treated HeLa cells shows an increased deformability compared with nontreated ones; c) bright field and d) actin-GFP fluorescent images of a CD-treated HeLa cell.
Monitoring the cellular mechanical properties during drug treatment is important for prognostics. Conventionally, this monitoring requires that the cells are incubated with drugs, then processed and delivered to another cell-deforming device. However, such a multi-procedure operation prevents real-time monitoring of the changes in cell stiffness. Our method integrates cell deformability measurements into existing platforms to monitor cell mechanical properties in the same chamber. The method simplifies handling of cell samples and enables monitoring of effects of the drugs in situ and in real time, while integrating with existing microfluidic cell culture systems.
3.5. Measurement of Cell Deformability of Subpopulations from Mixture
Analyzing the deformability of each cell subpopulation in complex cell samples will benefit multiple clinical applications. To probe the mechanical properties of the tumor cells from a cancer patient, in which both benign and metastatic cells exist, conventional techniques require complex sample preparation: separating each subpopulations in the cell mixture, culturing the specific tumor cells, and measuring the mechanical properties based on the purified tumor cells. This sample-purification process, however, is difficult to perform on cells that have similar cellular properties. Our method can probe the deformability of each subpopulation in a cell mixture, by directly combining chemical biomarkers with the mechanical biomarker.
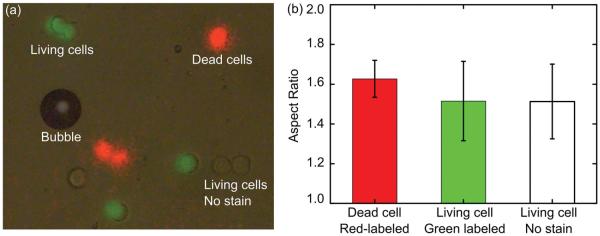
To demonstrate this capability, a cell sample was prepared containing two cell types (protein-denatured and living HeLa cells) and three fluorescent biomarkers (red fluorescence from PI, green fluorescence from calcium AM, and no stain). The superimposed fluorescent images and the deformability of each subpopulation are in Figure 5. In a single operation, about 20 cells were traced and their deformability was analyzed (Figure 5b). Protein-denatured cells exhibited more deformation (mean: 1.627, standard deviation: 0.0930, N = 5) than living cells. In protein-denatured cells, cytoskeleton proteins fail to maintain the cell’s mechanical integrity; while the living cells labeled with calcium AM (mean: 1.515, standard deviation: 0.1997, N = 7) and the unlabeled living cells (mean: 1.513, standard deviation: 0.1881, N = 6) demonstrated similar deformability properties, indicating similar mechanical properties. The number of cells which may be traced in a single experiment is determined by the area of the microscopic field of view. In this case, a 50× objective was used and about 20 individual cells were traced and identified simultaneously. With the combination of chemical and mechanical biomarkers, this technique measures the deformability of each subpopulation of cells. This capability, accompanied with high-throughput measurement, has real-world applications such as finding variations among subpopulations in a cell mixture from a cancer patient.
Figure 5.
a) Stacked images of the cell mixture with different dyed colors; b) the deformability of each subpopulation in the cell mixtures is measured by tracing each stained cell.
4. Conclusion
An acoustically actuated, bubble-based technique was developed to probe the deformability of suspended cells in a microfluidic chamber. An optothermal effect generated a bubble which was positioned near cells of interest. Acoustic streaming around the oscillating bubble deformed the cells, and cell deformability was measured. First, using this technique, the deformability from multiple HeLa, HEK, and HUVEC cells was measured, and statistically relevant data was obtained. The technique probes the mechanical properties of multiple cells at once. Second, in situ measurement of the deformability of cells after treating with the Cytochalasin D was demonstrated, which proves that our technique can be integrated with drug-screening platforms. Third, the characterization of deformability variance in denatured and healthy HeLa cell confirms that our technique can combine both fluorescent biomarkers and mechanical biomarkers in the same platform. With these unique properties, our technique will serve as a useful tool for biological studies as well as biophysical diagnoses and prognoses.
5. Experimental Section
Experimental Setups
Microsized bubbles were generated with a focused laser beam by the optothermal effect (Figure 1a).[36,54,58] Specifically, a diode laser of wavelength 405 nm was coupled into an upright optical microscope (Eclipse LV-100, Nikon, Japan) and was focused by an objective lens (LU Plan Fluor, 50×, NA = 0.8, Nikon, Japan) onto a glass slide (24 × 50 mm, VWR, USA) with a gold film of thickness 50 nm.[59] The diameter of the focused laser beam on the gold film was 30 μm. The laser power on the sample plane, measured by a power meter (FieldMaxII-TO, Coherent, USA), was adjustable from 0 to 46 mW. The location of the laser spot was controlled by moving the chamber in the XY plane with a motorized stage (Model C152V2, Prior Inc., USA). The gold-coated glass slide also served as the bottom of the microfluidic chamber (Figure 1b), and it was bonded to a polydimethylsiloxane (PDMS) microfluidic chamber by plasma treatment (Figure 1b). The PDMS chamber of length, width, and depth of 10, 10, and 60 μm, respectively, was fabricated by standard soft lithography and mold-replica techniques.
After bubbles were generated, they were actuated by a piezo transducer (Piezo Ceramic Transducer 20 × 2.1 mmR Disc, Steiner & Martins Inc., USA). The piezo transducer was bonded to the same glass slide with the microfluidic chamber by double-sided polyimide tape (Masking Products, USA) to generate acoustic waves (Figure 1b).[60–62] The stimulating electrical signal was generated from a function generator (8116A, Hewlett Packard, USA) and connected to a signal amplifier (Model 25A250A, Amplifier Research, USA). The frequency is ≈100 kHz. When the bubble was actuated by the acoustic waves, acoustic streaming was generated around the bubble due to oscillation of air–liquid interface. Cells suspended around the bubble were attracted to the bubble and then were pushed away (Figure 1c). As a result, significant deforming of cells was observed (Figure 1d).
Data Analysis
The cells were imaged with a CCD camera (DS-Fi1, Nikon, Japan) through the same objective lens that focused the laser beam. The outline of a cell at each frame was extracted by ImageJ and estimated as an ellipse. The long and short axes were estimated using the line-measurement function of ImageJ. The deformability of cells was defined as the aspect ratio between long axis (a in Figure 1e) and short axis (b in Figure 1e). The mean deformability of a cell type was obtained by measuring multiple cells around an oscillating bubble (Figure 1f).
To trace the motion and deformation of each cell in the cell mixtures, fluorescent images and bright-field videos are captured twice on the same imaging area. In this work, three types of images were taken: before the acoustic actuation of bubble, green fluorescent images for calcein AM stained fresh cells and red fluorescent images for propidium iodide stained protein-denatured cells were taken; during the acoustic actuation, bright-field videos were taken for recording the cells moving and deforming in the acoustic field. Since these three types of images/videos were taken using one camera, they could be superimposed together (Figure S5, Supporting Information). By stacking the images together, one could obtain various information including chemical properties of each single cells, the moving trajectory of each cell, and the deformation of each cell.
Cell Preparation
HeLa cells, Human umbilical vein endothelial cells (HUVEC), and Human Embryonic Kidney 293 cells (HEK 293) were chosen for testing of mechanical properties. HeLa cells were grown in Dulbecco’s Modified Eagle Medium: Nutrient Mixture F-12 (DMEM/F12) media (Gibco, CA, USA), supplemented with 10% fetal bovine serum (Atlanta Biologicals, GA, USA), penicillin (100 U mL−1), and 100 μg mL−1 streptomycin (Mediatech, VA, USA). HUVEC were cultured using EndoGRO-LS Complete Culture Medium (Millipore, Germany). HEK 293 were cultured using Minimum Essential Medium with Earle’s salts (Cellgro, Corning, USA) supplemented with 10% FBS and 1% penicillin–streptomycin solution. The cell lines were maintained in T-25 cell culture flasks, in a 37 °C incubator at 5% CO2 level, and were cultured twice per week. Before each experiment, an adherent culture was released from flasks using 0.05% trypsin digestion (Cellgro, Corning, USA), and then rinsed with Trypsin neutralizer solution (Gibco, Life Technologies, USA). After centrifugation at 800 rpm for 5 min and rinsing with PBS buffer (1×, pH 7.4), cells were re-suspended in a highly viscous working medium, containing 5% (w/w) sodium alginate (Sigma, USA) dissolved in PBS buffer (1×, pH 7.4), in a final concentration of about 2 × 105 cells mL−1.
Cortical actin in the suspended cells was fluorescently visualized by Actin-GFP (CellLight, BacMam 2.0, Life Technologies, USA), following the protocol provided by the manufacturer. The cortical actin was visualized with fluorescent microscopy in the excitation wavelength of 488 nm, and at the emission wavelength of 532 nm. Visualization of microtubule utilized the Microtubule-RFP (Cell-Light, BacMam 2.0, Life technologies, USA) with similar procedure to the actin stain. The fluorescent excitation wavelength and emission wavelength were 555 and 584 nm, respectively.
To test the change of deformability during the drug treatments, Cytochalasin D (Sigma-Aldrich, USA) was used to depolymerize the actin of the HeLa cells. Cytochalasin D was kept in Dimethyl sulfoxide (DMSO) of concentration of 5 mg mL−1 and at −20 °C. Cytochalasin D was added to the cell suspension, and the final concentration was 1 μg mL−1. After incubating for 20 min, cell deformation was measured.
The specimen of a cell mixture was prepared by mixing living and protein-denatured HeLa cells. The protein-denatured cells were prepared by adding 70% ethanol into the cell suspensions. They were then rinsed with PBS and mixed with the living cells in a PBS buffer. The protein-denatured cells were fluorescently labeled with propidium iodide (PI) stain, where PI was added into the medium at a ratio of 0.5 μl PI to 1 mL buffer. The living cells were fluorescently labeled with calcein AM (Life Technologies, USA) of a concentration of 0.5 × 10−6 M.
Supplementary Material
Acknowledgements
The authors acknowledge financial support from the National Institutes of Health (1 R01 GM112048-01A1 and 1R33EB01978501), the National Science Foundation (CBET-1438126 and IDBR-1455658), and the Penn State Center for Nanoscale Science (MRSEC) under grant DMR-1420620. Components of this work were conducted at the Penn State node of the NSF-funded National Nanotechnology Infrastructure Network.
Footnotes
Supporting Information
Supporting Information is available from the Wiley Online Library or from the author.
Contributor Information
Dr. Yuliang Xie, Department of Chemical Engineering, The Pennsylvania State University, University Park, PA 16802, USA
Dr. Nitesh Nama, Department of Engineering Science and Mechanics, The Pennsylvania State University, University Park, PA 16802, USA
Dr. Peng Li, Department of Engineering Science and Mechanics, The Pennsylvania State University, University Park, PA 16802, USA
Dr. Zhangming Mao, Department of Engineering Science and Mechanics, The Pennsylvania State University, University Park, PA 16802, USA
Dr. Po-Hsun Huang, Department of Engineering Science and Mechanics, The Pennsylvania State University, University Park, PA 16802, USA
Dr. Chenglong Zhao, Department of Physics & Electro-Optics Program, University of Dayton, Dayton, OH 45469, USA
Prof. Francesco Costanzo, Department of Engineering Science and Mechanics, The Pennsylvania State University, University Park, PA 16802, USA Center for Neural Engineering, The Pennsylvania State University, University Park, PA 16802, USA.
Prof. Tony Jun Huang, Department of Chemical Engineering, The Pennsylvania State University, University Park, PA 16802, USA; Department of Engineering Science and Mechanics, The Pennsylvania State University, University Park, PA 16802, USA.
References
- [1].Di Carlo D. J. Lab. Autom. 2012;17:32. doi: 10.1177/2211068211431630. [DOI] [PubMed] [Google Scholar]
- [2].Suresh S. Acta Biomater. 2007;3:413. doi: 10.1016/j.actbio.2007.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Hoffman BD, Crocker JC. Annu. Rev. Biomed. Eng. 2009;11:259. doi: 10.1146/annurev.bioeng.10.061807.160511. [DOI] [PubMed] [Google Scholar]
- [4].Costa KD. Dis. Markers. 2004;19:139. doi: 10.1155/2004/482680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Haghparast SMA, Kihara T, Shimizu Y, Yuba S, Miyake J. J. Biosci. Bioeng. 2013;116:380. doi: 10.1016/j.jbiosc.2013.03.003. [DOI] [PubMed] [Google Scholar]
- [6].Liu H, Tan Q, Geddie WR, Jewett MAS, Phillips N, Ke D, Simmons CA, Sun Y. Cell Biochem. Biophys. 2014;68:241. doi: 10.1007/s12013-013-9702-9. [DOI] [PubMed] [Google Scholar]
- [7].Xu W, Mezencev R, Kim B, Wang L, McDonald J, Sulchek T. PLoS One. 2012;7:e46609. doi: 10.1371/journal.pone.0046609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Pelling AE, Veraitch FS, Chu CP-K, Mason C, Horton MA. Cell Motil. Cytoskeleton. 2009;66:409. doi: 10.1002/cm.20391. [DOI] [PubMed] [Google Scholar]
- [9].MacQueen LA, Thibault M, Buschmann MD, Wertheimer MR. J. Biomech. 2012;45:2797. doi: 10.1016/j.jbiomech.2012.08.040. [DOI] [PubMed] [Google Scholar]
- [10].Ding X, Shi J, Lin S-CS, Yazdi S, Kiraly B, Huang TJ. Lab Chip. 2012;12:2491. doi: 10.1039/c2lc21021e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Li S, Ding X, Guo F, Chen Y, Lapsley MI, Lin SS, Wang L, Mccoy JP, Cameron CE, Huang TJ. Anal. Chem. 2013;85:5468. doi: 10.1021/ac400548d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Mao X, Huang TJ. Lab Chip. 2012;12:4006. doi: 10.1039/c2lc90100e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Kim D-H, Wong PK, Park J, Levchenko A, Sun Y. Annu. Rev. Biomed. Eng. 2009;11:203. doi: 10.1146/annurev-bioeng-061008-124915. [DOI] [PubMed] [Google Scholar]
- [14].Polacheck WJ, Li R, Uzel SGM, Kamm RD. Lab Chip. 2013;13:2252. doi: 10.1039/c3lc41393d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Zheng Y, Nguyen J, Wei Y, Sun Y. Lab Chip. 2013;13:2464. doi: 10.1039/c3lc50355k. [DOI] [PubMed] [Google Scholar]
- [16].Bow H, Pivkin IV, Silva D-M, Goldfless SJ, Dao M, Niles JC, Suresh S, Han J. Lab Chip. 2011;11:1065. doi: 10.1039/c0lc00472c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Rosenbluth MJ, Lam WA, Fletcher DA. Lab Chip. 2008;8:1062. doi: 10.1039/b802931h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Gossett DR, Tse HTK, Lee SA, Ying Y, Lindgren AG, Yang OO, Rao J, Clark AT, Di Carlo D. Proc. Natl. Acad. Sci. USA. 2012;109:7630. doi: 10.1073/pnas.1200107109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Abkarian M, Faivre M, Stone HA. Proc. Natl. Acad. Sci. USA. 2006;103:538. doi: 10.1073/pnas.0507171102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Guo Q, Duffy SP, Matthews K, Santoso AT, Scott MD, Ma H. J. Biomech. 2014;47:1767. doi: 10.1016/j.jbiomech.2014.03.038. [DOI] [PubMed] [Google Scholar]
- [21].Myrand-Lapierre M-E, Deng X, Ang RR, Matthews K, Santoso AT, Ma H. Lab Chip. 2015;15:159. doi: 10.1039/c4lc01100g. [DOI] [PubMed] [Google Scholar]
- [22].Zhang Z, Chen X, Xu J. Biomicrofluidics. 2015;9:024108. doi: 10.1063/1.4916645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Aghaamoo M, Zhang Z, Chen X, Xu J. Biomicrofluidics. 2015;9:034106. doi: 10.1063/1.4922081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Du E, Dao M, Suresh S. Extreme Mech. Lett. 2014;1:35. doi: 10.1016/j.eml.2014.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Lekka M, Laidler P. Nat. Nanotechnol. 2009;4:72. doi: 10.1038/nnano.2009.004. author reply 72. [DOI] [PubMed] [Google Scholar]
- [26].Hochmuth RM. J. Biomech. 2000;33:15. doi: 10.1016/s0021-9290(99)00175-x. [DOI] [PubMed] [Google Scholar]
- [27].Baghini Shojaei-E., Zheng Y, Sun Y. Ann. Biomed. Eng. 2013;41:1208. doi: 10.1007/s10439-013-0791-9. [DOI] [PubMed] [Google Scholar]
- [28].Tandiono T, Klaseboer E, Ohl S-W, Siak-Wei Ow D, Choo AB-H, Li F, Ohl CD. Soft Matter. 2013;9:8687. [Google Scholar]
- [29].Quinto-Su PA, Kuss C, Preiser PR, Ohl C-D. Lab Chip. 2011;11:672. doi: 10.1039/c0lc00182a. [DOI] [PubMed] [Google Scholar]
- [30].Wottawah F, Schinkinger S, Lincoln B, Ananthakrishnan R, Romeyke M, Guck J, Käs J. Phys. Rev. Lett. 2005;94:098103. doi: 10.1103/PhysRevLett.94.098103. [DOI] [PubMed] [Google Scholar]
- [31].Sraj I, Eggleton CD, Jimenez R, Hoover E, Squier J, Chichester J, Marr DWM. J. Biomed. Opt. 2013;15:047010. doi: 10.1117/1.3470124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Guck J, Schinkinger S, Lincoln B, Wottawah F, Ebert S, Romeyke M, Lenz D, Erickson HM, Ananthakrishnan R, Mitchell D, Käs J, Ulvick S, Bilby C. Biophys. J. 2005;88:3689. doi: 10.1529/biophysj.104.045476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Zheng Y, Nguyen J, Wang C, Sun Y. Lab Chip. 2013;13:3275. doi: 10.1039/c3lc50427a. [DOI] [PubMed] [Google Scholar]
- [34].MacQueen LA, Buschmann MD, Wertheimer MR. J. Micro-mech. Microeng. 2010;20:065007. [Google Scholar]
- [35].Zhang K, Jian A, Zhang X, Wang Y, Li Z, Tam H-Y. Lab Chip. 2011;11:1389. doi: 10.1039/c0lc00520g. [DOI] [PubMed] [Google Scholar]
- [36].Xie Y, Zhao C, Zhao Y, Li S, Rufo J, Yang S, Guo F, Huang TJ. Lab Chip. 2013;13:1772. doi: 10.1039/c3lc00043e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Ahmed D, Chan CY, Lin S-CS, Muddana HS, Nama N, Benkovic SJ, Huang TJ. Lab Chip. 2013;13:328. doi: 10.1039/c2lc40923b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Ahmed D, Mao X, Shi J, Juluri BK, Huang TJ. Lab Chip. 2009;9:2738. doi: 10.1039/b903687c. [DOI] [PubMed] [Google Scholar]
- [39].Ahmed D, Mao X, Juluri BK, Huang TJ. Microfluid. Nanofluid. 2009;7:727. [Google Scholar]
- [40].Riley N. Theor. Comput. Fluid Dyn. 1998;10:349. [Google Scholar]
- [41].Lee CP, Wang TG. J. Acoust. Soc. Am. 1990;88:2367. [Google Scholar]
- [42].Longuet-Higgins MS. Proc. R. Soc. London, Ser. A. 1998;454:725. [Google Scholar]
- [43].Hamilton MF, Ilinskii YA, Zabolotskaya EA. J. Acoust. Soc. Am. 2003;113:153. doi: 10.1121/1.1528928. [DOI] [PubMed] [Google Scholar]
- [44].Chindam C, Nama N, Lapsley MI, Costanzo F, Huang TJ. J. Appl. Phys. 2013;114:194503. doi: 10.1063/1.4827425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Ding X, Li P, Lin S-CS, Stratton ZS, Nama N, Guo F, Slotcavage D, Mao X, Shi J, Costanzo F, Huang TJ. Lab Chip. 2013;13:3626. doi: 10.1039/c3lc50361e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Nama N, Huang P-H, Huang TJ, Costanzo F. Lab Chip. 2014;14:2824. doi: 10.1039/c4lc00191e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Xie Y, Chindam C, Nama N, Yang S, Lu M, Zhao Y, Mai JD, Costanzo F, Huang TJ. Sci. Rep. 2015;5:12572. doi: 10.1038/srep12572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Nama N, Barnkob R, Mao Z, Kähler CJ, Costanzo F, Huang TJ. Lab Chip. 2015;15:2700. doi: 10.1039/c5lc00231a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Li P, Mao Z, Peng Z, Zhou L, Chen Y, Huang P, Truica CI. Proc. Natl. Acad. Sci. USA. 2015;112:4970. doi: 10.1073/pnas.1504484112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Ding X, Peng Z, Lin S-CS, Geri M, Li S, Li P, Chen Y, Dao M, Suresh S, Huang TJ. Proc. Natl. Acad. Sci. USA. 2014;111:12992. doi: 10.1073/pnas.1413325111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Guo F, Li P, French JB, Mao Z, Zhao H, Li S, Nama N, Fick JR. Proc. Natl. Acad. Sci. USA. 2015;112:43. doi: 10.1073/pnas.1422068112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Hart T, Hamilton MF. J. Acoust. Soc. Am. 1988;84:1488. [Google Scholar]
- [53].Hamilton MF, Blackstock DT. Nonlinear Acoustics. Academic Press; New York: 1998. [Google Scholar]
- [54].Zhao C, Xie Y, Mao Z, Zhao Y, Rufo J, Yang S, Guo F, Mai JD, Huang TJ. Lab Chip. 2014;14:384. doi: 10.1039/c3lc50748c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Neuman KC, Block SM. Rev. Sci. Instrum. 2004;75:2787. doi: 10.1063/1.1785844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Ashkin A, Dziedzic JM, Bjorkholm JE, Chu S. Opt. Lett. 1986;11:288. doi: 10.1364/ol.11.000288. [DOI] [PubMed] [Google Scholar]
- [57].Tho P, Manasseh R, Ooi A. J. Fluid Mech. 2007;576:191. [Google Scholar]
- [58].Xie Y, Yang S, Mao Z, Li P, Zhao C, Cohick Z, Huang P-H, Huang TJ. ACS Nano. 2014:812175. doi: 10.1021/nn503826r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Zhao C, Liu Y, Zhao Y, Fang N, Huang TJ. Nat. Commun. 2013;4:2305. doi: 10.1038/ncomms3305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Huang P-H, Xie Y, Ahmed D, Rufo J, Nama N, Chen Y, Chan CY, Huang TJ. Lab Chip. 2013;13:3847. doi: 10.1039/c3lc50568e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Huang P-H, Nama N, Mao Z, Li P, Rufo J, Chen Y, Xie Y, Wei C-H, Wang L, Huang TJ. Lab Chip. 2014;14:4319. doi: 10.1039/c4lc00806e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Huang P-H, Ren L, Nama N, Li S, Li P, Yao X, Cuento RA, Wei C-H, Chen Y, Xie Y, Nawaz AA, Alevy YG, Holtzman MJ, McCoy JP, Levinec SJ, Huang TJ. Lab Chip. 2015;15:3125. doi: 10.1039/c5lc00539f. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.