Integrating occupancy models and structural equation models to understand species occurrence

Abstract

Understanding the drivers of species occurrence is a fundamental goal in basic and applied ecology. Occupancy models have emerged as a popular approach for inferring species occurrence because they account for problems associated with imperfect detection in field surveys. Current models, however, are limited because they assume covariates are independent (i.e., indirect effects do not occur). Here, we combined structural equation and occupancy models to investigate complex influences on species occurrence while accounting for imperfect detection. These two methods are inherently compatible because they both provide means to make inference on latent or unobserved quantities based on observed data. Our models evaluated the direct and indirect roles of cattle grazing, water chemistry, vegetation, nonnative fishes, and pond permanence on the occurrence of six pond-breeding amphibians, two of which are threatened: the California tiger salamander (Ambystoma californiense), and the California red-legged frog (Rana draytonii). While cattle had strong effects on pond vegetation and water chemistry, their overall effects on amphibian occurrence were small compared to the consistently negative effects of nonnative fish. Fish strongly reduced occurrence probabilities for four of five native amphibians, including both species of conservation concern. These results could help to identify drivers of amphibian declines and to prioritize strategies for amphibian conservation. More generally, this approach facilitates a more mechanistic representation of ideas about the causes of species distributions in space and time. As shown here, occupancy modeling and structural equation modeling are readily combined, and bring rich sets of techniques that may provide unique theoretical and applied insights into basic ecological questions.

Introduction

Much of ecology is concerned with explaining and predicting where species occur in space and time. While species distributions are directly and indirectly influenced by a diverse suite of abiotic and biotic factors, most statistical treatments do not formally differentiate between direct and indirect effects (Guisan and Thuiller 2005). Structural equation modeling (SEM) provides one means by which to formally represent causal assumptions in the form of direct and indirect causal pathways, helping to close the gap between biological mechanisms and statistical methodology (Bollen 1989, Grace 2006).

Structural equation models combine causal assumptions with observations to generate causal inferences (Pearl 2000). Often, these assumptions are displayed in a path diagram that represents model components and causal relationships (i.e. how one variable affects another). These path diagrams encode both direct and indirect effects, such as those involved in complex processes that structure communities (Clough 2012, Alsterberg et al. 2013). As a result, SEM provides a framework for clarifying, representing, and evaluating hypotheses in ecology that can outperform traditional associational statistical methods. For example, the relationship between productivity and biodiversity has historically been evaluated statistically in a bivariate context, despite the multidimensionality of the hypotheses that have been put forward to explain the relationship. By explicitly representing causal relationships between productivity and diversity, along with disturbance and stressors in a SEM, the mechanistic relationship between productivity and biodiversity becomes more clear, with more predictive power than bivariate approaches (Grace et al. 2014). In addition, SEM is flexible, with recent developments facilitating non-linear effects and a wide range of distributions, broadening the potential applicability of SEM in ecology (Lee 2007). Finally, SEM differentiates between latent and observable variables. Latent variables cannot be observed directly, but observations can provide information on latent quantities. A classic example is the presence or absence of a species.

In practice, studies of species occurrence are notoriously plagued by imperfect detection because species may be present but unobserved. This can be problematic when trying to explain species distributions because false absences create bias in estimated coefficients for covariates that explain occurrence. For instance, if turbidity increases the probability of occurrence of an aquatic organism, but decreases detectability (i.e. the organism is harder to observe), detection events will not appear to be related to turbidity. However, adjusting for imperfect detection facilitates unbiased estimation of the true relationship between such a factor and species occurrence. Such adjustments can be made via occupancy modeling, a method in which repeat surveys are used to estimate probabilities of detection and draw inferences on true occupancy states (MacKenzie et al. 2002). Occupancy models are classic hierarchical models, where the latent binary occurrence state is partly observed, and the extra zeros in detection histories are modeled as potentially arising from a combination of true and false absences. As the appreciation and application of occupancy models has increased, they have been extended to include multiple species, temporal dynamics including colonization and extinction, estimation of species richness, habitat ephemerality, and even disease dynamics (Dorazio et al. 2010, MacKenzie et al. 2011, Miller 2012). These developments have been instrumental in improving inferences about the processes that govern species distributions. However, many existing models require independent covariates for occurrence and detection. This limitation represents a challenge to understanding even moderately complex processes that drive species distributions that may include a combination of direct and indirect effects on occurrence and detectability.

Here, we show that combining SEM with occupancy models overcomes this limitation and provides a means by which to more directly represent processes that influence species occurrence. We aim to illustrate the practical and conceptual compatibility of occupancy modeling and structural equation modeling by developing a causal model of species occurrence and community composition that explicitly accounts for non-detection. We use pond-breeding amphibians as an applied case example. First, we outline the logic behind the model by summarizing the relevant empirical knowledge for our system in terms of the effects of pond permanence, cattle grazing, nonnative fishes, water chemistry, and vegetation on amphibian occurrence. We then discuss the data collection scheme and formally relate our observations to the processes under consideration by developing observation, process, and parameter (prior) models. As a model verification step, we demonstrate the recovery of parameters from our SEM using simulation (Rykiel 1996). Last, we present results for the case study and discuss the value, limitations, and future directions for this approach.

Study system

The amphibian community in freshwater ponds of the San Francisco Bay Area of California, USA includes the Pacific chorus frog (Pseudacris regilla), western toad (Anaxyrus boreas), California newt (Taricha torosa), California tiger salamander (Ambystoma cailforniense), California red-legged frog (Rana draytonii), and nonnative American bullfrog (Lithobates catesbeianus) (Stebbins 2003). Of the native species, two are federally protected and are of broad conservation concern (A. californiense and R. draytonii), and A. boreas has declined in specific regions (Lannoo 2005). Some populations of these species are currently threatened by invasive species including nonnative fishes and bullfrogs, which potentially act as predators and competitors for native amphibians (Fisher and Shaffer 1996, Lawler et al. 1999, Preston et al. 2012). Further, widespread cattle grazing in this region has the potential to affect the population dynamics of amphibians at breeding sites directly via trampling, and indirectly by removing vegetation and increasing the concentration of nitrogenous compounds in wetlands (Robins and Vollmar 2002, Roche et al. 2012). The ponds we considered included both temporary and permanent water bodies up to 7 meters in depth.

Data collection

From 2009 to 2013, field crews used standardized methods to assess amphibian site occupancy in 171 wetlands in the San Francisco Bay Area, USA (Contra Costa, Alameda, Santa Clara, and San Mateo counties) (Johnson et al. 2013). For simplicity, we used only one year of data from each site (with years chosen at random). The sites consisted of both artificially created livestock ponds and natural wetlands. Crews surveyed wetlands twice per summer using a combination of visual encounter, seine, and dipnet surveys (Crump and Bury 1994). Visual encounter surveys involved a single observer walking the perimeter of the wetland and recording all species observed. Dipnet sweeps were conducted every 3 m around the pond perimeter (1.4 mm mesh and 2600 cm² net area) and three to four seine net hauls were performed in the deepest regions of each pond (4 mm mesh size and 1 × 2 m net area). For each survey, we recorded all life stages of each observed amphibian species. We considered sites “occupied” if larval amphibians were present, which indicates adult presence, successful fertilization, some degree of larval development, and potential for metamorphosis (i.e. breeding activity).

We quantified cattle grazing intensity, percentage of shoreline vegetated, pond permanence, water chemistry, and the presence of nonnative fish. To measure cattle grazing intensity, we recorded the number of cow paddies within three meters of shoreline and recorded shoreline perimeter with a handheld GPS unit to quantify cow paddy density at each pond. As a second measure of grazing intensity, we made a qualitative judgment of whether the wetland was disturbed by cattle based on evidence of tracks and trampling. Water samples were collected in acid-washed Nalgene bottles, filtered, frozen, and analyzed for ammonium (NH⁴+) and total dissolved nitrogen (TDN) concentrations using standard protocols (see: http://snobear.colorado.edu/Kiowa/Kiowaref/procedure.html). Imagery from Google Earth was used to help determine whether wetlands were permanent, based on consistent presence of water year round. Last, crews estimated the percentage of pond shoreline that was vegetated and recorded whether fish were present or absent using observations from all sampling methods. The most common fish species were nonnative, including mosquitofish (Gambusia affinis), largemouth bass (Micropterus salmoides), and bluegill sunfish (Lepomis macrochirus).

Conceptual model

Drawing upon previous literature, we developed a multivariate hypothesis about the drivers of amphibian community composition in this system (Figure 1). We expected fish to strongly affect community composition, particularly species with poor avoidance strategies and high palatability (Kruse and Stone 1984, Kats et al. 1988, Adams 2000, Welsh et al. 2006). Further, pond permanence should increase bullfrog occurrence because bullfrogs have a multi-year larval development period that is longer than most western native species (Collins 1979). We hypothesized that livestock would physically alter wetland ecosystems via trampling and grazing, and chemically alter wetlands via inputs of nitrogenous waste products in urine and feces (Kauffman et al. 1983, Jansen and Healey 2003, Knutson et al. 2004, Schmutzer et al. 2008, Adams et al. 2009). Previous studies indicate that characteristics of shoreline vegetation influence amphibian breeding and that water chemistry can alter reproductive success and occupancy probability (Freda and Dunson 1986, Rowe and Dunson 1995, Rouse et al. 1999, Jansen and Healey 2003, Brodman et al. 2003, Egan and Paton 2004, Burne and Griffin 2005, Earl and Whiteman 2009). Separating out the causal pathways through which grazing alters amphibian occupancy is important from a practical standpoint, as each one might be targeted differently with management interventions (e.g., limiting cattle-induced damage to vegetation versus limiting the total intensity of grazing).

Figure 1.

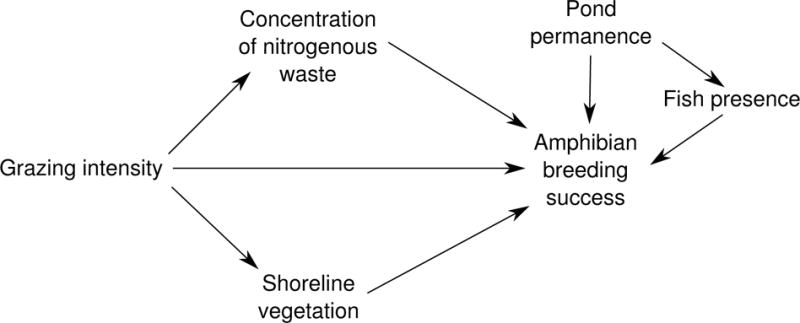
Conceptual model showing influences on amphibian breeding success. Nodes represent concepts of interest, and directional arrows represent causal effects (e.g. grazing intensity affects shoreline vegetation)

Model formalization

To formalize the model of Figure 1, we adopted a hierarchical Bayesian approach, developing model components related to observations, processes in the system, and priors for unknown parameters (Lee 2007, Cressie et al. 2009, Dorazio et al. 2010).

Observation model

While early structural equation models assumed normally distributed observed indicator variables, current methods are extremely flexible in terms of likelihood functions and relationships between variables, broadening the applicability of these methods in ecology (Grace 2006, Lee 2007). We consider the presence/absence state of a species at a location to be a hidden (latent) binary variable which gives rise to imperfect detection/nondetection data. The use of a latent state variable is a key conceptual link between the fields of SEM and occupancy modeling. The flexibility of this approach is demonstrated in the following sections where we apply a variety of observation models from the exponential family, a moderately complex finite-mixture distribution, and a combination of continuous and discrete latent variables.

We considered grazing intensity by cattle to be a continuous latent quantity that cannot be observed directly, whose value is indicated by evidence of disturbance and the density of cow paddies in the vicinity of a wetland. Specifically, cattle disturbance was modeled as a Bernoulli random variable with latent grazing intensity (ξ) as a continuous covariate:

$$\begin{array}{c}{Y}_1\left[j,k\right]\sim \mathit{\text{Bernoulli}}\left(p_{Y_1}\left[j\right]\right)\\ \mathit{\text{logit}}\left(p_{Y_1}\left[j\right]\right)={\beta }_{Y_1,0}+{\beta }_{Y_1,1}\mathrm{\xi }\left[j\right]\end{array}$$

for the j^th site and the k^th survey, with square brackets representing indexing. Observed cow paddy counts are treated as a second indicator (specifically, a multi-method indicator) (Grace 2006) and modeled as a Poisson random variable with an offset for shoreline perimeter of site j (μ_perim[j]) in meters:

$$\begin{array}{l}{Y}_2[j,k]\sim \mathit{\text{Poisson}}(\mathrm{\lambda }[j,k])\\ \frac{{\mathrm{\lambda }}_{j,k}}{{\mu }_{\mathit{\text{perim}}}[j,k]}=e^{{\beta }_{Y_2,0}+{\beta }_{Y_2,1}\mathrm{\xi }[j]}\end{array}$$

Perimeter observations are subject to measurement error and variation within a season. Therefore, we modeled latent mean perimeter values for each site (μ_perim), which represents the expected pond perimeter value for site j:

$$\begin{array}{c}\mathit{\text{log}}\left(\mathit{\text{perim}}\left[j,k\right]\right)\sim N\left({\mu }_{\mathit{\text{perim}}}\left[j\right],{\sigma }_w\right)\\ {\mu }_{\mathit{\text{perim}}}\left[j\right]\sim N\left({\alpha }_{\mathit{\text{perim}}},{\sigma }_a\right)\end{array}$$

where σ_w represents measurement error and variation within a season, α_perim is the (log) average perimeter across all wetlands, and σ_a is the variability in perimeter among wetlands.

Shoreline vegetation, v, ranged from 0–100% with a non-negligble number of 0%, 100%, and intermediate observations. Therefore, we treated these observations as arising from a zero-one inflated beta distribution, which is a finite mixture distribution with a Bernoulli component that produces 0’s and 1’s, and a beta component that produces values on the interval (0, 1) (Ospina and Ferrari 2012):

$$\begin{array}{l}P\left(v;\alpha ,{\mu }_v,\varphi \right)=\{\begin{array}{ll}\alpha \left(1-{\mu }_v\right)& v=0\\ \alpha {\mu }_v& v=0\\ \left(1-\alpha \right)f\left(v;{\mu }_v,\varphi \right)& 0<v<1\end{array}\\ \mathit{\text{logit}}\left({\mu }_v\left[j\right]\right)={\beta }_{v,0}+{\beta }_{v,1}{\eta }_1\left[j\right]\\ \mathit{\text{logit}}\left(\alpha \right)=a_0+a_2{\mu }_v^2\end{array}$$

Here, α determines the extent to which the beta or binomial mixture components dominate the probability density function. The second degree polynomial term with coefficient a₂ causes extreme values of the logit-expected shoreline vegetation cover μ_v to increase the probability of an observer recording either 0% or 100% shoreline vegetation cover. This formulation essentially imposes a minimum probability of observers recording a discrete value when the true shoreline vegetation is 50%, and increases the probability of 0% or 100% observations as the true cover approaches those values. Last, f(v; μ_v, ϕ) is the probability density function of the beta distribution, parameterized in terms of its mean (μ_v) and variance (ϕ), which represents the combination of observation error and within-summer variation in true shoreline vegetation cover (Ospina and Ferrari 2012).

Log-transformed concentrations of ammonium and total dissolved N in the water were used as multi-method indicators of latent N concentration. Because both total dissolved N and $N{H}_4^{+}$ concentrations tend to increase over the course of the summer due to exogenous inputs and pond drying, we also included an effect of survey number k, coded as an indicator variable for the 2nd survey, such that I(k = 2) = 1, and I(k = 1) = 0.

$$\mathit{\text{log}}\left(N{H}_4^{+}\left[j,k\right]\right)\sim N\left({\beta }_{N{H}_4^{+},0}+{\beta }_{N{H}_4^{+},1}{\eta }_2\left[j\right]+{\beta }_{N{H}_4^{+},2}I\left(k\right),{\sigma }_{N{H}_4^{+}}\right)$$

$$\mathit{\text{log}}\left(N\left[j,k\right]\right)\sim N\left({\beta }_{N,0}+{\beta }_{N,1}{\eta }_2\left[j\right]+{\beta }_{N,2}I\left(k\right),{\sigma }_N\right)$$

We adopt an occupancy modeling approach for the data model describing amphibian detection and non-detection. Observations of the i^th species at the j^th site on the k^th repeat survey are represented by Y [i, j, k]. We treated these observations as Bernoulli random variables with probability p[i, j, k]z[i, j], where p is the probability of detection and z is the latent binary presence/absence state. The true occurrence state z is only partly observed. If species i was seen at site j on any survey, it was present, but if it was not seen on any survey, it is possible that it was present but unobserved (MacKenzie et al. 2002):

$$Y\left[i,j,k\right]\sim \mathit{\text{Bernoulli}}\left(p\left[i,j,k\right]z\left[i,j\right]\right)$$

We treated fish presence and pond permanence as directly observed quantities, which is supported by consistency of observations within and across years in this system.

Process model

Our process model represents the latent processes connecting the latent quantities: grazing intensity ξ, shoreline vegetation η₁, N concentration η₂, the true occupancy states z, and the probability of detection P (Figure 2). In the SEM lexicon, process models are sometimes referred to as structural models. Note that there is an additional pathway from fish to nitrogen that was not initially hypothesized, but revealed in the process of model evaluation (see Model Assessment below).

Figure 2.

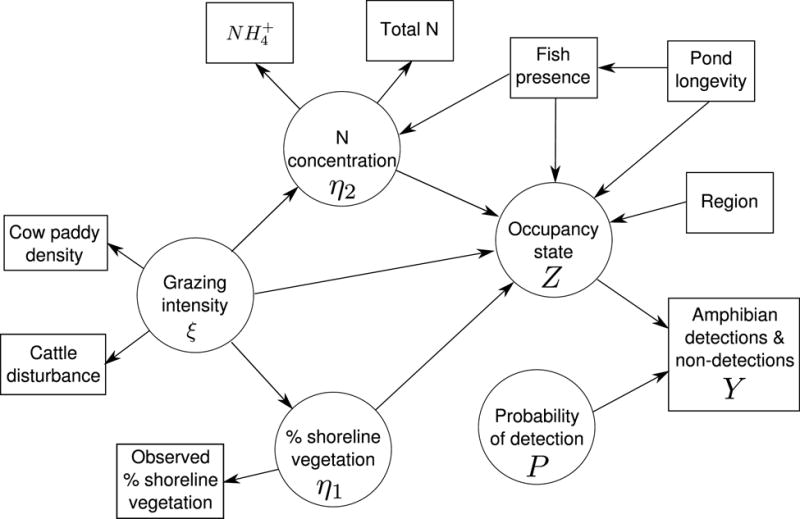
Directed acyclic graph illustrating relationships between unknown quantities (circles) and observed indicator variables (rectangles).

We treat grazing intensity as an exogenous latent variable, unaffected by the other latent quantities, with mean 0 and standard deviation 1 as an identifiability constraint. Due to cattle grazing on and trampling of shoreline vegetation, we modeled a linear effect of cattle grazing intensity ξ on shoreline vegetation η₁:

$${\eta }_1\sim N\left({\gamma }_1\mathrm{\xi },1\right)$$

where the standard deviation term, similarly set to 1 for identifiability, represents the influence of other, unmodeled factors on shoreline vegetation cover. Nitrogenous inputs from cattle excretion in and around wetlands are treated similarly. Following a graphical check of independence assertions, we included an effect of fish presence (γ₃) on nitrogen:

$${\eta }_2\sim N\left({\gamma }_2\mathrm{\xi }+{\gamma }_3\mathit{\text{fish}},1\right).$$

We represented true occupancy states as Bernoulli random variables with probability of occupancy ψ[i, j] for the i^th species at the j^th site, such that z[i, j] ∼ Bernoulli(ψ[i, j]). We use a logit-link to model the effects of observed and latent covariates on ψ:

$$\mathit{\text{logit}}\left(\psi \left[i,j\right]\right)={\alpha }_{\mathit{\text{species}}}\left[i\right]+{\alpha }_{\mathit{\text{region}}}\left[i,r\left[j\right]\right]+{\alpha }_{\mathit{\text{site}}}\left[i,j\right]$$

where α_species accounts for species-specific differences in overall occupancy across the entire study area, α_region accounts for regional differences in occupancy rates within each species (with region r being indexed by site j). Last, α_site represents the local effects of fish, pond permanence, grazing, shoreline vegetation and nitrogen concentrations. These terms can be decomposed as follows:

$${\alpha }_{\mathit{\text{region}}}\left[i,j\right]\sim N\left(0,{\sigma }_{{\alpha }_{\mathit{\text{region}}}}\left[i\right]\right)$$

This varying intercept term accounts for among-region variation within species in occupancy, with varying species-specific standard deviations, to account for the fact that the degree of regional variation in occupancy rates varies among species. Local covariate effects enter the final term:

$${\alpha }_{\mathit{\text{site}}}\left[i,j\right]={\beta }_{\psi }\left[i,1\right]\mathit{\text{fish}}\left[j\right]+{\beta }_{\psi }\left[i,2\right]\mathit{\text{perm}}\left[j\right]+{\beta }_{\psi }\left[i,3\right]{\eta }_1\left[j\right]+{\beta }_{\psi }\left[i,4\right]{\eta }_2\left[j\right]+{\beta }_{\psi }\left[i,5\right]\mathrm{\xi }\left[j\right]$$

Species vary in their detection probabilities and p may also vary between first and second visits:

$$\mathit{\text{logit}}\left(p\left[i,j,k\right]\right)={\mathrm{\alpha }}_p\left[i\right]+{\beta }_{p}k$$

where α_p is a species-specific mean and the last term represents the effect of early vs. late summer surveys.

Priors

We assumed logit-normal species responses to covariates with covariate-specific community means and variance parameters that represent among-species variability, such that:

$$\begin{array}{l}{\beta }_{\psi }\sim N\left({\mu }_{{\beta }_{\psi }},{\sigma }_{{\beta }_{\psi }}\right)\\ {\beta }_p\sim N\left({\mu }_{{\beta }_p},{\sigma }_{{\beta }_p}\right)\end{array}$$

Further, we assumed that for each species, mean detection probabilities would be logit-normally distributed around community level means:

$${\alpha }_p\sim N\left({\mu }_{{\alpha }_p},{\sigma }_{{\alpha }_p}\right)$$

Hierarchical parameters corresponding to community-level variance terms received semi-informative half-Cauchy priors that were weighted towards small values to reduce bias relative to commonly used uniform priors (Gelman 2006). We adopt vague priors for all other parameters except the loading terms for indicator variables which were constrained to be positive (e.g., increases in latent grazing intensity ξ correspond to increases in its indicators Y₁ and Y₂). Last, prior information based on previous work has entered the model in the form of included effect pathways (e.g., we assume that amphibian community composition does not affect grazing intensity).

Estimation

We used Stan, and the R package rstan to draw samples from the joint posterior distribution of all parameters (R Core Team 2014, Stan Development Team 2014a, 2014b, 2014c). Although this model could be implemented with WinBUGS, OpenBUGS, or JAGS, the simultaneous updating of all parameters via the No-U-Turn sampler in Stan results in faster convergence and more efficient sampling (Hoffman and Gelman 2014). Running three chains in parallel with 30000 iterations took about 80 minutes on a quad-core i7 laptop. Convergence was assessed using visual inspections of trace plots and the Gelman-Rubin potential scale reduction factor (Gelman and Rubin 1992, Brooks and Gelman 1998).

Model assessment

As this is a new method, we conducted a simulation analysis to ensure adequate recovery of parameter estimates across a range of known values. We simulated approximately 100 datasets with structure identical to our model, and the same amount of information (observations) present in our dataset. We then attempted to recover the known parameters by fitting the model to our simulated datasets (Gimenez et al. 2012). Any simulations that did not reach convergence at the MCMC step were discarded.

Independence assumptions were evaluated graphically using scatter plots to detect missing causal pathways (Grace et al. 2012). This revealed a positive correlation between fish presence and N (both total dissolved N and $N{H}_4^{+}$), leading to the inclusion of an additional effect of fish on N that we had not initially hypothesized. Mechanistically, this pathway may represent the joint effects of fish locking up N in their tissues, and suppressing zooplankton through predation, leading to release of phytoplankton from grazing and greater uptake of N from the water (Andersson et al. 1978, Henrikson et al. 1980).

Results

Parameter recovery

Our simulations demonstrated parameter recovery with 95% highest density posterior intervals (HDIs) including the true population level parameters over 90% of the time (Figure A1). Furthermore, we were able to recover effects of local factors (β_ψ), identifying large effects as being non-zero (Figure A2). These results increased confidence in parameter estimates for the empirical data and gave an indication of the power that we might have to detect effects of local drivers of occurrence with a dataset of comparable size.

Empirical results

Nonnative fish and pond permanence directly affected amphibian community composition, with fish exerting the most consistent and strongest effects. Nonnative fish reduced the probability of occurrence for four of five native amphibians (all species except western toads and bullfrogs; Figure 3). Species-specific effects were observed for pond permanence, which had a strong positive effect on bullfrog and red-legged frog occurrence. Shoreline vegetation, nitrogenous compounds, and cattle grazing exerted relatively weak direct effects, with all HDIs including zero. Similarly, all HDIs for indirect effects of fish (via nitrogen) and cattle (via nitrogen and shoreline vegetation) on amphibian occurrence included zero.

Figure 3.

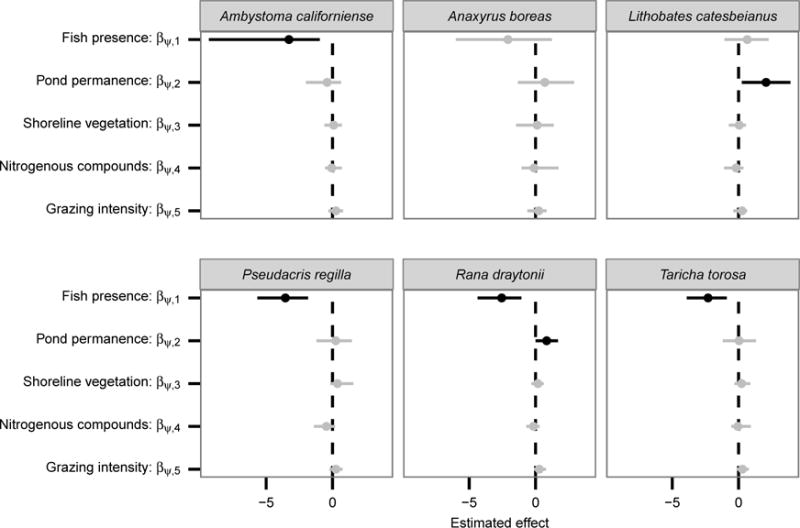
Estimated direct effects on occurrence probabilities for each species. Black corresponds to parameters for which HDIs excluded zero, and grey correpsonds to HDIs including zero

Consistent with our expectations and previous work, cattle grazing decreased shoreline vegetation (HDI: (−0.556, −0.206)) and increased nitrogenous compounds in the water column (HDI: (0.097, 0.450)). The grazing submodel combined information from cow paddy density counts and disturbance classifications to generate values of latent grazing intensity for each site (Figure 4A–B). As we expected based on field observations, many sites experience moderate to high levels of grazing, while fewer experience very low levels of grazing.

Figure 4.

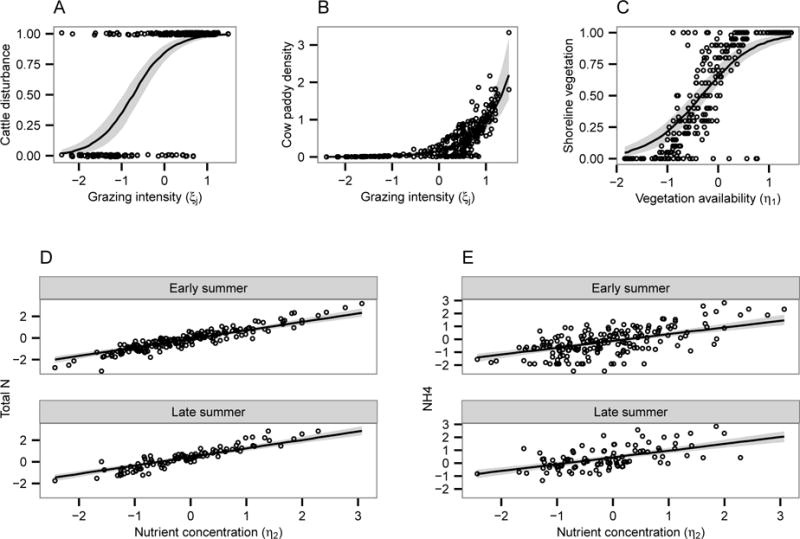
Fit of the submodels to the observed indicator variables. Shaded regions encompass the 95% HDI, with observed data shown as jittered points (x-axis values represent posterior medians).

Regionally, some species were far more variable in their distribution among parks than others. For example, although local factors tended to have minimal effects on the distribution of western toads (Figure 3), among-region variability was quite high for this species (Figure A3). In contrast, Pacific chorus frogs had low among-park variability, being nearly ubiquitous.

Most amphibian species were easier to detect during the first survey, probably due to metamorphosis occurring before or during the late-summer visit when evidence of successful breeding is no longer detectable (Figure A4). The inclusion of the visit number covariate (first vs. second) accounted for this discrepancy in the sense that species-specific covariate effects can still be recovered (Figure A2).

The shoreline vegetation submodel performed well, capturing the fact that some shorelines were either devoid or completely covered by vegetation, with variability between these two extremes (Figure 4C). The latent N variable and observed log-transformed total dissolved N and $N{H}_4^{+}$ concentrations showed good fit, with increasing N concentrations in late summer compared to early summer (Figure 4D–E). Graphical checks of independence assertions indicated no further causal pathways for inclusion (Figure A5).

Discussion

Our approach demonstrates the integration of SEM with occupancy modeling using a large-scale survey of pond breeding amphibians to gain a better understanding of the drivers of community composition. Importantly, this approach allows for explicit differentiation between observed data and underlying processes, accounting for a variety of measurement error models including the imperfect measurement process that gives rise to species detection data. We also embedded other types of observation models to account for more complicated likelihood functions, including the zero-one inflated beta distribution that was used to model observations of shoreline vegetation cover. With this approach, latent ecological processes hypothesized to drive occurrence can be explicitly represented and their direct and indirect consequences formally evaluated.

The potential advantages of integrating occupancy and structural equation frameworks include: 1) developing more mechanistic approaches for understanding species distributions influenced by simultaneous related processes; 2) inheriting a formal method for evaluating potential outcomes that would result from management interventions; and 3) clarifying hypotheses by requiring that assumptions be represented in a formal causal model. Unlike purely associational methods, the causal assumptions embedded within structural equation models facilitate unique predictions that can be used to answer applied management questions.

Well-specified SEMs yield unique management insights based on “do” operators, which can estimate the consequences of targeted interventions from effect decompositions (Pearl 1998). “Do” operators could be used to predict changes in occupancy following a management intervention that reduces grazing intensity or removes fish. Indeed, this was one of the original arguments for the development of structural equation models in the mid-20th century (Marschak 1950, Koopmans 1953). Causal inferences drawn from such analyses can be no better than the validity of the assumptions used to construct the model, however. Processes that drive the species distributions can be represented best when there is substantive knowledge to construct such models. This brings up two issues: how mechanistic is “mechanistic enough”, and how valid are the assumed causal relationships? First, it would be unreasonable to expect to construct an infinitely accurate and specific causal model for the occurrence of any species (Shipley 2002). However, an adequate model may capture the most important drivers of occurrence and provide “good-enough” predictions for management interventions. This point underlines the role of interventional tests of such models - if the true outcome of management intervention deviates from anticipated effects, then the validity of the underlying causal model must be questioned.

Although not a substitute for interventions, tests of model fit to observational data can also be useful for identifying potentially missing pathways based on independence relationships among variables in the causal network. Here, we employed graphical checks of independence assumptions for observed variables, but better methods could be developed. Information theoretic and d-separation tests exist for path analytic models, and other indices of model fit have long been used for traditional linear structural equation models that assume multivariate normality of errors (Grace 2006, Shipley 2013). However, methods for evaluating occupancy model fit are still relatively new and mostly rely on out-of-sample data (Zipkin et al. 2012) or bootstrapping (MacKenzie and Bailey 2004). Developing methods to evaluate the fit of hierarchical occupancy-type structural equation models with non-normal indicators and binary, partially observed latent variables is a non-trivial task, but one that would increase the utility of this method. Advances in the study of probabilistic graphical models may provide solutions, but such advances are only just beginning to be applied by ecologists (Koller and Friedman 2009, Grace et al. 2012). Aside from d-separation tests, management experiments provide another way to test the predictive power of these types of models.

Management implications

Our results have direct relevance to the management of threatened amphibian populations within lowland wetlands in California, particularly when land managers are faced with multiple potential challenges simultaneously. Livestock grazing, which is common throughout the western United States (Fleischner 1994), has been a topic of uncertainty with regard to amphibian conservation. While several studies indicate negative overall effects of grazing on populations of specific amphibian species (Knutson et al. 2004, Schmutzer et al. 2008), others indicate the potential for positive effects of grazing on diversity and the perseverance of native communities (Marty 2005).

Based on our analysis, livestock grazing in the Bay Area of California had minimal effects on the occurrence of six amphibian species, two of which are native species of conservation concern. This finding suggests that current grazing levels employed on these parks may be compatible with management aimed at conserving threatened amphibians. However, we did not explore the effects of grazing on amphibian abundance or temporal dynamics such as persistence and colonization. Such approaches may reveal effects of grazing that were not seen in this study.

Most ponds in this data set were initially constructed to serve as watering sites for livestock. Because most original natural wetlands in California have been destroyed for agriculture and development, particularly in the Central Valley (Garone 2011), such livestock ponds may now serve as vital habitat refuges for declining species. This trend is particularly important for the California tiger salamander and California red-legged frog, which are the focus of considerable conservation efforts due largely to habitat destruction (Lannoo 2005).

In sharp contrast to the minimal effects of grazing, we found strong negative effects of nonnative fish on native amphibian occupancy for all species except western toads and nonnative bullfrogs. This finding supports a large body of research showing that native pond-breeding amphibians that lack evolutionary history with fishes are unlikely to persist once predatory fish have been introduced to a breeding site. The most common fish species at our field sites were mosquitofish and centrarchids (bass, bluegill and other sunfish), which are native to the eastern United States. These species likely prevent amphibian reproduction through direct predation on multiple life stages of native amphibians. The lack of an effect on toads is consistent with prior work showing that toxicity and schooling behavior of toad larvae provides resistance to predation by fish (Kruse and Stone 1984, Welsh et al. 2006). Bullfrogs, which require permanent water bodies to complete metamorphosis, have co-evolved with fish in their native range, are unpalatable, and are not strongly affected by fish presence (Walters 1975, Kruse and Francis 1977, Szuroczki and Richardson 2011).

Taken together, our results indicate that land management strategies should prioritize removal of nonnative fish rather than limitation of livestock grazing. Fish removal via pond draining has been shown to be effective in restoring populations of threatened amphibians within the study region (Alvarez et al. 2003). Considering the needs of interests groups involved and the prevalence of grazing, this strategy is perhaps more feasible than dramatically limiting access of livestock to ponds, which may have unintended side effects including elimination of pond breeding habitat due to overgrowth by vegetation. While more research is needed to evaluate both temporal effects of grazing, and how grazing affects amphibian abundance, our analysis indicates that fish introductions have more severe impacts than cattle grazing.

Conclusion

Structural equation modeling provides a framework to evaluate why species occur in some areas and not others, allowing a more direct confrontation of some of the most fundamental questions in ecology. Occupancy modeling provides a solution to the problem of imperfect detection and can account for many different processes giving rise to detection data. Combining these approaches provides a means to evaluate complex causal processes driving occurrence while accounting for false-absences in empirical occurrence data. This framework potentially facilitates deeper insights into biological processes, making a clear separation between imperfectly observed data and underlying states. From a pragmatic standpoint, it is clearly advantageous to be able to represent both direct and indirect determinants of species occurrence rather than being limited to treating covariates as being independent. This approach also provides the practical advantage of inheriting a suite of methods to anticipate the effects of management interventions (“do” operators), and to account for many different sampling schemes in the occupancy modeling literature. Future extensions of this method could deepen connections between SEM and other classes of occupancy models, including dynamic multi-year occupancy models, models of abundance such as N-mixture models, Dail-Madsen models, their multi-species extensions, and spatial models (Royle 2004, Royle and Kéry 2007, Dail and Madsen 2011, Dorazio and Connor 2014, Lamb et al. 2014).

The full value of this approach may be most apparent, and perhaps palatable to individuals unfamiliar with SEM, when coupled with controlled field experiments, where the validity of the underlying causal model may be tested directly. Compared to fields like sociology and economics, ecology as a field is perhaps in a unique position to reap benefits from SEM because it is both complex and relatively amenable to experimental manipulation.

Appendix A

Supplemental figures (1–5) containing simulation results, among-region standard deviations, detection probabilities, and graphical independence checks.