The number of seizures needed in the EMU

Summary

Objective

The purpose of this study was to develop a quantitative framework to estimate the likelihood of multifocal epilepsy based on the number of unifocal seizures observed in the epilepsy monitoring unit (EMU).

Methods

Patient records from the EMU at Massachusetts General Hospital (MGH) from 2012 to 2014 were assessed for the presence of multifocal seizures as well the presence of multifocal interictal discharges and multifocal structural imaging abnormalities during the course of the EMU admission. Risk factors for multifocal seizures were assessed using sensitivity and specificity analysis. A Kaplan-Meier survival analysis was used to estimate the risk of multifocal epilepsy for a given number of consecutive seizures. To overcome the limits of the Kaplan-Meier analysis, a parametric survival function was fit to the EMU subjects with multifocal seizures and this was used to develop a Bayesian model to estimate the risk of multifocal seizures during an EMU admission.

Results

Multifocal interictal discharges were a significant predictor of multifocal seizures within an EMU admission with a p < 0.01, albeit with only modest sensitivity 0.74 and specificity 0.69. Multifocal potentially epileptogenic lesions on MRI were not a significant predictor p = 0.44. Kaplan-Meier analysis was limited by wide confidence intervals secondary to significant patient dropout and concern for informative censoring. The Bayesian framework provided estimates for the number of unifocal seizures needed to predict absence of multifocal seizures. To achieve 90% confidence for the absence of multifocal seizure, three seizures are needed when the pretest probability for multifocal epilepsy is 20%, seven seizures for a pretest probability of 50%, and nine seizures for a pretest probability of 80%.

Significance

These results provide a framework to assist clinicians in determining the utility of trying to capture a specific number of seizures in EMU evaluations of candidates for epilepsy surgery.

Patients are admitted to the epilepsy monitoring unit (EMU) for two primary indications: to confirm the diagnosis of epilepsy and/or to localize the ictal focus in anticipation of epilepsy surgery. In the first instance the number of events needed to fulfill the goal of admission is clear; the patient's events that are concerning for epilepsy need to be captured at least once.¹ For the presurgical admissions the number of seizures needed is less obvious. First the primary seizure focus needs to be characterized by electrographic signature and semiology. It is often helpful to capture several seizures to ensure consistency in the semiology and electroencephalography (EEG) pattern. The other main consideration is the exclusion of multifocal epilepsy. The number of seizures needed for this requirement is less certain.

Intuitively, certain factors make some patients more likely to have multifocal epilepsy. A review of the epilepsy surgery literature suggests that risk factors include multifocal lesions on magnetic resonance imaging (MRI) and multifocal interictal discharges.² These factors should increase the pretest probability of finding multifocal epilepsy during an EMU admission. It follows that patients with these risk factors might be required to have more seizures from a single focus before excluding the possibility of multifocal epilepsy. Although rules of thumb have been suggested such as capturing a minimum of five seizures,³ or four seizures, are needed for patients with bilateral epileptiform interictal discharges a rigorous justification has been lacking.⁴ The present study is intended to provide a principled guide to selecting the target number of seizures, while taking into account the pretest probabilities of multifocal epilepsy.

The EMU population at Massachusetts General Hospital (MGH) was investigated to address this question via several complementary methods. First the population was assessed for risk factors of multifocal epilepsy. Then a Kaplan-Meier survival analysis was performed to assess the proportion of patients with multifocal epilepsy that has not declared itself after a given number of seizures in the EMU. Ultimately a Bayesian framework was developed to define a likelihood function,⁵ which provides a means to augment the clinician's intuition about the question “How many more seizures do we need?”

Methods

Patient data collection

After institutional review board (IRB) approval, the MGH EMU (2012–2014) database was queried for all patients >18 years of age who were admitted to the EMU and had a confirmed epileptic seizure during admission (n = 117). Patients with epileptic encephalopathies were excluded. Imaging and EEG results were collected for risk factor assessment. The EMU admission records were assessed for number of seizures and EEG localization of seizures. The patient was determined to have multifocal epilepsy confirmed by EMU admission if scalp EEG ictal onsets occurred in at least two distinct quadrants. This study is intended toward initial phase I monitoring so the study population was limited to patients that did not have intracranial monitoring. Imaging reports, EEG/EMU reports, and epilepsy surgery conferences notes were assessed for presence of potentially epileptogenic lesions on structural imaging and for the presence and distribution of interictal discharges on EEG before and during EMU admission.

Risk factor assessment

Fisher's exact test was used for comparison of the proportion of patients with multifocal interictal discharges and multifocal imaging within the groups of patients with unifocal vs multifocal seizures. The sensitivity, specificity, positive predictive value, and negative predicative values of candidate risk factors were calculated with 95% Wilson confidence intervals.⁶

Survival analysis

A Kaplan-Meier survival analysis was performed using number of seizures as the independent variable, and the dependent variable is the proportion of patients with multifocal epilepsy that has yet to be uncovered after a specified number of seizures.⁷ Survival analysis considers subject dropout to account for patients with multifocal epilepsy that went undiscovered because of the finite nature of an EMU admission. The 95% confidence intervals were created using the Greenwood estimator of variance.⁸ The analysis was undertaken for four populations, including the entire EMU cohort, subjects with multifocal interictal discharges, subjects with multifocal imaging, and subjects without either of these risk factors.

Bayesian analysis

Survival analysis is limited because a minority of patients has a large number of seizures during their EMU admission. It is difficult to estimate the true proportion of multifocal epilepsy if only have a few seizures are captured during their EMU admission. Although the Kaplan-Meier technique accounts for subject dropout, if there is high subject dropout, the confidence intervals become wider as the number of seizures increase and an even more insidious bias can be introduced that is not reflected in the confidence intervals. Kaplan-Meier analysis requires the critical assumption of noninformative censoring. This assumption becomes more relevant as subject dropout increases. In this case the assumption of noninformative censoring means that patients that leave the EMU after a specified number of seizures have the same chance of having a multifocal seizure as the patient who is required to stay in the EMU for more seizures. This would imply that a patient who leaves the EMU after 3 seizures is not different from the patient who leaves after 15 seizures. For a lot of reasons this may not be true. For one thing, if the physician has an underlying assumption of multifocal epilepsy they may require the patient to stay longer in the EMU, or if the patient has an inherently more aggressive epileptic process and has a significant number of seizures in a short period of time, this group of patients may also be more prone to multifocal epilepsy. If there is only minor patient dropout, violations of noninformative censoring typically do not have a large effect, but in the case of significant dropout it introduces bias.⁹ This bias is difficult to overcome in either a retrospective or prospective manner for this patient population. There are inherent limitations because EMU admissions are constrained by time, financial concerns, and patient willingness.

A method to overcome this difficulty is to use Bayes' Formula.

$$Pr(\mathrm{H}1|\mathrm{K})=\frac{Pr(\mathrm{H}1)Pr(\mathrm{K}|\mathrm{H}1)}{Pr(\mathrm{H}1)Pr(\mathrm{K}|\mathrm{H}1)+Pr(\mathrm{H}0)Pr(\mathrm{K}|\mathrm{H}0)}$$

In this formula, H0 represents the hypothesis of unifocal epilepsy and H1 is the probability of multifocal epilepsy. K is the number of unifocal seizures, so Pr(H1/K) is the probability of multifocal epilepsy given K number of unifocal seizures. Pr(H1) is the pretest probability of multifocal epilepsy. This number is between 0 and 1 and is estimated by the clinician based on the patient's likelihood of multifocal epilepsy. This estimate eliminates the need to know exactly the true proportion of patients with multifocal epilepsy. Instead the initial estimate is modified by the new information gained during the test, in this case the number of unifocal seizures. All of the quantities in the formula are known except Pr(K/H1). This is the probability of having K unifocal seizures given the knowledge of multifocal epilepsy. This probability can be modeled as a function with the dependent variable being the probability of having multifocal epilepsy that has not be discovered after a certain number of seizures with the independent variable being the number of unifocal seizures. This function was defined by fitting the distribution of seizures from the 31 subjects from MGH EMU that had confirmed multifocal epilepsy. This patient population is not subject to concerns of censorship, because all members of this group had multifocal seizures. It is assumed that this is a representative sample of multifocal epilepsy that would present to a typical EMU. The distribution of seizures for the 31 subjects was fit to common distributions and evaluated to minimize the Akaike information criterion (AIC) and by visual inspection.¹⁰ The function was then used in Bayes' formula to calculate the number of unifocal seizures for various pretest probabilities of multifocal epilepsy. A complementary method using a Monte-Carlo simulation of 10,000 EMU admissions based on the distribution of seizures from the MGH EMU was used to test the reliability of the results. The methods for this simulation are found in Data S1. Matlab with Statistics Toolbox Release 2013b (MathWorks, Natick, MA, U.S.A.) was used for all statistical analysis and modeling.

Results

Population/demographics

One hundred seventeen subjects between 2012 and 2014 met the inclusion criteria of age >18 years, absence of an epileptic encephalopathy, and at least one electrographic seizure. Median age of the population was 41 years (interquartile range [IQR] 27–53). The population was 45.3% women. The median number of seizures during EMU admission was 6 (IQR 3–10). Multifocal epilepsy was found in 31 subjects (26.5%). For patients with multifocal epilepsy confirmed in the EMU, the median age for this population was 42 (IQR 32–55), the median number of seizures was 9 (IQR 5.5–11.5), and the median proportion of seizures from the dominant focus was 0.67 (IQR 0.60–0.78). Fifty subjects had multifocal interictal discharges. Twenty-eight subjects had multiple potentially epileptogenic lesions on structural imaging. Fourteen had both multifocal interictal discharges and multifocal imaging. Fifty-four subjects had neither multifocal imaging nor multifocal interictal discharges. The breakdown of the proportion of patients with multifocal epilepsy discovered in the EMU by risk is listed in Table 1.

Table 1. Risk factors for multifocal seizures.

Risk factor	Multifocal EMU		Unifocal EMU	p-Value
EEG (multifocal)	0.74 (0.57–0.86)		0.31 (0.22–0.41)	<0.01
MRI (multifocal)	0.29 (0.16–0.47)		0.22 (0.15–0.32)	0.44
Both EEG/MRI	0.25 (0.14–0.42)		0.07 (0.03–0.14)	<0.01
Predict multifocal	Sensitivity	Specificity	PPV	NPV
EEG (multifocal)	0.74 (0.54–0.86)	0.69 (0.59–0.78)	0.46 (0.33–0.60)	0.88 (0.78–0.94)
MRI (multifocal)	0.29 (0.16–0.47)	0.78 (0.68–0.85)	0.32 (0.18–0.51)	0.76 (0.65–0.85)
Both EEG/MRI	0.25 (0.14–0.42)	0.93 (0.86–0.97)	0.56 (0.32–0.78)	0.78 (0.69–0.85)

PPV positive predictive value, NPV, negative predictive value. Bolded text represents p-value < 0.05.

95% Confidence intervals provided in parenthesis.

Kaplan-Meier survival analysis

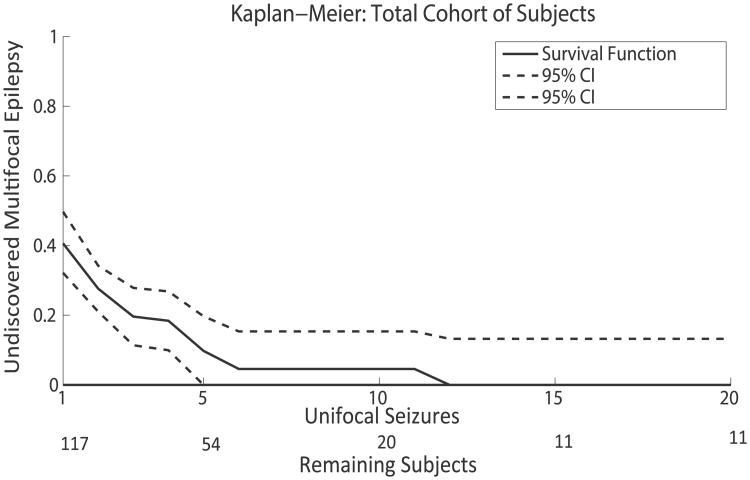
The Kaplan-Meier analysis was run on four populations: total cohort, multifocal interictal discharges, multifocal imaging, and absence of both multifocal imaging and multifocal interictal discharges. Figure 1 is a Kaplan-Meier estimate of the survival function for the total cohort of subjects. Table 2 provides specific data points for the Kaplan-Meier analysis including subgroups. Even in the total cohort of patients there are a limited number of subjects with a large number of seizures, and in subgroups this problem is more acute. The dropout of subjects is apparent in Figure 1 and as well as in the wide confidence intervals in all the subgroups in Table 2.

Figure 1.

Kaplan-Meier estimate of the survival function for all 117 subjects. Data presented with 95% confidence intervals (CIs). The number of subjects available at each seizure level is presented under the x-axis over the heading Remaining Subjects.

Epilepsia © ILAE

Table 2. Proportion of subjects with multifocal epilepsy not discovered after a specific number of seizures based on a Kaplan-Meier analysis.

Number of seizures	Total cohort	Multifocal interictals	Multifocal imaging	No risk factors
3	0.19 (0.11–0.28)	0.29 (0.15–0.43)	0.15 (0.10–0.33)	0.11 (0.01–0.22)
5	0.10 (0.00–0.20)	0.11 (0.00–0.27)	0.05 (0.00–0.25)	0.08 (0.00–0.20)
10	0.05 (0.00–0.15)	0.00 (0.00–0.17)	0.00 (0.00–0.21)	0.08 (0.00–0.20)
15	0.00 (0.00–0.13)	0.00 (0.00–0.17)	0.00 (0.00–0.21)	0.00 (0.00–0.19)

95% Confidence intervals are in parenthesis.

Bayes' model

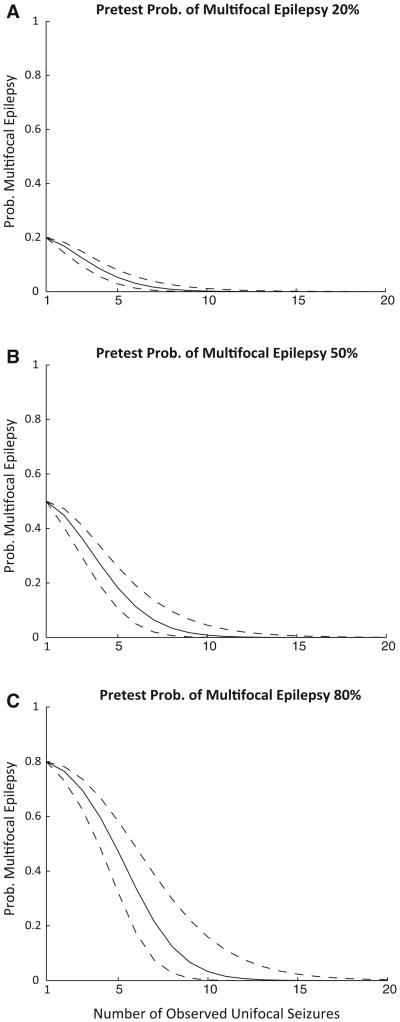
A Weibull distribution was selected after evaluation of the common parametric survival distributions using visual inspection and minimization of AIC.¹¹ Potentially relevant pretest probabilities for multifocal epilepsy including 20%, 50%, and 80% are displayed graphically in Figure 2, a graph of the posttest probability of multifocal epilepsy as a function of number of unifocal seizures. Table 3 provides a quick reference for the number of seizures needed for specific confidence levels. To calculate posttest probabilities from pretest probabilities other than those listed, a Matlab function is provided as Data S2. A Monte-Carlo simulation was developed as complementary assessment method. The results are similar to the Weibull distribution fit of the multifocal epilepsy population and can be found in Data S1.

Figure 2.

The probability of multifocal epilepsy for a given number of unifocal seizures based on the results of the Bayesian analysis with a parametric survival function for subjects with multifocal epilepsy. Pretest probabilities of multifocal epilepsy include 20% (A), 50% (B), and 80% (C). The 95% percent confidence intervals are presented as dashed lines.

Epilepsia © ILAE

Table 3. Risk of multifocal epilepsy from Bayesian analysis.

No. of seizures for confidence level	Pretest probability
	80%	50%	20%
>0.80	8 (6–10)	5 (4–6)	1
>0.90	9 (7–12)	7 (6–8)	4 (3–5)
>0.95	10 (8–13)	8 (6–10)	5 (5–7)

The number of seizures needed to achieve a given confidence level of unifocal epilepsy for different pretest probabilities of multifocal epilepsy. The 95% confidence intervals for number of seizures needed are presented in parenthesis.

Discussion

The number of seizures needed in the EMU has not been investigated extensively in the epilepsy literature, but recommendations have been made for the number of seizures needed in presurgical evaluations varying from 2 to 5.^3,12 The purpose of this investigation is not to provide prescriptive numbers of seizures needed for each EMU patient, but to provide a quantitative framework to help guide clinical intuition.

There are concerns beyond excluding multifocal epilepsy in deciding the number of seizures captured during an EMU admission. Factors including payor and patient limitations often limit the EMU admission length. Nonetheless an estimate of the confidence that a patient's risk of multifocal seizures remains an important consideration for patient management.

Scalp EEG has inherent limitations of spatial resolution and cerebral coverage that ultimately limits its utility in defining the ictal onset zone. Two nearby epileptogenic foci may have similar surface EEG patterns if they are within the 2–10 cm resolution of scalp EEG. Similarly, a single epileptogenic focus can have varying patterns of early propagation that can appear multifocal on surface EEG. Despite these limitations, scalp EEG EMU recordings provide critical information in the early stages of an epilepsy surgery work-up and help define the areas in question for phase II monitoring. One of the pernicious questions in a presurgical EMU admission is “How many seizures do we need to capture?”

This study considers several ways to approach this question. First, two potential risk factors for multifocal epilepsy were assessed: multifocal interictal and multifocal structural imaging. Multifocal interictal was confirmed as a risk factor, but multifocal imaging was not. The inherent limitation in this methodology is that surely some patients with multifocal epilepsy were discharged from the EMU before having seizures from two distinct foci, thus limiting the accuracy of this finding. To address this concern, a Kaplan-Meier survival analysis was used to account for patient dropout, although important concerns remain with this approach. A principal assumption of this methodology is that the censoring is not informative. That means that the subjects that drop out of the study have the same probability of going on to have multifocal epilepsy as those that stay in the EMU. This assumption may not hold true. Often patients that present a particular concern for multifocal epilepsy are required to stay in the EMU longer, which would violate this assumption. Also there is concern that patients with relatively more frequent seizures may also be more likely to have multifocal epilepsy; this would also violate the assumption. The necessarily finite timeframe of an EMU admission makes a direct clinical assessment of this matter cumbersome.

To address the shortcomings of the Kaplan-Meier analysis, another approach was employed. The rate at which subjects with multifocal epilepsy declare themselves was assessed empirically using the MGH EMU database. This distribution was then fit to a Weibull parametric survival function. By using Bayes' theorem, the clinical suspicion of multifocal epilepsy is incorporated into the calculation, and the Weibull function is used to define the rate at which patients with multifocal epilepsy declare themselves. Using the extensive epilepsy surgical literature regarding risk factors of poor surgical outcomes, presumably some from multifocal epilepsy as well as other sources of information such as the relevance of interictal discharges in predicting multifocal epilepsy found in this study allow for a reasonable estimate of a pretest probability. For example, if a patient is found to have unilateral temporal interictal discharges and concordant magnetic resonance imaging (MRI) evidence of hippocampal sclerosis, a reasonable pretest probability of multifocal seizures is 20%.^13,14 If a patient has bilateral hippocampal changes, the postsurgical data would suggest the estimate would be closer to 50%.^2,15,16 Similarly, if multifocal interictal discharges are apparent, several studies have placed surgical failure near 50%.^17–19 In the current study, subjects with multifocal interictal discharges had a 54% chance of unifocal epilepsy during the EMU admission and a 68% chance of unifocal epilepsy with multifocal imaging. These numbers likely underestimate the degree to which multifocal discharges correspond to multifocal epilepsy, as some cases of multifocal epilepsy surely were not discovered in the EMU, but are still a reasonable first guess that is refined by Bayes' equation. If a strong concern for multifocal epilepsy exists, the pretest probability could be estimated at even higher than 50%. This study provides specific numbers for pretest probabilities of multifocal epilepsy at 20%, 50%, and 80%; a Matlab function is available in the Data S2 that allows for other pretest probabilities.

This study utilizes a Bayesian approach, which requires the estimation of a pretest probability. Although some find that estimating such a number seems unscientific and subject to inherent bias, the counter argument is that avoiding this pretest estimate fails to take into account all pretest information, which imposes its own kind of bias. There are several reviews that discuss the strengths and weakness of Bayesian approach to classic clinical trials.^20,21 The weaknesses of standard risk factor analysis for this problem were discussed earlier, but primarily there is a lack of a gold standard for the proportion of multifocal epilepsy. These concerns could be somewhat addressed by a prospective cohort study, but practical considerations still limit the amount of time any one patient should be required to stay in the EMU. An alternative standard for defining multifocal epilepsy would be surgical failures that have seizure-onset zones in an area distinct from the prior surgical target. This standard has its own concerns in that it is subject to selection bias and has a lower power with many fewer subjects. Instead in this model the subjects with confirmed multifocality were used as a representative sample of the larger population of true multifocal epilepsy, and Bayes' theorem was then used to estimate the chance that the specific patient has multifocal epilepsy.

Another important consideration is if the subjects used in this study represent a generalizable population of patients with multifocal epilepsy. Patients with confirmed multifocal epilepsy from the MGH EMU were used to fit the parametric survival function that is used as an estimate for all patients with multifocal epilepsy. This generalization would not hold true if the patient population differed significantly from the MGH population with regard to the distribution of seizures for patients that have multifocal epilepsy. For this study to be generalizable to populations other than the MGH cohort, it must be inferred that patients with multifocal epilepsy have a similar proportion of their seizures from the nondominant focus. Populations where this assumption may be violated include the neonatal population where the distributions of seizures can change dramatically, with new seizure foci arising after numerous unifocal seizures. It was because of this concern that pediatric populations were excluded from this study, and it is likely less of a concern for adult populations were the causes and course of epilepsy are less protean, and the findings of this study are more applicable. In centers where the complexity and age of patients is substantially different from our center, the survival function could be different enough to affect the applicability of these results to their center's population. This possibility can be addressed in future, multicenter studies aimed at replicating and extending the findings herein. Alternatively, or in addition, other centers may wish to consider replicating this study in their own population and develop their own lab standard. The results of the study were designed to fit the common clinical practice of using the number of seizures in the EMU as a determinate in length of stay and provides a useful framework to augment clinical intuition on the cost(risk)/benefit of waiting to capture more seizures.

Another concern is the evolving experience from the responsive neurostimulation device that suggests there may be patients with bitemporal epilepsy that have fluctuations in the dominant seizure focus over the course of months. The paradigm developed here would be insensitive to these patients because it is based on the time scale of the typical EMU admission, which is days to at most weeks and would not capture the long-scale evolution that may exist in these patients. The current study is intended to predict how likely a multifocal seizure would occur if the patient were to stay in the EMU longer and is ultimately not capable of predicting long term trends. It is unclear how any EMU admissions could capture multifocal seizures that fluctuate over the course of months, and other techniques would have to be considered.

There are several readily apparent clinical applications for these data. Not only can they serve as a rough guide for the number of seizures needed for specific patients, they can also serve as a guide for when to abort an EMU admission. Take for example the common EMU scenario. A patient has been in the EMU for 10 days with likely right temporal lobe epilepsy by clinical criteria: clear right temporal interictals, right mesial temporal sclerosis on MRI, and three seizures originating from the right temporal region. The chance of unifocality by this study is about 90%; to change that to 95% at least one more seizure is needed. The length of time in the EMU necessary to capture another seizure may not warrant the minimal change in probability. A different scenario would be a patient with tuberous sclerosis and several areas of interictals and multiple semiologies. The pretest probability of unifocal epilepsy is likely on the order of 20%. In this case, going from two unifocal seizures to eight would show a dramatic difference in the posttest probability of unifocal epilepsy and might be worth the wait.

Supplementary Material

matlab supplemental

Data S1. Method and Results of Monte-Carlo Simulation of EMU Admissions.

Data S2. Matlab function to generate a posterior probability of multifocal seizures from an inputed pretest probability.

Key Points.

1. Multifocal interictal discharges predict multifocal seizures during an EMU admission with a sensitivity of 0.74 and specificity of 0.69.

2. Kaplan-Meier analysis provides estimates of the proportion of patients with undiscovered multifocal epilepsy but is limited by high subject dropout.

3. The numbers of unifocal seizures needed for a 90% confidence of unifocal epilepsy for pretest probabilities of multifocal epilepsy of 20%, 50%, and 80% are 3, 7, and 9, respectively.

Biography

Dr. Aaron F Struck is an epilepsy fellow at Massachusetts General Hospital.