Current State of Theoretical and Experimental Studies of the Voltage-Dependent Anion Channel (VDAC)

Abstract

Voltage-dependent anion channel (VDAC), the major channel of the mitochondrial outer membrane provides a controlled pathway for respiratory metabolites in and out of the mitochondria. In spite of the wealth of experimental data from structural, biochemical, and biophysical investigations, the exact mechanisms governing selective ion and metabolite transport, especially the role of titratable charged residues and interactions with soluble cytosolic proteins, remain hotly debated in the field. The computational advances hold a promise to provide a much sought-after solution to many of the scientific disputes around solute and ion transport through VDAC and hence, across the mitochondrial outer membrane. In this review, we examine how Molecular Dynamics, Free Energy, and Brownian Dynamics simulations of the large β-barrel channel, VDAC, advanced our understanding. We will provide a short overview of non-conventional techniques and also discuss examples of how the modeling excursions into VDAC biophysics prospectively aid experimental efforts.

1. Introduction

There is a significant progress in our understanding of ion channel transport properties, ability to distinguish between ions, and gating on a structural level [1–3]. However, this is mostly true for ion channels from the excitable cells, such as K⁺, Na⁺, Cl⁻ channels. Our understanding of molecular mechanisms of functioning of large, or so-called, transport or “nutrient” channels, such as mitochondrial channels, general and specific bacterial porins, and different toxin channels, is far behind the progress in the field of “conventional” highly-selective ion channels. Specifically, mitochondrial channels compose a separate class of channels characterized by unique properties that distinguish them from other channels, including evolutionary related bacterial porins [4, 5]. Mitochondrial channels are directly involved in regulation of the normal function of mitochondria and in metabolic changes in response to environmental challenges and different kinds of stress, such as apoptosis [4–9].

One of the most studied mitochondrial channels is the Voltage-Dependent Anion Channel (VDAC) [6, 8, 10–13]. VDAC serves as a major pathway for metabolites exchange between the cytosol and mitochondria and thus, controls a significant portion of the outer membrane permeability [6, 8, 10, 11, 13, 14]. It also is the most abundant protein in the mitochondrial outer membrane (MOM) and is shown to be involved in a wide variety of mitochondria-associated pathologies from various forms of cancer to neurodegeneration [14]. Therefore, it is not surprising that VDAC has emerged lately as a promising pharmacological target [15].

Small ions, such as Ca ²⁺, Na⁺, K⁺, Cl⁻, or OH⁻, and water soluble mitochondrial metabolites of a relatively high molecular weight, such as ATP, ADP, pyruvate, succinate, and inorganic phosphate, all cross MOM through one pathway, the VDAC. Therefore, determination of the molecular basis of VDAC’s ion selectivity, ion and metabolites permeability, and regulation is crucial to understanding the function and physiological role of this important mitochondrial channel.

In this review, we will focus on the main developments in the quantitative description of VDAC structure-function relationships driven by the recently solved structures, novel and existing experimental techniques as well as insights provided by computational experiments. Rapid development of better sampling algorithms [1, 2, 16–23], powerful hardware solutions (ANTON simulations) [24–26], protein-protein docking schemes [27–32], post-processing techniques for extraction of thermodynamic and kinetic information from Molecular Dynamics (MD) simulations [33–38] together with analytical approaches [39–43] contributed greatly to the intimate coupling between functional and structural information available for VDAC channel, leading to a refined picture of the mitochondrial functioning. Keeping with the focus of this special issue on the computational techniques applied to outstanding problems of the biomembrane transport, we will describe necessary details of novel theoretical methods in corresponding sections of our review to provide reader with the essential background information. Computational techniques not only complemented experimental observations but also led to a-priori identification of the binding sites for ATP in VDAC, thus connecting existing structures (both NMR and X-ray) [44–47] to the long-standing proposition of VDAC’s crucial role in providing and regulating metabolite transport in and out of mitochondria. We will conclude our review with a discussion of the unresolved issues such as gating mechanisms where experiments and simulations working together are expected to move the field forward.

2. VDAC Structure and Permeation Properties

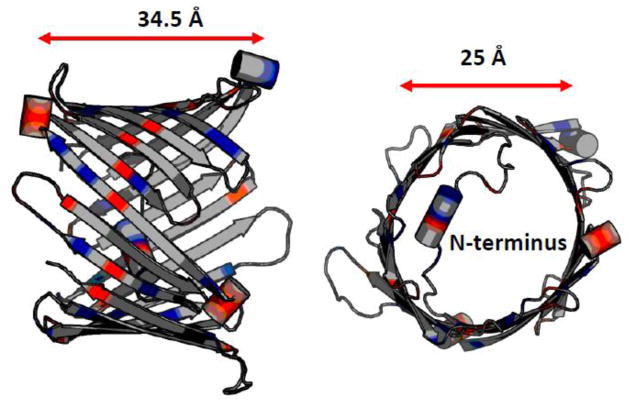
The first available model of VDAC was proposed by Colombini and co-workers and was primarily deduced from the extensive electrophysiological studies of VDAC in combination with point-directed mutagenesis [48–51]. According to this now-called “functional” model, VDAC pore is formed by 13 β-strands and one transmembrane α-helix. Later, the 3D structure of VDAC1, the most abundant isoform among three mammalian VDAC isoforms [13], was determined using solution nuclear magnetic resonance (NMR) and x-ray crystallographic methods (see Figure 1). Structural studies revealed that both mammalian VDAC1 and zebra fish VDAC2 (the latest solved structure) form βbarrels composed of 19 β-strands with the α-helix-break-α-helix N-terminus located inside the pore [45, 46, 52, 53]. Although in both models VDAC adopts β-barrels of similar dimensions of ~ 2.7 nm in diameter and the height of ~ 3 nm [46] and displays similar charge distributions, the “true” model of functional VDAC is still the subject of ongoing debates [44, 54]. The fact that most of the available electrophysiological data could be explained by both models makes this dilemma even more problematic.

Figure 1.

There are three VDAC isoforms in mammals encoded by three different genes, VDAC1, 2, and 3 [13, 55, 56] with >70% of sequence homology. All three isoforms are expressed in most tissues and could substitute each other in maintaining mitochondrial functions [57]. They also have specific indispensable roles in cell function. VDAC1 is the most abundant isoform among three and obviously, is the most characterized, biochemically, functionally, and structurally and therefore, all data described in this review are referred to VDAC1. Recently, VDAC2 has started to get more attention of the researches because of this only isoform is appeared to be lethal for mice embryos and only VDAC2 is required for mitochondrial Bak/tBid - induced apoptosis [58]. In a contrast, VDAC1 or 3 deficient mice are viable but characterized with impaired mitochondrial energetics [56, 59]. The major difference between mammalian VDAC2 and 1 is a small 11-amino acids extension of the N-terminus of VDAC2, but the latest study showed that this difference [53] is not account for a specific role of VDAC2 in import of Bak to mitochondria in apoptosis [60]. The only available so far structural data on VDAC2 have been obtained for zebra fish VDAC2 (zfVDAC2) which shares >90% of homology with mammalian VDAC2 and lacks the N-terminal extension. Abramson and co-authors have found that zfVDAC2 forms 19 β-strands β-barrel with N-terminus located inside the pore very similar to mammalian or human VDAC1 with most difference found in alignments of the cytoplasmic loops connecting β-strands 1 and 2 or 5 and 6. In consistence with structural study (Schredelseker et al, 2014), Hajnoczky group[60] demonstrated that zfVDAC2 substitutes mammalian VDAC2 in inducing MOM permeabilization in Bak/tBid – induced apoptosis. Thus, both studies structural [53] and physiological[61] agree on that zfVDAC2 is a good model for mammalian VDAC2. More structural, computational, and biophysical studies are needed to understand physiological importance and distinctiveness of VDAC2 among other isoforms.

Ion channel reconstitution is so far the best available method for direct functional studies of organelle channels, including mitochondrial VDAC. When reconstituted into planar lipid membranes VDAC forms large, 4 nS (in 1 M KCl) channels, permeable to non-charged polymers up to a few kDa [62–64] and to ATP [65, 66]. The characteristic and conserved property of VDAC channels reconstituted into lipid bilayers is voltage gating [63, 67]. Under applied voltages of > 30 mV the current reduces to ~0.5 of the open-state current. The voltage required to induce channel gating depends measurably on experimental conditions, such as membrane lipid composition, salt concentration, and pH. Importantly, there is one unique open state and a variety of low-conducting so called “closed” states [8, 10, 68]. So far all available structural data on VDAC are explicitly related to its open conformation. Therefore, all computational studies on VDAC are restricted to its open state which is characterized by weak anion selectivity with a permeability ratio between Cl⁻ and K⁺ of P_Cl−/P_K+ ≅ 2 [48, 68]. Usually, the preference for anions is explained by net positive +3 charge of the pore interior. The characteristic feature of VDAC’s low conducting states is their either less anionic than of the open state or cationic selectivity [68]. There is no obvious connection between the conductance of a particular closed state and its selectivity [63], which suggests a complex nature of VDAC’s closed states.

2.1 Molecular Dynamics Simulations of VDAC and Mechanism of Ion Permeation

When it comes to direct simulation of ion permeation with MD, there are a number of challenges and conceptual assumptions. The most popular approach widely used for estimation of ion conductance of a membrane channel is the one that assumes a constant electrical field acting in the system [69, 70]. The electric field (E) across the entire simulation box is perpendicular to the membrane plane and creates a transmembrane potential with a voltage difference of V = LE, where L is the length of the simulation box in the direction of the applied field. The main advantage of this very popular method is that its implementation is simple [3].

However, the approximation is hardly an ideal representation of membrane potentials emerging as a result of non-homogenous microscopic charge distributions on both sides of the bilayer. Several alternative approaches were developed, such as double phospholipid bilayer systems, which explicitly include two reservoirs into the simulation with uneven ion distributions [71–74]. The results of modelling permeation processes in various narrow and wide channels with the method, including VDAC, were truly remarkable, but the computational burden was significant due to a sharp increase in number of particles in the simulation box [71–74]. The main drawback in charge-imbalance methods is that the number of ions in the system remains relatively small and a single permeation act may cause significant change in the transmembrane potential [70].

This very detailed application of the constant-electrical field in MD simulations to studies of permeation through the various structures of VDAC channel available at the time was reported by the groups of Wonpil Im and Richard Pastor [75]. Im and colleagues directly addressed the problem of connecting available structures (NMR and X-ray) to permeation properties of the channel [75, 76]. By pulling together over 1.5 microseconds of all-atom MD simulations, the authors reported I–V relations in the applied voltage interval from −100 to +100 mV. The finding of this study shows that the conductance estimated from MD simulations in 1M of KCl (4.8 nS) is in good agreement with the ones reported experimentally. Furthermore, the VDAC structure used for the study displays clear anion preferences, which are in accord with the values measured experimentally e.g. 1/2 ratio for K⁺ vs. Cl⁻ permeability. The authors noted great structural diversity in the ensembles of structures from NMR studies by Wagner and colleagues [45]. In particular, NMR structures show different barrel conformations, not found in the deposited X-ray coordinates. The authors [75] used a simple metric (ratio of short (b) and long axis (a) of the channel) allowing to estimate evolution of effective cross-sections of this channel and hence permeation properties associated with different structures. They noted that there are several NMR structures with the low b/a ratios (~0.65) that were not sampled in MD simulations under applied voltages.

The interesting observation, corroborated later in simulation studies of Noskov and colleagues [77] is that while the N-terminus is still rather “flexible”, it remains inside the beta-barrel region during MD simulation. MD simulations performed under higher applied voltages (up to 1 V) showed that these voltages were not sufficient to drive N-terminus helix outside of the β-barrel region. It remained stably inside the β-barrel region with only a tail of the N-terminus reaching out to cis- or trans- sides of the channel.

Zachariae, de Groot, and colleagues [73, 74] pointed out that N-terminus may play a very essential structural role, preventing a collapse of the β-barrel and the gating dynamics may be attributed to the dynamics of the barrel itself. Nevertheless, all of the studies performed with an applied electrical field noted that dynamics of the unstructured tail of the N-terminus is clearly bi-phasic and depends on the direction of the electrical field [75, 77].

In 2015, Eddy et al. combined solid-state NMR, electrophysiology, and all-atom MD simulations of VDAC1 channel [78] to further test the extent of the interactions between the N-terminus and β-barrel walls [61]. The study focused on the cross-validating of the available crystal structure against a wealth of experimental data. The authors chose to focus on the comparison between VDAC1 wild type and its phosphorylation mimetic mutant VDACS193E [79] with S193 residue positioned inside the β-barrel with its side chain pointing toward the channel lumen and in direct proximity to A14 from the N-terminus (4–6 Å in the structure). In the early functional model [10] of the VDAC, S193 is positioned at a very different location in a loop outside the β-barrel and the path of ion flow and not in a region spanning the membrane. The authors found that the structural proximity between S193E and the N-terminus is in agreement with the analysis of chemical shifts obtained from NMR experiments. The simulation studies indicate that mutations affect predominantly local dynamics of the N-terminus and have a minor impact on the channel stability and conductance mechanisms. Electrophysiological experiments confirmed that the VDACS193E mutant forms typical VDAC channel with nearly identical voltage-gating behavior, conductance, and selectivity compared with those of the wild type channel [78]. The authors concluded that VDACS193E is not always closed as was previously suggested based on AFM measurements [79]. These results provide further evidence in support of that the N-terminus alone is not responsible for voltage gating, although it may be involved with other regions of the protein.

Both the MD and MAS NMR data show that the N-terminal domain screens or obstructs the charged residue of S193E from contributing to the channel’s interior surface charge, thus explaining the absence of the effect of extra negative charge on the channel properties and especially on ion selectivity. However, it has to be mentioned here that in the functional model, where the analogous residue from fungal and human VDAC is positioned in a loop outside of the transmembrane region and outside the pore [10], the channel ion selectivity and gating would also remain unaffected by replacing S193 with a negatively charged residue. This is one of many examples of the existing uncertainty in the field when functional data could be explained fairly well by both structural and functional VDAC models.

Taking together, structural and functional data obtained with a variety of different methods combined with recent MD simulations strongly support usefulness of the structural data available for the presumably open state of the VDAC1 channel. The results from various methods display a reasonable agreement with the electrophysiological experiments, while casting some doubts on the proposed structural mechanisms assigned to VDAC gating process where a flexible N-terminus moving inside the pore [46, 80] or out of the channel lumen [81, 82] provides for VDAC gating.

Given the structural variability observed in the NMR ensembles and simulations with applied voltages, it is reasonable to doubt validity of MD-based conductance from a single-structure based simulation. Ensemble-wide MD simulations with applied electrical field remain rather rare because of the computational burden. A viable strategy could be based on application of continuum electrostatic modelling [83], Poisson-Nernst-Plank (PNP) electro-diffusion theory, or more detailed approaches based on Brownian Dynamics (BD) simulations [1]. They are considerably less costly and may be a practical alternative for large channels such as VDAC.

2.2 Ion Permeation in VDAC Studied with Brownian Dynamics Simulations

Grand-Canonical Monte-Carlo/Brownian Dynamics (GCMC/BD) represents an attractive computational approach for simulating the permeation process through wide channels over long time scales [76, 84–89]. The approach consists of generating the trajectory of the ions as a function of time by numerically integrating the stochastic equation of motions using effective potential functions to calculate the microscopic forces acting on mobile particles in the system. BD can be easily combined with the Monte-Carlo loops to create Grand-Canonical Ensemble with dual reservoirs. Therefore, GCMC-BD algorithms allow direct simulations of systems with asymmetric buffers and applied electrical potentials.

The effective many-body potential can be used to describe ion dynamics in the field created by a static electrical potential due to protein charges and dielectric boundaries, reaction fields and acting membrane potential [87, 88]. The inclusion of trans-membrane potential into the scheme is rather straightforward and can be achieved by solving modified version of the Poisson-Boltzmann equation [90]. In the case of wide water-field pores such as VDAC, a continuum electrostatic description in which the solvent is represented as a featureless dielectric medium is often a useful and adequate approximation. Thus, the equation of motion governing dynamics of the system is a specific form of the general Langevin equation developed by Ermak and McCammon [91]:

$$\begin{array}{c}{\stackrel{.}{\mathit{r}}}_{\mathit{\iota }}=-\frac{D_i(r_i)}{k_{B}T}{\nabla }_{i}W(r_1,r_2,\cdots )+{\nabla }_i{D}_i(r_i)+{\mathit{\xi }}_{\mathit{i}}(\mathit{\tau })\\ W(r_1,r_2,\cdots )={\sum }_{ij}{u}_{ij}(\mid r_i-r_j\mid )+{\sum }_i{U}_{\mathit{core}}(r_i)+\mathrm{\Delta }{W}_{sf}(r_1,r_1,\cdots )+\mathrm{\Delta }{W}_{rf}(r_1,r_1,\cdots ),\end{array}$$ (1)

where ṙ_ı is the velocity and r_i is a position of the i-th ion, u_ij representing the direct ion-ion interaction, U_core is a repulsive potential preventing core-core overlap of the ions with the channel and membrane, ΔW_sf is the shielded static field coming from the permanent protein charge distribution and the transmembrane potential, and ΔW_rf is the reaction field arising from the electrostatic polarization of the various dielectric boundaries and the implicit salt in the outer region, D_i(r_i) is a position dependent diffusion coefficient of the i-th ion, and ξ_i(τ) is a term introducing a Gaussian random noise to the system dynamics as <ξ_i(τ)· ξ_i(0) > = 6D_i(r_i) δ_ij(t). [85, 92]

The Grabe and Coalson labs were first to use the mean-field approach combined with PNP electro-diffusion modelling to test the permeation properties of the structures available [93]. They found that PNP models driven by the diffusion properties extracted from all-atom MD simulations allow accurate evaluation of both experimentally reported conductance and weak anion preference of the channel. The authors examined different gating scenarios with PNP computations and concluded that neither of them (N-terminus movement in the electrical field) leads to a conclusive mechanism of gating.

To explore the role played by structural heterogeneity of different models from NMR studies, Im and colleagues [76] used GCMC/BD simulations to obtain ensemble averages and distributions of conducted states and to map a tentative mechanisms responsible for measured conductance. The results were rather striking. While all of the structures studied appear to be anion selective “on average”, the absolute values of the structure-specific computed conductance (average of ten simulations) span a range of values from 0.29 to > 0.6 nS in 100 mM of KCl (the experimentally measured conductance of VDAC isolated from rat liver is 0.45 nS). The average conductance in the NMR ensemble was found to be 0.36 nS in 100 mM of KCl. These findings illustrate that the single-structure based simulations are fairly limited. The general mechanisms responsible for (weakly) selective Cl⁻ transport also emerged. It appears that a number of acidic residues (Asp¹⁶, Asp³⁰, Glu⁸⁴, and Asn²⁰⁷) are central to attract and retain cations. K⁺ tends to display significantly longer residence times compared to a Cl⁻. Together with the higher free-energy barrier for K⁺ to enter the channel found in the ensemble of the structures, the K⁺-protein attractive interactions result in the difference in ion transport rates for K⁺ and Cl⁻ and determine the anion selectivity of VDAC.

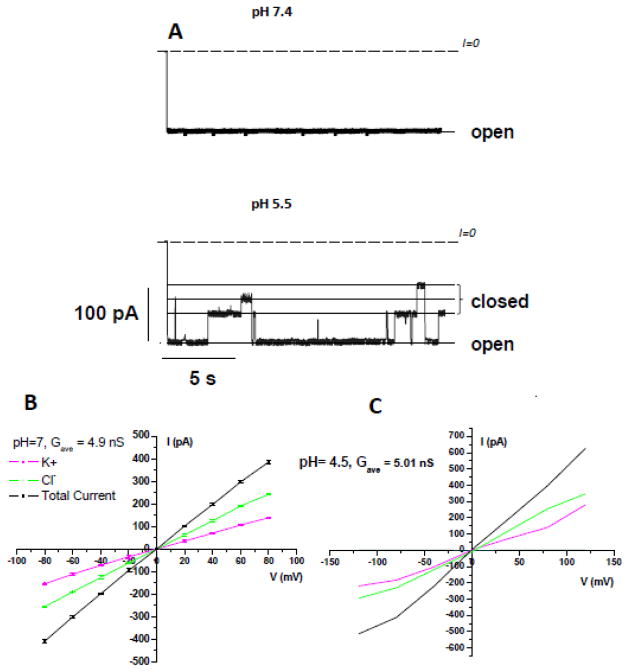
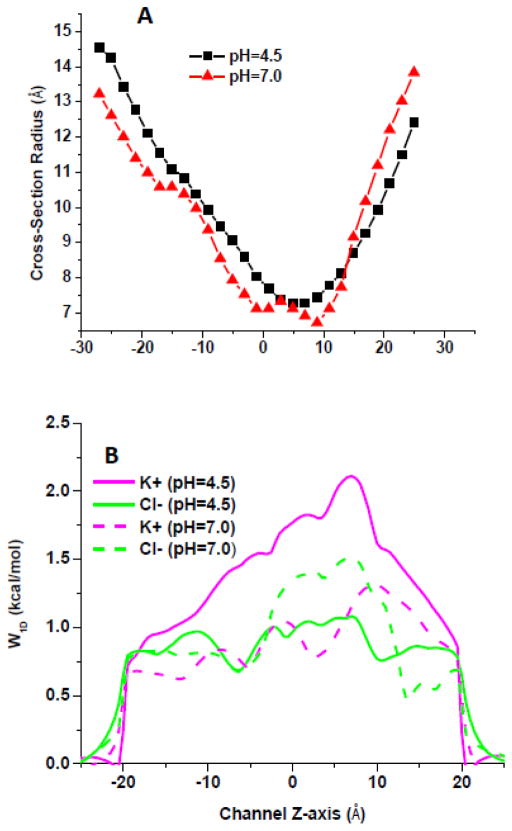
To test this elegant hypothesis, we performed GCMC/BD simulations of VDAC1 channel at pH 7.4 and 4.5 using the protocol of Lee et al. and novel effective potentials for KCl solutions [76, 87]. The ionization state of relevant residues was defined based on pK_a values computed using a protocol developed previously [94]. We performed 200 ns MD simulations for the channels with protonation states set at pH7 and 4.5 using this protocol. It was experimentally shown that acidification causes significant increase of VDAC gating (Figure 2A) and anion selectivity and a mild increase of channel conductance [95]. The change in the protonation states of major acidic residues has an obvious impact on the average cross-section radius (Figure 3A), but it is hard to relate the change in the channel structure such as a modest widening around the constriction zone with a decrease in pH to the channel’s conductance. The ten structures were selected based on RMSD clustering of the equilibrated channels in the DOPE bilayer for subsequent GCMC/BD simulations.

Figure 2.

Figure 3.

The resulting I–V relations obtained in a symmetric 1M of KCl in the applied voltage interval from −120 to 120 mV suggest that a decrease in the pH to 4.5 combined with a titration of Asp and Glu resulted in an average conductance similar to that of VDAC1 at pH 7.4 e.g. 4.9 nS and 5.0 nS, respectively (Figure 2B). This is a somewhat lower effect of acidification compared with the channel conductance increase of 10–20% at pH change from 7.4 to 4.5 found in electrophysiological experiments [95, 96]. The composition of the current at lower pH values is drastically different. The average ratio for Cl⁻/K⁺ changed from ~1.9 to > 5. The average (out of 10 simulations of 1 microsecond duration) 1D PMFs (W_1D(z)) for permeant cations and corresponding ion pathways for two pH values are shown in Figure 3B. The results from less-resource consuming methods such as BD appear to be in a general agreement with measured VDAC conductance at lower pH [95].

2.3 Molecular Mechanisms of Metabolite Transport in VDAC channel

VDAC’s main function is to conduct and regulate fluxes of ATP and ADP. Therefore, the permeability of the channel to adenine nucleotides is the most relevant physiological question to address in in vitro studies. The fluxes of ATP through VDAC were directly measured in experiments with multichannel membranes using the luciferin/luciferase assay for ATP [65, 66]. The calculated ATP⁴⁻ flux through a single channel was found to be ~ 70 times lower than Cl⁻ flux [66]. The effective diffusion coefficient of ATP inside the channel estimated by direct measurements of ATP fluxes in multichannel experiments and from ATP-induced ion current fluctuations inside the pore in single-channel measurements was found to be ~ 10 times smaller than the ATP diffusion coefficient in the bulk [66, 97]. These results suggested the existence of weak binding site(s) for ATP inside the VDAC pore. Measurements of VDAC single-channel conductance in the presence of ATP, ADP, AMP, NADH, and NADPH revealed weak, in the range of millimolar, binding of adenine nucleotides to the VDAC pore and the ability of VDAC to differentiate between these nucleotides, notwithstanding their very close molecular weights and charge [97–99].

The studies of the structural mechanisms implicated that ATP-selective binding and the consequent transport through the channel were facilitated by a number of structures available in the field. In 2008, Choudhary et al. [93] noted that highly-charged ATP⁴⁻ molecule may bind too tightly to the lumen of the channel and a partial charge neutralization by mobile counterions is expected to play a role in transport energetics. However, the flexibility of the metabolite molecule poses a formidable computational challenge. The direct simulation of metabolite transport from all-atom MD with an applied electrical field is attractive, but rather resource-demanding. The first and very impressive application of a microsecond-long MD simulation to ATP transport through VDAC1 happened only in 2014 with the use of the specialized ANTON machine [47].

2.3.1 1D Umbrella-Sampling Simulations of ATP Transport through VDAC

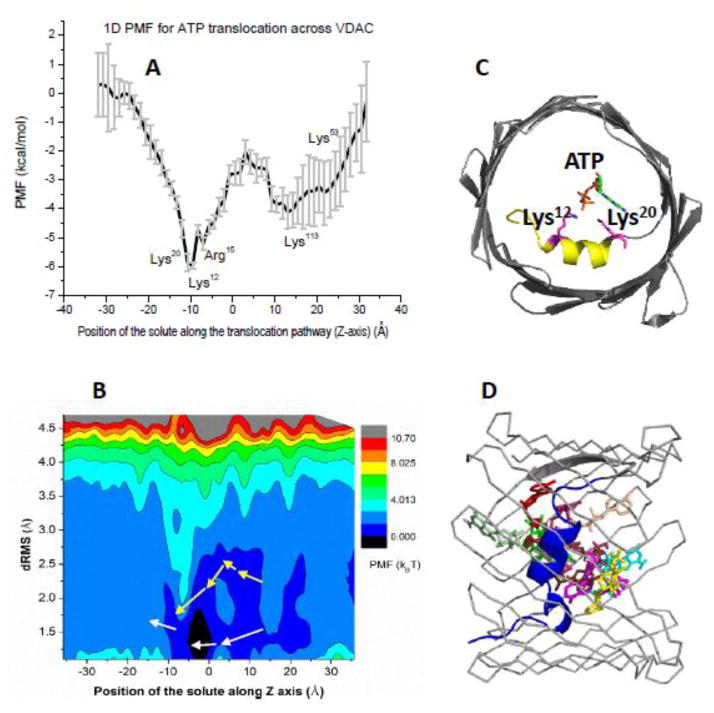
An attractive alternative can be found in enhanced sampling techniques such as Umbrella-Sampling (US), meta-dynamics or other similarly-spirited approaches discussed in this special volume of BBA-Biomembranes. All atom Free Energy simulations are arguably the most powerful tool for obtaining equilibrium thermodynamic properties along a reaction coordinate required to connect transport mechanisms and pore specificity for a given solute. In 2013, Noskov and colleagues have used atomistic simulations combined with conventional US to obtain 1D free energy profile for ATP transport through VDAC1 [77] (Figure 4A). The computed profile clearly identifies a tentative binding site for the solute and maps location of the barrier.

Figure 4.

The idea of residues forming ATP-selective binding sites along the permeation pathway provides an elegant explanation for experimental data from side-directed mutagenesis and electrophysiological recordings. The authors computed an effective equilibrium dissociation constant K_D from 1D PMF in presence of a cylindrical constraint can be expressed as:

$$K_D^{-1}(\mathit{effective})=\pi R^2{\int }_{z_{\mathit{min}}}^{z_{\mathit{max}}}\mathrm{d}z{\mathrm{e}}^{-w(z)/k_{B}T}$$ (2)

where R is the radius of the cylindrical restraint oriented normal to the z-axis with z_min=−2 Å and z_max=12.5 Å. The W(z) was offset to zero for an ion in the bulk phase [1].

According to 1D PMF shown in Figure 4A, an ATP molecule shows a well-pronounced binding with slightly different affinities, separated by a well-defined barrier loosely centred at the N-terminus. The barrier to escape the binding well around the middle of the channel to the mitochondrial side is 6k_BT, whereas the barrier to overcome for transport from the second binding site to the cytosolic side is ~4k_BT.

Tomasello et al [100] showed that the C-terminus of VDAC is not accessible to cleavage by cytosolic caspases and therefore faces the mitochondrial side of the MOM. In keeping with the predictions by Choudhary et al. [93], ATP remains fully hydrated with only a small drop in hydration from ~34 to ~29 water molecules while in the channel lumen. The average number of counterions for the ATP molecule drops down from N_K+ ~ 4 to N_K+ ~ 2.3 upon entering the channel and is partially compensated by interactions with basic residues lining up the pore. The estimated dissociation constant for ATP is ~125 μM, which is in a reasonable agreement with experimental data [97].

The pore radius shown in Figure 3A provides some explanations for the observed asymmetry of the PMF. The per-residue decomposition of interaction energies emphasized the role of two basic residues from the N-terminus (Lys¹² and Lys²⁰) in the formation of stable binding site for ATP. The second binding site located near the cytosolic entrance is formed by two basic residues from β-sheets (Lys⁵³ and Lys¹¹³) and Asn⁵⁵, which stabilizes the nucleobase of adenosine. While binding affinity obtained directly from the 1D-PMF is in general agreement with experiment, it was unclear if it is sufficient for flux optimization observed experimentally. Is this binding optimal enough to ensure optimized flux of ATP molecules as suggested by previous studies? The obtained profiles of PMF of translocating ATP combined with a known pore dimensions allow a simple modelling of flux efficiency. One can always asses two translocation probabilities for ATP molecule in the effective potential of mean force W(z) in two cases: (i) when the potential of mean force includes all the interactions discussed above and (ii) when the only component of the potential is the entropic one due to confinement described by a position-dependent radius R(z) with the attractive interactions between the channel and ATP “switched off” [77].

It was shown that the translocation probability for a particle at the channel entrance in the case of an unbiased empty channel with entrances of equal radii R on both sides of the membrane can be expressed as [39–43]:

$$P=\frac{1}{2+\frac{4D_b}{\pi R}{\int }_{z_{\mathit{right}}}^{z_{\mathit{left}}}\frac{exp(-w(z)/k_{B}T)}{D(z)}dz}$$ (3)

where k_b and T have their usual meaning of the Boltzmann constant and absolute temperature, and D_b and D_z are the ATP diffusion coefficients in the bulk and inside the channel, respectively. The diffusion coefficient of ATP in the VDAC pore was estimated as an order of magnitude smaller than in the bulk and is in agreement with the MD results. The translocation probability for ATP molecule computed with 1D-PMF that includes all the interactions found in the simulations, case (i), is P_PMF= 0.43. In the presence of only entropic contribution of the VDAC channel confinement, case (ii), P_ent= 0.045, which is small, as expected. Thus, attractive interactions revealed by the molecular dynamics simulations [77] increase the probability of ATP translocation through the channel by ~10 times. Notably, notwithstanding this impressive efficiency gain, the binding constant reflects the relatively weak binding of ATP to the channel. It has also to be stressed that use of the 1D PMF for this purpose assumes effective averaging along a simplified translocation path normal to the bilayer plane. Some of the key features or alternative pathways for ATP translocation may be left out of the picture by averaging out the degrees of freedom and projecting them onto 1D permeation coordinate.

2.3.2 Long-time scale MD simulations combined with Markov-State-Model analysis

The major structural development in understanding of ATP binding and translocation came in 2014 with the solution of crystal structure of VDAC-ATP complex and heroic efforts in a microsecond-long simulations based on this structure [47]. The complex structure solved at 2.28 Å resolution shows only a single ATP-binding site, next to the N-terminal α-helix. The bound metabolite molecule is directly coordinated by the Lys¹² and Lys²⁰ (Figure 4C) in excellent agreement with the results from the simulation study published in 2013 [77]. The importance of Lys²⁰ in ATP binding has also been demonstrated for human VDAC1 by NMR investigations. Therefore, there is an apparent consensus on the location of the high-affinity binding site for the ATP molecule.

In an effort to map molecular details of the ATP flux through the pore, Grabe and colleagues carried out a series of the multi-microsecond all atom MD simulations with the ANTON special-purpose supercomputer with and without biasing electrical potentials. The authors reported a very complex flux picture with several different permeation scenarios that depend on the flexibility of ATP. The wealth of sampling information provided by long MD simulations was analyzed within a framework of Markov-State-Model (MSM) approach [36]. The structural clustering enabled by an exhaustive sampling allows for identification of major states along the permeation reaction coordinate. Representative conformation for each state is known as the generator. The clustering can be used next to construct the transition probability matrix, P_i,j(τ), for ATP starting in state i and moving to state j inside the channel using a maximum-likelihood reversible estimator.

The MSM techniques has been used successfully to various biological phenomena before, including ion permeation in DNA-blocked pores, dynamics of dyes in lipid bilayers, and conformational dynamics of proteins [36, 88]. While MSM requires an exhaustive sampling of the conformational space, it may help to untangle usually noisy data-sets produced by long MD simulations and organize them into an elegant theoretical framework for the process kinetics and thermodynamics. Grabe and colleagues used MSM to evaluate the mean first passage time (MFPT) between states found in MSM to find out that mean translocation time for ATP from MD simulations is expected to be ~15–32 μs. The average transport rate based on MSM analysis is ~49,000 ATP/s, a result is in excellent agreement with the experimental value of 50,000 ATP/s measured for Neurospora crassa VDAC in channel reconstituted experiments [66, 97].

An important finding enabled by ANTON-based simulations and MSM studies is that permeation occurs via a number of distinct and often intersecting routes [47]. The pathway averaged in 1D PMF computations reported above is well-conserved in MSM analysis of Grabe et al. However, flexibility of the metabolite and its full hydration allow other pathways to emerge at a low-energetic cost. It appears that in a majority of cases the rate-limiting step is a dissociation of ATP from the α-helix of the VDAC N-terminus. It was also noted that one of the pathways, though a rare one, labeled pathway 5 (shown in Figure 4B with yellow arrows) can be associated with the highest possible ATP flux rates. The applications of multi microsecond-long MD simulations remain to be a rarity and therefore, it is instrumental to investigate if more computationally amenable techniques allow one to reveal complex permeation dynamics. Even in a pushing-an-envelope application of all-atom MD simulations reported by Grabe and Abramson labs, in a majority of cases complete permeation of ATP did not happened.

An attractive approach is to increase dimensionality in the US simulations [20, 101, 102]. While the number of computations is steeply rising, we can keep them relatively short by enhancing sampling. A very promising new technology that emerged in the field is built on the combination of well-established Replica-Exchange Techniques with multi-dimensional US simulations (Hamiltonian-Replica Exchange – H-REMD).

2.3.3 2D H-REMD Simulations: General Overview

The 2D US/H-REMD algorithm design used in this work was identical to the one published previously by Jiang and colleagues [20]. It builds on the previous work in tempered-simulation applications to sampling enhancements [103–106]. Similar to traditional T-REMD [105, 107] where running replicas at different temperatures provides substantial acceleration in sampling, the rate at which the sampling of reaction path can be considerably enhanced by coordinate swapping between independent simulations generated for different Hamiltonians generated by Umbrella-Sampling, Thermodynamic Integration of Free Energy Perturbation simulations [21, 101, 107–111]. For PMF calculation with US, considering N copies of a system that are identical except for some differences in a small number of parameters, it is possible to make ordered lists of these systems such that the difference in the parameters is smallest for the nearest neighbours in the list. In the current application of US in 2 dimensions (2D), different biasing windows potentials are required for each of the simulated systems. Assuming quadratic potentials, there are 2 parameters (p₁, p₂) and the associated US biasing window potential is as follows:

$$w(p_1,p_2)=k_1{(x-p_1)}^2+k_2{(x-p_2)}^2$$ (4)

The only variation is with the actual numerical values of the parameters p₁, k_1,p₂, and k₂. Therefore, an ordered list of systems is defined by (p₁^j, p₂^j), with j going from 1 to N. Assuming N is even for simplicity, the rule for attempted exchanges during the replica-exchange MD simulation can be defined. First, there is an attempt to exchange between the members of the list and their nearest neighbors according to the odd ↔ even rule, i.e., 1 ↔ 2, 3 ↔ 4, . . . (N – 1) ↔ N; then, there is an attempt to exchange their nearest neighbors according to the even ↔ odd rule, i.e., 2 ↔ 3, 4 ↔ 5, . . . (N – 2) ↔ (N – 1). Each neighboring exchange means that all the numerical values of the parameters of the members, or equivalently, instant configurations are simply swapped with the the conventional Metropolis Monte Carlo exchange criterion.

2.3.4 2D H-REMD Simulations: Extension to studies of ATP permeation across VDAC channel

To study ATP transport across VDAC channel we consider a combination of 2-Dimensional (2D) umbrella sampling simulations with the distributed replica-exchange protocol. The initial permeation coordinate was generated on the basis of our previous 1D US simulations [77], where position of the solute’s center of mass was used a 1D reaction coordinate varying from −32 to 32 Å with 1 Å bin widths. To account for the flexibility of the ATP molecule we added a second reaction coordinate defined as RMSD difference between two stable states of the molecule as sampled in 500 ns-long T-REMD simulations for an ATP molecule in water. The d-RMS coordinate was varied from 0.5 to 4.5 Å with 0.5 Å bin widths. Therefore the 2D US system was sampled with 512 windows used for the H-REMD simulations. The cylindrical constraint with a radius of 20 Å was applied to the solute ensuring that PMF is bounded in the bulk phase. The harmonic biasing potentials with a force constant of 5 kcal/(mol·Å²) along the channel axis, Z axis, was used to sample permeation coordinate, while the force constant for dRMSD coordinate was set to 10 kcal/(mol·Å²).

The 2D-PMF profiles were rebuilt with the weighted histogram analysis method (WHAM) [112, 113], and the tolerance for WHAM was set to 10⁻⁵. One of the major challenges in applications of the US simulation is how to assess efficiency and completeness of our sampling. The statistical uncertainties were estimated according to Zhu and Hummer [33] using the metric of relative entropy (η_i) (also known as Kullbak-Liebner divergence) as an estimator for the sampling efficiency using Equation 6. Essentially it allows to use histograms obtained directly from the simulation and the histograms predicted from the WHAM results to assess if the sampling is sufficient:

$${\eta }_i=\int p_i^{\mathit{obs}}(x)ln\frac{p_i^{\mathit{obs}}(x)}{p_i^{\mathit{WHAM}}(x)}dx$$ (6)

where p_i is the probability distribution in window i. Large values of relative entropy indicate that the samplings are inconsistent and were used as a criteria for need (or lack of whereof) in additional sampling. $p_i^{\mathit{obs}}(x)$ is the observed distributions from 2D US H-REMD simulations for a given reaction coordinate, while $p_i^{\mathit{WHAM}}(x)$ is a the consensus distribution after solution of 2D WHAM equations. Based on the criteria described above we performed 4 ns per-window 2D H-REMD runs using NAMD software package[114–116]. The composition of the 2D H-REMD windows and spacing was tested for “ideal” exchange criteria was selected to satisfy exchange probability of about 30 % according to the protocol used by Faraldo-Gomez and Roux [108, 117]. Therefore, the total simulation time for the entire ensemble of replicas was over 2 micro-seconds. To complete sampling for ATP permeation we had to use Director’s Discretional Allocation from the Argonne National Lab with 5,000,000 core-hours on a Blue Gene machine.

The resulting 2D PMF map is shown in Figure 4B. In excellent agreement with the results of multi-microsecond long simulation, ATP in the pore exhibit rather broad distribution of states (2D PMF surface from −8 to 8 Å and 10-most probable structural clusters from MSM analysis – Figure 4D). Even in the high-affinity binding sites found in all of the simulations studies, bound ATP shows RMSD dynamics at the order of 1–2 Å with favourable binding to the channel, a significant range for a small solute. The pathways identified from the MSM analysis appear to be present on the 2D PMF map. For example, the pathway 5 can be characterized by a stable but not dominant conformation of the ATP molecule, which is more compact than the dominant state (Figure 4B). While the interactions between the permeant metabolite and N-terminus basic residues are decreased, the ATP molecule interacts strongly with the residues on the β-barrel wall (Lys⁹⁶ and Lys¹¹⁹) partially compensating the decrease in excellent agreement with the results of microsecond-long MD simulations.

2.4 The Role of pH in Ion Transport through VDAC

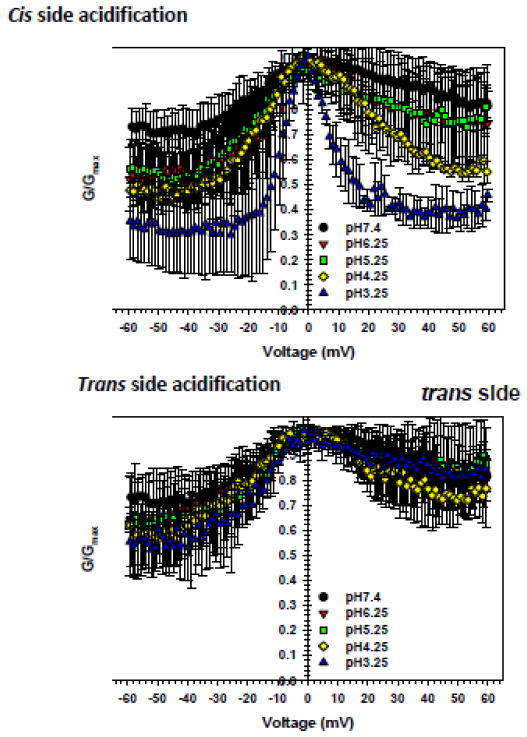
pH titration of negative charges together with His residues titration results in a total increase of the net positive charge inside the pore, which leads to an increase in anion selectivity of the open state and some increase of channel conductance [95, 96]. The VDAC’s open state reversal potential, which is a voltage corresponding to the zero current through the channel measured in salt gradient across the membrane, increases significantly, for ~ 15 mV (in 1.0 M vs. 0.2 M KCl gradient), when pH decreases from 7.4 to 3 with the most of the effect seen at pH < 5 [95]. Open state conductance increases only mildly, for ~ 40%, in response to the same pH decrease in agreement with the results of BD simulations discussed above. The most dramatic effect of acidification was found on VDAC gating when voltage sensitivity of VDAC closure increased at pH < 5.0 [95]. Analysis of the pH dependences of the gating and open channel parameters, such as ion selectivity and conductance, yielded similar pK_a values of ~ 4.0 [95]. Although simulations of the effect of low pH on VDAC’s two basic characteristics, channel conductance and selectivity, yield a satisfactory agreement with the experimental electrophysiological data, the description of pH effect on VDAC gating requires, first of all, structure of the VDAC closed state(s) and a comprehensive model of VDAC gating, which still are have to be solved. One of the successful efforts to employ MD simulations to understand VDAC complex gating behaviour was recently undertaken to explain a surprising asymmetry in the sensitivity of voltage gating to pH changes. It was found that one side of the channel, the so-called cis side that corresponds to the compartment to which VDAC is added in the reconstitution setup, is highly sensitive to acidification while the opposite, trans side of the channel, is almost insensitive to pH changes [95]. Considering a rather symmetrical distribution of charges over the VDAC’s β-strands (Figure 1) that constitute the channel wall [46] these results were quite puzzling.

MD simulations suggested a higher number of stable salt bridges clustered at the cis side of the pore (Figure 5), which are more susceptible to disruption at low pH and, therefore, a pH decrease at the cis side leads to the preferential closure of the channel [95]. The schematic model emerges from the fixed-charge (not dynamic pH titration) simulations of the channel at different pH. Interestingly, an asymmetric distribution of the salt bridges favoring one side of the channel pore is not unique to the VDAC family; similar patters exist in the voltage sensors of K⁺ channels [118, 119]. A role of this structural feature in a cooperative gating transition has been suggested. A similar mechanism was also proposed to explain apparent asymmetry in gating of Mg²⁺-selective CorA channel, where formation of inter-protamer salt bridges stabilizes different gating states of the system. Therefore, it may be a generic mechanism adopted by membrane proteins to operate in environments with pH gradients.

Figure 5.

Considering that the cis side of reconstituted VDAC in the planar membrane setup most likely corresponds to the cytosolic channel entrance [120], the pronounced sensitivity of the cytosolic side of VDAC to acidification could be physiologically relevant via the channel response to the large changes of cytosolic pH during ischemia and reperfusion injury [121, 122].

2.5 The Interactions between VDAC and Soluble Proteins

One of the first important indications that VDAC is not just a “molecular sieve” which passes the molecules of the size less than its pore dimensions, was finding that ATP does not translocate through VDAC’s low-conducting or closed states induced by applied voltage [65]. Another confirmation of that VDAC is not just a passive conduit for adeno-nucleotide fluxes, but actively controls their transport was a discovery of the exceptionally potent cytosolic regulator of VDAC permeability, a dimeric tubulin [123]. Already in 1995, Valdur Saks and co-authors suggested an existence of a cytosolic protein associated with cytoskeleton, the so-called “Factor-X” which controls MOM permeability in vivo [124]. This suggestion was based on their finding that in isolated mitochondria respiration is characterized by an apparent K_m for exogenous ADP, which is 10-fold lower than that in permeabilized cells with oxidative metabolism [124, 125]. It took more than 10 years to identify this illusive factor as one of the most abundant cytosolic proteins, tubulin [123, 126]. Dimeric tubulin induces highly efficient and reversible blockage of VDAC reconstituted into planar lipid membranes [120, 123]. The heterodimer of α- and β-tubulin is a 100 kDa acidic water-soluble protein composed of compactly folded α-helices and β-strands with a well-defined crystal structure [127]. Tubulin C-terminal tails (CTTs) are composed of unstructured peptides of 11–15 amino-acids [128] exposed out of the protein surface. Both α- and β-tubulin CTTs are highly negatively charged and are essentially poly-Glu peptides. The facts that tubulin blocks VDAC only when a negative potential is applied from the side of tubulin addition and that tubulin with proteolytically cleaved CTTs does not induce characteristic VDAC blockages suggest that the negatively charged CTTs are responsible for the channel blockage. Based on these observations, a model of VDAC-tubulin interaction was proposed where the negatively charged tubulin CTT partially blocks the positively charged VDAC pore [9, 120, 123]. The tubulin-blocked state is still highly ion-conductive, about 0.4 of the open state conductance in 1 M KCl, so that VDAC inhibition by tubulin is limited by the value of this residual conductance. Therefore, the important result is that the tubulin-blocked state is virtually impermeable for ATP [62]. In addition, the blocked state is characterized by reduced dimensions compared with the open state and the cation selectivity which is reversed from the anion selectivity of the open state [62].

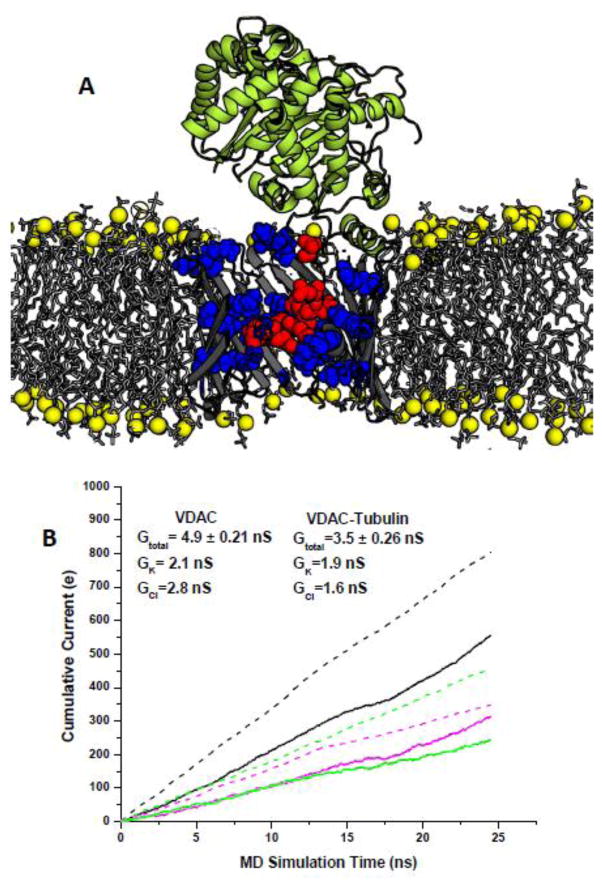
The preliminary molecular-level understanding of the interactions between tubulin and VDAC was achieved by using protein-protein docking with the RosettaDock software suite [27, 28]. It employs a Monte Carlo (MC) search with low-resolution runs followed by high-resolution refinements. The docked structures were clustered to produce four different starting complexes for MD simulations with similar ranking. Next, an extensive set of equilibrium and non-equilibrium (under applied electric field) simulations was used to establish conductance of the open and blocked channel. It was found that the presence of the unstructured C-terminal tail of α-tubulin in the VDAC pore decreases its conductance by about 60% and switches its selectivity from anion- to cation-preferring channels (Figure 6A and 6B). The negatively charged C-terminus of a bound α-tubulin molecule is complimented by the VDAC pore providing matching basic residues that form stable salt bridges involving Arg¹⁵, Lys²⁰, Lys¹², and Lys³² of VDAC. All of these residues participate in formation of a high-affinity ATP site and therefore disruption of ATP transport in the tubulin-blocked state is hardly surprising. Potential of Mean Force (PMF) computations for the VDAC-tubulin complex show that the tubulin-blocked state renders ATP transport virtually impossible.

Figure 6.

Altogether these results show that, due to the electrostatic and steric barriers induced by tubulin blockage, ATP is excluded from the tubulin-blocked state of VDAC, thus verifying the functional role of VDAC-tubulin interaction in regulating mitochondrial respiration. Experiments with isolated mitochondria [123, 126] and human hepatoma HepG2 cells [129, 130] confirmed that VDAC–tubulin interaction is important for mitochondrial respiration in intact cells. One of the intriguing implication of VDAC regulation by tubulin is its coupling with the Warburg-type aerobic glycolysis characteristic of many tumor cells [131], where the VDAC-tubulin complex may play a role of “glycolytic switch” in cells towards aerobic glycolysis or oxidative phosphorylation [120, 132].

3. Unsolved Problems in VDAC Structure and Function

A conserved property of VDAC channels in vitro is the ability to adopt a unique fully open state and multiple “closed” states of significantly smaller conductance (Figure 2A, low panel). The states differ in their ability to pass non-electrolytes and to conduct ions [133]. VDAC gating involves large conformational changes leading to a substantial decrease of the channel volume [134] and pore inner dimensions [63, 68], as was found in electrophysiological studies on reconstituted VDAC. Closed states are characterized by a set of different states with the selectivity ranging from a weak cationic selectivity to a weak anion-selective one, as compared with weak anionic selectivity in the open state, and are virtually impermeable to negatively charged metabolites such as ATP [63, 65, 66, 133]. First suggested model of VDAC gating involved translocation of a large positively charged voltage sensor domain towards one of the membrane surfaces, thereby reducing the size of the pore and inverting its selectivity [50, 68]. However, the molecular identity of the voltage sensor has not been resolved yet because charged residues affecting voltage gating are spread over the entire VDAC folding pattern including its N-terminus. Although there is a general agreement on the N-terminus location inside the VDAC pore in the open state and a crucial role in VDAC gating [93, 135, 136], its position in the closed states is still a subject of discussions. Addressing this question, the N-terminal α-helix of mouse VDAC1 was cross-linked to the β-barrel by using double cysteine mutations of L10C on the N-terminus and A170C on β-strand 11 followed by reconstitution of the mutant VDAC1 into planar lipid membranes [61]. It was found that VDAC with the N-terminus covalently bound to the channel wall had indistinguishably similar channel properties, including voltage gating, to VDAC1 wild type, suggesting that the N-terminal region is either immobile or does not move independently of the rest of the voltage sensor [61]. Based on these data the model of the N-terminus independently moving to provide voltage gating seems unlikely.

The growing body of evidence suggests that the gating dynamics in VDAC can be mostly modelled by the “collapsing” beta-barrel rather that one mobile element (proposed N-terminus), a.k.a. voltage sensor. NMR data in combination with MD simulation demonstrated a noticeable dynamics of βstrands 1–6 and 16–19 [73]. The analysis of the B-factor of the VDAC crystal structure showed that it increased measurably in the region of the wall opposite to β-strands 8–15 reinforced by the adjusted N-terminus and that the α-helix had a more rigid structure than the remainder of the pore [61]. Confirmation of intrinsic flexibility of the VDAC β-barrel was obtained with the VDAC mutant lacking the N-terminal α-helix, which characterized by sharp increase of the overall motion of β-barrel and its pronounced elliptical shape [74]. Recent advanced measurements of the electrochemical impedance spectra under applied voltage allowed associating spectral changes with the structural transition upon VDAC gating [137]. The observed spectral changes were interpreted as alterations of the angle of the β-strands’ tilt and could be visualized as expansion of the β-barrel, supporting the motion of all β-barrel upon voltage gating. The complexity of VDAC gating was re-examined in a recently study of the characteristic for large β-barrel channels hysteresis of voltage gating where it was conclusively demonstrated that gating cannot be described by a two-state Markov model [67]. Authors concluded that during closing and opening the channel explores different regions of a multidimensional free energy landscape, so that on the way to the closed states the system is far from equilibrium, whereas during opening it mostly follows quasi-equilibrium paths. Taken together, these observations imply that VDAC gating most likely is drastically different from conventional gating models adopted in studies of K⁺ channels with rather well-defined structures of open and closed states. Instead, we may have to consider a multitude of open and, especially, closed states with different permeation properties. The connectivity between these states and hence the mechanism of gating are a subject of future investigations.

The agreement between different approaches to sample ATP transport is encouraging and experimental data are in support. However, the exact mechanism by which other metabolites are excluded [98] is a subject of further investigations. Recently, Krammer et al. [138] reported a detailed application of MD and Adopted-Force Biased MD simulations to VDAC-facilitated transport of metabolites with different charges. The study emphasized the role of clusters of basic residues in the selectivity mechanisms. The authors proposed that a cluster of residues located in the N-terminal helix (high-affinity ATP binding site) represents a major selectivity filter excluding smaller ions or cations lacking charge complementarity. The metabolite specificity is expected to depend on charge screening effects and can be regulated by stabilization of different permeation pathways. Hence, an emerging picture of VDAC specificity is inherently dynamic and tuneable to local electrical fields controlled by the trans-membrane potentials and pH gradients. More work is required to identify different factors controlling selective flux of metabolites and its intimate linkage to protein dynamics

Another important question to address in future computational experiments is molecular mechanism(s) of VDAC regulation by cytosolic proteins. It was recently reported that in addition to tubulin, another abundant cytosolic protein, a neuronal intrinsically disordered α-synuclein involved in etiology of Parkinson disease (PD), effectively blocks VDAC [139]. Rostovtseva et al [139] have shown that monomeric α-synuclein not only reversibly blocks VDAC conductance, similarly to what has been shown to tubulin, but also is able to translocate through the VDAC pore. Experiments with yeast model of PD supported electrophysiological results by demonstrating that VDAC is indeed required for α-synuclein toxicity in yeast. Considering an intimate association of α-synuclein with PD progression [140] and yet unknown functions of this soluble synaptic protein in the brain, a newly proposed (patho)physiological role of α-synuclein as VDAC regulator asks for detailed testing by computational methods.

It turns out that VDAC interaction with both, tubulin and α-synuclein, strongly depends on the specific lipid composition of planar membranes in which VDAC is reconstituted [141]. Tubulin binding to the lipid membrane is a step preceding blocking the pore by the tubulin C-terminus and thus defining the on-rate of VDAC-tubulin binding. Therefore, tubulin- and α-synuclein-membrane interactions should be included into the whole picture of VDAC regulation by cytosolic proteins. These findings suggest another intriguing role of mitochondrial lipids in regulation of MOM permeability and hence mitochondrial respiration, but also bring another level of complexity in our understanding of VDAC functioning. In general, VDAC regulation by tubulin and α-synuclein is an example of the effective and dynamic interaction of membrane ion channel with water soluble protein regulated by membrane lipids.

4. Conclusions

The combination of structural, functional, and modelling studies of the Voltage-Dependent Anion Channel offered molecular-level insights into ion and metabolite transport across mitochondrial outer membranes, often inaccessible to a single approach. While the specific applications and the knowledge that emerged over the years were discussed in different sections of this mini-review, it is our intent to conclude this review with a note summarizing the role of modelling studies in unravelling permeation principles in membrane proteins. A recent sharp increase in a method resolution and/or accessible sampling lengths often promotes a reexamination of the microscopic factors that give rise to selective metabolite transport. Some of those computational experiments explored fairly artificial situations (e.g. use of a static electrical field), whereas others involved a set of approximate models such as continuum electrostatic. Classical notions adopted in the field that postulate one and only selective permeation pathway were critically re-evaluated by multi-microsecond long MD simulations and novel applications of 2D H-REMD Free Energy simulations. They are sharing now the stage with additional and less familiar concepts based on the co-existence of different permeation pathways with different efficiency. This creates the apparent need (for the computational community) of treating the conductance and selectivity of large channels based on the ensembles of structures. Much of the progress in VDAC studies has relied on a combination of all-atom MD simulations on known structures with the explicit solvent and membrane and the use of the diffusion constants and relevant states extracted from MD trajectories.

This information can be easily inputted into the Brownian Dynamics algorithms, thus creating a multi-scale platform for studies of ion permeation in wide and narrow channels. Until now, most efforts have implicitly been focused on the factors governing conductance and ion selectivity of the VDAC open state, with a fair amount of attention devoted to the notions of thermodynamic equilibrium in formation of VDAC complexes with metabolites or other proteins. More efforts will be required to better understand the phenomenon of conformation-driven selectivity of different VDAC states, which remains poorly understood, similarly to the situation with the mysterious gating mechanism. We have no doubts that research into VDAC gating will continue to advance with the availability of additional structural data and with improvements in the computational models.

Highlights.

• Structural underpinning of selective metabolite transport by VDAC channels are discussed

• Multi-scale models employed in the field appear to further establish physiological relevance of structural models of VDAC1 obtained with NMR and X-ray studies

• pH regulation of VDAC gating and selective transport results from asymmetric distribution of basic and acidic residues.