Computational Approaches to Detect Allosteric Pathways in Transmembrane Molecular Machines

Abstract

Many of the functions of transmembrane proteins involved in signal processing and transduction across the cell membrane are determined by allosteric couplings that propagate the functional effects well beyond the original site of activation. Data gathered from breakthroughs in biochemistry, crystallography, and single molecule fluorescence have established a rich basis of information for the study of molecular mechanisms in the allosteric couplings of such transmembrane proteins. The mechanistic details of these couplings, many of which have therapeutic implications, however, have only become accessible in synergy with molecular modeling and simulations. Here, we review some recent computational approaches that analyze allosteric coupling networks (ACNs) in transmembrane proteins, and in particular the recently developed Protein Interaction Analyzer (PIA) designed to study ACNs in the structural ensembles sampled by molecular dynamics simulations. The power of these computational approaches in interrogating the functional mechanisms of transmembrane proteins is illustrated with selected examples of recent experimental and computational studies pursued synergistically in the investigation of secondary active transporters and GPCRs.

Graphical Abstract

INTRODUCTION

In response to specific stimuli, molecular machines in a cell need to function in a regulated and coordinated manner. In many cases, the initiation of one machine, e.g., by cognate ligand binding at a receptor protein, is followed by functional impacts that extend well beyond the initial active site(s) and need to be propagated to a distant, so-called allosteric site(s), which may in turn regulate the functions of other machines. Such processes have been found to play key mechanistic roles in the functions of many, if not all proteins [1–4]. Thus studying the mechanistic interplay between active and allosteric sites, which is often referred to as allostery [5–7], is essential to achieve an understanding of the functional role of a particular molecular machine, and to move on to the discovery of means for therapeutic intervention [8].

From the perspective of statistical thermodynamics, allosteric mechanisms can result from changes in either or both enthalpic or entropic interactions across the entire molecular machine [1, 2]. From the perspective of physical observables, allostery is characterized by identifiable changes in conformation and dynamics: on the one hand, the identification of conformational changes between well-defined structural end states has been instrumental in the mechanistic understanding of the role of allostery in protein function in numerous examples; on the other hand, revealing the ensemble nature of allostery offered a unified and dynamic perspective in such an understanding, especially for disordered proteins or the molecular machines that are regulated by multiple factors [1].

The analysis of functional mechanisms of transmembrane proteins that transduce signals from the extracellular side to activate intracellular signaling cascades, transport materials in and out of the cells, or facilitate the communication and organization of cells, provides elegant examples of allostery and its complexity. To illuminate the functional mechanisms of these transmembrane molecular machines, in addition to characterizing their direct interactions with the cognate interacting partners on both sides of the membrane, the core issue is to delineate the allosteric coupling between the extracellular and intracellular sides through the transmembrane domain. Allosteric mechanisms have been suggested by the conformational changes revealed in numerous transmembrane macromolecular systems by means of direct structural determination such as X-ray crystallography and NMR experiments, and by biochemical analysis of the modes of function. For example, G-protein coupled receptors (GPCRs) transduce external signals to the cytoplasmic side of the cell by binding the cognate ligand on the extracellular side of the transmembrane domain, or even an extracellular domain, and consequently bind and activate G-proteins and arrestin at their intracellular face. Careful mutagenesis studies and the determination of structural changes associated with the process lead to the conclusion that the signal is propagated through the transmembrane domain of the receptor, which connotes an allosteric mechanism.

The functional mechanisms of secondary active pumps, which are specialized to transport substrates against their electrochemical gradient across the membrane by using the thermodynamic drive of co- or counter-transported ions, differ from those of GPCRs but are equally dependent on allosteric processes (reviewed in [4]). The transport mechanism in these pumps has long been considered to follow the alternating-access model [9], according to which the transporter is alternatingly accessible to either the extra- or intra-cellular side of the membrane, in order to facilitate the coupling of the translocation of substrate with the ion gradient. These changes in accessibility usually require large and coordinated conformational changes of transmembrane domain(s) upon binding of substrates and ions. In particular, recent progress in crystallography, computational modeling, and functional studies of the neurotransmitter:sodium symporter family indeed reveal large rearrangements of the proteins from the outward-open to inward-open states [10–12] (reviewed in [13–15]). In the mechanism of excitatory amino acid transporters (EAATs), entire protein domains move with respect to one another: in each of the three monomers of an EAAT homologue, the transport domain binds and transports substrate and ions across the membrane by undergoing an elevator-like motion with respect to the trimerization domain, a domain which participates in the larger scaffold of the entire trimer [16–18]. While it has been shown that each monomer can transport substrate and ions individually of the other monomers [19, 20], however, there is also evidence for allosteric coupling between these monomers [21].

Recently, important clues about allosteric changes were obtained experimentally with fluorescence resonance energy transfer (FRET) and electron paramagnetic resonance (EPR) spectroscopy methods that directly and indirectly detect and monitor protein dynamics. Studies for transporter proteins at the single-molecule level [22, 23] have shown, for example, that the binding of the substrate Ala from the extracellular side of a leucine transporter (LeuT) facilitates the intracellular gate opening by altering the transition dynamics between the open and closed states, rather than the occupancies of these two states [22].

With the important discoveries summarized above, the experimental approaches have laid the foundations for an understanding of the molecular mechanisms underlying the functions of the complex molecular machines that depend on allostery, and have provided general directions for elucidating the mechanistic details of protein allostery at the atomistic (interaction) level. However, it is difficult to deduce allosteric pathways connecting distal sites across entire molecular machines without using molecular modeling, simulations, and specific physics-based methods of analysis. By sampling the conformational distributions of molecular machines, computational approaches implementing such methods serve to interpret the experimental results and integrate them into a comprehensive mechanistic picture. In this review we discuss such computational approaches applied to deduce, from both enthalpic and entropic perspectives, the allosteric pathways in the form of allosteric coupling networks and their configurational changes. We compare such approaches on the same target proteins, and conclude with some general considerations regarding the development of the computational methods and their validation with experimental results for different transmembrane protein families.

COMPUTATIONAL APPROACHES USED IN THE IDENTIFICATION OF ALLOSTERIC MECHANISMS

The allosteric changes in conformation or dynamics can be represented as changes in an allosteric coupling network (ACN), with vertices for molecular elements and edges for their couplings. As discussed below, such a network can be deduced in the form of (i) a network of physical interactions, termed allosteric interaction network (AIN), or (ii) a network of equilibrium correlations between the dynamic behaviors of structural elements at different structural resolution, from atoms or residues to segments, domains, or entire proteins.

To deduce AINs at the atomic or residue level, the pairwise interactions being considered are of electrostatic or Lenard-Jones types, and are inferred from certain geometric criteria, such as contact distances, or angles of relative orientation between these elements [24, 25]. For example, polar interactions identified by the program HBPLUS [26] between donor and acceptor atoms are defined to have a donor-to-acceptor distance of less than a 3.9 Å cutoff, and donor-hydrogen-acceptor angle of at least 90°. At the segment, domain, or inter-protein level, these pairwise interactions can be summarized from the atomic and residual level, e.g., by counting individual atomic interactions [25], or by computing interface areas in protein-protein interactions [27, 28]. The pairwise interactions thus defined form networks across the entire proteins, which can be analyzed by various means. Many methods rely on the analysis of the AIN by using graph theoretical statistics [29–31], such as centrality, which quantifies the extent by which a given residue plays a role in the overall connectivity of the AIN. While these methods do not always directly reveal allosteric networks, interaction hubs in these networks [30, 32] indicate densely connected elements, and differences of these networks highlight interactions that may stabilize one crystal structure (conformational state) over others [33].

Harmonic Interaction Network Approaches

The harmonic interaction network (HIN) approaches have been proposed as a computationally efficient way to model allosteric couplings between molecular components from a single ground state conformation (such as a crystal structure) by identifying correlated elastic dynamics [34, 35]. For example, in the initial Gaussian network model (GNM) for proteins [36], residues i and j with a Cα-Cα reference distance R⁰_ij of no more than a cutoff R_c were assigned an interaction potential,

$$V_{\mathit{\text{GNM}}}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\gamma \sum _{i,j}{({\overrightarrow{R}}_{\mathit{\text{ij}}}-{\overrightarrow{R}}_{\mathit{\text{ij}}}^0)}^2$$

where γ is a uniform force constant parameter, and ${\overrightarrow{R}}_{\mathit{\text{ij}}}\text{ and }{\overrightarrow{R}}_{\mathit{\text{ij}}}^0$ are the variable and reference Cα-Cα distance vectors between residues i and j. In the GNM, the modeled elastic fluctuations are isotropic, i.e. they are independent and thus equally distributed among the different directions of the orthogonal coordinate system; therefore, only the magnitudes of these fluctuations are considered in the GNM. In contrast, in the anisotropic network model (ANM) developed subsequently [34] the potential function is defined as

$$V_{\mathit{\text{ANM}}}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\gamma \sum _{i,j}{(R_{\mathit{\text{ij}}}-R_{\mathit{\text{ij}}}^0)}^2$$

so it is able to distinguish between different fluctuation directions [37].

Any suitable potential, such as V_GNM, V_ANM or even a physical force-field potential V_FF [38, 39], can be used to construct a HIN model in the form of a symmetric matrix H (Kirchhoff matrix for V_GNM, Hessian matrix for V_ANM or V_FF). It turns out that the inverse of this matrix, H⁻¹, is proportional to the matrix of equilibrium fluctuation covariances between molecular components (atoms or residues), e. g., the fluctuation covariance matrix of a GNM with elements C_ij = 〈ΔR_i · ΔR_j〉 for residue i and j, which is $C=\frac{3k_{B}T}{\gamma }{H}^{-1}$. From a spectral decomposition of this matrix, it is possible to compute principal components (eigenmodes) of the elastic dynamics of a particular conformational state in form of eigenvectors ${\overrightarrow{u}}_k$ and eigenvalues λ_k of H, quantifying the directions and relative magnitudes of the eigenmodes, respectively [34, 40]. In this way, the harmonic interaction network methods relate the residues that interact in the potential function to networks of correlated motions at equilibrium.

When using the HIN approaches to study allostery, it is implicitly assumed that perturbations, such as ligand binding or mutations at key position in an interaction network, modulate the dominant eigenmodes. This assumption appears to be reasonable and has yielded important mechanistic insights about collective conformational changes, e.g., in response to different ligands binding to GPCRs [41], or to mutations at the intracellular gate of LeuT [42]. The successful investigation of such perturbations has been extended to even larger membrane protein systems (as reviewed in [34]), such as the role of inter-domain or lipid-protein interactions in the conformational transition energy in GltPh [43, 44]. However, as these computationally efficient approaches are limited to consideration of dynamics from the properties of a single structure, they were not designed to integrate information of the functionally relevant conformational ensemble of the macromolecular system under study. In most cases, however, such information is critical to the characterization of the allosteric mechanisms. In contrast, molecular dynamics (MD) simulations in combination with essential dynamics [45] and other analysis methods utilizing the dynamics trajectories, are means to integrate directly the information from functionally relevant conformational ensembles, albeit at a higher computational cost, as discussed in the next section.

Molecular dynamics based approaches

Molecular dynamics (MD) simulations ergodically sample the conformational equilibrium of a molecular system by numerically solving Newton’s equations of motions [46]. MD simulations have been traditionally used to sample the equilibrium ensemble of a single conformational state, but with the advent of ever increasing computational power and significantly improved enhanced sampling techniques, MD is now being routinely used to explore many conformational states available to a molecular system under certain conditions; this can offer direct clues for allosteric mechanisms involving transitions among such states [47]. These developments are especially important for mechanistic studies of transmembrane proteins, for which high-resolution crystal structures of all the functionally relevant conformational states are still difficult to acquire [25, 48, 49].

With suitable analysis methods applied to trajectories from MD simulations of a membrane protein structure and its environments (solvent, lipids, ions, etc.), it is possible to achieve a quantitative inference of allosteric coupling networks from equilibrium coupled motions between molecular components [50–54], or to identify an allosteric interaction networks from changes in pairwise interaction frequencies between these molecular components when the system is perturbed [25, 55–57]. Both approaches exploit fundamental concepts derived from statistical physics and/or information theory and, as a result, both yield dynamical representations of the elements of the allosteric coupling represented by an ACN. In the following, we discuss these complementary ACN strategies.

Equilibrium coupled motions

In the approaches that reveal equilibrium coupled motions, the elements of the ACN are quantifiable from ensembles generated from MD simulations of a single state of a protein through the quantification of correlation or mutual information between equilibrium fluctuations of structural elements [58]. These quantities are commonly derived from the covariance matrices of the atomic fluctuations [58], and while these matrices were originally used as the end point of analysis [59], various methods have been developed to extract features of allostery from these matrices. Commonly, the principal components of the atomic fluctuations are obtained by diagonalizing the atomic fluctuation covariance matrix; the highest variance motions are then extracted to yield the “essential dynamics” [45, 60]. These methods are analogous to the harmonic interaction models obtained from single structures, as described above, but they encode the actual dynamics of the system represented in the MD simulations. In pursuing allostery, this type of analysis relies on the assumption that external perturbations (e.g., ligand binding) modulate the motions encoded in the essential dynamics. However, it is also possible that external perturbations affect not only the highest variance motions but a large number of low variance motions in a non-trivial manner, and therefore methods have been developed to search specifically for networks that pertain to allosteric couplings between specific residues or clusters of residues. We refer to these methods as analyses of dynamical network models, DNM [51, 61, 62].

In the DNM, network representations of the protein are built by treating each residue as a node and assigning weights to the edges between each node, e_ij, using the atomic fluctuation correlation between the residues, e_ij = −log(|r_ij|). In this representation, maximally correlated residues have an edge weight of 0, whereas maximally uncorrelated residues have an edge weight of ∞. This representation allows for the calculation of allosteric pathways through the protein by using shortest pathway algorithms from graph theory and network theory. In this framework, an allosteric pathway is defined as a sequence of residues, each of which has high pairwise correlation with the residues before it and after it. In addition, this framework has been extended to account for sub-optimal pathways [63], and allows for the quantification of statistics such as the centrality and the identification of structures such as communities [64]. This method has been illustrated in applications to tRNA:synthetase complexes [51], in which the identified allosteric pathways pinpointed interactions between conserved residues and specific nucleotides that were shown with mutagenesis experiments to affect synthetase kinetics.

An alternative to the original dynamic network analysis in DNM, which is based on linear correlations, is to use the mutual information from Shannon information theory [65], which captures non-linear dependencies. The mutual information, I(X,Y), is defined as the difference between the marginal entropies, H(X) and H(Y), and the joint entropy, H(X,Y),

$$I(X,Y)=H(X)+H(Y)-H(X,Y)$$

where the entropy of discrete distributions is defined as

$$H(X)=-\sum p(x)\text{log}(p(x))$$

where x is individual realizations of X, and for continuous distributions is defined as

$$H(X)=-\int p(x)\text{log}(p(x))\mathit{\text{dx}}$$

Many approaches have been developed based on the mutual information [53, 66, 67]. The non-linear dependences can be captured in dynamical network analysis through use of the generalized correlation coefficient [68], and this approach has been successful in application to analyses of ACNs in thrombin [69] and imidazole glycerol phosphate synthase [70].

While DNM and mutual information methods can identify pathways with high consecutive pairwise correlation or mutual information, these formulations do not guarantee that all components of the pathway are correlated. Indeed, higher-order correlations between multiple residues in the network, which can be described using higher-order mutual information [71], are required for a system to transmit information through the network [54]. To find networks that transmit information through such higher-order correlations, a new type of quantitative analysis was developed, termed N-body Information Theory (NbIT) [54]. NbIT searches for multi-body information theoretical motifs that are characteristic of allosteric systems; the most basic motif is the 3-body information, which defines the most basic non-trivial allosteric system of three residues, and is calculated as

$$I(X,Y,Z)=I(X,Y)-I(X,Y|Z)$$

where I(X,Y|Z) is the conditional mutual information,

$$I(X,Y|Z)=H(X,Z)+H(Y,Z)-H(X,Y,Z)-H(Z)$$

As illustrated by the successful application of NbIT in the analysis of membrane proteins [54, 72, 73], this method can be used to identify more complex multi-body information motifs, such as the coordination of several structural components by a central coordinator, and can decompose functional sites into residues involved in internal collective motion (“stabilizers”) versus information transmission between sites (“communicators”). An extension of NbIT for additional applications, such as quantifying rigid-body motion, has also been described [73]. Notably, the current implementations of NbIT use a quasi-harmonic approximation for the configurational entropy for computational efficacy, but in principle, the method can use any entropy estimator. Furthermore, the robustness of the result can be assessed using bootstrapping and other statistical tools (the original implementation used an outlier detection method to identify residues that significantly contributed the ACN).

Allosteric interaction network (AIN)

In the approaches that rely on the generalization and analysis of the AINs identifiable in a particular molecular mechanism, the distributions of the interaction networks in different states are computed and compared according to the interactions sampled from MD simulations. To quantify the comparisons, the distributions can be approximated as lists of interaction frequencies with standard errors, so that significant differences of these distributions between different simulated states/conditions are identified as significant differences of individual pairwise interactions. We have implemented this approach in an application algorithm called Protein Interaction Analyzer (PIA) [25] (the code is available from the authors upon request). In PIA, two residues are considered to interact if the distance between any two heavy atoms from these two residues is smaller than the sum of their van der Waals radii plus 0.6 Å, with special considerations for the residue pairs within 4 residues in sequence (see [25] for details). Thus, such an interaction is considered to be significantly different between two simulated conditions a and b, if the difference in their interaction frequencies, df ≡ f_a − f_b, is statistically significantly different from zero: abs(df) − 2Δdf ≥ 0. The quantity $\Delta \mathit{\text{df}}\equiv \sqrt{\Delta f_a^2+\Delta f_b^2}$ is the standard error for the difference of f_a and f_b calculated through standard error propagation [74]. The standard errors Δf_a and Δf_b are calculated as $\Delta f=\frac{\sigma }{\sqrt{n}}$, where σ is the standard deviation of the binary interaction time traces, and is the number of statistically independent and identically distributed simulation samples (i.e., the MD frames in the case of PIA). In PIA, n is calculated as $n=\frac{t_{\mathit{\text{tot}}}}{2\tau }$, where t_tot is the total simulation time of a simulated condition, and τ is the maximum of autocorrelation times computed for a set of selected global observables of the molecule from the MD simulations. In the recent applications of PIA [25, 49], we used τ = 60 ns according to the global observables analysis of total radius of gyration, total accessible surface area, total potential energy, and total water count of the extracellular vestibule. The specific autocorrelation times are estimated from the smallest lag time, at which the standard autocorrelation function has decayed to e⁻¹ = 0.368[75, 76]. Alternatively, if a large number of statistically independent and identically distributed simulations are available, one can instead approximate the standard errors Δf directly from a bootstrap analysis [76] of entire simulation trajectories. In the new version of the method, we perform a more rigorous two-sided Z-test, where $Z=\frac{\mathit{\text{df}}}{\Delta \mathit{\text{df}}}$, to determine whether the interaction frequencies are significantly different when larger sampling dataset is available (Z-test assumes a normal distribution of the binary interaction data, which requires n > 30). For example, to achieve a p-value less than 0.05, the null hypothesis is rejected if abs(Z) is greater than ~2.35.

As illustrated in our recent application of this type of analysis [25], mechanistically significant differences in AINs are revealed from the combination of the PIA analysis with proper identifications of conformational states (see below). In turn, such differences serve to identify the allosteric pathways, as we demonstrated in that study [25].

Distinct Conformational States in the Molecular Dynamics Study of Allosteric Mechanisms

Experimentally accessed states of the analyzed molecules, representing conformations that are either substantiated by direct structural determinations (e.g., by crystallography), or derived from geometrical and time-related parameters obtained from single-molecule FRET experiments, are essential starting points or points of reference in the investigation of allosteric mechanisms with MD simulations and computational analyses. Other functionally relevant states that are yet to be determined experimentally, if possible, may potentially be accessed and characterized by MD simulations [15].

For the ACN analysis based on MD simulations, it thus becomes necessary to detect and evaluate whether the transition from one state to another has occurred, and whether each state has been adequately sampled in the MD simulations. While RMSD-based clustering approaches have been used for the detection of conformational transitions, it is not necessarily possible to assess from RMSD-based clustering whether or not sampling was adequate and ergodic. For this clustering, the measure of all-to-all RMSDs between simulation frames has been shown to be much more informative than a measure based on scalar RMSDs with respect to individual reference structures, as this reference may be arbitrarily selected and misleading [75]. However, because all-to-all RMSDs are computationally much more demanding than scalar RMSDs (quadratic vs. linear scaling), a promising alternative has been proposed to cluster the frames in the MD simulation trajectories in a more efficient manner. Such a protocol has been implemented in the recently documented program suite called PIA (see preceding section, above) that was used in our recently published analysis of allostery in LeuT [25].

In the initial stage of the clustering protocol in PIA, the frames in each MD trajectory are clustered based on a dissimilarity matrix of pairwise Cα-ifRMSDs (i.e., iterative fit RMSD of all the Cα atoms, as described in [48]) for all frames, using the agglomerative nesting algorithm and the average cluster linkage criterion. For each trajectory i, the clustering algorithm identifies nc_i clusters, where nc_i is the total simulation time of trajectory i divided by a stride of Q. Q represents a simplification of the clustering complexity, which becomes necessary due to the quadratic scaling of the all-to-all RMSD calculations when the data set becomes larger. Thus, in order to efficiently analyze large data sets without loss of accuracy, the value of Q is set as large as possible according to benchmarks from a variety of simulation systems, so that the clustering results would exhibit only minimum differences from those without using the simplification. For example, in the recent study [25], by using the reference Q = 0.24 ns or larger Qs < 20 ns, the differences in the final resulting cluster memberships are less than 3%.

In the second (“meta”) stage of the PIA clustering protocol, the centroid frames from each of these preliminary clusters from all the trajectories in the study are combined and clustered with the same type of dissimilarity matrix and using the same algorithm and criterion as in the initial stage. To separate clusters sufficiently according to the ifRMSD measure, the clustering is performed iteratively to identify the largest number of “meta” clusters conditional on that the minimum inter-cluster distance (obtained as the average of ifRMSDs between all the frames of two clusters) of the resulting clusters is above a threshold r_thres. The value of r_thres is determined by the most frequent pairwise ifRMSD between all the frames of a reference state.

In the assembly stage, as each centroid frame included in the meta stage represents a cluster of frames obtained in the initial stage, these clusters of frames from the original trajectories are assembled to form the final clusters according to the memberships of their centroid frames in the clustering results of the meta stage.

This clustering protocol is used to identify in each MD trajectory the segment that has evolved sufficiently far away from the starting point of the simulation (such a starting point does not necessarily represent the condition being simulated). An example demonstrating this use is the identification in our recent report [25] of evolved segments in the simulation of an outward-open conformation of LeuT in the absence of substrate, for which the starting point was obtained by removing the substrate from the binding site of the LeuT in its outward-occluded conformation [48, 77]. The advantage of this procedure is that the evolved segments could be identified with consistent criteria (i.e., the values of r_thres and Q described above) across all the examined trajectories. This controlled procedure enables the unbiased inclusion of only the identified evolved segments obtained from independent trajectories for each of the simulated conditions (see [25] for a definition of the conditions) in the subsequent (comparative) ACN analysis.

ANALYSIS OF ALLOSTERIC MECHANISMS IN THE FUNCTION OF MEMBRANE PROTEINS

The detailed analysis of signal propagation in the allosteric mechanisms of transmembrane proteins is complicated by the anisotropic environment in which the process takes place. Compared to similar studies of globular proteins, the characterization of the conformational changes presents the additional challenge of taking into consideration the role of the lipid bilayer. This is illustrated below for two classes of molecular machines in the membrane: transporter proteins, and GPCRs.

Analysis of allosteric mechanisms in transporter proteins

By coupling energy sources to the translocation of substrate against its concentration gradient, several classes of transporter proteins function by alternating the opening and closing of access gates in the permeation pathway, and traversing multiple conformational states in a transport cycle [13, 14]. Consequently, large and complicated conformational changes are expected in this molecular process due to the allosteric nature of the energy coupling and substrate-binding effects on the translocation process [78]. Therefore, computational analysis of the allosteric mechanisms, taking advantage of the breakthrough high-resolution structural information provided by crystallographic data, is essential in order to understand the transport mechanisms in atomistic detail.

Indeed, the recent computational investigation of substrate translocation mechanism of a bacterial EAAT homologue GltPh, the mechanistic role of interactions between the transporter and the surrounding lipid membrane, as well as allosteric communications of the three monomers in a GltPh trimer [44] was enabled by the available structures [16, 17, 79]. The study was based on the harmonic interaction network [44], in which the standard ANM used for non-membrane proteins was extended to account for the effect of the lipid molecules in the surrounding membrane [44]. This was achieved in an implicit model by replacing the uniform force constant γ with force constants along (γ_z) and perpendicular (γ_x, γ_y) to the membrane normal, and setting γ_x = γ_y = sγ_z, where s>0 is a scaling parameter. In an explicit account of the membrane, its effect was modeled by adding “membrane centroids” as explicit nodes to the anisotropic network. The results from both of these modeling strategies indicate that the membrane reduces the transition energy between the outward- and inward-facing conformations of GltPh [44].

Another study of GltPh, based on MD simulations, further suggested that the elevator-like motion of the transport domain relative to the trimerization domain in the mechanism of substrate translocation [17] is facilitated by a transient reduction in their contact interface and the penetration of solvent into the space made available by the separation [43]. In fact, this facilitation is allosteric in nature, as the transient interface changes occurred beyond the actual binding site of the translocated substrate. It is interesting to note that this computational finding resolved an apparent controversy between the crystal structures of the outward-open and inward-open states of GltPh - both of which show this interface to be tight and completely “dry” [16, 17, 79] - and results from accessibility analyses with the SCAM method that suggested accessibility to this interface [80]. The resolution of the conundrum by the results from computation is based on the transient accessibility to residues in the interface that is created in the process of substrate translocation. Notably, a recent investigation of a dynamically “unlocked” GltPh mutant using a combination of single molecule FRET, crystallography, and computational simulations [18] indicated that such an allosterically triggered opening of the interface, which was also observed for the wild type both computationally [43] and in the crystal structure of a transport intermediate [81], may be transiently filled by lipid from the membrane environment.

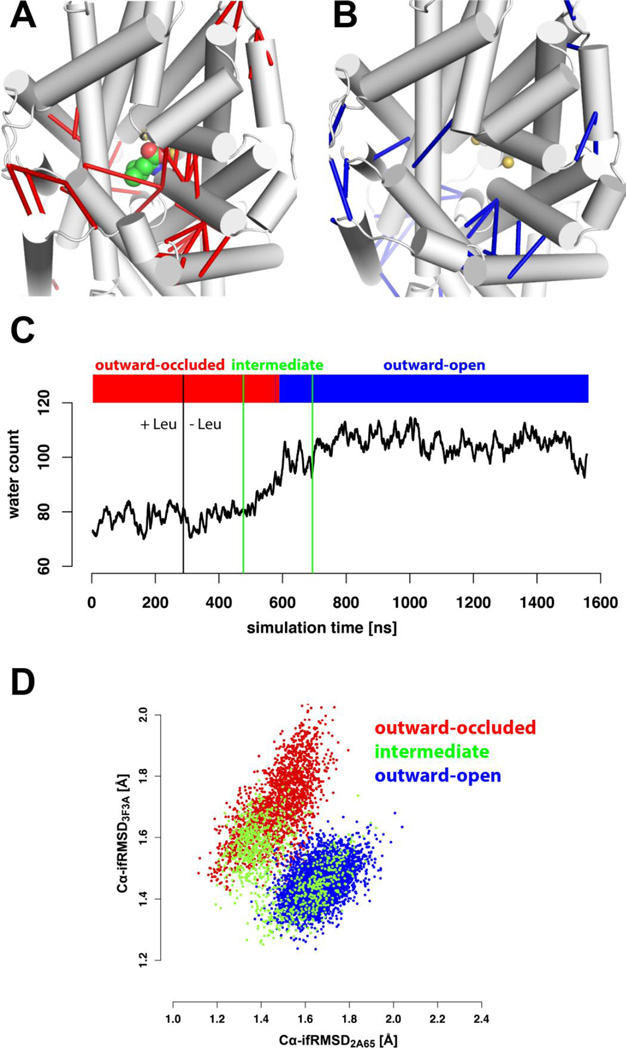
In the analysis of allosteric mechanisms based on MD simulations of the structurally known LeuT transporter, a spontaneous opening of the extracellular vestibule (EV) from an outward-occluded to an outward-open state (Fig. 1A,B) was observed after the substrate had been removed from the outward-occluded state [48, 77]. This opening was characterized by a spontaneous filling of the EV with water molecules (Fig. 1C). In this study we found that two conformational states traversed by a representative MD simulation trajectory can be clearly differentiated with the use of the clustering analysis module in the PIA, and these were found to correspond to different opening sizes of the EV, as indicated by distinctly different numbers of water molecules it contains. The increased water count in the EV correlates with the transition stage (defined according to the autocorrelation time, see Fig. 1) that overlaps with both the outward-occluded and outward-open states (Fig. 1D). Thus the effect of the absence of substrate is found to be allosterically propagated to the extracellular portions of the protein, and is responsible for triggering the conformational transition. The structural basis of such allosteric propagation is traceable as a network reconfiguration of specific residue-residue interactions identified with the PIA (Fig. 1, movie S1).

Figure 1. The Pairwise Interaction Analyzer reveals significant changes in pairwise interactions in the simulated overall transition of LeuT from an “outward-occluded” to an “outward-open” conformation.

LeuT is viewed from the top into the extracellular vestibule in an outward-occluded (panel A), an outward-open (panel B) conformation; leucine substrate and sodium ions are represented as space-filling spheres. In panels A and B, each of these snapshots is overlaid by red (or blue) bars that indicate pairwise interactions (polar or LJ-type) that are significantly more (or less) frequent in the occluded than in the open state (“red” interactions with the leucine substrate are omitted for clarity). In panel C, the water count in LeuT’s extracellular vestibule is plotted against simulation time in an MD simulation initiated in the presence of bound Leu substrate, and continued at 360 ns (black vertical line) in the absence of substrate. This plot is overlaid with corresponding PIA clustering results identifying two conformational states marked as red and blue simulation stages. The intermediate simulation stage (green vertical lines) is defined as the transition point at 560 ns plus and minus twice the maximum autocorrelation time of 60ns. The maximum autocorrelation time is determined from the maximum of any autocorrelation time computed for any chosen global observables of the transporter (total radius of gyration, total accessible surface area, total potential energy, total water count of the extracellular vestibule) for any LeuT simulation performed in [25]. Each autocorrelation time was estimated from the smallest lag time, at which the standard (Pearson) autocorrelation function has decayed to e⁻¹ = 0.368 [75, 76]. In panel D, the structural deviations (iRMSD values) of the MD simulation from the crystal structures of LeuT representing “outward-occluded” and “outward-open” states (PDB codes: “2A65” and “3F3A”, respectively) are plotted, and colored according to the corresponding simulation stages indicated in panel (C).

An intuitive interpretation of these changes is provided by the representation of PIA results in an interaction network of coarse-grained structural elements. In this representation, an interaction between two structural elements (e.g. the extracellular parts of two transmembrane helices) that can be respectively strengthened or weakened, is defined if pairwise residue-residue interaction(s) exist that are more frequent, or less frequent, in one state than in the other [25]. The detailed analysis using this representation in [25] shows that by comparing the WT conditions with those established by various perturbations (e.g., mutations of critical gating residues, or binding of Li⁺ instead of Na⁺), it is possible to reveal the major allosteric communication pathways between the extracellular and intracellular side of the transporter. This is inferred from the way in which the perturbations impact the coarsegrained interaction networks [25]. Strikingly, the predicted phenotypes from these network analyses were shown to correlate closely with experimental findings, including the subtle but significant differences between two mutations located within the same critical intracellular gate (Fig. 2A,B) [25]. These correlations demonstrate both the strength and the sensitivity of the allosteric analysis undertaken with the computational approaches.

Figure 2. Coarse-grained representations of the detected pairwise interaction differences in the simulations of transmembrane proteins.

The transmembrane helices in LeuT and the dopamine D2 receptor (D₂R) are divided into extracellular (“e”), middle (“m”, dark gray), and intracellular (“i”) sub-segments (panels A and C). Sub-segments are represented as circles with their relative positions in each region essentially retaining those in the three-dimensional structure; functional sites are indicated by squares and are connected to the sub-segments that form these sites with blue edges (the sub-segments that are unique to arrestin binding [110] are shown in dotted blue edges); the negatively charged Glu290 of LeuT in panel B is highlighted in red. Such coarse-grained representations of interaction differences are shown for the compared conditions in representative examples of transporter and GPCR proteins: the simulated LeuT-R5A and -Y268A constructs (in panel B) [25], and the D₂R model bound to a Na⁺-sensitive antagonist sulpiride in the presence and absence of bound Na⁺ (in panel D) [49]. An arrow is drawn between two sub-segments if any of the residue pairs in these sub-segments exhibits significant differences in the interaction frequencies in the equilibrated stages. The arrows are colored in orange if the interactions are significantly more frequent in the investigated condition (i.e., Y268A in panel B and the presence of bound Na⁺ in panel D) than in the reference condition, in green if the interactions are less frequent, and in black if the sub-segment pair involves both types (orange and green) of interactions. For LeuT, the comparative analysis shows that the interactions among the structural elements in the Y268A construct tend to be stronger at the extracellular side, whereas in R5A they tend to be stronger at the intracellular side; in the case of D₂R, the analysis shows the presence of Na⁺ induces changes in the AIN that propagate both extracellularly to the ligand binding sites (OBS and SBP) and intracellularly to the G protein and arrestin binding sites.

The analysis of the allosteric mechanism in LeuT has also been performed using the NbIT analysis method [54] applied to MD simulations of the leucine-bound occluded state. This analysis revealed a strong allosteric coupling between the substrate binding site and the intracellular residues involved in gating. This coupling was shown to be mediated by the TM6b segment, which was also identified to be essential in the previously described PIA results [25]. Furthermore, an essential binding site residue, Phe259, was identified as the primary mediator of allosteric communication. This finding led to the hypothesis that the extent to which substrates in the binding site interact with Phe259 may determine the extent to which they allosterically modulate gating. This hypothesis is supported by x-ray crystallography studies [11] of LeuT bound to various substrates known to be transported with different rates. In these closely comparable crystals one of the few, and most significant, conformational differences observable among the otherwise very similar structures, is the interaction between Phe259 and the various substrates.

Applied to an even more complex system, an NbIT-based analysis of the allosteric coupling between domain rearrangements in MD simulations of the human dopamine transporter (hDAT) [72] used hierarchical mutual information clustering (MIC) to cluster several structural coordinates based on their correlation during the spontaneous transition of the transporter to an inward-open conformation. In this study, the results of MIC revealed an ACN that involved both the protein and the lipid membrane. Thus, the contacts between the N-terminal domain and the lipid membrane, were found to be coupled to distance changes among the intracellular portions of several helical segments involved in the inward opening.

Analysis of allosteric mechanisms in GPCRs

The functional effects of the orthosteric ligands of GPCRs must be propagated allosterically across the transmembrane domain from the binding site at the extracellular end of the protein to the intracellular surface in order to activate or inhibit interactions at the intracellular end of the protein. It is well established that the binding of different ligands to a site considered to be the canonical orthosteric binding site (OBS, at which endogenous ligands bind [82]) in GPCRs can stabilize to different extents the multiple conformational states that the receptors can adopt [83, 84]. This differential stabilization can also be affected by ligands binding to other sites in the GPCR that have been termed “allosteric sites” [85]. Results from experimental analyses of the structure and dynamics of GPCRs indicate that this ligand-determined modulation of interactions with the other proteins involved in the signaling process is likely involve conserved allosteric pathways [86]. Moreover, this canonical process can also be allosterically modulated by ligands binding outside of the OBS (reviewed in [87]), by homo- or hetero-oligomerization of receptors (reviewed in [88]), or both [89]. Consequently, the application of computational approaches to identify the allosteric coupling in the mechanisms of GPCRs may have to consider the context of the system being studied.

Early computational studies of the ACN linking the ligand-binding site and the cytoplasmic surface of GPCRs were based on the statistical analysis of the evolutionary data [90]. The thermodynamic coupling between distantly positioned residues were inferred from analyses of the amino acid frequencies in multiple sequence alignment (MSA) to detect evolutionarily conserved networks of residues [91]. In this method, the statistical coupling between two positions i and j is defined as the degree to which amino acid frequencies at position i change in response to a perturbation of frequencies at the position j. Briefly, the overall empirical evolutionary conservation parameter for position i is defined as $\Delta G_i^{\mathit{\text{stat}}}=kT*\sqrt{{\sum }_x{\left(\text{ln}\frac{P_i^x}{P_{\mathit{\text{MSA}}}^x}\right)}^2}$, where $P_i^x$ is the probability of amino acid x at position i, $P_{\mathit{\text{MSA}}}^x$ is the mean amino acid frequencies in the MSA and kT^* is an arbitrary energy constant. The coupling between positions i and j is expressed in terms of the difference in $\Delta G_i^{\mathit{\text{stat}}}$ before and after the perturbation is made at position j. Application of this method to class A GPCRs led to the identification of a cluster of 47 positions that forms a physically connected network of coupled residues from the ligand binding site to the cytoplasmic regions [90].

More recent efforts to characterize ACNs are based on the analysis of interaction network from MD simulations. Based on the comparison of the antagonist-bound inactive and the agonist-bound active structures of the human β₂-adrenergic receptor, which revealed that the changes in the ligand binding site and on the cytoplasmic side are possibly coupled through a connector region during the activation process [92], the Shaw group performed MD simulations to characterize the dynamics of the ACN connecting these sites [93]. The dynamic coupling between sites was analyzed by first categorizing the conformational state of each of the functionally relevant sites into the inactive, intermediate, or active state using a combination of RMSD and distance measurements. Then the inter-dependence of relative conformational populations amongst the three sites was computed. The results showed that these sites are loosely coupled, whereby a conformational transition in one site influences the probability of the conformational state in the neighboring sites; for instance, the ligand-binding site adopts an active conformation 78% and 11% of the time when the connector is in its active or inactive conformations, respectively. Thus, although these sites do not all move in concert with one another, the activation of one site favors activation in the neighboring site [93]. Similarly, highly dynamic and correlated residue motions between the ligand-binding and G-protein-binding sites were shown by community network analysis applied to an accelerated MD simulation study of the M2 muscarinic acetylcholine receptor (M2R) [94].

The allosteric mechanism of ligand-determined propagation of conformational changes to the intracellular end of the 5-HT_2A receptor (5-HT_2AR) was described recently from MD simulations aimed at understanding functional selectivity mechanisms [95]. Specifically, RMSD distribution analysis from the MD trajectories of the receptor bound to diverse ligands shows that one structural element in particular, the second intracellular loop, ICL2, adopts distinct conformations in 5-HT_2AR complexes with different agonist ligands. Interestingly, previous NbIT analysis of ICL2 had suggested that 5-HT binding led to increased rigid-body motion, indicating a potential mechanism by which allosteric modulation of ICL2 was involved in activation [73]. Analysis of binding site interactions of the various 5-HT_2AR agonists, evaluated from the evolution of receptor-ligand contacts in the trajectories, showed that specific modes of interaction were classifiable in accordance with the measured pharmacological outcomes of receptor activation by these ligands. In particular, differences in contact frequency of ligands with specific components of the binding site were shown to be associated in the same manner with both the pharmacological classification of the ligand, and with the conformational propensities of the ICL2; these correlations were unrelated to the degree of structural similarity among the ligands. Notably, these findings identify a role for a specific structural component of the GPCR, the ICL2, in discriminant signaling pathway activations, based on differential ways of connecting the OBS to the intracellular receptor-effector interface [95].

A graph theory-based approach has also been used to analyze the ACN in GPCRs from MD simulations. The Fanelli group used networks of interacting amino acids and cross-correlation of atomic fluctuations to obtain communication pathways between the extracellular and intracellular halves of GPCRs such as the adenosine A_2A and luteinizing hormone receptors [96, 97]. In this method [98], the strength of interaction between residues i and j is defined as $I_{\mathit{\text{ij}}}=\frac{n_{\mathit{\text{ij}}}}{\sqrt{N_i{N}_j}}\times 100$, where n_ij is the number of atom-atom pairs between the side chains of residues i and j within a distance cutoff, and N_i and N_j are normalization factors for residue types i and j taking into account of the differences in size of the side chains and their propensity to make the maximum number of contacts with other residues in protein structures. Any residue pair ij for which I_ij is above a heuristic cutoff is considered to be interacting. Using this approach, the results of the pathway analysis on the MD simulations of antagonist-bound adenosine A_2A receptor in the monomeric and dimeric forms showed contributions of highly conserved residues in TMs 1, 2, 6, and 7 in the information flow between the two sides of the transmembrane domain and across the dimer interface [97].

As described above, the functional conformational dynamics of GPCRs - and thus their ACNs – are propagated not only from the canonical OBS, but also from allosteric ligand binding sites. Although allosteric sites are not well characterized for GPCRs in general, a few potential sites have been identified from crystallography and MD simulations. These include (i) the Na⁺ binding site revealed in the β₁AR and adenosine A_2A structures, involving the highly conserved residue Asp^2.50 (reviewed in [99]); (ii) the cholesterol-binding site, first identified in the carazolol- and timolol-bound β₂AR structures, involving the highly conserved Trp^4.50 [100]; and (iii) the extracellular vestibule (EV), identified in the M2R structure bound to both an orthosteric agonist iperoxo and an allosteric modulator LY2119620 [101]. Compared to the M2R structure that is bound only with iperoxo, LY2119620 induces a slight contraction of the EV, likely stabilizing the contracted OBS and the opening on the intracellular side in the active conformation. Interestingly, the allosteric binding pocket in the EV revealed by the bound LY2119620 overlaps significantly with that identified by a MD simulation study of M2R in which the allosteric coupling between the EV and OBS was demonstrated by the impact of allosteric modulator binding on the size of the OBS [102].

Among these allosteric sites, the Na⁺ site has been the most extensively studied for its effect on ligand-binding in GPCRs by several groups using MD simulations [49, 103–106]. In our recent work on the allosteric effect of Na⁺-binding in the dopamine D2-like receptors, PIA analysis [25] was used to calculate and compare the frequencies of pairwise residue interactions between the clusters of MD frames representing the simulated Na⁺-bound and Na⁺-unbound conditions [49]. The results of the network analysis of the MD simulations of D₂R bound with Na⁺-sensitive antagonist sulpiride, for example, indicated that the presence of Na⁺ not only strengthens the residue-residue interactions in the vicinity of the Na⁺-binding site, but also induces changes in the AIN that propagate towards the ligand binding site at the extracellular end of the receptor, and towards the intracellular G protein binding site [49] (Fig. 2C,D). In contrast, the binding modes of the Na⁺-insensitive ligand, spiperone, appear to mask the impact of the bound Na⁺. Thus, in addition to the proposed role of Na⁺ binding in receptor activation [99], the MD simulations and allosteric network analysis also revealed sub-states of the inactive state that are differentially stabilized by Na⁺-sensitive or Na⁺-insensitive antagonists [49].

The nature of the allosteric mechanism that connects ligand binding sites to specific intracellular regions of GPCRs has engendered great interest with the realization that ligands binding to the same site can cause differential coupling of the receptor to intracellular effectors, a phenomenon termed “functional selectivity” or “ligand bias” [107]. Thus, it is reasonable to expect that functionally selective or biased ligands preferentially stabilize conformations associated with specific signaling profiles [95, 108, 109]. Elucidation of the molecular mechanism of the allosteric changes underlying such differential conformational stabilization is critical for achieving a comprehensive understanding the function of GPCRs, and is therefore a current focus of the application of the rich spectrum of complementary computational approaches reviewed and described here.

CONCLUDING REMARKS

Given the importance of allostery in the functional mechanisms of most proteins, the computational analysis approaches designed to identify, characterize and quantify allosteric mechanisms are likely to grow both in number and in effectiveness. In reviewing such computational approaches aimed at allosteric mechanisms in transmembrane proteins we focused on those in which allosteric coupling networks (ACNs) were sought from structural or simulated molecular dynamics information. An advantage of formulating ACNs in the computational analysis comes from their ability to provide a framework for integrating various experimental results into a comprehensive mechanistic picture, and to predict sites of perturbation of an ACN that can be used to investigate further the allosteric mechanisms e.g., by using mutagenesis or binding of ligands.

Two classes of computational approaches to identify ACNs were discussed: those that identify allosteric interaction networks (AINs) between structural components (atoms, residues, segments, domains), and those that identify the couplings between structural components by means of mutual information or correlations of their equilibrium fluctuations. With specific examples of allosteric mechanisms in transporters and GPCRs we illustrated the strength of the AIN approach implemented in the PIA that relies on (i) the efficient identification of simulated trajectory segments that best represent the simulated condition with a hierarchical clustering procedure; (ii) the efficient computation and (statistical) data handling of large frequency tables of any pairwise interaction across the entire simulated (membrane) protein; and iii) the coarse-grained representation of the AINs at sub-segment level to extract the mechanistic implications and correlate them with experimental findings. Indeed, in combination with experimental studies, the applications of the PIA on MD simulation data of membrane proteins, such as the transporter proteins or GPCRs, have revealed important insights in the functional mechanisms of these molecular machines, with specific emphasis on the transmembrane connectivity of the allosteric coupling among the functional sites.

It is noteworthy, however, that the two classes of approaches discussed here (based on allosteric networks represented by the AINs, and on quantified couplings between molecular components), shed light on two complementary aspects of the underlying thermodynamics of the allosteric coupling in the ACN. An important goal for the near future is to unify these complementary approaches – while AINs can reveal the network of conformational changes that occur in response to perturbation(s), coupling-based methods can reveal the intrinsic properties of the free energy landscape that lead to the response observed by AINs. Notably, however, the signal-to-noise ratio and thus the success of both approaches in analyzing MD data depends on (i) adequate sampling, (ii) a suitable definition of a conformational state, and (iii) sufficient approximations of interaction distributions (in PIA) and entropies (in NbIT). These remains key challenges that must be addressed rigorously. In addition, it is difficult to assess the functional relevance of the perturbations treated by these methods solely by computations, so this has to be guided by cognate experimental findings, but it is clear that it is the change in the free energy landscape induced by perturbations that ultimately drives the biological processes.

Supplementary Material

Supplementary Information. Movies S1. The dynamic changes of the interaction network during the simulated transition from an “outward-occluded” to an “outward-open” conformation. Molecular representations are the same as in Fig. 1A and B. Movie shows significant residue interaction changes between the open and occluded conformational end state.

Highlights.

• The allosteric mechanisms of transmembrane proteins are critical for their functions.

• Computational methods that analyze allosteric coupling network (ACN) are reviewed.

• The methods detect equilibrium coupled motions and allosteric interaction network.

• The application algorithm Protein Interaction Analyzer (PIA) is described in detail.

• Selected examples for computational detection of allostery in transmembrane proteins.